22.03.201931.01.2019

Примеры на применение производной – Примеры применения производной к исследованию функций

• by alexxlab
• Комментариев к записи Примеры на применение производной – Примеры применения производной к исследованию функций нет
• Советы абитуриенту

Применение производной. Построение графиков с применением производных

Математика берет свои истоки со времен Античности. Благодаря ней архитектура, строительство и военное дело дали новый виток развития, достижения, которые были получены с помощью математики, привели к движению прогресса. И по сей день математика остается главной наукой, которая встречается во всех остальных отраслях.

Чтобы быть образованными, дети с первого класса начинают постепенно вливаться в эту среду. Очень важно разбираться в математике, так как она, в той или иной степени, встречается каждому человеку на протяжении всей его жизни. В этой статье будет разобран один из ключевых элементов – нахождение и применение производных. Не всякий человек может представить, насколько широко используется это понятие. Рассмотрим более 10 применений производных в определенных областях или науках.

Применение производной к исследованию функции

Производная – это такой предел отношения приращения функции к увеличению ее аргумента, когда показатель аргумента стремится к нулю. Производная – незаменимая вещь при исследовании функции. Например, с помощью нее можно определить возрастание и убывание последней, экстремумы, выпуклости и вогнутости. Дифференциальные исчисления входят в обязательную программу обучения студентов 1 и 2 курса математических вузов.

Область определения и нули функции

Первый этап любого исследования графика начинается с выяснения области определения, в более редких случаях – значения. Область определения задается по оси абсциссы, если говорить другими словами, то это числовые значения на оси OX. Часто область определения уже задана, но если она не задана, то следует оценить значение аргумента х. Допустим, если при каком-то значениях аргумента функция не имеет смысла, то этот аргумент исключается из области определения.

Нули функции находятся простым способом: функцию f(x) следует приравнивнять к нулю и решить полученное уравнение относительно одной переменной x. Полученные корни уравнения являются нулями функции, то есть в этих x функция равна 0.

Возрастание и убывание

Применение производной для исследования функций на монотонность может рассматриваться с двух позиций. Монотонная функция – это категория, которая имеет только положительные значения производной, либо только отрицательные. Простыми словами – функция только возрастает или только убывает на всем исследуемом промежутке:

1. Параметр возрастания. Функция f(x) будет возрастать, если производная f`(x) больше нуля.
2. Параметр убывания. Функция f(x) будет убывать, если производная f`(x) меньше нуля.

Касательная и угловой коэффициент

Применение производной к исследованию функции определяется еще и касательной (прямой, направленной под углом) к графику функции в данной точке. Касательная в точке (x₀) – прямая, которая проходит через точку и принадлежит функции, координаты которой (x₀, f(x₀)), и имеющая угловой коэффициент f`(x₀).

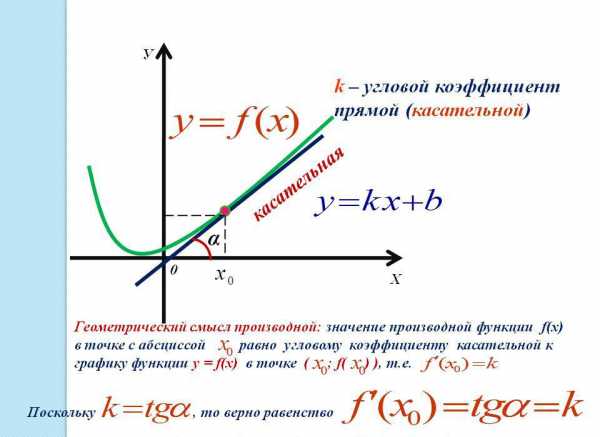
y = f(x₀) + f`(x₀)(x – x₀) – уравнение касательной к данной точке графика функции.

Геометрический смысл производной: производная функции f(x) равняется угловому коэффициенту образованной касательной к графику этой функции в данной точке x. Угловой коэффициент, в свою очередь, равняется тангенсу угла наклона касательной к оси ОХ (абсцисс) в положительном направлении. Это следствие является основополагающим к применению производной к графику функции.

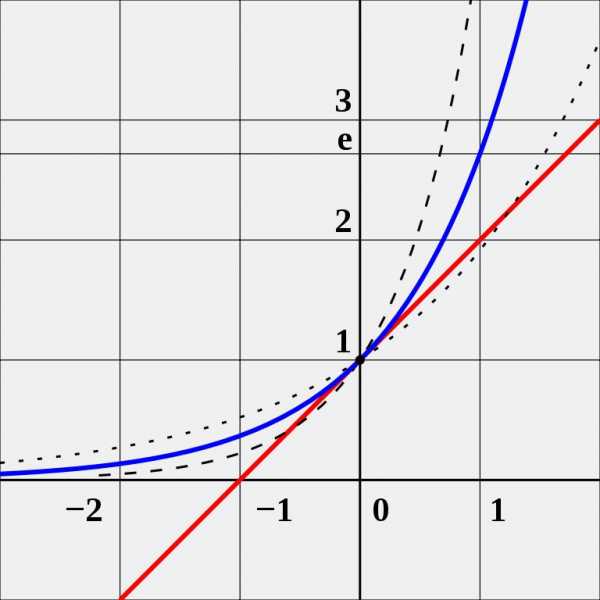
Точки экстремума

Применение производной к исследованию включает в себя нахождение точек максимума и минимума.

Для того чтобы найти и определить точки минимума и максимума, необходимо:

• Отыскать производную функции f(x).
• Приравнять полученное уравнение к нулю.
• Найти корни уравнения.
• Определить точки максимума и минимума.

Чтобы найти экстремумы функции:

• Отыскать точки минимума и максимума по способу выше.
• Подставить эти точки в первоначальное уравнение и высчитать y_наиб. и y_наим.

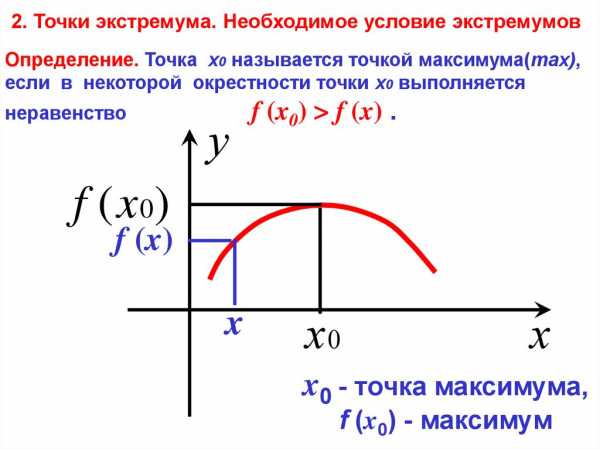
Точка максимума функции – это наибольшее значение функции f(x) на промежутке, другими словами x_наиб.

Точка минимума функции – это наименьшее значение функции f(x) на промежутке, другими словами x_наим.

Точки экстремума – то же самое, что и точки максимума и минимума, а экстремум функции (y_{наиб. и} у_наим) – значения функций, которые соответствуют точкам экстремума.

Выпуклости и вогнутости

Определить выпуклость и вогнутость можно, прибегая к применению производной для построения графиков:

• Функция f(x), исследуемая на промежутке (a, b), является вогнутой, если функция расположена ниже всех своих касательных, находящихся внутри этого интервала.
• Функция f(x), исследуемая на промежутке (a, b), является выпуклой, если функция расположена выше всех своих касательных, находящихся внутри этого интервала.

Точка, которая разделяет выпуклость и вогнутость, называется точкой перегиба функции.

Чтобы найти точки перегиба:

• Найти критические точки второго рода (вторую производную).
• Точками перегиба являются те критические точки, которые разделяют два противоположенных знака.
• Вычисление значений функций в точках перегиба функции.

Частные производные

Применение производных такого типа есть в задачах, где используется больше одной неизвестной переменной. Чаще всего такие производные встречаются при построении графика функции, если быть точнее, то поверхности в пространстве, где вместо двух осей – три, следовательно, три величины (две переменные и одна постоянная).

Основное правило при вычислении частных производных – выбираем одну переменную, а остальные рассматриваем как постоянные. Следовательно, при вычислении частной производной постоянная величина становится как-будто числовым значением (во многих таблицах производных они обозначаются как C = const). Смысл такой производной – это скорость изменения функции z = f(x, y) по оси OX и OY, то есть характеризует крутизну впадин и выпуклостей построенной поверхности.

Производная в физике

Применение производной в физике имеет широкое распространение и значение. Физический смысл: производная пути по времени – скорость, а ускорение – производная скорости по времени. Из физического смысла можно провести множество ответвлений в различные разделы физики, при этом полностью сохраняя смысл производной.

С помощью применения производной находятся такие величины:

• Скорость в кинематике, где вычисляется производная от пройденного пути. Если находится вторая производная от пути или первая производная от скорости, то находится ускорение тела. Помимо этого, возможно нахождение мгновенной скорости материальной точки, однако для этого необходимо знать приращение ∆t и ∆r.
• В электродинамике: вычисление мгновенной силы переменного тока, а также ЭДС электромагнитной индукции. Вычисляя производную, можно найти максимальную мощность. Производная от количества электрического заряда – сила тока в проводнике.

Производная в химии и биологии

Химия: производная используется для определения скорости протекания химической реакции. Химический смысл производной: функция p = p(t), в данном случае p – количество вещества, которое вступает в химическую реакцию во времени t. ∆t – приращение времени, ∆p – приращение количества вещества. Предел отношения ∆p к ∆t, при котором ∆t стремится к нулю, называется скоростью протекания химической реакции. Среднее значение химической реакции – отношение ∆p/∆t. При определении скорости необходимо точно знать все необходимые параметры, условия, знать агрегатное состояние вещества и среду протекания. Это довольно большой аспект в химии, который широко применяется в различных отраслях и деятельности человека.

Биология: понятие производной используют при вычислении средней скорости размножения. Биологический смысл: имеем функцию y = x(t). ∆t – приращение по времени. Тогда с помощью некоторых преобразований получаем функцию y`= P(t) = x`(t) – активность жизнедеятельности популяции времени t (средняя скорость размножения). Такое применение производной позволяет вести статистику, отслеживать темпы размножения и так далее.

Производная в географии и экономике

Производная позволяет географам решать такие задачи, как нахождение численности населения, вычислять значения в сейсмографии, рассчитать радиоактивность ядерно-геофизических показателей, вычислить интерполяцию.

В экономике важную часть расчетов занимает дифференциальное исчисление и вычисление производной. В первую очередь это позволяет определить пределы необходимых экономических величин. Например, наибольшую и наименьшую производительность труда, издержки, прибыль. В основном эти величины рассчитываются по графикам функций, где находят экстремумы, определяют монотонность функции на нужном участке.

Заключение

Роль данного дифференциального исчисления задействована, как было отмечено в статье, в различных научных структурах. Применение производных функций – важный элемент в практической части науки и производства. Не зря нас в старшей школе и университете учили строить сложные графики, исследовать и работать над функциями. Как видим, без производных и дифференциальных исчислений невозможно было бы рассчитать жизненно важные показатели и величины. Человечество научилось моделировать различные процессы и исследовать их, решать сложные математические задачи. Действительно, математика – царица всех наук, потому что эта наука лежит в основе всех других естественных и технических дисциплин.

fb.ru

Применение производной к построению графиков функций

Понятие производной можно применять для построения графиков функций, так как с помощью производных мы можем выяснить промежутки возрастания и убывания, промежутки выпуклости и вогнутости функции, найти точки экстремума функции (точки минимума и максимума), а также наибольшее и наименьшее значения функции данной функции. Однако, помимо этих данных, для более точного построения графиков функции нам необходимы еще некоторые сведения. Поэтому вначале приведем схему исследования функций, которой и будем пользоваться в дальнейшем.

Схема для исследования функций

1. Найти область определения функции;

2. Найти область значения функции;

3. Выяснить является ли функция четной, нечетной и периодической.

4. Найти точки пересечения с осями координат;

5. Выяснить промежутки знакопостоянства функции;

6. Найти производную функции;

7. Найти точки минимума и максимума функции;

8. Найти промежутки монотонности функции;

9. Найти наибольшее и наименьшее значение функции;

10. Найти вторую производную функции;

11. Найти промежутки выпуклости и вогнутости функции;

12. Найти пределы функции на концах области определения;

13. Если необходимо, найти значение функции в дополнительных точках;

14. Построить график функции.

Задачи на исследование и построение графиков функций.

Пример 1

Исследовать и построить график функции:

\[y=2x+1\]

1. Область определении – все действительные числа.

2. Область значения – все действительные числа.

3. функция ни четна, ни нечетна, непериодическая.

4. Точки пересечения с осями координат:

   При $y=0$, $2x+1=0,\ x=-\frac{1}{2}$. Точка пересечения с осью $Ox:\left(-\frac{1}{2},0\right)$.

   При $x=0$, $y=1$. Точка пересечения с осью $Ox:\left(0,1\right)$.

5. При $x\in \left(-\infty ,-\frac{1}{2}\right)$ функция отрицательна, при $x\in \left(-\frac{1}{2},\infty \right)$ функция положительна.

6. Производная:

   \[y’=2>0\]

7. Точек минимума и максимума нет.

8. Функция возрастает на всей области определения.

9. Функция не имеет наибольшего и наименьшего значений.

10. $y”=0$

11. Функция не имеет промежутков выпуклости и вогнутости.

12. ${\mathop{lim}_{x\to -\infty } y\ }=-\infty $, ${\mathop{lim}_{x\to +\infty } y\ }=+\infty $

13. График:

    Рисунок 1.

Пример 2

Исследовать и построить график функции:

\[y=\frac{5x^2+x+1}{x}\]

1. Область определения: $\left(-\infty ,0\right)(0,\infty )$.

2. Область значения:$\left(-\infty ,1-2\sqrt{5}\right][1+2\sqrt{5},\infty )$

3. Функция ни четна, ни нечетна, непериодическая.

4. Точек пересечения с осями координат нет.При $x\in \left(-\infty ,0\right)$ функция отрицательна, при $x\in \left(0,\infty \right)$ функция положительна.

5. При $x\in \left(-\infty ,0\right)$ функция отрицательна, при $x\in \left(0,\infty \right)$ функция положительна.

6. Производная:

   \[y’=\frac{10x^2+x-5x^2-x-1}{x^2}=\frac{5x^2-1}{x^2}\]

7. Найдем точки минимума:

   \[\frac{5x^2-1}{x^2}=0\] \[x\ne 0,\ x=\pm \frac{\sqrt{5}}{5}\]

   Рисунок 2.

   Максимум функции: $\left(-\frac{\sqrt{5}}{5},1-2\sqrt{5}\right)$

   Минимум функции: $\left(\frac{\sqrt{6}}{6},1+2\sqrt{5}\right)$

8. Из рисунка выше видим, что функция возрастает при $x\in \left(-\infty ,-\frac{\sqrt{5}}{5}\right)\left(\frac{\sqrt{5}}{5},\infty \right)$ и убывает при $x\in \left(-\frac{\sqrt{5}}{5},0\right)\left(0,\frac{\sqrt{5}}{5}\right)$

9. Наибольшее и наименьшее значение:

   $f\left(-\frac{\sqrt{5}}{5}\right)=1-2\sqrt{5}$ – наименьшее значение,

   $f\left(\frac{\sqrt{5}}{5}\right)=1-2\sqrt{5}$ – наибольшее значение.

10. $y”=\frac{{10x}^3-{10x}^3+2x}{x^4}=\frac{2}{x^3}$

11. Найдем промежутки выпуклости и вогнутости:

    \[\frac{2}{x^3}=0\] \[x\ne 0\]

    Методом интервалов получаем, что

    Функция вогнута при $x\in \left(0,\infty \right)$ и выпукла при $x\in \left(-\infty ,0\right)$.

12. ${\mathop{lim}_{x\to 0-0} y\ }=-\infty $, ${\mathop{lim}_{x\to 0+0} y\ }=+\infty $, ${\mathop{lim}_{x\to -\infty } y\ }=-\infty $, ${\mathop{lim}_{x\to +\infty } y\ }=+\infty $

13. График:

Рисунок 3.

spravochnick.ru

Применение производной к исследованию функций

Одними из основных аспектов применения производной к исследованию функции являются: исследование функции на возрастание и убывание, исследование функций на выпуклость и вогнутость, нахождение точек экстремума функции, а также наибольшего и наименьшего значения функции. Рассмотрим их отдельно.

Экстремумы функции

Определение 1

Точки $x_0$ называются точками экстремума функции, если они являются точками максимума и минимума для функции $f(x)$.

Определение 2

$x_0$ называется критической точкой функции $f(x)$, если:

1) $x_0$ – внутренняя точка области определения;

2) $f'(x_0)=0$ или не существует.

Для исследования функции на существование точек экстремума, мы будем использовать теорему о достаточных условиях существования экстремума:

Теорема 1

Достаточное условие экстремума

Пусть точка $x_0$ является критической для функции $y=f(x)$ и лежит в интервале $(a,b)$. Пусть на каждом интервале $\left(a,x_0\right)\ и\ (x_0,b)$ производная $f'(x)$ существует и сохраняет постоянный знак. Тогда:

1) Если на интервале $(a,x_0)$ производная $f’\left(x\right)>0$, а на интервале $(x_0,b)$ производная $f’\left(x\right)

2) Если на интервале $(a,x_0)$ производная $f’\left(x\right)0$, то точка $x_0$ – точка минимума для данной функции.

3) Если и на интервале $(a,x_0)$, и на интервале $(x_0,b)$ производная $f’\left(x\right)>0$ или производная $f’\left(x\right)

Схема исследования функции на экстремум

1) Найти область определения функции $f(x)$;

2) Найти производную $f'(x)$;

3) Найти точки, в которых выполняется равенство $f’\left(x\right)=0$;

4) Найти точки, в которых $f'(x)$ не существует;

5) Отметить на координатной прямой все найденные точки и область определения данной функции;

6) Определить знак производной $f'(x)$ на каждом получившемся промежутке;

7) Сделать выводы о наличии максимумов и минимумов на каждом промежутке, используя теорему 2.

Монотонность функции

Определение 3

Функция $y=f(x)$, определенная на промежутке $X$, называется возрастающей, если для любых точек $x_1,x_2\in X$ при $x_1

Определение 4

Функция $y=f(x)$, определенная на промежутке $X$, называется возрастающей, если для любых точек $x_1,x_2\in X$ при $x_1f(x_2)$.

Определение 5

Функция $y=f(x)$, определенная на промежутке $X$, называется неубывающей, если для любых точек $x_1,x_2\in X$ при $x_1

Определение 6

Функция $y=f(x)$, определенная на промежутке $X$, называется невозрастающей, если для любых точек $x_1,x_2\in X$ при $x_1

Схема исследования функции на возрастание и убывание

1) Найти область определения функции $f(x)$;

2) Найти производную $f'(x)$;

3) Найти точки, в которых выполняется равенство $f’\left(x\right)=0$;

4) Найти точки, в которых $f'(x)$ не существует;

5) Отметить на координатной прямой все найденные точки и область определения данной функции;

6) Определить знак производной $f'(x)$ на каждом получившемся промежутке;

7) Сделать вывод: на промежутках, где $f’\left(x\right)0$ функция возрастает.

Наибольшее и наименьшее значение функции

Определение 7

Функция $y=f(x)$, определенная на промежутке $X$, достигает своего наибольшего значения, если существует точка $x_0\in X$, такая, что для всех $x\in X$ выполняется неравенство

\[f\left(x\right)\le f(x_0)\]

Определение 8

Функция $y=f(x)$, определенная на промежутке $X$, достигает своего наименьшего значения, если существует точка $x_0\in X$, такая, что для всех $x\in X$ выполняется неравенство

\[f\left(x\right)\ge f(x_0)\]

Схема нахождения наибольшего и наименьшего значений функции $f(x)$ на отрезке $[a,b]$

1) Найти производную $f'(x)$;

2) Найти точки, в которых производная $f’\left(x\right)=0$;

3) Найти точки, в которых производная $f'(x)$ не существует;

4) Выбрать из полученных в пунктах 2 и 3 точек те, которые принадлежат отрезку $[a,b]$;

5) Вычислить значение функции в точках, полученных в пункте 4, а также на концах отрезка $[a,b]$;

6) Выбрать из полученных значений наибольшее и наименьшее значение.

Выпуклость и вогнутость функции

Определение 9

Функция $y=f(x)$, определенная на промежутке $X$, называется выпуклой, если для любых точек $x_1,x_2\in X$ выполняется неравенство

\[f\left(\frac{x_1+x_2}{2}\right)\le \frac{{f(x}_1)+f(x_2)}{2}\]

Определение 10

Функция $y=f(x)$, определенная на промежутке $X$, называется вогнутой, если для любых точек $x_1,x_2\in X$ выполняется неравенство

\[f\left(\frac{x_1+x_2}{2}\right)\ge \frac{{f(x}_1)+f(x_2)}{2}\]

Замечание 1

Если в определении выпуклости и вогнутости функции нестрогие знаки заменить на строгие, то мы получим, соответственно, определение строго выпуклой и строго вогнутой функции.

Схема исследования функции на возрастание и убывание

1) Найти область определения функции $f(x)$;

2) Найти вторую производную $f”(x)$;

3) Найти точки, в которых выполняется равенство $f”\left(x\right)=0$;

4) Найти точки, в которых $f”(x)$ не существует;

5) Определить знак производной $f”(x)$ на каждом получившемся промежутке;

6) Сделать вывод: на промежутках, где $f”\left(x\right)0$ функция вогнута.

Задачи на применение производной

Пример 1

Исследовать функцию на возрастание, убывание, выпуклость, вогнутость и наличие точек максимумов и минимумов:$f(x)=\frac{x^2-2x+1}{4}$

Решение:

1) Область определения – все действительные числа;

2) $f’\left(x\right)=\frac{2x-2}{4}=\frac{x-1}{2}$;

3) $f’\left(x\right)=0$;

\[\frac{x-1}{2}=0\] \[x=1\]

4) $f'(x)$ существует во всех точках области определения;

5) Координатная прямая:

Рисунок 1.

6) Определить знак производной $f'(x)$ на каждом промежутке:

\[f’\left(x\right) >0,\ при\ (1,+\infty )\] \[f’\left(x\right)7) Изобразим все на одном рисунке:

Рисунок 2.

Получаем:

Функция убывает, при $\left(-\infty ,1\right)$, функция возрастает, при $(1,+\infty )$.

Точка $x=1$ – точка минимума, точки максимума нет.

8) $f”\left(x\right)=\frac{1}{2}>0$

Функция вогнута на всей области определения.

spravochnick.ru

Применение производной в физике, технике, биологии, жизни

Разделы: Математика, Конкурс «Презентация к уроку»

---

Презентация к уроку

Загрузить презентацию (40,2 МБ)

Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.

---

Тип урока: интегрированный.

Цель урока: изучить некоторые аспекты применения производной в различных областях физики, химии, биологии.

Задачи: расширение кругозора и познавательной деятельности учащихся, развитие логического мышления и умения применять свои знания.

Техническое обеспечение: интерактивная доска; компьютер и диск.

ХОД УРОКА

I. Организационный момент

II. Постановка цели урока

– Урок хотелось бы провести под девизом Крылова Алексея Николаевича советского математика и кораблестроителя: «Теория без практики мертва или бесполезна, практика без теории невозможна или пагубна».

– Повторим основные понятия и ответим на вопросы:

– Скажите основное определение производной?
– Что вы знаете о производной (свойства, теоремы)?
– Знаете ли вы какие-нибудь примеры задач с применением производной в физике, математике и биологии?

Рассмотрение основного определения производной и его обоснование (ответ на первый вопрос):

Производная – одно из фундаментальных понятий математики. Умение решать задачи с применением производной требует хорошего знания теоретического материала, умения проводить исследование различных ситуаций.

Поэтому сегодня на уроке мы закрепим и систематизируем полученные знания, рассмотрим и оценим работу каждой группы и на примере некоторых задач покажем, как при помощи производной решать другие задачи и нестандартные задачи с применением производной.

III. Объяснение нового материала

1.  Мгновенная мощность есть производная работы по времени:

W = lim  ΔA/Δt   ΔA – изменение работы.

2. Если тело вращается вокруг оси, то угол поворота есть функция времени t
Тогда угловая скорость равна:

W = lim Δφ/Δt = φ׳(t) Δt → 0

3. Сила тока есть производная Ι = lim Δg/Δt = g′, где g – положительный электрический заряд переносимый через сечение проводника за время Δt.

4. Пусть ΔQ – количество теплоты, необходимое для изменения температуры за Δt времени, тогда   lim ΔQ/Δt = Q′ = C – удельная теплоёмкость.

5. Задача о скорости течения химической реакции

m(t) – m(t0) – количество вещества, вступающее в реакцию от времени t0 до t

V= lim Δm/Δt = m  Δt → 0

6. Пусть m – масса радиоактивного вещества. Скорость  радиоактивного распада: V = lim Δm/Δt = m׳(t)       Δt→0

В дифференцированной форме закон радиоактивного распада имеет вид: dN/dt = – λN, где N – число ядер не распавшихся время t.

Интегрируя это выражение, получаем: dN/N = – λdt     ∫dN/N = – λ∫dt  lnN = – λt + c, c = const при t = 0 число радиоактивных ядер N = N0, отсюда имеем: ln N0 = const, следовательно

n N = – λt + ln N0.

Потенциируя это выражение получаем:

 – закон радиоактивного распада, где N0 – число ядер в момент времени  t0 = 0, N – число ядер, не распавшихся за время t.

7. Согласно уравнению теплообмена Ньютона скорость потока теплоты dQ/dt прямо     пропорциональна площади окна S и разности температур  ΔT между внутренним и внешним стёклами и обратно пропорциональна его толщине d:

dQ/dt =A S/d ΔT

8. Явлением Диффузии называется процесс установления равновесного распределения          

Внутри фаз концентрации. Диффузия идёт в сторону, выравнивая концентрации.

m = D Δc/Δx   c – концентрация
m = D c׳x  x – координата, D – коэффициент диффузии

Закон Фика:

9. Было известно, что электрическое поле возбуждает либо электрические заряды, либо магнитное поле, которое имеет единственный источник – электрический ток. Джеймс Кларк Максвелл ввёл одну поправку в открытые до него законы электромагнетизма: магнитное поле возникает также и при изменении электрического поля. Маленькая на первый взгляд поправка имела грандиозные последствия: появилась пусть пока и на кончике пера, совершенно новый физический объект – электромагнитная волна. Максвелл виртуозно владел, в отличии от Фарадея, которому казалось возможным её существование, вывел уравнение для электрического поля:

∂E/∂x = M∂B/Mo ∂t   Mo = const t

Изменение электрического поля вызывает появление магнитного поля в любой точке пространства, другими словами, скорость изменения электрического поля определяет величину магнитного поля. Под большим электрическим током – большее магнитное поле.

IV. Закрепление изученного

– Мы с вами изучали производную и её свойства. Хотелось бы прочитать философское высказывание Гильберта: «У каждого человека есть определённый кругозор. Когда этот кругозор сужается до бесконечного малого, то он обращается в точку. Тогда человек и говорит что это и есть его точка зрения.»
Давайте попробуем измерить точку зрения на применении производной!

Сюжет «Листик» (применение производной в биологии, физике, жизни)

Рассмотрим падение как неравномерное движение зависящее от времени.

Итак: S = S(t)   V = S′(t) = x′(t), a = V′(t) = S″(t)

(Теоретический опрос: механический смысл производной).

1. Решение задач

Решите самостоятельно задачи.

2. F = ma  F = mV′   F = mS″

Запишем II закон Портона, и учитывая механический смысл производной перепишем его в виде: F = mV′   F = mS″

Сюжет «Волки, Суслики»

Вернёмся к уравнениям: Рассмотрим дифференциальные уравнения показательного роста и убывания : F = ma  F = mV’  F = mS”
Решение многих задач физики, технической биологии и социальных наук сводятся к задаче нахождения функций  f'(x) = kf(x),  удовлетворяющих дифференциальному уравнению, где k = const .

Формула Человека

Человек во столько раз больше атома, во сколько раз он меньше звезды:

Отсюда следует, что
Это и есть формула, определяющая место человека во вселенной. В соответствии с ней размеры человека представляют среднее пропорциональное звезды и атома.

Закончить урок хотелось бы словами Лобачевского: «Нет ни одной области математики, как бы абстрактна она ни была, которая когда-нибудь не окажется применимой к явлениям действительного мира».

V. Решение номеров из сборника:

Самостоятельное решение задач на доске, коллективный разбор решений задач:

№ 1 Найти скорость движения материальной точки в конце 3-й секунды, если движение точки задано уравнением s = t^2 –11t + 30.

№ 2 Точка движется прямолинейно по закону s = 6t – t^2. В какой момент ее скорость окажется равной нулю?

№ 3 Два тела движутся прямолинейно: одно по закону s = t^3 – t^2 – 27t,  другое — по закону s = t^2 + 1. Определить момент, когда скорости этих тел окажутся равными.

№ 4 Для машины, движущейся со скоростью 30 м/с, тормозной путь определяется формулой s(t) =30t—16t^2, где s(t) –  путь в метрах, t – время торможения в секундах. В течении какого времени осуществляется торможение до полной остановки машины? Какое расстояние пройдет машина с начала торможения до полной ее остановки?

№5 Тело массой 8 кг движется прямолинейно по закону s = 2t^2+ 3t – 1. Найти кинетическую энергию тела (mv^2/2) через 3 секунды после начала движения.

Решение: Найдем скорость движения тела в любой момент времени:
V = ds / dt = 4t + 3
Вычислим скорость тела в момент времени t = 3:
V t=3 = 4 * 3 + 3=15 (м/с).
Определим кинетическую энергию тела в момент времени t = 3:
mv2/2 = 8 – 15^2 /2 = 900 (Дж).

№6 Найти кинетическую энергию тела через 4 с после начала движения, если его масса равна 25 кг, а закон движения имеет вид s = Зt^2— 1.

№7 Тело, масса которого 30 кг, движется прямолинейно по закону s = 4t^2 + t. Доказать, что движение тела происходит под действием постоянной силы.
Решение: Имеем s’ = 8t + 1, s” = 8. Следовательно, a(t) = 8 (м/с^2), т. е. при данном законе движения тело движется с постоянным ускорением 8 м/с^2. Далее, так как масса тела постоянна (30 кг), то по второму закону Ньютона действующая на него сила F = ma = 30 * 8 = 240 (H) – также постоянная величина.

№8 Тело массой 3 кг движется прямолинейно по закону s(t) = t^3 – 3t^2 + 2. Найти силу, действующую на тело в момент времени t = 4с.

№9 Материальная точка движется по закону s = 2t^3 – 6t^2 + 4t. Найти ее ускорение в конце 3-й секунды.

VI. Применение производной в математике:

Производная в математике показывает числовое выражение степени изменений величины, находящейся в одной и тоже точке, под влиянием различных условий.

Формула производной встречается нам ещё в 15 веке. Великий итальянский математик Тартальи, рассматривая и развивая вопрос – на сколько зависит дальность полёта снаряда от наклона орудия – применяет её в своих трудах.

Формула производной часто встречается в работах известных математиков 17 века. Её применяют Ньютон и Лейбниц.

Посвящает целый трактат о роли производной в математике известный учёный Галилео Галилей. Затем производная и различные изложения с её применением стали встречаться в работах Декарта, французского математика Роберваля и англичанина Грегори. Большой вклад по изучению производной внесли такие умы, как Лопиталь, Бернулли, Лангранж и др.

1. Построить график и исследовать функцию:

Решение данной задачи:

 

Минутка релаксации

VII. Применение производной в физике:

При изучении тех или иных процессов и явлений часто возникает задача определения скорости этих процессов. Её решение приводит к понятию производной, являющемуся основным понятием дифференциального исчисления.

Метод дифференциального исчисления был создан в XVII и XVIII вв. С возникновением этого метода связаны имена двух великих математиков – И. Ньютона и Г.В. Лейбница.

Ньютон пришёл к открытию дифференциального исчисления при решении задач о скорости движения материальной точки в данный момент времени (мгновенной скорости).

В физике производная применяется  в основном для вычисления наибольших или наименьших значений каких-либо величин.

Решение задач:

 №1 Потенциальная энергия U поля частицы, в котором находится другая, точно такая же частица имеет вид: U = a/r² – b/r, где a и b — положительные постоянные, r — расстояние между частицами. Найти: а) значение r0 соответствующее равновесному положению частицы; б) выяснить устойчиво ли это положение; в) Fmax значение силы притяжения; г) изобразить примерные графики зависимости U(r) и F(r).

Решение данной задачи:  Для определения r0 соответствующего равновесному положению частицы исследуем f = U(r) на экстремум.

Используя связь между потенциальной энергией поля

U и F, тогда F = – dU/dr, получим F = – dU/dr = – (2a/r3+ b/r2) = 0; при этом r = r0;  2a/r3 = b/r2 => r0 = 2a/b; Устойчивое или неустойчивое равновесие определим по знаку второй производной:
d2U/dr02= dF/dr0 = – 6a/r02 + 2b/r03 = – 6a/(2a/b)4 + 2b/(2a/b)3 = (– b4/8a3) < 0;
равновесие устойчивое.

Для определения Fmax  притяжения исследую на экстремумы функцию:F = 2a/r3 — b/r2;
dF/dr = –6a/r4 + 2b/ r3 = 0; при r = r1 = 3a/b; подставляя, получу Fmax = 2a/r31 — b/r31 = – b3/27a2; U(r) = 0;       при r = a/b;       U(r)min при r = 2, a/b = r0;F = 0;   F(r)max при r = r1 = 3a/b;
Ответ:  F(r)max при r = r1 = 3a/b;

№2 Цепь с внешним сопротивлением R = 0,9 Ом питается от батареи из k = 36 одинаковых источников, каждый из которых имеет ЭДС  E=2 В и внутреннее сопротивление r0 = 0,4 Ом. Батарея включает n групп, соединенных параллельно, а в каждой из них содержится m последовательно соединенных аккумуляторов. При каких значениях m, n будет получена максимальная J во внешнем R.

Решение данной задачи:

При последовательном соединении аккумуляторов Eгр = m*E; rгр = r0*m;
а при параллельном соединении одинаковых rбат = r0m/n; Eбат = m*E,
По закону Ома J = mE/(R+ r0m/n) = mEn/(nR + r0m)
Т.к. k – общее число аккумуляторов, то k = mn;
J = kE/(nR + r0m) = kE/(nR + kr0/n);
Для нахождения условия при котором J тока в цепи максимальная исследую функцию J = J(n) на экстремум взяв производную по n и приравняв ее к нулю.
J’n – (kE(R — kr0/n2))/ (nR + kr0/n)2 = 0;
n2 = kr/R
n = √kr/R = √3,6*0,4/0,9 = 4;
m = k/n = 36/4 = 9;
при этом Jmax = kE/(nR + mr0) = 36*2/(4*0,9 + 9*0,4) = 10 А;

Ответ: n = 4, m = 9.

№3 Платформа массой М начинает двигаться вправо под действием постоянной силы F. Из неподвижного бункера на нее высыпается песок. Скорость погрузки постоянна и равна µ кг/с. Пренебрегая трением, найти зависимость от времени ускорения а платформы в процессе погрузки. Определить ускорение а1 платформы в случае, если песок не насыпается на платформу, а из наполненной высыпается через отверстие в ее дне с постоянной скоростью µ кг/с.

Решение данной задачи: Рассмотрим сначала случай, когда песок насыпается на платформу
Движение системы платформа – песок можно описать с помощью второго закона Ньютона:
dP/dt = FΣ
P – импульс системы платформа – песок, FΣ – сила, действующая на систему платформа – песок.
Если через p обозначить импульс платформы, то можно написать:dp/dt = F
Найдем изменение импульса платформы за бесконечно малый промежуток времени Δt: Δp = (M + µ(t + Δt))(u + Δu) – (M + µt)u = FΔt;
где u – скорость платформы.
Раскрыв скобки и, проведя сокращения получаем:
Dp = µuΔt + MΔu+ Δµut + ΔµuΔt = FΔt
Разделим на Δt и перейдем к пределу Δt → 0        
Mdu/dt + µtdu/dt + µu= F или d[(M + µt)u]/dt = F
Это уравнение можно проинтегрировать, считая начальную скорость платформы равной нулю: (M + µt)u = Ft.
Следовательно: u = Ft/(M + µt)
Тогда, ускорение платформы: a = du/dt = (F(M + µt) – Ftµ)/(M + µt)² = FM / (M + µt)²

Рассмотрим случай, когда песок высыпается из наполненной платформы.
Изменение импульса за малый промежуток времени:
Δp = (M – µ(t + Δt))(u+ Δu) +Δµtu – (M – µt)u = FΔt
Слагаемое Δµtu есть импульс количества песка, которое высыпалось из платформы за время Δt. Тогда:
Δp = MΔu  –  µtΔu  –  ΔµtΔu = FΔt
Разделим на Δt и перейдем к пределу Δt → 0
(M – µt)du/dt = F
Или a1= du/dt= F/(M – µt)

Ответ: a = FM / (M + µt)², a1= F/(M – µt)

 

VIII. Самостоятельная работа:

Найти производные функций:

Прямая у = 2х является касательной к функции: у = х³+ 5х² + 9х + 3. Найдите абсциссу точки касания.

IX. Подведение итогов урока:

– Каким вопросам был посвящен урок?
– Чему научились на уроке?
– Какие теоретические факты обобщались на уроке?
– Какие рассмотренные задачи оказались наиболее сложными? Почему?

 Список литературы:

1. Амелькин  В.В., Садовский А.П. Математические модели и дифференциальные уравнения. – Минск: Высшая школа, 1982.  –  272с.
2. Амелькин В.В. Дифференциальные уравнения в приложениях. М.: Наука. Главная редакция физико-математической литературы, 1987.  –  160с.
3. Еругин Н.П. Книга для чтения по общему курсу дифференциальных уравнений. –  Минск: Наука и техника, 1979.  –  744с
4. .Журнал «Потенциал» Ноябрь 2007 №11
5. «Алгебра и начала анализа» 11 класс С.М. Никольский, М.К. Потапов и др.
6. «Алгебра и математический анализ» Н.Я. Виленкин и др.
7. «Математика» В.Т. Лисичкин, И.Л. Соловейчик, 1991 год

12.04.2013

xn--i1abbnckbmcl9fb.xn--p1ai

Примеры применения производной к исследованию функции: ↑ и ↓

 

При  исследовании функции очень часто приходится применять производные. Одной из основных задач при исследовании функции является определение промежутков возрастания и убывания функции. Это исследование очень легко можно произвести с помощью производной функции.

Признаки возрастания функции

Если f’(x)>0 на некотором промежутке, то функция f(x) возрастает на данном промежутке

Признак убывания функции

Если f’(x)<0 на некотором промежутке, то функция f(x) убывает на данном промежутке.

Строгое доказательство этих двух признаков изучается в курсе математического анализа, здесь же мы его приводить не будем.

Применение этих признаков на конкретном примере

Найти промежутки возрастания и убывания функции f(x) = x^3 – 2*x^2 + x.

Найдем производную этой функции f’(x) = (x^3 – 2*x^2 + x)’ = 3*x^2 – 4*x +1. 

Найдем стационарные точки, то есть точки, в которых производная равна нулю.

Решим уравнение f’(x)=0. 

3*x^2 – 4*x +1=0. 

Это несложное квадратное уравнение решаем любым из известных вам способов, получаем два корня: х1=1/3, х2=1. 

Определим знак производной в промежутках на которые эти два корня разбили всю числовую ось. Для этого разложим квадратный трехчлен на множители.

Получим f’(x) = 3*(x-1/3)*(x-1).

Производная положительна на промежутке x<1/3 и на промежутке х>1. А значит, функция на этих промежутках возрастает.

На промежутке от 1/3 до 1 производная отрицательна, следовательно, в этом интервале функция убывает.

 

Точки максимума и минимума – экстремумы функции

 

Помимо, определения промежутков возрастания и убывания функции, с помощью производной при исследовании функции находят точки максимума и минимума этой функции.

Точки максимума и минимума функции называют еще точками экстремума. 

Для отыскания точек экстремума существует отдельный признак.

Достаточное условие существование экстремума в точке.

Пусть f(x) некоторая дифференцируемая на интервале (a;b)  функция. Точка х0 принадлежит этому интервалу и f’(x0)=0.

Тогда:

• 1. если при переходе через стационарную точку х0 функция f(x) и её производная меняет знак, с «плюса» на  «минус», тогда точка х0 является точкой максимума функции.
• 2. если при переходе через стационарную точку х0 функция f(x) и её производная меняет знак, с «минуса» на  «плюс», тогда точка х0 является точкой минимума функции 

Для функции рассмотренной выше найдем точки экстремума функции и значения функции в них.

Мы нашли две стационарные точки: х1=1/3, х2=1.

Так как слева от точки х=1/3 функция возрастает, а справа убывает, точка х=1/3 будет являться точкой максимума.

Точка х=1 будет являться точкой минимума, так как сева от нее функции убывает, а справа возрастает.

Посчитаем значение функции в точках максимума и минимума.

f(1/3) = (1/3)^3 – 2*(1/3)^2 +1/3 = 4/27.

f(1) = 0.

Нужна помощь в учебе?

Предыдущая тема: Критические точки функции: максимумы и минимумы
Следующая тема:&nbsp&nbsp&nbspОсновное свойство первообразной: теорема и наглядные примеры

Все неприличные комментарии будут удаляться.

www.nado5.ru

Производная и ее применение для решения прикладных задач

Министерство образования и науки Украины

Министерство образования и науки АР Крым

Малая академия наук школьников Крыма «Искатель»

Секция математики

Керченский городской филиал

Производная и ее применение для решения прикладных задач

Работу выполнил:

Коваленко Александр,

учащийся 11-Б класса

керченского учебно-воспитательного

комплекса общеобразовательной

школы

I-II ступеней- морской технический лицей

Научный руководитель:

Герасимова Валентина Леонидовна,

учитель математики,

учитель-методист

КУВК ош – МТЛ

Керчь 2008

Содержание

Введение

1. Производная и ее применение для решения прикладных задач

1.1 Исторические сведения

1.2 Понятие производной, ее геометрический и физический смысл

1.3 Дифференциал

2. Перечень прикладных задач

3. Примеры решения прикладных задач

3.1 Исследование функций и построение их графиков.

3.2 Нахождение наибольшего и наименьшего значения функции, решение прикладных задач (задач на оптимум).

3.3 Определение периода функции

3.4 Нахождение приближенных значений функции

3.5 Нахождение величины угла между прямыми и кривыми.

3.6 Разложение на множители и упрощение выражений.

3.7 Вычисление суммы

3.8 Сравнение чисел и доказательство неравенств

3.9 Решение неравенств

3.10 Доказательство тождеств

3.11. Решение уравнений

3.12 Решение систем уравнений

3.13 Отбор кратных корней уравнения

3.14 Вычисление пределов функции с помощью правила Лопиталя

3.15 Решение физических задач, связанных с нахождением скорости, ускорения и т.д.

3.16 Решение экономических задач

3.17 Разложение функций в ряд с помощью формулы Тейлора

3.18 Задача о линеаризации функции

Заключение

Список литературы

Введение

Из всех теоретических успехов знания вряд

ли какой-нибудь считается столь высоким три-

умфом человеческого духа, как изобретение ис-

числения бесконечно малых во второй половине

XVII века.

Ф. Энгельс

Тема исследовательской работы выбрана не случайно, поскольку применение производной позволяет более эффективно решать многие задачи повышенной сложности. Применение производной для решения задач требует от учащихся нетрадиционного мышления. Следует отметить, что знание нестандартных методов и приемов решения задач способствует развитию нового, нешаблонного мышления, которое можно успешно применять также и в других сферах человеческой деятельность (вычислительная техника, экономика, физика, химия и т.д.) Это доказывает актуальность данной работы.

Целью работы было: изучение применения производной для решения задач по алгебре и началам анализа, физике, экономике; углубление и расширение знаний по теме «Производная».При изучении изменяющихся величин очень часто возникает вопрос о скорости, о быстроте происходящего изменения. Так мы говорим о скорости движения самолета, поезда, автобуса, ракеты, о скорости падения камня, вращения шкива и т.д. Можно говорить о скорости выполнения определенной работы, о скорости протекания химической реакции, о быстроте роста населения в данном городе. О скорости можно говорить по отношению к любой величине, которая изменяется с течением времени. Для всего этого используется понятие производной.

Физические производные величины:

υ(t) = х^/ (t) – скорость

a (t)=υ^/ (t) – ускорение

J (t) = q^/ (t) – сила тока

C(t) = Q^/ (t) – теплоемкость

d(l )=m^/ (l ) – линейная плотность

K (t) = l ^/ (t) – коэффициент линейного расширения

ω (t)= φ^/ (t) – угловая скорость

а (t)= ω^/ (t) – угловое ускорение

N(t) = A^/ (t) – мощность

Дифференциальное исчисление широко применяется для экономического анализа как математический аппарат. В экономике очень часто требуется найти наилучшее или оптимальное значение показателя: наивысшую производительность труда, максимальную прибыль, максимальный выпуск, минимальные издержки и т. д. Каждый показатель представляет собой функцию от одного или нескольких аргументов. Таким образом, нахождение оптимального значения показателя сводится к нахождению экстремума функции.

Производная в экономических формулах:

П (t) = υ^/ (t) – производительность труда,

где υ (t) – объем продукции

J(x) = y^/ (x) – предельные издержки производства,

где y– издержки производства в зависимости от объема выпускаемой продукции x.

В работе рассмотрены прикладные задачи, способы решения которых можно использовать для решения нестандартных задач по алгебре и началам анализа, при подготовке к государственной итоговой аттестации, внешнему независимому оцениванию. Достаточно большое число задач раскрывают потенциальные возможности анализа бесконечно малых величин.

1. Производная и ее применение для решения прикладных задач

1.1 Исторические сведения

Ряд задач дифференциального исчисления был решен еще в древности. Они встречались у Евклида. Ряд таких задач был решен Архимедом, разработавшим способ проведения касательной, примененный им к спирали, но применимый для других кривых. Основное понятие дифференциального исчисления – понятие производной – возникло в XVII в. В связи с необходимостью решения ряда задач из физики, механики и математики. Дифференциальное исчисление было создано Ньютоном и Лейбницем на основе двух задач: 1) о разыскании касательной к произвольной линии2) о разыскании скорости при произвольном законе движенияЕще раньше понятие производной встречалось в работах итальянского математика Тартальи (около 1500 – 1557 гг.) – здесь появилась касательная в ходе изучения вопроса об угле наклона орудия, при котором обеспечивается наибольшая дальность полета снаряда. В 17 веке на основе учения Г.Галилея о движении активно развивалась кинематическая концепция производной. Различные изложения стали встречаться в работах у Декарта, французского математика Роберваля, английского ученого Л. Грегори. Большой вклад в изучение дифференциального исчисления внесли Лопиталь, Бернулли, Лагранж, Эйлер, Гаусс.

1.2 Понятие производной, ее геометрический и физический смысл

Понятие производной

Пусть y = f(x) есть непрерывная функция аргумента x, определенная в промежутке (a; b), и пусть х₀ – произвольная точка этого промежутка

Дадим аргументу x приращение ∆x, тогда функция y = f(x) получит приращение ∆y = f(x + ∆x) – f(x). Предел, к которому стремится отношение ∆y / ∆x при ∆x → 0, называется производной от функции f(x).

y'(x)=

Геометрический смысл производной состоит в том, что она равна угловому коэффициенту касательной. Рассмотрим график функции

(рис.). Видно,

что

, т.е. это отношение равно угловому

коэффициенту секущей mm. Если

, то секущая,

поворачиваясь вокруг точки М, в пределе переходит в

касательную

, так как касательная является предельным

положением секущей, когда точки пересечения сливаются.

Таким образом,

.

Уравнение касательной

, где – координаты точки касания, а – текущие координаты точки касательной прямой.

Физический смысл производной заключается в скорости изменения функции.

Пусть s = s (t ) — закон прямолинейного движения. Тогда v (t ₀ ) = s ‘(t ₀ ) выражает мгновенную скорость движения в момент времени t ₀ . Вторая производная a (t ₀ ) = s ”(t ₀ ) выражает мгновенное ускорение в момент времени t ₀ .Вообще производная функции y = f (x ) в точке x ₀ выражает скорость изменения функции в точке x ₀ , то есть скорость протекания процесса, описанного зависимостью y = f (x ).

13 Дифференциал

Пусть дана функция

и – внутренняя точка её области определения. Придадим аргументу приращение и рассмотрим приращение функции

Если это приращение

можно представить в виде где величина не зависит от приращения, а – бесконечно малая при величина, имеющая больший порядок малости, чем , то произведение называется дифференциалом функции в точке и обозначается .

mirznanii.com

§ 4. Применение производной к исследованию функций

Исследование функции удобно проводить по следующему плану.

1. Область определения функции.

2. Точки пересечения графика функции с осями координат.

3. Четность, нечетность функции.

4. Исследование функции на непрерывность. Вертикальные асимптоты.

5. Невертикальные асимптоты.

6. Интервалы монотонности. Экстремумы.

7. Интервалы выпуклости, вогнутости. Точки перегиба.

8. Дополнительные точки, (по мере необходимости).

9. Построение графика.

Подчеркнем, что пункт 8 не является необходимым. его выполняют, если необходимо уточнить график.

 

Пример 1. Исследовать функцию и построить ее график.

1. Область определения ().

2. Пусть х=0, тогда у=0. Пусть у=0, тогда  и . Итак, (0;0) и – точки пересечение графика с осями координат.

3. у(-х) =  – функция не является ни четной, ни нечетной.

4. Функция непрерывна во всей области определения. Вертикальных асимптот нет.

5. Невертикальные асимптоты

Найдем k и b, если они существуют.  поэтому при невертикальной асимптоты не существует. Аналогично можно показать, что и при невертикальных асимптот не существует.

6. Вычислим  Найдем критические точки:  х = 1 – критическая точка. Кроме того, y’ не существует при х = 0 – тоже критическая точка. Нанесем критические точки на числовую прямую и определим знаки производной в образовавшихся интервалах.

Таким образом, на интервалах (-и (1;+ функция возрастает, на интервале (0;1) убывает.

у_max = f(0) = 0, y_min = f(1)= –1.

7. Вычислим

у” не обращается в нуль ни при каком значении х и у” не существует при х=0. х=0 – критическая точка второго порядка. Нанесем критическую точку на числовую прямую и определим знаки второй производной в образовавшихся интервалах.

Таким образом, на интервалах ( и  график функции вогнутый, точек перегиба нет.

8. Заметим, что , то есть в точке (0;0) график имеет вертикальную касательную.

Пример 2. Исследовать функцию y = x-2arctg x и построить ее график.

1. Область определения (.

2. Пусть х = 0, тогда у = 0-2arctg 0 = 0.

Пусть y = 0, тогда х-2arctg x = 0; х = 2arctg x – решить такое уравнение точнo не удается.

Найдена точка (0;0) пересечения с осями координат.

3.  функция нечетная.

4. Функция непрерывна во всей области определения. Вертикальных асимптот нет.

5. Невертикальные асимптоты.

y = kx+b

 – асимптота при .

Выясним, есть ли асимптоты при 

.

 – асимптота при 

6. y‘

 и х = 1 – критические точки. Нанесем критические точки на числовую прямую и определим знаки производной в образовавшихся интервалах.

На интервалах  функция возрастает, на интервале

(-1;1)– убывает.

7.  y” = 0; 4х = 0; х = 0 – критическая точка второго порядка. Нанесем ее на числовую прямую и определим знаки второй производной в образовавшихся интервалах.

На интервале ( график выпуклый, на интервале  – вогнутый.

х = 0 – абсцисса точки перегиба.

8. .

Пример 3. Исследовать функцию  и построить ее график.

1. Область определения  так как при  и х=2 в знаменателе получается нуль.

2. Пусть х=0, тогда у=0.

Пусть у=0, тогда 

(0;0) – точка пересечения графика с осями координат.

3. = – функция нечетная.

4. Функция имеет разрывы в точках х = -2 и х = 2, так как значения f(-2) и f(2) не определены.  ;   Это означает, что в точках  и х = 2 функция имеет разрывы II рода и прямые  и х = 2 являются вертикальными асимптотами.

5. Найдем невертикальные асимптоты.

  следовательно, прямая у=0 является горизонтальной асимптотой при  и .

6.        Вычислим  при всех значениях х, принадлежащих области определения функции. Точки  и х = 2 – критические, так как в них производная не существует.

На интервалах  функция убывает. Экстремумов нет.

7.      Вычислим 

y” = 0; ; 

х = 0;  х = 2 – критические точки второго порядка.

На интервалах  и (0;2) график функции выпуклый, а на интервалах (-2;0) и  – вогнутый; х = 0 – абсцисса точки перегиба.

 

ya-znau.ru

---