Примеры резонанс – Я хотел бы узнать 3 примера резонанса из жизни, желательно с полным разяснением. - Центр социальной реабилитации инвалидов и детей-инвалидов Фрунзенского района Санкт-Петербурга

19.06.201925.11.2018

Примеры резонанс – Я хотел бы узнать 3 примера резонанса из жизни, желательно с полным разяснением.

Содержание

Примеры резонансных явлений

Резонанс играет очень большую роль в самых разнообразных явлениях, причем в одних — полезную, в других — вредную. Приведем несколько примеров, относящихся к механическим колебаниям.

Идя по доске, перекинутой через ров, можно попасть шагами в резонанс с собственным периодом системы (доски с человеком на ней), и доска начинает тогда сильно колебаться (изгибаться вверх и вниз). То же самое может случиться и с мостом, по которому проходит войсковая часть или проезжает поезд (периодическая сила обусловливается ударами ног или ударами колес на стыках рельсов). Так, например, в 1906г. в Петербурге обрушился так называемый Египетский мост через реку Фонтанку. Это произошло при переходе через мост кавалерийского эскадрона, причем четкий шаг лошадей, отлично обученных церемониальному маршу, попал в резонанс с периодом моста. Для предотвращения таких случаев войсковым частям при переходе через мосты приказывают обычно идти не «в ногу», а вольным шагом. Поезда же большей частью переезжают мосты на медленном ходу, чтобы период ударов колес о стыки рельсов был значительно больше периода свободных колебаний моста. Иногда применяют обратный способ «расстройки» периодов: поезда проносятся через мосты на максимальной скорости.

Случается, что период ударов колес на стыках рельсов совпадает с периодом колебаний вагона на рессорах, и вагон тогда очень сильно раскачивается. Корабль также имеет свой период качаний на воде. Если морские волны попадают в резонанс с периодом корабля, то качка становится особенно сильной. Капитан меняет тогда скорость корабля или его курс. В результате период волн, набегающих на корабль, изменяется (вследствие изменения относительной скорости корабля и воли) и уходит от резонанса.

Неуравновешенность машин и двигателей (недостаточная центровка, прогиб вала) является причиной того, что при работе этих машин возникает периодическая сила, действующая на опору машины — фундамент, корпус корабля и т. п. Период силы может совпасть при этом с периодом свободных колебаний опоры или, например, с периодом колебаний изгиба самого вращающегося вала или с периодом крутильных колебаний этого вала. Получается резонанс, и вынужденные колебания могут быть настолько сильны, что разрушают фундамент, ломают валы и т. д. Во всех таких случаях принимаются специальные меры, чтобы избежать резонанса или ослабить его действие (расстройка периодов, увеличение затухания — демпфирование и др.).

Очевидно, для того чтобы с помощью наименьшей периодической силы получить определенный размах вынужденных колебаний, нужно действовать в резонанс. Тяжелый язык большого колокола может раскачать даже ребенок, если он будет натягивать веревку с периодом свободных колебаний языка. Но самый сильный человек не раскачает язык, дергая веревку не в резонанс.

На явлении резонанса основало действие прибора, предназначенного для определения частоты переменного тока, сила которого изменяется по гармоническому закону (см. том II, § 153). Такие приборы, носящие название язычковых частотомеров, обычно применяются для контроля постоянства частоты в электрической сети. Внешний вид прибора изображен на рис. 28, а. Он состоит из набора упругих пластинок с грузиками на концах (язычков), причем массы грузиков и жесткости пластинок подобраны так, что частоты соседних язычков отличаются на одно и то же число герц. У частотомера, изображенного на рис. 28, а, частоты язычков идут через каждые . Эти частоты написаны на шкале против язычков.

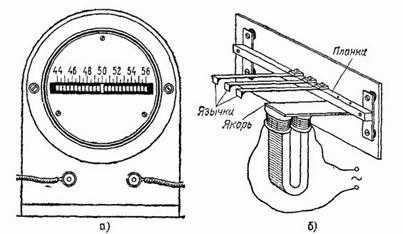
Рис. 28. Язычковый частотомер: а) внешний вид; б) схема устройства

Устройство частотомера схематически показано на рис. 28, б. Исследуемый ток пропускается через обмотку электромагнита. Колебания якоря передаются планке, с которой связаны основания всех язычков и которая укреплена на гибких пластинках. Таким образом, на каждый язычок действует гармоническая сила, частота которой равна частоте тока. Язычок, попавший в резонанс с этой силой, колеблется с большей амплитудой и показывает на шкале свою частоту, т. е. частоту тока.

В дальнейшем мы еще не раз встретимся с явлением резонанса, когда будем изучать звуковые и электрические колебания. Именно эти колебания дадут нам особенно яркие примеры полезного применения резонанса.

sfiz.ru

Резонанс напряжений. Что такое резонанс в электрической цепи

Резонанс является одним из самых распространенных в природе физических явлений. Явление резонанса можно наблюдать в механических, электрических и даже тепловых системах. Без резонанса у нас не было бы радио, телевидения, музыки и даже качелей на детских площадках, не говоря уже об эффективнейших диагностических системах, применяемых в современной медицине. Одним из самых интересных и полезных видов резонанса в электрической цепи является резонанс напряжений.

Элементы резонансной цепи

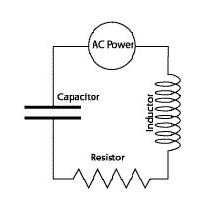
Явление резонанса может возникнуть в так называемой RLC-цепи, содержащей следующие компоненты:

R – резисторы. Эти устройства, относящиеся к так называемым активным элементам электрической цепи, преобразуют электрическую энергию в тепловую. Другими словами, они удаляют энергию из контура и преобразуют ее в тепло.
L – индуктивность. Индуктивность в электрических цепях – аналог массы или инерции в механических системах. Этот компонент не очень заметен в электрической цепи, пока не попробуешь сделать в ней какие-либо изменения. В механике, например, таким изменением является изменение скорости. В электрической цепи – изменение тока. Если оно по какой-либо причине происходит, индуктивность противодействует такому изменению режима цепи.
С – обозначение для конденсаторов, которые представляют собой устройства, хранящие электрическую энергию подобно тому, как пружины сохраняют механическую энергию. Индуктивность концентрирует и сохраняет магнитную энергию, в то время как конденсатор концентрирует заряд и тем самым хранит электрическую энергию.

Понятие резонансного контура

Ключевыми элементами резонансного контура являются индуктивность (L) и емкость (C). Резистор имеет тенденцию к гашению колебаний, поэтому он удаляет энергию из контура. При рассмотрении процессов, происходящих в колебательном контуре, мы его временно игнорируем, но необходимо помнить, что подобно силе трения в механических системах электрическое сопротивление в цепях невозможно устранить.

Резонанс напряжений и резонанс токов

В зависимости от способа соединения ключевых элементов резонансный контур может быть последовательным и параллельным. При подключении последовательного колебательного контура к источнику напряжения с частотой сигнала, совпадающей с собственной частотой, при определенных условиях в нем возникает резонанс напряжений. Резонанс в электрической цепи с параллельно соединенными реактивными элементами называется резонансом токов.

Собственная частота резонансного контура

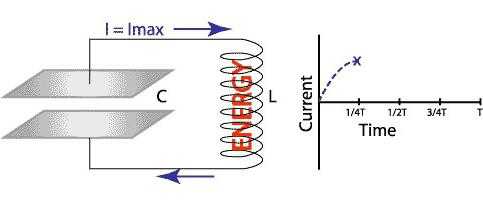
Мы можем заставить систему колебаться с собственной частотой. Для этого сначала необходимо зарядить конденсатор, как показано на верхнем рисунке слева. Когда это будет выполнено, ключ переводится в положение, показанное на том же рисунке справа.

В момент времени “0” вся электрическая энергия сохраняется в конденсаторе, и ток в контуре равен нулю (рисунок внизу). Обратите внимание, что верхняя пластина конденсатора заряжена положительно, а нижняя – отрицательно. Мы не можем видеть колебания электронов в цепи, но мы можем измерить ток амперметром, а при помощи осциллоскопа отследить характер зависимости тока от времени. Отметим, что T на нашем графике – это время, необходимое для завершения одного колебания, носящего в электротехнике название “период колебания”.

Ток течет по часовой стрелке (рисунок внизу). Энергия передается из конденсатора в катушку индуктивности. На первый взгляд может показаться странным, что индуктивность содержит энергию, однако это похоже на кинетическую энергию, содержащуюся в движущейся массе.

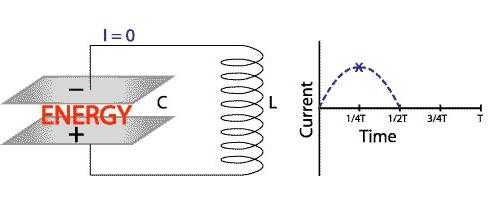
Поток энергии возвращается обратно в конденсатор, но обратите внимание, что полярность конденсатора теперь изменилась. Другими словами, нижняя пластина теперь имеет положительный заряд, а верхняя пластина – отрицательный заряд (рисунок внизу).

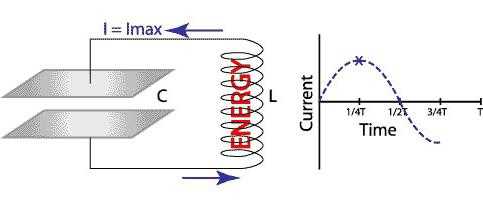
Теперь система полностью обратилась, и энергия начинает поступать из конденсатора опять в индуктивность (рисунок внизу). В итоге энергия полностью возвращается к своей отправной точке и готова начать цикл заново.

Частота колебаний может быть аппроксимирована следующим образом:

где: F – частота, L – индуктивность, C – емкость.

Рассмотренный на этом примере процесс отражает физическую суть резонанса напряжений.

Исследование резонанса напряжений

В реальных схемах LC всегда присутствует небольшое сопротивление, которое с каждым циклом уменьшает прирост амплитуды тока. После нескольких циклов ток уменьшается до нуля. Этот эффект называется “затухание синусоидального сигнала”. Скорость затухания тока до нулевого значения зависит от величины сопротивления в цепи. Тем не менее, сопротивление не изменяет частоту колебаний резонансного контура. Если сопротивление достаточно велико, синусоидальные колебания в контуре не возникнут вообще.

Очевидно, там, где существует собственная частота колебаний, есть возможность возбуждения резонансного процесса. Мы делаем это, включая в последовательную цепь источник питания переменного ток (АС), как показано на рисунке слева. Термин “переменный” означает, что выходное напряжение источника колеблется с определенной частотой. Если частота источника питания совпадает с собственной частотой контура, возникает резонанс напряжений.

Условия возникновения

Сейчас мы рассмотрим условия возникновения резонанса напряжений. Как показано на последнем рисунке, мы вернули резистор в контур. При отсутствии резистора в контуре ток в резонансной цепи будет нарастать до некоторого максимального значения, определяемого параметрами элементов контура и мощностью источника питания. Увеличение сопротивления резистора в резонансной цепи повышает тенденцию к затуханию тока в контуре, но не влияет на частоту резонансных колебаний. Как правило, режим резонанса напряжений не наступает, если сопротивление цепи резонанса удовлетворяет условию R = 2(L/C)^0,5.

Использование резонанса напряжений для передачи радиосигнала

Явление резонанса напряжений является не только любопытнейшим физическим феноменом. Оно играет исключительную роль в технологии беспроводных коммуникаций – радио, телевидении, сотовой телефонии. Передатчики, используемые для беспроводной передачи информации, в обязательном порядке содержат схемы, предназначенные для резонирования на определенной для каждого устройства частоте, называемой несущей частотой. При помощи передающей антенны, подключенной к передатчику, он излучает электромагнитные волны на несущей частоте.

Антенна на другом конце приемо-передающего тракта получает этот сигнал и подает его на приемный контур, предназначенный для резонирования на частоте несущей. Очевидно, что антенна принимает множество сигналов на различных частотах, не говоря уже о фоновом шуме. Благодаря наличию на входе приемного устройства, настроенного на несущую частоту резонансного контура, приемник выбирает единственно правильную частоту, отсеивая все ненужные.

После детектирования амплитудно-модулированного (AM) радиосигнала, выделенный из него низкочастотный сигнал (НЧ) усиливается и подается на звуковоспроизводящее устройство. Это простейшая форма радиопередачи очень чувствительна к шумам и помехам.

Для повышения качества принимаемой информации разработаны и успешно используются другие, более совершенные способы передачи радиосигнала, которые также базируются на использовании настроенных резонансных систем.

Частотная модуляция или FM-радио решает многие из проблем радиопередачи с амплитудно-модулированным передающим сигналом, однако это достигается ценой существенного усложнения системы передачи. В FM-радио системные звуки в электронном тракте превращаются в небольшие изменения несущей частоты. Часть оборудования, которое выполняет это преобразование, называется “модулятор” и используется с передатчиком.

Соответственно, к приемнику должен быть добавлен демодулятор для преобразования сигнала обратно в форму, которая может быть воспроизведена через громкоговоритель.

Другие примеры использования резонанса напряжения

Резонанс напряжений как основополагающий принцип заложен также в схемотехнике многочисленных фильтров, широко применяемых в электротехнике для устранения вредных и ненужных сигналов, сглаживания пульсаций и генерирования синусоидальных сигналов.

fb.ru

Лучший пример резонанса, объясняющий его суть

Образование 30 ноября 2016

Прежде чем приступить к знакомству с явлениями резонанса, следует изучить физические термины, связанные с ним. Их не так много, поэтому запомнить и понять их смысл будет несложно. Итак, обо всем по порядку.

Что такое амплитуда и частота движения?

Представьте обычный двор, где на качелях сидит ребенок и машет ножками, чтобы раскачаться. В момент, когда ему удается раскачать качели и они достигают равномерного движения из одной стороны в другую, можно подсчитать амплитуду и частоту движения.

Амплитуда – это наибольшая длина отклонения от точки, где тело находилось в положении равновесия. Если брать наш пример качелей, то амплитудой можно считать наивысшую точку, до которой раскачался ребенок.

А частота – это количество колебаний или колебательных движений в единицу времени. Измеряется частота в Герцах (1 Гц = 1 колебание в секунду). Возвратимся к нашим качелям: если ребенок проходит за 1 секунду только половину всей длины качания, то его частота будет равна 0,5 Гц.

Как частота связана с явлением резонанса?

Мы уже выяснили, что частота характеризует число колебаний предмета в одну секунду. Представьте теперь, что слабо качающемуся ребенку взрослый человек помогает раскачаться, раз за разом подталкивая качели. При этом данные толчки также имеют свою частоту, которая будет усиливать либо уменьшать амплитуду качания системы “качели-ребенок”.

Допустим, взрослый толкает качели в то время, когда они движутся навстречу к нему, в таком случае частота не будет увеличивать амлитуду движения подвесных качелей. То есть сторонняя сила (в данном случае толчки) не будет способствовать усиления колебания системы.

В случае если частота, с которой взрослый раскачивает ребенка, будет численно равна самой частоте колебания качелей, может возникнуть являение резонанса. Другими словами, пример резонанса – это совпадение частоты самой системы с частотой вынужденных колебаний. Логично представить, что частота вынужденных колебаний и резонанс взаимосвязаны.

Видео по теме

Где можно наблюдать пример резонанса?

Важно понимать, что примеры проявления резонанса встречаются практически во всех сферах физики, начиная от звуковых волн и заканчивая электричеством. Смысл резонанса заключается в том, что когда частота вынуждающей силы равна собственной частоте системы, то в этот момент амплитуда колебаний достигает наивысшего значения.

Следующий пример резонанса даст понимание сути. Допустим, вы шагаете по тонкой доске, перекинутой через речку. Когда частота ваших шагов совпадет с частотой или периодом всей системы (доска-человек), то доска начинает сильно колебаться (гнуться вниз и вверх). Если вы продолжите двигаться такими же шагами, то резонанс вызовет сильную амплитуду колебания доски, которая выходит за пределы допустимого значения системы и это в конечном счете приведет к неминуемой поломке мостика.

Существуют также те сферы физики, где можно использовать такое явление, как полезный резонанс. Примеры могут удивить вас, ведь обычно мы используем его интуитивно, даже не догадываясь о научной стороне вопроса. Так, например, мы используем резонанс, когда пытаемся вытащить машину из ямы. Вспомните, ведь легче всего достичь результат только тогда, когда толкаешь машину в момент ее движения вперед. Этот пример резонанса усиливает амплитуду движения, тем самым помогая вытащить машину.

Примеры вредного резонанса

Сложно сказать, какой резонанс в нашей жизни встречается больше: хороший или же наносящий нам вред. Истории известно немалое количество ужасающих последствий явления резонанса. Вот самые известные события, на которых можно наблюдать пример резонанса.

Во Франции, в городе Анжера, в 1750 году отряд солдат шел в ногу через цепной мост. Когда частота их шагов совпала с частотой свободных колебаний моста, размахи колебаний (амплитуда) резко увеличились. Наступил резонанс, и цепи оборвались, а мост обрушился в реку.
Бывали случаи, когда в деревнях дом был разрушен из-за проезжающего по главной дороге грузового автомобиля.

Как видите, резонанс может иметь весьма опасные последствия, вот почему инженерам следует тщательно изучать свойства строительных объектов и правильно вычислять их частоты колебаний.

Полезный резонанс

Резонанс не ограничивается только плачевными последствиями. При внимательном изучении окружающего мира можно наблюдать множество хороших и выгодных для человека результатов резонанса. Вот один яркий пример резонанса, позвляющий получать людям эстетическое удовольствие.

Устройсто многих музыкальных инструментов работает по принципу резонанса. Возьмем скрипку: корпус и струна образуют единую колебательную систему, внутри которой имеется штифт. Именно через него передаются частоты колебаний из верхней деки в нижнюю. Когда лютьер водит смычком по струне, то последняя, подобно стреле, побеждает своей силой упругости трение канифольной поверхности и летит в обратную сторону (начинает движение в противоположную область). Возникает резонанс, который передается в корпус. А внутри его есть специальные отверстия – эфы, сквозь которые резонанс выводится наружу. Именно таким образом он контролируется во многих струнных инструментах (гитара, арфа, виолончель и др).

Источник: fb.ru Духовное развитие
Прощенное воскресенье и его суть

Человек – существо совершенное и бренное в одно и то же время. С одной стороны, мы созданы по образу и подобию Божиему. Значит, у нас есть все чтобы сделать свою жизнь и судьбу окружающих нас людей счастливой. В…

Новости и общество
Возмездие – это что такое? Каким может быть возмездие и в чем его суть?

Возмездие – это понятие, которое довольно сложно выразить простыми словами. Наверное, причиной тому абстрактность этого явления. Не говоря уже о том, что каждый человек немного по-своему видит основную концепцию…

Новости и общество
Денежное обращение и его суть

Поскольку деньги меняют форму стоимости (деньги-товар, товар-деньги), они постоянно балансируют между тремя субъектами, первыми из которых являются физические лица, вторыми – хозяйствующие субъекты, а в роли …

Новости и общество
Факторный анализ : пример составления и его особенности

Для того, чтобы выяснить, насколько прибыльным или убыточным является предприятие, недостаточно просто считать деньги. Чтобы понять это наверняка, а главное, способствовать увеличению прибыли, нужно регулярно проводит…

Образование
Какая неофициальная расшифровка СНГ ярче отражает его суть?

До сих пор нет однозначного ответа на вопрос о причинах распада Советского Союза. Наиболее либерально настроенные историки, да и просто обыватели считают, что произошло это по вполне закономерным причинам, дескать &la…

Образование
Пластический обмен, его суть и роль для организма

Пластический обмен носит еще название анаболизма или ассимиляции и является совокупностью всех ферментативных биохимических реакций, в результате которых синтезируются биоорганические соединения.Пластический об…

Отношения
Как быть лучше бывшей и завоевать его?

Времена, когда молодых людей совершенно юными и невинными сватали родители, давно миновали. Мы не торопимся вступать в брак, зато у нас могут быть не одни отношения с противоположным полом до замужества. По этому пово…

Финансы
Вмененный налог – его суть и некоторые особенности

У крупных предприятий для ведения бухгалтерского учета есть штат специалистов, обладающих нужными знаниями. У малого бизнеса, будь это небольшая организация или индивидуальный предприниматель, возможность нанять таких…

Образование
Лучшие примеры человечности из жизни

Человечность – это одно из самых важных и в то же время сложных понятий. Ему невозможно дать однозначное определение, ведь проявляется оно в самых разных качествах человека. Это и стремление к справедливости, и …

Компьютеры
Что такое DLC? Лучшие примеры

Для того чтобы ответить на вопрос о том, что такое DLC, необходимо обратиться к игровой индустрии. Давайте представим такую ситуацию: купленная игра уже давно как пройдена вдоль и поперек, в ней больше нет никаких дос…

monateka.com

Лучший пример резонанса, объясняющий его суть

Что такое амплитуда и частота движения?

Как частота связана с явлением резонанса?

Где можно наблюдать пример резонанса?

Примеры вредного резонанса

Во Франции, в городе Анжера, в 1750 году отряд солдат шел в ногу через цепной мост. Когда частота их шагов совпала с частотой свободных колебаний моста, размахи колебаний (амплитуда) резко увеличились. Наступил резонанс, и цепи оборвались, а мост обрушился в реку.
Бывали случаи, когда в деревнях дом был разрушен из-за проезжающего по главной дороге грузового автомобиля.

Полезный резонанс

4u-pro.ru

Резонанс

Навигация:

Библиотека DJVU
Photogallery

БСЭ

Статистика:

Значение слова “Резонанс” в Большой Советской Энциклопедии

Резонанс (франц. resonance, от лат. resono — звучу в ответ, откликаюсь), явление резкого возрастания амплитуды вынужденных колебаний в какой-либо


Рис. 1. Механическая колебательная система.

колебательной системе, наступающее при приближении частоты периодического внешнего воздействия к некоторым значениям, определяемым свойствами самой системы. В простейших случаях Резонанс наступает при приближении частоты внешнего воздействия к одной из тех частот, с которыми происходят собственные колебания в системе, возникающие в результате начального толчка. Характер явления Резонанс существенно зависит от свойств колебательной системы. Наиболее просто Резонанс протекает в тех случаях, когда периодическому воздействию подвергается система с параметрами, не зависящими от состояния самой системы (т. н. линейные системы).

Типичные черты Резонанс можно выяснить, рассматривая случай гармонического воздействия на систему с одной степенью свободы: например, на массу m, подвешенную на пружине, находящуюся под действием гармонической силы F = F₀ coswt (рис. 1), или электрическую цепь, состоящую из последовательно соединённых индуктивности L, ёмкости С, сопротивления R и источника электродвижущей силы Е, меняющейся по гармоническому закону (рис. 2). Для определенности в дальнейшем рассматривается первая из этих моделей, но всё сказанное ниже можно распространить и на вторую модель. Примем, что пружина подчиняется закону Гука (это предположение необходимо, чтобы система была линейна), т. е., что сила, действующая со стороны пружины на массу m, равна kx, где х — смещение массы от положения равновесия, k — коэффициент упругости (сила тяжести для простоты не принимается во внимание). Далее, пусть при движении масса испытывает со стороны окружающей среды сопротивление, пропорциональное её скорости и коэффициенту трения b, т. е. равное k (это необходимо, чтобы система оставалась линейной). Тогда уравнение движения массы m при наличии гармонической внешней силы F имеет вид:

(1)

где F₀— амплитуда колебания, w — циклическая частота, равная 2p/Т, Т — период внешнего воздействия, — ускорение массы m. Решение этого уравнения может быть представлено в виде суммы двух решений. Первое из этих решений соответствует свободным колебаниям системы, возникающим под действием начального толчка, а второе — вынужденным колебаниям. Собственные колебания в системе вследствие наличия трения и сопротивления среды всегда затухают, поэтому по истечении достаточного промежутка времени (тем большего, чем меньше затухание собственных колебаний) в системе останутся одни только вынужденные колебания. Решение, соответствующее вынужденным колебаниям, имеет вид:

, (2)

причём tgj = . Т. о., вынужденные колебания представляют собой гармонические колебания с частотой, равной частоте внешнего воздействия; амплитуда и фаза вынужденных колебаний зависят от соотношения между частотой внешнего воздействия и параметрами системы.

Зависимость амплитуды смещений при вынужденных колебаниях от соотношения между величинами массы m и упругости k легче всего проследить, полагая, что m и k остаются неизменными, а изменяется частота внешнего воздействия. При очень медленном воздействии (w ® 0) амплитуда смещений x₀ »_{F₀/k. С увеличением частоты w амплитуда x₀ растет, т. к. знаменатель в выражении (2) уменьшается. Когда w приближается к значению (т. е. к значению частоты собственных колебаний при малом их затухании), амплитуда вынужденных колебаний достигает максимума — наступает Резонанс Далее с увеличением w амплитуда колебаний монотонно убывает и при w ® ¥ стремится к нулю.}

Амплитуду колебаний при Резонанс можно приближённо определить, полагая w = . Тогда x₀ = F₀/bw, т. е. амплитуда колебаний при Резонанс тем больше, чем меньше затухание b в системе (рис. 3). Наоборот, при увеличении затухания системы Резонанс становится всё менее резким, и если b очень велико, то Резонанс вообще перестаёт быть заметным. С энергетической точки зрения Резонанс объясняется тем, что между внешней силой и вынужденными колебаниями устанавливаются такие фазовые соотношения, при которых в систему поступает наибольшая мощность (т. к. скорость системы оказывается в фазе с внешней силой и создаются наиболее благоприятные условия для возбуждения вынужденных колебаний).

Если на линейную систему действует периодическое, но не гармоническое внешнее воздействие, то Резонанс наступит только тогда, когда во внешнем воздействии содержатся гармонические составляющие с частотой, близкой к собственной частоте системы. При этом для каждой отдельной составляющей явление будет протекать так же, как рассмотрено выше. А если этих гармонических составляющих с частотами, близкими к собственной частоте системы, будет несколько, то каждая из них будет вызывать резонансные явления, и общий эффект, согласно суперпозиции принципу, будет равен сумме эффектов от отдельных гармонических воздействий. Если же во внешнем воздействии не содержится гармонических составляющих с частотами, близкими к собственной частоте системы, то Резонанс вообще не наступает. Т. о., линейная система отзывается, «резонирует» только на гармонические внешние воздействия.

В электрических колебательных системах, состоящих из последовательно соединённых ёмкости С и индуктивности L (рис. 2), Резонанс состоит в том, что при приближении частот внешней эдс к собственной частоте колебательной системы, амплитуды эдс на катушке и напряжения на конденсаторе порознь оказываются гораздо больше амплитуды эдс, создаваемой источником, однако они равны по величине и противоположны по фазе. В случае воздействия гармонической эдс на цепь, состоящую из параллельно включенных ёмкости и индуктивности (рис. 4), имеет место особый случай Резонанс (антирезонанс). При приближении частоты внешней эдс к собственной частоте контура LC происходит не возрастание амплитуды вынужденных колебаний в контуре, а наоборот, резкое уменьшение амплитуды силы тока во внешней цепи, питающей контур. В электротехнике это явление называется Резонанс токов или параллельным Резонанс Это явление объясняется тем, что при частоте внешнего воздействия, близкой к собственной частоте контура, реактивные сопротивления обеих параллельных ветвей (ёмкостной и индуктивной) оказываются одинаковыми по величине и поэтому в обеих ветвях контура текут токи примерно одинаковой амплитуды, но почти противоположные по фазе. Вследствие этого амплитуда тока во внешней цепи (равного алгебраической сумме токов в отдельных ветвях) оказывается гораздо меньшей, чем амплитуды тока в отдельных ветвях, которые при параллельном Резонанс достигают наибольшей величины. Параллельный Резонанс, так же как и последовательный Резонанс, выражается тем резче, чем меньше активное сопротивление ветвей контура Резонанс Последовательный и параллельный Резонанс называются соответственно Резонанс напряжений и Резонанс токов.

В линейной системе с двумя степенями свободы, в частности в двух связанных системах (например, в двух связанных электрических контурах; рис. 5), явление Резонанс сохраняет указанные выше основные черты. Однако, т. к. в системе с двумя степенями свободы собственные колебания могут происходить с двумя различными частотами (т. н. нормальные частоты, см. Нормальные колебания), то Резонанс наступает при совпадении частоты гармонического внешнего воздействия как с одной, так и с другой нормальной частотой системы. Поэтому, если нормальные частоты системы не очень близки друг к другу, то при плавном изменении частоты внешнего воздействия наблюдаются два максимума амплитуды вынужденных колебаний (рис. 6). Но если нормальные частоты системы близки друг к другу и затухание в системе достаточно велико, так что Резонанс на каждой из нормальных частот «тупой», то может случиться, что оба максимума сольются. В этом случае кривая Резонанс для системы с двумя степенями свободы теряет свой «двугорбый» характер и по внешнему виду лишь незначительно отличается от кривой Резонанс для линейного контура с одной степенью свободы. Т. о., в системе с двумя степенями свободы форма кривой Резонанс зависит не только от затухания контура (как в случае системы с одной степенью свободы), но и от степени связи между контурами.

В связанных системах также существует явление, которое в известной мере аналогично явлению антирезонанса в системе с одной степенью свободы. Если в случае двух связанных контуров с различными собственными частотами настроить вторичный контур L₂C₂ на частоту внешней эдс, включенной в первичный контур L₁C₁ (рис. 5), то сила тока в первичном контуре резко падает и тем резче, чем меньше затухание контуров. Объясняется это явление тем, что при настройке вторичного контура на частоту внешней эдс в этом контуре возникает как раз такой ток, который в первичном контуре наводит эдс индукции, примерно равную внешней эдс по амплитуде и противоположную ей по фазе.

В линейных системах со многими степенями свободы и в сплошных системах Резонанс сохраняет те же основные черты, что и в системе с двумя степенями свободы. Однако в этом случае, в отличие от систем с одной степенью свободы, существенную роль играет распределение внешнего воздействия по отдельным координатам. При этом возможны такие специальные случаи распределения внешнего воздействия, при которых, несмотря на совпадения частоты внешнего воздействия с одной из нормальных частот системы, Резонанс всё же не наступает. С энергетической точки зрения это объясняется тем, что между внешней силой и вынужденными колебаниями устанавливаются такие фазовые соотношения, при которых мощность, поступающая в систему от источника возбуждения по одной координате, равна мощности, отдаваемой системой источнику по другой координате. Пример этого — возбуждение вынужденных колебаний в струне, когда внешняя сила, совпадающая по частоте с одной из нормальных частот струны, приложена в точке, которая соответствует узлу скоростей для данного нормального колебания (например, сила, совпадающая по частоте с основным тоном струны, приложена у самого конца струны). При этих условиях (вследствие того, что внешняя сила приложена к неподвижной точке струны) эта сила не совершает работы, мощность от источника внешней силы в систему не поступает и сколько-нибудь заметного возбуждения колебаний струны не возникает, т. е. Резонанс не наблюдается.

Резонанс в колебательных системах, параметры которых зависят от состояния системы, т. е. в нелинейных системах, имеет более сложный характер, чем в системах линейных. Кривые Резонанс в нелинейных системах могут стать резко несимметричными, и явление Резонанс может наблюдаться при различных соотношениях частот воздействия и частот собственных малых колебаний системы (т. н. дробный, кратный и комбинационный Резонанс). Примером Резонанс в нелинейных системах может служить т. н. феррорезонанс, т. е. резонанс в электрической цепи, содержащей индуктивность с ферромагнитным сердечником, или ферромагнитный резонанс, представляющий собой явление, связанное с Резонанс элементарных (атомных) магнитов вещества при приложении высокочастотного магнитного поля (см. Радиоспектроскопия).

Если внешнее воздействие производит периодические изменение энергоёмких параметров колебательной системы (например, ёмкости в электрическом контуре), то при определённых соотношениях частот изменения параметра и собственной частоты свободных колебаний системы возможно параметрическое возбуждение колебаний, или параметрический Резонанс

Резонанс весьма часто наблюдается в природе и играет огромную роль в технике. Большинство сооружений и машин способны совершать собственные колебания, поэтому периодические внешние воздействия могут вызвать их Резонанс; например Резонанс моста под действием периодических толчков при прохождении поезда по стыкам рельсов, Резонанс фундамента сооружения или самой машины под действием не вполне уравновешенных вращающихся частей машин и т. д. Известны случаи, когда целые корабли входили в Резонанс при определённых числах оборотов гребного вала. Во всех случаях Резонанс приводит к резкому увеличению амплитуды вынужденных колебаний всей конструкции и может привести даже к разрушению сооружения. Это вредная роль Резонанс, и для устранения его подбирают свойства системы так, чтобы её нормальные частоты были далеки от возможных частот внешнего воздействия, либо используют в том или ином виде явление антирезонанса (применяют т. н. поглотители колебаний, или успокоители). В др. случаях Резонанс играет положительную роль, например: в радиотехнике Резонанс — почти единственный метод, позволяющий отделить сигналы одной (нужной) радиостанции от сигналов всех остальных (мешающих) станций.

Лит.: Стрелков С. П., Введение в теорию колебаний, 2 изд., М., 1964; Горелик Г. С., Колебания и волны, Введение в акустику, радиофизику и оптику 2 изд. М., 1959.

Рис. 1. Механическая колебательная система.

Рис. 5. Пример двух связанных электрических контуров.

C и индуктивности L.” href=”a_pictures/18/10/213268392.jpg”>C и индуктивности L.” title=”Рис. 2. Электрическая колебательная система с последовательными включением емкости C и индуктивности L.” src=”a_pictures/18/10/th_213268392.jpg”>
Рис. 2. Электрическая колебательная система с последовательными включением емкости C и индуктивности L.

Рис. 4. Электрическая колебательная система с включенными параллельно емкостью и индуктивностью.

Рис. 6. Резонансная кривая с двумя максимумами.

Рис. 3. Зависимость амплитуд смещений от частоты внешнего воздействия для различных значений b (b6 < b5 < … < b1).

Статья про слово “Резонанс” в Большой Советской Энциклопедии была прочитана 66051 раз

Интересное

bse.sci-lib.com

Примеры резонансов – Энциклопедия по машиностроению XXL

Г Т данном примере резонанс не наступил [c.478]

Пример резонанс в диэлектрическом цилиндре. В качестве примера рассмотрим задачу о диэлектрическом круге в вакууме. Собственные функции легко находятся в явном виде [c.97]

Другой, чрезвычайно важный, пример резонанса, понимаемого в широком смысле разгон ионов и электронов в циклотроне и синхротроне ) под действием магнитного поля (постоянного в циклотроне, плавно нарастающего в синхротроне) и синусоидального электрического поля, изменяющегося в подходящем темпе. [c.104]

Второй пример резонанс маятника под действием периодических толчков. Рассмотрим со спектральной точки зрения действие периодических толчков на маятник (гл. III, 4). Разложение в ряд Фурье силы /(i) имеет здесь вид, указанный в 2 (если исключить гармоники очень высокого номера — те, периоды которых сравнимы с длительностью толчка или меньше его). Результаты этого параграфа указывают, что резонанс наступает при значениях собственной частоты маятника равных ш, 2ш, Зш,… При каждой из этих настроек маятник совершает сильные колебания, весьма близкие к синусоидальным частотам ш, 2ш, Зш,. .. [c.507]

Хороший пример резонанса Ферми дает колебательный спектр как мы знаем, на основе классификации колебании к 4.4) у молеку- [c.107]

Второй возможный способ объяснения зависимости, изображенной на рис. 2.26 основывается на эффекте аэроакустического резонанса. Наиболее типичный пример такого эффекта — возбуждение клиновых тонов (рис. 3.27). [c.137]

Противоположный пример мы имеем в радиотехнике, где резонанс оказывается очень полезным и используется для отделения сигналов одной радиостанции от сигналов всех остальных (настройка приемника). [c.248]

До сих пор мы рассматривали системы, имеющие только одну степень свободы, и на примерах убедились в том, что основной характеристикой колебательной системы является частота ее собственных колебаний. В зависимости от частоты собственных колебаний определяется степень опасности возникновения резонанса и величина напряжений при вынужденных колебаниях. [c.475]

Вместе с тем раскачка системы возможна и в том случае, когда внешняя сила будет достигать максимума не в такт каждому отклонению, а через один, два, три такта. Следовательно, в параметрических колебаниях существует не одно резонансное состояние, а целый ряд состояний. Более детальное исследование вопроса показывает, что резонансное состояние наступает не только при точном выполнении указанных соотношений частот. Существуют целые области резонансных состояний. Ширина этих областей зависит от амплитуды параметрического воздействия (в рассматриваемом примере от величины Ро)- Наиболее существенным является резонанс при отношении [c.497]

Рассмотренная система с параметрическим возбуждением не является единственной в своем роде. Можно указать на целый ряд простых и сложных систем, в которых возможно возникновение параметрического резонанса. На рис. 558 показано три таких примера. [c.498]

В реальности всегда существуют силы сопротивления. Их роль в развитии резонанса проанализируем на примере осциллятора с вязким трением [c.235]

Где ш, е, п — постоянные параметры. Используем результаты предыдущего примера и проанализируем возможность появления резонанса для уравнения Мейсснера, аналогичного уравнению Матье [c.248]

Теперь мы можем воспользоваться критерием параметрического резонанса. Как и в примере 3.10.2, построим матрицу монодромии. Пусть решения у 1([c.252]

В соответствии с теоремой 3.10.2 изучим сначала условие резонанса ац + й22 > 2. Как и в примере 3.10.2, обозначим тх = Т2 = а. 2 2-Рассматриваемое условие резонанса принимает вид [c.253]

После сравнения полученных формул с аналогичными формулами примера 3.10.2 видим, что заштрихованные области на рис.3 10.1 вместе с их границей дают правильное представление об условиях резонанса и в рассматриваемом случае.С> [c.253]

Из приведенного примера видно, что параметрический резонанс возникает при некотором соотношении между периодом колебаний маятника Т и периодом возмущающей силы Т, Очевидно, это соотношение имеет следующий вид [c.309]

Обычный резонанс возникает при точном совпадении частоты свободных колебаний и частоты возмущающей силы, если полагать отсутствующими диссипативные силы. В случае параметрического резонанса существуют области частот возмущающей силы, при которых возникают явления резонанса. При этом из приведенного примера видно, что резонанс может возникнуть при частоте возмущающей силы, вдвое большей частоты свободных колебаний. [c.321]

Пример 90. Каков должен быть статический прогиб рессор железнодорожных вагонов для того, чтобы при скорости V = 16,7 м/с (приблизительно 60 км/час) и длине I каждого рельса в 12 м вагон не попадал в резонанс с толчками на стыках [c.81]

Пример 3. Устойчивость резонанса. Рассмотрим простейший линейный колебательный контур, на который действует возмущение, изменяющееся по гармоническому закону. Дифференциальное уравнение движения имеет вид [c.149]

Простейшим примером ядерного взаимодействия является сильное притяжение между нуклонами, находящимися на очень малых (10 см) расстояниях друг от друга внутри атомного ядра. В дальнейшем (часть третья) мы узнаем, что существуют и другие частицы (я- и /С-мезоны, гипероны, антинуклоны, антигипероны, квазичастицы, или резонансы), которые также участвуют в сильном ядерном взаимодействии. Переносчиками ядерного взаимодействия, т. е. ядерными квантами, являются я-ме-зоны (см. 79). [c.201]

Резонансный характер изменения сечения ядерной реакции при изменении кинетической энергии бомбардирующей частицы впервые был установлен именно на примере (а, р)-реакций на легких ядрах. Однако правильное объяснение механизма возникновения резонансов было дано Бором значительно позже (1936 г.). Это связано с тем, что ширина уровней и расстояние между ними для промежуточного ядра, образующегося в рассматриваемых реакциях, отличаются от соответствующих величин для реакций, идущих под действием медленных нейтронов на тяжелых ядрах, значительно большей величиной (Г 1 кэв, А 0,1 — 1 Мэе). [c.443]

Существует два основных метода выявления и исследования резонансов метод недостающей массы и метод эффективной массы. Рассмотрим их на примере реакций [c.280]

Рассмотрим в качестве примера параметрических колебаний стержень постоянного сечения, лежащий на упругом основании (рис. 7.29). Стержень нагружен осевой периодической силой. Требуется получить области главного параметрического резонанса методом Рэлея, ограничившись первым приближением (одночленным). Уравнение изгибных параметрических колебаний стержня имеет вид [c.230]

Пример 14.6. Определить, какова должна быть величина статического прогиба рессор железнодорожного вагона, чтобы при скорости вагона ло 40 м/с вагон не попадал в резонанс с толчками иа стыках рельсов. Длина рельса l=i2 м. [c.271]

Примеры. 48.1. Груз массы /и =0,5 кг, подвешенный на пружине, погружен в масло. На верхний конец пружины действует вынуждающая сила, изменяющаяся со временем по закону F = =0,98 sin (ut. Жесткость пружины k = 49 Н/м, а коэффициент сопротивления масла г = 0,5 кг/с. Найти частоту изменения вынуждающей силы, при которой возникает резонанс, н амплитуды колебания груза при резонансе. Определить амплитуду вынужденных колебаний груза при частоте изменения вынуждающей силы, вдвое большей и вдвое меньшей резонансной частоты. [c.192]

Когда требуется усилить один определенный тон, выгодно использовать явление резонанса. Для этого нужен такой излучатель, частота собственных колебаний которого равна частоте усиливаемого звука. Примером такого излучателя является резонансный ящик камертона. В том же случае, когда необходимо в равной мере усиливать различные звуки (например, звуки человеческой речи), нужно, наоборот, всячески избегать явлений резонанса. Только при этом возможно воспроизвести правильное соотношение амплитуд составляющих колебаний. Следовательно, для равномерного усиления различных звуков колебания мембраны должны быстро затухать, а частота ее собственных колебаний должна быть больше частоты воспроизводимых звуков. [c.236]

Несравненно большей точностью обладают методы, основанные на явлении ядерного магнитного, резонанса, состоящего в том,что спин ядра, находящегося в сильном постоянном магнитном поле, может опрокидываться под действием слабого высокочастотного поля определенной (резонансной) частоты. Для примера [c.51]

Даже в окрестности резонанса форма сечения может отличаться от брейт-вигнеровской (4.43). Это наблюдается в том случае, когда, например, наряду с резонансным рассеянием имеется большой фон нерезонансного рассеяния. Для примера на рис. 4.12 приведено сечение упругого рассеяния медленных нейтронов на ядре изотопа урана Асимметричная форма резонансных пиков есть [c.144]

В этом простом случае флаттер имеет характер резонанса. Возможно, простейшим примером резонанса является маятник, точка опоры которого продолжает совершать колебательное движение с частотой, равной частоте маятника. Легко доказать эксиернментальпо, что в этом случае маятник будет испытывать значительные колебания. Явление резонанса ловко используют люди, иредсказываюгцие с помогцью маятника скрытые процессы. Например, они предсказывают сугцество-вапие воды или руды под землей. Они настраивают маятник на частоту своего пульса, так что малейшее движение руки заставляет маятник колебаться со значительной амплитудой. Наш простой случай с флаттером основан па подобном же принципе. [c.163]

Преобразование к резонансным переменным — не единственный способ описания топологических изменений адиабатического инварианта вблизи резонанса. Имеется определенная свобода выбора инварианта, так как если / — инвариант невозмущенной системы, то и любая функция / (J) тоже инвариант. Выбирая йПси =0 вблизи резонансных значений J, можно учесть изменения в топологии возмущенной системы. Этот метод, разработанный Дуннетом и др. [111 ] (метод ДЛТ), описан в п. 2.4г и иллюстрируется на том же примере резонанса волна—частица. [c.122]

Некоторые формы собственных колебаний того и другого типов показаны на рис. 94 это—фотографии хладнле-вых фигур, полученных на вращающемся кон сном громкоговорителе с вертикально ориентированной осью==). Формы а и Ь соответствуют резонансам второго типа (следует обратить внимание на скопление порошка в центральной части диафрагмы, что свидетельствует о малости амплитуд катушки) форма I получается при более высокой частоте, нежели форма а. Форма с иллюстрирует одну из очень сложных конфигураций, получающихся при наложении радиальных и тангенциальных волн. Наконец, форма с1, наблюдаемая при достаточно высоких частотах, представляет пример резонанса первого типа с 8 узловыми кругами. [c.196]

Пример 15.4. На двух балках (рис. 538) установлен двигател ,, в котором имеется несбалансированная вращающаяся масса m(,g= 40 к Г). Радиус дисбаланса г = 0,1 см. Число оборотов массы н = 3000 оЩмин. Вес двигателя 180 кГ. Длина балок I = 1,5 м. В качестве профиля выбран швеллер К 12 (см. таблицу в приложениях). Для сечения каждой балки У ,. = 304 сж . Требуется произвести проверку на резонанс. [c.472]

Пример 164. Для определения коэффициента вязкости жидкости наблюдают колебания диска, подвешенного на упругой вертикальной проволоке в жидкости. К диску приложен переменный момент, равный /М sin (/ /) (УИ = onst), при котсором наблюдается явление резонанса. Момент сопротивления движению диска в жидкости равен S o, где р, — коэффициент вязкости жидкости, S — сумма площадей верхнего и нижнего оснований диска, ш — его угловая скорость. [c.348]

Реакция с ядрами gLi является исторически первой реакцией, осуществленной в 1932 г. Э. Уолтоном и Д. Кокрофтом с искусственно ускоренными протонами. В этой реакции наблюдается резонанс при энергии протонов 3 Мэе, что соответствует уровню энергии ядра 4Ве на высоте 19,8 Мэе. Третья из выписанных реакций является примером реакции с резко выраженными резонансами. Испускаемые при этом а-частицы по величине энергии можно подразделить на пять групп 8,12 Мэе-, 1,97 Мэе 1,21 Мэе и т. д. При испускании а-частиц с S -= 8,12 Мэе возникающее ядро оказывается в нормальном состоянии, при испускании же а-частиц с меньшей энергией ядро оказывается в возбужденном состоянии. [c.285]

Устойчивость 1шнейных автономных систем. Устойчивость резонанса. Примеры [c.142]

Рассмотрение частного случая. Рассмотрим в качестве примера соль СиС12-2НзО, свойства которой хорошо изучены и которая не представляег собой слишком сложный случай антиферромагнетизма. Решетка этой солп обладает орторомбической симметрией. В Лейдене были изучены намагниченность в постоянных п переменных магнитных полях [137, 138], теплоемкость [139], электронный резонанс [140, 141] п протонный резонанс [142, 143] этой соли. [c.412]

Если б мало по сравнению с единицей, то наибольшая амплитуда вынужденных колебаний во много раз превышает статическое отклонение Хо- Прослеженная нами на частном примере зависимость амплитуды вынужденных колебаний от соотношения между со и Шо оказывается характерной для так называемых резонансных аспектов, наблюдаемых при вынужденных колебаниях разнообразных колебательных систем. Возрастание амплитуд вынужденных колебаний в области, где ш близко к Шц, представляет собой наиболее типичную черту явмния резонанса. Кривые, подобные изображенной на рис. 388, называются амплитудными резонансными кривыми. [c.607]

Для вынужденных колебаний в линейной колебательной системе в области резонанса это сразу видно из полученных выше зависимостей амплитуды и фазы вынужденных колебаний от частоты виеншей силы (графики этих зависимостей приведены на рис. 388 и 389). Вследствие сильной зависимости амплитуды и фазы вынужденных колебаний от Частоты, соотношение между амплитудами и фазами разных гармоник в спектре внешней силы н в спектре вынужденных колебаний нарушается и форма вынужденных колебаний может очень существенно отличаться от формы внешней силы. Пример этого был приведен выше для маятника, раскачиваемого толчками, при малом затухании форма вынужденных колебаний будет близка к гармонической. [c.621]

Параметрические колебания возбуждаются в системе только при определенном соотношении между частотой изменения параметра систе.мы и частотой собственных колебаний системы, и в этом отношении они сходны с явлением резонанса.. В примере с маятником частота изменения его длины вдвое превышала частоту собственных колебаний, так как полупериоду колебания маятника еоответство-вал полный период изменения его длины. В примере с качелями частота изменения параметра также вдвое превышала частоту собственных колебаний системы. [c.192]

Ри была обнаружена промежуточная структура, а у ядер 230ХН и других — подбарьерные резонансы. Пример промежуточной структуры в сечении деления ядер вц приведен на рис. 40.2. Эти явления нашли объяснения в модели двугорбого барьера [3, 14]. В табл. 40.6 приведен ряд основных характеристик делящихся ядер при взаимодействии ззу с тепловыми нейт- [c.1093]

Резонанс напряжения на емкости с1макс С л получается при 7 =1 —1/2Q , т. е. при более низкой чем со,, частоте р, а резонанс напряжения на индуктивности ul макс при у = = 1/(1 — 1/2Q2), т. е. на более высокой чем щ частоте р. Все три максимума совпадают только при Qq- -oo (практически при Qo>10 )- На этом примере легко убедиться в том, что при небольших величинах добротности электрических колебательных контуров (Qn = 2 — 5) резонансные максимумы Ul, с, ur отличаются друг от друга по частоте на несколько процентов, что может быть весьма существенно при использовании таких систем в радиоизмерительных устройствах. [c.85]

Полученное уравнение является дифференциальным уравнением вынужденных колебаний. Общее решение соответствующего однородного уравнения Xi = А sin kt -j- а), а частное решение зависит от соотношения р и А . В примере р = к, т. е. ил1еем случай резонанса. Так как сопротивление отсутствует, то Х2 = = —[lit/ 2p)] os pt н общее решение принимает вид [c.140]

mash-xxl.info

Примеры резонанс – Я хотел бы узнать 3 примера резонанса из жизни, желательно с полным разяснением.

Примеры резонансных явлений