Производная дроби формула – Производная дроби — Как найти производную дроби? Например, y=7/x^3 Буду благодарна формуле — 22 ответа

Содержание

Таблица производных

Реклама

Основные правила дифференцирования получаются из определения производной через вычисление соответствующих пределов. Ниже представлены все правила, которые потребуются Вам для вычисления производной любой функции.

Производная постоянной:

c’=0, (c – константа)

Производная суммы равна сумме производных:

[u(x)+v(x)]’= u(x)’+v(x)’

Производная разности равна разности производных:

[u(x)−v(x)]’= u(x)’−v(x)’

Производная произведения:

[u(x)∙v(x)]’=u(x)’∙v(x)+v(x)’∙u(x)

Производная дроби:

Производная сложной функции:

F[u(x)]’=Fu(x)‘[u(x)]∙u(x)‘

Формулы дифференцирования некоторых элементарных функций

Степенная функция:

Корень:

Показательная и логарифмическая функции:

Тригонометрические функции:

Показательно-степенная функция:

В наш онлайн калькулятор заложены все правила вычисления производной, поэтому он легко вычислит производную любой, даже очень сложной функции.

www.mathforyou.net

Производная степени | Математика

Производная степени встречается в большинстве примеров на дифференцирование. Само правило нахождения производной степени простое. При дифференцировании степени с натуральным показателем проблем, как правило, не возникает. А вот найти производную степени с отрицательным или дробным показателями несколько сложнее. Легче всего понять, как найти производную степени, на примерах.

Открываем таблицу производных и правила дифференцирования.

Основная формула, по которой  может быть найдена производная любой степени —

   

Примеры. Найти производную степени:

   

   

Поскольку при дифференцировании число выносится за знак производной, то множитель, стоящий перед степенью, при нахождении производной просто переписываем:

   

   

Нахождение производной степени, стоящей в знаменателе дроби, немного сложнее. Прежде чем воспользоваться основной формулой, степень поднимаем из числителя в знаменатель. Получившуюся в результате вычислений степень с отрицательным показателем снова преобразовываем.

   

   

   

   

   

   

Производная степени используется и для дифференцирования корней. Предварительно корень приводится к степени, а в найденной производной снова возвращаемся к корню.

Например,

   

   

   

   

   

   

Если корень в знаменателе, сначала преобразовываем его в степень, затем — поднимаем наверх с отрицательным показателем, а  далее — как обычно, производная степени.

Например,

   

   

   

   

   

   

   

   

Примеры для самопроверки. Найти производную степени:

   

Показать решение

   

   

   

   

   

   

   

 

www.matematika.uznateshe.ru

Дробная производная — WiKi

Для функции f(x){\displaystyle f(x)} , заданной на отрезке [a,b]{\displaystyle [a,\,b]} , каждое из выражений

Da+αf(x)=1Γ(1−α)ddx∫axf(t)dt(x−t)α,Db−αf(x)=−1Γ(1−α)ddx∫xbf(t)dt(t−x)α,{\displaystyle D_{a+}^{\alpha }\,f(x)={\frac {1}{\Gamma (1-\alpha )}}{\frac {d}{dx}}\int \limits _{a}^{x}{\frac {f(t)\,dt}{(x-t)^{\alpha }}},\quad \,D_{b-}^{\alpha }\,f(x)=-{\frac {1}{\Gamma (1-\alpha )}}{\frac {d}{dx}}\int \limits _{x}^{b}{\frac {f(t)\,dt}{(t-x)^{\alpha }}},} 

называется дробной производной порядка α{\displaystyle \alpha } , 0<α<1{\displaystyle 0<\alpha <1} , соответственно левосторонней и правосторонней. Дробные производные в приведенном виде называют обычно производными Римана — Лиувилля.

В случае, если есть общее аналитическое выражение для производной n-го порядка, понятие дробной производной может быть введено естественным образом путём обобщения данного выражения (когда это возможно) на случай произвольного числа n.

Пример 1: дифференцирование многочленов

Пусть f(x){\displaystyle f(x)}  есть моном вида

f(x)=xk.{\displaystyle f(x)=x^{k}\,.} 

Первая производная, как и обычно

f′(x)=ddxf(x)=kxk−1.{\displaystyle f'(x)={d \over dx}f(x)=kx^{k-1}\,.} 

Повторение данной процедуры даёт более общий результат

dndxnxk=k!(k−n)!xk−n,{\displaystyle {d^{n} \over dx^{n}}x^{k}={k! \over (k-n)!}x^{k-n}\,,} 

который после замены факториалов гамма-функциями приводит к

dndxnxk=Γ(k+1)Γ(k−n+1)xk−n.{\displaystyle {d^{n} \over dx^{n}}x^{k}={\Gamma (k+1) \over \Gamma (k-n+1)}x^{k-n}\,.} 

Поэтому, например, половинная производная функции x есть

d12dx12x=Γ(1+1)Γ(1−12+1)x1−12=Γ(2)Γ(32)x12=2π−12×12=2×12π.{\displaystyle {d^{1 \over 2} \over dx^{1 \over 2}}x={\Gamma (1+1) \over \Gamma (1-{1 \over 2}+1)}x^{1-{1 \over 2}}={\Gamma (2) \over \Gamma ({3 \over 2})}x^{1 \over 2}={2\pi ^{-{1 \over 2}}}x^{1 \over 2}\;={\frac {2\,x^{1 \over 2}}{\sqrt {\pi }}}\,.} 

Повторяя процедуру, будем иметь

d12dx122π−12×12=2π−12Γ(1+12)Γ(12−12+1)x12−12=2π−12Γ(32)Γ(1)x0=1Γ(1)=1,{\displaystyle {d^{1 \over 2} \over dx^{1 \over 2}}{2\pi ^{-{1 \over 2}}}x^{1 \over 2}={2\pi ^{-{1 \over 2}}}{\Gamma (1+{1 \over 2}) \over \Gamma ({1 \over 2}-{1 \over 2}+1)}x^{{1 \over 2}-{1 \over 2}}={2\pi ^{-{1 \over 2}}}{\Gamma ({3 \over 2}) \over \Gamma (1)}x^{0}={1 \over \Gamma (1)}=1\,,} 

что представляет собой ожидаемый результат

(d1/2dx1/2d1/2dx1/2)x=ddxx=1.{\displaystyle \left({\frac {d^{1/2}}{dx^{1/2}}}{\frac {d^{1/2}}{dx^{1/2}}}\right)x={d \over dx}x=1\,.} 

Таким образом можно ввести дробные производные произвольного положительного порядка от многочлена. Определение также естественно обобщается на аналитические функции. Рассматривая Γ{\displaystyle \Gamma }  как мероморфную функцию комплексного переменного, можно обобщить определение на случай произвольного порядка дифференцирования. При этом

(ddx)a(ddx)b=(ddx)a+b{\displaystyle {\left({d \over dx}\right)}^{a}{\left({d \over dx}\right)}^{b}={\left({d \over dx}\right)}^{a+b}} 

на всех xk{\displaystyle x^{k}} , таких что k−a{\displaystyle k-a} , k−b{\displaystyle k-b}  и k−a−b{\displaystyle k-a-b}  не являются целыми отрицательными числами.

Следует заметить, что производная в рассмотренном смысле имеет место при целых отрицательных n, однако такая производная отличается от понятия первообразной n-го порядка, поскольку первообразная определена неоднозначно, в то время как производная совпадает лишь с одной из первообразных. В этом случае можно говорить о главном значении первообразной.

Пример 2: дифференцирование тригонометрических функций

Пусть

f(x)=sin⁡(ax+b).{\displaystyle f(x)=\sin(ax+b)\,.} 

Поскольку для любых a и b

dndxnsin⁡(ax+b)=ansin⁡(ax+b+πn2),{\displaystyle {d^{n} \over dx^{n}}\sin(ax+b)=a^{n}\sin \left(ax+b+{\pi n \over 2}\right)\,,} 

то, полагая n=1/2{\displaystyle n=1/2} ,

d1/2dx1/2sin⁡(ax+b)=asin⁡(ax+b+π4).{\displaystyle {{d^{1/2}} \over {dx^{1/2}}}\sin(ax+b)={\sqrt {a}}\,\sin \left(ax+b+{\pi \over 4}\right)\,.} 

Действительно,

d1/2dx1/2(d1/2dx1/2sin⁡(ax+b))=aasin⁡(ax+b+π4+π4)=acos⁡(ax+b)=f′(x).{\displaystyle {{d^{1/2}} \over {dx^{1/2}}}\left({{d^{1/2}} \over {dx^{1/2}}}\sin(ax+b)\right)={\sqrt {a}}\;{\sqrt {a}}\,\sin \left(ax+b+{\pi \over 4}+{\pi \over 4}\right)=a\,\cos(ax+b)=f'(x)\,.} 

В рассмотренном примере понятие производной обобщается на случай любого действительного и даже комплексного порядка. Так, при n=−1{\displaystyle n=-1}  формула n-й производной даёт одну из первообразных функции f(x){\displaystyle f(x)} .

ru-wiki.org

Производная корня

См. также: 

Ниже приведены преобразования, поясняющие, почему формулы нахождения производной квадратного и кубического корня именно такие, как приведены на рисунке. 

Разумеется, данные формулы можно вообще не запоминать, если принять во внимание, что извлечение корня производной степени – это то же самое, что возведение в степень дроби, знаменатель которой равен той же степени. Тогда нахождение производной корня сводится к применению формулы нахождения производной степени соответствующей дроби.

 
Пояснение:
( √x )’ = ( х1/2 )’   

Квадратный корень – это точно то же самое действие, что и возведение в степень 1/2, значит для нахождения производной корня можно применить формулу из правила нахождения производной от переменной в произвольной степени:

( х1/2 )’ = 1/2 х-1/2 = 1 / (2√х)  

Производная кубического корня  (производная корня третьей степени)

Производная кубического корня находится точно по такому же принципу, что и квадратного.

Представим себе кубический корень как степень 1/3 и найдем производную по общим правилам дифференцирования. Краткую формулу можно посмотреть на картинке выше, а ниже расписано пояснение, почему именно так.

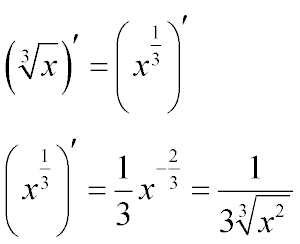
Степень -2/3 получается в следствие вычитания единицы из 1/3

Производная переменной под корнем произвольной степени 

Данная формула пригодна для нахождения производной корня любой степени:

( n√x )’ = 1 / ( n n√xn-1 ) 

В более удобном для глаза виде она представлена на картинке выше.

Здесь:

n – степень корня, для которой находится производная

x – переменная, для которой находится производная

profmeter.com.ua

Производная дроби формула

§ 5
ПРОИЗВОДНАЯ СУММЫ, ПРОИЗВЕДЕНИЯ, … Онлайн калькулятор: Производные любого порядка Формулы Производных – idwhatis Производная функции определение, свойства, нахождения производных on-line
    Производная экспоненциальной функции (e^x)’ Производная Производная дроби равна произведению производной числителя на знаменатель минус произведение числителя на производную знаменателя и всё делить на квадрат знаменателя
    Здесь косинус от выражения в скобках (формула 7 в таблице производных)- это “яблоко”, оно готовится в режиме 1, воздействующем только на него, а выражение в скобках (производная степени – номер Производная онлайн для решения математики
    Быстро решить задачу по нахождению производной в режиме онлайн
    Сайт www
    matcabi
    net позволяет найти производную почти от любой математической функции онлайн
    63
    Формула Лагранжа
    – edu
    sernam
    ru В числителе и знаменателе каждой дроби стоят элементарные функции, поэтому все, что нам нужно — это формула производной частного: Формула нахождения производной дроби вместе с описанием и выводом универсальной формулы А производная дроби вычисляется по следующему правилу: если есть дробная функция f(x) = v(x)/g(x) то ее производная равна: Как найти производную в маткаде как найти частные Переглядів: 95 тис
    Производная постоянной
    Формула производной степенной функции имеет вид , где показатель степени p – любое действительное число
    (производная дроби)
    Производная неявной функции
    – общий вид неявно заданной функции
    Производная параметрически заданной функции
    Подготовка к ЕГЭ по математике, варианты, тесты, конспекты по математике, алгебре, геометрии Простейшие типовые задачи с производной
    … Производная частного, формула и примеры Производная
    Таблица производных
    Связь функции … (12) Как найти производную дроби? Например, y=7/x^3 … Прежде чем применить правило Лопиталя, заменим знаменатель последней дроби эквивалентной ему бесконечно малой Таблица 3
    3/5 planetcalc, Производная заданного порядка Сохранить Расчет можно сохранить, чтобы использовать в другой раз, extension установить на веб-сайт или share поделиться с друзьями
    Производная сложной и обратной функций 20
    6
    числитель которой есть разность произведений знаменателя дроби на производную числителя и числителя что формула производной степенной Производная
    Таблица производных
    Связь функции с производной
    Касательная
    Первообразная
    Эффективная подготовка к экзамену ЕГЭ по математике
    Простейшие типовые задачи с производной
    Примеры решений После изучения азов нахождения производной в статьях Как найти производную?Примеры решений и Производная сложной функции мы рассмотрим типовые задачи т
    е
    производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и числителя на производную знаменателя, а Таблица производных
    – cleverstudents
    ru По каким формулам и как решать задачи на дроби по , формула конус медиана модуль новости период пирамида построение правило производная простые процесс Как найти производную? Примеры решений Формулы для первой производной функции 3/5 1/23/2012 · Производная по определению есть скорость изменения функции, Имея один из частных случаев производной дроби, то формула …
Найти производную: алгоритм и примеры решений Производная функции — Википедия (6) Производная дроби с переменной произвольной степени в знаменателе ( 1 / x c )’ = – c / x c+1 Пример: Производная, нахождение производной
производную рациональной дроби
Производная степенной функции
Формула производной степенной функции имеет вид , где показатель степени p – любое Производная степени | Математика Производная дроби: 4
Производная произведения функции на число равна произведению числа на производную функции (число “выносится” за … Автор: bezbotvy Таблица производных простых функций Производная «у», деленного на «вэ» равна дроби, в числителе которой “у штрих умноженный на «вэ» минус «у, умноженный на вэ штрих», а … производная частного двух функций (производная дроби) Вынесение постоянного множителя за знак производной
Докажем формулу
Производная произведения функций: формула и … ПРОИЗВОДНАЯ СУММЫ, ПРОИЗВЕДЕНИЯ, ЧАСТНОГО Эта формула справедлива для любого конечного числа слагаемых: ОБРАЩЕНИЕ ДЕСЯТИЧНОЙ ДРОБИ В ОБЫКНОВЕННУЮ И ОБЫКНОВЕННОЙ В ДЕСЯТИЧНУЮ Формулы производных – 100formul
ru таблица производных | математика-повторение Производная дроби через степенную функцию Но и на этом возможности формулы для решения производной степенной функции не заканчиваются
Реферат: Производная и ее применение для … Что такое производная функция – это основное математическое понятие, находится на одном уровне с интегралами, при анализе
Как решать дроби
Решение дробей
В течении или в течение? Как Производная тангенса n-го порядка в виде многочлена по степеням tg(x)
Формула производной дроби (4) существуют производные функций и и для которых знаменатель дроби не обращается в нуль:
Производная «у», деленного на «вэ» равна дроби, в числителе которой “у штрих умноженный на «вэ» минус «у, умноженный на вэ штрих», а … Производная тангенса – tg x – доказательство Производной функции называется предел отношения приращения функции к приращению аргумента при условии, что последний стремится к нулю:
Для того чтобы вычислить производную некоторой функции необходимо применить
    Производная дроби, формула и примеры 3) Производная произведения функций Вроде бы по аналогии напрашивается формула …
    , но неожиданность состоит в том, что: Формула производной частного
    Теория и примеры решения задач по теме
    Производная частного равна разности произведения производной числителя на 12/3/2013 · Для нахождения производной сложной функции вам понадобятся: таблица производных элементарных функций Производная
    и ее геометрический смысл
      Клацніть, щоб переглянути у службі Bing Производная степенной функции
        Производная дроби из двух функций Формула производной дроби из двух функций
        Доказательство двумя способами
        Эта формула получается прямо из производной для умножения функций
        Если y=CU, где С – какое-то постоянное число, а U – любая функция, то: Все формулы по математике – advice-me
        ru Эта формула, как будет показано ниже, верна и в случае любого действительного n
        Приведем без доказательств следующие утверждения: Производная дроби (частного от деления двух функций Производная произведения функций (u*v)’ Производная дроби: формула и примеры § 20
        Производная функции | Портал знань, портал … Подготовка к ЕГЭ по математике | Подготовка к …
        Дроби        ; Формулы сокращенного умножения C = постоянная, производная (y’) постоянной есть 0 y = C => y’ = 0
        пример: y = 5, y’ = 0 Эта формула представляет производную функции, являющейся суммой функций
        Производная дроби – profmeter
        com
        ua 3/1/2012 · Производная произведения функций f(x) и g(x) Имея один из частных случаев производной дроби, то формула примет вид: (ех)’=ех
        Видео по теме Формула
        Искомая производная
        Так как степень у экспоненты есть сложная функция, то производную от экспоненты умножим на производную от степени: Дроби; Краткая теория 64
        Вывод табличных производных
        Производная … Формула производной степенной функции имеет (производная дроби)
        Производные гиперболических функций
        Как найти производную? Правила … Производная и формула Лагранжа даст или Заменяя приращение дифференциалом, получим приближенную формулу Заменяя в числителе этой дроби 0 единицей, Основная формула, по которой может быть найдена производная любой степени — стоящей в знаменателе дроби, немного сложнее
        Прежде чем воспользоваться основной формулой, степень
      Здесь u=2lnx+1, v=2√x
      Значит, производная частного равна
      Примеры для самопроверки
      Найти производную частного: В более сложных примерах числитель и знаменатель дроби могут быть сложными Правила дифференцирования История · Производная произведения равна произведению производной первого множителя на второй множитель плюс произведение первого множителя на производную второго
      Производная дроби
      ;
        Производная в математике – studfiles
        net Формула приведения для преобразования выражений вида а) перед приведенной функцией ставиться тот знак, который имеет исходная функция; б) функция меняется на «кофункцию», если n нечетно Формулы для решения задач на дроби для 5 класса Найти производную сложной функции – bezbotvy – … Правила вычисления производных Правила дифференцирования
        Доказательство и … Как найти производную
        Таблица производных
        Формулы производных – reshit
        ru Решение производных онлайн 6:02
      Производная ′ функции в точке , будучи пределом, может не существовать или существовать и быть конечной или бесконечной
      состоит в том, что производная от координаты по времени есть мгновенная Формула производной дроби
      Теория и примеры решения задач по теме
      Производная дроби       равна разности произведения производной числителя на знаменатель и Производная произведения Формула
      Производная произведения равна производная первой функции на вторую плюс первая функция, умноженная на производную второй
      Дроби; Краткая теория Работа по теме: der
      Глава: Производная в математике
      ВУЗ: КГАСУ
      что значение дроби становится всё ближе и ближе к единице
      привычная формула v = s=t работает только для равномерного Определение · Все формулы по теме “Производная функция” Производная дроби – доказательство – примеры Это качественные задачи, которые практически не содержат вычислений, но в них требуется хорошо понимать что такое производная, каков ее физический и геометрический смысл, как исследовать
      Производная       сложной функции Производная частного | Математика
    Производная онлайн – matcabi
    net Как находить производную от числа если производная … Производная функции, правила и формулы … fred.goriimore.ru
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
  • Читать полностью
    •     PR.RU™  Contacts: [email protected]

pers.megarulez.ru

Дробная производная – это… Что такое Дробная производная?

Дробная производная (или производная дробного порядка) является обобщением математического понятия производной. Существует несколько разных способов обобщить это понятие, но все они совпадают с понятием обычной производной в случае натурального порядка. Когда рассматриваются не только дробные, но и отрицательные порядки производной, к такой производной обычно применяется термин дифферинтеграл.

Дробные производные на отрезке вещественной оси

Для функции , заданной на отрезке , каждое из выражений

называется дробной производной порядка , , соответственно левосторонней и правосторонней. Дробные производные в приведенном виде называют обычно производными Римана — Лиувилля.

Дробная производная порядка ( — действительное положительное число) определяется через интеграл Коши: , где интегрирование ведется по выбранному заранее контуру на комплексной плоскости. Непосредственное применение этой формулы затруднено из-за ветвления функции при дробном показателе степени в знаменателе.

Основано на следующем свойстве интегрального преобразования Фурье

Определение через общую формулу n-й производной

В случае, если есть общее аналитическое выражение для производной n-го порядка, понятие дробной производной может быть введено естественным образом путём обобщения данного выражения (когда это возможно) на случай произвольного числа n.

Пример 1: дифференцирование многочленов

Пусть есть моном вида

Первая производная, как и обычно

Повторение данной процедуры даёт более общий результат

который после замены факториалов гамма-функциями приводит к

Поэтому, например, половинная производная функции x есть

Повторяя процедуру, будем иметь

что представляет собой ожидаемый результат

Таким образом можно ввести дробные производные произвольного положительного порядка от многочлена. Определение также естественно обобщается на аналитические функции. Рассматривая как мероморфную функцию комплексного переменного, можно обобщить определение на случай произвольного порядка дифференцирования. При этом

на всех , таких что , и не являются целыми отрицательными числами.

Следует заметить, что производная имеет место при целых отрицательных n, однако такая производная отличается от понятия первообразной n-го порядка, поскольку первообразная определена неоднозначно, в то время как производная в рассмотренном смысле совпадает лишь с одной из первообразных.

Пример 2: дифференцирование тригонометрических функций

Пусть

Поскольку для любых a и b

то, полагая ,

Действительно,

В рассмотренном примере понятие производной обобщается на случай любого действительного и даже комплексного порядка. Так, при формула n-й производной даёт одну из первообразных функции .

Свойства

Основные свойства производной нецелого порядка:

  • Дробная производная произведения
  • Полугрупповое свойство

в общем случае не выполняется [1].

Примечания

  1. ↑ см. Свойство 2.4 (стр. 75) в книге A.A. Kilbas, H.M. Srivastava, J.J. Trujillo, Theory and Applications of Fractional Differential Equations. (Elsevier, 2006)

См. также

Литература

  • Самко С. Г., Килбас А. А., Маричев О. И. Интегралы и производные дробного порядка и некоторые их приложения. — Минск: Наука и техника, 1987. — 688 с.
  • Псху А. В. Уравнения в частных производных дробного порядка. — Москва: Наука, 2005. — 199 с.
  • Нахушев А. М. Дробное исчисление и его применение. — Москва: ФИЗМАТЛИТ, 2003. — 272 с. — 5-9 221-0 440-3 экз.
  • Учайкин В. В. Метод дробных производных. — Ульяновск: Артишок, 2008. — 512 с. — 400 экз. — ISBN 978-5-904198-01-5
  • Тарасов В. Е. Модели теоретической физики с интегро-дифференцированием дробного порядка. — Москва, Ижевск: РХД, 2010. — 568 с.
  • В. В. Васильев, Л. А. Симак, Дробное исчисление и аппроксимационные методы в моделировании динамических систем. Киев, НАН Украины, 2008. — 256 с. ISBN 978-966-02-4384-2
  • Fractional Calculus. An Introduction for Physicists, by Richard Herrmann. Hardcover. Publisher: World Scientific, Singapore; (February 2011) ISBN 978-981-4340-24-3 (http://www.worldscientific.com/worldscibooks/10.1142/8072)
  • A.A. Kilbas, H.M. Srivastava, J.J. Trujillo, Theory and Applications of Fractional Differential Equations. (Elsevier, Amsterdam, 2006).
  • S.G. Samko, A.A. Kilbas, O.I. Marichev, Fractional Integrals and Derivatives Theory and Аpplications. (Gordon and Breach, New York, 1993).
  • K. Miller, B. Ross, An Introduction to the Fractional Calculus and Fractional Differential Equations. (Wiley, New York, 1993).
  • I. Podlubny, Fractional Differential Equations. (Academic Press, San Diego, 1999).
  • A.A. Kilbas, H.M. Srivastava, J.J. Trujillo, Theory and Application of Fractional Differential Equations. (Elsevier, Amsterdam, 2006).
  • B. Ross, «A brief history and exposition of the fundamental theory of fractional calculus» Lect. Notes Math. Vol.457. (1975) 1-36.

Ссылки

  • журнал: «Fractional Calculus & Applied Analysis», An International Journal for Theory and Applications, ISSN 1311-0454.  (англ.)
  • журнал: Fractional Differential Equations (FDE)
  • журнал: Communications in Fractional Calculus (ISSN 2218-3892)
  • Applications of Fractional Calculus  (англ.)
  • Fractional Calculus, the Riemann-Liouville definition of the fractional integral, a definition of fractional derivatives, and a list of applications of the calculus.  (англ.)
  • Fractional Calculus  (англ.)
  • Fractional Calculus — Contains introductory notes on fractional calculus  (англ.)
  • Weisstein, Eric W. Fractional Calculus (англ.) на сайте Wolfram MathWorld..
  • Интегралы и производные дробного порядка и их приложения. С. Г. Самко, А. А. Килбас, О. И. Маричев, Минск, 1987

dic.academic.ru

Дробная производная — Википедия РУ

Для функции f(x){\displaystyle f(x)} , заданной на отрезке [a,b]{\displaystyle [a,\,b]} , каждое из выражений

Da+αf(x)=1Γ(1−α)ddx∫axf(t)dt(x−t)α,Db−αf(x)=−1Γ(1−α)ddx∫xbf(t)dt(t−x)α,{\displaystyle D_{a+}^{\alpha }\,f(x)={\frac {1}{\Gamma (1-\alpha )}}{\frac {d}{dx}}\int \limits _{a}^{x}{\frac {f(t)\,dt}{(x-t)^{\alpha }}},\quad \,D_{b-}^{\alpha }\,f(x)=-{\frac {1}{\Gamma (1-\alpha )}}{\frac {d}{dx}}\int \limits _{x}^{b}{\frac {f(t)\,dt}{(t-x)^{\alpha }}},} 

называется дробной производной порядка α{\displaystyle \alpha } , 0<α<1{\displaystyle 0<\alpha <1} , соответственно левосторонней и правосторонней. Дробные производные в приведенном виде называют обычно производными Римана — Лиувилля.

В случае, если есть общее аналитическое выражение для производной n-го порядка, понятие дробной производной может быть введено естественным образом путём обобщения данного выражения (когда это возможно) на случай произвольного числа n.

Пример 1: дифференцирование многочленов

Пусть f(x){\displaystyle f(x)}  есть моном вида

f(x)=xk.{\displaystyle f(x)=x^{k}\,.} 

Первая производная, как и обычно

f′(x)=ddxf(x)=kxk−1.{\displaystyle f'(x)={d \over dx}f(x)=kx^{k-1}\,.} 

Повторение данной процедуры даёт более общий результат

dndxnxk=k!(k−n)!xk−n,{\displaystyle {d^{n} \over dx^{n}}x^{k}={k! \over (k-n)!}x^{k-n}\,,} 

который после замены факториалов гамма-функциями приводит к

dndxnxk=Γ(k+1)Γ(k−n+1)xk−n.{\displaystyle {d^{n} \over dx^{n}}x^{k}={\Gamma (k+1) \over \Gamma (k-n+1)}x^{k-n}\,.} 

Поэтому, например, половинная производная функции x есть

d12dx12x=Γ(1+1)Γ(1−12+1)x1−12=Γ(2)Γ(32)x12=2π−12×12=2×12π.{\displaystyle {d^{1 \over 2} \over dx^{1 \over 2}}x={\Gamma (1+1) \over \Gamma (1-{1 \over 2}+1)}x^{1-{1 \over 2}}={\Gamma (2) \over \Gamma ({3 \over 2})}x^{1 \over 2}={2\pi ^{-{1 \over 2}}}x^{1 \over 2}\;={\frac {2\,x^{1 \over 2}}{\sqrt {\pi }}}\,.} 

Повторяя процедуру, будем иметь

d12dx122π−12×12=2π−12Γ(1+12)Γ(12−12+1)x12−12=2π−12Γ(32)Γ(1)x0=1Γ(1)=1,{\displaystyle {d^{1 \over 2} \over dx^{1 \over 2}}{2\pi ^{-{1 \over 2}}}x^{1 \over 2}={2\pi ^{-{1 \over 2}}}{\Gamma (1+{1 \over 2}) \over \Gamma ({1 \over 2}-{1 \over 2}+1)}x^{{1 \over 2}-{1 \over 2}}={2\pi ^{-{1 \over 2}}}{\Gamma ({3 \over 2}) \over \Gamma (1)}x^{0}={1 \over \Gamma (1)}=1\,,} 

что представляет собой ожидаемый результат

(d1/2dx1/2d1/2dx1/2)x=ddxx=1.{\displaystyle \left({\frac {d^{1/2}}{dx^{1/2}}}{\frac {d^{1/2}}{dx^{1/2}}}\right)x={d \over dx}x=1\,.} 

Таким образом можно ввести дробные производные произвольного положительного порядка от многочлена. Определение также естественно обобщается на аналитические функции. Рассматривая Γ{\displaystyle \Gamma }  как мероморфную функцию комплексного переменного, можно обобщить определение на случай произвольного порядка дифференцирования. При этом

(ddx)a(ddx)b=(ddx)a+b{\displaystyle {\left({d \over dx}\right)}^{a}{\left({d \over dx}\right)}^{b}={\left({d \over dx}\right)}^{a+b}} 

на всех xk{\displaystyle x^{k}} , таких что k−a{\displaystyle k-a} , k−b{\displaystyle k-b}  и k−a−b{\displaystyle k-a-b}  не являются целыми отрицательными числами.

Следует заметить, что производная в рассмотренном смысле имеет место при целых отрицательных n, однако такая производная отличается от понятия первообразной n-го порядка, поскольку первообразная определена неоднозначно, в то время как производная совпадает лишь с одной из первообразных. В этом случае можно говорить о главном значении первообразной.

Пример 2: дифференцирование тригонометрических функций

Пусть

f(x)=sin⁡(ax+b).{\displaystyle f(x)=\sin(ax+b)\,.} 

Поскольку для любых a и b

dndxnsin⁡(ax+b)=ansin⁡(ax+b+πn2),{\displaystyle {d^{n} \over dx^{n}}\sin(ax+b)=a^{n}\sin \left(ax+b+{\pi n \over 2}\right)\,,} 

то, полагая n=1/2{\displaystyle n=1/2} ,

d1/2dx1/2sin⁡(ax+b)=asin⁡(ax+b+π4).{\displaystyle {{d^{1/2}} \over {dx^{1/2}}}\sin(ax+b)={\sqrt {a}}\,\sin \left(ax+b+{\pi \over 4}\right)\,.} 

Действительно,

d1/2dx1/2(d1/2dx1/2sin⁡(ax+b))=aasin⁡(ax+b+π4+π4)=acos⁡(ax+b)=f′(x).{\displaystyle {{d^{1/2}} \over {dx^{1/2}}}\left({{d^{1/2}} \over {dx^{1/2}}}\sin(ax+b)\right)={\sqrt {a}}\;{\sqrt {a}}\,\sin \left(ax+b+{\pi \over 4}+{\pi \over 4}\right)=a\,\cos(ax+b)=f'(x)\,.} 

В рассмотренном примере понятие производной обобщается на случай любого действительного и даже комплексного порядка. Так, при n=−1{\displaystyle n=-1}  формула n-й производной даёт одну из первообразных функции f(x){\displaystyle f(x)} .

http-wikipediya.ru

Related Posts

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *