Реферат история появления алгебры как науки – ,
- Реферат – Математика как наука. История развития и становления
- Урок-конференция на тему: История развития алгебры
- История появления алгебры как науки
- Реферат по алгебре ученицы Храмцовой Ольги на тему История возникновения алгебры (7 класс)
- Но главное не в этом. Два достижения греческой математики далеко пережили своих творцов. Первое — греки построили математику как целостную науку с собственной методологией, основанной на чётко сформулированных законах логики.
- Второе — они провозгласили, что законы природы постижимы для человеческого разума, и математические модели — ключ к их познанию.
- Реферат по алгебре ученицы Храмцовой Ольги на тему – История возникновения алгебры – (7 класс)
- Но главное не в этом. Два достижения греческой математики далеко пережили своих творцов. Первое — греки построили математику как целостную науку с собственной методологией, основанной на чётко сформулированных законах логики.
- Второе — они провозгласили, что законы природы постижимы для человеческого разума, и математические модели — ключ к их познанию.
Реферат – Математика как наука. История развития и становления
Математика как наука. История развития и становления
Самой древней математической деятельностью был счет. Счет был необходим, чтобы следить за поголовьем скота и вести торговлю. Некоторые первобытные племена подсчитывали количество предметов, сопоставляя им различные части тела, главным образом пальцы рук и ног. Наскальный рисунок, сохранившийся до наших времен от каменного века, изображает число 35 в виде серии выстроенных в ряд 35 палочек-пальцев. Первыми существенными успехами в арифметике стали концептуализация числа и изобретение четырех основных действий: сложения, вычитания, умножения и деления. Первые достижения геометрии связаны с такими простыми понятиями, как прямая и окружность. Дальнейшее развитие математики началось примерно в 3000 до н. э. благодаря вавилонянам и египтянам.
^ Вавилония и Египет
Вавилония
Источником наших знаний о вавилонской цивилизации служат хорошо сохранившиеся глиняные таблички, покрытые т. н. клинописными текстами, которые датируются от 2000 до н. э. и до 300 н. э. Математика на клинописных табличках в основном была связана с ведением хозяйства. Арифметика и нехитрая алгебра использовались при обмене денег и расчетах за товары, вычислении простых и сложных процентов, налогов и доли урожая, сдаваемой в пользу государства, храма или землевладельца. Многочисленные арифметические и геометрические задачи возникали в связи со строительством каналов, зернохранилищ и другими общественными работами. Очень важной задачей математики был расчет календаря, поскольку календарь использовался для определения сроков сельскохозяйственных работ и религиозных праздников. Деление окружности на 360, а градуса и минуты на 60 частей берут начало в вавилонской астрономии.
Вавилоняне создали и систему счисления, использовавшую для чисел от 1 до 59, основание 10. Символ, обозначавший единицу, повторялся нужное количество раз для чисел от 1 до 9. Для обозначения чисел от 11 до 59 вавилоняне использовали комбинацию символа числа 10 и символа единицы. Для обозначения чисел, начиная с 60 и больше, вавилоняне ввели позиционную систему счисления с основанием 60. Существенным продвижением стал позиционный принцип, согласно которому один и тот же числовой знак (символ) имеет различные значения в зависимости от того места, где он расположен. Примером могут служить значения шестерки в записи (современной) числа 606. Однако нуль в системе счисления древних вавилонян отсутствовал, из-за чего один и тот же набор символов мог означать и число 65 (60 + 5), и число 3605 (602+ 0 + 5). Возникали неоднозначности и в трактовке дробей. Например, одни и те же символы могли означать и число 21, и дробь 21/60 и (20/60 + 1/602). Неоднозначность разрешалась в зависимости от конкретного контекста.
Вавилоняне составили таблицы обратных чисел (которые использовались при выполнении деления), таблицы квадратов и квадратных корней, а также таблицы кубов и кубических корней. Им было известно приближение числа. Клинописные тексты, посвященные решению алгебраических и геометрических задач, свидетельствуют о том, что они пользовались квадратичной формулой для решения квадратных уравнений и могли решать некоторые специальные типы задач, включавших до десяти уравнений с десятью неизвестными, а также отдельные разновидности кубических уравнений и уравнений четвертой степени. На глиняных табличках запечатлены только задачи и основные шаги процедур их решения. Так как для обозначения неизвестных величин использовалась геометрическая терминология, то и методы решения в основном заключались в геометрических действиях с линиями и площадями. Что касается алгебраических задач, то они формулировались и решались в словесных обозначениях.
Около 700 до н. э. вавилоняне стали применять математику для исследования движений Луны и планет. Это позволило им предсказывать положения планет, что было важно как для астрологии, так и для астрономии.
В геометрии вавилоняне знали о таких соотношениях, например, как пропорциональность соответствующих сторон подобных треугольников. Им была известна теорема Пифагора и то, что угол, вписанный в полуокружность, — прямой. Они располагали также правилами вычисления площадей простых плоских фигур, в том числе правильных многоугольников, и объемов простых тел. Число пи вавилоняне считали равным 3.
Египет
Наше знание древнеегипетской математики основано, главным образом, на двух папирусах, датируемых примерно 1700 до н. э. Излагаемые в этих папирусах математические сведения восходят к еще более раннему периоду — ок. 3500 до н. э. Египтяне использовали математику, чтобы вычислять вес тел, площади посевов и объемы зернохранилищ, размеры податей и количество камней, требуемое для возведения тех или иных сооружений. В папирусах можно найти также задачи, связанные с определением количества зерна, необходимого для приготовления заданного числа кружек пива, а также более сложные задачи, связанные с различием в сортах зерна; для этих случаев вычислялись переводные коэффициенты.
Но главной областью применения математики была астрономия, точнее, расчеты, связанные с календарем. Календарь использовался для определения дат религиозных праздников и предсказания ежегодных разливов Нила. Однако уровень развития астрономии в Древнем Египте намного уступал уровню ее развития в Вавилоне.
Древнеегипетская письменность основывалась на иероглифах. Система счисления того периода также уступала вавилонской. Египтяне пользовались непозиционной десятичной системой, в которой числа от 1 до 9 обозначались соответствующим числом вертикальных черточек, а для последовательных степеней числа 10 вводились индивидуальные символы. Последовательно комбинируя эти символы, можно было записать любое число. С появлением папируса возникло так называемое иератическое письмо-скоропись, способствовавшее, в свою очередь, появлению новой числовой системы. Для каждого из чисел от 1 до 9 и для каждого из первых девяти кратных чисел 10, 100 и т. д. использовался специальный опознавательный символ. Дроби записывались в виде суммы дробей с числителем, равным единице. С такими дробями египтяне производили все четыре арифметические операции, но процедура таких вычислений оставалась очень громоздкой.
Геометрия у египтян сводилась к вычислениям площадей прямоугольников, треугольников, трапеций, круга, а также формулам вычисления объемов некоторых тел. Надо сказать, что математика, которую египтяне использовали при строительстве пирамид, была простой и примитивной.
Задачи и решения, приведенные в папирусах, сформулированы чисто рецептурно, без каких бы то ни было объяснений. Египтяне имели дело только с простейшими типами квадратных уравнений и арифметической и геометрической прогрессиями, а потому и те общие правила, которые они смогли вывести, были также самого простейшего вида. Ни вавилонская, ни египетская математики не располагали общими методами; весь свод математических знаний представлял собой скопление эмпирических формул и правил.
Хотя майя, жившие в Центральной Америке, не оказали влияния на развитие математики, их достижения, относящиеся примерно к 4 в., заслуживают внимания. Майя, по-видимому, первыми использовали специальный символ для обозначения нуля в своей двадцатеричной системе. У них были две системы счисления: в одной применялись иероглифы, а в другой, более распространенной, точка обозначала единицу, горизонтальная черта — число 5, а специальный символ обозначал нуль. Позиционные обозначения начинались с числа 20, а числа записывались по вертикали сверху вниз.
^ Греческая математика
Классическая Греция
С точки зрения 20 в. родоначальниками математики явились греки классического периода (6 – 4 вв. до н. э.). Математика, существовавшая в более ранний период, была набором эмпирических заключений. Напротив, в дедуктивном рассуждении новое утверждение выводится из принятых посылок способом, исключавшим возможность его неприятия.
Настаивание греков на дедуктивном доказательстве было экстраординарным шагом. Ни одна другая цивилизация не дошла до идеи получения заключений исключительно на основе дедуктивного рассуждения, исходящего из явно сформулированных аксиом. Одно из объяснений приверженности греков методам дедукции мы находим в устройстве греческого общества классического периода. Математики и философы (нередко это были одни и те же лица) принадлежали к высшим слоям общества, где любая практическая деятельность рассматривалась как недостойное занятие. Математики предпочитали абстрактные рассуждения о числах и пространственных отношениях решению практических задач. Математика делилась на арифметику — теоретический аспект и логистику — вычислительный аспект. Заниматься логистикой предоставляли свободнорожденным низших классов и рабам.
Греческая система счисления была основана на использовании букв алфавита. Аттическая система, бывшая в ходу с 6 – 3 вв. до н. э., использовала для обозначения единицы вертикальную черту, а для обозначения чисел 5, 10, 100, 1000 и 10 000 начальные буквы их греческих названий. В более поздней ионической системе счисления для обозначения чисел использовались 24 буквы греческого алфавита и три архаические буквы. Кратные 1000 до 9000 обозначались так же, как первые девять целых чисел от 1 до 9, но перед каждой буквой ставилась вертикальная черта. Десятки тысяч обозначались буквой М (от греческого мириои — 10 000), после которой ставилось то число, на которое нужно было умножить десять тысяч
Дедуктивный характер греческой математики полностью сформировался ко времени Платона и Аристотеля. Изобретение дедуктивной математики принято приписывать Фалесу Милетскому (ок. 640 – 546 до н. э.), который, как и многие древнегреческие математики классического периода, был также философом. Высказывалось предположение, что Фалес использовал дедукцию для доказательства некоторых результатов в геометрии, хотя это сомнительно.
Другим великим греком, с чьим именем связывают развитие математики, был Пифагор (ок. 585 – 500 до н. э.). Полагают, что он мог познакомиться с вавилонской и египетской математикой во время своих долгих странствий. Пифагор основал движение, расцвет которого приходится на период ок. 550 – 300 до н. э. Пифагорейцы создали чистую математику в форме теории чисел и геометрии. Целые числа они представляли в виде конфигураций из точек или камешков, классифицируя эти числа в соответствии с формой возникающих фигур (“фигурные числа”). Слово “калькуляция” (расчет, вычисление) берет начало от греческого слова, означающего “камешек”. Числа 3, 6, 10 и т. д. пифагорейцы называли треугольными, так как соответствующее число камешков можно расположить в виде треугольника, числа 4, 9, 16 и т. д. — квадратными, так как соответствующее число камешков можно расположить в виде квадрата, и т. д.
Из простых геометрических конфигураций возникали некоторые свойства целых чисел. Например, пифагорейцы обнаружили, что сумма двух последовательных треугольных чисел всегда равна некоторому квадратному числу. Они открыли, что если (в современных обозначениях) n2—квадратное число, то n2+2n+1 = (n+1)2. Число, равное сумме всех своих собственных делителей, кроме самого этого числа, пифагорейцы называли совершенным. Примерами совершенных чисел могут служить такие целые числа, как 6, 28 и 496. Два числа пифагорейцы называли дружественными, если каждое из чисел равно сумме делителей другого; например, 220 и 284 — дружественные числа (и здесь само число исключается из собственных делителей).
Для пифагорейцев любое число представляло собой нечто большее, чем количественную величину. Например, число 2, согласно их воззрению, означало различие и потому отождествлялось с мнением. Четверка представляла справедливость, так как это первое число, равное произведению двух одинаковых множителей.
Пифагорейцы также открыли, что сумма некоторых пар квадратных чисел есть снова квадратное число. Например, сумма 9 и 16 равна 25, а сумма 25 и 144 равна 169. Такие тройки чисел, как 3, 4 и 5 или 5, 12 и 13, называются пифагоровыми числами. Они имеют геометрическую интерпретацию: если два числа из тройки приравнять длинам катетов прямоугольного треугольника, то третье число будет равно длине его гипотенузы. Такая интерпретация, по-видимому, привела пифагорейцев к осознанию более общего факта, известного ныне под названием теоремы Пифагора, согласно которой в любом прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.
Рассматривая прямоугольный треугольник с единичными катетами, пифагорейцы обнаружили, что длина его гипотенузы равна корню из двух, и это повергло их в смятение, ибо они тщетно пытались представить число в виде отношения двух целых чисел, что было крайне важно для их философии. Величины, непредставимые в виде отношения целых чисел, пифагорейцы назвали несоизмеримыми; современный термин — “иррациональные числа”. Около 300 до н. э. Евклид доказал, что число несоизмеримо. Пифагорейцы имели дело с иррациональными числами, представляя все величины геометрическими образами. Если 1 и считать длинами некоторых отрезков, то различие между рациональными и иррациональными числами сглаживается. Произведение чисел и есть площадь прямоугольника со сторонами длиной мы и сегодня иногда говорим о числе 25 как о квадрате 5, а о числе 27 — как о кубе 3.
Древние греки решали уравнения с неизвестными посредством геометрических построений. Были разработаны специальные построения для выполнения сложения, вычитания, умножения и деления отрезков, извлечения квадратных корней из длин отрезков; ныне этот метод называется геометрической алгеброй.
Приведение задач к геометрическому виду имело ряд важных последствий. В частности, числа стали рассматриваться отдельно от геометрии, поскольку работать с несоизмеримыми отношениями можно было только с помощью геометрических методов. Геометрия стала основой почти всей строгой математики, по крайней мере, до1600. И даже в 18 в., когда уже были достаточно развиты алгебра и математический анализ, строгая математика трактовалась как геометрия, и слово “геометр” было равнозначно слову “математик”.
Именно пифагорейцам мы во многом обязаны той математикой, которая затем была систематизированно изложена и доказана в “Началах” Евклида. Есть основания полагать, что именно они открыли то, что ныне известно как теоремы о треугольниках, параллельных прямых, многоугольниках, окружностях, сферах и правильных многогранниках.
Одним из самых выдающихся пифагорейцев был Платон (ок. 427 – 347 до н. э.). Платон был убежден, что физический мир постижим лишь посредством математики. Считается, что именно ему принадлежит заслуга изобретения аналитического метода доказательства. Аналитический метод начинается с утверждения, которое требуется доказать, и затем из него последовательно выводятся следствия до тех пор, пока не будет достигнут какой-нибудь известный факт; доказательство получается с помощью обратной процедуры. Принято считать, что последователи Платона изобрели метод доказательства, получивший название “доказательство от противного”. Заметное место в истории математики занимает Аристотель, ученик Платона. Аристотель заложил основы науки логики и высказал ряд идей относительно определений, аксиом, бесконечности и возможности геометрических построений.
Величайшим из греческих математиков классического периода, уступавшим по значимости полученных результатов только Архимеду, был Евдокс (ок. 408 – 355 до н. э.). Именно он ввел понятие величины для таких объектов, как отрезки прямых и углы. Располагая понятием величины, Евдокс логически строго обосновал пифагорейский метод обращения с иррациональными числами.
Работы Евдокса позволили установить дедуктивную структуру математики на основе явно формулируемых аксиом. Ему же принадлежит и первый шаг в создании математического анализа, поскольку именно он изобрел метод вычисления площадей и объемов, получивший название “метода исчерпывания”. Этот метод состоит в построении вписанных и описанных плоских фигур или пространственных тел, которые заполняют (“исчерпывают”) площадь или объем той фигуры или того тела, которое является предметом исследования. Евдоксу же принадлежит и первая астрономическая теория, объясняющая наблюдаемое движение планет. Предложенная Евдоксом теория была чисто математической; она показывала, каким образом комбинации вращающихся сфер с различными радиусами и осями вращения могут объяснить кажущиеся нерегулярными движения Солнца, Луны и планет.
Около 300 до н. э. результаты многих греческих математиков были сведены в единое целое Евклидом, написавшим математический шедевр “Начала”. Из немногих проницательно отобранных аксиом Евклид вывел около 500 теорем, охвативших все наиболее важные результаты классического периода. Свое сочинение Евклид начал с определения таких терминов, как прямая, угол и окружность. Затем он сформулировал десять самоочевидных истин, таких, как “целое больше любой из частей”. И из этих десяти аксиом Евклид смог вывести все теоремы. Для математиков текст “Начал” Евклида долгое время служил образцом строгости, пока в 19 в. не обнаружилось, что в нем имеются серьезные недостатки, такие как неосознанное использование не сформулированных в явном виде допущений.
Аполлоний (ок. 262 – 200 до н. э.) жил в александрийский период, но его основной труд выдержан в духе классических традиций. Предложенный им анализ конических сечений — окружности, эллипса, параболы и гиперболы — явился кульминацией развития греческой геометрии. Аполлоний также стал основателем количественной математической астрономии.
Александрийский период
В этот период, который начался около 300 до н. э., характер греческой математики изменился. Александрийская математика возникла в результате слияния классической греческой математики с математикой Вавилонии и Египта. В целом математики александрийского периода были больше склонны к решению чисто технических задач, чем к философии. Великие александрийские математики — Эратосфен, Архимед, Гиппарх, Птолемей, Диофант и Папп — продемонстрировали силу греческого гения в теоретическом абстрагировании, но столь же охотно применяли свой талант к решению практических проблем и чисто количественных задач.
Эратосфен (ок. 275 – 194 до н. э.) нашел простой метод точного вычисления длины окружности Земли, ему же принадлежит календарь, в котором каждый четвертый год имеет на один день больше, чем другие. Астроном Аристарх (ок. 310 – 230 до н. э.) написал сочинение “О размерах и расстояниях Солнца и Луны”, содержавшее одну из первых попыток определения этих размеров и расстояний; по своему характеру работа Аристарха была геометрической.
Величайшим математиком древности был Архимед (ок. 287 – 212 до н. э.). Ему принадлежат формулировки многих теорем о площадях и объемах сложных фигур и тел, вполне строго доказанные им методом исчерпывания. Архимед всегда стремился получить точные решения и находил верхние и нижние оценки для иррациональных чисел. Например, работая с правильным 96-угольником, он безукоризненно доказал, что точное значение числа p находится между 31/7и 310/71. Архимед доказал также несколько теорем, содержавших новые результаты геометрической алгебры. Ему принадлежит формулировка задачи о рассечении шара плоскостью так, чтобы объемы сегментов находились между собой в заданном отношении. Архимед решил эту задачу, отыскав пересечение параболы и равнобочной гиперболы.
Архимед был величайшим математическим физиком древности. Для доказательства теорем механики он использовал геометрические соображения. Его сочинение “О плавающих телах” заложило основы гидростатики. Согласно легенде, Архимед открыл носящий его имя закон, согласно которому на тело, погруженное в воду, действует выталкивающая сила, равная весу вытесненной им жидкости, во время купания, находясь в ванной, и не в силах совладать с охватившей его радостью открытия, выбежал обнаженный на улицу с криком: “Эврика!” (“Открыл!”).
Во времена Архимеда уже не ограничивались геометрическими построениями, осуществимыми только с помощью циркуля и линейки. Архимед использовал в своих построениях спираль, а Диоклес (конец 2 в. до н. э.) решил проблему удвоения куба с помощью введенной им кривой, получившей название циссоиды.
В александрийский период арифметика и алгебра рассматривались независимо от геометрии. Греки классического периода имели логически обоснованную теорию целых чисел, однако александрийские греки, восприняв вавилонскую и египетскую арифметику и алгебру, во многом утратили уже наработанные представления о математической строгости. Живший между 100 г. до н. э. и 100 г. н. э. Герон Александрийский трансформировал значительную часть геометрической алгебры греков в откровенно нестрогие вычислительные процедуры. Однако, доказывая новые теоремы евклидовой геометрии, он по-прежнему руководствовался стандартами логической строгости классического периода.
Первой достаточно объемистой книгой, в которой арифметика излагалась независимо от геометрии, было “Введение в арифметику” Никомаха (ок. 100 н. э.). В истории арифметики ее роль сравнима с ролью “Начал” Евклида в истории геометрии. На протяжении более 1000 лет она служила стандартным учебником, поскольку в ней ясно, четко и всеобъемлюще излагалось учение о целых числах (простых, составных, взаимно простых, а также о пропорциях). Повторяя многие пифагорейские утверждения, Введение Никомаха вместе с тем шло дальше, так как Никомах видел и более общие отношения, хотя и приводил их без доказательства.
Знаменательной вехой в алгебре александрийских греков стали работы Диофанта (ок. 250). Одно из главных его достижений связано с введением в алгебру начал символики. В своих работах Диофант не предлагал общих методов, он имел дело с конкретными положительными рациональными числами, а не с их буквенными обозначениями. Он заложил основы т. н. диофантова анализа — исследования неопределенных уравнений.
Высшим достижением александрийских математиков стало создание количественной астрономии. Гиппарху (ок. 161 – 126 до н. э.) мы обязаны изобретением тригонометрии. Его метод был основан на теореме, утверждающей, что в подобных треугольниках отношение длин любых двух сторон одного из них равно отношению длин двух соответственных сторон другого. В частности, отношение длины катета, лежащего против острого угла А в прямоугольном треугольнике, к длине гипотенузы должно быть одним и тем же для всех прямоугольных треугольников, имеющих один и тот же острый угол А. Это отношение известно как синус угла А. Отношения длин других сторон прямоугольного треугольника получили название косинуса и тангенса угла А. Гиппарх изобрел метод вычисления таких отношений и составил их таблицы. Располагая этими таблицами и легко измеримыми расстояниями на поверхности Земли, он смог вычислить длину ее большой окружности и расстояние до Луны. По его расчетам, радиус Луны составил одну треть земного радиуса; по современным данным отношение радиусов Луны и Земли составляет 27/1000. Гиппарх определил продолжительность солнечного года с ошибкой всего лишь в 61/2минуты; считается, что именно он ввел широты и долготы.
Греческая тригонометрия и ее приложения в астрономии достигли пика своего развития в “Альмагесте” египтянина Клавдия Птолемея (умер в 168 н. э.). В “Альмагесте” была представлена теория движения небесных тел, господствовавшая вплоть до 16 в., когда ее сменила теория Коперника. Птолемей стремился построить самую простую математическую модель, сознавая, что его теория — всего лишь удобное математическое описание астрономических явлений, согласованное с наблюдениями. Теория Коперника одержала верх именно потому, что как модель она оказалась проще.
Упадок Греции
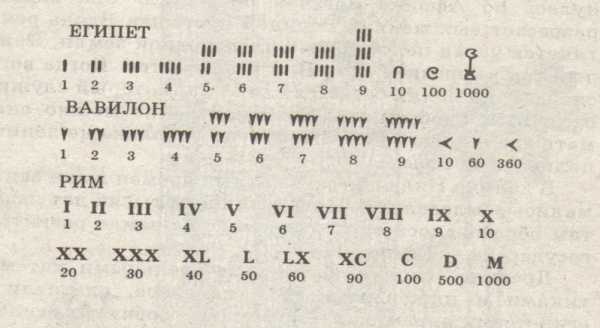
После завоевания Египта римлянами в 31 до н. э. великая греческая александрийская цивилизация пришла в упадок. Цицерон с гордостью утверждал, что в отличие от греков, римляне не мечтатели, а потому применяют свои математические знания на практике, извлекая из них реальную пользу. Однако в развитие самой математики вклад римлян был незначителен. Римская система счисления основывалась на громоздких обозначениях чисел. Главной ее особенностью был аддитивный принцип. Даже вычитательный принцип, например, запись числа 9 в виде IX, вошел в широкое употребление только после изобретения наборных литер в 15 в. Римские обозначения чисел применялись в некоторых европейских школах примерно до 1600, а в бухгалтерии и столетием позже.
^ Индия и арабы
Преемниками греков в истории математики стали индийцы. Индийские математики не занимались доказательствами, но они ввели оригинальные понятия и ряд эффективных методов. Именно они впервые ввели нуль и как кардинальное число, и как символ отсутствия единиц в соответствующем разряде. Махавира (850 н. э.) установил правила операций с нулем, полагая, однако, что деление числа на нуль оставляет число неизменным. Правильный ответ для случая деления числа на нуль был дан Бхаскарой (р. в 1114), ему же принадлежат правила действий над иррациональными числами. Индийцы ввели понятие отрицательных чисел (для обозначения долгов). Самое раннее их использование мы находим у Брахмагупты (ок. 630). Ариабхата (р. 476) пошел дальше Диофанта в использовании непрерывных дробей при решении неопределенных уравнений.
Наша современная система счисления, основанная на позиционном принципе записи чисел и нуля как кардинального числа и использовании обозначения пустого разряда, называется индо-арабской. На стене храма, построенного в Индии ок. 250 до н. э., обнаружено несколько цифр, напоминающих по своим очертаниям наши современные цифры.
Около 800 индийская математика достигла Багдада. Термин “алгебра” происходит от начала названия книги АЛЬ-джебр Ва-л-мукабала” (“Восполнение и противопоставление”), написанной в 830 астрономом и математиком аль-Хорезми. В своем сочинении он воздавал должное заслугам индийской математики. Алгебра аль-Хорезми была основана на трудах Брахмагупты, но в ней явственно различимы вавилонское и греческое влияния. Другой выдающийся арабский математик Ибн аль-Хайсам (ок. 965 – 1039) разработал способ получения алгебраических решений квадратных и кубических уравнений. Арабские математики, в их числе и Омар Хайям, умели решать некоторые кубические уравнения с помощью геометрических методов, используя конические сечения. Арабские астрономы ввели в тригонометрию понятие тангенса и котангенса. Насирэддин Туси (1201 – 1274) в “Трактате о полном четырехугольнике” систематически изложил плоскую и сферическую геометрии и первым рассмотрел тригонометрию отдельно от астрономии.
И все же самым важным вкладом арабов в математику стали их переводы и комментарии к великим творениям греков. Европа познакомилась с этими работами после завоевания арабами Северной Африки и Испании, а позднее труды греков были переведены на латынь.
^ Средние века и Возрождение
Средневековая Европа
Римская цивилизация не оставила заметного следа в математике, поскольку была слишком озабочена решением практических проблем. Цивилизация, сложившаяся в Европе раннего Средневековья (ок. 400 – 1100), не была продуктивной по прямо противоположной причине: интеллектуальная жизнь сосредоточилась почти исключительно на теологии и загробной жизни. Уровень математического знания не поднимался выше арифметики и простых разделов из “Начал” Евклида. Наиболее важным разделом математики в Средние века считалась астрология; астрологов называли математиками. А поскольку медицинская практика основывалась преимущественно на астрологических показаниях или противопоказаниях, медикам не оставалось ничего другого, как стать математиками.
Около 1100 в западноевропейской математике начался почти трехвековой период освоения сохраненного арабами и византийскими греками наследия Древнего мира и Востока. Поскольку арабы владели почти всеми трудами древних греков, Европа получила обширную математическую литературу. Перевод этих трудов на латынь способствовал подъему математических исследований. Все великие ученые того времени признавали, что черпали вдохновение в трудах греков.
Первым заслуживающим упоминания европейским математиком стал Леонардо Пизанский (Фибоначчи). В своем сочинении “Книга абака” (1202) он познакомил европейцев с индо-арабскими цифрами и методами вычислений, а также с арабской алгеброй. В течение следующих нескольких веков математическая активность в Европе ослабла. Свод математических знаний той эпохи, составленный Лукой Пачоли в 1494, не содержал каких-либо алгебраических новшеств, которых не было у Леонардо.
Возрождение
Среди лучших геометров эпохи Возрождения были художники, развившие идею перспективы, которая требовала геометрии со сходящимися параллельными прямыми. Художник Леон Баттиста Альберти (1404 – 1472) ввел понятия проекции и сечения. Прямолинейные лучи света от глаза наблюдателя к различным точкам изображаемой сцены образуют проекцию; сечение получается при прохождении плоскости через проекцию. Чтобы нарисованная картина выглядела реалистической, она должна была быть таким сечением. Понятия проекции и сечения порождали чисто математические вопросы. Например, какими общими геометрическими свойствами обладают сечение и исходная сцена, каковы свойства двух различных сечений одной и той же проекции, образованных двумя различными плоскостями, пересекающими проекцию под различными углами? Из таких вопросов и возникла проективная геометрия. Ее основатель — Ж. Дезарг (1593 – 1662) с помощью доказательств, основанных на проекции и сечении, унифицировал подход к различным типам конических сечений, которые великий греческий геометр Аполлоний рассматривал отдельно.
^ Начало современной математики
Наступление 16 в. в Западной Европе ознаменовалось важными достижениями в алгебре и арифметике. Были введены в обращение десятичные дроби и правила арифметических действий с ними. Настоящим триумфом стало изобретение в 1614 логарифмов Дж. Непером. К концу 17 в. окончательно сложилось понимание логарифмов как показателей степени с любым положительным числом, отличным от единицы, в качестве основания. С начала 16 в. более широко стали употребляться иррациональные числа. Б. Паскаль (1623 – 1662) и И. Барроу (1630 – 1677), учитель И. Ньютона в Кембриджском университете, утверждали, что такое число, как корень из двух, можно трактовать лишь как геометрическую величину. Однако в те же годы Р. Декарт (1596 – 1650) и Дж. Валлис (1616 – 1703) считали, что иррациональные числа допустимы и сами по себе, без ссылок на геометрию. В 16 в. продолжались споры по поводу законности введения отрицательных чисел. Еще менее приемлемыми считались возникавшие при решении квадратных уравнений комплексные числа, такие как названные Декартом “мнимыми”. Эти числа были под подозрением даже в 18 в., хотя Л. Эйлер (1707 – 1783) с успехом пользовался ими. Комплексные числа окончательно признали только в начале 19 в., когда математики освоились с их геометрическим представлением.
Достижения в алгебре
В 16 в. итальянские математики Н. Тарталья (1499 – 1577), С. Даль Ферро (1465 – 1526), Л. Феррари (1522 – 1565) и Д. Кардано (1501 – 1576) нашли общие решения уравнений третьей и четвертой степеней. Чтобы сделать алгебраические рассуждения и их запись более точными, было введено множество символов, в том числе “+”, “–”, “=”, “>” и “<“. Самым существенным новшеством стало систематическое использование французским математиком Ф. Виетом (1540 – 1603) букв для обозначения неизвестных и постоянных величин. Это нововведение позволило ему найти единый метод решения уравнений второй, третьей и четвертой степеней. Затем математики обратились к уравнениям, степени которых выше четвертой. Работая над этой проблемой, Кардано, Декарт и И. Ньютон (1643 – 1727) опубликовали (без доказательств) ряд результатов, касающихся числа и вида корней уравнения. Ньютон открыл соотношение между корнями и дискриминантом [b2 – 4ac] квадратного уравнения, а именно, что уравнение ax2+ bx + c = 0 имеет равные действительные, разные действительные или комплексно сопряженные корни в зависимости оттого, будет ли дискриминант b2 – 4ac равен нулю, больше или меньше нуля. В 1799 К. Фридрих Гаусс (1777 – 1855) доказал т. н. основную теорему алгебры: каждый многочлен n-й степени имеет ровно n корней.
Основная задача алгебры — поиск общего решения алгебраических уравнений — продолжала занимать математиков и в начале 19 в. Когда говорят об общем решении уравнения второй степени ax2+ bx + c = 0, имеют в виду, что каждый из двух его корней может быть выражен с помощью конечного числа операций сложения, вычитания, умножения, деления и извлечения корней, производимых над коэффициентами a, b и с. Молодой норвежский математик Н. Абель (1802 – 1829) доказал, что невозможно получить общее решение уравнения степени выше 4 с помощью конечного числа алгебраических операций. Однако существует много уравнений специального вида степени выше 4, допускающих такое решение. Накануне своей гибели на дуэли юный французский математик Э. Галуа (1811 – 1832) дал решающий ответ на вопрос о том, какие уравнения разрешимы в радикалах, т. е. корни каких уравнений можно выразить через их коэффициенты с помощью конечного числа алгебраических операций. В теории Галуа использовались подстановки или перестановки корней, и было введено понятие группы, которое нашло широкое применение во многих областях математики.
Развитие теории групп служит хорошим примером преемственности творческой работы в математике. Галуа построил свою теорию, опираясь на работу Абеля, Абель опирался на работу Ж. Лагранжа (1736 – 1813). В свою очередь многие выдающиеся математики, в том числе Гаусс и А. Лежандр (1752 – 1833) в своих работах неявно использовали понятие группы. Ньютон не был чрезмерно скромен, когда заявил: “Если я видел дальше других, то потому, что стоял на плечах гигантов”.
Аналитическая геометрия
Аналитическая, или координатная, геометрия была создана независимо П. Ферма (1601 – 1665) и Р. Декартом для того, чтобы расширить возможности евклидовой геометрии в задачах на построение. Однако Ферма рассматривал свои работы лишь как переформулировку сочинения Аполлония. Подлинное открытие — осознание всей мощи алгебраических методов — принадлежит Декарту. Евклидова геометрическая алгебра для каждого построения требовала изобретения своего оригинального метода и не могла предложить количественную информацию, необходимую науке. Декарт решил эту проблему: он формулировал геометрические задачи алгебраически, решал алгебраическое уравнение и лишь затем строил искомое решение — отрезок, имевший соответствующую длину. Собственно аналитическая геометрия возникла, когда Декарт начал рассматривать неопределенные задачи на построение, решениями которых является не одна, а множество возможных длин.
Аналитическая геометрия использует алгебраические уравнения для представления и исследования кривых и поверхностей. Декарт считал приемлемой кривую, которую можно записать с помощью единственного алгебраического уравнения относительно х и у. Такой подход был важным шагом вперед, ибо он не только включил в число допустимых такие кривые, как конхоида и циссоида, но также существенно расширил область кривых. В результате, в 17 – 18 вв. множество новых важных кривых, таких как циклоида и цепная линия, вошли в научный оби
www.ronl.ru
Урок-конференция на тему: История развития алгебры
Алгебра 7 классУрок — конференция
«История развития алгебры»
(с использованием ИКТ)
Учителя математики
МОУ «ООШ» с.Колычево
Кузнецовой Л.Н.
2009г.
Урок-конференция на тему:
История развития алгебры.
Цели: познакомить с историей возникновения алгебры, великими математиками, внесшими свой вклад в развитие алгебры;
расширять кругозор;
развивать коммуникативную и информационно-познавательную компетентности.
Тип урока: Урок – конференция
Подготовка к уроку: Ученикам темы докладов, сообщений предложить за неделю (проследить, чтобы затронуты были все темы).
Ход проведения занятия:
Организационный момент.
Сообщение учителя
Мы изучаем алгебру. На сегодняшнем уроке мы попробуем вникнуть в суть алгебры, узнаем историю происхождения термина «алгебра», и постараемся проследить историю развития этой науки. Вместе с тем узнаем, какие ученые – математики внесли свой вклад в развитие алгебры, придав ее ту форму, которую она сохранила до настоящего времени.
Суть алгебры
Алгебра, вместе с арифметикой, есть наука о числах и через посредство чисел – о величинах. Различие между арифметикой и алгеброй состоит в том, что первая наука исследует свойства данных, определенных величин, между тем как алгебра занимается изучением общих величин, значение которых может быть произвольное, а, следовательно, алгебра изучает только те свойства величин, которые независимы от их значений. Т.о, алгебра есть обобщенная арифметика. Алгебру можно определить, как «науку о количественных соотношениях».
В настоящее время, отчасти из педагогических соображений, отчасти вследствие исторического развития этой науки, алгебру делят на низшую и высшую. К низшей алгебре относят теорию простейших операций над алгебраическими выражениями, решение уравнений первой и второй степени, теорию степеней и корней, теорию логарифмов, теорию комбинаторики. С некоторыми понятиями вы уже знакомы, остальное вам, только, предстоит узнать на уроках алгебры.
3.Актуализация знаний.
Фронтальный опрос по изученному материалу.
Что называют «коэффициентом»?
Приведите пример выражения с переменными.
Как читаются знаки ? Какое неравенство называют строгим, а какое нестрогим?
Какие выражения называют тождественно равными?
Что значит решить уравнение?
Дайте определение корня уравнения.
Дайте определение линейного уравнения.
Что такое функция?
Что называется графиком функции?
Дайте определение линейной функции.
Что является графиком линейной функции?
Сформулируйте определение степени с натуральным показателем.
Сформулируйте правила свойств степеней.
После работы по определениям заслушиваются сообщения учащихся.
4. На доске (можно также приготовить мини программки) записываются темы сообщений, докладов. (в программках указываются докладчики):
Что изучает алгебра?
Древнейшие сочинения по алгебре.
Возникновение науки алгебры.
Развитие алгебры.
(Происхождение символики. Презентация)
Учитель является наблюдателем за ходом конференции, для этого нужны часы (хорошо, если песочные) и колокольчик (символизирует истечение времени докладчика).
После сообщений, докладов, презентации, слушателям предлагается задать вопросы выступающим ученикам.
После обсуждения учитель предлагает следующие вопросы для обсуждения всем присутствующим на конференции, которые заранее вывешены на доске.
История развития алгебры:
Каково происхождение слова «алгебра»?
Кто ввел в алгебру знак равенства?
Кто является создателем буквенной символики?
Какой математик обозначил переменные и постоянные строчными буквами латинского алфавита?
Какой древнегреческий математик много сделал в области решения уравнений?
С именем какого ученого связана система координат?
Кто ввел в математику термин «функция»?
Как называется формула возведения двучлена в степень?
Кто ввел термины «абсцисса», «ордината», «координаты»?
Кто впервые ввел обозначения степеней в той форме, которую используют в алгебре до настоящего времени?
Сообщения учащихся
Что изучает алгебра.
Алгебра-часть математики, которая изучает общие свойства, действия над различными величинами и решение уравнений, связанных с этими действиями.
В процессе развития алгебра из науки об уравнениях преобразовалась в науку об операциях, более или менее сходных с действиями над числами.
Например решим задачу: возрасты трёх братьев-30,20 и 6. Через сколько лет возраст старшего будет равен сумме возрастов младших братьев?
Решение
Обозначив искомое число лет через X, составим уравнение: 30+X=(20+X)+(6+X), решив его получим, что X=4. То есть через 4 года возраст старшего будет равен сумме возрастов младших братьев.
Близкий к описанию метод решения задач был известен ещё в II тысячелетий до н.э. писцам Древнего Египта (однако они не применяли буквенной символики).
В сохранившихся до наших дней математических папирусах имеются задачи, которые приводят к уравнениям не только первой степени с одним неизвестным вида ах=b, как в задаче о возрасте братьев, но и вида ax2=b.
Ещё более сложные задачи умели решать с начала II тысячелетия до н.э. в Древнем Вавилоне : в математических текстах, выполненных клинописью на глиняных пластинках , есть квадратные и биквадратные уравнения , системы уравнений с двумя неизвестными и даже простейшие кубические уравнения . при этом вавилоняне также не использовали буквы.
Возникновение науки алгебры
Алгебра как искусство решать уравнения зародилась у вавилонян, у которых было для него специальное название, перешедшее в арабский язык.
Узбекский математик аль-Хорезми (727-ок.850), живший в древней столице Хорезма городе Ургенч, написал в начале IX века свою книгу, которая стала родоначальником европейских учебников алгебры.
О назвал её Книга о восстановлении и противопоставлении.
« Восстановление» означает превращение вычитаемого ( по современному – «отрицательного» ) числа в положительное при перенесении из одной половины уравнения в другую. Так как в те времена отрицательные числа не считались настоящими, то операция аль – джебр ( алгебра) , как бы возвращающая число из небытия в бытие, казалось чудом этой науки, которую в Европе долго после этого называли «великим искусством» , рядом с «малым искусством» – арифметикой.
Термин «алгебра» как название «искусства восстания» у арабов же перешел в медицину. Выправление кости ломанной руки или ноги также являлось восстановлением потерянного органа, и искусство врача, которое возвращает человеку руку или ногу, также стали называть алгеброй.
Такой двойной смысл слова «алгебра» объясняет один странный на первый взгляд факт. Во второй части известного романа Сервантеса «Дон Кихот» ( глава XV ) рассказывается, как Дон Кихот сбил с лошади своего противника, как тот лежал на земле, не будучи в состоянии шевелить не руками ни ногами, как Дон Кихоту удалось найти алгебраиста для оказания помощи побеждённому противнику.
Так сказано в оригинале романа, так же говориться в более ранних русских изданиях ; только в более поздних «алгебраист» заменён «костоправом». Объясняется это тем, что в испанском и португальском языках слово «алгебра», как и в арабском языке, означает не только часть математики, но и «искусство вправлять вывихи» словом «алгебраист» называется не только знающий алгебру, но и врач – специалист по болезням рук и ног.
Уже аль-Хорезми видел характерную способность алгебры в том, что она решает задачи, рассматриваемые и в арифметике, в общем виде. Достигается это тем, что числа обозначаются буквами, которые, в зависимости от условия задачи, могут получать разные числовые значения. Поэтому алгебру часто называли общей или универсальной арифметикой. Употребление букв в алгебре появилось в результате очень долгого развития. В первом алгебраическом трактате аль-Хорезми буквенная символика отсутствовала, поэтому и в трудах европейских математиков символика появилась гораздо позже.
Древнейшие сочинения по алгебре.
Первое дошедшее до нас сочинения содержащие исследование алгебраических вопросов, есть трактат Диофанта, жившего в середине 4го века. В этом трактате мы встречаем, например, правило знаков (минус на минус даёт плюс), исследование степеней чисел, и решение множества неопределённых вопросов. Из 13 книг, составлявших полное сочинение Диофанта, до нас дошло только 6,в которых решаются уже довольно трудные алгебраические задачи.
Задачи, приводящие к решению простейших уравнений, люди решали на основе здравого смысла с этого времени ,как они стали людьми. Ещё за 3-4 тысячи лет до н.э. египтяне и вавилоняне умели решать простейшие уравнения, вид которых и приёмы решения были похожи на современные. Греки унаследовали знания египтян и пошли дальше. Наибольших успехов в развитии учения об уравнениях достиг греческий ученый Диофант Александровский(4 век до н.э.),о котором писали:
Посредством уравнений ,теорем
Он уйму всяких разрешал проблем:
И засуху предсказывал, и ливни.
Поистине его познанья дивны.
Знаменита надпись на его могильном камне:
Прах Диофанта гробница покоит : дивись ей- и камень
Мудрым искусством его скажет усопшего век.
Волей богов шестую часть жизни он прожил ребёнком,
И половину шестой встретил с пушком на щеках.
Только минула седьмая, с подругою он обручился.
С нею пять лет проведя, сына дождался мудрец.
Только полжизни отцовской возлюбленный сын его прожил.
Отнят он был ранней могилой своей.
Дважды два года родитель оплакивал горе.
Тут и увидел предел жизни печальной своей.
Мы можем задачу ,рассказывающую о жизни Диофанта ,перевести на язык алгебры.
Все годы жизни-x лет
Шестую часть в детстве –х/6
двенадцатую- в юности -х/12
после седьмой и ещё пяти лет, родился сын-х\7+5
умерший по достижению половины числа лет жизни отца- х/2
после чего Диофанта прожил-4 года.
Составим уравнение:
х/6+ х/12+х/7+5+х/2+4=х
Находим:х=84 Диофант прожил 84 года.
Знаменитое сочинение Диофанта «Арифметика» в 13 книгах. Эта книга рассматривается как эпоха в развитии математики потому, что она содержит в себе первые следы искусства; характерны для алгебры. Диофант изобрёл большое число способов решения уравнений, содержащих две или более переменных, и требуется найти все целые или натуральные их решения. Поэтому их часто называют диофантовыми уравнениями.
Презентация
Развитие алгебры. (Происхождение символики)
Обсуждение сообщений, докладов, презентации. Работа по вопросам.
Обобщение всего услышанного и увиденного на уроке.
Заключение
Нет возможности в этом кратком изложении обозреть успехи, которым алгебра обязана названным и не названным математикам. Мы, лишь. вкратце упоминаем о главных пунктах совершенствовании алгебры. С того времени алгебра входит в более тесную связь с геометрией, после разработки Декартом аналитической геометрии, а также с анализом бесконечно малых величин, изобретенным Ньютоном и Лейбницом. Классические труды Эйлера и Лагранжа довели алгебру до высокой степени совершенства. Позже работы Гаусса, Абеля, Коши, Галуа и многих других создали новые точки зрения на важнейшие алгебраические вопросы и придали алгебре высокую степень изящества и простоты.
referat.znate.ru
История появления алгебры как науки
Деление и история алгебры, происхождение ее термина. Древнейшие сочетания по алгебре, появление от арабов и ее развитие в Европе в эпоху Возрождения. Решение уравнений третей и четвёртой степени. Некоторые математические знаки и даты их возникновения.
Отправить свою хорошую работу в базу знаний просто. Используйте форму, расположенную ниже
Студенты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны.
Размещено на http://www.allbest.ru/
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
“ВОРОНЕЖСКИЙ ГОСУДАРСТВЕННЫЙ ИНСТИТУТ
Кафедра математических и естественно – научных дисциплин.
студент 1 курса 1 группы
Карлова Елена Сергеевна
1. Деление алгебры
2. История алгебры
2.1 Происхождение термина “алгебра”
2.2 Древнейшие сочетания по алгебре
2.3 Алгебра арабов
2.4 Возрождение алгебры в Европе
2.5 Решение уравнений третей и четвёртой степени
2.6 Развитие алгебры в странах Европы
2.7 Приобретение алгеброй законченного вида
3. Некоторые математические знаки и даты их возникновения
Список используемой литературы
Алгебра, вместе с арифметикой, есть наука о числах и через посредство чисел – о величинах вообще. Не занимаясь изучением свойств каких-нибудь определенных, конкретных величин, обе эти науки исследуют свойства отвлеченных величин, как таковых, независимо от того, к каким конкретным приложениям они способны. Различие между арифметикой и алгеброй состоит в том, что первая наука исследует свойства данных, определенных величин, между тем как алгебра занимается изучением общих величин, значение которых может быть произвольное, а, следовательно, алгебра изучает только те свойства величин, которые общи всем величинам, независимо от их значений. Таким образом, алгебра есть обобщенная арифметика. Это подало повод Ньютону назвать свой трактат об алгебре “Общая арифметика”. Гамильтон, полагая, что подобно тому, как геометрия изучает свойства пространства, алгебра изучает свойства времени, назвал алгебру “Наукою чистого времени” – название, которое Морган предлагал изменить на “Исчисление последовательности”. Однако такие определения не выражают ни существенных свойств алгебры, ни исторического ее развития. Алгебру можно определить как “науку о количественных соотношениях”.
1. Деление алгебры
В настоящее время, отчасти из педагогических соображений, отчасти вследствие исторического развития этой науки, алгебру делят на низшую и высшую. К низшей алгебре относят теорию простейших арифметических операций над алгебраическими выражениями, решение уравнений первой и второй степени, теорию степеней и корней, теорию логарифмов и комбинаторику. К высшей алгебре относят теорию уравнений произвольных степеней, теорию исключений, теорию симметрических функций, теорию подстановок, и, наконец, изложение различных частных способов отделения корней уравнений, определения числа вещественных или мнимых корней данного уравнения с численными коэффициентами, и приближённое или аналитическое (когда это возможно) уравнений произвольных степеней.
2. История алгебры
2.1 Происхождение термина “алгебра”
2.2 Древнейшие сочетания по алгебре
Первое дошедшее до нас сочинение, содержащее исследование алгебраических вопросов, есть трактат Диофанта, жившего в середине IV века. В этом трактате мы встречаем, например, правило знаков (минус на минус дает плюс), исследование степеней чисел, и решение множества неопределенных вопросов, которые в настоящее время относятся к теории чисел. Из 13 книг, составлявших полное сочинение Диофанта, до нас дошло только 6, в которых решаются уже довольно трудные алгебраические задачи. Нам неизвестно о каких бы то ни было иных сочинениях об алгебре в древности, кроме утерянного сочинения знаменитой дочери Теона, Гипатии.
2.3 Алгебра арабов
2.4 Возрождение алгебры в Европе
2.5 Решение уравнений третей и четвёртой степени
В 1505 году Сципион Феррео впервые решил один частный случай кубического уравнения. Это решение однако не было им опубликовано, но было сообщено одному ученику – Флориде. Последний, находясь в 1535 году в Венеции, вызвал на состязание уже известного в то время математика Тарталью из Брешии и предложил ему несколько вопросов, для разрешения которых нужно было уметь решать уравнения третьей степени. Но Тарталья уже нашел раньше сам решение таких уравнений и, мало того, не только одного того частного случая, который был решен Феррео, но и двух других частных случаев. Тарталья принял вызов и сам предложил Флориде также свои задачи. Результатом состязания было полное поражение Флориде. Тарталья решил предложенные ему задачи в продолжение двух часов, между тем как Флориде не мог решить ни одной задачи, предложенной ему его противником (число предложенных с обеих сторон задач было 30). Тарталья продолжал, подобно Феррео, скрывать свое открытие, которое очень интересовало Кардано, профессора математики и физики в Милане. Последний готовил к печати обширное сочинение об арифметике, алгебре и геометрии, в котором он хотел дать также решение уравнений 3-ей степени. Но Тарталья отказывался сообщить ему о своем способе. Только когда Кардано поклялся над Евангелием и дал честное слово дворянина, что он не откроет способа Тартальи для решения уравнений и запишет его в виде непонятной анаграммы, Тарталья согласился, после долгих колебаний, раскрыть свою тайну любопытному математику и показал ему правила решений кубических уравнений, изложенные в стихах, довольно туманно. Остроумный Кардано не только понял эти правила в туманном изложении Тартальи, но и нашел доказательства для них. Не взирая, однако, на данное им обещание, он опубликовал способ Тартальи, и способ этот известен до сих пор под именем “формулы Кардано”.
Вскоре было открыто и решение уравнений четвертой степени. Один итальянский математик предложил задачу, для решения которой известные до той поры правила были недостаточны, а требовалось умение решать биквадратные уравнения. Большинство математиков считало эту задачу неразрешимою. Но Кардано предложил ее своему ученику Луиджи Феррари, который не только решил задачу, но и нашел способ решать уравнения четвертой степени вообще, сводя их к уравнениям третьей степени. В сочинении Тартальи, напечатанном в 1546 году, мы также находим изложение способа решать не только уравнения первой и второй степени, но и кубические уравнения, причем рассказывается инцидент между автором и Кардано, описанный выше. Сочинение Бомбелли, вышедшее в 1572 г., интересно в том отношении, что рассматривает так называемый неприводимый случай кубического уравнения, который приводил в смущение Кардано, не сумевшего решить его посредством своего правила, а также указывает на связь этого случая с классическою задачей о трисекции угла. алгебра уравнение математический
2.6 Развитие алгебры в странах Европы
В Англии первый трактат об алгебре принадлежит Роберту Рекорду, преподавателю математики и медицины в Кембридже. Его сочинение об алгебре называется “The Whetstone of Wit”. Здесь впервые вводится знак равенства (=). Во Франции в 1558 году появилось первое сочинение об алгебре, принадлежащее Пелетариусу; в Голландии Стевин в 1585 г. не только изложил исследования, известные уже до него, но и ввел некоторые усовершенствования в алгебру. Например, он уже обозначал неизвестные. Правда, для обозначения неизвестных он использовал всего лишь числа, обведенные в кружочек. Так первая неизвестная (теперь обычно обозначаемая x) у него обозначалась обведенной в кружочек единицей, вторая – обведенной двойкой, и так далее. Громадные успехи сделала алгебра после сочинений Виета, который первый рассмотрел общие свойства для уравнений произвольных степеней и показал способы для приблизительного нахождения корней каких бы то ни было алгебраических уравнений. Он же первый обозначил величины, входящие в уравнения буквами, и тем придал алгебре ту общность, которая составляет характеристическую особенность алгебраических исследований нового времени. Он же подошел весьма близко к открытию формулы бинома, найденной впоследствии Ньютоном, и, наконец, в его сочинениях можно даже встретить разложение отношения стороны квадрата вписанного в круг к дуге круга, выраженное в виде бесконечного произведения. Фламандец Албер Жирар или Жерар, трактат которого об алгебре появился в 1629 г. первый ввел понятие мнимых величин в науку. Агличанин Гарриот показал, что всякое уравнение может рассматриваться, как произведение некоторого числа множителей первого порядка, и ввел в употребление знаки > и <. Его труды были опубликованы в 1631 г. Варнером.
2.7 Приобретение алгеброй законченного вида
3. Некоторые математические знаки и даты их возникновения
Отношение длины окружности к диаметру
Основание натурального логарифма
Корень квадратный из -1
Список используемой литературы
1. История математике в школе, Г.И.Глейзер, Москва, Просвещение 1964г.
2. Очерки по истории математики, Б.В.Болгарский, Минск, “Высшая школа” 1979г.
3.Математика, Я познаю мир, Москва, АСТ 2000г.
4. Энциклопедический словарь юного математика, Москва, Педагогика – пресс 1999г.
Размещено на Allbest.ru
Подобные документы
Оценка алгебры Ли как одного из классических объектов современной математики. Основные определения и особенности ассоциативной алгебры. Нильпотентные алгебры Ли, эквивалентность различных определений нильпотентности. Описание алгебр Ли малых размерностей.
Предмет и методы изучения дифференциальной векторно-матричной алгебры, ее структура. Векторное решение однородных и неоднородных дифференциальных уравнений. Численное решение векторно-матричных уравнений. Формулы построения вычислительных процедур.
Решение уравнения гармонического осциллятора при помощи разложения в ряд Тейлора. Применение метода индуцированной алгебры. Решение уравнения гармонического осциллятора при помощи метода индуцированной алгебры. Сравнение работоспособности методов решений.
Решение биквадратных, симметричных и кубических уравнений, содержащих радикалы. Решение уравнений четвертой степени методом понижения степени и разложения на множители. Применение бинома Ньютона. Графический метод решения уравнений повышенной степени.
Понятие текстовых задач, их типология, роль и место в курсе школьной алгебры. Психолого-педагогические основы формирования умения решать текстовые задачи, этапы и методы обучения. Разработка системы задач по алгебре для самостоятельного решения учащимися.
Задачи вычислительной линейной алгебры. Математическое моделирование разнообразных процессов. Решение систем линейных алгебраических уравнений большой размерности. Метод обратной матрицы и метод Гаусса. Критерии совместности и определенности системы.
Понятие и свойства n-арных операций, универсальной алгебры и сигнатуры. Характеристика централизаторов конгруэнции универсальных алгебр и доказательство их основных свойств. Нильпотентные и абелевы алгебры, формулировка и метод доказательства их лемм.
Теоретические аспекты обучения решению уравнений в 8 классе. Основные направления изучения линий уравнений в школьном курсе алгебры. Методика изучения квадратных уравнений. Методико-педагогические основы обучения решению квадратных уравнений.
История развития алгебры как научной дисциплины. Расширения Галуа как универсальный метод решения уравнений любой степени. Определение понятия коммуникативной (абелевой) группы. Сущность кольца и его свойства. Примеры использования конечного поля.
Операции над логическими высказываниями: булевы функции и выражение одних таких зависимостей через другие. Пропозициональные формулы и некоторые законы логики высказываний. Перевод выражений естественного языка на символическую речь алгебры логики.
Работы в архивах красиво оформлены согласно требованиям ВУЗов и содержат рисунки, диаграммы, формулы и т.д.
referat-4all.ru
Реферат по алгебре ученицы Храмцовой Ольги на тему История возникновения алгебры (7 класс)
«История возникновения алгебры»
Автор: Храмцова Ольга
Ученица 7 «А» класса МБОУ «Гимназия №2»
Руководитель: Чижова В.Н
В новом учебном году мы начали изучать новый для нас предмет – алгебру. Основной задачей алгебры является поиск общего решения алгебраических уравнений. Алгебра дает возможность не только выполнять вычисления, но и учит делать это быстрее и рациональнее. Алгебра, вместе с арифметикой, есть наука о числах и через посредство чисел – о величинах вообще. Не занимаясь изучением свойств каких-нибудь определенных, конкретных величин, обе эти науки исследуют свойства отвлеченных величин. Различие между арифметикой и алгеброй состоит в том, что первая наука исследует свойства данных, определенных величин, между тем как алгебра занимается изучением общих величин, значение которых может быть произвольное. Следовательно, алгебра изучает только те свойства величин, которые общи всем величинам, независимо от их значений.
Таким образом, алгебра есть обобщенная арифметика. Это подало повод Ньютону назвать свой тракт об алгебре «Общая арифметика». Гамильтон, полагая, что подобно тому, как геометрия изучает свойства пространства, алгебра изучает свойства времени, назвал алгебру «Наукою чистого времени». Однако такие определения не выражают ни существенных свойств алгебры, ни исторического ее развития. Алгебру можно определить как «науку о количественных соотношениях».
В данной работе мы рассмотрим историю возникновения такой сложной, но, в то же время, интересной науки.
– изучение истории развития алгебры;
– ознакомление с открытиями основоположников этой науки;
– подготовка к выступлению на научно-практической конференции;
– изучение материала по истории развития алгебры;
Исаак Ньютон – известный английский математик, механик, астроном и физик, создатель классической механики, с 1703 года президент Лондонского королевского общества, писал: «Алгебра – есть не что иное, как математический язык, приспособленный для обозначения отношений между количествами».
Алгебра – часть математики, которая изучает общие свойства, действия над различными величинами и решение уравнений, связанных с этими действиями.
Слово «алгебра» возникло после появления тракта хорезмского математика и астронома Мухаммеда бен Мусса Аль-Хорезми «Китабаль-джебр Валь-мукабала» («Книга о восстановлении и противопоставлении»). Термин «аль-джебр», взятый из названия этой книги, в дальнейшем стал употребляться как «алгебра». А имя Аль-Хорезми в видоизмененной форме Algorithmus превратилось в нарицательное слово «алгоритм».
Данный трактат оказал большое влияние на развитие математики в Западной Европе. В нем алгебра впервые рассматривается как самостоятельная отрасль математики, вводятся правила действий с алгебраическими количествами и систематически решаются уравнения 1-й и 2-й степеней.
С помощью другого трактата «Книга об индийском счете» европейцы познакомились с индийскими методами записи чисел, с употреблением нуля и с поместным значением цифр. Оба трактата в 12 веке были переведены на латинский язык и долгое время служили основными учебниками по математике.
Алгебра, как искусство решать уравнения, зародилась очень давно. Это было связано с потребностями практики и в результате поиска общих приемов решения однотипных задач.
Арифметика и нехитрая алгебра использовались при обмене денег и расчетах за товары, вычислении простых и сложных процентов, налогов и доли урожая, сдаваемой в пользу государства, храма или землевладельца. Многочисленные арифметические и геометрические задачи возникали в связи со строительством каналов, зернохранилищ и другими общественными работами. В египетских папирусах можно найти задачи, помогающие вычислять вес тел, площади посевов, объемы зернохранилищ, размеры податей и количество камней, требуемое для возведения тех или иных сооружений. А также более сложные задачи, связанные с использованием переводных коэффициентов.
Самые ранние, дошедшие до нас рукописи свидетельствуют о том, что в Древнем Вавилоне и Древнем Египте были известны приемы решения линейных уравнений. В математических папирусах имеются задачи, которые приводят к уравнениям не только первой степени с одним неизвестным, но и вида ax 2 = b.
Дошедший до нас трактат греческого математика Диофанта, жившего в III веке, содержит исследование алгебраических вопросов. В своём труде он дал решение задач приводящих к так называемым диофантовым уравнениям, впервые ввёл буквенную символику в алгебру. Также в его работах мы встречаем правило знаков (минус на минус дает плюс), исследование степеней чисел и решение множества неопределенных вопросов, которые в настоящее время относятся к теории чисел. 
Из 13 книг, составлявших полное собрание сочинений Диофанта, до нас дошло только 6, в которых решаются уже довольно трудные алгебраические задачи. 
Нам неизвестно о каких бы то ни было иных сочинениях об алгебре в древности, кроме утерянного сочинения знаменитой дочери Теона – Гипатии.
Эта женщина – математик, астроном и философ была убита в 415 году фанатами-христианами. Она является автором комментариев к Аполлонию Пермскому и Диофанту.
В процессе развития алгебра из науки об уравнениях преобразовалась в науку об операциях, сходных с действиями над числами.
В настоящее время алгебру делят на низшую и высшую. К низшей алгебре относят теорию простейших арифметических операций над алгебраическими выражениями, решение уравнений первой и второй степени, теорию степеней и корней, теорию логарифмов и комбинаторику. К высшей алгебре относят теорию уравнений произвольных степеней, теорию исключений, теорию симметрических функций, теорию подстановок, и, наконец, изложение различных частных способов отделения корней уравнений, определения числа вещественных или мнимых корней данного уравнения с численными коэффициентами.
Ступени развития алгебры
В эволюции алгебры различают три ступени развития: риторическую, синкопирующую и символическую.
Риторическая, или словесная, математика не пользуется символами. На этой ступени находится греческая математика начала III века (до Диофанта), арабская и европейская математика до XIV века.
Однако и там имеются особые знаки для некоторых математических понятий. У египтян используют иероглифы. Скарабей – для понятия «равно»; ноги, идущие против чтения – для понятия «больше»; уходящие ноги – для понятия «меньше»; иероглиф совы – неизвестное, искомое.
Первые записи выглядели как зарубки на палке. Если надо отсчитать тысячи, пройдет больше часа. Это была очень неудобная запись! Поэтому пять тысяч лет назад в Вавилоне, Египте и Китае почти одновременно родился новый способ записи чисел. Люди додумались писать числа по разрядам. Египтянам, чтобы написать цифру 7 приходилось рисовать семь палочек.
А вот число 1873 египтяне писали так:
Для запоминания результатов счёта инки использовали не зарубки, а узелки. Греческая система счисления была основана на использовании букв алфавита.
Очень интересная система счета была у народа Майя, который жил в Центральной Америке. У индейцев Майя была в то время развитая культура. Они считали двадцатками. У них была двадцатеричная система счета. Числа от 1 до 20 обозначались точками и черточками. Если под числом рисовался значок в виде глаза, то это число нужно было увеличить в 20 раз. Изображение в виде глаза играло у народов Майя ту же роль, что у нас цифра 0.
Число 45 Майя записывали так:
Вторая ступень развития – это синкопирующая математика. В этот период для обозначения часто встречающихся понятий используются отдельные буквы и сокращения. Диофант употреблял перевернутую букву ψ (пси), Лука Пачоли употреблял буквы «p» и «m» для обозначения плюса и минуса.
Третья ступень – символическая математика. Этот период в развитии математики приходится на начало XV века. До этого времени изложение алгебры велось в основном словесно. Буквенные обозначения и математические знаки появились постепенно. Знаки «+» и «–» впервые встречаются у немецких алгебраистов XV века.
Решительный шаг в использовании алгебраической символики был сделан в XVI веке, когда французский математик Франсуа Виет и его современники стали применять буквы для обозначения не только чисел неизвестных (что делалось и ранее), но и любых чисел. Однако эта символика еще отличалась от современной. 
Виет ввел буквенные обозначения для коэффициентов и неизвестного в уравнениях: например, искомое – буква N (Numers), квадрат искомого – Q (Quadrates), куб – С (Cubes), равно – aequ (aequali).
Запись следующих уравнений у Виета выглядела так:
x 3 – 3x = 1 NC – 3 N aequ 1
x 3 – 8x 2 + 16x = 40 1 С – 8Q +16 N aequ 40 
Англичанин Харриот в 1631 году заменяет большие буквы малыми. Затем французский математик и философ, основоположник «декардовой» системы координат в геометрии Рене Декарт предлагает известные числа обозначать первыми буквами латинского алфавита a, b, c,…, а неизвестные – последними буквами x, y, z.
Декарт в 1637 году вводит для обозначения равенства известный всем знак «=».
В 1631 году Харриот предлагает для обозначения неравенства использовать теперешние знаки «>» и «<». В конце XV века знаки сложения «+» и вычитания «–», предложенные Видманом, получают широкое распространение. Круглые скобки появились у Таргальи в 1556 году, но лишь в середине XVIII века скобки стали употребляться во всех математических книгах. 
Знак умножения « » впервые в 1661 году ввел У.Аутрид.
Современные знаки умножения в виде « ∙ » и деления в виде « : » впервые использовал немецкий философ, математик и физик Готфрид Лейбниц. Знак деления в 1684 году, а умножения – в 1698 году. В 1674 году усовершенствуя счетную машину Б. Паскаля, конструирует «компьютер», умеющий выполнять основные арифметические действия.
В 1675 году Лейбниц создает дифференциальное и интегральное исчисление, обнародовав главные результаты своего открытия в 1684. Именно Лейбницу принадлежат термины «дифференциал», «дифференциальное исчисление», «дифференциальное уравнение», «функция», «переменная», «постоянная», «координаты», «абсцисса», «алгебраические и трансцендентные кривые», «алгоритм».
История появления цифр и чисел
Понятие о натуральных числах формировалось постепенно и осложнялось неумением первобытного человека отделять числовую абстракцию от её конкретного представления. Вследствие этого счёт долгое время оставался только вещественным, то есть использовались пальцы, камешки, пометки. Археолог Б. А. Фролов обосновывает существование счёта уже в верхнем палеолите, который был более двух миллионов лет назад. До появления цифр в том виде, который известен нам сейчас, разные народы использовали своё написание цифр и чисел. Рассмотрим некоторые из них.
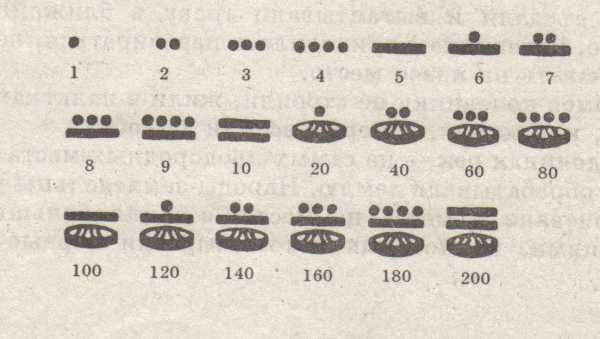
Изображение цифр и чисел у племени Майя
Изображение цифр в Индии (I век)
От этих индийских значков произошли современные цифры
Изображение цифр и чисел в Древнем Египте
Существовали и более экзотичные варианты. Например, туземцы островов Торресова пролива использовали двоичную систему для записи чисел.
В хозяйственной жизни далекого прошлого люди обходились сравнительно небольшими числами, так называемым малым счетом наших предков.
Счет доходил до числа 10 000, которое в самых старых памятниках называется тьма, то есть темное число. В дальнейшем граница малого счета была отодвинута до 10 8 , до числа тьма тём. Но наряду с этим малым числом, если получался великий счет и перечень, употреблялась вторая система, называвшаяся великим числом или счетом или числом великим словенским. При счете употреблялись более высокие разряды: тьма – 10 6 , легион – 10 12 , леодр – 10 24 , ворон – 10 48 , иногда еще колода – десять воронов – 10 49 , хотя колоду следует принять как 10 96 . Для обозначения этих больших чисел наши предки придумали способ, не встречающийся ни у одного из известных нам народов: число единиц любого из перечисленных высших разрядов обозначалось той же буквой, что и простые единицы, но окружность для каждого числа собственным бордюром.
Величайшие греческие математики не додумались до этого способа письма чисел. Таких больших чисел не требовала и не требует и теперь никакая практическая задача.
Архимед, величайший древнегреческий математик, сосчитал, что число песчинок во всем мировом пространстве, как это понимал в то время, не превышает 10 63 . Славянский честолюбец сказал бы, что это число песчинок не больше тысяч легионов воронов 10 63 = 10 3 * 10 12 * 10 48 . Число песчинок во всем мировом пространстве того времени действительно могло казаться наибольшим мыслимым числом.
Вавилоняне создали систему счисления, использовавшую для чисел от 1 до 59, основание 10. Символ, обозначавший единицу, повторялся нужное количество раз для чисел от 1 до 9. Для обозначения чисел от 11 до 59 вавилоняне использовали комбинацию символа числа 10 и символа единицы. Для обозначения чисел, начиная с 60 и больше, вавилоняне ввели позиционную систему счисления с основанием 60. Существенным продвижением стал позиционный принцип, согласно которому один и тот же числовой знак (символ) имеет различные значения в зависимости от того места, где он расположен. Примером могут служить значения шестерки в записи (современной) числа 606. Однако нуль в системе счисления древних вавилонян отсутствовал, из-за чего один и тот же набор символов мог означать и число 65 (60 + 5), и число 3605 (602 + 0 + 5). Вавилоняне составили таблицы обратных чисел, которые использовались при выполнении деления, таблицы квадратов и квадратных корней, а также таблицы кубов и кубических корней. Им было известно приближение числа.
Греческая система счисления была основана на использовании букв алфавита. Аттическая система, бывшая в ходу с VI по III век до нашей эры, использовала для обозначения единицы вертикальную черту, а для обозначения чисел 5, 10, 100, 1000 и 10 000 начальные буквы их греческих названий. В более поздней ионической системе счисления для обозначения чисел использовались 24 буквы греческого алфавита и три архаические буквы. Кратные 1000 до 9000 обозначались так же, как первые девять целых чисел от 1 до 9, но перед каждой буквой ставилась вертикальная черта. Десятки тысяч обозначались буквой М (от греческого “мириои” – 10 000), после которой ставилось то число, на которое нужно было умножить десять тысяч.
Для пифагорейцев любое число представляло собой нечто большее, чем количественную величину. Например, число 2, согласно их воззрению, означало различие и потому отождествлялось с мнением. Четверка представляла справедливость, так как это первое число, равное произведению двух одинаковых множителей.
Пифагорейцы также открыли, что сумма некоторых пар квадратных чисел есть снова квадратное число. Например, сумма 9 и 16 равна 25, а сумма 25 и 144 равна 169. Такие тройки чисел, как 3, 4 и 5 или 5, 12 и 13, называются пифагоровыми числами.
Римская система счисления основывалась на громоздких обозначениях чисел. Главной ее особенностью был вычитательный принцип, например, запись числа 9 в виде IX, вошел в широкое употребление только после изобретения наборных литер в 15 веке. Римские обозначения чисел применялись в некоторых европейских школах примерно до 1600 года, а в бухгалтерии и столетием позже.
Основные этапы развития
Когда понятие абстрактного числа окончательно утвердилось, следующей ступенью стали операции с числами. Натуральное число — это идеализация конечного множества однородных, устойчивых и неделимых предметов (людей, овец, дней и т. п.). Для счёта важно иметь математические модели таких важнейших событий, как объединение таких множеств в одно или, наоборот, отделение части множества. Так появились операции сложения и вычитания, умножения и деления. Свойства и взаимосвязь операций открывались постепенно.
Древнеегипетские математические тексты относятся к началу II тысячелетия до нашей эры. Математика тогда использовалась в астрономии, мореплавании, землемерии, при строительстве домов, плотин, каналов и военных укреплений. Денежных расчётов, как и самих денег, в Египте не было. Египтяне писали на папирусе, который сохраняется плохо, и поэтому в настоящее время знаний о математике Египта существенно меньше, чем о математике Вавилона или Греции. Вероятно, она была развита лучше, чем можно представить, исходя из дошедших до нас документов, что подтверждается тем, что греческие математики учились у египтян.
Основной сохранившийся папирус Ахмеса, записанный в 1650 году до нашей эры, содержит 84 математические задачи. Все задачи из папируса имеют прикладной характер и связаны с практикой строительства, размежеванием земельных наделов и т. п. Задачи сгруппированы не по методам, а по тематике. По преимуществу это задачи на нахождение площадей треугольника, четырёхугольников и круга, разнообразные действия с целыми числами и дробями, пропорциональное деление, нахождение отношений, возведение в разные степени, определение среднего арифметического, арифметические прогрессии, решение уравнений первой и второй степени с одним неизвестным.
В папирусе есть целый ряд свидетельств того, что математика в Древнем Египте тех лет начинала приобретать теоретический характер. Так, египетские математики умели извлекать корни и возводить в степень, решать уравнения, были знакомы с арифметической и геометрической прогрессией и даже владели зачатками алгебры.
Вавилоняне писали клинописными значками на глиняных табличках, которые в немалом количестве дошли до наших дней. Поэтому мы имеем довольно полное представление о математических достижениях учёных Вавилонского государства. Вавилонская расчётная техника была намного совершеннее египетской, а круг решаемых задач существенно шире. Есть задачи на решение уравнений второй степени, геометрические прогрессии. При решении применялись пропорции, средние арифметические, проценты. Методы работы с прогрессиями были глубже, чем у египтян. Линейные и квадратные уравнения решались ещё в эпоху Хаммурапи. При этом использовалась геометрическая терминология (произведение ab называлось площадью, abc — объёмом, и т. д.). Встречаются также кубические уравнения и системы линейных уравнений. Венцом планиметрии была теорема Пифагора.
Шумеры и вавилоняне использовали 60-ричную позиционную систему счисления, увековеченную в нашем делении круга на 360°, часа на 60 минут и минуты на 60 секунд.
Всё же богатая теоретическая основа математики Вавилона не имела целостного характера и сводилась к набору разрозненных приёмов, лишённых доказательной базы. Систематический доказательный подход в математике появился только у греков.
Цифры в древнем Китае обозначались специальными иероглифами, которые появились во II тысячелетии до н. э., и начертание их окончательно установилось к III веку до н. э. Эти иероглифы применяются и в настоящее время.
Вычисления производились на специальной счётной доске суаньпань (см. на фотографии), по принципу использования аналогичной русским счётам. Нуль сначала обозначался пустым местом, специальный иероглиф появился около XII века н. э. Для запоминания таблицы умножения существовала специальная песня, которую ученики заучивали наизусть.
Китайцам было известно многое, в том числе: вся базовая арифметика (включая нахождение наибольшего общего делителя и наименьшего общего кратного), действия с дробями, пропорции, отрицательные числа, площади и объёмы основных фигур и тел, теорема Пифагора и алгоритм подбора пифагоровых троек, решение квадратных уравнений. Был даже разработан метод фан-чэн для решения систем произвольного числа линейных уравнений — аналог классического европейского метода Гаусса.
Математика в современном понимании этого слова родилась в Греции. Во-первых, пифагорейская школа выдвинула тезис «Числа правят миром». Это означало, что истины математики есть в известном смысле истины реального бытия. Во-вторых, для открытия таких истин пифагорейцы разработали законченную методологию. Сначала они составили список первичных, интуитивно очевидных математических истин (аксиомы, постулаты). Затем с помощью логических рассуждений из этих истин выводились новые утверждения, которые также обязаны быть истинными. Так появилась дедуктивная математика. Греческая математика впечатляет, прежде всего, богатством содержания. Многие учёные нового времени отмечали, что мотивы своих открытий почерпнули у древних. Зачатки анализа заметны у Архимеда, корни алгебры — у Диофанта, аналитическая геометрия — у Аполлония.
Но главное не в этом. Два достижения греческой математики далеко пережили своих творцов. Первое — греки построили математику как целостную науку с собственной методологией, основанной на чётко сформулированных законах логики.
Второе — они провозгласили, что законы природы постижимы для человеческого разума, и математические модели — ключ к их познанию.
Индийский способ записи чисел изначально был изысканным. Несколько видоизменившись, эти значки стали современными цифрами, которые мы называем арабскими. Около 500 года н. э. неизвестный индийский математик изобрёл новую систему записи чисел — десятичную позиционную систему. В ней выполнение арифметических действий оказалось неизмеримо проще, чем в старых, с буквенными кодами, как у греков, или шестидесятиричных, как у вавилонян. Индусы разработали полные алгоритмы всех арифметических операций, включая извлечение квадратных и кубических корней.
К V—VI векам относятся труды Ариабхаты, выдающегося индийского математика и астронома. В его труде «Ариабхатиам» встречается множество решений вычислительных задач. В VII веке работал другой известный индийский математик и астроном, Брахмагупта.
Начиная с Брахмагупты, индийские математики свободно обращаются с отрицательными числами, трактуя их как долг. Наибольшего успеха средневековые индийские математики добились в области теории чисел и численных методов. Индийцы далеко продвинулись в алгебре. Их символика богаче, чем у Диофанта, хотя несколько громоздка (засорена словами).
Западная Европа (IV-XV века)
В V веке наступил конец Западной Римской империи, и территория Западной Европы надолго превратилась в поле сражений с завоевателями и разбойниками (гунны, готы, венгры, арабы, норманны и т. п.). Развитие науки прекратилось. Потребность в математике ограничивается арифметикой и расчётом календаря церковных праздников.
Стабилизация и восстановление европейской культуры начинаются с XI века. Появляются первые университеты (Салерно, Болонья). Расширяется преподавание математики. Первое знакомство европейских учёных с античными открытиями происходило в Испании. В конце XII века на базе нескольких монастырских школ был создан Парижский университет, где обучались тысячи студентов со всех концов Европы. Почти одновременно возникают Оксфорд и Кембридж в Британии. В XII веке там переводятся с греческого и арабского на латинский основные труды великих греков и их исламских учеников. С XIV века главным местом научного обмена становится Византия. Особенно охотно переводились и издавались «Начала» Евклида; постепенно они обрастали комментариями местных геометров.
Интерес к науке растёт, и одно из проявлений этого — смена числовой системы. Долгое время в Европе применялись римские цифры. В XII—XIII веках публикуются первые в Европе изложения десятичной позиционной системы записи (сначала переводы Аль-Хорезми, потом собственные руководства), и начинается её применение. С XIV века индо-арабские цифры начинают вытеснять римские даже на могильных плитах. Только в астрономии ещё долго применялась шестидесятеричная вавилонская арифметика.
Первым крупным математиком средневековой Европы стал в XIII веке Леонардо Пизанский, известный под прозвищем Фибоначчи. Основной его труд «Книга абака», изданная в 1202 году. Абаком Леонардо называл арифметические вычисления. Его изложение по полноте и глубине сразу стало выше всех античных и исламских прототипов, и долгое время было непревзойдённым. Эта книга оказала огромное влияние на распространение математических знаний, популярность индийских цифр и десятичной системы в Европе.
В XIV веке университеты появляются почти во всех крупных странах: Прага, Краков, Вена, Гейдельберг и Лейпциг. 
Лука Пачоли, крупнейший алгебраист XV века, друг Леонардо да Винчи, дал ясный, хотя не слишком удобный набросок алгебраической символики. Видный немецкий математик и астроном XV века Иоганн Мюллер напечатал первый в Европе труд, посвящённый тригонометрии.
Западная Европа (XVI век)
XVI век стал переломным для европейской математики. Первым крупным достижением стало открытие общего метода решения уравнений третьей и четвёртой степени. Итальянские математики дель Ферро, Тарталья и Феррари решили проблему, с которой несколько веков не могли справиться лучшие математики мира. При этом обнаружилось, что в решении иногда появлялись «невозможные» корни из отрицательных чисел. После анализа ситуации европейские математики назвали эти корни «мнимыми числами» и выработали правила обращения с ними, приводящие к правильному результату. Так в математику впервые вошли комплексные числа.
Важнейший шаг к новой математике сделал француз Франсуа Виет. Он окончательно сформулировал символический язык арифметики — буквенную алгебру. С её появлением открылась возможность проведения исследований невиданной ранее глубины и общности. Символика Виета не была похожа на принятую ныне, современный её вариант позднее предложил Декарт.
Третье великое открытие XVI века — изобретение логарифмов сделал Джон Непер. Сложные расчёты упростились во много раз, а математика получила новую неклассическую функцию с широкой областью применения.
В 1585 году фламандец Симон Стевин издаёт книгу «Десятая» о правилах действий с десятичными дробями, после чего десятичная система одерживает окончательную победу и в области дробных чисел.
Западная Европа (XVII век)
В XVII веке быстрое развитие математики продолжается. Рене Декарт исправляет стратегическую ошибку античных математиков и восстанавливает алгебраическое понимание числа. Более того, он указывает способ перевода геометрических предложений на алгебраический язык с помощью системы координат. Аналитический метод Декарта немедленно взяли на вооружение Валлис, Ферма и многие другие видные математики.
Пьер Ферма, Гюйгенс и Якоб Бернулли открывают новый раздел математики, которому суждено большое будущее — теорию вероятностей.
Во второй половине XVII века появляется научная периодика. Французская Академия наук с 1699 года издаёт свои записки (Memoires).
Западная Европа (XVIII век)
XVIII век в математике можно кратко охарактеризовать как век анализа, который стал главным объектом приложения усилий математиков. Главным методом познания природы становится составление и решение дифференциальных уравнений. Далеко продвинулись теория и техника интегрирования. В науке на первом месте стоят такие известные имена как
Стремительно развивается линейная алгебра. Первое подробное описание общего решения линейных систем дал в 1750 году Габриэль Крамер. Центрами математических исследований становятся Академии наук. В конце XVIII века появляются специализированные математические журналы.
Западная Европа (XIX век)
Неоспоримая эффективность применения математики в естествознании подталкивала учёных к мысли, что познание в математике есть часть познания реального мира. Но в XIX веке эволюционное развитие математики было нарушено, и этот, казавшийся непоколебимым, тезис был поставлен под сомнение. В алгебре и геометрии появляются многочисленные нестандартные структуры с необычными свойствами: неевклидовы и многомерные геометрии, конечные поля и т. п. Объектами математического исследования всё больше становятся нечисловые объекты: события, векторы, функции, и т. д. Возникает и получает широкое развитие математическая логика. В целом в XIX веке роль и престиж математики в науке и экономике заметно растут. Соответственно растёт и её государственная поддержка. Математика вновь становится по преимуществу университетской наукой. Появляются первые математические общества: Лондонское, Американское, Французское, Московское.
В XIX веке молодая российская математика уже выдвинула учёных мирового уровня. Первым из них стал Михаил Васильевич Остроградский. Как и большинство российских математиков , он разрабатывал преимущественно прикладные задачи анализа, занимался теорией чисел.
Фундаментальными вопросами математики в России первой половины XIX века занялся только Николай Иванович Лобачевский, который выступил против догмата евклидовости пространства.
Он построил геометрию Лобачевского и глубоко исследовал её необычные свойства. Опубликовал труды по алгебре, математическому анализу и теории вероятностей. Лобачевский настолько опередил своё время, что был оценён по заслугам только спустя много лет после смерти. Несколько важных открытий общего характера сделала Софья Ковалевская.
Во второй половине XIX века российская математика, при общем прикладном уклоне, публикует и немало фундаментальных результатов. Пафнутий Львович Чебышёв, математик-универсал, сделал множество открытий в самых разных областях математики — теории чисел, теории вероятностей, теории приближения функций.
Западная Европа (XX век)
Престиж профессии математика стал в XX столетии заметно выше. Невозможно сколько-нибудь полно перечислить сделанные открытия.
В начале века Эмми Нётер и Ван дер Варден завершили построение основ абстрактной алгебры. Герман Минковский в 1907 году разработал модель кинематики теории относительности. Капитальные результаты получены в теории алгоритмов.
А. Н. Колмогоров завершил общепризнанную аксиоматику теории вероятностей. Его фундаментальные труды по теории функций, математической логике, топологии, дифференциальным уравнениям, функциональному анализу и особенно по теории вероятностей и теории информации были высоко оценены.
В 1960-х годах Абрахам Робинсон опубликовал изложение нестандартного анализа — альтернативного подхода к обоснованию математического анализа на основе актуальных бесконечно малых.
Во второй половине XX века, в связи с появлением компьютеров, произошла существенная переориентация математических усилий. Значительно выросла роль таких разделов, как численные методы, теория оптимизации, общение с очень большими базами данных, имитация искусственного интеллекта, кодирование звуковых и видеоданных и т. п. Возникли новые науки — кибернетика и информатика.
Начало современного этапа в развитии математики характеризовалось изменениями во всех ее основных разделах: геометрии, алгебре и анализе.
Коренные изменения в алгебре наметились еще в XIX веке. Если алгебра минувшего времени оперировала числом, то современная алгебра распространяется на величины гораздо более общего характера: события, функции, множества, операции над векторами и над движениями разного рода. Алгебра в своём развитии прошла много сложных этапов, начиная с узелковой системы счёта и заканчивая математическим анализом и теорией вероятности, начиная с элементарных зарубок и заканчивая линейными уравнениями и интегралами.
В данной работе мы ознакомились с историей развития алгебры, узнали, как она формировалась в процессе эволюции человечества, изучили историю возникновения цифр и чисел. Узнали имена основоположников математики и ознакомились с содержанием некоторых их работ и открытий. Теперь мы знаем, что современный вид алгебраической символике придал Рене Декарт ещё в середине XVII века (трактат «Геометрия»), Исаак Ньютон усовершенствовал этот процесс («Универсальная арифметика»), а Эйлер внёс некоторые оставшиеся тонкости и уточнения.
В настоящее время сильно разрослись методы применения алгебры в различных науках: геометрии, анализе, физике, кристаллографии. Обширными разделами алгебры являются теория групп и линейная алгебра. Бурное развитие всех отраслей науки и техники неразрывно связано с развитием алгебры как науки. На базе алгебры в эпоху тотальной компьютеризации возникли новые науки. Изучение основ алгебры в современных условиях становится все более существенным элементом общеобразовательной подготовки молодого поколения.
1. Очерки по истории математики, Б.В.Болгарский, Минск, «Высшая школа», 1979 г.
2. Математика, Я познаю мир, Москва, АСТ, 2000 г.
3. Алгебра, учебник для 7 класса общеобразовательных учреждений, А.Г.Мордкович, Москва, Мнемозина, 2009 г.
4. Энциклопедический словарь юного математика, Москва, Педагогика-пресс, 1999 г.
5. История математики в школе, Г.И.Глейзер, Москва, Просвещение, 1964
6. История математики в трёх томах, под ред. А.П.Юшкевича, Москва, Наука, 1970-1972 г.г.
7. История математики в двух томах, К.А.Рыбников, Москва изд. МГУ, 1960-1963 г.г.
Некоторые математические знаки и даты их возникновения
Отношение длины окружности к диаметру
Основание натурального логарифма
Корень квадратный из –1
,
Десятичная система счисления чисел
referat-4all.ru
Реферат по алгебре ученицы Храмцовой Ольги на тему – История возникновения алгебры – (7 класс)
«История возникновения алгебры»
Автор: Храмцова Ольга
Ученица 7 «А» класса МБОУ «Гимназия №2»
Руководитель: Чижова В.Н
В новом учебном году мы начали изучать новый для нас предмет – алгебру. Основной задачей алгебры является поиск общего решения алгебраических уравнений. Алгебра дает возможность не только выполнять вычисления, но и учит делать это быстрее и рациональнее. Алгебра, вместе с арифметикой, есть наука о числах и через посредство чисел – о величинах вообще. Не занимаясь изучением свойств каких-нибудь определенных, конкретных величин, обе эти науки исследуют свойства отвлеченных величин. Различие между арифметикой и алгеброй состоит в том, что первая наука исследует свойства данных, определенных величин, между тем как алгебра занимается изучением общих величин, значение которых может быть произвольное. Следовательно, алгебра изучает только те свойства величин, которые общи всем величинам, независимо от их значений.
Таким образом, алгебра есть обобщенная арифметика. Это подало повод Ньютону назвать свой тракт об алгебре «Общая арифметика». Гамильтон, полагая, что подобно тому, как геометрия изучает свойства пространства, алгебра изучает свойства времени, назвал алгебру «Наукою чистого времени». Однако такие определения не выражают ни существенных свойств алгебры, ни исторического ее развития. Алгебру можно определить как «науку о количественных соотношениях».
В данной работе мы рассмотрим историю возникновения такой сложной, но, в то же время, интересной науки.
– изучение истории развития алгебры;
– ознакомление с открытиями основоположников этой науки;
– подготовка к выступлению на научно-практической конференции;
– изучение материала по истории развития алгебры;
Исаак Ньютон – известный английский математик, механик, астроном и физик, создатель классической механики, с 1703 года президент Лондонского королевского общества, писал: «Алгебра – есть не что иное, как математический язык, приспособленный для обозначения отношений между количествами».
Алгебра – часть математики, которая изучает общие свойства, действия над различными величинами и решение уравнений, связанных с этими действиями.
Слово «алгебра» возникло после появления тракта хорезмского математика и астронома Мухаммеда бен Мусса Аль-Хорезми «Китабаль-джебр Валь-мукабала» («Книга о восстановлении и противопоставлении»). Термин «аль-джебр», взятый из названия этой книги, в дальнейшем стал употребляться как «алгебра». А имя Аль-Хорезми в видоизмененной форме Algorithmus превратилось в нарицательное слово «алгоритм».
Данный трактат оказал большое влияние на развитие математики в Западной Европе. В нем алгебра впервые рассматривается как самостоятельная отрасль математики, вводятся правила действий с алгебраическими количествами и систематически решаются уравнения 1-й и 2-й степеней.
С помощью другого трактата «Книга об индийском счете» европейцы познакомились с индийскими методами записи чисел, с употреблением нуля и с поместным значением цифр. Оба трактата в 12 веке были переведены на латинский язык и долгое время служили основными учебниками по математике.
Алгебра, как искусство решать уравнения, зародилась очень давно. Это было связано с потребностями практики и в результате поиска общих приемов решения однотипных задач.
Арифметика и нехитрая алгебра использовались при обмене денег и расчетах за товары, вычислении простых и сложных процентов, налогов и доли урожая, сдаваемой в пользу государства, храма или землевладельца. Многочисленные арифметические и геометрические задачи возникали в связи со строительством каналов, зернохранилищ и другими общественными работами. В египетских папирусах можно найти задачи, помогающие вычислять вес тел, площади посевов, объемы зернохранилищ, размеры податей и количество камней, требуемое для возведения тех или иных сооружений. А также более сложные задачи, связанные с использованием переводных коэффициентов.
Самые ранние, дошедшие до нас рукописи свидетельствуют о том, что в Древнем Вавилоне и Древнем Египте были известны приемы решения линейных уравнений. В математических папирусах имеются задачи, которые приводят к уравнениям не только первой степени с одним неизвестным, но и вида ax 2 = b.
Дошедший до нас трактат греческого математика Диофанта, жившего в III веке, содержит исследование алгебраических вопросов. В своём труде он дал решение задач приводящих к так называемым диофантовым уравнениям, впервые ввёл буквенную символику в алгебру. Также в его работах мы встречаем правило знаков (минус на минус дает плюс), исследование степеней чисел и решение множества неопределенных вопросов, которые в настоящее время относятся к теории чисел. 
Из 13 книг, составлявших полное собрание сочинений Диофанта, до нас дошло только 6, в которых решаются уже довольно трудные алгебраические задачи. 
Нам неизвестно о каких бы то ни было иных сочинениях об алгебре в древности, кроме утерянного сочинения знаменитой дочери Теона – Гипатии.
Эта женщина – математик, астроном и философ была убита в 415 году фанатами-христианами. Она является автором комментариев к Аполлонию Пермскому и Диофанту.
В процессе развития алгебра из науки об уравнениях преобразовалась в науку об операциях, сходных с действиями над числами.
В настоящее время алгебру делят на низшую и высшую. К низшей алгебре относят теорию простейших арифметических операций над алгебраическими выражениями, решение уравнений первой и второй степени, теорию степеней и корней, теорию логарифмов и комбинаторику. К высшей алгебре относят теорию уравнений произвольных степеней, теорию исключений, теорию симметрических функций, теорию подстановок, и, наконец, изложение различных частных способов отделения корней уравнений, определения числа вещественных или мнимых корней данного уравнения с численными коэффициентами.
Ступени развития алгебры
В эволюции алгебры различают три ступени развития: риторическую, синкопирующую и символическую.
Риторическая, или словесная, математика не пользуется символами. На этой ступени находится греческая математика начала III века (до Диофанта), арабская и европейская математика до XIV века.
Однако и там имеются особые знаки для некоторых математических понятий. У египтян используют иероглифы. Скарабей – для понятия «равно»; ноги, идущие против чтения – для понятия «больше»; уходящие ноги – для понятия «меньше»; иероглиф совы – неизвестное, искомое.
Первые записи выглядели как зарубки на палке. Если надо отсчитать тысячи, пройдет больше часа. Это была очень неудобная запись! Поэтому пять тысяч лет назад в Вавилоне, Египте и Китае почти одновременно родился новый способ записи чисел. Люди додумались писать числа по разрядам. Египтянам, чтобы написать цифру 7 приходилось рисовать семь палочек.
А вот число 1873 египтяне писали так:
Для запоминания результатов счёта инки использовали не зарубки, а узелки. Греческая система счисления была основана на использовании букв алфавита.
Очень интересная система счета была у народа Майя, который жил в Центральной Америке. У индейцев Майя была в то время развитая культура. Они считали двадцатками. У них была двадцатеричная система счета. Числа от 1 до 20 обозначались точками и черточками. Если под числом рисовался значок в виде глаза, то это число нужно было увеличить в 20 раз. Изображение в виде глаза играло у народов Майя ту же роль, что у нас цифра 0.
Число 45 Майя записывали так:
Вторая ступень развития – это синкопирующая математика. В этот период для обозначения часто встречающихся понятий используются отдельные буквы и сокращения. Диофант употреблял перевернутую букву ψ (пси), Лука Пачоли употреблял буквы «p» и «m» для обозначения плюса и минуса.
Третья ступень – символическая математика. Этот период в развитии математики приходится на начало XV века. До этого времени изложение алгебры велось в основном словесно. Буквенные обозначения и математические знаки появились постепенно. Знаки «+» и «–» впервые встречаются у немецких алгебраистов XV века.
Решительный шаг в использовании алгебраической символики был сделан в XVI веке, когда французский математик Франсуа Виет и его современники стали применять буквы для обозначения не только чисел неизвестных (что делалось и ранее), но и любых чисел. Однако эта символика еще отличалась от современной. 
Виет ввел буквенные обозначения для коэффициентов и неизвестного в уравнениях: например, искомое – буква N (Numers), квадрат искомого – Q (Quadrates), куб – С (Cubes), равно – aequ (aequali).
Запись следующих уравнений у Виета выглядела так:
x 3 – 3x = 1 NC – 3 N aequ 1
x 3 – 8x 2 + 16x = 40 1 С – 8Q +16 N aequ 40 
Англичанин Харриот в 1631 году заменяет большие буквы малыми. Затем французский математик и философ, основоположник «декардовой» системы координат в геометрии Рене Декарт предлагает известные числа обозначать первыми буквами латинского алфавита a, b, c,…, а неизвестные – последними буквами x, y, z.
Декарт в 1637 году вводит для обозначения равенства известный всем знак «=».
В 1631 году Харриот предлагает для обозначения неравенства использовать теперешние знаки «>» и «<». В конце XV века знаки сложения «+» и вычитания «–», предложенные Видманом, получают широкое распространение. Круглые скобки появились у Таргальи в 1556 году, но лишь в середине XVIII века скобки стали употребляться во всех математических книгах. 
Знак умножения « » впервые в 1661 году ввел У.Аутрид.
Современные знаки умножения в виде « ∙ » и деления в виде « : » впервые использовал немецкий философ, математик и физик Готфрид Лейбниц. Знак деления в 1684 году, а умножения – в 1698 году. В 1674 году усовершенствуя счетную машину Б. Паскаля, конструирует «компьютер», умеющий выполнять основные арифметические действия.
В 1675 году Лейбниц создает дифференциальное и интегральное исчисление, обнародовав главные результаты своего открытия в 1684. Именно Лейбницу принадлежат термины «дифференциал», «дифференциальное исчисление», «дифференциальное уравнение», «функция», «переменная», «постоянная», «координаты», «абсцисса», «алгебраические и трансцендентные кривые», «алгоритм».
История появления цифр и чисел
Понятие о натуральных числах формировалось постепенно и осложнялось неумением первобытного человека отделять числовую абстракцию от её конкретного представления. Вследствие этого счёт долгое время оставался только вещественным, то есть использовались пальцы, камешки, пометки. Археолог Б. А. Фролов обосновывает существование счёта уже в верхнем палеолите, который был более двух миллионов лет назад. До появления цифр в том виде, который известен нам сейчас, разные народы использовали своё написание цифр и чисел. Рассмотрим некоторые из них.

Изображение цифр и чисел у племени Майя
Изображение цифр в Индии (I век)

От этих индийских значков произошли современные цифры
Изображение цифр и чисел в Древнем Египте
Существовали и более экзотичные варианты. Например, туземцы островов Торресова пролива использовали двоичную систему для записи чисел.
В хозяйственной жизни далекого прошлого люди обходились сравнительно небольшими числами, так называемым малым счетом наших предков.
Счет доходил до числа 10 000, которое в самых старых памятниках называется тьма, то есть темное число. В дальнейшем граница малого счета была отодвинута до 10 8 , до числа тьма тём. Но наряду с этим малым числом, если получался великий счет и перечень, употреблялась вторая система, называвшаяся великим числом или счетом или числом великим словенским. При счете употреблялись более высокие разряды: тьма – 10 6 , легион – 10 12 , леодр – 10 24 , ворон – 10 48 , иногда еще колода – десять воронов – 10 49 , хотя колоду следует принять как 10 96 . Для обозначения этих больших чисел наши предки придумали способ, не встречающийся ни у одного из известных нам народов: число единиц любого из перечисленных высших разрядов обозначалось той же буквой, что и простые единицы, но окружность для каждого числа собственным бордюром.
Величайшие греческие математики не додумались до этого способа письма чисел. Таких больших чисел не требовала и не требует и теперь никакая практическая задача.
Архимед, величайший древнегреческий математик, сосчитал, что число песчинок во всем мировом пространстве, как это понимал в то время, не превышает 10 63 . Славянский честолюбец сказал бы, что это число песчинок не больше тысяч легионов воронов 10 63 = 10 3 * 10 12 * 10 48 . Число песчинок во всем мировом пространстве того времени действительно могло казаться наибольшим мыслимым числом.
Вавилоняне создали систему счисления, использовавшую для чисел от 1 до 59, основание 10. Символ, обозначавший единицу, повторялся нужное количество раз для чисел от 1 до 9. Для обозначения чисел от 11 до 59 вавилоняне использовали комбинацию символа числа 10 и символа единицы. Для обозначения чисел, начиная с 60 и больше, вавилоняне ввели позиционную систему счисления с основанием 60. Существенным продвижением стал позиционный принцип, согласно которому один и тот же числовой знак (символ) имеет различные значения в зависимости от того места, где он расположен. Примером могут служить значения шестерки в записи (современной) числа 606. Однако нуль в системе счисления древних вавилонян отсутствовал, из-за чего один и тот же набор символов мог означать и число 65 (60 + 5), и число 3605 (602 + 0 + 5). Вавилоняне составили таблицы обратных чисел, которые использовались при выполнении деления, таблицы квадратов и квадратных корней, а также таблицы кубов и кубических корней. Им было известно приближение числа.
Греческая система счисления была основана на использовании букв алфавита. Аттическая система, бывшая в ходу с VI по III век до нашей эры, использовала для обозначения единицы вертикальную черту, а для обозначения чисел 5, 10, 100, 1000 и 10 000 начальные буквы их греческих названий. В более поздней ионической системе счисления для обозначения чисел использовались 24 буквы греческого алфавита и три архаические буквы. Кратные 1000 до 9000 обозначались так же, как первые девять целых чисел от 1 до 9, но перед каждой буквой ставилась вертикальная черта. Десятки тысяч обозначались буквой М (от греческого “мириои” – 10 000), после которой ставилось то число, на которое нужно было умножить десять тысяч.
Для пифагорейцев любое число представляло собой нечто большее, чем количественную величину. Например, число 2, согласно их воззрению, означало различие и потому отождествлялось с мнением. Четверка представляла справедливость, так как это первое число, равное произведению двух одинаковых множителей.
Пифагорейцы также открыли, что сумма некоторых пар квадратных чисел есть снова квадратное число. Например, сумма 9 и 16 равна 25, а сумма 25 и 144 равна 169. Такие тройки чисел, как 3, 4 и 5 или 5, 12 и 13, называются пифагоровыми числами.
Римская система счисления основывалась на громоздких обозначениях чисел. Главной ее особенностью был вычитательный принцип, например, запись числа 9 в виде IX, вошел в широкое употребление только после изобретения наборных литер в 15 веке. Римские обозначения чисел применялись в некоторых европейских школах примерно до 1600 года, а в бухгалтерии и столетием позже.
Основные этапы развития
Когда понятие абстрактного числа окончательно утвердилось, следующей ступенью стали операции с числами. Натуральное число — это идеализация конечного множества однородных, устойчивых и неделимых предметов (людей, овец, дней и т. п.). Для счёта важно иметь математические модели таких важнейших событий, как объединение таких множеств в одно или, наоборот, отделение части множества. Так появились операции сложения и вычитания, умножения и деления. Свойства и взаимосвязь операций открывались постепенно.
Древнеегипетские математические тексты относятся к началу II тысячелетия до нашей эры. Математика тогда использовалась в астрономии, мореплавании, землемерии, при строительстве домов, плотин, каналов и военных укреплений. Денежных расчётов, как и самих денег, в Египте не было. Египтяне писали на папирусе, который сохраняется плохо, и поэтому в настоящее время знаний о математике Египта существенно меньше, чем о математике Вавилона или Греции. Вероятно, она была развита лучше, чем можно представить, исходя из дошедших до нас документов, что подтверждается тем, что греческие математики учились у египтян.
Основной сохранившийся папирус Ахмеса, записанный в 1650 году до нашей эры, содержит 84 математические задачи. Все задачи из папируса имеют прикладной характер и связаны с практикой строительства, размежеванием земельных наделов и т. п. Задачи сгруппированы не по методам, а по тематике. По преимуществу это задачи на нахождение площадей треугольника, четырёхугольников и круга, разнообразные действия с целыми числами и дробями, пропорциональное деление, нахождение отношений, возведение в разные степени, определение среднего арифметического, арифметические прогрессии, решение уравнений первой и второй степени с одним неизвестным.
В папирусе есть целый ряд свидетельств того, что математика в Древнем Египте тех лет начинала приобретать теоретический характер. Так, египетские математики умели извлекать корни и возводить в степень, решать уравнения, были знакомы с арифметической и геометрической прогрессией и даже владели зачатками алгебры.
Вавилоняне писали клинописными значками на глиняных табличках, которые в немалом количестве дошли до наших дней. Поэтому мы имеем довольно полное представление о математических достижениях учёных Вавилонского государства. Вавилонская расчётная техника была намного совершеннее египетской, а круг решаемых задач существенно шире. Есть задачи на решение уравнений второй степени, геометрические прогрессии. При решении применялись пропорции, средние арифметические, проценты. Методы работы с прогрессиями были глубже, чем у египтян. Линейные и квадратные уравнения решались ещё в эпоху Хаммурапи. При этом использовалась геометрическая терминология (произведение ab называлось площадью, abc — объёмом, и т. д.). Встречаются также кубические уравнения и системы линейных уравнений. Венцом планиметрии была теорема Пифагора.
Шумеры и вавилоняне использовали 60-ричную позиционную систему счисления, увековеченную в нашем делении круга на 360°, часа на 60 минут и минуты на 60 секунд.
Всё же богатая теоретическая основа математики Вавилона не имела целостного характера и сводилась к набору разрозненных приёмов, лишённых доказательной базы. Систематический доказательный подход в математике появился только у греков.
Цифры в древнем Китае обозначались специальными иероглифами, которые появились во II тысячелетии до н. э., и начертание их окончательно установилось к III веку до н. э. Эти иероглифы применяются и в настоящее время.
Вычисления производились на специальной счётной доске суаньпань (см. на фотографии), по принципу использования аналогичной русским счётам. Нуль сначала обозначался пустым местом, специальный иероглиф появился около XII века н. э. Для запоминания таблицы умножения существовала специальная песня, которую ученики заучивали наизусть.
Китайцам было известно многое, в том числе: вся базовая арифметика (включая нахождение наибольшего общего делителя и наименьшего общего кратного), действия с дробями, пропорции, отрицательные числа, площади и объёмы основных фигур и тел, теорема Пифагора и алгоритм подбора пифагоровых троек, решение квадратных уравнений. Был даже разработан метод фан-чэн для решения систем произвольного числа линейных уравнений — аналог классического европейского метода Гаусса.
Математика в современном понимании этого слова родилась в Греции. Во-первых, пифагорейская школа выдвинула тезис «Числа правят миром». Это означало, что истины математики есть в известном смысле истины реального бытия. Во-вторых, для открытия таких истин пифагорейцы разработали законченную методологию. Сначала они составили список первичных, интуитивно очевидных математических истин (аксиомы, постулаты). Затем с помощью логических рассуждений из этих истин выводились новые утверждения, которые также обязаны быть истинными. Так появилась дедуктивная математика. Греческая математика впечатляет, прежде всего, богатством содержания. Многие учёные нового времени отмечали, что мотивы своих открытий почерпнули у древних. Зачатки анализа заметны у Архимеда, корни алгебры — у Диофанта, аналитическая геометрия — у Аполлония.
Но главное не в этом. Два достижения греческой математики далеко пережили своих творцов. Первое — греки построили математику как целостную науку с собственной методологией, основанной на чётко сформулированных законах логики.
Второе — они провозгласили, что законы природы постижимы для человеческого разума, и математические модели — ключ к их познанию.
Индийский способ записи чисел изначально был изысканным. Несколько видоизменившись, эти значки стали современными цифрами, которые мы называем арабскими. Около 500 года н. э. неизвестный индийский математик изобрёл новую систему записи чисел — десятичную позиционную систему. В ней выполнение арифметических действий оказалось неизмеримо проще, чем в старых, с буквенными кодами, как у греков, или шестидесятиричных, как у вавилонян. Индусы разработали полные алгоритмы всех арифметических операций, включая извлечение квадратных и кубических корней.
К V—VI векам относятся труды Ариабхаты, выдающегося индийского математика и астронома. В его труде «Ариабхатиам» встречается множество решений вычислительных задач. В VII веке работал другой известный индийский математик и астроном, Брахмагупта.
Начиная с Брахмагупты, индийские математики свободно обращаются с отрицательными числами, трактуя их как долг. Наибольшего успеха средневековые индийские математики добились в области теории чисел и численных методов. Индийцы далеко продвинулись в алгебре. Их символика богаче, чем у Диофанта, хотя несколько громоздка (засорена словами).
Западная Европа (IV-XV века)
В V веке наступил конец Западной Римской империи, и территория Западной Европы надолго превратилась в поле сражений с завоевателями и разбойниками (гунны, готы, венгры, арабы, норманны и т. п.). Развитие науки прекратилось. Потребность в математике ограничивается арифметикой и расчётом календаря церковных праздников.
Стабилизация и восстановление европейской культуры начинаются с XI века. Появляются первые университеты (Салерно, Болонья). Расширяется преподавание математики. Первое знакомство европейских учёных с античными открытиями происходило в Испании. В конце XII века на базе нескольких монастырских школ был создан Парижский университет, где обучались тысячи студентов со всех концов Европы. Почти одновременно возникают Оксфорд и Кембридж в Британии. В XII веке там переводятся с греческого и арабского на латинский основные труды великих греков и их исламских учеников. С XIV века главным местом научного обмена становится Византия. Особенно охотно переводились и издавались «Начала» Евклида; постепенно они обрастали комментариями местных геометров.
Интерес к науке растёт, и одно из проявлений этого — смена числовой системы. Долгое время в Европе применялись римские цифры. В XII—XIII веках публикуются первые в Европе изложения десятичной позиционной системы записи (сначала переводы Аль-Хорезми, потом собственные руководства), и начинается её применение. С XIV века индо-арабские цифры начинают вытеснять римские даже на могильных плитах. Только в астрономии ещё долго применялась шестидесятеричная вавилонская арифметика.
Первым крупным математиком средневековой Европы стал в XIII веке Леонардо Пизанский, известный под прозвищем Фибоначчи. Основной его труд «Книга абака», изданная в 1202 году. Абаком Леонардо называл арифметические вычисления. Его изложение по полноте и глубине сразу стало выше всех античных и исламских прототипов, и долгое время было непревзойдённым. Эта книга оказала огромное влияние на распространение математических знаний, популярность индийских цифр и десятичной системы в Европе.
В XIV веке университеты появляются почти во всех крупных странах: Прага, Краков, Вена, Гейдельберг и Лейпциг. 
Лука Пачоли, крупнейший алгебраист XV века, друг Леонардо да Винчи, дал ясный, хотя не слишком удобный набросок алгебраической символики. Видный немецкий математик и астроном XV века Иоганн Мюллер напечатал первый в Европе труд, посвящённый тригонометрии.
Западная Европа (XVI век)
XVI век стал переломным для европейской математики. Первым крупным достижением стало открытие общего метода решения уравнений третьей и четвёртой степени. Итальянские математики дель Ферро, Тарталья и Феррари решили проблему, с которой несколько веков не могли справиться лучшие математики мира. При этом обнаружилось, что в решении иногда появлялись «невозможные» корни из отрицательных чисел. После анализа ситуации европейские математики назвали эти корни «мнимыми числами» и выработали правила обращения с ними, приводящие к правильному результату. Так в математику впервые вошли комплексные числа.
Важнейший шаг к новой математике сделал француз Франсуа Виет. Он окончательно сформулировал символический язык арифметики — буквенную алгебру. С её появлением открылась возможность проведения исследований невиданной ранее глубины и общности. Символика Виета не была похожа на принятую ныне, современный её вариант позднее предложил Декарт.
Третье великое открытие XVI века — изобретение логарифмов сделал Джон Непер. Сложные расчёты упростились во много раз, а математика получила новую неклассическую функцию с широкой областью применения.
В 1585 году фламандец Симон Стевин издаёт книгу «Десятая» о правилах действий с десятичными дробями, после чего десятичная система одерживает окончательную победу и в области дробных чисел.
Западная Европа (XVII век)
В XVII веке быстрое развитие математики продолжается. Рене Декарт исправляет стратегическую ошибку античных математиков и восстанавливает алгебраическое понимание числа. Более того, он указывает способ перевода геометрических предложений на алгебраический язык с помощью системы координат. Аналитический метод Декарта немедленно взяли на вооружение Валлис, Ферма и многие другие видные математики.
Пьер Ферма, Гюйгенс и Якоб Бернулли открывают новый раздел математики, которому суждено большое будущее — теорию вероятностей.
Во второй половине XVII века появляется научная периодика. Французская Академия наук с 1699 года издаёт свои записки (Memoires).
Западная Европа (XVIII век)
XVIII век в математике можно кратко охарактеризовать как век анализа, который стал главным объектом приложения усилий математиков. Главным методом познания природы становится составление и решение дифференциальных уравнений. Далеко продвинулись теория и техника интегрирования. В науке на первом месте стоят такие известные имена как
Стремительно развивается линейная алгебра. Первое подробное описание общего решения линейных систем дал в 1750 году Габриэль Крамер. Центрами математических исследований становятся Академии наук. В конце XVIII века появляются специализированные математические журналы.
Западная Европа (XIX век)
Неоспоримая эффективность применения математики в естествознании подталкивала учёных к мысли, что познание в математике есть часть познания реального мира. Но в XIX веке эволюционное развитие математики было нарушено, и этот, казавшийся непоколебимым, тезис был поставлен под сомнение. В алгебре и геометрии появляются многочисленные нестандартные структуры с необычными свойствами: неевклидовы и многомерные геометрии, конечные поля и т. п. Объектами математического исследования всё больше становятся нечисловые объекты: события, векторы, функции, и т. д. Возникает и получает широкое развитие математическая логика. В целом в XIX веке роль и престиж математики в науке и экономике заметно растут. Соответственно растёт и её государственная поддержка. Математика вновь становится по преимуществу университетской наукой. Появляются первые математические общества: Лондонское, Американское, Французское, Московское.
В XIX веке молодая российская математика уже выдвинула учёных мирового уровня. Первым из них стал Михаил Васильевич Остроградский. Как и большинство российских математиков , он разрабатывал преимущественно прикладные задачи анализа, занимался теорией чисел.
Фундаментальными вопросами математики в России первой половины XIX века занялся только Николай Иванович Лобачевский, который выступил против догмата евклидовости пространства.
Он построил геометрию Лобачевского и глубоко исследовал её необычные свойства. Опубликовал труды по алгебре, математическому анализу и теории вероятностей. Лобачевский настолько опередил своё время, что был оценён по заслугам только спустя много лет после смерти. Несколько важных открытий общего характера сделала Софья Ковалевская.
Во второй половине XIX века российская математика, при общем прикладном уклоне, публикует и немало фундаментальных результатов. Пафнутий Львович Чебышёв, математик-универсал, сделал множество открытий в самых разных областях математики — теории чисел, теории вероятностей, теории приближения функций.
Западная Европа (XX век)
Престиж профессии математика стал в XX столетии заметно выше. Невозможно сколько-нибудь полно перечислить сделанные открытия.
В начале века Эмми Нётер и Ван дер Варден завершили построение основ абстрактной алгебры. Герман Минковский в 1907 году разработал модель кинематики теории относительности. Капитальные результаты получены в теории алгоритмов.
А. Н. Колмогоров завершил общепризнанную аксиоматику теории вероятностей. Его фундаментальные труды по теории функций, математической логике, топологии, дифференциальным уравнениям, функциональному анализу и особенно по теории вероятностей и теории информации были высоко оценены.
В 1960-х годах Абрахам Робинсон опубликовал изложение нестандартного анализа — альтернативного подхода к обоснованию математического анализа на основе актуальных бесконечно малых.
Во второй половине XX века, в связи с появлением компьютеров, произошла существенная переориентация математических усилий. Значительно выросла роль таких разделов, как численные методы, теория оптимизации, общение с очень большими базами данных, имитация искусственного интеллекта, кодирование звуковых и видеоданных и т. п. Возникли новые науки — кибернетика и информатика.
Начало современного этапа в развитии математики характеризовалось изменениями во всех ее основных разделах: геометрии, алгебре и анализе.
Коренные изменения в алгебре наметились еще в XIX веке. Если алгебра минувшего времени оперировала числом, то современная алгебра распространяется на величины гораздо более общего характера: события, функции, множества, операции над векторами и над движениями разного рода. Алгебра в своём развитии прошла много сложных этапов, начиная с узелковой системы счёта и заканчивая математическим анализом и теорией вероятности, начиная с элементарных зарубок и заканчивая линейными уравнениями и интегралами.
В данной работе мы ознакомились с историей развития алгебры, узнали, как она формировалась в процессе эволюции человечества, изучили историю возникновения цифр и чисел. Узнали имена основоположников математики и ознакомились с содержанием некоторых их работ и открытий. Теперь мы знаем, что современный вид алгебраической символике придал Рене Декарт ещё в середине XVII века (трактат «Геометрия»), Исаак Ньютон усовершенствовал этот процесс («Универсальная арифметика»), а Эйлер внёс некоторые оставшиеся тонкости и уточнения.
В настоящее время сильно разрослись методы применения алгебры в различных науках: геометрии, анализе, физике, кристаллографии. Обширными разделами алгебры являются теория групп и линейная алгебра. Бурное развитие всех отраслей науки и техники неразрывно связано с развитием алгебры как науки. На базе алгебры в эпоху тотальной компьютеризации возникли новые науки. Изучение основ алгебры в современных условиях становится все более существенным элементом общеобразовательной подготовки молодого поколения.
1. Очерки по истории математики, Б.В.Болгарский, Минск, «Высшая школа», 1979 г.
2. Математика, Я познаю мир, Москва, АСТ, 2000 г.
3. Алгебра, учебник для 7 класса общеобразовательных учреждений, А.Г.Мордкович, Москва, Мнемозина, 2009 г.
4. Энциклопедический словарь юного математика, Москва, Педагогика-пресс, 1999 г.
5. История математики в школе, Г.И.Глейзер, Москва, Просвещение, 1964
6. История математики в трёх томах, под ред. А.П.Юшкевича, Москва, Наука, 1970-1972 г.г.
7. История математики в двух томах, К.А.Рыбников, Москва изд. МГУ, 1960-1963 г.г.
Некоторые математические знаки и даты их возникновения
Отношение длины окружности к диаметру
Основание натурального логарифма
Корень квадратный из –1
,
Десятичная система счисления чисел

referat-4all.ru



