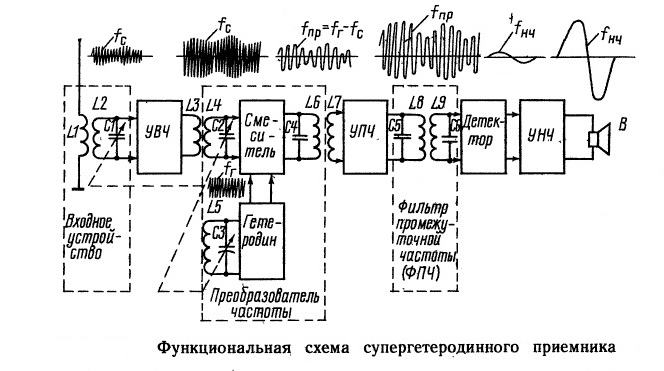
Решение дифференциальных уравнений с разделяющимися переменными калькулятор – Решение дифференциального уравнения с разделяющимися переменными – 25 Сентября 2012 – Примеры решений задач

Задача 1. \(\sqrt{y^2+1}dx=xydy.\)

Решение. Это уравнение с разделяющимися переменными. Деля обе его части на произведение \(\sqrt{y^2+1}\cdot x\), получаем

$$\frac{dx}{x}=\frac{ydy}{\sqrt{y^2+1}},\; x\neq 0,$$

откуда

$$\int {\frac{dx}{x}}=\int {\frac{ydy}{\sqrt{y^2+1}}}+C,$$

или

$$\ln\left|x \right|-\sqrt{y^2+1}=C.$$

Таким образом, все решения данного уравнения имеют вид

$$\ln\left|x \right|-\sqrt{y^2+1}=C,\; x=0.$$

Задача 2. \((x^2-1)y’+2xy^2=0,\; y(0)=1.\)

Решение. Сначала находим все решения этого уравнения. Имеем

$$(x^2-1)dy+2xy^2dx=0,$$

откуда, разделив переменные \(x\) и \(y\), получаем

$$\frac{dy}{y^2}+\frac{2xdx}{x^2-1}=0.$$

Интегрируя обе части полученного уравнения, находим

$$-\frac{1}{y}+ \ln \left|x^2-1 \right|=C.$$

Для получения всех решений исходного уравнения к последнему семейству интегральных кривых присоединим еше решение \(y=0.\)

Далее, из совокупности всех интегральных кривых выделим ту кривую, которая проходит через точку \((0,1)\). Полагая \(x=0\) и \(y=1\), находим \(C=-1.\) Таким образом, функция

$$y=\frac{1}{1+ \ln \left|x^2-1 \right|}$$

является решением поставленной задачи.

Задача 3. \(xy’+y=y^2,\; y(1)=0,5.\)

Решение. Записывая уравнение в виде

$$xdy+(y-y^2)dx=0$$

и разделяя переменные, имеем

$$\frac{dy}{y-y^2}+\frac{dx}{x}=0.$$

Интегрируя, получаем

$$xy(1-y)=C.$$

Заметим, что несмотря на деление обеих частей уравнения на \(x(y-y^2)\), его решения \(x=0,\: y=0\) и \(y=1\) не были потеряны. Наконец, подставив \(x=1,\: y=0,5\), находим \(C=\frac{1}{4}\). Следовательно, дифференцируемая кривая

$$4xy(1-y)-1=0$$

— решение поставленной задачи.

Задача 4. \(e^{-s}\left(1+\frac{ds}{dt} \right)=1.\)

Решение. Переписав уравнение в виде

$$\frac{ds}{dt}=e^s-1,$$

разделяем переменные \(s\) и \(t\):

$$\frac{ds}{e^s-1}=dt.$$

Проинтегрировав полученное уравнение, находим \(\ln \left|\frac{e^s-1}{e^s} \right|=t+ \ln C,\) или \(s=-\ln (1+Ce^t).\)

2012-01-17 • Просмотров [ 10195 ]

primat.org

Содержание

Решение дифференциальных уравнений

Математические модели происходящих процессов чаще всего описываются дифференциальными уравнениями. Поэтому остро стоит проблема нахождения их решения. Будем считать, что искомые функции рассматриваемых дифференциальных уравнений зависят от одной переменной.

Методы решения дифференциальных уравнений

1. К простейшим дифференциальным уравнениям первого порядка относятся уравнения вида

   

Решение таких уравнений находится с помощью операции интегрирования:

   

2. Дифференциальные уравнения вида

   

сводятся к дифференциальным уравнениям делением обеих частей равенства на . В результате получаем дифференциальное уравнение

   

Тогда, согласно выше написанному, его решение

   

3. Дифференциальным уравнением с разделяющимися переменными называется уравнение вида или .

Например.

Дифференциальное уравнение или называется дифференциальным уравнением с разделенными переменными.

Например.

Общее решение такого уравнения ищется с помощью интегрирования обеих частей равенства :

   

Дифференциальные уравнения с разделяющимися переменными сводятся к дифференциальным уравнениям с разделенными переменными делением на произведение :

   

Подробнее о дифференциальных уравнениях с разделяющимися переменными читайте в отдельной статье.

4. Дифференциальные уравнения вида

   

сводятся к дифференциальным уравнениям с разделяющимися переменными с помощью замены

   

5. Однородным дифференциальным уравнением n-го порядка

называется уравнение , удовлетворяющее условию

   

Однородные дифференциальные уравнения можно свисти к уравнению вида или , которое с помощью замены

   

(или ) сводится к дифференциальному уравнению с разделяющимися переменными.

Подробнее об однородных дифференциальных уравнениях читайте в отдельной статье.

6. Дифференциальные уравнения , где коэффициенты – некоторые действительные числа.

Если , то данное уравнение является однородным и методика получения его решения описана выше.

Рассмотрим случай, когда хотя бы одно из чисел или отлично от нуля. Выполним заменой (введем новые переменные)

   

Здесь – некоторые числа. При этом

   

Подставляя эти выражения в исходное дифференциальное уравнение, будем иметь:

   

или

   

Величины будем выбирать так, чтобы свободные коэффициенты в числителе и знаменателе последнего дифференциального уравнения равнялись нулю. То есть h и k найдем из системы

   

С учетом этого уравнение сводится к дифференциальному уравнению

   

которое является однородным.

ru.solverbook.com

Решение уравнений с разделяющимися переменными.

 

Найти решения дифференциальных уравнений:

1. ,  

Решение.

Это уравнение с разделяющимися переменными.

 

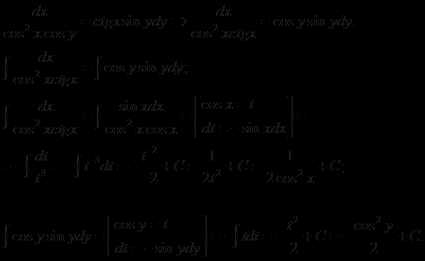
Таким образом,

Учитывая начальные условия, найдем С:

 

Таким образом, 

Ответ:  

 

 

 

2. 

Решение.

Это уравнение с разделяющимися переменными.

 

Следовательно,

 

Учитывая начальные условия, найдем С:

 

Таким образом,

Ответ: 

 

 

 

3. Указать тип дифференциального уравнения и найти его общее решение

 

 

Решение.

Это уравнение с разделяющимися переменными

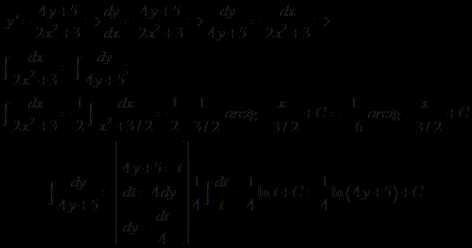
Таким образом,

Ответ: уравнение с разделяющимися переменными; 

 

 

 

4. 

Решение

Это уравнение с разделяющимися переменными.

 

Таким образом,

 

Найдем С из заданных начальных условий.

 

Отсюда получаем ответ.

Ответ: 

 

 

 

 5.    

 

Решение.

Это уравнение с разделяющимися переменными. 

 

Таким образом,

 

Переобозначим постоянную и получим ответ.

Ответ: 

  

 

 

 6.    

 

Решение.

Это уравнение с разделяющимися переменными.

 либо

  

 Таким образом,

  

 Учитывая начальные условия получаем:

 

 Ответ: 

  

 

 7.    

 

Решение.

 Это уравнение с разделяющимися переменными

  

Следовательно,

 .

Найдем постоянную , пользуясь начальными условиями:

  

 Таким образом, 

Ответ: 

 

  

 

8. 

 

 Решение.

Это уравнение с разделяющимися переменными.

 

Следовательно, 

Ответ: 

 

 

9. 

 

Решение.

 

 

Ответ: $y=\frac{x}{1+Cx}.$

  

 

10. 

 

 Решение.

Это уравнение с разделяющимися переменными.

 

 Следовательно,

 

Ответ: 

 

 

 

11.   

 

Решение.

Это уравнение с разделяющимися переменными.

 

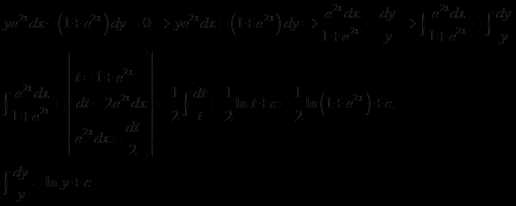
 Таким образом,

 

Ответ: 

  

 

12. Найти общее решение дифференциального уравнения первого порядка 

 

Решение.

Это уравнение с разделяющимися переменными.

 

Таким образом,

 

 Ответ: 

 

 

13.  Найти общее решение

 

 

 Решение.

Это уравнение с разделяющимися переменными.

 

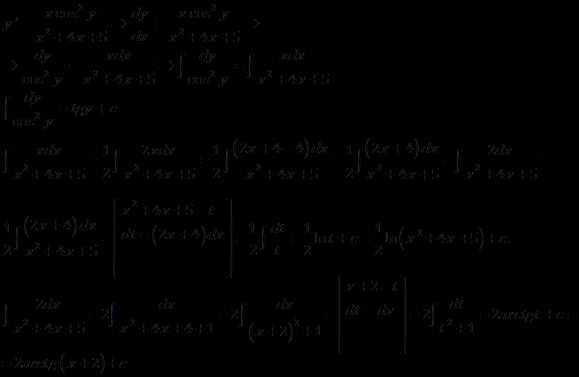
Отсюда,

 

Таким образом,

 

Ответ: .

  

 

 

14.   Решить дифференциальные уравнения

 

 

 Решение.

 Это уравнение с разделяющимися переменными

 

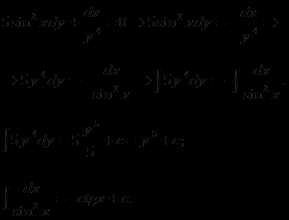
Следовательно,

 

Ответ: 

  

 

 

 

 

kontrolnye.com

Решение уравнений с разделяющимися переменными.

 

Найти решения дифференциальных уравнений:

1. ,  

Решение.

Это уравнение с разделяющимися переменными.

 

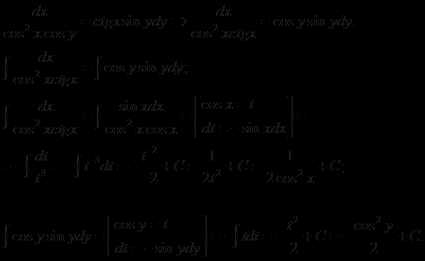
Таким образом,

Учитывая начальные условия, найдем С:

 

Таким образом, 

Ответ:  

 

 

 

2. 

Решение.

Это уравнение с разделяющимися переменными.

 

Следовательно,

 

Учитывая начальные условия, найдем С:

 

Таким образом,

Ответ: 

 

 

 

3. Указать тип дифференциального уравнения и найти его общее решение

 

 

Решение.

Это уравнение с разделяющимися переменными

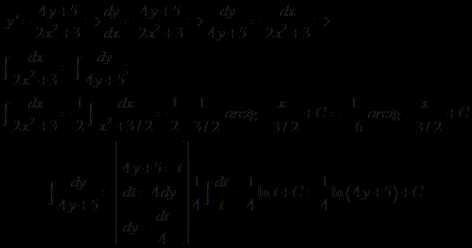
Таким образом,

Ответ: уравнение с разделяющимися переменными; 

 

 

 

4. 

Решение

Это уравнение с разделяющимися переменными.

 

Таким образом,

 

Найдем С из заданных начальных условий.

 

Отсюда получаем ответ.

Ответ: 

 

 

 

 5.    

 

Решение.

Это уравнение с разделяющимися переменными. 

 

Таким образом,

 

Переобозначим постоянную и получим ответ.

Ответ: 

  

 

 

 6.    

 

Решение.

Это уравнение с разделяющимися переменными.

 либо

  

 Таким образом,

  

 Учитывая начальные условия получаем:

 

 Ответ: 

  

 

 7.    

 

Решение.

 Это уравнение с разделяющимися переменными

  

Следовательно,

 .

Найдем постоянную , пользуясь начальными условиями:

  

 Таким образом, 

Ответ: 

 

  

 

8. 

 

 Решение.

Это уравнение с разделяющимися переменными.

 

Следовательно, 

Ответ: 

 

 

9. 

 

Решение.

 

 

Ответ: $y=\frac{x}{1+Cx}.$

  

 

10. 

 

 Решение.

Это уравнение с разделяющимися переменными.

 

 Следовательно,

 

Ответ: 

 

 

 

11.   

 

Решение.

Это уравнение с разделяющимися переменными.

 

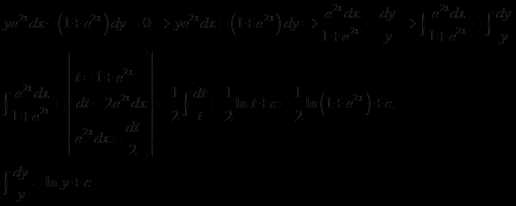
 Таким образом,

 

Ответ: 

  

 

12. Найти общее решение дифференциального уравнения первого порядка 

 

Решение.

Это уравнение с разделяющимися переменными.

 

Таким образом,

 

 Ответ: 

 

 

13.  Найти общее решение

 

 

 Решение.

Это уравнение с разделяющимися переменными.

 

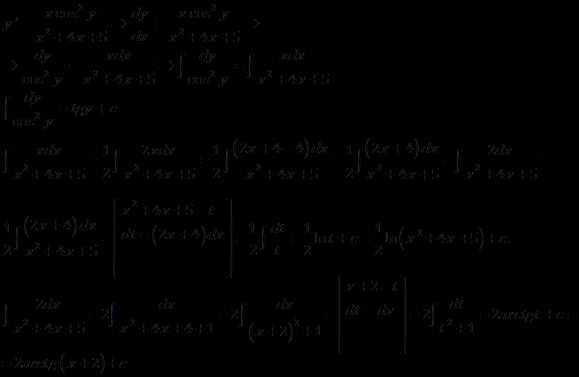
Отсюда,

 

Таким образом,

 

Ответ: .

  

 

 

14.   Решить дифференциальные уравнения

 

 

 Решение.

 Это уравнение с разделяющимися переменными

 

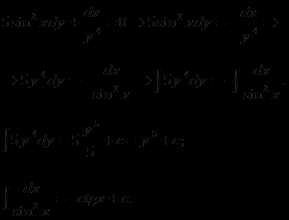
Следовательно,

 

Ответ: 

  

 

 

 

 

kontrolnye.com

Дифференциальные уравнения с разделяющимися переменными

Дифференциальное уравнение вида [cbm]\varphi(y)\,dy=f(x)\,dx[/cbm] называется уравнением с разделенными переменными .

Уравнение вида [cbm]\varphi_1(x)\psi_1(y)\,dx=\varphi_2(x)\psi_2(y)\,dy[/cbm] , в котором коэффициенты при дифференциалах распадаются на множители, зависящие только от [cbm]x[/cbm] и только от [cbm]y[/cbm] , называется уравнением с разделяющимися переменными.

Путем деления на произведение [cbm]\psi_1(y)\varphi_2(x)[/cbm] оно приводится к уравнению с разделенными переменными:

[cbm]\frac{\varphi_1(x)}{\varphi_2(x)}\,dx=\frac{\psi_2(y)}{\psi_1(y)}\,dy.[/cbm]

Общий интеграл этого уравнения имеет вид

[cbm]\int\frac{\varphi_1(x)}{\varphi_2(x)}\,dx-\int\frac{\psi_2(y)}{\psi_1(y)}\,dx=C.[/cbm]

Замечание. Деление на произведение [cbm]\psi_1(y)\varphi_2(x)[/cbm] может привести к потере частных решений, обращающих в ноль это произведение.

Дифференциальное уравнение вида

[cbm]\frac{dy}{dx}=f(ax+by+c),[/cbm]

где [cbm]a,b[/cbm] и [cbm]c[/cbm] — постоянные, заменой переменных [cbm]z=ax+by+c[/cbm] преобразуется в уравнение с разделяющимися переменными.

Пример 1. Решить уравнение [cbm]3e^x\operatorname{tg}y\,dx+(2-e^x)\sec^2{y}\,dy=0[/cbm] .

Решение. Разделим обе части уравнения на произведение [cbm](2-e^x)\operatorname{tg}y[/cbm] :

[cbm]\frac{3e^x}{2-e^x}\,dx+\frac{\sec^2y}{\operatorname{tg}y}\,dy=0.[/cbm]

Получили уравнение с разделенными переменными. Интегрируя его, найдем

[cbm]-3\ln|2-e^x|+\ln|\operatorname{tg}y|=C_1.[/cbm]

После потенцирования получим [cbm]\left|\frac{\operatorname{tg}y}{(2-e^x)^3}\right|=e^{C_1}[/cbm] откуда [cbm]\frac{\operatorname{tg}y}{(2-e^x)^3}=\pm e^{C_1}[/cbm]

Обозначая [cbm]\pm e^{C_1}=C[/cbm] , будем иметь [cbm]\frac{\operatorname{tg}y}{(2-e^x)^3}=C[/cbm] или [cbm]\operatorname{tg}y-C(2-e^x)^3=0[/cbm] . Мы получили общий интеграл данного уравнения.

При делении на произведение [cbm](2-e^x)\operatorname{tg}y[/cbm] предполагалось, что ни один из множителей не обращается в ноль. Приравняв каждый множитель нулю, получим соответственно [cbm]y=k\pi~(k\in\mathbb{Z}),~x\ln2[/cbm] .

Непосредственной подстановкой в исходное уравнение убеждаемся, что [cbm]y=k\pi[/cbm] и [cbm]x\ln{2}[/cbm] являются решениями этого уравнения. Они могут быть формально получены из общего интеграла при [cbm]C=0[/cbm] и [cbm]C=\infty[/cbm] . Последнее означает, что постоянная [cbm]C[/cbm] заменяется через [cbm]\frac{1}{C_2}[/cbm] , после чего общий интеграл примет вид

[cbm]\operatorname{tg}y-\frac{1}{C_2}(2-e^x)^3=0[/cbm] или [cbm]C_2\operatorname{tg}y-(2-e^x)^3=0[/cbm] .

Полагая в последнем равенстве [cbm]C_2=0[/cbm] , что соответствует [cbm]C=\infty[/cbm] , будем иметь, что [cbm](2-e^x)^3=0[/cbm] , откуда и получаем решение [cbm]x=\ln{2}[/cbm] исходного уравнения. Итак, функции [cbm]y=k\pi~(k\in\mathbb{Z})[/cbm] и [cbm]x=\ln{2}[/cbm] являются частными решениями данного уравнения. Поэтому окончательный ответ будет таким:

[cbm]\operatorname{tg}y-C(2-e^x)^3=0.[/cbm]

Пример 2. Найти частное решение уравнения [cbm](1+e^x)yy’=e^x[/cbm] , удовлетворяющее начальному условию [cbm]y|_{x=0}=1[/cbm] .

Решение. Имеем [cbm](1+e^x)y\frac{dy}{dx}=e^x.[/cbm] Разделяя переменные, получаем [cbm]y\,dy=\frac{e^x}{1+e^x}\,dx[/cbm] . Интегрируя, найдем общий интеграл

[cbm]\frac{y^2}{2}=\ln(1+e^x)+C.[/cbm]

(1)

Полагая [cbm]x=0[/cbm] и [cbm]y=1[/cbm] будем иметь [cbm]\frac{1}{2}=\ln{2}+C[/cbm] , откуда [cbm]C=\frac{1}{2}-\ln{2}[/cbm] .

Подставляя найденное значение [cbm]C[/cbm] , получаем частное решение

[cbm]y^2=1+\ln{\!\left(\frac{1+e^x}{2}\right)\!}^2,[/cbm] откуда [cbm]y=\pm\sqrt{1+\ln{\!\left(\frac{1+e^x}{2}\right)\!}^2}.[/cbm]

Из начального условия следует, что [cbm]y>0~(y|_{x=0}=1>0)[/cbm] , поэтому перед корнем берем знак плюс. Итак, искомое частное решение

[cbm]y=\sqrt{1+\ln{\!\left(\frac{1+e^x}{2}\right)\!}^2}.[/cbm]

Пример 3. Найти частные решения уравнения [cbm]y’\sin{x}=y\ln{x}[/cbm] , удовлетворяющие начальным условиям: a) [cbm]y|_{x=\pi/2}=e[/cbm] ; б) [cbm]y|_{x=\pi/2}=1[/cbm] .

Решение. Имеем [cbm]\frac{dy}{dx}\sin{x}=y\ln{y}[/cbm] . Разделяем переменные [cbm]\frac{dy}{y\ln{y}}=\frac{dx}{\sin{x}}[/cbm] . Интегрируя, найдем общий интеграл [cbm]\ln|\ln{y}|=\ln\left|\operatorname{tg}\frac{x}{2}\right|+\ln{C}[/cbm] . После потенцирования получим [cbm]\ln{y}=C\operatorname{tg}\frac{x}{2}[/cbm] или [cbm]y=\exp\!\left(C\operatorname{tg}\frac{x}{2}\right)[/cbm] , что является общим решением исходного уравнения.

а) Положим [cbm]x=\frac{\pi}{2},~y=e[/cbm] , тогда [cbm]e=C\operatorname{tg}\frac{x}{4}[/cbm] , откуда [cbm]C=1[/cbm] . Искомое частное решение [cbm]y=\exp\operatorname{tg}\frac{x}{2}[/cbm] .

б) Полагая в общем решении [cbm]x=\frac{\pi}{2},~y=1[/cbm] , будем иметь [cbm]1=\exp\!\left(C\operatorname{tg}\frac{\pi}{4}\right)[/cbm] откуда [cbm]C=0[/cbm] . Искомое частное решение [cbm]y=1[/cbm] .

Заметим, что в процессе получения общего решения постоянная [cbm]C[/cbm] входила под знак логарифма, и, значит, [cbm]C=0[/cbm] следует рассматривать как предельное значение. Это частное решение [cbm]y=1[/cbm] содержится среди нулей произведения [cbm]y\ln{x}\sin{x}[/cbm] , на которое мы делили обе части данного уравнения.

Пример 4. Найти такую кривую, проходящую через точку [cbm](0;-2)[/cbm] , чтобы тангенс угла наклона касательной в любой ее точке равнялся ординате этой точки, увеличенной на три единицы.

Решение. Исходя из геометрического свойства первой производной, получаем дифференциальное уравнение семейства кривых, удовлетворяющих требуемому в задаче свойству, а именно [cbm]\frac{dy}{dx}=y+3[/cbm] . Разделяя переменные и интегрируя, получаем общее решение

Так как искомая кривая должна проходить через точку [cbm](0;-2)[/cbm] , т.е. [cbm]y|_{x=0}=-2[/cbm] , то при [cbm]x=0[/cbm] получаем [cbm]-2=C-3[/cbm] , откуда [cbm]C=1[/cbm] . Искомая кривая определится уравнением [cbm]y=e^x-3[/cbm] .

Пример 5. Найти кривую, обладающую тем свойством, что длина ее дуги, заключенной между какими-либо двумя точками [cbm]P[/cbm] и [cbm]Q[/cbm] , пропорциональна разности расстояний этих точек от неподвижной точки [cbm]O[/cbm] .

Решение. Если фиксировать точку [cbm]P[/cbm] , то дуга [cbm]QP[/cbm] будет изменяться пропорционально разности [cbm]OQ[/cbm] и постоянной [cbm]OP[/cbm] . Введем полярные координаты, беря точку [cbm]O[/cbm] за полюс и [cbm]OP[/cbm] — за полярную ось (рис. 11). Дифференциал дуги кривой в полярных координатах [cbm](ds)^2=(dr)^2+(rd\varphi)^2[/cbm] .

Отсюда для нашей задачи имеем [cbm]k^2(dr)^2=(dr)^2+(rd\varphi)^2[/cbm] или [cbm]d\varphi=\sqrt{k^2-1}\frac{dr}{r}[/cbm] .

Интегрируя, находим [cbm]r=C\exp\frac{\varphi}{\sqrt{k^2-1}}[/cbm] (логарифмическая спираль).

Пример 6. Допустим, что при постоянной температуре скорость растворения твердого тела в жидкости пропорциональна количеству этого вещества, еще могущего раствориться в жидкости до насыщения последней (предполагается, что вещества, входящие в раствор, химически не действуют друг на друга, и раствор далек еще от насыщения, так как иначе линейный закон для скорости растворения неприменим). Найти зависимость количества растворившегося вещества от времени.

Решение. Пусть [cbm]P[/cbm] — количество вещества, дающее насыщенный раствор, и [cbm]x[/cbm] — количество уже растворившегося вещества. Тогда получаем дифференциальное уравнение [cbm]\frac{dx}{dt}=k(P-x)[/cbm] , где [cbm]k[/cbm] — известный из опыта коэффициент пропорциональности, a [cbm]t[/cbm] — время.

Разделяя переменные, найдем [cbm]\frac{dx}{P-x}=k\,dt[/cbm] .

Интегрируя, получаем [cbm]\ln|x-P|=\ln{C}-kt[/cbm] откуда [cbm]x=P+Ce^{-kt}[/cbm] .

В начальный момент [cbm]t=0[/cbm] имеем [cbm]x=0[/cbm] , поэтому [cbm]C=-P[/cbm] , так что окончательно [cbm]x=P(1-e^{-kt})[/cbm] .

Пример 7. В цилиндрическом сосуде объемом [cbm]V_0[/cbm] заключен атмосферный воздух, который адиабатически (без обмена тепла с окружающей средой) сжимается до объема [cbm]V_1[/cbm] . Вычислить работу сжатия.

Решение. Известно, что адиабатический процесс характеризуется уравнением Пуассона

[cbm]\frac{p}{p_0}=\left(\frac{V_0}{V}\right)^{k},[/cbm]

(3)

где [cbm]V_0[/cbm] — первоначальный объем газа, [cbm]p_0[/cbm] — первоначальное давление газа, [cbm]k[/cbm] — постоянная для данного газа величина.

Обозначим через [cbm]V[/cbm] и [cbm]p[/cbm] соответственно объем и давление газа в тот момент, когда поршень находится на высоте [cbm]h[/cbm] , а через [cbm]S[/cbm] — площадь поршня. Тогда при опускании поршня на величину [cbm]dh[/cbm] объем газа уменьшится на величину [cbm]dV=S\,dh[/cbm] . При этом будет выполнена работа

[cbm]dW=-pS\,dh \quad \text{or} \quad dW=-p\,dV.[/cbm]

(4)

Находя [cbm]p[/cbm] из (3) и подставляя в (4), получаем дифференциальное уравнение процесса

[cbm]dW=-\frac{p_0V_0^k}{V^k}\,dV.[/cbm]

Интегрируя это уравнение, будем иметь

[cbm]W=-p_0V_0^k\int\frac{dV}{V^k}=\frac{p_0V_0^k}{(k-1)V^{k-1}}+C,~k\ne1.[/cbm]

(5)

Согласно начальному условию [cbm]W|_{V=V_0}=0[/cbm] получим [cbm]C=\frac{p_0V_0}{1-k}[/cbm] .

Таким образом, работа адиабатического сжатия (от [cbm]V_0[/cbm] до [cbm]V[/cbm] ) будет [cbm]W=\frac{p_0V_0}{k-1}\left[\left({\!\frac{V_0}{V}\right)\!}^{k-1}-1\right][/cbm] .

При [cbm]V=V_1[/cbm] получаем [cbm]W=\frac{p_0V_0}{k-1}\left[\left({\!\frac{V_0}{V_1}\right)\!}^{k-1}-1\right][/cbm] .

Пример 8. Найти решение уравнения

[cbm]x^3\sin{y}\,y’=2,[/cbm]

(6)

удовлетворяющее условию [cbm]y\to\frac{\pi}{2}, \quad x\to\infty[/cbm]

(7)

Решение. Разделяя переменные и интегрируя, найдем общий интеграл уравнения: [cbm]\cos{y}=\frac{1}{x^2}+C[/cbm] .

Начальное условие даёт [cbm]\cos\frac{\pi}{2}=C[/cbm] , т. е. [cbm]C=0[/cbm] , так что частный интеграл будет иметь вид [cbm]\cos{y}=\frac{1}{x^2}[/cbm] . Ему соответствует бесконечное множество частных решений вида

[cbm]y=\pm\arccos\frac{1}{x^2}+2\pi{n},~n\in\mathbb{Z}\,.[/cbm]

(8)

Среди этих решений имеется только одно, удовлетворяющее начальному условию. Это решение найдем, переходя к пределу при [cbm]x\to\infty[/cbm] в равенстве (8):

[cbm]\frac{\pi}{2}=\pm\arccos0+2\pi{n}[/cbm] или [cbm]\frac{\pi}{2}=\pm\frac{\pi}{2}+2\pi{n}[/cbm] , откуда [cbm]\frac{1}{2}=\pm\frac{1}{2}+2n[/cbm] .

Нетрудно видеть, что получившиеся уравнение имеет два корня: [cbm]n=0[/cbm] и [cbm]n=\frac{1}{2}[/cbm] , причем корень [cbm]n=\frac{1}{2}[/cbm] , отвечающий- знаку минус перед [cbm]\arccos\frac{1}{x^2}[/cbm] , не подходит, так как [cbm]n\in\mathbb{Z}[/cbm] . Таким образом, искомое частное решение уравнения будет [cbm]y=\arccos\frac{1}{x^2}[/cbm] .

В вашем браузере отключен Javascript.
Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!