18.06.201925.11.2018

Решение ргз по физике – Физика решение задач по физике Чертова А.Г Прокофьева В.Л, скачать задачи по физике бесплатно, скачать задачи по физике бесплатно

• by alexxlab
• Комментариев к записи Решение ргз по физике – Физика решение задач по физике Чертова А.Г Прокофьева В.Л, скачать задачи по физике бесплатно, скачать задачи по физике бесплатно нет
• Советы абитуриенту

Методические указания к выполнению ргз

При выполнении РГЗ студенту необходимо руководствоваться следующим:

1. РГЗ выполняются на листах А4, вложенных в файл. На титульном листе приводятся сведения по следующему образцу:

ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ

Белгородский государственный технологический

Университет

им. В.Г. Шухова

Расчетно-графическое задание по физике

Выполнил:

студент группы ХТ-11

Иванов И.И.

Проверил:

Петров А.А.

Белгород

2013г.

2. После титульного листа прилагаются распечатанные условия заданий. РГЗ выполняются чернилами. Для замечаний преподавателя оставляются поля. Каждая задача должна начинаться с новой страницы.

3. Решения должны сопровождаться исчерпывающими, и краткими объяснениями, через раскрывающими физический смысл употребляемых формул или законов.

4. Необходимо решить задачу в общем виде, т.е. выразить искомую величину через буквенные обозначения величин, заданных в условии задачи. Сопоставить размерности левой и правой частей полученной формулы.

5. Подставить в рабочую формулу все величины, выраженные в системе СИ. Произвести вычисления и получить численное значение искомой величины. Полученное значение записать в ответ.

6. В конце контрольной работы указать учебники и учебные пособия, которые использовались при решении задач.

8. Контрольные работы, оформленные без соблюдения указанных правил не проверяются.

9. При защите РГЗ необходимо дать устное объяснение решенных задач и используемых при решении законов.

Письменное оформление решения задач

Общепринятый способ письменного оформления решения задачи по физике заключается в следующем.

Сначала записывают условие (текст) задачи полностью, без сокращений, а затем кратко. Краткая запись отражает, что дано в условии и что нужно определить, при этом все значения данных величин записывают слева в столбик в том порядке, в котором они встречаются в условии. Значение физической величины состоит из числового значения и наименования единицы этой величины. Например, в записи v = 5 м/с v – обозначение скорости, 5 м/с – значение ско­рости, 5 -числовое значение, м/с – единица скорости (точнее, обоз­начение единицы скорости – метр в секунду).

Снизу столбик данных значений подчеркивают горизонтальной чер­той и под ней пишут искомую величину. Справа столбик отделяют вертикальной чертой и пишут заголовок “Решение”.

. Решают задачу и записывают решение в общем виде, в буквенных обозначениях, при этом промежуточные вычисления не производят. В результате получается расчетная формула, в которой искомая величи­на выражена в обозначениях величин, заданных в условии задачи.

Решение должно сопровождаться! краткими, но исчерпывающими пояснениями, в которых дается обоснование используемых формул и объяснение обозначений. Необходимо делать схематический чертеж (рисунок), если это возможно в данной задаче. Рисунок помогает на­гляднее представить рассматриваемую в задаче ситуацию и более чет­ко описать ход решения.

После получения расчетной формулы ее проверяют следующим образом: в правую часть формулы вместо обозначений физических величин подставляют обозначения единиц СИ этих величин, произво­дят с ними необходимые действия и убеждаются в том, что полученная при этом единица соответствует искомой величине. Затем числовые значения величин выражают в единицах СИ, подставляют их в расчетную формулу и производят вычисления, соблюдая при этом прави­ла приближенных вычислений. В конце решения записы­вают ответ.

Рассмотрим пример оформления решения задачи по РГЗ

Задача. Электрон влетает со скоростью υ = 5 • 10⁶ м/с в однород­ное электростатическое поле, напряженность которого Е= 10³ В/м и направлена так же, как и скорость электрона. Сколько времени будет двигаться электрон до момента остановки и какой путь он при этом прой­дет? Заряд электрона е = 1,6 • 10^-19Кл, его масса m_e = 9,1 • 10

-31 кг.

υ=5∙106м/c

Е=1∙10³В/м Решение

e=1,6∙10^-19Кл В электростатическом поле на электрон действует сила F,

m_e=9,1∙10^-31кг модуль которой F = еЕ, а направление противоположно

t–? s–? направлению на­пряженности Ё. Электрон движется

прямолинейно (силой тяжести пре­небрегаем) в течение некоторого про­межутка времени t до остановки, при этом под действием силы F импульс электрона изменяется. Согласно вто­рому закону Ньютона,

Ft = m_eυ₂– m_eυ₁

где υ₂, υ₁ – скорость электрона в точках

2 и 1 соответственно.

Для проекций на ось ОХ уравнение имеет вид F_xt = m_eυ_2x –. m_eυ_1x. В данном случае F_x = —F, eυ_2x = 0, υ_1x= υ поэтому Ft = mυ, откуда t = m_eυ/F, или

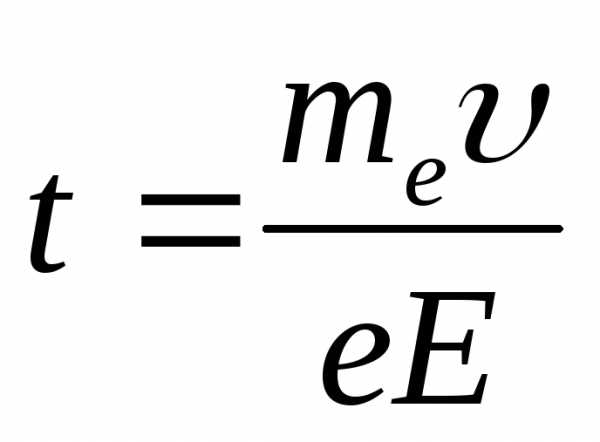(1)

Изменение кинетической энергии электрона равно работе силы F:

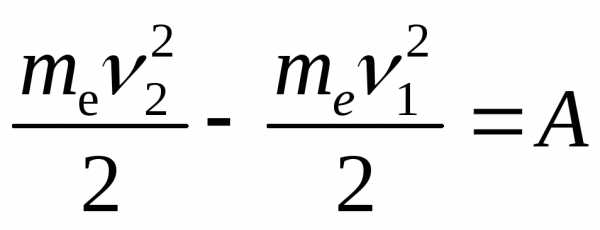
Учитывая, что υ₂=0; υ₁=υ A=F•s•cos180^О=-Fs, получаем тυ²/2 = Fs, где s – модуль перемещения, который в данном случае равен пройденному пути. Следовательно,

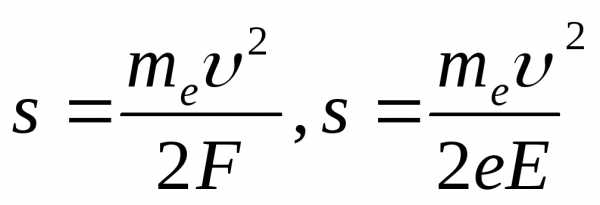(2)

Расчетные формулы (1) и (2) проверим с помощью действий над единицами физических величин:

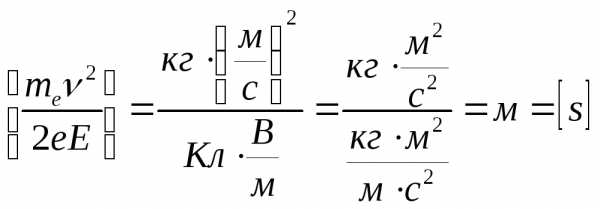
Подставим числовые значения величин в формулы (1) и (2) и про­изведем вычисления:

Ответ: t = 3•10 ^{– 8} c, s = 7•10 ^{– 2} м

studfiles.net

РГЗ1 по физике

РГЗ1 по физике, вариант 2

1.13Наблюдатель стоит в начале электропоезда. Первый вагон прошел мимо него за время. Какое время будет двигаться мимо него седьмой вагон? Движение поезда равноускоренное, его начальная скорость.

Решение:

Скорость поезда при заданных условиях будет описываться формулой:

Пройденное расстояние:

Будем обозначать через момент времени, когда начало-го вагона поравнялось с наблюдателем. Например,,.

По условию, , где– длина вагона.

Значит, .

Начало седьмого вагона поравняется с наблюдателем в момент , к этому времени проедут шесть вагонов, поэтому,.

Конец седьмого вагона — это начало восьмого: ,.

Ответ:

1.29Колесо автомашины вращается равноускоренно. После 50 полных оборотов частота вращения колеса возросла отn₁ = 4 об/с доn₂= 6 об/с. Определить угловое ускорение колеса.

Решение:

,

,

,

.

Ответ: = 1.26 рад/с².

2.28Грузик, привязанный к шнуру длиной l = 1.5 м, вращается в горизонтальной плоскости с частотой n = 28 об/мин. Какой уголс вертикалью образует шнур?

Решение:

n= 28 об/мин = 0.46 Гц

OX:,

OY: ,

,

,

,

,

,

Ответ:

3.13 Автомобиль массой m = 4 т подъезжает к горке высотой h = 10 м и длиной склона S = 80 м со скоростью V₀=36 км/ч. Какую среднюю мощность развивает автомобиль на подъеме, если его скорость на вершине горы при постоянной силе тяги оказалась V = 21,6 км/ч? Коэффициент трения принять равным.

Решение:

Автомобиль в начале горки имел кинетическую энергию Е_к1, к конце горки имел Е_к1+Е_p2. При этом двигатель совершил работу А₁и сила трения совершила работу А_тр. Изменение энергии тела равно работе сил, приложенных к телу:

Из этого уравнения находим А₁

, делаем рисунок, указываем силы, действующие на машину, видим как найти силу реакции опоры. Найдем энергию.

, время t ищется из, а ускорение ищется из.

Ответ:

3.39Движущееся тело массой m₁ударяется о неподвижное тело массой m₂. Считая удар неупругим и центральным, найти, какая часть первоначальной кинетической энергии переходит при ударе в теплоту. Задачу решить сначала в общем виде, а затем рассмотреть следующие случаи: 1)m₁= m₂; 2)m₁= 9m₂.

Решение:

Кинетическая энергия первого тела до удара ; кинетическая энергия второго тела до удара. После удара кинетические энергии обоих тел, где- общая скорость тел.

Следовательно, . Тогда кинетическая энергия, перешедшая при ударе в тепло:. Искомое отношение:.

1. Если m₁ = m₂, то

2. Если m₁ = 9m₂, то

Ответ:приm₁ = m₂ , , приm₁ = 9m₂ , .

4.13Через блок перекинута невесомая нить, к концам которой привязаны два груза. Груз массойm₂= 5 кг поднимается со скоростью, меняющейся по законуV= 5 + 0,8t(м/с), груз массойm₁опускается. Момент инерции блока, его радиусR= 0,2 м. Найти массу опускающегося грузаm₁. Трением пренебречь.

Решение:

Ускорение грузов будет а = 0,8 м/с²(из данного закона движения).

Заменим блок материальной точкой массы m₃, обращающейся по окружности радиусомR(это будет “инерционная” масса блока).

Составим простое уравнение сил (m₁большеm₂)

.

Подставим в него все известные значения: .

Осталось одно неизвестное m₁.

Ответ:

4.38Платформа в виде диска вращается по инерции около вертикальной оси с частотой n₁= 14 об/мин. На краю платформы стоит человек. Когда человек перешел в центр платформы, частота вращения возросла до n₂= 25 об/мин. Масса человека m = 70 кг. Определить массу платформыM. Момент инерции человека рассчитывать так же, как и для материальной точки.

Решение:

Закон сохранения момента импульса , или учитывая что,. Момент инерции, где- момент инерции диска,- момент инерции человека, момент инерции, где, а, т.к. расстояние между осью и человеком стало равно 0. Итакотсюда.

Ответ:

5.3Математический маятник установлен в лифте, который поднимается с ускорением а = 2,5 м/с². Определить период Т собственных колебаний маятника. Его длина равна 1 м.

Решение:

.

Ответ:T = 1.8 c.

5.28Даны амплитуда и период свободных колебаний пружинного маятника: А = 4 см, Т = 2 с. Написать уравнение этих колебаний. В момент возникновения колебаний х(0) = 0, х(0) < 0.

Решение:

x< 0 – пружина сжата на амплитуду 4 см , ФазаQ= 4,71, то есть сдвинута на 270ᵒ, угловая скорость

Уравнение гармонических колебаний

Подставив данные в формулу получим:

Ответ:

studfiles.net

РГЗ по физике

Министерство образования и науки Российской Федерации

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

Санкт-Петербургский государственный горный университет

Кафедра общей и технической физики

Расчетно-графическая работа № 1

Вариант 6

По дисциплине: Физика

(наименование учебной дисциплины согласно учебному плану)

Тема: «Электростатика»

Выполнил: студент гр. ОНГ-12-1______________ /Исманилов И. И./

^{(подпись) (Ф.И.О.)}

Проверил: профессор ____________ /Немов С. А./

^{(должность) (подпись) (Ф.И.О.)}

Санкт-Петербург

2013

Задача

Рассчитать потенциал электрического поля, создаваемого заряженной равномерно сферической поверхностью в точках, расположенных внутри сферы и вне ее на расстояниях от ее центра r, равном: 2, 4, 6, 8, 10, 12 см.

Исходные данные:

Расчет провести для двух случаев:

1. Сфера находится в воздухе;

2. Сфера находится в трансформаторном масле с диэлектрической проницаемостью ε=2,24.

Построить графики зависимостей потенциала электрического поля от расстояния сферы r для обоих случаев.

Теоретические сведения

Потенциал электрического поля это энергетическая характеристика поля. Он представляет собой работу которую нужно совершить против сил электрического поля для того чтобы переместить единичный положительный точечный заряд находящийся на бесконечности в данную точку поля.

Измеряется потенциал электрического поля в вольтах.

По определению, потенциал – скалярная физическая величина, равная отношению потенциальной энергии, которой обладает пробный заряд q₀, помещенный в данную точку поля, к величине этого заряда q:

φ=Wq₀/q

Потенциальная энергия пробного заряда Wq₀ вычисляется по формуле

Wq₀=q*q₀/4πεε₀r

Отсюда получаем, что потенциал равен

φ =q/4πεε₀r

Так как напряженность электростатического поля E равен

E= q/4πεε₀r²,

то получаем, что

φ=E*r

Ход работы

I. Проведение расчетов

1. Проведем расчет для случая, когда сфера находится в воздухе.

r, м	φ, В
0,02	1800
0,04	900
0,06	600
0,08	450
0,1	360
0,12	300

Пример расчета

r=0,02 м.

ε=1

q=4*10^-9Кл.

φ =q/4πεε₀r=4*10^-9/4π*1*8,8*10^-12*0,02=1800 (В.)

2. Сфера находится в трансформаторном масле.

r, м	φ, В
0,02	803,57
0,04	401,79
0,06	267,86
0,08	200,89
0,1	160,71
0,12	133,93

Пример расчета

r=0,04 м.

ε=2,24

q=4*10^-9Кл.

φ =q/4πεε₀r=4*10^-9/4π*2,24*8,8*10^-12*0,04=401,79 (В.)

II. Построение графиков зависимостей.

1. Зависимость потенциала φ электрического поля от расстояния до центра r в случае, когда сфера находится в воздухе .

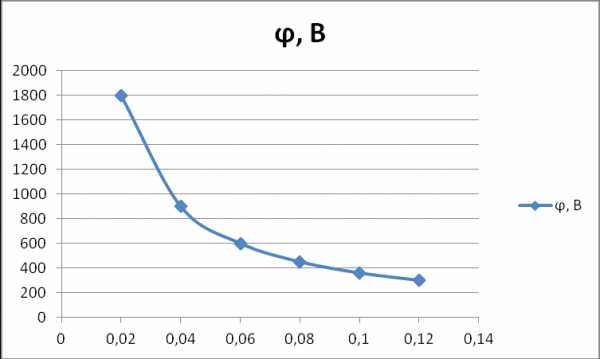
2.Зависимость потенциала электрического поля φ от расстояния до центра r в случае, когда сфера находится в трансформаторном масле.

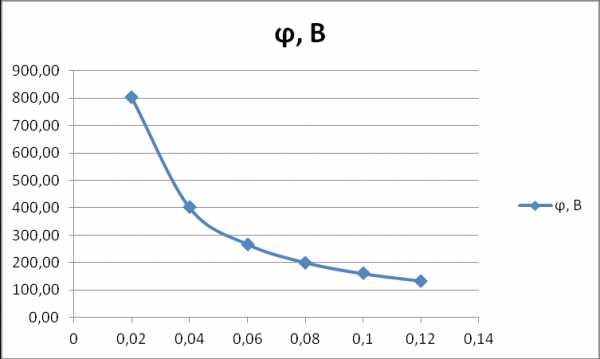
studfiles.net

РГЗ по физике 1633

Министерство образования Российской Федерации Ивановский государственный энергетический университет

Кафедра физики

ВОЛНЫ.

ВОЛНОВЫЕ И КВАНТОВЫЕ СВОЙСТВА СВЕТА

Расчетно−графические задания по физике

Составители: М. В. Дмитриев, В. Х. Костюк, Г. А. Шмелёва

Редактор М. Н. Шипко

Настоящие задания предназначены для обеспечения самостоятельной работы студентов по теме “ Волны. Волновые и квантовые свойства света”.

В заданиях учтены особенности учебных планов различных факультетов. Дана таблица вариантов контрольной работы для студентов заочной формы обучения.

Расчетно– графические	задания	утверждены	цикловой
методической комиссией ИФФ

Рецензент кафедра физики Ивановского государственного энергетического

университета

1. УПРУГИЕ И ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ. ОБЩАЯ ХАРАКТЕРИСТИКА ВОЛНОВЫХ ПРОЦЕССОВ

Уравнение плоской волны, распространяющейся вдоль оси X, имеет вид:

ξ = ACos(ωt −kx + ϕ0 ),

где ξ – смещение частицы среды, имеющей координатуx в

момент времени t ; A –	амплитуда смещения; ω – циклическая частота;
k – волновое число;ϕ0 –	начальная фаза.

Для одномерной волны уравнение волновой поверхности имеет

вид:

ϕ =ωt -kx +ϕ0 .

Скорость перемещения волновой поверхности равна:

dx =ω =λ =λv =V ,

dt k	T
где λ – длина волны;T = 2π / ω –	период колебаний; v – частота
колебаний.

Уравнение волны, распространяющейся в среде с затуханием: ξ = A0e− χt cos(ωt – kx + ϕ0 ),

где χ – коэффициент затухания; A0 – амплитуда волны в точкеx = 0 .

Объёмная плотность энергии упругой волны:

w = ρA2ω2Sin2 (ωt- kx+ϕ0 ),

где ρ – плотность среды.

Плотность потока энергии упругой волны U (вектор Умова),
распространяющейся в среде со скоростью V , равна:
U	= wV.

Поток энергии, переносимый волной через поверхность площадью

S , равен:

Fw = U× S= VwSCosα ,

где α – угол между вектором скорости и единичным вектором нормали к

поверхности S . Интенсивность волны:

I =U =wV =12 ρA2ω2V .

Уравнение плоской электромагнитной волны:

Ey	= E0Cos(ωt −kx + ϕ0 ),
H z	= H0Cos(ωt −kx + ϕ0 ),

где E0 ,H 0 – амплитуды векторов напряженности электрического и

магнитного поля соответственно. Модули амплитуды векторов напряжённости магнитного и электрического поля связаны соотношением:

H0 =

εε0

E0 ,

µµ

0

где

ε – относительная диэлектрическая

проницаемость среды,

μ –

относительная магнитная проницаемость среды, ε0 – электрическая

постоянная, μ0 – магнитная постоянная. Фазовая скорость волны:

U =

1

=

c

=

c

,

ε

0

μ

0

εμ

εμ

n

здесь c = 1 ε 0 μ0 – скорость электромагнитной волны в вакууме;

n = εμ – показатель преломления среды.

Объемная плотность энергии электромагнитной волны:

w =wE +wH =	εε E 2	+	μμ H 2	=	EH
	0		0		.
	2		2		V

Плотность потока энергии электромагнитной волны, называемая вектором Пойнтинга, равна:

где V – групповая скорость волны. В среде, обладающей дисперсией,

групповая скорость связана с фазовой скоростью волны соотношением:

u =dω =V − λdV .dk dλ

В вакууме вектор Пойнтинга равен :

P = wc.

Интенсивность электромагнитной волны:

I = P= 1

E0H 0= 1

εε 0

E02.

2

2

μμ0

Давление плоской электромагнитной волны:

P =w(1 +R) cos2 α ,

где R – коэффициент отражения,α – угол между направлением распространения волны и нормалью к поверхности.

Коэффициент отражения света в случае его падения по нормали к поверхности равен:

	I			n		− 1		2
R =		отр		=	21				,
		I				+ 1
			0	n
					21

где Iотр –	интенсивность	отраженного	света, I0 –	интенсивность
падающего	света, n21 –	относительный	показатель	преломления
вещества.

Задача 1. Тонкая длинная струна с закрепленными концами натянута вдоль координатной оси Х. Если вывести струну из положения равновесия, то все частицы струны движутся перпендикулярно ее положению равновесия (поперечные колебания). В каждый момент времени струна находится в плоскости ХОУ. В процессе колебания величина отклонения частиц струны от положения

равновесия y зависит от координатыx и

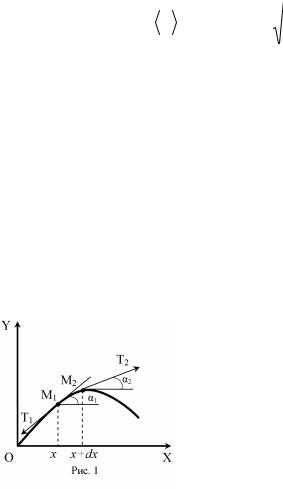
времени t. Найти зависимостьy(x,t). Решение. При фиксированном

значении t график функцииy(x,t) представляет форму колеблющейся струны в момент времениt (рис.1).

Частная производная dy/dx= yx’ (x,t) дает угловой коэффициент к

касательной в точке с абсциссой х.

Для заданного значения х функцияy(x,t) определяет закон движения точки струны с координатой х вдоль прямой, параллельной оси

OY, производная dy = y'(x,t) есть скорость движения этой точки,

dt t

вторая производная d 2 y – ускорение.

dt 2

Выделим бесконечно малый участок струны М1М2, проектирующейся на ось ОХ интервалом[x,x+dx]. На него действуют силы натяженияT1 иT2 . При малых колебаниях частиц струны угол

наклона касательной к любой точке струны мал, α ≈ sin α ≈ tgα . Приняв, что величина силы натяжения вдоль струны постоянна и равнаT0 , получим

− T1 sinα1 +T2 sinα2 =T0 (sinα2 − sinα1 )

2

T0 (tgα2 −tgα1 ) =T0 [y`x (x +dx,t) −y`x (x,t)] =T0 d 2y dx,dx

где tgα1 =y`x (x,t),tgα2 =y`x (x +dx,t).

Здесь	частное	приращение	производной		dy	при	переходе от
					dx
аргументов	(х,t)к	аргументам	(x+dx,t)	заменено			ее частным

d 2 y
дифференциалом		2 dx.
dx

Масса участка струны M1M 2 равна

mM1M2				= ρ (M1M 2 ),
где ρ – линейная плотность вещества струны (кг/м).
Запишем второй закон Ньютона для этого участка:
ρdx		d 2 y			= T		d 2 y		dx.
		dt 2			0 dx2
Обе части уравнения разделим на ρdx и получим уравнение:
	d 2 y			= V 2		d 2 y		,
	dt 2
						dx 2

T

где V 2 = ρ0 – положительная постоянная величина.

Это линейное дифференциальное уравнение второго порядка с постоянными коэффициентами называется одномерным волновым уравнением. Оно описывает свободные колебания струны.

В случае бесконечно длинной струны общее решение волнового

уравнения имеет вид:

y(x,t) = ϕ(x −Vt) +ψ (x +Vt).

Функция ϕ (x − Vt) в момент времениt=0 описывает перемещение волны вдоль оси ОХ в положительном направлении со

	скоростью V, которая равна	T0	. Функция ψ (x + Vt) описывает
		ρ
			1

волну, распространяющуюся вдоль оси ОХ в обратном направлении. Если точки струны колеблются по гармоническому закону

y(x,t) = Acos(ω (Vt – x)), то вдоль струны будет распространяться

V

волна со скоростью V, описываемая гармонической функцией.

Задача 2. Смещение от положения равновесия точки, находящейся на расстоянии 4см от источника колебаний, в момент времениt=T/6 равно половине амплитуды. Найти длину волны.

Решение. В уравнении плоской волны

y =Asin(ωt −kx)

подставим ω = 2π / T ,

k = 2π / λ

и выразим из

него в явном виде

длину волны:

2πx

λ =

.

2π

t – arcsin

y

T

A

Подставим числовые данные:

λ =

2 × 3,14× 4×10−2

= 0,48м.

2 × 3,14

×

T

– arcsin

0,5A

T

6

A

Задача 3. По какому закону изменяется с расстоянием амплитуда незатухающей цилиндрической воны?

Решение. Поток энергии, переносимой волной через цилиндрическую поверхность радиусаR, пропорционален интенсивности волны и площади поверхностиS

Φ = IR 2πRh ,

где h – высота цилиндра. Этот же поток энергии переносится волной и через цилиндрическую поверхность радиусаr. Следовательно,

IR 2πRh= Ir 2πrh,

Интенсивность волны пропорциональна квадратуамплитуды I ~ A2

Если источником волн является тонкая нить; то амплитуда AR

выбирается равной амплитуде волны на расстоянии R=1 м от оси нити. Закон убывания амплитуды с расстоянием от источника принимает вид:

A =AR .r

1.1. Написать уравнение плоской монохроматической волны, распространяющейся вдоль оси Х. Частицы среды колеблются вдоль осиZ. Известно, что амплитуда волны равнаА, циклическая частота ω, начальная фазаπ/6, длинаλ. Рассеянием энергии пренебречь.

1.2.Получить дифференциальное уравнение, решением которого является функция y(x, t) = A cos(wt − kx).

1.3.Получить дифференциальное уравнение, решением которого является функция y(x,t) = Aexp(−γx) cos(wt − kx). Какой физический

смысл имеет коэффициент γ ?

1.4. Плоская монохроматическая волна распространяется вдоль оси Υ. Амплитуда волныА=0,05 м. Считая, что в начальный момент времени смещение точкиР, находящейся в источнике, максимально, определить

смещение от положения равновесия точки М, находящейся на расстоянииy=λ/2 от источника колебаний в момент времениt=T/6.

1.5.В условии задачи 1.4 определить разность фаз колебаний точек

Ми Р.

1.6.В некоторый момент времени t1 в точкех1=0 фаза плоской монохроматической волны равна нулю. Какова будет фаза волны в точке

х2=10-3 м в тот же момент времени? Какова будет фаза волны в точкех2 в момент времениt2=10-2 c? Длина волныλ=10-4 м.

1.7. Плоские волны переходят из среды, в которой фазовая скорость волны равна V, в среду, в которой фазовая скорость в два раза больше. Что происходит при этом с частотойω и длиной волныλ ?

1.8. Какие из приведённых функций можно использовать при описании волновых движений: у = А(х − Vt)2 ,y = A(x − Vt) ,

y= Aln(x +Vt)?

1.9.Записать уравнение цилиндрической волны. Установить закон, по которому меняется амплитуда и интенсивность цилиндрической волны

сизменением расстояния от источника.

1.10.Записать уравнение сферической волны. Установить закон, по которому меняется амплитуда и интенсивность сферической волны с изменением расстояния от источника.

		1.11. В окрестностях точек 1 и 2
	n2	известны направления распространения
	n1	сферической волны (рис.1.1). Найти
	2	графическим построением положение
		источника излучения.
	1
	Рис. 1.1

1.12. В поглощающей среде вдоль оси Х распространяется плоская волна. Определить расстояние, на котором амплитуда волны уменьшается

в е раз. Коэффициент затухания волны известен и равенγ .

1.13. Указать направление, вдоль которого распространяется плоская волна, имеющая волновой вектор (k,0,0). Определить частотуν и длинуλ этой волны. Скорость распространения волны в среде равнаV.

1.14.Решить задачу 1.13, приняв волновой вектор равным (0,k,0).

1.15.Решить задачу 1.13, приняв волновой вектор равным (0,0,-k).

1.16.На больших расстояниях от точечного источника сферическая волна может рассматриваться как плоская. При каком характерном

размере d малый участок волновой поверхности может считаться плоским? Длина волныλ задана.

1.17.	Найти волновой вектор k и скорость волныV. Волна
описывается	уравнением f (x,y,z,t) =Acos(ωt − αx − βy − γz), где
α , βи γ–	постоянные.

1.18.Плоская волна с длиной λ распространяется вдоль

направления, образующего с осями Х, Υ, Z углыπ/3,π/4, иπ/3 соответственно. Написать уравнение волны. Амплитуда и частота равны соответственноА иν.

1.19. Доказать, что любая функция вида f (x + αt) является решением волнового уравнения. Каков физический смысл постоянной

α ?

1.20. Плоская волна задана уравнением

y(x,t) = 60 cos(1800t − 5,3x),

где смещение частиц среды y задано в мкм,t в с,х в м. Найти отношение амплитуды смещения частиц среды к длине волны.

1.21. Плоская волна задана уравнением y(x,t) = Acos(ωt − kx) . Для момента времениt=0 изобразите графики зависимости отх величин

у,∂y/∂tи ∂y/∂x.

10

studfiles.net

Кафедра физики

Методические материалы

Методические материалы для студентов всех форм обучения

Литература к занятиям

 

Интернет-ресурсы

 

Методические указания к лабораторному практикуму

 

Методические указания к выполнению РГЗ, ИДЗ, КР.

Графики лабораторных работ, ИДЗ, РГЗ.

	Направление	1 курс 1 семестр	1 курс 2 семестр	2 курс 3 семестр	2 курс 4 семестр
1	08.03.01 (С)	График л.р.	График л.р.
2	08.05.01. (СУЗ)	График л.р.	График л.р.	График л.р.
3	09.03.01. (ВТ)	График л.р.	График л.р.
4	09.03.02. (ИТ)		График л.р.	График л.р.	График л.р.
5	09.03.03. (ПИ)		График л.р.	График л.р.	График л.р.
6	09.03.04 (ПВ)	График л.р.	График л.р.
7	10.05.03 (КБ)	График л.р.	График л.р.
8	13.03.01 (ЭТ)	График л.р.	График л.р.
	13.03.01 (ЭТз, ЭПз)		График л.р
9	13.03.02 (Э, ЭА)
	13.03.02 (ЭЛз)
10	15.03.01 (МТ)		График л.р.	График л.р.
11	15.03.02 (МО)		График л.р.	График л.р.
12	15.03.04 (АП)	График л.р.	График л.р.	График л.р.
13	15.03.05 (ТМ)		График л.р.	График л.р.
14	15.03.06 (МР)	График л.р.	График л.р.	График л.р.
15	15.05.01 (ПМ)		График л.р.	График л.р.	График л.р.
16	18.03.01 (ХТ)	График л.р.		.
17	18.03.02 (ЭР)		График л.р.	График л.р.
18	19.03.01 (БТ)
19	20.03.01 (ТБ)		График л.р.	График л.р.
20	20.03.02 (ПР)
21	20.05.01 (ПБ)		График л.р.	График л.р.
22	21.03.02 (ЗК)		График л.р.	График л.р.
23	21.05.01 (ПГ)		График л.р.	График л.р.
24	21.05.04 (ГМ)		График л.р.	График л.р.	График л.р.
25	22.03.01 (МВ)	График л.р.	График л.р.
26	23.03.01 (ТТП)		График л.р.
27	23.03.02 (НК)		График л.р.	График л.р.
28	23.03.03 (ЭТА)		График л.р.
29	23.05.01 (НС)	График л.р.	График л.р.	График л.р.	График л.р.
	23.05.01 (НСз)		График л.р.	График л.р.	График л.р.
30	23.05.06 (ЖД)		График л.р.	График л.р.
31	27.03.01 (СТ)		График л.р.	График л.р.
32	27.03.02 (УК)
33	27.03.04 (УС)	График л.р.	График л.р.	График л.р.
34	28.03.02 (НИ)		График л.р.	График л.р.
35	29.03.04 (ТХ)			График л.р.

f.bstu.ru

РГЗ по физике – Электростатика

Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования Санкт-Петербургский государственный горный университет Кафедра общей и технической физики Расчетно-графическая работа № 1 Вариант 6 По дисциплине: Физика (наименование учебной дисциплины согласно учебному плану) Тема: «Электростатика» Выполнил: студент гр. ОНГ-12-1______________ /Исманилов И. И./ (подпись) (Ф.И.О.) Проверил: профессор ____________ /Немов С. А./ (должность) (подпись) (Ф.И.О.) Санкт-Петербург 2013 Задача Рассчитать потенциал электрического поля, создаваемого заряженной равномерно сферической поверхностью в точках, расположенных внутри сферы и вне ее на расстояниях от ее центра r, равном: 2, 4, 6, 8, 10, 12 см. Исходные данные: Заряд сферы q=4*10-9 Кл Радиус сферы R=2 cм Расчет провести для двух случаев: Сфера находится в воздухе; Сфера находится в трансформаторном масле с диэлектрической проницаемостью ε=2,24. Построить графики зависимостей потенциала электрического поля от расстояния сферы rдля обоих случаев. Теоретические сведения Потенциал электрического поля это энергетическая характеристика поля. Он представляет собой работу которую нужно совершить против сил электрического поля для того чтобы переместить единичный положительный точечный заряд находящийся на бесконечности в данную точку поля. Измеряется потенциал электрического поля в вольтах. По определению, потенциал – скалярная физическая величина, равная отношению потенциальной энергии, которой обладает пробный заряд q0, помещенный в данную точку поля, к величине этого заряда q: φ=Wq0/q Потенциальная энергия пробного заряда Wq0 вычисляется по формуле Wq0=q*q0/4πεε0r Отсюда получаем, что потенциал равен φ =q/4πεε0r Так как напряженность электростатического поля Eравен E= q/4πεε0r2, то получаем, что φ=E*r Ход работы I. Проведение расчетов 1. Проведем расчет для случая, когда сфера находится в воздухе. r, м φ, В 0,02 1800 0,04 900 0,06 600 0,08 450 0,1 360 0,12 300 Пример расчета r=0,02 м. ε=1 q=4*10-9Кл. φ =q/4πεε0r=4*10-9/4π*1*8,8*10-12*0,02=1800 (В.) Сфера находится в трансформаторном масле. r, м φ, В 0,02 803,57 0,04 401,79 0,06 267,86 0,08 200,89 0,1 160,71 0,12 133,93 Пример расчета r=0,04 м. ε=2,24 q=4*10-9Кл. φ =q/4πεε0r=4*10-9/4π*2,24*8,8*10-12*0,04=401,79 (В.) II. Построение графиков зависимостей. Зависимость потенциала φ электрического поля от расстояния до центра r в случае, когда сфера находится в воздухе . 2.Зависимость потенциала электрического поля φ от расстояния до центра rв случае, когда сфера находится в трансформаторном масле.

historich.ru

---