Решение задач с графиками по физике – “Андреева Т.А. учитель физики МБОУ СОШ 4. решение задач графическим способом, включающее построение графиков работа с предложенными графиками графическое.”. Скачать бесплатно и без регистрации.
- Комментариев к записи Решение задач с графиками по физике – “Андреева Т.А. учитель физики МБОУ СОШ 4. решение задач графическим способом, включающее построение графиков работа с предложенными графиками графическое.”. Скачать бесплатно и без регистрации. нет
- Советы абитуриенту
- Решение графических задач по физике
- Графические задачи по физике и графическое решение задач
- Об использовании графиков при решении задач по физике
- графические задачи по физике 7-9, проект
- Типовые задачи на уравнения и графики прямолинейного равноускоренного движения. Примеры решения задач по физике. 9-10 класс
- Методическая разработка по физике на тему “Методика решения графических задач (механика)”
- Методическая разработка на тему “Методика решения графических задач по молекулярной физике и термодинамике”
Решение графических задач по физике
Просмотр содержимого документа
«Решение графических задач по физике»
Решение графических задач по физике
В графических задачах объектом исследования являются графики зависимости физических величин. Графики могут быть даны в условии задачи или их надо построить в процессе решения задачи. Чтобы успешно решать графические задачи, их нужно уметь «читать», видеть характер зависимости между величинами. Рассмотрим решение некоторых графических задач.
Задача №1 (Задание из варианта ЕГЭ)
На рисунке приведен график зависимости проекции скорости тела от времени.
Проекция ускорения тела в интервале времени от 12 до 16 с представлена графиком
Чтобы успешно и быстро решить подобное задание, нужно знать формулу ускоренияа = . Выделите указанный участок на графике. За 4 с скорость изменилась от значения -10 м/с до значения 0 м/с. Значит, а = (0м/с – (-10 м/с))/4 с = 2,5 м/с2.
а 0, значит верный ответ №4.
Задача №2 (Задание из варианта ЕГЭ)
На графике показана зависимость скорости тела от времени. Каков путь, пройденный телом к моменту времени t = 4 c?
1) 7 м; 2) 6 м; 3) 5 м; 4) 4 м.
Не нужно «искать» путь за 4 с движения по формулам кинематики. Это отнимает много времени. Найдём путь как площадь полученной трапеции. Верхнее основание трапеции это отрезок времени 4 с, нижнее – 2 с. Высота трапеции 2 м/с. Далее находим площадь:S = = 6 м.
Аналогично решаются некоторые задачи по термодинамике.
Задача №3
Рабочий цикл тепловой машины изображен на рисунке.
Дано: ν=1 моль, P2 =6P1 , T4 =2T1 , T1 =300К
А ? (за весь цикл)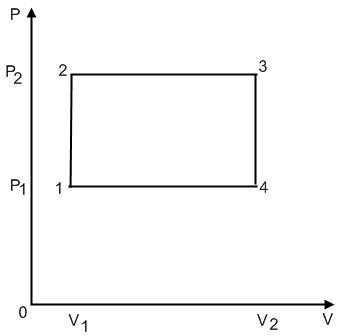
Сначала найдем работу, совершенную в каждом процессе.
A1-2 =0, A3-4 =0,
т.к. V-const,
A2-3 =P2 (V2 –V1),
A4-1 =P1 (V1 –V2). Работа за весь цикл равна:
A =A2-3 +A4-1 = P2 (V2 –V1)+ P1 (V1 –V2)=
=P2 (V2 –V1)- P1 (V2
= (V2 –V1 )5 P1.
Запишем уравнение
Менделеева-Клапейрона.
состояние (параметры в точке 1:P1 ,V1,T1):
P1V1 =νRT1 ;
2 состояние (точка 4): P1V2 =νRT4 ;Решая систему уравнений, получим:
(V2 –V1)P1= νRT4 – νRT1 .
(V2 –V1)P1= νR(T4 -T1)= νRT1.
(V2 –V1)= νRT1 /P1.
A= (V2 –V1)5P1=(νRT1 /P1) ∙5P1=5∙νRT 1.
A=12465Дж.
2 способ:
Найдём работу как площадь фигуры (прямоугольника): А = (P2 – P1)·(V2 – V1) = 5 P1· νRT1 /P1, т.к. P1V1 =νRT1 ;P1V2 =νRT4, откуда (V2 –V1)= νRT1 /P1.
Задача №4
Сравните графики движения тел и определите, какое из них имеет наибольшую скорость.
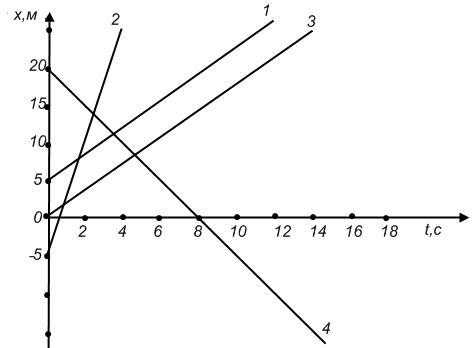
Можно вычислить скорости движения всех тел и затем их сравнить. Но есть более быстрый способ выполнения этого задания. Чем больше угол наклона графика к оси времени, тем больше скорость тела. Это согласуется с формулой скорости: v= , т.к. отношение изменения координаты (х –х0
multiurok.ru
Графические задачи по физике и графическое решение задач
Часто графическое представление физического процесса делает его более наглядным и тем самым облегчает понимание рассматриваемого явления. Позволяя порой значительно упростить расчеты, графики широко используются на практике для решения различных задач. Умение строить и читать их сегодня является обязательным для многих специалистов.
К графическим задачам мы относим задачи:
- на построение, где очень помогают, рисунки, чертежи;
- схемы, решаемые с помощью векторов, графиков, диаграмм, эпюр и номограмм.
1) Мячик бросают с земли вертикально вверх с начальной скоростью vо. Постройте график зависимости скорости мячика от времени, считая удары о землю абсолютно упругими. Сопротивлением воздуха пренебречь. [решение]
2) Пассажир, опоздавший к поезду, заметил, что предпоследний вагон прошел мимо него за t1 = 10 c, а последний — за t2 = 8 с. Считая движение поезда равноускоренным, определите время опоздания. [решение]
3) В комнате высотой H к потолку одним концом прикреплена легкая пружина жесткостью k, имеющая в недеформированном состоянии длину lо (lо < H). На полу под пружиной размещают брусок высотой x с площадью основания S, изготовленный из материала плотностью ρ. Построить график зависимости давления бруска на пол от высоты бруска. [решение]
4) Букашка ползет вдоль оси Ox. Определите среднюю скорость ее движения на участке между точками с координатами x1 = 1,0 м и x2 = 5,0 м, если известно, что произведение скорости букашки на ее координату все время остается постоянной величиной, равной
5) К бруску массой 10 кг, находящемуся на горизонтальной поверхности, приложена сила. Учитывая, что коэффициент трения равен 0,7, определите:
- cилу трения для случая, если F = 50 Н и направлена горизонтально.
- cилу трения для случая, если F = 80 Н и направлена горизонтально.
- построить график зависимости ускорения бруска от горизонтально приложенной силы.
- с какой минимальной силой нужно тянуть за веревку, чтобы равномерно перемещать брусок? [решение]
6) Имеются две трубы, подсоединенных к смесителю. На каждой из труб имеется кран, которым можно регулировать поток воды по трубе, изменяя его от нуля до максимального значения Jo = 1 л/с. В трубах течет вода с температурами t1 = 10° C и t2 = 50° C. Постройте график зависимости максимального потока воды, вытекающей из смесителя, от температуры этой воды. Тепловыми потерями пренебречь. [решение]
7) Поздним вечером молодой человек ростом h идет по краю горизонтального прямого тротуара с постоянной скоростью v. На расстоянии l от края тротуара стоит фонарный столб. Горящий фонарь закреплен на высоте H от поверхности земли. Постройте график зависимости скорости движения тени головы человека от координаты x. [решение]
Вы читате материалы из пособия для подготовки к олимпиадам по физике. Далее: многоступенчатые задачи по физике.
www.afportal.ru
Об использовании графиков при решении задач по физике
Графический метод в физических задачах
Графическими принято называть задачи, в которых условия даны в графической форме, то есть в виде функциональных диаграмм. Применение графического приёма позволяет рассмотреть широкий ряд задач, которые другим способов решить нельзя. По роли графиков в решении задач их можно подразделить на два вида:
* задачи, ответ на вопрос которых может быть найден в результате построения графика;
* задачи, ответ на вопрос которых может быть найден с помощью анализа графика
При решении большинства графических задач по физике требуются знания графического изображения математических функций.
Виды функций
• 1) Линейная
Прямая линия – график линейной функции y = ax + b. Функция y монотонно возрастает при a > 0 и убывает при a < 0. При b = 0 прямая линия проходит через начало координат т. 0 (y = ax – прямая пропорциональность)
В физике от времени линейно зависят: координата; путь,cкорость при прямолинейном равномерном движении; сила тока от напряжения на концах проводника и др.
Парабола – график функции квадратного трёхчлена у = ах² + bх + с. Имеет вертикальную ось симметрии. Если а > 0, имеет минимум, если а < 0 -максимум. Точки пересечения (если они есть) с осью абсцисс – корни соответствующего квадратного уравнения ax² + bx +с =0
В физике квадратичной функцией является зависимость х от t при равноускоренном движении.
Гипербола – график функции . При а > О расположена в I и III четвертях, при а < 0 – во II и IV. Асимптоты – оси координат. Ось симметрии – прямая у = х(а > 0) или у = – х(а < 0).
В физике обратной зависимостью является зависимость силы постоянного тока от сопротивления.
Экспонента (показательная функция по основанию е) у = еx. (Другое написание у = ехр(х)). Асимптота – ось абсцисс.
В физике – это зависимость числа распавшихся атомов радиоактивного вещества от времени.
Синусоида – периодическая функция с периодом Т = 2π у = а•sin(ωx+φ) – функция гармонических колебаний. Обозначения: а – амплитуда, ω – частота (ω = 2π/Т), φ – фаза (сдвиг).
В физике – графики колебательного движения.
Алгоритм решения графических задач
1) Вспомнить формулу, связывающую параметры, о которых идет речь в задаче.
2) Установить, каким видом зависимости (прямо пропорциональной, обратно пропорциональной, степенной, квадратичной) связаны данные параметры.
3) Получить теоретическую информацию из графика – прочесть график
4) Применить математические вычисления для определения искомой величины (например, силы из 2-го закона Ньютона, если известна масса и из графика определено ускорение)
5) Если установлена зависимость величин по графику в предложенных осях, перейти к её изображению в других осях.
Взаимосвязь между графиками движения
Особое внимание необходимо обратить на взаимосвязь между графиками. Следующие закономерности, которые изучаются в курсе математики, хорошо проявляются в физических графиках:
Тангенс угла, образованного касательной к данной точке графика координаты с осью времени, равен численному значению скорости в этот момент времени: tg 1 = V1:
Тангенс угла, образованного линией графика скорости с осью времени, равен численному значению ускорения в данный момент времени: tg 2 = a.
Площадь под графиком ускорения численно равна изменению скорости за данный промежуток времени S1 = V.
Площадь под графиком скорости численно равна изменению координаты тела за данный промежуток времени , то есть пройденному телом пути S2 = Х
Если график координаты отражает направление движения (участок 4 указывает на изменение направления движения), то график пути учитывает только закономерность изменения длины пути со временем, и направление движения по нему определить невозможно.
Обратите внимание на то, что линия графика координаты может устремляться как вверх, так и вниз, так как расстояние от точки отсчета до движущейся точки может и увеличиваться и уменьшаться (если тело движется к точке отсчета). А линия графика пути развивается только вверх, так как независимо от направления движения длина пройденного телом пути только увеличивается.. Поэтому в конкретных задачах удобнее и нагляднее пользоваться графиком координаты, а не графиком пути.
Решение физических задач с помощью нахождения площади фигуры, образовавшейся под графиком (умножение с помощью графиков)
Вы конечно же обратили внимание на то, что мы с помощью графика практически выполняли функцию умножения. Ведь если мы находили изменение скорости по графику ускорения, мы фактически перемножали а и t , затем эти произведения складывали по всему интервалу времени, получая всю площадь под графиком ускорения.
То же самое происходило и с графиком скорости. Перемножая V на t и складывая все эти элементарные произведения на всем заданном промежутке времени, мы считали площадь образовавшейся под графиком фигуры, которая численно была равна пройденному пути.
А это значит, что если нам нужно найти, например, работу переменной силы, которая равна А = (F X)i ( знак означает сумму), то достаточно на графике зависимости силы F от расстояния Х подсчитать площадь фигуры под графиком, мы получим искомое значение работы
При расчете механической мощности, равной N = (F V)i , по графику зависимости силы от скорости можно найти мощность, рассчитав площадь под линией графика.
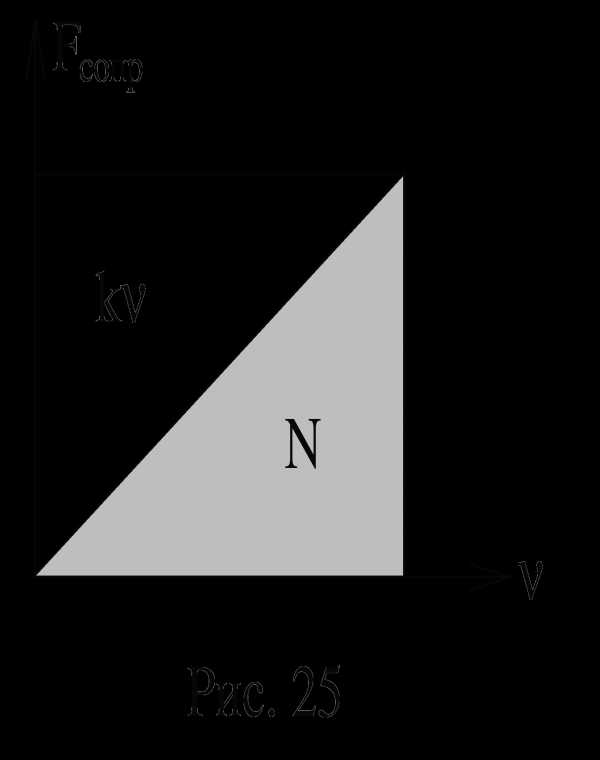
Особенно удобно пользоваться графическим расчетом мощности при решении задач с учетом силы сопротивления среды, которая чаще всего бывает пропорциональна скорости. Тогда мощность потерь составит (рис. 25) N = 1/2 kV2 (площадь под линией графика).
В задачах на расчет работы расширения идеального газа A = P V удобно использовать график в координатах Р и V .
В задачах на расчет электрической мощности Р = I U удобно использовать график с координатами I и U .И множество других расчетов можно упростить, используя графическую зависимость.
Деление с помощью графиков
С помощью графика можно не только перемножать величины. Деление тоже возможно с помощью графика. Так, чтобы А разделить на В, достаточно умножить А на 1/В. То есть если взять в качестве координатных осей ось А и ось 1/В, изобразить графически зависимость 1/В от А и подсчитать площадь под линией графика, то мы фактически и выполним операцию деления.
Задача 16. Муравей ползет от муравейника так, что скорость его перемещения обратно пропорциональна расстоянию до муравейника. На расстоянии 1 м от муравейника скорость муравья была 2 см/с. За какое время муравей проползет второй метр?
Решение. Так как скорость муравья V обратно пропорциональна расстоянию до муравейника Х, то зависимость эта имеет вид V = k/X, где k = V X. Подставив заданные значения Х = 1 м и V = 0,02 м/с, получаем значение k: k = 0,02.
Время перемещения равно t = X/V. Найдем зависимость 1/V от Х и отобразим ее в координатах (1/V ; Х).
1/V = X/k = X/0,02 = 50 Х. На графике это прямая, выходящая из начала координат .Построив ее, мы находим зависимость 1/V от координаты Х.
Время перемещения муравья численно равно площади под линией этого графика. И теперь мы можем ответить на любой вопрос относительно времени перемещения муравья.
Так, время перемещения на первом метре равно площади треугольника со сторонами 50 и 1, то есть t1 = 25 с.
Время движения на втором метре равно площади заштрихованной трапеции t2 = 75 c.
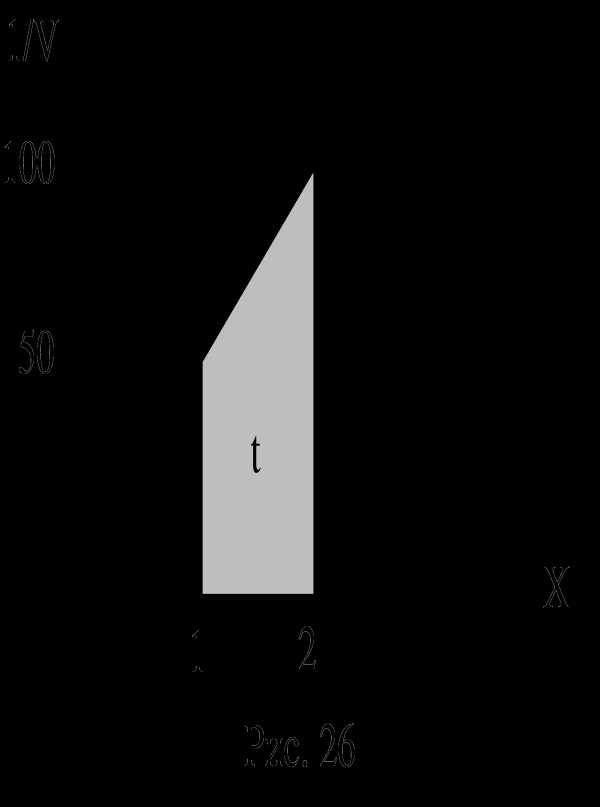
Время движения на первых двух метрах равно соответственно 100 с. И так далее.
То есть с помощью данного графика мы можем определить время перемещения муравья на любом участке.
Подобным образом мы можем решать многие задачи, например, рассчитывать сопротивление резистора при заданной зависимости 1/I от напряжения U. Или рассчитывать электроемкость при заданной зависимости 1/U от заряда Q.
infourok.ru
графические задачи по физике 7-9, проект
Слайд 1
Функциональные зависимости физических величин. Общие способы, приёмы и правила подхода к решению графических задач проект « ГОВОРЯЩАЯ ЛИНИЯ » МБОУ СОШ №8 Южно-Сахалинск Выполнили: Семёнов Владислав, Ивасиро Александр ученики 9класса «А»Слайд 2
тезис Решение задач – это один из методов познания взаимосвязи законов природы. Решение задач – одно из важных средств повторения, закрепления и самопроверки знаний. Большинство физических задач мы решаем аналитическим способом, но в физике существуют задачи, которые требуют графического решения или в которых представлен график. В этих задачах необходимо использовать умение читать и анализировать график.
Слайд 3
Актуальность темы. 1 ) Решение и анализ графических задач позволяют понять и запомнить основные законы и формулы по физике. 2 ) В КИМах для проведения ЕГЭ по физике и математике включены задания с графическим содержанием
Слайд 4
Цель проекта : 1. Издать пособие для самостоятельного обучения решению графических задач. 2. Создать электронную игру. Задачи: 1. Отобрать графические задачи по различным темам. 2. Выяснить общую закономерность в решении графических задач.
Слайд 5
Чтение графика Определение тепловых процессов Определение периода , амплитуды,… Определение Ек, Ер
Слайд 6
В курсе физики 7-9 можно выделить законы, которые выражаются прямой зависимостью : Х( t ), m ( ρ ) , I ( q ) , F упр( Δ x ), F тр( N ) , F ( m), P ( v ) , p ( F ) p ( h ) , F а( V т) … , квадратичной зависимостью: E к =mv 2 /2 E р =CU 2 /2 E р =kx 2 /2
Слайд 7
1 . С равнить ёмкость конденсаторов 2 .Какой из ниже указанных точек на диаграмме зависимости импульса тела от его массы соответствует минимальная скорость? Рассмотрим задачи 3 1 2
Слайд 8
1 .В каком соотношении находятся между собой коэффициенты жесткости? 2. Покоящиеся в начальный момент тело, под действием постоянной силы перемещается так, как показано на рисунке. Определить величину проекции этой силы, если масса тела 3кг.
Слайд 9
Обратите внимание , дана Р( V ), а вопрос о Ек 1 .В каком из нижеприведенных соотношений находятся кинетические энергии трех тел различных масс в момент времени, когда их скорости одинаковы? 2 .По проекции перемещения от времени для тела массой 2кг, определить импульс тела в момент времени 2с. (Начальная скорость равна нулю.)
Слайд 10
1 . Какой из нижеприведенных графиков наиболее точно соответствует зависимости проекции скорости от времени? (Начальная скорость равна нулю. ) Е От одной зависимости к другой От графика к графику
Слайд 11
2 . Тело массой 1кг изменяет свою проекцию скорости так, как показано на рисунке. Какой из нижеприведенных графиков зависимости проекции силы от времени, соответствует данному движению?
Слайд 12
В курсе физики встречаются задачи с несколькими способами решения 1. Вычислить среднюю скорость 2. Определить, в каком соотношении между собой находятся проекции перемещения тел в момент времени, когда скорости тел одинаковы. 10 5 0 V,x ; м/с t,c I II III
Слайд 13
Способ №1 10 5 0 V,x ; м/с t,c I II III a x= V 2x – V 1x t 2 – t 1 2 S=v 0 t+at 2 /2
Слайд 14
Способ № 2 10 5 0 Vx ; м/с t,c I II III Sx= ( V 0 x + Vx ) t/ 2
Слайд 15
Способ № 3 10 5 0 V,x ; м/с t,c I II III S 3 x= 1 *S S 2 x= 2 *S S 1 x : S 2 x : S 3 x= 3 : 2 : 1 S 1 x= 3 *S
Слайд 16
Лишний слайд Очевидно, третий способ решения не требует промежуточных вычислений, поэтому более быстрый, а значит, более удобный. Выясним, в каких задачах возможно такое использование площади.
Слайд 17
Анализ решённых задач показывает, что если произведение X и Y физическая величина, то она равна площади фигуры, ограниченной графиком. P=IU , A=Fs S=vt , V=at, v 0 =0 Δp/t=F , q=It Fa=V ρ g ,…. Х Y
Слайд 18
1 .На рисунке приведен график зависимости проекции скорости некоторого тела от времени. Определить проекцию перемещения и путь этого тела за 5 с после начала движения. Vx ; м/с 3 0 -2 3 t ; с 5 А ) 5 м, 13м В )13 м, 5м С )-1 м, 0м Д )9 м, -4м Е )15 м, 5м
Слайд 19
0 4 6 8 1 2 3 4 5 6 t, c V, м/с 2 .Определите среднюю скорость велосипедиста за время t=6с. Весь путь на всё время S х =S трапеции 4,7м / с
Слайд 20
Изменение импульса тела определяется площадью фигуры – прямоугольника, если сила постоянна , и прямоугольного треугольника, – если сила зависит от времени линейно. F t F t t F
Слайд 21
3 .Наибольшее изменения импульса тела за 2с F t 1 .А 2 .Б 3 .С 1 С Б А Подсказка : Ft=S ф = p
Слайд 22
4 .Используя зависимость импульса тела от времени, определить равнодействующую силу действующую на это тело. А ) 3Н B ) 8Н C ) 12Н D ) 2Н E ) 16 ловушка Р; кг* м/с 6 2 0 2 t ; c F= Δ p/t=(6-2)/2=2
Слайд 23
Механическая работа Механическая работа постоянной по модулю и направлению силы численно равна площади прямоугольника. Механическая работа силы, величина которой зависит от модуля перемещения по линейному закону, численно равна площади прямоугольного треугольника. S 0 F F * s = A = S прямоуг S 0 F A = S пр.треуг
Слайд 24
5 .На рисунке приведена зависимость силы действующей на тело от перемещения. Определить работу этой силы при перемещении тела на 20см. А) 20Дж. B) 8Дж. C) 0,8Дж. D) 40Дж. E) 0,4Дж. ловушка См в метры
Слайд 25
Вычислить заряд 4 I,A 6 2 U,B 4 8 12 16 20 24 Вычислить сопротивление Вычислить А, Δ Ек за 4с Вычислить Ер пружины
Слайд 26
6 .Под действием переменной силы, тело массой 1кг изменяет свою проекцию скорости с течением времени, так, как показано на рисунке. Определить работу равнодействующей этой силы за 8 секунд после начала движения А) 512Дж B) 128Дж C) 112Дж D) 64Дж E) 132Дж сложно A=FS , S= S (t=4c) =32м , F =ma, a =(v-v0)t=2 м / с 2
Слайд 27
заключение В результате своей работы мы выпустили брошюру с задачами графического содержания для самостоятельного решения и создали электронную игру. Работа оказалась полезной для подготовки к ЕГЭ, а также для учащихся, интересующихся физикой. В перспективе рассмотрение других видов задач и их решение.
Слайд 28
Функциональные зависимости физических величин. Общие способы, приёмы и правила подхода к решению графических задач проект « ГОВОРЯЩАЯ ЛИНИЯ » МБОУ СОШ №8 Южно-Сахалинск Выполнили: Семёнов Владислав, Ивасиро Александр ученики 9класса «А»
Слайд 29
Источники информации. 1. Лукашик В.И, Иванова Е.В Сборник задач по физике. Москва «Просвещение» 2000 2. Степанова Г.И Сборник задач по физике М. Просвещение 1995 3. Рымкевич А.П Сборник задач по физике Москва. Просвещение 1988. 4. www.afportal.ru 5. А.В. Перышкин, Е.М Гутник Учебник по физике 7, 8, 9 класс. 6. материалы ГИА 7. С.Е. Каменецкий, В.П.Орехов Методика решения задач по физике в средней школе. М: Просвещение, 1987. 8. В.А. Балаш Задачи по физике и методы их решения. Москва «просвещение» 1983
nsportal.ru
Типовые задачи на уравнения и графики прямолинейного равноускоренного движения. Примеры решения задач по физике. 9-10 класс
Типовые задачи на уравнения и графики прямолинейного равноускоренного движения. Примеры решения задач по физике. 9-10 класс
Задачи по физике – это просто!
Не забываем, что решать задачи надо всегда в системе СИ!
А теперь к задачам!
Элементарные задачи из курса школьной физики по кинематике.
Бесполезно разбирать эти задачи, если вы не знаете формул прямолинейного равноускоренного движения!
Тема трудная, и без азов, как вы сами понимаете, никуда!
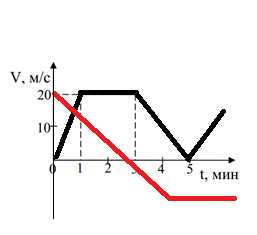
Задача на определение ускорения по заданному графику скорости
Дано: график скорости движущегося тела.
Найти: определить ускорение тела по графику скорости.
Задача на составление описания движения тела и построение графика скорости по заданному уравнению скорости
Дано: уравнение скорости движущегося тела.
Найти: составить описание движения тела, построить график скорости.

Задача на составление описания движения и уравнения скорости по заданному графику скорости
Дано: график скорости движущегося тела.
Найти: составить описание движения и уравнение скорости.

Задачи на составление описания движения тела и построение графика скорости по заданному уравнению движения
Задача 1
Дано: уравнение движения тела.
Найти: составить описание движения тела, построить график скорости.

Задача 2
Дано: уравнение движения тела.
Найти: составить описание движения тела, построить график скорости.

Также полезно рассмотреть решения подобных задач при задании уравнений движения c разными знаками коэффициентов при t и при отсутствии некоторых членов уравнения движения.
class-fizika.ru
Методическая разработка по физике на тему “Методика решения графических задач (механика)”
Методика решения графических задач
Методическая разработка по физике (раздел “Механика”), тема: “Методика решение графических задач” – включает в себя теоретический материал; алгоритм решения графических задач, примеры задач с подробным решением, задачи для самостоятельного решения. Задачи взяты из ОГЭ и ЕГЭ.
Разработка предназначена для учащихся старших классов.
“Мы должны учиться использовать свои знания так, чтобы они способствовали достижению наших целей.” – Н. Энкельманн
Составила: О.И.Добрынина
Содержание
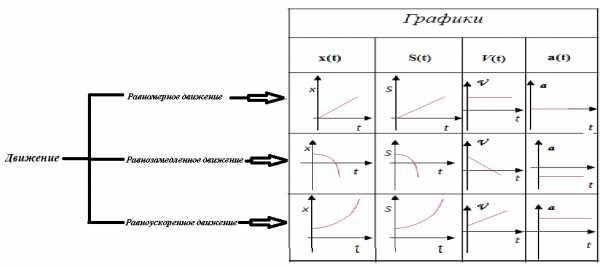
Информация о видах движения
Определение по графику зависимости х(t) , S(t)
Определение по графику зависимости ν (t)
Определение по графику зависимости а(t)
Алгоритм решения задач
Примеры задач
Введение
Графические задания в экзаменационной работе по физике составляет от объема примерно 10 – 20%. Ученику необходимо научиться «читать» графики. Что это значит? Ученик должен определять: вид движения, представленный на графике; начальное и конечное значения изменяющихся величин; место встречи; производить расчеты по имеющимся данным для нахождения физической величины. Данный материал позволит ученикам разобраться с типом решения графических задач и усвоить алгоритм их выполнения при самостоятельном изучении.
Равномерное прямолинейное движение является движение с постоянной скоростью.
Равнопеременное движение является движение, при котором за любые равные промежутки времени скорость тела изменяется на одинаковую величину
Механическое движение представляют графическим способом. Зависимость физических величин выражают при помощи функций. Обозначают:
х(t) – изменение координаты со временем,
S(t) – изменение пути со временем,
ν(t) – изменение скорости со временем,
а(t) – изменение ускорения со временем,
При равномерном движении:
График х(t) и S(t) – наклонная линия, изменяется согласно линейной зависимости
Так как ускорение равно нулю, то график а(t) – прямая линия, идущая по оси времени
Скорость со временем не изменяется, график ν(t) – прямая линия, идущая параллельно оси времени
При равнопеременном движении:
График х(t) и S(t) – парабола, изменяется согласно квадратной зависимости; ветвь параболы направленная вверх – равноускоренное движение, если ветвь параболы направлена вниз – равнозамедленное движение
Ускорение со временем не изменяется график а(t) – прямая линия, идущая параллельно оси времени; а > 0 – движение равноускоренное, если, а < 0 равнозамедленное
График ν(t) – наклонная линия, изменяется согласно линейной зависимости; если прямая удаляется от оси времени – равноускоренное движение, если прямая приближается к оси времени равнозамедленное движение
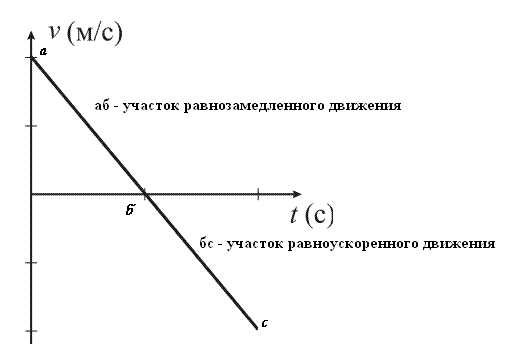
Если движение равноускоренное прямолинейное, то
Если движение равнозамедленное прямолинейное, то
Алгоритм решения задач на определение вида движущегося тела
Определите, физическую величину по вертикальной и горизонтальной осям графика
Установите, единицу измерения физической величины при необходимости выполните преобразования физической величины в основную единицу измерения
Вспомните уравнение х(t) или S(t) при равномерном и равнопеременном (равноускоренном прямолинейном, равнозамедленном прямолинейном) движении, какая эта зависимость от времени (линейная или параболическая), т.е
– равномерное движение: х = хо+ʋ0t -прямая линия
– равноускоренное движение: х = хо+ʋ0t+(ахt2)/2 –ветвь параболы
Sх = х-хо
При равномерном прямолинейном движении вектор ускорения равен нулю = 0.
При равнопеременном прямолинейном движении вектор ускорения – величина постоянная = const.
Формула ускорения равнопеременного прямолинейного движения:
Формула скорости равномерного прямолинейного движения:
Формула скорости равнопеременного прямолинейного движения:
4. Определите вид движения: равномерное, или равноускоренное, или равнозамедленное.
Примеры заданий
1.На рис. Представлен график зависимости координаты – х от времени – t четырех тел, движущихся вдоль оси ОХ. Ускоренному движению соответствует график
А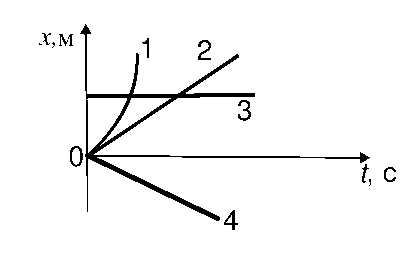 )1
)1
Б) 2
В)3
Г)4
Ответ: А
2.На рисунке даны графики, характеризующие движение пешехода. Опишите это движение, пользуясь обоими графиками.
Рис.а б
Ответ: Рис. а — представляет собой график изменения координаты, рис.б — график пути. На первом графике показано, что пешеход вернулся в то место, откуда он начал движение; на втором по ординате точки С можно определить весь пройденный им путь. Отрезки ОА и ВС соответствуют равномерному движению; АВ — остановке. В обоих направлениях скорость движения одинакова. Это видно по наклону прямых ОА и ВС к оси времени.
3. На каком из графиков (рис. 1) изображена зависимость проекции скорости материальной точки от времени при равноускоренном движении тела при υ0x ≠ 0?
Рис. 1 аРис. 1 бРис. 1 вРис. 1 г
Ответ: При равноускоренном движении уравнение проекции скорости υx = υ0x + ax·t. График – прямая линия, пересекающая ось 0υx в точке υx = υ0x, а тангенс угла наклона графика к оси 0t равен проекции ускорения (ax ≠ 0).Такой график изображен в условии на рис. б.
infourok.ru
Методическая разработка на тему “Методика решения графических задач по молекулярной физике и термодинамике”
ГБОУ «ЛИЦЕЙ «МЕЖДУНАРОДНАЯ КОСМИЧЕСКАЯ ШКОЛА ИМ. В.Н. ЧЕЛОМЕЯ»
МЕТОДИКА РЕШЕНИЯ ГРАФИЧЕСКИХ ЗАДАЧ ПО МОЛЕКУЛЯРНОЙ ФИЗИКЕ И ЕРМОДИНАМИКЕ
ГАШЕВА НАТАЛИЯ ЛЬВОВНА
учитель физики
высшей категории
г. Байконур
2014г
Содержание
Введение…………………………………………………………………стр.3
Методика решения графических задач. Общие вопросы…………….стр.5
Методика решения графических задач по теме «Изопроцессы в газах»…………………………………………………………………… стр.6
Методика решения графических задач по теме «Термодинамика»…стр.10
Заключение………………………………………………………………стр.14
Список литературы……………………………………………………..стр. 17
Введение
В овладении учащимися курсом физики решение задач является важнейшим средством реализации дидактических и воспитательных целей. Задачи служат инструментом формирования физических понятий, развития мышления учащихся, их самостоятельности. Решение задач воспитывает настойчивость, трудолюбие, любознательность. Задачи являются средством контроля качества и глубины усвоения материала.
… Обучение решению задач является органической частью преподавания физики, но, к сожалению, умение учащихся решать задачи находится на недостаточном, а иногда и низком уровне. Причин тому много. Основная причина, на мой взгляд, – отсутствие оптимальной технологии обучения, основанной на достижениях современной психологии. Кроме того, настоящая программа по физике претерпела существенные изменения: это сокращение учебных часов, и перераспределение тем в связи с введением профильного обучения, и изменение требований к минимуму содержания основного и среднего образования.
Таким образом, возникает вопрос: как в новых условиях организовать работу учащихся в школе и дома по решению задач, какие приемы использовать при обучении, какие задачи, сколько и в какой последовательности надо решать, чтобы с наименьшими затратами труда и времени выйти на желаемый результат.
Основная цель, которая ставится при решении задач, заключается в том, чтобы учащиеся глубже поняли физические закономерности, научились разбираться в них и применять их к анализу физических явлений, к практическим вопросам.
Для этого учителю необходимо произвести тщательный отбор задач, определить последовательность их решения. Отобранная система задач должна удовлетворять ряду требований. Основным дидактическим требованием является постепенность усложнения связей между величинами и понятиями, характеризующими процесс или явление, описываемое в задачах. Желательно начинать решение задач по теме или отдельному вопросу курса физики с тренировочных задач. Затем идут более сложные расчетные, экспериментальные и другие задачи, подбираемые последовательно, с возрастающим числом связей.
Необходимость такого отбора связана еще с тем, что в настоящее время существует достаточно широкий круг задачников по физике, содержащих задачи разного уровня сложности и ученики не всегда способны выбрать для себя необходимый задачник. Необходимо учитывать и такой фактор: в данной теме нельзя все время решать задачи только одного типа. Материал следует непрерывно повторять.
Цель моей работы – рассмотреть подборку графических задач по молекулярной физике и термодинамике, позволяющую учащимся усвоить материал на уровне, достаточном для того, чтобы справиться как с задачами базового уровня, предлагаемыми в ЕГЭ, так и с более сложными задачами.
Принцип подборки – от простых тренировочных задач к более сложным, носящим олимпиадный характер.
Методика решения графических задач. Общие вопросы
Под графическими задачами я понимаю задачи, в которых ответ на полученный вопрос не может быть получен без графика.
Трудности решения подобных задач связаны, на мой взгляд, прежде всего со снижением математической грамотности учащихся. Для того, чтобы облегчить ребятам процесс решения подобных задач, стоит иметь в кабинете физики справочные материалы или таблицы, позволяющие вспомнить, каким образом записываются уравнения линейной и квадратичной функций, что представляют собой графики этих функций при тех или иных значениях коэффициентов.
Кроме того, может помочь общий алгоритм решения подобных задач:
Установить, между какими величинами задается зависимость данным графиком.
Определить, какие параметры состояния остаются постоянными, а какие- меняются.
Описать график или отдельные участки графика математически с помощью известных физических законов, если это возможно.
Дополнить, если это необходимо, полученную систему уравнений математическими соотношениями.
Решив систему уравнений, получить ответ.
В молекулярной физике и термодинамике достаточно большое количество графических задач решается при изучении тем « Изопроцессы в газах», «Работа газа в термодинамике, «КПД циклов». Рассмотрим методику решения задач по данным темам.
Методика решения графических задач по теме «Изопроцессы в газах»
После изучения темы «Изопроцессы в газах» учащиеся четко должны знать основные признаки изопроцессов- это постоянство массы газа и одного из параметров состояния – p, V или T, а также уметь изображать графики этих процессов в осях V-p, V-T, p-T. На первом этапе –этапе узнавания- нужно рассмотреть задачи, в которых необходимо уметь определять, какой из процессов, происходящих с одной и той же массой газа, соответствует большему значению одного и того же параметра. А затем перейти к задачам, в которых необходимо оценить изменение того или иного параметра газа, изменение состояния которого не является изопроцессом. При решении последних довольно часто встречается ошибка, состоящая в неумении отличать процессы, протекающие по линейному закону, от изопрцессов.
Пример 1
Даны два изобарных процесса, происходящих с одной и той же массой газа, какой из них происходит при более высоком давлении?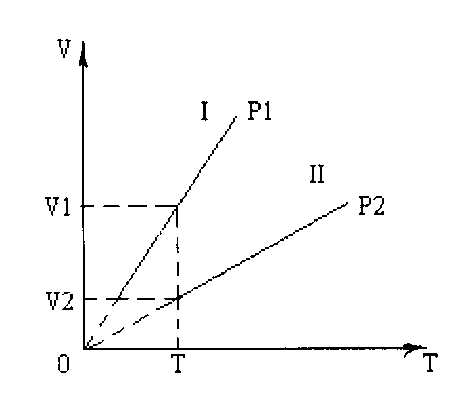
Решение
Рассмотрим состояния 1 и 2, которым соответствует одна и та же температура. Из уравнения Менделеева- Клапейрона pV= νRT следует, что если , то , т.е. чем больше угол наклона графика к оси абсцисс, тем меньше соответствующее давление.
Ответ: второй процесс происходит при более высоком давлении.
Пример 2
График изменения состояния идеального газа в осях V-T представляет собой прямую линию 1-2. Как изменилось давление газа в этом процессе? 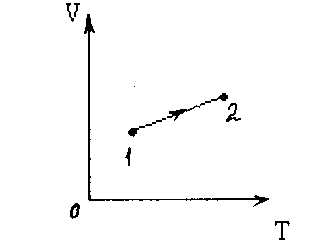
Достаточно часто учащиеся считают, что перед ними изобарный процесс. Поэтому необходимо, прежде всего показать, что график не проходит через начало координат, потому давление газа не может быть постоянным. Для этого продолжим отрезок, изображающий график, пунктирной линией до пересечения с осью ординат.
Метод решения подобных задач состоит в том, что через интересующие нас состояния проводится система изобар, изотерм или изохор, по положению которых по отношению к системе координат можно сравнить интересующие нас параметры. В данном случае угол наклона изобары, проходящей через состояние 2, меньше, поэтому ей соответствует большее давление.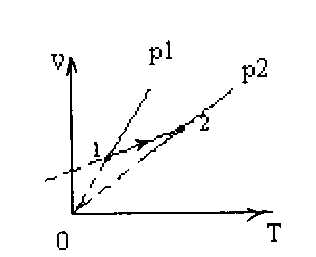
Ответ давление в данном процессе увеличивается.
Пример 3
Укажите точки, в которых достигается наибольшая и наименьшая температура идеального газа, в ходе процесса, изображенного на рисунке (рис.1). 
Чтобы ответить на вопрос этой задачи, построим семейство изотерм (рис.2) Чем дальше от координатных осей находится изотерма, тем выше соответствующая ей температура. Т.о. самой высокой будет температура в точке А, а самой низкой – в точке В. На участке графика ВСА температура газа увеличивается, а на участке АДБ – уменьшается.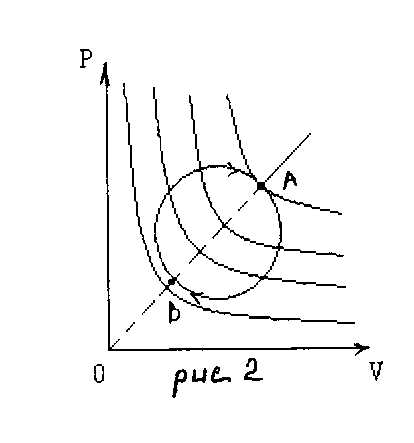
После подробного разбора перечисленных задач, я думаю, несложно будет справиться с заданиями ЕГЭ.
Рассмотрим одну из задач.
В сосуде, закрытом поршнем, находится идеальный газ. График зависимости объема газа от температуры при изменении его состояния показан на рисунке. В каком состоянии давление газа наибольшее?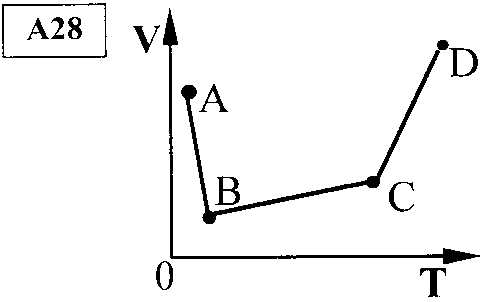
А; 2) В; 3) С; 4) D.
Ответ: 3.
Следующий тип задач – задачи на построение диаграмм изменения состояния газа в различных координатных плоскостях. Подобные задачи способствуют более прочному усвоению закономерностей изопроцессов. Решение данных задач можно осуществлять по следующему плану:
Установить, между какими величинами задается зависимость данным графиком.
Определить, какие параметры состояния остаются постоянными, а какие – меняются.
Определить, какой процесс изображает график ( или отдельный участок графика), назвать его.
Записать, если возможно, закон, описывающий этот процесс.
Изобразить процесс в других координатных осях.
Подробный предварительный анализ графика позволяет избежать ошибок при построении в других координатных плоскостях, а называние процесса – закрепить знания о закономерностях, его описывающих.
Пример 4
На рисунке дан график изменения состояния идеального газа в координатных осях V-T. Представить этот график в осях p-V и p-T.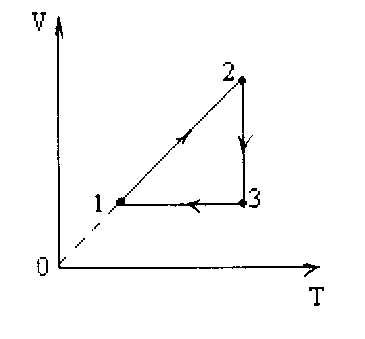
Сначала проанализируем график.
1-2: Vp= const, V- изобарное расширение;
2-3: T= const, V- изотермическое сжатие, pV=const.
3-1: V=const, T изохорное охлаждение.
Теперь построим график в других координатных плоскостях.
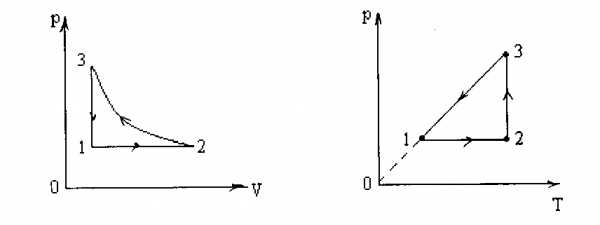
Рассмотрим также задачу, в которой речь идет о построении в других координатных осях диаграммы процесса, содержащей участки, не являющиеся изопроцессами.
Пример 5
Один моль идеального газа участвует в некотором процессе, изображенном в координатах p-V. Продолжения отрезков прямых 1-2 и 3-4 проходят через начало координат, а кривые 1-4 и 2-3 являются изотермами. Изобразить этот процесс в координатах V-T, найти объем V3, если известны объемы V1, V2 ,V3 (Рис.1)
Решение.
Для нахождения объема V3 учтем, что участки 1-4 и 2-3 – изотермы. По закону Бойля- Мариотта p1V1=p4V4, p2V2=p3V3. Т.к. продолжения отрезков прямых 1-2 и 3-4 проходят через начало координат, то для них р1/р2=V1/V2, p4/p3=V4/V3. Отсюда V3= V2V4/V1. Для построения графика в плоскости T-V запишем соотношение p=αV, а также уравнение Менделеева – Клапейрона pV= νRT. Выразим Т и подставим р. Тогда Т= αV2/(νR). Отсюда следует, что для участков 1-2 и 3-4 зависимость температуры от объема квадратичная, графиком такой зависимости является парабола с вершиной в начале координат. График цикла в осях Т- V, имеет вид, указанный на рисунке 2.
Учащимся , интересующимся физикой, можно предложить построить в других координатных плоскостях «Ботинок» или «Елочку», а затем придумать свои замкнутые циклы в виде привычных и непривычных предметов. Эту идею я позаимствовала из статьи Е.А. Ольховской .
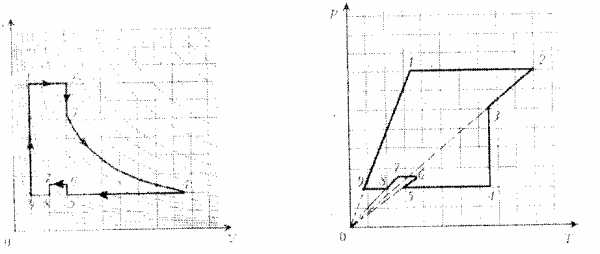
При построении графиков изопроцессов основное внимание следует обратить на p-V- диаграммы, особенно когда цикл содержит несколько изотерм одновременно. Если температуры изотерм относятся, например, как Т1:Т2:Т3:…= 3:4:5…, то расстояния между такими изотермами уменьшается с повышением температуры.
Вновь к графикам изопроцессов приходится вернуться при решении задач по термодинамике. Рассмотрим подобные задачи.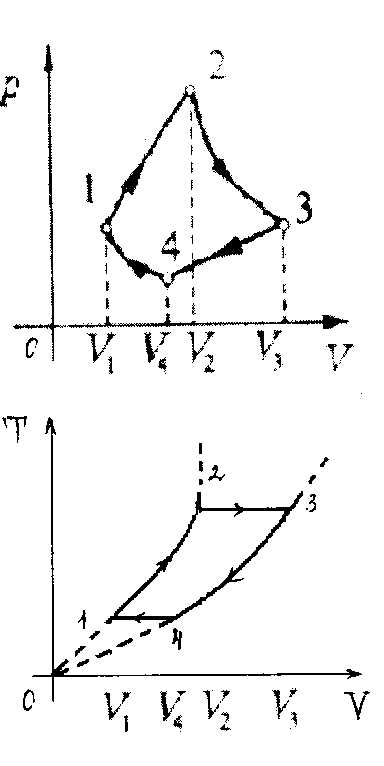
Методика решения задач по термодинамике
В основе термодинамики лежат несколько установленных на опыте фундаментальных физических законов. Первый закон термодинамики представляет собой обобщенный закон сохранения энергии: внутренняя энергия макроскопической системы может быть изменена как в результате работы внешних сил, так и при сообщении теплоты: ΔU=Q+A’, где A’ – работа внешних сил.
Для решения многих задач его удобно записывать в другой форме: Q=ΔU+A, где A – работа, совершенная системой над внешними силами. Исторически первый закон термодинамики был сформулирован именно так.
К графическим задачам можно отнести, во-первых, задачи, в которых рассчитывается работа газа в некотором процессе. А во-вторых, задачи, в которых рассматриваются циклические процессы, происходящие с некоторым количеством газа, и для которых нужно определить КПД.
Перед решением таких задач необходимо напомнить учащимся, в чем состоит графический смысл работы и формулировку первого закона термодинамики.
Работа газа численно равна площади фигуры, ограниченной графиком процесса в координатной плоскости p–V, осью абсцисс и прямыми, проходящими через соответствующие значения объема, параллельно оси ординат.
Перед решением задач на расчет КПД цикла надо также обратить внимание на то, что изменение температуры ΔТ связано с изменением внутренней энергии. Если ΔTЕсли газ совершает работу , то при ΔV, т.е. знак работы совпадает со знаком изменения объема.
Сначала решаем задачи на расчет работы, производимой газом в процессе, изображенном графически. При решении таких задач нужно обратить внимание на то, что судить о работе можно только в случае, когда график процесса изображен в плоскости p-V.
Пример 1.
Над идеальным газом проводят два циклических процесса: 1-2-3-1 и 3-2-4-3. В каком из них газ совершает большую работу? Смотри рисунок.
Чтобы ответить на вопрос задачи, необходимо построить диаграмму этих процессов в плоскости p-V.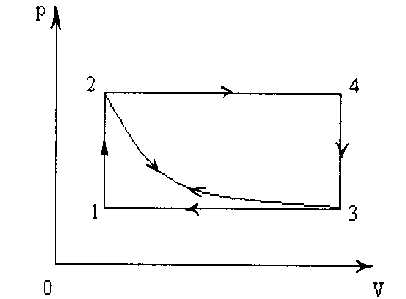
Т.к. работа, совершенная газом за цикл, численно равна площади фигуры, ограниченной циклом в осях (p,V), то из рисунка видно, что большая работа совершена в циклическом процессе 3-2-4-3, т.к. площадь фигуры, ограниченной этим циклом, больше.
Начнем с задачи, которая носит подготовительный характер. Впоследствии, при решении задач подобный анализ можно проводить устно. При рассмотрении данной задачи я ввожу обозначения- стрелочка указывает направление поступления теплоты, если она направлена внутрь цикла, то на данном участке тепло поступает в систему из окружающей среды, если наоборот, то система отдает тепло.
Пример 2.
В цилиндре под поршнем находится воздух. Его состояние последовательно меняется следующим образом:
а) при постоянном объеме увеличивается давление;
б) при постоянном давлении увеличивается объем;
в) при постоянной температуре увеличивается объем;
г) при постоянном давлении воздух возвращается в исходное состояние.
Начертить диаграмму в координатах p – V и указать, при каких из перечисленных изменений воздух получает теплоту и при каких отдает.
Решение.
1-2: V=const => A=0; p↑=>T↑=>ΔT>0=>ΔU>0.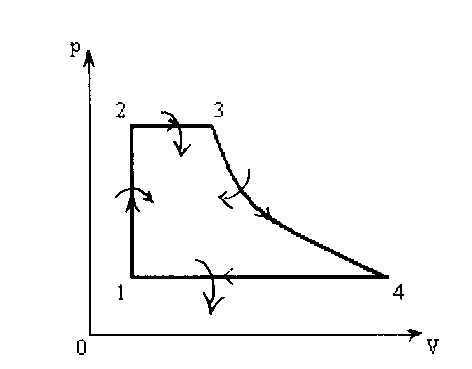
Q=ΔU=>Q12>0.
2-3: p=const=>V↑=>ΔV>0=>А>0, V ~T => V↑ <=> T↑ => ΔT>0, ΔU>0. По первому началу термодинамики Q23=ΔU+A=>Q23>0.
3-4: T=const=>ΔU=0; V↑=>ΔV>0=>A>0. Q34=A=>Q34>0.
4-1: p=const, V↓ => ∆V<0 => A<0. V~T => V↓ и T↓ => ∆T<0, ∆U<0. По первому закону термодинамики Q41=∆U+A=> Q41<0.
Еще один тип задач – задачи на расчет КПД тепловой машины, которая работает по заданному циклу.
Пример 3
С одним молем идеального одноатомного газа осуществляется цикл, состоящий из изохоры (1-2), адиабаты (2-3) и изобары (3-1). Температуры в точках 1,2,3 равны Т1,Т2 и Т3 соответственно. Определите КПД цикла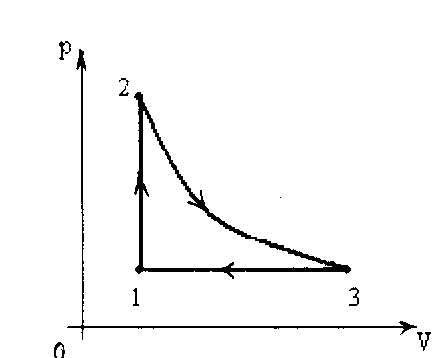
К решению этой задачи можно подойти по-разному.
С одной стороны Положительная работа совершается газом только в процессе 2-3. A23=-ΔU2-3, т.к. процесс 2-3 адиабатный и Q23=0. ΔU2-3=½ i ν R(T3-T2). i-число степеней свободы, у одноатомного газа i=3.
В процессе 3-1 работу над газом совершают внешние силы. Т.к. 3-1- изобарный процесс, то A31=νR(T1-T3), A31<0, потому что T13 .
Работа, совершенная газом за цикл, равна
A=A23+A31=-3/2 ν R (T3-T2)+νR (T1-T3=1/2νR(3T2+2T1-5T3).
Количество теплоты, полученное от нагревателя, Qн= 0,5iνR(T2-T1),т.к. газ получает энергию лишь на участке 1-2, причем процесс 1-2 изохорный, поэтому Qн=Q12=ΔU12=1/2iνR(T2-T1).
Т.о.
Можно подойти к решению по-другому: из предыдущих рассуждений следует, что Qн=Q12=1/2νR(T2-Т1). Qх– количество теплоты, отдаваемое холодильнику. Т.к. тепло отдается окружающей среде только на участке 3-1, то Qх=Q31. По первому началу термодинамики
К этому же результату можно прийти, воспользовавшись формулой
В этой формуле cр– удельная теплоемкость газа при постоянном объеме.
Тогда
Ответ:.
В рассмотренной задаче цикл состоял из процессов, для которых запись первого начала термодинамики хорошо известна. Но довольно часто на олимпиадах предлагаются задачи, в которых циклы состоят не из известных процессов, а из процессов, которые представляют собой либо линейную зависимость p(V), либо дугу окружности. Рассмотрим следующий пример.
Пример 4
В качестве рабочего вещества в тепловой машине используется некоторое количество идеального одноатомного газа, изменение состояния которого изображено на p,V-диаграмме. При надлежащем выборе масштаба по координатным осям цикл изображается двумя четвертями окружностей, причем точки пересечения дуг 1 и 2 лежат на биссектрисе угла, образуемого осями диаграммы. Найти КПД, если отношение максимального и минимального объемов газа в этом цикле 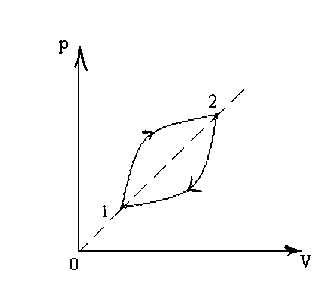
Решение.
Работа, совершенная газом в этом цикле численно равна площади фигуры, ограниченной графиком процесса. Радиус окружностей, соответствующих границам цикла, пропорционален (p2-p1) и (V2-V1), а площадь сегмента, длина дуги которого равна четверти окружности, составляет (0,25πr2-0,5r2).
Тогда работа за цикл равна А = Sфигуры= (0,5πr2-1)(p2-p1)(V2-V1).
Учитывая, что только на участке 1-3-2 газ совершает работу и только на этом участке при увеличении его объема увеличивается давление, а значит, растет температура и внутренняя энергия, можно утверждать, что только на этом участке газ получает энергию от нагревателя.
По первому началу термодинамики Q132=ΔU12+A132, ΔU12=1,5νR(T2-T1).
Из уравнения Менделеева-Клапейрона следует, что p1V1=νRT1, p2V2=νRT2=> ΔU12=1,5(p2V
infourok.ru



