Решение задач теория игр – Решение задач «СРОЧНО! 1 задача по теории игр» по теории игр заказать, купить
- Комментариев к записи Решение задач теория игр – Решение задач «СРОЧНО! 1 задача по теории игр» по теории игр заказать, купить нет
- Советы абитуриенту
Матричные игры: примеры решения задач
Матричной игрой в математической теории игр называется игра двух лиц с нулевой суммой, в которой в распоряжении каждого из них имеется конечное множество стратегий. Правила матричной игры определяет платёжная матрица, элементы которой – выигрыши первого игрока, которые являются также проигрышами второго игрока.
Матричная игра является антагонистической игрой. Первый игрок получает максимальный гарантированный (не зависящий от поведения второго игрока) выигрыш, равный цене игры, аналогично, второй игрок добивается минимального гарантированного проигрыша.
Под стратегией понимается совокупность правил (принципов), определяющих выбор варианта действий при каждом личном ходе игрока в зависимости от сложившейся ситуации.
Теперь обо всём по порядку и подробно.
В матричной игре её правила определяет платёжная матрица.
Рассмотрим игру, в которой имеются два участника: первый игрок и второй игрок. Пусть в распоряжении первого игрока имеется m чистых стратегий, а в распоряжении второго игрока – n чистых стратегий. Поскольку рассматривается игра, естественно, что в этой игре есть выигрыши и есть проигрыши.
В платёжной матрице элементами являются числа, выражающие выигрыши и проигрыши игроков. Выигрыши и проигрыши могут выражаться в пунктах, количестве денег или в других единицах.
Составим платёжную матрицу:
.
Если первый игрок выбирает i-ю чистую стратегию, а второй игрок – j-ю чистую стратегию, то выигрыш первого игрока составит a
ij единиц, а проигрыш второго игрока – также aij единиц.Так как aij + (- aij) = 0, то описанная игра является матричной игрой с нулевой суммой.
Простейшим примером матричной игры может служить бросание монеты. Правила игры следующие. Первый и второй игроки бросают монету и в результате выпадает “орёл” или “решка”. Если одновременно выпали “орёл” и “орёл” или “решка” или “решка”, то первый игрок выиграет одну единицу, а в других случаях он же проиграет одну единицу (второй игрок выиграет одну единицу). Такие же две стратегии и в распоряжении второго игрока. Соответствующая платёжная матрица будет следующей:
.
Задача теории игр – определить выбор стратегии первого игрока, которая гарантировала бы ему максимальный средний выигрыш, а также выбор стратегии второго игрока, которая гарантировала бы ему максимальный средний проигрыш.
Как происходит выбор стратегии в матричной игре?
Вновь посмотрим на платёжную матрицу:
.
Сначала определим величину выигрыша первого игрока, если он использует i-ю чистую стратегию. Если первый игрок использует i-ю чистую стратегию, то логично предположить, что второй игрок будет использовать такую чистую стратегию, благодаря которой выигрыш первого игрока был бы минимальным. В свою очередь первый игрок будет использовать такую чистую стратегию, которая бы обеспечила ему максимальный выигрыш. Исходя из этих условий выигрыш первого игрока, который обозначим как v1, называется максиминным выигрышем или нижней ценой игры.
При решении задач на цену игры и определение стратегии для этих величин у первого игрока следует поступать следующим образом. Из каждой строки выписать значение минимального элемента и уже из них выбрать максимальный. Таким образом, выигрыш первого игрока будет максимальным из минимальных. Отсюда и название – максиминный выигрыш. Номер строки этого элемента и будет номером чистой стратегии, которую выбирает первый игрок.
Теперь определим величину проигрыша второго игрока, если он использует j-ю стратегию. В этом случае первый игрок использует такую свою чистую стратегию, при которой проигрыш второго игрока был бы максимальным. Второй игрок должен выбрать такую чистую стратегию, при которой его проигрыш был бы минимальным. Проигрыш второго игрока, который обозначим как v2, называется минимаксным проигрышем или верхней ценой игры.
При решении задач на цену игры и определение стратегии
для определения этих величин у второго игрока следует поступать следующим образом. Из каждого столбца
выписать значение максимального элемента и уже из них выбрать минимальный. Таким образом, проигрыш второго
игрока будет минимальным из максимальных. Отсюда и название – минимаксный выигрыш. Номер столбца этого
элемента и будет номером чистой стратегии, которую выбирает второй игрок. Если второй игрок использует
“минимакс”, то независимо от выбора стратегии первым игроком, он проиграет не более
Пример 1. Дана матричная игра с платёжной матрицей
.
Определить максиминную стратегию первого игрока, минимаксную стратегию второго игрока, нижнюю и верхнюю цену игры.
Решение. Справа от платёжной матрицы выпишем наименьшие элементы в её строках и отметим максимальный из них, а снизу от матрицы – наибольшие элементы в столбцах и выберем минимальный из них:
Наибольший из наименьших элементов строк – 2, это нижняя цена игры, ей соответствует первая строка, следовательно, максиминная стратегия первого игрока первая. Наименьший из наибольших элементов столбцов – 5, это верхняя цена игры, ей соответствует второй столбец, следовательно, минимаксная стратегия второго игрока – вторая.
Теперь, когда мы научились находить нижнюю и верхнюю цену игры, максиминную и минимаксную стратегии, пришло время научиться обозначать эти понятия формально.
Итак, гарантированный выигрыш первого игрока:
.
Первый игрок должен выбрать чистую стратегию, которая обеспечивала бы ему максимальный из минимальных выигрышей. Этот выигрыш (максимин) обозначается так:
.
Первый игрок использует такую свою чистую стратегию, чтобы проигрыш второго игрока был максимальным. Этот проигрыш обозначается так:
.
Второй игрок должен выбрать свою чистую стратегию так, чтобы его проигрыш был минимальным. Этот проигрыш (минимакс) обозначается так:
.
Ещё пример из этой же серии.
Пример 2. Дана матричная игра с платёжной матрицей
.
Определить максиминную стратегию первого игрока, минимаксную стратегию второго игрока, нижнюю и верхнюю цену игры.
Решение. Справа от платёжной матрицы выпишем наименьшие элементы в её строках и отметим максимальный из них, а снизу от матрицы – наибольшие элементы в столбцах и выберем минимальный из них:
Наибольший из наименьших элементов строк – 3, это нижняя цена игры, ей соответствует вторая строка, следовательно, максиминная стратегия первого игрока вторая. Наименьший из наибольших элементов столбцов – 5, это верхняя цена игры, ей соответствует первый столбец, следовательно, минимаксная стратегия второго игрока – первая.
Если верхняя и нижняя цена игры одинаковая, то считается, что матричная игра имеет седловую точку. Верно и обратное утверждение: если матричная игра имеет седловую точку, то верхняя и нижняя цены матричной игры одинаковы. Соответствующий элемент одновременно является наименьшим в строке и наибольшим в столбце и равен цене игры.
Таким образом, если , то – оптимальная чистая стратегия первого игрока, а – оптимальная чистая стратегия второго игрока. То есть равные между собой нижняя и верхняя цены игры достигаются на одной и той же паре стратегий.
В этом случае матричная игра имеет решение в чистых стратегиях.
.
Найти нижнюю и верхнюю цену игры. Имеет ли данная матричная игра седловую точку?
Решение. Справа от платёжной матрицы выпишем наименьшие элементы в её строках и отметим максимальный из них, а снизу от матрицы – наибольшие элементы в столбцах и выберем минимальный из них:
Нижняя цена игры совпадает с верхней ценой игры. Таким образом, цена игры равна 5. То есть . Цена игры равна значению седловой точки . Максиминная стратегия первого игрока – вторая чистая стратегия, а минимаксная стратегия второго игрока – третья чистая стратегия. Данная матричная игра имеет решение в чистых стратегиях.
В большинстве случаев матричная игра не имеет седловой точки, поэтому соответствующая матричная игра не имеет решений в чистых стратегиях.
Но она имеет решение в оптимальных смешанных стратегиях. Для их нахождения нужно принять, что игра повторяется достаточное число раз, чтобы на основании опыта можно было предположить, какая стратегия является более предпочтительной. Поэтому решение связывается с понятием вероятности и среднего (математического ожидания). В окончательном же решении есть и аналог седловой точки (то есть равенства нижней и верхней цены игры), и аналог соответствующих им стратегий.Итак, чтобы чтобы первый игрок получил максимальный средний выигрыш и чтобы средний проигрыш второго игрока был минимальным, чистые стратегии следует использовать с определённой вероятностью.
Если первый игрок использует чистые стратегии с вероятностями , то вектор называется смешанной стратегией первого игрока. Иначе говоря, это “смесь” чистых стратегий. При этом сумма этих вероятностей равна единице:
.
Если второй игрок использует чистые стратегии с вероятностями , то вектор называется смешанной стратегией второго игрока. При этом сумма этих вероятностей равна единице:
.
Если первый игрок использует смешанную стратегию p, а второй игрок – смешанную стратегию q, то имеет смысл математическое ожидание выигрыша первого игрока (проигрыша второго игрока). Чтобы его найти, нужно перемножить вектор смешанной стратении первого игрока (который будет матрицей из одной строки), платёжную матрицу и вектор смешанной стратегии второго игрока (который будет матрицей из одного столбца):
.
Пример 4. Дана матричная игра с платёжной матрицей
.
Определить математическое ожидание выигрыша первого игрока (проигрыша второго игрока), если смешанная стратегия первого игрока , а смешанная стратегия второго игрока .
Решение. Согласно формуле математического ожидания выигрыша первого игрока (проигрыша второго игрока) оно равно произведению вектора смешанной стратегии первого игрока, платёжной матрицы и вектора смешанной стратегии второго игрока:
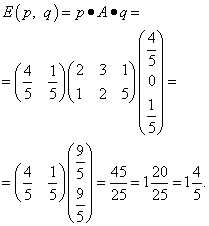
Оптимальной смешанной стратегией первого игрока называется такая смешанная стратегия , которая обеспечивала бы ему максимальный средний выигрыш , если игра повторяется достаточное число раз.
Оптимальной смешанной стратегией второго игрока называется такая смешанная стратегия , которая обеспечивала бы ему минимальный средний проигрыш , если игра повторяется достаточное число раз.
По аналогии с обозначениями максимина и минимакса в случах чистых стратегий оптимальные смешанные стратегии обозначаются так (и увязываются с математическим ожиданием, то есть средним, выигрыша первого игрока и проигрыша второго игрока):
,
.
В таком случае для функции E существует седловая точка, что означает равенство .
Для того, чтобы найти оптимальные смешанные стратегии и седловую точку, то есть решить матричную игру в смешанных стратегиях, нужно свести матричную игру к задаче линейного программирования, то есть к оптимизационной задаче, и решить соответствующую задачу линейного программирования.
Для того, чтобы решить матричную игру в смешанных стратегиях, нужно составить прямую задачу линейного программирования и двойственную ей задачу. В двойственной задаче расширенная матрица, в которой хранятся коэффициенты при переменных в системе ограничений, свободные члены и коэффициенты при переменных в функции цели, транспонируется. При этом минимуму функции цели исходной задачи ставится в соответствие максимум в двойственной задаче.
Функция цели в прямой задаче линейного программирования:
.
Система ограничений в прямой задаче линейного программирования:
Функция цели в двойственной задаче:
.
Система ограничений в двойственной задаче:
Оптимальный план прямой задачи линейного программирования обозначим
,
а оптимальный план двойственной задачи обозначим
Линейные формы для соответствующих оптимальных планов обозначим и ,
а находить их нужно как суммы соответствующих координат оптимальных планов.
В соответствии определениям предыдущего параграфа и координатами оптимальных планов, в силе следующие смешанные стратегии первого и второго игроков:
,
.
Математики-теоретики доказали, что цена игры следующим образом выражается через линейные формы оптимальных планов:
,
то есть является величиной, обратной суммам координат оптимальных планов.
Нам, практикам, остаётся лишь использовать эту формулу для решения матричных игр в смешанных стратегиях. Как и формулы для нахождения оптимальных смешанных стратегий соответственно первого и второго игроков:
,
,
в которых вторые сомножители – векторы. Оптимальные смешанные стратегии также, как мы уже определили в предыдущем параграфе, являются векторами. Поэтому, умножив число (цену игры) на вектор (с координатами оптимальных планов) получим также вектор.
Пример 5. Дана матричная игра с платёжной матрицей
.
Найти цену игры V и оптимальные смешанные стратегии и .
Решение. Составляем соответствующую данной матричной игре задачу линейного программирования:
Приводим задачу к канонической форме и решаем задачу и двойственную ей задачу симплекс-методом.
Получаем решение прямой задачи:
.
Находим линейную форму оптимальных планов как сумму найденных координат:
.
Получаем решение двойственной задачи:
.
Находим линейную форму оптимальных планов как сумму найденных координат:
.
Находим цену игры:
.
Находим оптимальную смешанную стратегию первого игрока:
.
Находим оптимальную смешанную стратегию второго игрока:
.
Пусть дана игра с платёжной матрицей
Если эта матричная игра имеет седловую точку, то она имеет решение в чистых стратегиях, как показано в параграфах 1 и 2.
Если же игра не имеет седловой точки, то она имеет решение в оптимальных смешанных стратегиях. Для этого простейшего случая матричной игры при её решениях путём сведения к задаче линейного программирования были найдены формулы стратегий игроков и цены игры, благодаря которым такая игра решается менее трудоёмким способом.
Формула для нахождения оптимальной смешанной стратегии первого игрока:
.
Формула для нахождения оптимальной смешанной стратегии второго игрока:
.
Формула для нахождения цены игры:
.
Пример 6. Дана матричная игра с платёжной матрицей
.
Найти оптимальные смешанные стратегии игроков и цену игры.
Решение. Оптимальные смешанные стратегии первого игрока получаем по соответствующей из приведённых формул:
.
Оптимальные смешанные стратегии второго игрока получаем также по соответствующей формуле:
.
Цена игры:
.
Матричная игра, седловая точка, чистые стратегии, смешанные стратегии… А для чего всё это? Рассмотрим на примере, как с помощью матричных игр решаются экономические задачи.
Пример 7. Составить матричную игру для следующей задачи.
Предприятие может выпускать три вида продукции (A1, A2, A3), получая при этом прибыль, зависящую от спроса, который может быть в одном из четырёх состояний (B1, B2, B3, B4). Дана матрица, элементы которой aij характеризуют прибыль, которую получит предприятие при выпуске i-й продукции с j-м состоянием спроса.
| B1 | B2 | B3 | B1 | |
| A1 | 3 | 3 | 6 | 8 |
| A2 | 9 | 10 | 4 | 2 |
| A3 | 7 | 7 | 5 | 4 |
Решение. Задача сводится к матричной игре предприятия A против спроса B.
Прежде чем решать задачу, можно упростить игру, проведя анализ платёжной матрицы и отбросив стратегии, заведомо невыгодные или дублирующие. Вторая стратегия (второй столбец матрицы) является явно невыгодной для игрока B по сравнению с первой (элементы второго столбца больше элементов первого столбца), так как цель игрока B – уменьшить выигрыш игрока A. Поэтому второй столбец можно отбросить. Получим следующую матрицу:
.
Далее составляется и решается задача линейного программирования. Это мы уже умеем.
Поделиться с друзьями
Материалы по векторам и матрицам
Линейное программирование
function-x.ru
Решение задач по теории игр
Определения теории игр
Предметом рассмотрения теории игр является изучение конфликтных ситуаций.
Под конфликтной ситуацией понимается ситуация преследования различных целей участников конфликта в условиях неопределенности. При этом результаты действий каждого из участников конфликта зависят от предыдущих действий других участников. В теории игр математическая модель конфликтной ситуации называется игрой, а стороны, участвующие в конфликте – игроками. Исходом конфликта является выигрыш (или проигрыш, т.е. выигрыш с отрицательным знаком) игроков. Условия, в которых происходит развитие конфликта, считаются неопределенными. Эта неопределенность может иметь различное происхождение. Так заранее могут быть неизвестны как цели игроков, так и поведение игроков в процессе развития конфликтной ситуации. Все условия, в которых происходит развитие конфликта, могут носить как частично заданный, так и вероятностный характер. Действие игрока в конфликтной ситуации называется ходом. Ходы игроков могут быть намеренными и случайными. Набор ходов игроков называется стратегией.
Как же решают такие задачи в теории игр?
Для математического моделирования конфликтной ситуации в теории игр принимают некоторые упрощающие допущения. Например, допускается, что игра игроками ведется по определенным правилам. Кроме этого упрощенная математическая модель строится без учета второстепенных факторов. Для решения задач в теории игр существует несколько методов. Один из них основан на допущении о том, что ходы игроков носят оптимальный характер. Под оптимальностью подразумевается рациональность ходов, производимых игроками. Т.е. делается предположение, что каждый из игроков при каждом своем ходе стремится получить максимально возможную на данном этапе выгоду. При этом другие игроки в данных условиях при такой стратегии первого игрока стремятся получить минимальный проигрыш. При этом предполагается, что игроки в течение игры не отклоняются от выбранных ими стратегий. Это так называемая матричная игра, которую можно представить формулой:
где — множества стратегий;
— функция двух переменных х и y, принадлежащих соответственно множествам и .
Согласно принципу оптимальности, при выборе первым игроком некой стратегии из множества , второй игрок может выбрать такую стратегию из множества , при которой выигрыш первого игрока будет равен наименьшему из значений . Поэтому предполагается, что первый игрок заранее будет стремиться выбрать свою стратегию так, чтобы этот минимальный выигрыш был наибольшим из возможных, т.е.
Обозначим
— нижняя цена игры .
Такая стратегия первого игрока в теории игр называется максиминной стратегией.
А принцип, согласно которому он действует, называется принципом максимина. При котором первый игрок гарантирует себе определенный выигрыш не зависимо от действий второго игрока.
Приняв эту стратегию, первый игрок при любом поведении второго игрока гарантирует себе выигрыш не меньший, чем значение .
Стратегия же второго игрока при следующем ходе определяется как:
Обозначим
Здесь — верхняя цена игры .
Стратегия второго игрока называется минимаксной стратегией.
Принимая такую стратегию второй игрок при любых действиях первого игрока проигрывает не более значения игры .
Допуская, что игроки придерживаются выбранных стратегий до конца игры, т.е.
, — выигрыши игроков равны .
Получаем, что выигрыши игры в таком случае находятся в интервале между значениями нижней и верхней цены игры и . Т.е.
Если оба игрока действуют согласно одному принципу – принципу минимакса, то
Для игры, заданной матрицей выигрышей это равенство можно записать в виде:
Тогда нахождение решения такой задачи можно представить в виде следующей схемы:
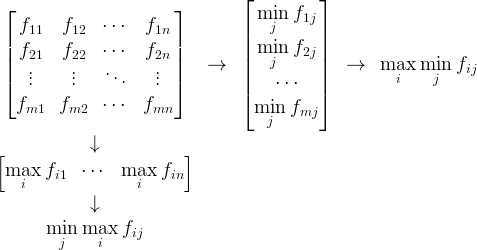
Общее значение максимина и минимакса в теории игр называют значением матричной игры.
Заключение
Под понятием игрок в теории игр подразумевается не только конкретное лицо, но и может приниматься некая группа (компания, страна), имеющая в конфликте определенные интересы. А под конфликтной ситуацией могут рассматриваться ситуации из различных областей жизнедеятельности (экономики, экологии, и т.п.). Выигрыш игроков может носить не только количественный характер, но и состоять из рекомендаций по достижению целей, преследуемых в конфликте. Таким образом, с помощью теории игр, можно предложить решить конфликтную ситуацию выбором определенных рациональных ходов — стратегий, необходимых для достижения целей игроков.
Решение задач на заказ
Мы также практикуем платное решение задач по теории игр и другим математическим дисциплинам. Заказать решение у нас на сайте. Узнать цену можно бесплатно.
Смотрите также:
reshatel.org
Тема 8_Лекция 9_Теория игр
ТЕМА 8. ТЕОРИЯ МАТРИЧНЫХ ИГР
Лекция 9
1. Постановка задачи выбора в условиях неопределенности
2.Основные определения и теоремы теории игр
3.Примеры решения задач при парной игре с нулевой суммой.
1. Постановка задачи выбора в условиях неопределенности
Ранее мы познакомились с задачами выбора решения, когда каждой альтернативе (варианту выбора) соответствовал определенный исход. Это был, таким образом, выбор в условиях определенности.
В реальных задачах часто приходится иметь дело с ситуацией, когда альтернатива неоднозначно определяет последствия сделанного выбора. Другими словами, имеется набор возможных исходов y Y, из которых один окажется совмещенным с выбранной альтернативой, но с какой именно – в момент выбора неизвестно, но станет ясно только тогда, когда выбор уже сделан, и ничего изменить нельзя. Хотя с разной альтернативой x X связано одно и то же множество исходов Y, для разных альтернатив разные исходы имеют неодинаковое значение.
1.1 Задание неопределенности с помощью матрицы
В случае дискретного набора альтернатив и исходов описанную выше стиуацию можно представить в виде матрицы
X, Y
y1
y2
y3
yj
…
ym
x1
a11
a12
a13
a1i
…
a1m
x2
a21
a22
a23
a2i
…
a2m
xi
ai1
ai2
ai3
aii
…
aim
…
…
…
…
…
…
…
xn
an1
an2
an3
ani
…
anm
Вектор y = (y1,….ym) – это все возможные исходы. Числа aii выражают оценку ситуации, когда сделан выбор альтернативы хi и реализовался исход yi. В разных случаях числа aii могут иметь различный смысл (“выигрыш”, “потери”, “платеж”).
Возможны два варианта:
все строки ai = (ai1, …. aim) (т.е. мы видим, это тоже вектор) одинаковы и проблемы выбора между альтернативами нет;
строки различны, следовательно, возникает проблемв выбора альтернативы.
В случае непрерывных множеств X и Y ситуация описывается аналогично с помощью задаваемых на этих множествах функциях a (x,y), x X, y Y.
Мы несколько определились с ситуацией, однако всего этого пока недостаточно для формальной постановки задачи выбора. Реальные задачи могут быть самыми разными и требуют, соответственно, самых разных методов решения.
2.Основные определения и теоремы теории игр
Теория игр относится к разделу прикладной математики исследующей математические модели принятия решений в условиях конфликта, противоречий и неопределенности. Задачей теории игр является нахождение оптимальной стратегии поведения в условиях конфликта, неопределенности или противодействия какой то стороны в этой ситуации независимо от того сознательно или неосознанно это происходит. Игровые математические модели позволяют не только найти оптимальную стратегию, которая не всегда однозначна, но и оценить каждый вариант решения с различных иногда противоречивых точек зрения, а так же глубже разобраться во всех сложностях и неопределенностях реальной ситуации для принятия до конца продуманного решения.
Началом теории игр как последовательной математической теории поведения можно считать выход в свет 50 лет назад монографии Дж. фон Неймана и О. Моргенштерна. Французский математик Э. Мулен так характеризует значение теории игр для социально-экономических наук: «По нашему мнению, теория игр представляет собой набор инструментов для построения моделей в экономических и политических теориях. Единственным, но вполне достаточным оправданием существования теории игр служит её растущее применение в этих дисциплинах. Она является поистине неиссякаемым источником гибких концепций, каждая из которых проливает свет на определенные стороны социальных взаимоотношений.».
Вначале введем несколько фундаментальных понятия теории игр, после этого дадим определение этому разделу прикладной математики.
Конфликт – это противоречие, вызванное противоположными интересами сторон.
Конфликтная ситуация – ситуация в которой участвуют стороны интересы которых полностью или частично противоположны.
Игра – это действительный или формальный конфликт, в котором имеется по крайней мере два участника, каждый из которых стремится к достижению собственных целей
Правилами игры называют допустимые действия каждого из игроков, направленные на достижение некоторой цели.
Платежом называется количественная оценка результатов игры.
Парная игра – игра в которой участвуют только две стороны (два игрока).
Игра с нулевой суммой – парная игра при которой сумма платежа равна нулю, т. е. если проигрыш одного игрока, равен выигрышу другого.
Стратегия игрока – это однозначный выбор игрока в каждой из возможных ситуаций, когда этот игрок должен сделать личный ход.
Оптимальная стратегия – это такая стратегия игрока, которая при многократном повторении игры обеспечивает ему максимально возможный средний выигрыш или минимально возможный средний проигрыш.
Пусть мы имеем парную игру с нулевой суммой, один игрок может выбрать при данном ходе i -ю стратегию из m своих возможных (i=1..m), а второй, не зная выбора первого j -ю стратегию из n своих возможных стратегий (j=1..n). В результате первый игрок выигрывает величину , а второй проигрывает эту величину. Из этих величин составим матрицуA.
A
Платежная матрица – так назовем матрицу A или еще по другому матрицей игры.
Конечной игрой размерности (m n) называется игра определенная матрицей А имеющей m строк и n столбцов.
Максимином или нижней ценой игры назавем число ,
а соответствующая ему стратегия (строка) максиминной.
Минимаксом или верхней ценой игры назавем число
,
а соответствующая ему стратегия (столбец) минимаксной.
Теорема 1.1. Нижняя цена игры всегда не превосходит верхнюю цену игры.
Игрой с седловой точкой называется игра для которой .
Ценой игры называется величина , если.
В случае игры с седловой точкой , игрокам выгодно придерживатся максиминной и минимаксной стратегий и не выгодно отклонятся от них . В таких случаях про игру говорят, что в ней имеет место равновесие в чистых стратегиях.
Возможна игра и с несколькими седловыми точками. Тогда игра имеет несколько оптимальных решений, но с одинаковой ценой игры.
Чаще встречаются матричные игры без седловой точки, когда и тогда для нахождения её решения используются смешанные стратегии.
Смешанной стратегией игрока называется вектор, каждая из компонент которого показывает относительную частоту использования игроком соответствующей чистой стратегии.
Теорема 1.2. Основная теорема теории матричных игр. Всякая матричная игра с нулевой суммой имеет решение в смешанных стратегиях.
Теорема 1.3. Если один из игроков применяет оптимальную смешанную стратегию, то его выигрыш равен цене игры в не зависимости от того, с какими частотами будет применять второй игрок свои стратегии (в том числе и чистые стратегии).
2. Примеры решения задач при парной игре с нулевой суммой
Задача 1.1.
Найти решение игры, заданной матрицей А
А=.
Решение. Прежде всего проверим наличие седловой точки в данной матрице.
Для этого найдем нижнюю и верхнюю цену игры.
Минимальные элементы по строкам равны (2 и 3) тогда нижняя цена игры = max (2; 3) = 3. Максимальные элементы по столбцам равны (3 и 6) тогда верхняя цена игры = min (3; 6) = 3. Отсюда видно, что = =3 и мы имеем седловую точку .= 3, т.е. задача имеет решение в чистых стратегиях.
Оптимальные чистые стратегии для первого и второго игроков равны соответственно U* = (0; 1), Z* = (1; 0), а цена игры = 3.
Задача 1.2.
Найти решение игры, заданной матрицей А
А=.
Решение. Прежде всего проверим наличие седловой точки в данной матрице.
Для этого найдем нижнюю и верхнюю цену игры.
Минимальные элементы по строкам равны (2 и 3) тогда нижняя цена игры = max (2; 3) = 3. Максимальные элементы по столбцам равны (4 и 6) тогда верхняя цена игры = min (4; 6) = 4. Отсюда видно, что и мы имеем игру, которая имеет решение в смешанных стратегиях, а цена игры .
Предположим, что для первого игрока смешанная стратегия задается вектором U = (u1; u2). Первый игрок, если придерживается своей оптимальной стратегии, независимо от стратегии второго игрока получает цену игры , т.е.
4u1* + 3u2* = (1)
2u1* + 6u2* = .
Кроме этого относительные частоты связаны условием:
u1* + u2* = 1.
Решаем полученную систему трех линейных уравнений с тремя неизвестными. Получим оптимальную стратегию первого игрока и цену игры:
U* = ( u1* ; u2*) = (3/5; 2/5), = 18/5.
Составим уравнения для нахождения оптимальной стратегии второго игрока, если при любой чистой стратегии первого, второй проигрывает цену игры:
4z1* + 2z2* = = 18/5 (2)
3z1* + 6z2* = = 18/5.
Решаем полученную систему двух линейных уравнений с двумя неизвестными. Получим оптимальную стратегию второго игрока:
Z* = ( z1* ; z2*) = (4/5; 1/5).
Рассмотрим геометрическую интерпретацию этой задачи в смешанных стратегиях. Для этого в плоскости введем систему координат и на горизонтальной оси Ou отложим вероятность применения первым игроком его двух стратегий, сумма этих вероятностей равна 1, поэтому весь график расположится на отрезке единичной длины. В точках 0 стратегия (1; 0), а в 1 стратегия (0; 1).
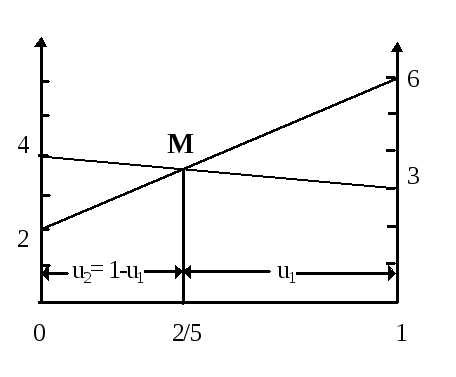
По оси ординат в точке 0 отложим выигрыши первого игрока по первой его стратегии при обеих стратегиях второго, а в точке 1 при второй стратегии первого игрока. Соединим эти платежи по столбцам, тогда пересечение прямых дадут решение системы уравнений (1), а ордината этой точки цену игры .
Анологично можно построить график для нахождения оптимальной стратегии второго игрока.
Мы рассмотрели только самый простой вариант парной матричной игры с нулевой суммой, но она достаточно наглядно показывает, что иногда можно количественно оценить и выбрать оптимальный вариант поведения в конфликтной ситуации.
studfiles.net
Теория игр
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
Государственное образовательное учреждение высшего профессионального образования
“ЧЕЛЯБИНСКИЙ ГОСУДАРСТВЕННЫЙ ПЕДАГОГИЧЕСКИЙ УНИВЕРСИТЕТ”
Кафедра информатики и методики преподавания информатики
Квалификационная работа
ТЕОРИЯ ИГР В НАЧАЛЬНОЙ ШКОЛЕ
Исполнитель:
Новикова Ксения Сергеевна,
студентка группы 591
Научный руководитель:
Дмитриева О.А.,
ассистент кафедры ИМПИ
Зав. кафедрой:
Матрос Д. Ш.,
докт. пед. наук, профессор
Дата допуска к защите:
Челябинск 2007
Содержание
Введение
Глава I Основные положения Теории игр
1.1 Предмет и задачи теории игр
1.2 Решение матричной игры в чистых стратегиях
1.3 Решение матричной игры в смешанных стратегиях
1.4 Решение игр графическим методом
1.5 Сведение матричной игры к задаче линейного программирования
1.6 Игры с природой
Выводы по I главе
Глава II Разработка элективного курса “Элементы теории игр в начальной школе”
2.1 Место компьютера в начальной школе
2.3 Игра как метод обучения в начальной школе
2.4 Анализ программ и стандарта по информатике в начальной школе
2.5 Элективный курс
2.6 Педагогический эксперимент
2.7 Описание программного продукта
Выводы по II главе
Заключение
Список использованной литературы
Приложения
Теория игр была основана Джоном фон Нейманом и Оскаром Моргенштерном в их первой работе “The Theory of Games and Economic Behavior”, изданной в 1944 году. В 1928 году в математических анналах фон Нейманом была опубликована статья “О теории общественных игр”, в которой впервые было применено понятие “теория игр”. Использование этого понятия объясняется схожестью логики принятия решений в таких играх, как шахматы и покер. Характерным для таких ситуаций является то, что результат для принимающего решение зависит не только от его решения, но и от того, какое решение примут другие. Поэтому оптимальный исход не может быть получен в результате принятия решения одним лицом.
Другим предшественником теории игр по праву считается французский математик Э. Борель (1871-1956). Некоторые фундаментальные идеи были независимо предложены А. Вальдом (1902-1950), заложившим основы нового подхода к статистической теории принятия решений.
Первые приложения теория игр нашла в математической статистике. Во время второй мировой войны и сразу после нее теорией игр серьезно заинтересовались военные, которые увидели в ней аппарат для исследования стратегических решений. Ее использовали как плодотворный источник теоретических моделей в экономике и социологии. Методы теории игр используются также в теории операций и в линейном программировании.
В начальной школе для обучения детей используют различные правила и инструкции, поэтому в этом возрасте можно развивать у них алгоритмическое мышление, которое не только приводит к более прочному усвоению знаний, но и к вхождению в компьютерный мир.
Изучение “Теории игр” в начальной школе поможет сформировать у детей умение анализировать условие задачи, продумывать последовательность действий, направленных на ее выполнение. Контролировать правильность своих действий на всех этапах работы и корректировать их в случаях допущенной ошибки, то есть направить учащихся на формирование широкого спектра умений, которые будут необходимы в дальнейшей учебной и учебно-трудовой деятельности ребенка, а в будущем и любой профессиональной деятельности.
Цель: изучение теоретических положений по теории игр и создание элективного курса “Элементы теории игр в начальной школе” с методической поддержкой.
Объект исследования: Теория игр
Предмет исследования: Обучение теории игр в начальной школе.
Задачи исследования:
изучить теоретический материал
отобрать задачи для практической реализации
разработать алгоритмы решения задач
программно реализовать отобранные задачи
разработать элективный курс
создать электронное пособие
Гипотеза: если в процессе обучения использовать понятие выигрышной стратегии, то это будет способствовать развитию логического мышления и сообразительности у младших школьников, а также повысит общий уровень подготовки по информатике.
Новизна работы заключается в следующем:
На данный момент не существует школьного курса по теме теории игр в начальной школе.
Создана программная поддержка, позволяющая осуществить эффективное изучение данной темы в начальной школе.
Разработан элективный курс “Элементы теории игр в начальной школе” и программно-методическая поддержка к нему.
В процессе целенаправленной человеческой деятельности возникают ситуации, в которых интересы отдельных лиц (участников, групп, сторон) либо прямо противоположны (антагонистичны), либо, не будучи непримиримыми, все же не совпадают. Простейшими и наиболее наглядными примерами таких ситуаций являются спортивные игры, арбитражные споры, военные учения (маневры), борьба между блоками избирателей за своих кандидатов, в международных отношениях – отстаивание интересов своего государства и т.п. Здесь каждый из участников сознательно стремится добиться наилучшего результата за счет другого участника. Подобного рода ситуации встречаются и в различных сферах производственной деятельности.
Все ситуации, когда эффективность действия одного из участников зависит от действий других, можно разбить на два типа: интересы участников совпадают, и они могут договориться о совместных действиях; интересы участников не совпадают. В этих случаях может оказаться невыгодным сообщать другим участникам свои решения, так как кто-нибудь из них сможет воспользоваться знанием чужих решений и получит больший выигрыш за счет других участников. Ситуации такого типа называются конфликтными.
Для указанных ситуаций характерно, что эффективность решений, принимаемых в ходе конфликта каждой из сторон, существенно зависит от действий другой стороны. При этом ни одна из сторон не может полностью контролировать положение, так как и той и другой стороне решения приходится принимать в условиях неопределенности. Так, при определении объема выпуска продукции на одном предприятии нельзя не учитывать размеров выпуска аналогичной продукции на других предприятиях. В реальных условиях нередко возникают ситуации, в которых антагонизм отсутствует, но существуют противоположные тенденции. Например, для нормального функционирования производства, с одной стороны, необходимо наличие запасов разнообразных ресурсов, но с другой – стремление к чрезвычайному увеличению этих запасов вызывает дополнительные затраты по их содержанию и хранению. В приведенных примерах конфликтные ситуации возникают в результате сознательной деятельности людей. Однако на практике встречаются неопределенности, которые порождаются не сознательным противодействием другой стороны, а недостаточной информированностью об условиях проведения планируемой операции.
Раздел математики, изучающий конфликтные ситуации на основе их математических моделей, называется теорией игр. Таким образом, теория игр – это математическая теория конфликтных ситуаций, разрабатывающая рекомендации по наиболее рациональному образу действий каждого из участников в ходе конфликтной ситуации, т.е. таких действий, которые обеспечивали бы ему наилучший результат. Игровую схему можно придать многим ситуациям в экономике. Здесь выигрышем могут быть эффективность использования дефицитных ресурсов, производственных фондов, величина прибыли, себестоимость и т.д.
Необходимо подчеркнуть, что методы и рекомендации теории игр разрабатываются применительно к таким специфическим конфликтным ситуациям, которые обладают свойством многократной повторяемости. Если конфликтная ситуация реализуется однократно или ограниченное число раз, то рекомендации теории игр теряют смысл.
Чтобы проанализировать конфликтную ситуацию по ее математической модели, ситуацию необходимо упростить, учтя лишь важнейшие факторы, существенно влияющие на ход конфликта.
Определение 1. Игрой называется упрощенная математическая модель конфликтной ситуации, отличающаяся от реального конфликта тем, что ведется по определенным правилам.
Игра – это совокупность правил, определяющих возможные действия (чистые стратегии) участников игры. Суть игры в том, что каждый из участников принимает такие решения в развивающейся конфликтной ситуации, которые, как он полагает, могут обеспечить ему наилучший исход. Исход игры – это значение некоторой функции, называемой функцией выигрыша (платежной функцией), которая может задаваться либо аналитически выражением, либо таблично (матрицей). Величина выигрыша зависит от стратегии, применяемой игроком.
Человечество издавна пользуется такими формализованными моделями конфликтных ситуаций, которые являются играми в буквальном смысле слова. Примерами могут служить шашки, шахматы, карточные игры и т.д. Все эти игры носят характер соревнования, протекающего по известным правилам и заканчивающего “победой” (выигрышем) того или иного игрока.
Такие формально регламентированные, искусственно организованные игры представляют собой наиболее подходящий материал для иллюстрации и усвоения основных понятий теории игр. Терминология, заимствованная из практики таких игр, применяется и при анализе других конфликтных ситуаций: стороны, участвующие в них, условно именуются “игроками “, а результат столкновения – “выигрышем ” одной из сторон.
mirznanii.com
Типовые задачи, решаемые с помощью теории игр
Пример 1
Предприниматель располагает тремя видами товаров А1, А2, А3, которые он стремится реализовать на рынке, где возможна продажа конкурентом аналогичных товаров – В1, В2, В3 соответственно.
Предпринимателю не известно, какой вид товаров преимущественно конкурент будет продавать на рынке, а конкуренту не известно, какие товары предпринимателя на этом рынке появятся
Предприниматель располагает данными о том, какова вероятность продать тот или иной товар при наличии на рынке товаров конкурента. Эти данные образуют матрицу игры (табл. 2).
Таблица 2. Матрица игры для примера 1.
Предприниматель | Конкурент | |||
B1 | B2 | B3 | αi | |
A1 | 0,5 | 0,4 | 0,9 | 0,4* |
A2 | 0,2 | 0,9 | 0,1 | 0,1 |
A3 | 0,8 | 0,0 | 1,0 | 0,0 |
βj | 0,8* | 0,9 | 1,0 | |
Необходимо дать предпринимателю рекомендации по рациональному выбору вида товаров для продвижения их на рынок в условиях конкуренции, при котором обеспечивается получение наилучшего возможного результата – наибольшей вероятности продаж, что бы ни предпринимал конкурент.
Решение
Выписываем справа минимумы строк и из них выбираем наибольший αi = 0,4 (отмечен звездочкой). Это нижняя цена игры, или максимин. Затем выписываем внизу максимумы столбцов и из них выбираем наименьший βj = 0,8 (отмечен звездочкой). Это верхняя цена игры, или минимакс.
Решение заключается в том, что необходимо систематически применять максиминную стратегию – товар типа A1. При этом предпринимателю гарантируется результат не менее р = 0,4, что бы ни предпринимал конкурент (его замыслы нам не известны). Для конкурента наилучшая стратегия – выбор товара вида В1; при этом он гарантирует себе результат не более q = 0,8 (чем прибыль предпринимателя больше, тем для него хуже).
Поскольку в рассмотренном примере нет седловой точки (α ≠ β), это означает, что полученные рекомендации верны лишь для случая, когда конкурент не располагает данными об избранном предпринимателем решении. Это так называемая неустойчивая стратегия. Если конкурент узнает о том, что предприниматель стал применять товар типа А2 он сразу же начнет применять товар вида В3 и тем самым улучшит свой результат до р = 0,1.
В тех случаях, когда в подобной задаче конкурент располагает данными о выборе предпринимателя, необходимо искать решение в смешанных .стратегиях.
Пример 2 (продолжение примера 1)
Пусть предпринимателю стали известны возможные количества единиц каждого из его товаров, которые могут быть проданы при различных вариантах появления товаров конкурента на рынке (табл. 3).
Необходимо дать предпринимателю рекомендации, при использовании которых среднеожидаемое количество проданных товаров будет наибольшим, что бы ни предпринимал конкурент.
Таблица 3. Матрица игры для примера 2.
Предприниматель | Конкурент | |||
B1 | B2 | B3 | αi | |
A1 | 5 | 6 | 8 | 5 |
A2 | 8 | 7 | 7 | 7* |
A3 | 9 | 7 | 6 | 6 |
βj | 9 | 7* | 8 | |
studfiles.net
Типовые задачи, решаемые с помощью теории игр
Пример 1
Предприниматель располагает тремя видами товаров А1, А2, А3, которые он стремится реализовать на рынке, где возможна продажа конкурентом аналогичных товаров – В1, В2, В3 соответственно.
Предпринимателю не известно, какой вид товаров преимущественно конкурент будет продавать на рынке, а конкуренту не известно, какие товары предпринимателя на этом рынке появятся
Предприниматель располагает данными о том, какова вероятность продать тот или иной товар при наличии на рынке товаров конкурента. Эти данные образуют матрицу игры (табл. 2).
Таблица 2. Матрица игры для примера 1.
Предприниматель | Конкурент | |||
B1 | B2 | B3 | αi | |
A1 | 0,5 | 0,4 | 0,9 | 0,4* |
A2 | 0,2 | 0,9 | 0,1 | 0,1 |
A3 | 0,8 | 0,0 | 1,0 | 0,0 |
βj | 0,8* | 0,9 | 1,0 | |
Необходимо дать предпринимателю рекомендации по рациональному выбору вида товаров для продвижения их на рынок в условиях конкуренции, при котором обеспечивается получение наилучшего возможного результата – наибольшей вероятности продаж, что бы ни предпринимал конкурент.
Решение
Выписываем справа минимумы строк и из них выбираем наибольший αi = 0,4 (отмечен звездочкой). Это нижняя цена игры, или максимин. Затем выписываем внизу максимумы столбцов и из них выбираем наименьший βj = 0,8 (отмечен звездочкой). Это верхняя цена игры, или минимакс.
Решение заключается в том, что необходимо систематически применять максиминную стратегию – товар типа A1. При этом предпринимателю гарантируется результат не менее р = 0,4, что бы ни предпринимал конкурент (его замыслы нам не известны). Для конкурента наилучшая стратегия – выбор товара вида В1; при этом он гарантирует себе результат не более q = 0,8 (чем прибыль предпринимателя больше, тем для него хуже).
Поскольку в рассмотренном примере нет седловой точки (α ≠ β), это означает, что полученные рекомендации верны лишь для случая, когда конкурент не располагает данными об избранном предпринимателем решении. Это так называемая неустойчивая стратегия. Если конкурент узнает о том, что предприниматель стал применять товар типа А2 он сразу же начнет применять товар вида В3 и тем самым улучшит свой результат до р = 0,1.
В тех случаях, когда в подобной задаче конкурент располагает данными о выборе предпринимателя, необходимо искать решение в смешанных .стратегиях.
Пример 2 (продолжение примера 1)
Пусть предпринимателю стали известны возможные количества единиц каждого из его товаров, которые могут быть проданы при различных вариантах появления товаров конкурента на рынке (табл. 3).
Необходимо дать предпринимателю рекомендации, при использовании которых среднеожидаемое количество проданных товаров будет наибольшим, что бы ни предпринимал конкурент.
Таблица 3. Матрица игры для примера 2.
Предприниматель | Конкурент | |||
B1 | B2 | B3 | αi | |
A1 | 5 | 6 | 8 | 5 |
A2 | 8 | 7 | 7 | 7* |
A3 | 9 | 7 | 6 | 6 |
βj | 9 | 7* | 8 | |
studfiles.net
Теория игр Примеры и задачи
Рекомендовано кафедрой математического моделирования экономических процессов Финансового университета при Правительстве Российской Федерации в качестве учебного пособия для студентов, обучающихся по направлению подготовки бакалавров и магистров
Теория игр. Примеры и задачи: Учебное пособие / В.П. Невежин. – М.: Форум, 2012. – 128 с.: 60×90 1/16. – (Высшее образование). (обложка)
ISBN 978-5-91134-645-4
Предлагаемое учебное пособие предназначено для студентов, изучающих в рамках Государственного образовательного стандарта такие дисциплины, как «Теория игр», «Элементы теории игр», «Теория игр и стратегическое поведение фирм», «Математические методы и модели исследования операций» и т. п.
Важным достоинством данного пособия является то, что в нем по каждой рассматриваемой теме из теории игр приводится краткая теоретическая справка, рассматривается решение типового примера, а затем предлагаются задания для самостоятельной работы студентов. Приведенные задания могут быть использованы как для промежуточного контроля знаний, так и в качестве практических заданий на экзамене или зачете.
Предназначено для студентов экономических вузов, обучающихся по программам «бакалавр экономики» и магистерским программам, а также преподавателей, ведущих обучение по данным дисциплинам.
Введение 3
Глава 1. АНТАГОНИСТИЧЕСКИЕ МАТРИЧНЫЕ ИГРЫ 6
1.1. Основные положения теории игр 6
1.2. Построение платежной матрицы 14
Задачи для самостоятельной работы 16
1.3. Принцип доминирования 26
Задачи для самостоятельной работы 28
1.4. Определение границ выигрыша и наличия седловой точки .. 29
Задачи для самостоятельной работы 30
1.5. Игра 2×2 32
Задачи для самостоятельной работы 36
1.6. Игра 2 х N 37
Задачи для самостоятельной работы 42
1.7. Игра М х 2 44
Задачи для самостоятельной работы 47
1.8. Игра Л/х УУ 49
Задачи для самостоятельной работы 56
1.9. Общая схема решения парных игр с нулевой суммой 58
Глава 2. БЕСКОАЛИЦИОННЫЕ ИГРЫ 59
2.1. Игры двух лиц с произвольной суммой .,. 60
2.2. Задачи для самостоятельной работы 71
Глава 3. СТАТИСТИЧЕСКИЕ ИГРЫ 77
3.1. Игры с природой 77
3.2. Классические критерии в играх с природой 82
3.2.1. Критерий Байеса—Лапласа (В-L-критерий) 82
3.2.2. Критерий Лапласа 83
3.2.3. Критерий Вальда 83
3.2.4. Минимаксный критерий (ММ-критерий) 84
3.2.5. Критерий Сэвиджа 85
Примеры игр с природой с применением классических критериев 85
3.3. Производные критерии в играх с природой 90
3.3.1. Критерий Гурвица 90
3.3.2. Критерий Ходжа—Лемана 92
3.3.3. Критерий Гермейера 92
3.3.4. BL (ММ)-критерий 93
3.3.5. Критерий произведений 94
Примеры игры с природой с применением производных критериев 95
3.4. Задачи для самостоятельной работы 98
Список рекомендуемой литературы 110
Ответы на задания 111
Ответы на задачи раздела 1.2 111
Ответы на задачи раздела 1.4 115
Ответы на задачи раздела 1.5 115
Ответы на задачи раздела 1.6 116
Ответы на задачи раздела 1.7 117
Ответы на задачи раздела 1.8 / 118
Ответы на задачи раздела 3.4 120
textarchive.ru



