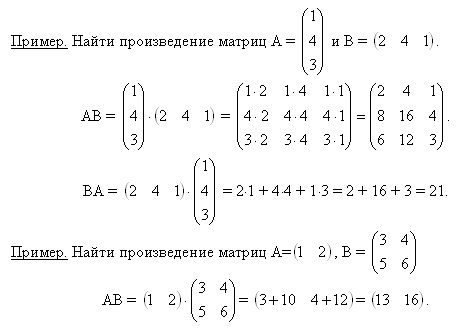
С действие матрицами – умножение, сложение, вычитание. Как решать, с чего начать
- Комментариев к записи С действие матрицами – умножение, сложение, вычитание. Как решать, с чего начать нет
- Советы абитуриенту
Матрицы действия с ними
Контрольная работа на тему:
«Матрицы, действия с ними»
Историческая справка
Понятие Матрица (в математике) было введено в работах У. Гамильтона и А. Кэли в середине 19 века. Основы теории созданы К. Вейерштрассом и Ф. Фробениусом (2-я половина 19 века и начало 20 века). И.А. Лаппо-Данилевский разработал теорию аналитических функций от многих матричных аргументов и применил эту теорию к исследованию систем дифференциальных уравнений с аналитическими коэффициентами. Матричные обозначения получили распространение в современной математике и её приложениях. Исчисление Матрица (в математике) развивается в направлении построения эффективных алгоритмов для численного решения основных задач.
Раскрытие темы
Понятие о матрице
Матрица – множество чисел, образующих прямоугольную таблицу, которая содержит m-строк и n-столбцов. Для обозначения матрицы используется надпись:
aij, I – номер строки, j – номер столбца.
Элементы матрицы, стоящие на диагонали, идущие из верхнего левого угла называют главной диагональю, другую диагональ называют побочной.
пример 1.
Элементы главной диагонали: 1,6,5. Побочной диагонали: 3,6,3. (пример 1)
пример 2.
Если количество строк m матрицы не равно количеству столбцов n, то матрица называется прямоугольной (пример 2).
Если количество столбцов матрицы совпадают с количеством строк, то матрица называется квадратной (пример 1).
Количество строк или столбцов в квадратной матрице называются ее порядком.
Если все элементы квадратной матрицы, кроме элементов главной диагонали, равны нулю, то матрица называется диагональной (пример 3).
пример3
Если все числа главной диагонали равны единице, то матрица называется единичной (пример 4).
пример 4
Если в прямоугольной матрице m*n m=1, то получается матрица-строка (пример 5).
xT = (2 3 5). пример 5.
Если n=1, то получается матрица-столбец (пример 6).
пример 6.
Матрицы-строки матрицы-столбцы называются векторами.
Свойства матриц:
Действия с матрицами
Сложение матриц
Матрицы одинакового размера можно складывать.
Суммой двух таких матриц А и В называется матрица С, элементы которой равны сумме соответствующих элементов матриц А и В. Символически будем записывать так: А+В=С.
Пример.
Легко видеть, что сложение матриц подчиняется переместительному и сочетательному законам:
А+В=В+А
(А+В)+С=А+(В+С).
Нулевая матрица при сложении матриц выполняет роль обычного нуля при сложении чисел: А+0=А.
Вычитание матриц.
Разностью двух матриц А и В одинакового размера называется матрица С, такая, что
С+В=А
Из этого определения следует, что элементы матрицы С равны разности соответствующих элементов матриц А и В.
Обозначается разность матриц А и В так: С=А – В.
Пример.
3. Умножение матриц
Рассмотрим правило умножения двух квадратных матриц второго порядка.
Произведением матрицы А на матрицу В называется матрица С=АВ.
Правила умножения прямоугольных матриц:
Умножение матрицы А на матрицу В имеет смысл в том случае, когда число столбцов матрицы А совпадает с числом строк в матрице В.
В результате умножения двух прямоугольных матриц получается матрица, содержащая столько строк, сколько строк было в первой матрице и столько столбцов, сколько столбцов было во второй матрице.
4. Умножение матрицы на число
При умножении матрицы A на число a все числа, составляющие матрицу A, умножаются на число a. Например, умножим матрицу на число 2. Получим , т.е. при умножении матрицы на число множитель «вносится» под знак матрицы.
Транспонирование матрицы
Транспонированная матрица – матрица AТ, полученная из исходной матрицы A заменой строк на столбцы.
Формально, транспонированная матрица для матрицы A размеров m*n – матрица AT размеров n*m, определённая как AT[i, j] = A [j, i].
Например,
Свойства транспонированных матриц
1. (AT)T = A
2. (A + B)T = AT + BT
3. (AB)T = BTAT
4. detA = detAT
Список литературы
Баврин, Матросов В.Л. Высшая математика: Учебник для студентов ВУЗов – М.: 2002.
Беллман Р. Введение в теорию матриц. – М.: Мир, 1969
Дж. Голуб, Ч. Ван Лоун Матричные вычисления. – М.: Мир, 1999.
coolreferat.com
Действия с матрицами
Действия с матрицамиДанное методическое пособие поможет Вам научиться выполнять действия с матрицами: сложение (вычитание) матриц, транспонирование матрицы, умножение матриц, нахождение обратной матрицы. Весь материал изложен в простой и доступной форме, приведены соответствующие примеры, таким образом, даже неподготовленный человек сможет научиться выполнять действия с матрицами. Для самоконтроля и самопроверки Вы можетебесплатно скачать матричный калькулятор >>>.
Я буду стараться минимизировать теоретические выкладки, кое-где возможны объяснения «на пальцах» и использование ненаучных терминов. Любители основательной теории, пожалуйста, не занимайтесь критикой, наша задача – научиться выполнять действия с матрицами.
Начнем.
Матрица – это прямоугольная таблица каких-либо элементов. В качестве элементов мы будем рассматривать числа, то есть числовые матрицы.
Обозначение: матрицы обычно обозначают прописными латинскими буквами
Пример: рассмотрим матрицу «два на три»:
Данная матрица состоит из шести элементов:
Все числа (элементы) внутри матрицы существуют сами по себе, то есть ни о каком вычитании речи не идет:
Это просто таблица (набор) чисел!
Также договоримся не переставлять числа, если иного не сказано в объяснениях. У каждого числа свое местоположение, и перетасовывать их нельзя!
Рассматриваемая матрица имеет две строки:
и три столбца:
СТАНДАРТ: когда говорят о размерах матрицы, то сначала указывают количество строк, а только потом – количество столбцов. Мы только что разобрали по косточкам матрицу «два на три».
Если количество строк и столбцов матрицы совпадает, то матрицу называют квадратной, например: – матрица «три на три».
Если в матрице один столбец или одна строка , то такие матрицы также называют векторами.
На самом деле понятие матрицы мы знаем еще со школы, рассмотрим, например точку с координатами «икс» и «игрек»: . По существу, координаты точки записаны в матрицу «один на два». Кстати, вот Вам и пример, почему порядок чисел имеет значение: и – это две совершенно разные точки плоскости.
Теперь переходим непосредственно к изучению действий с матрицами:
1) Действие первое. Вынесение минуса из матрицы (внесение минуса в матрицу).
Вернемся к нашей матрице . Как вы наверняка заметили, в данной матрице слишком много отрицательных чисел. Это очень неудобно с точки зрения выполнения различных действий с матрицей, неудобно писать столько минусов, да и просто в оформлении некрасиво выглядит.
Вынесем минус за пределы матрицы, сменив у КАЖДОГО элемента матрицы знак:
У нуля, как Вы понимаете, знак не меняется, ноль – он и в Африке ноль.
Обратный пример: . Выглядит безобразно.
Внесем минус в матрицу, сменив у КАЖДОГО элемента матрицы знак:
Ну вот, гораздо симпатичнее получилось. И, самое главное, выполнять какие-либо действия с матрицей будет ПРОЩЕ. Потому-что есть такая математическая народная примета: чем больше минусов – тем больше путаницы и ошибок.
2) Действие второе. Умножение матрицы на число.
Пример:
Всё просто, для того чтобы умножить матрицу на число, нужно каждый элемент матрицы умножить на данное число. В данном случае – на тройку.
Еще один полезный пример:
– умножение матрицы на дробь
Сначала рассмотрим то, чего делать НЕ НАДО:
Вносить дробь в матрицу НЕ НУЖНО, во-первых, это только затрудняет дальнейшие действия с матрицей, во-вторых, затрудняет проверку решения преподавателем (особенно, если – окончательный ответ задания).
И, тем более, НЕ НАДО делить каждый элемент матрицы на минус семь:
Из статьи Математика для чайников или с чего начать, мы помним, что десятичных дробей с запятой в высшей математике стараются всячески избегать.
Единственное, что желательно сделать в этом примере – это внести минус в матрицу:
А вот если бы ВСЕ элементы матрицы делились на 7 без остатка, то тогда можно (и нужно!) было бы поделить.
Пример:
В этом случае можно и
Примечание: в теории высшей математики школьного понятия «деление» нет. Вместо фразы «это поделить на это» всегда можно сказать «это умножить на дробь». То есть, деление – это частный случай умножения.
3) Действие третье. Транспонирование матрицы.
Для того чтобы транспонировать матрицу, нужно ее строки записать в столбцы транспонированной матрицы.
Пример:
Транспонировать матрицу
Строка здесь всего одна и, согласно правилу, её нужно записать в столбец:
– транспонированная матрица.
Транспонированная матрица обычно обозначается надстрочным индексом или штрихом справа вверху.
Пошаговый пример:
Транспонировать матрицу
Сначала переписываем первую строку в первый столбец:
Потом переписываем вторую строку во второй столбец:
И, наконец, переписываем третью строку в третий столбец:
Готово. Грубо говоря, транспонировать – это значит повернуть матрицу набок.
4) Действие четвертое. Сумма (разность) матриц.
Сумма матриц действие несложное.
НЕ ВСЕ МАТРИЦЫ МОЖНО СКЛАДЫВАТЬ. Для выполнения сложения (вычитания) матриц, необходимо, чтобы они были ОДИНАКОВЫМИ ПО РАЗМЕРУ.
Например, если дана матрица «два на два», то ее можно складывать только с матрицей «два на два» и никакой другой!
Пример:
Сложить матрицы и
Для того чтобы сложить матрицы, необходимо сложить их соответствующие элементы:
Для разности матриц правило аналогичное, необходимо найти разность соответствующих элементов.
Пример:
Найти разность матриц ,
А как решить данный пример проще, чтобы не запутаться? Целесообразно избавиться от лишних минусов, для этого внесем минус в матрицу :
Примечание: в теории высшей математики школьного понятия «вычитание» нет. Вместо фразы «из этого вычесть это» всегда можно сказать «к этому прибавить отрицательное число». То есть, вычитание – это частный случай сложения.
5) Действие пятое. Умножение матриц.
Чем дальше в лес, тем толще партизаны. Скажу сразу, правило умножения матриц выглядит очень странно, и объяснить его не так-то просто, но я все-таки постараюсь это сделать, используя конкретные примеры.
Дата добавления: 2015-08-27; просмотров: 68 | Нарушение авторских прав
Как умножить матрицы? | Обратите внимание, что ! Это почти всегда так! | Как вычислить определитель? | Свойства определителя. Понижение порядка определителя | Эффективные методы вычисления определителя | Свойства определителя | При транспонировании матрицы величина её определителя не меняется | Если две строки (или два столбца) определителя поменять местами, то определитель сменит знак | Из строки (столбца) определителя можно вынести общий множитель | Если две строки (столбца) определителя пропорциональны (как частный случай – одинаковы), то данный определитель равен нулю |
mybiblioteka.su – 2015-2019 год. (0.009 сек.)
mybiblioteka.su
Действия с матрицами
Действия с матрицами
Данное методическое пособие поможет Вам научиться выполнять действия с матрицами: сложение (вычитание) матриц, транспонирование матрицы, умножение матриц, нахождение обратной матрицы. Весь материал изложен в простой и доступной форме, приведены соответствующие примеры, таким образом, даже неподготовленный человек сможет научиться выполнять действия с матрицами. Для самоконтроля и самопроверки Вы можете бесплатно скачать матричный калькулятор >>>.
Я буду стараться минимизировать теоретические выкладки, кое-где возможны объяснения «на пальцах» и использование ненаучных терминов. Любители основательной теории, пожалуйста, не занимайтесь критикой, наша задача – научиться выполнять действия с матрицами.
Начнем.
Матрица – это прямоугольная таблица каких-либо элементов. В качестве элементов мы будем рассматривать числа, то есть числовые матрицы. ЭЛЕМЕНТ – это термин. Термин желательно запомнить, он будет часто встречаться, не случайно я использовал для его выделения жирный шрифт.
Обозначение: матрицы обычно обозначают прописными латинскими буквами
Пример: рассмотрим матрицу «два на три»:
Данная матрица состоит из шести элементов:
Все числа (элементы) внутри матрицы существуют сами по себе, то есть ни о каком вычитании речи не идет:
Это просто таблица (набор) чисел!
Также договоримся не переставлять числа, если иного не сказано в объяснениях. У каждого числа свое местоположение, и перетасовывать их нельзя!
Рассматриваемая матрица имеет две строки:
и три столбца:
СТАНДАРТ: когда говорят о размерах матрицы, то сначала указывают количество строк, а только потом – количество столбцов. Мы только что разобрали по косточкам матрицу «два на три».
Если количество строк и столбцов матрицы совпадает, то матрицу называют квадратной, например: – матрица «три на три».
Если в матрице один столбец или одна строка , то такие матрицы также называют векторами.
На самом деле понятие матрицы мы знаем еще со школы, рассмотрим, например точку с координатами «икс» и «игрек»: . По существу, координаты точки записаны в матрицу «один на два». Кстати, вот Вам и пример, почему порядок чисел имеет значение: и – это две совершенно разные точки плоскости.
Теперь переходим непосредственно к изучению действий с матрицами:
1) Действие первое. Вынесение минуса из матрицы (внесение минуса в матрицу).
Вернемся к нашей матрице . Как вы наверняка заметили, в данной матрице слишком много отрицательных чисел. Это очень неудобно с точки зрения выполнения различных действий с матрицей, неудобно писать столько минусов, да и просто в оформлении некрасиво выглядит.
Вынесем минус за пределы матрицы, сменив у КАЖДОГО элемента матрицы знак:
У нуля, как Вы понимаете, знак не меняется, ноль – он и в Африке ноль.
Обратный пример: . Выглядит безобразно.
Внесем минус в матрицу, сменив у КАЖДОГО элемента матрицы знак:
Ну вот, гораздо симпатичнее получилось. И, самое главное, выполнять какие-либо действия с матрицей будет ПРОЩЕ. Потому-что есть такая математическая народная примета: чем больше минусов – тем больше путаницы и ошибок.
2) Действие второе. Умножение матрицы на число.
Пример:
Всё просто, для того чтобы умножить матрицу на число, нужно каждый элемент матрицы умножить на данное число. В данном случае – на тройку.
Еще один полезный пример:
– умножение матрицы на дробь
Сначала рассмотрим то, чего делать НЕ НАДО:
Вносить дробь в матрицу НЕ НУЖНО, во-первых, это только затрудняет дальнейшие действия с матрицей, во-вторых, затрудняет проверку решения преподавателем (особенно, если – окончательный ответ задания).
И, тем более, НЕ НАДО делить каждый элемент матрицы на минус семь:
Из статьи Математика для чайников или с чего начать, мы помним, что десятичных дробей с запятой в высшей математике стараются всячески избегать.
Единственное, что желательно сделать в этом примере – это внести минус в матрицу:
А вот если бы ВСЕ элементы матрицы делились на 7 без остатка, то тогда можно (и нужно!) было бы поделить.
Пример:
В этом случае можно и НУЖНО умножить все элементы матрицы на , так как все числа матрицы делятся на 2 без остатка.
Примечание: в теории высшей математики школьного понятия «деление» нет. Вместо фразы «это поделить на это» всегда можно сказать «это умножить на дробь». То есть, деление – это частный случай умножения.
3) Действие третье. Транспонирование матрицы
Для того чтобы транспонировать матрицу, нужно ее строки записать в столбцы транспонированной матрицы.
Пример:
Транспонировать матрицу
Строка здесь всего одна и, согласно правилу, её нужно записать в столбец:
– транспонированная матрица.
Транспонированная матрица обычно обозначается надстрочным индексом или штрихом справа вверху.
Пошаговый пример:
Транспонировать матрицу
Сначала переписываем первую строку в первый столбец:
Потом переписываем вторую строку во второй столбец:
И, наконец, переписываем третью строку в третий столбец:
Готово. Грубо говоря, транспонировать – это значит повернуть матрицу набок.
4) Действие четвертое. Сумма (разность) матриц.
Сумма матриц действие несложное.
НЕ ВСЕ МАТРИЦЫ МОЖНО СКЛАДЫВАТЬ. Для выполнения сложения (вычитания) матриц, необходимо, чтобы они были ОДИНАКОВЫМИ ПО РАЗМЕРУ.
Например, если дана матрица «два на два», то ее можно складывать только с матрицей «два на два» и никакой другой!
Пример:
Сложить матрицы и
Для того чтобы сложить матрицы, необходимо сложить их соответствующие элементы:
Для разности матриц правило аналогичное, необходимо найти разность соответствующих элементов.
Пример:
Найти разность матриц ,
А как решить данный пример проще, чтобы не запутаться? Целесообразно избавиться от лишних минусов, для этого внесем минус в матрицу :
Примечание: в теории высшей математики школьного понятия «вычитание» нет. Вместо фразы «из этого вычесть это» всегда можно сказать «к этому прибавить отрицательное число». То есть, вычитание – это частный случай сложения.
5) Действие пятое. Умножение матриц.
Чем дальше в лес, тем толще партизаны. Скажу сразу, правило умножения матриц выглядит очень странно, и объяснить его не так-то просто, но я все-таки постараюсь это сделать, используя конкретные примеры.
Какие матрицы можно умножать?
Чтобы матрицу можно было умножить на матрицу необходимо, чтобы число столбцов матрицы равнялось числу строк матрицы .
Пример:
Можно ли умножить матрицу на матрицу ?
, значит, умножать данные матрицы можно.
А вот если матрицы переставить местами, то, в данном случае, умножение уже невозможно!
, следовательно, выполнить умножение невозможно, и вообще, такая запись не имеет смысла
Не так уж редко встречаются задания с подвохом, когда студенту предлагается умножить матрицы, умножение которых заведомо невозможно.
Следует отметить, что в ряде случаев можно умножать матрицы и так, и так.
Например, для матриц, и возможно как умножение , так и умножение
Как умножить матрицы?
Умножение матриц лучше объяснить на конкретных примерах, так как строгое определение введет в замешательство (или помешательство) большинство читателей.
Начнем с самого простого:
Пример:
Умножить матрицу на матрицу
Я буду сразу приводить формулу для каждого случая:
– попытайтесь сразу уловить закономерность.
Пример сложнее:
Умножить матрицу на матрицу
Формула:
В результате получена так называемая нулевая матрица.
Попробуйте самостоятельно выполнить умножение (правильный ответ ).
Обратите внимание, что ! Это почти всегда так!
Таким образом, переставлять матрицы в произведении нельзя!
Если в задании предложено умножить матрицу на матрицу , то и умножать нужно именно в таком порядке. Ни в коем случае не наоборот.
Переходим к матрицам третьего порядка:
Умножить матрицу на матрицу
Формула очень похожа на предыдущие формулы:
А теперь попробуйте самостоятельно разобраться в умножении следующих матриц:
Умножьте матрицу на матрицу
Вот готовое решение, но постарайтесь сначала в него не заглядывать!
Будет время, распишу подробнее
6) Действие шестое. Нахождение обратной матрицы.
Данная тема достаточно обширна, и вынес даннай вопрос на отдельную страницу.
А пока спектакль закончен.
Желаю успехов!
lablek.ru
Простейшие действия с матрицами — МегаЛекции
Введение
Данное пособие написано для того, чтобы помочь студентам, обучающимся на факультете заочного и дистанционного обучения по направлению «Электроэнергетика и электротехника» и профилю «электрооборудование и электрохозяйство предприятий, организаций и учреждений», в изучении линейной и векторной алгебры, аналитической геометрии, а также в выполнении контрольных работ по высшей математике по соответствующим темам: № 1, №2, №3.
В пособии содержатся три раздела, в каждом из которых имеется необходимый теоретический материал, пример выполнения соответствующей контрольной работы и задания для самостоятельного выполнения в десяти вариантах. Номер варианта определяется по последней цифре зачётной книжки (шифра).
Работу следует выполнять в тонкой ученической тетради в клетку. Выполненную работу следует снабдить титульным листом, образец которого можно найти на доске объявлений у деканата.
Поскольку пособие содержит достаточно большой теоретический материал, полезно сохранить его до конца обучения в вузе, так как он может быть востребован при дальнейшем изучении математики и других дисциплин.
Раздел 1. Контрольная работа по высшей математике №1
Теоретический материал по линейной алгебре
Комплексные числа и действия с ними
Под комплексным числом в алгебраической форме записи понимается выражение где и – действительные числа, а – мнимая единица, для которой справедлива формула
Числа вида отождествляются с действительными числами, числа вида называются чисто мнимыми. Сопряженным числом к числу называется комплексное число Два комплексных числа иравны, если и
Сложение, вычитание, умножение и деление комплексных чисел определяются следующим образом.
1)
2)
3)
Примечание. Формулу умножения двух комплексных чисел не обязательно запоминать, так как она получается, если формально перемножить двучлены и по обычному правилу умножения двучленов и затем заменить на –1.
Примеры.
1. Найти сумму и произведение комплексных чисел и
Находим сумму:
Умножим:
2. Найти частное комплексных чисел и
Для нахождения частного умножим числитель и знаменатель дроби на число, сопряженное знаменателю:
Комплексное число можно изобразить точкой на плоскости имеющей координаты На оси изображаются действительные числа, поэтому она называется действительной осью; на оси расположены чисто мнимые числа; она называется мнимой осью.
Можно также сопоставить числу вектор, направленный из начала координат в точку Длина этого вектора , т.е. расстояние от начала координат до точки называется модулем комплексного числа и обозначается
Из рисунка находим Следовательно:
Такая форма записи комплексного числа называется тригонометрической. Угол , образованный радиус-вектором с положительным направлением действительной оси называется аргументом комплексного числа и обозначается . В инженерных приложениях угол также называется фазой. Величина угла определяется с точностью до слагаемого Главным называется значение , удовлетворяющее условию: .
Главное значение аргумента можно вычислить по следующим формулам:
Пусть – любое действительное число. Символом обозначается комплексное число С помощью этого обозначения всякое комплексное число может быть записано в показательной форме (формула Эйлера):
Пример. Представить в тригонометрической и показательной форме комплексное число
Находим модуль Аргумент находим по формуле:
.
Следовательно
Матрицы и действия с ними
Матрица представляет собой прямоугольный массив чисел, образующих строки и столбцы одинаковой длины.
Для краткого обозначения матриц применяются латинские буквы A, B, C и т.д. Если в матрице m строк и n столбцов, то говорят, что матрица имеет размер . В общем виде элементы матрицы принято обозначать латинскими буквами a, b, c и т.д. Элемент, стоящий в i-той строке (т.е. в строке с номером i) и j-том столбце (т.е. столбце с номером j), обозначается и т.д. Учитывая введенные обозначения, произвольная матрица А может быть записана так:
.
Кроме больших круглых скобок, массив чисел, образующих матрицу может быть заключен в большие квадратные скобки или ограничен сдвоенными чертами. Многоточие в записи означает, что за элементом следуют элементы и т.д. до ; за элементом следуют элементы и т.д. до элемента . Элементами матрицы могут быть любые действительные и комплексные числа.
Если в матрице число строк и столбцов совпадает, т.е. , то матрица называется квадратной, а число указывает порядок матрицы.
Направление из левого верхнего в правый нижний угол квадратной матрицы называется главной диагональю, а элементы — диагональными элементами. Их сумма , кратко обозначаемая , называется следом матрицы . Направление, перпендикулярное главной диагонали, называется побочной диагональю.
Если в квадратной матрице все элементы, стоящие выше или ниже одной из диагоналей, равны 0, например,
то такие матрицы называются треугольными.
Если равны 0 все элементы, кроме стоящих на главной диагонали, то такая матрица называется диагональной:
.
Если все диагональные элементы равны 1, то такая матрица называется единичной:
.
Матрица, не обязательно квадратная, все элементы которой равны 0, называется нулевой.
Матрица, состоящая из одного столбца, называется матрицей-столбцом, матрица, состоящая из одной строки, называется матрицей-строкой.
Две матрицы называются равными, если они одного размера и все соответствующие элементы совпадают.
Под нормой матрицы А понимается действительное число , аналогичное понятию модуля для действительных чисел. Из элементов матрицы А ее норму можно составить различными способами, в дальнейшем за норму будем принимать корень квадратный из суммы квадратов всех элементов матрицы:
Простейшие действия с матрицами
1) Транспонирование.
Матрица называется транспонированной по отношению к матрице А, если строки одной матрицы являются столбцами другой и наоборот, например,
.
2) Сложение (вычитание) матриц.
Чтобы найти сумму или разность двух матриц, нужно сложить или вычесть соответствующие элементы этих матриц, например,
;
.
Замечание: исходя из определения, складывать или вычитать можно только матрицы одного размера.
3) Умножение на число (скаляр).
Чтобы умножить матрицу на число, нужно все ее элементы умножить на это число, например,
.
Следствие: общий множитель всех элементов матрицы можно выносить за знак матрицы.
Умножение матриц
Матрица С называется произведением матрицы А на матрицу В, если ее элементы вычисляются следующим образом:
.
Т.е. элемент матрицы С, стоящий в -той строке и -том столбце, равен сумме произведений соответствующих элементов -той строки матрицы А и -того столбца матрицы В (соответствующих — это значит, что первый элемент строки умножаем на первый элемент столбца, второй — на второй и так до последней пары элементов).
Из определения данного действия следует, что умножать можно только такие матрицы, в которых число столбцов матрицы А (т.е. число элементов в ее строке) равно числу строк матрицы В (т.е. числу элементов в ее столбце). Такие матрицы называются согласованными для умножения. Из определения умножения можно также заключить, что умножение матрицы А размера на матрицу В размера дает матрицу С размера .
Заметим, что квадратные матрицы одного порядка всегда согласованы для умножения.
Пример.
.
.
Для данных матриц обратное умножение В на А невозможно, т.к. число столбцов в В равно 2, а число строк в матрице А равно 4. Но даже, если возможны оба произведения, они в общем случае могут не совпадать. Проверим:
;
;
.
Свойства умножения матриц
1) В общем случае , т.е. в общем случае перестановочное свойство умножения не выполняется.
Матрицы, для которых оно выполняется, называются перестановочными.
2) Сочетательное свойство: .
3) Распределительное свойство умножения относительно сложения:
4) Умножение на единичную матрицу не меняет матрицы: .
5) Умножение на нулевую матрицу дает нулевую матрицу: ;
замечание: из того факта, что произведение двух матриц равно 0, не следует обязательно, что либо одна из них, либо обе вместе равны 0.
Матричные уравнения
Используя различные действия с матрицами, можно составлять матричные уравнения — соотношения между неизвестной матрицей Х и известными матрицами.
Например, АХ = В или ХА = В, АХВ = С, АХ + В = С, ХА — В = С и т.д.
Рассмотрим одно из простейших матричных уравнений:
.
В школьном курсе алгебры рассматривалось соответствующее ему уравнение для действительных чисел:
Решением этого линейного уравнения является , где число называется обратным к и удовлетворяет соотношению: .
Введем подобное понятие и для матриц. Матрица называется обратной к , если она удовлетворяет условию:
,
где — единичная матрица.
Из определения обратной матрицы следует, что ее можно найти только для квадратных матриц.
Существование обратной матрицы дает возможность решать матричные уравнения, например, рассмотрим уравнение . Умножим обе части уравнения слева на матрицу, обратную :
.
Аналогично можно найти решение уравнения , умножая теперь уже справа обе части уравнения на :
.
Рекомендуемые страницы:
Воспользуйтесь поиском по сайту:
megalektsii.ru



