19.06.201902.02.2019

Штейнера формула – Теорема Гюйгенса — Штейнера — Википедия

• by alexxlab
• Комментариев к записи Штейнера формула – Теорема Гюйгенса — Штейнера — Википедия нет
• Советы абитуриенту

Теорема Штейнера.

В приведенных примерах оси проходят через центр инерции тела. Мо­мент инерции относительно других осей вращения определяется при по­мощи теоремы Штейнера: момент инерции тела относительно произвольной оси вращения равен сумме момента инерции Jc относительно параллельной оси, проходящей через центр инерции тела, и величины произведения массы тела на квадрат расстояния между ними. где m масса тела, а – расстояние от центра инерции тела до выбранной оси вращения,т.е.

, где m – масса тела, а – расстояние от центра

инерции тела до выбранной оси вращения.

Покажем на одном примере применение теоремы Штейнера. Вычислим момент инерции тонкого стержня относительно оси, проходящей через его край перпендикулярно стержню. Прямое вычисление сводится к тому же ин­тегралу (*),но взятому в других пределах:

Расстояние до оси, проходящей через центр масс, равно а = ℓ/2.По теореме Штейнера получаем тот же результат.

.

§22.Основной закон динамики вращательного движения.

Формулировка закона: Скорость изменения момента импульса относительно полюса равна главному моменту силы относительно того же полюса, т.е.

.

В проекциях на оси координат: .

Если вращение тела происходит относительно неподвижной оси, то основной закон динамики вращательного движения примет вид: . В данном случае момент импульса легко выразить через угловую скорость и момент инерции тела относительно рассматриваемой оси:. Тогда основной закон динамики вращательного движения примет вид:

. Если тело не рассыпается и не деформируется, то

, вследствие чего 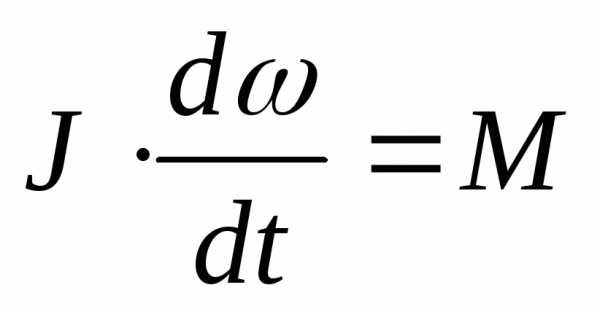. Если ко всему, тои, оно равно:.

Элементарная работа, совершаемая моментом силы, при вращательном движении относительно неподвижной оси вычисляется по формуле: (*). Полная работа. Если, то.

На основании формулы (*), получим выражение для кинетической энергии вращательного движения твёрдого тела относительно неподвижной оси. Т.к. , то. После интегрирования, получим окончательный результат для кинетической энергии вращательного движения относительно неподвижной оси.

§23.Закон сохранения момента импульса.

Как уже указывалось, законы сохранения энергии и импульса связаны с однородностью времени и пространства, соответственно. Но у трехмер­ного пространства, в отличие от одномерного времени, имеется еще одна симметрия. Пространство само по себе

изотропно,в нем нет выделен­ных направлений. С этой симметрией связанзакон сохранениямомента импульса.Эта связь проявляется в том, что момент количества движе­ния, является одной из основных величин, описывающих вращательное движение.

По определению момент импульса отдельной частицы равен .

Направление вектора Lопределяется по правилу буравчика (штопора), а его величина равна L = r p sin ,где

  угол между направлениями радиус-вектора частицы и ее импульса. Величина ℓ = r sinравна рас­стоянию от начала координатОдо прямой, вдоль которой направлен импульс частицы. Эта величина называетсяплечом импульса.ВекторLзависит от выбора начала координат, поэтому говоря о нем, обычно указывают: “момент импульса относительно точки

О“.

Рассмотрим производную по времени от момента импульса:

.

Первое слагаемое равно нулю, т.к. . Во втором слагаемом, согласно второму закону Ньютона, производную по импульсу можно заменить на действующую на тело силу. Векторное произведение радиус-вектора на силу называетсямоментом силыотносительно точкиО: .

Направление момента силы определяется тем же правилом буравчика. Его величина М = r F sin ,где

•  угол между радиус-вектором и силой. Аналогично тому, как это было сделано выше, определяется и плечо силы

ℓ = r sin — расстояние от точкиОдо линии действия силы. В итоге получаем уравнение движения для момента импульса частицы:.

По форме уравнение аналогично второму закону Ньютона: вместо им­пульса частицы стоит момент импульса, а вместо силы —момент силы. Если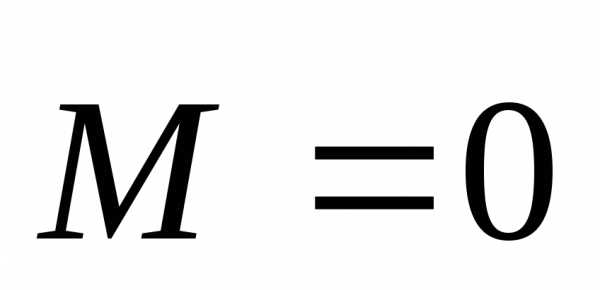,то,т.е. момент импульса постоянен в отсутствие внешних моментов сил.

Формулировка закона: Момент импульса замкнутой системы относительно полюса не изменяется с течением времени.

В частном случае вращения относительно неподвижной оси, имеем: , где

начальные момент инерции и угловая скорость тела относительно рассматриваемой оси, а

конечные момент инерции и угловая скорость тела относительно рассматриваемой оси.

Закон сохранения полной механической энергии с учётом вращательного движения:

полная механическая энергия консервативной системы постоянна: .

Пример: Найти скорость системы при прохождении расстояния h.

Дано: m, M, h. Найти: V – ?

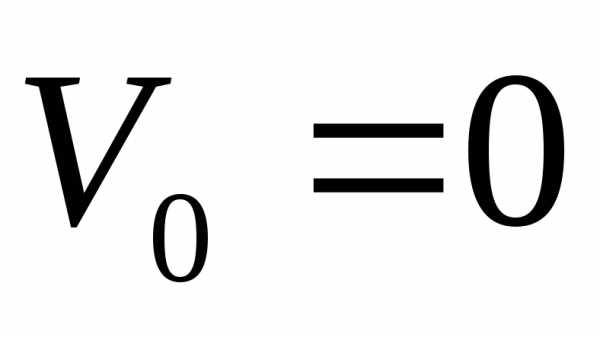
studfiles.net

Теорема Гюйгенса – Штейнера. (Викимеханика.Теорема Гюйгенса – Штейнера\.)

Теоре́ма Гю́йгенса — Ште́йнера, или просто теорема Штейнера (названа по имени швейцарского математика Якоба Штейнера и голландского математика, физика и астронома Христиана Гюйгенса): момент инерции тела  относительно произвольной оси равен сумме момента инерции этого тела  относительно параллельной ей оси, проходящей через центр масс тела, и произведения массы тела  на квадрат расстояния  между осями:

где

 — известный момент инерции относительно оси, проходящей через центр масс тела,

 — искомый момент инерции относительно параллельной оси,

 — масса тела,

 — расстояние между указанными осями.

Момент инерции, по определению:

Радиус-вектор  можно расписать как разность двух векторов:

,

где  — радиус-вектор расстояния между старой и новой осью вращения. Тогда выражение для момента инерции примет вид:

Вынося за сумму , получим:

Поскольку старая ось проходит через центр масс, то суммарный импульс тела будет равен нулю:

Тогда:

Откуда и следует искомая формула:

,

где  — известный момент инерции относительно оси, проходящей через центр масс тела.

Момент инерции стержня относительно оси, проходящей через его центр и перпендикулярной стержню, (назовём её осью ) равен

Тогда согласно теореме Штейнера его момент относительно произвольной параллельной оси будет равен

где  — расстояние между искомой осью и осью . В частности, момент инерции стержня относительно оси, проходящей через его конец и перпендикулярной стержню, можно найти положив в последней формуле :

Теорема Гюйнеса — Штейнера допускает обобщение на тензор момента инерции, что позволяет получать тензор  относительно произвольной точки из тензора  относительно центра масс. Пусть  — смещение от центра масс, тогда

где

 — вектор смещения от центра масс, а  — символ Кронекера.

Как видно, для диагональных элементов тензора (при ) формула имеет вид теоремы Гюйгенса — Штейнера для момента относительно новой оси.

1. Википедия – свободная энциклопедия ru.wikipedia.org

Автор: Сова Е.О. (2-ТМ-55)

dafedin.myxwiki.org

16) Теорема Гюйгенса — Штейнера

Механика

1)Измерение – процесс нахождения значения физической величины опытным путем с помощью средств измерения.

Прямые – это измерения, при которых искомое значение физической величины находят непосредственно из опытных данных. Косвенные – это измерения, при которых значение величины определяют на основании известной зависимости между искомой величиной и величинами, значения которых находят прямыми измерениями. 

Погрешность измерения — оценка отклонения измеренного значения величины от её истинного значения. 

Окончательный результат измерения должен быть представлен в стандартной форме записи. Для этого:

1. Абсолютную погрешность измерения округляют до первой значащей цифры, если она не единица;

2. Если первая значащая цифра в абсолютной погрешности единица, то абсолютную погрешность представляют в виде числа с двумя значащими цифрами. Значащими цифрами числа называют все его цифры, начиная с первой слева, отличной от нуля.

3. Числовое значение результата измерения представляется, так чтобы и среднее значение и абсолютная погрешность имели одинаковое число десятичных знаков после запятой.

Среднее значение результата измерения округляют до того разряда, до которого округлена абсолютная погрешность.

4. Среднее значение результата представляют в виде числа, содержащего до запятой одну значащую цифру, умноженного на десять в соответствующей степени.

2)

3) Механика для описания движения тел в зависимости от условий конкретных задач использует разные физические модели.Простейшей моделью является матери­альная точка — тело, обладающее массой, размерами которого в данной задаче мож­но пренебречь.

Система отсчета – совокупность системы координат и часов, связанных с телом, относительно которого изучается движение.

Векторный способ Положение материальной точки задается с помощью радиуса-вектора относительно некоторой неподвижной точки О.

Координатный способ

При описании этим способом с телом отчета связывают какую-либо систему координат (например, декартову).

– закон движения материальной точки

Естественный способ

В нем движение описывается с помощью параметров самой траектории, и он используется, когда траектория известна.

– закон движения точки

 – средняя путевая скорость

 – путь

4) Траектория – это линия, по которой движется тело (материальная точка). Траектория движения может быть прямой (тело перемещается в одном направлении) и криволинейной, то есть механическое движение может быть прямолинейным и криволинейным.

Путь – это длина траектории. Путь является скалярной величиной и в международной системе единиц СИ измеряется в метрах (м). Расчёт пути выполняется во многих задачах по физике.

Вектор перемещения (или просто перемещение) – это направленный отрезок прямой, соединяющий начальное положение тела с его последующим положением. Перемещение – величина векторная. Вектор перемещения направлен от начальной точки движения к конечной.

Ско́рость — векторная физическая величина, характеризующая быстроту перемещения и направление движения материальной точки относительно выбранной системы отсчёта; по определению, равна производной радиус-вектора точки по времени

Средняя скорость движения – это физическая величина, равная отношению вектора перемещения точки к интервалу времени, за который это перемещение произошло.

Мгновенной скоростью _мгн называется скорость в данный момент времени.

Мгновенная скорость определяется как предел отношения вектора перемещения к интервалу времени, за который это перемещение происходит, при стремлении интервала времени к нулю:

В классической механике абсолютная скорость точки равна векторной сумме её относительной и переносной скоростей:

Данное равенство представляет собой содержание утверждения теоремы о сложении скоростей^[1].

Скорость движения тела относительно неподвижной системы отсчёта равна векторной сумме скорости этого тела относительно подвижной системы отсчета и скорости (относительно неподвижной системы) той точки подвижной системы отсчёта, в которой в данный момент времени находится тело.

5)  Ускоре́ние — скорость изменения скорости, то есть первая производная от скорости по времени, векторная величина, показывающая, на сколько изменяется вектор скорости тела при его движении за единицу времени

В общем случае ускорение направлено под углом к скорости. Составляющая ускорения, направленная вдоль скорости, называется тангенциальным ускорением . Она характеризует изменение скорости по модулю.

Составляющая ускорения, направленная к центру кривизны траектории, т.е. перпендикулярно (нормально) скорости, называется нормальным ускорением . Она характеризует изменение скорости по направлению.

Здесь R – радиус кривизны траектории в данной точке. Тангенциальное и нормальное ускорение взаимноперпендикулярны, поэтому модуль полного ускорения

Углова́я ско́рость — векторная величина характеризующая скорость вращения материальной точки вокруг центра вращения. Вектор угловой скорости по величине равен углу поворота точки вокруг центра вращения за единицу времени: Углово́е ускоре́ние — псевдовекторная физическая величина, характеризующая быстроту изменения угловой скорости движения материальной точки по окружности. При вращении точки вокруг неподвижной оси, угловое ускорение по модулю равно[1]:

6) Си́ла — векторная физическая величина, являющаяся мерой интенсивности воздействия на данное тело других тел, а также полей. Приложенная к массивномутелу сила является причиной изменения его скорости или возникновения в нёмдеформаций и напряжений

Масса – величина, измеряющая количество вещества в теле, мера инерции тела по отношению к действующей на него силе

1 закон Ньютона

Если на тело не действуют силы или их действие скомпенсировано, то данное тело находится в состоянии покоя или равномерного прямолинейного движения..

2 закон Ньютона

Ускорение тела прямо пропорционально равнодействующей сил, приложенных к телу, и обратно пропорционально его массе:

3 закон Ньютона

Силы, с которыми тела взаимодействуют друг с другом, равны по модулю и направлены вдоль одной прямой в противоположные стороны.

7) Центр масс

        центр инерции, геометрическая точка, положение которойхарактеризует распределение масс в теле или механической системе. Координаты Ц. м. определяютсяформулами

         , 

        или для тела при непрерывном распределении масс

         

8)Внутренние силы – это силы взаймодействия между точками самой системы

Внешние силы – силы приложенные к точкам системы со стороны тел не пренадлежащих системе .

Замкнутые системы – системы где действуют только внутренние силы изолированные от внешних сил

консервати́вные си́лы (потенциальные силы) — это силы, работа которых не зависит от видатраектории, точки приложения этих сил и закона их движения, и определяется только начальным и конечным положением этой точки^[1]. Равносильным определением является и следующее: консервативные силы — это такие силы, работа которых по любой замкнутой траектории равна 0.

9) Сила трения — это сила, возникающая при соприкосновении двух тел и препятствующая их относительному движению.

• Трение скольжения — сила, возникающая при поступательном перемещении одного из контактирующих/взаимодействующих тел относительно другого и действующая на это тело в направлении, противоположном направлению скольжения.

• Трение качения — момент сил, возникающий при качении одного из двух контактирующих/взаимодействующих тел относительно другого.

• Трение покоя — сила, возникающая между двумя контактирующими телами и препятствующая возникновению относительного движения. Эту силу необходимо преодолеть для того, чтобы привести два контактирующих тела в движение друг относительно друга. Возникает при микроперемещениях (например, при деформации) контактирующих тел. Она действует в направлении, противоположном направлению возможного относительного движения.

• сухое, когда взаимодействующие твёрдые тела не разделены никакими дополнительными слоями/смазками (в том числе и твердыми смазочными материалами) — очень редко встречающийся на практике случай. Характерная отличительная черта сухого трения — наличие значительной силы трения покоя;

• жидкостное (вязкое), при взаимодействии тел, разделённых слоем твёрдого тела (порошком графита),жидкости или газа (смазки) различной толщины — как правило, встречается при трении качения, когда твёрдые тела погружены в жидкость, величина вязкого трения характеризуется вязкостью среды;

 При деформации тела возникает сила, которая стремится восстановить прежние размеры и форму тела. Эта сила возникает вследствие электромагнитного взаимодействия между атомами и молекулами вещества. Ее называют силой упругости.

Для тонкого растяжимого стержня закон Гука имеет вид:

Здесь  — сила, которой растягивают (сжимают) стержень,  — абсолютное удлинение (сжатие) стержня, а — коэффициент упругости (или жёсткости).

10)механи́ческая эне́ргия описывает сумму потенциальной и кинетической энергий, имеющихся в компонентах механической системы. Механическая энергия — это энергия, связанная с движением объекта или его положением, и имеет способность совершать механическую работу

Закон сохранения механической энергии утверждает, что если тело или система подвергается действию только консервативных сил, то полная механическая энергия этого тела или системы остаётся постоянной. В изолированной системе, где действуют только консервативные силы, полная механическая энергия сохраняется.^[3]

Кинети́ческая эне́ргия — скалярная функция, являющаяся мерой движения материальной точки и зависящая только от массы и модуля скорости материальных точек, образующих рассматриваемую физическую систему^[1], энергия механической системы, зависящая от скоростей движения её точек в выбранной системе отсчёта. Часто выделяют кинетическую энергию поступательного и вращательногодвижения^[2].

Более строго, кинетическая энергия есть разность между полной энергией системы и её энергией покоя; таким образом, кинетическая энергия — часть полной энергии, обусловленная движением^[

Чтобы увеличить расстояние тела от центра Земли (поднять тело), над ним следует совершить работу. Эта работа против силы тяжестизапасается в виде потенциальной энергии тела.

Кривая — зависимость потенциальной энергии от координаты.

Связь между энергией и массой неизбежно следует из закона сохранения энергии и того факта, что масса тела зависит от скорости его движения.

11)

Ek1 + Ep1 = Ek2 + Ep2.

Сумма кинетической и потенциальной энергии тел, составляющих замкнутую систему и взаимодействующих между собой посредством сил тяготения и сил упругости, остается неизменной.

12) И́мпульс (Коли́чество движе́ния) — векторная физическая величина, являющаяся мерой механического движения тела. В классической механике импульс тела равен произведению массы m этого тела на его скорость v, направление импульса совпадает с направлением вектора скорости:

В замкнутой системе векторная сумма импульсов всех тел, входящих в систему, остается постоянной при любых взаимодействиях тел этой системы между собой.

13)

Абсолютно упругим ударом называется столкновение, при котором сохраняется механическая энергия системы тел.

Абсолютно неупругим ударом называют такое ударное взаимодействие, при котором тела соединяются (слипаются) друг с другом и движутся дальше как одно тело.

При абсолютно неупругом ударе механическая энергия не сохраняется. Она частично или полностью переходит во внутреннюю энергию тел (нагревание).

14) Мощность — это физическая величина, равная отношению работы ко времени, за который эта работа была выполнена. Коэффициент полезного действия (КПД) — это физическая величина, равная отношению полезной работы к полной работы. КПД обозначается буквой η и измеряется в процентах. Полезная работа всегда меньше полной. КПД всегда меньше 100%.

Работой A, совершаемой постоянной силой называется физическая величина, равная произведению модулей силы и перемещения, умноженному на косинус угла α между векторами силыи перемещения (рис. 1.18.1): 

15) Моме́нт ине́рции — скалярная (в общем случае — тензорная) физическая величина, мера инертности во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости).

Тензор инерции — в механике абсолютно твёрдого тела — тензорная величина, связывающая момент импульса тела и кинетическую энергию его вращения с его угловой скоростью:

где  — тензор инерции,  — угловая скорость,  — момент импульса

Моментом инерции механической системы относительно неподвижной оси («осевой момент инерции») называется величина J_a, равная сумме произведений масс всех n материальных точек системы на квадраты их расстояний до оси:

,

Момент инерции твёрдого тела относительно какой-либо оси зависит от массы, формы и размеров тела, а также и от положения тела по отношению к этой оси. Согласно теореме Штейнера (теореме Гюйгенса-Штейнера), момент инерции тела J относительно произвольной оси равен сумме момента инерции этого тела J_c относительно оси, проходящей через центр масс тела параллельно рассматриваемой оси, и произведения массы тела m на квадрат расстояния d между осями:

где m — полная масса тела.

Например, момент инерции стержня относительно оси, проходящей через его конец, равен:

Кинетическая энергия вращательного движения — энергия тела, связанная с его вращением.

Основные кинематические характеристики вращательного движения тела — его угловая скорость () и угловое ускорение. Основные динамические характеристики вращательного движения — момент импульса относительно оси вращения z:

и кинетическая энергия

где I_z — момент инерции тела относительно оси вращения.

17) Момент силы — векторная физическая величина, равная векторному произведению радиус-вектора, на вектор этой силы

Плечо силы- величина, равная кратчайшему расстоянию от данной точки (центра) до линии действия силы. 

– Это выражение носит название основного уравнения динамики вращательного движения и формулируется следующим образом: изменение момента количества движения твердого тела, равно импульсу момента всех внешних сил, действующих на это тело.

18) Момент импульса материальной точки относительно некоторого начала отсчёта определяется векторным произведением её радиус-вектора и импульса:

где  — радиус-вектор частицы относительно выбранного неподвижного в данной системе отсчёта начала отсчёта,  — импульс частицы.

Изменение во времени момента импульса системы равно суммарному моменту всех внешних сил

.

Закон изменения момента импульса: приращение момента импульса равно импульсу суммарного момента внешних сил за время 

 .

Закон сохранения момента импульса: момент импульса замкнутой системы, взятый относительно любой точки инерциальной системы отсчета, не изменяется при любых процессах, происходящих внутри данной системы

.

 – сохранение проекции импульса.

19) Рассмотрим действие внешней силы , приложенной к точке массой . За время элементарная масса проходит путь Работа силы на этом пути определяется проекцией силы на направление перемещения, которая очевидно, равна тангенциальной составляющей силы.

Но равна модулю момента силы относительно оси вращения. Работа , и будет положительна, если имеет такое же направление, как и  отрицательное, если направление векторов и  противоположны.

С учетом, что 

Работа всех сил, приложенных к телу

(5.13)

Полная работа

(

20) Упругими называют деформации, которые исчезают после прекращения действия сил, а тела восстанавливают свою форму и объем.

Пластическими называют деформации, которые сохраняются после прекращения действия сил, а тела не восстанавливают свою первоначальную форму и объем.

Предел упругости — максимальная величина механического напряжения, при которой деформация данного материала остаётся упругой, то есть полностью исчезает после снятия нагрузки.

21)

Поступательное движение		Вращательное движение
Перемещение	S	Угловое перемещение	φ
Линейная скорость		Угловая скорость
Ускорение		Угловое ускорение
Масса	m	Момент инерции	I
Импульс		Момент импульса
Сила	F	Момент силы	M

Таблицу можно продолжать и далее.

Работа: 

 Кинетическая энергия 

22) Неинерциа́льная систе́ма отсчёта — система отсчёта, в которой не выполняется первый закон Ньютона — «закон инерции», говорящий о том, что каждое тело, в отсутствие действующих на него сил, покоится либо движется по прямой и с постоянной скоростью. Всякая система отсчета, движущаяся с ускорением или поворачивающаяся относительно инерциальной, является неинерциальной. Второй закон Ньютона также не выполняется в неинерциальных системах отсчёта. Для того чтобы уравнение движения материальной точки в неинерциальной системе отсчёта по форме совпадало с уравнением второго закона Ньютона, дополнительно к «обычным» силам, действующим в инерциальных системах, вводят силы инерции.

Силы инерции — силы, обусловленные ускоренным движением неинерциальной системы отсчета (НСО) относительно инерциальной системы отсчета (ИСО). Основной закон динамики для неинерциальных систем отсчета: , где — сила, действующая на тело со стороны других тел;

  — сила инерции, действующая на тело относительно поступательно движущейся НСО.  — ускорение НСО относительно ИСО. Она появляется, например, в самолете при разгоне на взлетной полосе;

  — центробежная сила инерции, действующая на тело относительно вращающейся НСО.  — угловая скорость НСО относительно ИСО,  — расстояние от тела до центра вращения;

  — кориолисова сила инерции, действующая на тело, движущееся со скоростью  относительно вращающейся НСО.   — угловая скорость НСО относительно ИСО (вектор направлен вдоль оси вращения в соответствии с правилом правого винта).

23) В механике большое значение имеет принцип независимости действия сил: если на материальную точку действует одновременно несколько сил, то каждая из этих сил сообщает материальной точке ускорение согласно второму закону Ньютона, как будто других сил не было. Согласно этому принципу силы и ускорения можно разлагать на составляющие, использование которых приводит к существенному упрощению решения задач.

Например, нормальное и тангенциальное ускорения материальной точки определяются соответствующими составляющими силы, сообщающая материальной точке нормальное ускорение, направлена к центру кривизны траектории и потому называется центростремительной силой

24)

Первый постулат: законы физики имеют одинаковую форму во всех инерциальных системах отсчета. Этот постулат явился обобщением принципа относительности Ньютона не только на законы механики, но и на законы остальной физики. Первый постулат — принцип относительности.

Второй постулат: свет распространяется в вакууме с определенной скоростью с, не зависящей от скорости источника или наблюдателя. 

Эти два постулата образуют основу теории относительности А. Эйнштейна.

 

studfiles.net

Теорема Штейнера или теорема параллельных осей для вычисления момента инерции

При математическом описании вращательного движения важно знать момент инерции системы относительно оси. В общем случае процедура нахождения этой величины предполагает реализацию процесса интегрирования. Облегчить вычисления позволяет так называемая теорема Штейнера. Рассмотрим ее подробнее в статье.

Что такое момент инерции?

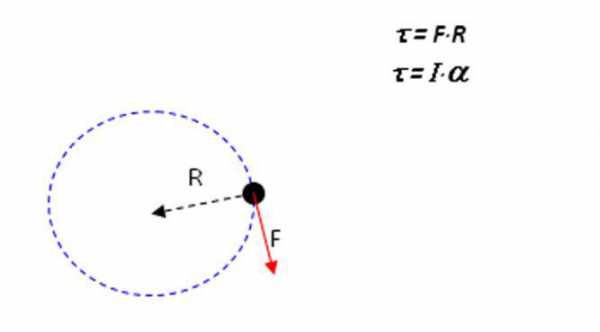
До того как привести формулировку теоремы Штейнера, следует разобраться с самим понятием момента инерции. Допустим, имеется некоторое тело определенной массы и произвольной формы. Этим телом может быть, как материальная точка, так и любой двумерный и трехмерный объект (стержень, цилиндр, шар и т.д.). Если рассматриваемый объект совершает круговое движение вокруг некоторой оси с постоянным угловым ускорением α, тогда можно записать следующее уравнение:

M = I*α

Здесь величина M представляет суммарный момент сил, который придает ускорение α всей системе. Коэффициент пропорциональности между ними – I, называется моментом инерции. Эта физическая величина рассчитывается по следующей общей формуле:

I = ∫_m (r²*dm)

Здесь r – это дистанция между элементом с массой dm и осью вращения. Это выражение означает, что необходимо найти сумму произведений квадратов расстояний r² на элементарную массу dm. То есть момент инерции не является чистой характеристикой тела, что его отличает от линейной инерции. Он зависит от распределения массы по всему объекту, который вращается, а также от расстояния до оси и от ориентации тела относительно нее. Например, стержень будет иметь разный I, если его вращать относительно центра масс и относительно конца.

Момент инерции и теорема Штейнера

Известный швейцарский математик, Якоб Штейнер, доказал теорему о параллельных осях и моменте инерции, которая теперь носит его фамилию. Эта теорема постулирует, что момент инерции для абсолютно любого твердого тела произвольной геометрии относительно некоторой оси вращения равен сумме момента инерции относительно оси, которая пересекает центр масс тела и параллельна первой, и произведения массы тела на квадрат дистанции между этими осями. Математически эта формулировка записывается так:

I_Z = I_O + m*l²

I_Z и I_O – моменты инерции относительно оси Z и параллельной ей оси O, которая проходит через центр масс тела, l – расстояние между прямыми Z и O.

Теорема позволяет, зная величину I_O, рассчитать любой другой момент I_Z относительно оси, которая параллельна O.

Доказательство теоремы

Формулу теоремы Штейнера можно легко получить самостоятельно. Для этого рассмотрим произвольное тело на плоскости xy. Пусть начало координат проходит через центр масс этого тела. Рассчитаем момент инерции I_O которая проходит через начало координат перпендикулярно плоскости xy. Поскольку расстояние до любой точки тела выражается формулой r = √ (x² + y²), тогда получаем интеграл:

I_O = ∫_m (r²*dm) = ∫_m ( (x²+y²) *dm)

Теперь переместим параллельно ось вдоль оси x на расстояние l, например, в положительном направлении, тогда расчет для новой оси момента инерции будет выглядеть следующим образом:

I_Z = ∫_m (( (x+l)²+y²)*dm)

Раскроем полный квадрат в скобках и разделим подынтегральные суммы, получим:

I_Z = ∫_m ( (x²+l²+2*x*l+y²)*dm) = ∫_m ( (x²+y²)*dm) + 2*l*∫_m (x*dm) + l²*∫_mdm

Первое из этих слагаемых является величиной I_O, третье слагаемое, после проведения интегрирования, дает член l²*m, а вот второе слагаемое равно нулю. Обнуление указанного интеграла связано с тем, что он берется от произведения иксов на элементы массы dm, что в среднем дает ноль, так как центр масс находится в начале координат. В итоге, получается формула теоремы Штейнера.

Рассмотренный случай на плоскости можно обобщить на объемное тело.

Проверка формулы Штейнера на примере стержня

Приведем простой пример, на котором продемонстрируем, как пользоваться рассмотренной теоремой.

Известно, что для стержня длиной L и массой m момент инерции I_O (ось проходит через центр масс) равен m*L²/12, а момент I_Z (ось проходит через конец стержня) равен m*L²/3. Проверим эти данные, воспользовавшись теоремой Штейнера. Поскольку расстояние между двумя осями равно L/2, тогда получаем момент I_Z:

I_Z = I_O + m*(L/2)² = m*L²/12 + m*L²/4 = 4*m*L²/12 = m*L²/3

То есть мы проверили формулу Штейнера и получили такое же значение для I_Z, что и в источнике.

Аналогичные вычисления можно проводить и для других тел (цилиндра, шара, диска), получая при этом необходимые моменты инерции, и не производя интегрирования.

Момент инерции и перпендикулярные оси

Рассмотренная теорема касается параллельных осей. Для полноты информации полезно также привести теорему для перпендикулярных осей. Она формулируется так: для плоского объекта произвольной формы момент инерции относительно перпендикулярной ему оси будет равен сумме двух моментов инерции относительно двух взаимно перпендикулярных и лежащих в плоскости объекта осей, при этом все три оси должны проходить через одну точку. Математически это записывается так:

I_z = I_x + I_y

Здесь z, x, y – три взаимно перпендикулярные оси вращения.

Существенное отличие этой теоремы от теоремы Штейнера заключается в том, что она применима только к плоским (двумерным) твердым объектам. Тем не менее на практике ее достаточно широко используют, мысленно разрезая тело на отдельные слои, а затем, складывая полученные моменты инерции.

fb.ru

Теорема Штейнера – Момент инерции. Формулировка и доказательство теоремы

Теорема Штейнера. Момент инерции. Формулировка и доказательство теоремы

Скачать реферат по математике «Теорема Штейнера. Момент инерции» в формате doc

Скачать презентацию «Теорема Штейнера. Момент инерции» в формате ppt

Уважаемые посетители сайта Школьный портал, предлагает Вашему вниманию работу по математике на тему «Теорема Штейнера. Момент инерции», где представлены материалы теоретического и практического характера, рекомендации по решению задач с использованием указанной теоремы.

Теорема Штейнера, или, как именуется она в других источниках, теорема Гюйгенса-Штейнера, получила свое название в честь ее автора – Якоба Штейнера (швейцарского математика), а также благодаря дополнениям – Христиана Гюйгенса (голландского физика, астронома и математика). Рассмотрим кратко их вклад в историю математики и других наук.

 Теорема Штейнера — об авторах теоремы

Якоб Штейнер
(1796—1863)

Якоб Штейнер (1796—1863) — один из великих математиков, который считается основателем, как синтетической геометрии кривых линий, так и поверхностей второго и высших порядков.

Что касается Христиана Гюйгенса, то его вклад в различные науки тоже не мал. Он значительно усовершенствовал телескоп (до 92-кратного увеличения изображения), открыл кольца Сатурна и спутник его — Титан, а в 1673 году в своем довольно содержательном труде «Маятниковые часы», представил работы по кинематике ускоренного движения.

Теорема Штейнера — формулировка

Согласно теореме Штейнера, установлено, что момент инерции тела при расчете относительно произвольно оси соответствует сумме момента инерции тела относительно такой оси, которая проходит через центр масс и является параллельной данной оси, а также плюс произведение квадрата расстояния между осями и массы тела, по следующей формуле (1):

J= J₀ + md²      (1)

Где в формуле принимаем соответственно величины: d – расстояние между осями ОО₁║О’O₁’;
J₀– момент инерции тела, рассчитанный относительно оси, что проходит сквозь центр масс и будет определяться соотношением (2):

J₀ = J_d = mR²/2       (2)

Так как d = R, тогда и момент инерции относительно оси, которая проходит через указанную на рисунке точку А будет определяется формулой (3):

J = mR² + mR²/2 = ³/₂ mR²       (3)

Более подробная информация о теореме представлена в реферате и презентации, которые можно скачать по ссылкам перед статьей.

Теорема Штейнера. Момент инерции – содержание работы

Введение

Часть 1. Динамика вращения твердого тела
1.1. Моменты инерции шара и диска
1.2. Теорема Гюйгенса-Штейнера
1.3. Динамика вращательного движения твердого тела — теоретические основы
• Момент импульса
• Момент силы
• Момент инерции относительно оси вращения
• Главный закон динамики вращательного движения твердого тела относительно неподвижной оси

Часть 2. Рекомендации по решению различных типовых задач

Часть 3. Решение задач на определение момента инерции
3.1. Классические примеры решения задач
3.2. Нахождение момента инерции диска и шара
• Задачи на определение момента инерции диска
• Задачи на определение момент инерции шара
Заключение
Список литературы

Просмотреть презентацию «Теорема Штейнера. Момент инерции» можно ниже ↓

Скачать презентацию «Теорема Штейнера. Момент инерции»

nashashcola.ru

Теорема Штейнера Википедия

Иллюстрация теоремы для момента площади

Теоре́ма Гю́йгенса — Ште́йнера (теорема Гюйгенса, теорема Штейнера): момент инерции J{\displaystyle J} тела относительно произвольной неподвижной оси равен сумме момента инерции этого тела JC{\displaystyle J_{C}} относительно параллельной ей оси, проходящей через центр масс тела, и произведения массы тела m{\displaystyle m} на квадрат расстояния d{\displaystyle d} между осями^[1]:

J=JC+md2,{\displaystyle J=J_{C}+md^{2},}

где

J{\displaystyle J} — искомый момент инерции относительно параллельной оси,

JC{\displaystyle J_{C}} — известный момент инерции относительно оси, проходящей через центр масс тела,

m{\displaystyle m} — масса тела,

d{\displaystyle d} — расстояние между указанными осями.

Теорема названа по имени швейцарского математика Якоба Штейнера и голландского математика, физика и астронома Христиана Гюйгенса.

Вывод

Будем рассматривать абсолютно твёрдое тело, образованное совокупностью материальных точек^[2].

По определению момента инерции для JC{\displaystyle J_{C}} и J{\displaystyle J} можно записать

JC=∑i=1nmi(ri)2,{\displaystyle J_{C}=\sum _{i=1}^{n}m_{i}(\mathbf {r} _{i})^{2},}

J=∑i=1nmi(ri′)2,{\displaystyle J=\sum _{i=1}^{n}m_{i}(\mathbf {r} ‘_{i})^{2},}

где r{\displaystyle \mathbf {r} } — радиус-вектор точки тела в системе координат с началом, расположенным в центре масс, а r′{\displaystyle \mathbf {r} ‘} — радиус-вектор точки в новой системе координат, через начало которой проходит новая ось.

Радиус-вектор r′i{\displaystyle \mathbf {r’} _{i}} можно расписать как сумму двух векторов:

ri′=ri+d,{\displaystyle \mathbf {r} ‘_{i}=\mathbf {r} _{i}+\mathbf {d} ,}

где d{\displaystyle \mathbf {d} } — радиус-вектор расстояния между старой (проходящей через центр масс) и новой осями вращения. Тогда выражение для момента инерции примет вид

J=∑i=1nmi(ri)2+2∑i=1nmirid+∑i=1nmi(d)2.{\displaystyle J=\sum _{i=1}^{n}m_{i}(\mathbf {r} _{i})^{2}+2\sum _{i=1}^{n}m_{i}\mathbf {r} _{i}\mathbf {d} +\sum _{i=1}^{n}m_{i}(\mathbf {d} )^{2}.}

Вынося d{\displaystyle \mathbf {d} } за сумму, получим

J=∑i=1nmi(ri)2+2d∑i=1nmiri+d2∑i=1nmi.{\displaystyle J=\sum _{i=1}^{n}m_{i}(\mathbf {r} _{i})^{2}+2\mathbf {d} \sum _{i=1}^{n}m_{i}\mathbf {r} _{i}+d^{2}\sum _{i=1}^{n}m_{i}.}

По определению центра масс, для его радиус-вектора rc{\displaystyle \mathbf {r} _{c}} выполняется

rc=∑imiri∑imi.{\displaystyle \mathbf {r} _{c}={\frac {\sum \limits _{i}m_{i}\mathbf {r} _{i}}{\sum \limits _{i}m_{i}}}.}

Поскольку в системе координат с началом, расположенным в центре масс, радиус-вектор центра масс равен нулю, то равна нулю и сумма ∑i=1nmiri{\displaystyle \sum _{i=1}^{n}m_{i}\mathbf {r} _{i}}.

Тогда

J=∑i=1nmi(ri)2+d2∑i=1nmi,{\displaystyle J=\sum _{i=1}^{n}m_{i}(\mathbf {r} _{i})^{2}+d^{2}\sum _{i=1}^{n}m_{i},}

откуда и следует искомая формула:

J=JC+md2,{\displaystyle J=J_{C}+md^{2},}

где JC{\displaystyle J_{C}} — известный момент инерции относительно оси, проходящей через центр масс тела.

Если тело состоит не из материальных точек, а образовано непрерывно распределённой массой, то во всех приведённых выше формулах суммирование заменяется интегрированием. Ход рассуждения при этом остаётся прежним.

Следствие. Из полученной формулы очевидно, что J>JC{\displaystyle J>J_{C}}. Поэтому можно утверждать: момент инерции тела относительно оси, проходящей через центр масс тела, является наименьшим среди всех моментов инерции тела относительно осей, имеющих данное направление.

Пример

Момент инерции стержня относительно оси, проходящей через его центр и перпендикулярной стержню (назовём её осью C{\displaystyle C}) равен

JC=mL212.{\displaystyle J_{C}={\frac {mL^{2}}{12}}.}

Тогда, согласно теореме Штейнера, его момент относительно произвольной параллельной оси будет равен

J=JC+md2,{\displaystyle J=J_{C}+md^{2},}

где d{\displaystyle d} — расстояние между этой осью и осью C{\displaystyle C}. В частности, момент инерции стержня относительно оси, проходящей через его конец и перпендикулярной стержню, можно найти, положив в последней формуле d=L/2{\displaystyle d=L/2}:

J=JC+m(L2)2=mL212+mL24=mL23.{\displaystyle J=J_{C}+m\left({\frac {L}{2}}\right)^{2}={\frac {mL^{2}}{12}}+{\frac {mL^{2}}{4}}={\frac {mL^{2}}{3}}.}

Пересчёт тензора инерции

Теорема Гюйгенса — Штейнера допускает обобщение на тензор момента инерции, что позволяет получать тензор J^ij{\displaystyle {\hat {J}}_{ij}} относительно произвольной точки из тензора I^ij{\displaystyle {\hat {I}}_{ij}} относительно центра масс. Пусть a{\displaystyle \mathbf {a} } — смещение от центра масс, тогда

J^ij=I^ij+m(a2δij−aiaj),{\displaystyle {\hat {J}}_{ij}={\hat {I}}_{ij}+m(a^{2}\delta _{ij}-a_{i}a_{j}),}

где

a=(a1,a2,a3){\displaystyle \mathbf {a} =(a_{1},a_{2},a_{3})} — вектор смещения от центра масс, а δij{\displaystyle \delta _{ij}} — символ Кронекера.

Как видно, для диагональных элементов тензора (при i=j{\displaystyle i=j}) формула имеет вид теоремы Гюйгенса — Штейнера для момента относительно новой оси.

См. также

Примечания

1. ↑ Тарг С. М. Краткий курс теоретической механики. — 11-е изд. — М.: «Высшая школа», 1995. — С. 268—269. — 416 с. — ISBN 5-06-003117-9.
2. ↑ Абсолютно твёрдое тело, образованное совокупностью материальных точек, — это такая механическая система, у которой расстояния между составляющими её точками постоянны.

wikiredia.ru

Теорема Гюйгенса — Штейнера – Calculations & Formula

English

Deutsch

Español

Français

Hrvatski

Italiano

Polski

Türkçe

Русский

中文

日本語

한국어

Legal notice a span.text:after, .ynmenu-multi > a span.text:after, .ynmenu-content > a span.text:after, .ynmenu-mixed > a span.text:after { display: none !important; } ]]>

a span.text { color: #transparent !important; } .ynmenu-style-metro li[data-level=’1′].ynmenu-level1-idmenu-1 > a { background-color: #transparent; } .ynmenu-style-metro li[data-level=’1′].ynmenu-level1-idmenu-1.ynmenu-standard li.over > a { background-color: #transparent; } .ynmenu-style-metro li[data-level=’1′].ynmenu-level1-idmenu-1 > ul, .ynmenu-style-metro li[data-level=’1′].ynmenu-level1-idmenu-1.ynmenu-standard ul, .ynmenu-style-metro li[data-level=’1′].ynmenu-level1-idmenu-1 > .ynmenu-mixed-main { border-color: #transparent; border-top-color: 4px solid #transparent; } .ynmenu-style-metro li[data-level=’1′].ynmenu-level1-idmenu-1.ynmenu-multi li a { color: #transparent; } .ynmenu-style-metro li[data-level=’1′].ynmenu-level1-idmenu-1.ynmenu-multi li li.over > a > .text { color: #transparent; } .ynmenu-style-metro li[data-level=’1′].ynmenu-level1-idmenu-1.ynmenu-multi li li.over > a > .text { background-color: #transparent; } ]]>
• Community
  a span.text { color: #transparent !important; } ]]>
  • Groups
    a span.text { color: #transparent !important; } ]]>
    • Local and Branch
    a span.text { color: #transparent !important; } ]]>
    • Manufacturer & Supplier
    a span.text { color: #transparent !important; } ]]>
    • CAD, PLM, ERP
    a span.text { color: #transparent !important; } ]]>
    • Mixed Zone
    a span.text { color: #transparent !important; } ]]>
    • Functionality focused…
    a span.text { color: #transparent !important; } ]]>
    • Made by CAD
    a span.text { color: #transparent !important; } ]]>
    • Type of machine
    a span.text { color: #transparent !important; }

b2b.partcommunity.com

---