03.03.202030.12.2018

Сила тяготения формула физика – Закон всемирного тяготения | Формулы и расчеты онлайн

• by alexxlab
• Комментариев к записи Сила тяготения формула физика – Закон всемирного тяготения | Формулы и расчеты онлайн нет
• Советы абитуриенту

Формула силы тяжести | Все формулы

Сила тяжести, действующая на тело, находящееся на поверхности Земли равна массе тела, умноженной на постоянную  м/с.

  

Здесь  – сила тяжести,  – масса,  — ускорение свободного падения.

Единица измерения силы – Н (ньютон).

Для тела, находящегося на определённой высоте над Землёй сила тяжести может быть найдена по формуле:

  

Здесь  – гравитационная постоянная,  – масса тела,  – масса Земли ( кг),  – высота тела над Землёй,  – радиус Земли ( м).

Из-за того, что Земля имеет сплюснутую форму, то есть её радиус не везде одинаков, ускорение свободного падения меняется в зависимости от географической широты, от  на экваторе до  на полюсах.  – его среднее значение.

Сила тяжести действует на тело, имеющее опору или подвес. Если тело их не имеет, то есть находится в состоянии свободного падения, то говорят, что тело находится в невесомости. Сила тяжести всегда направлена к центру Земли.

Примеры решения задач по теме «Сила тяжести»

xn--b1agsdjmeuf9e.xn--p1ai

Формула силы тяготения в физике. Тяготение (гравитация)

Все мы ходим по Земле потому, что она нас притягивает. Если бы Земля не притягивала все находящиеся на ее поверхности тела, то мы, оттолкнувшись от нее, улетели бы в космос. Но этого не происходит, и всем известно о существовании земного притяжения.

Притягиваем ли мы Землю? Притягивает Луна!

А притягиваем ли мы сами к себе Землю? Смешной вопрос, правда? Но давайте разберемся. Вы знаете, что такое приливы и отливы в морях и океанах? Каждый день вода уходит от берегов, неизвестно где шляется несколько часов, а потом, как ни в чем не бывало, возвращается обратно.

Так вот вода в это время находится не неизвестно где, а примерно посредине океана. Там образуется что-то наподобие горы из воды. Невероятно, правда? Вода, которая имеет свойство растекаться, сама не просто стекается, а еще и образует горы. И в этих горах сосредоточена огромная масса воды.

Просто прикиньте весь объем воды, который отходит от берегов во время отливов, и вы поймете, что речь идет о гигантских количествах. Но раз такое происходит, должна же быть какая-то причина. И причина есть. Причина кроется в том, что эту воду притягивает к себе Луна.

Вращаясь вокруг Земли, Луна проходит над океанами и притягивает к себе океанические воды. Луна вращается вокруг Земли, потому что она притягивается Землей. Но, выходит, что она и сама при этом притягивает к себе Землю. Земля, правда, для нее великовата, но ее влияние оказывается достаточным для перемещения воды в океанах.

Сила и закон всемирного тяготения: понятие и формула

А теперь пойдем дальше и подумаем: если два громадных тела, находясь неподалеку, оба притягивают друг друга, не логично ли предположить, что и тела поменьше тоже будут притягивать друг друга? Просто они намного меньше и сила их притяжения будет маленькой?

Оказывается, что такое предположение абсолютно верно. Абсолютно между всеми телами во Вселенной существуют силы притяжения или, другими словами, силы всемирного тяготения.

Первым такое явление обнаружил и сформулировал в виде закона Исаак Ньютон. Закон всемирного тяготения гласит: все тела притягиваются друг к другу, при этом сила их притяжения прямо пропорциональна массе каждого из тел и обратно пропорциональна квадрату расстояния между ними:

F = G * (m_1 * m_2) / r^2 ,

где F величина вектора силы притяжения между телами, m_1 и m_2 массы этих тел, r расстояние между телами, G гравитационная постоянная.

Гравитационная постоянная численно равна силе, которая существует между телами массами 1 кг, находящимися на расстоянии 1 метр. Эта величина найдена экспериментально: G=6,67*〖10〗^(-11) Н* м^2⁄〖кг〗^2 .

Возвращаясь к нашему исходному вопросу: «притягиваем ли мы Землю?», мы можем с уверенностью ответить: «да». Согласно третьему закону Ньютона мы притягиваем Землю ровно с такой же силой, с какой Земля притягивает нас. Силу эту можно рассчитать из закона всемирного тяготения.

А согласно второму закону Ньютона воздействие тел друг на друга какой-либо силой выражается в виде придаваемого ими друг другу ускорения. Но придаваемое ускорение зависит от массы тела.

Масса Земли велика, и она придает нам ускорение свободного падения. А наша масса ничтожно мала по сравнению с Землей, и поэтому ускорение, которое мы придаем Земле, практически равно нулю. Именно поэтому мы притягиваемся к Земле и ходим по ней, а не наоборот.

Почему выпущенный из рук камень падает на Землю? Потому что его притягивает Земля, скажет каждый из вас. В самом деле, камень падает на Землю с ускорением свободного падения. Следовательно, на камень со сто-роны Земли действует сила, направленная к Земле. Согласно третьему закону Ньютона и камень действует на Землю с такой же по модулю силой, направленной к камню. Иными словами, между Землей и камнем действуют силы взаимного притяжения.

Ньютон был первым, кто сначала догадался, а потом и строго доказал, что причина, вызывающая падение камня на Землю, движение Луны вокруг Земли и планет вокруг Солнца, одна и та же. Это сила тяготения, действующая между любыми телами Вселенной. Вот ход его рассуждений, приведенных в главном труде Ньютона «Математические начала натуральной философии»:

«Брошенный горизонтально камень отклонится под действием тяжести от прямолинейного пути и, описав кривую траекторию, упадет наконец на Землю. Если его бросить с большей скоростью, то он упадет дальше» (рис. 1).

Продолжая эти рассуждения, Ньютон приходит к выводу, что если бы не сопротивление воздуха, то траектория камня, брошенного с высокой горы с определенной скоростью, могла бы стать такой, что он вообще никогда не достиг бы поверхности Земли, а двигался вокруг нее «подобно тому, как планеты описывают в небесном пространстве свои орбиты».

Сейчас нам стало настолько привычным движение спутников вокруг Земли, что разъяснять мысль Ньютона подробнее нет необходимости.

Итак, по мнению Ньютона, движен

tsiolkovsky.ru

Законы силы, формулы

Существует ряд законов, которые характеризуют физические процессы при механических движениях тел.

Выделяют следующие основные законы сил в физике:

• закон силы тяжести;
• закон всемирного тяготения;
• законы силы трения;
• закон силы упругости;
• законы Ньютона.

Закон силы тяжести

Замечание 1

Сила тяжести является одним из случаев проявления действия гравитационных сил.

Силу тяжести представляют в виде такой силы, которая действует на тело со стороны планеты и придает ему ускорение свободного падения.

Свободное падение можно рассмотреть в виде $mg = G\frac{mM}{r^2}$, откуда получаем формулу ускорения свободного падения:

$g = G\frac{M}{r^2}$.

Формула определения силы тяжести будет выглядеть следующим образом:

${\overline{F}}_g = m\overline{g}$

Сила тяжести имеет определенный вектор распространения. Он всегда направлен вертикально вниз, то есть по направлению к центру планеты. На тело действует силы тяжести постоянно и это означает, что оно совершает свободное падение.

Траектория движения при действии силы тяжести зависит от:

• модуля начальной скорости объекта;
• направления скорости движения тела.

С этим физическим явлением человек сталкивается ежедневно.

Силу тяжести можно также представить в виде формулы $P = mg$. При ускорении свободного падения учитываются также дополнительные величины.

Если рассматривать закон всемирного тяготения, который сформулировал Исаак Ньютон, все тела обладают определенной массой. Они притягиваются друг к другу с силой. Ее назовут гравитационной силой.

$F = G\frac{m_1m_2}{r^2}$

Эта сила прямо пропорциональна произведению масс двух тел и обратно пропорциональна квадрату расстояния между ними.

$G = 6,7\cdot {10}^{-11}\ {H\cdot m^2}/{{kg}^2\ }$, где $G$ — это гравитационная постоянная и она имеет по международной системе измерений СИ постоянное значение.

Определение 1

Весом называют силу, с которой тело действует на поверхность планеты после возникновения силы тяжести.

В случаях, когда тело находится в состоянии покоя или равномерно движется по горизонтальной поверхности, тогда вес будет равен силе реакции опоры и совпадать по значению с величиной силы тяжести:

$Р = тg$

При равноускоренном движении вертикально вес будет отличаться от силы тяжести, исходя из вектора ускорения. При направлении вектора ускорения в противоположную сторону возникает состояние перегрузки. В случаях, когда тело вместе с опорой двигаются с ускорением $а = g$, тогда вес будет равен нулю. Состояние с нулевым весом называют невесомостью.

Напряженность поля тяготения высчитывается следующим образом:

$g = \frac{F}{m}$

Величина $F$ — сила тяготения, которая действует на материальную точку массой $m$.

Тело помещается в определенную точку поля.

Потенциальная энергия гравитационного взаимодействия двух материальных точек, имеющих массы $m_1$ и $m_2$, должны находиться на расстоянии $r$ друг от друга.

Потенциал поля тяготения можно найти по формуле:

$\varphi = \Pi / m$

Здесь $П$ — потенциальная энергия материальной точки с массой $m$. Она помещена в определенную точку поля.

Законы силы трения

Замечание 2

Сила трения возникает при движении и направлена против скольжения тела.

Статическая сила трения будет пропорциональна нормальной реакции. Статическая сила трения не лежит в зависимости от формы и размеров трущихся поверхностей. От материала тел, которые соприкасаются и порождают силу трения, зависит статический коэффициент трения. Однако законы трения нельзя назвать стабильными и точными, поскольку часто наблюдаются в результатах исследований различные отклонения.

Традиционное написание силы трения предполагает использование коэффициента трения ($\eta$), $N$ – сила нормального давления.

$F=\eta N$

Также выделяют внешнее трение, силу трения качения, силу трения скольжения, вязкую силу трения и другие виды трения.

Закон силы упругости

Сила упругости равна жёсткости тела, которую помножили на величину деформации:

$F = k \cdot \Delta l$

В нашей классической формуле силы по поиску силы упругости главное место занимают величины жесткости тела ($k$) и деформации тела ($\Delta l$). Единицей измерения силы является ньютон (Н).

Подобная формула может описать самый простой случай деформации. Его принято называть законом Гука. Он гласит, что при попытке любым доступным способом деформировать тело, сила упругости будет стремиться вернуть форму объекта в первоначальный вид.

Для понимания и точного процесса описания физического явления вводят дополнительные понятия. Коэффициент упругости показывает зависимость от:

• свойств материала;
• размеров стержня.

В частности, выделяют зависимость от размеров стержня или площади поперечного сечения и длины. Тогда коэффициент упругости тела записывают в виде:

$k = \frac{ES}{L}$

В такой формуле величина $E$ является модулем упругости первого рода. Также ее называют модулем Юнга. Она отражает механические характеристики определенного материала.

При проведении расчётов прямых стержней применяется запись закона Гука в относительной форме:

$\Delta l = \frac{FL}{ES}$

Отмечается, что применение закона Гука будет носить эффективный характер только при относительно небольших деформациях. Если идет превышение уровня предела пропорциональности, то связь между деформациями и напряжениями становится нелинейной. Для некоторых сред закон Гука нельзя применять даже при небольших деформациях.

spravochnick.ru

Сила тяжести, формулы

Определение 1

Сила тяжести считается приложением к центру тяжести тела, определяемому путем подвешивания тела на нити за его различные точки. При этом точка пересечения всех направлений, которые отмечены нитью, и будет считаться центром тяжести тела.

Понятие силы тяжести

Замечание 1

Сила тяжести $mg$ считается состоящей из гравитационного притяжения планеты, определяемого как $\frac{GMm}{r_2}$ и также центробежной силы инерции $mw2a$.

Силой тяжести в физике считают силу, действующую на любое физическое тело, пребывающее вблизи земной поверхности либо иного астрономического тела. Сила тяжести на поверхности планеты, по определению, будет складываться из гравитационного притяжения планеты, а также центробежной силы инерции, спровоцированной суточным вращением планеты.

Иные силы (например, притяжение Солнца и Луны) по причине их малости не учитываются или изучаются отдельно в формате временных изменений гравитационного поля Земли. Сила тяжести сообщает всем телам, в независимости от их массы, равное ускорение, представляя при этом консервативную силу. Она вычисляется на основании формулы:

$\vec {P} = m\vec{g}$,

где $\vec{g}$-ускорение, которое сообщается телу силой тяжести, обозначенное как ускорение свободного падения.

На тела, передвигающиеся относительно поверхности Земли, помимо силы тяжести, также оказывает непосредственное воздействие сила Кориолиса, представляющая силу, используемую при изучении движения материальной точки по отношению к вращающейся системе отсчета. Присоединение силы Кориолиса к воздействующим на материальную точку физическим силам позволит учитывать воздействие вращения системы отсчета на подобное движение.

Важные формулы для расчета

Соответственно закону всемирного тяготения, сила гравитационного притяжения, воздействующая на материальную точку с ее массой $m$ на поверхности астрономического сферически симметричного тела с массой $M$, будет определяться соотношением:

$F={G}\frac{Mm}{R^2}$, где:

• $G$—гравитационная постоянная,
• $R$— радиус тела.

Указанное соотношение оказывается справедливым, если предположить сферически симметричное распределение массы по объему тела. Тогда сила гравитационного притяжения направляется непосредственно к центру тела.

Модуль центробежной силы инерции $Q$, воздействующей на материальную частицу, выражен формулой:

$Q = maw^2$, где:

• $a$— расстояние между частицей и осью вращения астрономического тела, которое рассматривается,
• $w$—угловая скорость его вращения. При этом центробежная сила инерции становится перпендикулярной оси вращения и направленной в сторону от нее.

В векторном формате выражение для центробежной силы инерции записывается так:

$\vec{Q} = {mw^2\vec{R_0}}$, где:

$\vec {R_0}$— вектор, перпендикулярный оси вращения, который проведен от нее к указанной материальной точке, пребывающей вблизи поверхности Земли.

При этом сила тяжести $\vec {P}$ будет равнозначна сумме $\vec {F}$ и $\vec {Q}$:

$\vec{P} = \vec{F} = \vec{Q}$

Закон притяжения

Без присутствия силы тяжести стало бы невозможным происхождение многих, сейчас кажущихся нам естественными, вещей: так, не было бы схождение с гор лавин, течения рек, дождей. Атмосфера Земли может сохраняться исключительно благодаря воздействию силы тяжести. Планеты с меньшей массой, например, Луна или Меркурий, растеряли всю свою атмосферу довольно стремительными темпами и стали беззащитными перед потоками агрессивного космического излучения.

Атмосфера Земли сыграла решающее значение при процессе формирования жизни на Земле, ее. Помимо силы тяжести, на Земле воздействует также сила притяжения Луны. За счет ее близкого соседства (в космических масштабах), на Земле возможно существование отливов и приливов, а многие биологические ритмы являются совпадающими с лунным календарем. Силу тяжести, таким образом, нужно рассматривать в формате полезного и важного закона природы.

Замечание 2

Закон притяжения считается универсальным и возможен к применению в отношении любых двух тел, обладающих определенной массой.

В ситуации, если масса одного взаимодействующего тела оказывается намного больше массы второго, говорится о частном случае гравитационной силы, для которого существует специальный термин, такой как «сила тяжести». Он применим к задачам, ориентированным на определение силы притяжения на Земле или иных небесных телах. При подставлении значения силы тяжести в формулу второго закона Ньютона, получаем:

$F = ma$

Здесь $а$ – ускорение силы тяжести, принуждающее тела стремиться друг к другу. В задачах, связанных с задействованием ускорения свободного падения, такое ускорение обозначают буквой $g$. С помощью собственного интегрального исчисления, Ньютону математически удалось доказать постоянную сосредоточенность силы тяжести в центре большего тела.

spravochnick.ru

Referat. Сила тяжести — PhysBook

Сила тяжести

Частным, но крайне важным для нас видом силы всемирного тяготения является сила притяжения тел к Земле. Эту силу называют силой тяжести. Согласно закону всемирного тяготения, она выражается формулой

\(~F_T = G \frac{mM}{(R+h)^2}\) , (1)

где m – масса тела, М – масса Земли, R – радиус Земли, h – высота тела над поверхностью Земли. Сила тяжести направлена вертикально вниз, к центру Земли.

• Более точно, помимо этой силы, в системе отсчета, связанной с Землей, на тело действует центробежная сила инерции \(~\vec F_c\) , которая возникает из-за суточного вращения Земли, и равна \(~F_c = m \cdot \omega^2 \cdot r\) , где m – масса тела; r – расстояние между телом и земной осью. Если высота тела над поверхностью Земли мала по сравнению с ее радиусом, то \(~r = R \cos \varphi\) , где R – радиус Земли, φ – географическая широта, на которой находится тело (рис. 1). С учетом этого \(~F_c = m \cdot \omega^2 \cdot R \cos \varphi\) .

Рис. 1

Силой тяжести называется сила, действующая на любое находящееся вблизи земной поверхности тело.

Она определяется как геометрическая сумма действующей на тело силы гравитационного притяжения к Земле \(~\vec F_g\) и центробежной силы инерции \(~\vec F_c\) , учитывающей эффект суточного вращения Земли вокруг собственной оси, т.е. \(~\vec F_T = \vec F_g + \vec F_c\) . Направление силы тяжести является направлением вертикали в данном пункте земной поверхности.

НО величина центробежной силы инерции очень мала по сравнению с силой притяжения Земли (их отношение составляет примерно 3∙10^-3), то обычно силой \(~\vec F_c\) пренебрегают. Тогда \(~\vec F_T \approx \vec F_g\) .

Ускорение свободного падения

Сила тяжести сообщает телу ускорение, называемое ускорением свободного падения. В соответствии со вторым законом Ньютона

\(~\vec g = \frac{\vec F_T}{m}\) .

С учетом выражения (1) для модуля ускорения свободного падения будем иметь

\(~g_h = G \frac{M}{(R+h)^2}\) . (2)

На поверхности Земли (h = 0) модуль ускорения свободного падения равен

\(~g = G \frac{M}{R^2}\) ,

а сила тяжести равна

\(~\vec F_T = m \vec g\) .

Модуль ускорения свободного падения, входящего в формулы, равен приближенно 9,8 м/с².

Из формулы (2) видно, что ускорение свободного падения не зависит от массы тела. Оно уменьшается при подъеме тела над поверхностью Земли: ускорение свободного падения обратно пропорционально квадрату расстояния тела от центра Земли.

Однако если высота h тела над поверхностью Земли не превышает 100 км, то при расчетах, допускающих погрешность ≈ 1,5%, этой высотой можно пренебречь по сравнению с радиусом Земли (R = 6370 км). Ускорение свободного падения на высотах до 100 км можно считать постоянным и равным 9,8 м/с².

И все же у поверхности Земли ускорение свободного падения не везде одинаково. Оно зависит от географической широты: больше на полюсах Земли, чем на экваторе. Дело в том, что земной шар несколько сплюснут у полюсов. Экваториальный радиус Земли больше полярного на 21 км.

Другой, более существенной причиной зависимости ускорения свободного падения от географической широты является вращение Земли. Второй закон Ньютона справедлив в инерциальной системе отсчета. Такой системой является, например, гелиоцентрическая система. Систему же отсчета, связанную с Землей, строго говоря, нельзя считать инерциальной. Земля вращается вокруг своей оси и движется по замкнутой орбите вокруг Солнца.

Вращение Земли и сплюснутость ее у полюсов приводит к тому, что ускорение свободного падения относительно геоцентрической системы отсчета на разных широтах различно: на полюсах g_пол ≈ 9,83 м/с², на экваторе g_экв ≈ 9,78 м/с², на широте 45° g ≈ 9,81 м/с². Впрочем, в наших расчетах мы будем считать ускорение свободного падения приближенно равным 9,8 м/с².

Из-за вращения Земли вокруг своей оси ускорение свободного падения во всех местах, кроме экватора и полюсов, не направлено точно к центру Земли.

Кроме того, ускорение свободного падения зависит от плотности пород, залегающих в недрах Земли. В районах, где залегают породы, плотность которых больше средней плотности Земли (например, железная руда), g больше. А там, где имеются залежи нефти, g меньше. Этим пользуются геологи при поиске полезных ископаемых.

Вес тела

Вес тела – это сила, с которой тело, вследствие его притяжения к Земле, действует на опору или подвес.

Рассмотрим, например, тело, подвешенное к пружине, другой конец которой закреплен (рис. 2). На тело действует сила тяжести \(~\vec F_T = m \vec g\) направленная вниз. Оно поэтому начинает падать, увлекая за собой нижний конец пружины. Пружина окажется из-за этого деформированной, и появится сила упругости \(~\vec F_{ynp}\) пружины. Она приложена к верхнему краю тела и направлена вверх. Верхний край тела будет поэтому «отставать» в своем падении от других его частей, к которым сила упругости пружины не приложена. Вследствие этого и тело деформируется. Возникает еще одна сила упругости – сила упругости деформированного тела. Она приложена к пружине и направлена вниз. Вот эта сила и есть вес тела.

Рис. 2

По третьему закону Ньютона обе эти силы упругости равны по модулю и направлены в противоположные стороны. После нескольких колебаний тело на пружине оказывается в покое. Это значит, что сила тяжести \(~m \vec g\) по модулю равна силе упругости F_упр пружины. Но этой же силе равен и вес тела.

Таким образом, в нашем примере вес тела, который мы обозначим буквой \(~\vec P\) , по модулю равен силе тяжести:

\(~P = m g\) .

Второй пример. Пусть тело А находится на горизонтальной опоре В (рис. 3). На тело А действует сила тяжести \(~m \vec g\) и сила реакции опоры \(~\vec N\) . Но если опора действует на тело с силой \(~\vec N\) то и тело действует на опору с силой \(~\vec P\) , которая в соответствии с третьим законом Ньютона равна по модулю и противоположна по направлению \(~\vec N\) \[~\vec P = -\vec N\] . Сила \(~\vec P\) и есть вес тела.

Рис. 3

Если тело и опора неподвижны или движутся равномерно и прямолинейно, т. е. без ускорения, то, согласно второму закону Ньютона,

\(~\vec N + m \vec g = 0\) .

Так как

\(~\vec N = -\vec P\) , то \(~-\vec P + m \vec g = 0\) .

Следовательно,

\(~\vec P = m \vec g\) .

Значит, если ускорение а = 0, то вес тела равен силе тяжести.

Но это не значит, что вес тела и сила тяжести, приложенная к нему, одно и то же. Сила тяжести приложена к телу, а вес приложен к опоре или подвесу. Природа силы тяжести и веса тоже различна. Если сила тяжести является результатом взаимодействия тела и Земли (сила тяготения), то вес появляется в результате совсем другого взаимодействия: взаимодействия тела А и опоры В. Опора В и тело А при этом деформируются, что приводит к появлению сил упругости. Таким образом, вес тела (как и сила реакции опоры) является частным видом силы упругости.

Вес обладает особенностями, существенно отличающими его от силы тяжести.

Во-первых, вес определяется всей совокупностью действующих на тело сил, а не только силой тяжести (так, вес тела в жидкости или воздухе меньше, чем в вакууме, из-за появления выталкивающей (архимедовой) силы). Во-вторых, вес тела, существенно зависит от ускорения, с которым движется опора (подвес).

Вес тела при движении опоры или подвеса с ускорением

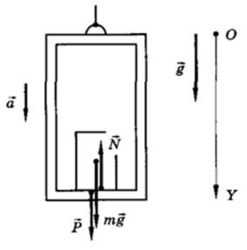
Можно ли увеличить или уменьшить вес тела, не изменяя самого тела? Оказывается, да. Пусть тело находится в кабине лифта, движущегося с ускорением \(~\vec a\) (рис. 4 а, б).

• 

  а

• 

  б

Рис. 4

Согласно второму закону Ньютона

\(~\vec N + m \vec g = m \vec a\) , (3)

где N – сила реакции опоры (пола лифта), m – масса тела.

По третьему закону Ньютона вес тела \(~\vec P = -\vec N\) . Поэтому, учитывая (3), получим

\(~\vec P = m (\vec g – \vec a)\) .

Направим координатную ось Y системы отсчета, связанной с Землей, вертикально вниз. Тогда проекция веса тела на эту ось будет равна

\(~P_y = m (g_y – a_y)\) .

Так как векторы \(~\vec P\) и \(~\vec g\) сонаправлены с осью координат Y, то Р_y = Р и g_y = g. Если ускорение \(~\vec a\) направлено вниз (см. рис. 4, а), то a_y = а, и равенство принимает следующий вид:

\(~P = m (g – a)\) .

Из формулы следует, что лишь при а = 0 вес тела равен силе тяжести. При а ≠ 0 вес тела отличается от силы тяжести. При движении лифта с ускорением, направленным вниз (например, в начале спуска лифта или в процессе его остановки при движении вверх) и по модулю меньшим ускорения свободного падения, вес тела меньше силы тяжести. Следовательно, в этом случае вес тела меньше веса того же тела, если оно находится на покоящейся или равномерно движущейся опоре (подвесе). По этой же причине вес тела на экваторе меньше, чем на полюсах Земли, так как вследствие суточного вращения Земли тело на экваторе движется с центростремительным ускорением.

Рассмотрим теперь, что произойдет, если тело движется с ускорением \(~\vec a\), направленным вертикально вверх (см. рис. 4, б). В данном случае получаем

\(~P = m (g + a)\) .

Вес тела в лифте, движущемся с ускорением, направленным вертикально вверх, больше веса покоящегося тела. Увеличение веса тела, вызванное ускоренным движением опоры (или подвеса), называется перегрузкой. Перегрузку можно оценить, найдя отношение веса ускоренно движущегося тела к весу покоящегося тела:

\(~k = \frac{m (g + a)}{m g} = 1 + \frac{a}{g}\) .

Тренированный человек способен кратковременно выдерживать примерно шестикратную перегрузку. Значит, ускорение космического корабля, согласно полученной формуле, не должно превосходить пятикратного значения ускорения свободного падения.

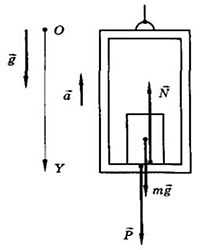
Невесомость

Возьмем в руки пружину с подвешенным к ней грузом, а лучше пружинные весы. По шкале пружинных весов можно отсчитать вес тела. Если рука, держащая весы, покоится относительно Земли, весы покажут, что вес тела по модулю равен силе тяжести mg. Выпустим весы из рук, они вместе с грузом начнут свободно падать. При этом стрелка весов устанавливается на нуле, показывая, что вес тела стал равным нулю. И это понятно. При свободном падении и весы и груз движутся с одинаковым ускорением, равным g. Нижний конец пружины не увлекается грузом, а сам следует за ним, и пружина не деформируется. Поэтому нет силы упругости, которая действовала бы на груз. Значит, и груз не деформируется и не действует на пружину. Вес исчез! Груз, как говорят, стал невесомым.

Невесомость объясняется тем, что сила всемирного тяготения, а значит, и сила тяжести сообщают всем телам (в нашем случае – грузу и пружине) одинаковое ускорение

g. Поэтому всякое тело, на которое действует только сила тяжести или вообще сила всемирного тяготения, находится в состоянии невесомости. В таких условиях находятся свободно падающие тела, например тела в космическом корабле. Ведь и космический корабль, и тела в нем тоже находятся в состоянии длительного свободного падения. Впрочем, в состоянии невесомости, хотя и непродолжительно, находится каждый из вас, спрыгивая со стула на пол или подпрыгивая вверх.

Это же можно доказать и математически. При свободном падении тела \(~\vec a = \vec g\) и \(~P = m (g – g) = 0\) .

Литература

1. Кикоин И.К., Кикоин А.К. Физика: Учеб. для 9 кл. сред. шк. – М.: Про-свещение, 1992. – 191 с.
2. Луцевич А.А., Яковенко С.В. Физика: Учеб. пособие. – Мн.: Выш. шк., 2000. – 495 с.
3. Физика: Механика. 10 кл.: Учеб. для углубленного изучения физики / М.М. Балашов, А.И. Гомонова, А.Б. Долицкий и др.; Под ред. Г.Я. Мякишева. – М.: Дрофа, 2002. – 496 с.

www.physbook.ru

Гравитационное взаимодействие. Закон всемирного тяготения

Из законов динамики нам хорошо известно, что для того, чтобы тело двигалось ускоренно, на него должна действовать сила, как в данном примере с автомобилем на рис. 1. Равнодействующая направлена таким образом, что машина ускоряется.

Рис. 1. Иллюстрация действий сил на тело

В то же время мы хорошо знаем, что земля сообщает одинаковое ускорение любым падающим на нее телам. Эту силу, с которой действует земля на падающие тела, мы традиционно называем сила тяжести. На рис. 2 проиллюстрировано действие силы тяжести.

Рис. 2. Иллюстрация действия силы тяжести

В конце XVII века Исаак Ньютон, которому на тот момент было всего 22 года, предположил, что свойство притягивать тела характерно не только для земли, но и для любых тел, обладающих массами (рисунок. 3). Такую силу он назвал

силой всемирного тяготения,а взаимодействие, ответственное за появление этой силы, было названо гравитационным (от латинского gravitas – «тяжесть»).

Рис. 3. Взаимодействие двух тел обладающих массой

Закон всемирного тяготения позволяет описывать не только падение тел на землю, но и движение планет, звезд, приливы, отливы и множество других универсальных явлений, которые протекают в природе. Попробуем восстановить ход рассуждений Ньютона, а он получил математическую формулу, описывая движение Луны вокруг Земли, и тоже получить закон всемирного тяготения.

Если Земля сообщает любому телу, находящемуся на ее поверхности, ускорение свободного падения g, которое, как мы знаем, по модулю равно g = 9,8 , то Луне притяжение Земли сообщает центростремительное ускорение. Запишем некоторые характеристики.

Радиус Земли (он нам понадобится в расчетах) R₃ = 6370 км, орбиты Луны R_Л = 384000 км, период обращения Луны вокруг Земли, так называемый лунный месяц Т = 27,3 суток.

Воспользуемся этими данными и рассуждениями для дальнейших выводов.

Ньютон предположил, что сила, с которой Земля притягивает те или иные объекты, зависит от расстояния между объектом и центром Земли. Известно, что расстояние от Луны до центра Земли примерно в 60 раз больше чем радиус Земли, т. е. расстояние от любого тела находящегося на поверхности Земли.

А во сколько же раз отличается ускорение, приобретаемое телами в результате такого притяжения? Для начала рассчитаем ускорение, которое приобретает Луна в результате своего притяжения Землей. Ускорение, которым обладает любое тело, находящееся на поверхности Земли, вы и так хорошо знаете, это ускорение свободного падения.

Переходим к расчетам.Центростремительное ускорение Луны, вызванное притяжением Земли, может быть рассчитано по формуле:

Угловая скорость нам не известна, но мы прекрасно знаем, что угловая скорость связана с периодом вращения таким соотношением:

Получим:

Само по себе это значение может ничего нам не говорить, но сравним его с величиной ускорения свободного падения g = 9,8  и тоже вызванной земным притяжением. Итак, находим отношение:

Почему выделяем именно 60²? Дело в том, что Луна по отношению к поверхности Земли расположена как раз на расстоянии приблизительно в 60 раз больше, чем сам радиус Земли.

На тот момент из исследований Галилео Галилея было хорошо известно, что ускорение, приобретаемое телами в результате притяжения Землей, не зависит от их массы, т. е. если яблоко у поверхности Земли обладает ускорением 9,8, вызванным земным притяжением:

то, помещенное на орбиту Луны, оно будет обладать точно таким же ускорением, как и Луна, т. е. в 3600 раз меньшим, чем ускорение свободного падения у поверхности Земли:

Исходя из наших расчетов, мы с вами получаем, что сила, с которой Земля притягивает Луну, обратно пропорциональна квадрату расстояния между центрами этих объектов:

Кроме этого, из второго закона Ньютона мы знаем, что сила прямо пропорциональна массе объекта. Т. е. в данном случае сила прямо пропорциональна массе Луны или другого небесного тела:

Из третьего закона Ньютона мы знаем, что сила действия вызывает аналогичное противодействие, направленное в противоположную сторону, значит, сила взаимодействия между Землей и Луной будет пропорциональна не только массе Луны, но и массе Земли тоже:

Объединяя все это в одну пропорциональность, мы можем получить, что сила, с которой взаимодействуют Земля и Луна, пропорциональна произведению их масс и обратно пропорциональна квадрату расстояния между ними:

А если обобщать и говорить не только о Земле и Луне, то запишем аналогичную пропорциональность, но уже для двух произвольных масс. Итак, сила взаимодействия между ними пропорциональна произведению этих масс и обратно пропорциональна квадрату расстояния между этими телами:

Если же перейти к строгому равенству, то мы получаем ту самую формулировку, которая впервые появилась в знаменитом труде Ньютона «Математические начала натуральной философии» (1687) и носит название закона всемирного тяготения.

Формулировка

Закон всемирного тяготения: тела притягиваются друг к другу с силой, модуль которой пропорционален произведению их масс и обратно пропорционален квадрату расстояния между ними. Сила направлена вдоль прямой, соединяющей центры тел.

Математическая запись этой формулы

 

---

Как Луна влияет на Землю

Несмотря на то, что Луна расположена от Земли достаточно далеко, расстояние составляет порядка 400 000 км, ее влияние на Землю все-таки весьма ощутимо. Итак, поговорим о том, как Луна влияет на вес тел, находящихся на Земле. Сразу оговоримся: мы не будем учитывать влияние Солнца и других небесных тел, так как оно по сравнению с влиянием Луны значительно меньше.

Мы не будем сейчас вдаваться в детальные подробности того, как мы получили те данные, о которых сейчас поговорим, а остановимся лишь на результате. Если подсчитать, воспользовавшись законом всемирного тяготения, влияние Луны на вес тел на Земле, то окажется что в наиболее близкой к Луне и в наиболее удаленной от Луны точках земной поверхности вес тела несколько уменьшается, а в точке, лежащей на средней линии, вес тела немного увеличивается. При этом изменение веса, показанное на рисунке 4 красным цветом, в два раза меньше, чем изменение веса, показанное на рисунке 5 также красным цветом, для точек наиболее близкой и наиболее удаленной.

Рис. 4. Изменение веса в зависимости от расстояния до Луны

Рис. 5. Изменение веса в зависимости от расстояния до Луны

Если бы Луны вообще не было на земной орбите, то вес тела уменьшился бы совершенно незначительно. Если перейти от ньютонов к единицам ускорения , то эта величина составляла бы всего лишь 0,0001 . По сравнению, например, с ускорением свободного падения 10  (мы здесь его округлили от 9,8 до 10), вы видите, что разница составляет порядка одной стомиллионной доли. Немного? Да, немного, но если сравнивать с радиусом Земли те изменения, которые привносит такое небольшое измерение ускорения в результате отсутствия Луны, то мы получим, что Rз = 6400 км. И эти стомиллионные доли изменения приводят к тому, что высота уровня воды в точках, показанных на рис. 4, поднимается на 54 см, в точках, показанных на рис. 5, она падает на 27 см (см. рис. 3).

Речь идет о явлении приливов и отливов. Именно Луна определяет наличие приливов и отливов на Земле.

Благодаря вращению Земли места подъемов и опусканий уровня воды постоянно перемещаются. Именно такие постоянные перемещения мы и ощущаем в виде приливов и отливов. Конечно же, приливы и отливы зависят и от географического места на Земле, например, на Черном море или на Каспийском море приливы практически не наблюдаются, однако в Охотском море есть бухта, в которой высота приливных волн достигает нескольких метров.

Еще одно интересное влияние Луны на Землю – в результате приливов и отливов, волна, которая бежит вдоль земли трется о поверхность земли и, значит, несколько замедляет вращение Земли. Интересно, что тот факт, что мы всегда видим Луну повернутой к нам одним боком, тоже предопределил теперь уже влияние Земли на Луну.

А сейчас поговорим об ограничениях, о границах применимости той формулировки закона всемирного тяготения, которую мы записали. В каких случаях он справедлив? К примеру, есть два тела А и В. Они, согласно закону всемирного тяготения, притягиваются друг к другу. Если эти тела притягиваются и, например, находятся на расстоянии, показанном на рисунке 6, то какую величину брать в качестве r (расстояния между ними) – либо самое маленькое между ними, либо расстояние между наиболее дальними краями, или же расстояние между серединками? А где взять эту серединку? Итак, возникает вопрос: применима ли формула закона всемирного тяготения для тел неправильной формы, находящихся на таком расстоянии друг от друга?

Рис. 6. Положение тел А и В

Ответ мы можем получить, для этого увеличим расстояние между телами. Когда мы их разнесли достаточно далеко друг от друга, нужно ли учитывать их размеры? Нет, ведь их размеры по сравнению с расстоянием между ними очень малы, поэтому в данном случаи мы их можем полагать материальными точками. Итак, первое ограничение:

1. Закон всемирного тяготения применим для тел, размеры которых несущественны по сравнению с расстоянием между ними. Такие тела мы называем материальными точками. Это первое условие.

Однако есть ситуации, когда можно рассматривать тела, обладающие реальными размерами и находящиеся на небольшом расстоянии друг от друга. Это тела примерно такой формы, как показано на рисунке 7.

Рис. 7. Положение тел сферической формы

Представьте себе, что это идеальные сферы. Если тела, обладающие сферической формой, или, говорят, сферической симметрией, находятся даже на небольшом расстоянии друг от друга, мы можем пользоваться формулой закона всемирного тяготения в качестве расстояния r. В этом случае мы берем расстояние между центрами тел, именно в такой форме мы пользуемся законом всемирного тяготения, когда рассматриваем наше притяжение к центру Земли.

Второе условие, при котором можно применять закон всемирного тяготения в той форме, которую мы записали:

2. Тела должны обладать сферической симметрией.

Поняв, в каких случаях можно применять формулу для закона всемирного тяготения, вернемся к величине G (коэффициенту пропорциональности):

Эта величина носит название гравитационной постоянной. Выясним какой смысл у гравитационной постоянной G. Запишем еще раз закон всемирного тяготения:

Отсюда несложно получить, что гравитационная постоянная G может быть вычислена по формуле:

Итак, отсюда мы получаем физический смысл гравитационной постоянной. В самом деле, если мы возьмем две материальные точки, расположенные на расстоянии 1 м друг от друга, а масса этих материальных точек равна 1 кг, то гравитационная постоянная будет численно равна силе, с которой притягиваются эти две точки. Физический смысл гравитационной постоянной: она численно равна силе, с которой мысленно притягиваются две материальные точки массами по 1 кг, расположенные в вакууме на расстоянии 1 м друг от друга.

Поговорим о том, как вычислить гравитационную постоянную. Из курса физики 9 класса вы знаете, что эта же формула для гравитационной постоянной для закона всемирного тяготения в случае притяжения к Земле может быть заменена формулой для силы тяжести:

Где м – это масса тела, а g – ускорение свободного падения. Отсюда несложно получить фомулу для гравитационной постоянной:

Можно оценить гравитационную постоянную. Получилось следующее значение гравитационной постоянной:

Эта величина и носит название гравитационной постоянной и является так называемой универсальной физической постоянной, т. е. одинаковой в любой точке Вселенной.

 

---

Модельное представление опыта Кавендиша

Величину гравитационного взаимодействия определяет величина гравитационной постоянной, одной из фундаментальных физических констант. Она составляет:

Как видите, это сравнительно небольшая, даже маленькая величина. Как же ее измерить? Впервые она была измерена несколько сотен лет назад английским ученым Генри Кавендишем. Если говорить об этом человеке, то он был нетипичным ученым, он задолго до Кулона определил закон взаимодействия электрических зарядов, первым в истории науки определил среднюю плотность Земли с достаточно большой точностью. Однако он практически не занимался публикацией своих открытий, они стали известны уже после его смерти.

Для определения гравитационной постоянной Кавендиш сконструировал так называемые крутильные весы, принципиальная схема которых показана на рисунке 8.

Рис. 8. Принципиальная схема крутильных весов

Обратите внимание: на деревянном коромысле подвешены сравнительно небольшие свинцовые шары одинаковой массы. Само деревянное коромысло подвешено на тончайшей посеребренной медной проволочке длиной порядка 1 м. Если к этим шарам подносить массивные также свинцовые шары, то вследствие гравитационного притяжения нить будет немного закручиваться и шарики массы m будут притягиваться к шарикам массы М. В какой-то момент сила гравитационного взаимодействия уравновесится с силой упругости закрученной нити и система придет в равновесие. Сравнивая эти две силы, Кавендиш и определял гравитационную постоянную.

Вы понимаете, что значение гравитационной постоянной очень мало, поэтому углы на которые отклонялась нить также очень малы, он их регистрировал при помощи сложных оптических приборов. Также для того, чтобы избежать конвекционных потоков, т. е. влияния потоков воздуха, вся система была помещена в воздушный колпак, показанный на рисунке 9.

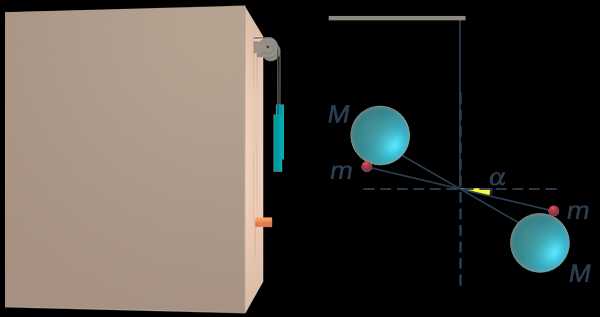
Рис. 9. Воздушный колпак

Интересно, что Кавендиш в своих опытах не измерял напрямую значение гравитационной постоянной, он ставил своей целью как раз определить значение средней плотности Земли, и он определили его как:

Тогда эта величина была неизвестна, и он сказал, что плотность Земли в 5,48 раз больше, чем плотность воды. Современное значение плотности, измеренное более точными приборами, составляет:

Отличие всего в 0,04, менее чем в 1 %. Настолько точно несколько сотен лет назад ученому удалось поставить эксперимент. Какой вывод сделал Кавендиш из значения, которое он получил? Дело в том, что средняя плотность поверхностных слоев Земли составляет порядка:

Отсюда вывод: раз средняя плотность значительно выше, значит где-то в глубине Земли, глубоко, находятся плотные породы, например железо или какие-то другие плотные металлы.

Сама гравитационная постоянная, по всей видимости, впервые в науку была введена французским ученым Пуассоном в трактате по механике в 1811 году, и вычислил он ее как раз из результатов опыта Генри Кавендиша.

Подводим итоги.

1. Взаимодействие, свойственное всем телам во Вселенной и проявляющееся в их взаимном притяжении друг к другу, называют гравитационным, а само явление – всемирным тяготением или гравитацией.

2. Закон всемирного тяготения имеет следующий вид:

Сила взаимодействия между двумя телами массами , находящимися на расстоянии  друг от друга, прямо пропорционально произведению масс этих тел и обратно пропорционально квадрату расстояния между ними.

Направление силы вдоль прямой, соединяющей центры тел, представлено на рисунке 10.

Рис. 10. Направление силы вдоль прямой, соединяющей центры тел

3. Справедлив этот закон в таком виде для:

а) если тела можно положить материальными точками, т. е. их размерами можно пренебречь по сравнению с расстоянием между телами;

б) если тела обладают сферической симметрией.

Напомним, что мы с вами записали и поняли, чему равна гравитационная постоянная и обсудили ее универсальный характер:

Именно гравитационное взаимодействие как одно из четырех универсальных физических взаимодействий является наиболее ответственным за движение крупных небесных тел – планет, звезд, целых галактик.

 

---

Законы движение небесных тел (законы Кеплера)

Вам хорошо известно, что к появлению законов всемирного тяготения привело наблюдение за телами космических масштабов, за планетами, за солнцем, за кометами, за метеоритами и т. д. Именно о том, какие закономерности появились при наблюдении за такими телами, мы и поговорим, а точнее, мы поговорим о законах, которые впервые получил Иоганн Кеплер. На основаниях наблюдений своего учителя, датского астронома Тихо Браге, и собственных наблюдений он провел огромную аналитическую работу и получил три закона движения космических тел. Именно из этих законов и благодаря этим законам в свое время Ньютон и получил закон всемирного тяготения.

Первый закон Кеплера: все планеты Солнечной системы движутся по эллиптическим орбитам, в одном из фокусов эллипса находится Солнце.

Эллипс &ndash

interneturok.ru

Сила: явление тяготения и сила тяжести

Что такое сила?

Каждый из нас постоянно встречается с различными случаями действия тел друг на друга. В результате взаимодействия скорость движения какого-либо тела меняется.

Тело может начать движение или остановиться, а может изменить направление скорости своего движения.

Когда мы пинаем мяч – он начинает двигаться

Когда мяч попадает в сетку ворот, то останавливается

А если мы промазали и мяч попадает в штангу – то отскакивает от нее в другую сторону, т.е. изменяет направления скорости.

Часто не указывают, какое тело и как действовало на данное тело. Просто говорят, что на тело действует сила или к нему приложена сила. То есть, рассматривая пример с мячем, нам не всегда важно, что конкретно на него повлияло. Мы просто говорим, что у тела изменилась скорость под воздействием силы. Следовательно, силу можно рассматривать как причину изменения скорости движения.

В физике силой называют физическую величину, характеризующую изменение скорости тела.

Во всех наших примерах мы воздействовали на мяч с определенной силой, и при этом менялась его скорость.

Признаки действия силы на тело

Сила – это векторная величина, характеризующая действие тел друг на друга, то есть являющаяся мерой этого действия.

Известны четыре признака действия на тело силы:Признак 1 – у тела может измениться значение скорости
(Все мы любим боулинг. Толкая руками шар, мы можем привести его в движение. Скорость шара меняется под действием руки человека. ИЛИ когда мы пинаем футбольный мяч)Признак 2 – У тела может измениться направление движения

( Это когда мяч врезался в штангу ИЛИ изменяем направления летящего шарика ракеткой или другим предметом)

Признак 3 – у тела может произойти изменение размеров тела

(Это надувание надувного матраса или воздушного шарика)

  

 Признак 4 – У тела может произойти изменение формы тела.

(Мы можем сжать ластик в руках или мнем баскетбольный мяч при игре или жмем руку)

Если есть хотя бы один из этих признаков, то говорят: “На тело действует некоторая сила”.

Сила, действующая на тело, может не только изменить скорость всего тела, но и отдельных его частей. Обратите внимание, когда мы мнем баскетбольный мяч руками, то скорость изменяется не у всего тела, а только у некоторых его частей. Например, мы сжимаем мяч пальцами, и только часть его частиц начинает двигаться. Это называется – деформация тела.

Деформация – изменение взаимного положения частиц тела, связанное с их перемещением друг относительно друга.

Деформацией называется любое изменение формы и размера тела. Еще один пример деформации – Батут, прикрепленный к опорам, прогибается, если на него встает человек.

Направление и единица измерения силы

Сила – физическая величина, которую можно измерить..

Известно. что сила является причиной изменения скорости тела. То есть, мы можем измерить, как сильно мы пнули мяч или толкнули шар в боулинге.Однако, сила имеет еще и направление, потому что мяч мы можем пнуть абсолютно в любую сторону также как и толкнуть шар, и от нас зависит, куда он полетит или покатится.

То есть сила – это величина векторная.

Обозначается в физике буквой F со стрелочкой над ней.

За единицу силы, принята сила, которая за время 1с изменяет скорость тела массой 1 кг на 1 м/с.

В честь английского физика Ньютона эта единица названа ньютоном.

Единица измерения силы – Ньютон, обозначается [H]

Часто применяют и другие единицы – килоньютоны(кН), миллиньютоны (мН):

1кН=1000 Н,

1Н = 0,001 кН.

Сила, как и скорость, является векторной величиной. Она характеризуется не только числовым значением, но и направлением.

На чертеже силу изображают в виде отрезка прямой со стрелкой на конце. 

Начало отрезка – точка А есть точка приложения силы. Длина отрезка условно обозначает в определенном масштабе модуль силы.

Итак, можно сказать, что результат действия силы на тело зависит от ее модуля, направления и точки приложения.

Сила притяжения земли

Все мы были на футболе и наблюдали за полетами футбольного мяча. Можно сделать одно наблюдение: как бы сильно не пинал мяч футболист, рано или поздно мяч оказывается на Земле.

Как бы мы не радовались победе нашей команды и подпрыгивали высоко-высоко, все равно приземлялись обратно.Любой предмет, будучи поднятым над поверхностью, стремится к Земле.

То есть, мы приходим к выводу, что есть какая-то неизменная сила, которая притягивает все предметы к Земле. Почему же это происходит? Как называется это явление?

Вот ответ на эти вопросы – На эти тела действует сила – сила притяжения к Земле. Из-за притяжения к Земле падают тела, поднятые над Землей, а потом опущенные.

Сила вытаскивания ноги с зыбучих песков со скоростью 0,1 м/с

 равна силе поднятия легкового автомобиля. 

Интересный факт: зыбучие пески – это ньютоновская жидкость, 

которая не может поглотить человека полностью. 

Поэтому увязшие в песках люди умирают от обезвоживания, 

солнечного облучения или по другим причинам. .

Сила тяжести и сила тяготения

В курсе физике явление которые мы описали выше, носит понятие силы тяжести или силы тяготения. Это одно и то же? Не совсем.

Сила притяжения к Земле называется силой тяжести. Сила тяжести действует на все тела, находящиеся на поверхности Земли. Но не только тела притягиваются к Земле – они сами притягивают к себе Землю. Как по расписанию, по два раза за каждые сутки поднимаются огромные волны на морях и океанах – это можно наблюдать на берегу в виде приливов и отливов. За счет чего? За счет того, что луна действует на Землю. Это взаимодействие. Впервые его описал английский физик Исаак Ньютон. Он утверждал, что все тела во Вселенной притягиваются друг к другу. И.Ньютон установил, «что чем больше массы взаимодействующих тел, тем сила, с которой они взаимодействуют, будет больше. Силы притяжения между телами уменьшаются, если увеличивается расстояние между ними». Вот это явление и называется силой всемирного тяготения.

Притяжение всех тел Вселенной друг к другу называется всемирным тяготением.

Явление тяготения обусловливает силу тяжести. 

Сила, с которой Земля притягивает к себе тело, называется силой тяжести.

Для нас с вами, как для жителей Земли, сила тяжести играет огромную роль. Именно благодаря ей, мы не улетаем в открытый космос, как и все предметы вокруг нас и даже воздух, которым мы дышим. 

В физике сила тяжести обозначается такой же буквой, как и любая другая сила, но с добавлением индекса: 

Fт или Fтяж.

Она всегда направлена вертикально вниз.Сила тяжести прямо пропорциональна массе данного тела.

Если сравнивать два тела с разной массой, то тело с большей массой – тяжелее. Тело же с меньшей массой – легче.

Во сколько раз масса одного тела больше массы другого тела, во столько же раз и сила тяжести, действующая на первое тело, больше силы тяжести, действующей на второе. Когда массы тел одинаковы, то одинаковы и действующие на них силы тяжести.

spishy-u-antoshki.ru

---