Системы счисления доклад по информатике – Реферат и презентация на тему “Системы счисления”
- Комментариев к записи Системы счисления доклад по информатике – Реферат и презентация на тему “Системы счисления” нет
- Советы абитуриенту
- Реферат Десятичная система счисления
- система счисления. Виды систем счисления
- Доклад по информатике «Системы счисления, используемые в компьютере» Работу Попова Мария Михайловна
- Реферат по информатике и информационно-коммуникационным технологиям Тема:«Системы счисления» Введение
- МБОУ Ангеловская СОШ
- Реферат по информатике и информационно-коммуникационным технологиям Тема:«Системы счисления» Введение
- Современный человек в повседневной жизни постоянно сталкивается с числами и цифрами – они с нами везде. Различные системы счисления используются всегда, когда появляется потребность в числовых расчётах, начиная с вычислений учениками младших классов, выполняемых карандашом на бумаге, заканчивая вычислениями, выполняемыми на суперкомпьютерах. История систем счисления
- Система счисления – это определённый способ представления чисел и соответствующие ему правила действия над ними. Цель создания системы счисления- выработка наиболее удобного способа записи количественной информации. Древние системы счисления:
- Единичная система
- Древнегреческая нумерация
- Славянская нумерация
- Римская нумерация
- Позиционные и непозиционные системы счисления
- Запись числа в позиционной системе счисления
- Любое целое число в позиционной системе можно записать в форме многочлена: Хs=An · Sn-1 + An-1 · Sn-2 + An-2 · Sn-3 +…+ A2 · S1 + A1 · S0 где S – основание системы счисления, А – цифры числа, записанного в данной системе счисления, n – количество разрядов числа. Так, например число 629310запишется в форме многочлена следующим образом: 629310=6·103 + 2·102 + 9·101 + 3·100 Примеры позиционных систем счисления:
- История двоичной системы счисления
- Двоичная система счисления была придумана математиками и философами ещё до появления компьютеров (XVII — XIX вв.). Пропагандистом двоичной системы был знаменитый Г.В. Лейбниц. Он отмечал особую простоту алгоритмов арифметических действий в двоичной арифметике в сравнении с другими системами и придавал ей определенный философский смысл. В 1936 — 1938 годах американский инженер и математик Клод Шеннон нашёл замечательные применения двоичной системы при конструировании электронных схем. Двоичная система счисления
- Двоичная система счисления (бинарная система счисления, binary) — позиционная система счисления с основанием 2. Неудобством этой системы счисления является необходимость перевода исходных данных из десятичной системы в двоичную при вводе их в машину и обратного перевода из двоичной в десятичную при выводе результатов вычислений. Главное достоинство двоичной системы — простота алгоритмов сложения, вычитания, умножения и деления. Сложение, вычитание, умножение и деление в двоичной системе счисления
- Двоичное кодирование в компьютере
- В конце ХХ века, века компьютеризации, человечество пользуется двоичной системой ежедневно, так как вся информация, обраба- тываемая современными ЭВМ, хранится в них в двоичном виде. В современные компьютеры мы можем вводить текстовую информацию, числовые значения, а также графическую и звуковую информацию. Количество информации, хранящейся в ЭВМ, измеряется ее «длиной» (или «объемом»), которая выражается в битах (от английского binary digit – двоичная цифра). Перевод чисел из одной системы счисления в другую
- Заключение
- Высшим достижением древней арифметики является открытие позиционного принципа представления чисел.
- Нужно признать важность не только самой распространенной системы, которой мы пользуемся ежедневно. Но и каждой по отдельности. Ведь в разных областях используются разные системы счисления, со своими особенностями и характерными свойствами.
- Перевод двоичного числа в десятичное
- Для перевода двоичного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 2, и вычислить по правилам десятичной арифметики: Х10= Аn·2n-1 + Аn-1·2n-2 + Аn-2·2n-3 +…+А2·21 + А1·20 Перевод восьмеричного числа в десятичное
- Для перевода восьмеричного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 8, и вычислить по правилам десятичной арифметики: Х10= Аn·8n-1 + Аn-1·8n-2 + Аn-2·8n-3 +…+А2·81 + А1·80 Перевод шестнадцатеричного числа в десятичное
- Для перевода шестнадцатеричного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 16, и вычислить по правилам десятичной арифметики: Х10= Аn·16n-1 + Аn-1·16n-2 + Аn-2·16n-3 +…+А2·161 + А1·160 Перевод десятичного числа в двоичную систему
- Для перевода десятичного числа в двоичную систему его необходимо последовательно делить на 2 до тех пор, пока не останется остаток, меньший или равный 1. Число в двоичной системе записывается как последовательность последнего результата деления и остатков от деления в обратном порядке. Пример: Число 2210 перевести в двоичную систему счисления: 2210=101102 Перевод десятичного числа в восьмеричную систему
- Для перевода десятичного числа в восьмеричную систему его необходимо последовательно делить на 8 до тех пор, пока не останется остаток, меньший или равный 7. Число в восьмеричной системе записывается как последовательность цифр последнего результата деления и остатков от деления в обратном порядке. Пример: Число 57110 перевести в восьмеричную систему счисления: 57110=10738 Перевод десятичного числа в шестнадцатеричную систему
- Для перевода десятичного числа в шестнадцатеричную систему его необходимо последовательно делить на 16 до тех пор, пока не останется остаток, меньший или равный 15. Число в шестнадцатеричной системе записывается как последовательность цифр последнего результата деления и остатков от деления в обратном порядке. Пример: Число 746710 перевести в шестнадцатеричную систему счисления: 746710=1D2B16 Перевод чисел из двоичной системы в восьмеричную
- Чтобы перевести число из двоичной системы в восьмеричную, его нужно разбить на триады (тройки цифр), начиная с младшего разряда, в случае необходимости дополнив старшую триаду нулями, и каждую триаду заменить соответствующей восьмеричной цифрой. При переводе необходимо пользоваться двоично-восьмеричной таблицей: Пример: Число 10010112 перевести в восьмеричную систему счисления: 001 001 0112=1138 Перевод из двоичной системы в шестнадцатеричную
- Чтобы перевести число из двоичной системы в шестнадцатеричную, его нужно разбить на тетрады (четверки цифр). Двоично-шестнадцатеричная таблица: Пример: Число 10111000112 перевести в шестнадцатеричную систему счисления: 0010 1110 00112=2E316 Перевод восьмеричного числа в двоичное
- Для перевода восьмеричного числа в двоичное необходимо каждую цифру заменить эквивалентной ей двоичной триадой. Пример: Число 5318 перевести в двоичную систему счисления: 5318=101 011 0012 Перевод шестнадцатеричного числа в двоичное
- Для перевода шестнадцатеричного числа в двоичное необходимо каждую цифру заменить эквивалентной ей двоичной тетрадой. Пример: Число ЕЕ816 перевести в двоичную систему счисления: ЕЕ816=1110111010002 Перевод из восьмеричной системы счисления в шестнадцатеричную и обратно
- При переходе из восьмеричной системы счисления в шестнадцатеричную и обратно, необходим промежуточный перевод чисел в двоичную систему. Пример 1: Число FEA16 перевести в восьмеричную систему счисления: FEA16=1111111010102=111 111 101 0102=77528 Пример 2: Число 66358 перевести в шестнадцатеричную систему счисления: 66358=1101100111012=1101 1001 11012=D9D16 Единичная система
- В древние времена, когда появилась потребность в записи чисел, количество предметов, изображалось нанесением черточек или засечек на какой-либо твердой поверхности. Археологами найдены такие «записи» при раскопках культурных слоев, относящихся к периоду палеолита (10–11 тысяч лет до н.э.). В такой системе применялся только один вид знаков – палочка. Каждое число обозначалось с помощью строки, составленной из палочек, количество которых равнялось обозначаемому числу. Древнегреческая нумерация
- Славянская нумерация
- В России славянская нумерация сохранилась до конца XVII века. Южные и восточные славянские народы для записи чисел пользовались алфавитной нумерацией. Славянская нумерация сохранялась только в богослужебных книгах. Над буквой, обозначавшей цифру, ставился специальный значок: («титло»). Для обозначения тысяч перед числом (слева внизу) ставился особый знак . Римская нумерация
- Древние римляне пользовались нумерацией, которая сохраняется до настоящего времени под именем «римской нумерации». Мы пользуемся ей для обозначения веков, юбилейных дат, наименования съездов и конференций, для нумерации глав книги или строф стихотворения. Обозначение чисел в ионийской системе нумерации
- Обозначение чисел в древнеславянской системе нумерации
- Доклад – Позиционные системы счисления
Реферат Десятичная система счисления
скачатьРеферат на тему:
План:
- Введение
- 1 История
- 2 Основные сведения
- 2.1 Двоично-десятичное кодирование
- 2.2 Таблица сложения в десятичной системе счисления
- 2.3 Таблица умножения в десятичной системе
Введение
Десяти́чная систе́ма счисле́ния — позиционная система счисления по целочисленному основанию 10. Одна из наиболее распространённых систем. В ней используются цифры 1, 2, 3, 4, 5, 6, 7, 8, 9, 0 (ноль), называемые арабскими цифрами. Предполагается, что основание 10 связано с количеством пальцев рук у человека.
1. История
Десятичная непозиционная система счисления с единичным кодированием десятичных цифр возникла во второй половине третьего тысячелетия до н. э. в древнем Египте. В другой великой цивилизации — вавилонской — за две тысячи лет до н. э. внутри шестидесятеричных разрядов использовалась позиционная десятичная система счисления с единичным кодированием десятичных цифр.
Древнейшая известная запись позиционной десятичной системы обнаружена в Индии в 595 г. Нуль в то время применялся не только в Индии, но и в Китае. В этих старинных системах для записи одинакового числа использовались символы, рядом с которыми дополнительно помечали, в каком разряде они стоят. Потом перестали помечать разряды, но число всё равно можно прочитать, так как у каждого разряда есть своя позиция. А если позиция пустая, её нужно пометить нулём. В поздних вавилонских текстах такой знак стал появляться, но в конце числа его не ставили. Лишь в Индии нуль окончательно занял своё место, эта запись распространилась затем по всему миру.
Индийская нумерация пришла сначала в арабские страны, затем и в Западную Европу. О ней рассказал среднеазиатский математик аль-Хорезми. Простые и удобные правила сложения и вычитания чисел, записанных в позиционной системе, сделали её особенно популярной. А поскольку труд аль-Хорезми был написан на арабском, то за индийской нумерацией в Европе закрепилось неправильное название — «арабская» (арабские цифры).
1.1. Кипу инков
Прообразом баз данных, широко использовавшихся в Центральных Андах (Перу, Боливия) в государственных и общественных целях в I—II тысячелетии н. э., была узелковая письменность Инков — кипу, состоявшая как из числовых записей десятичной системы[2], так и не числовых записей в двоичной системе кодирования[3]. В кипу применялись первичные и дополнительные ключи, позиционные числа, кодирование цветом и образование серий повторяющихся данных[4]. Кипу впервые в истории человечества использовалось для применения такого способа ведения бухгалтерского учёта как двойная запись[5].
2. Основные сведения
Один десятичный разряд в десятичной системе счисления иногда называют декадой. В цифровой электронике одному десятичному разряду десятичной системы счисления соответствует один десятичный триггер.
Целое число
- , где — это целые числа, называемые цифрами, удовлетворяющие неравенству
Обычно для ненулевого числа x требуют, чтобы старшая цифра an − 1 в десятичном представлении x была также ненулевой.
Например, число сто три представляется в десятичной системе счисления в виде:
С помощью n позиций в десятичной системе счисления можно записать целые числа от 0 до 10n − 1, то есть, всего 10n различных чисел.
Дробные числа записываются в виде строки цифр с разделителем десятичная запятая, называемой десятичной дробью:
где n — число разрядов целой части числа, m — число разрядов дробной части числа.
2.1. Двоично-десятичное кодирование
В двоичных компьютерах применяют двоично-десятичное кодирование десятичных цифр (Binary-Coded Decimal), при этом для одной двоично-десятичной цифры отводится четыре двоичных разряда (двоичная тетрада). Двоично-десятичные числа требуют большего количества бит для своего хранения. [6] Так, четыре двоичных разряда имеют 16 состояний, и при двоично-десятичном кодировании 6 из 16 состояний двоичной тетрады не используются.[7]
2.2. Таблица сложения в десятичной системе счисления
| + | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 2 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 3 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 4 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 5 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 6 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 7 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 8 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 9 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 10 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
2.3. Таблица умножения в десятичной системе
| × | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 2 | 0 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 |
| 3 | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 |
| 4 | 0 | 4 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 | |
| 5 | 0 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 |
| 6 | 0 | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 | 60 |
| 7 | 0 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 | 70 |
| 8 | 0 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 | 80 |
| 9 | 0 | 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 | 90 |
| 10 | 0 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
wreferat.baza-referat.ru
система счисления. Виды систем счисления
В курсе информатики, вне зависимости, школьном или университетском, особое место уделяется такому понятию как системы счисления. Как правило, на него выделяют несколько уроков или практических занятий. Основная цель – не только усвоить основные понятия темы, изучить виды систем счисления, но и познакомиться с двоичной, восьмеричной и шестнадцатеричной арифметикой.
Что это значит?
Начнем с определения основного понятия. Как отмечает учебник “Информатика”, система счисления – это система записи чисел, в которой используется специальный алфавит или определенный набор цифр.
В зависимости от того, меняется ли значение цифры от ее положения в числе, выделяют две: позиционную и непозиционную системы счисления.
В позиционных системах значение цифры меняется вместе с ее положением в числе. Так, если взять число 234, то цифра 4 в ней означает единицы, если же рассмотреть число 243, то тут она будет уже означать десятки, а не единицы.
В непозиционных системах значение цифры статично, вне зависимости от ее положения в числе. Наиболее яркий пример – палочковая система, где каждая единица обозначается с помощью черточки. Неважно, куда вы припишите палочку, значение числа измениться лишь на единицу.
Непозиционные системы
К непозиционным системам счисления относятся:
- Единичная система, которая считается одной из первых. В ней вместо цифр использовались палочки. Чем их было больше, тем больше было значение числа. Встретить пример чисел, записанных таким образом, можно в фильмах, где речь идет о потерянных в море людях, заключенных, которые отмечают каждый день с помощью зарубок на камне или дереве.
- Римская, в которой вместо цифр использовались латинские буквы. Используя их, можно записать любое число. При этом его значение определялось с помощью суммы и разницы цифр, из которых состояло число. Если слева от цифры находилось меньшее число, то левая цифра вычиталась из правой, а если справа цифра была меньше или равна цифре слева, то их значения суммировались. Например, число 11 записывалось как XI, а 9 – IX.
- Буквенные, в которых числа обозначались с помощью алфавита того или иного языка. Одной из них считается славянская система, в которой ряд букв имел не только фонетическое, но и числовое значение.
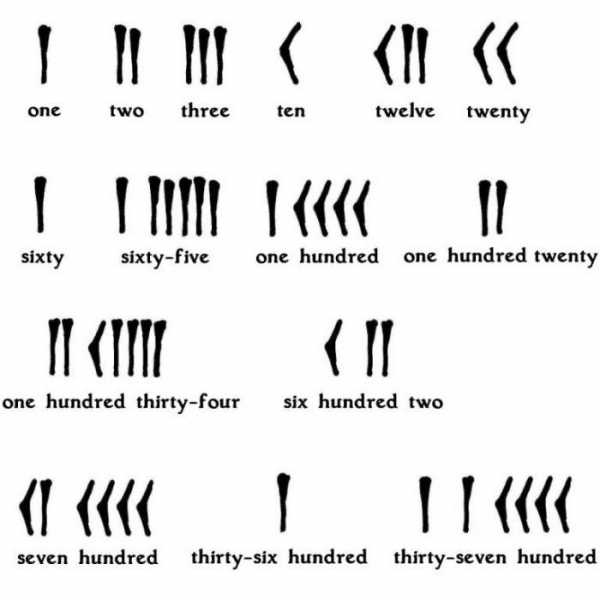
- Вавилонская система счисления, в которой использовалось всего два обозначения для записи – клинья и стрелочки.
- В Египте тоже использовались специальные символы для обозначения чисел. При записи числа каждый символ мог использоваться не более девяти раз.
Позиционные системы
Большое внимание уделяется в информатике позиционным системам счисления. К ним относятся следующие:
- двоичная;
- восьмеричная;
- десятичная;
- шестнадцатеричная;
- шестидесятеричная, используемая при счете времени (к примеру, в минуте – 60 секунд, в часе – 60 минут).
Каждая из них обладает своим алфавитом для записи, правилами перевода и выполнения арифметических операций.
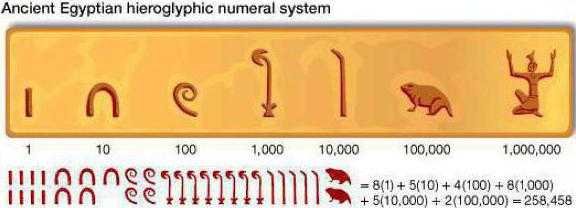
Десятичная система
Данная система является для нас наиболее привычной. В ней используются цифры от 0 до 9 для записи чисел. Они также носят название арабских. В зависимости от положения цифры в числе, она может обозначать разные разряды – единицы, десятки, сотни, тысячи или миллионы. Ее мы пользуемся повсеместно, знаем основные правила, по которым производятся арифметические операции над числами.
Двоичная система
Одна из основных систем счисления в информатике – двоичная. Ее простота позволяет компьютеру производить громоздкие вычисления в несколько раз быстрее, нежели в десятичной системе.
Для записи чисел используется лишь две цифры – 0 и 1. При этом, в зависимости от положения 0 или 1 в числе, его значение будет меняться.
Изначально именно с помощью двоичного кода компьютеры получали всю необходимую информацию. При этом, единица означала наличие сигнала, передаваемого с помощью напряжения, а ноль – его отсутствие.

Восьмеричная система
Еще одна известная компьютерная система счисления, в которой применяются цифры от 0 до 7. Применялась в основном в тех областях знаний, которые связаны с цифровыми устройствами. Но в последнее время она употребляется значительно реже, так как на смену ей пришла шестнадцатеричная система счисления.
Двоично-десятичная система
Представление больших чисел в двоичной системе для человека – процесс довольно сложный. Для его упрощения была разработана двоично-десятичная система счисления. Используется она обычно в электронных часах, калькуляторах. В данной системе из десятичной системы в двоичную преобразуется не все число, а каждая цифра переводится в соответствующий ей набор нулей и единиц в двоичной системе. Аналогично происходит и перевод из двоичной системы в десятичную. Каждая цифра, представленная в виде четырехзначного набора нулей и единиц, переводится в цифру десятичной системы счисления. В принципе, нет ничего сложного.
Для работы с числам в данном случае пригодится таблица систем счисления, в которой будет указано соответствие между цифрами и их двоичным кодом.
Шестнадцатеричная система
В последнее время все большую популярность приобретает в программировании и информатике система счисления шестнадцатеричная. В ней используются не только цифры от 0 до 9, но и ряд латинских букв – A, B, C, D, E, F.

При этом, каждая из букв имеет свое значение, так A=10, B=11, C=12 и так далее. Каждое число представляется в виде набора из четырех знаков: 001F.
Перевод чисел: из десятичной в двоичную
Перевод в системах счисления чисел происходит по определенным правилам. Наиболее часто встречается перевод из двоичной в десятичную систему и наоборот.
Для того, чтобы перевести число из десятичной системы в двоичную, необходимо последовательно делить его на основание системы счисления, то есть, число два. При этом, остаток от каждого деления необходимо фиксировать. Так будет происходить до тех пор, пока остаток от деления не будет меньше или равен единице. Проводить вычисления лучше всего в столбик. Затем полученные остатки от деления записываются в строку в обратном порядке.
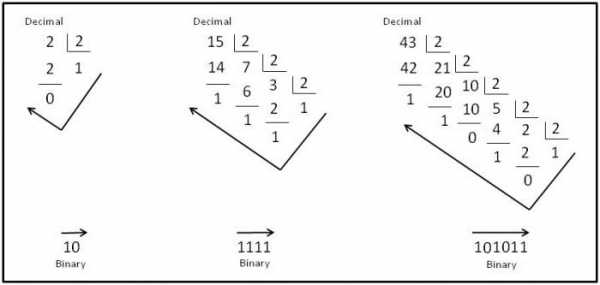
Например, переведем число 9 в двоичную систему:
Делим 9, так как число не делится нацело, то берем число 8, остаток будет 9 – 1 = 1.
После деления 8 на 2 получаем 4. Снова делим его, так как число делится нацело – получаем в остатке 4 – 4 = 0.
Проводим ту же операцию с 2. В остатке получаем 0.
В итоге деления у нас получается 1.
Далее записываем все полученные нами остатки в обратном порядке, начиная с итога деления: 1001.
Вне зависимости от итоговой системы счисления, перевод чисел из десятичной в любую другую будет происходить по принципу деления числа на основу позиционной системы.
Перевод чисел: из двоичной в десятичную
Довольно легко переводить числа и в десятичную систему счисления из двоичной. Для этого достаточно знать правила возведения чисел в степень. В данном случае, в степень двойки.
Алгоритм перевода следующий: каждую цифру из кода двоичного числа необходимо умножить на двойку, причем, первая двойка будет в степени m-1, вторая – m-2 и так далее, где m – количество цифр в коде. Затем сложить результаты сложения, получив целое число.
Для школьников этот алгоритм можно объяснить проще:
Для начала берем и записываем каждую цифру, умноженную на двойку, затем проставляем степень двойки с конца, начиная с нуля. Потом складываем полученное число.
Для примера разберем с вами полученное ранее число 1001, переведя его в десятичную систему, и заодно проверим правильность наших вычислений.
Выглядеть это будет следующим образом:
1*23 + 0*22+0*21+1*20= 8+0+0+1 =9.
При изучении данной темы удобно использовать таблицу со степенями двойки. Это существенно уменьшит количество времени, необходимое для проведения вычислений.
Другие варианты перевода
В некоторых случаях перевод может осуществляться между двоичной и восьмеричной системой счисления, двоичной и шестнадцатеричной. В таком случае можно пользоваться специальными таблицами или же запустить на компьютере приложение калькулятор, выбрав во вкладке вид вариант «Программист».
Арифметические операции
Вне зависимости от того, в каком виде представлено число, с ним можно проводить привычные для нас вычисления. Это может быть деление и умножение, вычитание и сложение в системе счисления, которую вы выбрали. Конечно, для каждой из них действуют свои правила.
Так для двоичной системы разработаны свои таблицы для каждой из операций. Такие же таблицы используются и в других позиционных системах.
Заучивать их необязательно – достаточно просто распечатать и иметь под рукой. Также можно воспользоваться калькулятором на ПК.

Одна из важнейших тем в информатике – система счисления. Знание этой темы, понимание алгоритмов перевода чисел из одной системы в другую – залог того, что вы сможете разобраться в более сложных темах, таких как алгоритмизация и программирование и сможете самостоятельно написать свою первую программу.
fb.ru
| Тамбовский областной медицинский колледж Доклад по информатике «Системы счисления, используемые в компьютере» Работу выполнил: Попова Мария Михайловна Студентка 1 курса Проверил: Учитель информатики Малькова С. И. г. Мичуринск 2018 СОДЕРЖАНИЕ 1.ВВЕДЕНИЕ 2. Сущность различных систем счисления 3. Перевод чисел из одной системы счисления в другую 4.ЗАКЛЮЧЕНИЕ 5.ЛИТЕРАТУРА ВВЕДЕНИЕ В повседневной жизни мы, как правило, пользуемся десятичной системой счисления. Но это лишь одна из многих систем, которая получила свое распространение, вероятно, по той причине, что у человека на руках 10 пальцев. Однако эта В разные исторические периоды развития человечества для подсчетов и вычислений использовались те или иные системы счисления. Например, довольно широко была распространена двенадцатеричная система. Многие предметы (ножи, вилки, тарелки, носовые платки и т. д.) и сейчас считают дюжинами. Число месяцев в году двенадцать. Двенадцатеричная система счисления сохранилась в английской системе мер (например, 1 фут = 12 дюймам) и в денежной системе (1 шиллинг = 12 пенсам). В древнем Вавилоне существовала весьма сложная шестидесятеричная система. Она, как и двенадцатеричная система, в какой-то степени сохранилась и до наших дней (например, в системе измерения времени: 1 час = 60 минутам, 1 минута = 60 секундам, аналогично в системе измерения углов: 1 градус = 60 минутам, 1 минута = 60 секундам). У некоторых африканских племен была распространена пятеричная система счисления, у ацтеков и народов майя, населявших в течение многих столетий обширные области американского континента, – двадцатеричная система. У некоторых племен Австралии и Полинезии встречалась двоичная система. В данной работе будут рассмотрены различные системы счисления. СУЩНОСТЬ РАЗЛИЧНЫХ СИСТЕМ СЧИСЛЕНИЯ Вначале проанализируем различия между цифрами и числами: число – это абстрагированная от конкретики запись количества (например, число 25 – это двадцать пять предметов чего угодно и не только предметов, а, скажем, лет или килограммов), а цифра – это специальный знак для обозначения количества единиц. Следует обратить внимание, что цифры – это тоже записи чисел, например 8 – это не только цифра, но и число. Слово «цифра» происходит от позднелатинского слова «cifra», первые цифры появились у египтян и вавилонян, причем интересно, что цифры, как специальные знаки, образовались позже, чем буквы. Так, многие народы (греки, финикияне, Поделитесь с Вашими друзьями: |
coolnew.ru
МБОУ Ангеловская СОШРефератВведениеСовременный человек в повседневной жизни постоянно сталкивается с числами и цифрами – они с нами везде. Различные системы счисления используются всегда, когда появляется потребность в числовых расчётах, начиная с вычислений учениками младших классов, выполняемых карандашом на бумаге, заканчивая вычислениями, выполняемыми на суперкомпьютерах. Цель создания системы счисления- выработка наиболее удобного способа записи количественной информации. Хs=An · Sn-1 + An-1 · Sn-2 + An-2 · Sn-3 +…+ A2 · S1 + A1 · S0Так, например число 629310запишется в форме многочлена следующим образом:Примеры позиционных систем счисления:История двоичной системы счисленияДвоичная система счисления была придумана математиками и философами ещё до появления компьютеров (XVII — XIX вв.).В 1936 — 1938 годах американский инженер и математик Клод Шеннон нашёл замечательные применения двоичной системы при конструировании электронных схем. Неудобством этой системы счисления является необходимость перевода исходных данных из десятичной системы в двоичную при вводе их в машину и обратного перевода из двоичной в десятичную при выводе результатов вычислений.Сложение, вычитание, умножение и деление в двоичной системе счисленияДвоичное кодирование в компьютереВ конце ХХ века, века компьютеризации, человечество пользуется двоичной системой ежедневно, так как вся информация, обраба- тываемая современными ЭВМ, хранится в них в двоичном виде.Перевод чисел из одной системы счисления в другуюЗаключение
Перевод двоичного числа в десятичноеХ10= Аn·2n-1 + Аn-1·2n-2 + Аn-2·2n-3 +…+А2·21 + А1·20 Х10= Аn·8n-1 + Аn-1·8n-2 + Аn-2·8n-3 +…+А2·81 + А1·80 Х10= Аn·16n-1 + Аn-1·16n-2 + Аn-2·16n-3 +…+А2·161 + А1·160 Пример: Число 2210 перевести в двоичную систему счисления: 2210=101102 Пример: Число 57110 перевести в восьмеричную систему счисления: 57110=10738
Перевод десятичного числа в шестнадцатеричную системуДля перевода десятичного числа в шестнадцатеричную систему его необходимо последовательно делить на 16 до тех пор, пока не останется остаток, меньший или равный 15. Число в шестнадцатеричной системе записывается как последовательность цифр последнего результата деления и остатков от деления в обратном порядке.
Пример: Число 10010112 перевести в восьмеричную систему счисления:Перевод из двоичной системы в шестнадцатеричнуюЧтобы перевести число из двоичной системы в шестнадцатеричную, его нужно разбить на тетрады (четверки цифр).Пример: Число 10111000112 перевести в шестнадцатеричную систему счисления:Перевод восьмеричного числа в двоичноеДля перевода восьмеричного числа в двоичное необходимо каждую цифру заменить эквивалентной ей двоичной триадой.
5318=101 011 0012
Пример: Число ЕЕ816 перевести в двоичную систему счисления:Перевод из восьмеричной системы счисления в шестнадцатеричную и обратноПри переходе из восьмеричной системы счисления в шестнадцатеричную и обратно, необходим промежуточный перевод чисел в двоичную систему.FEA16=1111111010102=111 111 101 0102=7752866358=1101100111012=1101 1001 11012=D9D16 Археологами найдены такие «записи» при раскопках культурных слоев, относящихся к периоду палеолита (10–11 тысяч лет до н.э.).Древнегреческая нумерацияСлавянская нумерацияВ России славянская нумерация сохранилась до конца XVII века. Южные и восточные славянские народы для записи чисел пользовались алфавитной нумерацией. Славянская нумерация сохранялась только в богослужебных книгах. Над буквой, обозначавшей цифру, ставился специальный значок: («титло»). Для обозначения тысяч перед числом (слева внизу) ставился особый знак . Обозначение чисел в ионийской системе нумерацииОбозначение чисел в древнеславянской системе нумерации |
Единичная система
Древнегреческая нумерация
Славянская нумерация
Римская нумерация
dok.opredelim.com
Доклад – Позиционные системы счисления
РАБОТА ПО
ИНФОРМАТИКЕ
ТЕМА «Позиционные системы счисления»
Ученицы
11 класса «А»
Калашниковой Анны
МОСКВА 2004 год
План
1) Арифметические основы построения ЭВМ
2) Непозиционные и позиционные системы счисления
3) Непозиционные системы счисления
4) Позиционные системы счисления
5) Системы счисления
6) Десятичная система счисления
7) Двоичная система счисления
8) Восьмеричная система счисления
9) Шестнадцатиричная система счисления
10) Перевод из одной системы счисления в другую
11) Перевод целых чисел
12) Перевод правильных дробей
13) Правила перевода из системы счисления в систему счисления
14) Представление чисел в различных системах счисления
15) Вопросы и задачи. Ответы и решения.
16) Средства процессора Word, используемые в данной работе.
17) Список литературы.
Арифметические основы построения ЭВМ
Непозиционные и позиционные системы счисления
Системой счисления называется совокупность правил для обозначения (записи) действительных чисел с помощью цифровых знаков. Для записи чисел в конкретных системах счисления используется некоторый конечный алфавит, состоящий из цифр а1, а2, а3,…., аn. При этом каждой цифре аi в записи числа ставится в соответствие определенный количественный эквивалент. Различают непозиционные и позиционные системы счисления.
Непозиционные системы счисления
В ней количественный эквивалент каждой цифры, входящей в запись данного числа, не зависит от места (позиции) этой цифры в ряду других цифр. Пример: римская система счисления. В ней для записи различных целых чисел используются символы I, V, X, L, C, D, M и т.д., обозначающие соответственно 1, 5, 10, 50, 100, 500, 1000 и т.д. Например, запись MCMLXXXV означает число 1985. Общим недостатком непозиционных систем является сложность представления в них достаточно больших чисел, так как при этом получается чрезвычайно громоздкая запись чисел или требуется очень большой алфавит используемых цифр. В ЭВМ применяют только позиционные системы счисления, в которых количественный эквивалент каждой цифры алфавита зависит не только от вида этой цифры, но и от ее местоположения в записи числа.
Позиционные системы счисления
В позиционных системах счисления вес каждой цифры изменяется в зависимости от ее позиции в последовательности цифр, изображающих число. Любая позиционная система характеризуется своим основанием. Основание позиционной системы счисления — это количество различных знаков или символов, используемых для изображения цифр в данной системе. За основание можно принять любое натуральное число — два, три, четыре, шестнадцать и т.д. Следовательно, возможно бесконечное множество позиционных систем.
Системы счисления
Десятичная система счисления.
Пришла в Европу из Индии, где она появилась не позднее VI века н.э. В этой системе 10 цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, но информацию несет не только цифра, но и место, на котором цифра стоит (то есть ее позиция). В десятичной системе счисления особую роль играют число 10 и его степени: 10, 100, 1000 и т.д. Самая правая цифра числа показывает число единиц, вторая справа — число десятков, следующая — число сотен и т.д. Позиции цифр в записи числа называют его разрядами. В десятичной системе счисления вес каждого разряда в 10 раз больше веса предыдущего. Всякое число в десятичной системе счисления можно представить в виде суммы различных целых степеней десяти с соответствующими коэффициентами аi (0-9), взятыми из алфавита данной системы счисления. Например: 245,83 = 2 * 102 + 4 * 101 + 5 * 100 + 8 * 10-1 + 3 * 10-2. Любое десятичное позиционное число N можно представить с помощью целых степеней десяти, взятых с соответствующими коэффициентами, т.е.
N10 = am * 10m + am-1 * 10m-1 + …+ a1*10+ +a0 * 100 + a-1 * 10-1 +…+ a-n * 10-n.
Двоичная система счисления.
В этой системе всего две цифры — 0 и 1. Особую роль здесь играет число 2 и его степени: 2, 4, 8 и т.д. Самая правая цифра числа показывает число единиц, следующая цифра — число двоек, следующая — число четверок и т.д. Двоичная система счисления позволяет закодировать любое натуральное число — представить его в виде последовательности нулей и единиц. В двоичном виде можно представлять не только числа, но и любую другую информацию: тексты, картинки, фильмы и аудиозаписи. Инженеров двоичное кодирование привлекает тем, что легко реализуется технически. Наиболее простыми с точки зрения технической реализации являются двухпозиционные элементы, например, электромагнитное реле, транзисторный ключ.
Восьмеричная система счисления.
В этой системе счисления 8 цифр: 0, 1, 2, 3, 4, 5, 6, 7. Цифра 1, указанная в самом младшем разряде, означает — как и в десятичном числе — просто единицу. Та же цифра 1 в следующем разряде означает 8, в следующем 64 и т.д. Число 100 (восьмеричное) есть не что иное, как 64 (десятичное). Чтобы перевести в двоичную систему, например, число 611 (восьмеричное), надо заменить каждую цифру эквивалентной ей двоичной триадой (тройкой цифр). Легко догадаться, что для перевода многозначного двоичного числа в восьмиричную систему нужно разбить его на триады справа налево и заменить каждую триаду соответствующей восьмеричной цифрой.
Шестнадцатиричная система счисления.
Запись числа в восьмеричной системе счисления достаточно компактна, но еще компактнее она получается в шестнадцатеричной системе. В качестве первых 10 из 16 шестнадцатеричных цифр взяты привычные цифры 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, а вот в качестве остальных 6 цифр используют первые буквы латинского алфавита: A, B, C, D, E, F. Цифра 1, записанная в самом младшем разряде, означат просто единицу. Та же цифра 1 в следующем — 16 (десятичное), в следующем — 256 (десятичное) и т.д. Цифра F, указанная в самом младшем разряде, означает 15 (десятичное). Перевод из шестнадцатеричной системы в двоичную и обратно производится аналогично тому, как это делается для восьмеричной системы.
Перевод из одной системы счисления в другую
Перевод целых чисел
Для перевода целых чисел из одной системы счисления с основанием S в другую с основанием S1 надо это число последовательно делить на основание S1 новой системы счисления до тех пор, пока не получится частное меньше S1. Число в новой системе запишется в виде остатков деления, начиная с последнего. Это последнее частое дает цифру старшего разряда в новой системе счисления. Деление выполняют в исходной системе счисления. Например:
37710=1011110012
Перевод правильных дробей
Для перевода правильной дроби из одной системы счисления в другую необходимо эту дробь последовательно умножать на основание той системы, в которую она переводится, перемножаются только дробные части. Дробь в новой системе записывается в виде целых частей получающихся произведений, начиная с первого. Например:
0,6875 0,67510=0,100112
* 2
1,3750
* 2
0,7500
* 2
1,5000
* 2
1,0000
При переводе неправильных десятичных дробей необходимо пользуясь рассмотренными правилами выполнить отдельно перевод целой и дробной частей.
Правила перевода из системы счисления в систему счисления
1) Для перевода чисел из любой системы счисления в десятичную необходимо:
А) Старшую цифру исходного числа умножить на основание старой системы счисления и прибавить следующую цифру исходного числа
Б)Результат опять умножить на основание старой системы счисления и прибавить следующую цифру исходного числа
В) Процесс перевода заканчивается после прибавления последней самой младшей цифры исходного числа
2) Для перевода чисел из десятичной системы счисления в любую необходимо делить исходное число на основание новой системы счисления до тех пор пока последнее частное не станет меньше основания новой системы счисления. Результат складывается из остатков деления, начиная с последнего.
3) Для перевода чисел из любой системы счисления в любую необходимо исходное число перевести в десятичную систему по первому правилу (умножением), полученное десятичное число перевести в искомую систему по второму правилу (деление).
4) Для перевода чисел из систем счисления, которые являются степенью двойки необходимо:
А) из 16-ричной в 2-ичную: для перевода 16-ричного числа в двоичную систему необходимо каждую цифру 16-ричного числа заменить 4-х разрядным двоичным значением.
Б) из 8-ричной в 2-ичную: Каждую цифру 8-ричного числа необходимо заменить 3-х разрядным двоичным значением.
Представление чисел в различных системах счисления | |||
Системы счислений | |||
Десятичная | Двоичная | Восьмеричная | Шестнадцатиричная |
1 | 1 | 1 | 1 |
2 | 10 | 2 | 2 |
3 | 11 | 3 | 3 |
4 | 100 | 4 | 4 |
5 | 101 | 5 | 5 |
6 | 110 | 6 | 6 |
7 | 111 | 7 | 7 |
8 | 1000 | 10 | 8 |
9 | 1001 | 11 | 9 |
10 | 1010 | 12 | А |
11 | 1011 | 13 | В |
12 | 1100 | 14 | С |
13 | 1101 | 15 | D |
14 | 1110 | 16 | E |
15 | 1111 | 17 | F |
Вопросы и задачи. Ответы и решения
1) Дать определение системы счисления. Назвать и охарактеризовать свойства системы счисления.
2) Какие символы используются для записи чисел в двоичной системе счисления, восьмеричной, шестнадцатеричной?
3) Зашифруйте следующие десятичные числа, преобразовав их в двоичные (восьмеричные, шестнадцатеричные): 0, 1, 18, 25, 128.
4) Дешифруйте следующие двоичные числа, преобразовав их в десятичные: 0010, 1011, 11101, 0111, 0101.
5) Дешифруйте следующие восьмеричные числа, преобразовав их в десятичные: 777, 375, 111, 1015.
6) Дешифруйте следующие шестнадцатеричные числа, преобразовав их в десятичные: 15, A6, 1F5, 63.
7) 2. Перевести данное число в десятичную систему счисления: 0000012; 1000011111,01012; 1216,048; 29A,516
8) Перевести данное число из десятичной системы счисления в двоичную: а) 46410; б) 380,187510; в) 115,9410
· 10000012 =1× 26 +0× 25 +0× 24 +0× 23 +0× 22 + 0× 21 +1× 20= 64+1=6510.
· 1000011111,01012 =1×29 + 1×24 + 1×23 + 1×22 + 1×21 + 1×20+ 1×2-2 + 1×2-4 = 512 + 16 + 8 + 4 + 2 + 1 + 0,25 + 0,0625 = 543,312510 .
· 1216,048 =1×83 +2×82 +1×81 +6×80+4× 8-2 = 512+128+8+6+0,0625 = 654,062510 .
· 29A,516 = 2×162 +9×161 +10×160+5×16-1 = 512+144+10+0,3125 = 656,312510 .
· а) 46410 » 1110100002; б) 380,187510 » 101111100,00112; в) 115,9410 » 1110011,11110(2)
Средства процессора Word, используемые в данной работе.
· Главным средством процессора Word, использованный в этой работе, является форматирование текста. Основной текст расположен «по ширине», заголовки – выравнивание «по центру», остальные части текста – «по левому краю» или «по правому краю».
· В данной работе было применено форматирование абзацев, изменение шрифтов и стилей, использование списков и использование границ.
· Также в тексте присутствует таблица, созданная в программе Excel, а затем копированная в данный текст. Этот способ более удобен, чем создание таблиц непосредственно в Word’е.
· В данный реферат включен рисунок. Он был нарисован в самом простом редакторе Paint. После этого вставлен в текст.
· В эту работу были вставлены некоторые символы.
Список литературы
· Л.З.Шауцукова, «Основы информатики в вопросах и ответах», Издательский центр «Эль-Фа», Нальчик, 1994
· Введение в информатику. Лабораторные работы. / Авт.-сост. А.П. Шестаков; Перм. ун-т. — Пермь, 1999
· Теоретический материал из лекций по информатике в МГАПИ.
www.ronl.ru



