08.03.202030.12.2018

Сложные пределы – Сложные пределы и методы их решения

• by alexxlab
• Комментариев к записи Сложные пределы – Сложные пределы и методы их решения нет
• Советы абитуриенту

Сложные пределы и методы их решения

В этой статье собраны наиболее интересные и сложные случаи пределов, решение которых требует определенных навыков и знаний. В большинстве случаев, пределы, изучаемые в
базовом курсе высшей математики, просты и решаются в одно-два действия. Однако иногда приходится сталкиваться со сложными примерами пределов, которые чтобы решить
нужно знать хитростные способы. Рассмотрим же их!

Пример 1. Решить предел

Чтобы решить данный предел, необходимы знания по теме первый замечательный предел и эквивалентные бесконечно малые функции. Ну а в начале долгого пути, нам предстоит сделать преобразования в числителе, используя свойства тригонометрических функций, и в знаменателе, используя обманный ход, но обо всем по порядку. Начнем с числителя, представим

в равнозначной записи и запишем числитель уже в новой форме:

Тот факт, что x стремится к нулю, позволяет нам считать что в будущем можно будет использовать свойства эквивалентных бесконечно малых. Поэтому, обращаем внимание на

логарифм, стоящий в знаменателе. Если его немного «отредактировать» и привести к нужному виду, то его смело можно будет использовать для получения эквивалентных
значений. Обращаемся к таблице эквивалентных бесконечно малых величин и видим, что для счастья нам не хватает единицы. Вот здесь-то мы и используем способ (как я его
называю) «искусственного добавления» числа:

Все довольно просто, мы не нарушая баланса выражения, добавили и убавили единицу к косинусу. С учетом всех знаков , преобразуем выражение:

В результате наших действий, мы получили идеальных кандидатов на эквивалентные замены. В числителе вынесли знак минус за скобки, получив тем самым

в знаменателе подготовили выражение с логарифмом. С ними все понятно, что же делать в синусом? Все просто, используем первый замечательный предел и получаем законную
единицу. Вычисляем:

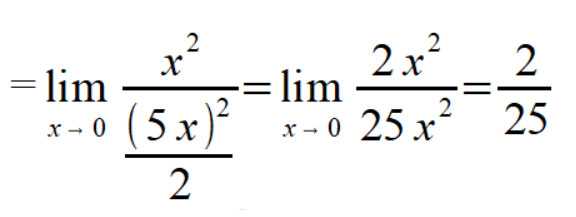
Краткие пояснения к тому, какие эквивалентные замены были произведены, а также как был использован первый предел:

— первый предел, при

Отдельной строкой хотелось бы остановиться на третьей формуле. Как известно, эквивалентная малая для логарифма выглядит следующим образом:

ln(1+x) ~x

В нашем случае, в роли х выступала вся скобка (-(1-cos(5x))).

Далее, мы повторно используем правило, но только уже для случая с косинусом:

при

В нашем случае, cos(x) — это cos(5x) и соответствующая замена была такой:

при

Ну вот и все. Предел был непростым, но интересным, и его решение, надеюсь, было вам понятным.

matematyka.ru

11. Предел сложной функции.

Th. Пусть ф-цияfзадана на множествеX, функцияg-на множествеYиf(X)Y. Если сущ-ет конечные или бесконечные пределы.

,

то при x→x₀ сущ-т предел (кон-й или беск-й) сложный функцииg[f(x)], причем

Пусть x_n→x_0, x_nX,n=1,2,…; тогда в силу (1) имеемy_n=f(x_n)→y_0, y_nY,n=1,2,…

Поэтому в силу (2) g(y_n)→z₀, ноy_n=f(x_n) =>g[f(x_n)]→z₀,n=1,2,.., т.е. имеет место рав-во (3).

Зам1. Если ф-ция gнепр-на в точкеy₀, т.е.,

то формулу (3) можно записать виде

Иначе говоря, предельный переход перестановочен с операцией взятия непр-ой ф-ции. В самом деле согласно Th..

Отсюда => в частности что непре-ая ф-ция от непр-й ф-ции непр-на, точнее:

След. Если ф-ция fнепр-на в точкеx₀, а ф-цияgнепр-на в точкеy₀=f(x₀), то и их композицияg°fнепрерывна в точкеx₀.

Действительно, непрерывность ф-ции fв точкеx₀ означает, что

Поэтому в силу непр-ти ф-ции gв точкеy₀ из формулы (5) получим

,

т.е. ф-ция g°fнепр-на в точкеx_0.

Зам2. Обычно, когда говорят, что некоторая ф-ция в данной точке имеет предел, что имеют в виду, что этот предел конечный, а случай бесконечного предела оговаривают особо.

12. Первый замечательный предел.

sin0=0

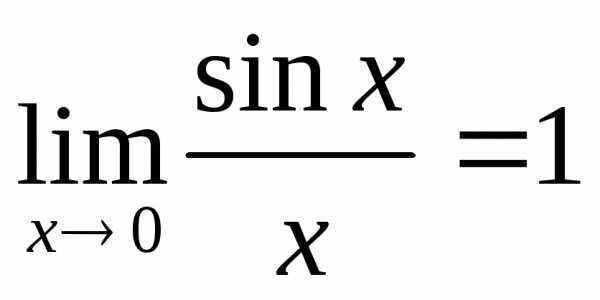
sinx~xв т.0!

Д-во:

I. 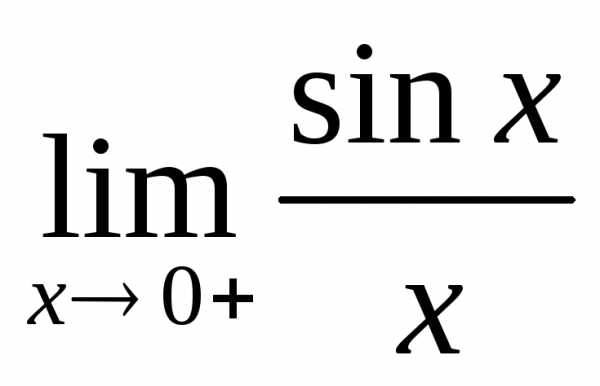x(0,)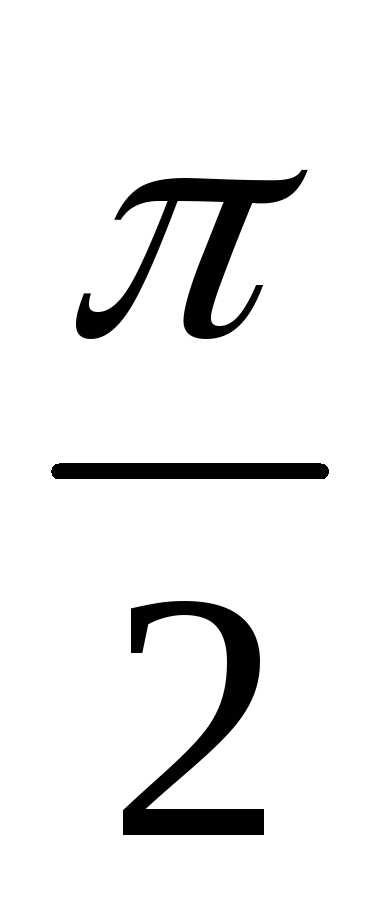

tgx=cd

S∆oda<S_{секторa}oda<S∆odc

S=

sinx<x<tgx

ab<ad<cd

sinx<x<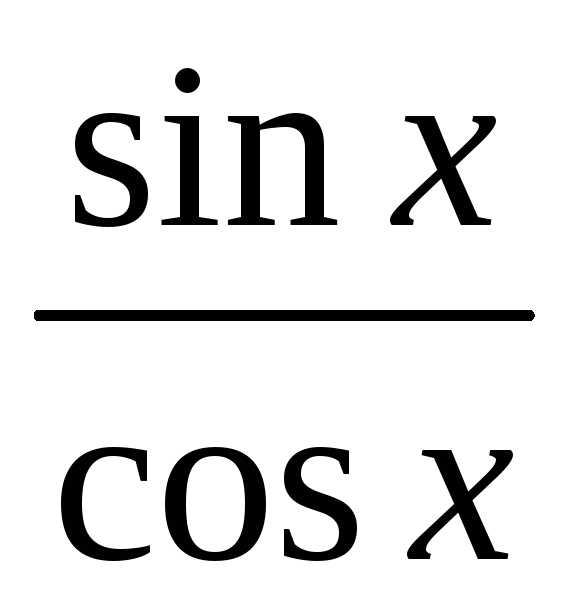

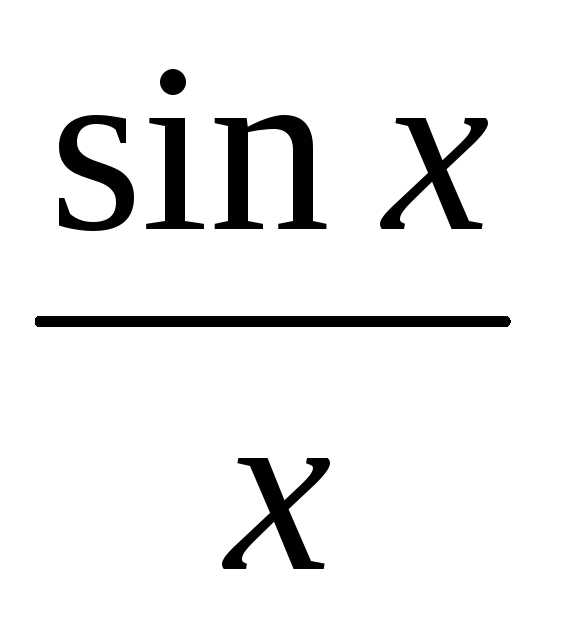<1<

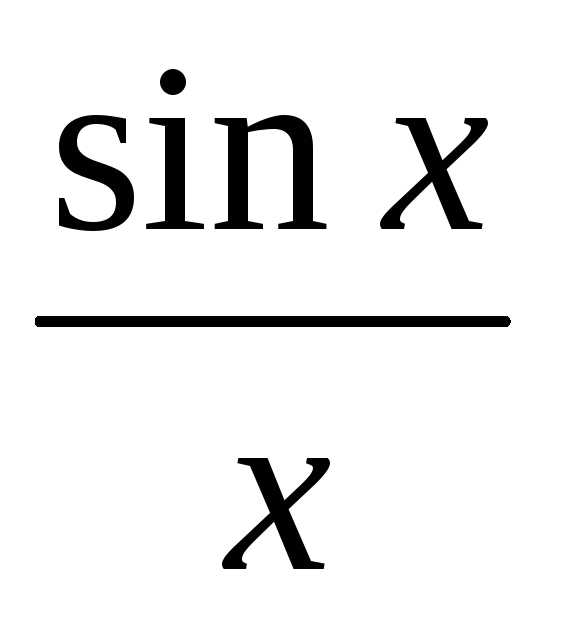cosx<<1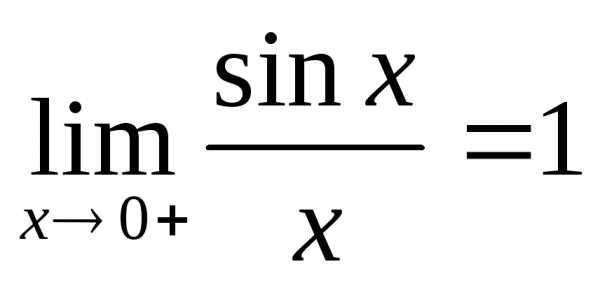

lim cosx=1

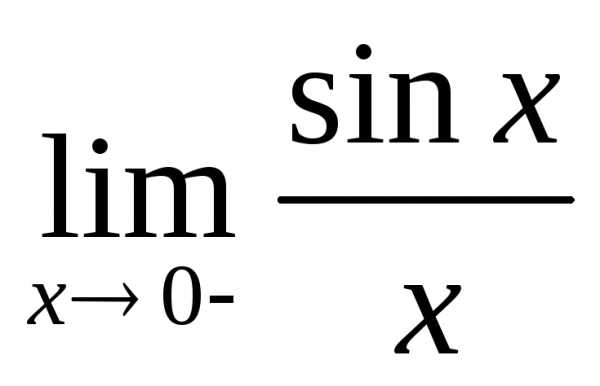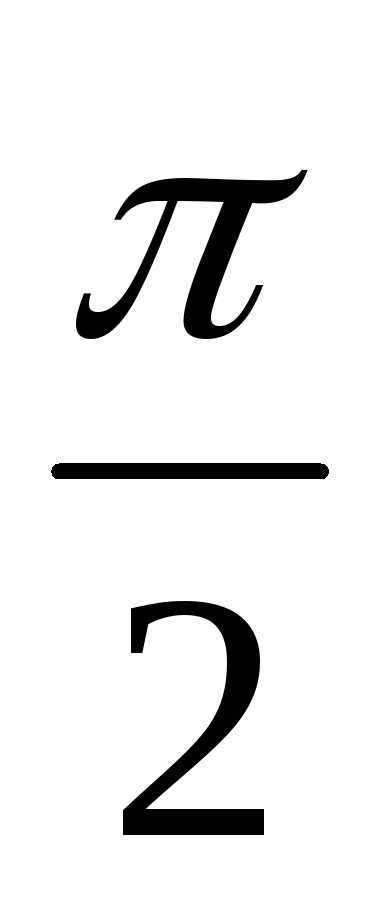II. x(-,0)

x=-t t(0,)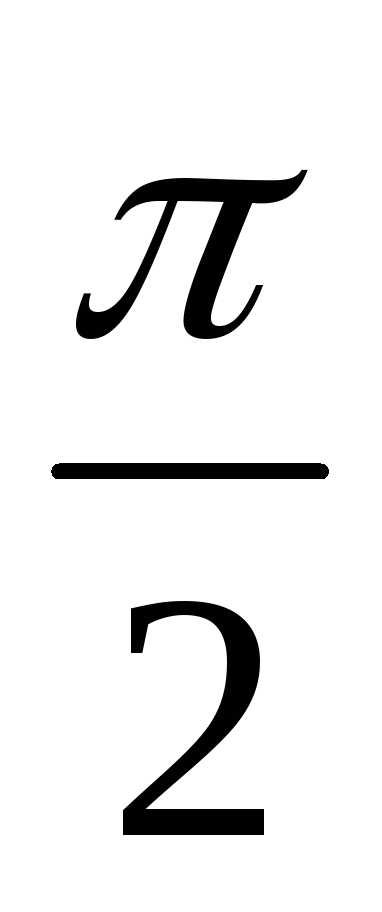

==

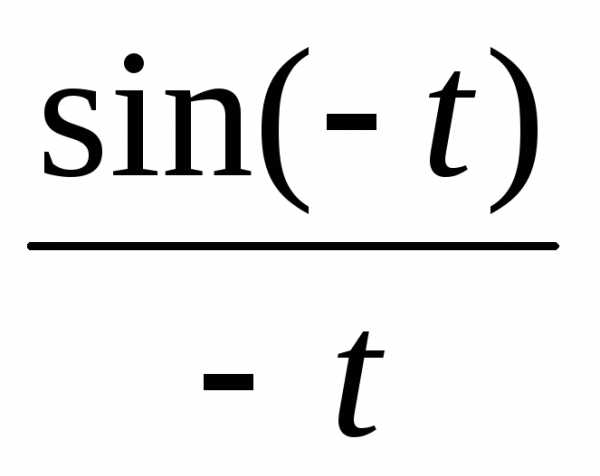13. Второй замечательный предел.

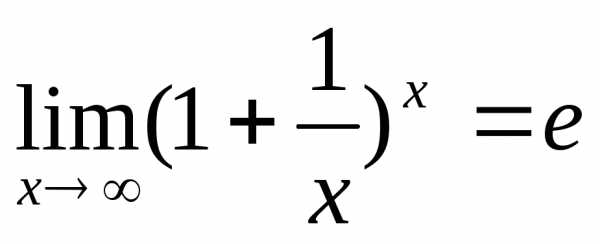
x_n→∞

1) x_n-натуральные значения

1,2,1,3,2,4,3

Для N:n>N|

|<

x_n-б.б. тоKn>Kx_n>N

>0 Kn>K||<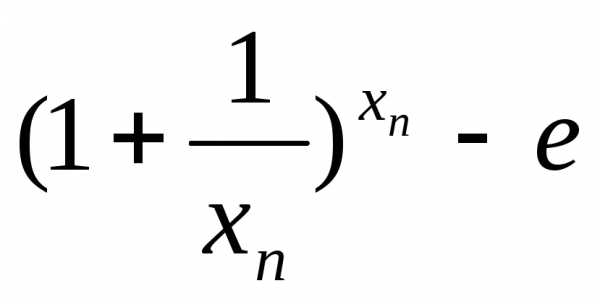

2) x_n>0 начин. с некот.n

[x_n]-целая часть

[x_n]≥x_n-1=> [x_n]-б.б. посл.

≤≤

∙

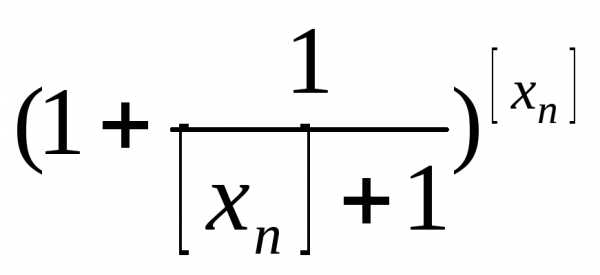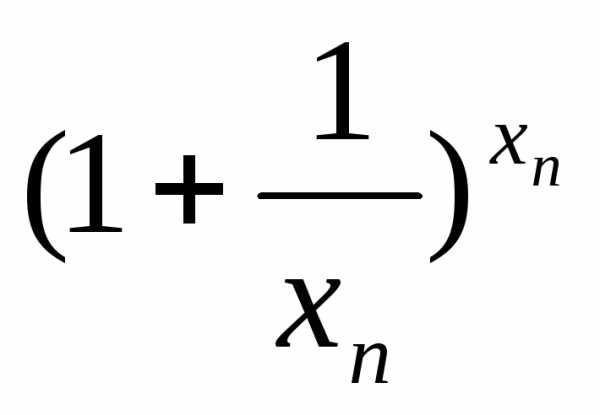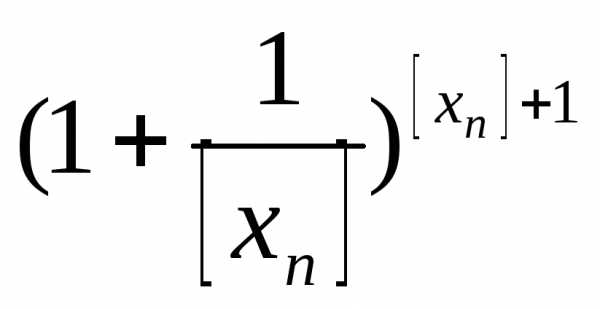
3) x_n<0 начин. с некот.n

x_n=-1-z_nz_n=-1-x_n

4) общая послед-ть x_n-произв-е

x_n+-положительныеx_n—-отрицательные

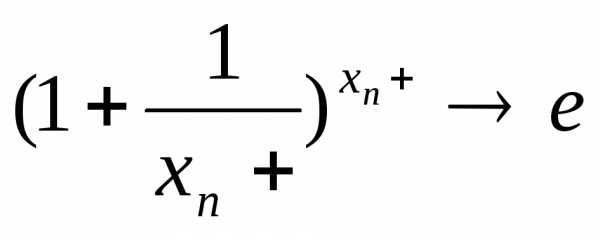
14. Сравнение бесконечно малых и бесконечно больших функций. Теоремы об эквивалентных бесконечно малых и бесконечно больших.

Две б.м. функций сравниваются между собой с помощью их отношения(сумма, разность и произведение).

Рассмотрим правило сравнения б.м. функций:

Пусть при хх₀функции(х) и(х) являются б.м., т.е.Lim(х){при хх₀}=0 иLim(х){при хх₀}=0, тогда Правила:

1)Если Lim(х)/(х){при хх₀}=0, то(х) – б.м. более высокого порядка, чем(х).

2)Если Lim(x)/(х){при хх₀}=А0, то(х) и(х) – б.м. одного порядка.

3)Если Lim(х)/(х){при хх₀}=1, то(х) и(х) – эквивалентные б.м.. Иногда нужно оценивать как высок порядок б.м. более высокого порядка, поэтому

4)Если Lim(х)/bⁿ(х){при хх₀}=А0, то(х) – б.м.n-го порядка относительно(х)

Замечания: Для сравнения б.м. функций, при х∞, х+\-∞, хх

0+\-. Существует аналогичное правило.

1) Если α(x)=(β(x)) в т.а

то α(x)+β(x)~ β(x) в т.а

=> они эквивалентны

2) α(x),β(x) б.м. в а

α(x)∙β(x)= (α(x))

3) α(x)~α₁(x)

β(x)~β₁(x) в т. а

M(x), N(x) б.б. в а

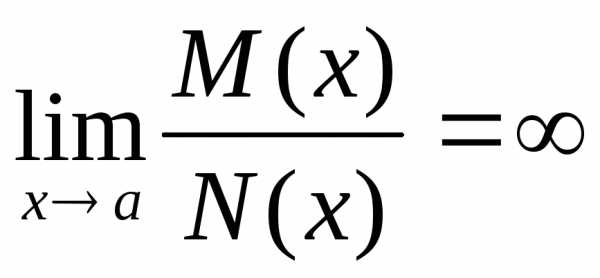
Для раскрытия неопределённостей вида [0/0] часто бывает полезным применить принцип замены б. м. эквивалентными.

1.sinx~xпри х->0

2.tgx~x

arcsin x ~ x

arctg x ~x

(1- cos x)~ x

e^x-1 ~x

a^x-1 ~xlna

ln(1+x)~x

log_а(1+x)~ xlog_аe

(1+x)к -1~kx,k>0

studfiles.net

Предел и непрерывность сложной функции

Теорема о непрерывности сложной функции
Пусть функция g(t)  непрерывна в точке t₀. И пусть функция f(x)  непрерывна в точке x₀ = g(t₀).
Тогда сложная функция  f(g(t)) непрерывна в точке t₀.
Доказательство ⇓

Теорема о пределе непрерывной функции от функции
Пусть существует предел функции g(t) при t → t₀, и он равен x₀:
.
Здесь точка t₀ может быть конечной или бесконечно удаленной: .
И пусть функция f(x)  непрерывна в точке x₀.
Тогда существует предел сложной функции f(g(t)), и он равен f(x₀):
.
Доказательство ⇓

Эта теорема означает, что знак предела можно применять к аргументу непрерывной функции:
.

По сравнению с предыдущей теоремой, здесь на функцию g(t) наложено менее жесткое условие. А именно: функция g(t) может быть не определена в точке t₀, или ее значение в этой точке может отличаться от x₀. Также точка t₀ может быть бесконечно удаленной.

Теорема о пределе сложной функции
Пусть функция имеет предел и отображает проколотую окрестность точки на проколотую окрестность точки . Пусть функция определена на этой окрестности и имеет на ней предел .
Здесь – конечные или бесконечно удаленные точки: . Окрестности и соответствующие им пределы могут быть как двусторонние, так и односторонние.
Тогда существует предел сложной функции и он равен :
.
Доказательство ⇓

Если функция определена в точке и имеет значение , то эта функция является непрерывной в этой точке и, для вычисления предела, нужно воспользоваться предыдущей теоремой. Теорема о пределе сложной функции применяется в том случае, когда функция не определена в точке или имеет значение, отличное от предельного . Поэтому, для применения этой теоремы, должна существовать проколотая окрестность точки , чтобы множество значений функции на этой окрестности не содержало точку :
.

Пример

Найти односторонние пределы сложной функции в точке :
  и  .

Решение

Функцию можно рассматривать как композицию двух элементарных функций:
,
где .

Рассмотрим функцию . Она определена для всех значений переменной , за исключением точки и имеет в этой точке односторонние пределы:
.

Возьмем произвольную левую проколотую окрестность точки :
, где .
Функция отображает эту окрестность в левую окрестность бесконечно удаленной точки , которая, разумеется, является проколотой.

Таким образом, чтобы найти левый предел сложной функции в точке , надо найти левый предел функции в бесконечно удаленной точке. Этот предел хорошо известен и равен нулю:
.
Тогда
.
Схематично процесс решения можно записать так:
При .
При .

Аналогично для предела справа:
При .
При .

Ответ

;
.

Доказательства теорем

Доказательство теоремы о непрерывности сложной функции

Формулировка ⇑

1. Покажем сначала, что существует такая окрестность точки , на которой определена сложная функция .

Воспользуемся определением непрерывности функции в точке по Коши. Поскольку функция непрерывна в точке , то она определена на некоторой окрестности этой точки, и имеется такая функция , так что для любого ,
(1.1)     при  .
Здесь конечно подразумевается, что функция выбрана так, что окрестность лежит в окрестности , на которой определена функция .

Поскольку функция непрерывна в точке , то она определена на некоторой окрестности этой точки, и имеется такая функция , так что для любого ,
(1.2)     при  .
Здесь также подразумевается, что окрестность лежит в окрестности , на которой определена функция .

Таким образом, при некотором фиксированном положительном значении , функция определена, по крайней мере на окрестности точки , и ее множество значений лежит в окрестности , на которой определена функция . Поэтому существует такая окрестность точки :
,
на которой определена сложная функция .

2. Теперь покажем, что
.

Перепишем неравенства (1.1) и (1.2), справедливые для любых и :
(1.1)     при  .
(1.2)     при  .

Возьмем произвольное положительное число . Тогда на основании (1.1) имеем:
  при  .
Поскольку и , то из (1.2) следует, что
  при  .
Тогда
  при  .

Тем самым мы нашли такую функцию , при которой, для любого ,
  при  .
Это означает, что
.

Теорема доказана.

Доказательство теоремы о пределе непрерывной функции от функции

Формулировка ⇑

1. Покажем сначала, что существует такая проколотая окрестность точки , на которой определена сложная функция .

Воспользуемся определением непрерывности функции в точке по Коши. Поскольку функция непрерывна в точке , то она определена на некоторой окрестности этой точки, и имеется такая функция , так что для любого ,
(2.1)     при  .
Здесь конечно подразумевается, что окрестность лежит в окрестности , на которой определена функция .

Воспользуемся определением предела функции в точке по Коши. Поскольку функция имеет предел в точке , то она определена на некоторой проколотой окрестности этой точки, и для любого , существует положительное число , зависящее от , так что
(2.2)     при  .
Здесь означает проколотую δ – окрестность точки . Подразумевается, что эта окрестность лежит в окрестности , на которой определена функция .

Таким образом, при некотором фиксированном положительном значении , функция определена, по крайней мере на проколотой окрестности точки , и ее множество значений лежит в окрестности , на которой определена функция . Тем самым мы нашли такую окрестность точки :
,
на которой определена сложная функция .

2. Теперь покажем, что
.

Перепишем неравенства (2.1) и (2.2), справедливые для любых и :
(2.1)     при  .
(2.2)     при  .

Возьмем произвольное положительное число . Тогда на основании (2.1) имеем:
  при  .
Поскольку , то из (2.2) следует, что
  при  .
Тогда
  при  .

Тем самым мы нашли такую функцию , при которой, для любого ,
  при  .
Это означает, что
.

Теорема доказана.

Доказательство теоремы о пределе сложной функции

Формулировка ⇑

1. Покажем сначала, что существует такая проколотая окрестность точки , на которой определена сложная функция .

Воспользуемся определением предела функции в точке по Коши. Поскольку функция имеет предел в точке , то она определена на некоторой проколотой окрестности этой точки. И для любого , существует положительное число , зависящее от , так что для всех , принадлежащих проколотой σ – окрестности точки ,
(3.1)     при  .
Здесь конечно подразумевается, что зависимость выбрана таким способом, что окрестность лежит в окрестности , на которой определена функция .

Аналогичным образом, поскольку функция имеет предел в точке , то она определена на некоторой проколотой окрестности этой точки, и для любого , существует положительное число , зависящее от , так что для всех , принадлежащих проколотой δ – окрестности точки :
,
значения функции принадлежат σ – окрестности точки :
.
По условию теоремы, . Тогда значения функции принадлежат проколотой σ – окрестности точки :
(3.2)     при  .
Подразумевается, что окрестность лежит в окрестности , на которой определена функция .

Таким образом, при некотором фиксированном положительном значении , функция определена, по крайней мере на проколотой окрестности точки , и ее множество значений лежит в проколотой окрестности , на которой определена функция . Тем самым мы нашли окрестность точки :
,
на которой определена сложная функция .

2. Теперь покажем, что
.

Перепишем неравенства (3.1) и (3.2), справедливые для любых и :
(3.1)     при  ;
(3.2)     при  .

Возьмем произвольное положительное число . Тогда на основании (3.1) имеем:
  при  .
Поскольку , то из (3.2) следует, что
  при  .
Тогда
  при  .

Тем самым мы нашли такую функцию , при которой, для любого ,
  при  .
Это означает, что
.

Теорема доказана.

Использованная литература:
О.И. Бесов. Лекции по математическому анализу. Часть 1. Москва, 2004.

Автор: Олег Одинцов.     Опубликовано: 15-09-2018

1cov-edu.ru

Теория

Т10)

Предел суммы двух функций: Предел суммы двух функций равен сумме пределов:

Предел произведения двух функций: Предел произведения двух функций равен произведению пределов:

Дано:

Доказательство: ,,

(Предел суммы и частного доказывается аналогично)

Предел частного двух функций: Предел частного двух функций равен частному пределов, если предел делителя не равен нулю:

Т11)

Теорема о пределе сложной функции: Пусть функцияf(x) определена в проколотой окрестности точкии принимает значения в проколотой окрестноститочки, причем. Тогда, если функцияg(y) определена на, и ,то и

Т12)

Теорема о знакопостоянстве функции, име­ющей ненулевой предел: Если, то существует окрестность точки а, в которой и знаксовпадает со знаком значенияb.

Доказательство: по условию , т.е., илисправедливы неравенства.

Возьмём за число. Тогда,,являются числами одного знака. Следовательно, в силу неравенства,и имеет знак числаbв указанной-окрестности точки а.

Т13)

Теорема о предельном переходе в неравенстве:

Если для двух функций и, имеющих пределы соответственноивыполняется неравенство, то и для их пределов выполняется то же неравенство, т.е.,,

Доказательство

. По теореме о знакопостоянстве функции и ее предела имеем , т.е.. Теорема доказана.

Т14)

Теорема о пределе промежуточной функции:

Пусть для всех xиз некоторой проколотой окрестности(точкивыполняется двойное неравенство, и пусть существуют пределыи, равные одному и тому же числуa. Тогда и

Т15)

Первый замечательный предел: (Геометрический способ)

c

B

X

A

O

Доказательство:

Проведем геометрическое доказательство, основанное на очевидном соотношении между тремя площадями:

Нами выбран круг единичного радиуса и угол х, выраженный в радианах, в интервале от 0 до п/2. Найдем три указанные площади и подставим в имеющееся неравенство:

Преобразовываем:

Сокращаем:

Затем делим на sinx

Так как предел косинуса при равен 1, то интересующий нас предел оказался заключен между двумя другими, имеющими одинаковый предел. Тогда от сюда следует, что

Второй замечательный предел:

Для функции верны следующие утверждения:

Т16) Сравнение бесконечно малых и бесконечно больших функций. Теоремы об эквивалентных бесконечно малых и бесконечно больших функциях:

1. Бесконечно малые функции и их сравнение.

Пусть y=f1(x) и y=f2(x) – некоторые две функции, а x стремится к некоторому x0 (конечному или бесконечному). Если при этом f1(x)→0 и f2(x)→0, то есть если

Это значит, что f2(x) несравненно меньше f1(x) при x→x0 (f2(x) несравненно быстрее, чем , стремится к нулю при x→x0). В этом случае говорят, что функция f2(x) является бесконечно малой функцией более высокого (высшего) порядка малости, чем функция f1(x), при x→x0. И обозначают этот факт так:

(читается: f2(x) есть «о малое» от f1(x) при x→x0). Суть записи (4.3) состоит, как сказано выше, в том, что бесконечно малая функция f2(x) является бесконечно малой частью другой бесконечно малой функции f1(x) при x→x0.

Вариант 2:

Это значит, что при x→x0 бесконечно малые функции f1(x) и f2(x) практически не отличаются друг от друга. В этом случае говорят, что функция f2(x) эквивалентна (равносильна) функции f1(x) при x→x0 . И обозначается это так:

В этом случае говорят, что бесконечно малые при x→x0 функции f1(x) и f2(x) – одного порядка малости. И записывают этот факт так:

2. Бесконечно большие функции и их сравнение.

Пусть

то есть функции y=f1(x) и y=f2(x) при x→x0 по абсолютной величине стремятся к бесконечности. Тогда они называются бесконечно большими при x→x0.

Сравнивают бесконечно большие функции по тому же принципу, что и бесконечно малые. А именно:

1) Если

то функция f2(x) называется бесконечно большой функцией низшего порядка роста, чем бесконечно большая функция f1(x). А функция f1(x) – соответственно высшего порядка роста, чем f2(x).

В частности, очевидно, что функции y=x; y=x2; y=x3; y=ex являются бесконечно большими при x→+∞, причем каждая последующая из них – высшего порядка роста, чем предыдущая. И вообще, можно доказать (см. главу 4, §4), что любая степенная функция y=xn (n>0) при x→+∞ является бесконечно большой функцией низшего порядка роста, чем любая показательная функция y=ax (a>1). То есть

17) Непрерывность функции действительного переменного в точке. Теорема о непрерывности сложной функции:

Функция f(x) называется непрерывной в точке а, если:

1)функция f(x) определена в точке а,

2)имеет конечный предел при x стремящемся к а,

3)этот предел равен значению функции в этой точке:

Второе определение непрерывности:

Функция f(x) называется непрерывной в точке а, если она определена в этой точке и бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции:

Приращение функции:

Определение означает, что при

Сложная функция, являющаяся композицией конечного числа непрерывных в точке функций, непрерывна в точке.

Т18) Точки разрыва и их классификация. Доказательство непрерывности функции.

Определение. Точка х0 называется точкой разрыва функции f(x), если f(x) не определена в точке х0 или не является непрерывной в этой точке.

Определение. Точка х0 называется точкой разрыва 1- го рода, если в этой точке функция f(x) имеет конечные, но не равные друг другу левый и правый пределы.

Для выполнения условий этого определения не требуется, чтобы функция была определена в точке х = х0, достаточно того, что она определена слева и справа от нее.

Из определения можно сделать вывод, что в точке разрыва 1 – го рода функция может иметь только конечный скачок. В некоторых частных случаях точку разрыва 1 – го рода еще иногда называют устранимой точкой разрыва, но подробнее об этом поговорим ниже.

Определение. Точка х0 называется точкой разрыва 2 – го рода, если в этой точке функция f(x) не имеет хотя бы одного из односторонних пределов или хотя бы один из них бесконечен.

http://msu–students.ru/math.html

studfiles.net

Второй замечательный предел, следствия, примеры

Второй замечательный (особый) предел часто вызывает трудности у студентов, хотя сам предел довольно прост и понятен на практике. Он позволяет раскрывать неопределенности вида единица в степени бесконечность . Замечательный предел имеет следующий вид

где “е”-экспонента.

Следствия второго замечательного предела

1)
2)
3)
4)
5)
6)

На практике следствия второго предела реже встречаются на практике чем он сам, однако без них некоторые задачи в простой способ не решить.

Примеры на замечательный предел

Рассмотрим некоторые примеры из сборника А.В. Тевяшев, А.Г. Литвин, Г.М. Кривошеева и др.”Высшая математика в примерах и задачах. Ч.5 Тесты” (Харьков, 2007, ст. 99).

Пример 6.1. Найти предел функции
а)

Решение.
Преобразуем функцию к виду при котором возможно применить формулу замечательного предела

В результате можем применить правило замечательного предела

 

б)

Решение.
Подобно предыдущему примеру превращаем функцию в скобках чтобы применить замечательный предел

Нужно отметить, что в этом примере и во многих подобных константы в степенях, как правило вклада не несут. Функцию можно расписать следующим образом

Предел умышленно расписан в виде произведения двух множителей чтобы Вы убедились что константы в степенях вклада не несут. Их цель запутать Вас, если плохо знаете теоретический материал или сомневаетесь в правильности решения. Во всех последующих примерах мы не будем расписывать примеры на произведение двух границ, однако помните, что они не меняют конечного результата (вклад – множитель единица).

————————————

в)

Решение.
Выполняем преобразование заданной функции

Запись в таком виде сделана специально, потому что степень нужно свести к подобному виду

В такой простой способ получили искомый предел функции. В дальнейшем необходимые замены или подсказки будут выделены цветом из общего решения.

 

г)

Решение.
Выполним замену переменных в пределе

и определенные преобразования для нахождения предела

Бывают случаи, когда прямо применить правило второго замечательного предела довольно сложно, в таких ситуациях используйте простые замены которые Вам понятны и позволяют в быстрый способ найти предел.

 

Пример 6. 2 Вычислить предел функции

а)

Решение.
Сводим функцию к правилу замечательного предела

Подставляем и вычисляем, выполняя нужные манипуляции с показателями

 

в)

Решение.
За известным уже алгоритмом преобразуем функцию

Применяя определение второго важного предела находим

 

Пример 6. 3 Определить предел функции
б)

Решение.
Сведем функцию для применения замечательного предела

Подставляем в границу и упрощаем

 

г)

Решение.
“Как найти предел ? – скажете Вы, ведь переменная равна минус бесконечности.
В этом примере видим что аргумент стремится к минус бесконечности, кроме того функция в скобках следует не до единицы, а до 2 при больших аргументах.

Учитывая что степень отрицательный получим следующее значение предела

Во всех примерах второго замечательного предела следует сначала проверять условие что выражение в скобках стремится к единице. Если нет, то предел функции в зависимости от степени будет равен или нулю или бесконечности. Те из Вас кто часто решает примеры такие проверки осуществляет автоматически. Остальные сводят границу в экспоненте в определенном степени, но все равно вылезает множителем или ноль или бесконечность. В конечном варианте правы все, однако в первом случае тратится гораздо меньше времени, которое так необходима на контрольных работах, тестах, ВНО. Поэтому выбирайте для себя простой путь и делайте в обучении правильные выводы.

 

Пример 6. 5 Найти предел функции
а)

Решение.
Заданный пример на вид отличается от предыдущих, однако решение получаем по такой же схеме. Выполняем преобразования функции в скобках под правило замечательного предела

Осталось в степени выделить обратный множитель

и подставить в границу

По такой схеме вычисляйте все подобные пределы, она проста и не требует дополнительных пояснений.

————————————

в)

Решение.
К рассматриваемому примеру великих преобразований делать не нужно. Он имеет достаточно простую запись и решение осуществляем в одну строку

Практикуйте с подобными пределами, используйте удобные для себя схемы сведения задач под необходимое правило. Не бойтесь делать ошибки – без них обучение не обходится!

yukhym.com

Как решать пределы?

В данной статье вы узнаете о том, как решать пределы?

Решение пределов является одним из важных разделов математического и вычислительного анализа. Многие ученики и учащиеся вузов справляются с данной проблемой свободно, когда другие постоянно задают один и тот же вопрос: «Как решать пределы?». Нахождение пределов тема актуальная. Существует множество способов решения пределов. Идентичные пределы можно найти согласно закону Лопиталя и без его помощи. Однако сначала нам следует разобраться, что же такое предел?

Предел имеет три части

Первая — это всем известный значок lim, вторая, это то, что написано под ним.

Например: x -> 1. Данная запись будет читаться так (икс стремиться к 1).

Третья часть это сама функция, которая стоит после знака lim.

Хотелось бы уточнить, значение икс стремится к 1, это то значение x, при котором х принимает определенные значения, которые близки к единице или почти с ней совпадают.

Решать пределы, дело легкое, если в них разобраться.

Первое правило решения пределов

В случае если предоставлена нам функция, попросту подставьте число в функцию. Это элементарные пределы, которые действительно встречаются в примерах и очень часто.

Есть пределы, где х->? Тогда бесконечность это та функция, где икс бесконечно возрастает. Значение такой функции является (1-х). Чтобы решить данный предел, нам необходимо следуя нашему первому правилу подставить значение (1-х) в функцию и получить ответ.

Из вышесказанного, для того чтобы обучиться решать наиболее непростые пределы, вы обязаны помнить правила решение элементарных пределов.

• Правило первое: Дана функция, подставляем число в функцию.
• Правило второе: Дана бесконечность, подставляем (1-х) в функцию.

Как только вы это поймете, то сразу начнете замечать элементарные пределы и сможете их решить. Вот мы и научились решать легкие пределы. Теперь ознакомимся с решением более сложных пределов.

Существует множество пределов с ? Одним из таких вариантов является предел вида ?/?

Такая функция возможна, когда х->?, а предел выражен в виде дроби.

Многие интересуются, просто ли решить такой предел?

Первое, что вы должны запомнить, вам необходимо найти в числителе х по старшинству, т.е. в самой большей степени из всех х, которые есть в числителе.

lim+(х->?)?((2х^2-3х-4)/(3х^2+1+х))^ ?

Мы видим, что старшая степень в числителе это 2

Теперь, нам необходимо сделать тоже самое только со знаменателем. В знаменателе старшая степень тоже 2.

Принцип: Для того чтобы разрешить эту функцию, нам следует и делимое и делитель разделить на х в самой старшей степени в пределе. В случае если бы она равнялась 2. Если бы степень числителя равна была 4, а знаменателя 2, то мы бы выбирали 4. Потому, что это самая старшая степень в данной нам функции. Смотрите, как быстро мы обучились решать пределы вида ?/?

Теперь рассмотрим, решение самых сложных пределов. Это вид 0/0.

Подобные пределы очень напоминают нам решение пределов вида бесконечность на бесконечность. Но есть отличие, которое важно помнить при решении. Когда икс стремится к бесконечности, то он бесконечно увеличивается, а тут он равен 0, т.е. конечному числу.

Чтобы разрешить подобную функцию, нам следует, и числители и знаменатель разложить на множители. Чтобы получить элементарный дискриминант, известный нам с 6 класса. Вычисляем дискриминант и подставляем ответы в нашу функцию. Находим конечный ответ.

Правило: если в числителе или знаменателе можно некое число вынести за данную скобку, то мы, не думая, обязательно выносим.

Существует множество разных способов решения более сложных пределов. Одним из них является метод замены. Заменить любую переменную легче, чем постоянно раскладывать на множители. Очень часто такой способ применяется для того, чтобы из сложного предела сделать первый замечательный предел.

Давайте рассмотрим детальнее на примере

Пример: lim+(х->0)?(arctg4x/7x)^ ?

Решение: Мы видим, что наша функция представлена в виде неопределенности 0/0 , которую мы уже прошли

                     lim+(х->0)?(arctg4x/7x)^ ? = 0/0

Мы видим в пределе арктангенс, нехорошая функция, от которой нам необходимо избавиться. Очень комфортно нам будет, если мы арктангенс превратим в одну простую и легкую букву.

Сделаем замену: arctg заменим на у. И в процессе решения арктангенс будем именовать как у. Если наш икс стремится к нулю, арктангенс мы заменили на у, тогда записываем, что у тоже стремится к нулю. Все, что нам осталось в знаменателе выразить икс через игрек. Для этого в обе части равенства мы добавляем tg

Выражения приобретёт такой вид:

tg ( arctg4x)=tgy

С левой стороны две функции мы убираем, они взаимообратные и пропадают.

У нас остается:

4х = tgу, отсюда: х= tgy/4

А теперь осталось самое элементарное:

lim+(х->0)?(y/(7*tgy/4))^ ?

Дальше решаем первый замечательный предел.

Идем дальше. В пределах есть не только один замечательный предел, а их оказывается два. Сейчас мы не только разберемся с понятием второго замечательного предела, но и научимся его решать. Второй замечательный предел существует для решения неопределенности вида 1^? В математике она записывается так а(х) ->? Такой вид данной функции самый простой, есть функции и сложнее, самое важное, чтобы она стремилась к бесконечности.

Следует запомнить, что как только наш предел оказывается в степени, это главный знак того, что такое выражение нам поможет решить второй замечательный предел. Сейчас мы подробнее остановимся на примере, который встречается очень часто, советую его изучить детально.

Дан нам предел: lim+(х->?)?((x-2)/(x+1))^(2x+3) ?

Этот предел вида (?/?)^?Второй замечательный предел такой вид не решает, как мы знаем, он решает вид 1^?, для этого нашу функцию необходимо преобразить в другой вид. В знаменателе мы видим х+1, значит, в числителе тоже должно быть х+1

lim+(х->?)?((х+1-3)/(х+1))^(2х+3) ?

Теперь нам необходимо почленно разделить числитель на знаменатель. Тогда же наше основание будет похоже на нашу неопределенность, но там знак минус, который нам мешает. Делаем дробь с тремя этажами и видим нашу неопределённость ?/?. А такую функцию мы уже умеем вычислять. Делим обе части дроби на х, и готово. У нас получился ответ.

Хочу поздравить вас, дорогие читатели, вы научились решать пределы. Надеюсь, моя статья была познавательной, увлекательной и интересной!

xn--80aakeqfhfoqvpv.xn--p1ai

---