Связь работы и кинетической энергии – Кинетическая энергия. Связь между работой тела и изменением его кинетической энергии. Потенциальная энергия тела в поле земного тяготения.
- Комментариев к записи Связь работы и кинетической энергии – Кинетическая энергия. Связь между работой тела и изменением его кинетической энергии. Потенциальная энергия тела в поле земного тяготения. нет
- Советы абитуриенту
- 10. Работа и кинетическая энергия.
- 8.Кинетическая энергия. Связь работы с кинетической энергией.
- Работа и кинетическая энергия
- 6. Работа переменной силы.
- 3.2. Кинетическая энергия механической системы и её связь с работой
- 3.2. Кинетическая энергия механической системы и её связь с работой
- 3.1. Работа. Кинетическая энергия
10. Работа и кинетическая энергия.
Уравнение движения тела под действием внешней силы имеет вид
или, в проекции на направление движения,
Умножив обе части равенства на , получим
.
Левая часть равенства есть полный дифференциал некоторой функции:
,
Если система замкнута, то иFτ = 0. Тогда и
Если полный дифференциал некоторой функции, описывающей поведение системы, равен нулю, то эта функция может служить характеристикой состояния данной системы. Функция состояния системы, определяемая только скоростью ее движения, называется кинетической энергией.
Кинетическая энергия системы есть функция состояния движения этой системы. K – аддитивная величина:
K –
относительная величина, её значение
зависит от выбора системы координат
(так же как и –
относительная величина).
Энергия измеряется в СИ в единицах
произведения силы на расстояние, т.е. в
ньютонах на метр. 1 Н·м = 1 Дж.
Кроме
того, в качестве единицы измерения
энергии используется внесистемная
единица – электрон-вольт (эВ). 1 эВ =
1,6·10
При решении задач полезна формула, связывающая кинетическую энергию с импульсом p. Получим её:
отсюда
Теперь рассмотрим связь кинетической энергии с работой. Если постоянная сила действует на тело, то оно будет двигаться в направлении силы. Тогда элементарная работа по перемещению тела из точки 1 в точку 2, будет равна произведению силы F на перемещение dr :
dA = F dr, отсюда ,
Окончательно получаем:
Следовательно, работа силы, приложенной к телу на пути r, численно равна изменению кинетической энергии этого тела:
Или изменение кинетической энергии dK равно работе внешних сил:
dK = dA.
Работа, так же как и кинетическая энергия, измеряется в джоулях. Скорость совершения работы (передачи энергии) называется мощность. Мощность есть работа, совершаемая в единицу времени.
Мгновенная мощность , или
Средняя мощность
Измеряется мощность в ваттах. 1 Вт = 1 Дж/с.
11. Законы сохранения в механике
Кинетическая энергия тела массой m, движущегося со скоростью :
.
Потенциальная энергия тела массой m, находящегося на высоте h, в поле сил тяжести с ускорением свободного падения :
.
Энергия пружины с коэффициентом жесткости k, сжатой или растянутой на :
.
Импульс тела массой m, движущегося со скоростью :
.
Закон сохранения энергии:
В замкнутых системах полная энергия (потенциальная + кинетическая + тепловая) системы тел сохраняется.
.
Если при этом можно пренебречь переходом механической энергии (потенциальная + кинетическая) втепловую, то сохраняется механическая энергия системы.
Абсолютно упругим ударом называется такое кратковременное взаимодействие тел, после которого тела полностью восстанавливают свою форму, а их суммарная кинетическая энергия не изменяется. При абсолютно упругом ударе выполняются закон сохранения импульса и закон сохранения механической энергии.
Абсолютно неупругим ударом называется такое кратковременное взаимодействие тел, после которого соударяющиеся тела образуют единое тело, движущееся с определенной скоростью, а суммарная кинетическая энергия тел уменьшается. При абсолютно неупругом ударе выполняется закон сохранения импульса, а механическая энергия не сохраняется, часть ее превращается во внутреннюю энергию тел.
Закон сохранения импульса:
Полный импульс замкнутой системы тел остается постоянным.
.
Работа постоянной силы :
,
где s – модуль перемещения, а – угол между векторами силы и перемещения.
Работа так же может быть найдена по следующей формуле:
.
Мощность – работа A совершенная за единицу времени:
.
Силы:
– сила упругости.
– сила тяжести.
8.Кинетическая энергия. Связь работы с кинетической энергией.
Кинетическая энергия. Физическая величина, равная половине произведения массы тела на квадрат его скорости, называется кинетической энергией тела.
Кинетическая энергия тела обозначается буквой Eк:.
Работа равнодействующей сил, приложенных к телу, равна изменению кинетической энергии тела. Это утверждение называют теоремой о кинетической энергии.
Так как изменение кинетической энергии равно работе силы, кинетическая энергия выражается в тех же единицах, что и работа, т. е. в джоулях. Если начальная скорость движения тела массой m равна нулю и тело увеличивает свою скорость до значения , то работа силы равна конечному значению кинетической энергии тела:.
Кинетическая энергия тела массой m, движущегося со скоростью , равна работе, которую должна совершить сила, действующая на покоящееся тело, чтобы сообщить ему эту скорость.
9. Потенциальная энергия. Связь работы с потенциальной энергией. Принцип минимума потенциальной энергии.
Потенциальная энергия – энергия, определяемая взаимным расположением тел или отдельных частей тела относительно друг друга, т.е. потенциальная энергия зависит от конфигурации системы.
Соотношение, связывающее работу потенциальной силы с изменением потенциальной энергии системы, имеет вид: ,где – приращение потенциальной энергии.
Принцип минимума потенциальной энергии состоит в том, что любая система стремится перейти в такое состояние, при котором ее потенциальная энергия окажется минимальной.
10. Закон сохранение механической энергии: в системе тел, между которыми действуют только консервативные силы, полная механическая энергия сохраняется, т. е. не изменяется со временем.
Консервативные силы это все силы кроме силы трения и сопротивления. В этом случае с течением времени полная механическая энергия системы уменьшается. Но механическая энергия не исчезает, она переходит в другие виды энергии, например, при силе трения во внутреннюю энергию.
11. Закон сохранения импульса
Последнее выражение и является законом сохранения импульса: импульс замкнутой системы сохраняется, т. е. не изменяется с течением времени.
12.Столкновение тел. Упругий и неупругий удар
Примером применения законов сохранения импульса и энергии при решении реальной физической задачи является удар абсолютно упругих и неупругих тел.
Абсолютно упругий удар — столкновение двух тел, в результате которого в обоих взаимодействующих телах не остается никаких деформаций и вся кинетическая энергия, которой обладали тела до удара, после удара снова превращается в кинетическую энергию
Абсолютно неупругий удар — столкновение двух тел, в результате которого тела объединяются, двигаясь дальше как единое целое. Продемонстрировать абсолютно неупругий удар можно с помощью шаров из пластилина (глины), движущихся навстречу друг другу
13. Динамика вращательного движения. Момент силы. Момент импульса.
Вращательным движением тела вокруг фиксированной оси называют движение, при котором произвольная точка тела, кроме тех, что лежат на оси вращения, движется по окружности в плоскости, перпендикулярной оси вращения, с центром, лежащим на этой оси.
Момент
силы относительно оси —
это скалярная величина, которая
является характеристикой вращательного
действия силы, равная произведению
модуля силы, действующей на твердое
тело, на плечо силы этой силы относительно
данной оси:
M = Fd. Моме́нт
и́мпульса характеризует количество
studfiles.net
Работа и кинетическая энергия
Чтобы у тела изменилась скорость, на тело должна подействовать сила. Но изменение скорости происходит при перемещении тела.
Можно установить прямую связь между силой, действующей на тело, его перемещением и изменением скорости тела на рассматриваемом участке траектории движения.
Пусть на тело массы m, двигавшееся со скоростью начала действовать сила под углом к направлению движения тела. Под действием этой силы тело совершает перемещение и скорость тела изменяется от до
Сделаем чертеж и опишем сюжет на математическом языке.
Выберем инерциальную систему отсчета, свяжем ее с Землей.
Точку отсчета совместим с тем положением тела, когда на него только начала действовать сила. В этот же момент начнем отсчитывать время.
Так как движение происходит в одном направлении, ограничимся одной координатной осью. Выберем направление, совпадающее с направлением движения.
Закончим отсчет времени в тот момент, когда скорость тела достигла искомой величины
Изобразим на чертеже кинематические характеристики движения тела: его перемещение, начальную и конечную скорости, ускорение, а также динамическую характеристику – силу.
Запишем второй закон Ньютона в векторной форме и в проекции на выбранное направление. x: F ∙ cos α = m ∙ a.
В связи с поставленной задачей, домножим правую и левую часть уравнения на S:
F ∙ S ∙ cos α = m ∙ a ∙ S.
Из кинематики известно, что ускорение движения связано с начальной и конечной скоростью движения соотношением:
С учетом этого имеем:
|
|
Это утверждение называется теоремой об изменении кинетической энергии тела.
Работа силы и кинетическая энергия – величины скалярные.
Чтобы получить единицу работы, надо в определяющее уравнение работы подставить единицы силы – 1 Н и перемещения – 1 м. Получаем: 1 Н∙м. Эта единица имеет собственное название – 1 джоуль (1 Дж).
Если тело движется по инерции, силы на него не действуют, работа не совершается и кинетическая энергия не изменяется.
Если на тело действует сила, но тело покоится, работа силы равна нулю.
Если на тело действует сила и тело движется, но угол между направлениями силы и перемещения равен 90°, работа силы также равная нулю.
В зависимости от величины угла между векторами перемещения и силы, работа силы может быть положительной и отрицательной.
files.school-collection.edu.ru
6. Работа переменной силы.
Работа, совершаемая постоянной силой F при перемещении тела M на прямолинейном участке пути s равна A=Fs=Fscos(). Работа – скалярная величина. Если cos()>0, то работа – положительна.
Консервативная (потенциальная) сила – сила, работа которой определяется только начальным и конечным положениями тела и не зависит от формы пути.
Примером работы, совершаемой переменной силой, может служить работа упругой или квазиупругой силы F=-kx, где k – упругость, x – смещение тела, на которое действует упругая сила F относительно положения равновесия (x=0).
Мощность – величина, характеризующая скорость выполнения работы. N=dA/dt.
Консервативные силы и потенциальные поля.
Поле, в котором работа силы не зависит от формы пути, а зависит лишь от положения начальной и конечной точек траектории, называют потенциальными, а силы, действующие в нём, – консервативными.
В потенциальном поле работа сил по любому замкнутому контуру равна нулю.
7.Кинетическая энергия и её связь с работой внешних и внутренних сил.
Кинетической энергией называют энергию, зависящую от скорости движения тела.
Всякое движущее тело может производить работу. Кинетическая энергия определяется работой, которую может совершать тело вследствие того, что оно обладает определённой скоростью.
А= –m(d/dt). Элементарная работа, совершаемая движущимся телом против силы F на пути dx равна A=-Fdx=-m(d/dx)=-md.
Если скорость тела уменьшается от 1 до 2, то A=m12/2- m22/2, т.е. работа равна убыли кинетической энергии тела, т.к. работа совершается против внешних сил. Если внешние силы, действуя на тело, совершают работу, то кинетическая энергия тела, движущегося со скоростью равна Eк=m2/2.
При изменении скорости тела на d кинетическая энергия изменяется на dEк=d(m2/2)=md.
8. Закон сохранения механической энергии.
E=Eк+U=const.
Для консервативных систем, в которых не происходит преобразование механической энергии в другие формы энергии (нет трений и других сил, зависящих от скорости), полная энергия системы при ей движении остаётся неизменной.
9. Момент силы.
Пусть некоторое тело под действием силы F, приложенной в точке А, приходит во вращение вокруг оси ОО’.
Сила действует в плоскости, перпендикулярной оси. Перпендикуляр р, опущенный из точки О (лежащей на оси) на направление силы, называют плечом силы. Произведение силы на плечо определяет модуль момента силы относительно точки О: M=Fp=Frsin(rF).
Момент силы есть вектор, определяемый векторным произведением радиус-вектора точки приложения силы и вектора силы. M=[rF].
Момент импульса материальной точки.
Момент импульса – вектор, совпадающий по направлению с вектором угловой скорости.
Момент импульса материальной точки равен L=I.
Связь между моментом силы и моментом импульса.
Основное уравнение динамики вращательного движения.
Рассмотрим вначале материальную точку А массой m, движущуюся по окружности радиусом r. Пусть на неё действует постоянная сила F, направленная по касательной к окружности. Согласно второму закону Ньютона, эта сила вызывает тангенциальное ускорение. a=F/m или F= am. a=r => F=rm; Fr=mr2; M=Fr; I= mr2 => M=I или = M/I.
Угловое ускорение точки при её вращении вокруг неподвижной оси пропорционально вращающему моменту и обратно пропорционально моменту инерции.
10.Момент инерции.
Инертность тел при вращательном движении зависит не только от массы, но и от её распределения в пространстве относительно оси вращения. Мерой инертности при вращательном движении служит величина, называемая моментом инерции тела относительно оси вращения.
Если тело однородно и его плотность =m/V, то
Момент инерции тела зависит от того, относительно какой оси оно вращается и как распределена масса тела по объёму.
Тонкий стержень | Перп. (центр) | ml2/12 |
Перп. (конец) | ml2/3 | |
Кольцо, обруч, труба, маховик | Перп. плоскости основания | mR2 |
Диск (цилиндр) | mR2/2 | |
Шар | Центр щара | 2mR2/5 |
Момент импульса вращающегося тела равен сумме моментов импульсов отдельных его частей L=sum(miri2)=I.
studfiles.net
3.2. Кинетическая энергия механической системы и её связь с работой
Рассмотрим
простейшую систему, состоящую из одной
частицы (материальной точки) массы m,
движущейся под действием сил, результирующая
которых равна .
.
Запишем уравнение движения частицы:
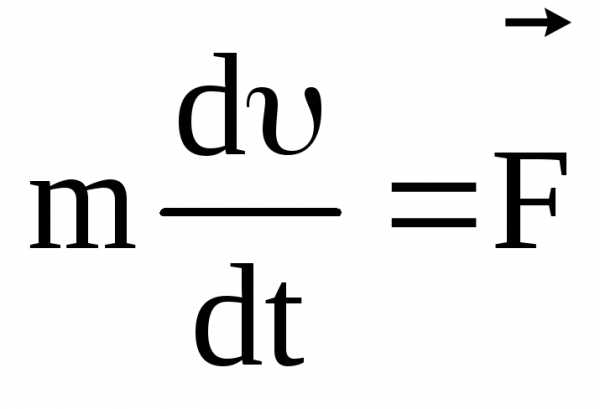 .
.
Умножим скалярно
обе части этого равенства на элементарное
перемещение частицы 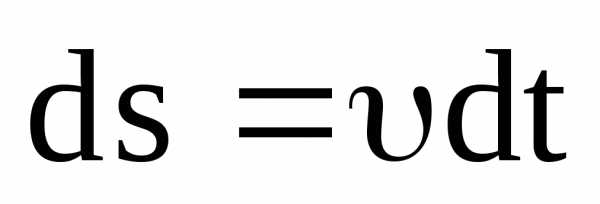 :
:
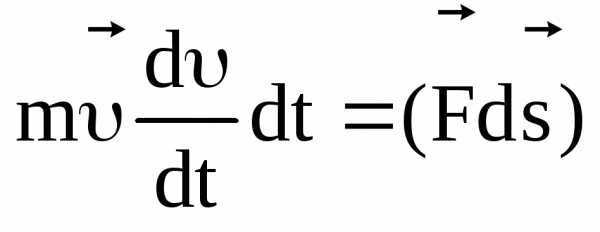 ,
,
. (3.7)
Скалярное
произведение 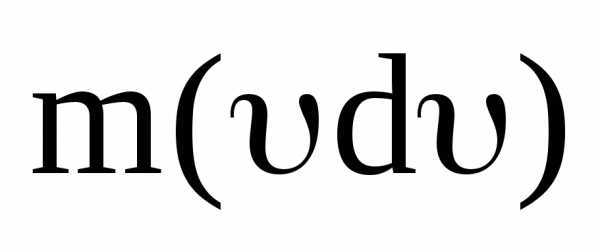 распишем через модули векторов и косинус
угла между ними
распишем через модули векторов и косинус
угла между ними
.
Поскольку
косинус угла между векторами  и
и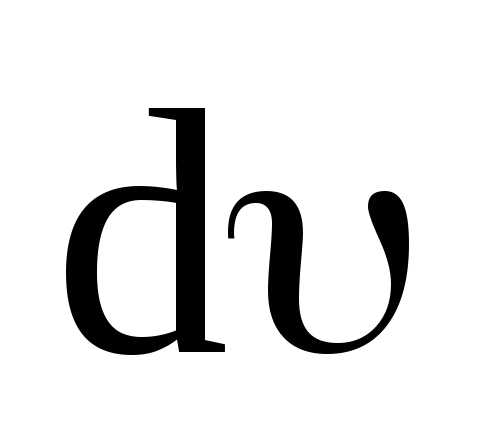 равен единице, то равенство (3.7) перепишется
в виде
равен единице, то равенство (3.7) перепишется
в виде
. (3.8)
Произведение
mdравно производной от величины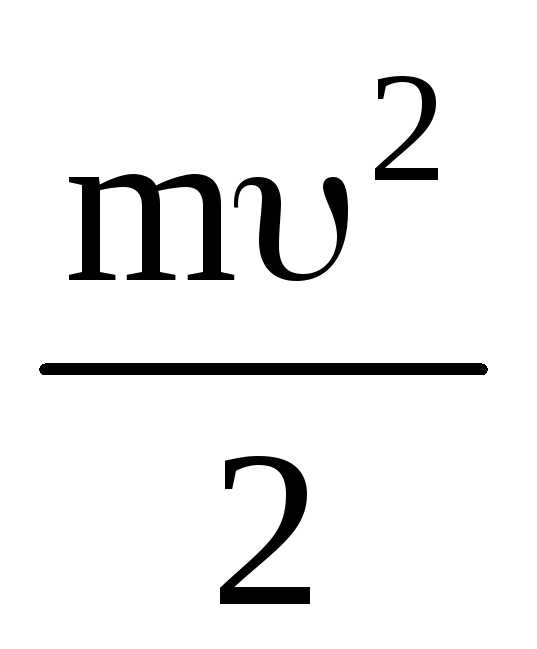 ,
т.е.
,
т.е.
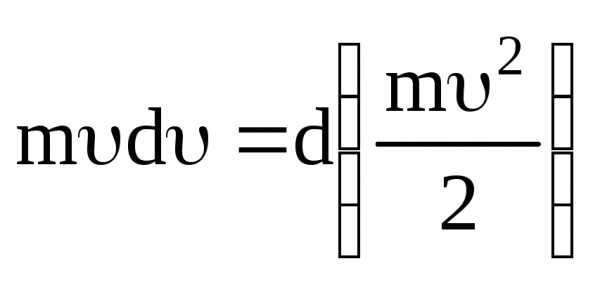 .
.
Заменив полученным выражением левую часть формулы (3.8), придем к соотношению
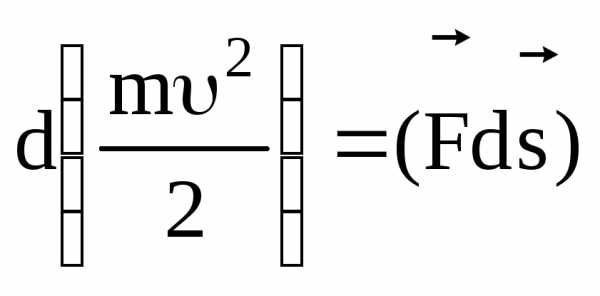 .
(3.9)
.
(3.9)
Если результирующая сил, действующих на частицу, равна нулю,
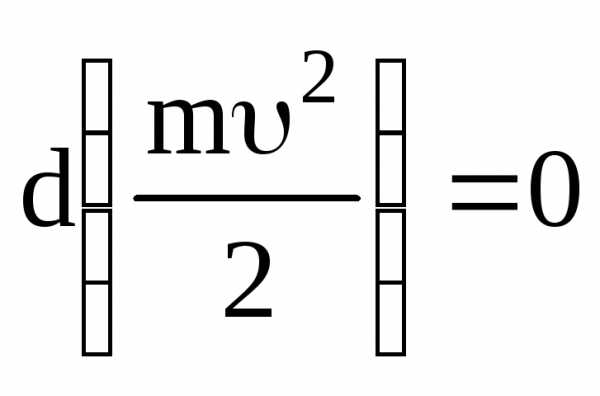 ,
то сама величина
,
то сама величина
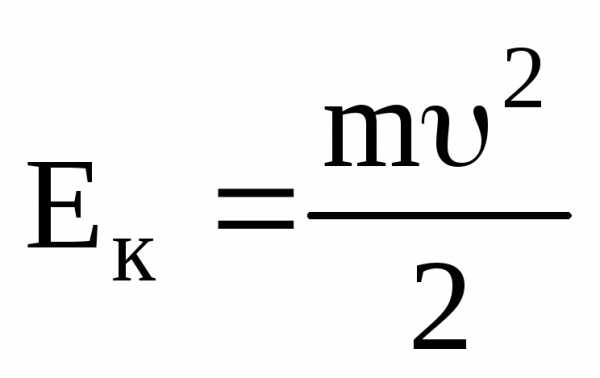 (3.10)
(3.10)
остается постоянной.
Эта величина называется кинетической энергией частицы.
Приняв во внимание, что произведение равно модулю импульса частицы р, выражению (3.10) можно придать вид
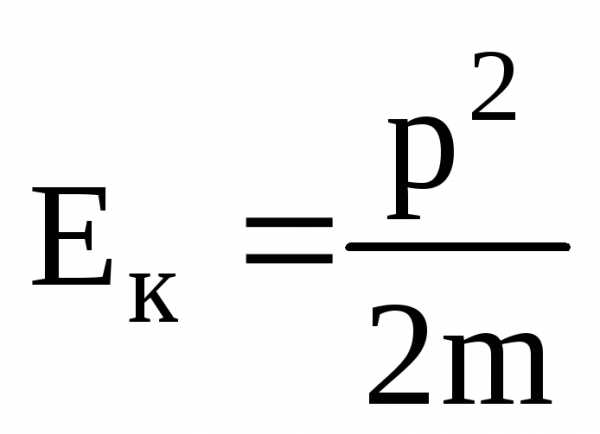 .
.
Если сила F, действующая на частицу не равна нулю, кинетическая энергия получит за времяdt приращение
, (3.11)
где ds- перемещение частицы за времяdt.
Величина
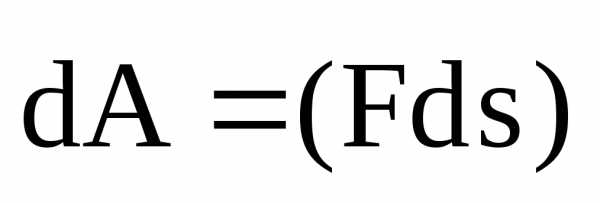
называется работой, совершаемой
силой  на пути
на пути (ds- модуль перемещения
(ds- модуль перемещения ).
Из (3.11) следует, что работа характеризует
изменение кинетической энергии,
обусловленное действием силы на
движущуюся частицу:
).
Из (3.11) следует, что работа характеризует
изменение кинетической энергии,
обусловленное действием силы на
движущуюся частицу:
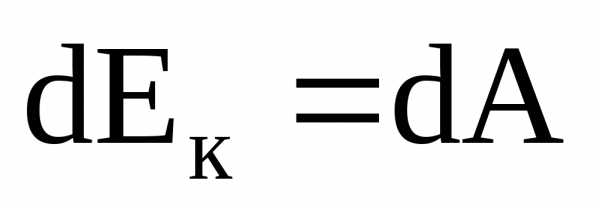 .
.
Проинтегрируем (т.е. просуммируем) обе части равенства (3.9) вдоль траектории движения частицы от точки 1 до точки 2:
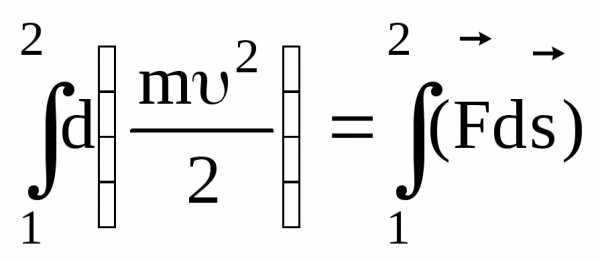 .
(3.12)
.
(3.12)
Левая часть равенства представляет собой приращение кинетической энергии частицы
. (3.13)
Правая часть
есть работа А12силы на пути 1-2
на пути 1-2
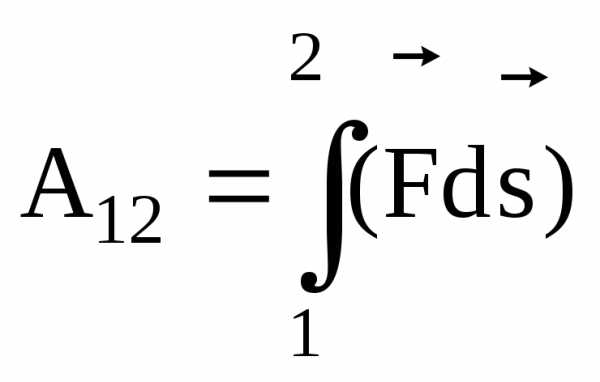 .
(3.14)
.
(3.14)
Подставляя (3.13) и (3.14) в соотношение (3.12), получим
.
Таким образом, работа результирующей всех сил, действующих на частицу, идет на приращение кинетической энергии частицы. Энергия, так же, как и работа, в системе СИ измеряется в джоулях (Дж):
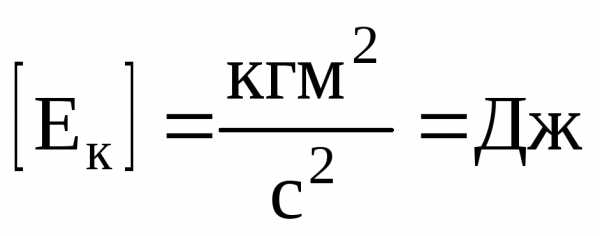 .
.
3.3. Потенциальная энергия материальной точки во внешнем силовом поле и ее связь с силой, действующей на материальную точку
Если частица в каждой точке пространства подвержена воздействию других тел, то говорят, что частица находится в поле сил. Так, например, частица вблизи поверхности Земли находится в поле сил тяжести. В каждой точке пространства на нее действует сила, равная произведению массы на ускорение силы тяжести, т.е. mg.
Пусть заряженная частица находится в электрическом поле точечного заряда q. Это поле характерно тем, что направление силы, действующей на частицу в любой точке пространства, проходит через неподвижный центр (зарядq), а величина силы зависит только от расстояния до этого центра:F=F(r). Поле сил, обладающих таким свойством, называется центральным. Поле сил тяжести является частным случаем центрального поля сил (с центром, расположен-ным в бесконечности).
Если в каждой
точке поля сила, действующая на частицу,
одинакова по величине и направлению
( =сonst),
поле называется однородным.
=сonst),
поле называется однородным.
Силовое поле можно описать с помощью функции П(x,y,z,t) такой, что компоненты силы в декартовой системе координат равны
. (3.15)
Такое поле называется потенциальным. Функция П(x,y,z,t) носит название потенциальной функции (или потенциала). Поле, не изменяющееся со временем, называется стационарным. В этом случае П=П(x,y,z). Поле, изменяющееся со временем, называется нестационарным. В этом случае П=П(x,y,z,t). Известно, что если обозначить- скалярную функцию координатx,y,z, то
, (3.16)
где 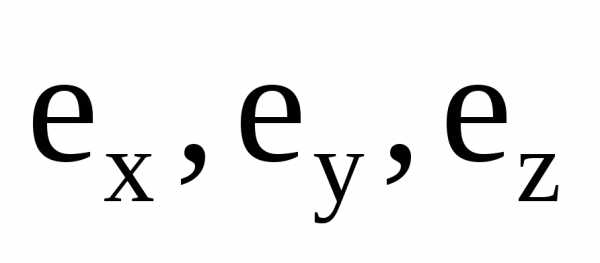 – орты координат. Вектор с компонентами
– орты координат. Вектор с компонентами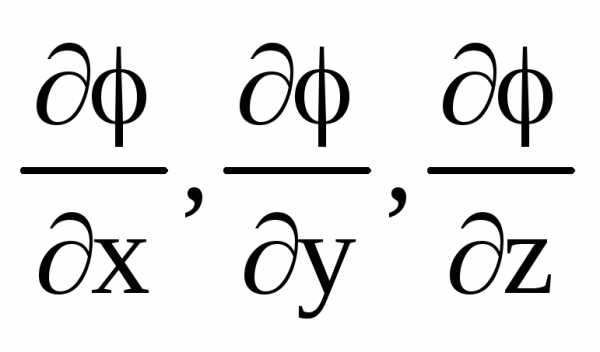 называется градиентом функциии обозначается символомgradилисимволический
вектор,(набла) –
называется оператором Гамильтона.читается «набла фи».
называется градиентом функциии обозначается символомgradилисимволический
вектор,(набла) –
называется оператором Гамильтона.читается «набла фи».
Сравнивая (3.15) и (3.16), можно видеть, что в случае потенциального силового поля
. (3.17)
Подставляя (3.17) в выражение для работы, получим
,
.
Если поле стационарно, то правая часть этого уравнения представляет собой полный дифференциал функции П(x,y,z,). Следовательно, работа, совершенная над частицей в стационарном силовом поле:
. (3.18)
Проинтегрируем соотношение (3.18) вдоль некоторой траектории от точки 1 до точки 2:
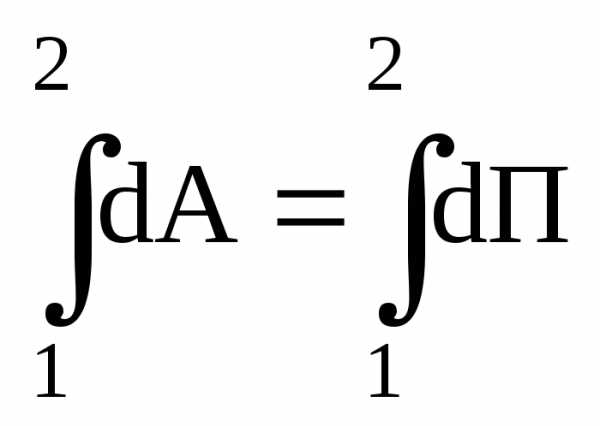 .
.
Левая часть этой формулы дает работу А12, совершенную силами поля на пути 1-2. Сумма элементарных приращенийdП функции П равна полному приращению этой функции на пути 1-2:
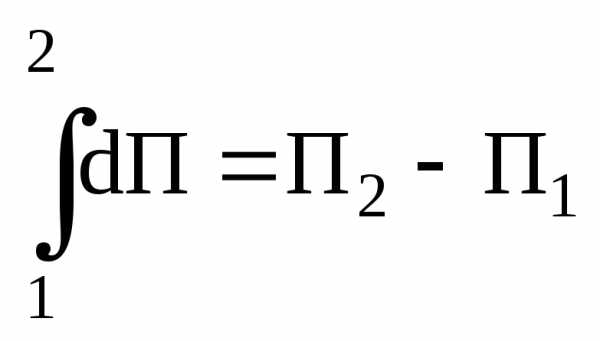 .
.
Таким образом, работа на пути 1-2 равна полному приращению функции П на пути 1-2:
А12=П2-П1. (3.19)
Форма траектории, по которой осуществлялось интегрирование, была совершенно произвольна. Отсюда заключаем, что работа, совершаемая над частицей силами стационарного потенциального поля, не зависит от пути, по которому движется частица, а определяется только начальным и конечным положением частицы в пространстве.
Силы, работа которых не зависит от пути, по которому частицы переходят из одного положения в другое, называется консервативными. Силы, действующие на частицу в стационарном потенциальном поле, являются консервативными. Работа консервативных сил на замкнутом пути равна нулю.
Консервативными силами являются силы тяготения, силы упругости, силы электростатического происхождения, так как их работа не зависит от формы пути.
В формуле (3.19), определяющей работу, совершенную силами поля на пути (1-2) П1и П2– значения потенциальной функции П(x,y,z) в начальной и конечной точках. Эта работа идет на приращение кинетической энергии частицы:
. (3.20)
Обозначим – П(x,y,z)=Eп. Соотношение (3.20) примет вид
;
.
Полученный результат означает, что величина (Eк+Eп) для частицы, находящейся в поле консервативных сил, остается постоянной (является интегралом движения). СлагаемоеEкесть кинетическая энергия частицы. Все величины в (3.19) имеют одинаковую размерность – размерность энергии. ФункциюEп(x,y,z) называют потенциальной энергией частицы во внешнем поле сил. Величину Е, равную сумме кинетической и потенциальной энергии частицы, называют полной механической энергией частицы.
В равенстве (3.19) П(x,y,z) заменим на –Eп(x,y,z), получим
.
Работа, совершаемая над частицей консервативными силами, равна убыли потенциальной энергии частицы. Иначе, работа, совершается за счет запаса потенциальной энергии.
Заменив в соотношении (3.18) функцию П(x,y,z) потенциальной энергией, найдем связь между потенциальной энергией и силой:
.
Таким образом, сила, действующая на частицу в стационарном потенциальном силовом поле, равна градиенту потенциальной энергии в данной точке, взятому с обратным знаком. Компоненты силы определяются следующими выражениями:
.
Конкретный вид функции Eп(x,y,z) зависит от характера силового поля. Чтобы найти потенциальную энергию частицы в поле силы тяжести (рис.3.3), вспомним, что работа, совершаемая над частицей силами этого поля, равна
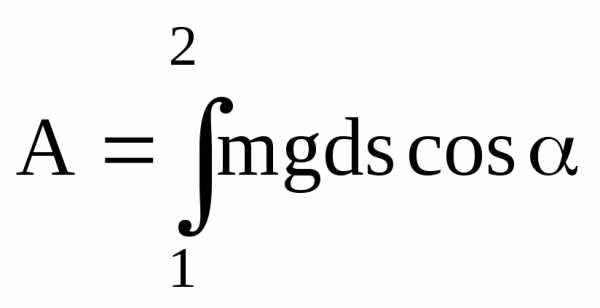 ;
;
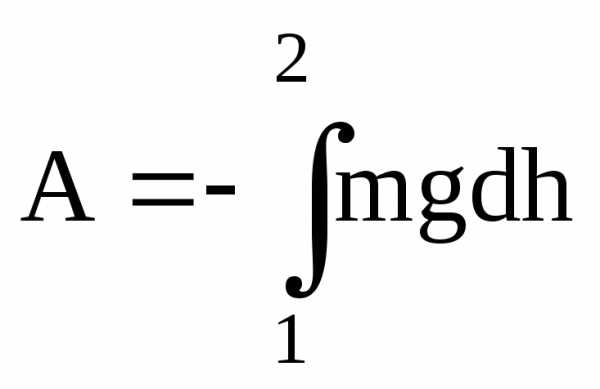 .
.
С другой стороны, .
h 2 h2 dh h1 1 mg s Рис.3.3 | Сравнивая эти соотношения, можно видеть, что потенциа-льная энергия частицы в поле силы тяжести определяется выражением: , где h- отсчитывается от произ-вольного уровня. |
studfiles.net
3.2. Кинетическая энергия механической системы и её связь с работой
Рассмотрим
простейшую систему, состоящую из одной
частицы (материальной точки) массы m,
движущейся под действием сил, результирующая
которых равна .
.
Запишем уравнение движения частицы:
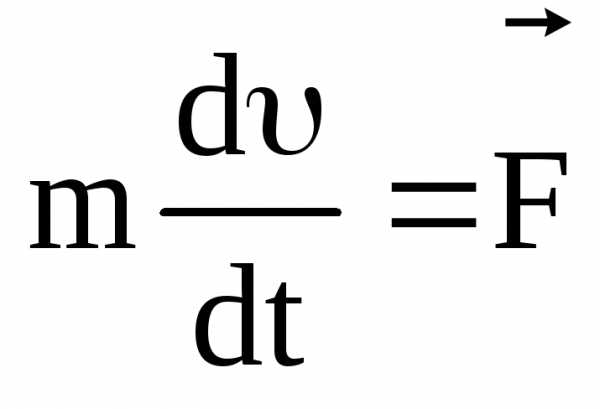 .
.
Умножим скалярно
обе части этого равенства на элементарное
перемещение частицы 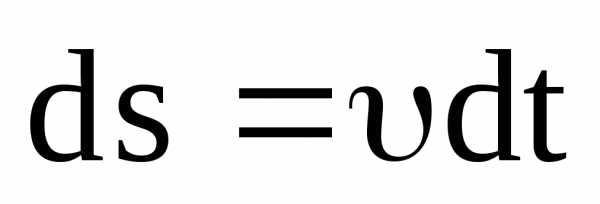 :
:
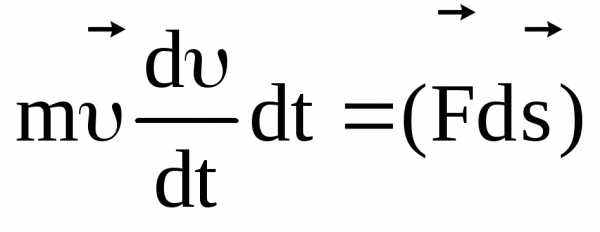 ,
,
. (3.7)
Скалярное
произведение 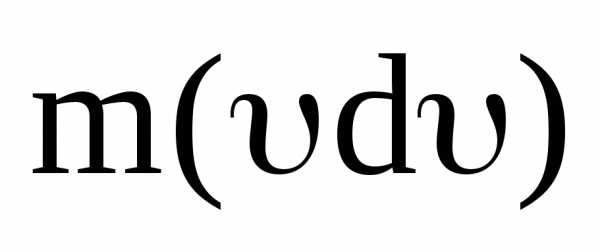 распишем через модули векторов и косинус
угла между ними
распишем через модули векторов и косинус
угла между ними
.
Поскольку
косинус угла между векторами  и
и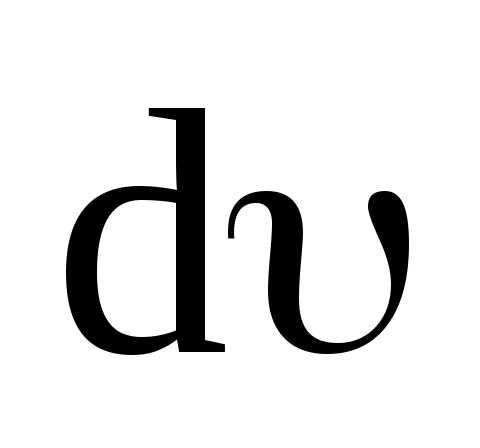 равен единице, то равенство (3.7) перепишется
в виде
равен единице, то равенство (3.7) перепишется
в виде
. (3.8)
Произведение
mdравно производной от величины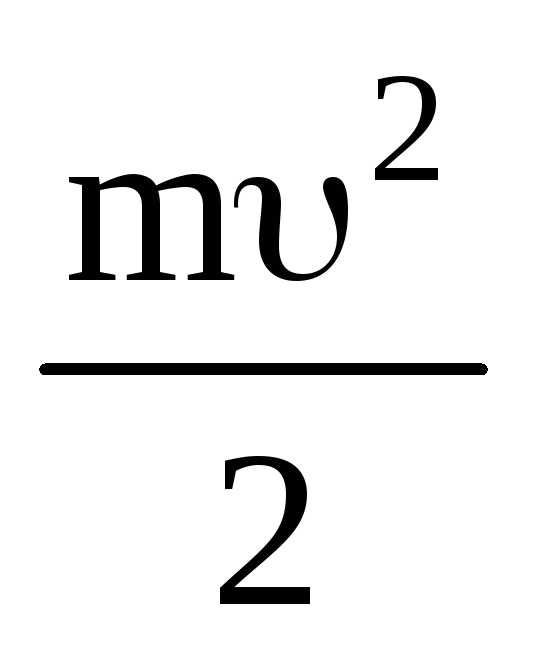 ,
т.е.
,
т.е.
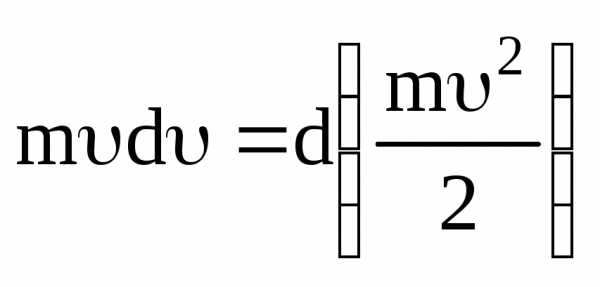 .
.
Заменив полученным выражением левую часть формулы (3.8), придем к соотношению
. (3.9)
Если результирующая сил, действующих на частицу, равна нулю,
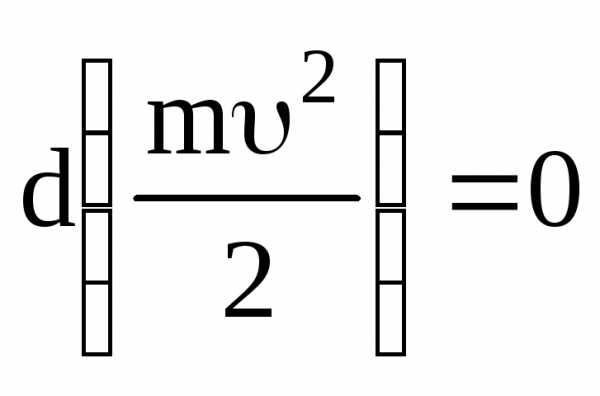 ,
то сама величина
,
то сама величина
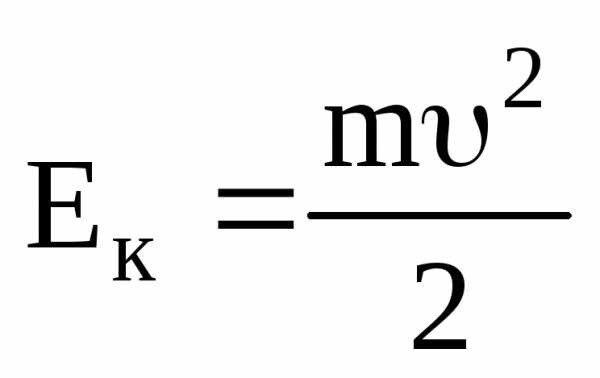 (3.10)
(3.10)
остается постоянной.
Эта величина называется кинетической энергией частицы.
Приняв во внимание, что произведение равно модулю импульса частицы р, выражению (3.10) можно придать вид
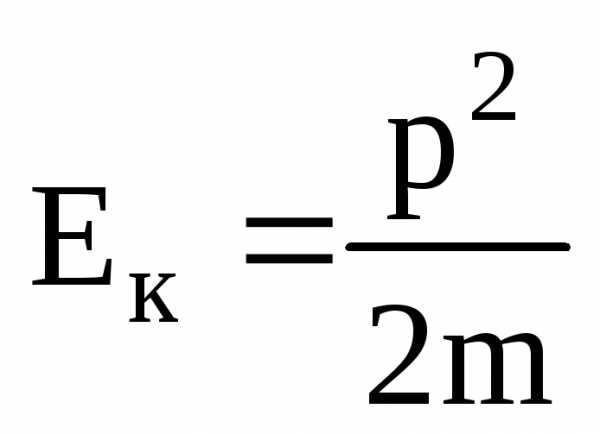 .
.
Если сила F, действующая на частицу не равна нулю, кинетическая энергия получит за времяdt приращение
, (3.11)
где ds- перемещение частицы за времяdt.
Величина
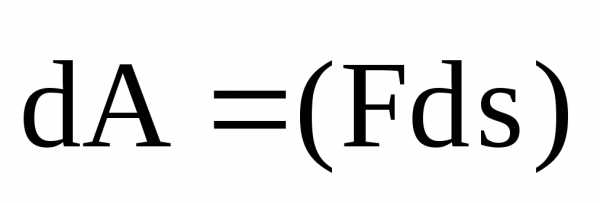
называется работой, совершаемой
силой  на пути
на пути (ds- модуль перемещения
(ds- модуль перемещения ).
Из (3.11) следует, что работа характеризует
изменение кинетической энергии,
обусловленное действием силы на
движущуюся частицу:
).
Из (3.11) следует, что работа характеризует
изменение кинетической энергии,
обусловленное действием силы на
движущуюся частицу:
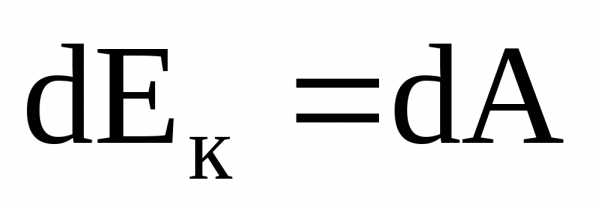 .
.
Проинтегрируем (т.е. просуммируем) обе части равенства (3.9) вдоль траектории движения частицы от точки 1 до точки 2:
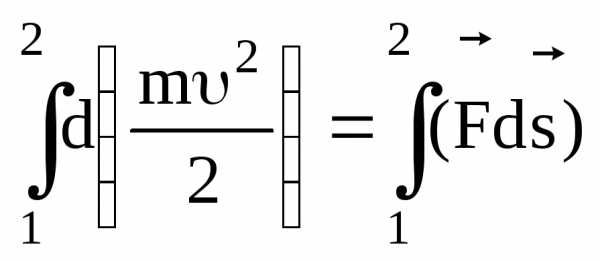 .
(3.12)
.
(3.12)
Левая часть равенства представляет собой приращение кинетической энергии частицы
. (3.13)
Правая часть
есть работа А12силы на пути 1-2
на пути 1-2
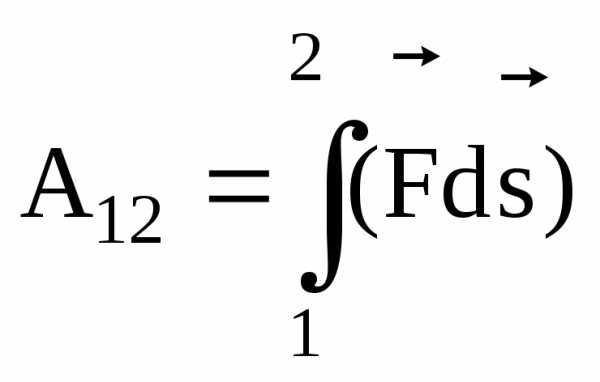 .
(3.14)
.
(3.14)
Подставляя (3.13) и (3.14) в соотношение (3.12), получим
.
Таким образом, работа результирующей всех сил, действующих на частицу, идет на приращение кинетической энергии частицы. Энергия, так же, как и работа, в системе СИ измеряется в джоулях (Дж):
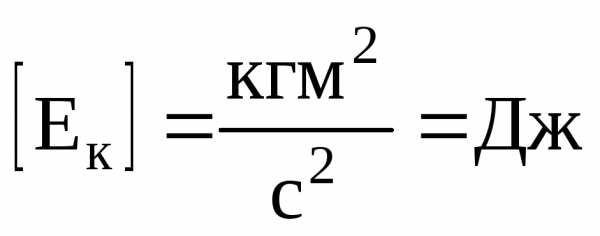 .
.
3.3. Потенциальная энергия материальной точки во внешнем силовом поле и ее связь с силой, действующей на материальную точку
Если частица в каждой точке пространства подвержена воздействию других тел, то говорят, что частица находится в поле сил. Так, например, частица вблизи поверхности Земли находится в поле сил тяжести. В каждой точке пространства на нее действует сила, равная произведению массы на ускорение силы тяжести, т.е. mg.
Пусть заряженная частица находится в электрическом поле точечного заряда q. Это поле характерно тем, что направление силы, действующей на частицу в любой точке пространства, проходит через неподвижный центр (зарядq), а величина силы зависит только от расстояния до этого центра:F=F(r). Поле сил, обладающих таким свойством, называется центральным. Поле сил тяжести является частным случаем центрального поля сил (с центром, расположен-ным в бесконечности).
Если в каждой
точке поля сила, действующая на частицу,
одинакова по величине и направлению
( =сonst),
поле называется однородным.
=сonst),
поле называется однородным.
Силовое поле можно описать с помощью функции П(x,y,z,t) такой, что компоненты силы в декартовой системе координат равны
. (3.15)
Такое поле называется потенциальным. Функция П(x,y,z,t) носит название потенциальной функции (или потенциала). Поле, не изменяющееся со временем, называется стационарным. В этом случае П=П(x,y,z). Поле, изменяющееся со временем, называется нестационарным. В этом случае П=П(x,y,z,t). Известно, что если обозначить- скалярную функцию координатx,y,z, то
, (3.16)
где 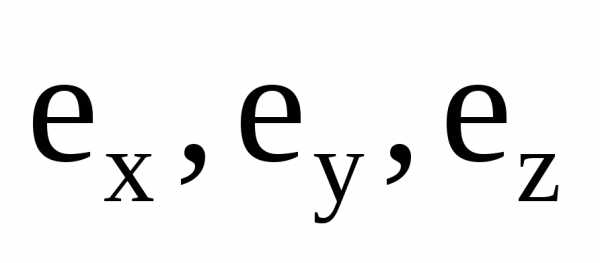 – орты координат. Вектор с компонентами
– орты координат. Вектор с компонентами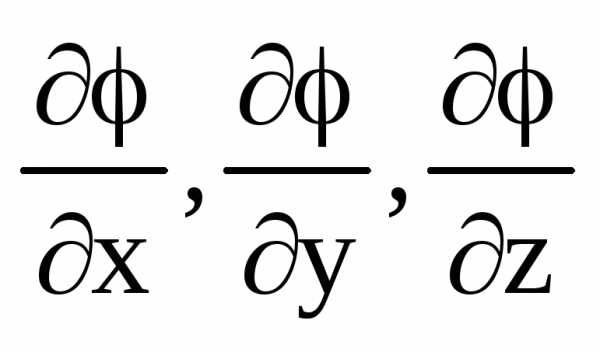 называется градиентом функциии обозначается символомgradилисимволический
вектор,(набла) –
называется оператором Гамильтона.читается «набла фи».
называется градиентом функциии обозначается символомgradилисимволический
вектор,(набла) –
называется оператором Гамильтона.читается «набла фи».
Сравнивая (3.15) и (3.16), можно видеть, что в случае потенциального силового поля
. (3.17)
Подставляя (3.17) в выражение для работы, получим
,
.
Если поле стационарно, то правая часть этого уравнения представляет собой полный дифференциал функции П(x,y,z,). Следовательно, работа, совершенная над частицей в стационарном силовом поле:
. (3.18)
Проинтегрируем соотношение (3.18) вдоль некоторой траектории от точки 1 до точки 2:
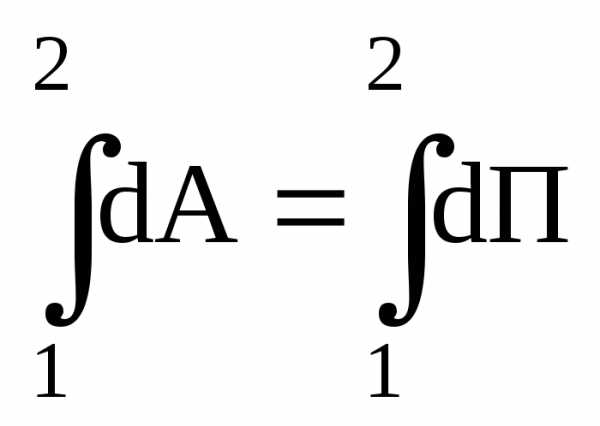 .
.
Левая часть этой формулы дает работу А12, совершенную силами поля на пути 1-2. Сумма элементарных приращенийdП функции П равна полному приращению этой функции на пути 1-2:
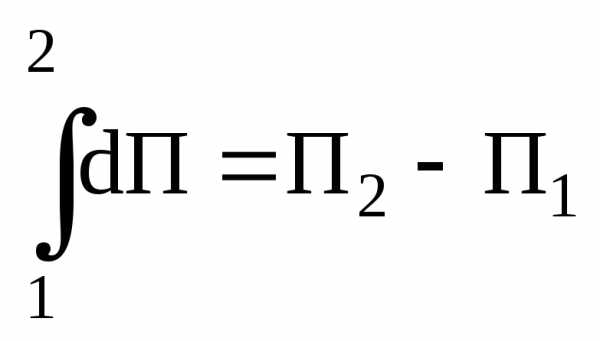 .
.
Таким образом, работа на пути 1-2 равна полному приращению функции П на пути 1-2:
А12=П2-П1. (3.19)
Форма траектории, по которой осуществлялось интегрирование, была совершенно произвольна. Отсюда заключаем, что работа, совершаемая над частицей силами стационарного потенциального поля, не зависит от пути, по которому движется частица, а определяется только начальным и конечным положением частицы в пространстве.
Силы, работа которых не зависит от пути, по которому частицы переходят из одного положения в другое, называется консервативными. Силы, действующие на частицу в стационарном потенциальном поле, являются консервативными. Работа консервативных сил на замкнутом пути равна нулю.
Консервативными силами являются силы тяготения, силы упругости, силы электростатического происхождения, так как их работа не зависит от формы пути.
В формуле (3.19), определяющей работу, совершенную силами поля на пути (1-2) П1и П2– значения потенциальной функции П(x,y,z) в начальной и конечной точках. Эта работа идет на приращение кинетической энергии частицы:
. (3.20)
Обозначим – П(x,y,z)=Eп. Соотношение (3.20) примет вид
;
.
Полученный результат означает, что величина (Eк+Eп) для частицы, находящейся в поле консервативных сил, остается постоянной (является интегралом движения). СлагаемоеEкесть кинетическая энергия частицы. Все величины в (3.19) имеют одинаковую размерность – размерность энергии. ФункциюEп(x,y,z) называют потенциальной энергией частицы во внешнем поле сил. Величину Е, равную сумме кинетической и потенциальной энергии частицы, называют полной механической энергией частицы.
В равенстве (3.19) П(x,y,z) заменим на –Eп(x,y,z), получим
.
Работа, совершаемая над частицей консервативными силами, равна убыли потенциальной энергии частицы. Иначе, работа, совершается за счет запаса потенциальной энергии.
Заменив в соотношении (3.18) функцию П(x,y,z) потенциальной энергией, найдем связь между потенциальной энергией и силой:
.
Таким образом, сила, действующая на частицу в стационарном потенциальном силовом поле, равна градиенту потенциальной энергии в данной точке, взятому с обратным знаком. Компоненты силы определяются следующими выражениями:
.
Конкретный вид функции Eп(x,y,z) зависит от характера силового поля. Чтобы найти потенциальную энергию частицы в поле силы тяжести (рис.3.3), вспомним, что работа, совершаемая над частицей силами этого поля, равна
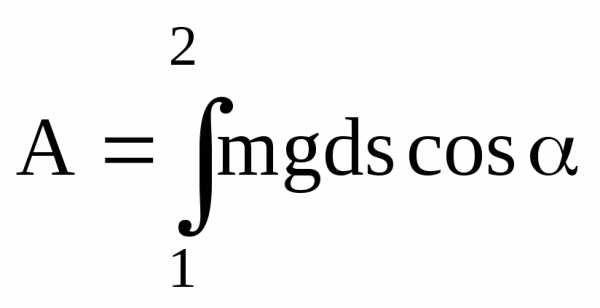 ;
;
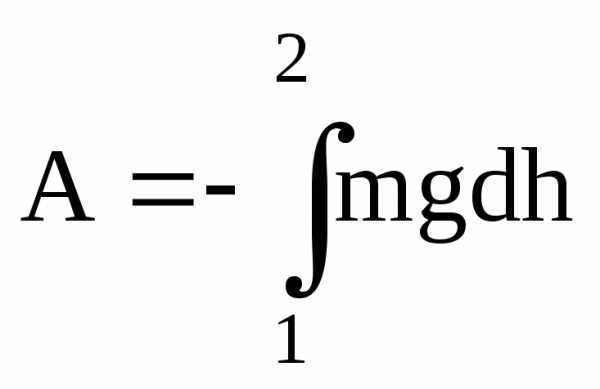 .
.
С другой стороны, .
h 2 h2 dh h1 1 mg s Рис.3.3 | Сравнивая эти соотношения, можно видеть, что потенциа-льная энергия частицы в поле силы тяжести определяется выражением: , где h- отсчитывается от произ-вольного уровня. |
studfiles.net
3.1. Работа. Кинетическая энергия
3. РАБОТА И ЭНЕРГИЯ
В предыдущем разделе рассмотрены законы динамики, которые позволяют рассчитать, как будет двигаться тело массой т под действием силыF. Но задачи механики не сводятся лишь к расчёту траекторий тел. В ряде случаев важно не только то, как будет двигаться тело, но и какую для этого необходимо совершить работу, какой энергией будет обладать тело в процессе движения и в какой форме будет существовать энергия. Именно эти проблемы и будут рассмотрены в данном разделе.
Пусть вдоль оси х движется частица массойт. Пусть на частицу действует постоянная силаF, параллельная осих. Динамическое уравнение, спроецированное на осьх, будет иметь вид
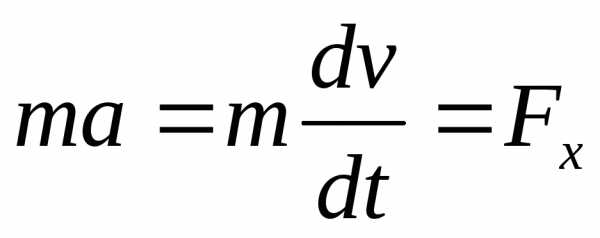
Умножим обе части этого уравнения на скорость частицы vи перенесём величинуdt в правую часть
Учитывая, что 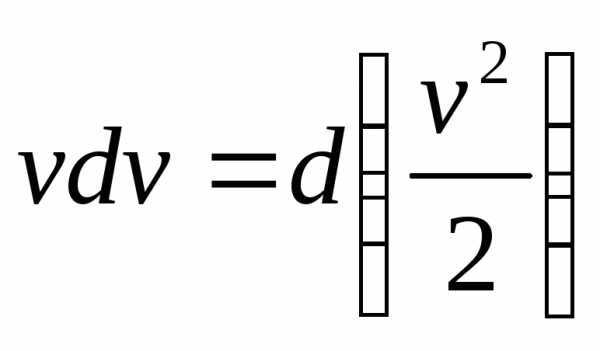 иvdt=dх,
гдеdх– элементарное
перемещение частицы за времяdt,
получаем
иvdt=dх,
гдеdх– элементарное
перемещение частицы за времяdt,
получаем
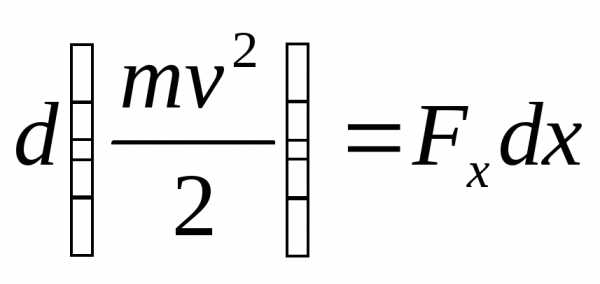
Величина 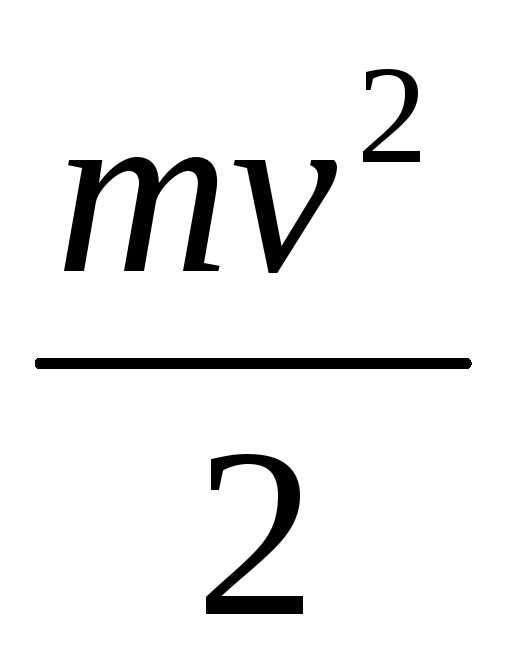 называетсякинетической энергией, а величинаFxdх–элементарнойработой. С
использованием этих терминов полученное
соотношение можно прочесть следующим
образом: элементарная работа, совершённая
на бесконечно малом перемещенииdx силойF, идёт на
приращение кинетической энергии частицы.
называетсякинетической энергией, а величинаFxdх–элементарнойработой. С
использованием этих терминов полученное
соотношение можно прочесть следующим
образом: элементарная работа, совершённая
на бесконечно малом перемещенииdx силойF, идёт на
приращение кинетической энергии частицы.
Если частица под действием силы F совершила конечное перемещение из точки1 в точку 2, то связь работы и кинетической энергии имеет следующий вид:
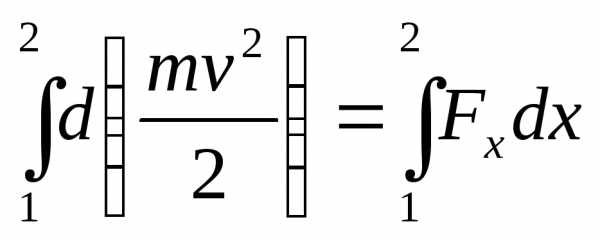
Взяв интегралы, получим
или
W2–W1=A12,
Где v1,v2– скорости частицы в точках 1 и 2,W1,W2– значения кинетической энергии в тех же точках.
Полученное соотношение показывает, что и в этом случае работа, совершённая силой Fна перемещении из точки 1 в точку 2, идёт на приращение кинетической энергии частицы.
Обратите внимание на то, что в ходе анализа не учитывалось, какая именно сила действовала на частицу. Поэтому работа любой силы идёт на приращение кинетической энергии.
Отметим, что выражение для расчета кинетической энергии можно записать и в другом виде:
где p– импульс рассматриваемой частицы.
Как было уже показано, элементарная работа равна Fxdx. В выражение для элементарной работы входит проекция силыF на осьх (в данном случае это направление движения). Эта проекция равнаFcos, где- угол между силой и направлением движения. С учётом сказанного выражение для элементарной работы, совершённой силойF на элементарном перемещенииdr, равнаFdrcosa (поскольку элементарное перемещениеdr совпадает с осьюх, модуль перемещенияdr равен приращению координатыdx).
Из векторной алгебры известно, что результат скалярного произведения двух векторов равен произведению модулей векторов на косинус угла между ними. Следовательно, элементарную работу можно выразить в векторной форме. Элементарная работа равна скалярному произведению вектора силы на вектор перемещения Fdr=Fdrcos.
Работа, совершённая силой F на конечном перемещении тела из точки 1 в точку 2, равна
Это выражение является определением механической работы.
Работа есть скалярная величина, так как результат скалярного произведения силы на перемещение является скаляром. Работа может быть положительной (если угол <90o), отрицательной (если угол>90o) и равной нулю (если угол=90o).
Физический смысл работы таков: работа является мерой энергии, переданной в ходе механического воздействия на тело.
Если на движущуюся материальную точку или тело действуют одновременно несколько сил, то работа будет равна
т.е. полная работа, совершаемая несколькими силами, равна алгебраической сумме работ всех сил, действующих на тело.
Полную работу нескольких сил можно рассчитать и иначе: заменить действующие силы одной, равной векторной сумме всех сил, приложенных к телу (она называется равнодействующей силой), и подсчитать работу этой силы:
F=F1+F2+…+Fk
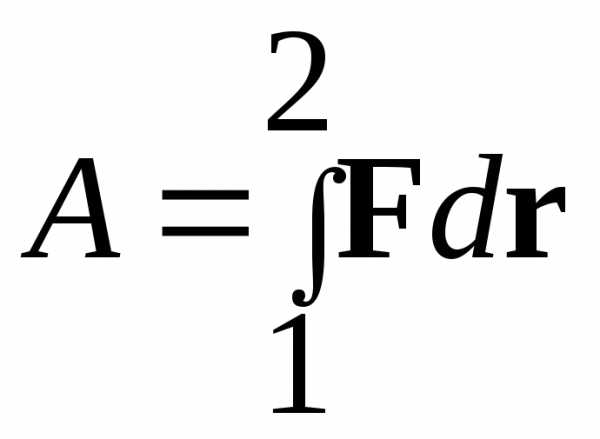 .
.
В системе СИ единицей измерения работы и энергии является джоуль [A]=Дж (Дж=кг.м/с2).
Вкачестве примера найдём работу, совершаемую некоторыми силами.
studfiles.net