Теоретическая механика общие теоремы динамики – Методичка (Общие теоремы динамики), условие Типового расчета №2 » СтудИзба
- Комментариев к записи Теоретическая механика общие теоремы динамики – Методичка (Общие теоремы динамики), условие Типового расчета №2 » СтудИзба нет
- Советы абитуриенту
- Лекция 13 общие теоремы динамики механической системы
- 7) Общие теоремы динамики для материальной точки их значение.
- ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ МАТЕРИАЛЬНОЙ ТОЧКИ ЛЕКЦИИ ПО ТЕОРЕТИЧЕСКОЙ
- Общие теоремы динамики и общее уравнение механики
- О принципе виртуальных перемещений
- Лекции 36 часов (2 часа в неделю)
- 3. ОБЪЕМ ДИСЦИПЛИНЫ И ВИДЫ УЧЕБНОЙ РАБОТЫ
- Издательство ГОУ ВПО ТГТУ
- МЕТОДИЧЕСКИЕ УКАЗАНИЯ
- 3. ОБЪЕМ ДИСЦИПЛИНЫ И ВИДЫ УЧЕБНОЙ РАБОТЫ
- 1. Геометрия масс (продолжение) Рис. 10.1
- ОСНОВЫ АНАЛИТИЧЕСКОЙ МЕХАНИКИ. Ковалев Л.А.
- Автоколебания системы с сухим трением
- Семинар 5. Частные производные
- МЕТОДИЧЕСКИЕ УКАЗАНИЯ
- ТЕОРЕТИЧЕСКАЯ МЕХАНИКА ЛЕКЦИЯ 3
- Лекция 16. Общие принципы динамики
- ЧЕБЫШЕВСКИЙ СБОРНИК Том 14 Выпуск 1 (2013)
- Условия сохранения покоя твердого тела
- внутренними. Будем обозначать их
- ТЕОРЕТИЧЕСКАЯ МЕХАНИКА ЛЕКЦИЯ 4
- 9.8 Релятивистская динамика
- Лекция 6. Прямая на плоскости
- Разработка модели мехатронной системы
- Нелинейные динамические системы
- 12.1. Теорема о движении центра масс
- I КОЛЕБАНИЕ УЗЛА ФЕРМЫ. Пример решения
- ДИНАМИКА. Описание движения твердого тела
- Теоретическая механика
- Общие теоремы динамики.
- Теоретическая механика
Лекция 13 общие теоремы динамики механической системы
При
большом количестве материальных точек,
входящих в состав механической системы,
или, если в её состав входят абсолютно
твёрдые тела ( ),
совершающие непоступательное движение,
применение системы дифференциальных
уравнений движения при решении основной
задачи динамики механической системы
оказывается практически неосуществимым.
Однако при решении многих инженерных
задач нет необходимости в определении
движения каждой точки механической
системы в отдельности. Иногда бывает
достаточно сделать выводы о наиболее
важных сторонах изучаемого процесса
движения, не решая полностью систему
уравнений движения. Эти выводы из
дифференциальных уравнений движения
механической системы составляют
содержание общих теорем динамики. Общие
теоремы, во-первых, освобождают от
необходимости в каждом отдельном случае
производить те математические
преобразования, которые являются общими
для разных задач и их раз и навсегда
производят при выводе теорем из
дифференциальных уравнений движения.
Во-вторых, общие теоремы дают связь
между общими агрегированными
характеристиками движения механической
системы, имеющими наглядный физический
смысл. Эти общие характеристики, такие
как количество движения, кинетический
момент, кинетическая энергия механической
системы называются
),
совершающие непоступательное движение,
применение системы дифференциальных
уравнений движения при решении основной
задачи динамики механической системы
оказывается практически неосуществимым.
Однако при решении многих инженерных
задач нет необходимости в определении
движения каждой точки механической
системы в отдельности. Иногда бывает
достаточно сделать выводы о наиболее
важных сторонах изучаемого процесса
движения, не решая полностью систему
уравнений движения. Эти выводы из
дифференциальных уравнений движения
механической системы составляют
содержание общих теорем динамики. Общие
теоремы, во-первых, освобождают от
необходимости в каждом отдельном случае
производить те математические
преобразования, которые являются общими
для разных задач и их раз и навсегда
производят при выводе теорем из
дифференциальных уравнений движения.
Во-вторых, общие теоремы дают связь
между общими агрегированными
характеристиками движения механической
системы, имеющими наглядный физический
смысл. Эти общие характеристики, такие
как количество движения, кинетический
момент, кинетическая энергия механической
системы называются
Первая мера движения – количество движения механической системы
z Mk O y x Рис. 13.1 | Пусть
дана механическая система, состоящая
из 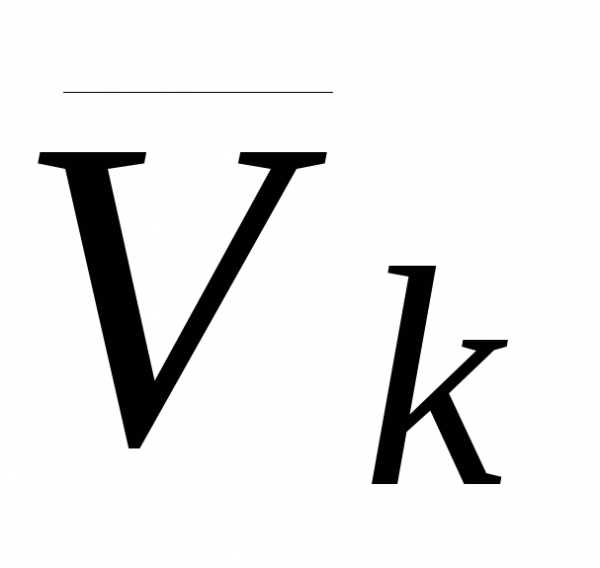 –
скорость точки –
скорость точки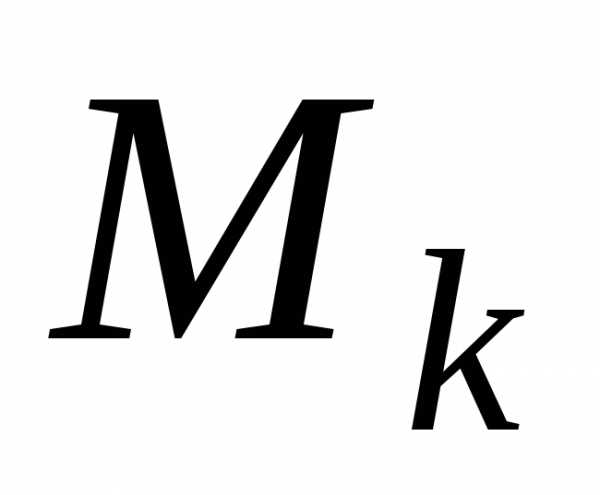 . . |
Количеством движения материальной точки называется векторная мера её движения, равная произведению массы точки на её скорость:
.
Количеством движения механической системы называется векторная мера её движения, равная сумме количеств движения её точек:
 , (13.1)
, (13.1)
или в проекциях на оси координат
.
Преобразуем правую часть формулы (23.1):
,
где
–
масса всей системы,
Следовательно, количество движения механической системы равно количеству движения её центра масс, если сосредоточить в нём всю массу системы:
 .
.
Пример: Рис. 13.2 | Количество
движения колеса массой М,
катящегося без скольжения по
горизонтальной плоскости со скоростью так как скорость центра масс колеса совпадает со скоростью оси колеса. |
Импульс силы
Произведение
силы на элементарный промежуток времени
её действия  называется элементарным импульсом
силы.
называется элементарным импульсом
силы.
Импульсом
силы  за промежуток времени [0,t]
называется интеграл от элементарного
импульса силы
за промежуток времени [0,t]
называется интеграл от элементарного
импульса силы
 .
.
Теорема об изменении количества движения механической системы
Пусть
на каждую точку  механической
системы действуют равнодействующая
внешних сил
механической
системы действуют равнодействующая
внешних сил и равнодействующая внутренних сил
и равнодействующая внутренних сил
Рассмотрим основные уравнения динамики механической системы
(13.2)
Складывая почленно уравнения (13.2) для n точек системы, получим
(13.3)
Первая
сумма в правой части равна главному
вектору  внешних сил системы. Вторая сумма равна
нулю по свойству внутренних сил системы.
Рассмотрим левую часть равенства (13.3):
внешних сил системы. Вторая сумма равна
нулю по свойству внутренних сил системы.
Рассмотрим левую часть равенства (13.3):
.
Таким образом, получим:
 , (13.4)
, (13.4)
или в проекциях на оси координат
(13.5)
Равенства (13.4) и (13.5) выражают теорему об изменении количества движения механической системы:
Эту теорему можно представить также в интегральной форме, проинтегрировав обе части равенства (13.4) по времени в пределах от t0 до t:
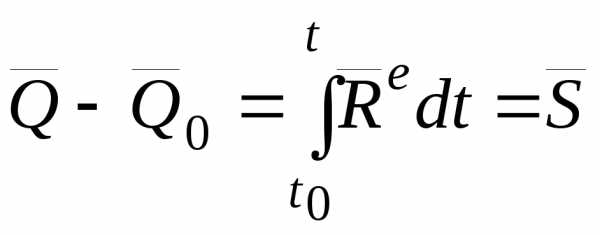 , (13.6)
, (13.6)
где , а интеграл в правой части – импульс внешних сил за
время t–t0.
Равенство (13.6) представляет теорему в интегральной форме:
Приращение количества движения механической системы за конечное время равно импульсу внешних сил за это время.
Теорему называют также теоремой импульсов.
В проекциях на оси координат, теорема запишется в виде:
.
Следствия (законы сохранения количества движения) 1).
Если главный вектор внешних сил за
рассматриваемый промежуток времени
равен нулю, то количество движения
механической системы постоянно, т.е.
если  ,.
,.
2). Если проекция главного вектора внешних сил на какую-либо ось за рассматриваемый промежуток времени равна нулю, то проекция количества движения механической системы на эту ось постоянна,
т.е.
если  то.
то.
studfiles.net
7) Общие теоремы динамики для материальной точки их значение.
Для решения многих задач динамики удобно пользоваться так называемыми общими теоремами, являющимися следствиями основного закона динамики.
Количество движения, кинетическая энергия точки, импульс силы, работа силы, мощность.
Значение состоит в том, что они устанавливают наглядные зависимости между основными динамическими характеристиками движения материальных тел и открывают тем самым новые возможности исследования механических движений, широко применяемые в инженерной практике. Кроме того, теоремы позволяют изучать отдельные, практически важные стороны данного явления, не изучая явление в целом. Применение теорем избавляет от необходимости проделывать для каждой задачи те операции интегрирования, которые раз и навсегда производятся при выводе этих теорем; тем самым упрощая процесс решения.
8) Количество движения точки. Элементарный импульс и импульс силы за конечный промежуток времени.
Количеством движения мат точки называется вектор, имеющий направление вектора скорости, и модуль, равный произведению массы точки m на модуль скорости её движения v.
Элементарный импульс сил
– этовекторная величина, равная произведению вектора силы на элементарный промежуток времени. Это векторная величина имеющая направление силы (ds=F·dt)Импульс силы за конечный промежуток времени.

9) Теорема об изменении количества движения точки в дифференциальной и конечной формах.
В диф. Форме.
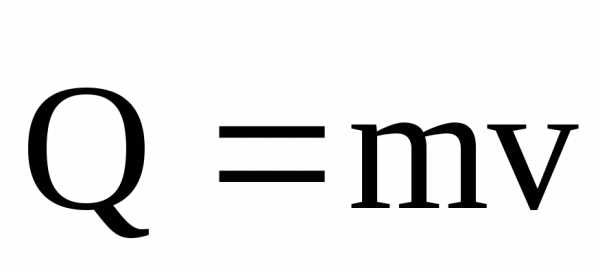 –количество
движения материальной точки,
–количество
движения материальной точки,  – элементарный импульс силы.– элементарное изменение количества
движения материальной точки равно
элементарному импульсу силы, приложенной
к этой точке (теорема в дифференц-ной
форме) или
– элементарный импульс силы.– элементарное изменение количества
движения материальной точки равно
элементарному импульсу силы, приложенной
к этой точке (теорема в дифференц-ной
форме) или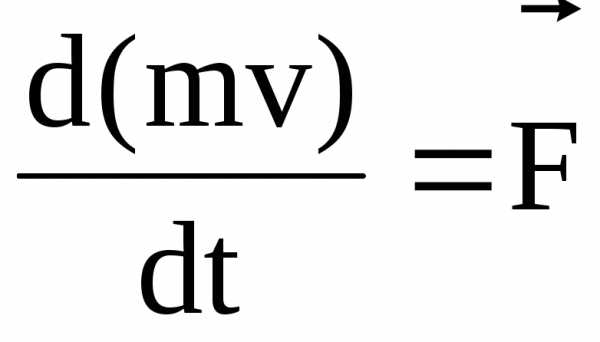 –
производная по времени от количества
движения материальной точки равна
равнодействующей сил, приложенных к
этой точке.
–
производная по времени от количества
движения материальной точки равна
равнодействующей сил, приложенных к
этой точке.
В конечной(интегральной )форме:
Проинтегрируем: 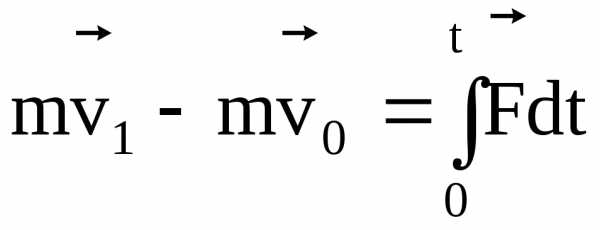 – изменение количества движения
материальной точки занекоторый
промежуток времени равно
геометрической сумме
импульсов
сил, приложенных
к этой точке, за тот же промежуток
времени.
– изменение количества движения
материальной точки занекоторый
промежуток времени равно
геометрической сумме
импульсов
сил, приложенных
к этой точке, за тот же промежуток
времени.  –
импульс силы за промежуток времени
[0,t]. В проекциях на оси координат:
–
импульс силы за промежуток времени
[0,t]. В проекциях на оси координат: и т.д.
и т.д.
10) Момент количества движения точки относительно центра и оси. Относительно центра
Моментом количества движения мат.точки относительно центра называется вектор, модуль которого = произведению модуля количества движения на кратчайшее расстояние от центра до линии действия вектора количества движения, I-й плоскости в которой лежат упоминающиеся линии и направленный так, что бы глядя от его конца видеть движение, совершающееся против часовой стрелки. mц(mυ)=r·(mυ)
Момент количества движения точки относительно оси.
Моментом количества движения мат.точки относительно оси называется скалярная величена = произведению проекции количества движения мат.точки на плоскость перпендикулярную данной оси и на кратчайшее расстояние от точки пересечения данной оси с этой плоскостью до прямой, на которой лежит прямая вектора количества движения.
mz(mυ)=±h(mυxy) (h-плечо вектора mυ)
studfiles.net
ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ МАТЕРИАЛЬНОЙ ТОЧКИ ЛЕКЦИИ ПО ТЕОРЕТИЧЕСКОЙ
 ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ МАТЕРИАЛЬНОЙ ТОЧКИ ЛЕКЦИИ ПО ТЕОРЕТИЧЕСКОЙ МЕХАНИКЕ. ДИНАМИКА ЛЕКЦИЯ 5
ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ МАТЕРИАЛЬНОЙ ТОЧКИ ЛЕКЦИИ ПО ТЕОРЕТИЧЕСКОЙ МЕХАНИКЕ. ДИНАМИКА ЛЕКЦИЯ 5
 Цель лекции Ознакомиться с общими теоремами динамики материальной точки и примерами их практического применения. План лекции Введение • Теорема об изменении импульса точки • Теорема об изменении момента импульса точки • Движение в центральном поле • Теорема об изменении кинетической энергии точки • Работа силы. Потенциальные силы Заключение 2 Цель лекции
Цель лекции Ознакомиться с общими теоремами динамики материальной точки и примерами их практического применения. План лекции Введение • Теорема об изменении импульса точки • Теорема об изменении момента импульса точки • Движение в центральном поле • Теорема об изменении кинетической энергии точки • Работа силы. Потенциальные силы Заключение 2 Цель лекции
 ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ ТОЧКИ теоремы об изменении … импульса момента импульса кинетической энергии Зачем нам нужны теоремы для точки? оптимальная методика решения задач 3 Введение на основе теорем динамики для точки мы построим теоремы для механической системы
ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ ТОЧКИ теоремы об изменении … импульса момента импульса кинетической энергии Зачем нам нужны теоремы для точки? оптимальная методика решения задач 3 Введение на основе теорем динамики для точки мы построим теоремы для механической системы
 ИМПУЛЬС ТОЧКИ Импульс (количество движения) точки – вектор, равный произведению массы точки на вектор ее скорости 4 Теорема об изменении импульса
ИМПУЛЬС ТОЧКИ Импульс (количество движения) точки – вектор, равный произведению массы точки на вектор ее скорости 4 Теорема об изменении импульса
 ИМПУЛЬС СИЛЫ Элементарным импульсом силы называется вектор, равный произведению силы на элементарный промежуток времени Импульсом силы за конечный промежуток времени называется вектор 5 Теорема об изменении импульса
ИМПУЛЬС СИЛЫ Элементарным импульсом силы называется вектор, равный произведению силы на элементарный промежуток времени Импульсом силы за конечный промежуток времени называется вектор 5 Теорема об изменении импульса
 ТЕОРЕМА ОБ ИЗМЕНЕНИИ ИМПУЛЬСА Производная по времени от импульса материальной точки равна равнодействующей приложенных к точке сил Изменение импульса материальной точки за некоторый временной интервал равно импульсу равнодействующей приложенных к точке сил на этом интервале 6 Теорема об изменении импульса
ТЕОРЕМА ОБ ИЗМЕНЕНИИ ИМПУЛЬСА Производная по времени от импульса материальной точки равна равнодействующей приложенных к точке сил Изменение импульса материальной точки за некоторый временной интервал равно импульсу равнодействующей приложенных к точке сил на этом интервале 6 Теорема об изменении импульса
 ДОКАЗАТЕЛЬСТВО • Запишем дифф. уравнение движения точки • Учитывая постоянство массы точки и определение ее ускорения получим или • Умножив обе части уравнения на элементарный промежуток времени и проинтегрировав, получим или 7 Теорема об изменении импульса Теорема доказана
ДОКАЗАТЕЛЬСТВО • Запишем дифф. уравнение движения точки • Учитывая постоянство массы точки и определение ее ускорения получим или • Умножив обе части уравнения на элементарный промежуток времени и проинтегрировав, получим или 7 Теорема об изменении импульса Теорема доказана
 ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА • Пусть • В этом случае Если равнодействующая приложенных к материальной точке сил равна нулю, то импульс точки сохраняется во все время движения Если проекция на какую-нибудь ось равнодействующей приложенных к точке сил равна нулю, то проекция импульса точки на эту ось сохраняется 8 Теорема об изменении импульса
ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА • Пусть • В этом случае Если равнодействующая приложенных к материальной точке сил равна нулю, то импульс точки сохраняется во все время движения Если проекция на какую-нибудь ось равнодействующей приложенных к точке сил равна нулю, то проекция импульса точки на эту ось сохраняется 8 Теорема об изменении импульса
 ПРИМЕР 9 Теорема об изменении импульса Определить время движения точки до остановки ?
ПРИМЕР 9 Теорема об изменении импульса Определить время движения точки до остановки ?
 МОМЕНТ ИМПУЛЬСА ТОЧКИ Момент импульса (момент количества движения) точки вектор, определяемый равенством – радиус-вектор точки, проведенный из центра O 10 Теорема об изменении момента импульса
МОМЕНТ ИМПУЛЬСА ТОЧКИ Момент импульса (момент количества движения) точки вектор, определяемый равенством – радиус-вектор точки, проведенный из центра O 10 Теорема об изменении момента импульса
 МОМЕНТ ИМПУЛЬСА ТОЧКИ O 11 Теорема об изменении момента импульса
МОМЕНТ ИМПУЛЬСА ТОЧКИ O 11 Теорема об изменении момента импульса
 ТЕОРЕМА ОБ ИЗМЕНЕНИИ МОМЕНТА ИМПУЛЬСА Производная по времени от момента импульса материальной точки относительно некоторого неподвижного центра равна моменту равнодействующей приложенных к точке сил относительно этого же центра 12 Теорема об изменении момента импульса
ТЕОРЕМА ОБ ИЗМЕНЕНИИ МОМЕНТА ИМПУЛЬСА Производная по времени от момента импульса материальной точки относительно некоторого неподвижного центра равна моменту равнодействующей приложенных к точке сил относительно этого же центра 12 Теорема об изменении момента импульса
 ДОКАЗАТЕЛЬСТВО • Запишем теорему об изменении импульса точки • Умножим обе части уравнения векторно на радиус-вектор точки • Рассмотрим выражение • Таким образом, 13 Теорема об изменении момента импульса • Теорема доказана
ДОКАЗАТЕЛЬСТВО • Запишем теорему об изменении импульса точки • Умножим обе части уравнения векторно на радиус-вектор точки • Рассмотрим выражение • Таким образом, 13 Теорема об изменении момента импульса • Теорема доказана
 ПРОЕКЦИИ МОМЕНТА ИМПУЛЬСА 14 Теорема об изменении момента импульса
ПРОЕКЦИИ МОМЕНТА ИМПУЛЬСА 14 Теорема об изменении момента импульса
 ЗАКОН СОХРАНЕНИЯ МОМЕНТА ИМПУЛЬСА • Пусть • В этом случае Если момент равнодействующей приложенных к материальной точке сил относительно какого-либо центра равен нулю, то момент импульса точки сохраняется 15 Теорема об изменении момента импульса
ЗАКОН СОХРАНЕНИЯ МОМЕНТА ИМПУЛЬСА • Пусть • В этом случае Если момент равнодействующей приложенных к материальной точке сил относительно какого-либо центра равен нулю, то момент импульса точки сохраняется 15 Теорема об изменении момента импульса
 ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ ЦЕНТРАЛЬНОЙ СИЛЫ Действующую на материальную точку силу называют центральной, если она всегда направлена к некоторому неподвижному центру. Пример 16 Теорема об изменении момента импульса ?
ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ ЦЕНТРАЛЬНОЙ СИЛЫ Действующую на материальную точку силу называют центральной, если она всегда направлена к некоторому неподвижному центру. Пример 16 Теорема об изменении момента импульса ?
 ДВИЖЕНИЕ ПЛАНЕТ Как изменяется модуль скорости планеты при движении по эллиптической траектории 17 Теорема об изменении момента импульса ?
ДВИЖЕНИЕ ПЛАНЕТ Как изменяется модуль скорости планеты при движении по эллиптической траектории 17 Теорема об изменении момента импульса ?
 ДВИЖЕНИЕ ПЛАНЕТ Определим закон изменения площади сектора . модуль 18 Теорема об изменении момента импульса направление ?
ДВИЖЕНИЕ ПЛАНЕТ Определим закон изменения площади сектора . модуль 18 Теорема об изменении момента импульса направление ?
 ДВИЖЕНИЕ ПЛАНЕТ 19 Теорема об изменении момента импульса
ДВИЖЕНИЕ ПЛАНЕТ 19 Теорема об изменении момента импульса
 ДВИЖЕНИЕ ПЛАНЕТ Каждая планета движется в плоскости, проходящей через центр Солнца, причём за равные промежутки времени радиус-вектор, соединяющий Солнце и планету, описывает равные площади 20 Теорема об изменении момента импульса
ДВИЖЕНИЕ ПЛАНЕТ Каждая планета движется в плоскости, проходящей через центр Солнца, причём за равные промежутки времени радиус-вектор, соединяющий Солнце и планету, описывает равные площади 20 Теорема об изменении момента импульса
 ДВИЖЕНИЕ ПЛАНЕТ Иоганн Кеплер (1571 – 1630) 21 Теорема об изменении момента импульса
ДВИЖЕНИЕ ПЛАНЕТ Иоганн Кеплер (1571 – 1630) 21 Теорема об изменении момента импульса
 КИНЕТИЧЕСКАЯ ЭНЕРГИЯ ТОЧКИ- скалярная величина, равная половине произведения массы точки на квадрат ее скорости 22 Теорема об изменении энергии
КИНЕТИЧЕСКАЯ ЭНЕРГИЯ ТОЧКИ- скалярная величина, равная половине произведения массы точки на квадрат ее скорости 22 Теорема об изменении энергии
 РАБОТА СИЛЫ траектория точки – прямая 23 Теорема об изменении энергии
РАБОТА СИЛЫ траектория точки – прямая 23 Теорема об изменении энергии
 РАБОТА СИЛЫ 24 Теорема об изменении энергии
РАБОТА СИЛЫ 24 Теорема об изменении энергии
 РАБОТА СИЛЫ Элементарная работа силы – величина, равная скалярному произведению вектора силы на вектор элементарного перемещения Работа силы на конечном перемещении – интеграл от элементарной работы, взятый вдоль этого перемещения 25 Теорема об изменении энергии
РАБОТА СИЛЫ Элементарная работа силы – величина, равная скалярному произведению вектора силы на вектор элементарного перемещения Работа силы на конечном перемещении – интеграл от элементарной работы, взятый вдоль этого перемещения 25 Теорема об изменении энергии
 ТЕОРЕМА ОБ ИЗМЕНЕНИИ ЭНЕРГИИ Изменение кинетической энергии точки на некотором перемещении равно сумме работ всех действующих на нее сил на этом же перемещении 26 Теорема об изменении энергии
ТЕОРЕМА ОБ ИЗМЕНЕНИИ ЭНЕРГИИ Изменение кинетической энергии точки на некотором перемещении равно сумме работ всех действующих на нее сил на этом же перемещении 26 Теорема об изменении энергии
 ДОКАЗАТЕЛЬСТВО Запишем дифф. уравнение движения точки Спроектируем его на тангенциальную ось Представим тангенциальное ускорение в виде и учтем, что проекция силы 27 Теорема об изменении энергии
ДОКАЗАТЕЛЬСТВО Запишем дифф. уравнение движения точки Спроектируем его на тангенциальную ось Представим тангенциальное ускорение в виде и учтем, что проекция силы 27 Теорема об изменении энергии
 ДОКАЗАТЕЛЬСТВО Умножим обе части уравнения на элементарное перемещение и проинтегрировав, получим Теорема доказана 28 Теорема об изменении энергии
ДОКАЗАТЕЛЬСТВО Умножим обе части уравнения на элементарное перемещение и проинтегрировав, получим Теорема доказана 28 Теорема об изменении энергии
 ПРИМЕР Бусинка двигается по проволоке, изогнутой в форме полуокружности. Определить ее скорость в точке B, если в начальный момент она находилась в покое. Трением пренебречь. 29 Теорема об изменении энергии
ПРИМЕР Бусинка двигается по проволоке, изогнутой в форме полуокружности. Определить ее скорость в точке B, если в начальный момент она находилась в покое. Трением пренебречь. 29 Теорема об изменении энергии
 ПРИМЕР • Будем считать бусинку материальной точкой • Изобразим силы, действующие на нее в некоторый момент времени … • … и элементарное перемещение 30 Теорема об изменении энергии
ПРИМЕР • Будем считать бусинку материальной точкой • Изобразим силы, действующие на нее в некоторый момент времени … • … и элементарное перемещение 30 Теорема об изменении энергии
 ПРИМЕР • Запишем теорему об изменении кинетической энергии 31 Теорема об изменении энергии
ПРИМЕР • Запишем теорему об изменении кинетической энергии 31 Теорема об изменении энергии
 ПРИМЕР Согласно теореме Замечание Можно ли получить этот результат более простым способом? 32 Теорема об изменении энергии
ПРИМЕР Согласно теореме Замечание Можно ли получить этот результат более простым способом? 32 Теорема об изменении энергии
 ПОТЕНЦИАЛЬНЫЕ СИЛЫ Градиентом называется вектор с компонентами Сила называется потенциальной (консервативной), если ее можно представить в виде градиента некоторой скалярной функции, называемой потенциалом 33 Теорема об изменении энергии
ПОТЕНЦИАЛЬНЫЕ СИЛЫ Градиентом называется вектор с компонентами Сила называется потенциальной (консервативной), если ее можно представить в виде градиента некоторой скалярной функции, называемой потенциалом 33 Теорема об изменении энергии
 ПОТЕНЦИАЛЬНЫЕ СИЛЫ Работа потенциальной силы не зависит от формы траектории точки и закона ее движения и определяется только начальным и конечным положением точки 34 Теорема об изменении энергии
ПОТЕНЦИАЛЬНЫЕ СИЛЫ Работа потенциальной силы не зависит от формы траектории точки и закона ее движения и определяется только начальным и конечным положением точки 34 Теорема об изменении энергии
 ПОТЕНЦИАЛЬНЫЕ СИЛЫ. ПРИМЕР Попробуем построить потенциал для силы тяжести 35 Теорема об изменении энергии
ПОТЕНЦИАЛЬНЫЕ СИЛЫ. ПРИМЕР Попробуем построить потенциал для силы тяжести 35 Теорема об изменении энергии
 ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ Замечание Потенциал определяется с точностью до некоторой не зависящей от координат постоянной Потенциальной энергией точки, находящейся под действием консервативной силы, называется величина Пусть 36 Теорема об изменении энергии
ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ Замечание Потенциал определяется с точностью до некоторой не зависящей от координат постоянной Потенциальной энергией точки, находящейся под действием консервативной силы, называется величина Пусть 36 Теорема об изменении энергии
 ПОЛНАЯ МЕХАНИЧЕСКАЯ ЭНЕРГИЯ Запишем теорему об изменении кинетической энергии для точки, находящейся под действием потенциальной силы Для точки, находящейся под действием потенциальной силы, можно ввести полную механическую энергию как сумму ее потенциальной и кинетической энергий. При движении точки она сохраняется. Если на точку действует несколько потенциальных сил 37 Теорема об изменении импульса
ПОЛНАЯ МЕХАНИЧЕСКАЯ ЭНЕРГИЯ Запишем теорему об изменении кинетической энергии для точки, находящейся под действием потенциальной силы Для точки, находящейся под действием потенциальной силы, можно ввести полную механическую энергию как сумму ее потенциальной и кинетической энергий. При движении точки она сохраняется. Если на точку действует несколько потенциальных сил 37 Теорема об изменении импульса
 РАБОТА ПОТЕНЦИАЛЬНЫХ СИЛ 38 Теорема об изменении энергии
РАБОТА ПОТЕНЦИАЛЬНЫХ СИЛ 38 Теорема об изменении энергии
 ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ 1. Какие из уравнений динамики точки записываются в виде векторных уравнений, а какие – скалярных? 2. Что такое импульс материальной точки? 3. Как определяется импульс силы за конечный промежуток времени? 4. При каких условиях количество движения системы не изменяется? 5. Как определяется и момент количества движения точки? 6. Чему равна проекция момента количества движения точки относительно центра на ось? 39 Заключение
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ 1. Какие из уравнений динамики точки записываются в виде векторных уравнений, а какие – скалярных? 2. Что такое импульс материальной точки? 3. Как определяется импульс силы за конечный промежуток времени? 4. При каких условиях количество движения системы не изменяется? 5. Как определяется и момент количества движения точки? 6. Чему равна проекция момента количества движения точки относительно центра на ось? 39 Заключение
 ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ 7. Как происходит движение материальной точки под действием центральной силы? Как формулируется закон Кеплера? 8. Как определяется работа постоянной силы на прямолинейном перемещении точки, к которой она приложена? А если сила переменная и точка перемещается по кривой? 9. Что понимают под элементарной работой силы и как она связана с работой силы на конечном перемещении точки, к которой она приложена? Когда элементарная работа равна нулю? 40 Заключение
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ 7. Как происходит движение материальной точки под действием центральной силы? Как формулируется закон Кеплера? 8. Как определяется работа постоянной силы на прямолинейном перемещении точки, к которой она приложена? А если сила переменная и точка перемещается по кривой? 9. Что понимают под элементарной работой силы и как она связана с работой силы на конечном перемещении точки, к которой она приложена? Когда элементарная работа равна нулю? 40 Заключение
 ТЕМА СЛЕДУЮЩЕЙ ЛЕКЦИИ Динамика механической системы 41 Заключение
ТЕМА СЛЕДУЮЩЕЙ ЛЕКЦИИ Динамика механической системы 41 Заключение
present5.com
Общие теоремы динамики и общее уравнение механики
О принципе виртуальных перемещений
ИПМ иммвкелдыша РАН Электронная библиотека Препринты ИПМ Препринт 65 за 010 г Боровин ГК, Лапшин ВВ О принципе виртуальных перемещений Рекомендуемая форма библиографической ссылки: Боровин ГК, Лапшин ВВ
ПодробнееЛекции 36 часов (2 часа в неделю)
1 Календарный план курса теоретической и прикладной механики на осенний семестр 2012/13 учебного года. Факультет разработки нефтяных и газовых месторождений. Специальность: 131 201 Физические процессы
Подробнее3. ОБЪЕМ ДИСЦИПЛИНЫ И ВИДЫ УЧЕБНОЙ РАБОТЫ
ЦЕЛИ И ЗАДАЧИ ДИСЦИПЛИНЫ. Целью данной дисциплины является изучение общих законов движения и равновесия материальных тел и возникающих при этом взаимодействий между телами. Изучение курса теоретической
ПодробнееИздательство ГОУ ВПО ТГТУ
Издательство ГОУ ВПО ТГТУ Учебное издание ТЕОРЕТИЧЕСКАЯ МЕХАНИКА ОБЩЕЕ УРАВНЕНИЕ ДИНАМИКИ УРАВНЕНИЯ ЛАГРАНЖА Методические указания Составители: ЛОМАКИНА Ольга Владимировна ГАЛАЕВ Валентин Иванович Редактор
ПодробнееМЕТОДИЧЕСКИЕ УКАЗАНИЯ
МЕТОДИЧЕСКИЕ УКАЗАНИЯ В теоретической механике изучаются свойства и законы механического движения и равновесия материальных объектов. Курс теоретической механики делится на три основных раздела: статику,
Подробнее3. ОБЪЕМ ДИСЦИПЛИНЫ И ВИДЫ УЧЕБНОЙ РАБОТЫ
1. ЦЕЛИ И ЗАДАЧИ ДИСЦИПЛИНЫ. Теоретическая механика одна из фундаментальных общенаучных дисциплин физико-математического цикла. Целью данной дисциплины является изучение общих законов движения и равновесия
ПодробнееПример. Два стержня DC и C шарнирно соединены в точке C между собой и в точках и с неподвижными опорами (рис., а). Известно, что силы F 1 1 кh, F кh и пара сил с моментом М кн м ; длины L L L м. 1 3 Рис.,
Подробнее1. Геометрия масс (продолжение) Рис. 10.1
ЛЕКЦИЯ 10 ЭЛЛИПСОИД ИНЕРЦИИ. КИНЕТИЧЕСКИЙ МОМЕНТ И КИНЕТИЧЕСКАЯ ЭНЕРГИЯ ПРИ ВРАЩЕНИИ ВОКРУГ НЕПОДВИЖНОЙ ТОЧКИ. ДИНАМИЧЕСКИЕ УРАВНЕНИЯ ЭЙЛЕРА. СЛУЧАЙ ЭЙЛЕРА 1. Геометрия масс (продолжение) Рис. 10.1 Выберем
ПодробнееОСНОВЫ АНАЛИТИЧЕСКОЙ МЕХАНИКИ. Ковалев Л.А.
ОСНОВЫ АНАЛИТИЧЕСКОЙ МЕХАНИКИ Лекция Аналитическая механика это раздел теоретической механики, в котором изучение равновесия и движения механических систем основано на дифференциальных и интегральных принципах
ПодробнееАвтоколебания системы с сухим трением
# 06, июнь 2016 УДК 534.113 Автоколебания системы с сухим трением Черкасов К. Ю., студент Россия, 105005, г. Москва, МГТУ им. Н.Э. Баумана, кафедра «Динамика и управление полетом ракет и космических аппаратов»
ПодробнееСеминар 5. Частные производные
Семинар 5 Частные производные О. Пусть M 0 (x 1,, x m ) внутренняя точка D(f). Частной производной (ч.п.) функции f(x 1,, x m ) по переменной x k в точке M 0 называется предел f xk (M 0 ) = f (M x 0 )
ПодробнееМЕТОДИЧЕСКИЕ УКАЗАНИЯ
Министерство образования Российской Федерации ОРЕНБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ Кафедра теории механизмов и машин Л.И. Кудина МЕТОДИЧЕСКИЕ УКАЗАНИЯ и варианты заданий для выполнения контрольной
ПодробнееТЕОРЕТИЧЕСКАЯ МЕХАНИКА ЛЕКЦИЯ 3
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА 2 СЕМЕСТР ЛЕКЦИЯ 3 УРАВНЕНИЯ ЛАГРАНЖА ПЕРВОГО РОДА ПРИНЦИП ДАЛАМБЕРА-ЛАГРАНЖА (ОБЩЕЕ УРАВНЕНИЕ ДИНАМИКИ) ПРИНЦИП ВИРТУАЛЬНЫХ ПЕРЕМЕЩЕНИЙ РАБОТА СИЛ ИНЕРЦИИ ТВЁРДОГО ТЕЛА Лектор:
ПодробнееЛекция 16. Общие принципы динамики
Оглавление Принцип Германа Эйлера – Даламбера… 2 Сила инерции… 2 Принцип Даламбера для материальной точки… 2 Принцип Даламбера для системы материальных точек… 3 Принцип Даламбера для несвободной
ПодробнееЧЕБЫШЕВСКИЙ СБОРНИК Том 14 Выпуск 1 (2013)
ЧЕБЫШЕВСКИЙ СБОРНИК Том 14 Выпуск 1 (013) УДК 511.3 К РАСПРЕДЕЛЕНИЮ ПРОСТЫХ ЧИСЕЛ В МНОГОЧЛЕНАХ ВТОРОЙ СТЕПЕНИ С ЦЕЛЫМИ КОЭФФИЦИЕНТАМИ И. И. Ильясов (г. Актобе, Казахстан) Аннотация В работе доказывается:
ПодробнееУсловия сохранения покоя твердого тела
Лекция 3 1 Условия покоя произвольной дискретной механической системы Необходимые условия равновесия внешних сил системы. Рассмотрим дискретную систему n материальных точек. Система находится в покое,
Подробнеевнутренними. Будем обозначать их
Профессор ВА Яковенко Лекция 7 Динамика механических систем Внешние и внутренние силы Движение системы материальных точек Центр масс и центр тяжести механической системы Движение центра масс Закон сохранения
ПодробнееТЕОРЕТИЧЕСКАЯ МЕХАНИКА ЛЕКЦИЯ 4
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА 2 СЕМЕСТР ЛЕКЦИЯ 4 ОБОБЩЁННЫЕ КООРДИНАТЫ И СИЛЫ УРАВНЕНИЯ РАВНОВЕСИЯ СИСТЕМЫ В ОБОБЩЁННЫХ КООРДИНАТАХ ВИРТУАЛЬНЫЙ ДИФФЕРЕНЦИАЛ ПОТЕНЦИАЛЬНЫЕ СИЛЫ Лектор: Батяев Евгений Александрович
ПодробнееУДК 69.783 В. В. К о р о в и н, А. В. П о п о в, В. И. У с ю к и н КВАТЕРНИОННЫЕ ПАРАМЕТРЫ РОДРИГА ГАМИЛЬТОНА В МОДЕЛИ КОСМИЧЕСКОЙ ТРОСОВОЙ СВЯЗКИ Рассмотрена задача пространственного движения космической
Подробнее9.8 Релятивистская динамика
9.8 Релятивистская динамика Принцип относительности Эйнштейна требует, чтобы все законы природы имели один и тот же вид во всех инерциальных системах отсчета. Этому принципу должны удовлетворять, в том
ПодробнееЛекция 6. Прямая на плоскости
Лекция 6 Прямая на плоскости Уравнение прямой, проходящей через заданную точку и имеющей заданный вектор нормали l O b y На плоскости, где введена прямоугольная система координат, рассмотрим прямую l.
ПодробнееРазработка модели мехатронной системы
Министерство образования и науки Российской Федерации Калужский филиал федерального государственного бюджетного образовательного учреждения высшего профессионального образования «Московский государственный
ПодробнееНелинейные динамические системы
П Р ОБ ЛЕ М Ы М ЕХАН ИКИ И УП РАВ ЛЕН ИЯ Нелинейные динамические системы Вып. 47 Межвузовский сборник научных трудов 5 УДК 53.3+6-5 М.Х. Тешаев Бухарский инженерно-технологический институт Республика Узбекистан
Подробнее12.1. Теорема о движении центра масс
Глава 12 ДИНАМИКА СИСТЕМЫ 12.1. Теорема о движении центра масс ПОСТАНОВКА ЗАДАЧИ. Механизм, состоящий из n связанных между собой тел, установлен на призме, находящейся на горизонтальной плоскости. Трение
ПодробнееI КОЛЕБАНИЕ УЗЛА ФЕРМЫ. Пример решения
I КОЛЕБАНИЕ УЗЛА ФЕРМЫ Пример решения Задача. В шарнире C плоской фермы находится точка с массой m = = 9 кг (рис. 1). Материал стержней имеет модуль упругости E, m C площадь сечения стержней F, жесткость
ПодробнееДИНАМИКА. Описание движения твердого тела
Л5 ДИНАМИКА Описание движения твердого тела 1 Прямолинейное движение Прямолинейным движением твердого тела будем называть такое движение системы материальных точек при котором скорости прямолинейного движения
Подробнееdocplayer.ru
Теоретическая механика
ГОУ ВПО «Алтайский государственный университет
им. И.И. Ползунова»
В.М. Щербаков
Учебное пособие для студентов
дистанционной формы обучения
Барнаул 2009
Статика твердого тела
1 Основные понятия и аксиомы статики
§ 1 Основные понятия статики
Статика – раздел теоретической механики, в котором рассматривается учение о силах и условия равновесия тел под действием этих сил.
В теоретической механике в качестве материальных объектов рассматриваются:
— материальная точка – материальное тело, обладающее массой и способностью взаимодействовать с другими телами, но размерами которого в данной конкретной задаче можно пренебречь.
— механическая система – система взаимосвязанных материальных точек.
Под механической системой в абстрактном смысле можно понимать любое механическое устройство.
Абсолютно твёрдое тело – неизменяемая система материальных точек.
Сила – мера механического взаимодействия материальных объектов.
По своей природе сила – векторная величина и в общем случае характеризуется:
-численной величиной (модулем)
-линией действия и направлением
-точкой приложения.
вектор силы
точка приложения
линия действия
де
Рисунок 1
Линия действия силы – прямая, с которой совпадает вектор силы.
Совокупность нескольких сил, действующих на данное тело или механическую систему, называется системой сил.
Системы сил, оказывающие одинаковое механическое воздействие на материальный объект называются эквивалентными системами сил.
Одна сила, эквивалентная некоторой системе сил, называется равнодействующей силой.
Система сил, приложенная к материальному объекту, не нарушающая характер его механического движения, называется системой взаимно уравновешивающихся сил.
Силы, действующие на механическую систему, делят на внешние и внутренние.
Внешними называют силы, действующие на материальные точки данной механической системы со стороны материальных объектов, не входящих в эту систему.
Внутренними силами называют силы взаимодействия между материальными объектами данной механической системы.
§ 2 Аксиомы статики
В основе любых естественных наук, какой является и механика, лежат объективные законы природы, установленные опытным путем.
Эти законы называются аксиомами. Аксиомы не доказываются, их справедливость подтверждается многовековой практикой.
В статике используются аксиомы:
1. Аксиома покоя: Система взаимно уравновешивающихся сил не может нарушить исходного покоя механического объекта.
2. Аксиома равновесия двух сил: Две силы взаимно уравновешиваются только в том случае, если они имеют общую линию действия, равны по величине и направлены в разные стороны.
3. Аксиома присоединения или исключения взаимно уравновешивающихся сил: Если к механическому объекту, находящемуся под действием некоторой системы сил присоединить(или исключить) систему взаимно уравновешивающихся сил, то получится система сил, эквивалентная заданной.
Из аксиомы (3) вытекает важное следствие:
-механическое состояние твердого тела не изменится вследствие переноса силы вдоль её линии действия.
Рисунок 2
Вывод: Вектор силы – скользящий вектор.
4. Аксиома параллелограмма сил: Равнодействующая двух пересекающихся сил приложена в точке их пересечения и представляется диагональю параллелограмма, построенного на этих силах.
Рисунок 3.
Из аксиомы(4) вытекает следствие, получившее название
Теорема о трёх силах: Если три непараллельные силы взаимно уравновешены, то они лежат в одной плоскости и линии их действия пересекаются в одной точке.
F3
Рисунок 4.
Доказательство: Пусть силы F1,F2,F3 взаимно уравновешены. Заменим силы F2 и F3 их равнодействующей R, приложенной в точке их пересечения В. Силы R и F1 эквивалентны исходной системе сил. Две же силы взаимно уравновешены, если они имеют общую линию действия. Следовательно линия действия силы F1 также пройдёт через точку В.
studfiles.net
Общие теоремы динамики.
Дифференциальные уравнения движения системы.
Применяем второй (основной) закон динамики, получим
(2)
Аналогичного вида уравнения получим для любой точки системы, т.е. всего для рассматриваемой системы будет иметь nтаких уравнений (k= 1, 2….n). Эта система уравнений представляет собойдифференциальные уравнения движения механической системы в векторной форме.
Проектируя равенства (2) на какие-нибудь координатные оси, получим систему дифференциальных уравнений движения системы в проекциях на эти оси.
В результате интегрирования системы дифференциальных уравнений ( что очень сложно) получить законы движений каждой точки системы. Гораздо удобнее определять некоторые сумарные характеристики движения всей системы в целом, а по ним, если требуется, найти и соответствующие параметры движения отжельных точек системы.
Такими характеристиками являются меры движения системы: количество движения, момент количества движения, кинетическая инергия.
Приче м каждая из этих мер для системы определяется как сумма соответствующих мер движения всех ее точек.
Соответственно и воздействия на систему рассматриваются суммарно ( главный вектор и главный момент приложенных к системе сил, суммы работ и т.п.).
Зависсимость между мерами движения системы и мерами воздействия на нее выражают общие теоремы системы материальных точек.
Общие теоремы динамики системы являются следствиями системы уравнений (2).
2) Масса системы. Центр масс.
Механическая система – это система материальных точек, каждая из которых имеет определенную массу и занимает в данный момент времени определенное положение в пространстве.
Для удобства решения задач динамики механические системы желательно некоторые обобщенные (т.е. суммарные ) характеристики, которые бы отражали и массу системы, и ее «геометрию масс», т.е. расположение в пространстве материальных точек системы.
Масса системы М равна арифметической сумме масс всех точек или тел, образующих систему:
Центром масс механической системы называют геометрическую точку С, радиус вектор которой
(1)
где радиус- вектор точек, образующих систему.
– массы точек механической системы
М – масса системы.
Центр масс системы явл не материальной точкой, а геометрической. Он может не совпадать ни с одной материальной точкой системы. Центр масс системы характеризует распределение масс в системе.
Теорема о движении центра масс механической системы.
Теорема: Центр масс системы движется как материальная точка, масса которой равна массе всей системы и к которой приложены все действующие на систему внешние силы.
(3)
Где – ускорение центра масс.
– главный вектор внешних сил.
Проецируя обе части уравнения на координатные оси, получим:
где ,,- координаты центра масс.
Из теоремы о движения центра масс можно получить следующие важные следствия, которые выражают закон сохранения центра масс механической системы.
Если геометрическая система всех внешних сил, действующих на систему, равна 0 () то это значит , чтоили, т.е. центр масс этой системы движется с постоянной по модулю и направлению скоростью (иначе, равномерно и прямолинейно). В частном случае, если вначале центр масс был в покое () то он и останется в покое т.е ().
Если внешние силы, действующие на систему, таковы, что сумма их проекций на какую-нибудь ось (например, ось Х равна 0 , тоилит.е. проекция скорости центра масс системы на эту ось есть величина постоянная. В частном случае , если в начальный момент, то и в любой последующий момент времени это значение сохранится , а следовательно координатацентра масс системы не изменится т.е.=const.
Теоремы об изменении количества движения точки и системы
Определение: количеством движения материальной точки называется векторная величина ,равная произведению массы точки на вектор ее скорости. Векторприложен к движущейся точке.
Определение: Количеством движения механической системы называется вектор, равный геометрической сумме количеств движения всех точек системы.
(4)
Вектор является свободным вектором. Как правило скорости всех точек системы различны и поэтому непосредственное суммирование векторов в правой части равенства является затруднительным.
Воспользуемся формулой для определения центра масс механической системы (1)
Или запишем в виде
дифференциируя обе части выражения по времени получим:
или
(5)
Сравнивая формулы (4) и (5) получим , что количество движения системы равно произведению массы всей системы на скорость ее центра масс.
(6)
Вектор является обобщенной векторной характеристикой движения всей механической системы. В общем случае движение системы ее количество движения можно рассматривать как характеристику поступательной части движения системы вместе с центром масс. Если при движении системы (тела) центр масс неподвижен, то количество движения будет равно 0. Например количество движения тела, вращающегося вокруг неподвижной оси, проходящей через его центр масс.
Запишем второй закон динамики для материальной точки: учитывая чтополучим(7)
В каждый момент времени производная по времени от количества движения точки равна действующей на точку силе.
Если обе части равенства (7) умножить на dt, то получимвекторная величина, стоящая в правой части этого равенства, характеризует действие, оказываемое на тело силой за элементарный промежуток времениdt эту величинуназывают элементарным импульсом силы, т.е.
(8)
Импульс силыза конечный промежуток времениt2 – t1 равен
(10)
Уравнение (10) выражает теорему об изменении количества движения точки в конечной интегральной форме:
Теорема: изменение количества движения точки за некоторый промежуток времени равно импульсу действующей на точку силы ( или равнодействующей всех приложенных к ней сил)за тот же промежуток времени.
При решении задач пользуются уравнениями этой теоремы в проекциях на координатные оси.
Рассмотрим механическую систему, состоящую из nматериальных точек. Тогда для каждой точки можно применить теорему об изменении количества движения в дифференциальной форме:
( k= 1, 2….n).
Суммируя эти равенства, получим
т.к. по свойству внутренних сил
то получим:
(11)
Уравнение (11) выражает теорему об изменении количества движения системы в дифференциальной форме:
Теорема:Производная по времени от количества движения системы равна векторной сумме действующих на систему внешних сил.
В проекциях на координатные оси:
; ;
Умножая обе части равенства (11) на dtи интегрируя, получим:
(12)
Уравнение (12) выражает теорему об зменении количества движения системы в интегральной форме:
Теорема: изменение количества движения системы за какое-либо время равно сумме импульсов всех внешних сил, действующих на систему за то же время.
Из теоремы об изменении количества движения системы можно получить следующие важные следствия, которые выражают закон сохранения количества движения системы.
Если геометрическая сумма всех внешних сил, действующих на систему, равна 0 (), то значит, что при этом, т.е. вектор количества движения системы будет постоянен по модулю и направлению.
Если внешние силы, действующие на систему, таковы, что сумма их проекций на какую-либо ось равна 0, то значит .
studfiles.net
Теоретическая механика
Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования
«Кубанский государственный технологический университет»
Часть 2 динамика
Утверждено Редакционно-издательским
советом университета в качестве
учебного пособия
Краснодар
2011
УДК 531.1/3 (075)
Д.722
Теоретическая механика. Часть 2. Динамика: Учебное пособие / Л.И.Драйко; Кубан. гос. технол.ун-т. Краснодар, 2011. 123 с.
ISBN 5-230-06865-5
Излагается в краткой форме теоретический материал, даны примеры решения задач, большинство из которых отражает реальные вопросы техники, уделено внимание выбору рационального способа решения.
Предназначено для бакалавров заочной и дистанционной форм обучения строительных, транспортных и машиностроительных направлений.
Табл. 1 Илл. 68 Библиогр. 20 назв.
Научный редактор канд.техн.наук,доц. В.Ф.Мельников
Рецензенты: зав.кафедрой теоретической механики и теории механизмов и машин Кубанского аграрного университета проф. Ф.М. Канарев; доцент кафедры теоретической механики Кубанского государственного технологического университета М.Е. Мултых
Печатается по решению Редакционно-издательского совета Кубанского государственного технологического университета.
Переиздание
ISBN 5-230-06865-5 КубГТУ 1998г.
Предисловие
Данное учебное пособие предназначено для студентов заочной формы обучения строительных, транспортных и машиностроительных специальностей, но может быть использовано при изучении раздела «Динамика» курса теоретической механики студентами заочниками других специальностей, а также студентами дневной формы обучения при самостоятельной работе.
Пособие составлено в соответствии с действующей программой курса теоретической механики, охватывает все вопросы основной части курса. Каждый раздел содержит краткий теоретический материал, снабженный иллюстрациями и методическими рекомендациями для его использования при решении задач. В пособии разобрано решение 30 задач, отражающих реальные вопросы техники и соответствующих контрольным заданиям для самостоятельного решения. Для каждой задачи представлена расчетная схема, наглядно иллюстрирующая решение. Оформление решения соответствует требованиям, предъявляемым к оформлению контрольных работ студентов-заочников.
Автор выражает глубокую признательность преподавателям кафедры теоретической механики и теории механизмов и машин Кубанского аграрного университета за большой труд по рецензированию учебного пособия, а также преподавателям кафедры теоретической механики Кубанского государственного технологического университета за ценные замечания и советы по подготовке учебного пособия к изданию.
Все критические замечания и пожелания будут приняты автором с благодарностью и в дальнейшем.
Введение
Динамика является наиболее важным разделом теоретической механики. Большинство конкретных задач, которые приходится в инженерной практике, относится к динамике. Используя выводы статики и кинематики, динамика устанавливает общие законы движения материальных тел под действием приложенных сил.
Простейшим материальным объектом является материальная точка. За материальную точку можно принять материальное тело любой формы, размерами которого в рассматриваемой задаче можно пренебречь. За материальную точку можно принимать тело конечных размеров, если различие в движении его точек для данной задачи не существенно. Это бывает в случае, когда размеры тела малы по сравнению с расстояниями, которые проходят точки тела. Каждую частицу твердого тела можно считать материальной точкой.
Силы, приложенные к точке или материальному телу, в динамике оцениваются по их динамическому воздействию, т. е. по тому, как они изменяют характеристики движения материальных объектов.
Движение материальных объектов с течением времени совершается в пространстве относительно определенной системы отсчета. В классической механике, опирающейся на аксиомы Ньютона, пространство считается трехмерным, его свойства не зависят от движущихся в нем материальных объектов. Положение точки в таком пространстве определяется тремя координатами. Время не связано с пространством и движением материальных объектов. Оно считается одинаковым для всех систем отсчета.
Законы динамики описывают движение материальных объектов по отношению к абсолютным осям координат, условно принятым за неподвижные. Начало абсолютной системы координат принимается в центре Солнца, а оси направляются на отдаленные, условно не подвижные звезды. При решении многих технических задач условно не подвижными можно считать координатные оси, связанные с Землей.
Параметры механического движения материальных объектов в динамике устанавливаются путем математических выводов из основных законов классической механики.
Первый закон (закон инерции):
Материальная точка сохраняет состояние покоя или равномерного и прямолинейного движения до тех пор, пока действие каких-либо сил не выведет ее из этого состояния.
Равномерное и прямолинейное движение точки называют движением по инерции. Покой является частным случаем движения по инерции, когда скорость точки равна нулю.
Всякая материальная точка обладает инертностью, т. е. стремится сохранить состояние покоя или равномерного прямолинейного движения. Система отсчета, по отношению к которой выполняется закон инерции, называется инерциальной, а движение, наблюдаемое по отношению к этой системе, называется абсолютным. Любая система отсчета, совершающая относительно инерциальной системы поступательное прямолинейное и равномерное движение, будет также инерциальной системой.
Второй закон (основной закон динамики):
Ускорение
материальной точки относительно
инерциальной системы отсчета
пропорционально приложенной к точке
силе и совпадает с силой по направлению: 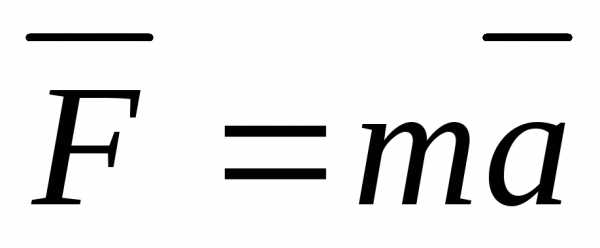 .
.
Из основного закона
динамики следует, что при силе 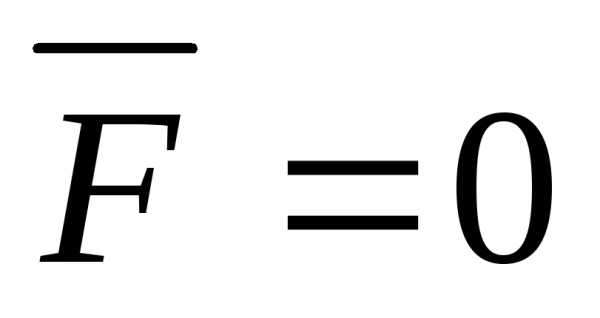 ускорение
ускорение .
Масса точки характеризует степень
сопротивляемости точки изменению ее
скорости, т. е. является мерой инертности
материальной точки.
.
Масса точки характеризует степень
сопротивляемости точки изменению ее
скорости, т. е. является мерой инертности
материальной точки.
Третий закон (закон действия и противодействия):
Силы, с которыми два тела действуют друг на друга, равны по модулю и направлены вдоль одной прямой в противоположные стороны.
Силы, именуемые действием и противодействием, приложены к разным телам и поэтому уравновешенной системы не образуют.
Четвертый закон (закон независимости действия сил):
При одновременном действии нескольких сил ускорение материальной точки равно геометрической сумме ускорений, которые имела бы точка при действии каждой силы в отдельности:
, где  ,
, ,…,
,…,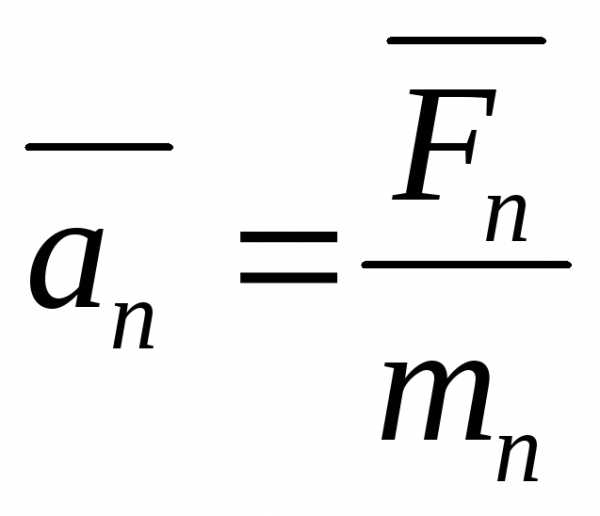 .
.
studfiles.net




 материальных точек.Положение
каждой точки массой
материальных точек.Положение
каждой точки массой определяется в инерциальной системе
отсчёта
определяется в инерциальной системе
отсчёта радиус-вектором
радиус-вектором (рис. 13.1)
(рис. 13.1) (скорость оси колеса) (рис. 13.2) равно
(скорость оси колеса) (рис. 13.2) равно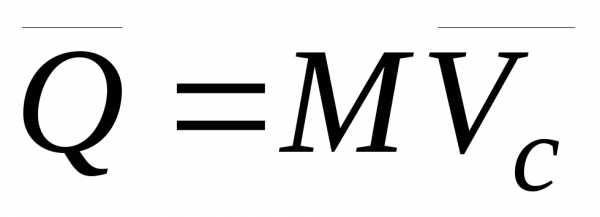 ,
,

