28.04.201902.02.2019

Техника быстрого счета на пальцах – Ментальная Арифметика на Пальцах

• by alexxlab
• Комментариев к записи Техника быстрого счета на пальцах – Ментальная Арифметика на Пальцах нет
• Советы абитуриенту

Ментальная Арифметика на Пальцах

Вы когда-нибудь задумывались, почему у восточных сорабанских счетчиков- математиков, которые занимаются Ментальной Арифметикой есть 4 отдельных бусинки? Они находится в базе 10, а не 4 или 5, так зачем организовать такой счет таким образом?

Ответ счета в Ментальной Арифметики может исходить только с объяснением математики пальцев. Если вы посмотрите на этот аккуратный способ подсчета до 99 на ваших двух руках, то вы поймете Соробан — Абакус! Четыре бусинки означают четыре пальца на руке и отдельную бусину для большого пальца это нашу пятерку.

Человеческая рука несет пять пальцев; у двух рук их десять. Несомненно, этот факт отвечает за универсальное принятие десятичной системы.

Дети учатся рассчитывать, считая пальцы в математике, сначала до 5 с одной стороны, а затем до 10 на две руки. Тем не менее, есть простой способ подсчитать до 10 с помощью всего 5 пальцев одной руки и до 100, используя обе руки.

Вот как это сделать:

Сложенный кулак может стоять на 10, если вы не планируете использовать секундную стрелку или 0, если вы это сделаете:

Вторая рука используется таким же образом, но для подсчета в математике 10 секунд:

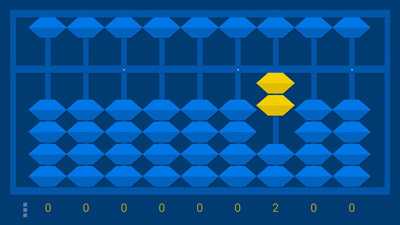
С фотографиями  и скриншотами из онлайн—счетов Soroban мы можем показать эту идею. Он работает лучше всего, если вы считаете. Сначала используйте четыре пальца правой руки для подсчета 1, 2, 3, 4. Это соответствует четырем шарикам в первом ряду Соробана, показанным желтым.

Затем вещи становятся немного более абстрактными. Большой палец — 5, сам по себе, точно так же, как и одинокий желтый шарик. Мы переходим от прямого подсчета к символам или иначе образности:

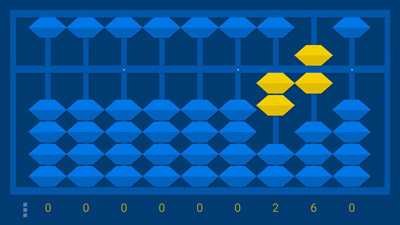
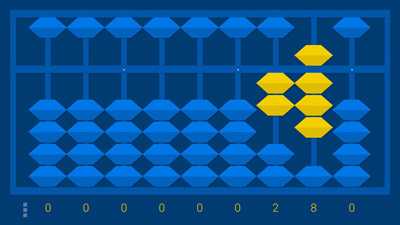
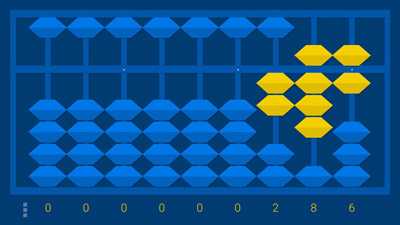
Вы добавляете пальцы в большой палец, чтобы подсчитать 6, 7, 8, 9. Представьте, что маленький ребенок играет с традиционными играми с пальцами с родителями. Дети могут мгновенно распознавать (сублицировать) количества от 1 до 4, но подсчет западных пальцев проходит до 10 — намного выше диапазона субтитизации. В отличие от подсчета западных пальцев, эта система вводит группы и символы (большой палец — 5), а также добавление, как только вы покидаете диапазон субтитизации. Другими словами, система следит за тем, как работают умы детей.

Что происходит, когда вы достигаете 10? Что-то очень полезное и захватывающее! Вы можете использовать другую руку, которая означает значение нового места — и новый ряд бус на абакусе. Цифры, бусины и пальцы — все вместе, как рука в перчатке.

Вот еще одно отличие этой системы от подсчета ваших 10 пальцев. Вы можете сосчитать весь путь до 99 на ваших двух руках!

И если вы объедините силы с другом, вы можете показать еще большие цифры.

Вот видео, показывающее, как считать весь путь от 1 до 99:

Ментальная Арифметика удивительная наука, которая помогает понимать самую из всех точных наук нашу любимую математику. Изучайте и любите математику, она откроет вам много тайн, которые всегда очевидны и интересны. Ваша Ментальная Арифметика.

Поделиться ссылкой:

Похожее

mentalar.ru

Ментальная арифметика в домашних условиях для ребенка 6-7 лет

О ментальной арифметике в России узнали сравнительно недавно, около 20 лет назад. Цена на занятия с профессиональными преподавателями менар растет от года к году. По этой причине многие мамы и папы решают заниматься ментальной арифметикой с детьми самостоятельно. Опытом и секретами домашнего обучения быстрому счету поделимся в этой статье.

Из этой статьи вы узнаете

Можно ли заниматься дома

Обучать малышей счету на абакусе не обязательно в специализированных центрах. Если родители мобильны, готовы тратить время и силы на самообразование и развитие детей, то домашние занятия по ментальной арифметике станут не только хобби, но и семейным видом общения, игр.

Сторонники развивающих уроков дома с мамой настаивают на нескольких плюсах и минусах самостоятельного непрофессионального обучения.

Преимущества

• Знакомая обстановка помогает расслабиться, дети не испытывают стресса.
• Родители учитывают индивидуальные особенности малыша при планировании занятий.
• Отсутствие платы за обучение.
• Экономия времени. Добираться до обучающих центров не нужно.
• Самообразование для родителей.

Недостатки

• Отсутствие опыта у домашних педагогов.
• Минимальное количество информации о методе в Сети, книжных магазинах. Педагоги спеццентров стараются держать тонкости преподавания в тайне.

Занятия ментальной арифметикой дома – неплохой способ саморазвития и обучения ребенка. Но решаться на этот шаг нужно при хорошей дидактической, методологической подготовке родителей. Иначе вы рискуете совершить массу ошибок. А исправлять недочеты гораздо сложнее, чем сразу научить правильно.

Важно! Для самообучения и подготовки к урокам используйте видеокурсы из Сети, книги, советы психологов. Для экономии средств распечатывайте лекции, тренировочные задания на домашнем принтере.

Что такое абакус

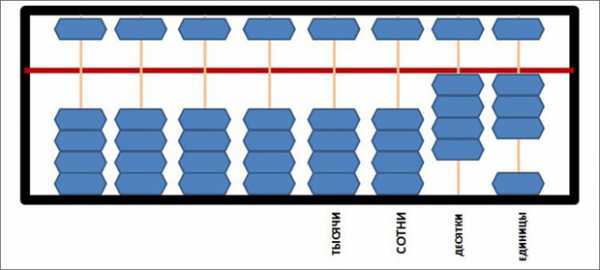
Это помощник для обучения детей быстрому счету. По внешнему виду напоминает русские счеты, но в перевернутом виде. Абакус, по-японски соробан, состоит из рамки и бусин, надетых на спицы.

Счетная область разделена на два блока:

1. Верхний. На каждой спице по 1 костяшке. Этот ряд кратен 5. Их называют братья.

2. Нижний. По 4 костяшки на каждой спице. Бусины кратны 1. Это друзья.

Вертикальный ряд спиц в нижнем блоке обозначает разряд цифр. Справа — налево: единицы, десятки, сотни и т.д.

При счете разделительная планка между нижним и верхним рядами должна располагаться горизонтально. Чтобы показать число, нужно поднимать костяшки вверх. Если все бусины опущены — на счетах 0.

Важно! Разобраться в устройстве абакуса сложно только теоретически. Если взять счеты в руки, выставить пару чисел пальцами самостоятельно, то понимание работы древнейшего математического прибора быстро приходит к детям и взрослым.

Посмотрите, как легко и просто можно раскладывать различные числа на абакусе:

Этапы подготовки

Поэтапное следование советам профессиональных педагогов поможет сделать процесс обучения ментальной арифметике дома продуктивным и интересным:

1. Пройдите азы ментальной математики сами, усвойте и закрепите материал основательно с помощью самоучителя.
2. Оборудуйте домашний класс счетами, пособиями.
3. Составьте примерную программу уроков, план на 1–2 месяца.
4. На первом занятии познакомьте юного ученика с абакусом. Пусть пощупает, попробует передвинуть костяшки.
5. Посмотрите с ребенком видеоурок, схемы сложения цифр на абакусе.
6. Заведите тетрадь с зарисованными схемами выкладывания комбинаций на счетах.
7. При откладывании цифр пользуйтесь указательным и большим пальцем.
8. После объяснения принципа работы переходите к сложению однозначных, двузначных чисел.
9. Не торопитесь. Переход к более сложной ступени должен быть постепенным.
10. Переходить к вычитанию нужно после автоматизации решения примеров на сложение.
11. Занимайтесь регулярно. Назначьте точное время, дни для уроков, старайтесь не отступать от намеченного плана.
12. Занятие должно длиться около 30 минут.
13. Учитывайте возраст детсадовца, школьника, уровень математических знаний при составлении плана.
14. Отработайте умножение и деление на счетах.
15. Попробуйте работать только пальцами, без абакуса. Визуализация – самый сложный этап обучения.
16. Практикуйте ментальный счет только пальцами на каждом занятии по 10 минут.

Как складывать на абакусе

Итак, маленький математик с вашей помощью освоил счеты для ментальной арифметики, познакомился с основными принципами работы. Пора переходить к первым простейшим примерам сложения.

Скачайте задачи для домашних занятий в интернете бесплатно и решите их сами, потом предлагайте дошкольнику. На первом уроке используйте однозначные и двузначные числа. Попробуем сложить 14 и 22. Действовать нужно по следующему алгоритму:

1. Отложите на спицах первое число – 13. Для этого в ряду десятков поднимите 1 бусину на нижнем ряду; на спице, отвечающей за единицы, отложите 3 костяшки.
2. Прибавляем 23. Для этого в ряду единиц добавляете 3 бусины, в ряду десятков – 2.
3. Получаем 36.

Выполняйте математические действия слева направо. Для поднимания бусин пользуйтесь большим пальцем, для опускания – указательным. При нехватке костей в нижнем блоке нужно пользоваться помощью братьев из верхней части рамки, кратных 5.

Например, для выкладывания числа 80 бусин в ряду десятков не хватит, их всего 4. Для этого нужно отложить 5 десятков в верхнем блоке. Получится 50. И добавить 3 бусины на нижнем блоке — еще 30. В сумме получается 80.

Важно! Умение формируется постепенно. Не торопитесь сами и не подгоняйте ребенка. В качестве помощи используйте видеоуроки, методические пособия.

Посмотрите видеоурок, в котором показаны азы сложения:

Продолжение обучения:

В этом видео разобраны более сложные примеры на сложение:

Учимся вычитать

Отнимать цифры на абакусе тоже несложно. Перед первым уроком посмотрите видео базового курса. Вводное занятие в домашних условиях начните с теории. Объясните ребенку следующие аспекты:

1. Начинать вычитать нужно с большего разряда. В трехзначных цифрах – с сотен, в двузначных – с десятков.
2. Не нужно забывать пользоваться верхним блоком, костяшками-братьями.

Приведем несколько примеров на вычитание. Для малышей тренировка должна начинаться с однозначных цифр.

От 8 отнимем 3

1. На первой спице в верхнем блоке опустите костяшку, получится 5.
2. В нижнем поднимите еще 3 бусины. Так выставляется цифра 8.
3. Теперь отнимаем 3.
4. Опускаем 3 костяшки в нижнем ряду.
5. Остается 5.

От 13 отнимаем 4

1. Выставляем на абакусе число 13.
2. В ряду десятков поднимайте 1 косточку. Это 10.
3. В ряду единиц — 3 бусины. Равно 13.
4. Отнимаем 4.
5. В ряду единиц бусин для вычитания не хватает, поэтому опускаем костяшку из блока десятков.
6. Затем поднимаем бусину верхнего блока, кратного 5, в ряду единиц и 1 бусину в нижнем ярусе.
7. Ответ – 9.

Примеры расчета представлены на схемах. Их можно распечатать, иметь под рукой во время занятий. Спустя пару уроков выкладывание цифр на счетах станет автоматическим. Малышу нужно впервые предложить представлять ментальную карту для решения простых задач. Опорные таблицы для устного счета без абакуса понадобятся только в первое время.

Умножение

Изучение принципа умножения на абакусе чуть сложнее, чем предыдущие задачи. Придется немного напрячься. Начинайте перемножать с большего разряда, двигаясь от сотен к единицам поэтапно. Большой палец двигает костяшки вверх, указательный – вниз.

Вначале советуем вам посмотреть обучающее видео на эту тему:

И еще один дополнительный урок по умножению:

Умножим 13 на 22

1. Сначала берем десятки у обеих цифр. Умножаем устно: 10 x 20 = 200.
2. Откладываем получившийся результат на счетах.
3. Теперь действуем так же с единицами первого числа и десятками второго. Умножаем 3 x 20 = 60.
4. Откладываем на счетах.
5. На этом этапе берем десятки первого числа и перемножаем с единицами второго. 10 x 2 = 20.
6. Передвигаем костяшки.
7. Осталось перемножить единицы обеих цифр: 3 x 2 = 6.
8. Откладываем и оцениваем результат на счетах.
9. Получилось 286.

Важно! При изучении умножения и деления не прерывайте уроки надолго, лучше тренироваться 2–3 раза в неделю по 30–40 минут. Иначе новая информация быстро забывается, навык теряется.

Деление

Проходить деление на абакусе нужно сразу после понимания и автоматизации умножения. Учебный процесс начните с пояснений принципов работы на счетах. Ребенок должен действовать так:

1. Мысленно разделить абакус на две половины по ширине. Это поля для знаменателя и ответа.
2. Цифру для деления выставить справа.
3. Слева будет ответ.
4. Писать итог деления нужно с крайнего столбца.

Посмотрите видео, в котором подробно объяснен принцип деления:

Продолжите изучать деление в этом ролике:

Делим 62 на 2

• Сначала отложим первое число (62) на абакусе.
• Делим десяток: 60 : 2 = 30.
• Откладываем в поле ответа 3 костяшки в крайнем ряду.
• Делим единицы: 2 : 2 = 1.
• Откладываем 1 костяшку в поле ответа в следующем ряду.
• Оцениваем итог. Получилось 31.

Делим 864 на 4

• Откладываем 864 на счетах.
• Оставляем в поле ответа не менее трех рядов свободными.
• Делим 800 на 4, получается 200.
• Поднимаем 2 костяшки в крайнем ряду для ответа.
• Делим 60 на 4. Получаем число с остатком. Придется умножить 4 на число меньше 6, но ближайшее к 4. Умножаем: 4 х 1, получается 4.
• Поднимаем 1 костяшку во втором ряду для ответа.
• Умножаем полученные 4 на 6 для восстановления равновесия чисел. Получается 24.
• Теперь делим 24 на 6. Ответ: 4.
• Поднимаем 4 костяшки в третьем ряду в поле ответов.
• Оцениваем результат – 216.

Важно! Учебный процесс на начальном этапе приобретения навыка деления можно сопровождать работой на калькуляторе. Регулярно проверяйте себя и ребенка на точность результата.

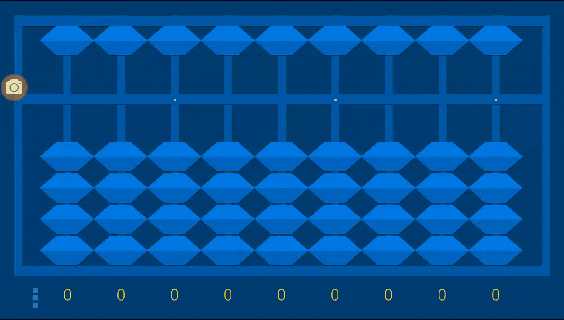
Как пользоваться пальцами без использования счетов

Конечный результат обучения ментальному счету – это решение арифметических задач на пальцах, без абакуса. Знакомство с этим методом практической работы начинайте с простых упражнений.

Считать на пальцах нужно следующим образом:

1. Представьте, что рука — это абакус.
2. Пальцы левой руки отвечают за числа, кратные 10. Большой палец – это 50.
3. Правая рука — это числа от 1 до 9, большой палец обозначает цифру 5.
4. Сжатые кулаки — 0.

Приведем несколько примеров счета на руках.

Как показать цифру 35

Вытягиваем три пальца левой руки – это 30, большой палец правой руки – это 5.

Показываем число 98

Разворачиваем все пальцы левой руки. Они обозначают цифру 90. На правой руке поднят большой палец – это 5, и три других пальчика. В итоге получается 90 и 8.

С помощью счета без абакуса можно складывать, отнимать, делить и умножать. Пальчики выполняют роль костяшек. Спустя 10–12 уроков по ментальной карте, то есть с помощью визуализации, ребенок будет решать примеры довольно быстро.

Именно этот метод является эффективным способом обучения быстрому счету. Ребенок не будет тратить время на передвижение бусин на счетах, запоминать их расположение. Движения пальцами автоматизируются поэтапно, от простых примеров к сложным.

Книги по ментальной арифметике

Обойтись без пособий и решебников для домашнего обучения ментальной арифметике просто невозможно. Приведем небольшой список самых популярных и доступных для понимания учебников. Используйте их как самоучитель, сборник примеров и домашних заданий.

«Матемагия. Секреты ментальной математики». А. Бенжамин

Раскрывает секреты ментальной арифметики. После ее прочтения родителю будут доступны многие методы работы с ребенком дома. Автор рассказывает о математических трюках, способах молниеносно решить сложнейшие задачи устно.

В процессе усвоения материала у ребенка улучшается память, внимание. По итогам курса обучения школьник научится извлекать квадратный корень, переводить кубические величины в квадратные и наоборот без калькулятора, в уме.

Блокнот-тренажер «Не ментальная арифметика». Ш. Ахмадуллин

Автор обещает научить детей быстрому устному счету за 21 день. В сборник включены теоретическая информация, упражнения для пробных занятий, задания высшего уровня. Можно использовать в детском саду, школе. Книга предназначена для детей от 7 до 11 лет.

По отзывам родителей, блокнот заинтересовывает детей с первого занятия. Игра постепенно переходит в серьезную работу. Ребенок чувствует уверенность на уроках математики, повышается самооценка, успеваемость.

«Ментальная арифметика. Знакомство». Р. Багаутдинов, Р. Ганиев

Изучать ментальный счет по данному пособию можно с 5 лет. Этапный метод подготовки к развитию навыка решения задач на пальцах включает в себя теорию, простые упражнения, задачи повышенной сложности.

В книге огромное количество фотографий, изображений формул для вычитания, сложения многозначных цифр. Ребенок воспринимает информацию на слух, зрительно. Дети научатся считать с помощью ментальной карты за 1–2 месяца.

«Ментальная арифметика. Учебник для преподавателей и родителей»

Издается компанией «Анаста». В комплект входят четыре книги: учебник, «Методика для занятий с детьми», два решебника. Приобретать методическую литературу нужно в комплекте. К учебникам прилагаются флеш-карты для тренировки памяти, внимания.

Дидактический сборник используется на занятиях с детьми от 4 лет. Издатели гарантируют быстрое запоминание материала благодаря большому количеству интересных занятий, упражнений, психологической составляющей метода обучения.

«Ментальная арифметика. Сложение и вычитание». С. Эрташ

Это рабочий тренажер по ментальной арифметике и дидактический сборник в одном флаконе. Задачник помогает понять принципы преподавания быстрого счета в домашних условиях, в центрах «Менар», содержит доступную информацию для детей и родителей.

Математический гений быстро перейдет от низкого уровня к сложному благодаря играм, схемам, формулам, интересным задачам. Автор предлагает несколько способов сложения и вычитания: традиционный — на счетах, комбинированный, на пальцах (устный). Учебник предназначен для детей 4–6 лет.

Ментальная арифметика – это лишь один из методов развития ребенка раннего возраста. Использовать домашний тип обучения нужно в том случае, если вы уверены в своих силах, есть много свободного времени. В противном случае доверьте малыша специалистам, домашние задания готовьте вместе.

После успешного усвоения основ быстрого счета, автоматизации движения пальцами продолжайте самообучение дома. Делайте это регулярно, чтобы не потерять навык работы с ментальной картой.

ВАЖНО! *при копировании материалов статьи обязательно указывайте активную ссылку на первоисточник: https://razvitie-vospitanie.ru/intellect/mentalnaya_arifmetika_v_domashnih_usloviyah.html

Если вам понравилась статья — поставьте лайк и оставьте свой комментарий ниже. Нам важно ваше мнение!

razvitie-vospitanie.ru

быстрая методика для 1-2 класса

Довольно часто родители сталкиваются с задачей научить ребенка считать. Может показаться, что в этом нет ничего сложного, однако для маленького ребенка порой бывает очень трудно научиться счету. Малышам, как правило, свойственно запоминать только то, что им интересно, поэтому взрослым нужно постараться сначала заинтересовать кроху, тогда процесс приобретения новых знаний пройдет намного легче.

Если подавать арифметику как сухое скучное занятие, ребенка будет сложно заинтересовать им

Оптимальный возраст для начала обучения ребенка счету

Начинать учить детей счету лучше всего в тот период, когда их мозг очень активно развивается. Обычно это происходит в возрасте до 6-7 лет. Родителям важно еще до момента поступления в школу начинать развивать у малыша навыки обучения счету.

Дети уже в раннем возрасте, как только начинают разговаривать, проявляют интерес к счету. Родителям необходимо поддерживать этот интерес с помощью специальных развивающих игр.

Основные правила обучения счету

Эта статья рассказывает о типовых способах решения Ваших вопросов, но каждый случай уникален! Если Вы хотите узнать у меня, как решить именно Вашу проблему — задайте свой вопрос. Это быстро и бесплатно!

Если вы хотите обучить малыша счету, необходимо придерживаться главных правил обучения:

1. Получаемый объем информации ребенком. Занятия следует совершать три раза в день, продолжительность каждого из которых не должна превышать 10 минут. Таким образом у ребенка не появится усталость от изобилия информации, не исчезнет интерес к новым знаниям.
2. Не повторять пройденный материал каждый день. Его лучше вспоминать лишь в тех случаях, когда накопленные знания потребуются для решения более тяжелых заданий.
3. Не давать малышу слишком сложные задания. Не стоит ругать ребенка, если у него не получается достичь желаемого результата. Возможно, ему на самом деле тяжело справиться с поставленной задачей. Подбирайте ребенку такие задачи, которые ему под силу решить.
4. Закреплять полученные знания в повседневной жизни. Чаще занимайтесь с ребенком подсчетом всего, что находится вокруг: машины, птички на дереве, количество тарелок на столе, автобусов на дороге и т. д.
5. Соблюдайте очередность этапов. По мнению психологов, процесс приобретения новых знаний у ребенка состоит из трех этапов: этап привыкания, этап понимания полученной информации, запоминание материала.

Самое главное – не торопить малыша. Наберитесь терпения, чаще общайтесь с крохой, сравнивайте при разговоре предметы, говорите о числах, оказывайте поддержку и помощь в получении знаний.

Учить ребенка счету можно и на прогулке, где попадаются примечательные интересные предметы

Методики обучения малыша

Чтобы научить ребенка правильному счету в уме, необходимо использовать следующие методы:

1. Пальцы рук. Этот метод один из самых популярных среди родителей. Его суть заключается в подсчете пальчиков на руках. Метод помогает развивать зрительную память малыша, моторику рук, а также способствует быстрому обучению считать предметы.
2. Материал для счета. Идеально подходит для обучения малыша считать примеры. В качестве материала подойдут обычные игрушки или определенные развивающие наборы. При выборе такого набора отдавайте предпочтение более ярким и красочным, убедитесь, что они сделаны из экологически чистых и безопасных материалов.
3. Развивающие детские книги (рекомендуем прочитать: какие книги можно купить для 4-летнего ребенка?). В настоящий момент в магазинах представлен огромный ассортимент интересных книг для развития ребенка дошкольного возраста. Старайтесь выбирать учебное пособие, написанное простым и понятным языком для малыша, чтобы в ваше отсутствие он мог сам продолжать учиться считать предметы.

Следите за тем, чтобы мозг ребенка не перезагружался во время занятий. Слишком большой объем информации способен утомить малыша и не принесет желаемого результата. В начале занятий учите его считать примеры до 10, уделяйте этому не более 10-15 минут, в дальнейшем можете заниматься с малышом до 30 минут. Во время каждого нового занятия повторяйте ранее пройденный материал.

Учимся считать до 10

Начинать малыша учить счету до 10 можно уже в два-три года. Сначала он должен обучиться считать до 5, а потом до 10. В таком возрасте малыши уже знают, что у них есть две ножки и значит надо надеть два носка. В 3-4 года можно ребенку давать более сложные задания. Самое главное, чтобы ребенок стал понимать значение слов «поровну», «больше», «меньше». Можете приводить ему простые примеры: «У Маши было три мандарина, а Кати – два. У какой девочки больше фруктов, а у какой меньше?»

Чтобы малышу было легче освоить счет до 10, предложите ему посчитать свои пальчики. Дайте крохе задание сложить 2+1, пусть он поднимет один пальчик на левой руке и два на правой, а затем посчитает общее количество поднятых пальчиков.

Такие же манипуляции можно проводить, чтобы малыш научился вычитать: ребенок загибает несколько пальчиков, а потом считает количество оставшихся в поднятом положении. То же самое можно проделывать с различными предметами: карандашами, ручками и т. д.

Учимся считать до 20

Когда малыш научится счету до 10, переходите к обучению счета до 20. В качестве материала для счета хорошо подойдут машины на улицы. По дороге в детский сад можете предложить посчитать их количество. Когда ребенок хорошо освоит урок, попробуйте посчитать автомобили в обратном порядке.

Обычно намного проще малыша научить считать до 20, чем до 10. Просто ему необходимо объяснить, что прибавляется окончание «-надцать».

Малышу может показать довольно трудным складывать числа от 1 до 20, поэтому занятия нужно проводить с игровым уклоном. К примеру, можно сказать: восьмерка решила прибавить к себе тройку. Она сначала взяла у тройки двойку и превратилась в десятку. Тройка стала единичкой. Сколько же будет, если восьмерка прибавит к себе тройку?

Мозгу малыша требуются ежедневные тренировки. Если малыш в раннем возрасте начнет заниматься устным счетом, то будет обладать хорошо развитыми умственными способностями.

Обучение устному счету

Когда малышу исполнится 5 лет, старайтесь отучать его от использования счетного материала, в том числе и своих пальцев. Пусть он учиться устному счету. Если в первое время ему это очень помогало, то в дальнейшем только будет мешать процессу приобретения новых знаний.

После пяти лет детей необходимо учить сложению и вычитанию чисел в пределах до 10 на автомате, т.е. нужно добиться того, чтобы малыш запоминал результаты вычислений. Для достижения этих целей хорошо помогает использование математических цепочек. Не забывайте, что в процессе получения знаний должен сохраняться игровой характер. Для больших чисел есть отдельные методики.

Учимся считать в 1 классе

Для каждого малыша наступает важный момент в жизни — он идет в 1 класс. Это время, когда формируется основа всех знаний о будущем. В первом классе у ребенка происходит смена деятельности, но особенность познавать все с помощью игр не исчезает. Малыш примеряет на себя роль ученика, развивает умения самоорганизации. Ему необходимо освоить навыки планирования своей работы, контроля и оценки своих поступков, общения со сверстниками и учителем.

Большое внимание у первоклассников уделяется устной работе. Для обучения первоклассников счету в уме и закрепления полученных ранее знаний педагоги применяют некоторые способы с игровым уклоном:

1. Метод кубиков Зайцева. Является очень распространенным методом игрового характера, цель которого – быстро обучиться счету. Малыши с большим интересом набираются знаний, используя кубики. Суть метода состоит в использовании нескольких таблиц, с помощью которых дети намного проще и быстрее обучаются сложению и вычитанию чисел в уме. Данный способ можно применять и родителям во время развивающих занятий с чадом в дошкольном возрасте. В наборе кубиков Зайцева есть обучающее пособие и диск с песнями, что позволяет стать процессу приобретения новых знаний очень интересным и простым.
2. Метод Глена Домана. Этот метод заключается в том, что дети учатся считать с помощью специальных карточек, на которых изображены точки. Способ позволяет развивать зрительную память малыша, и умение считать количество предметов.

Учителя в своей практике могут применять и другие методики обучения счету, поэтому родителям желательно заранее уточнить, каким способом будет проходить процесс обучения в школе. Чтобы достичь высокого результата, специалисты советуют не использовать разные методы обучения — это может не лучшим образом сказаться на ребенке.

Методика Домана может применяться и для раннего возраста, но во время подготовки к школе она особенно эффективна

Учимся считать во 2 классе

Следующее важное испытание для малыша – поступление во второй класс. Некоторые педагоги следуют выполнению только школьной программы и не оказывают должного внимания процессу обучению своих учеников. Получается так, что ребенок вроде и умеет складывать и вычитать, но в то же время он неспособен понять, почему из одного числа получается другое.

В математике очень важно соблюдать последовательность действий и регулярно тренировать память. Только в таком случае малыш сможет уверенно считать в уме двузначные числа.

Если же родители столкнулись с проблемой неуспеваемости их ребенка в школе, педагоги советуют больше заниматься с ним дома. Примеры для домашних занятий:

1. Сложить в уме двузначные числа 30+34. Можно предложить малышу разбить 34 на 30 и 4. Так малышу будет проще выполнить сложение. Как можно чаще тренируйте зрительную память при выполнении повседневных дел.
2. Выполнить сложение 40+35. Некоторым детям намного легче выполнять сложение в обратную сторону. Для этого нужно округлить меньшее число до ближайшего десятка: 40+40. Затем просто отнять лишнюю часть: 80-5=75.
3. Тренируйтесь складывать и вычитать в уме простые примеры. Например: 2+3 или 2+2. Потом начинайте усложнять задачи: 3+7=10, 10-2=8, 10-8=2. Если малыш будет хорошо уметь решать простые задачи, то для него не составят труда задания с двузначными и трехзначными числами.
4. Если у ребенка богатая фантазия, можно предложить ему считать предметы или животных в уме. Каждый малыш индивидуален, поэтому родители должны выбрать наиболее подходящую методику обучения, исходя из его особенностей.

Устный счет будет легче освоить ребенку-фантазеру, который заменит скучные числа животными или игрушками

Рекомендации родителям

Не стоит думать, что желаемый результат будет достигнут быстро, наберитесь терпения. Малышу не так просто обучиться счету, как может показаться на первый взгляд.

Специалисты советуют придерживаться следующих рекомендаций:

• Следить во время занятий, как малыш реагирует на процесс обучения. Если ему скучно и неинтересно, лучше попробовать другую методику.
• Не заставляйте кроху заниматься обучением против его воли. Таким образом вы не добьетесь желаемого результата.
• Не нервничайте во время занятий и не ругайте малыша.
• Регулярно повторяйте уже изученный материал.
• Хвалите малыша за каждое достижение.

Научить ребенка быстро считать не так уж и сложно (рекомендуем прочитать: как научить ребенка писать цифру 2 и другие цифры?). Просто родителям необходимо подойти к этому со всей ответственностью, проявить любовь, терпение и понимание к малышу, тогда результат не заставит себя ждать.

Поделитесь с друьями!

vseprorebenka.ru

Таблица умножения на пальцах. Как выучить?

Возможность умножения на пальцах — это ценный навык, и человечеству известно как считать на пальцах таблицу умножения, по крайней мере, с XV века. У нас могут быть мобильные калькуляторы, но во многих случаях, на самом деле, проще держать телефон в кармане и умножать на пальцах. Эта методика также может оказаться полезной для малышей, которые столкнулись с проблемами во время заучивания бесконечных математических формул.

Учить таблицу умножения на пальцах можно начинать после того, как ребенку будет известно умножение от одного до пяти. Уже на основе этих знаний можно развить навык в прямом смысле ручного умножения. Итак, приступим?

Таблица умножения на пальцах рук: девять

Держите руки перед собой ладонями вверх. Каждый из ваших десяти пальцев представляет собой число. Перемещаясь от большого пальца левой руки к большому пальцу правой руки, подсчитайте числа от одного до десяти.

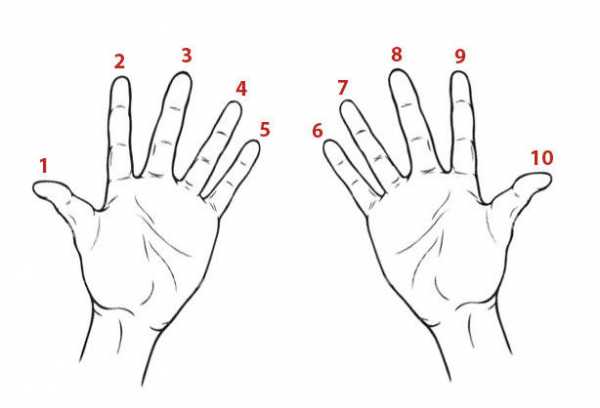
Направьте палец, цифра которого соответствует числу, которое вы хотите умножить на девять, вниз к вашему телу. Так, например, если вы хотите решить, сколько будет 9×3, вам нужно будет удерживать средний палец левой рукой. Средний палец представляет номер три, потому что, если вы считаете свои пальцы от одного до десяти, начиная с большого пальца левой руки, ваш средний палец является третьим по счету.

Производим подсчет

Решается задача посредством подсчета пальцев в левую и в правую сторону. Сначала подсчитайте пальцы слева от вашего согнутого пальца — в этом случае их будет два. Затем подсчитайте пальцы справа от вашего согнутого пальца — в этом случае должно быть семь. Первая цифра ответа равна двум, а вторая цифра — семи. В итоге ответ равен 27!

Так работает таблица умножения на 9 на пальцах. Попробуйте это с другими числами кратными девяти. Как бы вы умножили 9 на 2? Как насчет 9 на 7? Этот метод невероятно прост и понятен даже малышам. Как показывает практика, дети более охотно и успешно изучают математику, зная этот интересный способ подсчета произведения двух чисел!

Таблица умножения на пальцах на шесть, семь, восемь и десять

Держите руки так, чтобы ваши ладони были обращены к вашему телу, а ваши пальцы обращены друг к другу. Снова каждый палец будет представлять собой число. Ваш мизинец представляет собой номер шесть. Безымянный палец будет иметь значение семи, средний — восьми. Указательные пальцы ваших рук будут символизировать девятку, а большие пальцы — десятку. Итак, как выучить таблицу умножения на пальцах?

Схема расчета

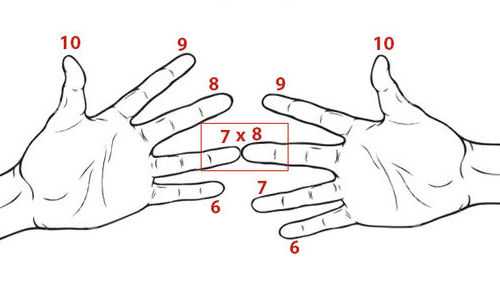
Для того, чтобы подсчитать произведение двух чисел, вам необходимо соприкоснуться двумя пальцами, числа которых соответствуют цифрам, которые вам необходимо умножить.

Например, если вы хотите высчитать, чему будет равно 7 * 6, вам необходимо коснуться безымянным пальцем левой руки (поскольку она представляет цифру слева) мизинца правой руки, поскольку он означает цифру справа. Опять же, помните, что каждый палец представляет собой число, и в этом случае ваш безымянный палец представляет семь, а ваш мизинец представляет шесть. Поэтому вам нужно соединить их чтобы решить эту математическую проблему.

Возможно, вам придется странным образом сгибать свое запястье, чтобы подсчитать произведение двух чисел! А кто говорил, что будет легко?

Для того чтобы убедиться, что вы правильно поняли технику таблицы умножения на пальцах на шесть, семь, восемь и десять, проверьте себя. Если вам необходимо вычислить, чему будет равно произведение 9 и 7, то какие пальцы вы бы соединили? Подумайте! Ответ будет в следующем предложении.

Итак, считайте, что вы выучили таблицу умножения на пальцах на шесть, семь, восемь и десять, если в качестве ответа, какие пальцы вам необходимо соединить, чтобы высчитать, чему равно произведение 9 и 7, вы выбрали указательный палец вашей левой руки и безымянный палец правой руки. Дело за малым!

Как считать?

Следующий шаг — просто подсчитать пальцы, что соприкасаются, а также пальцы под ними. Они будут представлять десятичные числа. В этом случае вы будете считать безымянный палец на левой руке, мизинец на левой руке и мизинец на правой руке. Каждый палец, который вы учитываете будет равняться 10. В этом случае общая сумма составляет 30.

Умножьте оставшиеся пальцы. Следующим шагом будет сложить количество пальцев на каждой руке, не считая пальцы, которые соприкасаются друг с другом. Сначала подсчитайте количество пальцев на левой руке, которые находятся над касающимися пальцами — в этом случае их будет 3. Затем подсчитайте количество пальцев правой руки над касающимися пальцами — в этом случае их будет 4. 3 * 4 = 12. Сложите два полученных числа вместе, чтобы найти свой ответ. В этом случае вам необходимо добавить 30 к 12. Общая сумма будет равна 42. Если 7 умножить на 6, то ответ совпадет и будет равняться 42!

Таблица умножения на пальцах может поначалу показаться сложной, однако, если тщательно разобраться, то выучить ее намного проще, чем бесконечные формулы в настоящей математической таблице.

Умножьте на 10, прибегая к помощи этого же метода. Например, если вы хотите найти ответ, чему будет равняться 10, умноженная на 7, то начните с касания большим пальцем левой руки безымянного пальца правой руки. Подсчитайте количество пальцев под соединяющимися пальцами, включая пальцы, которые касаются друг друга. В общей сложности у вас должно получиться 7, что означает 70. Затем подсчитайте количество пальцев над касающимися пальцами правой и левой руки. Здесь должно быть 0 слева и 3 справа от вас. Теперь умножьте 3 на 0 = 0 и добавьте 70 к 0 для ответа. Ответ 10 на 7 = 70!

Итог

Попробуйте это с другими кратными шести, семи, восьми и десяти. Как бы вы умножали 8 и 8 пальцами? Что насчет 8 и 10? Если вас интересует вопрос, как научить таблице умножения на пальцах своего ребенка, то просто постарайтесь включить практику подсчета произведения различных чисел в ежедневную рутину. Вы и не заметите, как малыш начнет не только быстро считать произведение двух чисел, но и в конечном итоге запомнит таблицу умножения.

В этом и заключается вся привлекательность данного способа — он веселый, заставляет думать логически, включать математические способности и при этом развивает память. Что может быть лучше для ребенка? Давайте напоследок подсчитаем, чему будет равно произведение 6 и 10? А 8 и 9? Что насчет 7 и 8? Вот такая вот занимательная математика.

fb.ru

Приемы быстрого счета

ПРИЕМЫ БЫСТРОГО СЧЕТА

Введение

1.Актуальность темы

В наш век высоких технологий и повсеместного использования компьютера умение быстро и правильно производить в уме достаточно сложные вычисления ни в коем случае не утратило своей актуальности. Гибкость ума является предметом гордости людей, а способность, например, быстро производить в уме вычисления вызывает откровенное удивление. Такие навыки помогут человеку в учебе, в быту, в профессиональной деятельности. Кроме того, быстрый счет – настоящая гимнастика для ума, приучающая в самых сложных жизненных ситуациях находить в кратчайшее время хорошие и нестандартные решения. Производя математические вычисления в уме, человек пользуется, по сути, теми же правилами, что и при письменных вычислениях

Большинство наших детей считают плохо. То ли думать им лень (зачем загружать себя лишней работой, если есть калькуляторы), то ли в свое время этому никто не научил. Приемов рациональных вычислений в учебниках практически нет. Сложные формулы и алгоритмы школьной программы все дальше и дальше уводят учеников от простых, понятных навыков устного счета.

Я выбрала тему «Приемы быстрого счета» потому, что я люблю математику и хотела бы научиться считать быстро и правильно, не прибегая к использованию калькулятора.

Актуальность моей темы заключается в следующем: то, что быстрый счет помогает людям в повседневной жизни, а ученикам на «отлично» заниматься по математике

.Цели исследовательской работы: изучить методы и приемы быстрого счета и доказать необходимость умения быстрого счета и эффективного использования этих приемов.

.Задачи:

А) Посмотреть и изучить книги по данной теме.

В) Выбрать наиболее оптимальные методы и приемы быстрого счета.

. Объект исследования: методы и приемы быстрого счета.

Как люди научились считать

Никто не знает, как впервые появилось число, как первобытный человек начал считать. Однако десятки тысяч лет назад первобытный человек собирал плоды деревьев, ходил на охоту, ловил рыбу, научился делать каменный топор и нож, и ему приходилось считать различные предметы, с которыми он встречался в повседневной жизни. Постепенно возникало необходимость отвечать на жизненно важные вопросы: поскольку плодов достанется каждому, чтобы хватило всем, сколько расходовать сегодня, чтобы оставить про запас; сколько нужно сделать ножей и т.п. Таким образом, сам не замечая, человек начал считать и вычислять.

Вначале человек научился выделять единичные предметы. Например, из стаи волков, стада оленей он выделял одного вожака, из выводка птенцов – одного птенца и т. д. Научившись выделять один предмет из множества других, говорили: “один”, а если их было больше – “много” Даже для названия числа “один” часто пользовались словом, которым обозначался единичный предмет, например: “луна”, “солнце”. Такое совпадение названия предмета и числа сохранилось в языке некоторых народов до наших дней.

Частые наблюдения множеств, состоящих из пары предметов (глаза, уши, крылья, руки), привели человека к представлению о числе два. До сих пор слово “два” на некоторых языках звучит так же, как “глаза” или “крылья”.

« Если предметов было больше двух, то первобытный человек говорил «много». Лишь постепенно человек научился считать до трех, затем до пяти и до десяти и т.д. Название каждого числа отдельным словом было великим шагом вперед.

Для счета люди использовали пальцы рук, ног. Ведь и маленькие дети тоже учатся считать по пальцам. Однако этот способ годился только в пределах 20.

Выход нашелся: считать на пальцах до 10, а затем начинать сначала, отдельно подсчитывая количество десятков. Система счисления на основе десяти возникла как естественное развитие пальцевого счета.

По мере развития речи люди начали использовать слова для обозначения чисел. Отпала необходимость показывать кому-то пальцы, камешки или реальные предметы, чтобы назвать их количество. Для изображения чисел стали применяться рисунки, чертежи или символы. Существовали и системы с отдельными символами для каждой цифры до 9 включительно, как в арабской системе счисления, которую мы сейчас используем, а у греков имелся специальный символ и для 10.

При помощи пальцев рук люди научились не только считать большие числа, но и выполнять действия сложения и вычитания.

Древние торговцы для удобства счета начали накладывать зерна и раковины на специальную дощечку, которая со временем стала называться абаком.

Особенно сложны и трудны были в старину действия умножения и деления — особенно последнее. «Умноженье — мое мученье, а с делением — беда», — говорили в старину. Тогда не существовало еще, как теперь, одного выработанного практикой приема для каждого действия. Напротив, в ходу была одновременно чуть не дюжина различных способов умножения и деления — приемы один другого запутаннее, твердо запомнить которые не в силах был человек средних способностей. Каждый учитель счетного дела держался своего излюбленного приема, каждый «магистр деления» (были такие специалисты) восхвалял собственный способ выполнения этого действия.

В книге В. Беллюстина «Как постепенно дошли люди до настоящей арифметики» (1914) изложено 27 способов умножения, причем автор замечает: «весьма возможно, что есть и еще (способы), скрытые в тайниках книгохранилищ, разбросанные в многочисленных, главным образом, рукописных сборниках». Наш современный способ умножения описан там под названием «шахматного». Был также и очень интересный, точный, легкий, но громоздкий способ «галерой» или «лодкой», названный так в силу того, что при делении чисел этим способом получается фигура, похожая на лодку или галеру. У нас такой способ употреблялся до середины XVIII века. На протяжении своей книги в 640 страниц Леонтий Магницкий («Арифметика» – старинный русский учебник математики, которую Ломоносов называл «вратами своей учености») пользуется исключительно способом «галеры», не употребляя, впрочем, этого названия.

Упоминаются такие способы, как «загибанием», «решеткой», «задом наперед», «ромбом», «треугольником» и многие многие другие. Многие такие приемы для умножения чисел долгие и требуют обязательной проверки.

Интересно, что и наш способ умножения не является совершенным; можно придумать еще более быстрые и еще более надежные.

Таблица умножения на «пальцах».

Таблица умножения – те необходимые в жизни каждого человека знания, которые требуется элементарно заучить, что на первых школьных порах дается совсем не элементарно. Это потом уже с легкостью мага мы “щелкаем” примеры на умножение: 2·3, 3·5, 4·6 и так далее. С возрастом, правда, все чаще забываемся на множителях ближе к 9, особенно если счетной практики давно не ведали, отчего отдаемся во власть калькулятора или надеемся на свежесть знаний друга. Однако, овладев одной незамысловатой техникой “ручного” умножения, мы можем запросто отказаться от услуг калькулятора. Но сразу уточним, что говорим только о школьной таблице умножения, то есть для чисел от 2 до 9, умножаемых на числа от 1 до 10.

Умножение для числа 9 – 9·1, 9·2 … 9·10 – легче выветривается из памяти и труднее пересчитывается вручную методом сложения, однако именно для числа 9 умножение легко воспроизводится “на пальцах”. Растопырьте пальцы на обеих руках и поверните руки ладонями от себя. Мысленно присвойте пальцам последовательно числа от 1 до 10, начиная с мизинца левой руки и заканчивая мизинцем правой руки (это изображено на рисунке).

Допустим, хотим умножить 9 на 6. Загибаем палец с номером, равным числу, на которое мы будем умножать девятку. В нашем примере нужно загнуть палец с номером 6. Количество пальцев слева от загнутого пальца показывает нам количество десятков в ответе, количество пальцев справа – количество единиц. Слева у нас 5 пальцев не загнуто, справа – 4 пальца. Таким образом, 9·6=54. Ниже на рисунке детально показан весь принцип “вычисления”.

Еще пример: нужно вычислить 9·8=?. По ходу дела скажем, что в качестве “счетной машинки” не обязательно могут выступать пальцы рук. Возьмите, к примеру, 10 клеточек в тетради. Зачеркиваем 8-ю клеточку. Слева осталось 7 клеточек, справа – 2 клеточки. Значит 9·8=72. Все очень просто.

Умножение для числа 8 – 8·1, 8·2 … 8·10 – действия здесь похожи на умножение для числа 9 за некоторыми изменениями. Во-первых, поскольку числу 8 не хватает уже двойки до круглого числа 10, нам необходимо каждый раз загибать сразу два пальца – с номером x и следующий палец с номером x+1. Во-вторых, тотчас же после загнутых пальцев мы должны загнуть еще столько пальцев, сколько осталось незагнутых пальцев слева. В-третьих, это напрямую работает при умножении на число от 1 до 5, а при умножении на число от 6 до 10 нужно отнять от числа x пятерку и выполнить расчет как для числа от 1 до 5, а к ответу затем добавить число 40, потому что иначе придется выполнять переход через десяток, что не совсем удобно “на пальцах”, хотя в принципе это не так сложно. Вообще надо заметить, что умножение для чисел ниже 9 тем неудобнее выполнять “на пальцах”, чем ниже число расположено от 9.

Теперь рассмотрим пример умножения для числа 8. Допустим, хотим умножить 8 на 4. Загибаем палец с номером 4 и за ним палец с номером 5 (4+1). Слева у нас осталось 3 незагнутых пальца, значит нам необходимо загнуть еще 3 пальца после пальца с номером 5 (это будут пальцы с номерами 6, 7 и 8). Осталось 3 пальца не загнуто слева и 2 пальца – справа. Следовательно, 8·4=32.

Еще пример: вычислить 8·7=?. Как было сказано выше, при умножении на число от 6 до 10 нужно отнять от числа x пятерку, выполнить расчет с новым числом x-5, а затем добавить к ответу число 40. У нас x=7, значит загибаем палец с номером 2 (7-5=2) и следующий палец с номером 3 (2+1). Слева один палец остался не загнут, значит загибаем еще один палец (с номером 4). Получаем: слева 1 палец не загнут и справа – 6 пальцев, что обозначает число 16. Но к этому числу нужно еще добавить 40: 16+40=56. В итоге 8·7=56.

Приемы быстрого счета

Феномен особых способностей в устном счёте встречается с давних пор. Как известно, ими обладали многие учёные, в частности, Андре Ампер и Карл Гаусс. Однако, умение быстро считать было присуще и многим людям, чья профессия была далека от математики и науки в целом.

До второй половины XX века на эстраде были популярны выступления специалистов в устном счёте. Иногда они устраивали показательные соревнования между собой. Известными российскими «суперсчетчиками» являются Арон Чиквашвили, Давид Гольдштейн, Юрий Горный, зарубежными: Борислав Гаджански, Вильям Клайн, Томас Фулер и другие.

Хотя некоторые специалисты уверяли, что дело во врождённых способностях, другие аргументированно доказывали обратное: «дело не только и не столько в каких-то исключительных, „феноменальных способностях, а в знании некоторых математических законов, позволяющих быстро производить вычисления» и охотно раскрывали эти законы.

Истина, как обычно, оказалась на некоей «золотой середине» сочетания природных способностей и грамотного, трудолюбивого их пробуждения, взращивания и использования. Те, кто следуя Трофиму Лысенко уповают исключительно на волю и напористость, со всеми уже хорошо известными способами и приёмами устного счёта обычно при всех стараниях не поднимаются выше очень и очень средних достижений. Более того, настойчивые попытки «хорошенько нагрузить» мозг такими занятиями как устный счёт, шахматы вслепую и т. п. легко могут привести к перенапряжению и заметному падению умственной работоспособности, памяти и самочувствия (а в наиболее тяжёлых случаях – и к шизофрении). С другой стороны и одарённые люди при беспорядочном использовании своих талантов в такой области как устный счёт быстро «перегорают» и перестают быть в состоянии длительно и устойчиво показывать яркие достижения. Один из примеров удачного сочетания обоих условий (природной одарённости и большой грамотной работы над собой) показал наш соотечественник уроженец Алтайского края Юрий Горный.

Пожалуй, единственная научно обоснованная и достаточно подробно разработанная система резкого повышения быстроты устного счета создана была в годы второй мировой войны цюрихским профессором математики Я. Трахтенбергом. Она известна под названием “Системы быстрого счета”. История ее создания необычная. В 1941 году гитлеровцы бросили Трахтенберга в концлагерь. Чтобы уцелеть в нечеловеческих условиях и сохранить нормальной свою психику, Трахтенберг начал разрабатывать принципы ускоренного счета. За четыре страшных года пребывания в концлагере профессору удалось создать стройную систему ускоренного обучения детей и взрослых основам быстрого счета. После войны Трахтенберг создал и возглавил Цюрихский математический институт, получивший мировую известность.

Также разработкой приемов быстрого счета занимались другие ученые: Яков Исидорович Перельман, Георгий Берман и другие.

Приведу приемы умножения чисел, получившие наибольшее описание в литературе.

Умножение двузначного числа на 11

1. Умножение на 11 числа, сумма цифр которого не превышает 10.

Чтобы умножить на 11 число, сумма цифр которого 10 или меньше 10, надо мысленно раздвинуть цифры этого числа, поставить между ними сумму этих цифр, а затем к первой цифре прибавить 1, а вторую и последнюю (третью) цифру оставить без изменения.

х 11 = 7 (7+2) 2 = 792;

х 11 = 3 (3+5) 5 = 385;

2. Умножение на 11 числа, сумма цифр которого больше 10.

Чтобы умножить на 11 число, сумма цифр которого 10 или больше 10, надо мысленно раздвинуть цифры этого числа, поставить между ними сумму этих цифр, а затем к первой цифре прибавить 1, а вторую и последнюю (третью) цифру оставить без изменения.

х 11 = 7 (7+8) 8 = 7(13)8 = 858.

х 11 = 9 (9+4) 4 = 9 (13) 4 = 1034;

Умножение на одиннадцать (по Трахтенбергу).

Разберем на примере: 633 умножить на 11.

Ответ пишется под 633 по одной цифре справа налево, как указано в правилах.

Первое правило. Напишите последнюю цифру числа 633 в качестве правой цифры результата

633 * 11

3

Второе правило. Каждая последующая цифра числа 633 складывается со своим правым соседом и записывается в результат. 3 + 3 будет 6. Перед тройкой записываем результат 6.

* 11

63

Применим правило еще раз: 6 + 3 будет 9. Записываем и эту цифру в результате:

* 11

963

Третье правило. Первая цифра числа 633, то есть 6, становится левой цифрой результата:

* 11

6963

Ответ: 6963.

Умножение на одиннадцать по Берману

Берман вывел, что при умножении на одиннадцать, число нужно умножить на 10 и прибавить само себя, то есть то число, которое мы умножаем.

Пример : 110 * 11 = 110 * (10 + 1) = 110 * 10 + 110 * 1 = 1100 + 110 =1210 Ответ: 1210.

Пример: 123 * 11 = 123 * (10 +1) = 123 * 10 + 123 * 1 = 1230 + 123 =1353 Ответ: 1353.

Умножение на число 111, 1111 и т.д, зная правила умножения двузначного числа на число 11

Если сумма цифр первого множителя меньше 10, надо мысленно раздвинуть цифры этого числа на 2, 3 и т.д. шага, сложить цифры и записать соответствующее количество раз их сумму между раздвинутыми цифрами. Количество шагов всегда меньше количества единиц на 1.

Пример:

24 х 111 = 2 (2 + 4) (2+4) 4 = 2664 (количество шагов – 2)

х 1111 = 2 (2 +4) (2 +4) (2+4) 4 = 26664 (количество шагов – 3)

При умножении числа 72 на 111111 цифры 7 и 2 надо раздвинуть на 5 шагов. Эти вычисления можно легко произвести в уме.

72 х 111111 = 7999992 (количество шагов – 5)

Если единиц во втором множителе 7, то шагов будет на один меньше, т.е. 6.

Если единиц 8, то шагов будет 7 и т.д.

х 11111111 = 677777771

Эти вычисления можно легко произвести в уме.

Умножение двузначного числа на 111, 1111, 1111 и т.д., сумма цифр которого равна 10 или больше 10

Немного сложнее выполнить устное умножение, если сумма цифр первого множителя равна 10 или более 10.

Примеры:

48 х 111 = 4 (4+8) (4+8) 8 = 4 (12) (12) 8 = (4 +1) (2+1) 28 = 5328.

В этом случае к первой цифре надо прибавить 1. Получим 5.

Далее 2 + 1 = 3. А последние цифры 2 и 8 оставляем без изменения.

56 х 11111 = 5(5+6)(5+6)(5+6)(5+6)6 = 5(11)(11)(11)(11)6 = 622216

67 х 1111 = 6(6+7)…7 = 6(13)…7 = 74437

Умножение двузначного числа на 101

Пожалуй, самое простое правило: припишите ваше число к самому себе. Умножение закончено. Пример:

* 101 = 5757 57 –> 5757

быстрый счет умножение число

Умножение трехзначного числа на 999.

Любопытная особенность числа 999 проявляется при умножении на него всякого другого трехзначного числа. Тогда получается шестизначное произведение: первые три цифры его есть умножаемое число, только уменьшенное на единицу, а остальные три цифры (кроме последней) – «дополнения» первых до 9. Например:

* 999 = 572 427

999

Умножение на двенадцать (по Трахтенбергу)

Правило умножения на 12: нужно удваивать поочередно каждую цифру и прибавлять к ней поочередно ее «соседа».

Пример: 63247 * 12

Необходимо записывать цифры множимого через интервал и каждую цифру результата писать точно под цифрой числа 63247, из которой она образовалась.

63247 * 12 дважды 7 будет = 14, переносим 1

4

063247 * 12 дважды 4 + 7 + 1 = 16, переносим 1

64

063247 * 12 дважды 2 + 4 + 1 = 9

964

Следующие шаги аналогичны.

Окончательный ответ : 063247 * 12

758964

Умножение на двенадцать ( по Берману)

При умножении на 12 можно число умножить сначала на 6, а затем на 2.6, в свою очередь, можно разбить на 2 множителя – это 3 и 2.

Пример : 136 * 12 = 136 * 6 * 2 = 816 * 2 = 1632 или

* 12 = 136 * 3 * 2 * 2 = 408 * 2 * 2 = 816 * 2 = 1632

Умножение на шесть (по Трахтенбергу).

Нужно прибавить к каждой цифре половину «соседа».

Пример: 0622084 * 6

0622084 * 6 4 является правой цифрой этого числа и, так 4 как «соседа» у нее нет, прибавлять нечего.

0622084 * 6 Вторая цифра 8, ее «сосед» – 4. Мы берем 8 04 прибавляем половину 4 (2) и получаем 10, ноль пишем, 1 в перенос.

0622084 * 6 Следующая цифра ноль. Мы прибавляем к ней

половину «соседа» 8 (4), то есть 0 + 4 = 4 плюс

перенос (1).

Остальные шаги аналогичны.

Ответ : 0622084 * 6

Правило умножения на 6 : является «сосед» четным или нечетным – никакой роли не играет. Мы смотрим только на саму цифру: если она четная, прибавляем к ней целую часть половины «соседа», если нечетная, то кроме половины «соседа» прибавляем еще 5.

Пример: 0443052 * 6

0443052 * 6 2 – четная и не имеет «соседа», напишем ее снизу

0443052 * 6 5 – нечетная: 5 + 5 и плюс половина «соседа» 2 (1)

будет 11. Запишем 1 и в перенос 1

0443052 * 6 половина от 5 будет 2, и прибавим перенос 1, будет 3

0443052 * 6 3 – нечетная, 3 + 5 =8

0443052 * 6 4 + половина от 3 (1) будет 5

0443052 * 6 4 + половина от 4 (2) будет 6

0443052 * 6 ноль + половина от 4 (2) будет 2

Ответ : 2658312

Система быстрого счета по Трахтенбергу основана на закономерностях умножения чисел. Чтобы умножить на 11, 12, 6 и т. д. надо знать алгоритм выполнения. Этим система неудобна, надо в памяти держать много правил быстрого счета, но система Трахтенберга показывает как красива математика, если человек открывает тайны ее закономерностей, изучает их и учится применять на практике.

Выводы исследования

Как мы видим, быстрый счет это уже не тайна за семью печатями, а научно разработанная система. Раз есть система, значит ее можно изучать, ей можно следовать, ею можно овладеть.

Все рассмотренные мною методы устного умножения говорят о многолетнем интересе и ученых, и простых людей к игре с цифрами.

Используя некоторые из этих методов на уроках или дома, можно развить скорость вычислений, привить интерес к математике, добиться успехов в изучении всех школьных предметов.

Список литературы

Бантова М. А. Система формирования вычислительных навыков. //Нач. шк – 1993.-№ 11.-с. 38-43.

Белошистая А. В. Приём формирования устных вычислительных умений в пределах 100 // Начальная школа. – 2001.- № 7

Берман Г. Н. Приемы счёта, изд. 6-е, М.: Физматгиз, 1959.

Боротьбенко Е И. Контроль навыков устных вычислений. //Нач. шк. – 1972. – № 7.- с. 32-34.

Воздвиженский А. Умственные вычисления. Правила и упрощённые примеры действий с числами. – 1908.

Волкова СИ., Моро М. И. Сложение и вычитание многозначных чисел. //Нач. шк.- 1998.-№ 8.-с.46-50

Воскресенский М. П. Приёмы сокращённых вычислений. – М.Д905.-148с.

Вроблевский. Как научится легко и быстро считать. – М.-1932.-132с.

Гольдштейн Д. Н. Курс упрощённых вычислений. М.: Гос. учебно-пед. изд., 1931.

Гольдштейн Д. Н. Техника быстрых вычислений. М.: Учпедгиз, 1948.

Гончар Д. Р. Устный счёт и память: загадки, приёмы развития, игры // В сб. Устный счёт и память. Донецк:Сталкер, 1997 г.

Демидова Т. Е., Тонких А. П. Приёмы рациональных вычислений в начальном курсе математики // Начальная школа. – 2002. – № 2. – С. 94-103.

Катлер Э. Мак-Шейн Р. Система быстрого счёта по Трахтенбергу. – М.: Учпедгиз.- 1967. ?150с.

Липатникова И. Г. Роль устных упражнений на уроках математики //Начальная школа. – 1998. – № 2.

Мартель Ф. Приемы быстрого счёта. – Пб. ?1913. ?34с.

Мартынов И. И. Устный счёт для школьника, что гаммы для музыканта. // Начальная школа. – 2003. – № 10. – С. 59-61.

Мелентьев П. В. «Быстрые и устные вычисления.» М.: «Гостехиздат», 1930.

Перельман Я. И. Быстрый счёт. Л.: Союзпечать, 1945.

Пекелис В. Д. «Твои возможности, человек!» М.: «Знание», 1973.

Робер Токэ «2 + 2 = 4» (1957) (англоязычное издание: «Магия чисел» (1960)).

Сорокин А. С. Техника счёта. М.: «Знание», 1976.

Сухорукова А. Ф. Больше внимания устным вычислениям. //Нач. шк. – 1975.-№ 10.-с. 59-62.

Фаддейчева Т. И. Обучение устным вычислениям // Начальная школа. – 2003. – № 10.

Фаермарк Д. С. «Задача пришла с картины.» М.: «Наука».

ЛИТЕРАТУРА

Берман Г. Н. Приемы счета, изд. 6-е, М., Физматгиз, 1959.

Гольдштейн Д. Н. Курс упрощенных вычислений. М., Гос. учебно-пед. изд., 1931.

Гольдштейн Д. Н. Техника быстрых вычислений. М., Учпедгиз, 1948.

Катлер. Э., Мак – Шеин Р. Система быстрого счета по Трахтенбергу. Пер. с англ. М., “Просвещение”, 1967.

Перельман Я. И. Быстрый счет. Л.; Союзпечать, 1945.

Сорокин А. С. Техника счета. М., “Знание”, 1976.

. Перельман А.И. Быстрый счет. 1941г.

. Шейнина О.С. Соловьева Г.М. Занятие школьного кружка 5-6 классов. 2003г.

. Баврин И.И. Сельский учитель С.А.Рачинский и его задачи для умственного счета. 2003г.

. Спивак А.В. Тысяча и одна задача по математике. 2002г.

. Шарыгин И.Ф. Шевкин А.В. Математика. Задачи на смекалку. 2000г.

. Шевкин А.В.Школьная олимпиада по математике. 2003г.

yamiki.ru

Воображаемые счёты: сложные вычисления «на пальцах»

Маленькие дети в Южной Азии могут производить сложные математические вычисления за несколько секунд, просто щёлкая пальцами в воздухе.

Их секретный инструмент — воображаемые счёты-абак.

Новости с программы Mind Mathlon 2014, которая проходила в марте в Технологическом институте города Карачи, рассказывали о маленьких детях, которые просто щёлкают пальцами и производят сложнейшие вычисления с невероятной точностью.

Очевидно, детей научили использовать пальцы в качестве бусинок на счётах, что позволило им складывать и вычитать со скоростью калькулятора.

Эта техника довольно проста, но чтобы её освоить, требуется несколько лет практики. Пальцы правой руки — единицы. Поднятый вверх большой палец правой руки — число 5. Каждый палец левой руки соответствует десяткам. А поднятый вверх большой палец левой руки — это число 50. То есть два больших пальца, поднятых вверх — это 55.

Удивительная особенность этой техники в том, что использовать её может любой: слабовидящий ребёнок, участвующий в вышеуказанной программе, считал ничуть не хуже всех остальных. 11-летние дети запросто умножали 10-значные числа и даже извлекали квадратный корень из 6-значного числа, и всё это без калькулятора, карандаша и бумаги.

Ясин Атальф генеральный директор лаборатории робототехники, пояснил, что детей просто научили двигать воображаемые бусинки на воображаемых счётах-абак.

Эта техника популярна среди школьников в ряде азиатских стран, например, в Китае, Японии и Индии.

Майкл Франк из Стенфордского университетаи Дэвид Баннер из Университета Калифорнии отправились в школу в штате Гуджарат в Индии, чтобы понять, как эта техника работает.

В частности специалисты хотели понять, как детям удаётся следить за всеми 15 столбцами воображаемых счёт, в то время как многие люди едва смогут отследить 3 или 4 столбца. Они изучали детей, которые обучались технике только один год. И эти дети не могли выполнять арифметические действия с числами, в которых больше трёх или четырёх знаков. Это означало, что эти дети в состоянии держать в голове лишь три или четыре столбца своих «счёт».

А ещё специалисты установили, что работа на воображаемых счётах не зависит от языковых систем. В других похожих техниках учащимся приходится представлять числа, оперируя их названиями на том или ином языке. А воображаемые счёты-абак — задача полностью визуальная, и от языка никак не зависит.

По словам Альтафа, эта «психическая математика» подойдёт каждому, кто желает отточить свои навыки счёта в уме. Но чтобы добиться действительно впечатляющих результатов, потребуется не один год напряжённой работы.

Алексей Степанов02.02.2015

www.factroom.ru

---