06.07.202017.12.2018

В чем измеряется период вращения в физике – в каких единицах и каким символом обозначается период вращения и частото вращения?

• by alexxlab
• Комментариев к записи В чем измеряется период вращения в физике – в каких единицах и каким символом обозначается период вращения и частото вращения? нет
• Советы абитуриенту

Равномерное движение по окружности, формулы и примеры

Равномерное движение тела по окружности — это частный и наиболее простой случай криволинейного движения. Хотя при таком движении модуль скорости остается постоянным, это движение с ускорением, которое является следствием изменения направления вектора скорости.

В окружающем нас мире мы часто сталкиваемся с подобным движением — при любом вращении твердого тела вокруг некоторой закрепленной оси все точки этого тела движутся по окружностям.

Основные характеристики и формулы

Пусть материальная точка движется по окружности радиуса (рис.1). Начало декартовой системы координат поместим в центр окружности. Тогда положение точки на окружности однозначно определяется углом поворота между осью и радиус-вектором точки.

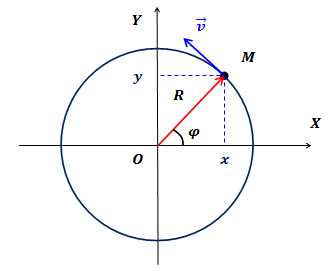
Рис.1. Равномерное движение тела по окружности

Условились положительным считать направление вращения против часовой стрелки.

Декартовые координаты точки однозначно определяются углом поворота точки:

   

При движении точки по окружности ее координата, то есть угол поворота , изменяется или становится функцией времени. Поэтому закон движения в этом случае — это зависимость угла поворота от времени: .

Единицей измерения угла поворота в системе СИ является радиан.

Период вращения — это время, за которое точка совершает один полный оборот по окружности, т.е. поворачивается на угол .

Частота вращения — это число полных оборотов, совершаемых точкой при равномерном движении по окружности, в единицу времени:

   

В системе СИ частота измеряется в

Частота и период связаны между собой формулой:

   

Примеры решения задач

ru.solverbook.com

Частота вращения Википедия

Углова́я частота́ (синонимы: радиальная частота, циклическая частота, круговая частота, частота вращения) — скалярная физическая величина, мера частоты вращательного или колебательного движения. В случае вращательного движения угловая частота равна модулю вектора угловой скорости. В Международной системе единиц (СИ) и системе СГС угловая частота выражается в радианах в секунду, её размерность обратна размерности времени (радианы безразмерны).

Угловая частота является производной по времени от фазы колебания:

ω=∂φ/∂t.{\displaystyle \omega =\partial \varphi /\partial t.}

Другое распространённое обозначение ω=φ˙.{\displaystyle \omega ={\dot {\varphi }}.}

Угловая частота связана с частотой ν соотношением^[1]

ω=2πν.{\displaystyle \omega ={2\pi \nu }.}

В случае использования в качестве единицы угловой частоты градусов в секунду связь с обычной частотой будет следующей:

ω=360∘ν.{\displaystyle \omega ={360^{\circ }\nu }.}

В случае вращательного движения угловая частота численно равна углу, на который повернется вращающееся тело за единицу времени (то есть равна модулю вектора угловой скорости), в случае колебательного движения — приращению полной фазы колебания за единицу времени. Численно угловая (циклическая) частота равна числу циклов (колебаний, оборотов) за 2π единиц времени.

Введение циклической частоты (в её основной размерности — радианах в секунду) позволяет упростить многие формулы в теоретической физике и электронике. Так, резонансная циклическая частота колебательного LC-контура равна ωLC=1/LC,{\displaystyle \omega _{LC}=1/{\sqrt {LC}},} тогда как обычная резонансная частота νLC=1/(2πLC).{\displaystyle \nu _{LC}=1/(2\pi {\sqrt {LC}}).}

В то же время ряд других формул усложняется. Решающим соображением в пользу циклической частоты стало то, что переводные множители 2π и 1/(2π), появляющиеся во многих формулах при использовании радианов для измерения углов и фаз, исчезают при введении циклической частоты.

См. также

Примечания

1. ↑ Угловая частота (неизв.). Большой энциклопедический политехнический словарь. Проверено 27 октября 2016.

wikiredia.ru

Частота вращения – это… Что такое Частота вращения?



Частота вращения

Угловая скорость (синяя стрелка) в полторы единицы по часовой стрелке

Угловая скорость (синяя стрелка) в одну единицу против часовой стрелки

Углова́я ско́рость — векторная величина, характеризующая скорость вращения тела. Вектор угловой скорости по величине равен углу поворота тела в единицу времени:

,

а направлен по оси вращения согласно правилу буравчика, то есть, в ту сторону, в которую ввинчивался бы буравчик с правой резьбой, если бы вращался в ту же сторону.

Единица измерения угловой скорости, принятая в системах СИ и СГС) — радианы в секунду. (Примечание: радиан, как и любые единицы измерения угла, — физически безразмерен, поэтому физическая размерность угловой скорости — просто [1/секунда]). В технике также используются обороты в секунду, намного реже — градусы в секунду, грады в секунду. Пожалуй, чаще всего в технике используют обороты в минуту — это идёт с тех времён, когда частоту вращения тихоходных паровых машин определяли, просто «вручную» подсчитывая число оборотов за единицу времени.

Вектор (мгновенной) скорости любой точки (абсолютно) твердого тела, вращающегося с угловой скоростью определяется формулой:

где  — радиус-вектор к данной точке из начала координат, расположенного на оси вращения тела, а квадратными скобками обозначено векторное произведение. Линейную скорость (совпадающую с модулем вектора скорости) точки на определенном расстоянии (радиусе)

r от оси вращения можно считать так: v = rω. Если вместо радианов применять другие единицы углов, то в двух последних формулах появится множитель, не равный единице.

• В случае плоского вращения, то есть когда все векторы скоростей точек тела лежат (всегда) в одной плоскости («плоскости вращения»), угловая скорость тела всегда перпендикулярна этой плоскости, и по сути — если плоскость вращения заведомо известна — может быть заменена скаляром — проекцией на ось, ортогональную плоскости вращения. В этом случае кинематика вращения сильно упрощается, однако в общем случае угловая скорость может менять со временем направление в трехмерном пространстве, и такая упрощенная картина не работает.
• Производная угловой скорости по времени есть угловое ускорение.
• Движение с постоянным вектором угловой скорости называется равномерным вращательным движением (в этом случае угловое ускорение равно нулю).
• Угловая скорость (рассматриваемая как свободный вектор) одинакова во всех инерциальных системах отсчета, однако в разных инерциальных системах отсчета может различаться ось или центр вращения одного и того же конкретного тела в один и тот же момент времени (то есть будет различной «точка приложения» угловой скорости).
• В случае движения одной единственной точки в трехмерном пространстве можно написать выражение для угловой скорости этой точки относительно выбранного начала координат:

, где  — радиус-вектор точки (из начала координат),  — скорость этой точки.  — векторное произведение,  — скалярное произведение векторов. Однако эта формула не определяет угловую скорость однозначно (в случае единственной точки можно подобрать и другие векторы , подходящие по определению, по другому — произвольно — выбрав направление оси вращения), а для общего случая (когда тело включает более одной материальной точки) — эта формула не верна для угловой скорости всего тела (так как дает разные для каждой точки, а при вращении абсолютно твёрдого тела по определению угловая скорость его вращения — единственный вектор). При всём при этом, в двумерном случае (случае плоского вращения) эта формула вполне достаточна, однозначна и корректна, так как в этом частном случае направление оси вращения заведомо однозначно определено.

• При измерении угловой скорости в оборотах в секунду (об/с), модуль угловой скорости равномерного вращательного движения совпадает с частотой вращения f, измеренной в герцах (Гц) (то есть в таких единицах ).

• В случае использования обычной физической единицы угловой скорости — радианов в секунду — модуль угловой скорости связан с частотой вращения так:

• Наконец, при использовании градусов в секунду связь с частотой вращения будет:

См. также

Wikimedia Foundation. 2010.

• Частота сети
• Частота сердечных сокращений

Смотреть что такое “Частота вращения” в других словарях:

• частота вращения ВК — частота вращения ветроколеса Угол, проходимый лопастью ВК за единицу времени, измеренный в оборотах в единицу времени или в радианах. [ГОСТ Р 51237 98] Тематики ветроэнергетика Синонимы частота вращения ветроколеса EN rotation speed …   Справочник технического переводчика

• частота вращения — частота вращения …   Справочник технического переводчика

• Частота вращения — 3.113 Частота вращения число оборотов в единицу времени. Источник: ГОСТ Р МЭК 1029 2 4 96: Машины переносные электрические. Частные тр …   Словарь-справочник терминов нормативно-технической документации

• частота вращения — sukimosi dažnis statusas T sritis automatika atitikmenys: angl. rotating speed; rotation frequency; rotational speed vok. Drehgeschwindigkeit, f; Rotationsgeschwindigkeit, f rus. скорость вращения, f; частота вращения, f pranc. fréquence de… …   Automatikos terminų žodynas

• частота вращения — sūkių dažnis statusas T sritis Standartizacija ir metrologija apibrėžtis Kūno sukimosi apie tam tikrą ašį dažnis, išreiškiamas sūkių skaičiumi per vienetinį laiko tarpą. atitikmenys: angl. rotating frequency; rotating speed; rotation frequency;… …   Penkiakalbis aiškinamasis metrologijos terminų žodynas

• Частота вращения w — 69. Частота вращения w Угловая скорость вращения поворотной части крана в установившемся режиме движения. Определяется при наибольшем вылете с рабочим грузом при установке крана на горизонтальной площадке и скорости ветра не более 3 м/с на высоте …   Словарь-справочник терминов нормативно-технической документации

• частота вращения — sukimosi dažnis statusas T sritis fizika atitikmenys: angl. rotation frequency vok. Rotationsfrequenz, f; Umlauffrequenz, f rus. частота вращения, f pranc. fréquence de rotation, f …   Fizikos terminų žodynas

• ЧАСТОТА ВРАЩЕНИЯ — величина, равная отношению числа оборотов, совершённых телом, ко времени вращения. Обозначается обычно п. Единица Ч. в. (в СИ) с 1. Внесистемные единицы об/мин и об/с …   Большой энциклопедический политехнический словарь

• частота вращения — rotation frequency Число оборотов вращающегося звена в единицу времени. Шифр IFToMM: Раздел: СТРУКТУРА МЕХАНИЗМОВ …   Теория механизмов и машин

• частота вращения ротора (вала) ГТД в режиме сопровождения — частота вращения режима сопровождения Частота вращения ротора ГТД при запуске в момент отключения пускового устройства. [ГОСТ 23851 79] Тематики двигатели летательных аппаратов Синонимы частота вращения режима сопровождения …   Справочник технического переводчика

xzsad.academic.ru

Частота вращения – это… Что такое Частота вращения?



Частота вращения

Угловая скорость (синяя стрелка) в полторы единицы по часовой стрелке

Угловая скорость (синяя стрелка) в одну единицу против часовой стрелки

Углова́я ско́рость — векторная величина, характеризующая скорость вращения тела. Вектор угловой скорости по величине равен углу поворота тела в единицу времени:

,

а направлен по оси вращения согласно правилу буравчика, то есть, в ту сторону, в которую ввинчивался бы буравчик с правой резьбой, если бы вращался в ту же сторону.

Единица измерения угловой скорости, принятая в системах СИ и СГС) — радианы в секунду. (Примечание: радиан, как и любые единицы измерения угла, — физически безразмерен, поэтому физическая размерность угловой скорости — просто [1/секунда]). В технике также используются обороты в секунду, намного реже — градусы в секунду, грады в секунду. Пожалуй, чаще всего в технике используют обороты в минуту — это идёт с тех времён, когда частоту вращения тихоходных паровых машин определяли, просто «вручную» подсчитывая число оборотов за единицу времени.

Вектор (мгновенной) скорости любой точки (абсолютно) твердого тела, вращающегося с угловой скоростью определяется формулой:

где  — радиус-вектор к данной точке из начала координат, расположенного на оси вращения тела, а квадратными скобками обозначено векторное произведение. Линейную скорость (совпадающую с модулем вектора скорости) точки на определенном расстоянии (радиусе) r от оси вращения можно считать так: v = rω. Если вместо радианов применять другие единицы углов, то в двух последних формулах появится множитель, не равный единице.

• В случае плоского вращения, то есть когда все векторы скоростей точек тела лежат (всегда) в одной плоскости («плоскости вращения»), угловая скорость тела всегда перпендикулярна этой плоскости, и по сути — если плоскость вращения заведомо известна — может быть заменена скаляром — проекцией на ось, ортогональную плоскости вращения. В этом случае кинематика вращения сильно упрощается, однако в общем случае угловая скорость может менять со временем направление в трехмерном пространстве, и такая упрощенная картина не работает.
• Производная угловой скорости по времени есть угловое ускорение.
• Движение с постоянным вектором угловой скорости называется равномерным вращательным движением (в этом случае угловое ускорение равно нулю).
• Угловая скорость (рассматриваемая как свободный вектор) одинакова во всех инерциальных системах отсчета, однако в разных инерциальных системах отсчета может различаться ось или центр вращения одного и того же конкретного тела в один и тот же момент времени (то есть будет различной «точка приложения» угловой скорости).
• В случае движения одной единственной точки в трехмерном пространстве можно написать выражение для угловой скорости этой точки относительно выбранного начала координат:

, где  — радиус-вектор точки (из начала координат),  — скорость этой точки.  — векторное произведение,  — скалярное произведение векторов. Однако эта формула не определяет угловую скорость однозначно (в случае единственной точки можно подобрать и другие векторы , подходящие по определению, по другому — произвольно — выбрав направление оси вращения), а для общего случая (когда тело включает более одной материальной точки) — эта формула не верна для угловой скорости всего тела (так как дает разные для каждой точки, а при вращении абсолютно твёрдого тела по определению угловая скорость его вращения — единственный вектор). При всём при этом, в двумерном случае (случае плоского вращения) эта формула вполне достаточна, однозначна и корректна, так как в этом частном случае направление оси вращения заведомо однозначно определено.

• При измерении угловой скорости в оборотах в секунду (об/с), модуль угловой скорости равномерного вращательного движения совпадает с частотой вращения f, измеренной в герцах (Гц) (то есть в таких единицах ).

• В случае использования обычной физической единицы угловой скорости — радианов в секунду — модуль угловой скорости связан с частотой вращения так:

• Наконец, при использовании градусов в секунду связь с частотой вращения будет:

См. также

Wikimedia Foundation. 2010.

• Частота сети
• Частота сердечных сокращений

Смотреть что такое “Частота вращения” в других словарях:

• частота вращения ВК — частота вращения ветроколеса Угол, проходимый лопастью ВК за единицу времени, измеренный в оборотах в единицу времени или в радианах. [ГОСТ Р 51237 98] Тематики ветроэнергетика Синонимы частота вращения ветроколеса EN rotation speed …   Справочник технического переводчика

• частота вращения — частота вращения …   Справочник технического переводчика

• Частота вращения — 3.113 Частота вращения число оборотов в единицу времени. Источник: ГОСТ Р МЭК 1029 2 4 96: Машины переносные электрические. Частные тр …   Словарь-справочник терминов нормативно-технической документации

• частота вращения — sukimosi dažnis statusas T sritis automatika atitikmenys: angl. rotating speed; rotation frequency; rotational speed vok. Drehgeschwindigkeit, f; Rotationsgeschwindigkeit, f rus. скорость вращения, f; частота вращения, f pranc. fréquence de… …   Automatikos terminų žodynas

• частота вращения — sūkių dažnis statusas T sritis Standartizacija ir metrologija apibrėžtis Kūno sukimosi apie tam tikrą ašį dažnis, išreiškiamas sūkių skaičiumi per vienetinį laiko tarpą. atitikmenys: angl. rotating frequency; rotating speed; rotation frequency;… …   Penkiakalbis aiškinamasis metrologijos terminų žodynas

• Частота вращения w — 69. Частота вращения w Угловая скорость вращения поворотной части крана в установившемся режиме движения. Определяется при наибольшем вылете с рабочим грузом при установке крана на горизонтальной площадке и скорости ветра не более 3 м/с на высоте …   Словарь-справочник терминов нормативно-технической документации

• частота вращения — sukimosi dažnis statusas T sritis fizika atitikmenys: angl. rotation frequency vok. Rotationsfrequenz, f; Umlauffrequenz, f rus. частота вращения, f pranc. fréquence de rotation, f …   Fizikos terminų žodynas

• ЧАСТОТА ВРАЩЕНИЯ — величина, равная отношению числа оборотов, совершённых телом, ко времени вращения. Обозначается обычно п. Единица Ч. в. (в СИ) с 1. Внесистемные единицы об/мин и об/с …   Большой энциклопедический политехнический словарь

• частота вращения — rotation frequency Число оборотов вращающегося звена в единицу времени. Шифр IFToMM: Раздел: СТРУКТУРА МЕХАНИЗМОВ …   Теория механизмов и машин

• частота вращения ротора (вала) ГТД в режиме сопровождения — частота вращения режима сопровождения Частота вращения ротора ГТД при запуске в момент отключения пускового устройства. [ГОСТ 23851 79] Тематики двигатели летательных аппаратов Синонимы частота вращения режима сопровождения …   Справочник технического переводчика

dic.academic.ru

Угловая скорость. Формула угловой скорости :: SYL.ru

Расстояние и время, которое уходит на преодоление этого расстояния, связывает физическое понятие – скорость. И у человека, как правило, не вызывает вопросов определение этой величины. Все понимают, что двигаться на автомобиле со скоростью 100 км/ч – значит за один час проехать 100 километров.

А как быть, если тело вращается? Например, обычный бытовой вентилятор делает с десяток оборотов в секунду. И в то же время скорость вращения лопастей такова, что их запросто можно остановить рукой без вреда для себя. Земля вокруг своей звезды – Солнца – делает один оборот за целый год, а это более 30 миллионов секунд, но скорость её движения по околозвёздной орбите составляет около 30 километров за одну секунду!

Как же связать привычную скорость с быстротой вращения, как выглядит формула угловой скорости?

Понятие угловой скорости

Понятие угловой скорости используется в изучении законов вращения. Оно применяется ко всем вращающимся телам. Будь то вращение некоторой массы вокруг другой, как в случае с Землёй и Солнцем, или же вращение самого тела вокруг полярной оси (суточное вращение нашей планеты).

Отличие угловой скорости от линейной в том, что она фиксирует изменение угла, а не расстояния в единицу времени. В физике угловую скорость принято обозначать буквой греческого алфавита «омега» – ω.

Классическая формула угловой скорости вращения рассматривается так.

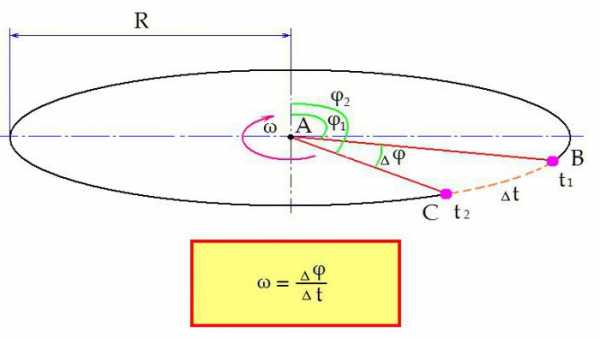
Представим, что вокруг некоторого центра А вращается физическое тело с постоянной скоростью. Его положение в пространстве относительно центра определяется углом φ. В некоторый момент времени t1 рассматриваемое тело находится в точке В. Угол отклонения тела от начального φ1.

Затем тело перемещается в точку С. Оно находится там в момент времени t2. Время, понадобившееся для данного перемещения:

∆t = t2 – t1.

Меняется и положение тела в пространстве. Теперь угол отклонения равен φ2. Изменение угла за период времени ∆t составило:

∆φ = φ2 – φ1.

Теперь формула угловой скорости формулируется следующим образом: угловая скорость определяется как отношение изменения угла ∆φ за время ∆t.

Единицы измерения угловой скорости

Скорость движения тела линейная измеряется в разных величинах. Движение автотранспорта по дорогам привычно указывают в километрах в час, морские суда делают узлы – морские мили в час. Если же рассматривать движение космических тел, то тут чаще всего фигурируют километры в секунду.

Угловая скорость в зависимости от величины и от предмета, который вращается, также измеряется в разных единицах.

Радианы в секунду (рад/с) – классическое мерило скорости в международной системе единиц (СИ). Показывают – на сколько радиан (в одном полном обороте 2 ∙ 3,14 радиан) успевает повернуться тело за одну секунду.

Обороты в минуту (об/мин) – самая распространённая единица для обозначения скоростей вращения в технике. Валы двигателей как электрических, так и автомобильных выдают именно (достаточно посмотреть на тахометр в своём автомобиле) обороты в минуту.

Обороты в секунду (об/с) – используется реже, прежде всего в образовательных целях.

Период обращения

Иногда для определения скорости вращения удобнее пользоваться другим понятием. Периодом обращения принято называть время, за которое некое тело делает оборот 360° (полный круг) вокруг центра вращения. Формула угловой скорости, выраженная через период обращения, принимает вид:

ω = 2П / Т.

Выражать периодом обращения быстроту вращения тел оправдано в случаях, когда тело вращается относительно медленно. Вернёмся к рассмотрению движения нашей планеты вокруг светила.

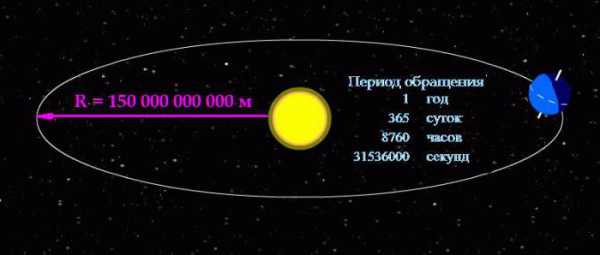
Формула угловой скорости позволяет вычислить её, зная период обращения:

ω = 2П/31536000 = 0,000000199238499086111 рад/с.

Глядя на полученный результат, можно понять, почему, рассматривая вращение небесных тел, удобнее пользоваться именно периодом обращения. Человек видит перед собой понятные цифры и наглядно представляет себе их масштаб.

Связь угловой и линейной скоростей

В некоторых задачах должны быть определены линейная и угловая скорость. Формула трансформации проста: линейная скорость тела равняется произведению угловой скорости на радиус вращения. Как это показано на рисунке.

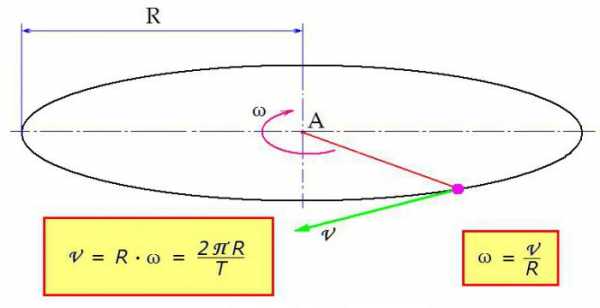
«Работает» выражение и в обратном порядке, с его помощью определяется и угловая скорость. Формула через скорость линейную получается путём несложных арифметических манипуляций.

www.syl.ru

Период вращения – это… Что такое Период вращения?



Период вращения

Период вращения космического объекта — это период времени, которое требуется объекту для совершения полного оборота вокруг своей оси относительно звёзд.

Период вращения (физический термин) — промежуток времени, в течение которого точка совершает полный оборот, двигаясь по окружности.

Период вращения Земли относительно точки весеннего равноденствия называется звёздными сутками^[1].

Периоды вращения некоторых объектов:

См. также

Примечания

Категории:

• Небесная механика
• Время в астрономии

Wikimedia Foundation. 2010.

• Новодевичий монастырь (значения)
• Политическая карьера Арнольда Шварценеггера

Смотреть что такое “Период вращения” в других словарях:

• Период вращения (астрономия) — Период вращения небесного тела это количество времени, требуемое объекту для совершения полного оборота вокруг своей оси относительно неподвижных звёзд. Совпадает с понятием «звёздные сутки», однако применительно к конкретным астрономическим… …   Википедия

• период — а, м. période f. <лат. periodus<гр. periodos обход, круговращение, орбита небесного тела. 1. Промежуток времени, в который протекает та или иная часть общего процесса. БАС 1. Бывают в жизни его периоды во время которых выступает он из… …   Исторический словарь галлицизмов русского языка

• Период — (Period) Промежуток времени, период как этап общественного развития, период в науках Период года, период работы, период регистрации, налоговый период, отчетный период, гарантийный период, ледниковый период Содержание Содержание Раздел 1. в других …   Энциклопедия инвестора

• Период обращения — Сидерический период обращения (от лат. sidus, звезда; род. падеж sideris)  промежуток времени, в течение которого какое либо небесное тело спутник совершает вокруг главного тела полный оборот относительно звёзд. Понятие «cидерический период… …   Википедия

• период — сущ., м., употр. часто Морфология: (нет) чего? периода, чему? периоду, (вижу) что? период, чем? периодом, о чём? о периоде; мн. что? периоды, (нет) чего? периодов, чему? периодам, (вижу) что? периоды, чем? периодами, о чём? о периодах 1. Периодом …   Толковый словарь Дмитриева

• ПЕРИОД — (греч. periodos путь кругом). 1) промежуток времени между двумя важными историческими событиями. 2) в астрономии то же, что цикл; в арифметике: число цифр, повторяющихся, в том же порядке, бесчисленное множество раз. 3) особенно развитое сложное… …   Словарь иностранных слов русского языка

• Период колебаний — Эту статью следует викифицировать. Пожалуйста, оформите её согласно правилам оформления статей …   Википедия

• Период колебания — Период колебаний  наименьший промежуток времени, за который система совершает одно полное колебание (то есть возвращается в то же состояние, в котором она находилась в первоначальный момент, выбранный произвольно). Содержание 1 Периоды простейших …   Википедия

• Синодический период — обращения (от греч. σύνοδος  соединение)  промежуток времени между двумя последовательными соединениями Луны или какой нибудь планеты Солнечной системы с Солнцем при наблюдении за ними с Земли. При этом соединения планет с Солнцем… …   Википедия

• Сидерический период — обращения (от лат. sidus, звезда; род. падеж sideris)  промежуток времени, в течение которого какое либо небесное тело спутник совершает вокруг главного тела полный оборот относительно звёзд. Понятие «сидерический период обращения»… …   Википедия

dic.academic.ru

Что такое угловая скорость и как ее рассчитывают?

Обычно, когда говорят о перемещении, мы представляем себе объект, который движется по прямой. Скорость такого движения принято называть линейной, и расчёт ее средней величины выполняется просто: достаточно найти отношение пройденного расстояния к времени, за которое оно было телом преодолено. Если же объект перемещается по окружности, то в этом случае уже определяется не линейная, а угловая скорость. Что это за величина и как ее рассчитывают? Об этом как раз и пойдет разговор в данной статье.

Угловая скорость: понятие и формула

Когда материальная точка движется по окружности, быстроту ее перемещения можно характеризовать величиной угла поворота радиуса, который соединяет движущийся объект с центром данной окружности. Понятно, что эта величина в зависимости от времени постоянно меняется. Быстрота, с которой этот процесс происходит, и есть не что иное, как угловая скорость. Другими словами, это отношение величины отклонения радиус-вектора объекта к промежутку времени, которое потребовалось объекту на совершение такого поворота. Формула угловой скорости (1) может быть записана в таком виде:

w = φ / t, где:

φ – угол поворота радиуса,

t – период времени вращения.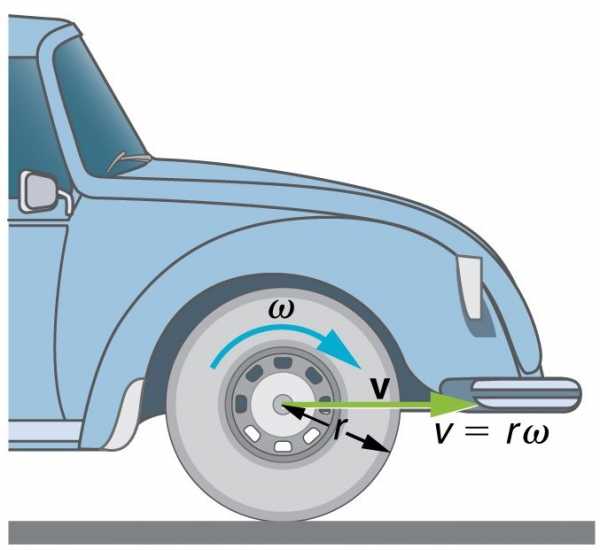

Единицы измерения величины

В международной системе общепринятых единиц (СИ) для характеристики поворотов принято использовать радианы. Поэтому 1 рад/с – основная единица, которая используется в расчетах угловой скорости. В то же время никто не запрещает применять градусы (напомним, что один радиан равен 180/пи, или 57˚18’). Также угловая скорость может выражаться в числе оборотов за минуту или за секунду. Если перемещение по окружности происходит равномерно, то данная величина может быть найдена по формуле (2):

w = 2π*n,

где n – частота вращения.

В противном случае подобно тому, как это делают для обычной скорости, рассчитывают среднюю, или мгновенную угловую скорость. Следует отметить, что рассматриваемая величина является векторной. Для определения ее направления обычно используют правило буравчика, которое часто применяется в физике. Вектор угловой скорости направлен в ту же сторону, в которую происходит поступательное движение винта с правой резьбой. Другими словами, он устремлен вдоль оси, вокруг которой вращается тело, в ту сторону, откуда вращение видно происходящим против движения часовой стрелки.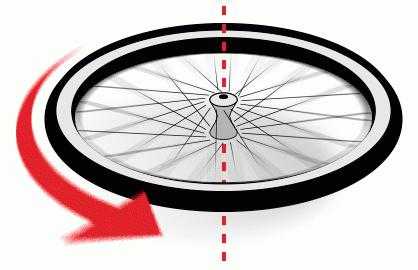

Примеры расчета

Предположим, требуется определить, чему равна линейная и угловая скорость колеса, если известно, что его диаметр равен одному метру, а угол вращения изменяется в соответствии с законом φ=7t. Воспользуемся нашей первой формулой:

w = φ / t = 7t / t = 7 с^-1.

Это и будет искомая угловая скорость. Теперь перейдем к поиску привычной нам быстроты перемещения. Как известно, v = s / t. Учитывая, что s в нашем случае – это длина окружности колеса (l =2π*r), а 2π – один полный оборот, получается следующее:

v = 2π*r / t = w * r = 7 * 0.5 = 3.5 м/с

Вот еще одна задачка на эту тему. Известно, что радиус Земли на экваторе равен 6370 километров. Требуется определить линейную и угловую быстроту движения точек, находящихся на этой параллели, которое возникает в результате вращения нашей планеты вокруг своей оси. В данном случае нам понадобится вторая формула:

w = 2π*n = 2*3,14 *(1/(24*3600)) = 7,268 *10^-5 рад/с.

Осталось выяснить, чему равна линейная скорость: v = w*r = 7,268 *10^-5 *6370 * 1000 = 463 м/с.

fb.ru

---