04.02.201922.12.2018

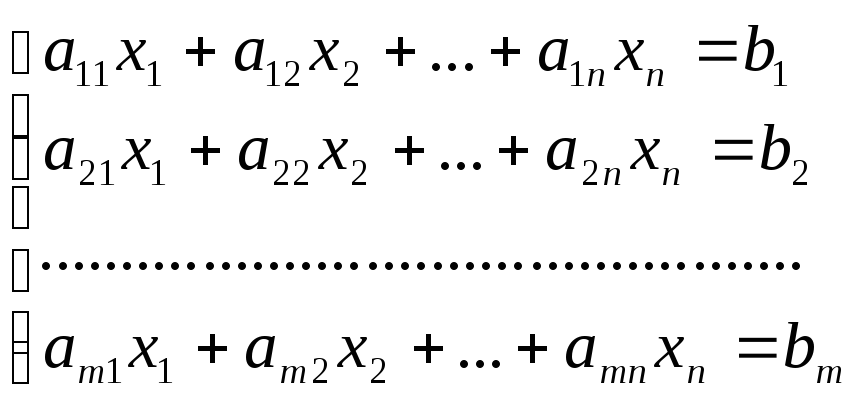
В матрице две одинаковые строки в – определение и свойства. Вычисление детерминантов. Правило Крамера. Метод Гаусса решения системы, страница 2

• by alexxlab
• Комментариев к записи В матрице две одинаковые строки в – определение и свойства. Вычисление детерминантов. Правило Крамера. Метод Гаусса решения системы, страница 2 нет
• Советы абитуриенту

определение и свойства. Вычисление детерминантов. Правило Крамера. Метод Гаусса решения системы, страница 2

Из свойства 1 следует равноправность строк и столбцов. Именно, если справедливо какое-либо утверждение о детерминантах, касающееся строк соответствующих матриц, то верно и аналогичное утверждение, касающееся столбцов, и обратно.

Свойство 2. Если элементы одной строки или столбца детерминанта равны нулю, то и детерминант равен нулю.

Доказательство: Доказательство вытекает из доказанной ранее теоремы. Раскроим детерминант по   -й строке

что и требовалось доказать.

Свойство 3. Для того чтобы умножить детерминант на число, достаточно умножить на это число строку (столбец).

Доказательство: Доказательство вытекает из доказанной ранее теоремы. Раскроим детерминант по   -й строке

Таким образом каждый элемент -й строки умножился на , что и требовалось доказать.

Свойство 4. Если одна из строк (столбцов) является суммой двух строк (столбцов), то её детерминант есть сумма детерминантов соответствующих матриц.

Доказательство: Доказательство вытекает из доказанной ранее теоремы. Раскроим детерминант по   -й строке

что и требовалось доказать.

Свойство 5. Если в матрице поменять местами какие-нибудь две строки (столбца), то ее детерминант изменит знак.

Доказательство: Доказательство мы проведем методом полной индукции. Непосредственно очевидно, что для матриц второго порядка она справедлива 

Здесь  матрица, у которой поменяли местами строки.

Допустим, что формула верна для матриц порядка , и докажем ее для матрицы порядка . Детерминант матрицы порядка мы разложим по любому столбцу, отличному от переставляемых столбцов. Переставляемые столбцы входят в каждый дополнительный минор, и если предложение справедливо для матриц порядка , при перестановке столбцов каждый минор меняет знак. Отсюда вытекает, что знак изменится и у детерминанта, что и заканчивает доказательство.

В качестве следствий из свойства 4 мы получим следующие свойство.

Свойство 6.  Если в матрице есть два две одинаковые строки (одинаковых столбца), то .

Доказательство: Действительно, при перестановке одинаковых столбцов мы не изменяем матрицу, а изменим знак у детерминанта. Отсюда  и, следовательно, , что и требовалось доказать.

Свойство 7. Справедливы следующие формулы

,      

Здесь  – символ Кронекера, который определён следующим образом

Доказательство: Если то мы получаем детерминант, раскрытый по -ой строке. Если же то получается детерминант, у которого две строки равные, а он по 5 свойству детерминантов равен нулю, что и требовалось доказать.

Свойство 8. Детерминант матрицы не изменится, если к какой-нибудь строке (какому – нибудь  ее столбцу) прибавить линейную комбинацию остальных строк (столбцов) этой матрицы.

Доказательство: К -й строке прибавим линейную комбинацию остальных строк, а затем раскроем определитель по -й строке.

  По свойству 7 .

Тогда получаем   свойство доказано.

3.  Вычисление детерминантов.

Используя свойства детерминантов, его можно привести к диагональному виду

Полученный детерминант вычисляется по формуле .

Метод сведение детерминанта к диагональному виду называется методом последовательных исключений, который впервые предложил Гаусс.

Опишем его. Пусть , это предположение не ограничивает общность рассуждений, в силу свойств детерминантов (если , то поменяем местами столбцы, поменяв знак на противоположный ). Умножим первую строку на  и сложим со второй строкой, тогда на первом месте во второй строке будет ноль. Умножим первую строку на  и сложим с третей строкой, тогда на первом месте в третей строке будет ноль и так далее. Мы получим детерминант

в котором . Аналогичным образом сделаем нули во втором столбце под элементом  и так далее. Если в процессе вычислений в одной из строк все элементы получатся равные нулю, то и детерминант будет равен нулю.

4. Системы линейных уравнений

Систему уравнений вида

    

мы будем называть системой  линейных уравнений с  неизвестными . Коэффициенты этих урав­нений мы будем записывать в виде матрицы

называемой матрицей системы. Числа, стоящие в пра­вых частях уравнений, образуют столбец , называемый столбцом свободных членов.

Определение. Совокупность  чисел  называется решением системы, если каждое уравне­ние системы обращается в тождество после подстановки в него чисел  вместо соответствующих неизвестных .

vunivere.ru

Определители

Определители

С понятием определителя мы уже сталкивались при изучении векторного произведения в разделе 10. Там были введены определители матриц второго и третьего порядка. В этом разделе мы дадим определение определителя квадратной матрицы любого порядка. Это определение будет рекуррентным, то есть чтобы установить, что такое определитель матрицы порядка , нужно уже знать, что такое определитель матрицы порядка. Такое рекуррентное определение и было использовано для введенияопределителя матрицы третьего порядка. Отметим также, что определитель существует только у квадратных матриц.

Определитель квадратной матрицы будем обозначатьили.

Определение 14.6Определителем квадратной матрицывторого порядка называется число. Определителем квадратной матрицыпорядка,, называется число

где — определитель матрицы порядка, полученной из матрицывычеркиванием первой строки и столбца с номером.

Легко проверить, что это определение для определителей второго и третьего порядка совпадает с данным ранее в разделе 10.

Для наглядности запишем, как можно вычислить определитель матрицы четвертого порядка:

        Замечание 14.7Реальное вычисление определителей для матриц выше третьего порядка на основе определения используется в исключительных случаях. Как правило, вычисление ведется по другим алгоритмам, которые будут рассмотрены позже и которые требуют меньше вычислительной работы.

        Замечание 14.8Вопределении 14.6было бы точнее сказать, что определитель есть функция, определенная на множестве квадратных матриц порядкаи принимающая значения в множестве чисел.

        Замечание 14.9В литературе вместо термина “определитель” используется также термин “детерминант”, имеющий тот же самый смысл. От слова “детерминант” и появилось обозначение.

Рассмотрим некоторые свойства определителей, которые сформулируем в виде предложений.

Предложение 14.6При транспонировании матрицы определитель не меняется, то есть .

Предложение 14.7Определитель произведения квадратных матриц равен произведению определителей сомножителей, то есть .

Предложение 14.8Если в матрице поменять местами две строки, то ее определитель сменит знак.

Ввиду ограниченности курса доказательства этих трех свойств мы опускаем. Читатель может найти их в учебниках по линейной алгебре [3],[5]или же может без особых сложностей проверить их на матрицах второго и третьего порядков.

Предложение 14.9Если матрица имеет две одинаковые строки, то ее определитель равен нулю.

        Доказательство.     Поменяем местами две одинаковые строки. В силу

предложения 14.8определитель сменит знак. С другой стороны, так как строки были одинаковыми, то матрица не изменилась и, следовательно, не изменился и ее определитель. Получим, что, откуда следует, что.

В дальнейшем нам потребуется складывать строки и умножать строку на число. Эти действия над строками (столбцами) мы будем выполнять так же, как действия над матрицами-строками (матрицами-столбцами), то есть поэлементно. Результатом будет служить строка (столбец), как правило, не совпадающая со строками исходной матрицы. При наличии операций сложения строк (столбцов) и умножения их на число мы можем говорить и о линейных комбинациях строк (столбцов), то есть суммах с числовыми коэффициентами.

Предложение 14.10Если строку матрицы умножить на число , то ее определитель умножится на это число.

        Доказательство.     Пусть– исходная матрица,– матрица, полученная изумножением первой строки на число:

Тогда

где — определитель матрицы, полученной из матрицыили, что то же самое, из матрицывычеркиванием первой строки и-ого столбца.

Вынесем множитель за знак суммы и получим

Пусть теперь матрица получается из матрицыумножением-ой строки на число. Поменяем местами первую и-ую строки в матрицеи то же самое проделаем в матрице. Получим две новых матрицыи. Попредложению 14.8

(14.10)

Очевидно, что матрица получается из матрицыумножением первой строки на число. Как только что было доказано,. Таким образом, из второго равенства (14.10) находим, отсюда с помощью первого равенства (14.10) получаем.

Предложение 14.11Если матрица содержит нулевую строку, то ее определитель равен нулю.

        Доказательство.     Нулевую строку можно рассматривать как строку из единиц, умноженную на число ноль. Попредложению 14.10определитель такой матрицы равен нулю, умноженному на определитель матрицы, содержащей строку из единиц. Результат такого умножения всегда будет ноль.

Предложение 14.12Если одна из строк матрицы равна другой, умноженной на число (строки пропорциональны), то определитель матрицы равен нулю.

        Доказательство.    Попредложению 14.10определитель исходной матрицы равен числу, умноженному на определитель матрицы, у которой есть две одинаковые строки. Попредложению 14.9определитель последней матрицы равен нулю. Поэтому и определитель исходной матрицы равен нулю.

Предложение 14.13Пусть в матрице -ая строка имеет вид. Тогда, где матрицаполучается из матрицызаменой-ой строки на строку, а матрица– заменой-ой строки на строку.

        Доказательство.     Пусть первая строка матрицыимеет вид. Тогда

Для случая утверждение доказано.

Пусть . Обозначим через,,матрицы,, и, в которых поменяли местами первую и-ую строки. По только что доказанному (для) утверждению. Попредложению 14.8,,. Следовательно,. Умножив обе части последнего равенства на, получим требуемое утверждение.

Предложение 14.14Если к одной из строк матрицы добавить другую, умноженную на число, то определитель матрицы не изменится.

        Доказательство.     Пусть к-ой строке матрицыприбавлена-ая строка, умноженная на число. Новую матрицу обозначим. В матрицеэлементы-ой строки имеют вид. Попредложению 14.13, где– матрица, полученная из матрицызаменой-ой строки на-ую строку, умноженную на число. Попредложению 14.12, то есть.

Предложение 14.15Если одна из строк матрицы является линейной комбинацией других ее строк, то определитель матрицы равен нулю.

        Доказательство.     Попредложению 14.13определитель исходной матрицы равен сумме определителей матриц, в каждой из которых есть пропорциональные строки. Попредложению 14.12все эти определители равны нулю. Следовательно, и определитель исходной матрицы тоже равен нулю.

Определение 14.7Алгебраическим дополнением к элементуматрицыназывается число, равное, где– определитель матрицы, полученной из матрицывычеркиванием-ой строки и-ого столбца.

Алгебраическое дополнение к элементу матрицыобозначается.

        Пример 14.4Пусть. Тогда

        

Замечание 14.10Используя алгебраические дополнения,определение 14.6определителя можно записать так:

        

Предложение 14.16Разложение определителя по произвольной строке. Для определителя матрицы справедлива формула

        Доказательство.     Если, положим. Пусть. Тогда-ую строку поменяем местами со строкой с номером. Определитель сменит знак. Затем строку с номеромпоменяем местами со строкой с номером. Определитель снова сменит знак. Процесс перестановки строк будем продолжать до тех пор, пока-ая строка матрицыне станет первой строкой новой матрицы, которую мы обозначим. Отметим, что в матрице, начиная со второй строки, стоят строки матрицы, причем порядок их следования не изменился.

При переходе от матрицы к матрицеопределитель сменит знакраз (проверьте для случая). Таким образом

(14.11)

Это соотношение верно и при . Поопределению 14.6определителя,

где — определитель матрицы, полученной из матрицывычеркиванием первой строки и-ого столбца. Первая строка матрицысовпадает с-ой строкой матрицы, поэтому. Результат вычеркивания в матрицепервой строки и-ого столбца будет таким же, как при вычеркивании в матрице-ой строки и-ого столбца. Поэтому, где– определитель матрицы, полученной при вычеркивании в матрице-ой строки и-ого столбца. Следовательно,

В силу равенства (14.11) получим

По определению 14.7алгебраического дополнения получим. Тогда из предыдущего равенства вытекает

что и требовалось доказать.     

        Пример 14.5Вычислите.

Решение.Воспользуемся разложением по третьей строке, так выгоднее, поскольку в третьей строке два числа из трех — нули. Получим

        

Предложение 14.17Для квадратной матрицы порядкапривыполнено соотношение

(14.12)

        Доказательство.     Пусть– матрица, полученная из матрицы, в которой-ая строка заменена-ой строкой этой же матрицы, а сама-ая строка осталась без изменения. Таким образом, в матрицеесть две одинаковые строки и в силупредложения 14.9.

С другой стороны, используя разложение определителя по -ой строке (предложение 14.16), получим

где — алгебраическое дополнение к элементу. Так как все строки матрицы, кроме-ой, совпадают со строками матрицы, то. Так как по построению матрицы, то

Так как , то равенство (14.12) доказано.

Предложение 14.18Все свойства определителя, сформулированные для строк ( предложения 14.8–14.17), справедливы и для столбцов, в частности, справедливо разложение определителя по -ому столбцу

(14.13)

и равенство

при .

        Доказательство.     В силупредложения 14.6определитель не меняется при транспонировании матрицы, а ее столбцы становятся строками транспонированной матрицы, для которой доказываемые свойства имеют место.

Предложение 14.19Определитель треугольной матрицы равен произведению элементов ее главной диагонали.

        Доказательство.     Воспользуемся индукцией по порядку матрицы. Для:

утверждение верно. Предположим, что доказываемое утверждение верно для матриц порядка . Покажем, что оно верно для матрицы порядка.

Если — верхняя треугольная матрица, то используем разложение по первому столбцу (равенство (14.13) при):

Справа стоит определитель треугольной марицы порядка . По предположению индукции этот определитель равен. Поэтому.

Если — нижняя треугольная матрицы, то нужно воспользоваться разложением по первой строке. В остальном рассуждения аналогичны.

Итак, утверждение верно для матрицы порядка . Предложение доказано.

Следствие 14.1Определитель единичной матрицы равен единице, .

Перечисленные выше свойства позволяют находить определители матриц достаточно высоких порядков при сравнительно небольшом объеме вычислений. Алгоритм вычислений следующий.

Алгоритм создания нулей в столбце.

Пусть требуется вычислить определитель матрицы порядка. Если, то поменяем местами первую строку и любую другую, в которой первый элемент не нуль. В результате определитель, будет равен определителю новой матрицы с противоположным знаком. Если же первый элемент каждой строки равен нулю, то матрицаимеет нулевой столбец и попредложениям 14.11,14.18ее определитель равен нулю.

Итак, считаем, что уже в исходной матрице . Первую строку оставляем без изменений. Прибавим ко второй строке первую строку, умноженную на число. Тогда первый элемент второй строки будет равен

Остальные элементы новой второй строки обозначим ,. Определитель новой матрицы попредложению 14.14равен.

Первую строку умножим на число и прибавим к третьей. Первый элемент новой третьей строки будет равен

Остальные элементы новой третьей строки обозначим ,. Определитель новой матрицы попредложению 14.14равен.

studfiles.net

3. Теорема о равноправности строк и столбцов матрицы определителя.

Теорема: Определитель порожденный матрицей не изменится если в ней поменять местами строки со столбцами.

Доказательство: А) Определим вначале знак члена определителя при произвольном порядке сомножителей.

a_{α1, β1}, a_{α2, β2}… a_{αk, βk}… a_{αl, βl}… a_{αn, βn}(*)

α₁, α₂… α_k… α_l…α_n(1) – перестановка номеров строк.

β₁, β₂… β_k… β_l…β_n(1’) – перестановка индексов столбцов.

Обозначим число инверсий в перестановке (1) – S_1, в перестановке (1’) – S₁’. Рассмотрим сумму S₁+ S₁’, и покажем, что четность или нечетность этой суммы не меняется ни при каком изменении порядка множителей. Ясно что от одного порядка множителей к другому можно перейти с помощью конечного числа транспозиций множества. Поэтому достаточно доказать, что характер четности числа S₁+ S₁’ не изменится при одной транспозиции множества в произведении(*).

a_{α1, β1}, a_{α2, β2}… a_{αl, βl}… a_{αk, βk}… a_{αn, βn}(**)

α₁, α₂… α_l… α_k…α_n(2)

β₁, β₂… β_l… β_k…β_n(2’)

Число инверсий в перестановке (2) – S₂, в перестановке(2’) – S₂’. Рассмотрим число S₂+S₂’. S₁ и S₂ имеют разный характер четности. S₁’ и S₂’ имеют разный характер четности следовательно суммы S₁+ S₁’ и S₂+S₂’ имеют одинаковый характер четности. Напишем множители рассматриваемого члена определителя (*) в порядке следования строк: a_{1, j1}, a_{2, j2}…a_{n, jn}(3).

Обозначим число инверсий столбцов через S, число инверсий в перестановке строк =0. Таким образом по доказанному числа 0+S и S₁+S₁’ имеют одинаковый характер четности. Следовательно, знак члена определителя (*):

(-1)^S=(-1)^S1+S1’

В)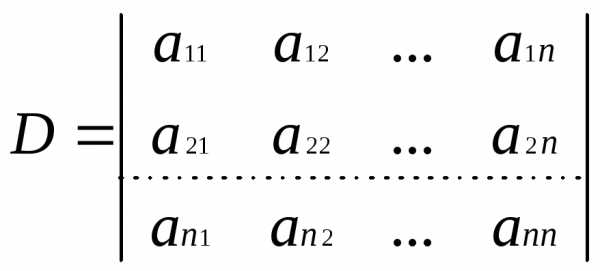

Рассмотрим произвольный член определителя D: a_{α1, β1}, a_{α2, β2}… a_{αn, βn}– он будет и членом определителя D₁, т.к. в нем в качестве множителя взят один и только один элемент из каждой строки и столбца матрицы определителя D₁(в D первые индексы – номера строк, вторые – номера столбцов, а в определителе D₁ – наоборот).

Покажем что знаки этого члена, как в D, так и в D₁ будут одинаковы. Это следует из того что знаки этого члена и в Dи в D₁ определяются суммой числа инверсий в перестановках первых и вторых индексов. D=D₁ .(ч.т.д.)

4. Теорема о перестановке 2х строк матрицы оределителя. Определитель с двумя одинаковыми строками.

Теорема: Если в матрице определителя поменять местами 2 строки, то определитель изменит знак на противоположный.

Доказательство:

a_{1, γ1}*a_{2, γ2}*…*a_{k, γk}*…*a_{l, γl}*…*a_{n, γn} – член определителя D, он будет и членом определителя D₁, но знак его здесь будет противоположный.

Знак этого члена определителя в D: γ₁,γ₂…γ_k…γ_l…γ_n(1)

А в D₁: a_{1, γ1}*a_{2, γ2}*…* a_{l, γl} *…* a_{k, γk} *…*a_{n, γn}

γ₁,γ₂…γ_l…γ_k…γ_n(2)

Перестановки (1) и (2) отличаются одной транспозицией, значит характер четности этих перестановок разный. Следовательно рассматриваемый член в D и в D₁ имеет разные знаки. Следовательно D= – D₁.(ч.т.д.)

Следствие: Определитель с двумя одинаковыми строками равен 0.

Доказательство: Допустим в матрице определителя D две одинаковые строки. Поменяем местами эти две одинаковые строки. Определитель соответствующий новой матрице обозначим D₁. Согласно доказанной теореме D= – D₁. Но т.к. мы поменяли две одинаковые строки и матрица не изменилась, следовательно, D=D₁. Получаем 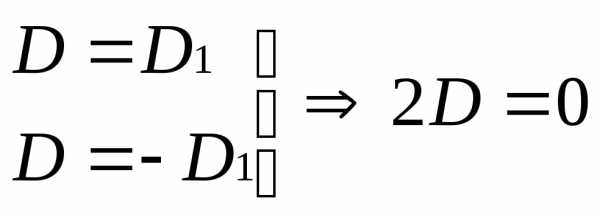иD=0.(ч.т.д.)

studfiles.net

. Свойства определителей

СВОЙСТВО 1. Величина определителя не изменится, если все его строки заменить столбцами, причем каждую строку заменить столбцом с тем же номером, то есть

.

СВОЙСТВО 2. Перестановка двух столбцов или двух строк определителя равносильна умножению его на -1. Например,

.

СВОЙСТВО 3. Если определитель имеет два одинаковых столбца или две одинаковые строки, то он равен нулю.

СВОЙСТВО 4. Умножение всех элементов одного столбца или одной строки определителя на любое число kравносильно умножению определителя на это число k. Например,

.

СВОЙСТВО 5. Если все элементы некоторого столбца или некоторой строки равны нулю, то сам определитель равен нулю. Это свойство есть частный случае предыдущего (при k=0).

СВОЙСТВО 6. Если соответствующие элементы двух столбцов или двух строк определителя пропорциональны, то определитель равен нулю.

СВОЙСТВО 7. Если каждый элемент n-го столбца или n-й строки определителя представляет собой сумму двух слагаемых, то определитель может быть представлен в виде суммы двух определителей, из которых один в n-м столбце или соответственно в n-й строке имеет первые из упомянутых слагаемых, а другой – вторые; элементы, стоящие на остальных местах, у вех трех определителей одни и те же. Например,

СВОЙСТВО 8. Если к элементам некоторого столбца (или некоторой строки) прибавить соответствующие элементы другого столбца (или другой строки), умноженные на любой общий множитель, то величина определителя при этом не изменится. Например,

.

Дальнейшие свойства определителей связаны с понятием алгебраического дополнения и минора. Минором некоторого элемента называется определитель, получаемый из данного путем вычеркиванием строки и столбца, на пересечении которых расположен этот элемент.

Алгебраическое дополнение любого элемента определителя равняется минору этого элемента, взятому со своим знаком, если сумма номеров строки и столбца, на пересечении которых расположен элемент, есть число четное, и с обратным знаком, если это число нечетное.

Алгебраическое дополнение элемента мы будем обозначать большой буквой того же наименования и тем же номером, что и буква, кторой обозначен сам элемент.

СВОЙСТВО 9. Определитель

равен сумме произведений элементов какого-либо столбца (или строки) на их алгебраические дополнения.

Иначе говоря, имеют место следующие равенства:

, ,

, ,

, .

6) Миноры и алгебраические дополнения.

Определение. Минором элемента определителя – го порядка называют определитель – го порядка, который получается из данного определителя вычеркиванием – й строки и – го столбца, на пересечении которых стоит элемент .

Обозначение: .

Определение. Алгебраическим дополнением элемента определителя – го порядка называют его минор, взятый со знаком плюс, если – четное число и со знаком минус в противном случае.

Обозначение: .

Теорема. (О разложении определителя.)

Определитель равен сумме произведений элементов любой строки (или любого столбца) определителя на их алгебраические дополнения:

, ;       (1)

или

, .       (2)

7) Обра́тная ма́трица — такая матрица A⁻¹, при умножении на которую, исходная матрица A даёт в результате единичную матрицу E:

Квадратная матрица обратима тогда и только тогда, когда она невырожденная, то есть её определитель не равен нулю. Для неквадратных матриц и вырожденных матриц обратных матриц не существует. Однако возможно обобщить это понятие и ввести псевдообратные матрицы, похожие на обратные по многим свойствам.

8) Ранг матрицы — наивысший из порядков миноров этой матрицы, отличных от нуля

Обычно ранг матрицы  обозначается  () или . Оба обозначения пришли к нам из иностранных языков, потому и употребляться могут оба. 

Свойства

Теорема (о базисном миноре): Пусть r = rang A M — базисный минор матрицы A, тогда:

• базисные строки и базисные столбцы линейно независимы;

• любая строка (столбец) матрицы A есть линейная комбинация базисных строк (столбцов).

Следствия:

• Если ранг матрицы равен r, то любые p:p > r строк или столбцов этой матрицы будут линейно зависимы.

• Если A — квадратная матрица, и det A = 0 <=> строки и столбцы этой матрицы линейно зависимы.

• Пусть r = rang A, тогда максимальное количество линейно независимых строк (столбцов) этой матрицы равно r.

• Теорема (об инвариантности ранга при элементарных преобразованиях): Введём обозначение элементарными преобразованиями. Тогда справедливо утверждение: Если , то их ранги равны для матриц, полученных друг из друга

studfiles.net

Math.by – Вычисление определителя матрицы

Теория

Рассмотрим произвольную квадратную матрицу n-го порядка:

С каждой такой матрицей свяжем определенную численную характеристику, называемую определителем , соответствующим данной матрице. В дальнейшем мы будем говорить об элементах, строках и столбцах определителя, подразумевая под этими терминами соответственно элементы, строки и столбцы отвечающей этому определителю матрицы.

Определение: Определителем |А| матрицы первого порядка A=(а₁₁), или определителем первого порядка, называется число равное матричному элементу а₁₁:

Определение: Определителем |А| матрицы второго порядка A=(а_ij), или определителем второго порядка, называется число определяемое формулой:

Определение: Определителем |А| матрицы третьего порядка A=(а_ij), или определителем третьего порядка, называется число, определяемое формулой:

Определение: Определителем |А| квадратной матрицы n-го порядка A=(а_ij), или определителем n-го порядка, называется число, равное алгебраической сумме n! членов, каждый из которых является произведением n элементов матрицы, взятых по одному из каждой строки и каждого столбца, причем знак каждого члена определяется как (—1)^N, где N — число инверсий в перестановке из номеров столбцов элементов матрицы в произведении, если при этом номера строк образуют возрастающую последовательность n чисел:

Основные свойства определителей:

• при перестановке местами двух параллельных строк или столбцов определителя его знак меняется на обратный;
• определитель, содержащий две одинаковых строки или столбца, равен нулю;
• если одну из строк определителя умножить на какое-либо число, то получится определитель, равный исходному определителю, умноженному на это число;
• при транспонировании матрицы её определитель не меняет своего значения;
• если в определителе вместо любой строки записать сумму этой строки и любой другой строки, умноженной на некоторое число, то полученный новый определитель будет равен исходному;
• если каждый элемент какой-либо строки или столбца определителя представляем в виде суммы двух слагаемых, то этот определитель может быть разложен на сумму двух соответствующих определителей;
• общий множитель элементов какой-либо строки или столбца определителя можно выносить за знак определителя.

www.math.by

Определители квадратных матриц.

Определитель матрицы – это число, характеризующее квадратную матрицу А и тесно связанное с решением систем линейных уравнений. Определитель матрицы А обозначается или . Любой квадратной матрице А порядка n ставится в соответствие по определенному закону вычисленное некоторое число, называемое определителем, или детерминантом, n-го порядка этой матрицы. Рассмотрим определители второго и третьего порядков.

Пусть дана матрица

,

тогда ее определитель второго порядка вычисляется по формуле

.

Пример. Вычислить определитель матрицы А:

Ответ: -10.

Определитель третьего порядка вычисляется по формуле

.

Пример. Вычислить определитель матрицы В

 

.

Ответ: 83.

Вычисление определителя n-го порядка производится на основании свойств определителя и следующей теоремы Лапласа: определитель равен сумме произведений элементов любой строки (столбца) матрицы на их алгебраические дополнения:

.

Алгебраическое дополнение элемента равно , где – минор элемента , получаемый путем вычеркивания в определителе i-ой строки и j-го столбца.

Минором порядка элемента матрицы А называется определитель матрицы (n-1)-го порядка, полученный из матрицы А вычеркиванием i-ой строки и j-го столбца.

Пример. Найти алгебраические дополнения всех элементов матрицы А:

.

Ответ: .

Пример. Вычислить определитель матрицы треугольной матрицы:

.

Ответ: -15.

Свойства определителей:

1. Если какая-либо строка (столбец) матрицы состоит из одних нулей, то ее определитель равен 0.

2. Если все элементы какой-либо строки (столбца) матрицы умножить на число , то ее определитель умножится на это число.

3. При транспонировании матрицы ее определитель не изменится.

4. При перестановке двух строк (столбцов) матрицы ее определитель меняет знак на противоположный.

5. Если квадратная матрица содержит две одинаковые строки (столбца), то ее определитель равен 0.

6. Если элементы двух строк (столбцов) матрицы пропорциональны, то ее определитель равен 0.

7. Сумма произведения элементов какой-либо строки (столбца) матрицы на алгебраические дополнения элементов другой строки (столбца) этой матрицы равна 0.

8. Определитель матрицы не изменится, если к элементам какой-либо строки (столбца) матрицы прибавить элементы другой строки (столбца), предварительно умноженные на одно и то же число.

9. Сумма произведений произвольных чисел на алгебраические дополнения элементов любой строки (столбца) равна определителю матрицы, полученной из данной заменой элементов этой строки (столбца) на числа .

10. Определитель произведения двух квадратных матриц равен произведению их определителей.

 

Обратная матрица.

Определение. Матрица называется обратной по отношению к квадратной матрице А, если при умножении этой матрицы на данную как справа, так и слева получается единичная матрица:

.

Из определения следует, что только квадратная матрица имеет обратную; в этом случае и обратная матрица является квадратной того же порядка. Если определитель матрицы отличен от нуля, то такая квадратная матрица называется невырожденной.

Необходимое и достаточное условие существования обратной матрицы: Обратная матрица существует (и единственна) тогда и только тогда, когда исходная матрица невырожденная.

Первый алгоритм вычисления обратной матрицы:

1. Находим определитель исходной матрицы. Если определитель не равен нулю, то исходная матрица невырожденная и обратная матрица существует.

2. Находим матрицу , транспонированную к А.

3. Находим алгебраические дополнения элементов транспонированной матрицы и составляем из них присоединенную матрицу .

4. Вычисляем обратную матрицу по формуле: .

5. Проверяем правильность вычисления обратной матрицы, исходя из ее определения .

 

Пример. Найти матрицу, обратную к данной:

.

Ответ: .

Второй алгоритм вычисления обратной матрицы:

Обратную матрицу можно вычислить на основании следующих элементарных преобразований над строками матрицы:

– перемена местами двух строк;

– умножение строки матрицы на любое число, отличное от нуля;

– прибавление к одной строке матрицы другой строки, умноженной на любое число, отличное от нуля.

Для того чтобы вычислить обратную матрицу для матрицы А, необходимо составить матрицу , затем путем элементарных преобразований привести матрицу А к виду единичной матрицы Е, тогда на месте единичной матрицы получим матрицу .

Пример. Вычислить обратную матрицу для матрицы А:

.

Составляем матрицу В вида:

.

Элемент = 1 и первую строку, содержащую данный элемент, назовем направляющими. Осуществим элементарные преобразования, в результате которых первый столбец преобразуется в единичный столбец с единицей в первой строке. Для этого ко второй и третьей строкам прибавим первую строку, соответственно умноженную на 1 и -2. В результате этих преобразований получим:

.

Окончательно получим

.

Откуда .

Ранг матрицы.Рангом матрицы А называется наивысший порядок отличных от нуля миноров этой матрицы. Ранг матрицы А обозначается rang(A) или r(A).

Из определения следует: а) ранг матрицы не превосходит меньшего из ее размеров, т.е. r(А) меньше или равен минимальному из чисел m или n; б) r(A)=0 тогда и только тогда, когда все элементы матрицы А равны нулю; в) для квадратной матрицы n-го порядка r(A)=n тогда и только тогда, когда матрица А – невырожденная.

Пример: вычислить ранги матриц:

.

Ответ: r(A)=1. Ответ: r(A)=2.

Назовем элементарными преобразованиями матрицы следующие:

1) Отбрасывание нулевой строки (столбца).

2) Умножение всех элементов строки (столбца) матрицы на число, не равное нулю.

3) Изменение порядка строк (столбцов) матрицы.

4) Прибавление к каждому элементу одной строки (столбца) соответствующих элементов другой строки (столбца), умноженных на любое число.

5) Транспонирование матрицы.

Ранг матрицы не изменяется при элементарных преобразованиях матрицы.

Примеры: Вычислить матрицу , где

; ;

Ответ: .

Пример: Вычислить матрицу , где

; ; ; E – единичная матрица.

Ответ: .

Пример : Вычислить определитель матрицы

.

Ответ: 160.

Пример: Определить, имеет ли матрица А обратную, и если имеет, то вычислить ее:

.

Ответ: .

Пример : Найти ранг матрицы

.

Ответ: 2.

 

2.4.2. Системы линейных уравнений.

 

Система m линейных уравнений с n переменными имеет вид:

,

где , – произвольные числа, называемые соответственно коэффициентами при переменных и свободными членами уравнений. Решением системы уравнений называется такая совокупность n чисел ( ), при подстановке которых каждое уравнение системы обращается в верное равенство.

Система уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет решений. Совместная система уравнений называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения.

Теорема Крамера: Пусть – определитель матрицы А, составленной из коэффициентов при переменных “х”, а – определитель матрицы, получаемой из матрицы А заменой j-го столбца этой матрицы столбцом свободных членов. Тогда, если , то система имеет единственное решение, определяемое по формулам: (j=1, 2, …, n). Эти уравнения получили названия формул Крамера.

Пример. Решить системы уравнений по формулам Крамера:

Ответы: (4, 2, 1). (1, 2, 3) (1, -2, 0)

Метод Гаусса – метод последовательного исключения переменных, заключается в том, что с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которой последовательно, начиная с последних по номеру переменных, находятся все остальные переменные.

Пример: Решить системы уравнений методом Гаусса.

Ответы: (1, 1, 1). (1, -1, 2, 0). (1, 1, 1).

Для совместных систем линейных уравнений верны следующие утверждения:

· если ранг матрицы совместной системы равен числу переменных, т.е. r = n, то система уравнений имеет единственное решение;

· если ранг матрицы совместной системы меньше числа переменных, т.е. r<n, то система неопределенная и имеет бесконечное множество решений.

 

2.4.3. Технология выполнения операций над матрицами в среде EXCEL.

 

Рассмотрим некоторые аспекты работы с табличным процессором Excel, которые позволяют упростить расчеты, необходимые для решения оптимизационных задач. Табличный процессор – это программный продукт, предназначенный для автоматизации обработки данных табличной формы.

Работа с формулами.В программах электронных таблиц формулы служат для выполнения множества разнообразных расчетов. С помощью Excel можно быстро создать формулу. Формула состоит из трех основных частей:

– знак равенства;

– совокупность значений или ссылки на ячейки, с которыми выполняются расчеты;

– операторы.

Использование в формулах функций. Чтобы облегчить ввод формул, можно воспользоваться функциями Excel. Функции – это встроенные в Excel формулы. Для активизации той или иной формулы следует нажать кнопки Вставка, Функции. В появившемся окне Мастер функций слева содержится перечень типов функций. После выбора типа справа будет помещен список самих функций. Выбор функций осуществляется щелчком клавиши мыши на соответствующем названии.

При выполнении операций над матрицами, решении систем линейных уравнений, решении оптимизационных задач можно применять следующие функции Excel:

– МУМНОЖ – умножение матриц;

– ТРАНСП – транспонирование матрицы;

– МОПРЕД – вычисление определителя матрицы;

– МОБР – вычисление обратной матрицы.

Кнопка находится на панели инструментов. Функции для выполнения операций с матрицами находятся в категории Математические.

Умножение матриц с помощью функции МУМНОЖ. Функция МУМНОЖ возвращает произведение матриц (матрицы хранятся в массивах 1 и 2). Результатом является массив с таким же числом строк, как массив 1, и с таким же числом столбцов, как массив 2.

Пример. Найти произведение двух матриц А и В в среде Excel (см. рис 2.9):

; .

– Введите матрицы А в ячейки А2:C3 и В в ячейки E2:F4.

– Выделите диапазон ячеек для результата умножения – h3:I2.

– Введите формулу умножения матриц =МУМНОЖ(A2:C3, E2:F4).

– Нажмите клавиши CTRL+SHIFT+ENTER.

Вычисления обратной матрицы с помощью функции МОБР.

Функция МОБР возвращает обратную матрицу для матрицы, хранящейся в массиве. Синтаксис: МОБР(массив). На рис. 2.10 приведено решение примера в среде Excel.

Пример. Найти матрицу, обратную к данной:

.

 

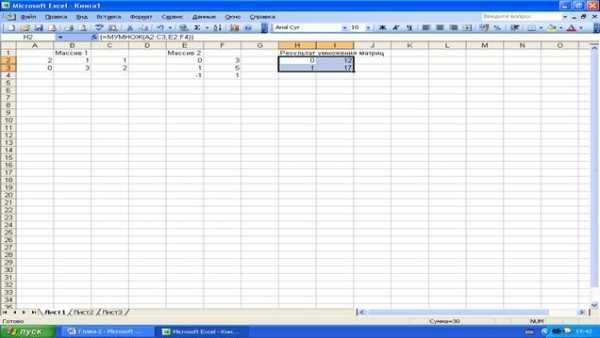
Рисунок 2.9. Исходные данные для умножения матриц.

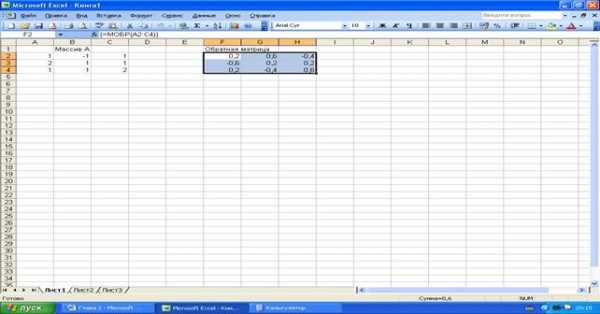
Рисунок 2.10. Исходные данные для вычисления обратной матрицы.

 

 

Похожие статьи:

poznayka.org

I. Матрицы и определители. § Матрицы. Матрицей

Глава I. Матрицы и определители.

§ 1. Матрицы.

Матрицей называется прямоугольная таблица, состоящая из чисел, записанных в строк и столбцов. Матрицы обозначаются большими латинскими буквами. Элементы матрицы нумеруются следующим образом:

.

Обрати внимание: число находится в -й строке и -м столбце!

Множество матриц размерности обозначается . Если число строк равно количеству столбцов (), то матрица называется квадратной. В общем случае она прямоугольная.

Если две матрицы имеют одну и ту же размерность:

,

то их можно складывать и вычитать. Пусть , , тогда

, .

Любую матрицу можно умножить на число по правилу:

.

Если , то матрица называется матрицей-строкой:

.

Если , получим матрицу-столбец:

.

§ 2. Умножение матриц.

Оно производится необычно и довольно непросто. Поэтому рассмотрим сначала самый простой случай, когда матрица-строка умножается на матрицу-столбец.

• 
  Строка на столбец.
  

Умножение можно производить только тогда, когда количество элементов в строке равно количеству элементов в столбце:

, .

В этом случае

.

• 
  Произвольные матрицы.
  

Матрицу можно умножить на матрицу только в случае, если количество столбцов первой матрицы равно количеству строк второй матрицы. В результате умножения получается матрица , каждый элемент которой есть результат умножения -й строки матрицы на -й столбец матрицы :

.

Матрицы оказываются очень полезными при решении систем уравнений. Рассмотрим, например, систему

Если обозначить матрицы

, , ,

то с помощью умножения матриц эту систему можно записать так:

.

§ 3. Метод Гаусса.

Система

называется системой линейных неоднородных уравнений с неизвестными (СЛУ). Матрица из коэффициентов при неизвестных

называется основной матрицей. Матрица

–

столбец неизвестных. Матрица

–

столбец свободных членов.

Метод Гаусса решения СЛУ.

1. 
   К основной матрице справа надо приписать столбец свободных членов . Получится расширенная матрица:
   

.

2. 
   Привести расширенную матрицу к ступенчатому виду, т.е. к такому виду, чтобы каждая нижняя строка имела слева больше нулей, чем верхняя:
   

.

Для приведения расширенной матрицы к ступенчатому виду можно:

• 
  Переставлять строки. Это равносильно перестановке уравнений в системе, поэтому ни на что не влияет.
  
• 
  Умножать любую строку на любое число и прибавлять к другой строке. Это равносильно умножению уравнения системы на число (это делать можно) и сложению двух уравнений системы (что тоже делать можно).
  
• 
  Отбрасывать нулевые строки. Такие строки равносильны уравнениям 0 = 0, которые можно из системы выбросить.
  

Рангом матрицы называется число её ненулевых строк после приведения её к ступенчатому виду. Обозначается:

.

Замечание.

По ходу приведения расширенной матрицы к ступенчатому виду может получиться строка, где все элементы равны нулю за исключением последнего. Это означает, что ранг основной матрицы меньше ранга расширенной матрицы. В этом случае система несовместна (решений нет). Такая строка равносильна уравнению , где . Если одно уравнение не имеет решений, то и система решений не имеет. Справедлива

теорема Кронекера-Капелли.

Система линейных уравнений совместна тогда и только тогда, когда ранг основной матрицы равен рангу расширенной:

.

Здесь – это не произведение матриц и , а расширенная матрица, получающаяся приписыванием справа к основной матрице столбца свободных членов .

3. 
   Поделить каждую строку на её первый элемент (каждая строка будет начинаться с 1).
   
4. 
   Преобразованиями, аналогичными п.2, привести матрицу к виду
   

.

5. 
   Записать ответ.
   

§ 4. Перестановки.

Первые 5 натуральных чисел, записанные в произвольном порядке – это перестановки 5-го порядка:

, , .

В общем случае перестановки -го порядка выглядят так:

, .

Вообще, перестановкой конечного множества различных чисел называется биективное отображение этого множества на себя.

Инверсией (нарушением порядка) называется ситуация, когда , но , т.е. когда число, которое больше, находится левее.

Перестановка называется чётной, если число инверсий чётное. Перестановка называется нечётной, если число инверсий нечётное.

Теорема.

Если в перестановке поменять местами 2 числа, у неё изменится чётность.

Доказательство.

1 случай.

Если числа соседние:

,

то, очевидно, если поменять их местами, количество инверсий либо увеличится на 1, либо уменьшится на 1, поэтому чётность перестановки поменяется, ч.т.д.

2 случай.

Если числа несоседние:

,

мы поступим так:

• 
  Меняя местами с соседними справа числами, передвинем это число вправо вплотную к :
  

.

При этом, согласно 1-му случаю, чётность перестановки должна смениться раз.

• 
  Поменяем местами и :
  

.

После этого чётность перестановки сменится ещё один раз.

Меняя местами с соседними слева числами, вернём на то место, где стояло число . При этом, согласно 1-му случаю, чётность перестановки снова должна смениться раз.

Подведём итог: чётность перестановки менялась суммарно

раз,

а это нечётное число. Следовательно, чётность перестановки изменилась, ч.т.д.

§ 5. Определители.

Пусть , т.е. – квадратная матрица. Элементы , , …, образуют главную диагональ квадратной матрицы. Молнией мы назовём произведение элементов, взятых по одному из каждой строки и из каждого столбца. Например, в матрице

молнией будет

.

Зарядом молнии мы назовём число , где – число инверсий в перестановке . Например, у молнии число равно количеству инверсий в перестановке , т.е. . Следовательно, заряд этой молнии равен .

Определителем матрицы называется сумма всех её молний, взятых со своими зарядами:

.

Упражнение 1.

Получить формулы для вычисления определителей второго и третьего порядков:

,

Упражнение 2.

Чтобы в тройном интеграле перейти к сферическим координатам, надо вычислить якобиан. Теперь это уже определитель третьего порядка:

Проверить последнее равенство.

§ 6. Свойства определителей.

1. 
   Если в матрице есть нулевая строка (столбец), то её определитель равен нулю:
   

.

Подумай, почему?

2. 
   Если в матрице поменять местами два столбца, то её определитель сменит знак:
   

.

Доказательство.

Рассмотрим произвольную молнию исходной матрицы:

.

Её заряд равен , где – число инверсий в перестановке

.

Если поменять местами столбцы, молния останется такой же:

,

а её заряд будет зависеть от числа инверсий в перестановке

.

Согласно теореме § 4, у этой перестановки другая чётность по сравнению с перестановкой . Поэтому заряд у молнии станет противоположным. Тем самым мы доказали, что при перестановке столбцов каждая молния сменит свой знак, следовательно, и определитель также сменит свой знак.

Замечание.

При вычислении определителей строки и столбцы равноправны, поэтому все утверждения, справедливые относительно столбцов, справедливы и относительно строк. Т.е. если в матрице поменять местами две строки, то её определитель также сменит знак.

3. 
   Если в матрице есть две одинаковые строки (столбца), то её определитель равен нулю:
   

.

Если поменять местами одинаковые строки, то, очевидно, определитель не изменится. Но, по предыдущему свойству, он должен поменять знак на противоположный. Таким образом, получаем:

,

откуда и следует, что .

4. 
   Из любой строки (столбца) общий множитель можно выносить за знак определителя:
   

.

Подумай, почему?

5. 
   Если элементы какой-то строки представлены в виде суммы, то:
   

.

Подумай, почему?

6. 
   Если к -й строке прибавить -ю, умноженную на любое число , (не равное нулю), то определитель от этого не изменится.
   

Доказательство.

для -й строки применим свойство 5:

во втором слагаемом из -й строки вынесем множитель (свойство 4):

.

второй определитель равен нулю (свойство 3), ч.т.д.

Квадратная матрица называется треугольной, если все элементы, стоящие ниже главной диагонали равны нулю:

.

7. 
   Определитель треугольной матрицы равен произведению элементов её главной диагонали:
   

.

Подумай, почему?

Рассмотренные свойства определителей дают нам второй способ вычисления определителя матрицы (не через сумму молний):

• 
  Преобразованиями, описанными в методе Гаусса, привести матрицу к ступенчатому виду. Получится треугольная матрица.
  
• 
  Воспользоваться свойством 7.
  

§ 7. Миноры. Алгебраические дополнения.

Мы уже знаем, что определитель 3-го порядка можно представить в виде суммы определителей 2-го порядка:

.

Аналогично можно вычислить определитель 4-го и вообще любого порядка:

.

Пусть . Минором элемента называется определитель -го порядка, составленный из элементов, находящихся не в -й строке и не в -м столбце. Минор элемента обозначается . Таким образом, предыдущие два разложения являются результатом применения формулы

.

Алгебраическим дополнением элемента называется его минор, взятый со своим знаком:

.

Так что предыдущая формула для вычисления определителя ещё более упрощается:

.

Эта формула позволяет вычислить определитель, разложив его по 1-й строке. На практике её удобнее применять к той строке, где больше нулей. (Подумай, почему?) Для произвольной -й строки она имеет вид:

.

Так как в квадратной матрице строки и столбцы равноправны, аналогичная формула имеет место и для разложения определителя по -му столбцу:

.

Её полезно применять, когда какой-то столбец имеет много нулей. Последние две формулы дают третий способ вычисления определителей (не через молнии и не через приведение к треугольному виду).

Теорема.

Сумма произведений элементов -й строки на алгебраические дополнения другой, -й строки, равна нулю:

.

Доказательство.

Рассмотрим определитель, -я строка которого состоит из элементов -й строки. По свойству 3 определителей, он равен нулю:

Расписав его по элементам -й строки, мы получим:

, ч.т.д.

§ 8. Обратная матрица.

Квадратная матрица называется единичной, если на её главной диагонали – единицы, а все остальные элементы равны нулю:

.

Она так называется потому, что от умножения на неё любой квадратной матрицы той же размерности последняя не меняется:

.

Пусть – квадратная матрица. Матрица называется обратной для , если

.

Матрица называется союзной для , если она специальным образом составлена из алгебраических дополнений к элементам матрицы :

.

Теорема.

.

Доказательство.

.

То, что элементы главной диагонали равны , следует из третьего способа вычисления определителей. А то, что все остальные элементы равны нулю, следует из теоремы предыдущего параграфа: сумма произведений элементов -й строки на алгебраические дополнения другой, -й строки, равна нулю. Теорема доказана.

Следствие (способ нахождения обратной матрицы).

Если умножить равенство

слева на , получим:

,

,

.

Эта формула даёт нам алгоритм нахождения обратной матрицы:

1. 
   Найти определитель. Если он равен нулю, то обратной матрицы не существует. Если определитель матрицы равен нулю, она называется вырожденной.
   
2. 
   Вычислить алгебраические дополнения для каждого элемента матрицы .
   
3. 
   Составить из них союзную матрицу (там особая нумерация строк и столбцов).
   
4. 
   Каждый элемент союзной матрицы разделить на .
   

Вычисление обратной матрицы – процесс небыстрый, но очень полезный. Как мы помним, первый способ решения СЛУ

– это метод Гаусса. Однако если основная матрица – квадратная, и если мы нашли для неё обратную матрицу , то мы фактически и решили СЛУ:

.

Эта формула даёт второй способ решения СЛУ, если число уравнений равно числу неизвестных.

Ну, а третий (самый удобный) способ решения СЛУ – это

§ 9. Правило Крамера.

Распишем подробно равенство :

.

Чтобы найти, например, , надо 1-ю строку обратной матрицы умножить столбец :

.

Пользуясь третьим способом вычисления определителей, можно считать, что в числителе стоит определитель, расписанный по первому столбцу:

,

только вместо первого столбца основной матрицы находится столбец свободных членов .

Если обозначить числитель за , получим простенькую формулу:

.

Рассуждая аналогичным образом, можно получить общую формулу для нахождения любого неизвестного :

,

где – определитель, составленный из элементов основной матрицы , в которой -й столбец заменён столбцом свободных членов:

.

Такой способ нахождения неизвестных называется правилом Крамера.

Замечание.

Из правила Крамера, в частности, следует, что если , то система имеет единственное решение.

Обрати внимание: единственным универсальным способом решения СЛУ является метод Гаусса. Остальные два способа (с помощью обратной матрицы и по правилу Крамера) применимы только в случае, когда основная матрица – квадратная, и когда её определитель не равен нулю.

§ 10. Системы линейных однородных уравнений.

Если в СЛУ столбец свободных членов нулевой, получается система линейных однородных уравнений (СЛОУ):

Она всегда совместна, ибо, очевидно, имеет нулевое решение:

.

Если , решать её надо методом Гаусса. Если же :

то всё зависит от определителя основной матрицы. Если , то, по замечанию предыдущего параграфа, система имеет единственное решение. Но одно решение у СЛОУ есть всегда (нулевое), поэтому оно и будет составлять ответ. Тем самым мы доказали, что если основная матрица квадратная, то

СЛОУ имеет ненулевые решения тогда и только тогда, когда .

lib2.podelise.ru

---