Вычисление производных примеры – Производная сложной функции. Примеры нахождения производных сложных функций.
- Комментариев к записи Вычисление производных примеры – Производная сложной функции. Примеры нахождения производных сложных функций. нет
- Советы абитуриенту
Вычисление производных.
На этом занятии мы будем учиться применять формулы и правила дифференцирования.
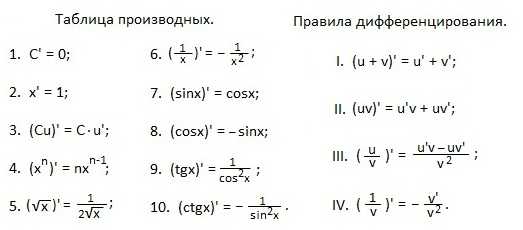
Примеры. Найти производные функций.
1. y=x7+x5-x4+x3-x2+x-9. Применяем правило I, формулы 4, 2 и 1. Получаем:
y’=7x6+5x4-4x3+3x2-2x+1.
2. y=3x6-2x+5. Решаем аналогично, используя те же формулы и формулу 3.
y’=3∙6x5-2=18x5-2.
Применяем правило I, формулы
Применяем правило IV, формулы 5 и 1.
В пятом примере по правилу I производная суммы равна сумме производных, а производную 1-го слагаемого мы только что находили (пример 4), поэтому, будем находить производные 2-го и 3-го слагаемых, а для 1-го слагаемого можем сразу писать результат.
 Дифференцируем 2-ое и 3-е слагаемые по формуле 4. Для этого преобразуем корни третьей и четвертой степеней в знаменателях к степеням с отрицательными показателями, а затем, по 4 формуле, находим производные степеней.
Дифференцируем 2-ое и 3-е слагаемые по формуле 4. Для этого преобразуем корни третьей и четвертой степеней в знаменателях к степеням с отрицательными показателями, а затем, по 4 формуле, находим производные степеней.
Посмотрите на данный пример и полученный результат. Уловили закономерность? Хорошо. Это означает, что мы получили новую формулу и можем добавить ее в нашу таблицу производных.
Решим шестой пример и выведем еще одну формулу.
Используем правило IV и формулу 4. Получившиеся дроби сократим.
Смотрим на данную функцию и на ее производную. Вы, конечно, поняли закономерность и готовы назвать формулу:
Учим новые формулы!
www.mathematics-repetition.com
Логарифмическая производная – примеры вычисления
Пусть
(1)
есть дифференцируемая функция от переменной x. В начале мы рассмотрим ее на множестве значений x, для которых y принимает положительные значения: . В дальнейшем мы покажем, что все полученные результаты применимы и для отрицательных значений .
В некоторых случаях, чтобы найти производную функции (1), ее удобно предварительно прологарифмировать
,
а затем вычислить производную. Тогда по правилу дифференцирования сложной функции,
.
Отсюда
(2) .
Производная от логарифма функции называется логарифмической производной:
.
Логарифмическая производная функции y = f(x) – это производная натурального логарифма этой функции: (ln f(x) )′.
Случай отрицательных значений y
Теперь рассмотрим случай, когда переменная может принимать как положительные, так и отрицательные значения. В этом случае возьмем логарифм от модуля и найдем его производную:
.
Отсюда
(3) .
То есть, в общем случае, нужно найти производную от логарифма модуля функции .
Сравнивая (2) и (3) мы имеем:
.
То есть формальный результат вычисления логарифмической производной не зависит от того, взяли мы по модулю или нет. Поэтому, при вычислении логарифмической производной, мы можем не беспокоится о том, какой знак имеет функция .
Прояснить такую ситуацию можно с помощью комплексных чисел. Пусть, при некоторых значениях x, отрицательна: . Если мы рассматриваем только действительные числа, то функция не определена. Однако, если ввести в рассмотрение комплексные числа, то получим следующее:
.
То есть функции и отличаются на комплексную постоянную :
.
Поскольку производная от постоянной равна нулю, то
.
Свойство логарифмической производной
Из подобного рассмотрения следует, что логарифмическая производная не изменится, если умножить функцию на произвольную постоянную :
.
Действительно, применяя свойства логарифма, формулы производной суммы и производной постоянной, имеем:
.
Применение логарифмической производной
Применять логарифмическую производную удобно в тех случаях, когда исходная функция состоит из произведения степенных или показательных функций. В этом случае операция логарифмирования превращает произведение функций в их сумму. Это упрощает вычисление производной.
Далее мы приводим примеры вычисления производных для следующих функций:
; ; .
Пример 1
Найти производную функции:
.
Решение
Логарифмируем исходную функцию:
.
Дифференцируем по переменной x.
В таблице производных находим:
.
Применяем правило дифференцирования сложной функции.
;
;
;
;
(П1.1) .
Умножим на :
.
Итак, мы нашли логарифмическую производную:
.
Отсюда находим производную исходной функции:
.
Примечание
Если мы хотим использовать только действительные числа, то следует брать логарифм от модуля исходной функции:
.
Тогда
;
.
И мы получили формулу (П1.1). Поэтому результат не изменился.
Ответ
Пример 2
С помощью логарифмической производной, найдите производную функции
.
Решение
Логарифмируем:
(П2.1) .
Дифференцируем по переменной x:
;
;
;
;
;
.
Умножим на :
.
Отсюда мы получаем логарифмическую производную:
.
Производная исходной функции:
.
Примечание
Здесь исходная функция неотрицательная: . Она определена при . Если не предполагать, что логарифм может быть определен для отрицательных значений аргумента, то формулу (П2.1) следует записать так:
.
Поскольку
и
,
то это не повлияет на окончательный результат.
Ответ
.
Пример 3
Найдите производную
.
Решение
Дифференцирование выполняем с помощью логарифмической производной. Логарифмируем, учитывая что :
(П3.1) .
Дифференцируя, получаем логарифмическую производную.
;
;
;
(П3.2) .
Поскольку , то
.
Примечание
Проделаем вычисления без предположения, что логарифм может быть определен для отрицательных значений аргумента. Для этого возьмем логарифм от модуля исходной функции:
.
Тогда вместо (П3.1) имеем:
;
.
Сравнивая с (П3.2) мы видим, что результат не изменился.
Ответ
.
Автор: Олег Одинцов. Опубликовано: Изменено:
1cov-edu.ru
Примеры вычисления производных. Функция f(x)=x2. Типовые задачи
Дополнительные сочиненияНа уроке рассматривается тема: «Примеры вычисления производных. Функция f(x)=x2. Типовые задачи». На этом занятии приобретаются навыки вычисления производных для простейших функций и применения алгоритма по нахождению производной для функции f(x)=x2.
Тема: Производная
Урок: Примеры вычисления производных. Функция f(x)=x^2. Типовые задачи.
1. Вычисление производных простейших функций
Дано: .
Найти: .
На предыдущем уроке рассматривали для конкретной функции нахождение производной и изучили весь алгоритм ее нахождения. На данном примере повторим этот алгоритм.
Решение.
Будем сопровождать решение иллюстрацией (см. рис. 1).
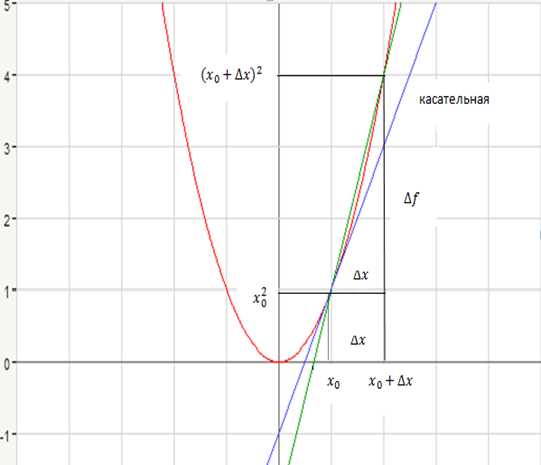
Рис. 1. График функции .
Если зафиксировать точку , то можно получить значение функции в этой точке. Если задать приращение аргументу , то получим новое значение аргумента, а именно , и новое значение функции – .
Итак, выяснили, что . Дали приращение аргументу, и получили значение функции при новом значении аргумента .
Дальше надо найти приращение функции. Приращение функции – это значение функции в новой точке минус значение функции в старой точке
.
Имеем приращение аргумента и приращение функции. На рисунке (см. рис.1) – это катеты треугольника. Также имеем секущую, которая наклонена под углом . При эта секущая будет стремиться занять положение касательной. Дальше нужно найти разностное отношение и упростить его так, чтобы сократить .
.
Как и в предыдущем примере мы получили слагаемое, которое не зависит от и слагаемое, которое от него зависит. Проанализируем, что будет если устремить к нулю. В данном случае получим, что
Ответ:
. Так как – произвольное, то ответ можно записать для произвольной точки , то есть
.
Проанализируем ситуацию на графике. В точке секущая заняла положение касательной и угол наклона касательной – . , где – тангенс угла наклона касательной, которая проведена к кривой в точке с абсциссой .
2. Решение стандартной задачи
Решим стандартную задачу.
Дано: .
Найти
Решение.
1) Найдем значение производной в любой точке .
.
2) Нужно найти значение производной в конкретной точке
.
3. Сопутствующие задачи
Для функции , в точке , найти угол наклона касательной. Для простоты возьмем тангенс угла наклона касательной.
Решение.
1) Найдем производную функции: .
2) Найдем .
3) Учтем геометрический смысл производной, то есть .
Ответ. . Если нужно найти сам угол , то его тоже можно найти так:
.
Таким образом рассмотрели конкретную функцию , закрепили применение алгоритма по нахождению производной и решили сопутствующие задачи, проиллюстрировав все это на чертеже.
4. Производная степенной функции. Анализ производной
Итак, решив две задачи, выяснили, что и . Это
наводит на мысль о том, что можно написать производную для любого показателя
Проанализируем возможности использования производной. Для этого нарисуем графики функций (см. рис.2-3).
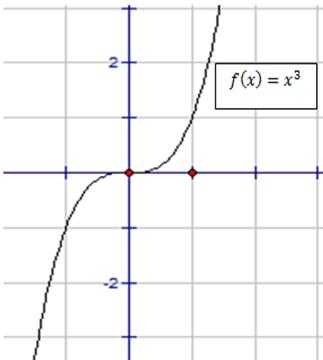
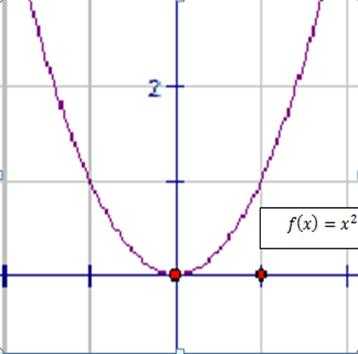
Рис. 2. Кубическая парабола. Рис. 3. Парабола.
Разница между ними видна. Первая функция возрастает при всех . Вторая функция убывает на промежутке (] и возрастает на промежутке [0;+). В точке – вершине параболы – функция имеет точку минимума.
Нарисуем график производной для первой функции (см. рис.4).
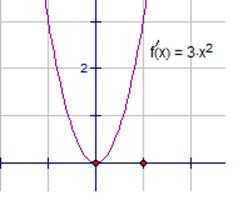
Рис. 4 График производной функции .
, то есть . Так как , то – возрастает на всей числовой прямой. Будет сформулирована соответствующая теорема, которая базируется на свойствах производной. Пока выясняем смысл производной и зачем она нужна, причем видим, что с ростом скорость растет, и крутизна кривой тоже увеличивается.
Нарисуем график производной для второй функции (см. рис.5).

Рис. 5 График производной функции .
Это линейная функция . Это означает, что при () производная отрицательная, а при – производная положительная. Вспомним физический смысл производной. Производная – это мгновенная скорость. Если в момент времени мгновенная скорость положительна, то мы от дома уезжаем, и расстояние от дома увеличивается. Это и видно на графике, так как функция увеличивается. Значит, если , то . Если производная меньше нуля, то это означает, что мы приближаемся к дому, расстояние уменьшается. Если , то функция убывает, что мы и видим на графике.
Выясним, что происходит в точке .
. Производная равна нулю. Тангенс угла наклона равен нулю. В этой точке может быть либо точка максимума, либо точка минимума.
5. Некоторые задачи на физический и геометрический смысл производной
Рассмотрим некоторые задачи на физический и геометрический смысл производной.
Допустим задан график производной функции (см. рис.6).
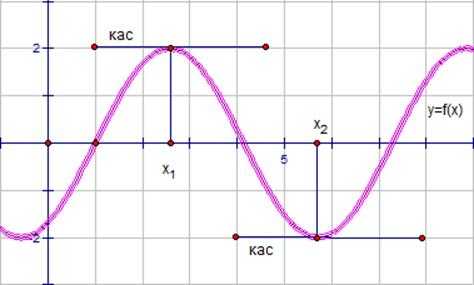
Рис. 6. График производной произвольной функции.
Заданы точки и . Найти производную в этих точках. Касательная в точке параллельна оси X.
Напомним, что – геометрический смысл производной. Это означает, что .
Задача 2.
Заданы точки и . Сравнить, что больше: или (см. рис.6).
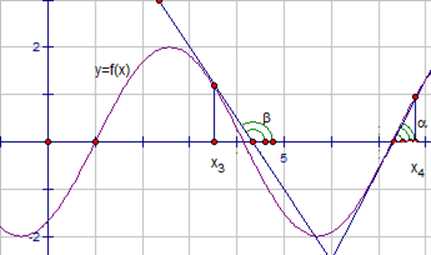
Рис.6. График производной функции.
По графику видно, что если в точке с абсциссой провести касательную, то ее угол наклона β – тупой. Это означает, что . Если провести касательную в точке и посмотреть на угол , то можно увидеть, что он острый. Это означает, что . Итак, – отрицательна, –положительна, отсюда .
6. Итог урока
На уроке рассмотрели применение алгоритма по нахождению производной для функции f(x)=x2.
Рекомендации для самостоятельного решения: 27.1-28.9
Список рекомендованной литературы
1. Алгебра и начала анализа, 10 класс (в двух частях). Учебник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. –М.: Мнемозина, 2009.
2. Алгебра и начала анализа, 10 класс (в двух частях). Задачник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. –М.: Мнемозина, 2007.
3. Виленкин Н. Я., Ивашев-Мусатов О. С., Шварцбурд С. И. Алгебра и математический анализ для 10 класса (учебное пособие для учащихся школ и классов с углубленным изучением математики).-М.: Просвещение, 1996.
4. Галицкий М. Л., Мошкович М. М., Шварцбурд С. И. Углубленное изучение алгебры и математического анализа.-М.: Просвещение, 1997.
5. Сборник задач по математике для поступающих во ВТУЗы (под ред. М. И.Сканави).-М.:Высшая школа, 1992.
6. Мерзляк А. Г., Полонский В. Б., Якир М. С. Алгебраический тренажер.-К.: А. С.К., 1997.
7. ЗвавичЛ. И., Шляпочник Л. Я., Чинкина Алгебра и начала анализа. 8-11 кл.: Пособие для школ и классов с углубленным изучением математики (дидактические материалы).-М.: Дрофа, 2002.
8. Саакян С. М., Гольдман А. М., Денисов Д. В. Задачи по алгебре и началам анализа (пособие для учащихся 10-11 классов общеобразов. учреждений).-М.: Просвещение, 2003.
9. Карп А. П. Сборник задач по алгебре и началам анализа : учеб. пособие для 10-11 кл. с углубл. изуч. математики.-М.: Просвещение, 2006.
10. Глейзер Г. И. История математики в школе. 9-10 классы (пособие для учителей).-М.: Просвещение, 1983
Дополнительные веб-ресурсы
1. Интернет-портал Mathematics. ru .
2. Портал Естественных Наук .
3. Интернет-портал Exponenta. ru .
Сделай дома
№ 41.5; 41.37 (а, г) (Алгебра и начала анализа, 10 класс (в двух частях). Задачник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. –М.: Мнемозина, 2007.)
dp-adilet.kz



