Вывод формулы момент инерции сферы – Момент инерции шара, теория и примеры
- Комментариев к записи Вывод формулы момент инерции сферы – Момент инерции шара, теория и примеры нет
- Советы абитуриенту
- Момент инерции шара, теория и примеры
- Помогите решить / разобраться (Ф)
- V. Вывод формулы для определения момента инерции.
- definition of Момент инерции and synonyms of Момент инерции (Russian)
- Помогите решить / разобраться (Ф)
- Центробежный момент инерции Википедия
- вывод формулы для момента инерции полого толстостенного цилиндра
Момент инерции шара, теория и примеры
Это скалярная (в общем случае тензорная) величина. Для непрерывного однородного тела, вращающегося около оси, момент инерции определяют как:
где r – функция положения материальной точки в пространстве; – плотность тела; –объем элемента тела.
Момент инерции однородного шара
Однородный по объем шар можно представить как систему сферических слоев (или тонких дисков), обладающих массами ().

По условию шар является однородным, плотность его можно представить как:
где – объем всего шара; m – масса всего шара.
В качестве элементарной массы выберем сферический слой радиуса r (указанный на рис.1). Его массу можно представить как:
При этом объем рассматриваемого сферического слоя равен:
Момент инерции тонкого диска (толщина диска ) равен:
Выделенный нами диск находится на расстоянии h от центра шара. Радиус рассматриваемого нами диска связан с расстоянием h выражением:
Тогда формулу (4) преобразуем к виду:
Просуммируем моменты инерции всех дисков:
Получили, что момент инерции однородного шара, относительно его диаметра равен:
Момент инерции полого шара (сферы)
Момент инерции сферы удобно находить, используя полярный момент инерции. Это момент инерции тела относительно некоторой точки, назовем ее O. Он равен произведению всех масс точек тела на квадраты расстояний от них до точки О. Если через полюс О провести прямоугольные оси, то полярный момент () равен:
Полярный момент инерции равен половине суммы моментов инерции тела относительно трех прямоугольных осей, которые проходят через полюс:
В центре тяжести тела полярный момент инерции имеет минимальной значение.
Рассмотрим сферу радиуса R. Для нее удобно сначала найти полярный момент инерции относительно ее центра ():
Согласно формуле (10) и зная, что для сферы , имеем:
Получаем, что момент инерции сферы (полого шара) равен:
Примеры решения задач
ru.solverbook.com
Помогите решить / разобраться (Ф)
Если вам нужен именно вывод… Я бы вывел следующим образом:Будем считать что функция плотности задана на поверхности и за ось примем . Площадь сферы обозначим
Переходим к цилиндрическим координатам:
Мысленно разбиваем диаметр вдоль оси на равных отрезков и получаем соответственно разбиение сферы на сферических поясов (и шапочки на полюсах) одинаковой высоты . Далее проводим меридианов и соответственно разбиваем каждый сферический пояс на сферические “квадраты” ( в полюсах- треугольники) каждый с угловой мерой . Получаем в общей сложности кусочков.
В каждом кусочке /элементе сферы – выбираем точку с координатами , и находим значение плотности Момент каждого кусочка относительно оси приблизительно равен
Чтобы найти площадь кривой поверхности, вообще говоря необходимо привлекать частные производные, но в нашем случае (сферы) спасает теорема, утверждающая, что если сферические пояса имеют одинаковую высоту, то их площади равны. (Доказывается средствами матана 2 курса или просто смотри в инете ). Поэтому равны и площади всех элементов нашего разбиения сферы .
Далее все это суммируем по обоим индексам, устремляем к бесконечности и получаем двойной интеграл по поверхности как советовали в самом начале.

Ну а если, как частный случай, масса распределена равномерно, то вытаскивая за интегралы и умножив на получаем
где – масса сферы. Проинтегрировав, получите ответ данный Архиповым.
dxdy.ru
V. Вывод формулы для определения момента инерции.
Пусть при вращении диск поднялся, на высоту h =h1 – h2 (рис. 1). Тогда приращение потенциальной энергии равно
.
При опускании нижнего диска потенциальная энергия переходит в кинетическую энергию вращательного движения
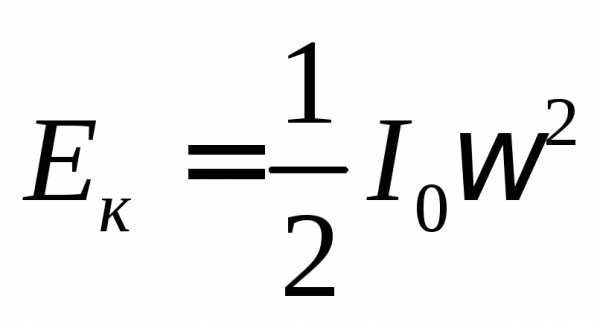 ,
,
где I0 – момент инерции нижнего диска, – угловая скорость диска.
Вмомент прохождения диском положения равновесия угловая скорость, а, следовательно, и кинетическая энергия, принимает максимальное значение, т.е. = 0.
Если пренебречь трением, то на основании закона сохранения энергии для колеблющегося диска можно записать:
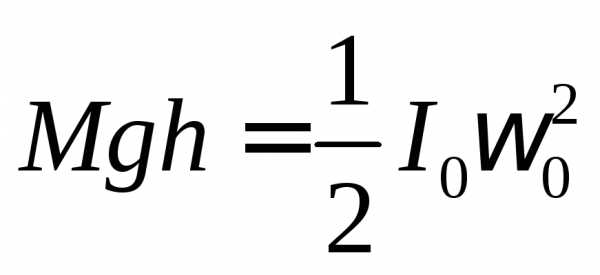 .
(2)
.
(2)
Угловая скорость , являющаяся первой производной от смещения по времени, может быть записана
Максимальное значение угловой скорости равно:
. (3)
На основании выражений (2) и (3) имеем:
Найдем величину h при повороте диска на малый угол 0, считая, что h1 + h2 2l:
. (5)
Из рис.1 ясно, что
и .
Подставляя
значение  и
и 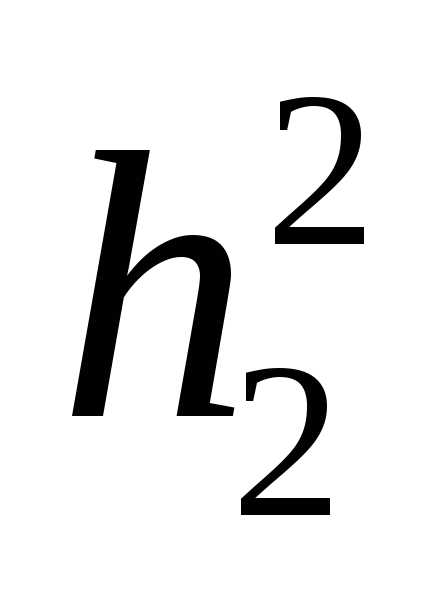 в (5), получим:
в (5), получим:
.
Вследствие малости угла 0 синус можно заменить аргументом:
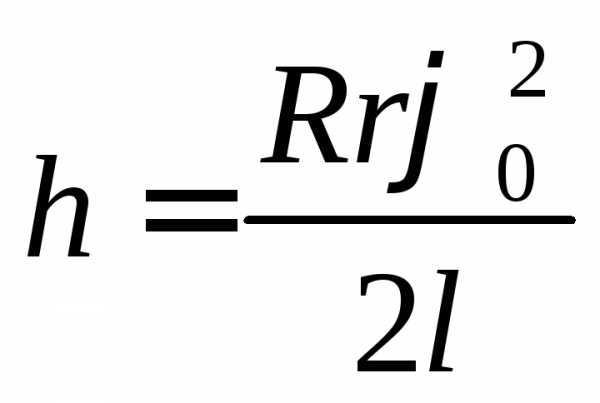 .
(6)
.
(6)
Подставив выражения (3) и (6) в формулу (2), получим:
, или
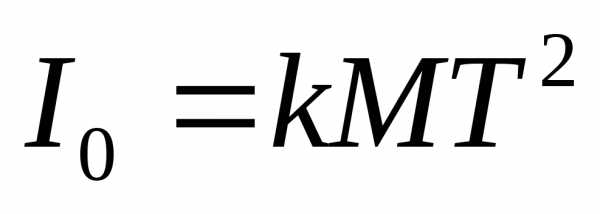
где 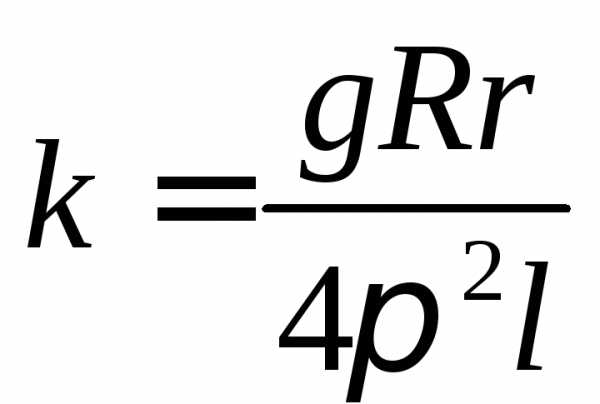 – постоянная установки.
– постоянная установки.
IV. Порядок выполнения лабораторной работы
1. Определение момента инерции i0 диска без нагрузки.
а) Заставить диск совершать крутильные колебания с малой амплитудой (10 15 градусов). Секундомером измерить времяtсовершенияnполных колебаний (n– задаётся преподавателем). Все измерения провести несколько раз. Все значения занести в табл.1.
б) Провести статистическую обработку времени t по методу Стьюдента.
в) Определить период колебаний диска Т = t /n, занести данные в таблицу 1.
г) Занести в табл.2 массу диска М и постоянную установкиk.
д) По формуле (7) рассчитать значение момента инерции диска
е) Вычислить относительные и абсолютные погрешности по формулам (8) – (9) и занести результаты в таблицу 3.
(8)
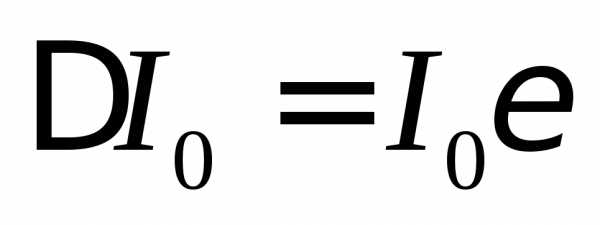 .
(9)
.
(9)
Абсолютная погрешность периода колебаний определяется следующим образом
.
Таблица 1
№/№ п/п | t | t | t2 | Sn | t(,n) | t сл | tпр | t | n | T | T |
с | с | с2 | с | – | с | c | с | – | с | с | |
1 | |||||||||||
2 | |||||||||||
3 | |||||||||||
… | |||||||||||
cреднее |
Таблица 2
k | M | m | d | I0 | I1 | I2 | I3 | |
м2с–2 | кг | кг | м | кгм2 | кгм2 | кгм2 | кгм2 | |
Среднее значение | ||||||||
Абсолютная погрешность | 510-4 | |||||||
Относительная погрешность |
studfiles.net
definition of Момент инерции and synonyms of Момент инерции (Russian)
У этого термина существуют и другие значения, см. Момент.Момент инерции — скалярная физическая величина, мера инертности во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости).
Единица измерения СИ: кг·м².
Обозначение: I или J.
Различают несколько моментов инерции — в зависимости от многообразия, от которого отсчитывается расстояние точек.
Осевой момент инерции
Осевые моменты инерции некоторых тел.
Моментом инерции механической системы относительно неподвижной оси («осевой момент инерции») называется величина Ja, равная сумме произведений масс всех n материальных точек системы на квадраты их расстояний до оси:
,
где:
- mi — масса i-й точки,
- ri — расстояние от i-й точки до оси.
Осевой момент инерции тела Ja является мерой инертности тела во вращательном движении вокруг оси подобно тому, как масса тела является мерой его инертности в поступательном движении.
,
где:
Если тело однородно, то есть его плотность всюду одинакова, то
Теорема Гюйгенса-Штейнера
Момент инерции твёрдого тела относительно какой-либо оси зависит не только от массы, формы и размеров тела, но также от положения тела по отношению к этой оси. Согласно теореме Штейнера (теореме Гюйгенса-Штейнера), момент инерции тела J относительно произвольной оси равен сумме момента инерции этого тела Jc относительно оси, проходящей через центр масс тела параллельно рассматриваемой оси, и произведения массы тела m на квадрат расстояния d между осями:
Если — момент инерции тела относительно оси, проходящей через центр масс тела, то момент инерции относительно параллельной оси, расположенной на расстоянии от неё, равен
,
где — полная масса тела.
Например, момент инерции стержня относительно оси, проходящей через его конец, равен:
Осевые моменты инерции некоторых тел
Вывод формул
Тонкостенный цилиндр (кольцо, обруч)
Вывод формулы
Момент инерции тела равен сумме моментов инерции составляющих его частей. Разобъём тонкостенный цилиндр на элементы с массой dm и моментами инерции dJi. Тогда
Поскольку все элементы тонкостенного цилиндра находятся на одинаковом расстоянии от оси вращения, формула (1) преобразуется к виду
Толстостенный цилиндр (кольцо, обруч)
Вывод формулы
Пусть имеется однородное кольцо с внешним радиусом R, внутренним радиусом R1, толщиной h и плотностью ρ. Разобьём его на тонкие кольца толщиной dr. Масса и момент инерции тонкого кольца радиуса r составит
Момент инерции толстого кольца найдём как интеграл
Поскольку объём и масса кольца равны
получаем окончательную формулу для момента инерции кольца
Однородный диск (сплошной цилиндр)
Вывод формулы
Рассматривая цилиндр (диск) как кольцо с нулевым внутренним радиусом (R1 = 0), получим формулу для момента инерции цилиндра (диска):
Сплошной конус
Вывод формулы
Разобьём конус на тонкие диски толщиной dh, перепендикулярные оси конуса. Радиус такого диска равен
где R – радиус основания конуса, H – высота конуса, h – расстояние от вершины конуса до диска. Масса и момент инерции такого диска составят
Интегрируя, получим
Сплошной однородный шар
Вывод формулы
Разобъём шар на тонкие диски толщиной dh, перпендикулярные оси вращения. Радиус такого диска, расположенного на высоте h от центра сферы, найдём по формуле
Масса и момент инерции такого диска составят
Момент инерции сферы найдём интегрированием:
Тонкостенная сфера
Вывод формулы
Для вывода воспользуемся формулой момента инерции однородного шара радиуса R:
Вычислим, насколько изменится момент инерции шара, если при неизменной плотности ρ его радиус увеличится на бесконечно малую величину dR.
Тонкий стержень (ось проходит через центр)
Вывод формулы
Разобъём стержень на малые фрагменты длиной dr. Масса и момент инерции такого фрагмента равна
Интегрируя, получим
Тонкий стержень (ось проходит через конец)
Вывод формулы
При перемещении оси вращения из середины стержня на его конец, центр тяжести стержня перемещается относительно оси на расстояние l/2. По теореме Штейнера новый момент инерции будет равен
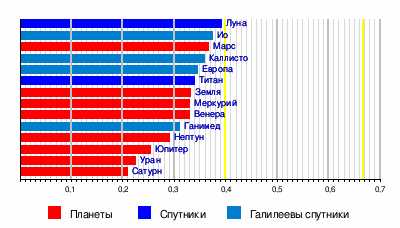
Безразмерные моменты инерции планет и их спутников
Большое значение для исследований внутренней структуры планет и их спутников имеют их безразмерные моменты инерции. Безразмерный момент инерции тела радиуса r и массы m равен отношению его момента инерции относительно оси вращения к моменту инерции материальной точки той же массы относительно неподвижной оси вращения, расположенной на расстоянии r (равному mr2). Эта величина отражает распределение массы по глубине. Одним из методов её измерения у планет и спутников является определение допплеровского смещения радиосигнала, передаваемого АМС, пролетающей около данной планеты или спутника. Для тонкостенной сферы безразмерный момент инерции равен 2/3 (~0,67), для однородного шара — 0,4, и вообще тем меньше, чем большая масса тела сосредоточена у его центра. Например, у Луны безразмерный момент инерции близок к 0,4 (равен 0,391), поэтому предполагают, что она относительно однородна, её плотность с глубиной меняется мало. Безразмерный момент инерции Земли меньше, чем у однородного шара (равен 0,335), что является аргументом в пользу существования у неё плотного ядра. [3][4]
Центробежный момент инерции
Центробежными моментами инерции тела по отношению к осям прямоугольной декартовой системы координат называются следующие величины:
где x, y и z — координаты малого элемента тела объёмом dV, плотностью ρ и массой dm.
Ось OX называется главной осью инерции тела, если центробежные моменты инерции Jxy и Jxz одновременно равны нулю. Через каждую точку тела можно провести три главные оси инерции. Эти оси взаимно перпендикулярны друг другу. Моменты инерции тела относительно трёх главных осей инерции, проведённых в произвольной точке O тела, называются главными моментами инерции тела.
Главные оси инерции, проходящие через центр масс тела, называются главными центральными осями инерции тела, а моменты инерции относительно этих осей — его главными центральными моментами инерции. Ось симметрии однородного тела всегда является одной из его главных центральных осей инерции.
Геометрический момент инерции
Геометрический момент инерции — геометрическая характеристика сечения вида
где — расстояние от центральной оси до любой элементарной площадки относительно нейтральной оси.
Геометрический момент инерции не связан с движением материала, он лишь отражает степень жесткости сечения. Используется для вычисления радиуса инерции, прогиба балки.
Единица измерения СИ — м4. В строительных расчетах, литературе и сортаментах металлопроката в частности указывается в см4.
Из него выражается момент сопротивления сечения:
- .
Центральный момент инерции
Центральный момент инерции (или момент инерции относительно точки O) — это величина
,
где:
Центральный момент инерции можно выразить через главные осевые или центробежные моменты инерции: .
Момент инерции тела относительно произвольной оси, проходящей через центр масс и имеющей направление, заданное единичным вектором , можно представить в виде квадратичной (билинейной) формы:
- (1),
где — тензор инерции. Матрица тензора инерции симметрична, имеет размеры и состоит из компонент центробежных моментов:
- ,
.
Выбором соответствующей системы координат матрица тензора инерции может быть приведена к диагональному виду. Для этого нужно решить задачу о собственных значениях для матрицы тензора :
,
где — ортогональная матрица перехода в собственный базис тензора инерции. В собственном базисе координатные оси направлены вдоль главных осей тензора инерции, а также совпадают с главными полуосями эллипсоида тензора инерции. Величины — главные моменты инерции. Выражение (1) в собственной системе координат имеет вид:
- ,
откуда получается уравнение эллипсоида в собственных координатах. Разделив обе части уравнения на
и произведя замены:
- ,
получаем канонический вид уравнения эллипсоида в координатах :
Расстояние от центра эллипсоида до некоторой его точки связано со значением момента инерции тела вдоль прямой, проходящей через центр эллипсоида и эту точку:
См. также
Примечания
Литература
- Матвеев. А. Н. Механика и теория относительности. М.: Высшая школа, 1986. (3-е изд. М.: ОНИКС 21 век: Мир и Образование, 2003. — 432с.) http://www.alleng.ru/d/phys/phys108.htm
- Трофимова Т. И. Курс физики. — 7-е изд. — М.: Высшая школа, 2001. — 542 с.
- Алешкевич В. А., Деденко Л. Г., Караваев В. А. Механика твердого тела. Лекции. Издательство Физического факультета МГУ, 1997. http://nature.web.ru/db/msg.html?mid=1186208&s=120000000
- Павленко Ю. Г. Лекции по теоретической механике. М.: ФИЗМАТЛИТ, 2002. — 392с. http://www.alleng.ru/d/phys/phys99.htm
- Яворский Б. М., Детлаф А. А. Физика для школьников старших классов и поступающих в вузы: учебное пособие — М.: Дрофа, 2002, 800с. ISBN 5-7107-5956-3
- Сивухин Д. В. Общий курс физики. В 5 т. Том I. Механика. 4-е изд. М.: ФИЗМАТЛИТ; Изд-во МФТИ, 2005. — 560 с. http://www.alleng.ru/d/phys/phys103.htm
- Беляев Н. М., Сопротивление материалов. Главная редакция физико-математической литературы изд-ва «Наука», 1976. — 608 с.
Ссылки
dictionary.sensagent.com
Помогите решить / разобраться (Ф)
Никак не могу согласиться с предыдущим оратором. Вот правильное решение.Упростим немного обозначения. Пусть и — внешний в внутренний радиусы кольца, и — массы дисков из того же материала, что кольцо, радиусами и . Известно, что моменты инерции таких дисков относительно осей, перпендикулярных дискам и проходящих через их центры масс, равны и . (Если это необходимо пояснить, переспросите.)
Представим теперь большой диск как наше кольцо и малый диск внутри кольца. Воспользовавшись аддитивностью массы и момента инерции, можно записать
Кроме того, массы дисков, очевидно, пропорциональны квадратам их радиусов
Из трех последних уравнений исключаем и и выражаем
Задачу можно решить и впрямую с помощью интегрирования, только совсем не так, как предлагает Eiktyrnir.
dxdy.ru
Центробежный момент инерции Википедия
Моме́нт ине́рции — скалярная (в общем случае — тензорная) физическая величина, мера инертности во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости).
Единица измерения в Международной системе единиц (СИ): кг·м².
Обозначение: I или J.
Различают несколько моментов инерции — в зависимости от типа базового множества до которого отсчитываются расстояния от элементарных масс.
Осевой момент инерции
Осевые моменты инерции некоторых телМоментом инерции механической системы относительно неподвижной оси («осевой момент инерции») называется величина Ja, равная сумме произведений масс всех n материальных точек системы на квадраты их расстояний до оси[1]:
- Ja=∑i=1nmiri2,{\displaystyle J_{a}=\sum _{i=1}^{n}m_{i}r_{i}^{2},}
где:
- mi — масса i-й точки,
- ri — расстояние от i-й точки до оси.
Осевой момент инерции тела Ja является мерой инертности тела во вращательном движении вокруг оси подобно тому, как масса тела является мерой его инертности в поступательном движении.
- Ja=∫(m)r2dm=∫(V)ρr2dV,{\displaystyle J_{a}=\int \limits _{(m)}r^{2}dm=\int \limits _{(V)}\rho r^{2}dV,}
где:
- dm = ρ dV — масса малого элемента объёма тела dV,
- ρ — плотность,
- r — расстояние от элемента dV до оси a.
Если тело однородно, то есть его плотность всюду одинакова, то
- Ja=ρ∫(V)r2dV.{\displaystyle J_{a}=\rho \int \limits _{(V)}r^{2}dV.}
Теорема Гюйгенса — Штейнера
Момент инерции твёрдого тела относительно какой-либо оси зависит от массы, формы и размеров тела, а также и от положения тела по отношению к этой оси. Согласно теореме Гюйгенса — Штейнера, момент инерции тела J относительно произвольной оси равен сумме момента инерции этого тела Jc относительно оси, проходящей через центр масс тела параллельно рассматриваемой оси, и произведения массы тела m на квадрат расстояния d между осями[1]:
- J=Jc+md2,{\displaystyle J=J_{c}+md^{2},}
где m — полная масса тела.
Например, момент инерции стержня относительно оси, проходящей через его конец, равен:
- J=Jc+md2=112ml2+m(l2)2=13ml2.{\displaystyle J=J_{c}+md^{2}={\frac {1}{12}}ml^{2}+m\left({\frac {l}{2}}\right)^{2}={\frac {1}{3}}ml^{2}.}
Осевые моменты инерции некоторых тел
Вывод формул
Тонкостенный цилиндр (кольцо, обруч)
Вывод формулы
Момент инерции тела равен сумме моментов инерции составляющих его частей. Разобьём тонкостенный цилиндр на элементы с массой dm и моментами инерции dJi. Тогда
- J=∑dJi=∑Ri2dm.(1).{\displaystyle J=\sum dJ_{i}=\sum R_{i}^{2}dm.\qquad (1).}
Поскольку все элементы тонкостенного цилиндра находятся на одинаковом расстоянии от оси вращения, формула (1) преобразуется к виду
- J=∑R2dm=R2∑dm=mR2.{\displaystyle J=\sum R^{2}dm=R^{2}\sum dm=mR^{2}.}
Толстостенный цилиндр (кольцо, обруч)
Вывод формулы
Однородный диск (сплошной цилиндр)
Вывод формулы
Рассматривая цилиндр (диск) как кольцо с нулевым внутренним радиусом (R1 = 0), получим формулу для момента инерции цилиндра (диска):
- J=12mR2.{\displaystyle J={\frac {1}{2}}mR^{2}.}
Сплошной конус
Вывод формулы
Разобьём конус на тонкие диски толщиной dh, перпендикулярные оси конуса. Радиус такого диска равен
- r=RhH,{\displaystyle r={\frac {Rh}{H}},}
где R – радиус основания конуса, H – высота конуса, h – расстояние от вершины конуса до диска. Масса и момент инерции такого диска составят
- dm=ρdV=ρ⋅πr2dh;{\displaystyle dm=\rho dV=\rho \cdot \pi r^{2}dh;}
- dJ=12r2dm=12πρr4dh=12πρ(RhH)4dh;{\displaystyle dJ={\frac {1}{2}}r^{2}dm={\frac {1}{2}}\pi \rho r^{4}dh={\frac {1}{2}}\pi \rho \left({\frac {Rh}{H}}\right)^{4}dh;}
Интегрируя, получим
- J=∫0HdJ=12πρ(RH)4∫0Hh5dh=12πρ(RH)4h55|0H==110πρR4H=(ρ⋅13πR2H)310R2=310mR2.{\displaystyle {\begin{aligned}J=\int _{0}^{H}dJ={\frac {1}{2}}\pi \rho \left({\frac {R}{H}}\right)^{4}\int _{0}^{H}h^{4}dh={\frac {1}{2}}\pi \rho \left({\frac {R}{H}}\right)^{4}\left.{\frac {h^{5}}{5}}\right|_{0}^{H}=={\frac {1}{10}}\pi \rho R^{4}H=\left(\rho \cdot {\frac {1}{3}}\pi R^{2}H\right){\frac {3}{10}}R^{2}={\frac {3}{10}}mR^{2}.\end{aligned}}}
Сплошной однородный шар
Вывод формулы
Разобьём шар на тонкие диски толщиной dh, перпендикулярные оси вращения. Радиус такого диска, расположенного на высоте h от центра сферы, найдём по формуле
- r=R2−h3.{\displaystyle r={\sqrt {R^{2}-h^{2}}}.}
Масса и момент инерции такого диска составят
- dm=ρdV=ρ⋅πr2dh;{\displaystyle dm=\rho dV=\rho \cdot \pi r^{2}dh;}
- dJ=12r2dm=12πρr4dh=12πρ(R2−h3)2dh=12πρ(R4−2R2h3+h5)dh.{\displaystyle dJ={\frac {1}{2}}r^{2}dm={\frac {1}{2}}\pi \rho r^{4}dh={\frac {1}{2}}\pi \rho \left(R^{2}-h^{2}\right)^{2}dh={\frac {1}{2}}\pi \rho \left(R^{4}-2R^{2}h^{2}+h^{4}\right)dh.}
Момент инерции шара найдём интегрированием:
- J=∫−RRdJ=2∫0RdJ=πρ∫0R(R4−2R2h3+h5)dh==πρ(R4h−23R2h4+15h5)|0R=πρ(R5−23R5+15R5)=815πρR5==(43πR3ρ)⋅25R2=25mR2.{\displaystyle {\begin{aligned}J&=\int _{-R}^{R}dJ=2\int _{0}^{R}dJ=\pi \rho \int _{0}^{R}\left(R^{4}-2R^{2}h^{2}+h^{4}\right)dh=\\&=\pi \rho \left.\left(R^{4}h-{\frac {2}{3}}R^{2}h^{3}+{\frac {1}{5}}h^{5}\right)\right|_{0}^{R}=\pi \rho \left(R^{5}-{\frac {2}{3}}R^{5}+{\frac {1}{5}}R^{5}\right)={\frac {8}{15}}\pi \rho R^{5}=\\&=\left({\frac {4}{3}}\pi R^{3}\rho \right)\cdot {\frac {2}{5}}R^{2}={\frac {2}{5}}mR^{2}.\end{aligned}}}
Тонкостенная сфера
Вывод формулы
Для вывода воспользуемся формулой момента инерции однородного шара радиуса R:
- J0=25MR2=815πρR5.{\displaystyle J_{0}={\frac {2}{5}}MR^{2}={\frac {8}{15}}\pi \rho R^{5}.}
Вычислим, насколько изменится момент инерции шара, если при неизменной плотности ρ его радиус увеличится на бесконечно малую величину dR.
- J=dJ0dRdR=ddR(815πρR5)dR==83πρR4dR=(ρ⋅4πR2dR)23R2=23mR2.{\displaystyle {\begin{aligned}J&={\frac {dJ_{0}}{dR}}dR={\frac {d}{dR}}\left({\frac {8}{15}}\pi \rho R^{5}\right)dR=\\&={\frac {8}{3}}\pi \rho R^{4}dR=\left(\rho \cdot 4\pi R^{2}dR\right){\frac {2}{3}}R^{2}={\frac {2}{3}}mR^{2}.\end{aligned}}}
Тонкий стержень (ось проходит через центр)
Вывод формулы
Разобьём стержень на малые фрагменты длиной dr. Масса и момент инерции такого фрагмента равна
- dm=mdrl;dJ=r2dm=mr2drl.{\displaystyle dm={\frac {mdr}{l}};\qquad dJ=r^{2}dm={\frac {mr^{2}dr}{l}}.}
Интегрируя, получим
- J=∫−l/2l/2dJ=2∫0l/2dJ=2ml∫0l/2r2dr=2mlr33|0l/2=2mll324=112ml2.{\displaystyle J=\int _{-l/2}^{l/2}dJ=2\int _{0}^{l/2}dJ={\frac {2m}{l}}\int _{0}^{l/2}r^{2}dr={\frac {2m}{l}}\left.{\frac {r^{3}}{3}}\right|_{0}^{l/2}={\frac {2m}{l}}{\frac {l^{3}}{24}}={\frac {1}{12}}ml^{2}.}
Тонкий стержень (ось проходит через конец)
Вывод формулы
При перемещении оси вращения из середины стержня на его конец, центр тяжести стержня перемещается относительно оси на расстояние l⁄2. По теореме Штейнера новый момент инерции будет равен
- J=J0+mr2=J0+m(l2)2=112ml2+14ml2=13ml2.{\displaystyle J=J_{0}+mr^{2}=J_{0}+m\left({\frac {l}{2}}\right)^{2}={\frac {1}{12}}ml^{2}+{\frac {1}{4}}ml^{2}={\frac {1}{3}}ml^{2}.}
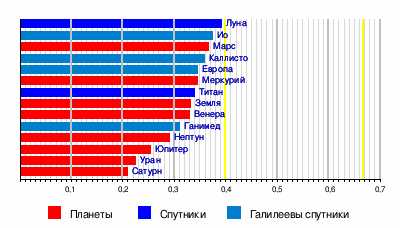
Безразмерные моменты инерции планет и спутников
Большое значение для исследований внутренней структуры планет и их спутников имеют их безразмерные моменты инерции. Безразмерный момент инерции тела радиуса r и массы m равен отношению его момента инерции относительно оси вращения к моменту инерции материальной точки той же массы относительно неподвижной оси вращения, расположенной на расстоянии r (равному mr2). Эта величина отражает распределение массы по глубине. Одним из методов её измерения у планет и спутников является определение доплеровского смещения радиосигнала, передаваемого АМС, пролетающей около данной планеты или спутника. Для тонкостенной сферы безразмерный момент инерции равен 2/3 (~0,67), для однородного шара — 0,4, и вообще тем меньше, чем большая масса тела сосредоточена у его центра. Например, у Луны безразмерный момент инерции близок к 0,4 (равен 0,391), поэтому предполагают, что она относительно однородна, её плотность с глубиной меняется мало. Безразмерный момент инерции Земли меньше, чем у однородного шара (равен 0,335), что является аргументом в пользу существования у неё плотного ядра[5][6].
Центробежный момент инерции
Центробежными моментами инерции тела по отношению к осям прямоугольной декартовой системы координат называются следующие величины[1][7]:
- Jxy=∫(m)xydm=∫(V)xyρdV,{\displaystyle J_{xy}=\int \limits _{(m)}xydm=\int \limits _{(V)}xy\rho dV,}
- Jxz=∫(m)xzdm=∫(V)xzρdV,{\displaystyle J_{xz}=\int \limits _{(m)}xzdm=\int \limits _{(V)}xz\rho dV,}
- Jyz=∫(m)yzdm=∫(V)yzρdV,{\displaystyle J_{yz}=\int \limits _{(m)}yzdm=\int \limits _{(V)}yz\rho dV,}
где x, y и z — координаты малого элемента тела объёмом dV, плотностью ρ и массой dm.
Ось OX называется главной осью инерции тела, если центробежные моменты инерции Jxy и Jxz одновременно равны нулю. Через каждую точку тела можно провести три главные оси инерции. Эти оси взаимно перпендикулярны друг другу. Моменты инерции тела относительно трёх главных осей инерции, проведённых в произвольной точке O тела, называются главными моментами инерции данного тела[7].
Главные оси инерции, проходящие через центр масс тела, называются главными центральными осями инерции тела, а моменты инерции относительно этих осей — его главными центральными моментами инерции. Ось симметрии однородного тела всегда является одной из его главных центральных осей инерции[7].
Геометрические моменты инерции
Геометрический момент инерции объёма относительно оси — геометрическая характеристика тела, выражаемая формулой[8]:
- JVa=∫(V)r2dV,{\displaystyle J_{Va}=\int \limits _{(V)}r^{2}dV,}
где, как и ранее r — расстояние от элемента dV до оси a.
Размерность JVa — длина в пятой степени (dimJVa=L5{\displaystyle \mathrm {dim} J_{Va}=\mathrm {L^{5}} }), соответственно единица измерения СИ — м5.
Геометрический момент инерции площади относительно оси — геометрическая характеристика тела, выражаемая формулой[8]:
- JSa=∫(S)r2dS,{\displaystyle J_{Sa}=\int \limits _{(S)}r^{2}dS,}
где интегрирование выполняется по поверхности S, а dS — элемент этой поверхности.
Размерность JSa — длина в четвёртой степени (dimJSa=L4{\displaystyle \mathrm {dim} J_{Sa}=\mathrm {L^{4}} }), соответственно единица измерения СИ — м4. В строительных расчетах, литературе и сортаментах металлопроката часто указывается в см4.
Через геометрический момент инерции площади выражается момент сопротивления сечения:
- W=JSarmax.{\displaystyle W={\frac {J_{Sa}}{r_{max}}}.}
Здесь rmax — максимальное расстояние от поверхности до оси.
Момент инерции относительно плоскости
Моментом инерции твёрдого тела относительно некоторой плоскости называют скалярную величину, равную сумме произведений массы каждой точки тела на квадрат расстояния от этой точки до рассматриваемой плоскости[9].
Если через произвольную точку O{\displaystyle O} провести координатные оси x,y,z{\displaystyle x,y,z}, то моменты инерции относительно координатных плоскостей xOy{\displaystyle xOy}, yOz{\displaystyle yOz} и zOx{\displaystyle zOx} будут выражаться формулами:
- JxOy=∑i=1nmizi2 ,{\displaystyle J_{xOy}=\sum _{i=1}^{n}m_{i}z_{i}^{2}\ ,}
- JyOz=∑i=1nmixi2 ,{\displaystyle J_{yOz}=\sum _{i=1}^{n}m_{i}x_{i}^{2}\ ,}
- JzOx=∑i=1nmiyi2 .{\displaystyle J_{zOx}=\sum _{i=1}^{n}m_{i}y_{i}^{2}\ .}
В случае сплошного тела суммирование заменяется интегрированием.
Центральный момент инерции
Центральный момент инерции (момент инерции относительно точки O, момент инерции относительно полюса, полярный момент инерции) JO{\displaystyle J_{O}} — это величина, определяемая выражением[9]:
- Ja=∫(m)r2dm=∫(V)ρr2dV,{\displaystyle J_{a}=\int \limits _{(m)}r^{2}dm=\int \limits _{(V)}\rho r^{2}dV,}
где:
Центральный момент инерции можно выразить через главные осевые моменты инерции, а также через моменты инерции относительно плоскостей[9]:
- JO=12(Jx+Jy+Jz),{\displaystyle J_{O}={\frac {1}{2}}\left(J_{x}+J_{y}+J_{z}\right),}
- JO=JxOy+JyOz+JxOz.{\displaystyle J_{O}=J_{xOy}+J_{yOz}+J_{xOz}.}
Тензор инерции и эллипсоид инерции
Момент инерции тела относительно произвольной оси, проходящей через центр масс и имеющей направление, заданное единичным вектором s→=‖sx,sy,sz‖T,|s→|=1{\displaystyle {\vec {s}}=\left\Vert s_{x},s_{y},s_{z}\right\Vert ^{T},\left\vert {\vec {s}}\right\vert =1}, можно представить в виде квадратичной (билинейной) формы:
- Is=s→T⋅J^⋅s→,{\displaystyle I_{s}={\vec {s}}^{T}\cdot {\hat {J}}\cdot {\vec {s}},\qquad } (1)
где J^{\displaystyle {\hat {J}}} — тензор инерции. Матрица тензора инерции симметрична, имеет размеры 3×3{\displaystyle 3\times 3} и состоит из компонент центробежных моментов:
- J^=‖Jxx−Jxy−Jxz−JyxJyy−Jyz−Jzx−JzyJzz‖,{\displaystyle {\hat {J}}=\left\Vert {\begin{array}{ccc}J_{xx}&-J_{xy}&-J_{xz}\\-J_{yx}&J_{yy}&-J_{yz}\\-J_{zx}&-J_{zy}&J_{zz}\end{array}}\right\Vert ,}
- Jxy=Jyx,Jxz=Jzx,Jzy=Jyz,{\displaystyle J_{xy}=J_{yx},\quad J_{xz}=J_{zx},\quad J_{zy}=J_{yz},\quad }Jxx=∫(m)(y2+z2)dm,Jyy=∫(m)(x2+z2)dm,Jzz=∫(m)(x2+y2)dm.{\displaystyle J_{xx}=\int \limits _{(m)}(y^{2}+z^{2})dm,\quad J_{yy}=\int \limits _{(m)}(x^{2}+z^{2})dm,\quad J_{zz}=\int \limits _{(m)}(x^{2}+y^{2})dm.}
Выбором соответствующей системы координат матрица тензора инерции может быть приведена к диагональному виду. Для этого нужно решить задачу о собственных значениях для матрицы тензора J^{\displaystyle {\hat {J}}}:
- J^d=Q^T⋅J^⋅Q^,{\displaystyle {\hat {J}}_{d}={\hat {Q}}^{T}\cdot {\hat {J}}\cdot {\hat {Q}},}
- J^d=‖JX000JY000JZ‖,{\displaystyle {\hat {J}}_{d}=\left\Vert {\begin{array}{ccc}J_{X}&0&0\\0&J_{Y}&0\\0&0&J_{Z}\end{array}}\right\Vert ,}
где Q^{\displaystyle {\hat {Q}}} — ортогональная матрица перехода в собственный базис тензора инерции. В собственном базисе координатные оси направлены вдоль главных осей тензора инерции, а также совпадают с главными полуосями эллипсоида тензора инерции. Величины JX,JY,JZ{\displaystyle J_{X},J_{Y},J_{Z}} — главные моменты инерции. Выражение (1) в собственной системе координат имеет вид:
- Is=JX⋅sx2+JY⋅sy2+JZ⋅sz2,{\displaystyle I_{s}=J_{X}\cdot s_{x}^{2}+J_{Y}\cdot s_{y}^{2}+J_{Z}\cdot s_{z}^{2},}
откуда получается уравнение эллипсоида в собственных координатах. Разделив обе части уравнения на Is{\displaystyle I_{s}}
- (sxIs)2⋅JX+(syIs)2⋅JY+(szIs)2⋅JZ=1{\displaystyle \left({s_{x} \over {\sqrt {I_{s}}}}\right)^{2}\cdot J_{X}+\left({s_{y} \over {\sqrt {I_{s}}}}\right)^{2}\cdot J_{Y}+\left({s_{z} \over {\sqrt {I_{s}}}}\right)^{2}\cdot J_{Z}=1}
и произведя замены:
- ξ=sxIs,η=syIs,ζ=szIs,{\displaystyle \xi ={s_{x} \over {\sqrt {I_{s}}}},\eta ={s_{y} \over {\sqrt {I_{s}}}},\zeta ={s_{z} \over {\sqrt {I_{s}}}},}
получаем канонический вид уравнения эллипсоида в координатах ξηζ{\displaystyle \xi \eta \zeta }:
- ξ2⋅JX+η2⋅JY+ζ2⋅JZ=1.{\displaystyle \xi ^{2}\cdot J_{X}+\eta ^{2}\cdot J_{Y}+\zeta ^{2}\cdot J_{Z}=1.}
Расстояние от центра эллипсоида до некоторой его точки связано со значением момента инерции тела вдоль прямой, проходящей через центр эллипсоида и эту точку:
- r2=ξ2+η2+ζ2=(sxIs)2+(syIs)2+(szIs)2=1Is.{\displaystyle r^{2}=\xi ^{2}+\eta ^{2}+\zeta ^{2}=\left({s_{x} \over {\sqrt {I_{s}}}}\right)^{2}+\left({s_{y} \over {\sqrt {I_{s}}}}\right)^{2}+\left({s_{z} \over {\sqrt {I_{s}}}}\right)^{2}={1 \over I_{s}}.}
См. также
Комментарии
- ↑ В правильности использования знака «+» в этой формуле можно убедиться, если сравнить моменты инерции полого толстостенного и сплошного цилиндров с одинаковыми массами. Действительно, у первого из этих цилиндров масса в среднем сосредоточена дальше от оси, чем у второго, поэтому и момент инерции этого цилиндра должен быть больше, чем у сплошного. Именно такое соотношение моментов инерции и обеспечивает знак «+». С другой стороны, в пределе при стремлении r1 к r2 формула для полого толстостенного цилиндра должна приобрести тот же вид, что и формула для полого тонкостенного цилиндра. Очевидно, что такой переход происходит только при использовании формулы со знаком «+».
Примечания
wikiredia.ru
вывод формулы для момента инерции полого толстостенного цилиндра
Мда… У Левченко ничего не видно, кроме того, что расчёт выполнен с помощью интеграла :))) Относительно какой оси вращения нужно вычислить момент инерции? Наверное, относительно геометрической оси цилиндра? Тогда можно и без интегралов вывести, если вспомнить, что момент инерции сплошного цилиндра (а также и диска) радиуса R и массы m равен 0,5 * m*R^2. В случае с толстостенным однородным цилиндром рассмотрим два цилиндра – сплошной и тот, что был вырезан из его полости. Момент первого обозначим 0,5 * M * R^2, а второго 0,5 * m * r^2 Так как момент инерции – величина аддитивная, – то искомый момент равен просто разности этих моментов: 0,5 * ( M * R^2 – m * r^2). Где R и r – внешний и внутренний радиусы толстостенного цилиндра, а M и m – массы сплошного и внутреннего. Остаётся только выразить массу через плотность материала ro и длину цилиндра L. M = ro * V = ro * pi * R^2 * L m = ro * pi * r^2 * L Искомый момент равен: 0,5 * ro * pi * L * (R^4 – r^4)
<img src=”//otvet.imgsmail.ru/download/18ff4d948d3a3c2f2437b0597287c91f_i-14.jpg” > Списывайте товорищи теретическую механику, ибо это большое зло для студента!
А тут можно и без интегралов сосчитать. Момент инерции – аддитивная величина. Момент инерции системы из двух тел равен сумме их индивидуальных моментов инерции. Для обычного цилиндра (сплошного) момент инерции равен 1/2 mR². Так что представим себе сплошной цилиндр радиуса R как систему из сплошного цилиндра радиуса r и пустотелого цилиндра толщиной стенки от r до R. Момент инерции “внутреннего” будет 1/2 mr², всей системы – 1/2 MR². Осталось только понять, как связаны m и М. Ну это как раз просто – масса пропорциональна квадрату радиуса. Так что если известны масса m0 и размеры трубы, то масса этой фиктивной вставки m1 определяется из пропорции R² : r² = (m1+m0) : m1. Всё, осталась простенькая арифметика.
touch.otvet.mail.ru



