Задачи по физике с векторами решение – Открытый интегрированный урок по физике и математике. Применение темы «Векторы» при решении задач практического содержания по физике.
- Комментариев к записи Задачи по физике с векторами решение – Открытый интегрированный урок по физике и математике. Применение темы «Векторы» при решении задач практического содержания по физике. нет
- Советы абитуриенту
- Работа с векторами. Примеры решения задач по физике. 10-11 класс
- Векторы в физике — 4. Примеры из физики — Phystech.Academy
- Секержицкий В.С. О векторных способах решения избранных задач кинематики
- Урок по физике и математике «Векторы»
- При решении задач по физике
- Векторы. Действия с векторами. Повторение к урокам физики в 9, 10 классе.
- Как решать задачи по физике на свободное падение. Примеры решения задач по физике. 9-10 класс
Работа с векторами. Примеры решения задач по физике. 10-11 класс
Работа с векторами. Примеры решения задач по физике. 10-11 класс
Задачи по физике – это просто!
Элементарные задачи из курса школьной физики.
Векторы в физике
Многие физические величины зависят от направления и называются векторными, например, скорость, перемещение, ускорение.
При работе с векторами (векторными величинами) существуют специальные обозначения, которые надо запомнить:
Изображение вектора на чертеже:
Если вектор параллелен координатной оси, то модуль вектора равен модулю проекции вектора на эту ось:
Проекция вектора может быть положительной или отрицательной (в зависимости от его положения относительно оси координат):
Если вектор перпендикулярен оси, то проекция вектора на эту ось равна нулю!
Как бы ни был направлен вектор, его модуль всегда можно рассчитать по формуле:
Сложение векторов (а это часто приходится выполнять в задачах) можно производить графически двумя способами – треугольника и параллелограмма.
Расчетные формулы прямолинейного равномерного движения
Расчетные формулы для прямолинейного равномерного движения – это формулы в проекциях векторов на координатную ось.
Скорость тела:
где
Vx – проекция вектора скорости на координатную ось х
Sx – проекция вектора перемещения на ось х
t –
время, за которое совершается данное перемещение
Координата тела в любой момент времени
или после подстановки скорости:
Последнюю формулу иначе называют уравнением прямолинейного равномерного движения:
где
xo – начальная координата тела
x –
конечная координата тела через время t после начала движения
Расстояние
между движущимися телами при прямолинейном равномерном движении в любой момент времени:где
l – расстояние между телами в любой момент времени движения
x1 – конечная координата первого тела на момент определения расстояния между телами
x2 – конечная координата второго тела на момент определения расстояния между телами
class-fizika.ru
Векторы в физике — 4. Примеры из физики — Phystech.Academy
Простейшие примеры векторов в физике – скорость и сила.
1. Всякое движение можно представить как результат сложения нескольких движений, его составляющих. Скорость результирующего движения изображается по величине и направлению диагональю параллелограмма, построенного на отрезках, изображающих составляющие скорости, как на сторонах. Рассмотрим конкретный пример.
Рыбак переправляется на лодке `A` через реку, которая течёт в сторону, указанную стрелкой.
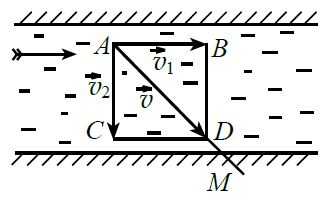
Пусть скорость течения воды `vec(v_1)` изображается по величине и направлению отрезком `AB`, а скорость `vec(v_2)` движения лодки относительно воды под влиянием усилий гребца изображается отрезком `AC` (в стоячей воде лодка двигалась бы по направлению `AC` со скоростью `vec(v_2)`). Лодка будет двигаться относительно берега по направлению `AM` со скоростью `vec v`, изображаемой диагональю `AD` параллелограмма, построенного на векторах `vec(v_1)` и `vec(v_2)` (в данном случае параллелограмм `ABCD` является прямоугольником).
2. Сила – как векторная величина – всегда имеет определённое направление, модуль, а также точку приложения.
Часто встречаются случаи, когда на тело действуют несколько сил. Тогда бывает удобно заменить их одной силой, которая производит на тело такое же действие, как и несколько одновременно действующих сил. Такую силу (если она существует) называют равнодействующей. Нахождение равнодействующей нескольких сил осуществляется с помощью правил векторного сложения, при этом слагаемые силы называют составляющими.
Так, несколько сил, действующих на одну и ту же точку тела, всегда можно заменить одной равнодействующей, как бы ни были направлены силы и каковы бы ни были их величины. Пусть, например, на тело действуют четыре силы `vec(F_1)`, `vec(F_2)`, `vec(F_3)` и `vec(F_4)`, приложенные к одной точке `O` и лежащие в одной плоскости.
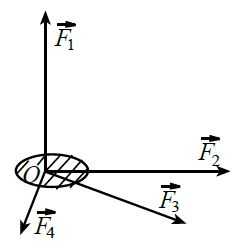
Тогда их равнодействующая `vec F` будет равна векторной сумме этих сил, найденной по правилу многоугольника.
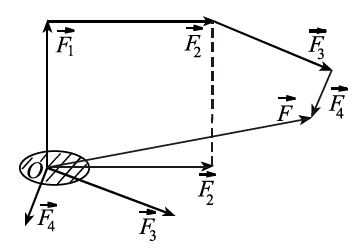
Найти равнодействующую `vec R` трёх равных по модулю сил, приложенных к телу в одной точке и расположенных в одной плоскости, если углы между всеми силами равны между собой.
`F_1 = F_2 = F_3 = F`.
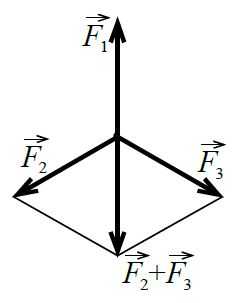
Углы между парами векторов `vec(F_1)` и `vec(F_2)`, `vec(F_2)` и `vec(F_3)`, а также между векторами `vec(F_1)` и `vec(F_3)`, равны друг другу и равны `120^@`. Сложим силы `vec(F_2)` и `vec(F_3)` по правилу параллелограмма. Вследствие равенства модулей сил `vec(F_2)` и `vec(F_3)` этот параллелограмм есть ромб. Сумма сил `vec(F_2) + vec(F_3)` есть диагональ ромба, поэтому углы между парами векторов `vec(F_2)` и `vec(F_2) + vec(F_3)`, а также `vec(F_3)` и `vec(F_2) + vec(F_3)` равны по `60^@`, т. е. векторы `vec(F_1)` и `vec(F_2) + vec(F_3)` направлены вдоль одной прямой, но в противоположные стороны. Силовой параллелограмм, построенный на векторах `vec(F_2)` и `vec(F_3)`, состоит из двух равносторонних треугольников, поэтому модуль силы
`|vec(F_2) + vec(F_3)| = F_2 = F_3 = F = F_1`, т. е `vec F_1 = – (vec(F_2) + vec(F_3))`,
откуда следует `vec(F_1) + vec(F_2) + vec(F_3) = 0`.
К телу приложено `6` сил, лежащих в одной плоскости и составляющих друг с другом углы в `60^@`. Силы последовательно равны `1`, `2`, `3`, `4`, `5` и `6 Н`. Найти равнодействующую `vec R` этих шести сил.
Сложение сил по правилу многоугольника здесь нецелесообразно. Поступим иначе. Сложим сначала попарно силы, направленные вдоль одной прямой.
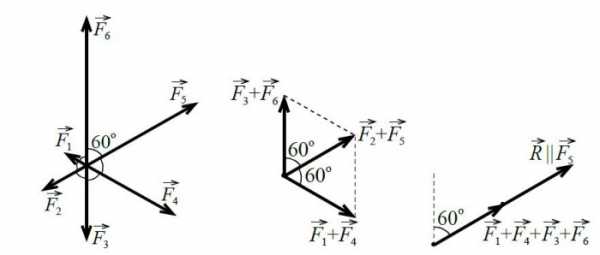
Получим
`|vec(F_2) + vec(F_4)| = 4 – 1 = 3`,
аналогично `|vec(F_2) + vec(F_5)| = 5 – 2 = 3` и `|vec(F_3) + vec(F_6)| = 6 – 3 = 3`.
Сумма сил `vec(F_2) + vec(F_5)` направлена вдоль вектора `vec(F_5)`. Туда же направлена и сумма сил `vec(F_1) + vec(F_4) + vec(F_3) + vec(F_6)`, причём модуль этой силы равен `3`. В итоге получаем, что сумма всех шести сил `vec(F_1) + vec(F_2) + vec(F_3) + vec(F_4) + vec(F_5) + vec(F_6)` направлена вдоль направления силы `vec(F_5)`, а модуль этой силы `|vec(F_1) + vec(F_2) + vec(F_3) + vec(F_4) + vec(F_5) + vec(F_6)| = 3 + 3 = 6 Н`.
Найти равнодействующую `vec R` пяти равных по модулю сил, приложенных к телу в одной точке и расположенных в одной плоскости, если углы между всеми соседними силами равны между собой.
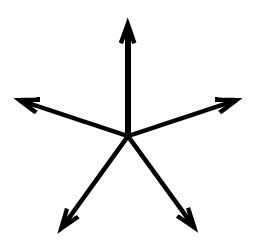
(Эти углы, разумеется, равны `360^@ //5 = 72^@`.)
В отличие от предыдущего примера здесь мы имеем нечётное число сил, поэтому невозможно образовать из них целое число пар. Поступим иначе. Возьмём какую-нибудь силу, например, `vec(F_1)`, а остальные сгруппируем в пары и попарно сложим их:
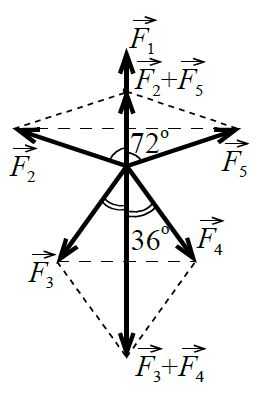
`vec(F_2) + vec(F_5)` и `vec(F_3) + vec(F_4)`.
Почему удобна именно такая группировка сил в пары? Дело в том, что обе суммы сил (и `vec(F_2) + vec(F_5)` и `vec(F_3) + vec(F_4)`) направлены вдоль линии действия силы `vec(F_1)`. Ясно, что равнодействующая всех сил будет направлена вдоль линии действия силы `vec(F_1)`. Модули сумм сил легко найти из геометрии. Например, в силовом параллелограмме, построенном на векторах `vec(F_2)` и `vec(F_5)`, который является ромбом, длина диагонали ромба (модуль силы `vec(F_2) + vec(F_5)`) равна удвоенной половинке диагонали, а та легко ищется из любого из 4-х прямоугольных треугольников, на которые ромб разбивается диагоналями. В результате
`|vec(F_2) + vec(F_5) | = 2F cos 72^@`,
где `F` – модуль любой из 5-ти исходных сил. Аналогично
`|vec(F_3) + vec(F_4)| = 2F cos 36^@`.
В итоге для модуля искомой силы получаем формулу
`R = F(1 + 2 cos 72^@ – 2 cos 36^@)` (*).
Для углов `72^@` и `36^@` нет таких простых формул, как для углов `30^@`, `45^@` или `60^@`. Пользуясь калькулятором, можно, однако, показать, что согласно формуле (*) `R = 0`.
Имеется и более красивое доказательство того, что результирующий вектор есть нулевой вектор. В самом деле, мы довольно произвольно взяли в качестве силы, которой не хватило пары, силу `vec(F_1)`. Если бы в качестве такой взять силу `vec(F_2)`, а в пары объединить `vec(F_1)` и `vec(F_3)` (одна пара) и `vec(F_4)` и `vec(F_5)`, то, повторив рассуждения, получим, что равнодействующая всех пяти сил `vec R` должна быть направлена вдоль линии действия силы `vec(F_2)`. Возможно ли, чтобы вектор был одновременно направлен вдоль двух несовпадающих друг с другом направлений (и `vec(F_1)`, и `vec(F_2)`; а на самом деле, как догадался читатель, ещё и вдоль направления действия сил `vec(F_3)`, `vec(F_4)` и `vec(F_5)`!)? Ненулевым вектор не может быть! Остаётся одна возможность: суммарный вектор – нулевой!
В примерах 10 и 11 мы искали по правилу параллелограмма суммы сил. В примере 12 нас интересовала лишь проекция равнодействующей силы на направление (например, силы `vec(F_1)`). В следующих примерах наш интерес будет также скорее не к равнодействующей силе, а только к каким-то её проекциям.
Электрический фонарь весом `Q = 16 Н` укреплён, как показано на рисунке.
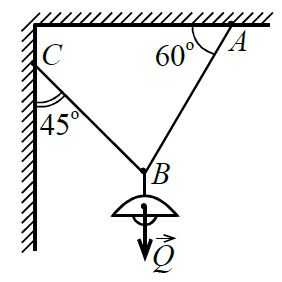
Определите отношение натяжений `T_1` и `T_2` в проволоках `BA` и `BC`, углы наклона которых даны на рисунке.
В условиях равновесия сумма всех сил, приложенных к точке `B`, равна нулю. Поэтому проекция равнодействующей всех сил на горизонтальное направление тоже равна нулю. Проекция силы со стороны проволоки, идущей к фонарю, на это направление равна нулю (эта сила вертикальна). Остаются вклады от двух натяжений со стороны проволок `BA` и `BC`. Горизонтальную ось направим слева направо. Тогда имеем: T1, гор+T2, гор=0T_{1,\;\mathrm{гор}}+T_{2,\;\mathrm{гор}}=0,
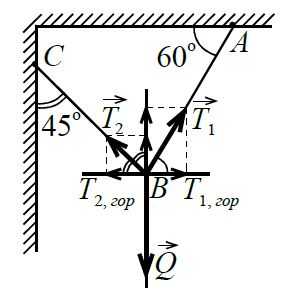
т. е.
`T_1 * cos 60^@ – T_2 cos 45^@ = 0`
(или `T_1 * sin 30^@ – T_2 sin 45^@ = 0`), откуда получаем `T_1//T_2 = sqrt2`.
Однородная массивная верёвка подвешена за два конца на разных высотах.
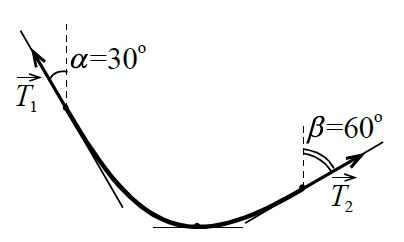
Масса верёвки `m`. Углы, которые составляет верёвка с вертикалью в точках закрепления, равны `30^@` и `60^@`. Определите силы натяжения верёвки вблизи её точек крепления.
Задача кажется очень трудной, т. к. не ясно, какую роль играет неизвестная нам форма верёвки, которую она примет под действием сил тяжести всех частей верёвки. (В предыдущем примере мы не интересовались провисанием проволок под действием силы тяжести, молчаливо считая провисание малым.) И всё же задача в той постановке, в какой дана, имеет простое решение. Мысленно проведём горизонтальную ось слева направо. Поскольку верёвка находится в равновесии, то сумма проекций всех сил на горизонтальное направление равна нулю. Сила тяжести верёвки имеет нулевую проекцию на это направление (эта сила направлена вертикально). Снова остаются вклады от двух натяжений:
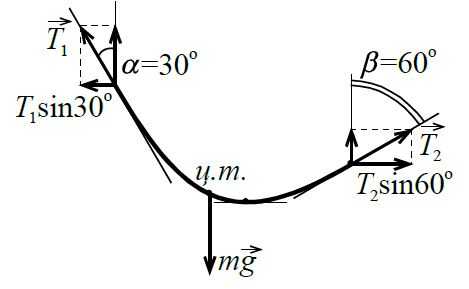
T1, гор+T2, гор=0T_{1,\;\mathrm{гор}}+T_{2,\;\mathrm{гор}}=0, или `- T_1 * sin 30^@ + T_2 sin 60^@ = 0`. Полагая `sin 30^@ = 1//2` и `sin 60^@ = sqrt3 //2`, находим `T_1 // T_2 = sqrt3`. Мысленно проведём ещё и вертикальную ось, направив её вниз. Сумма проекций всех сил на эту ось также равна нулю:
`mg – T_1 cos 30^@ – T_2 cos 60^@ = 0`.
Учитывая найденное ранее соотношение между `T_1` и `T_2` и значения `cos 60^@ = 1//2` и `cos 30^@ = sqrt3 //2`, получаем:
`mg – sqrt3 * T_2 * sqrt3 //2 – T_2 //2 = 0`,
откуда
`T_2 = mg//2` и `T_1 = sqrt3 mg//2`.
На гладкой наклонной плоскости с углом наклона лежит брусок массой m. Какую горизонтальную силу нужно приложить к бруску, чтобы он находился в покое?
Определите также модуль нормальной силы реакции на брусок со стороны наклонной плоскости.
Брусок по условию задачи покоится. Значит, сумма всех сил, приложенных к бруску, равна нулю. Равны нулю и суммы проекций сил на любые направления, в частности, на направление вдоль наклонной плоскости и перпендикулярное ему. Нормальная сила реакции `vec N` со стороны наклонной плоскости имеет равную нулю составляющую вдоль наклонной плоскости.
Проекция сила тяжести `m vec g` на ось `Ox` вдоль наклонной плоскости
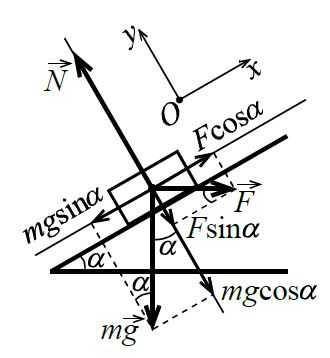
равна `- mg sin alpha`, а проекция горизонтальной силы `F` на эту ось равна `F cos alpha`. Других сил вдоль наклонной плоскости не действует (плоскость, по условию задачи, гладкая, т. е. сила трения пренебрежимо мала). Приравнивая нулю сумму проекций на ось `Ox` всех сил, действующих на тело, получаем: `- mg sin alpha + F cos alpha = 0`, откуда находим
`F = mg (sin alpha)/(cos alpha) = mg * bbb”tg” alpha`.
Для отыскания `N` обратимся к проекциям сил на направление `Oy`. Приравняем нулю и сумму проекций на ось `Oy`:
`N – mg cos alpha – F sin alpha = 0`,
откуда `N = mg cos alpha + F sin alpha`, или с учётом найденного значения `F`:
`N = mg cos alpha + mg (sin^2 alpha)/(cos alpha) = mg (cos^2 alpha + sin^2 alpha)/(cos alpha)`,
тогда с учётом основного тригонометрического тождества, `sin^2 alpha + cos^2 alpha = 1`, получаем окончательно
`N = (mg)/(cos alpha)`.
На шероховатой поверхности доски лежит брусок массой `m`. К нему приложена сила, направленная под углом `alpha` к горизонту.
Определите модуль нормальной силы реакции со стороны поверхности.
Поскольку брусок не проваливается и не подскакивает вверх, то сумма проекций сил на вертикальную ось равна нулю:
`N + F * sin alpha – mg = 0`,
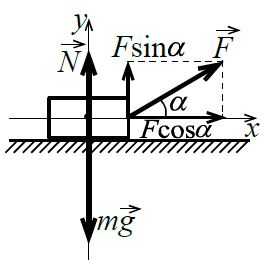
откуда находим
`N = mg – F * sin alpha`.
Часто совершенно безосновательно приравнивают силу реакции `N` силе тяжести `mg`. Мы видим, что даже в случае горизонтальной поверхности это в общем случае не так. Для наклонной плоскости это тоже не так. В предыдущем примере нормальная сила реакции равнялась `mg//cos alpha`. Кстати, если бы удерживающая сила `F` действовала там не вдоль горизонтали, а вдоль наклонной плоскости, то для удержания бруска на наклонной плоскости потребовалась бы сила величиной `F = mg sin alpha`, а нормальная сила реакции была бы равна `N = mg cos alpha` (и снова не равнялась бы `mg`!)
Докажите это самостоятельно.
Самолёт взлетает с аэродрома со скоростью v=220 км/чv=220\;\mathrm{км}/\mathrm ч под углом `alpha = 20^@` к горизонту. Найдите модули горизонтальной и вертикальной составляющих скорости самолёта.
В данном примере мы имеем дело с весьма простым случаем разложения скорости на два взаимно перпендикулярных направления:
`vec v = vec(v _sf”гор”) + vec(v_sf”верт”)`,
vгор=v cos α≈207 км/чv_\mathrm{гор}=v\;\cos\;\alpha\approx207\;\mathrm{км}/\mathrm ч, vверт=v sin α≈75 км/чv_\mathrm{верт}=v\;\sin\;\alpha\approx75\;\mathrm{км}/\mathrm ч.
В безветренную погоду самолёт летит со скоростью 180 км/ч180\;\mathrm{км}/\mathrm ч (50 м/с50\;\mathrm м/\mathrm с) относительно земли. С какой скоростью относительно земли будет лететь самолёт, если дует западный ветер со скоростью 10 м/с10\;\mathrm м/\mathrm с?
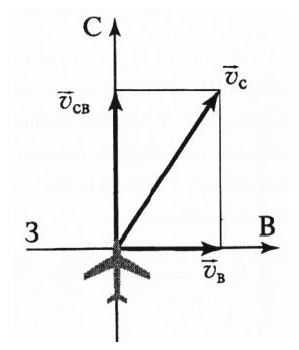
В данном случае мы имеем дело со сложением движений: `vec(v_sf”с”) = vec(v_sf”св”) + vec(v_sf”в”)`, где `vec(v_sf”св”)` – скорость самолёта относительно воздуха (модуль которой равен скорости самолёта относительно земли в безветренную погоду), а `vec(v_sf”в”)` – скорость воздуха. Далее по теореме Пифагора получаем:
vс=502+102=2600≈51 м/сv_\mathrm с=\sqrt{50^2+10^2}=\sqrt{2600}\approx51\;\mathrm м/\mathrm с.
Лодка пытается пересечь реку, текущую со скоростью u=3 км/чu=3\;\mathrm{км}/\mathrm ч. Скорость лодки в стоячей воде v=5 км/чv=5\;\mathrm{км}/\mathrm ч. Под каким углом `alpha` к нормали к берегу надо направить лодку, чтобы она двигалась поперек реки (без сноса)? Какой будет при этом модуль скорости лодки `v` относительно берега?
Как и в примере 9, мы также имеем дело со случаем сложения движений. Но там было проще: не требовалось выбирать никакой стратегии, рыбак лишь наблюдал, как снесёт его лодку течением воды в реке. Если бы вода в реке покоилась, то, направив корпус лодки под углом `alpha` к нормали, мы заставили бы её двигаться в направлении вектора `vec V`.
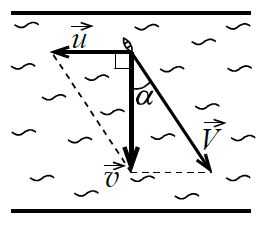
В действительности, вода в реке не стоячая, а имеет скорость `vec u` Поэтому сносимая течением лодка будет двигаться в направлении вектора `vec v` таком, что `vec v = vec V + vec u`. Учитывая, что оба треугольника в параллелограмме прямоугольные (по условию, лодка должна двигаться перпендикулярно берегам), находим
`sin alpha = u//V = 3//5`, `alpha ~~ 37^@`,
а по теореме Пифагора v=V2-u2=4 м/сv=\sqrt{V^2-u^2}=4\;\mathrm м/\mathrm с.
Лодка пытается пересечь реку, текущую со скоростью u=5 км/чu=5\;\mathrm{км}/\mathrm ч. Скорость лодки в стоячей воде V=3 км/чV=3\;\mathrm{км}/\mathrm ч. Под каким углом `alpha` к нормали к берегу надо направить корпус лодки, чтобы её снесло как можно меньше? Под каким углом `beta` к нормали к берегу будет при этом плыть лодка?
В данном примере скорость лодки относительно воды меньше, чем скорость воды в реке, `V < u`, поэтому реализовать план из предыдущего примера невозможно. Наша цель состоит в том, чтобы направить корпус лодки под таким углом `alpha` к нормали к берегу, чтобы сносимая течением лодка двигалась под углом `beta`, по возможности наименьшим.
В данном примере складывать скорости (лодки относительно воды `vec V` и воды в реке `vec u`) удобно по правилу треугольника, а не параллелограмма: приставим начало вектора `vec V` к концу вектора `vec u`. Выбирая оптимальный план (с наименьшим углом сноса), будем мысленно поворачивать вектор `vec V`. При этом конец вектора будет описывать окружность с центром в конце вектора `vec u`. Из рисунков видно, что минимальному углу сноса лодки `beta` соответствует случай, когда вектор `vec v = vec V + vec u` направлен по касательной к этой окружности. При этом вектор `vec V _|_ vec v` т. е. треугольник скоростей на рис. 36 в прямоугольный. Отсюда получаем:
`sin alpha = V//u = 3//5`; `alpha ~~37^@`; `beta = 90^@ – alpha ~~53^@`.
Лодку вытягивают из воды, стоя на крутом берегу и выбирая верёвку, которая привязана к носу лодки, со скоростью `v`.
Какой будет скорость лодки `u` в момент, когда верёвка будет составлять угол `alpha` с горизонтом? Верёвка нерастяжима.
Традиционная ошибка решающих эту задачу состоит в том, что пытаются разложить движение лодки на два направления – горизонтальное и вертикальное, делая (неправильное!) построение, как показано на рисунке
и получая неверный ответ `u = v * cos alpha`. Что здесь неправильно? В отличие от самолёта из примера 17, который двигался под отличным от нуля углом к горизонту, здесь лодка движется горизонтально! Сделаем другое разложение скорости лодки `vec u` по двум направлениям – вдоль верёвки (в данный момент времени!) и перпендикулярно ей.
Проекция вектора `vec u` на направление верёвки будет равна скорости `v`, с которой выбирают верёвку: `v = u cos alpha`, поэтому `u = v/(cos alpha)`.
Поясним ещё, почему проекция вектора `vec u` на направление верёвки будет равна скорости `v` с которой выбирают верёвку. Если мы имеем абсолютно твердое тело (АТТ), деформациями в котором можно пренебречь, или нерастяжимую нить (но уже максимально натянутую), то как бы ни двигались АТТ или нерастяжимая нить, они будут обладать следующим свойством. Возьмём две произвольные точки `A` и `B` нити или АТТ и мысленно соединим их прямой. Тогда составляющие скоростей выбранных точек вдоль этой прямой в любой момент времени будут равны друг другу: vA∥→=vB∥→\overrightarrow{v_{A\parallel}}=\overrightarrow{v_{B\parallel}}.
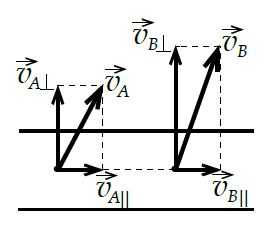
В противном случае изменялось бы расстояние между точками `A` и `B`. Составляющие скорости, перпендикулярные отрезку прямой `AB`, могут быть при этом любыми.
Две лодки 1 и 2 буксируют третью лодку с помощью двух тросов.
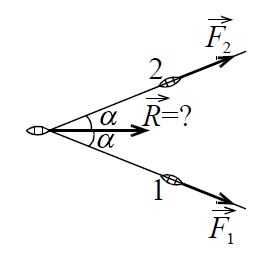
В некоторый момент времени силы натяжения тросов, идущих от лодок 1 и 2, равны друг другу по модулю и равны `F`. Угол между тросами равен `2 alpha`. Какая равнодействующая сила приложена к буксируемой лодке со стороны тянущих её лодок? Чему будет равна эта сила в случае малого угла `alpha` (когда буксирующие лодки тянут третью лодку почти в одном направлении)?
Две силы нужно сложить по правилу параллелограмма, который в данном случае будет ещё и ромбом с перпендикулярными друг другу диагоналями, разбивающими его на четыре равных прямоугольных треугольника. Из геометрии
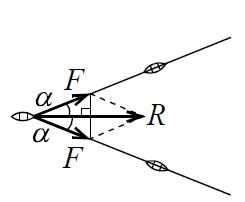
видно, что модуль равнодействующей силы `R` равен удвоенной длине прилежащего катета: `R = 2F cos alpha`. При стремлении угла между направлениями тросов к нулю `R -> 2F` (`cos alpha -> 1` при `alpha -> 0`).
Хитрее оказывается похожая задача, когда заданы не силы, а скорости.
Две лодки 1 и 2 буксируют третью лодку с помощью двух тросов.
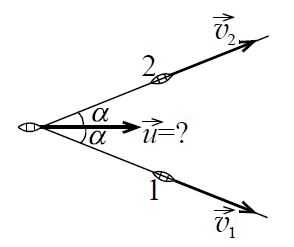
В некоторый момент времени модули скоростей лодок 1 и 2 равны друг другу и равны `v_1 = v_2 = v`. Найти модуль и направление скорости буксируемой лодки `u`. Тросы нерастяжимы. Чему будет равна эта скорость в случае малого угла `alpha` (когда буксирующие лодки тянут третью лодку почти в одном направлении)?
Ясно, что «решение» `u = 2v cos alpha` (как в предыдущем примере) не подходит, т. к. при `alpha -> 0` мы получили бы, что `u -> 2v`, чего не может быть. Если, например, две собаки в упряжке бегут с одинаковыми скоростями `v` в одном направлении, то и скорость упряжки будет равна этой же скорости `v` (если, конечно, упряжка не отцепилась или к ней не подключили дополнительно мотор).
Решение задачи такое же, как в примере 21. В данном примере важнейшими словами являются «Тросы нерастяжимы». Ясно, что правильное построение, учитывающее это условие, должно быть таким, как на рисунке ниже,
откуда немедленно получаем `v = u cos alpha`, поэтому `u = v/(cos alpha)`. Тогда в предельном случае, когда `alpha -> 0`, имеем `u -> v`, как и должно быть.
Заметим, что четырёхугольник весьма мало похож на параллелограмм из предыдущего примера. Еще меньше будет похож на параллелограмм этот четырёхугольник, когда модули скоростей `v_1 != v_2`.
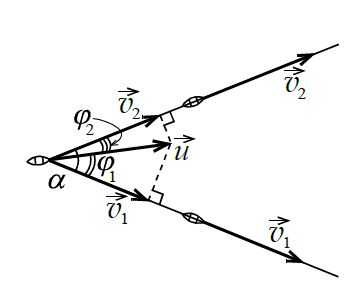
Две лодки буксируют третью с помощью двух тросов.
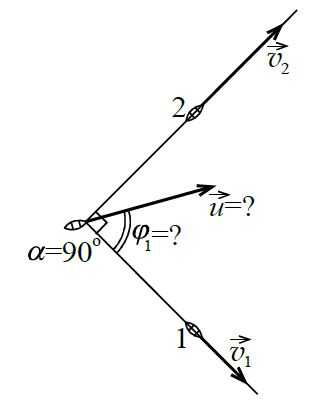
В некоторый момент времени скорость 2-ой лодки в 2 раза больше, чем скорость 1-ой, `v_2 = 2v_1 = 2v`, а угол между тросами равен `90^@`. В каком направлении и с какой скоростью движется в этот момент буксируемая лодка? Тросы нерастяжимы.
В данном случае четырёхугольник будет прямоугольником (т. е. всё же параллелограммом).
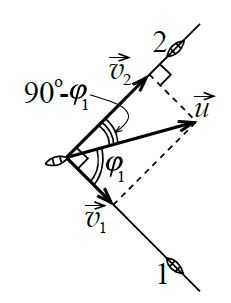
По определению тангенса угла tg`phi _1 = v_2 //v_1 = 2`, откуда, пользуясь калькулятором, находим `phi _1 ~~63^@`; `phi _2 = 90^@ – phi _1 ~~ 27^@`.
Модуль скорости буксируемой лодки найдём по теореме Пифагора (раз уж у нас «случайно» появились прямоугольные треугольники):
`u = sqrt(v_1^2 + v_2^2) = sqrt(v^2 + (2v)^2) = sqrt5 * v ~~ 2,2 v`.
phystech.academy
Секержицкий В.С. О векторных способах решения избранных задач кинематики
В ряде случаев векторный способ имеет преимущество перед координатным, не только упрощая решение конкретной задачи, но и превращая иногда сложные, на первый взгляд, задачи в подстановочные, решаемые практически устно. В данной статье мы рассмотрим возможность применения векторных способов к решению задач кинематики, большинство из которых предлагались в различные годы на олимпиадах школьников по физике.
1. Некоторые методы теоретической механики предполагают применение достаточно простого математического аппарата, вполне доступного студентам младших курсов вузов и учащимся старших классов (особенно с углубленным изучением физики). К таким методам относится, в частности, использование векторных способов решения задач кинематики. При изучении механики в школе предполагается знакомство с векторным способом кинематического описания движения (вводятся понятия векторов перемещения, скорости и ускорения), но значительно больше внимания уделяется координатному и естественному способам. Вместе с тем в ряде случаев векторный способ имеет преимущество перед координатным, не только упрощая решение конкретной задачи, но и превращая иногда сложные, на первый взгляд, задачи в подстановочные, решаемые практически устно.
В данной статье мы рассмотрим возможность применения векторных способов к решению задач кинематики, большинство из которых предлагались в различные годы на олимпиадах школьников по физике, т е считаются в школьном курсе физики задачами повышенной трудности.
2. При движении тела (материальной точки) его перемещение можно рассматривать как геометрическую сумму нескольких последовательных перемещений, например,
(1)
Соответствующий уравнению (1) многоугольник перемещений (треугольник в данном случае) представлен на рис. 1. Изменение скорости тела
(2)
Этому выражению соответствует треугольник скоростей (рис. 2).
При движении тела с постоянным по величине и направлению ускорением выражение для скорости в любой момент времени t имеет вид:
(3)
где при t = 0.
В общем случае направления векторов начальной скорости и ускорения могут не совпадать. Треугольник скоростей, соответствующий выражению (3), приведен на рис. 3.
Рис. 1.
Рис. 2.
Рис. 3.
Вектор перемещения при этом определяется следующим образом:
(4)
Треугольники перемещений представлены на рис. 4, а–в.
а
б
в
Рис. 4.
Наиболее эффективно применение векторного способа, основанного на построении треугольников скоростей и перемещений в тех случаях, когда известны направления векторов ускорения и одной из скоростей (например, начальной). Это относится, в частности, к задачам о движении тела под действием силы тяжести. Рассмотрим примеры.
Задача 1. Тело брошено вверх перпендикулярно плоскости, наклоненной под углом a к горизонту. На каком расстоянии от места броска тело упадет на эту наклонную плоскость? Сопротивлением движения пренебречь.
Решение. На рис. 5 изображен треугольник перемещений, соответствующий условию задачи и соотношению . Легко видеть, что , откуда время движения . Тогда искомое расстояние .
Рис. 5
Задача 2. На наклонную плоскость с углом a свободно падает мяч без начальной скорости. Пролетев расстояние h, он упруго отразился от плоскости. На каком расстоянии от места удара мяч упадет на плоскость вторично? Определите величину и направление его скорости в этот момент. Сопротивлением движению пренебречь.
Решение. При упругом ударе угол падения равен углу отражения, и скорость u0 отскока мяча равна конечной скорости его падения с высоты h: . Треугольник перемещений BCD (рис. 6), соответствующий соотношению , равнобедренный. Тогда и искомое расстояние
Соотношению соответствует треугольник перемещений BED (рис. 6), из которого по теореме синусов находим:
Величину скорости u можно определить по теореме косинусов из треугольника ECD:
Тогда
Итак, мяч вторично падает на наклонную плоскость со скоростью , вектор которой направлен к плоскости под углом .
Заметим, что основанные на принципе независимости движений координатные способы решения данных задач более трудоемкие, чем предложенные выше. Другие примеры решения задач кинематики с использованием треугольников перемещений и скоростей приведены в [1].
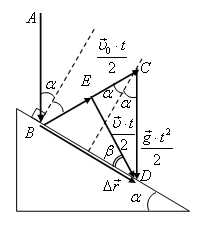
Рис. 6.
При движении двух материальных точек относительно некоторой систему отсчета, зная их перемещения , можно вычислить перемещение второго тела относительно первого:
(5)
Разность скоростей тел (относительная скорость) определяется выражением:
(6)
соответствующим закону сложения скоростей Галилея:
(7)
где – скорости первого и второго тел в неподвижной системе отсчета (естественно, «неподвижность» системы относительна), – скорость второго тела относительно первого. Треугольник и параллелограммы скоростей, соответствующие формулам (6) и (7), представлены на рис. 7, а-в.
а
б
в
Рис. 7.
Применим формулы (6) и (7) к решению задач
Задача 3. Две частицы брошены одновременно из одной точки с одинаковыми по модулю скоростями
Решение. Ускорения частиц одинаковы и равны g (движение под действием силы тяжести). Следовательно, относительное движение равномерное и прямолинейное, т.е. вторая частица движется относительно первой с постоянной скоростью (рис. 8). Тогда искомое расстояние .
Рис. 8.
Задача 4. Две частицы находятся на одной высоте на расстоянии l друг от друга. Им одновременно сообщили одинаковые по величине скорости, направления которых показаны на рис. 9. Найдите минимальное расстояние между частицами в процессе их движения. Частицы движутся в одной вертикальной плоскости, сопротивление отсутствует.
Рис. 9.
Решение. Свяжем систему отсчета с телом А. Тогда (рис 10)Ускорения обеих частиц одинаковы и равны g в системе отсчета, связанной с землей. Следовательно, относительная скорость постоянна по величине и направлению, траектория относительного движения – прямая. Искомое наименьшее расстояние между частицами (между точкой А и траекторией относительного движения на рис. 10) .
Рис. 10.
Задача 5. Собственная скорость пловца в п раз (n > 1) меньше скорости течения. Под каким углом к течению он должен стараться плыть, чтобы при переправе через реку снос был минимальным?
Решение. Воспользуемся формулой (7) и треугольником скоростей, представленным на рис 7, а. Здесь – скорость течения, – собственная скорость пловца (относительно воды), – скорость пловца относительно неподвижной системы отсчета (берега). Так как
Рис. 11.
Задача 6. Жесткий стержень АВ движется в плоскости рисунка 12, на котором показаны направления скоростей точек А и В. Найдите величину скорости uB, если uA = 5,0 м/с.
Рис. 12.
Решение. Так как расстояние между точками A и В неизменно (стержень жесткий), то скорость точки В относительно точки А может быть направлена только перпендикулярно стержню. Учитывая, что , строим параллелограмм скоростей (рис. 13), который в данное случае является прямоугольником. Тогда
Рис. 13.
Примеры решения аналогичных задач приведены в [2]. Очевидно, что применение векторных способов для решения ряда задач кинематики весьма эффективно, но в IX классе общеобразовательной школы для этого нет достаточной математической (тригонометрической) базы. В классах же с углубленным изучением физики, в курсах по выбору, при подготовке к олимпиадам изучение векторных способов решения задач вполне целесообразно. Опыт преподавания автором на протяжении нескольких лет факультативного спецкурса “Избранные задачи по физике и методы их решения” в лицее №1 г. Бреста показывает, что учащиеся XI класса достаточно легко воспринимают и усваивают векторные способы решения задач.
1. Койфман Ю.Г., Секержицкий В.С. Кинематика: о векторном cnocoбе решения избранных задач // Фокус. – 1993. – №4. – С. 61-68.
2. Секержицкий В.С. Кинематика: относительность движения // Фокус. – 1995. – №2. – С. 77-80.
www.alsak.ru
Урок по физике и математике «Векторы»
Интегрированный урок по физике и математике «Векторы».9 класс
Повторение и закрепление основных понятий в математике и физике,
связанных с векторами.
Повторить и закрепить основные понятия, связанные с векторами, закрепить умение решать задачи, применяя теоретический материал геометрии и физики. Применение темы «Векторы» при решении задач практического содержания.
Цель урока:
Обобщение знаний теоретического материала по теме «Векторы»;
Использование метапредметных способностей обучающихся для освоения новых знаний и применение УУД;
Использование математических знаний для изучения многообразных явлений и процессов физики;
Создание ситуации применения знаний, полученных на уроках математики и физики, на практике;
Активизация познавательной деятельности.
Задачи урока:
Сформировать у обучающихся осознанное понятие вектора;
Сформировать у обучающихся устойчивый навык решения геометрических и физических задач;
Развивать у учащихся умение пользоваться опорными знаниями в нестандартной ситуации;
Развивать навыки самостоятельной работы.
Ученик должен знать:
определение вектора и связанных с ним понятий,
находить сумму, разность и скалярное произведение двух векторов,
вычислять значение угла между векторами.
Ученик должен уметь:
применять теоретические знания при решении геометрических и физических задач.
Тип урока:
Комбинированный урок повторения изученного материала.
Технология:
Личностно-ориентированная, информационно-коммуникативная.
КЭС: векторы, сумма, разность, умножение вектора на число, координаты вектора, скалярное произведение двух векторов, вычисление значений угла между векторами, радиус-вектор, практическая значимость понятия «вектор».
Структура урока:
Организационный момент.
Повторение.
Обобщение и систематизация.
Практические задания на слайдах и тест.
Самостоятельная работа (выполнение теста).
Рефлексия.
Домашнее задание.
Сценарий урока:
1. Подготовка к восприятию материала:
Вступительное слово учителя математики:
«…нет ни одной области в математике, которая когда-либо не окажется применимой к явлениям действительного мира…» Н.И.Лобачевский
-Мы изучаем векторы. А где это применяется?
Векторная история это пограничная история, между математикой и физикой. Геометрический подход к физическим задачам наследуется еще от древних греков. Смещение от числовых, или скалярных, координат из аналитической геометрии к житейскому понятию «направление», смешанному с иллюстративно-художественным подходом, постепенно трансформировало образы мышления физиков.
Прежде, чем говорить об использовании векторов при решении физических задач, вспомним действия, которые можно выполнять с векторами.
(Задавая вопросы, учитель может использовать игровой компонент: бросая мячик, формулировать вопрос, принимая его, получать ответ).
– Какие способы сложения векторов вам известны? (Правило треугольника и правило параллелограмма)
– В чем принципиальное отличие этих правил? ( При сложении по правилу треугольника начало второго вектора совмещается с концом первого (слайд 2), а при сложении по правилу параллелограмма начала обоих векторов совпадают (слайд 3).)
– Что будет вектором суммы при сложении векторов по правилу треугольника? (Вектор, берущий начало в начале первого и заканчивающийся в конце второго вектора.)
– Что будет вектором суммы при сложении векторов по правилу параллелограмма? (Вектор, являющийся диагональю параллелограмма, построенного на исходных векторах, исходящий из общего начала слагаемых векторов.)
– Что будет вектором разности двух векторов? (Вектор, соединяющий концы векторов и идущий в направлении уменьшаемого (слайд 4)).
– А если нужно выполнить действие с векторами, которые не выходят из одной точки? (Один из векторов параллельным переносом перенести так, чтобы начала их совпали.)
– Что происходит при умножении вектора на положительное число? (Длина вектора изменяется во столько раз, на какое число выполняется умножение, а направление не изменяется).
– А если выполняем умножение на отрицательное число? (Направление меняется на противоположное (слайд 5)).
– Как называются получившиеся векторы? (Коллинеарные (сонаправленные и противоположно направленные)).
Задача 1.
Построить вектор , равный сумме трех заданных векторов (слайд 6).
Решение (слайд 7):
Задача 2.
Построить вектор . (слайд 8).
Решение (слайд 9).
Задача 3 (слайд 10).
Решение (слайд 11).
Задача 4 (слайд 12).
Решение (слайд 13).
– Как найти координаты вектора, зная координаты его начала и его конца (слайд 14)? (Чтобы найти координаты вектора, нужно из координат конца вычесть соответствующие координаты начала вектора (слайд 15)).
– Как найти длину вектора, зная координаты его начала и его конца (слайд 16)? ( Длина вектора равна корню из суммы квадратов разностей соответствующих координат начала и конца вектора) .
Задача 5(слайд 17).
Решение (слайд 18).
– Как найти координаты суммы двух векторов? (Найти сумму соответствующих координат (слайд 19)).
– Как найти координаты разности двух векторов? (Найти разность соответствующих координат (слайд 20)).
– Что называют «скаляром»? (Скаляр – это физический термин, обозначающий число).
-Почему умножение векторов называется скалярным? (Потому что в результате умножения двух векторов получается число).
– А что получается при умножении вектора на число (скаляр)? (Вектор).
– Как найти в этой ситуации координаты нового вектора? (Координаты исходного вектора умножить на скаляр (слайд 21)).
– Модуль вектора – это скаляр или вектор? (Скаляр, так как модуль – это длина вектора).
– Чему равен модуль вектора? (Корню из квадрата этого вектора (слайд 22)).
– Как найти модуль вектора, если нам известны его координаты? (Извлечь корень из суммы квадратов координат этого вектора (слайд 23)).
– Как найти скалярное произведение векторов, зная их координаты? (Сложить произведения соответствующих координат этих векторов (слайд 24)).
– Как найти скалярное произведение векторов другим способом? (Умножить произведение длин этих векторов на косинус угла между ними (слайд 25)).
В физике дается определение радиус-вектора.
Радиус-вектор – это направленный отрезок, проведенный из начала координат в данную точку пространства.
Если противоречие между двумя определениями, сформулированными в математике и физике? (В любом случае, сделать акцент на идею направления в обоих определениях)
Многие физические величины характеризуются подобно радиус-вектору не только числовым значением, но и направлением. Например: скорость, перемещение, импульс, напряженность электрического поля, сила и др. Эти физические величины называют векторными. Длину такого вектора называют модулем вектора.
Законы сложения и вычитания векторов мы будем использовать с вами на уроках физики неоднократно, изучая разные темы. Сейчас мы рассматриваем задачи по теме «Относительность механического движения, законы сложения скоростей и перемещений». Данные задачи обязательно встретятся вам на ГИА в этом году и при сдаче ЕГЭ по физике в 11 классе.
Рассмотрим сегодня на уроке задачи практического содержания по этой теме.
Задача 1.
Парашютист опускается вертикально вниз со скоростью 4 м/с в безветренную погоду. С какой скоростью он будет двигаться при горизонтальном ветре, скорость которого относительно Земли 3 м/с. На какое расстояние отнесет его от места падения, если он спускается с высоты 2км?
Работа над задачей.
Запишем закон сложения скоростей в векторном виде.
Сделаем чертеж, произведя сложение векторов скоростей.
Искомый вектор является гипотенузой прямоугольного треугольника. По теореме Пифагора вычислим её, найдя тем самым модуль скорости.
Зная, что при прямолинейном равномерном движении модуль перемещения пропорционален скорости, составим пропорцию и найдем модуль искомого перемещения. (Слайды 26 – 29).
Задача 2.
Штурман пытается провести судно в тумане через узкий проход между рифами. Представьте себе, что проход между рифами идет в северном направлении, Скорость океанского течения равна 5м/с, направлено оно на восток, а скорость, сообщаемая винтом судну 9 м/с. Выполните построение и покажите в каком направлении штурман должен вести судно по компасу.
Идет аналогичная работа над задачей.
(Слайды 30 – 32)
Задача 3.
Скорость лодки 4 м/с, скорость течения 2 м/с. Под каким углом к береговой линии должен лодочник вести лодку, чтобы попасть на противоположный берег строго против того места, от которого он отплыл? Сделайте чертеж.
(Слайды 33 – 35)
В конце урока предлагается тест по материалам урока. Вопросы теста по карточкам, которые выдают каждому обучающемуся.
Тест на тему «Векторы» ученика 9 класса гимназии №1799 «Экополис» _______________________________________________.
Начертите два неколлинеарных вектора. Найдите сумму векторов двумя способами.
M,H,P,O,S-произвольные точки. Найдите сумму ++++.
3. Лодка должна попасть на противоположный берег реки кратчайшим путем в системе отсчета, связанной с берегом. Скорость течения реки, а скорость лодки относительно воды . Модуль скорости лодки относительно берега должен быть равен
1) 2) 3) 4)
Ответ: 4
4. Два автомобиля движутся по прямой дороге: один – со скоростью (–10 м/с), другой – со скоростью (–25 м/с). Скорость второго автомобиля относительно первого равна
1) –35 м/с 2) –15 м/с 3) –20 м/с 4) 35 м/с
Ответ: 2
5. Пилот поднялся на воздушном шаре на высоту 800м, за это время шар был отнесен ветром в горизонтальном направлении на 600м. Найдите перемещение шара относительно земли?
1) 1400м 2)200м 3)1000м 4) 800м
Ответ: 3
Заключительная часть урока.
Подводится итог. Выставляются оценки за урок. Идет обобщение материала.
Домашнее задание.
1. Лодка с туристами потерпела крушение в 40 м от берега, налетев на пороги. Туристы поплыли к берегу со скоростью 2 м/с, относительно воды перпендикулярно линии берега, но быстрое течение со скоростью 10 м/с сносило их в сторону. С какой реальной скоростью относительно берега двигались туристы? На какое расстояние их снесло, когда они выплыли на берег? Сделайте чертежи.
2. Вертолет летел на юг со скоростью 20 м/с. С какой скоростью и под каким углом к меридиану будет лететь вертолет, если подует восточный ветер со скоростью 10 м/с?
3. Задачник Степановой Г.Н. №№ 61, 60,59.
Интегрированные уроки имеют огромное значение для создания предметных, метапредметных и личностных компетенции обучающихся, являются мощным мотивом к интеллектуальному труду, способствуют более глубокому усвоению материала, расширению границ изученного материала, развитию творческих способностей учащихся, которые развиваются в рамках двух дисциплин, умению логично, научно и доступно излагать свои мысли, математически грамотно говорить.
Литература:
Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Поздняк Л.В., Юдина И.И. Геометрия 7-9 кл. Просвещение,2006
Зив Б. Г., Мейлер В. М. Геометрия. Дидактические материалы для 8 класса. Просвещение,2006
Задачник Степановой Г.Н.для 7-9 классов
А.В. Пёрышкин, Е.М. Путник Физика -9 .Просвещение,2006
fiz.na5bal.ru
При решении задач по физике
Геометрический подход к физическим задачам наследуется еще от древних греков. Смещение от числовых, или скалярных, координат из аналитической геометрии к житейскому понятию направление, смешанному с иллюстративно-художественным подходом, постепенно трансформировало образы мышления физиков.
На уроках физики учитель дает определение радиус-вектора при изучении механических явлений. Радиус-вектор – это направленный отрезок, проведенный из начала координат в данную точку пространства. Многие физические величины характеризуются подобно радиус-вектору не только числовым значением, но и направлением. Например, скорость, перемещение, импульс, напряженность электрического поля, сила. Эти физические величины называют векторными. Длину такого вектора называют модулем вектора. Законы сложения и вычитания векторов также используют на уроках физики неоднократно, изучая разные темы в разных классах. Интуитивное понимание вектора у учащихся складывается с первых же уроков физики в 7 …
и 8 классе.
Проведем сравнение понятия вектора в физике и математике:
| в физике | в математике |
| Изучаем векторные величины (F, v, S ) | Изучаем векторы (a, b, c ) |
| Вектор имеет точку приложения (на теле) | Вектор можно отложить от любой точки плоскости |
| Правила сложения векторов | |
| Чаще применяем правило параллелограмма | Правило треугольника и правило параллелограмма |
| Длину вектора называем длиной | Длину вектора называем модулем |
Понимание вектора в физике и математике происходит поэтапно, когда ученики раскрывают и изучают следующие вопросы:
В математике:
· Координатная прямая.
· Координатная плоскость.
· Координаты точки.
В физике:
· Понятие системы отсчета.
· Координаты, которыми задается положение тела на прямой, на плоскости, в пространстве, и их количество.
Понятие вектор и нулевой вектор, в каком случае проекция вектора на ось считается положительной, отрицательной, равной нулю, — рассматривается как в математике, так и в физике.
Координаты вектора в физике рассматриваем относительно перемещения тела.
Интеграцию обоих предметов необходимо осуществлять при изучении сложения векторов. В математике это правило треугольника, параллелограмма, многоугольника, произведение векторов. В физике прикладной характер правил сложения векторов виден не при определении перемещения тела, а при сложении скоростей движущегося тела, при вычислении механической работы.
| В математике: | В физике: | |
| Координатная прямая. Координатная плоскость. Координаты точки. | Понятие системы отсчета. Координаты, которыми задается положение тела на прямой, на плоскости, в пространстве, и их количество. | |
| Вектор — направленный отрезок. | Вектор – как графическое представление перемещения тела. При прямолинейном движении в одном направлении путь и перемещение совпадают. | |
| Точка — это вектор нулевой длины или нулевой вектор. | Если начальное и конечное положение тела совпадают, то вектор перемещения равен нулю. При этом путь может иметь значение отличное от нуля. Например, когда тело движется по окружности. | |
| В каком случае проекция вектора на ось считается положительной, отрицательной, равной нулю? (Если от проекции начала вектора к проекции его конца надо двигаться по направлению оси, то проекция вектора на ось считают положительной. Если от проекции начала вектора к проекции его конца надо двигаться в направлении, противоположном направлению оси, то проекция отрицательная. Если вектор перпендикулярен оси координат, то проекция равна нулю). | ||
| Чтобы найти координаты вектора, необходимо из координат конца вектора вычесть координаты начала. x=x2-x1 , y=y2-y1 . | Вспомните, как связаны проекция вектора перемещения и координаты тела. (sx= х — х0, sy= y — y0) Вспомним формулы для расчета координат тела в любой момент времени (х = х0 + sx, y = y0+ sy). | |
| Операции сложения векторов. | ||
| Правило треугольника. Правило параллелограмма. Правило многоугольника. | При движении тела (материальной точки) его перемещение можно рассматривать как геометрическую сумму нескольких последовательных перемещений, например, . Соответствующий многоугольник (треугольник) перемещений выглядит таким образом: Если тело движется с постоянным по величине и направлению ускорением , то выражение для скорости в любой момент t времени имеет вид: . Прикладной характер правил сложения векторов виден не только при определении перемещения тела, но и при сложении скоростей движущегося тела. | |
| Произведение векторов изучают в 9 классе: Произведение векторов – скалярная величина. | Вычисление механической работы (в 10 классе): Механическая работа – скалярная величина. | |
Глубокое понимание вектора и действий с векторами у учеников сложится только посредством интеграции математического и физического определения этих понятий.
Рассмотрим пример задачи, при решении которой применяется теорема Пифагора.
Задача индийского математика XII века Бхаскары.
На берегу реки рос тополь одинокий.
Вдруг ветра порыв его ствол надломал.
Бедный тополь упал. И угол прямой
С теченьем реки его ствол составлял.
Запомни теперь, что в этом месте река
В четыре лишь фута была широка
Верхушка склонилась у края реки.
Осталось три фута всего от ствола,
Прошу тебя, скоро теперь мне скажи:
У тополя как велика высота?
Решение: По теореме Пифагора . Высота тополя равна м.
На уроках физики ученики сталкиваются с теоремой Пифагора чаще всего при изучении механических и оптических явлений.
В приложении к данному выступлению можно ознакомиться с подборкой задач на применение векторного анализа и правила треугольника (Приложение 3).
refac.ru
Векторы. Действия с векторами. Повторение к урокам физики в 9, 10 классе.

К уроку физики в 9,10 классе:
Повторение темы «Векторы. Действия с векторами»
Автор: Проценко Ольга Владимировна
учитель физики высшей категории
МОУ сош №3 г. Красный Кут
Саратовской области

Вектор.
Действия с векторами
Вектор – отрезок прямой линии, имеющий направление.
Обозначается стрелкой .
Величины, которые кроме числового значения имеют
еще и направление в пространстве, называются векторными
Пример: Скорость, сила, перемещение и т. Д.
Величины не имеющие направления называются скалярными.
Пример: время, масса, объем, путь и т. Д.
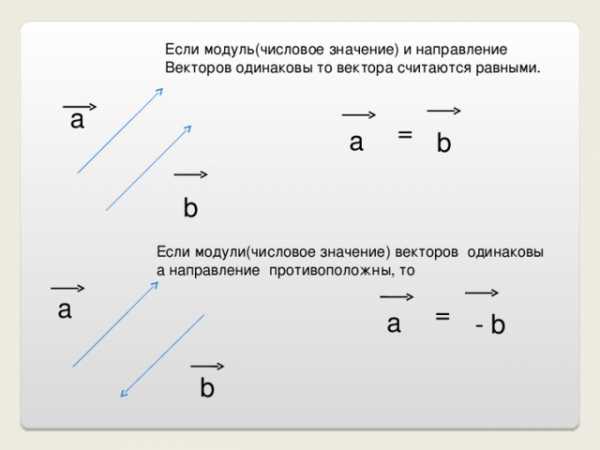
Если модуль(числовое значение) и направление
Векторов одинаковы то вектора считаются равными.
а
=
а
b
b
Если модули(числовое значение) векторов одинаковы
а направление противоположны, то
а
=
а
– b
b
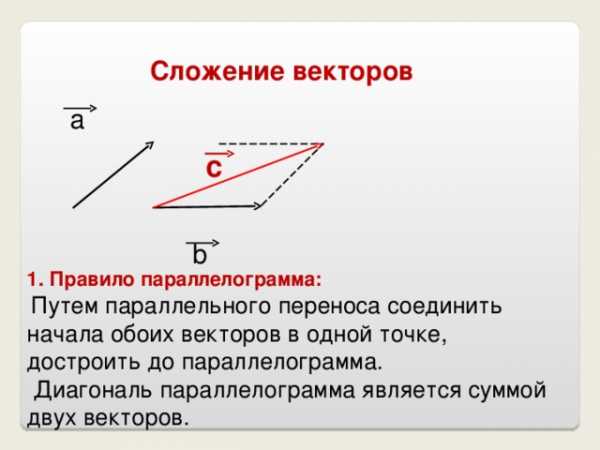
Сложение векторов
а
с
b
1. Правило параллелограмма:
Путем параллельного переноса соединить начала обоих векторов в одной точке, достроить до параллелограмма.
Диагональ параллелограмма является суммой двух векторов.
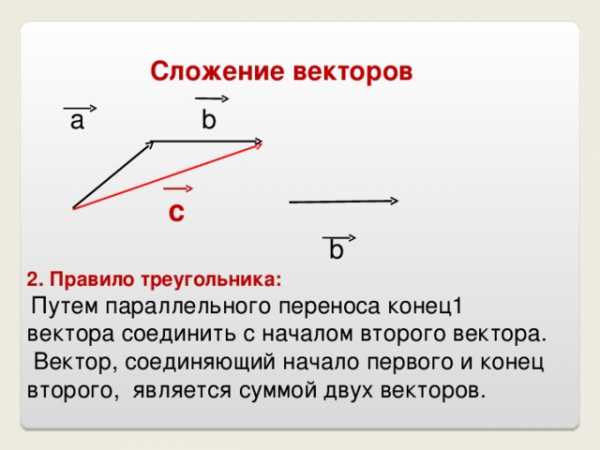
Сложение векторов
b
а
с
b
2. Правило треугольника:
Путем параллельного переноса конец1 вектора соединить с началом второго вектора.
Вектор, соединяющий начало первого и конец второго, является суммой двух векторов.
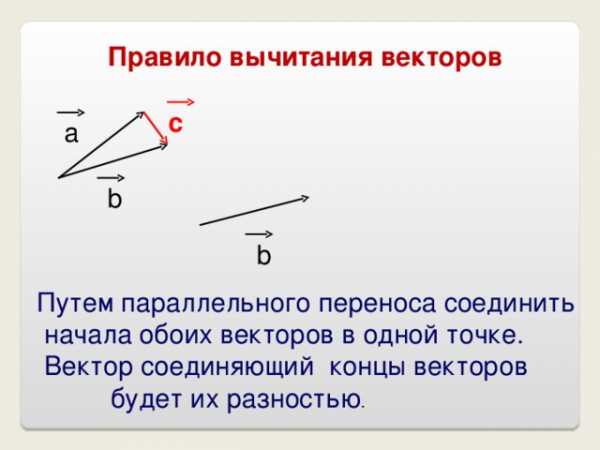
Правило вычитания векторов
с
а
b
b
Путем параллельного переноса соединить
начала обоих векторов в одной точке.
Вектор соединяющий концы векторов
будет их разностью .

Проекция вектора на координатной оси
- это линия на оси, полученная путем
опускания перпендикуляров на ось из
начала и конца вектора.
у
А
а х =0
а
Если вектор перпендикулярен оси
то его проекция на эту ось равна нулю.
В
х
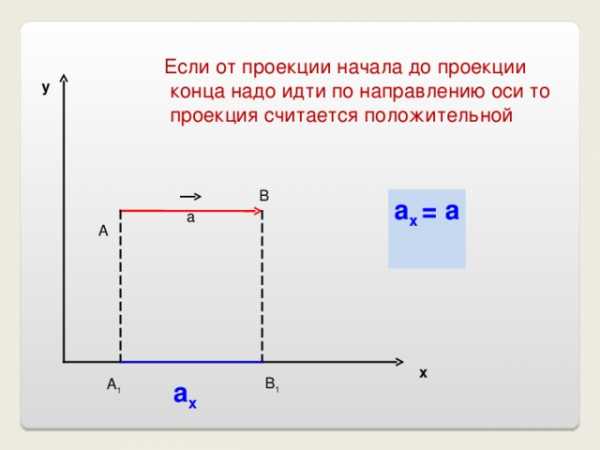
Если от проекции начала до проекции
конца надо идти по направлению оси то
проекция считается положительной
у
В
а х = а
а
А
х
В 1
А 1
а х
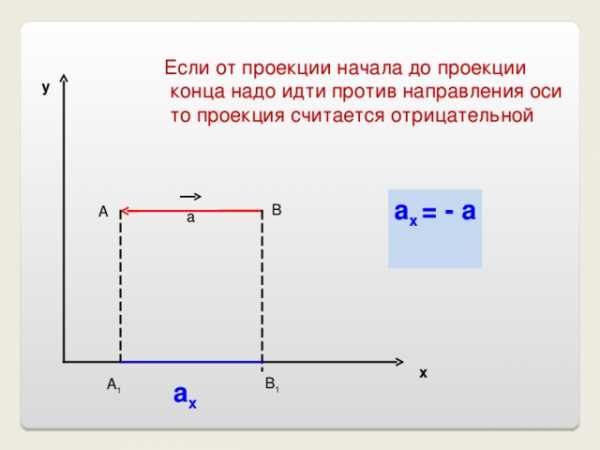
Если от проекции начала до проекции
конца надо идти против направления оси
то проекция считается отрицательной
у
а х = – а
В
А
а
х
В 1
А 1
а х
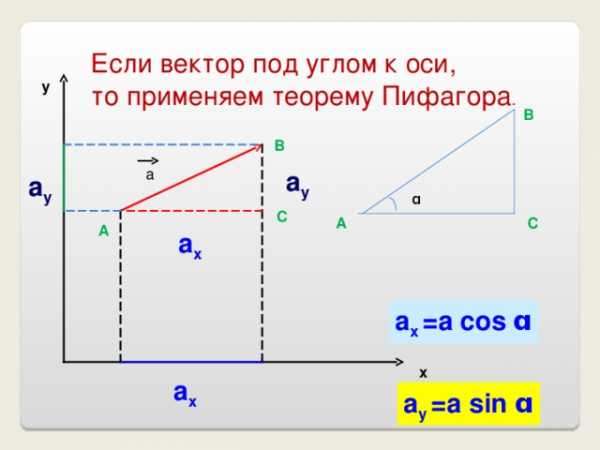
Если вектор под углом к оси,
то применяем теорему Пифагора .
у
В
В
а
а у
а у
ɑ
С
А
С
А
а х
а х =а cos ɑ
х
а х
а у =а sin ɑ

В начальный момент времени тело находилось в точке с
Координатами х 0 = – 2 м и у 0 = 4м, потом переместилось в точку с
координатами х 1 = 2 м и у 1 = 1 м. Найдите проекции вектора перемещения
на оси х и у. Начертите вектор перемещения и определите его модуль.
у
А
СВ = 4 м
АС = 3 м
АВ 2 = СВ 2 + АС 2
АВ = 5 м
4
3
2
1
В
С
х
1
2
3
-1
-2
kopilkaurokov.ru
Как решать задачи по физике на свободное падение. Примеры решения задач по физике. 9-10 класс
Как решать задачи по физике на свободное падение. Примеры решения задач по физике. 9-10 класс
Задачи по физике – это просто!
Не забываем, что решать задачи надо всегда в системе СИ!
А теперь к задачам!
Элементарные задачи из курса школьной физики по кинематике.
Школьные задачи по физике на свободное падение подразделяются на:
1. падение тела вниз при начальной скорости, равной нулю (9 кл., 10 кл.)
2. движение тела, брошенного вертикально вверх (9 кл., 10 кл.)
3. движение тела, брошенного под любым углом к горизонту, включая бросок в горизонтальном направлении (10 кл.)
Свободное падение – это движение тела только лишь под действием силы тяжести.
И хотя в реальных земных условиях действует еще сила сопротивления воздуха, но в школьных задачах она не учитывается!
В задачах на свободное падение тело движется с ускорением свободного падения g , вектор которого направлен всегда также, как вектор силы тяжести Fт.
Движение под действием постоянной силы – это равноускоренное движение, поэтому исходными формулами для решения являются 3 основные расчетные формулы равноускоренного движения: для расчета скорости, перемещения и координаты тела.
В 9 классе используются обычно расчетные формулы скорости и перемещения:
В 10 классе к ним добавляется расчетная формула координаты тела:
Эти формулы надо запомнить!
Вместе эти формулы составляют систему уравнений, достаточную для решения задачи любой сложности.
Если начальная скорость в задаче равна нулю, то формулы упрощаются.
Например:
Но нет нужды запоминать упрощенные формулы, достаточно помнить 3 основные!
Помните, при решении задач используют расчетные формулы в проекциях векторов!
Обратите внимание, что в этих формулах нет «минусов»!
Минус может появиться при расчете, когда при подстановке числовых значений придется учитывать знак проекции вектора на ось!
Для решения простой задачи выбираем нужную формулу.
Потренируйтесь в преобразовании формулы, если надо найти величину, в нее входящую!
В более сложных задачах решаем систему из двух уравнений.
Обычно это выглядит, как решение задачи по действиям с использованием двух (трех) формул.
Иногда встречаются трудные задачи, когда решение по действиям не удается, тогда решаем систему из двух (или трех) уравнений, используя все свои накопленные знания по алгебре (решение систем уравнений).
В решении необходимо сделать чертежи:
1. для падения вниз
2. при броске вертикально вверх
3. при броске под углом
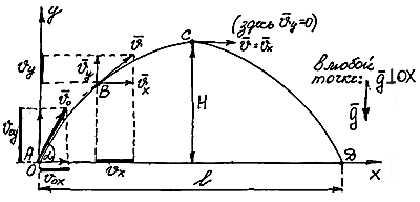
4. при броске в горизонтальном направлении
class-fizika.ru



