Закон ома сопротивление – Закон Ома — Википедия
Закон Ома
9.2Электрическое сопротивление
А сейчас давайте подумаем вот о чём. Пусть к концам проводника приложено постоянное напряжение U. Тогда на свободные заряды проводника действует сила со стороны стационарного электрического поля. Раз есть сила значит, эти заряды должны двигаться с ускорением; скорость их направленного движения будет увеличиваться, а вместе с ней будет возрастать и сила тока. Но закон Ома гласит, что сила тока будет постоянной. Как же так?
Дело в том, что сила со стороны стационарного поля не единственная сила, действующая на свободные заряды проводника.
Например, свободные электроны металла, совершая направленное движение, сталкиваются с ионами кристаллической решётки. Возникает своего рода сила сопротивления, действующая со стороны проводника на свободные заряды. Эта сила уравновешивает электрическую силу, с которой на свободные заряды действует стационарное поле. В результате скорость направленного движения заряженных частиц не меняется по модулю15; вместе с ней остаётся постоянной и сила тока.
Так что величина R названа сопротивлением не случайно. Она и в самом деле показывает, в какой степени проводник ¾сопротивляется¿ прохождению тока.
9.3Удельное сопротивление
Возьмём два проводника из одинакового материала с равными поперечными сечениями; пусть отличаются только их длины. Ясно, что сопротивление будет больше у того проводника, у которого больше длина. В самом деле, при большей длине проводника свободным зарядам труднее пройти сквозь него: каждый свободный электрон встретит на своём пути больше ионов кристаллической решётки. Аналогия такая: чем длиннее заполненная машинами улица, тем труднее будет через неё проехать.
Пусть теперь проводники отличаются только площадью поперечного сечения. Ясно, что чем больше площадь, тем меньше сопротивление проводника. Снова аналогия: чем шире шоссе, тем больше его пропускная способность, т. е. тем меньше его ¾сопротивление¿ движению машин.
Опыт подтверждает эти соображения и показывает, что сопротивление проводника прямо пропорционально его длине l и обратно пропорционально площади поперечного сечения S:
Коэффициент пропорциональности уже не зависит от геометрии проводника; он является характеристикой вещества проводника и называется удельным сопротивлением данного вещества. Величины удельных сопротивлений различных веществ можно найти в соответствующей таблице.
В каких единицах измеряется удельное сопротивление? Давайте выразим его из форму-
лы (47):
= RSl :
Получим:
[ ] = Ом м2 = Ом м:
м
Однако такая ¾теоретическая¿ единица измерения не всегда удобна. Она вынуждает при расчётах переводить площадь поперечного сечения в квадратные метры, тогда как на практике
15Точнее говоря, свободные электроны всё же двигаются равноускоренно, но только в промежутках между соударениями с ионами кристаллической решётки. В среднем же оказывается, что электроны перемещаются с постоянной скоростью.
studfiles.net
формула удельного сопротивления и закон Ома
Закон Ома является основным законом электрических цепей. При этом он позволяет объяснять многие явления природы. Например, можно понять, почему электричество не “бьет” птиц, которые сидят на проводах. Для физики закон Ома является крайне значимым. Без его знания невозможно было бы создавать стабильно работающие электрические цепи или вовсе не было бы электроники.
Зависимость I = I(U) и ее значение
История открытия сопротивления материалов напрямую связана с вольт-амперной характеристикой. Что это такое? Возьмем цепь с постоянным электрическим током и рассмотрим любой ее элемент: лампу, газовую трубку, металлический проводник, колбу электролита и т. д.
Меняя напряжение U (часто обозначается как V), подаваемое на рассматриваемый элемент, будем отслеживать изменение силы тока (I), проходящего через него. Как итог, мы получим зависимость вида I = I (U), которая носит название “вольт-амперная характеристика элемента” и является прямым показателем его электрических свойств.
Вольт-амперная характеристика может выглядеть по-разному для различных элементов. Самый простой ее вид получается при рассмотрении металлического проводника, что и сделал Георг Ом(1789 – 1854).
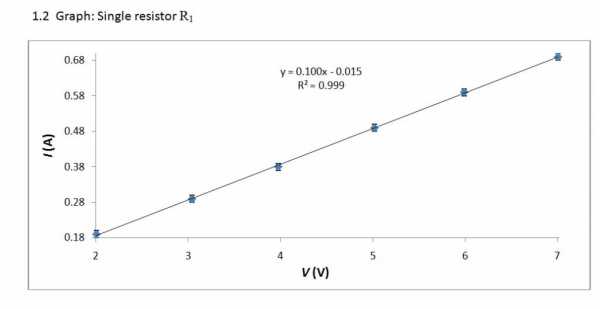
Вольт-амперная характеристика – это линейная зависимость. Поэтому ее графиком служит прямая линия.
Закон в простой форме
Исследования Ома по изучению вольт-амперных характеристик проводников показали, что сила тока внутри металлического проводника пропорциональна разности потенциалов на его концах (I ~ U) и обратно пропорциональна некоему коэффициенту, то есть I ~ 1/R. Этот коэффициент стал называться “сопротивление проводника”, а единица измерения электрического сопротивления – Ом или В/А.
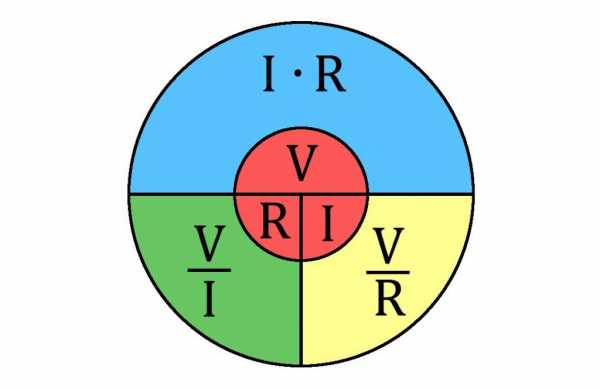
Стоит отметить еще вот что. Закон Ома часто используется для расчета сопротивления в цепях.
Формулировка закона
Закон Ома говорит, что сила тока (I) отдельно взятого участка цепи пропорциональна напряжению на этом участке и обратно пропорциональна его сопротивлению.
Следует заметить, что в таком виде закон остается верным только для однородного участка цепи. Однородной называется та часть электрической цепи, которая не содержит источника тока. Как пользоваться законом Ома в неоднородной цепи, будет рассмотрено ниже.
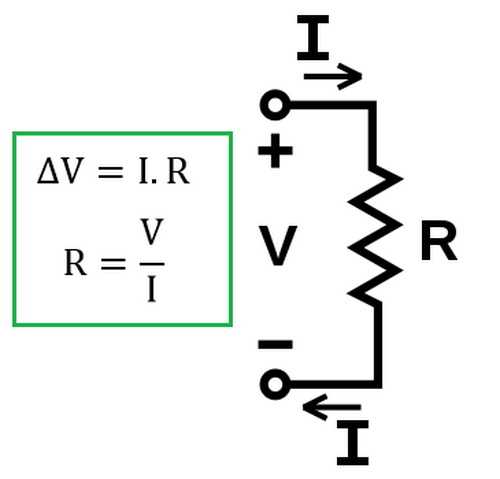
Позже опытным путем было установлено, что закон остается справедливым и для растворов электролитов в электрической цепи.
Физический смысл сопротивления
Сопротивление – это свойство материалов, веществ или сред препятствовать прохождению электрического тока. Количественно сопротивление в 1 Ом означает, что в проводнике при напряжении 1 В на его концах способен проходить электрический ток силой 1 А.
Удельное электрическое сопротивление
Экспериментальным методом было установлено, что сопротивление электрического тока проводника зависит от его размеров: длина, ширина, высота. А также от его формы (сфера, цилиндр) и материала, из которого он сделан. Таким образом, формула удельного сопротивления, например, однородного цилиндрического проводника будет: R = р*l/S.
Если в этой формуле положить s = 1 м2 и l = 1 м, то R численно будет равен р. Отсюда вычисляется единица измерения для коэффициента удельного сопротивления проводника в СИ – это Ом*м.

В формуле удельного сопротивления р – это коэффициент сопротивления, определяемый химическими свойствами материала, из которого изготовлен проводник.
Для рассмотрения дифференциальной формы закона Ома, необходимо рассмотреть еще несколько понятий.
Плотность тока
Как известно, электрический ток – это строго упорядоченное движение любых заряженных частиц. Например, в металлах носителями тока выступают электроны, а в проводящих газах – ионы.
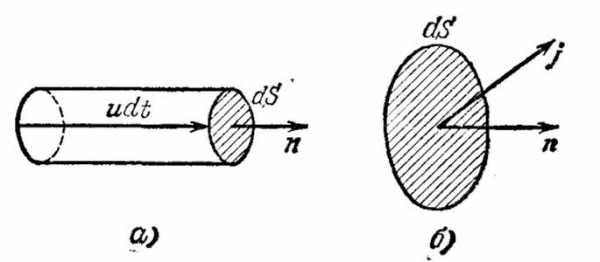
Возьмем тривиальный случай, когда все носители тока однородны – металлический проводник. Мысленно выделим в этом проводнике бесконечно малый объем и обозначим через u среднюю (дрейфовую, упорядоченную) скорость электронов во взятом объеме. Далее пусть n обозначает концентрацию носителей тока в единице объема.
Теперь проведем бесконечно малую площадь dS перпендикулярно вектору u и построим вдоль скорости бесконечно малый цилиндр с высотой u*dt, где dt – обозначает время, за которое все носители скорости тока, содержавшиеся в рассматриваемом объеме, пройдут сквозь площадку dS.
При этом электронами сквозь площадку будет перенесен заряд, равный q = n*e*u*dS*dt, где e – заряд электрона. Таким образом, плотность электрического тока – это вектор j = n*e*u, обозначающий количество заряда, переносимого в единицу времени через единицу площади.
Один из плюсов дифференциального определения закона Ома заключается в том, что часто можно обойтись без расчета сопротивления.
Электрический заряд. Напряженность электрического поля
Напряженность поля наряду с электрическим зарядом является фундаментальным параметром в теории электричества. При этом количественное представление о них можно получить из простых опытов, доступных школьникам.
Для простоты рассуждений будем рассматривать электростатическое поле. Это электрическое поле, которое не изменяется со временем. Такое поле может быть создано неподвижными электрическими зарядами.
Также для наших целей необходим пробный заряд. В его качестве будем использовать заряженное тело – настолько малое, что оно не способно вызывать какие-либо возмущения (перераспределение зарядов) в окружающих объектах.
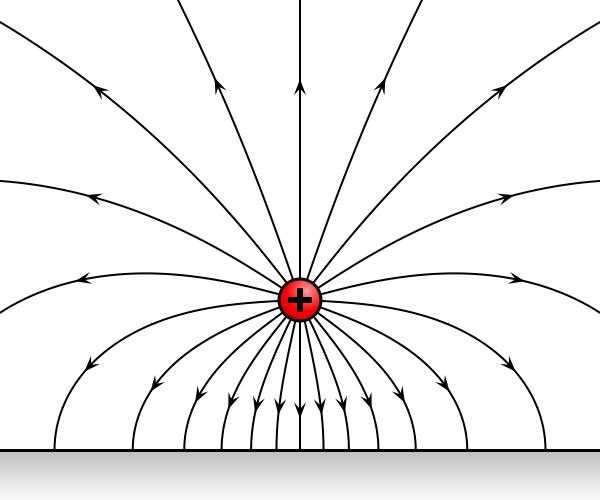
Рассмотрим поочередно два взятых пробных заряда, последовательно помещенных в одну точку пространства, находящуюся под воздействием электростатического поля. Получается, что заряды будут подвергаться неизменному во времени воздействию с его стороны. Пусть F1 и F2 – это силы, воздействующие на заряды.
В результате обобщения опытных данных было установлено, что силы F1 и F2 направлены либо в одну, либо в противоположные стороны, а их отношение F1/F2 является независимым от точки пространства, куда были поочередно помещены пробные заряды. Следовательно, отношение F1/F2 является характеристикой исключительно самих зарядов, и никак не зависит от поля.
Открытие данного факта позволило охарактеризовать электризацию тел и в дальнейшем было названо электрическим зарядом. Таким образом, по определению получается q1/q2 = F1/F2, где q1 и q2 – величина зарядов, помещаемых в одну точку поля, а F1 и F2 – силы, действующие на заряды со стороны поля.
Из подобных соображений были экспериментально установлены величины зарядов различных частиц. Условно положив в соотношение один из пробных зарядов равным единице, можно вычислить величину другого заряда, измерив соотношение F1/F2.
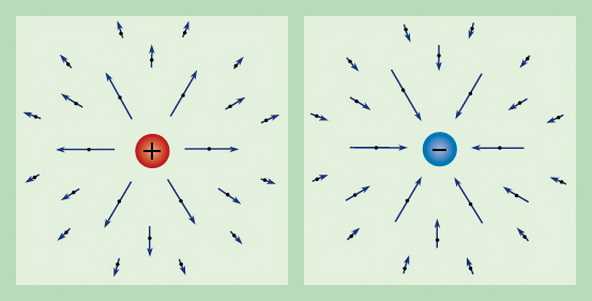
Через известный заряд можно охарактеризовать любое электрическое поле. Таким образом, сила, действующая на единичный пробный заряд, находящийся в состоянии покоя, называется напряженностью электрического поля и обозначается E. Из определения заряда получаем, что вектор напряженности имеет следующий вид: E = F/q.
Связь векторов j и E. Другая форма закона Ома
В однородном проводнике упорядоченное движение заряженных частиц будет происходить по направлению вектора E. А это значит, что векторы j и E будут сонаправлены. Как и при определении плотности тока, выделим в проводнике бесконечно малый цилиндрический объем. Тогда через поперечное сечение этого цилиндра будет проходить ток, равный j*dS, а напряжение, приложенное к цилиндру, будет равно E*dl. Также известна формула удельного сопротивления цилиндра.
Тогда, записав формулу силы тока двумя способами, получим: j = E/р, где величина 1/р носит название удельной электрической проводимости и является обратной к удельному электрическому сопротивлению. Ее принято обозначать σ (сигма) или λ (лямбда). Единицей измерения проводимости является См/м, где См – это Сименс. Единица, обратная Ом.
Таким образом, можно ответить на вопрос, поставленный выше, о законе Ома для неоднородной цепи. В таком случае на носителей тока будет действовать сила со стороны электростатического поля, которая характеризуется напряженностью E1, и другие силы, воздействующие на них со стороны другого источника тока, которые можно обозначить E2. Тогда Закон Ома применительно к неоднородному участку цепи будет иметь вид: j = λ(E1 + E2).
Подробнее о проводимости и сопротивлении
Способность проводника проводить электрический ток характеризуется его удельным сопротивлением, которое можно найти через формулу удельного сопротивления, или удельной проводимостью, рассчитывающейся как обратное проводимости. Величина данных параметров определяется как химическими свойствами материала проводника, так и внешними условиями. В частности температурой окружающей среды.
Для большинства металлов удельное сопротивление при нормальной температуре пропорционально ей, то есть р ~ T. Однако при низких температурах наблюдаются отклонения. У большого ряда металлов и сплавов при температурах, близких к 0°К, расчет сопротивления показывал нулевые значения. Это явление получило название сверхпроводимости. Таким свойством обладают, например, ртуть, олово, свинец, алюминий и др. Для каждого металла существует свое критическое значение температуры Tk, при которой наблюдается явление сверхпроводимости.
Также отметим, что определение удельного сопротивления цилиндра можно обобщить для проводов, состоящих из одного материала. В таком случае площадь поперечного сечения из формулы удельного сопротивления будет равна сечению провода, а l – его длине.
fb.ru
Закон Ома. Сопротивление и проводимость
⇐ ПредыдущаяСтр 2 из 8Следующая ⇒
Вспомните хорошо известные из школьного курса физики понятия.
Электрический ток (или сила тока) – количество заряда, проходящего через поперечное сечение проводника в единицу времени или производная заряда по времени i(t) = dq/dt.
Единица измерения тока – Ампер – А = Кл/с
Для цепей постоянного тока i(t) = const = I
Напряжение – разность электрических потенциалов между двумя точками цепи u(t) = φ1 – φ2.
В цепях постоянного тока u(t) = const = U.
Единица измерения напряжения – Вольт (В).
Одной из основных характеристик элемента цепи является зависимость тока от напряжения I = f (U), называемая вольт-амперная характеристика (ВАХ)
ВАХ бывают линейные (если график – прямая линия) и нелинейные. На рисунке 1.2 характеристики 1 и 3 – линейные, а 2 – нелинейная. Соответственно, элементы цепи с линейной ВАХ называются линейными, а с нелинейной – нелинейными.
Линейная цепь – это цепь, состоящая только из линейных элементов. Если хотя бы один элемент цепи имеет нелинейную ВАХ, то цепь уже является нелинейной.
Важным параметром элемента цепи является его сопротивление R – коэффициент пропорциональности между током и напряжением.
В линейной цепи сопротивление элемента при любом напряжении постоянно и не зависит ни от напряжения, ни от тока. Зависимость тока от напряжения определяется законом Ома:
U = IR, где R = const.
Сопротивление R легко определить по графику ВАХ по любым двум точкам. R = ΔU/ΔI.
Определите: на какой из линейных ВАХ на рисунке 2 сопротивление больше: 1 или 3?
В нелинейной цепи сопротивление в каждой точке ВАХ различно. В данном разделе будем рассматривать только более простые, линейные цепи. Нелинейные цепи будут рассматриваться в последующих главах.
Сопротивление R является характеристикой провод-ника и определяется следующим образом:
R = , где l – длина проводника, ρ – удельное со-противление, характеризующее материал проводника, S – площадь поперечного сечения.
Теоретически любой элемент цепи обладает сопро-тивлением, но на практике в расчётах цепь идеализирует-ся, и сопротивлением проводов пренебрегают и считают, что всё сопротивление заключается в нагрузках.
Элемент цепи, обладающий сопротивлением, назы-вают резистором, на схеме обозначается так:
Размеры резистора – 4х10.
Часто удобно использовать величину, обратную сопротивлению, и называемую
G = 1/R
Единицей проводимости называется Сименс (См).
1 См = 1/1 Ом.
Закон Ома в этом случае выглядит: I = GU
G = , где γ = 1/ ρ – удельная проводимость.
Рассмотрим участок ветви с резистором R (смотреть рисунок 1.3) и полярности величин.
Очевидно, всегда R > 0
Uab = φa – φb
Если φa > φb то Uab > 0 – напряжение положительно.
Ток считается положительным, если направление тока совпадает с направлением положительного напряжения и отрицательным, если его направление противоположно направлению положительного напряжения.
Рассмотрим теперь источник ЭДС (рисунок 1.4)
Стрелка источника ЭДС показывает направление положительного тока, который вызывает источник. Интересно, что направление напряжения на самом источнике ЭДС противоположно току.
Рассмотрим участок ветви, содержащий источник ЭДС и резистор (рисунок 1.5).
Некоторые студенты испытывают затруднения при анализе данной цепи. При данном направлении ЭДС, правильная формула:
Uab = UR – E = IR – E
Проанализируйте схему и запишите самостоятельно формулы при различных вариантах направлений напряжений, токов и источника.
Соединение сопротивлений
Во многих случаях расчёт электрической цепи можно упростить, путём преобразования её из сложного вида в более простой. При этом уменьшается число узлов, ветвей либо и то и другое.
Необходимое условие преобразования: токи и напряжения в остальных частях схемы, не подвергающих-ся преобразованию, не изменяются. Такое преобразование называется эквивалентным.
а) Последовательное соединение сопротивлений
Последовательное соединение – это такое, при ко-тором во всех элементах цепи течёт одинаковый ток. Элементы ветви соединены последовательно (рис. 1.6).
Такую ветвь можно заменить одним резистором с сопротивлением Rэкв, равным сумме сопротивлений всех резисторов.
Rэкв = = R1+R2+R3+…+Rn
Эквивалентное сопротивление при таком соедине-нии всегда больше сопротивления любого из элементов. Если все сопротивления равны
R1= R2= R3=…= R, то Rэкв = nR
Для проводимостей G формула будет выглядеть так:
Напряжение на зажимах ab равно сумме напряжений на каждом элементе ветви.
б) Параллельное соединение сопротивлений
Параллельное соединение сопротивлений – это такое соединение, при котором ко всем элементам цепи приложено одинаковое напряжение.
Параллельно соединены элементы между двумя узлами (рисунок 1.7).
Ток I в неразветвлённой части равен сумме токов в каждом элементе.
I = I1= I2+ I3+…+ In
Эквивалентная проводимость в этом случае равна сумме проводимостей всех элементов:
Gэкв = = G1+ G2+ G3+…+ Gn
Для сопротивлений R формула будет выглядеть так:
Как видите, формулы симметричны: при последова-тельном соединении складываются сопротивления, а при параллельном – проводимости.
Эквивалентное сопротивление при таком соедине-нии всегда меньше сопротивления любого из элементов.
Если все сопротивления равны R1= R2= R3=…= R, то
Rэкв = R/n
Ток в любой ветви пропорционален проводимости этой ветви.
Смешанное соединение сопротивлений – это такое соединение, которое можно представить в виде параллельного и последовательного.
На первый взгляд кажется, что любую схему соединения элементов можно представить в виде смешанного соединения и найти эквивалентное сопротивление путём преобразования параллельных и последовательных участков. Однако бывают случаи, когда соединение элементов не является смешанным. Примером такого случая может служить распространённая в электронике мостовая схема, показанная на рисунке 1.8.
Как найти сопротивление между точками a и d? После нескольких попыток упростить схему, легко убе-диться, что здесь нет участков ни с последовательным, ни с параллельным соединением. Для этого нужно приме-нить преобразование, описанное в следующем параграфе.
г) Преобразование «Звезда-треугольник»
Существует возможность эквивалентного преобра-зования треугольника сопротивлений, показанного на ри-сунке 1.9, в трёхлучевую звезду (рисунок 1.10).
При преобразовании одной схемы в другую, напря-жения и токи, как при любом эквивалентном преобразова-нии, не изменяются.
Формулы для преобразования из треугольника в звезду:
Формулы для преобразования из звезды в треугольник:
Rab = Ra+ Rb+ RaRb/Rс
Rac = Ra+ Rc+ RaRc/Rb
Rbc = Rc+ Rb+ RcRb/Ra
Если все сопротивления равны, то легко убедиться, что сопротивления в треугольнике в три раза больше, чем в звезде.
Теперь вернёмся к мостовой схеме на рисунке 8. Можно преобразовать в ней треугольник abc в звезду. Получим схему на рисунке 1.11.
В этой схеме сопротивления треугольника R
Теперь не вызывает затруднения найти сопротивле-ние Rad. Для этого нужно найти последовательные соеди-нения Rb-R4 и Rc-R5, затем параллельное соединение двух получившихся и затем – последовательное соедине-ние с Ra.
Также и в других подобных случаях преобразование «звезда-треугольник» может быть незаменимым.
Рекомендуемые страницы:
lektsia.com
Закон Ома для переменного тока
Мы с вами знаем формулировку закона Ома для цепей постоянного тока, которая гласит, что ток в такой цепи прямо пропорционален напряжению на элементе цепи и обратно пропорционален сопротивлению этого элемента постоянному току, протекающему через него.
Однако при изучении цепей переменного тока стало известно, что оказывается кроме элементов цепей с активным сопротивлением, есть элементы цепи с так называемым реактивным сопротивлением, то есть индуктивности и емкости (катушки и конденсаторы).
В цепи, содержащей только активное сопротивление, фаза тока всегда совпадает с фазой напряжения (рис 1.), т. е. сдвиг фаз тока и напряжения в цепи с чисто активным сопротивлением равен нулю.
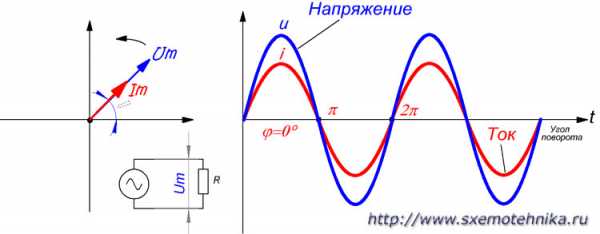
Рисунок 1. Напряжение и ток в цепи с чисто активным сопротивлением. Сдвиг фаз между током и напряжение в цепи переменного тока с чисто активным сопротивлением всегда равен нулю
Отсюда следует, что угол между радиус-векторами тока и напряжения также равен нулю.
Тогда, падение напряжения на активном сопротивлении определяется по формуле:
| (1) |
где, U-напряжение на элементе цепи,
I – ток через элемент цепи
R – активное сопротивление элемента
Формула (1) применима как для амплитудных, так и для эффективных значений тока и напряжения:
| (2) |
где, Um-амплитудное значение напряжения на элементе цепи,
Im – амплитудное значение тока через элемент цепи
R – активное сопротивление элемента
В цепи, содержащей чисто реактивное сопротивление — индуктивное или емкостное, — фазы тока и напряжения сдвинуты друг относительно друга на четверть периода, причем в чисто индуктивной цепи фаза тока отстает от фазы напряжения (рис. 2), а в чисто емкостной цепи фаза тока опережает фазу напряжения (рис. 3).
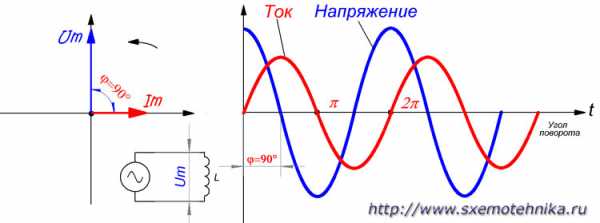
Рисунок 2. Напряжение и ток в цепи с чисто индуктивным сопротивлением. Фаза тока отстает от фазы напряжения на 90 градусов.
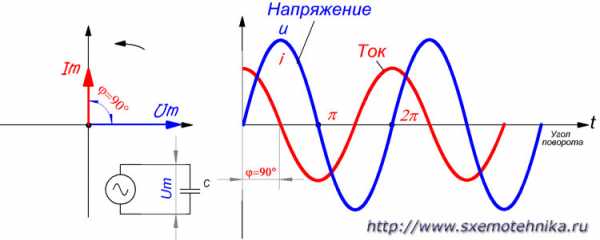
Рисунок 3. Напряжение и ток в цепи с чисто емкостным сопротивлением. Фаза тока опережает фазу напряжения на угол 90 градусов.
Отсюда следует, что в чисто реактивной цепи угол между радиус-векторами тока и напряжения всегда равен 90°, причем в чисто индуктивной цепи радиус-вектор тока при вращении движется позади радиус-вектора напряжения, а в чисто емкостной цепи он движется впереди радиус-вектора напряжения.
Падения напряжения на индуктивном и емкостном сопротивлениях определяются соответственно по формулам:
| (3) | |
| (4) |
где — UL-падение напряжение на чисто индуктивном сопротивлении ;
UС—падение напряжения на чисто емкостном сопротивлении;
I— значение тока в через реактивное сопротивление;
L— индуктивность реактивного элемента;
C— емкость реактивного элемента;
ω— циклическая частота.
Эти формулы применимы как для амплитудных, так и для эффективных значений тока и напряжения синусоидальной формы. Однако здесь следует отметить, что они ни в коем случае не применимы для мгновенных значений тока и напряжения, а также и для несинусоидальных токов.
Приведенные выше формулы являются частными случаями закона Ома для переменного тока.
Следовательно, полный закон Ома для переменного тока будет иметь вид:
| (5) |
Где Z – полное сопротивление цепи переменного тока.
Теперь остается только вычистислить полное сопротивление цепи, а оно зависит непосредсвенно от какие активные и реактивные элементы присутсвуют в цепи и как они соединены.
Закон Ома для различных типовых цепей переменного тока
Давайте выясним, как будет выглядеть закон Ома для цепи переменного тока, состоящей из активного и индуктивного сопротивлений, соединенных последовательно (рис. 4.)
Рисунок 4. Цепь переменного тока с последовательным соединением активного и индуктивного сопротивления.
Закон Ома для переменного синусоидального тока в случае последовательного соединения активного и индуктивного сопротивлений выражается следующей формулой:
| (6) |
где —эффективное значение силы тока в А;
U—эффективное значение напряжения в В;
R—активное сопротивление в Ом;
ωL—индуктивное сопротивление в ом.
Формула (6) будет также действительной, если в нее подставить амплитудные значения тока и напряжения.
В цепи, изображенной на рис. 5, соединены последовательно активное и емкостное сопротивления.
Рисунок 5. Цепь переменного тока с последовательным соединением активного и емкосного сопротивления.
А закон Ома для такой цепи принимает вид:
| (7) |
В общем случае, когда цепь содержит все три вида сопротивлений (рис. 6),
Рисунок 6. Цепь переменного тока с последовательным соединением активного, индуктивного и емкосного сопротивления.
Закон Ома при последовательном соединении активного, индуктивного и емкостного сопротивлений будет выглядеть так:
| (8) |
где I-сила тока в А;
U-напряжение в В;
R-активное сопротивление в Ом;
ωL-индуктивное сопротивление в Ом;
1/ωС-емкостное сопротивление в Ом.
Формула (8) верна только для эффективных и амплитудных значений синусоидального тока и напряжения.
Для того, что бы определить ток в цепях с параллельным соединением элементов (рисунок 7), то необходимо так же вычислить полное сопротивление цепи, как это делать можно прсмотреть здесь, зтем подставить значение полного сопротивления в общую формулу для закона Ома (5).
Рисунок 7. Полное сопротивление цепи при параллельном соединении активного и реактивных элементов. а) – параллельное соединение R и L; б) – параллельное соединение R и C.
Тоже самое касается и вычисления тока в колебательном контуре изображенном на рисунке 8.
Рисунок 8. Эквивалентная схема колебательного контура.
Таким образом закон Ома для переменного тока можно сформулировать следующим образом.
Значение тока в цепи переменного тока прямо пропорционально напряжению в цепи (или на участке цепи) и обратно пропорционально полному сопротивлению цепи (участка цепи)
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
Похожие материалы:
Добавить комментарий
www.sxemotehnika.ru
Закон Ома для участка цепи. Сопротивление (Ерюткин Е.С.). Видеоурок. Физика 10 Класс
На этом уроке мы рассмотрим связь параметров поля внутри проводника (разность потенциалов на определенном участке) с характеристикой тока (силой тока), сформулируем закон Ома для участка цепи, а также рассмотрим свойства проводников, влияющие на пропускание электрического тока (сопротивление)
Для существования электрического тока внутри проводника должно существовать электрическое поле, а для существования поля в проводнике необходима разность потенциалов. Разность потенциалов называют напряжением. Причем ток направлен в сторону уменьшения потенциалов (ток по договоренности обусловлен движением положительных зарядов), а свободные электроны, соответственно, движутся в обратную сторону. Рассмотрим движение частиц в металлическом проводнике.
Рис. 1. Движение частиц в металлическом проводнике
Допустим, на концах некоторого участка проводника существуют потенциалы и , причем .
В таком случае напряжение на участке (или разность потенциалов) равно .
Опытным путем было показано, что, чем больше напряжение на участке, тем больше сила тока, проходящего через него.
Немецкий ученый Георг Ом в 1826 году провел серию опытов и получил зависимость, которую впоследствии назвали законом Ома.

Рис. 2. Георг Ом
Для разных проводников он строил так называемые вольт-амперные характеристики – графики зависимости силы тока от напряжения.
Рис. 3. График зависимости силы тока от напряжения
В результате была обнаружена линейная связь силы тока с напряжением: увеличивая напряжение, увеличиваем и силу тока, это увеличение происходит прямо пропорционально: .
Однако, как видно из графиков, для каждого проводника коэффициент пропорциональности разный. Это означало, что каждый проводник обладает некоторой мерой проводимости тока, и для разных проводников она разная. Эту величину назвали электрическим сопротивлением. Обозначение сопротивления – R.
При одном и том же напряжении проводники с меньшим сопротивлением будут пропускать ток большей силы.
Используя опытные результаты, Омом был сформулирован закон, впоследствии названный законом Ома для участка цепи. Закон Ома для участка цепи:сила тока для однородного проводника на участке цепи прямо пропорциональна напряжению на этом участке и обратно пропорциональна сопротивлению проводника.
Сопротивление является главной характеристикой проводника. В чем же природа сопротивления? Чем обусловлена лучшая или худшая проводимость тока проводниками? Дело в том, что электроны, которые движутся в металле под действием электрического поля, не движутся в однородной среде, они постоянно взаимодействуют с узлами кристаллической решетки металла и атомами различных примесей, замедляясь. В перерывах же между ударами они движутся равноускоренно.
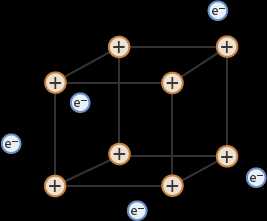
Рис. 4. Движение электронов в металлическом проводнике
Проводники могут быть твердые, жидкие, газообразные, плазменные и во всех них существует свое электрическое сопротивление.
После объяснения механизма сопротивления становится очевидным, что сопротивление зависит только от свойств проводника, в частности, материала, геометрических размеров и температуры. Какова же эта зависимость?
В данном случае это l – длина проводника;
S – площадь поперечного сечения проводника;
Ρ – удельное сопротивление.
Чем проводник длиннее, тем его электрическое сопротивление больше, а чем площадь поперечного сечения проводника больше, тем электрическое сопротивление меньше.
Удельное сопротивление– табличная величина, характеризующая способность материала к сопротивлению, показывает, каким сопротивлением обладает проводник длиной 1 метр, площадь поперечного сечения которого составляет 1 м2.
Единица измерения сопротивления – Ом:
Единица измерения удельного сопротивления: . По удельному сопротивлению мы можем судить о материале и о том, как его можно использовать. Все удельные сопротивления известных нам материалов собраны в таблице:
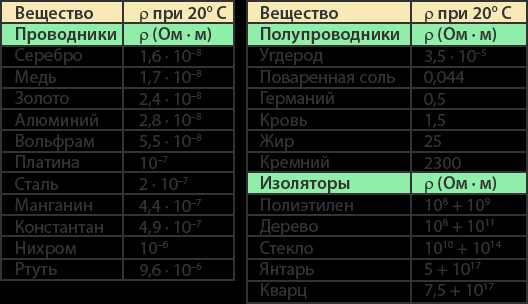
Рис. 5. Удельное сопротивление металлов
По признаку проводимости все материалы разделяются на три группы: проводники (удельное сопротивление порядка 10-8 Ом м), полупроводники (порядка 10-4-102 Ом м) и изоляторы (порядка 108-1017 Ом м).
Закон Ома для участка цепи имеет значение для расчета электрических цепей.
На следующем уроке мы рассмотрим, как соединяются электрические сопротивления (резисторы).
Список рекомендованной литературы
- Тихомирова С.А., Яворский Б.М. Физика (базовый уровень) – М.: Мнемозина, 2012.
- Генденштейн Л.Э., Дик Ю.И. Физика 10 класс. – М.: Илекса, 2005.
- Мякишев Г.Я., Синяков А.З., Слободсков Б.А. Физика. Электродинамика. – М., 2010.
Домашнее задание
- Для изготовления резистора сопротивления 126 Ом использовали никелевый провод с площадью сечения 0,1 мм2. Какая длина этого провода?
- Как изменится сопротивление оголенного провода, если его сложить в два раза?
- От чего зависит сопротивление?
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Интернет-портал Kakras.ru (Источник).
- Интернет-портал Class-fizika.narod.ru (Источник).
- Интернет-портал Uchifiziku.ru (Источник).
- Интернет-портал Electromechanics.ru (Источник).
interneturok.ru



