Закон постоянного тока ома – Формула полного расчета закона Ома для цепей постоянного и переменного токов
- Комментариев к записи Закон постоянного тока ома – Формула полного расчета закона Ома для цепей постоянного и переменного токов нет
- Советы абитуриенту
- Закон Ома.
- Есть ли отличия закона Ома для цепей переменного и постоянного напряжения?
- Закон Ома
- Закон Ома для переменного тока
- Электрический ток. Закон Ома. Законы постоянного тока.
- Закон Ома. Для цепей и тока. Формулы и применение
- В результате нового эксперимента Ом пришел к формуле:
- Х = a / b + l
- I = U / R
- Таким образом формула для расчета сопротивления проводника примет вид:
- R = p ⋅ l / s
- I = U / R + r
- Формула для расчета падения напряжения на индуктивном сопротивлении:
- U = I ⋅ ωL
- Формула для расчета падения напряжения на емкостном сопротивлении:
- U = I / ω ⋅ С
- Полный же будет выглядеть следующем образом:
- I = U / Z
- Формула полного расчета закона Ома для цепей постоянного и переменного токов
Закон Ома.
Закон Ома.Программа КИП и А
В программу «КИП и А», в разделе «Электрика» включен блок расчета закона Ома для постоянного и переменного тока. Сначала немного теории..
Для постоянного тока
Закон Ома определяет зависимость между током (I), напряжением (U) и сопротивлением (R) в участке электрической цепи. Наиболее популярна формулировка:
Сила тока в участке цепи прямо пропорциональна напряжению и обратно пропорциональна электрическому сопротивлению данного участка цепи, т.е.
| I = U / R | где | I – сила тока, измеряемая в Амперах, (A) |
| U – напряжение, измеряемое в Вольтах, (V) | ||
| R – сопротивление, измеряется в Омах, (Ω) |
Закон Ома, является основополагающим в электротехнике и электронике. Без его понимания также не представляется работа подготовленного специалиста в области КИП и А. Когда-то была даже распространена такая поговорка, – “Не знаешь закон Ома, – сиди дома..”.
Помимо закона Ома, важнейшим является понятие электрической мощности, P:
Мощность постоянного тока (P) равна произведению силы тока (I) на напряжение (U), т.е.
| P = I × U | где | P – эл. мощность, измеряемая в Ваттах, (W) |
| I – сила тока, измеряемая в Амперах, (A) | ||
| U – напряжение, измеряемое в Вольтах, (V) |
Комбинируя эти две формулы, выведем зависимость между силой тока, напряжением, сопротивлением и мощностью, и создадим таблицу:
| Сила тока, | I= | U/R | P/U | √(P/R) |
| Напряжение, | U= | I×R | P/I | √(P×R) |
| Сопротивление, | R= | U/I | P/I² | U²/P |
| Мощность, | P= | I×U | I²×R | U²/R |
Практический пример использования таблицы: Покупая в магазине утюг, мощностью 1 кВт (1 кВт = 1000 Вт), высчитываем на какой минимальный ток должна быть рассчитана розетка в которую предполагается включать данную покупку:
Несмотря на то, что утюг включается в сеть переменного тока, пренебрегаем его реактивным сопротивлением (см. ниже), и используем упрощенную формулу для постоянного тока. Находим в таблице I = P / U. Получаем: 1000 кВт / 220 В (напряжение сети) = 4,5 Ампера. Это и есть минимальный ток, который должна выдерживать розетка, при подключении к ней нагрузки мощностью 1 кВт.
Наиболее распространенные множительные приставки:
- Сила тока, Амперы (A): 1 килоампер (1 kА) = 1000 А. 1 миллиампер (1 mA) = 0,001 A. 1 микроампер (1 µA) = 0,000001 A.
- Напряжение, Вольты (V): 1 киловольт (1kV) = 1000 V. 1 милливольт (1 mV) = 0,001 V. 1 микровольт (1 µV) = 0,000001 V.
- Сопротивление, Омы (Om): 1 мегаом (1 MOm) = 1000000 Om. 1 килоом (1 kOm) = 1000 Om.
Для переменного тока
В цепи переменного тока закон Ома может иметь некоторые особенности, описанные ниже.
Импеданс, Z
В цепи переменного тока, сопротивление кроме активной (R), может иметь как емкостную (C), так и индуктивную (L) составляющие. В этом случае вводится понятие электрического импеданса, Z (полного или комплексного сопротивления для синусоидального сигнала). Упрощенные схемы комплексного сопротивления приведены на рисунках ниже, слева для последовательного, справа для параллельного соединения индуктивной и емкостной составляющих.
Последовательное включение R, L, C
Параллельное включение R, L, C
Также, полное сопротивление, Z зависит не только от емкостной (C), индуктивной (L) и активной (R) составляющих, но и от частоты переменного тока.
| Импеданс, Полное сопротивление, Z | |
| При последовательном включении R, L, C | При параллельном включении R, L, C |
| Z=√(R2+(ωL-1/ωC)2) | Z=1/ √(1/R2+(1/ωL-ωC)2) |
| где, | |
| ω = 2πγ – циклическая, угловая частота; γ – частота переменного тока. | |
Коэффициент мощности, Cos(φ)
Коэффициент мощности, в самом простом понимании, это отношение активной мощности (P) потребителя электрической энергии к полной (S) потребляемой мощности, т. е.
Cos(φ) = P / S
Он также показывает насколько сдвигается по фазе переменный ток, протекающий через нагрузку, относительно приложенного к ней напряжения.
Изменяется от 0 до 1. Если нагрузка не содержит реактивных составляющих (емкостной и индуктивной), то коэффициент мощности равен единице.
Чем ближе Cos(φ) к единице, тем меньше потерь энергии в электрической цепи.
Исходя из вышеперечисленных понятий импеданса Z и коэффициента мощности Cos(φ), характерных для переменного тока, выведем формулу закона Ома, коэффициента мощности и их производные для цепей переменного тока:
| I = U / Z | где | I – сила переменного тока, измеряемая в Амперах, (A) |
| U – напряжение переменного тока, измеряемое в Вольтах, (V) | ||
| Z – полное сопротивление (импеданс), измеряется в Омах, (Ω) |
Производные формулы:
| Сила тока, | I= | U/Z | P/(U×Cos(φ)) | √(P/Z) |
| Напряжение, | U= | I×Z | P/(I×Cos(φ)) | √(P×Z) |
| Полное сопротивление, импеданс | Z= | U/I | P/I² | U²/P |
| Мощность, | P= | I²×Z | I×U×Cos(φ) | U²/Z |
Программа «КИП и А» имеет в своем составе блок расчета закона Ома как для постоянного и переменного тока, так и для расчета импеданса и коэффициента мощности Cos(φ). Скриншоты представлены на рисунках внизу:
Закон Ома для постоянного тока
Закон Ома для переменного тока
Расчет полного сопротивления
Расчет коэффициента мощности Cos(φ)
www.axwap.com
Есть ли отличия закона Ома для цепей переменного и постоянного напряжения?
Закон Ома является одним из основных законов электротехники. Он довольно прост и применяется при расчете практически любых электрических цепей. Но данный закон имеет некоторые особенности работы в цепях переменного и постоянного тока при наличии в цепи реактивных элементов. Эти особенности нужно помнить всегда.
Закон Ома для цепи постоянного тока
Классическая схема закона Ома выглядит так:
А звучит и того проще – ток, протекающей на участке цепи, будет равен отношению напряжения цепи к ее сопротивлению, что выражается формулой:
Но ведь мы знаем, что помимо активного сопротивления R, существует и реактивные сопротивления индуктивности ХL и емкости XC. А ведь согласитесь, что электрические схемы с чисто активным сопротивлением встречаются крайне редко. Давайте рассмотрим схему, в которой последовательно включена катушка индуктивности L, конденсатор С и резистор R:
Помимо чисто активного сопротивления R, индуктивность L и емкость С имеют и реактивные сопротивления ХL и XC, которые выражены формулами:
Где ω это циклическая частота сети, равная ω = 2πf. f – частота сети в Гц.
Для постоянного тока частота равна нулю (f = 0), соответственно реактивное сопротивление индуктивности станет равным нулю (формула (1)), а емкости – бесконечности (2), что приведет к разрыву электрической цепи. Отсюда можно сделать вывод, что реактивное сопротивление элементов в цепях постоянного напряжения отсутствует.
Закон Ома для цепи переменного тока
Если рассматривать классическую электрическую цепь и на переменном токе, то она практически ничем не будет отличаться от постоянного тока, только источником напряжения (вместо постоянного — переменное):
Соответственно и формула для такого контура останется прежней:
Но если мы усложним схему и добавим к ней реактивных элементов:
Ситуация изменится кардинально. Теперь f у нас не равна нулю, что сигнализирует о том, что помимо активного, в цепь вводится и реактивное сопротивление, которое также может влиять на величину тока, протекаемого в контуре и приводить к резонансу. Теперь полное сопротивление контура (обозначается как Z) и оно не равно активному Z ≠ R. Формула примет следующий вид:
Соответственно немного изменится и формула для закона Ома:
Почему это важно?
Знание этих нюансов позволит избежать серьезных проблем, которые могут возникнуть при неправильном подходе к решению некоторых электротехнических задач. Например, в контур переменного напряжения подключена катушка индуктивности со следующими параметрами: f
Где:
В случае, если подать на эту же катушку постоянное напряжение с таким же значением, получим:
Мы видим, что ток катушки возрастает в разы, что приводит к выходу из строя элементов контура.
elenergi.ru
Закон Ома
Всем привет, дамы и господа! Сегодня наконец речь пойдет о законе Ома. Да-да, это то, без знания чего вас заклюют на любом радиолюбительском форуме или паблике сотни уважаемых господ, которые в теме, пусть и не всегда действительно глубоко. Да что там паблики! Если ты, мой юный друг, посещаешь школу, лицей, гимназию или другое, без сомнения превосходное, учебное заведение, неправильный ответ на этот вопрос может привести в ярость почтенного преподавателя физики и закончиться для тебя не самым лучшим образом.
Сегодняшний урок статья (мы же не в школе, в самом деле) направлена на предотвращения такого нехорошего сценария развития событий путем приобщения к еще одной очень важной (на самом деле так) тайне радиоэлектроники.
Закон Ома на самом деле весьма прост. На великом и ужасном языке математики он выглядит следующим образом:
В этой формуле I – уже известный нами ток, U – напряжение, R – cопротивление. Как вы видите, все величины мы рассмотрели ранее, они нам уже известны. В этой же статье мы рассмотрим, как они связаны между собой. Более того, мы уже видели раньше эту формулу в статье про сопротивлениe, правда тогда мы договорились, что не будем пока забегать вперед.
Видите, зависимость совсем проста. Дифференциалов и страшных интегралов тут нет, а делить, вроде как вы, надуюсь, умеете. Так что на самом деле все несложно.
Резонный вопрос – а откуда, собственно, эта связь взялась и сфига я должен ей верить? Если вы его задали – поздравляю, господа, вы на правильном пути. Действительно, с какой это стати верить всему написанному на слово?
Та или иная зависимость может родиться двумя способами: результаты эксперимента или математический вывод формулок. Ну, здесь настолько простая формулка, что ответ один – эта зависимость получена экспериментальным путем уважаемым господином Георгом Омом. Грубо говоря, он взял источник напряжения (были в те времена так называемые «вольтовые столбы», кому интересно – гуглите) и куски металлической проволоки. Изменяя число вольтовых столбов (т.е. изменяя напряжение источника) или количество отрезков проволоки (т.е. изменяя сопротивление нагрузки), Ом получил данную зависимость. В тонкости физики измерений тех лет мы вникать не будем, это тема отдельной статьи. Кому интересно – гугл в помощь. Кто по-прежнему не верит – эксперимент в помощь. Вы всегда можете взять источник питания, который выдает точно известное напряжение, можете купить в магазине резистор с точно известным сопротивлением и мультиметром в режиме амперметра измерить протекающий в цепи ток. Дальше остается результат этого измерения сравнить с расчетным значением тока в цепи по приведенной формуле. Если вы все сделали правильно, результат эксперимента должен совпасть с расчетным значением. Схемка, иллюстрирующая этот эксперимент, приведена на рисунке 1.
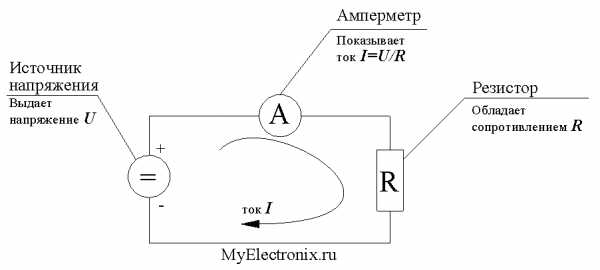
Рисунок 1 – Иллюстрация закона Ома
Математика – математикой, а настоящего инженера должна интересовать в первую очередь физика процесса. К сожалению, есть люди даже среди почтеннейшей касты преподавателей, которые не уделяют должного внимания физике происходящего процесса, ограничиваясь лишь написанием формул, часто вообще без понимания сути происходящего. Если вы относите себя к их числу и вас устраивает данное положение дел, вероятно, есть смысл сейчас же безотлагательно покинуть данный ресурс. Невыполнение данного требования может повлечь существенные изменения в вашей психике! Автор не несет за это никакой ответственности!
Итак, физика процесса. Возьмем источник напряжения. Разумеется, не ортодоксальные вольтовые столбы, а, например, лабораторный источник питания. Возьмем нагрузку. Например, обычный резистор 1,2 кОм. Выставим на источнике питания напряжение 12 В. Внимание, вопрос, господа знатоки. Какой будет протекать ток через резистор? Используя написанную нами выше формулку, получаем величину тока
Т. е. ток через резистор равен 0,1 А или 100 мА.
Допустим, мы хотим увеличить протекающий ток. Как это можно сделать? Очевидно, двумя способами – поднять напряжение источника питания или уменьшить сопротивление нагрузки-резистора.
А если уменьшить протекающий ток? Аналогично – уменьшаем напряжение. Или увеличиваем сопротивление.
Важно понимать, господа, что напряжение и сопротивление – это первичные величины. Они задаются конкретными девайсами – источником питания и резистором-нагрузкой. Они… как там это говорят… самобытны и самодостаточны. Они существуют сами по себе и, собственно, отлично живут без какого-то там тока.
Сопротивление резистора ни в коем случае не зависит от источника напряжения! Оно ни в коем случае не зависит от протекающего тока! Оно может зависеть от материала резистора, от температуры, от формы, еще от чего-нибудь, но никак не от напряжения и тока (слышу вой уважаемый зануд, что это не так для нелинейных элементов – тссс! Спокойно, господа, до них тоже доберемся). От чего именно оно зависит, мы уже рассматривали здесь.
Напряжение источника питания тоже тут величина первичная. Она определяется и формируется источником питания. А именно – переизбытком электронов на одном из электродов.
Ток же здесь – вторичная величина, т.е. расчетная. Он существо подневольное, можно сказать, раб системы. Он зависит от напряжения и сопротивления. Сдохнет источник питания – каюк и току, он пропадет. Прикажет долго жить резистор, устав постоянно сопротивляться – на токе, несомненно, это тоже отразится (уменьшится или увеличится – отдельный вопрос, который решать будет все тот же уже почерневший резистор). Это рабство просто отлично характеризует картинка, которую мы любезно позаимствуем с pikaby .
Даже по выражению лиц на картинке отлично видно, кто тут подневольное существо, а кто командует парадом .
Читатель может возразить: “А как же источники тока?” Да, действительно есть такое понятие как “источник тока“. Дескать, это такой девайс, у которого не напряжение первичная величина, а ток. То есть в теории он выдает через любое сопротивление строго один и тот же ток. Однако на практике возможности этих источников тока весьма ограничены. Как правило, они могут работать лишь при очень небольших нагрузочных сопротивлениях. Более того, если углубиться в физику процессов этих источников, то окажется, что там тоже идет игра за счет изменения напряжения. Поэтому-таки будем полагать, что первичной величиной является именно напряжение, а не ток. А про источники тока и источники напряжения потом поговорим более подробно.
В инженерной практике, равно как и в школьных задачах, возникает задача следующего рода. Мы намерили ток, например, величиной в 1 А через известный резистор с сопротивлением, скажем, 10 Ом. Вопрос задачи: определите напряжение источника питания.
Решается подобная задача весьма просто на основе того же закона Ома. Просто выражаем из уже написанной формулы напряжение:
Абсолютно аналогичным образом можно посчитать и сопротивление, если мы знаем напряжение и ток.
Итак, у нас теперь есть отличный инструмент, который связывает между собой напряжение, ток и сопротивление. Зная две из этих величины мы всегда сможем найти третью. Поверьте, на практике это встречается сплошь и рядом и это реально надо очень хорошо запомнить и понимать.
Ну что ж, господа, на этом, думаю, сегодня можно закругляться. Поскольку тема и правда очень важная, не буду вас сегодня грузить чем-то еще, лучше хорошо разобраться в этой. Всем огромной удачи и пока!
Вступайте в нашу группу Вконтакте
Вопросы и предложения админу: This email address is being protected from spambots. You need JavaScript enabled to view it.
myelectronix.ru
Закон Ома для переменного тока
После открытия в 1831 году Фарадеем электромагнитной индукции, появились первые генераторы постоянного, а после и переменного тока. Преимущество последних заключается в том, что переменный ток передается потребителю с меньшими потерями.
При увеличении напряжения в цепи, ток будет увеличиваться аналогично случаю с постоянным током. Но в цепи переменного тока сопротивление оказывается катушкой индуктивности и конденсатор. Основываясь на этом, запишем закон Ома для переменного тока: значение тока в цепи переменного тока прямо пропорционально напряжению в цепи и обратно пропорционально полному сопротивлению цепи.
где- I [А] – сила тока,
- U [В] – напряжение,
- Z [Ом] – полное сопротивление цепи.
Полное сопротивление цепи
В общем случае полное сопротивление цепи переменного тока (рис. 1) состоит из активного (R [Ом]), индуктивного, и емкостного сопротивлений. Иными словами, ток в цепи переменного тока зависит не только от активного омического сопротивления, но и от величины емкости (C [Ф]) и индуктивности (L [Гн]). Полное сопротивление цепи переменного тока можно вычислить по формуле:
где- – индуктивное сопротивление, оказываемое переменному току, обусловленное индуктивностью электрической цепи, создается катушкой.
- – емкостное сопротивление, создается конденсатором.
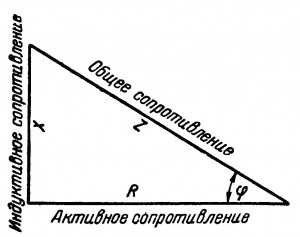
Полное сопротивление цепи переменного тока можно изобразить графически как гипотенузу прямоугольного треугольника, у которого катетами являются активное и индуктивное сопротивления.
Рис.1. Треугольник сопротивлений
Учитывая последние равенства, запишем формулу закона Ома для переменного тока:
– амплитудное значение силы тока.Рис.2. Последовательная электрическая цепь из R, L, C элементов.
Из опыта можно определить, что в такой цепи колебания тока и напряжения не совпадают по фазе, а разность фаз между этими величинами зависит от индуктивности катушки и емкости конденсатора:
Решение задач:
Цепь переменного тока состоит из последовательно соединенных конденсатора (емкостью С), катушки индуктивности (L) и активного сопротивления (R). На зажимы цепи подается действующее напряжение (U), частота которого ν. Чему равно действующее значение силы тока в цепи?
zakon-oma.ru
Электрический ток. Закон Ома. Законы постоянного тока.
Электрическим током называется упорядоченное движение электрических зарядов. За направление электрического тока принимают направленное движение положительных заряженных частиц. Однако в металлических проводниках ток создается движением электронов в направлении обратном току. Электрический ток может существовать в том случае, если существуют свободные носители зарядов. В металлах свободными носителями заряда являются электроны, в растворах и расплавах солей – ионы, в газах – ионы и электроны.
Отношение заряда Q, переносимого через поперечное сечение за единицу времени dt этому интервалу времени называется силой тока I.
Если сила тока со временем не изменяется, электрический ток называют постоянным.
Закон Ома для участка цепи: Сила тока I прямо пропорциональна напряжению на концах участка цепи U и обратно пропорциональна его электрическому сопротивлению R:
l – длина проводника, S – площадь его поперечного сечения, r – удельное электрическое сопротивление вещества проводника.
Закон Ома в дифференциальной форме.
j – плотность тока; g=1/r – удельная проводимость или электропроводность вещества проводника; E – напряженность поля в проводнике.
Если известны величины зарядов положительных и отрицательных носителей q+ и q–, их концентрации n+ и n– и их скорости v+ и v–, то плотность тока определяется следующим образом
.
Для металлов эта формула примет следующий вид
,
где e – заряд электрона, n – их концентрация, v – средняя скорость направленного движения.
Очевидно, для данного металла, плотность тока будет определятся средней скоростью движения зарядов, которая в свою очередь будет зависеть от температуры. Для жидкостей и газов с повышением температуры увеличивается и плотность тока, т.к. с ростом температуры увеличивается подвижность носителей зарядов и их концентрация. Для металлов повышение температуры приводит к раскачке узлов кристаллической решетки, что приводит к уменьшению скорости движения электронов, т.е. повышению удельного сопротивления металла. Для большинства металлов при температурах, близких к комнатной, удельное сопротивление r изменяется пропорционально абсолютной температуре T: .
При низкой температуре наблюдается отступление от этой закономерности (рис.1). В большинстве случаев зависимость r от T следует кривой 1. У некоторых металлов и сплавов при температуре порядка нескольких кельвин сопротивление скачком уменьшается до нуля (кривая 2). Это явление называется сверхпроводимостью. Тk – критическая температура, при которой данный проводник переходит в сверхпроводящее состояние.
При последовательном соединении (рис.2) проводников суммарное соединение проводников определяется формулой
Rобщ = R1 + R2 .
Для n одинаковых проводников
Rобщ =n R .
При параллельном соединении проводников (рис.3) суммарное соединение проводников определяется формулой
или .
Для n одинаковых проводников
infopedia.su
Закон Ома. Для цепей и тока. Формулы и применение
Георг Симон Ом начал свои исследования вдохновляясь знаменитым трудом Жана Батиста Фурье «Аналитическая теория тепла». В этой работе Фурье представлял тепловой поток между двумя точками как разницу температур, а изменение теплового потока связывал с его прохождением через препятствие неправильной формы из теплоизолирующего материала. Аналогично этому Ом обуславливал возникновение электрического тока разностью потенциалов.
Исходя из этого Ом стал экспериментировать с разными материалами проводника. Для того, чтобы определить их проводимость он подключал их последовательно и подгонял их длину таким образом, чтобы сила тока была одинаковой во всех случаях.
Важно при таких измерениях было подбирать проводники одного и того же диаметра. Ом, замеряя проводимость серебра и золота, получил результаты, которые по современным данным не отличаются точностью. Так, серебряный проводник у Ома проводил меньше электрического тока, чем золотой. Сам Ом объяснял это тем, что его проводник из серебра был покрыт маслом и из-за этого, по всей видимости, опыт не дал точных результатов.
Однако не только с этим были проблемы у физиков, которые в то время занимались подобными экспериментами с электричеством. Большие трудности с добычей чистых материалов без примесей для опытов, затруднения с калибровкой диаметра проводника искажали результаты тестов. Еще большая загвоздка состояла в том, что сила тока постоянно менялась во время испытаний, поскольку источником тока служили переменные химические элементы. В таких условиях Ом вывел логарифмическую зависимость силы тока от сопротивления провода.
Немногим позже немецкий физик Поггендорф, специализировавшийся на электрохимии, предложил Ому заменить химические элементы на термопару из висмута и меди. Ом начал свои эксперименты заново. В этот раз он пользовался термоэлектрическим устройством, работающем на эффекте Зеебека в качестве батареи. К нему он последовательно подключал 8 проводников из меди одного и того же диаметра, но различной длины. Чтобы измерить силу тока Ом подвешивал с помощью металлической нити над проводниками магнитную стрелку. Ток, шедший параллельно этой стрелке, смещал ее в сторону. Когда это происходило физик закручивал нить до тех пор, пока стрелка не возвращалась в исходное положение. Исходя из угла, на который закручивалась нить можно было судить о значении силы тока.
В результате нового эксперимента Ом пришел к формуле:
Х = a / b + l
Здесь X – интенсивность магнитного поля провода, l – длина провода, a – постоянная величина напряжения источника, b – постоянная сопротивления остальных элементов цепи.
Если обратиться к современным терминам для описания данной формулы, то мы получим, что Х – сила тока, а – ЭДС источника, b + l – общее сопротивление цепи.
Закона Ома для участка цепи
Закон Ома для отдельного участка цепи гласит: сила тока на участке цепи увеличивается при возрастании напряжения и уменьшается при возрастании сопротивления этого участка.
I = U / R
Исходя из этой формулы, мы можем решить, что сопротивление проводника зависит от разности потенциалов. С точки зрения математики, это правильно, но ложно с точки зрения физики. Эта формула применима только для расчета сопротивления на отдельном участке цепи.
Чтобы рассчитать сопротивление проводника, нужно перемножить его длину на удельное сопротивление его материала и разделить на площадь поперечного сечения.
Таким образом формула для расчета сопротивления проводника примет вид:
R = p ⋅ l / s
Закон Ома для полной цепи
Отличие закона Ома для полной цепи от закона Ома для участка цепи заключается в том, что теперь мы должны учитывать два вида сопротивления. Это «R» сопротивление всех компонентов системы и «r» внутреннее сопротивление источника электродвижущей силы. Формула таким образом приобретает вид:
I = U / R + r
Закон Ома для переменного тока
Переменный ток отличается от постоянного тем, что он изменяется с определенными временными периодами. Конкретно он изменяет свое значение и направление. Чтобы применить закон Ома здесь нужно учитывать, что сопротивление в цепи с постоянным током может отличатся от сопротивления в цепи с током переменным. И отличается оно в том случае если в цепи применены компоненты с реактивным сопротивлением. Реактивное сопротивление может быть индуктивным (катушки, трансформаторы, дроссели) и емкостными (конденсатор).
Попробуем разобраться, в чем реальная разница между реактивным и активным сопротивлением в цепи с переменным током. Вы уже должны были понять, что значение напряжение и силы тока в такой цепи меняется со временем и имеют, грубо говоря, волновую форму.
Если мы схематически представим, как с течением времени меняются эти два значения, у нас получится синусоида. И напряжение, и сила тока от нуля поднимаются до максимального значения, затем, опускаясь, проходят через нулевое значение и достигают максимального отрицательного значения. После этого снова поднимаются через нуль до максимального значения и так далее. Когда говорится, что сила тока или напряжение имеет отрицательное значение, здесь имеется ввиду, что они движутся в обратном направлении.
Весь процесс происходит с определенной периодичностью. Та точка, где значение напряжения или силы тока из минимального значения поднимаясь к максимальному значению проходит через нуль называется фазой.
На самом деле, это только предисловие. Вернемся к реактивному и активному сопротивлению. Отличие активного сопротивления от реактивного в том, что в цепи с активным сопротивлением фаза тока совпадает с фазой напряжения. То есть, и значение силы тока, и значение напряжения достигают максимума в одном направлении одновременно. В таком случае наша формула для расчета напряжения, сопротивления или силы тока не меняется.
Если же цепь содержит реактивное сопротивление, фазы тока и напряжения сдвигаются друг от друга на ¼ периода. Это означает, что, когда сила тока достигнет максимального значения, напряжение будет равняться нулю и наоборот. Когда применяется индуктивное сопротивление, фаза напряжения «обгоняет» фазу тока. Когда применяется емкостное сопротивление, фаза тока «обгоняет» фазу напряжения.
Формула для расчета падения напряжения на индуктивном сопротивлении:
U = I ⋅ ωL
Где L – индуктивность реактивного сопротивления, а ω – угловая частота (производная по времени от фазы колебания).
Формула для расчета падения напряжения на емкостном сопротивлении:
U = I / ω ⋅ С
С – емкость реактивного сопротивления.
Эти две формулы – частные случаи закона Ома для переменных цепей.
Полный же будет выглядеть следующем образом:
I = U / Z
Здесь Z – полное сопротивление переменной цепи известное как импеданс.
Сфера применения
Закон Ома не является базовым законом в физике, это лишь удобная зависимость одних значений от других, которая подходит почти в любых ситуациях на практике. Поэтому проще будет перечислить ситуации, когда закон может не срабатывать:
- Если есть инерция носителей заряда, например, в некоторых высокочастотных электрических полях;
- В сверхпроводниках;
- Если провод нагревается до такой степени, что вольтамперная характеристика перестает быть линейной. Например, в лампах накаливания;
- В вакуумных и газовых радиолампах;
- В диодах и транзисторах.
Похожие темы:
electrosam.ru
Формула полного расчета закона Ома для цепей постоянного и переменного токов
Закон Ома – простой и мощный математический инструмент, помогающий анализировать электрические схемы. Он лучше всего используется для понимания взаимосвязи между временными характеристиками цепи. Однако ему присущи некоторые ограничения. Следует понимать подобные ограничения, чтобы правильно использовать правило в реальных схемах.
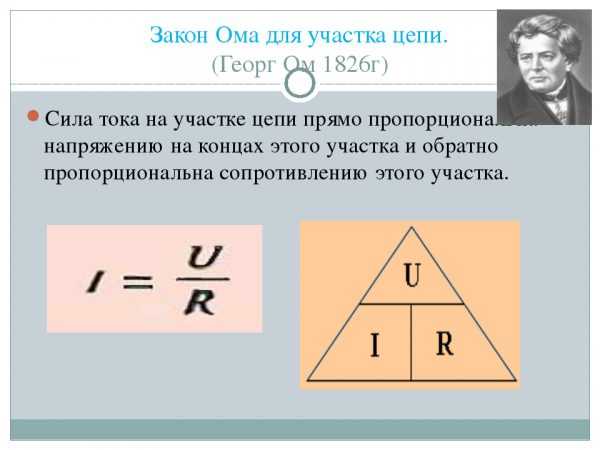
Классическая формула закона Ома
Согласно данному канону, ток увеличивается с увеличением напряжения. При фиксированном напряжении изменение сопротивления приводит к обратно пропорциональному изменению тока. Данное правило справедливо для сети только с активным сопротивлением.
Для информации. К этому принципу физики должно быть «конститутивное отношение», означающее только предположение, что некоторые материалы или даже вакуум поддерживают линейную вольт-амперную характеристику цепи. На самом же деле этого не может быть, поскольку нет такого понятия, как чистое сопротивление. Имеется в виду просто математическое упрощение. Каждому реальному резистору свойственна небольшая реальная индуктивность и емкость, и связанное с ними … сопротивление изменяется с температурой.
Закон Ома
Для участка контура
Фундаментальное правило физики имеет формулировку для цепей постоянного тока и не сопровождается нелинейными нагрузками, такими как транзисторы, диоды, конденсаторы. Переменный ток подчиняется данному правилу, но вместо известной формулы:
I = U/ R, где:
- I – ток через проводник в единицах «ампер»,
- U – напряжение, измеренное через проводник в единицах «вольт»,
- R – противодействующее сопротивление проводника в единицах «Ом»;
используется формула для расчета:
I = U / Z, где:
Z – импеданс контура.
Импеданс – это противодействие потоку электрических зарядов.
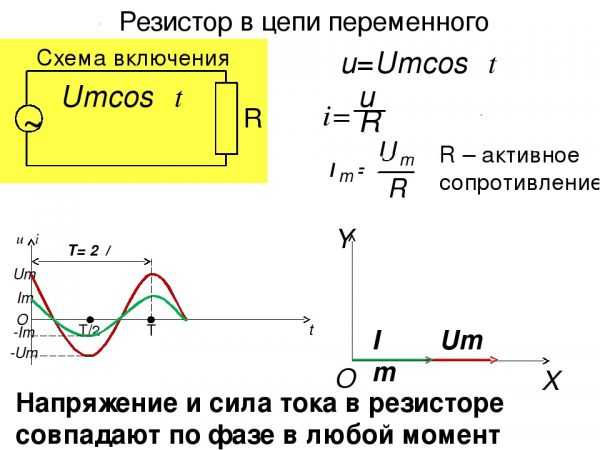
Физические параметры в контуре с активным сопротивлением
Линейная зависимость, описываемая данной функцией, на самом деле является исключением в природе. Закон применяется только при довольно ограниченном наборе условий (постоянной температуре, металлических проводниках с постоянными напряжениями).
В действительности вольт-амперное соотношение внутри физического материала обычно сложное и нелинейное. Различные нелинейные математические модели могут применяться только при четко определенных диапазонах напряжений, полярностях и температурах.
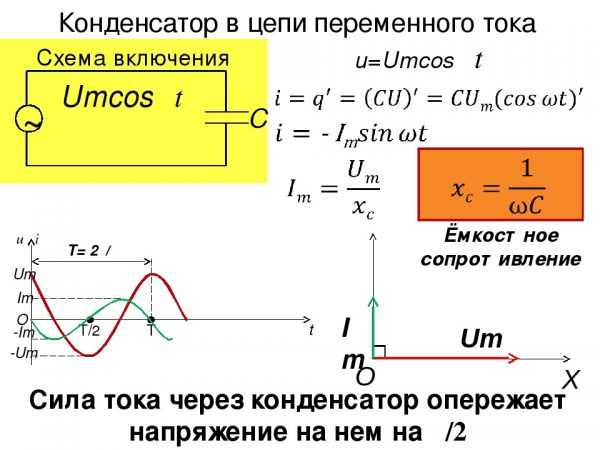
Параметры контура с реактивным сопротивлением
Для различных цепей
Когда резисторы (или лампочки) подключаются последовательно (серия), один и тот же ток проходит через каждый из них. При параллельной проводке токи не связаны друг с другом и определяются значением каждого резистора. В каждом случае величина тока определяется законом Ома:
- для последовательной схемы сопротивления складываются вместе,
- для параллельной схемы они берутся отдельно, и суммируется ток.
Математика последовательных соединений проще. Сопротивления в параллельных или более сложных конфигурациях требуют сведения к одному значению сопротивления.

Закон Ома для различных типовых цепей
Для высокого напряжения
Найти объекты, которые эмулируют резисторы на очень высокой частоте, довольно трудно. Если построить график U / I, то у большинства материалов под высоким напряжением графическая характеристика будет представлена непрямой линией. Такие материалы не подчиняются классическому закону физики.
Если есть возможность определить мгновенные значения для напряжения V и сопротивления R, то можно рассчитать мгновенный переменный ток. Получить такую величину весьма нелегко, и, следовательно, используются другие подходы, такие, как расчет по формуле со значениями реактивных составляющих и импеданса. Если амплитуда синусоиды сигнала от пика до пика находится в линейном диапазоне, то этот материал подчиняется закону Ома.
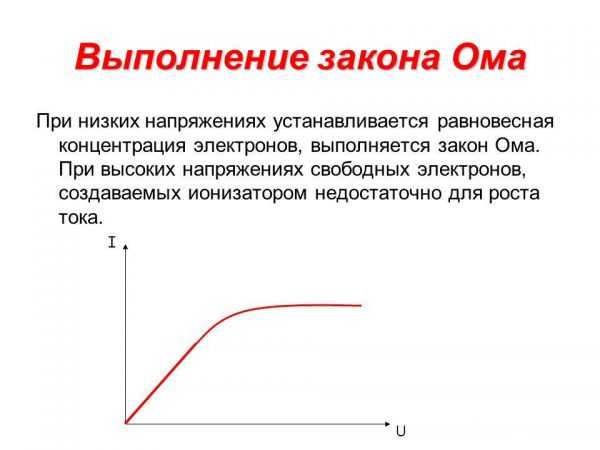
Основной закон физики для высокого напряжения
Важно! При высокой температуре закон Ома неприменим, потому что с увеличением температуры с течением времени сопротивление возрастает, из-за чего линейная зависимость между напряжением и током (как описано законом Ома) больше не существует. И ток начинает уменьшаться только из-за прироста сопротивления проводника.
Закон Ома для полной цепи
Замкнутый электрический контур делится на внешний и внутренний участки. Первый включает в себя разные сопротивления нагрузки, второй – сопротивление источника тока. В цепи ток течет как по внешнему и внутреннему контуру цепи.
Формула расчета физических параметров для полной цепи будет следующая:
I = E/R+r, где:
- E – ЭДС источника,
- R – сопротивление нагрузки,
- r – сопротивление источника тока.
Из данного соотношения видно, что, когда внешнее сопротивление становится меньше внутреннего, получается короткое замыкание.
Для информации. Закон Ома для переменного тока называется так из-за его формальной математической аналогии с основным правилом физики. По своей сути, это не должно противоречить канону физики, хотя под ним подразумеваются более сложные физические отношения.
Закон Ома для цепи переменного тока трактуется в иных формулах, нежели для постоянного тока. Поскольку в схеме имеются некоторые распределенные емкость и индуктивность, то правило физики формулируется в терминах импеданса, комплекснозначной функции частоты. Это позволяет охватить большинство случаев.
Видео
Оцените статью:elquanta.ru



