14.05.201925.11.2018

Законы ома для участка и полной цепи – 12.Обобщенный закон Ома в интегральной форме для участка цепи и полной цепи.

• by alexxlab
• Комментариев к записи Законы ома для участка и полной цепи – 12.Обобщенный закон Ома в интегральной форме для участка цепи и полной цепи. нет
• Советы абитуриенту

Решение задач на закон Ома для участка и полной цепи

Решение задач на закон Ома сводится к нахождению одной из трех неизвестных составляющих: тока, сопротивления или напряжения. Сам же закон описывает, как они соотносятся между собой.

Напомним, что согласно закону Ома сила тока прямо пропорциональна напряжению и обратно пропорциональна сопротивлению.

Формула закона Ома для участка цепи:

Формула закона Ома для полной цепи:

Задача 1

Утюг включенный в сеть напряжением 220 В, потребляет ток 1,2 А. Определите сопротивление утюга.

Дано  U = 220 В I = 1,2 А	Решение Согласно закону Ома для участка цепи:
Найти R – ?
Ответ: R = 183,3 Ом.

Задача 2

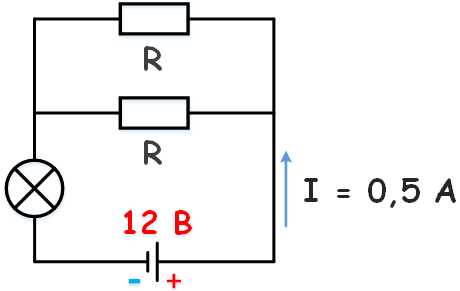
К аккумулятору с ЭДС 12 В, подключена лампочка и два параллельно соединенных резистора сопротивлением каждый по 10 Ом. Известно, что ток в цепи 0,5 А, а сопротивление лампочки R/2. Найти внутреннее сопротивление аккумулятора.

Дано  E = 12 В I = 0,5 А Rл = Rр/2 Rр = 10 Ом	Решение Найдем экв. сопротивление двух параллельно соединённых резисторов: Сопротивление лампочки: Согласно закону Ома для полной цепи:
Найти r – ?
Ответ: r = 14 Ом.

Задача 3

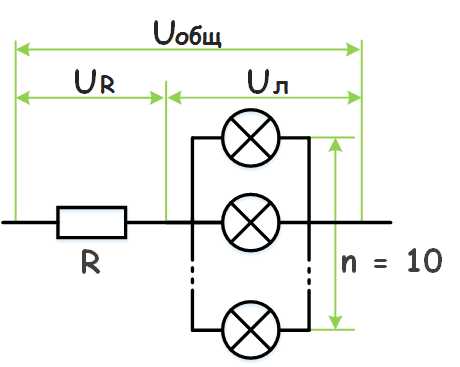
К участку цепи с напряжением 12 В через резистор сопротивлением 2 Ом подключены десять одинаковых лампочек сопротивлением 10 Ом. Найти напряжение на каждой лампочке.

Дано  Uобщ = 10 В Rр = 2 Ом Rл = 10 Ом	Решение Так как лампочки подключены параллельно, напряжение на них будет одинаковым, согласно закону Ома для участка цепи: При последовательном соединении ток в цепи общий: Выразим Uл через Uобщ: Найдем Rэкв: Окончательно получим:
Найти Uл – ?
Ответ: Uл = 4 В.

Задача 4

Как определить длину мотка медной проволоки, не разматывая его?

Решение:

Для решения данной задачи необходимо воспользоваться формулой:

отсюда длина проволоки

В этой формуле, l – длина проволоки, R – сопротивление, S – площадь поперечного сечения, ρ – удельное сопротивление металлов, в данном случае ρ для меди равно 0.0175 Ом/м.

Сопротивление R проволоки можно измерить с помощью омметра, а площадь S с помощью штангенциркуля, измерив  диаметр проволоки и по формуле Πr² вычислив ее значение. Значение удельного сопротивления ρ не только для меди, но и других металлов можно найти в справочнике, или тут. Подставив все известные величины в формулу, приведенную выше, получим длину проволоки.

Задача 5

Начертите схему электрической цепи, состоящей из источника тока, выключателя и двух ламп, включенных параллельно. Что произойдет в цепи при перегорании одной лампы?

Решение:

При перегорании одной из лампочек, вторая будет гореть, так как, при параллельном включении проводников токи I₁ и I₂ проходящие через них не зависят друг от друга и при разрыве параллельной цепочки ток продолжает протекать.

Просмотров: 890

electroandi.ru

Закон Ома для участка цепи

Когда электрическая цепь создана, свободные заряды (электроны) получают возможность двигаться. Это движение называется электрическим током, или иначе, потоком электричества. Такое движение подобно движению жидкости внутри полой трубы, но не во всём сохраняется такое подобие, есть и существенные различия.

Сила движения свободных зарядов определяется напряжением, которое является специфическим показателем потенциальной энергии. Напряжение всегда характеризуется двумя точками в электрической цепи, и потому правильнее говорить не о напряжении, а о падении напряжения между двумя точками цепи. Обычно слово падение опускают, подразумевая под обозначением «напряжение» – падение напряжения на определённом участке электрической цепи. Это значит, что употребляя термин «напряжение» всегда подразумеваются две точки участка цепи, начальная и конечная. Для одной точки понятие падения напряжения не имеет смысла, всегда две точки и конкретный участок цепи.

Свободные заряды, а в проводниках первого рода (металлы и сплавы) ими являются электроны, имеют свойство двигаться через проводник с некоторой степенью трения, оказывая сопротивление к своему движению под действие источника тока (ЭДС). Это противостояние так и называется — сопротивление

.

Величина тока в цепи зависит от величины напряжения, которое разгоняет свободные электроны, и от величины сопротивления участка цепи. Точно так же как и падение напряжения (напряжение), сопротивление является величиной характеризующей участок цепи, то есть сопротивление — это всегда между двумя точками цепи.

Ток существует в электрической цепи, а падение напряжения и сопротивление — это всегда участок цепи, всегда между двумя точками.

Для того, чтобы работать с этими параметрами электрической цепи, надо иметь возможность описать их количественно, точно так же как описывается масса, объем, длина и другие физические величины.

Вот стандартные единицы измерения для электрического тока, напряжения и сопротивления:

«Символ» – это обозначение физической величины в алгебраических уравнениях, на схемах, таблицах, технической документации, в дисциплинах физики и инженерии. Эти обозначения являются общепризнанными на международном уровне.

«Аббревиатура» – представляет собой алфавитный символ, который используется для сокращённой записи количества в единицах измерения. Своеобразная подкова Ω — это греческая буква «омега», именно ей и обозначают в электротехнике сопротивление.

Каждая единица измерения названа в честь известного исследователя электричества. Сила тока в честь француза Андре Мари Ампера, напряжение в честь Алессандро Вольта, и сопротивление в честь немецкого исследователя — Георга Симона Ома.

Закон Ома — взаимосвязь трёх величин

Все три величины: напряжение, ток и сопротивление, взаимосвязаны. Такую взаимосвязь обнаружил Георг Симон Ом и опубликовал в статье в 1827 году. Он математически исследовал гальваническую электрическую цепь.

Основным открытием Ома было то, что величина силы тока, проходящего через металлический проводник прямо пропорциональна напряжению, что и выразил он в виде математической записи — уравнения (формулы).

В этом алгебраическом выражении напряжение (V) равно величине силе тока (I) умноженной на сопротивление (R). Используя алгебраические методы, мы можем манипулировать этим уравнением и записать его ещё в двух вариантах, для I и для R соответственно:

Формулировка Закона Ома для участка цепи имеет следующее содержание:

Сила тока, протекающего в участке цепи, прямо пропорциональна падению напряжения на этом участке, и обратно пропорциональна сопротивлению этого участка.

Важно помнить, что сила тока всегда в участке цепи (ветви), а падение напряжения и сопротивление — это всегда на участке цепи.

Не может быть силы тока на участке цепи, или падения напряжения и сопротивления в участке цепи, потому как это нелогично, абсурдно. Неверное употребление в речи и письме предлогов «в» и «на» говорит об отсутствии понимания сути основных электрических величин: напряжения, тока и сопротивления говорящим или пишущим.

Без правильного понимания сути физических явлений и величин, которые характеризуют электрическую цепь, невозможно профессионально выполнять электротехнические работы, и тем более выполнять инженерные расчёты.

Прямая пропорциональность говорит о том, что при увеличении напряжения V в n раз, сила тока I увеличится также в n раз, то же самое касается уменьшения величины напряжения.

Обратная пропорциональность говорит сама за себя. Если сопротивление R увеличится в n раз, тогда сила тока I уменьшится в n раз. Если же сопротивление уменьшится в n раз, тогда сила тока I увеличится в n раз.

Дата: 21.06.2015

© Valentin Grigoryev (Валентин Григорьев)

electricity-automation.com

Закон Ома для электрической цепи

Электрический ток, как и любой процесс, подчиняется законам физики. Знаменитый немецкий физик Георг Симон Ом, именем которого названа единица измерения сопротивления, в 1826 году эмпирически вывел формулы, связывающие между собой ток, напряжение и сопротивление. Поначалу закон вызвал недоверие и критику в научных кругах. Затем правильность его рассуждений была подтверждена французом Клодом Пулье и труды Ома получили заслуженное признание.

Закон Ома для электрической цепи (полной)

Частный случай – закон Ома для участка цепи:

Обозначение	Единица измерения	Физический смысл
I	Ампер	Сила тока в цепи
ԑ	Вольт	Электродвижущая сила (э.д.с.) источника питания
r	Ом	Внутреннее сопротивление источника питания
R	Ом	Сопротивление нагрузки, подключенной и источнику
U	Вольт	Падение напряжения на сопротивлении нагрузки

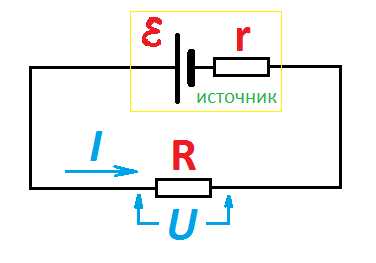Поясняющая схема к закону Ома

Добавим к этим формулам еще и электрическую мощность, выделяемую при прохождении тока:

В результате получается ряд формул, которые выводятся математически. Они связывают между собой все перечисленные физические величины.

Электродвижущая сила и внутреннее сопротивление

Электродвижущая сила источника напряжения характеризует его способность обеспечивать постоянную разность потенциалов на выводах. Эта сила имеет неэлектрическую природу: химическую у батареек, механическую – у генераторов.

Какова роль внутреннего сопротивления источника питания и что это такое? Допустим, вы замкнули накоротко выводы автомобильного аккумулятора медным проводником небольшого сечения. В физическом смысле вы подключили к источнику постоянного тока сопротивление, близкое к нулю. Если воспользоваться формулой для участка цепи, то через аккумулятор и проволоку должен пойти ток бесконечно большой величины. На деле этого не происходит, но проволока сгорит.

Теперь замкнем этой же проволокой батарейку. Ток через нее пойдет меньший. Это объясняется большим, чем у аккумулятора, значением внутреннего сопротивления. При малом сопротивлении нагрузки формула закона для полной цепи превращается в

В итоге ток через замкнутую накоротко батарейку будет иметь конечное значение, а мощность приведет к нагреву батарейки. Если бы мы замкнули аккумулятор более толстым проводом, выдержавшим ток короткого замыкания, то он ощутимо нагрел бы источник изнутри.

Э.Д.С. источника можно с некоторой точностью измерить вольтметром с высоким входным сопротивлением. Внутреннее же сопротивление источника нельзя измерить напрямую, а только рассчитать.

Закон Ома для переменного тока

На переменном токе в формуле закона Ома используется не активное, а полное сопротивление (Z).

Эта величина учитывает и активное, и реактивное сопротивление нагрузки, которое в свою очередь имеет индуктивную

и емкостную

составляющие.

Общее реактивное сопротивление цепи:

Знак (-) означает, что индуктивный и емкостной токи находятся в противофазе и друг друга компенсируют.

Оцените качество статьи. Нам важно ваше мнение:

electric-tolk.ru

Закон Ома для участка и полной замкнутой цепи

В 1826 г. немецкий ученый Георг Ом экспериментально установил прямую пропорциональную зависимость между силой тока I в проводнике и напряжением U на его концах: , гдеG – электрическая проводимость проводника. Величина, обратная проводимости называется электрическим сопротивле­ни­ем проводника R. Таким образом, закон Ома для участка цепи, не содержа­щего источника э.д.с., имеет вид . Учитывая, что в общем случае участок цепи может содержать и э.д.с.,закон Ома следует представить в виде .

Сопротивление проводника зависит от его размеров, формы и материала, из которого он изготовлен. Для однородного линейного проводника , гдеl – длина, S – площадь поперечного сечения проводника,  – удельное электриче­с­кое сопротивление, зависящее от материала, из которого изготовлен проводник. Единица сопротивления 1 Ом – это сопротивление такого проводника, в котором при напряжении 1В течет ток в 1А.

Если цепь замкнута, то ,, гдеR – общее сопротивление всей цепи, включая сопротивление источника э.д.с. Тогда закон Ома для замкнутой цепи следует записать , где – алгебраическая сумма всех э.д.с., имеющихся в этой цепи.

Принято называть сопротивление источника тока r – внутренним, а сопротив­ление всей остальной цепи R – внешним. Окончательный вид формулы закона Ома для замкнутой цепи . В системе единиц СИ напряжение и э.д.с. изме­ряются в Вольтах (В), сопротив­ление – в Омах (Ом), удельное электрическое сопротивление – в Ом-метрах (Омм), электрическая проводимость в Сименсах (См).

Рис.2.1. Отрезок проводни­ка.

Закон Ома можно записать и для плотности тока. Рассмотрим участок электрической длиной dl и поперечным сечением dS (рис.2.1). Сила тока на этом участке , сопротивление, падение на­пряжения, где Е – напряженность электрического поля в проводнике. Под­ставив эти параметры в закон Ома для участка цепи, получим. Отсюдаили, где-удельная электрическая проводи­мость проводника или удельная электропроводность. В векторном виде имеем (единицей измерения в системе СИ является сименс на метр (См/м)). Полученное выражение есть закон Ома в дифференциальной форме : плот­ность тока в любой точке внутри проводника прямо пропорциональна напря­женности поля в этой точке.

1.14 Сопротивление проводника. Явление сверхпроводимости.

Способность вещества проводить ток характеризуется его удельной проводи­мостью , либо удельным сопротивлением . Их величина определяется химичес­кой природой проводника и условиями, в частности температурой, при которой он находится. Для большинства металлов  растет с температурой приблизительно по линейному закону: ,- удельное сопротивление при 0С, t – температура по шкале Цельсия,  – темпе­ра­турный коэффициент сопротивления близкий к 1/273 К^-1 при не очень низких темпе­ратурах. Так как R, то , где- сопротивление при 0С. Преобра­зовав две последние формулы, можно записать и, где Т – температура по Кельвину. На основе температурной зависимости сопротивления метал­лов созда­нытермометры сопротивления – термисторы, позволяющие определять температуру с точно­стью до 0.003 К.

При низких температурах нарушается линейность зависимости сопротивления металлов от температуры и при температуре 0 К наблюдается остаточное сопротивление R_ост. Величина R_ост зави­сит от чистоты материала и наличия в нем механических напряжений. Лишь у иде­ально чистого металла с идеально правильной кристаллической решеткой R_ост 0 при Т0 (пунктирная часть кривой).

Кроме этого, в 1911 г. Г.Каммерлинг-Оннес обнару­жил, что при Т_к = 4.1К сопротивление ртути скачкообразно уменьшается практически до нуля. Эта температура была названа критической, а наблюдаемое яв­ление – сверхпроводимостью. Впо­следствии этот эффект был обнаружен у целого ряда дру­гих металлов (Ti, Al, Pb, Zn, V и др.) и их спла­вов в интервале температур 0.14-20 К. Вещества в сверхпроводящем состоянии обладают необычными свойствами. Однажды возбужденный в них ток может длительно существовать без источника тока. Переход в сверхпроводящее состояние сопровождается скачкообразным изме­нением теплоемкости, теплопроводности, маг­нитных свойств вещества. Выясни­лось, что внешнее магнитное поле не проникает в толщи­ну сверхпроводника, т.е. магнитная индукция внутри него всегда равна нулю. Явление сверхпроводимости объясняется на основе квантовой теории. К настоящему времени это явление обнаружено также у ряда композиционных веществ (например, соединений металлов и диэлектриков), при этом критическая температура доходит до температуры сжижения азота, что позволяет достаточно экономично использовать явление высокотемпературной сверхпроводимости в инженерной практике. Данное явление позволяет создавать: системы передачи без потерь электрического тока по проводам из таких веществ, системы для накопления электроэнергии, мощные электромагниты, магнитные подвески для различных целей.

1.15 Работа и мощность тока, закон Джоуля-Ленца.

Определим работу, совершаемую постоянным током в проводнике, имеющем сопротивление R и находящемся под напряжением . Так как ток пред­ставляет собой перемещение зарядаq под действием поля, то работу тока можно оп­ределить по формуле . Учитывая формулуи закон Ома, получим, или, или, гдеt – время протекания тока. Поделив обе части равенства на t, получим выраже­ния для мощности постоянного тока N

, ,. Работа тока в системе единиц СИ измеряется в доулях (Дж), а мощность – в ваттах (Вт). На практике применяются также внесистемные единицы работы тока: ватт-час (Втч) и киловатт-час (кВтч). 1Втч – работа тока мощностью 1Вт в течение одного часа. 1Втч=3.610³ Дж.

Опыт показывает, что ток всегда вызывает некоторое нагревание проводника. Нагревание обусловлено тем, что кинетическая энергия движущихся по проводнику электронов (т.е. энергия тока) при каждом их столкновении с ионами металличе­ской решетки переходит в теплоту Q. Если ток идет по неподвижному металличе­скому проводнику, то вся работа тока расходуется на его нагревание и, следуя за­кону сох­ранения энергии, можно записать . Данные соотношения выражаютзакон Джоуля-Ленца. Впервые этот закон был установлен опытным путем Д.Джоулем в 1843 г. и независимо от него Э.Ленцем в 1844 г. Применение теплового действия тока в технике началось с открытия в 1873 г. русским инженером А.Ладыгиным лампы накаливания.

На тепловом действии тока основан целый ряд электрических приборов и ус­та­новок: тепловые электроизмерительные приборы, электропечи, электросварочная аппаратура, бытовые электронагревательные приборы – чайники, кипятильники, утюги. В пищевой промышленности широко применяется метод электроконтактного нагрева, заключающийся в том, что электрический ток, проходя через продукт, об­ла­дающий определенным сопротивлением, вызывает его равномерное нагревание. На­пример, для производства колбасных изделий через дозатор фарш поступает в формы, торцевые стенки которых служат электродами. При такой обработке обес­пе­чивается равномерность нагрева по всему объему продукта, возможность под­держа­ния определенного температурного режима, наивысшая биологическая цен­ность из­делия, наименьшие длительность процесса и расход энергии.

Определим удельную тепловую мощность тока , т.е. количество теплоты, вы­деляющееся в единице объема за единицу времени. Выделим в проводнике элемен­тарный цилиндрический объем dV с поперечным сечением dS и длиной dl параллель­ной направлению тока, и сопротивлением ,. По закону Джоуля-Ленца, за времяdt в этом объеме выделится теплота . Тогдаи, используя закон Ома для плотности токаи соотно­шение, получим. Эти соотношения выражаютзакон Джоуля-Ленца в дифференциальной форме.

1.16. Правило Кирхгофа для разветвленных электрических цепей.

До сих пор нами рассматривались простейшие электрические цепи, состоя­щие из одного замкнутого неразветвленного контура. На всех его участках силы тока оди­наковы. Расчет I, R,  в такой цепи выполняется с помощью законов Ома.

Рис.2.2.Разветвленная электрическая цепь.

Более сложной является разветвленная электри­ческая цепь, состоящая из нескольких замкнутых кон­ту­ров, имеющих общие участки. В каждом контуре мо­жет быть несколько источников тока. Силы тока на от­дельных участках замкнутого контура могут быть раз­личными по величине и направлению (рис.2.2). В 1847 г. Г.Кирхгоф сформулировал два правила, значительно упрощающих расчет разветвленных цепей.

Первое правило Кирхгофа: алгебраическая сумма сил токов в узле равна нулю: .Узел – точка цепи, в которой сходятся не менее трех про­водников. В электрической цепи на рис.2.2 имеются два узла А и В. Ток, входящий в узел, считается положительным, выходящий – отрицательным. Например, для узла А первое правило Кирх­гофа следует записать .

Первое правило выражает закон сохранения электрического заряда, так как ни в одной точке цепи они не могут возникать или исчезать.

Второе правило Кирхгофа относится к любому замкнутому контуру, выде­ленному в разветвленной цепи: алгебраическая сумма произведений токов на со­противления, включая и внутренние, на всех участках замкнутого контура равна алгебраической сумме электродвижущих сил, встречающихся в этом контуре . Контур ‑ это замкнутый участок схемы, по которому можно пройти и вернуться в исходную точку. Второе правило Кирхгофа получается из закона Ома, записанного для всех участков от узла до узла (ветвей) разветвленной схемы. В электрической цепи на рис.2.2 имеются три контура:AMNBA, CABDC, CMNDC. При этом, токи I_i в ветвях контура, совпадающие с произвольно вы­бран­ным направлением обхода контура, считаются положительными, а направлен­ные на­встречу обхода – отрицательными. Э.д.с., проходимые от «+» к «-» считаются поло­жительными и наоборот. В рассматриваемой элек­трической цепи (рис.2.2) выберем обход контуров по часовой стрелке и запишем для них уравнения по II правилу Кирхгофа: для AMNBА ; дляCABDС ; дляCMNDС . В данном примере внутренними сопротивлениями источников тока пренебрегаем. Первое и второе правила Кирхгофа по­зволяют составить систему линейных алгебраичес­ких уравнений, которые связывают пара­метры (I, R, ) и позволяют, зная одни, найти другие.

Рис.2.3. а) Последовательное соеди­нение сопротивлений; б) Параллельное соединение со­противлений.

Простые электрические цепи имеют очень большое практическое применение. В повседневной жизни полезно знать, как под­ключить динамики или проигрыватель к сте­реосистеме, как подсоединить сигнализацию для охраны или автомобильный кас­сетный проигрыватель, как зарядить аккумуляторы или осветить новогоднюю елку.

Большинство электрических цепей содержит комбинацию последовательно или параллельно подключенных резисторов (резистор – это элемент цепи, обла­дающий только сопротивлением). Полное сопротивление участка цепи оп­ределяется отношением падения на­пряжения на нем к величине силы тока . При последовательном соединении (рис.2.3 а) через все резисторы течет один и тот же ток. При параллельном соединении (рис.2.3 б) полный ток равен сумме токов, те­кущих в отдельных резисторах.

При последовательном соединении падение на­пряже­ния на участке АВ равно , т.е. сумме падений напряжения на трех резисторах. Разделим обе части равенства наI и получим , т.е.. Таким образом, полное сопротивление участка цепи, состоящего из последо­ва­тельно соединенных резисторов, равно их алгебраической сумме.

При параллельном соединении (рис..2.3 б) мы имеем . Разделим обе части равенства наU, где U – падение напряжения на участке цепи АВ, причем , и получим. Из этого равенства следует. Величина обратная полному сопротивлению параллельно соединенных резис­торов равна алгебраической сумме величин их обратных сопротивлений.

В электрическую цепь может быть включено регулируемое (изменяющееся с помощью специального движка), сопротивление, которое называется реостатом. По назначению реостаты делятся на пусковые, служащие для ограничения силы тока во время пуска двигателей, и регулирующие – для регулировки силы тока в цепи (по­степенное снижение освещенности в театральных залах), регулировки скорости вращения электродвигателей и т.д. Реостат может быть использован в качестве так называемого датчика пере­мещения. В автоматических регуляторах уровня жидкос­ти в резервуарах применя­ется поплавково-реостатный датчик. Специальный поплавок крепится к движку реостата. Изменение уровня жидкости сдвигает поплавок, изменя­ет сопротивление реостата, и следовательно, силы тока в цепи, величина которого дает информацию об уровне.

studfiles.net

Закон Ома для участка цепи, формула, определение

Закон Ома для участка цепи, безусловно, можно описать известной из школьного курса физики формулой: I=U/R, но некоторые изменения и уточнения внести, думаю, стоит.

Возьмем замкнутую электрическую цепь (рисунок 1) и рассмотрим ее участок между точками 1-2. Для простоты я взял участок электрической цепи, не содержащий источников ЭДС (Е).

Итак, закон Ома для рассматриваемого участка цепи имеет вид:

φ1-φ2=I*R, где

• I – ток, протекающий по участку цепи.
• R – сопротивление этого участка.
• φ1-φ2 – разность потенциалов между точками 1-2.

Если учесть, что разность потенциалов это напряжение, то приходим к производной формулы закона Ома, которая приведена в начале страницы: U=I*R

Это формула закона Ома для пассивного участка цепи (не содержащего источников электроэнергии).

В неразветвленной электрической цепи (рис.2) сила тока во всех участках одинакова, а напряжение на любом участке определяется его сопротивлением:

• U₁=I*R₁
• U₂=I*R₂
• Un=I*Rn
• U=I*(R₁+R₂+…+Rn

Отсюда можно получить формулы, которые пригодятся при практических вычислениях. Например:

U=U₁+U₂+…+Un или U₁/U₂/…/Un=R₁/R₂/…/Rn

Расчет сложных (разветвленных) цепей осуществляется с помощью законов Кирхгофа.

ПРАВИЛО ЗНАКОВ ДЛЯ ЭДС

Перед тем как рассмотреть закон Ома для полной (замкнутой) цепи приведу правило знаков для ЭДС, которое гласит:

Если внутри источника ЭДС ток идет от катода (-) к аноду (+) (направление напряженности поля сторонних сил совпадает с направлением тока в цепи, то ЭДС такого источника считается положительной (рис.3.1). В противном случае – ЭДС считается отрицательной (рис.3.2).

Практическим применением этого правила является возможность приведения нескольких источников ЭДС в цепи к одному с величиной E=E₁+E₂+…+En, естественно, с учетом знаков, определяемых по вышеприведенному правилу. Например (рис.3.3) E=E₁+E₂-E₃.

При отсутствии встречно включенного источника E3 (на практике так почти никогда не бывает) имеем широко распространенное последовательное включение элементов питания, при котором их напряжения суммируются.

ЗАКОН ОМА ДЛЯ ПОЛНОЙ ЦЕПИ

Закон Ома для полной цепи – его еще можно назвать закон ома для замкнутой цепи, имеет вид I=E/(R+r).

Приведенная формула закона Ома содержит обозначение r, которое еще не упоминалось. Это внутреннее сопротивление источника ЭДС. Оно достаточно мало, в большинстве случаев при практических расчетах им можно пренебречь (при условии, что R>>r – сопротивление цепи много больше внутреннего сопротивления источника). Однако, когда они соизмеримы, пренебрегать величиной r нельзя.

Как вариант можно рассмотреть случай, при котором R=0 (короткое замыкание). Тогда приведенная формула закона Ома для полной цепи примет вид: I=E/r, то есть величина внутреннего сопротивления будет определять ток короткого замыкания. Такая ситуация вполне может быть реальной.

Закон Ома рассмотрен здесь достоточно бегло, но приведенных формул достаточно для проведения большинства расчетов, примеры которых, по мере размещения других материалов я буду приводить.

© 2012-2018 г. Все права защищены.

Все представленные на этом сайте материалы имеют исключительно информационный характер и не могут быть использованы в качестве руководящих и нормативных документов

eltechbook.ru

Закон Ома для участка цепи, содержащего ЭДС | Учеба-Легко.РФ

Закон Ома для участка цепи, содержащего источник ЭДС. Обобщенный закон Ома. Закон (правило) Ома для участка цепи, содержащего источник ЭДС, позволяет найти ток этого участка по известной разности потенциалов (φ_а – φ_с)на концах участка цепи и имеющейся на этом участке ЭДС E.

Так, по уравнению (1.2) для схемы рис. 2.6, а

I = (φ_a – φ_c + E) / R = (U_ac + E) / R;

по уравнению (2.2а) для схемы рис. 2.6, б

I = (φ_a – φ_c – E) / R = (U_ac – E) / R.

В общем случае

          (2.3а)

Уравнение (2.3а) математически выражает закон Ома для участка цепи, содержащего источник ЭДС; знак плюс перед Е соответствует рис. 2.6, а, знак минус – рис. 2.6, б. В частном случае при Е = 0 уравнение (2.3а) переходит в уравнение (2.3).

Закон Ома для полной цепи:

, (2)

где:

• — ЭДС источника напряжения(В),
• — сила тока в цепи (А),
• — сопротивление всех внешних элементов цепи (Ом),
• — внутреннее сопротивление источника напряжения (Ом).

Из закона Ома для полной цепи вытекают следствия:

• При r< сила тока в цепи обратно пропорциональна её сопротивлению. А сам источник в ряде случаев может быть назван источником напряжения
• При r>>R сила тока от свойств внешней цепи (от величины нагрузки) не зависит. И источник может быть назван источником тока.

Часто выражение:

(3)

(где есть напряжение или падение напряжения, или, что то же, разность потенциалов между началом и концом участка проводника) тоже называют «Законом Ома».

Таким образом, электродвижущая сила в замкнутой цепи, по которой течёт ток в соответствии с (2) и (3) равняется:

(4)

То есть сумма падений напряжения на внутреннем сопротивлении источника тока и на внешней цепи равна ЭДС источника. Последний член в этом равенстве специалисты называют «напряжением на зажимах», поскольку именно его показывает вольтметр, измеряющий напряжение источника между началом и концом присоединённой к нему замкнутой цепи. В таком случае оно всегда меньше ЭДС.

К другой записи формулы (3), а именно:

(5)

Применима другая формулировка:

Сила тока в участке цепи прямо пропорциональна напряжению и обратно пропорциональна электрическому сопротивлению данного участка цепи.

Выражение (5) можно переписать в виде:

(6)

где коэффициент пропорциональности G назван проводимость или электропроводность. Изначально единицей измерения проводимости был «обратный Ом» — Mо, впоследствии переименованный в Си́менс

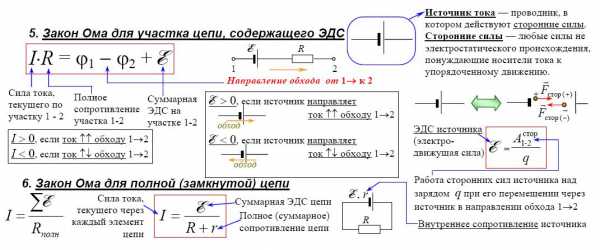
В заключение предлагаем Вашему вниманию шпаргалку по этой теме:

 

uclg.ru

---