Формула пи: Число Пи – значение, история, кто придумал
- Число Пи – значение, история, кто придумал
- Калейдоскоп формул для пи
- Март, четырнадцатое. Как вычислить число Пи
- ЧЕМУ РАВНО ЧИСЛО ПИ? – Ньютонов ⚛ физика
- Март, четырнадцатое
- 3,14 способа запомнить число π с большой точностью
- Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике – Планиметрия
- Пи
- Вычисление числа Пи (π) – Maths Careers
- PI
- Что такое Пи и как он появился?
- Как использовать функцию Excel PI
- – это красивая формула (с использованием числа Пи), показывающая, что математика пугающе совершенна – Кварц
Число Пи – значение, история, кто придумал
Все окружности похожи
Если сравнить окружности отличных друг от друга размеров, то можно заметить следующее: размеры разных окружностей пропорциональны. А это значит, что при увеличении диаметра окружности в некоторое количество раз, увеличивается и длина этой окружности в такое же количество раз. Математически это записать можно так:
| C1 | C2 | ||
| = | |||
| d1 | d2 | (1) |
где C1 и С2 – длины двух разных окружностей, а d1 и d2 – их диаметры.
Это соотношение работает при наличии коэффициента пропорциональности – уже знакомой нам константы π. Из отношения (1) можно сделать вывод: длина окружности C равна произведению диаметра этой окружности на независящий от окружности коэффициент пропорциональности π:
C = πd.
Также эту формулу можно записать в ином виде, выразив диаметр d через радиус R данной окружности:
С = 2πR.
Как раз эта формула и является проводником в мир окружностей для семиклассников.
Еще с древности люди пытались установить значение этой константы. Так, например, жители Месопотамии вычисляли площадь круга по формуле:
| C 2 | |||
| S | = | , | |
| 12 |
где S – площадь круга, C – длина окружности (круга). Если в эту формулу подставить уже знакомые школьнику выражения площади круга S = πr2 и длины окружности С = 2 πR, то мы получим:
Если в эту формулу подставить уже знакомые школьнику выражения площади круга S = πr2 и длины окружности С = 2 πR, то мы получим:
| (2πR)2 | ||
| πR2 | = | |
| 12 |
, откуда π = 3.
В древнем Египте значение для π было точнее. В 2000-1700 годах до нашей эры писец, именуемый Ахмесом, составил папирус, в котором мы находим рецепты разрешения различных практических задач. Так, например, для нахождения площади круга он использует формулу:
| 8 | 2 | |||||
| S | = | ( | d | ) | ||
| 9 |
Из каких соображений он получил эту формулу? – Неизвестно. Вероятно, на основе своих наблюдений, впрочем, как это делали и другие древние философы.
Вероятно, на основе своих наблюдений, впрочем, как это делали и другие древние философы.
По стопам Архимеда
– Какое из двух числе больше 22/7 или 3.14 ?
– Они равны.
– Почему ?
– Каждое из них равно π.
А. А. Власов. Из Экзаменационного билета.
Некоторы полагают, что дробь 22/7 и чисо π тождественно равны. Но это является заблуждением. Помимо вышеприведенного неверного ответа на экзамене (см. эпиграф) к этой группе можно также добавить одну весьма занимательную головоломку. Задание гласит: “переложите одну спичку так, чтобы равенство стало верным”.
Решение будет таковым: нужно образовать “крышу” для двух вертикальных спичек слева, используя одну из вертикальных спичек в знаменателе справа. Получится визуальное изображение буквы π.
Многие знают, что приближение π = 22/7 определил древнегреческий математик Архимед. В честь этого часто такое приближение называют “Архимедовым” числом. Архимеду удалось не только установить приближенное значение для π, но также найти точность этого приближения, а именно – найти узкий числовой промежуток, которому принадлежит значение π. В одной из своих работ Архимед доказывает цепь неравенств, которая на современный лад выглядела бы так:
Архимеду удалось не только установить приближенное значение для π, но также найти точность этого приближения, а именно – найти узкий числовой промежуток, которому принадлежит значение π. В одной из своих работ Архимед доказывает цепь неравенств, которая на современный лад выглядела бы так:
| 10 | 6336 | 14688 | 1 | |||||||||
| 3 | < | < | π | < | < | 3 | ||||||
| 71 | 1 | 1 | 7 | |||||||||
| 2017 | 4673 | |||||||||||
| 4 | 2 | |||||||||||
можно записать проще: 3,140 909 < π < 3,1 428 265. ..
..
Как видим из неравенств, Архимед нашел довольно-таки точное значение с точностью до 0,002. Самое удивительно то, что он нашел два первых знака после запятой: 3,14… Именно такое значение чаще всего мы используем в несложных расчетах.
Практическое применение
Едут двое в поезде:− Вот смотри, рельсы прямые, колеса круглые.
Откуда же стук?
− Как откуда? Колеса-то круглые, а площадь
круга пи эр квадрат, вот квадрат-то и стучит!
Как правило, знакомятся с этим удивительным числом в 6-7 классе, но более основательно им занимаются к концу 8-го класса. В этой части статьи мы приведем основные и самые важные формулы, которые пригодятся вам в решении геометрических задач, только для начала условимся принимать π за 3,14 для удобства подсчета.
Пожалуй, самая известная формула среди школьников, в которой используется π, это – формула длины и площади окружности. Первая – формула площади круга – записывается так:
где S – площадь окружности, R – ее радиус, D – диаметр окружности.
Длина окружности, или, как ее иногда называют, периметр окружности, вычисляют по формуле:
С = 2 πR = πd,
где C – длина окружности, R – радиус, d – диаметр окружности.
Понятно, что диаметр d равен двум радиусам R.
Из формулы длины окружности можно легко найти радиус окружности:
| C | C | ||
| R= | = | ||
| 2π | d |
Обозначения для этих формул остаются те же.
Диаметр окружности можно найти по формуле:
где D – диаметр, С – длина окружности, R – радиус окружности.
Это базовые формулы, знать которые должен каждый ученик. Также иногда приходится вычислять площадь не всей окружности, а только ее части – сектора. Поэтому представляем вам её – формулу для вычисления площади сектора окружности. Выглядит она так:
| α | |||
| S | = | πR2 | |
| 360˚ |
где S – площадь сектора, R – радиус окружности, α – центральный угол в градусах.
Такое загадочное 3,14
И правда, оно загадочно. Потому что в честь этих магических цифр устраивают праздники, снимают фильмы, проводят общественные акции, пишут стихи и многое другое.
Например, в 1998 году вышел фильм американского режиссера Даррена Аронофски под названием “Пи”. Фильм получил множество наград.
Каждый год 14 марта в 1:59:26 люди, интересующиеся математикой, празднуют “День числа Пи”. К празднику люди подготавливают круглый торт, усаживаются за круглый стол и обсуждают число Пи, решают задачи и головоломки, связанные с Пи.
Вниманием это удивительное число не обошли и поэты, неизвестный написал:
Надо только постараться и запомнить всё как есть – три, четырнадцать, пятнадцать, девяносто два и шесть.
Давайте развлечемся!
Вашему вниманию предлагаются интересные ребусы с числом Пи. Разгадайте слова, какие зашифрованы ниже.
1. π р
2. π L
3. π k
π k
Ответы: 1. Пир; 2. Надпил; 3. Писк.
Число Пи – справочные материалы
Чему равно число Пи
Как запомнить число Пи
Число Пи в Excel
Число Пи на клавиатуре и в Word
Фотографии числа Пи
Калейдоскоп формул для пи
Калейдоскоп формул для пи«…я считал, что есть две математики — алгебраическая и геометрическая, и что геометрическая математика принципиально “трансцендентна” для алгебраической. Возьмите, например, формулу длины окружности — там есть “геометрическое” число $\pi$. Или, скажем, синус — он определяется чисто геометрически.
Когда я обнаружил, что синус можно записать алгебраически в виде ряда, барьер обрушился, математика стала единой.»
— из интервью И. М. Гельфанда
«Калейдоскоп» ниже состоит из нескольких «алгебраических» формул для $\pi$ с краткими комментариями.
Он также опубликован (с сокращениями) в журнале «Квант» (№5 за 2020 год). 2$ (последнее равенство — это, по сути, основная теорема арифметики).
Более серьезное обсуждение вопроса можно найти, например, в книге «Введение в теорию чисел» Харди и Райта.
2$ (последнее равенство — это, по сути, основная теорема арифметики).
Более серьезное обсуждение вопроса можно найти, например, в книге «Введение в теорию чисел» Харди и Райта.
4. Формула Валлиса
Если подставить $x=\pi/2$ в разложение Эйлера синуса в бесконечное произведение, то получается равенство $$ \frac\pi2= \frac{2\cdot2\cdot4\cdot4\cdot6\cdot6\cdot\ldots}{1\cdot3\cdot3\cdot5\cdot5\cdot7\cdot\ldots} $$ Впрочем, Джон Валлис нашел эту формулу уже в середине XVII века, почти за 100 лет до формулы Эйлера, вычисляя некоторые интегралы.
В упоминавшейся выше статье Ягломов при помощи элементарной тригонометрии доказывается и формула Валлиса. А J. Wästlund нашел и доказательство (в духе «геометрического суммирования»), непосредственно связывающее произведение Валлиса с площадью круга — см. его статью (AMM, 2007) или лекцию Д. Кнута.
При помощи формулы Валлиса можно доказать, что если подкинуть монету $2n$ раз, то вероятность того, что орлов и решек выпадет в точности поровну, приблизительно равна $1/\sqrt{\pi n}$. наверх
наверх
Март, четырнадцатое. Как вычислить число Пи
Еще в древности люди заметили, что отношение длины окружности к ее диаметру близко к трем, но не точно три, а чуть больше. Причем это отношение не зависит ни от диаметра окружности, ни от места, где она проведена. В те времена это отношение, названное впоследствии числом Пи, не сильно выделялось из множества других чисел, которые можно определить опытным путем. Таких как отношение диагонали квадрата к его стороне или отношение площадей квадрата и равностороннего треугольника с такой же, как у квадрата, стороной.
Фото: depositphotos
Отцом числа Пи следует считать Архимеда, которого называют автором удивительных открытий, что отношение Пи не приближенно, а в точности связывает не только диаметр и длину окружности, но и площадь круга и квадрат его радиуса, объем шара и куб его радиуса и даже площадь сферы и квадрат ее радиуса. То есть Архимед доказал известные всем со школы формулы: L = 2πr, S1 = πr2, V = 4/3 x πr3 и S2 = 4πr2.
Архимеду принадлежит также первая не опытная, а теоретическая (методом построения описанных и вписанных в круг многоугольников) оценка числа Пи: 3 + (10/71)
Так Архимед представлял себе вычисление площади круга
Впоследствии математики поняли, что число Пи связывает объем многомерного шара и степень его радиуса при любой размерности пространства (с рациональным множителем, уже зависящим от размерности: для 2х измерений это 1, для 3х измерений — 4/3). Таким образом, число Пи не изменится даже для исследователей, живущих в пространствах с другим числом измерений.
Однако отношение длины окружности к ее диаметру меняется при искривлении пространства и совпадает с нашей константой только в «плоском» однородном случае, проще говоря в пространстве, для которого справедлива теорема Пифагора. Как утверждает теория относительности, рядом с горизонтом событий черной дыры пространство сильно искривлено. Неужели цивилизация, которой повезло возникнуть в подобном месте, может не подозревать о существовании константы Пи?
Как утверждает теория относительности, рядом с горизонтом событий черной дыры пространство сильно искривлено. Неужели цивилизация, которой повезло возникнуть в подобном месте, может не подозревать о существовании константы Пи?
Оказывается, число Пи неожиданно возникает просто из натурального ряда чисел. Английский математик Джон Валлис, старший современник Исаака Ньютона, открыл удивительную формулу:
Многоточие в конце формулы означает, что если мы перемножим достаточно много четных чисел в числителе и нечетных в знаменателе, то получим результат, сколь угодно близкий к числу Пи /2.
Еще более удивительную для непосвященных формулу с участием числа вывел великий математик Леонард Эйлер, бóльшую часть своей долгой научной карьеры проработавший в Петербургской академии наук:
Эта формула была признана «самой красивой теоремой в математике». Здесь e = 2,71828… — константа Эйлера, i = √-1 — мнимая единица и Пи — конечно, наше число Пи. На самом деле формулаЭйлера эквивалентна сразу двум равенствам:
где n! = 1×2 x 3···(n — 1) x n.
Конечно, затруднительно вычислять Пи из этих формул как корень уравнения бесконечной степени. А уравнения конечной степени с целыми коэффициентами, корнем которого было бы число Пи, не существует! Это доказал в конце XIX века немецкий математик Фердинанд фон Линдеман, решив заодно знаменитую античную проблему «квадратуры круга». То есть он показал, что, имея отрезок, равный диаметру круга, невозможно только с помощью циркуля и линейки построить квадрат, площадь которого равна площади круга.
Другая знаменитая формула Эйлера:
уже пригодна для приближенного вычисления числа Пи. И даже более подходит для этой цели, чем формула великого немецкого философа и математика Готфрида Лейбница:
Впоследствии выяснилось, что эту формулу задолго до Лейбница вывел индийский математик и астроном Мадхава. Формула Лейбница на самом деле является частным случаем формулы разложения арктангенса в ряд Тейлора:
при подстановке x = 1. Долгое время наиболее удобным для вычисления приближений числа Пи считалось равенство английского математика Джона Мэчина, который был секретарем Лондонского королевского общества, когда его возглавлял Исаак Ньютон. Вот это равенство Мэчина:
Вот это равенство Мэчина:
Для вычисления числа Пи по формуле Мэчина нужно сначала вычислить arctg1/5 и arctg1/239 с помощью приведенного выше разложения арктангенса в ряд Тейлора, которое, по-видимому, впервые нашел сам Исаак Ньютон.
Число возникает в математике в самых неожиданных местах. Например, математик Абрахам де Муавр (бежавший в Англию из Франции, где его преследовали как гугенота) обнаружил формулу:
Теперь ее называют формулой Эйлера-Пуассона, или интегралом Гаусса.
Сам Муавр, а также выдающиеся математики Пьер-Симон де Лаплас и Карл Фридрих Гаусс в разной степени общности и строгости доказали, что функция Φ(x) = e-x2/2/√2 (из формулы Эйлера-Пуассона следует, что интеграл от функции Φ по вещественной прямой равен 1) является плотностью нормального, или гауссова, распределения, которое является предельным для средних арифметических последовательности независимых случайных величин.
Гистограмма близка к графику функции Φ
Это означает, например, если мы будем n серий по m раз подбрасывать монету, вычислять разность между числом выпавших «орлов» и «решек» и записывать результат в таблицу, то при росте n и m построенная по таблице гистограмма будет все больше походить на график функции Φ. Эта теорема служит фундаментом для современной квантовой физики, обеспечивая возможность извлекать из многократных измерений случайных событий строгие закономерности.
Эта теорема служит фундаментом для современной квантовой физики, обеспечивая возможность извлекать из многократных измерений случайных событий строгие закономерности.
Казалось бы, тысячелетняя история исследований позволяет предположить, что мы не упустили ничего важного о числе. Однако в 1997 году, совсем недавно в историческом масштабе, произошла сенсация. Саймон Плафф нашел новое представление для числа в виде ряда:
которое не только требует гораздо меньше слагаемых для вычисления числа с заранее заданной точностью, но и позволяет вычислить любую цифру в двоичном представлении числа Пи, не вычисляя предыдущие цифры.
Владимир Потапов.
Читайте также: Безумие на «Википедии»: 11 статей, которые вас удивят
ЧЕМУ РАВНО ЧИСЛО ПИ? – Ньютонов ⚛ физика
***
Что общего между колесом от Лады Приоры, обручальным кольцом и блюдцем вашего кота? Вы, конечно, скажете красота и стиль! Но я осмелюсь с вами поспорить. Число Пи! Это число, объединяющее все окружности, круги и округлости, к коим в частности можно отнести и мамино кольцо, и колесо от любимой папиной машины и даже блюдце любимого кота Мурзика. Готов поспорить, что в рейтинге самых популярных физических и математических констант число Пи несомненно займет первую строчку. Но что скрывается за ним? Может какие-то страшные ругательства математиков? Давайте попробуем разобраться в этом вопросе.
Готов поспорить, что в рейтинге самых популярных физических и математических констант число Пи несомненно займет первую строчку. Но что скрывается за ним? Может какие-то страшные ругательства математиков? Давайте попробуем разобраться в этом вопросе.
Что же такое число «Пи»
и откуда оно взялось?Современное обозначение числа π (Пи) появилось благодаря английскому математику Джонсу в 1706 году. Это первая буква греческого слова περιφέρεια (периферия, или окружность).
Для тех, кто проходил математику давно, да и к тому же мимо, напомним, что число Пи — это отношение длины окружности к её диаметру. Величина является константой, то есть постоянна для любой окружности, независимо от её радиуса. Люди знали об этом еще в древности. Так в древнем Египте число Пи принимали равным отношению 256/81, а в ведических текстах приводится значение 339/108, Архимед же предлагал соотношение 22/7.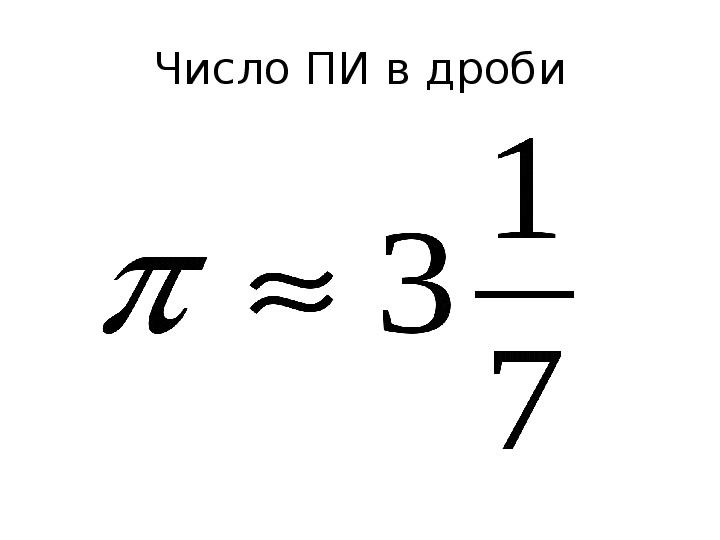 Но ни эти, ни многие другие способы выражения числа Пи не давали точный результат.
Но ни эти, ни многие другие способы выражения числа Пи не давали точный результат.
Оказалось, что число Пи трансцендентное, соответственно, и иррациональное. А это значит, его нельзя представить в виде простой дроби. Если же его выразить через десятичную, то последовательность цифр после запятой устремятся в бесконечность, к тому же периодически не повторяясь. Что все это значит? Очень просто. Хотите узнать номер телефона понравившейся девушки? Его наверняка можно найти в последовательности цифр после запятой числа Пи.
Телефон можно посмотреть здесь ↓
Число Пи с точностью до 1000 знаков.
π= 3,
1415926535 8979323846 2643383279 5028841971 6939937510 5820974944 5923078164 0628620899 8628034825 3421170679 8214808651 3282306647 0938446095 5058223172 5359408128 4811174502 8410270193 8521105559 6446229489 5493038196 4428810975 6659334461 2847564823 3786783165 2712019091 4564856692 3460348610 4543266482 1339360726 0249141273 7245870066 0631558817 4881520920 9628292540 9171536436 7892590360 0113305305 4882046652 1384146951 9415116094 3305727036 5759591953 0921861173 8193261179 3105118548 0744623799 6274956735 1885752724 8912279381 8301194912 9833673362 4406566430 8602139494 6395224737 1907021798 6094370277 0539217176 2931767523 8467481846 7669405132 0005681271 4526356082 7785771342 7577896091 7363717872 1468440901 2249534301 4654958537 1050792279 6892589235 4201995611 2129021960 8640344181 5981362977 4771309960 5187072113 4999999837 2978049951 0597317328 1609631859 5024459455 3469083026 4252230825 3344685035 2619311881 7101000313 7838752886 5875332083 8142061717 7669147303 5982534904 2875546873 1159562863 8823537875 9375195778 1857780532 1712268066 1300192787 6611195909 2164201989.
 .
.Не нашли? Тогда посмотрите здесь.
Все в числе «Пи»
Вообще это может быть не только номер телефона, а любая информация, закодированная с помощью цифр. К примеру, если представить все произведения Александра Сергеевича Пушкина в цифровом виде, то они хранились в числе Пи еще до того, как он их написал, даже до того, как он родился. В принципе, они хранятся там до сих пор. Кстати, ругательства математиков в π тоже присутствуют, да и не только математиков.
Словом, в числе Пи есть всё, даже мысли, которые посетят вашу светлую голову завтра, послезавтра, через год, а может, через два. В это очень трудно поверить, но даже если мы представим, что поверили, еще труднее будет получить оттуда информацию и расшифровать её. Так что вместо того, чтобы копаться в этих цифрах, может проще подойти к понравившейся девушке и спросить у неё номер?.. Но для тех, кто не ищет легких путей, ну или просто интересующихся, чему же равно число Пи, предлагаю несколько способов его вычисления. Считайте на здоровье.
Считайте на здоровье.
Чему равно число Пи?
Методы его вычисления:Экспериментальный метод.
Если число Пи это отношение длины окружности к её диаметру, то первый, пожалуй, самый очевидный способ нахождения нашей загадочной константы будет вручную произвести все измерения и вычислить число Пи по формуле π=l/d. Где l — длина окружности, а d — её диаметр. Все очень просто, необходимо лишь вооружится ниткой для определения длины окружности, линейкой для нахождения диаметра, и, собственно, длины самой нитки, ну и калькулятором, если у вас проблемы с делением в столбик. В роли измеряемого образца может выступить кастрюля или банка из под огурцов, неважно, главное? чтоб в основании была окружность.
Рассмотренный способ вычисления самый простой, но, к сожалению, имеет два существенных недостатка, отражающихся на точности полученного числа Пи. Во-первых, погрешность измерительных приборов (в нашем случае это линейка с ниткой), а во-вторых, нет никакой гарантии, что измеряемая нами окружность будет иметь правильную форму. Поэтому не удивительно, что математика подарила нам множество других методов вычисления π, где нет нужды производить точные измерения.
Поэтому не удивительно, что математика подарила нам множество других методов вычисления π, где нет нужды производить точные измерения.
Ряд Лейбница.
Существует несколько бесконечных рядов, позволяющих точно вычислять число Пи до большого количества знаков после запятой. Одним из самых простых рядов является ряд Лейбница. π = (4/1) — (4/3) + (4/5) — (4/7) + (4/9) — (4/11) + (4/13) — (4/15) …
Все просто: берем дроби с 4 в числителе (это то что сверху) и одним числом из последовательности нечетных чисел в знаменателе (это то что снизу), последовательно складываем и вычитаем их друг с другом и получаем число Пи. Чем больше итераций или повторений наших нехитрых действий, тем точнее результат. Просто, но не эффективно, к слову, необходимо 500000 итераций чтоб получить точное значение числа Пи с десятью знаками после запятой. То есть, нам придется несчастную четверку разделить аж 500000 раз, а помимо этого полученные результаты мы должны будем 500000 раз вычитать и складывать. Хотите попробовать?
Хотите попробовать?
Ряд Нилаканта
Нет времени возится с рядом Лейбница? Есть альтернатива. Ряд Нилаканта, хотя он немного сложнее, но позволяет быстрее получить нам искомый результат. π = 3 + 4/(2*3*4) — 4/(4*5*6) + 4/(6*7*8) — 4/(8*9*10) + 4/(10*11*12) — (4/(12*13*14) … Думаю, если внимательно посмотреть на приведенный начальный фрагмент ряда, все становится ясным, и комментарии излишни. По этому идем дальше.
Метод «Монте-Карло»
Довольно интересным методом вычисления числа Пи является метод Монте Карло. Столь экстравагантное название ему досталось в честь одноименного города в королевстве Монако. И причина тому случайность. Нет, его не назвали случайно, просто в основе метода лежат случайные числа, а что может быть случайней чисел, выпадающих на рулетках казино Монте Карло? Вычисление числа Пи не единственное применение этого метода, так в пятидесятых годах его использовали при расчетах водородной бомбы. Но не будем отвлекаться.
Возьмем квадрат со стороной, равной 2r, и впишем в него круг радиусом r. Если наугад ставить точки в квадрате, то вероятность P того, что точка угодит в круг, есть отношение площадей круга и квадрата. P=Sкр/Sкв=πr2/(2r)2=π/4.
Если наугад ставить точки в квадрате, то вероятность P того, что точка угодит в круг, есть отношение площадей круга и квадрата. P=Sкр/Sкв=πr2/(2r)2=π/4.
Теперь отсюда выразим число Пи π=4P. Остается только получить экспериментальные данные и найти вероятность Р как отношение попаданий в круг Nкр к попаданиям в квадрат Nкв. В общем виде расчетная формула будет выглядеть следующим образом: π=4Nкр / Nкв.
Хочется отметить, что для того, чтобы реализовать этот метод, в казино идти необязательно, достаточно воспользоваться любым более или менее приличным языком программирования. Ну а точность полученных результатов будет зависеть от количества поставленных точек, соответственно, чем больше, тем точнее. Желаю удачи 😉
Число Тау
(Вместо заключения).Люди, далекие от математики, скорее всего не знают, но так сложилось, что число Пи имеет брата, который больше его в два раза. Это число Тау(τ) , и, если Пи — это отношение длины окружности к диаметру, то Тау — это отношение этой длины к радиусу. И на сегодняшний день есть предложения некоторых математиков отказаться от числа Пи и заменить его на Тау, так как это во многом более удобно. Но пока это только предложения, и как говорил Лев Давидович Ландау: «Новая теория начинает господствовать тогда, когда вымрут сторонники старой».
Это число Тау(τ) , и, если Пи — это отношение длины окружности к диаметру, то Тау — это отношение этой длины к радиусу. И на сегодняшний день есть предложения некоторых математиков отказаться от числа Пи и заменить его на Тау, так как это во многом более удобно. Но пока это только предложения, и как говорил Лев Давидович Ландау: «Новая теория начинает господствовать тогда, когда вымрут сторонники старой».
Март, четырнадцатое
Каждый год 14 марта мы публикуем материал, посвященный числу 𝞹. Три года назад это была сложная математическая задача (вот, на всякий случай, ее решение), два года назад — материал про экспериментальные способы вычисления числа 𝞹, в прошлом году — веселая игра. На этот раз по просьбе N + 1 математик Владимир Потапов рассказал о том, как число 𝞹 можно вычислить математическим путем, с помощью различных — подчас необычных — формул.
Еще в древности люди заметили, что отношение длины окружности к ее диаметру близко к трем, но не точно три, а чуть больше. Причем это отношение не зависит ни от диаметра окружности, ни от места, где она проведена. В те времена это отношение, названное впоследствии числом 𝞹, не сильно выделялось из множества других чисел, которые можно определить опытным путем. Таких, как отношение диагонали квадрата к его стороне или отношение площадей квадрата и равностороннего треугольника с такой же, как у квадрата, стороной.
Отцом числа 𝞹 следует считать Архимеда, которого называют автором удивительных открытий, что отношение 𝞹 не приближенно, а в точности связывает не только диаметр и длину окружности, но и площадь круга и квадрат его радиуса, объем шара и куб его радиуса и даже площадь сферы и квадрат ее радиуса. То есть Архимед доказал известные всем со школы формулы: L = 2πr, S1 = πr2, V = 4/3 × πr3 и S2 = 4πr2.
То есть Архимед доказал известные всем со школы формулы: L = 2πr, S1 = πr2, V = 4/3 × πr3 и S2 = 4πr2.
Архимеду принадлежит также первая не опытная, а теоретическая (методом построения описанных и вписанных в круг многоугольников) оценка числа 𝞹: 3 + (10/71) < 𝞹 < 3 + (1/7). То есть он нашел первые три десятичные цифры числа 𝞹 = 3,14…, что и определило сегодняшнюю дату.
Так Архимед представлял себе вычисление площади круга
Впоследствии математики поняли, что число 𝞹 связывает объем многомерного шара и степень его радиуса при любой размерности пространства (с рациональным множителем, уже зависящим от размерности: для 2х измерений это 1, для 3х измерений — 4/3). Таким образом, число 𝞹 не изменится даже для исследователей, живущих в пространствах с другим числом измерений.
Однако отношение длины окружности к ее диаметру меняется при искривлении пространства и совпадает с нашей константой 𝞹 только в «плоском» однородном случае, проще говоря в пространстве, для которого справедлива теорема Пифагора. Как утверждает теория относительности, рядом с горизонтом событий черной дыры пространство сильно искривлено. Неужели цивилизация, которой повезло возникнуть в подобном месте, может не подозревать о существовании константы 𝞹?
Оказывается, число 𝞹 неожиданно возникает просто из натурального ряда чисел. Английский математик Джон Валлис, старший современник Исаака Ньютона, открыл удивительную формулу:
Многоточие в конце формулы означает, что если мы перемножим достаточно много четных чисел в числителе и нечетных в знаменателе, то получим результат, сколь угодно близкий к числу 𝞹/2.
Еще более удивительную для непосвященных формулу с участием числа 𝞹 вывел великий математик Леонард Эйлер, бóльшую часть своей долгой научной карьеры проработавший в Петербургской академии наук:
Эта формула была признана «самой красивой теоремой в математике». Здесь e = 2,71828… — константа Эйлера, i = √−1 — мнимая единица и 𝞹 — конечно, наше число 𝞹. На самом деле формулаЭйлера эквивалентна сразу двум равенствам:где n! = 1 × 2 × 3···(n − 1) × n.
Конечно, затруднительно вычислять 𝞹 из этих формул как корень уравнения бесконечной степени. А уравнения конечной степени с целыми коэффициетами, корнем которого было бы число 𝞹, не существует! Это доказал в конце XIX века немецкий математик Фердинанд фон Линдеман, решив заодно знаменитую античную проблему «квадратуры круга». То есть он показал, что, имея отрезок, равный диаметру круга, невозможно только с помощью циркуля и линейки построить квадрат, площадь которого равна площади круга.
Другая знаменитая формула Эйлера:
уже пригодна для приближенного вычисления числа 𝞹. И даже более подходит для этой цели, чем формула великого немецкого философа и математика Готфрида Лейбница:
Впоследствии выяснилось, что эту формулу задолго до Лейбница вывел индийский математик и астроном Мадхава. Формула Лейбница на самом деле является частным случаем формулы разложения арктангенса в ряд Тейлора:
при подстановке x = 1. Долгое время наиболее удобным для вычисления приближений числа 𝞹 считалось равенство английского математика Джона Мэчина, который был секретарем Лондонского королевского общества, когда его возглавлял Исаак Ньютон. Вот это равенство Мэчина:
Для вычисления числа 𝞹 по формуле Мэчина нужно сначала вычислить arctg1/5 и arctg1/239 с помощью приведенного выше разложения арктангенса в ряд Тейлора, которое, по-видимому, впервые нашел сам Исаак Ньютон.
Число 𝞹 возникает в математике в самых неожиданных местах. Например, математик Абрахам де Муавр (бежавший в Англию из Франции, где его преследовали как гугенота) обнаружил формулу:
Теперь ее называют формулой Эйлера-Пуассона, или интегралом Гаусса.
Сам Муавр, а также выдающиеся математики Пьер-Симон де Лаплас и Карл Фридрих Гаусс в разной степени общности и строгости доказали, что функция Φ(x) = e−x2/2/√2𝞹 (из формулы Эйлера-Пуассона следует, что интеграл от функции Φ по вещественной прямой равен 1) является плотностью нормального, или гауссова, распределения, которое является предельным для средних арифметических последовательности независимых случайных величин.
Гистограмма близка к графику функции Φ
Это означает, например, если мы будем n серий по m раз подбрасывать монету, вычислять разность между числом выпавших «орлов» и «решек» и записывать результат в таблицу, то при росте n и m построенная по таблице гистограмма будет все больше походить на график функции Φ. Эта теорема служит фундаментом для современной квантовой физики, обеспечивая возможность извлекать из многократных измерений случайных событий строгие закономерности.
Казалось бы, тысячелетняя история исследований позволяет предположить, что мы не упустили ничего важного о числе 𝞹. Однако в 1997 году, совсем недавно в историческом масштабе, произошла сенсация. Саймон Плафф нашел новое представление для числа 𝞹 в виде ряда:
которое не только требует гораздо меньше слагаемых для вычисления числа 𝞹 с заранее заданной точностью, но и позволяет вычислить любую цифру в двоичном представлении числа 𝞹, не вычисляя предыдущие цифры.
Владимир Потапов
3,14 способа запомнить число π с большой точностью
Число π показывает, во сколько раз длина окружности больше ее диаметра. Неважно, какого размера окружность, — как заметили по меньшей мере еще 4 тыс. лет назад, соотношение всегда остается одним и тем же. Вопрос только, чему оно равняется.
Чтобы высчитать его приблизительно, достаточно обыкновенной нитки. Грек Архимед в III веке до н.э. применял более хитрый способ. Он чертил внутри и снаружи окружности правильные многоугольники. Складывая длины сторон многоугольников, Архимед все точнее определял вилку, в которой находится число π, и понял, что оно приблизительно равно 3,14.
Методом многоугольников пользовались еще почти 2 тыс. лет после Архимеда, это позволило узнать значение числа π вплоть до 38-й цифры после запятой. Еще один-два знака — и можно с точностью до атома рассчитать длину окружности с диаметром как у Вселенной.
Пока одни ученые использовали геометрический метод, другие догадались, что число π можно рассчитывать, складывая, вычитая, деля или умножая другие числа. Благодаря этому “хвост” вырос до нескольких сотен цифр после запятой.
С появлением первых вычислительных машин и особенно современных компьютеров точность повысилась на порядки — в 2016 году швейцарец Петер Трюб определил значение числа π до 22,4 трлн знаков после запятой. Если напечатать этот результат в строчку 14-м кеглем нормальной ширины, то запись получится немногим короче, чем среднее расстояние от Земли до Венеры.
В принципе ничто не мешает добиться еще большей точности, но для научных расчетов в этом давно нет нужды — разве что для тестирования компьютеров, алгоритмов и для исследований в математике. А исследовать есть что. Даже про само число π известно не все. Доказано, что оно записывается в виде бесконечной непериодической дроби, то есть цифрам после запятой нет предела, и они не складываются в повторяющиеся блоки. Но вот с одинаковой ли частотой появляются цифры и их комбинации, неясно. Судя по всему, это так, но пока никто не привел строгого доказательства.
Дальнейшие вычисления проводятся в основном из спортивного интереса — и по той же причине люди пытаются запомнить как можно больше цифр после запятой. Рекорд принадлежит индийцу Раджвиру Мине, который в 2015 году назвал на память 70 тыс. знаков, сидя с завязанными глазами почти десять часов.
Наверное, чтобы превзойти его результат, нужен особый талант. Но просто удивить друзей хорошей памятью способен каждый. Главное — использовать одну из мнемонических техник, которая потом может пригодиться и для чего-нибудь еще.
Структурировать данные
Самый очевидный способ — разбить число на одинаковые блоки. Например, можно представить π как телефонную книгу с десятизначными номерами, а можно — как причудливый учебник истории (и будущего), где перечислены годы. Много так не запомнишь, но, чтобы произвести впечатление, хватит и пары десятков знаков после запятой.
Превратить число в историю
Считается, что самый удобный способ запомнить цифры — придумать историю, где им будет соответствовать количество букв в словах (ноль было бы логично заменить пробелом, но тогда большинство слов сольется; вместо этого лучше использовать слова из десяти букв). По этому принципу построена фраза “Можно мне большую упаковку кофейных зерен?” на английском языке:
May — 3,
I — 1
have — 4
a — 1
large — 5
container — 9
of — 2
coffee — 6
beans — 5
На эту тему
В дореволюционной России придумали похожее предложение: “Кто и шутя и скоро пожелает(ъ) Пи узнать число, уже знает(ъ)”. Точность — до десятого знака после запятой: 3,1415926536. Но проще запомнить более современный вариант: “Она и была, и будет уважаемая на работе”. Есть и стихотворение: “Это я знаю и помню прекрасно — пи, многие знаки мне лишни, напрасны”. А советский математик Яков Перельман сочинил целый мнемонический диалог:
— Что я знаю о кругах? (3,1415)
— Вот и знаю я число, именуемое пи — молодец! (3,1415927)
— Учи и знай в числе известном за цифрой цифру, как удачу примечать! (3,14159265359)
Американский математик Майкл Кит и вовсе написал целую книгу Not A Wake, в тексте которой содержится информация о первых 10 тыс. цифр числа π.
Заменить цифры буквами
Кому-то легче запомнить бессвязные буквы, чем случайные цифры. В этом случае цифры заменяются первыми буквами алфавита. Первое слово в названии рассказа Cadaeic Cadenza Майкла Кита появилось именно таким образом. Всего в этом произведении закодировано 3835 знаков числа пи — правда, тем же способом, что в книге Not a Wake.
В русском языке для подобных целей можно использовать буквы от А до И (последняя будет соответствовать нолю). Насколько удобно будет запоминать составленные из них комбинации — вопрос открытый.
Придумать образы для комбинаций цифр
Чтобы добиться по-настоящему выдающихся результатов, предыдущие методы не годятся. Рекордсмены используют технику визуализации: изображения запомнить легче, чем цифры. Сначала нужно сопоставить каждую цифру с согласной буквой. Получится, что каждому двухзначному числу (от 00 до 99) соответствует двухбуквенное сочетание.
Допустим, один — это “н”, четыре — “р”, пять — “т”. Тогда число 14 — это “нр”, а 15 — “нт”. Теперь эти пары следует дополнить другими буквами, чтобы получилось слова, например, “нора” и “нить”. Всего понадобится сто слов — вроде бы много, но за ними стоят всего десять букв, поэтому запомнить не так уж сложно.
Число π предстанет в уме как последовательность образов: три целых, нора, нить и т.п. Чтобы лучше запомнить эту последовательность, изображения можно нарисовать или распечатать на принтере и поставить перед глазами. Некоторые люди просто раскладывают соответствующие предметы по комнате и вспоминают числа, разглядывая интерьер. Регулярные тренировки по этому методу позволят запомнить сотни и даже тысячи знаков после запятой — или любую другую информацию, ведь визуализировать можно не только числа.
Марат Кузаев, Кристина Недкова
Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике – Планиметрия
Основные определения и свойства
| Фигура | Рисунок | Определения и свойства |
| Окружность | Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки – центра окружности | |
| Дуга | Часть окружности, расположенная между двумя точками окружности | |
| Круг | Конечная часть плоскости, ограниченная окружностью | |
| Сектор | Часть круга, ограниченная двумя радиусами | |
| Сегмент | Часть круга, ограниченная хордой | |
| Правильный многоугольник | Выпуклый многоугольник, у которого все стороны равны и все углы равны | |
Около любого правильного многоугольника можно описать окружность |
| Окружность |
Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки – центра окружности |
| Дуга |
Часть окружности, расположенная между двумя точками окружности |
| Круг |
Конечная часть плоскости, ограниченная окружностью |
| Сектор |
Часть круга, ограниченная двумя радиусами |
| Сегмент |
Часть круга, ограниченная хордой |
| Правильный многоугольник |
Выпуклый многоугольник, у которого все стороны равны и все углы равны Около любого правильного многоугольника можно описать окружность |
Определение 1. Площадью круга называют предел, к которому стремятся площади правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон.
Определение 2. Длиной окружности называют предел, к которому стремятся периметры правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон.
Замечание 1. Доказательство того, что пределы площадей и периметров правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон действительно существуют, выходит за рамки школьной математики и в нашем справочнике не приводится.
Определение 3. Числом π (пи) называют число, равное площади круга радиуса 1.
Замечание 2. Число π является иррациональным числом, т.е. числом, которое выражается бесконечной непериодической десятичной дробью:
Число π является трансцендентным числом, то есть числом, которое не может быть корнем алгебраического уравнения с целочисленными коэффициентами.
Формулы для площади круга и его частей
Формулы для длины окружности и её дуг
Площадь круга
Рассмотрим две окружности с общим центром (концентрические окружности) и радиусами радиусами 1 и R, в каждую из которых вписан правильный n – угольник (рис. 1).
Обозначим через O общий центр этих окружностей. Пусть внутренняя окружность имеет радиус 1.
Рис.1
Площадь правильного n – угольника, вписанного в окружность радиуса R, равна
Площадь правильного n – угольника, вписанного в окружность радиуса 1, равна
Следовательно,
Поскольку при увеличении n площадь правильного n – угольника, вписанного в окружность радиуса 1, стремится к π, то при увеличении n площадь правильного n – угольника, вписанного в окружность радиуса R, стремится к числу πR2.
Таким образом, площадь круга радиуса R, обозначаемая S, равна
S = πR2.
Длина окружности
Рассмотрим правильный n – угольник B1B2…Bn , вписанный в окружность радиуса радиуса R, и опустим из центраO окружности перпендикуляры на все стороны многоугольника (рис. 2).
Рис.2
Поскольку площадь n – угольника B1B2…Bn равна
то, обозначая длину окружности радиуса R буквой C, мы, в соответствии с определением 2, при увеличении n получаем равенство:
откуда вытекает формула для длины окружности радиуса R:
C = 2πR.
Следствие. Длина окружности радиуса 1 равна 2π.
Длина дуги
Рассмотрим дугу окружности, изображённую на рисунке 3, и обозначим её длину символом L(α), где буквой α обозначена величина соответствующего центрального угла.
Рис.3
В случае, когда величина α выражена в градусах, справедлива пропорция
из которой вытекает равенство:
В случае, когда величина α выражена в радианах, справедлива пропорция
из которой вытекает равенство:
Площадь сектора
Рассмотрим круговой сектор, изображённый на рисунке 4, и обозначим его площадь символом S (α) , где буквой α обозначена величина соответствующего центрального угла.
Рис.4
В случае, когда величина α выражена в градусах, справедлива пропорция
из которой вытекает равенство:
В случае, когда величина α выражена в радианах, справедлива пропорция
из которой вытекает равенство:
Площадь сегмента
Рассмотрим круговой сегмент, изображённый на рисунке 5, и обозначим его площадь символом S (α), где буквой α обозначена величина соответствующего центрального угла.
Рис.5
Поскольку площадь сегмента равна разности площадей кругового сектора MON и треугольника MON (рис.5), то в случае, когда величина α выражена в градусах, получаем
Следовательно,
В случае, когда величина α выражена в в радианах, получаем
Следовательно,
На сайте можно также ознакомиться с нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Пи
Нарисуйте круг диаметром (полностью поперек круга) 1
Тогда окружность (полностью по кругу) равна 3,14159265 … число, известное как Pi
Pi (произносится как «пирог») часто пишется с использованием греческого символа π
.Определение π:
Окружность
, разделенная на Диаметр
окружности.
Длина окружности, разделенная на диаметр круга, всегда равна π, независимо от того, насколько большой или малый круг!
Чтобы помочь вам вспомнить, что такое π … просто нарисуйте эту диаграмму.
В поисках Пи себя
Нарисуйте круг или используйте что-нибудь круглое, например тарелку.
Измерьте по краю (окружность ):
Получил 82 см
Измерьте поперек круга (диаметр ):
Получил 26 см
Разделить:
82 см / 26 см = 3.1538 …
Это довольно близко к π. Может, если точнее замерил?
Использование Pi
Мы можем использовать π, чтобы найти окружность, когда мы знаем диаметр
Окружность = π × Диаметр
Пример. Вы ходите по кругу диаметром 100 м. Как далеко вы прошли?
Пройденное расстояние = Окружность
= π × 100 м
= 314,159 … м
= 314 м (с точностью до м)
Также мы можем использовать π, чтобы найти диаметр, когда мы знаем окружность
Диаметр = Окружность / π
Пример: Сэм измерил 94 мм на внешней стороне трубы… каков его диаметр?
Диаметр = Окружность / π
= 94 мм / π
= 29,92 … мм
= 30 мм (с точностью до мм)
Радиус
Радиус составляет половину диаметра, поэтому мы также можем сказать:
Для круга радиусом из 1
Расстояние на полпути вокруг окружности равно π = 3,14159265 …
цифр
π примерно равно:
3.14159265358979323846…
Цифры продолжаются без единого шаблона.
π было вычислено с точностью до пятидесяти триллионов десятичных знаков, и все еще нет , нет шаблона для цифр
Приближение
Быстрое и простое приближение для π – 22/7
22/7 = 3,1428571 …
Но, как видите, 22/7 – это , не совсем верно . На самом деле π не равно отношению любых двух чисел, что делает его иррациональным числом.
Действительно хорошее приближение, лучше, чем 1 часть из 10 миллионов, составляет:
355/113 = 3,1415929 …
(подумайте о «113355», косой чертой посередине «113/355», затем переверните «355/113»)
Резюме:
| 22/7 | = | 3,14 28571 … |
| 355/113 | = | 3,141592 9 … |
| π | = | 3.14159265 … |
Запоминание цифр
Я обычно помню просто «3,14159», но вы также можете сосчитать буквы:
«Можно мне сегодня большую тару сливочного масла»
3 1 4 1 5 9 2 6 5
до 100 знаков после запятой
Вот π с первыми 100 десятичными знаками:
| 3,14159265358979323846264338327950288 4197169399375105820974944592307816 4062862089986280348253421170679… |
Самостоятельное вычисление числа Пи
Есть много специальных методов, используемых для вычисления π, и вот один из них, который вы можете попробовать сами: он называется серия Нилаканта (в честь индийского математика, жившего в 1444–1544 годах).
Это продолжается вечно и имеет такую схему:
3+ 4 2 × 3 × 4 – 4 4 × 5 × 6 + 4 6 × 7 × 8 – 4 8 × 9 × 10 +…
(Обратите внимание на узор + и -, а также на узор чисел под линиями.)
Это дает следующие результаты:
| Срок | Результат (до 12 знаков после запятой) |
|---|---|
| 1 | 3 |
| 2 | 3,166666666667 |
| 3 | 3,133333333333 |
| 4 | 3,145238095238 |
| … | … и т. Д.! … |
Возьмите калькулятор (или воспользуйтесь таблицей) и посмотрите, сможете ли вы добиться лучших результатов.
День Пи
ДеньПи отмечается 14 марта. Март – 3-й месяц, поэтому он выглядит как 3/14
.Вычисление числа Пи (π) – Maths Careers
В некотором смысле число Пи (π) действительно простое – вычисление числа Пи просто включает в себя разделение любой окружности на диаметр окружности.
С другой стороны, Пи (π) – это первое число, которое мы узнаем в школе, где мы не можем записать его как точную десятичную дробь – это загадочное число, состоящее из вечных цифр, которое очаровывало людей на протяжении тысячелетий. .
Мы узнаем, что можем начать записывать Пи (π) = 3,141592653589… .. но никогда не закончим. Пи (π) продолжается вечно и не имеет повторяющихся цифр – это то, что называется иррациональным числом. Фактически, если вы будете искать достаточно долго в числах числа Пи (π), вы сможете найти любое число, включая дату вашего рождения.
Пи (π) – тоже действительно полезное число. Он встречается повсюду в математике, а также имеет бесчисленное множество применений в инженерии и науке. Многие вещи круглые, и всякий раз, когда что-то круглое, обычно становится важным число Пи (π). Например, если инженер хочет рассчитать объем водопровода, он будет использовать следующую формулу для цилиндра:
(где радиус трубы, а высота трубы.)
Расчет числа Пи (π)
Поскольку у Pi (π) так много важных применений, нам нужно иметь возможность начать его вычисление, по крайней мере, с точностью до нескольких десятичных знаков.Кто-то должен был придумать приблизительное значение числа Пи (π), которое появляется на вашем калькуляторе – оно не было получено по волшебству!
Измерительные круги
Первый и наиболее очевидный способ вычисления числа Пи (π) – взять самый совершенный круг, который вы можете, а затем измерить его длину и диаметр, чтобы вычислить число Пи (π). Именно так поступили бы древние цивилизации, и именно так они впервые осознали, что внутри каждого круга скрыто постоянное соотношение. Проблема с этим методом заключается в точности – можете ли вы доверять своей рулетке, чтобы она показывала число Пи (π) с точностью до 10 или более десятичных знаков?
Использование многоугольников для аппроксимации числа Пи (π)
Древнегреческий математик Архимед изобрел остроумный метод вычисления аппроксимации числа Пи (π).Архимед начал с того, что вписал правильный шестиугольник внутри круга, а затем описал другой правильный шестиугольник за пределами того же круга. Затем он смог вычислить точные окружности и диаметры шестиугольников и, следовательно, смог получить грубое приближение Pi (π), разделив длину окружности на диаметр.
Затем Архимед нашел способ удвоить количество сторон своих шестиугольников. Затем он мог найти более точное приближение Pi (π), используя многоугольники с большим количеством сторон, которые были ближе к окружности.Он проделал это четыре раза, пока не использовал 96-сторонние многоугольники. Архимед точно рассчитал длину окружности и диаметр и, следовательно, мог приблизительно определить число Пи (π) между и. С тех пор дробь остается одним из самых популярных и запоминающихся приближений числа Пи (π).
Примерно через 600 лет после Архимеда китайский математик Цзу Чунчжи использовал аналогичный метод, чтобы вписать правильный многоугольник с 12 288 сторонами. Это привело к приближению числа Пи (π), которое является правильным с точностью до шести десятичных знаков.Прошло почти 600 лет, прежде чем был разработан совершенно новый метод, улучшающий это приближение.
Вычисление числа Пи (π) с использованием бесконечного ряда
Математики в конце концов обнаружили, что на самом деле существуют точные формулы для вычисления Pi (π). Единственная загвоздка в том, что каждая формула требует от вас делать что-то бесконечное количество раз. (Что имеет смысл, учитывая, что цифры числа Пи (π) продолжаются вечно). Одна из удивительных вещей, которые интересуют людей в отношении числа Пи (π), заключается в том, что существует не одна формула, а большое количество разных формул для людей учиться.
Один из самых известных и красивых способов вычисления Пи (π) – использовать серию Грегори-Лейбница:
Если вы продолжите этот шаблон до бесконечности, вы сможете точно вычислить, а затем просто умножить его на 4, чтобы получить … Однако если вы начнете складывать первые несколько членов, вы начнете получать приближение для числа Пи (π ). Проблема с серией, приведенной выше, заключается в том, что вам нужно сложить много членов, чтобы получить точное приближение Пи (π).Вам нужно сложить более 300 членов, чтобы получить число Пи (π) с точностью до двух десятичных знаков!
Другая серия, которая сходится быстрее, – это серия Nilakantha, которая была разработана в 15 -м веке. Быстрее сходится означает, что вам нужно выработать меньше терминов, чтобы ваш ответ стал ближе к Пи (π).
Nilakantha Серия:
Математики также нашли другие более эффективные ряды для вычисления Pi (π). Компьютерные программы могут складывать все больше и больше членов, вычисляя Pi (π) с необычайной степенью точности.В 2014 году мировым рекордом было то, что компьютер вычислил число Пи (π) с точностью до 13 300 000 000 000 десятичных разряда.
До появления компьютеров вычислить Пи (π) было намного сложнее. В 19 -ом веке Уильяму Шанксу потребовалось 15 лет, чтобы вычислить Пи (π) с точностью до 707 знаков после запятой. К сожалению, позже выяснилось, что он ошибся и был прав только с 527 десятичными знаками! Девять или десять цифр числа Пи (π), которые вы видите на своем калькуляторе, были известны, вероятно, с 1400 года.
Теперь, когда вы знаете, как вычислить Пи (π), вы всегда можете попробовать свои силы в запоминании десятичных знаков числа Пи (π). Самый последний рекорд был установлен в День Пи в 2019 году компанией Google, которая вычислила Пи с точностью до 31,4 триллиона знаков после запятой! С другой стороны, вы можете просто использовать следующую мнемонику для изучения первых шести десятичных знаков числа Пи (π): «Как бы я хотел вычислить Пи»
Длина каждого слова соответствует цифре в Пи (π).
| Как | Я | желание | Я | мог | рассчитать | Пи |
| 3 | 1 | 4 | 1 | 5 | 9 | 2 |
Статья Хейзел Льюис
PI
Пи – это отношение длины окружности окружности к диаметру.Это означает, что для любого круга вы можете разделить окружность (расстояние по окружности) по диаметру и всегда получается одно и то же число. Неважно, насколько большой или маленький круг, Пи остается прежним. Пи часто пишут с помощью символа и произносится «пирог», как и десерт.
История | Пи веб-сайты | Сделай сам Пи | Цифры | Формулы
Краткая история Пи
Древние цивилизации знали, что существует фиксированное соотношение окружности
до диаметра, который был примерно равен трем.Греки утонченные
процесс, и Архимеду приписывают первый теоретический расчет
Пи.
В 1761 году Ламберт доказал иррациональность числа Пи, т. Е. что это нельзя записать как отношение целых чисел.
В 1882 году Линдеман доказал, что Пи трансцендентен, что состоит в том, что Pi не является корнем какого-либо алгебраического уравнения с рациональными коэффициентами. Это открытие доказало, что нельзя «квадратировать круг», который была проблемой, которая занимала до того времени многих математиков.(Более информация о квадрате круг.)
Сколько здесь цифр? Это когда-нибудь закончится?
Поскольку Пи, как известно, является иррациональным числом, это означает, что цифры
никогда не заканчивать и не повторять каким-либо известным способом. Но вычисление цифр Пи
на протяжении всей истории интересовал математиков.
Некоторые потратили свою жизнь на вычисление цифр числа Пи, но до компьютеров,
было подсчитано менее 1000 цифр.В 1949 году компьютер рассчитал
2000 цифр и гонка началась. Были подсчитаны миллионы цифр,
с рекордом, установленным (по состоянию на сентябрь 1999 г.) суперкомпьютером на
Токийского университета, который рассчитал 206 158 430000 цифр. (первый
1000 цифр)
Подробнее об истории of Pi можно найти в архивах истории математики Mac Tutor.
Аппроксимация Пи
Архимед вычислил, что Пи находилось между 3 10/71 и 3 1/7 (также написано 223/71 < 22/7 ). 22/7 все еще является хорошим приближением. 355/113 лучше.
Веб-сайты Pi
Pi продолжает увлекать многих людей во всем мире. если ты
заинтересованы в получении дополнительной информации, существует множество веб-сайтов, посвященных
число Пи. Есть сайты, предлагающие тысячи, миллионы или миллиарды
цифр, пи-клубы, пи-музыка, люди, которые считают цифры, люди, которые
запоминать цифры, эксперименты с Пи и многое другое.Проверить это Yahoo
страницу с полным списком.
Классный эксперимент с Пи
Один из самых интересных способов узнать больше о Пи – это провести эксперименты с Пи.
сам. Вот знаменитая игла Buffon’s Needle.
В эксперименте с иглой Буффона вы можете уронить иглу линованный лист бумаги. Если следить за тем, сколько раз игла оказывается на линии, оказывается, что оно напрямую связано со значением числа Пи.
Буффона
Апплет для моделирования иглы (Майкл Дж. Хурбен)
Buffon’s
Needle (Джордж Риз, Управление математики, науки и технологий)
Образовательный университет Иллинойса Шампейн-Урбана)
Цифры из Pi
Первые 100 десятичных знаков
3,1415926535 8979323846 2643383279 5028841971 6939937510 5820974944 5923078164 0628620899 8628034825 3421170679…
Первые 1000 знаков после запятой
3,1415926535 8979323846 2643383279 5028841971 6939937510 5820974944 5923078164
0628620899 8628034825 3421170679 8214808651 3282306647 0938446095 5058223172
5359408128 4811174502 8410270193 8521105559 6446229489 5493038196 4428810975
6659334461 2847564823 3786783165 2712019091 4564856692 3460348610 4543266482
1339360726 0249141273 7245870066 0631558817 4881520920 9628292540 9171536436
78925
0113305305 4882046652 1384146951 9415116094 3305727036 5759591953 0921861173 8193261179 3105118548 0744623799 6274956735 1885752724 8912279381 8301194912 9833673362 4406566430 8602139494 6395224737 11798 6094370277 0539217176 2931767523 8467481846 7669405132 0005681271 4526356082 7785771342 7577896091 7363717872 1468440901 2249534301 4654958537 1050792279 6892589235 4201995611 212
60 8640344181 5981362977 4771309960 5187072113 4999999837 2978049951 0597317328 1609631859 5024459455 3469083026 4252230825 3344685035 2619311881 7101000313 7838752886 5875332083 8142061717 7669147303 5982534904 2875546873 1159562863 8823537875 9375195778 1857780532 1712268066 1300192787 6611195909 2164201989 5
миллион, 10 миллионов, 100 миллионов и 200 миллионов цифр
Формулы для Pi
Более сложный формулы и выводы
Формула Виета
2 / PI = 2/2 * (2 + 2 ) / 2 * (2 + (( 2 + 2))) / 2 *…c
Формула Лейбница
PI / 4 = 1/1 – 1/3 + 1/5 – 1/7 + …
Wallis Продукт
PI / 2 = 2/1 * 2/3 * 4/3 * 4/5 * 6/5 * 6/7 * …2 / PI = (1 – 1/2 2 ) (1 – 1/4 2 ) (1 – 1/6 2 ) …
Формула лорда Браункера
4 / PI = 1 + 1
----------------
2 + 3 2
------------
2 + 5 2
---------
2 + 7 2 ...
(ИП 2 ) / 8 = 1/1 2 + 1/3 2 + 1/5 2 + …
(PI 2 ) / 24 = 1/2 2 + 1/4 2 + 1/6 2 + …
Формула Эйлера
(ИП 2 ) / 6 = (n = 1 ..) 1 / n 2 = 1/1 2 + 1/2 2 + 1/3 2 + …
(или более широко…)
(n = 1 ..) 1 / n (2k) = (-1) (k-1) PI (2k) 2 (2k) B (2к) / (2 (2к)!)B (k) = k th число Бернулли. например. В 0 = 1 B 1 = -1 / 2 B 2 = 1/6 B 4 = -1 / 30 B 6 = 1/42 B 8 = -1 / 30 B 10 = 5/66. Дальнейшие числа Бернулли определяется как (n 0) B 0 + (n 1) B 1 + (n 2) B 2 +… + (n (n-1)) B (N-1) = 0 при условии, что все нечетные # Бернулли > 1 = 0. (n k) = биномиальный коэффициент = n! / (K! (N-k)!)
См. Power Summations # 2 для упрощенные выражения (без обозначения Бернулли) этих сумм для заданных значений k.
Что такое Пи и как он появился?
Вкратце, пи – это греческая буква, обозначающая р или π – это отношение длины окружности любого круга к диаметру этого круга.Независимо от размера круга это отношение всегда будет равно пи. В десятичной форме значение пи составляет примерно 3,14. Но пи – иррациональное число, что означает, что его десятичная форма не заканчивается (например, 1/4 = 0,25) и не становится повторяющейся (например, 1/6 = 0,166666 …). (Всего с 18 десятичными знаками число пи равно 3,141592653589793238.) Следовательно, полезно иметь сокращенное обозначение отношения длины окружности к диаметру. Согласно « A History of Pi » Петра Бекмана, греческая буква π была впервые использована для этой цели Уильямом Джонсом в 1706 году, вероятно, как сокращение периферии, и стала стандартной математической записью примерно 30 лет спустя.
Проведите небольшой эксперимент: с помощью циркуля нарисуйте круг. Возьмите один кусок веревки и поместите его на вершину круга ровно один раз. Теперь распрямите веревку; его длина называется окружностью круга. Измерьте окружность линейкой. Затем измерьте диаметр круга, который представляет собой длину от любой точки круга прямо через его центр до другой точки на противоположной стороне. (Диаметр в два раза больше радиуса, длины от любой точки круга до его центра.Если вы разделите окружность круга на диаметр, вы получите примерно 3,14 – независимо от того, какой размер круга вы нарисовали! У большего круга будет большая окружность и больший радиус, но соотношение всегда будет тем же. Если бы вы могли точно измерить и разделить, вы бы получили 3,141592653589793238 … или пи.
Иначе говоря, если вы разрежете несколько кусков веревки, длина которых равна диаметру, вам понадобится чуть больше трех из них, чтобы покрыть окружность круга.
Пи чаще всего используется в некоторых вычислениях, касающихся кругов. Пи не только связывает окружность и диаметр. Удивительно, но он также связывает диаметр или радиус круга с площадью этого круга по формуле: площадь равна пи, умноженному на квадрат радиуса. Кроме того, число пи часто неожиданно появляется во многих математических ситуациях. Например, сумма бесконечного ряда
1 + 1/4 + 1/9 + 1/16 + 1/25 + … + 1 / n2 + … равно π 2 /6
Важность числа Пи была признана не менее 4000 лет назад. A History of Pi отмечает, что к 2000 году до нашей эры «вавилоняне и египтяне (по крайней мере) знали о существовании и значении константы π», признавая, что каждый круг имеет одинаковое отношение длины окружности к диаметру. И вавилоняне, и египтяне имели грубые численные приближения к значению числа пи, а более поздние математики в Древней Греции, особенно Архимед, улучшили эти приближения. К началу 20 века было известно около 500 цифр числа Пи.С развитием вычислений, благодаря компьютерам, мы теперь знаем больше, чем первые шесть миллиардов цифр числа Пи.
Как использовать функцию Excel PI
В геометрии площадь, ограниченная кругом радиуса (r), определяется по следующей формуле: πr2 Греческая буква π («пи») представляет собой отношение длины окружности к ее диаметру. В Excel π равно …
.В геометрии сфера определяется как набор точек, находящихся на одинаковом расстоянии (r) от данной точки в трехмерном пространстве.Формула для расчета объема шара: Где r представляет собой …
В геометрии стандартная формула для расчета площади поверхности цилиндра: По сути, эта формула сначала вычисляет площадь стороны цилиндра на основе длины окружности, умноженной на …
В геометрии длина окружности радиуса (r) определяется по следующей формуле: = 2πr Греческая буква π («пи») представляет собой отношение длины окружности к ее диаметру.В Excel π равно …
.В геометрии формула для расчета объема цилиндра: Греческая буква π («пи») представляет собой отношение длины окружности к ее диаметру. В Excel π представлено в формуле с …
В геометрии формула для расчета объема конуса: Формула для расчета объема конуса основана на формуле для расчета объема пирамиды.Поскольку основанием конуса является …
В геометрии сфера определяется как набор точек, находящихся на одинаковом расстоянии (r) от данной точки в трехмерном пространстве. Формула для расчета площади поверхности шара: Греческий …
В геометрии формула для расчета площади поверхности правого конуса: Греческая буква π («пи») представляет собой отношение длины окружности к ее диаметру.В Excel π представлено в формуле …
Уравнение Эйлера– это красивая формула (с использованием числа Пи), показывающая, что математика пугающе совершенна – Кварц
В старшей школе я изучал высшую математику. У этого есть два применения: во-первых, я могу сказать людям, что когда-то изучал высшую математику. Во-вторых, я знаю об уравнении Эйлера.
Уравнения Эйлера не должно существовать. Автор-фантаст никогда бы не вообразил такую потрясающе совершенную формулу; это слишком красиво, чтобы казаться реальным в воображаемом мире.И все же это правда, причем абсолютно в том смысле, в каком может быть только математика. Возможно, я забыл, как вывести уравнение Эйлера из первых принципов (наряду с почти всеми остальными деталями из моих школьных уроков), но я всегда буду помнить получившуюся формулу. Это неопровержимое доказательство математического совершенства и напоминание о том, что мы никогда не сможем полностью понять смысл и причины математики.
Вот уравнение:
Если вы давно не изучали математику, возможно, это не так уж много.Но его разбивка показывает его красоту.
Во-первых, в честь дня числа Пи возьмите число Пи или 𝜋: иррациональное число, названное так потому, что оно продолжается бесконечно без повторения, 𝜋 было впервые обнаружено как число, которое описывает связь между длиной окружности и ее диаметром ( окружность = 𝜋 x диаметр.) Спустя столетия ученые определили, что 𝜋 также описывает направление ветра в реках и рябь света в физике. Однако изначально 𝜋 принадлежал к области математики, которая занимается формами и размерами: геометрия.
Другое известное иррациональное число,, происходит от логарифмов, которые являются частью исчисления – совершенно другой области математики. Полное значение требует времени, чтобы объяснить, но одна ключевая деталь, лежащая в основе его роли в логарифмах, заключается в том, что скорость роста x составляет x . Как и пи, e является основой множества различных формул. Численно это равно 2,71828… происходит постоянно, без повторения.
Затем – мнимое число.Это теоретическая концепция, которая никогда не может существовать на практике. 𝑖 означает квадратный корень из -1, что невозможно. Никакие два одинаковых числа нельзя умножить вместе, чтобы получить отрицательное значение, то есть не существует числового квадратного корня из -1. Квадратный корень из 4 равен 2, и у вас может получиться 2 яблока. Но вы никогда не сможете съесть √-1 яблок.
И все же возьмите эти три совершенно разных, сложных числа и объедините их в уравнение Эйлера, и вы получите волшебный результат: e в степени (𝑖, умноженное на пи) равно -1.Или:
Вы также можете записать это как:
Число один, конечно же, является первым натуральным числом, первым положительным целым числом и наиболее часто встречающимся лидером в наборах данных: Все просто, с чего мы начинаем подсчет. А число ноль – единственное неположительное натуральное число, наименьшая неотрицательная величина, ничего не означающая.
Другими словами, одно короткое уравнение включает пять самых важных чисел во всей математике.
Это почти нервирует.Взятые по отдельности, такие числа, как e, и, кажутся результатом несовершенных человеческих усилий понять сложность мира с помощью математических соотношений. Однако уравнение Эйлера показывает, что за этими числами стоит единство. Общая сумма математических знаний человека – это не более чем крошечная доля полной совершенной системы. И каждое число или уравнение, которое мы обнаруживаем, является отражением этой абстрактной внутренней истины, а не изобретением человека. {n + 1}} sin2n + 1π ≈2n + 1π для больших nnn.
Более полезный ряд включает в себя бесконечные сумм , а не произведения, потому что вычисление первых нескольких членов бесконечного выражения π \ piπ дает хорошее приближение к его значению. Самым простым является ряд Грегори-Лейбница, в котором используется оценка ряда Тейлора arctanx \ arctan xarctanx в 1:
.π4 = 1−13 + 15−17 + ⋯. \ Frac {\ pi} {4} = 1 – \ frac {1} {3} + \ frac {1} {5} – \ frac {1} {7 } + \ cdots.4π = 1−31 +51 −71 + ⋯.
Однако это сходится медленно, а это означает, что необходимо большое количество членов, чтобы получить хорошее приближение π \ piπ.Лучшая серия включает Machin-like формулы:
π4 = 4arctan15 − arctan1239π4 = 22arctan24478873121 + 17arctan685601693. \ Begin {align} \ frac {\ pi} {4} & = 4 \ arctan \ frac {1} {5} – \ arctan \ frac {1} {239} \\ \ frac {\ pi} {4} & = 22 \ arctan \ frac {24478} {873121} +17 \ arctan \ frac {685601} {693}.
