Как находится мгновенная скорость: Мгновенная скорость, теория и онлайн калькуляторы

11.07.201912.06.2021

Содержание

Мгновенная и средняя скорость

Если материальная точка находится в движении, то ее координаты подвергаются изменениям. Этот процесс может происходить быстро или медленно.

Определение 1

Величина, которая характеризует быстроту изменения положения координаты, называется скоростью.

Определение 2

Средняя скорость – это векторная величина, численно равная перемещению в единицу времени, и сонаправленная с вектором перемещения υ=∆r∆t; υ↑↑∆r.

Рисунок 1. Средняя скорость сонаправлена перемещению

Модуль средней скорости по пути равняется υ=S∆t.

Мгновенная скорость точки. Формулы

Мгновенная скорость характеризует движение в определенный момент времени. Выражение «скорость тела в данный момент времени» считается не корректным, но применимым при математических расчетах.

Определение 3

Мгновенной скоростью называют предел, к которому стремится средняя скорость υ при стремлении промежутка времени ∆t к 0:

υ=lim∆t∆r∆t=drdt=r˙.

Направление вектора υ идет по касательной к криволинейной траектории, потому как бесконечно малое перемещение dr совпадает с бесконечно малым элементом траектории ds.

Рисунок 2. Вектор мгновенной скорости υ

Имеющееся выражение υ=lim∆t∆r∆t=drdt=r˙ в декартовых координатах идентично ниже предложенным уравнениям:

υx=dxdt=x˙υy=dydt=y˙υz=dzdt=z˙.

Нужна помощь преподавателя?

Опиши задание — и наши эксперты тебе помогут!

Описать задание

Перемещение и мгновенная скорость

Запись модуля вектора υ примет вид:

υ=υ=υx2+υy2+υz2=x2+y2+z2.

Чтобы перейти от декартовых прямоугольных координат к криволинейным, применяют правила дифференцирования сложных функций. Если радиус-вектор r является функцией криволинейных координат r=rq1, q2, q3, тогда значение скорости запишется как:

υ=drdt=∑i=13∂r∂qi∂qi∂r=∑i=13∂r∂qiq˙i.

Рисунок 3. Перемещение и мгновенная скорость в системах криволинейных координат

При сферических координатах предположим, что q1=r; q2=φ; q3=θ, то получим υ, представленную в такой форме:

υ=υrer+υφeφ+υθφθ, где υr=r˙; υφ=rφ˙sin θ; υθ=rθ˙; r˙=drdt; φ˙=dφdt; θ˙=dθdt; υ=r1+φ2sin2θ+θ2.

Определение 4

Мгновенной скоростью называют значение производной от функции перемещения по времени в заданный момент, связанной с элементарным перемещением соотношением dr=υ(t)dt

Пример 1

Дан закон прямолинейного движения точки x(t)=0,15t2-2t+8. Определить ее мгновенную скорость через 10 секунд после начала движения.

Решение

Мгновенной скоростью принято называть первую производную радиус-вектора по времени. Тогда ее запись примет вид:

υ(t)=x˙(t)=0.3t-2; υ(10)=0.3×10-2=1 м/с.

Ответ: 1 м/с.

Пример 2

Движение материальной точки задается уравнением x=4t-0,05t2. Вычислить момент времени tост, когда точка прекратит движение, и ее среднюю путевую скорость υ.

Решение

Вычислим уравнение мгновенной скорости, подставим числовые выражения:

υ(t)=x˙(t)=4-0,1t.

4-0,1t=0;tост=40 с;υ0=υ(0)=4;υ=∆υ∆t=0-440-0=0,1 м/с.

Ответ: заданная точка остановится по прошествии 40 секунд; значение средней скорости равняется 0,1 м/с.

Мгновенная скорость движения

Другими словами, мгновенная скорость – это первая производная радиус-вектора по времени.

Вектор мгновенной скорости всегда направлен по касательной к траектории тела в сторону движения тела.

Мгновенная скорость дает точную информацию о движении в определенный момент времени. Например, при езде в автомобиле в некоторый момент времени водитель смотрит на спидометр и видит, что прибор показывает 100 км/ч. Через некоторое время стрелка спидометра указывает на величину 90 км/ч, а еще спустя несколько минут – на величину 110 км/ч. Все перечисленные показания спидометра – это значения мгновенной скорости автомобиля в определенные моменты времени. Скорость в каждый момент времени и в каждой точке траектории необходимо знать при стыковке космических станций, при посадке самолетов и т.д.

Имеет ли понятие «мгновенной скорости» физический смысл? Скорость – это характеристика изменения перемещения тела в пространстве. Однако, для того, чтобы определить, как изменилось перемещение, необходимо наблюдать за движением в течение некоторого времени. Даже самые совершенные приборы для измерения скорости такие как радарные установки, измеряют скорость за промежуток времени – пусть достаточно малый , однако это все-таки конечный временной интервал, а не момент времени. Выражение «скорость тела в данный момент времени» с точки зрения физики не является корректным. Однако, понятие мгновенной скорости очень удобно в математических расчетах, и им постоянно пользуются.

Примеры решения задач по теме «Мгновенная скорость»

Понравился сайт? Расскажи друзьям!

Мгновенная и средняя скорость | Физика

1.

Мгновенная скорость

В этом параграфе мы будем рассматривать неравномерное движение. Однако при этом нам пригодится то, что мы знаем о прямолинейном равномерном движении.

На рисунке 4.1 показаны положения разгоняющегося автомобиля на прямом шоссе с интервалом времени 1 с. Стрелка указывает на зеркальце заднего вида, положение которого мы рассмотрим далее более подробно.

Мы видим, что за равные интервалы времени автомобиль проходит разные пути, то есть движется неравномерно.

Уменьшим теперь последовательные интервалы времени в 20 раз – до 0,05 с – и проследим за изменением положения автомобиля в течение половины секунды (это нетрудно сделать, например, с помощью видеосъемки).

Чтобы не загромождать рисунок 4.2, на нем изображены только два положения автомобиля с промежутком времени 0,5 с. Последовательные положения автомобиля с интервалом 0,05 с отмечены положением его зеркальца заднего вида (показано красным цветом).

Мы видим, что когда последовательные равные промежутки времени достаточно малы, то пути, проходимые автомобилем за эти промежутки времени, практически одинаковы.

А это означает, что движение автомобиля в течение столь малых промежутков времени можно с хорошей точностью считать прямолинейным равномерным.

Оказывается, этим замечательным свойством обладает любое движение (даже криволинейное): если рассматривать его за достаточно малый промежуток времени Δt, оно очень похоже на прямолинейное равномерное движение! Причем чем меньше промежуток времени, тем больше это сходство.

Скорость тела за достаточно малый промежуток времени и называют его скоростью в данный момент времени t, если этот момент времени находится в промежутке Δt. А более точное ее название – мгновенная скорость.

Насколько малым должен быть промежуток времени Δt, чтобы в течение этого промежутка движение тела можно было считать прямолинейным равномерным, зависит от характера движения тела.

В случае разгона автомобиля это доли секунды. А, например, движение Земли вокруг Солнца можно с хорошей точностью считать прямолинейным и равномерным даже в течение суток, хотя Земля за это время пролетает в космосе больше двух с половиной миллионов километров!

Говоря далее о скорости, мы будем (если это особо не оговорено) подразумевать обычно мгновенную скорость.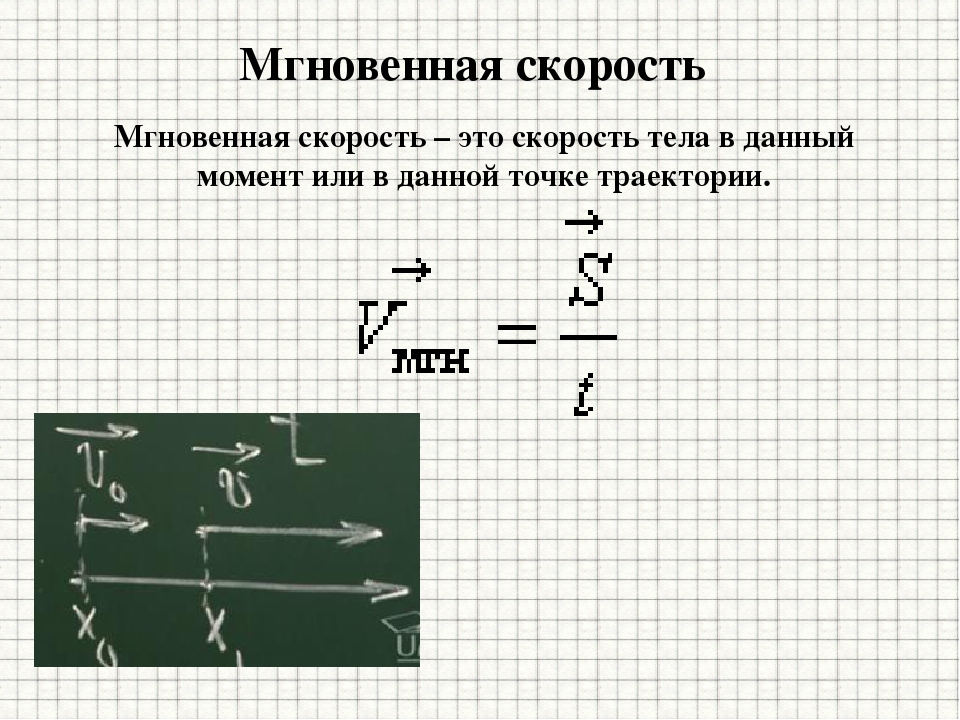

? 1. По рисунку 4.2 определите мгновенную скорость автомобиля. Длину автомобиля примите равной 5 м.

Значение мгновенной скорости автомобиля показывает спидометр (рис. 4.3).

Как найти мгновенную скорость по графику зависимости координаты от времени

На рисунке 4.4 изображен график зависимости координаты от времени для автомобиля, который движется по прямолинейному шоссе.

Мы видим, что он движется неравномерно, потому что график зависимости его координаты от времени – это кривая, а не отрезок прямой.

Покажем, как определить по этому графику мгновенную скорость автомобиля в какой-либо момент времени – скажем, при t = 3 с (точка на графике).

Для этого рассмотрим движение автомобиля за столь малый промежуток времени, в течение которого его движение можно считать прямолинейным равномерным.

На рисунке 4.5 показан интересующий нас участок графика при десятикратном увеличении (см., например, шкалу времени).

Мы видим, что этот участок графика практически неотличим от отрезка прямой (красный отрезок). За последовательные равные промежутки времени по 0,1 с автомобиль проходит практически одинаковые расстояния – по 1 м.

2. Чему равна мгновенная скорость автомобиля в момент t = 3 с?

Возвращаясь к прежнему масштабу чертежа, мы увидим, что прямая красного цвета, с которой практически совпадал малый участок графика, – касательная к графику зависимости координаты от времени в данный момент времени (рис. 4.6).

Итак, о мгновенной скорости тела можно судить по угловому коэффициенту касательной к графику зависимости координаты от времени:

чем больше угловой коэффициент касательной, тем больше скорость тела. (Описанный способ определения мгновенной скорости с помощью касательной к графику зависимости координаты от времени связан с понятием производной функции. Это понятие вы будете изучать в курсе «Алгебра и начала аиализа».) А в тех точках графика, где угол наклона касательной равен нулю, то есть касательная параллельна оси времени t, мгновенная скорость тела равна нулю.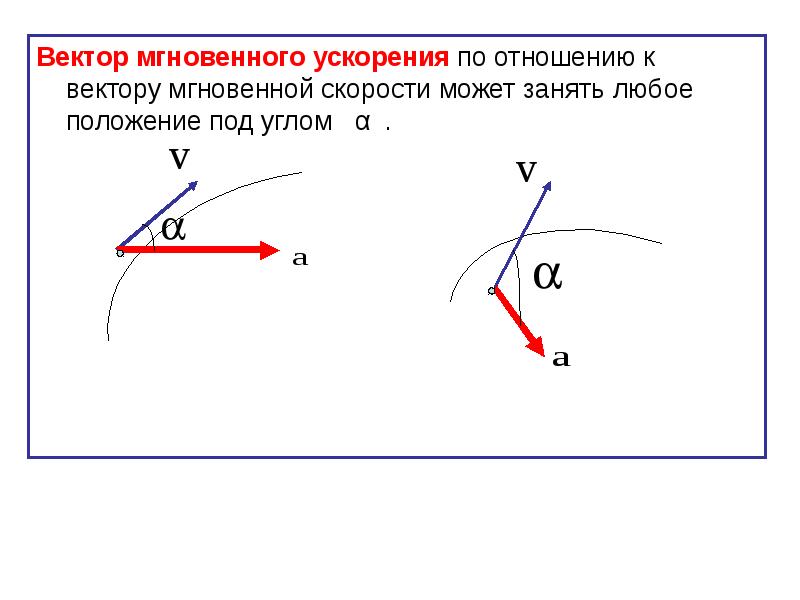

? 3. Рассмотрите рисунок 4.6.
а) В каких точках графика угол наклона касательной наибольший? наименьший?
б) Найдите наибольшую и наименьшую мгновенную скорость автомобиля в течение первых 6 с его движения.

2. Средняя скорость

Во многих задачах используют среднюю скорость, связанную с пройденным путем:

v_ср = l/t. (1)

Определенная таким образом средняя скорость является скалярной величиной, так как путь – это скалярная величина. (Иногда во избежание недоразумений ее называют средней путевой скоростью.)

Например, если автомобиль в течение трех часов проехал по городу 120 км (при этом он мог разгоняться, тормозить и стоять на перекрестках), то его средняя скорость равна 40 км/ч.

? 4. Насколько уменьшится средняя скорость только что упомянутого автомобиля, если из-за остановок в пробках общее время движения увеличится на 1 ч?

Средняя скорость на двух участках движения

Во многих задачах рассматривается движение тела на двух участках, на каждом из которых движение можно считать равномерным. В таком случае, согласно определению средней скорости (1), можно записать:

v_ср = (l₁ + l₂)/(t₁ + t₂), (2)

где l₁ и t₁ – путь и время для первого участка, а l₂ и t₂ – для второго. Рассмотрим примеры.
Саша выехал из поселка на велосипеде со скоростью 15 км/ч и ехал в течение часа. А потом велосипед сломался, и Саша еще час шел пешком со скоростью 5 км/ч.

? 5. Найдите:
а) путь, пройденный Сашей за все время движения;
б) общее время движения Саши;
в) среднюю скорость Саши.

В рассмотренном случае средняя скорость оказалась равной среднему арифметическому скоростей, с которыми Саша ехал и шел. Всегда ли это справедливо? Рассмотрим следующий пример.
Пусть Саша ехал на велосипеде в течение часа со скоростью 15 км/ч, а потом прошел такое же расстояние пешком со скоростью 5 км/ч.

? 6. Найдите:
а) путь, который Саша прошел пешком;
б) путь, пройденный Сашей за все время движения;
в) общее время движения Саши;
б) среднюю скорость Саши.

Рассмотрев этот случай, вы увидите, что на этот раз средняя скорость не равна среднему арифметическому скоростей езды и ходьбы. А если присмотреться еще внимательнее, то можно заметить, что во втором случае средняя скорость меньше, чем в первом. Почему?

? 7. Сравните промежутки времени, в течение которых Саша ехал и шел пешком в первом и втором случаях.

Обобщим рассмотренные выше ситуации.

Рассмотрим сначала случай, когда тело двигалось с разными скоростями в течение равных промежутков времени.

Пусть первую половину всего времени движения тело двигалось со скоростью v₁, а вторую половину – со скоростью v₂. Можно ли найти среднюю скорость движения на всем участке, если не известны ни общее время движения, ни путь, пройденный телом за все время движения?

Можно: для этого введем обозначения для всех нужных нам величин независимо от того, известны они или неизвестны. Это распространенный прием при решении многих задач.

Обозначим все время движения t, весь путь l, а пути, пройденные за первую и вторую половину времени движения, обозначим соответственно) l₁ и l₂.

? 8. Выразите через v₁, v₂ и t:
a) l₁ и l₂; б) l; в) среднюю скорость.

Найдя ответы на эти вопросы, вы узнаете, справедливо ли в общем случае утверждение: если тело двигалось на двух участках с разными скоростями в течение равных промежутков времени, то его средняя скорость на всем пути равна среднему арифметическому скоростей движения на двух участках.

Рассмотрим теперь случай, когда тело двигалось с разными скоростями первую и вторую половину пути.

Пусть теперь первую половину всего пути тело двигалось со скоростью v₁, а вторую половину – со скоростью v₂. Обозначим снова все время движения t, весь путь l, а промежутки времени, в течение которых тело двигалось на первом и втором участке, обозначим соответственно t₁ и t₂.

? 9. Выразите через v₁, v₂ и l:
а) t₁ и t₂; б) t; в) среднюю скорость.

Ответив на эти вопросы, вы узнаете, справедливо ли в общем случае утверждение: если тело двигалось на двух участках равной длины с разными скоростями, то его средняя скорость на всем пути не равна среднему арифметическому этих скоростей.

? 10. Докажите, что средняя скорость тела, которое двигалось на двух участках равной длины с разными скоростями, меньше, чем если бы оно двигалось на двух участках с теми же скоростями в течение равных промежутков времени.
Подсказка. Выразите для каждого из двух случаев среднюю скорость через скорости на первом и втором участках и сравните полученные выражения.

? 11. На первом участке пути тело двигалось со скоростью v₁, а на втором – со скоростью v₂. Чему равно отношение длин этих участков, если средняя скорость движения оказалась равной среднему арифметическому v₁ и v₂?

Дополнительные вопросы и задания

12. Одну треть всего времени движения поезд ехал со скоростью v₁, а оставшееся время – со скоростью v₂.
а) Выразите пройденный поездом путь через v₁, v₂ и все время движения t.
б) Выразите среднюю скорость поезда через v₁ и v₂.
в) Найдите числовое значение средней скорости при v₁ = 60 км/ч, v₂ = 90 км/ч.

13. Автомобиль ехал три четверти всего пути со скоростью v₁, а оставшийся участок пути – со скоростью v₂.
а) Выразите все время движения автомобиля через v₁, v₂ и весь пройденный путь l.
б) Выразите среднюю скорость движения автомобиля через v₁ и v₂.
в) Найдите числовое значение средней скорости при v₁ = 80 км/ч, v₂ = 100 км/ч.

14. Автомобиль ехал 2 ч со скоростью 60 км/ч. Сколько времени после этого он должен ехать со скоростью 80 км/ч, чтобы его средняя скорость на всем пути стала равной 66,7 км/ч?

15. Перенесите в тетрадь (по клеточкам) график зависимости координаты автомобиля от времени, изображенный на рисунке 4.4. Считайте, что автомобиль едет вдоль оси x.
а) Определите графически среднюю скорость за 6 с.
б) Используя касательную, определите, в какие примерно моменты времени мгновенная скорость автомобиля была равна его средней скорости за 6 с.

16. Тело движется вдоль оси x. Зависимость координаты тела от времени выражается формулой x = 0,2 * t².
а) Выберите удобный масштаб и изобразите график зависимости x(t) в течение первых 6 с.
б) С помощью этого графика найдите момент времени, в который мгновенная скорость тела была равна средней скорости за все время движения.

Мгновенная скорость | Физика

Рассмотрим автомобиль, движущийся прямолинейно и неравномерно (например, из Москвы в Санкт-Петербург, как на рис. 50). Понятно, что значения средней скорости этого автомобиля за различные промежутки времени при неравномерном движении могут меняться. Можно ли в этом случае ответить на вопрос: чему равна скорость автомобиля в какой-то конкретный момент времени? И существует ли вообще такая физическая величина? Ведь в определение средней скорости входит понятие определенного промежутка времени. А если этот промежуток времени будет равен нулю, то и перемещение тела, очевидно, будет равно нулю. Однако, наблюдая в движущимся автомобиле за спидометром, мы видим, что в каждый момент времени он показывает определенную величину, которая чаще всего изменяется со временем. Как же определить скорость тела в конкретный момент времени? Чтобы это сделать, рассмотрим очень маленький промежуток времени.

Под очень маленьким промежутком времени понимают такой промежуток, в течение которого движение тела практически неотличимо от равномерного прямолинейного движения. Это означает, что скорость тела в течение этого промежутка можно считать практически постоянной.

Из сказанного следует, что промежуток времени можно считать достаточно малым, если при его дальнейшем уменьшении полученные новые значения скорости практически не изменяются.

Понятно, что чем быстрее исследуемое тело изменяет свою скорость, тем меньше будет промежуток времени, в течение которого движение тела практически неотличимо от равномерного прямолинейного. И следовательно, тем меньший промежуток времени мы должны использовать для определения значения его скорости в конкретный момент времени.

Мгновенная скорость тела в данный момент времени t – это средняя скорость тела за достаточно малый промежуток времени Δt, начинающийся сразу после момента времени t.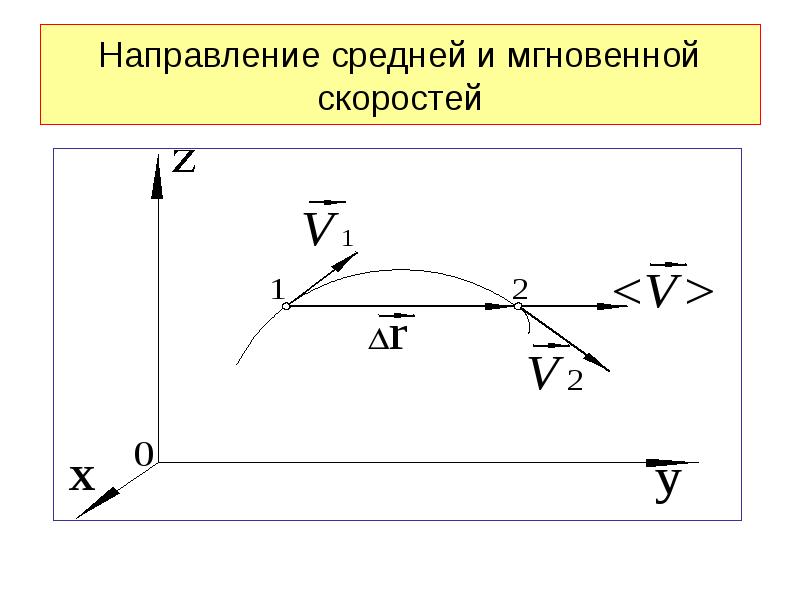

Так же как и средняя скорость, мгновенная скорость является вектором. Чтобы подчеркнуть это, часто говорят «вектор скорости v», а при необходимости указать момент времени, для которого определена скорость, говорят «скорость в момент времени t».

При описании движения обычно говорят о скорости, имея при этом в виду мгновенную скорость в момент времени t. Поэтому мгновенную скорость обычно называют просто скорость. Если же речь идет, например, о средней скорости, то обязательно используют прилагательное «средняя», а для средней путевой скорости — прилагательные «средняя» и «путевая».

Итоги

Скорость (мгновенная скорость) тела в данный момент времени t – это средняя скорость тела за достаточно малый промежуток времени Δt, начинающийся сразу после момента времени t.

Вопросы

Какой промежуток времени при определении скорости можно считать достаточно малым?
Что такое мгновенная скорость?
Изменяется ли с течением времени мгновенная скорость тела, которое движется равномерно и прямолинейно?
Какие физические модели используют при введении понятия мгновенной скорости?

Упражнение

Представьте себе, что вы выехали на автомобиле со своего места на стоянке, находящейся рядом с вашим домом, в 8 часов утра, а в 17 часов вечера вернули автомобиль на то же место. За день вы проехали путь s = 360 км. При этом в течение промежутка времени от 10 до 12 часов дня вы ехали по прямолинейной трассе строго на север с постоянной скоростью 60 км/ч. Определите вашу скорость (модуль и направление) в моменты времени: а) t = 11 часов; б) t = 17 часов.

Мгновенная скорость

Средняя скорость

Если тело перемещается неравномерно, то описывая его движение в качестве одного из параметров можно воспользоваться средней скоростью движения на отдельных отрезках пути. Но такое описание дает очень приближенную, грубую характеристику перемещения. Поскольку находя средние скорости, мы проводим замену неравномерного движения на движение с постоянной скоростью на избранных отрезках пути, думая, что скорость изменяется скачкообразно при переходе от одного отрезка времени к другому. Графиком пути, отражающем перемещение тела, с постоянной скоростью, отличающейся на разных временных отрезках, станет ломаная линия, имеющая звенья с различным наклоном.

Допустим, что материальная точка перемещается вдоль прямой линии, которая не совпадает с осями координат. При этом ее положение определяет радиус- вектор $\vec r_1$, соответствующий моменту времени $t_1$. В момент времени $t_2$ положение материальной точки в пространстве определяет вектор $\vec r_2$.

Вектор перемещения нашей материальной точки определим как:

$\Delta \vec r=\vec r_2-\vec r_1(1).$

Определение 1

Средняя скорость материальной точки будет определена выражением:

$ \vec v_{sr}=\frac{\Delta \vec r}{\Delta t}=\frac{\vec r_2-\vec r_1}{t_2-t_1}(2).$

Из формулы (2) видно, что в ней происходит деление вектора на скаляр, в результате мы имеем вектор, направление которого совпадает с направлением вектора перемещения.

Векторы скорости и перемещения обладают одинаковыми направлениями.

Переход от средней скорости к мгновенной скорости

В выражении (2) средняя скорость найдена для отрезка времени, равного $\Delta t$. Разделим данный временной отрезок на более мелкие. Если материальная точка перемещается неравномерно, то вновь найденные средние скорости будут отличаться, от средней скорости для всего отрезка $\Delta t$. Уменьшим временной отрезок $\Delta t$, станут меньше и отрезки времени внутри него. Средние скорости в уменьшенных промежутках времени будут отличаться от средней скорости на всем отрезке времени, но величина различия станет меньше.

Устремим рассматриваемый промежуток времени к нулю (∆t→0), средняя скорость при этом устремится к предельному значению, которое называют мгновенной скоростью.

Определение 2

Мгновенной скоростью или скоростью в данный момент времени называют векторную величину, равную:

$\vec v(t)= \frac {d\vec r}{dt}(3).$

Если тело перемещается равномерно, то мгновенная скорость его движения в каждый момент времени совпадает со скоростью этого движения. Говорят, что мгновенная скорость равномерного движения является постоянной.

Мгновенная скорость неравномерного перемещения – это переменный параметр, который принимает разные значения для разных моментов времени. При этом мгновенную скорость можно считать изменяющейся непрерывно на всем отрезке времени, на котором рассматривается движение. 2 (9).$

Направление мгновенной скорости

Будем описывать движение материальной точки через параметры траектории. При этом нам известны траектория движения точки и связь пути ($s$) и времени $t$. Путь отмеряется по траектории, от точки траектории, которую мы принимаем за начальную. При этом любая точка траектории характеризуется собственной величиной $s$. Из сказанного выше следует, что радиус-вектор – это функция от $s$, траекторию зададим уравнением:

$\vec r = \vec r(s)(10)$.

Получаем, что в определении мгновенной скорости (3) мы можем считать радиус – вектор как сложную функцию ($\vec r(s(t))$). При этом ее производную найдем, применяя правило дифференцирования сложной функции:

$\vec v=\frac{d\vec r}{dt}=\frac{d\vec r}{ds}\frac{ds}{dt}(11)$,

где по определению мгновенной скорости ее величина равна: $v=\frac{ds}{dt}$.

Обозначим $\Delta s$ – расстояние между парой точек по траектории; $|\Delta \vec r|$– расстояние между рассматриваемыми точками по кратчайшему расстоянию (прямой). При сближении наших точек разница между $\Delta s$ и $|\Delta \vec r|$ уменьшается, запишем:

$\frac{d\vec r}{ds}=\lim_{\Delta s\to 0} (\frac {\Delta \vec r}{\Delta s})=\lim_{\Delta s\to 0}(\frac{\Delta \vec r}{|\Delta r|}\frac {|\Delta r|}{\Delta s})=\vec \tau (12).$

где $\vec \tau$ – единичный вектор, являющийся касательным к траектории движения точки.

Принимая во внимание сказанное выше выражение (12) для мгновенной скорости можно записать как:

$\vec v=v\vec \tau$(13).

Из формулы (13) становится очевидно, что мгновенная скорость направлена по касательной к траектории движения материальной точки.

Рассматривая направления мгновенной скорости движения материальной точки подчеркнем, что:

Мгновенная скорость материальной точки перемещающейся по прямой – это вектор, который направлен по траектории ее движения.
При перемещении материальной точки по криволинейной траектории вектор мгновенной скорости имеет направление по касательной к траектории движения точки.

Скорость при равнопеременном движении

Самым простым способом неравномерного движения является равнопеременное перемещение тела, движение с постоянным ускорением. Это движение бывает:

равноускоренным, если скорость и ускорение имеют одинаковые направления, при этом величина скорости увеличивается;
равнозамедленное, при противоположном направлении скорости и ускорения, в этом случае скорость по модулю уменьшается.

При равнопеременном движении скорость в любой момент времени можно вычислить, если использовать выражение:

$\vec v(t)=\vec v_0+\vec a \bullet t (14),$

где $\vec v_0$ – начальная скорость движения точки; $\vec a$ – постоянное ускорения точки.

1. Мгновенная скорость.

Мгновенная скорость – это скорость тела в данный момент времени или в данной точке траектории. Это векторная физическая величина, численно равная пределу, к которому стремится средняя скорость за бесконечно малый промежуток времени:

Другими словами, мгновенная скорость – это первая производная радиус-вектора по времени.

2. Средняя скорость.

Средней скоростью на некотором участке называется величина равная отношению перемещения к промежутку времени, за который это перемещение произошло.

3. Угловая скорость. Формула. СИ.

Угловой скоростью называется векторная физическая величина равная первой производной угла поворота тела по времени. [рад/с]

4. Связь угловой скорости с периодом вращения.

Равномерное вращение характеризуется периодом вращения и частотой вращения.

5. Угловое ускорение. Формула. СИ.

Это физическая величина равная первой производной угловой скорости или второй производной угла поворота тела по времени. [рад/с²]

6. Как направлен вектор угловой скорости/углового ускорения.

Вектор угловой скорости направлен по оси вращения причем так чтобы вращение рассматриваемое с конца вектора угловой скорости, происходило против хода часовой стрелки(правило правой руки).

При ускоренном вращении вектор углового ускорения сонаправлен с вектором угловой скорости, а при замедленном − противоположен ему.

7/8. Связь между нормальным ускорением и угловой скоростью/Связь между тангенциальным и угловым ускорением.

9. Что определяет и как направлена нормальная составляющая полного ускорения? Нормальное ускорение СИ.Нормальное ускорение определяет быстроту изменения скоро-сти по направлению и направлено к центру кривизны траектории.

В СИ нормальное ускорение [м/с²]

10. Что определяет и как направлена тангенциальная составляющая полного ускорения.

Тангенциальное ускорение равно первой производной по времени от модуля скорости и определяет быстроту изменения скорости по модулю, и направлено по касательной к траектории.

11. Тангенциальное ускорение в СИ.

м/с²

12. Полное ускорение тела. Модуль этого ускорения.

13. Масса. Сила. Законы Ньютона.

Масса − это физическая величина, являющаяся мерой инерционных и гравитационных свойств тела. Единицей массы в СИ [m] = кг.

Сила − это векторная физическая величина, являющаяся мерой механического воздействия на тело со стороны других тел или полей, в результате, которого тело деформируется или приобретает ускорение. Единица измерения силы в СИ – Ньютон; кг*м/с²

Первый закон Ньютона (или закон инерции): если на тело не действуют силы или их действие скомпенсировано, то данное тело находится в состоянии покоя или равномерного прямолинейного движения.

Второй закон Ньютона: ускорение тела прямо пропорционально результирующей сил приложенных к нему и обратно пропорционально его массе. Второй закон Ньютона позволяет решать основную задачу механики. Поэтому его называется основным уравнением динамики поступательного движения.

Третий закон Ньютона: сила, с которой одно тело действует на другое, равна по величине и противоположна по направлению силе, с которой второе тело действует на первое.

Мгновенная скорость – это… Что такое Мгновенная скорость?

Ско́рость (часто обозначается , от англ. velocity или фр. vitesse) — векторная величина, характеризующая быстроту перемещения и направление движения материальной точки в пространстве относительно выбранной системы отсчёта. Этим же словом может называться скалярная величина, точнее модуль производной радиус-вектора.

В науке повсеместно используется также скорость в широком смысле, то есть как скорость изменения какой-либо величины (не обязательно радиус-вектора). Так, например, говорят об угловой скорости, скорости роста температуры, скорости химической реакции и т. д. Математически находится с помощью производной от данной величины (обычно по времени, либо от другого аргумента).

Скорость тела в механике

Вектор скорости материальной точки в каждый момент времени определяется производной по времени радиус-вектора этой точки:

Здесь v — модуль скорости, — направленный вдоль скорости единичный вектор касательной к траектории в точке .

Говорят, что тело совершает мгновенно-поступательное движение, если в данный момент времени скорости всех составляющих его точек равны. Так, например, равны скорости всех точек кабинки колеса обозрения (если, конечно, пренебречь колебаниями кабинки).

В общем случае, скорости точек, образующих твёрдое тело, не равны между собой. Так, например, для катящегося без проскальзывания колеса величина скорости точек на ободе относительно дороги принимает значения от нуля (в точке касания с дорогой) до удвоенного значения скорости автомобиля (в точке, диаметрально противоположной точке касания). Распределение скоростей в твёрдом теле определяется с помощью кинематической формулы Эйлера.

Если скорость тела (как векторная величина) не меняется во времени, то движение тела — равномерное (ускорение равно нулю).

Полезно отличать понятие средней скорости перемещения от понятия средней скорости пути, равной отношению пройденного точкой пути ко времени, за которое этот путь был пройден. В отличие от скорости перемещения, средняя скорость пути — скаляр.

Мгновенная и средняя скорость

Когда говорят о средней скорости , для различения, скорость согласно выше приведённому определению называют мгновенной скоростью. Так, хотя мгновенная скорость бегуна, кружащего по стадиону, в каждый момент времени отлична от нуля, его средняя скорость (перемещения) от старта до финиша оказывается равной нулю, если точки старта и финиша совпадают. Заметим, что при этом, средняя путевая скорость остаётся отличной от нуля.

Преобразование скорости

В классической механике Ньютона скорости преобразуются при переходе из одной инерциальной системы отсчёта в другую согласно преобразованиям Галилея. Если скорость тела в системе отсчёта S была равна , а скорость системы отсчёта S’ относительно системы отсчёта S равна , то скорость тела в при переходе в систему отсчёта S’ будет равна .

Для скоростей, близких к скорости света преобразования Галилея становятся несправедливы. При переходе из системы S в систему S’ необходимо использовать преобразования Лоренца для скоростей:

в предположении, что скорость направлена вдоль оси х системы S. Легко убедиться, что в пределе нерелятивистских скоростей преобразования Лоренца сводятся к преобразованиям Галилея.

Единицы измерения скорости

Соотношение между единицами скорости

1 м/с = 3,6 км/ч
1 узел = 1,852 км/ч = 0,514 м/c
Мах 1 ~ 330 м/c ~ 1200 км/ч (зависит от условий, в которых находится воздух)
c = 299 792 458 м/c

См. также

Wikimedia Foundation. 2010.

Формула мгновенной скорости

Скорость – это скорость изменения положения во времени. Скорость объекта может меняться по мере его движения. Мгновенная скорость – это скорость объекта в определенный момент времени. Если положение является функцией времени, то скорость зависит от изменения положения при изменении времени. Мгновенная скорость может быть найдена, поскольку это изменение во времени становится небольшим. Для расчета мгновенной скорости требуется найти предел функции положения, когда изменение во времени приближается к нулю.Скорость – это скалярная величина, означающая, что она имеет величину (значение), но не направление. По этой причине скорость никогда не может быть отрицательной. Единица измерения скорости – метры в секунду (м / с).

v = мгновенная скорость (м / с)

Δ = “изменение”, представленное греческой буквой “дельта” (без единиц измерения)

x (t) = положение как функция времени (м)

t = время (с)

Вопросы по формуле мгновенной скорости:

1) Когда объект падает и на него действует сила тяжести, его положение изменяется в соответствии с функцией x (t) = 4.9t ², а x (t) выражается в метрах. Какова мгновенная скорость при t = 5,0 с?

Ответ: Мгновенную скорость можно найти по формуле:

v = 9,8 т

v = 9,8 (5,0) м / с

v = 49,0 м / с

Мгновенная скорость при t = 5,0 с составляет 49,0 м / с.

2) Автомобиль останавливается на светофоре, а затем начинает движение по прямой дороге.Расстояние автомобиля от источника света определяется функцией x (t) = bt ³ – ct ², где постоянные b = 0,900 м / с ³ и c = 2,70 м / с ². Какой будет мгновенная скорость при t = 3,00 с?

Ответ: Мгновенную скорость можно найти по формуле:

При t = 3.00 с, мгновенная скорость:

v = 24,3 м / с – 16,2 м / с

v = 8,1 м / с

Мгновенная скорость автомобиля при t = 3,00 с составляет 8,1 м / с.

Формула мгновенной скорости

Средняя скорость и мгновенная скорость

Скорость

Силы и движение

Средняя скорость и мгновенная скорость

Повествование о физике для 11-14

Расчеты на основе различных измерений

По мере того, как интервал измерения средней скорости становится все короче и короче, эта скорость становится все ближе и ближе к мгновенной скорости.

То, что вы видите на спидометре автомобиля, – это скорость в данный момент или момент – мгновенная скорость. Это скорость , сейчас . Один из способов найти эту мгновенную скорость – измерить скорость вращения колес. Современные электронные устройства позволяют точно измерять короткие промежутки времени, а датчик может измерять угол в течение этих очень коротких промежутков времени, эффективно обеспечивая мгновенную скорость.

Однако по большей части мы измеряем более длительные поездки: расстояние, пройденное за более длительные промежутки времени от нескольких секунд до минут или даже часов.Итоговый расчет дает среднюю скорость. Мы не предполагаем, что автомобиль сохранял постоянную скорость в течение времени.

Средняя скорость, рассчитанная в конце поездки, может сказать вам, что:

Спортсмен, завершивший забег на 800 метров за 160 секунд, имел среднюю скорость 5 метров в секунду.
Автомобиль, который проехал 20 миль за 30 минут, имел среднюю скорость 40 миль в час.

Обычно используется термин скорость , а не средняя скорость .Многие учителя опускают термин средний , полагая, что это может добавить дополнительный уровень сложности. Тем не менее, мы бы порекомендовали вам побуждать ваших учеников по возможности различать мгновенную и среднюю скорости. Один из способов сделать это – ограничить использование средней скорости для обозначения всего путешествия. (Позже вы можете ослабить это, чтобы применить к длинным ногам в рамках одного путешествия, поэтому относитесь к ним как к серии мини-путешествий). Мгновенные скорости, напротив, могут тогда составлять , сейчас измерений во время поездки.По мере того, как путешествия разбиваются на более короткие и более короткие этапы, средние скорости становятся все более и более неотличимыми от мгновенных скоростей. Тем не менее, это хороший способ разделить функции двух измерений до тех пор, пока не возникнет необходимость в более сложном понимании (подробнее в теме SPT: Сила и движение).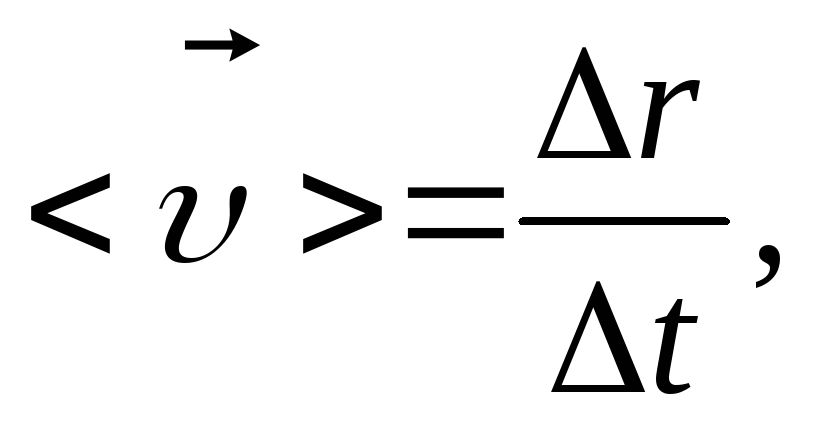

Мгновенная скорость

Обыденное понятие скорости возникает, когда мы рассматриваем, насколько быстро или медленно движется тело.Каким-то образом мы связываем смещение тела со временем, проведенным в таком смещении. В этом разделе мы определим, что в физике подразумевается под мгновенной скоростью, а также ее сходство и различие с мгновенной скоростью.

Мгновенная скорость

Когда вы путешествуете на машине, вы можете смотреть на спидометр, который показывает «скорость» в каждый момент времени. Хотя обычно мы просто называем это значение скоростью , мы ранее определили скорость как вектор.На самом деле автомобильный спидометр показывает вам величину вектора мгновенной скорости , которая соответствует скорости , вычисленной в момент времени , следуя процедуре, подобной той, которую мы выполняем для вычисления мгновенной скорости из . средняя скорость , то есть вычисление предела средней скорости, когда время приближается к нулю (∆t → 0).

Мгновенная скорость определяется как предел средней скорости, когда рассматриваемый временной интервал приближается к 0.Это дается выражением:

где:

V : Мгновенная скорость или просто скорость
∆s: Пройденное расстояние за рассматриваемый интервал
∆t: Время, необходимое телу для завершения движения

Единица измерения мгновенной скорости в Международной системе (S.I.) – метр в секунду [м / с] .

Значение мгновенной скорости совпадает с величиной мгновенной скорости в этой точке.Вот почему мы используем ту же букву ( V ), но заглавную, чтобы обозначить ее. Однако не путайте их: мгновенная скорость или просто скорость – это вектор, а мгновенная скорость – это скаляр. В следующем «эксперименте и обучении» вы увидите, что, как мы указывали ранее, когда мы берем очень близкие точки, значение средней скорости приближается к значению величины средней скорости. На пределе значения равны.

Экспериментируй и учись

Данные

Мгновенная скорость

На графике показана траектория, по которой следует тело, а также его начальное и конечное положение.

Переместите ползунок времени, чтобы увидеть, где будет находиться тело каждый раз, и обратите внимание, что по мере того, как время уменьшается, значения средней скорости и величина средней скорости приближаются к . Из этого мы можем вывести, что средняя скорость , когда время приближается к нулю , равна величине средней скорости, или, что то же самое, величина мгновенной скорости равна мгновенной скорости .

Пример

Знание того, что расстояние, которое проходит тело как функция времени, определяется следующим уравнением:

S (t) = t2 + 5 · t + 1

Вычислить:

а) Средняя скорость в первые 3 секунды.
б) Мгновенная скорость тела.

скорость, средняя скорость и мгновенная скорость и скорость с примерами

СКОРОСТЬ И СКОРОСТЬ

В последних разделах мы изучили скалярные и векторные концепции. Помимо определений этих понятий, мы попытаемся объяснить термины скорости и скорости. Как упоминалось в последнем разделе, расстояние и смещение – разные термины. Расстояние – это скалярная величина, а смещение – это векторная величина.Таким же образом мы можем разделить скорость и скорость. Скорость – это скалярная величина, относящаяся только к величине, а скорость – это векторная величина, которая должна учитывать как величину, так и направление.

СКОРОСТЬ

Скорость можно определить как «насколько быстро что-то движется» или с более научной точки зрения это можно объяснить как «расстояние, пройденное за единицу времени». В повседневной жизни мы используем первое определение и говорим, что более быстрый объект имеет более высокую скорость. Скорость не показывает нам направление движения, она просто дает величину расстояния, пройденного за данный момент времени.Другими словами, это скалярная величина. Мы используем символ v , чтобы показать скорость. Позвольте мне сформулировать то, о чем мы говорим выше;

Скорость = расстояние / время

Из приведенной выше формулы мы можем сказать, что скорость прямо пропорциональна расстоянию и обратно пропорциональна времени. Думаю, пора поговорить немного об единицах скорости.Автомобили обычно используют километр в час (км / ч) в качестве единицы скорости, однако на коротких дистанциях мы можем использовать метр в секунду (м / с) в качестве единицы скорости. В своих примерах и пояснениях я буду использовать м / с как единицу измерения.

Пример Рассчитайте скорость автомобиля, который преодолевает 450 м за 9 секунд.

СКОРОСТЬ

Скорость может быть определена как «скорость, имеющая направление». Как вы понимаете из определения, скорость – это векторная величина, имеющая как величину, так и направление.В повседневной жизни мы используем скорость и скорость как синонимы, но в физике они имеют разные значения. Мы можем определить скорость как «скорость изменения смещения», тогда как «скорость – это скорость изменения расстояния». При вычислении скорости мы смотрим на общее расстояние, однако при вычислении скорости мы должны учитывать направление, и короче говоря, мы можем просто смотреть на изменение положения, а не на все пройденное расстояние. Если человек идет на 5 м на восток, а затем на 5 м на запад, скорость этого человека, рассчитанная путем деления общего пройденного расстояния, равного 10 м, на затраченное время, однако, скорость, рассчитанная путем деления смещения на затраченное время, которое составляет 0 м, разделенное на затраченное время, дает нас ноль.Другими словами, если смещение равно нулю, мы не можем говорить о скорости.

Будьте осторожны !! Чтобы объект имел скорость, должно быть изменение положения.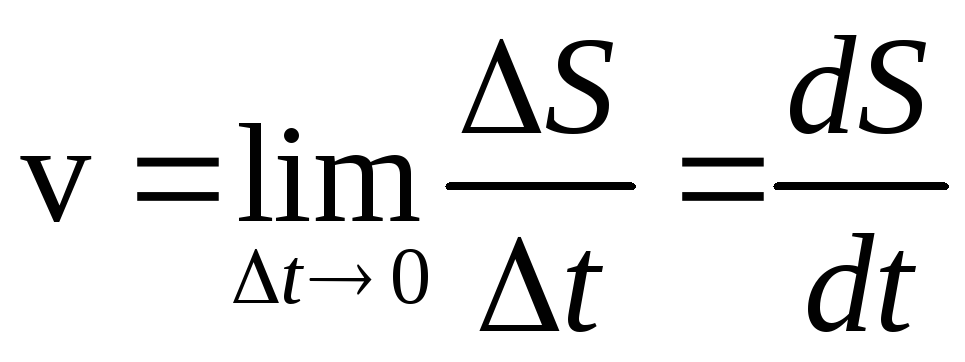

Пользуемся? символ, чтобы показать изменение чего-либо. Например, мы можем обозначить изменение положения как? X. .

Пример Рассчитайте скорость и скорость человека, перемещающегося на 45 м к северу и 36 м к югу за 27 секунд.

Сначала мы должны вычислить пройденное расстояние и перемещение человека, чтобы вычислить скорость и скорость.

Общее пройденное расстояние = 45 м + 6 м = 81 м

Скорость = общее расстояние / время движения = 81 м / 27 с = 3 м / с

Скорость = перемещение / время = (45-36) м / 27 с = 9 м / 27 с = 0,33 м / с

На этом примере мы показываем, что скорость и скорость – не одно и то же.

Средняя скорость и мгновенная скорость

Движущийся объект не имеет одинаковой скорости во время своего движения. Иногда он ускоряется, а иногда замедляется.В данный момент времени мы читаем со спидометра: мгновенная скорость . Например, автомобиль, движущийся с постоянной скоростью, едет в другой город, он должен остановиться на красный свет светофора или замедлить движение при возникновении нежелательных ситуаций на дороге. В конце поездки, если мы хотим узнать средней скорости автомобиля, мы делим общее расстояние на общее время поездки.

Предположим, что автомобиль проезжает 500 км за 5 часов.Когда мы вычисляем среднюю скорость, мы видим, что она составляет 100 км / ч. Конечно, машина не движется с постоянной скоростью 100 км / ч. У него много мгновенных скоростей, и 100 км / ч – это среднее из этих мгновенных скоростей.

Средняя скорость и мгновенная скорость

Мы можем следовать тем же шагам, что и при определении средней и мгновенной скорости, при определении средней и мгновенной скорости. Мгновенная скорость – это скорость в данный момент времени, однако, как и в случае скорости, средняя скорость вычисляется смещением за интервал времени.

Пример Человек, едущий со своей машиной на 150 м на восток и более чем на 70 м на запад, вычисляет среднюю скорость и скорость автомобиля, если поездка занимает 10 секунд.

Средняя скорость = смещение / временной интервал смещения = 150 м-70 м = 80 м

Средняя скорость = 80 м / 10 с = 8 м / с на восток

Средняя скорость = общее пройденное расстояние / временной интервал

Средняя скорость = (150 м + 70 м) / 10 с

Средняя скорость = 22 м / с

Это хороший пример, который ясно показывает разницу скорости и скорости.Мы должны указывать направление со скоростью, поскольку скорость является векторной величиной, однако скорость является скалярной величиной, и мы не учитываем направление.

Пример: Автомобиль едет по прямой, как показано на приведенном ниже графике. Найдите среднюю скорость этого автомобиля.

Экзамены по кинематике

Расстояние и смещение <Назад		Далее> Физические формулы Скорость и скорость / Шпаргалка

Кинематика

– Зачем нужна мгновенная скорость?

Если скорость объекта меняется, то его среднюю скорость за определенный промежуток времени все же можно вычислить, но это будет приблизительное значение, которое может иметь или не иметь смысла.

от 4,9 до 5,0 секунд и разделите на время. Получаем мгновенную скорость. Мы могли бы просто взять пройденное расстояние от 0 до 5 секунд и затем разделить его на время
.

Это правильно. Расстояние за определенный промежуток времени дает среднюю скорость, которая приблизительно равна мгновенной скорости. Обратите внимание, что оба временных интервала, 5 с или 0,1 с, приводят к измерению средней скорости. Но поскольку 0,1 с кажется «коротким», это «больше похоже на то, как мы измерили мгновенную скорость». Просто кажется, что это так, но это не значит, что это правда.

На самом деле важно то, насколько мгновенная скорость изменяется в течение интервала измерения. Если вы хотите измерить мгновенную скорость, вы должны сначала решить, насколько точным должно быть ваше измерение, скажем, процент ошибки, затем оценить, насколько скорость объекта может измениться с течением времени, и выбрать временной интервал, который достаточно мал, чтобы дать вам нужную точность.

Допустим, вы едете на велосипеде по холмистой местности. Под гору поедешь быстро, а вот в гору не так уж и много.Если вы потратите 50 минут на подъем и 10 минут на спуск, то измерение более часа даст бессмысленный результат. Может быть, вы в среднем проехали 12 км / ч, но на самом деле это было 10 км / ч в гору и 50 км / ч под гору.

Если ваша скорость на спуске постоянная, то измерение более 10 минут будет более точным. Если вы используете тормоза, которые изменяют скорость, вам нужно проводить измерения за более короткий интервал.

Обратите внимание, то же самое относится и к вектору скорости. Если вы бежите по кругу и усредняете вектор скорости за один поворот, то среднее значение будет нулевым вектором, независимо от скорости, потому что изменение направления вектора при повороте приводит к уменьшению всей векторной суммы до нуля.Чтобы измерить вектор скорости (включая направление), вы должны выбрать интервал, в котором не только скорость, но и направление остается «достаточно постоянным» для получения значимого среднего значения.

интересно использовать мгновенную скорость

Во-первых, он существует: объект движется с определенной скоростью, и если эта скорость меняется, вам нужен способ математического представления, если вы хотите записать уравнения.

Тогда пригодится для начальных условий: бросаешь камень, как далеко он уйдет? Это, помимо прочего, зависит от его мгновенной скорости, когда он покидает вашу руку.

Также требуется для расчета кинетической энергии.

Разница между мгновенной скоростью и скоростью

Скорость и скорость:

Скорость и скорость связаны с перемещением и расстоянием соответственно. Скорость – это расстояние в единицу времени, а скорость – это смещение в единицу времени. Скорость имеет величину, но не направление, т.е. скаляр, подобный расстоянию. Скорость зависит от направления, т.е.вектор похож на смещение. Формулы для скорости и скорости:

Скорость = скорость изменения расстояния = \ [\ frac {Изменение \: in \: Distance} {Изменение \: in \: Time} \]

Скорость = скорость change of displacement = \ [\ frac {Change \: in \: Displacement} {Change \: on \: Time} \]

Подобно расстоянию и смещению, которые имеют совершенно разные значения, независимо от их сходства, скорость и скорость также имеют разные смыслы. Тело / объект, движущийся с высокой скоростью, может преодолеть большое расстояние за короткий промежуток времени.В отличие от этого будет пройденное расстояние и время, затраченное на объект / тело, которое движется с низкой скоростью. У неподвижного объекта будет нулевая скорость. Например, человек, который быстро движется – один шаг вперед и один шаг назад, это означает, что он возвращается в исходное положение. Это приведет к нулевой скорости. Движение никогда не приведет к изменению положения, поскольку человек всегда стремится вернуться в исходную исходную точку. Чтобы максимизировать скорость, движущийся человек должен максимизировать расстояние, на которое он смещается от исходного положения.

Средняя скорость и средняя скорость:

Движущееся тело / объект часто претерпевает изменения. Средняя скорость – это расстояние, пройденное объектом, деленное на время, затраченное на путешествие.

Средняя скорость = \ [\ frac {Distance \: Traveled} {Time \: of \: Travel} \]

Принимая во внимание, что средняя скорость – это изменения положения, то есть смещение, деленное на затраченное время.

Средняя скорость = \ [\ frac {Displacement} {Time \: Taken} \]

Разница между средней скоростью и средней скоростью:

Критерии

Средняя скорость

Значение

Изменение смещения i.е. положение, деленное на затраченное время

Расстояние, пройденное объектом, деленное на затраченное время

Формула

Смещение / затраченное время

Пройденное расстояние / время перемещения

Знак

Это может быть либо положительное или отрицательное

Всегда будет положительным

Единицы измерения

м / с

Скалярное или векторное

Вектор

Скалярное

Мгновенное
Скорость изменения положения во времени называется скоростью.По мере движения объекта его скорость может соответственно меняться. Скорость объекта в любой данный момент называется мгновенной скоростью. Его можно определить, узнав среднюю скорость на очень коротком расстоянии и во времени.

Формула для мгновенной скорости:

Она равна скорости через определенный промежуток времени. Ниже приводится формула для определения мгновенной скорости:
Мгновенная скорость = предел, поскольку изменение во времени приближается к нулю (изменение позитрона / изменение во времени)

v = lim _Δt _→ ₀ _{= \ [\ frac {\ Delta x} {\ Delta t} = \ frac {\ Delta x} {\ Delta t} \]}

Здесь x – расстояние, пройденное телом.Мгновенная скорость измеряется в метрах в секунду (м / с), поскольку это скорость в конкретном временном интервале. Мгновенная скорость и скорость будут присутствовать в движущемся объекте. Пройденное расстояние относительно времени является скалярной величиной, и тем, насколько быстро объект перемещается, показывает это. У школьного автобуса меняется скорость. Спидометр будет показывать изменения скорости в течение определенного промежутка времени.

Скорость для различных объектов приведена ниже:

Объекты	м / с	м / ч
Бодрая прогулка	1.7	3,9
Спринтерский бегун	12,2	27
Официальный рекорд скорости на суше	341,1	763
Космический челнок на повторной стоянке	9037,5 звука на уровне моря	343	768

Разница между средней скоростью и мгновенной скоростью:

Средняя скорость	Мгновенная скорость
Общее расстояние, пройденное объектом определенный промежуток времени используется для расчета средней скорости.	Точная скорость движения объекта в данный момент времени – это мгновенная скорость.

Мгновенная скорость:

Скорость в определенный момент времени – это мгновенная скорость. Если скорость непостоянна, она будет отличаться от средней скорости. В то же время для объекта со стандартной скоростью в течение определенного периода времени его мгновенная скорость и средняя скорость будут одинаковыми.Вычисление мгновенной скорости в конкретный момент выполняется путем подстановки соответствующего значения времени переменной в первую производную уравнения смещения.

Мгновенная скорость = v = lim _Δt _→ ₀ _{= \ [\ frac {\ Delta s} {\ Delta t} = \ frac {\ Delta s} {\ Delta t} \]}

Где dS – вектор смещения. Разница между средней скоростью и мгновенной скоростью:

Средняя скорость	Мгновенная скорость
Чтобы найти среднюю скорость объекта, разделите его общее смещение на общее время, необходимое для движения объекта. из одного места в другое.	Скорость объекта в один момент времени – это Мгновенная скорость.

Видеоурок: Мгновенная скорость | Нагва

Стенограмма видео

В этом уроке мы будем говорить о мгновенной скорости. Мгновенная скорость относится к скорости, с которой движется объект в определенный момент времени.Это делает его очень полезным при описании движения объекта, скорость которого меняется со временем. В этом видео мы сосредоточимся на том, как можно вычислить мгновенную скорость объекта, глядя на график его смещения во времени. Как мы увидим, метод, который мы используем для вычисления мгновенной скорости объекта, зависит от того, движется ли он с постоянной скоростью или же его скорость меняется.

Обычно, когда мы вычисляем скорость объекта, мы думаем об этом уравнении.Скорость объекта определяется расстоянием, которое объект проходит, деленным на время, затраченное объектом на прохождение этого расстояния. Но на самом деле это уравнение сообщает нам только среднюю скорость, с которой движется объект за весь рассматриваемый нами период времени. Если бы мы смотрели на объект, который ускорялся или замедлялся, то мы могли бы обнаружить, что его мгновенная скорость, то есть его скорость в любой данный момент, отличается от его средней скорости. Чтобы проиллюстрировать разницу между средней скоростью и мгновенной скоростью, представим себе автомобиль, едущий по прямой дороге из точки А в точку Б.Предположим, что по пути автомобиль останавливается на светофоре, прежде чем поехать в пункт B.

Предположим также, что общее расстояние от A до B составляет 800 метров, а общее время, затраченное на поездку, составило 80 секунд. Давайте посмотрим, что произойдет, если мы подставим эти значения в нашу формулу скорости. Формула говорит нам, что наша скорость определяется делением расстояния, то есть 800 метров, на затраченное время, которое составляет 80 секунд, что дает нам ответ 10 метров в секунду.Однако, когда мы вычисляли это значение скорости, мы учли все время, в течение которого автомобиль стоял на светофоре. Если мы посмотрим на скорость автомобиля в разные моменты его движения, мы, вероятно, обнаружим, что большую часть времени его скорость отличалась от 10 метров в секунду.

Например, мы знаем, что когда автомобиль был остановлен, его скорость составляла ноль метров в секунду. И где-то еще на своем пути автомобиль должен был двигаться со скоростью более 10 метров в секунду, чтобы его скорость в среднем составляла 10 метров в секунду.Поэтому очень важно отметить, что это уравнение на самом деле просто говорит нам среднюю скорость, с которой перемещался объект, на основе общего пройденного расстояния и общего времени, затраченного на его путешествие. Если мы хотим узнать скорость, с которой автомобиль двигался в разных точках своего пути, то есть его мгновенную скорость в разных точках. Затем нам потребуется дополнительная информация о том, что именно машина делала между точкой A и точкой B.

В этом уроке мы сосредоточимся на том, как мы можем вычислить мгновенную скорость на основе графика смещения-времени.Для нашей машины график «смещение – время» может выглядеть так. Этот график показывает нам, что в момент времени, равный нулю секунд, автомобиль трогается с места на ноль метров. И это увеличивается в течение первых 20 секунд до водоизмещения 400 метров. Итак, эта часть графика показывает путь автомобиля от точки А до светофора. Следующая часть графика от 20 секунд до 60 секунд показывает, что водоизмещение автомобиля остается постоянным – 400 метров. Таким образом, эта часть графика соответствует тому моменту, когда автомобиль был остановлен на светофоре.И затем последняя часть графика от 60 секунд до 80 секунд показывает смещение автомобиля, увеличивающееся с 400 до 800 метров, представляя часть пути автомобиля после светофора, когда он двигался к точке B.

Так как же рассчитать мгновенную скорость автомобиля в разное время? Ответ заключается в том, что мы смотрим на наклон графика. В частности, мгновенная скорость объекта в любой момент времени определяется величиной наклона его графика смещения-времени в это время.Другими словами, мгновенная скорость нашей машины определяется крутизной этого графика в различных точках. И мы можем вычислить значение его скорости в любой момент времени, вычислив наклон графика в это время. Обратите внимание, что мы говорим о величине наклона графика. Это означает, что независимо от того, является ли наклон положительным или отрицательным, мы просто берем его значение с положительным знаком, поскольку это указывает его величину. И это потому, что скорость по определению может быть только положительной или нулевой.Не может принимать отрицательные значения.

Итак, этот график смещения – время, например, показывает нам объект, движущийся с относительно низкой скоростью, потому что наклон этой линии относительно мал. С другой стороны, этот график смещения-времени показывает нам объект, движущийся с относительно высокой скоростью, что мы знаем, потому что наклон этой линии относительно велик. Этот окончательный график смещения-времени также показывает объект, движущийся с высокой скоростью. Наклон графика отрицательный и относительно большой.Но поскольку скорость определяется просто величиной наклона графика смещения-времени, не имеет значения, что он отрицательный. Мы просто берем положительное значение. Положительное значение этого наклона примерно совпадает с наклоном этого графика. Фактически, оба этих графика показывают нам два объекта примерно с одинаковой скоростью.

Если мы посмотрим на график нашей машины, то увидим, что он состоит из трех прямых линий. Поскольку прямая линия имеет постоянный уклон, это говорит нам о том, что автомобиль движется с постоянной скоростью от нуля до 20 секунд, с другой постоянной скоростью от 20 до 60 секунд и с другой постоянной скоростью от 60 до 80 секунд.На самом деле это упрощение, и мы ожидаем, что график смещения-время для реальной машины будет изогнутым. Но мы воспользуемся этим примером, чтобы показать нам, как можно вычислить мгновенную скорость на основе графика смещения-времени, который состоит из прямых линий.

Итак, предположим, что мы хотим вычислить мгновенную скорость нашей машины в момент времени 70 секунд, который здесь. Для этого нам нужно вычислить наклон нашего графика в этой точке. Мы видим, что наклон графика вокруг этой точки между 60 и 80 секундами постоянный.Другими словами, график представляет собой прямую линию. Это означает, что величина наклона в интересующей нас точке совпадает с величиной наклона линии между 60 и 80 секундами. Таким образом, мгновенная скорость в 70 секунд определяется величиной наклона этого отрезка линии.

Напомним, что наклон прямой линии определяется разницей по вертикали между двумя точками на этой линии, деленной на разность по горизонтали между теми же двумя точками.Итак, давайте использовать конечные точки этого отрезка линии как две точки, которые мы будем использовать для вычисления наклона. Эта точка находится в 60 секундах по оси времени и 400 метрах по оси смещения. Итак, координаты этой точки – 60, 400. Эта вторая точка находится в 80 секундах по оси времени и 800 метрах по оси смещения. Итак, его координаты – 80, 800. Теперь мы можем использовать эти координаты, чтобы вычислить наклон этого отрезка линии. Разница по вертикали между двумя выбранными нами точками определяется разницей между их 𝑦-координатами, которые определяют их вертикальное положение на графике.Таким образом, вертикальная разница в этом случае составляет 800 минус 400.

Точно так же горизонтальная разница между этими двумя точками равна 80 минус 60. 800 минус 400 равно 400, а 80 минус 60 равно 20. И 400, разделенное на 20, равно 20. Таким образом, наклон линии на отметке 70 секунд равен 20. Теперь мы знаем, что мгновенная скорость определяется величиной наклона графика «смещение – время». Поскольку рассчитанный нами наклон положительный, у нас уже есть его величина, 20. И единицы для мгновенной скорости, которые мы вычислили, просто задаются теми единицами, которые используются для наших осей.Таким образом, в этом случае рассчитанная нами вертикальная разница измеряется в метрах, а рассчитанная нами горизонтальная разница измеряется в секундах. Это означает, что мгновенная скорость автомобиля в этот момент составляла 20 метров в секунду.

Если мы хотим узнать мгновенную скорость автомобиля в любой другой момент, нам просто нужно вычислить наклон графика в этот момент. Например, на момент времени 10 секунд мы можем увидеть, что наклон графика просто задается наклоном этого отрезка линии.И в этом конкретном случае это фактически то же самое, что и наклон этого отрезка линии. Хотя, конечно, так будет не всегда. Таким образом, мгновенная скорость за 10 секунд также составляет 20 метров в секунду. Если мы посмотрим на мгновенную скорость, скажем, за 50 секунд, мы увидим, что наклон графика в этой точке определяется наклоном этого отрезка линии. Поскольку этот отрезок линии горизонтален, мы можем сказать, что его наклон равен нулю, что означает, что мгновенная скорость в этой точке равна нулю метров в секунду.И это верно для любого места в пределах этого сегмента линии.

Итак, мы видим, что между 20 и 60 секундами мгновенная скорость автомобиля равна нулю. Но для времени, указанного на графике до 20 секунд или после 60 секунд, мгновенная скорость автомобиля составляет 20 метров в секунду. Теперь, когда мы рассмотрели, как мы можем вычислить мгновенную скорость объекта по прямолинейному графику смещение – время, давайте посмотрим, как мы можем вычислить мгновенную скорость объекта с помощью криволинейного графика смещения – времени. .

Как мы упоминали ранее, прямолинейный график, который мы только что рассматривали, на самом деле был упрощением того, как смещение автомобиля может меняться с течением времени. График смещения-время для реальной машины, совершающей описанный путь, вероятно, будет выглядеть примерно так. Этот график смещения-времени не состоит из прямых линий с постоянным наклоном и, следовательно, представляет постоянные скорости. Если мы посмотрим на этот участок графика, то увидим, как он меняется от относительно крутого к чуть менее крутому, пока не станет горизонтальным.Это постепенное изменение наклона представляет собой тот факт, что мгновенная скорость автомобиля, когда он замедляется, постепенно уменьшается до нуля.

Точно так же, если мы посмотрим на эту часть графика, мы увидим, что наклон постепенно и непрерывно увеличивается от нуля до некоторого положительного значения до более высокого положительного значения, представляя тот факт, что автомобиль постепенно ускоряется с места. Но как мы можем вычислить мгновенную скорость в этих точках? Мы можем сделать это, проведя касательные к графику.Касательная – это прямая линия, которая касается кривой таким образом, что и кривая, и касательная имеют одинаковый наклон в точке соприкосновения. Например, мы могли бы провести касательную к кривой в этой точке. Здесь кривая имеет такой наклон, поэтому касательная к кривой в этой точке выглядит так. Рисование касательной дает нам способ вычислить наклон кривой в заданной точке.

Эта касательная касается нашего графика примерно за 18 секунд. Таким образом, вычислив наклон этой касательной, мы найдем наклон графика в 18 секунд.Таким образом, мгновенная скорость автомобиля составляет 18 секунд. Поскольку касательная представляет собой прямую линию, мы можем найти ее наклон, указав две точки на прямой и разделив разницу по вертикали между этими точками на разницу по горизонтали. Поскольку мы только что нарисовали касательную на глаз, это означает, что наш ответ действительно будет оценкой наклона. Но мы можем свести к минимуму ошибку в нашем измеренном градиенте и сделать наш ответ как можно более точным, выбрав две точки так, чтобы они были ближе к концам линии.

Глядя на эту точку для начала, мы можем увидеть, что это время примерно восемь секунд, а смещение составляет ноль метров. Итак, координаты этой точки восемь, ноль. Теперь, глядя на эту точку, мы видим, что это время примерно 37 секунд и смещение 800 метров. Таким образом, координаты этой точки равны 37, 800. И снова наклон определяется как разность по вертикали, деленная на разность по горизонтали между этими точками. Вертикальная разница между точками определяется разницей между их вертикальными координатами, другими словами, 800 минус ноль.А по горизонтали разница 37 минус восемь. 800 минус ноль, конечно, 800. И 37 минус восемь равно 29. 800 делить на 29 дает 27,586. Итак, с точностью до одного десятичного знака это 27,6.

Итак, если касательная к нашему графику в момент времени 18 секунд имеет наклон 27,6, это означает, что сам график имеет наклон 27,6 в 18 секунд. Мгновенная скорость в это время определяется величиной 27,6, что составляет всего 27,6, потому что она уже положительна. И снова, единицы для нашей мгновенной скорости даются единицами, используемыми на вертикальной оси, деленными на единицы, используемые на горизонтальной оси.Это метры в секунду. Таким образом, мгновенная скорость автомобиля в момент времени 18 секунд составляет 27,6 метра в секунду.

Если бы мы хотели узнать мгновенную скорость автомобиля в другое время, например, 65 секунд. Мы бы еще раз нарисовали касательную к кривой в это время, вычислили бы наклон этой касательной, используя две точки около конца, а затем взяли бы величину этого наклона. Это означает, что если мы вычисляем отрицательный наклон, мы просто берем положительную версию этого числа.

Итак, давайте просто подведем итог тому, что мы узнали о вычислении мгновенной скорости. Мгновенная скорость – это скорость объекта в определенный момент времени. Он определяется величиной наклона графика смещения-времени в определенный момент времени. А для изогнутого графика смещение – время мы можем провести касательную к графику, чтобы помочь нам вычислить наклон в определенной точке.