Момент инерции задачи с решением – Примеры решения задач
- Примеры решения задач
- Задачи по теме «Момент инерции. Закон сохранения момента
- Примеры решения задач
- Примеры решения задач по теме «Динамика вращательного движения абсолютно твёрдого тела»
- 23. Механика твердого тела. Момент импульса: задачи с ответами
- Закон сохранения момента импульса задачи с решением — Ваше право
Примеры решения задач
Пример
1. Найти
момент инерции тонкого однородного
диска массой 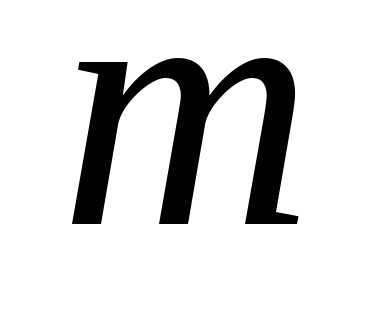 и радиуса
и радиуса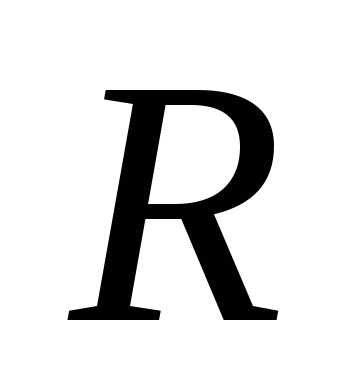 относительно: а) оси симметрии,
перпендикулярной к плоскости диска; б)
оси, совпадающей с диаметром диска.
относительно: а) оси симметрии,
перпендикулярной к плоскости диска; б)
оси, совпадающей с диаметром диска.
Р
е ш е н и е. а)Выберем
на диске цилиндрический слой радиуса 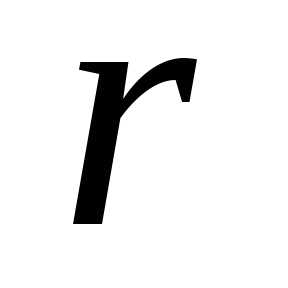 и шириной
и шириной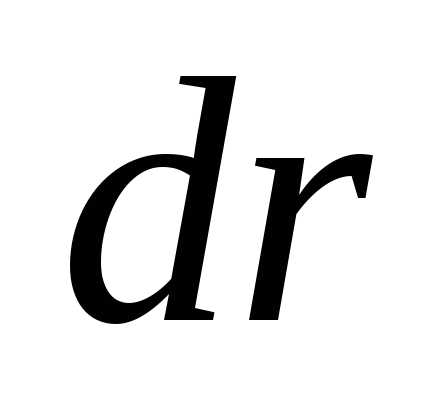 (см.
рис. 3а). Так как все элементы цилиндрического
слоя находятся на одном расстоянии
от центра кольца, его момент инерции
равен
(см.
рис. 3а). Так как все элементы цилиндрического
слоя находятся на одном расстоянии
от центра кольца, его момент инерции
равен
(14)
где 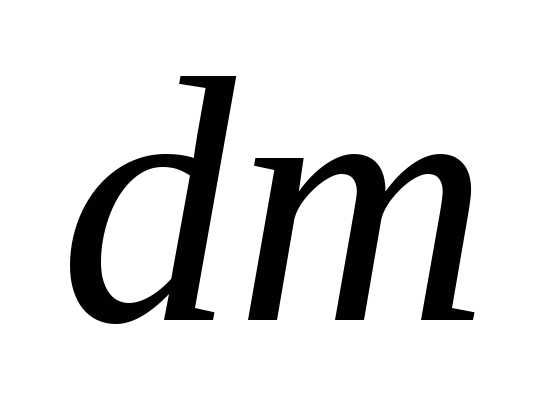
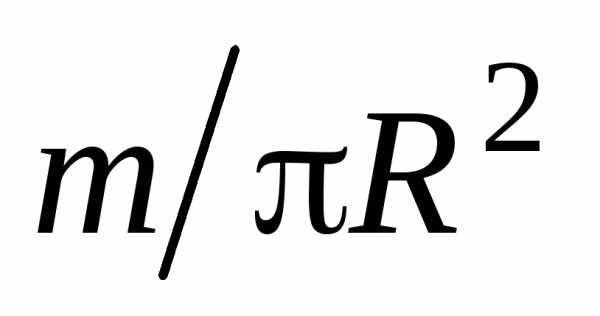 и умножив ее на площадь поверхности
кольца
и умножив ее на площадь поверхности
кольца т.е.
т.е. 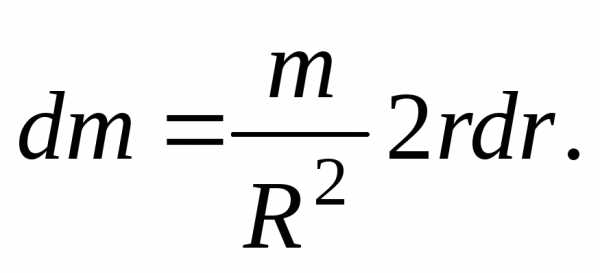
Подставляя
это значение в (14) интегрируя по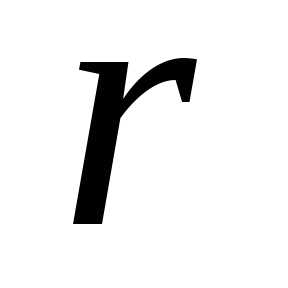 в пределах от 0 до
в пределах от 0 до ,
найдем момент инерции диска относительно
оси симметрии
,
найдем момент инерции диска относительно
оси симметрии
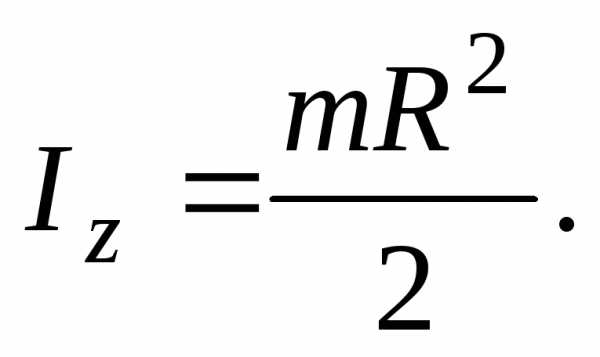 (15)
(15)
б)
Для нахождения момента инерции диска
относительно диаметра, например оси 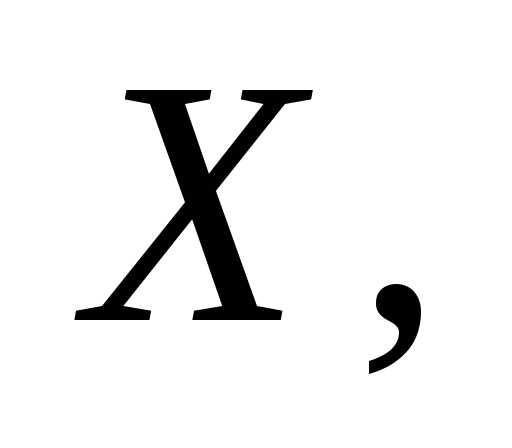
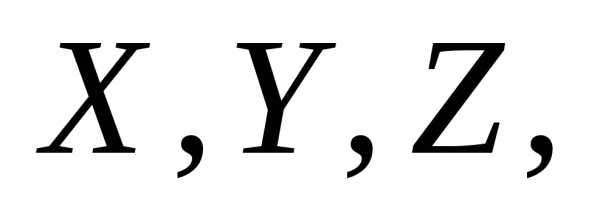 пересекающиеся в центре диска (рис. 3б).
Очевидно, что
пересекающиеся в центре диска (рис. 3б).
Очевидно, что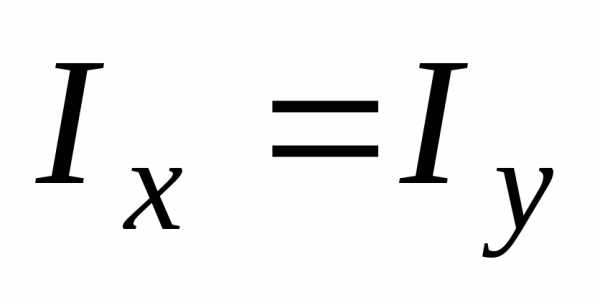 ,
тогда из уравнения (6) следует
,
тогда из уравнения (6) следует 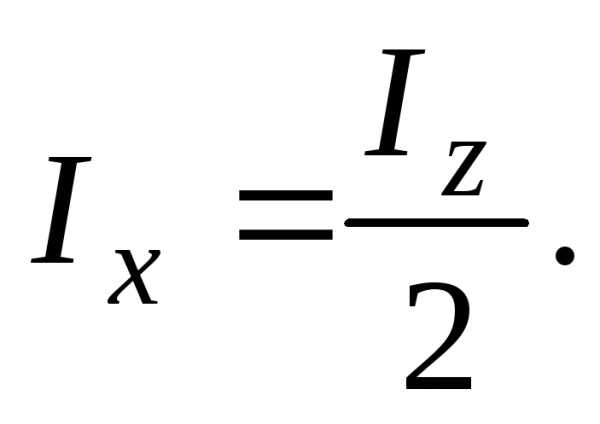
Подставляя
в это выражение значение 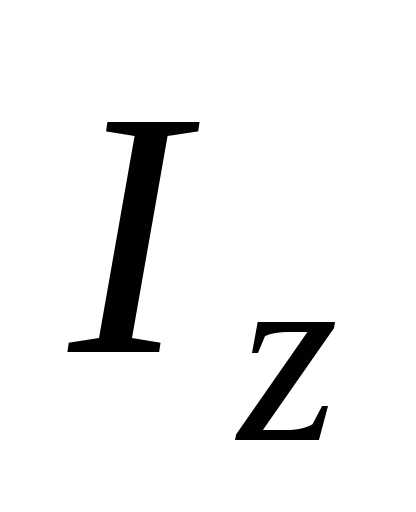 из уравнения (15), найдем момент инерции
диска относительно диаметра
из уравнения (15), найдем момент инерции
диска относительно диаметра
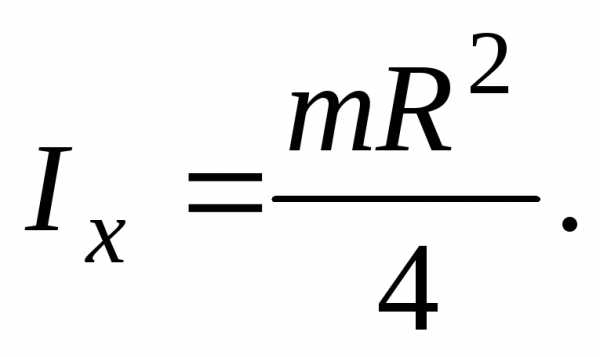
Пример
2. Найти
момент инерции однородного шара массы 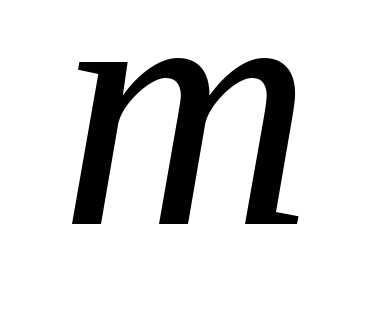 и радиуса
и радиуса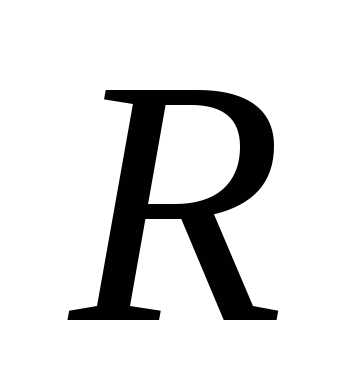 относительно оси, совпадающей с центром
шара.
относительно оси, совпадающей с центром
шара.
Ре ш е н и е. Вычисление момента инерции
шара прямым методом, т.е. с использованием
уравнения (1) довольно трудоемкая
математическая задача, поэтому для
нахождения этого момента инерции
воспользуемся соотношением (5). Проведем
три взаимно перпендикулярные оси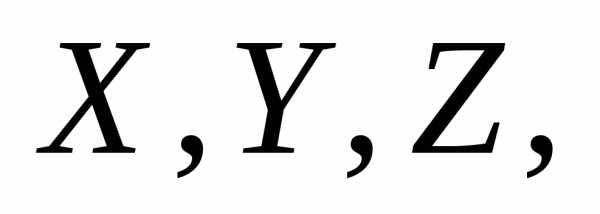 пересекающиеся в центре шара (см. рис.
4). Очевидно, что
пересекающиеся в центре шара (см. рис.
4). Очевидно, что
поэтому соотношение (5) перепишем в виде
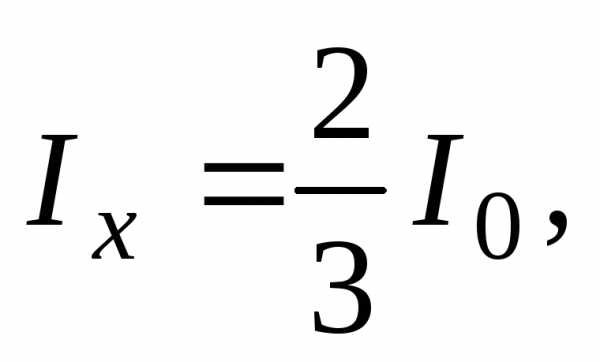 (16)
(16)
где 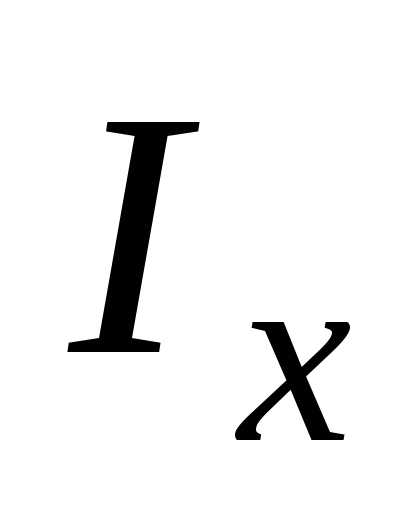 – искомый момент инерции,
– искомый момент инерции,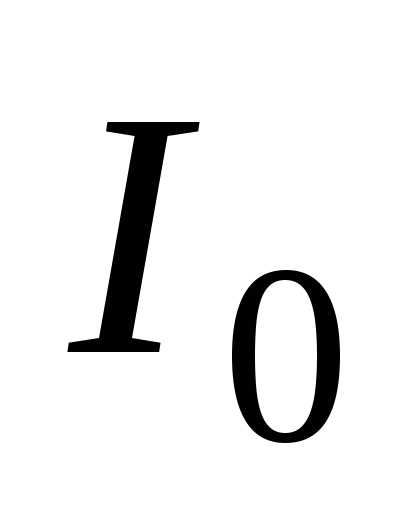 – момент инерции шара относительно
центра шара.
– момент инерции шара относительно
центра шара.
Для
нахождения момента инерции 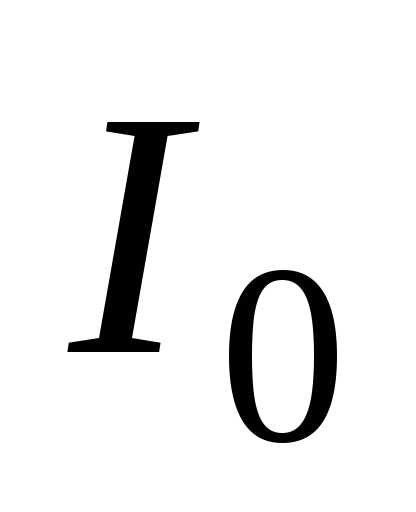
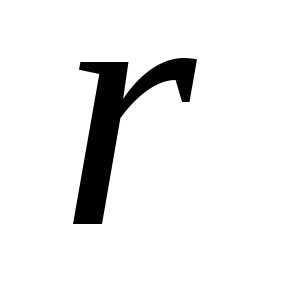 и толщиной
и толщиной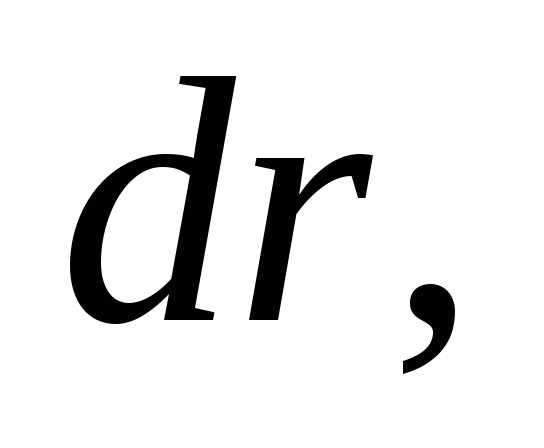 центр
которого совпадает с центром шара (на
рис. 4 он выделен цветом). Все элементы
этого слоя находятся на одинаковом
расстоянии от центра шара, поэтому его
момент инерции относительно центра
шара равен
центр
которого совпадает с центром шара (на
рис. 4 он выделен цветом). Все элементы
этого слоя находятся на одинаковом
расстоянии от центра шара, поэтому его
момент инерции относительно центра
шара равен 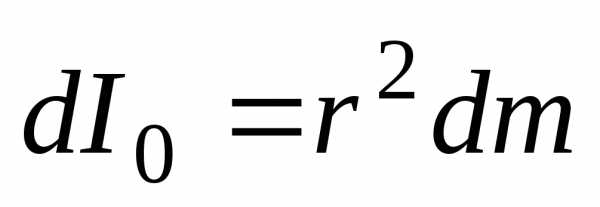 .
(17)
.
(17)
Объемная
плотность шара равна 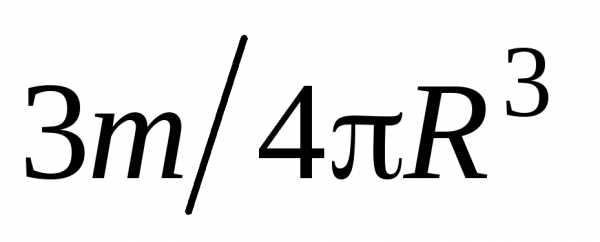 ,
умножая ее на объем тонкого сферического
слоя
,
умножая ее на объем тонкого сферического
слоя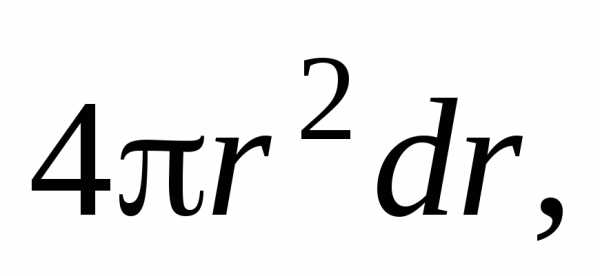 найдем массу сферического слоя
найдем массу сферического слоя
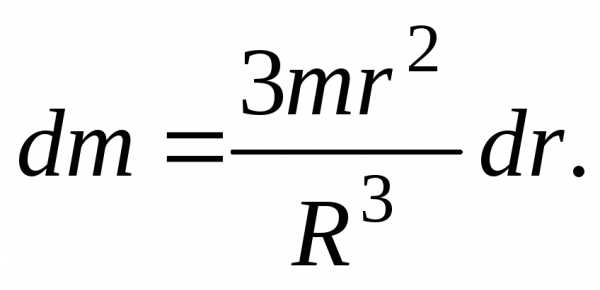
Подставляя
это выражение в (17) и интегрируя в пределах
от 0 до 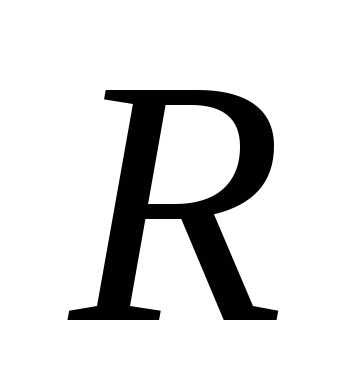 ,
найдем момент инерции шара относительно
центра
,
найдем момент инерции шара относительно
центра
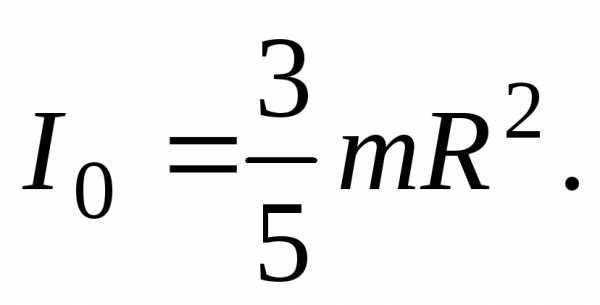
С учетом этого из уравнения (16) находим искомый момент инерции шара
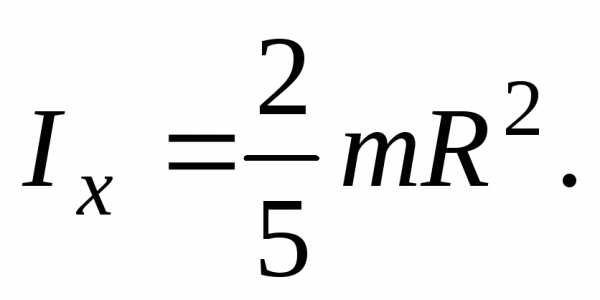
Пример
3. Однородный
цилиндр радиуса 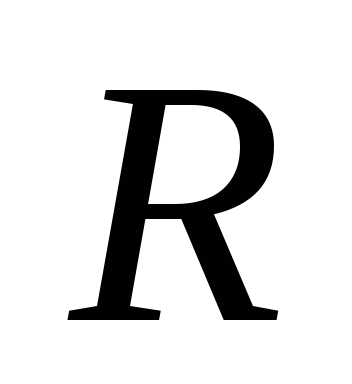 раскрутили вокруг его оси до угловой
скорости
раскрутили вокруг его оси до угловой
скорости и поместили затем в угол (рис.5) Коэффициент
трения между стенками угла и цилиндром
равен
и поместили затем в угол (рис.5) Коэффициент
трения между стенками угла и цилиндром
равен Сколько оборотов сделает цилиндр до
остановки?
Сколько оборотов сделает цилиндр до
остановки?
(18)
где 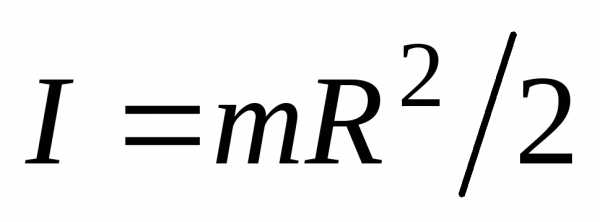 – момент инерции цилиндра относительно
этой оси. Знак “–” в левой части этого
уравнения обусловлен тем, что при
замедленном движении модуль углового
ускоренияТак как нам необходимо найти число
оборотов, которое сделает цилиндр до
остановки, исключим из уравнения (18)
время. Для этого умножим и разделим
левую часть уравнения (18) на
– момент инерции цилиндра относительно
этой оси. Знак “–” в левой части этого
уравнения обусловлен тем, что при
замедленном движении модуль углового
ускоренияТак как нам необходимо найти число
оборотов, которое сделает цилиндр до
остановки, исключим из уравнения (18)
время. Для этого умножим и разделим
левую часть уравнения (18) на
где – угловая скорость вращения цилиндра в некоторый момент времени. После преобразований получим
. (19)
Прежде чем решать это уравнение, найдем выражения для сил трения. Так как центр цилиндра покоится,
Запишем
это уравнение в проекциях на оси 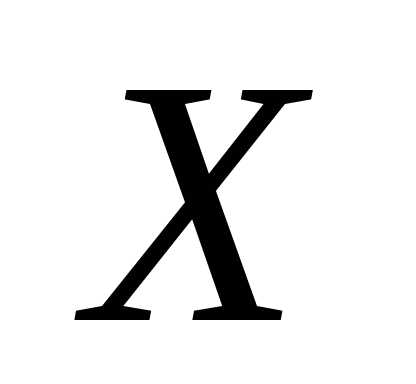 и
и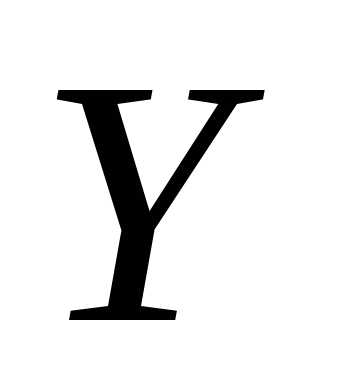 (см. рис. 5)
(см. рис. 5)
Решая эту систему уравнений, учитывая, что аполучим выражения для сил трения
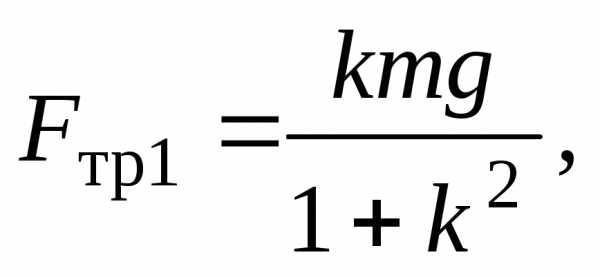
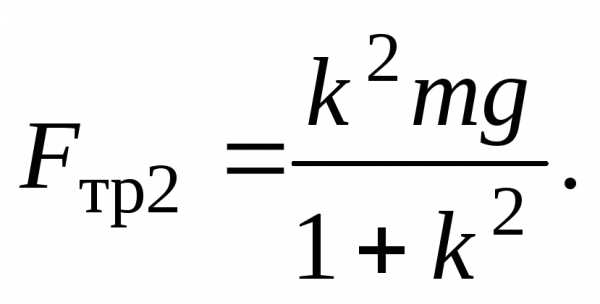
Подставляя эти
выражения в уравнение (19) и интегрируя
левую часть этого уравнения в пределах
от  до 0, а правую часть в пределах от 0 до
до 0, а правую часть в пределах от 0 до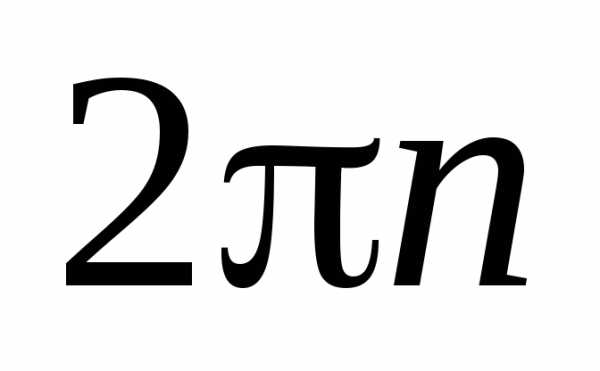 ,
найдем число оборотов
,
найдем число оборотов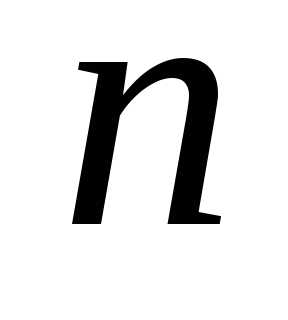
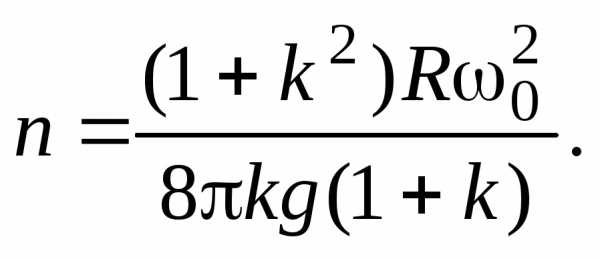
Пример
4. Однородный
шар скатывается без скольжения по
наклонной плоскости, составляющей угол  с горизонтом. Найти ускорение
с горизонтом. Найти ускорение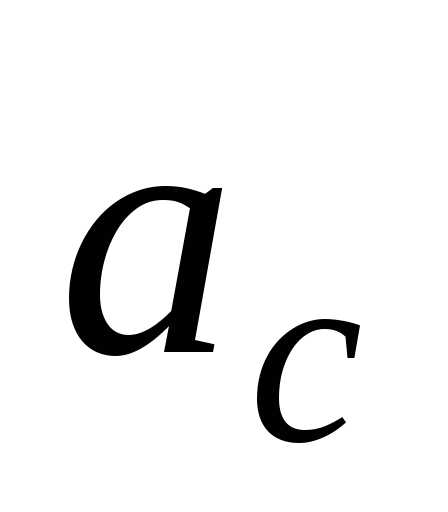 центра шара и кинетическую энергию шара
через время
центра шара и кинетическую энергию шара
через время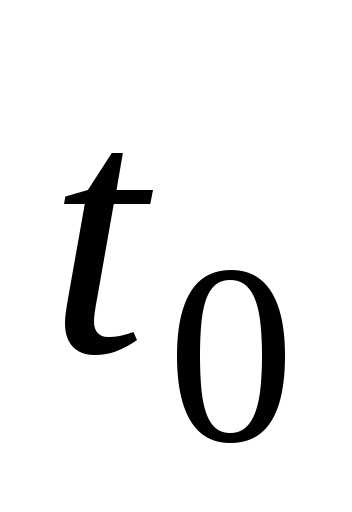 после начала движения.
после начала движения.
Р е ш е н и е. Решим задачу двумя способами.
а) Шар совершает
плоское движение. Свяжем подвижную
систему отсчета с центром шара. Эта
система движется поступательно
относительно наклонной плоскости, а
шар в этой системе вращается вокруг
оси, проходящей через его центр. Расставим
силы, действующие на шар в
процессе движения (см. рис.6). Запишем
теорему о движении центра масс в проекции
на ось 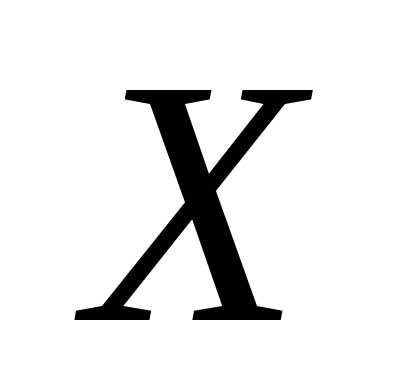
(20)
Уравнение вращательного движения шара вокруг оси, проходящей через центр масс имеет вид
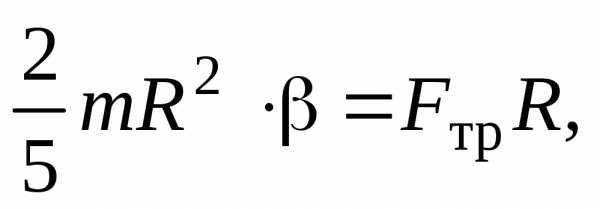 (21)
(21)
где 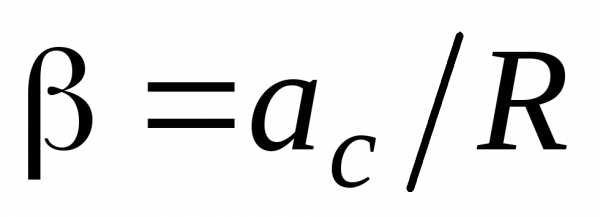 – угловое ускорение шара,
– угловое ускорение шара,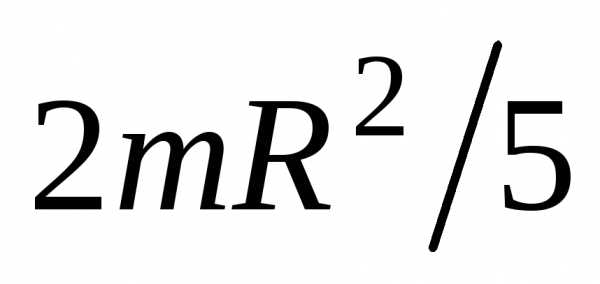 – момент инерции шара относительно оси
вращения. Решая совместно уравнения
(20) и (21), найдем ускорение центра шара
– момент инерции шара относительно оси
вращения. Решая совместно уравнения
(20) и (21), найдем ускорение центра шара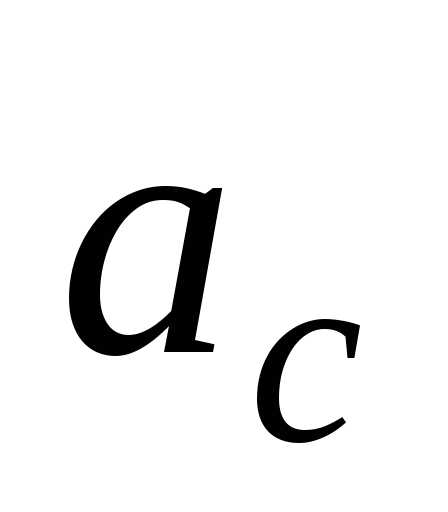 и его угловое ускорение
и его угловое ускорение
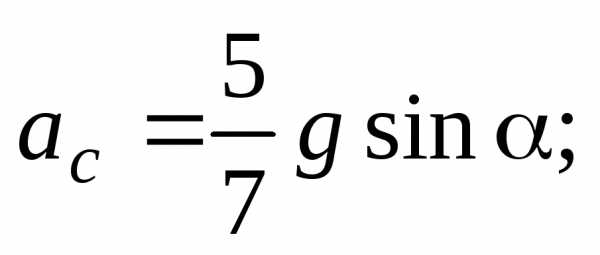
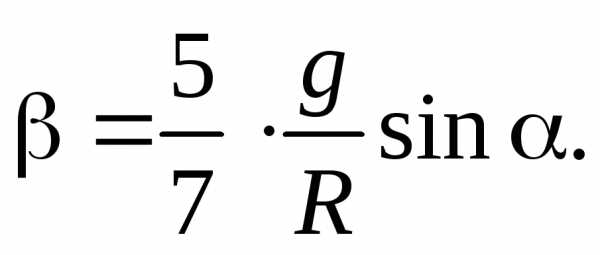 (22)
(22) Используя формулу
(13) для кинетической энергии тела,
совершающего плоское движение, и
учитывая, что в интересующий нас момент
времени
и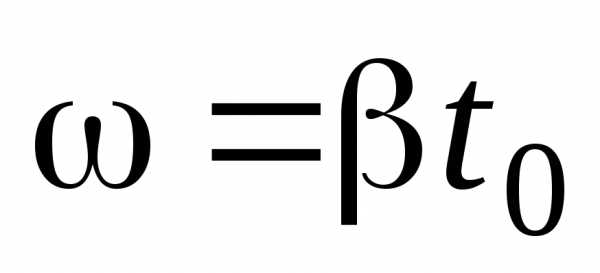 (т.к.
(т.к.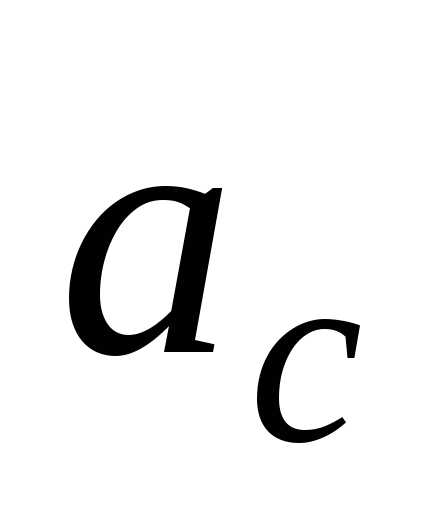 и
и постоянные), найдем кинетическую энергию
шара через время
постоянные), найдем кинетическую энергию
шара через время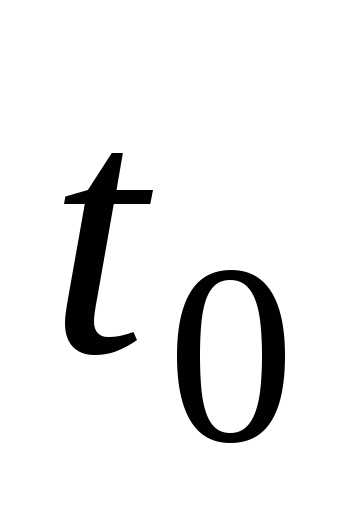 после начала движения
после начала движения
б) Так как шар
катится без проскальзывания, точка
соприкосновения шара  с наклонной плоскостью имеет скорость
равную нулю. Поэтому прямая, перпендикулярная
плоскости рисунка и проходящая через
точку
с наклонной плоскостью имеет скорость
равную нулю. Поэтому прямая, перпендикулярная
плоскости рисунка и проходящая через
точку
(23)
где 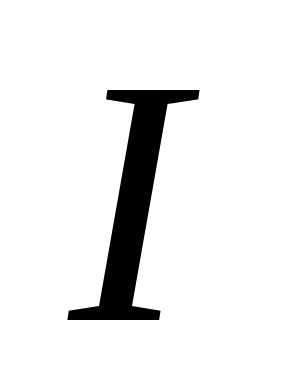 – момент инерции шара относительно
мгновенной оси вращения. Согласно
теореме Штейнера момент инерции
– момент инерции шара относительно
мгновенной оси вращения. Согласно
теореме Штейнера момент инерции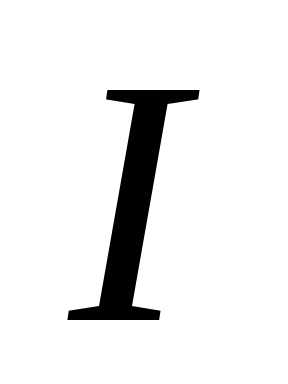 равен
равен
Подставляя это
выражение в уравнение (23), находим
ускорение центра шара 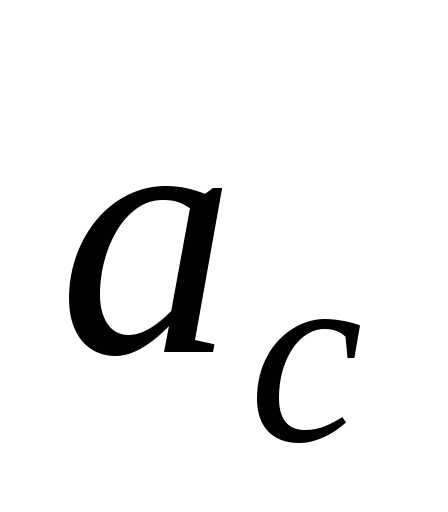 и его угловое ускорение
и его угловое ускорение (см. уравнения (22)).
(см. уравнения (22)).
Кинетическая энергия шара, в этом случае, определяется только вращательным движением
Заметим, что при
любом способе решения, кинетическую
энергию шара можно найти из закона
сохранения энергии (сила трения работы
не совершает, т.к. эта сила – сила трения
покоя). Пусть за время 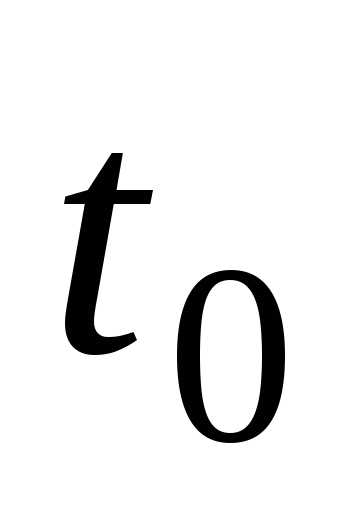 высота центра шара изменилась на
высота центра шара изменилась на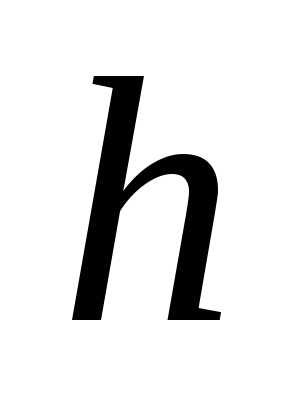 (см. рис.6), тогда
(см. рис.6), тогда
(24)
где 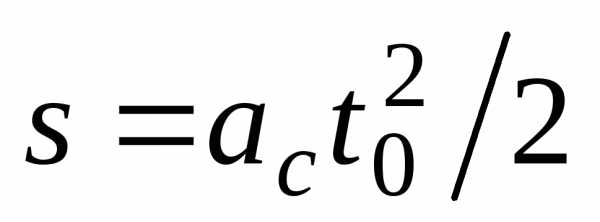 – расстояние, пройденное центром шара
за время
– расстояние, пройденное центром шара
за время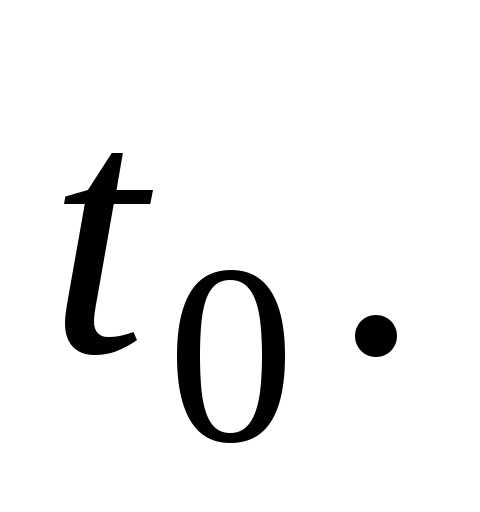 Подставляя
в (24) выражение для
Подставляя
в (24) выражение для и
и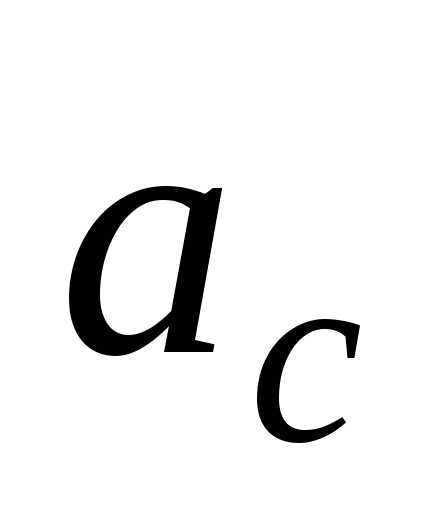 ,
находим кинетическую энергию шара
,
находим кинетическую энергию шара
Пример
5. Однородный
стержень длины 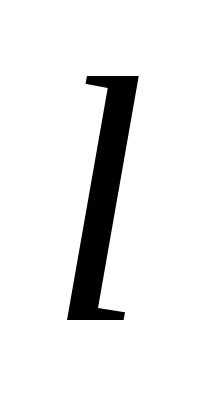 может вращаться вокруг горизонтальной
оси, перпендикулярной к стержню и
проходящей через один из его концов
(рис. 7). Систему равномерно вращают с
угловой скоростью
может вращаться вокруг горизонтальной
оси, перпендикулярной к стержню и
проходящей через один из его концов
(рис. 7). Систему равномерно вращают с
угловой скоростью вокруг вертикальной оси. Пренебрегая
трением, найти угол
вокруг вертикальной оси. Пренебрегая
трением, найти угол между стержнем и вертикалью.
между стержнем и вертикалью.
Р е ш е н и е. Решим задачу двумя способами. Первое решение приведем в инерциальной системе отсчета, т.е. в системе, в которой стержень вращается. Второе решение – в неинерциальной системе отсчета, жестко связанной со стержнем.
а) Система отсчета,
в которой будем решать задачу, на рис.
7 не показана. Решение задачи относительно
вертикальной оси вращения не даст
желаемого результата, т.к. моменты сил,
действующих на стержень (сила тяжести
и сила реакции в точке  ),
относительно этой оси равны нулю, и
величина момента импульса остается
постоянной.
),
относительно этой оси равны нулю, и
величина момента импульса остается
постоянной.
Поэтому
будем решать задачу относительно точки  подвеса стержня. Напомним, что уравнение
моментов относительно точки имеет вид
подвеса стержня. Напомним, что уравнение
моментов относительно точки имеет вид
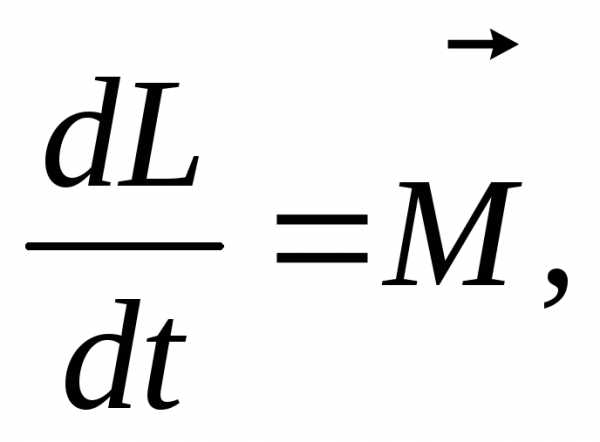
откуда видно, что
направление изменения момента импульса 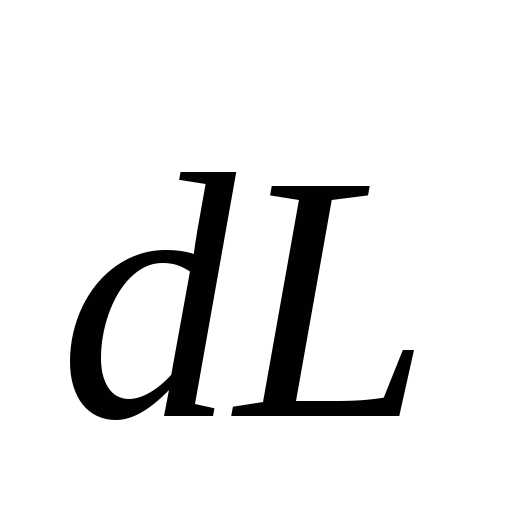 совпадает по направлению с направлением
момента сил
совпадает по направлению с направлением
момента сил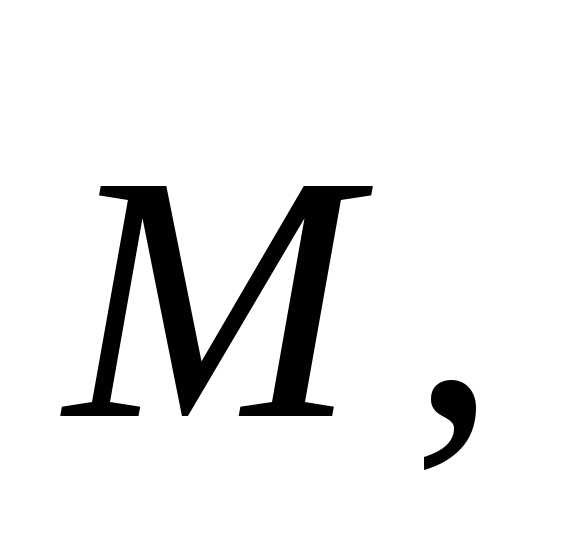 действующих на стержень, поэтому в
дальнейшем это уравнение будем записывать
для модулей
действующих на стержень, поэтому в
дальнейшем это уравнение будем записывать
для модулей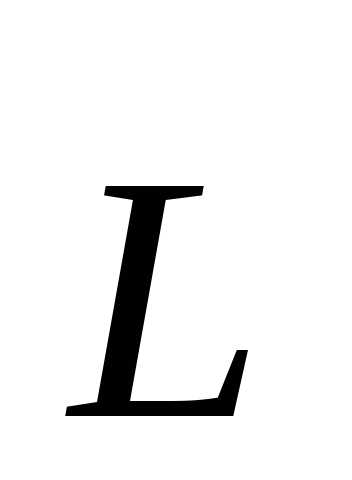 и
и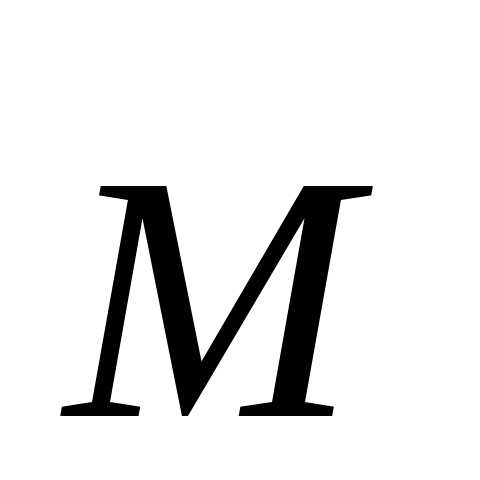
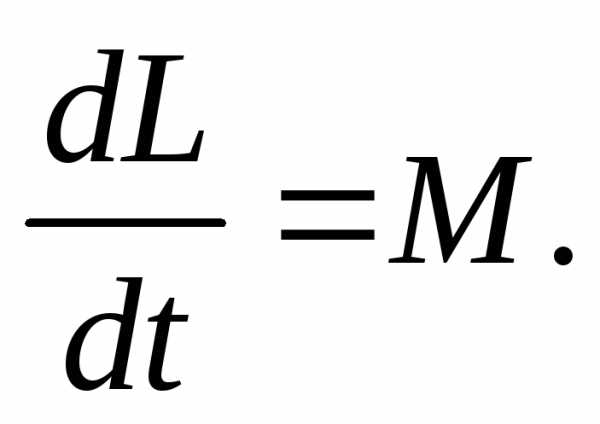 (25)
(25)
Момент силы реакции
в точке  равен нулю, т.к. плечо этой силы равно
нулю. Направление момента силы тяжести
показано на рис.7, а величина равна
равен нулю, т.к. плечо этой силы равно
нулю. Направление момента силы тяжести
показано на рис.7, а величина равна
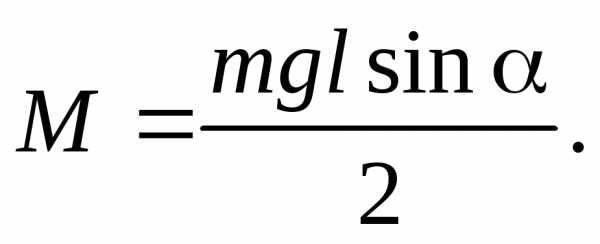 (26)
(26)
Найдем величину
и направление момента импульса 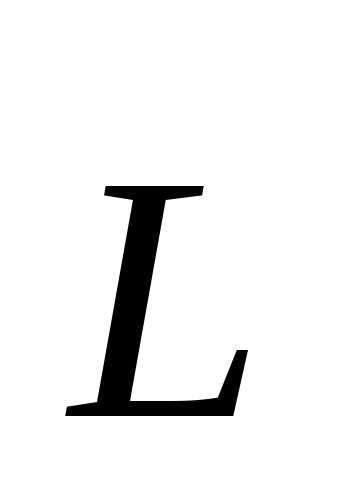 стержня относительно точки
стержня относительно точки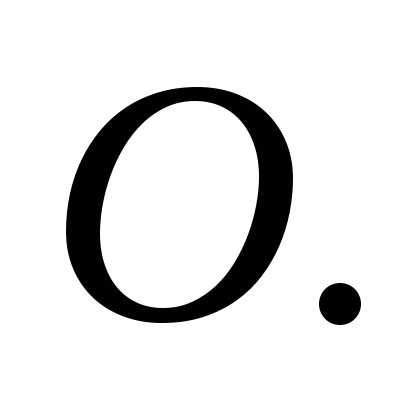 Для этого выделим на стержне небольшой
участок длиной
Для этого выделим на стержне небольшой
участок длиной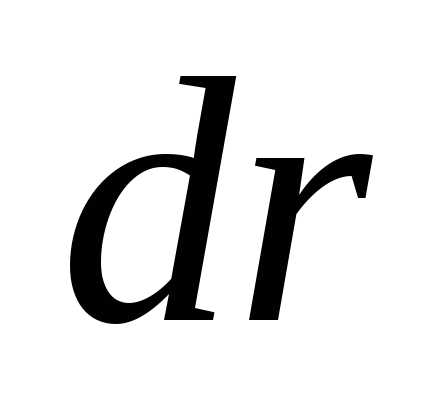 и массойположение которого относительно точки
и массойположение которого относительно точки зададим радиус-вектором
зададим радиус-вектором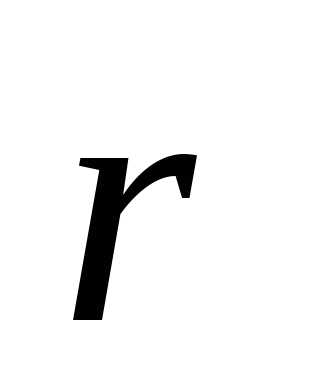 (см.
рис. 7). Обозначим величину момента
импульса этого участка как
(см.
рис. 7). Обозначим величину момента
импульса этого участка как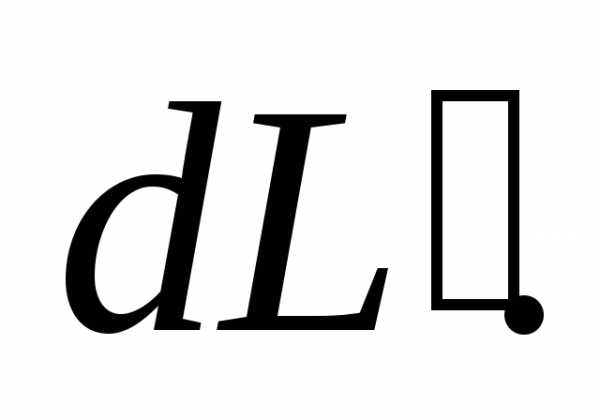 Так как стержень вращается вокруг
вертикальной оси, так как показано на
рисунке, скорость
Так как стержень вращается вокруг
вертикальной оси, так как показано на
рисунке, скорость этого участка будет направлена за
плоскость рисунка, поэтому как следует
из определения момента импульса
этого участка будет направлена за
плоскость рисунка, поэтому как следует
из определения момента импульса
,
он будет направлен
перпендикулярно стержню, как показано
на рис. 7. Очевидно, что направления всех
моментов импульса остальных участков
стержня будут иметь такое же направление,
поэтому результирующий момент импульса
будет также перпендикулярен стержню.
Учитывая, что векторы 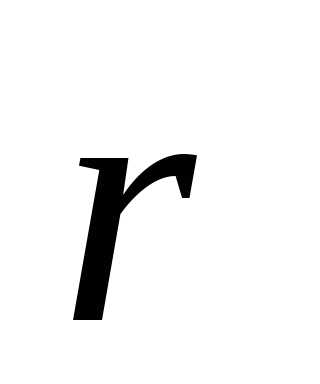 и
и взаимно перпендикулярны, величина
взаимно перпендикулярны, величина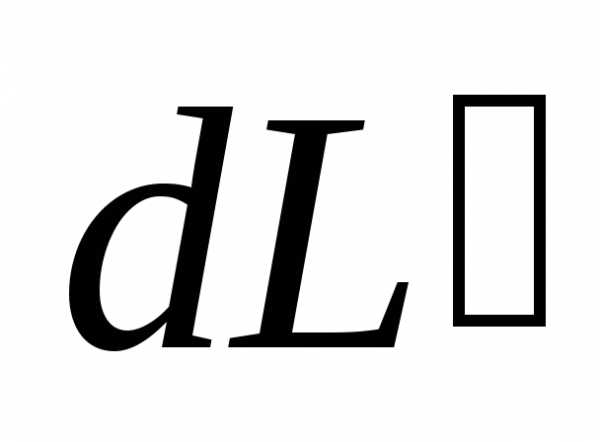 равна
равна
Интегрируя это уравнение
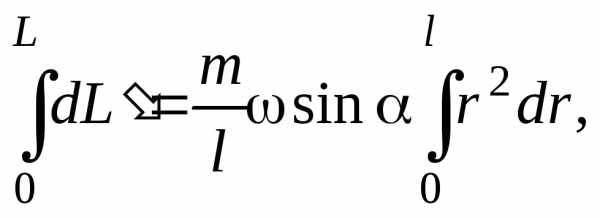
найдем величину
момента импульса стержня относительно
точки 
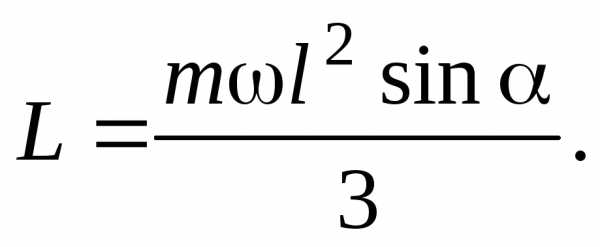
Момент
импульса поворачивается вместе со
стержнем, и за время 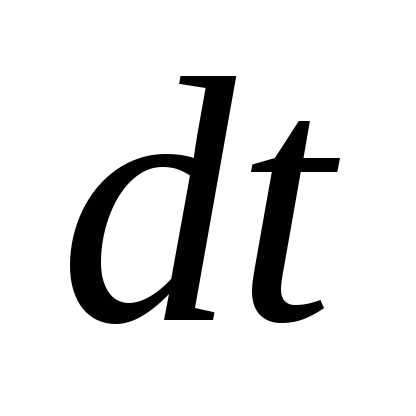 повернется на некоторый угол
повернется на некоторый угол ,
получив приращение
,
получив приращение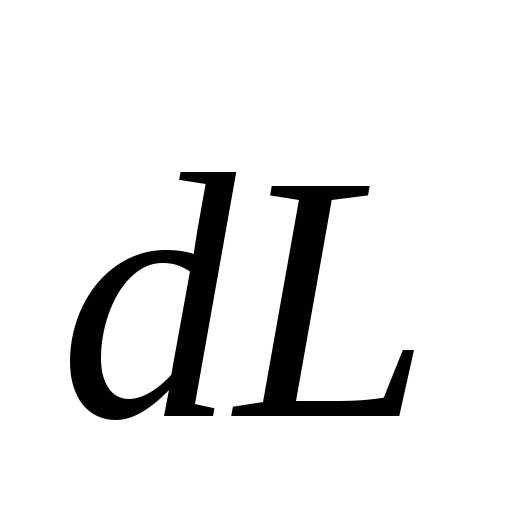 (см. рис.8).
Найдем величину этого приращения
(см. рис.8).
Найдем величину этого приращения
или
. (27)
Подставляя уравнение (26) и (27) в уравнением моментов (25), получим
где . Преобразуем это уравнение к виду
. (28)
Если величина
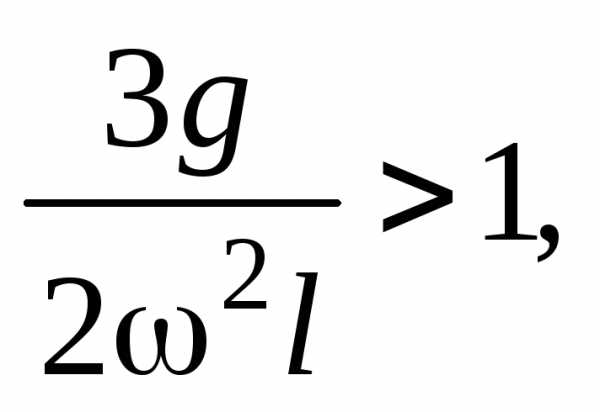
уравнение (28) имеет
одно решение 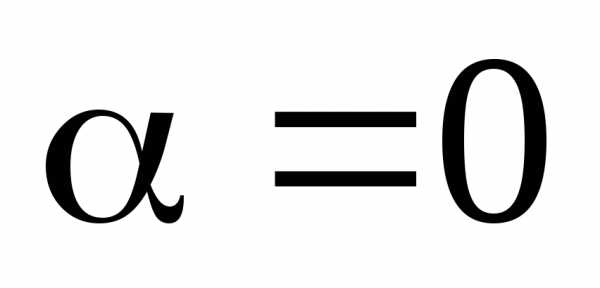 ,
и это положение устойчивое, т.е. стержень
будет занимать вертикальное положение
и будет вращаться вокруг собственной
оси.
,
и это положение устойчивое, т.е. стержень
будет занимать вертикальное положение
и будет вращаться вокруг собственной
оси.
Если то уравнение (28) будет иметь два решение
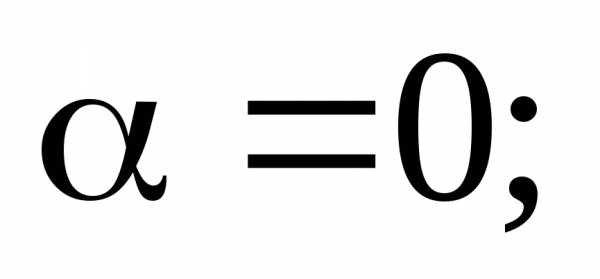 и
и 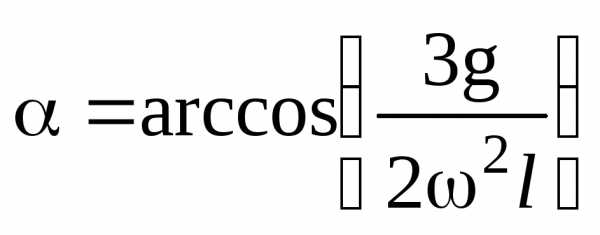 ,
,
причем можно показать, что первое решение перестает быть устойчивым, и стержень отклонится на угол, определяемый вторым решением.
б) Решим теперь задачу в неинерциальной системе отсчета, жестко связанной со стержнем. В этой системе отсчета на стержень, кроме сил взаимодействия действует центробежная сила инерции. Так как стержень находится в равновесии, сумма моментов сил, действующих на стержень, должна равняться нулю, т.е.
где 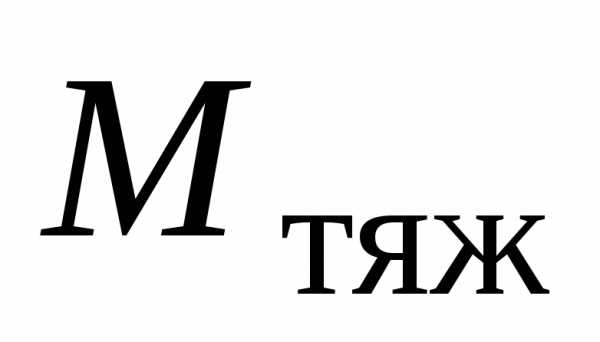 – величина момента силы тяжести,
– величина момента силы тяжести,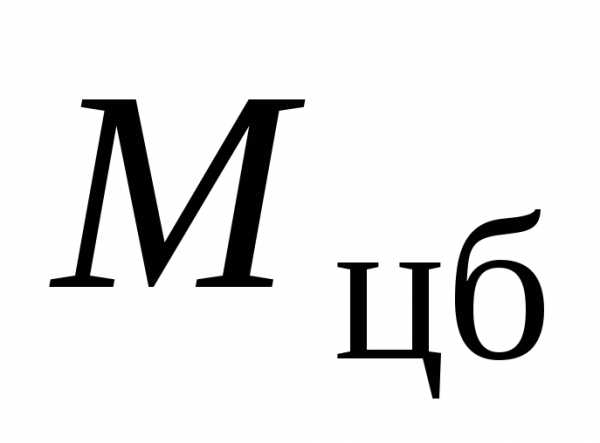 – величина момента центробежной силы
инерции относительно точки
– величина момента центробежной силы
инерции относительно точки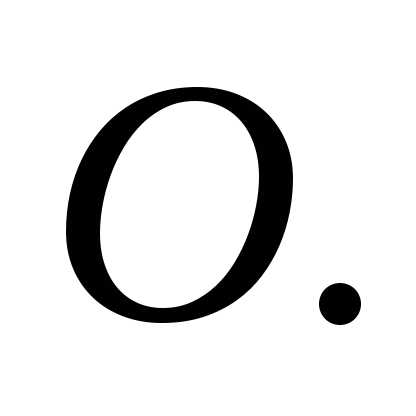 Величина момента силы тяжести определяется
уравнением (26).
Для нахождения момента центробежной
силы инерции воспользуемся рис. 7, считая,
что стержень покоится.
Величина момента силы тяжести определяется
уравнением (26).
Для нахождения момента центробежной
силы инерции воспользуемся рис. 7, считая,
что стержень покоится.
На выделенный участок стержня действует центробежная сила инерции
величина момента
которой, относительно точки  равна
равна
Интегрируя это выражение по всей длине стержня, получим
.
Подставляя это выражение и соотношение (26) в уравнение моментов (25), получим уравнение
,
в точности совпадающее с уравнением (28).
Надо заметить, что решение этой задачи в неинерциальной системе отсчета много проще, чем в инерциальной.
Пример
6. Однородная
тонкая квадратная пластинка массы 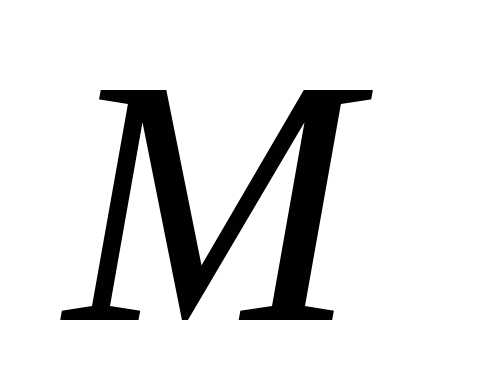 может свободно вращаться вокруг
неподвижной вертикальной оси, совпадающей
с одной из ее сторон. В центр пластины
по нормали к ней упруго ударяется шарик
массы
может свободно вращаться вокруг
неподвижной вертикальной оси, совпадающей
с одной из ее сторон. В центр пластины
по нормали к ней упруго ударяется шарик
массы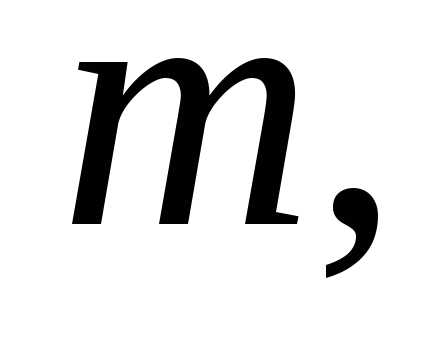 летевший со скоростью
летевший со скоростью Найти величину скорости шарика
Найти величину скорости шарика сразу после удара.
сразу после удара.
Р е ш е н и е. Система “пластина-шарик” незамкнута, так как для удержания оси пластины в неподвижном состоянии к ней необходимо приложить внешние силу. Однако надо заметить, что момент этих внешних сил относительно оси равны нулю, т.к. они приложены непосредственно к оси.
Для
решения задачи воспользуемся законами
сохранения энергии (удар упругий) и
законом сохранения момента импульса
(сумма момента внешних сил относительно
оси равен нулю). Будем считать, что длина
стороны пластины равна 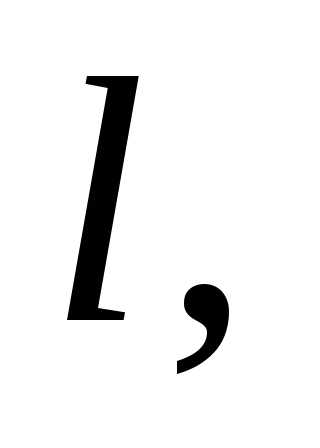 и шарик после удара будет лететь в
прежнем направлении, тогда
и шарик после удара будет лететь в
прежнем направлении, тогда
,
где 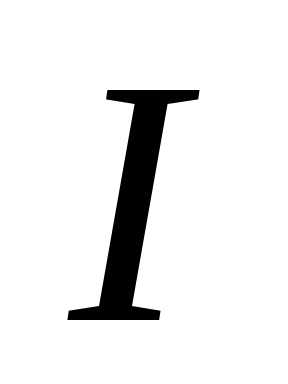 – момент инерции пластины относительно
оси,
– момент инерции пластины относительно
оси, – угловая скорость, с которой пластина
будет вращаться после удара вокруг оси.
– угловая скорость, с которой пластина
будет вращаться после удара вокруг оси.
Для простоты решения этой системы перепишем ее в виде
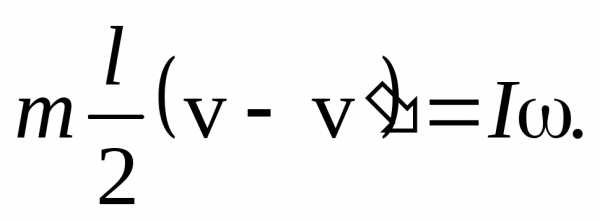 (29)
(29)
Разделив первое уравнение не второе, получим
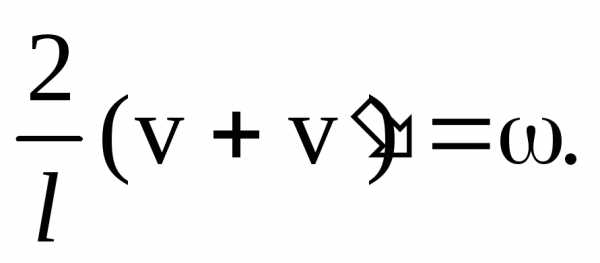 (30)
(30)
Решая
совместно уравнения (29) и(30) и учитывая,
что момент инерции пластины относительно
оси, совпадающей с одной из ее сторон
равен 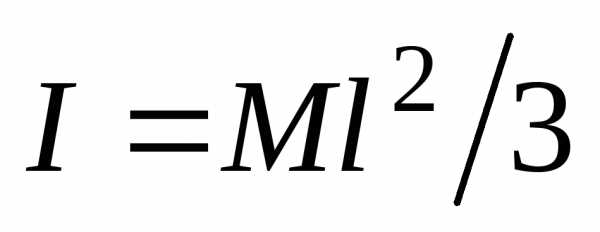 (докажите это самостоятельно), найдем
скорость шарика после удара
(докажите это самостоятельно), найдем
скорость шарика после удара
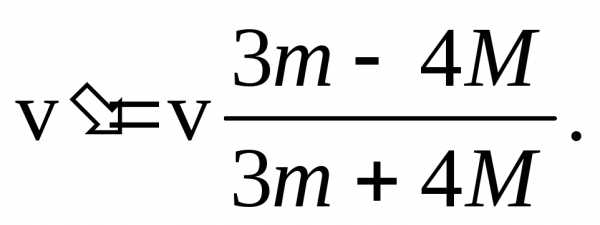
Заметим, что если , скорость шарика после удара становится отрицательной. Это означает, что пришарик полетит в обратную сторону.
Пример
7. Однородный
диск радиуса 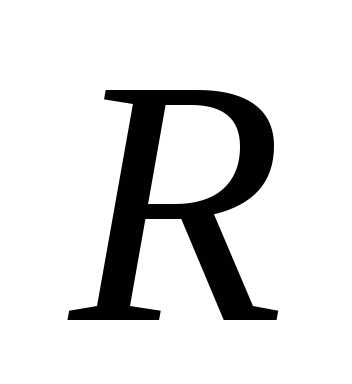 и массы
и массы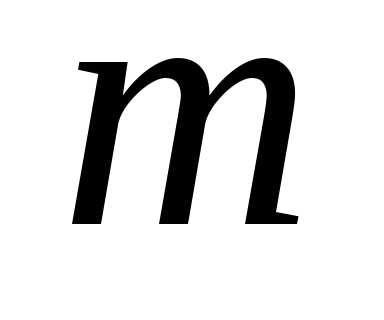 лежит на гладкой горизонтальной
поверхности. На боковую поверхность
диска плотно намотана нить, к свободному
концу
лежит на гладкой горизонтальной
поверхности. На боковую поверхность
диска плотно намотана нить, к свободному
концу которой приложили постоянную горизонтальную
силу
которой приложили постоянную горизонтальную
силу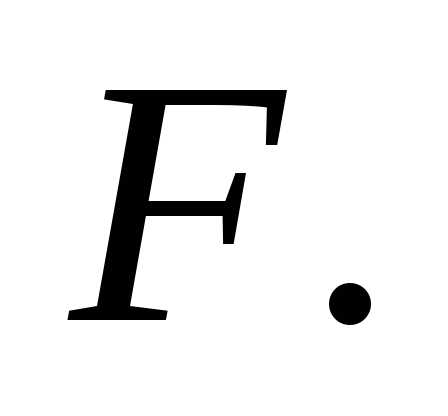 После начала движения диска точка
После начала движения диска точка переместилась на расстояние
переместилась на расстояние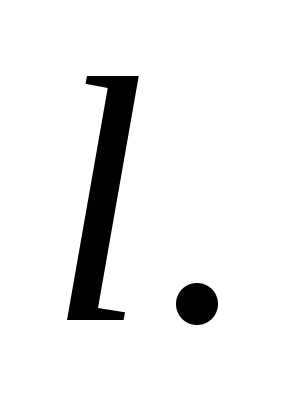 Найти угловую скорость диска к этому
моменту времени.
Найти угловую скорость диска к этому
моменту времени.
Р
е ш е н и е. Под действием силы 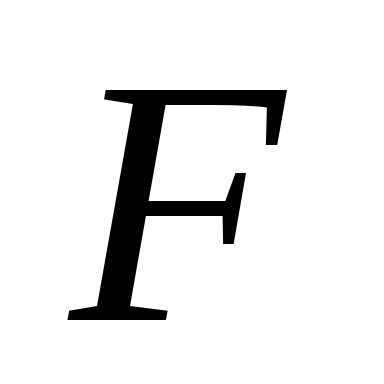 диск будет совершать плоское движение.
Свяжем подвижную систему отсчета с
центром масс диска. Величину ускорения
центра масс
диск будет совершать плоское движение.
Свяжем подвижную систему отсчета с
центром масс диска. Величину ускорения
центра масс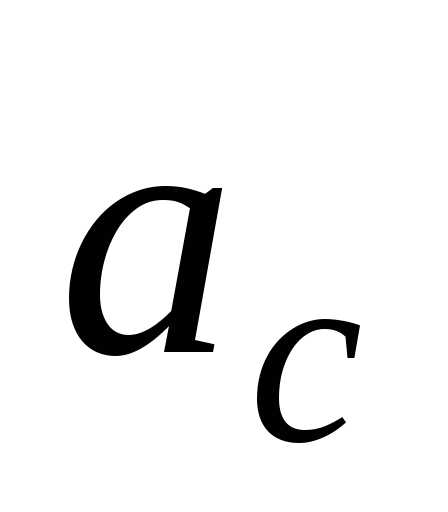 найдем из второго закона Ньютона,
записанного в проекции на направление
движения
найдем из второго закона Ньютона,
записанного в проекции на направление
движения
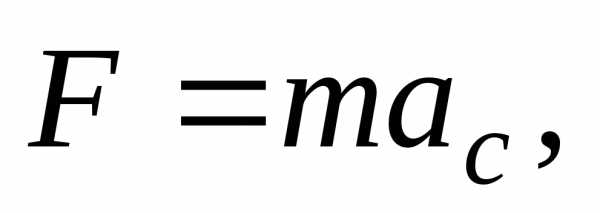

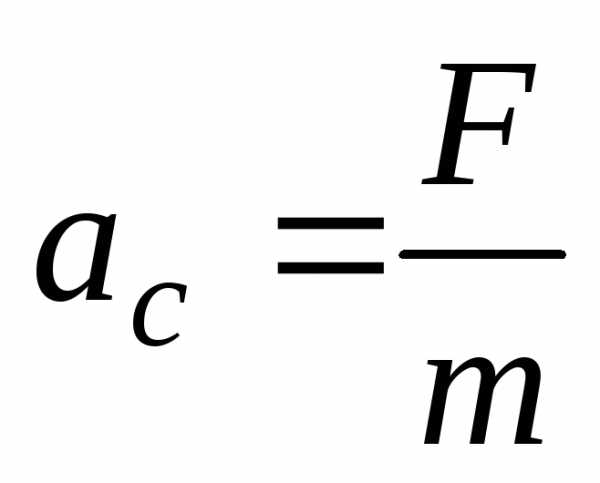 .
(31)
.
(31)
В
системе отсчета, связанной с центром
масс, диск вращается с угловым ускорением  ,
которое найдем из уравнения вращательного
движения диска
,
которое найдем из уравнения вращательного
движения диска
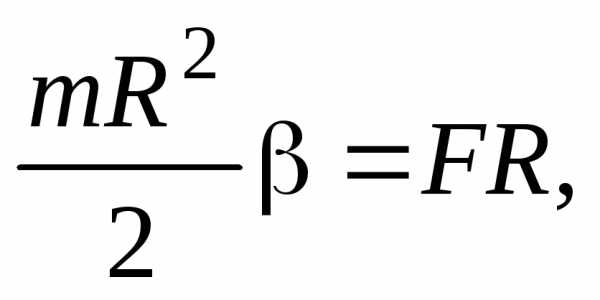

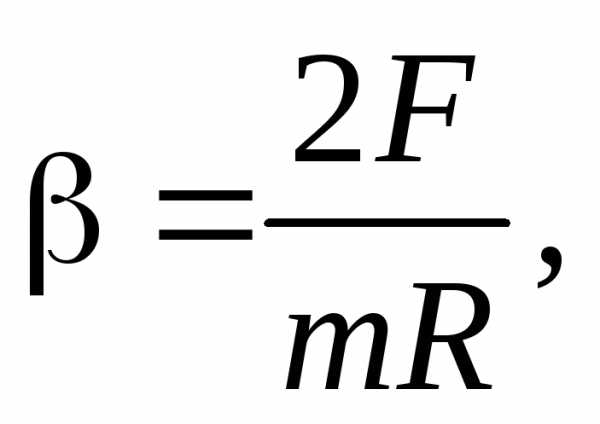 (32)
(32)
где 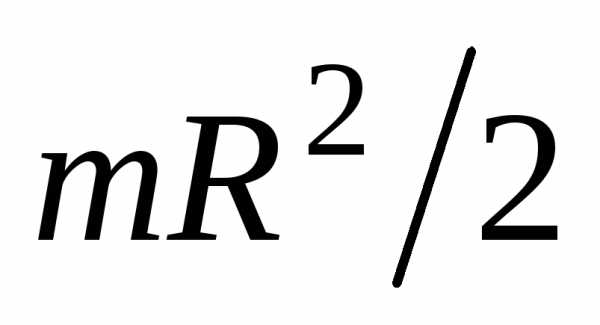 – момент инерции диска, относительно
оси вращения.
– момент инерции диска, относительно
оси вращения.
Найдем
величины скорости 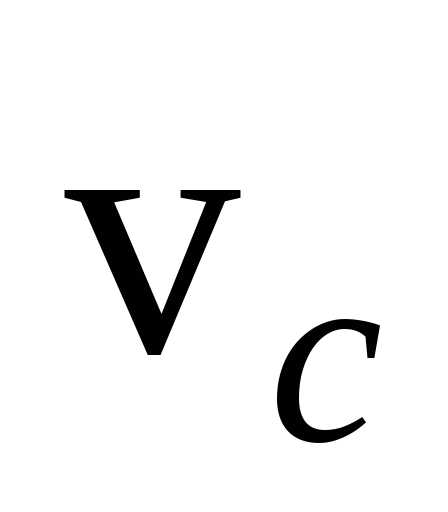 центра масс диска и угловой скорости
его вращения к моменту времени
центра масс диска и угловой скорости
его вращения к моменту времени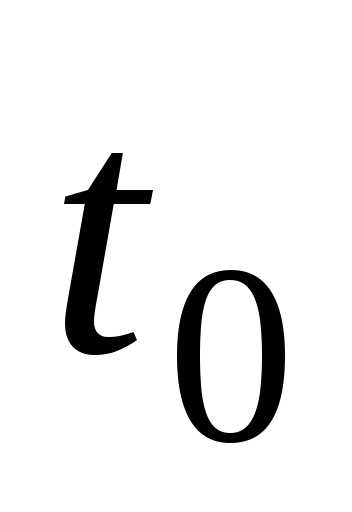 ,
когда точка приложения силы
,
когда точка приложения силы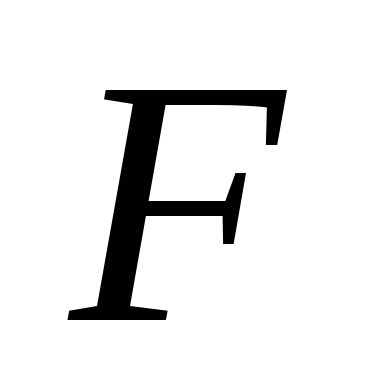 совершит перемещение
совершит перемещение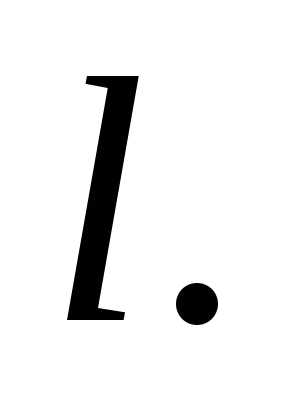 Так как в начальный момент времени диск
покоился, а величины ускорений
Так как в начальный момент времени диск
покоился, а величины ускорений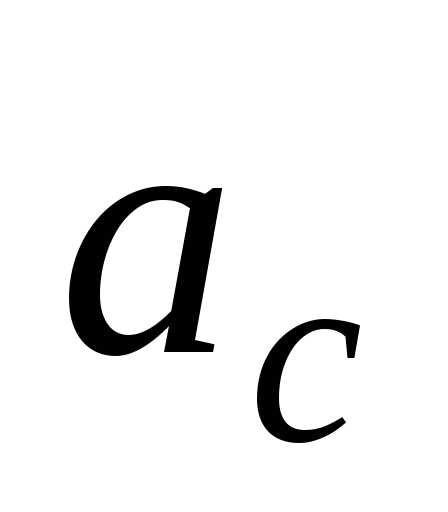 и
и не меняются с течением времени (см.
уравнения (31) и (32)), получим
не меняются с течением времени (см.
уравнения (31) и (32)), получим
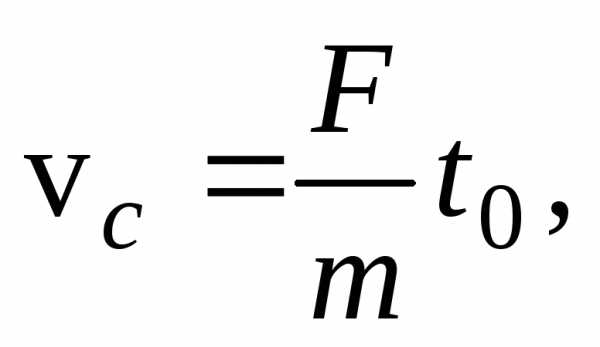
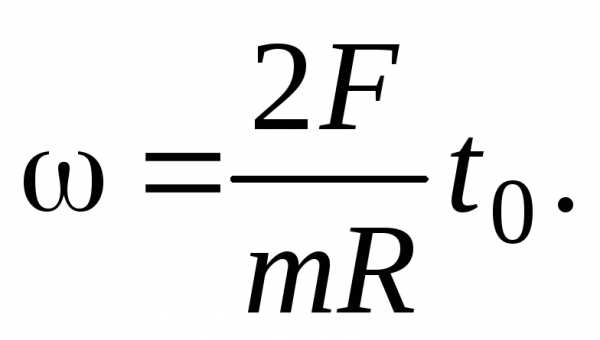
Исключая
из этих уравнений время 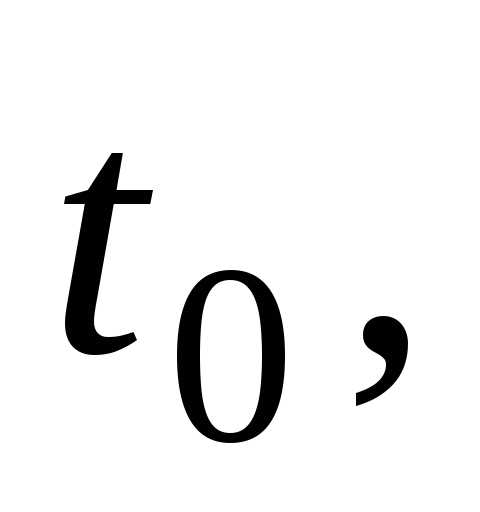 найдем связь между скоростью центра
масс и угловой скоростью вращения диска
найдем связь между скоростью центра
масс и угловой скоростью вращения диска
(33)
Запишем теорему об изменении кинетической энергии для диска
(34)
где  – работа всех сил, действующих на диск.
Силы тяжести и сила реакции опоры работу
на совершают, работу совершает только
постоянная сила
– работа всех сил, действующих на диск.
Силы тяжести и сила реакции опоры работу
на совершают, работу совершает только
постоянная сила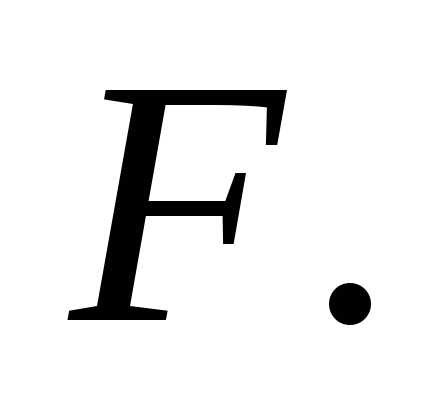 По определению работа постоянной силы
равна произведению модуля силы наперемещение
точки приложения силы,
таким образом
По определению работа постоянной силы
равна произведению модуля силы наперемещение
точки приложения силы,
таким образом
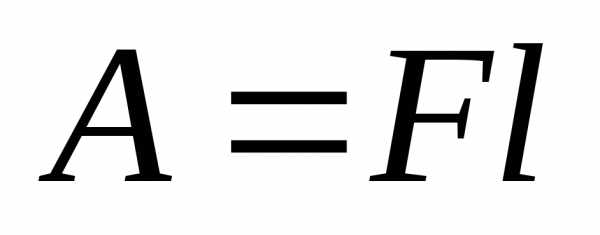 .
(35)
.
(35)
Подставляя
выражения (33) и (35) в уравнение (34), найдем
величину угловой скорости диска к
моменту времени, когда точка приложения
силы совершит перемещение 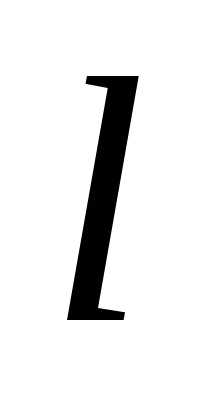
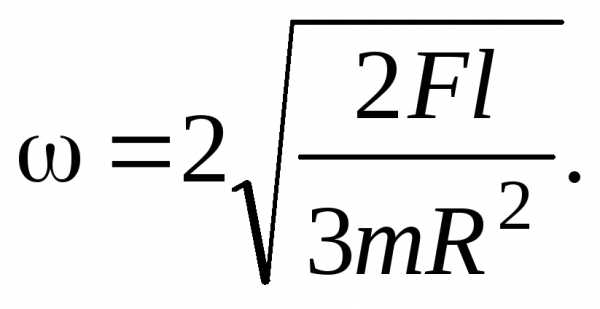
studfiles.net
Задачи по теме «Момент инерции. Закон сохранения момента
Приложение 1
Задачи по теме: «Момент инерции. Закон сохранения момента инерции и момента импульса».
На барабан радиусом R=0,5 м и с горизонтальной осью вращения намотан шнур, к концу которого привязан груз массой m = 10 кг. Найдите момент инерции барабана, если известно, что его угловое ускорение равно
 .
Тернием пренебречь.
.
Тернием пренебречь.
Дано: Решение:
m = 10 кг
R = 0, 5 м
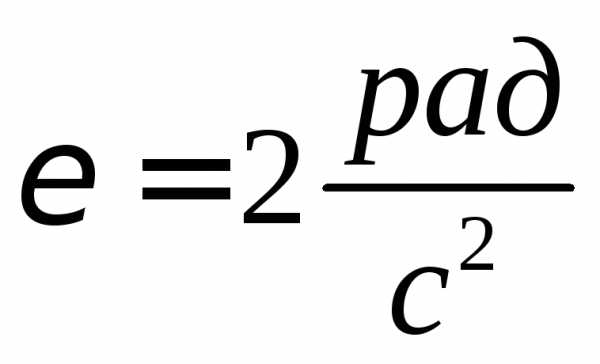
J = ?
Вращение барабана происходит под
действием силы F. Из второго закона Ньютона
ох: ma = mg – F
F = m (g – a)
 =
∆ω/∆t = ∆υ/R∆t = a/R → a = εR
=
∆ω/∆t = ∆υ/R∆t = a/R → a = εR
F = m (g – ε r)
M = Jε – момент силы через момент инерции для вращающегося тела.
M = Fd = FR – момент силы вращающей барабан.
По закону сохранения момента сил
Jε = FR
Jε = m (g – εR) R
J = (m ( g – εR) R)/ ε = 22,5 (кг м²)
Ответ: 22, 5 кг м2
К ободу однородного диска радиусом R=0,2м массой m=1,2 кг приложена постоянная сила 100 Н, при вращении на диск действует момент силы трения, равный 5 нм. Чему равно угловое ускорение диска?
Дано: Решение:
R = 0, 2 м Из оснавного управления динамики вращательного
m = 1, 2 кг движения M=Jε
F = 100 Н Сила действующая на обод F`= F – Fтр. Из M = 5 нм момента силы трения Fтр = M\R = 25 Н
ε = ? Момент силы F`- M=F`R по закону сохранения
момента сил.
Jε = F`R
J = mR² –момент инерции обруча
mR²ε = (F – Fтр.)R
Ответ: ε = 312, 5 с-2.
Шарик, диаметр которого равен 6 см, катится по полу и останавливается через t = 2с, пройдя расстояние S = 70 см. Определите коэффициент трения качения, считая его постоянным.
Дано: Решение:
d = 0, 06 м М=εJ – основное уравнение вращательного движения.
t = 2c J= 0,4mr2 – момент инерции шара.
S=
0,7м. 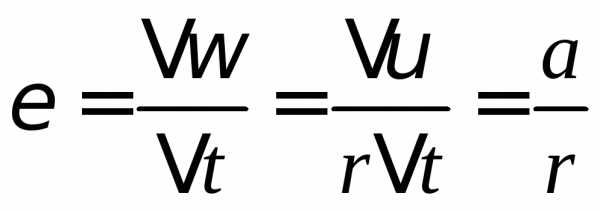
μ = ?
M= 0,4 m r2 a/ r= 0,4 a m r
Момент силы трения M = Fтр r
Fтр = μN= μmg
M = μmgr
По закону сохранения момента сил
μmgr=0,4amr
μ = 0,4a/g
S= at2/2  a=2S/t2 =
1,4/4 = 0,35 м/с2
a=2S/t2 =
1,4/4 = 0,35 м/с2
Ответ: 0,014.
Во сколько раз уменьшится угловая скорость вращения человека, если момент инерции изменится от 1 кг м² до 1,25 кг м²?
Дано: Решение:
L1 = J1ω1 – момент импульса в первом состоянии.
L2 = J2ω2 – момент импульса во втором состоянии.
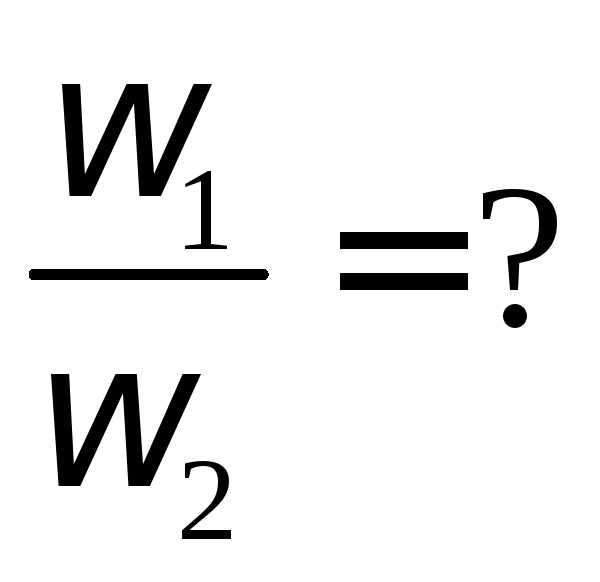 L1 = L2 – закон сохранения момента импульса.
L1 = L2 – закон сохранения момента импульса.
Ответ: 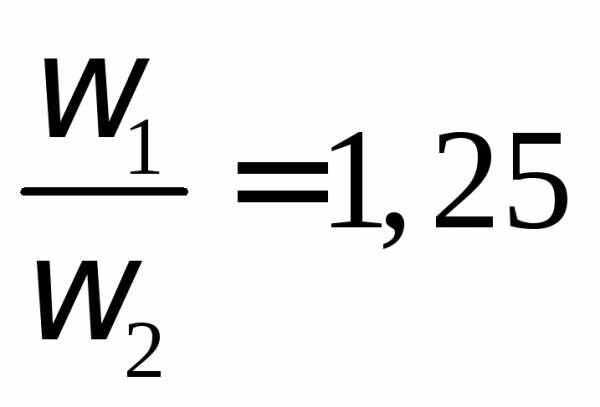
Найти момент импульса Земного шара М3 = 6·1024 кг, R3 = 6,4·10³ км, если точки поверхности Земли вращаются со скоростью 36 км/ ч.
Дано: Решение:
M3 = 6·1024 кг L = Jω J= 0,4 M3R3²- момент инерции шара.
R3 = 6,4·10 6 м ω = υ/ R
υ = 10 м\с L = 0,4 M3 υ R3= 15,36·10³º кг м²/с.
L = ?
Ответ: L = 15, 36·10³º кг м²/с
Комета Галлея движется вокруг солнца по вытянутому эллипсу. Наибольшее удаление от солнца равно 35,2 а. е., а наименьшее удаление – 0,6 а.е.. Найти отношение максимальной скорости кометы к минимальной.
Дано: Решение:
R1 = 35, 2 а. е. момент импульса при наибольшем
R2 = 0, 6 а. е. удалении.
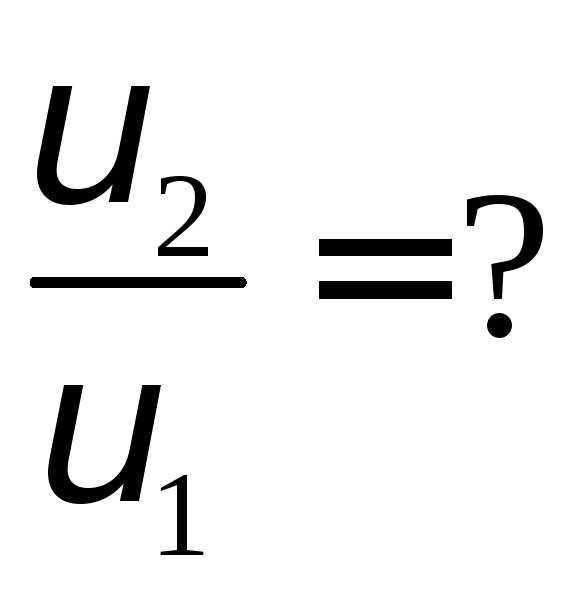
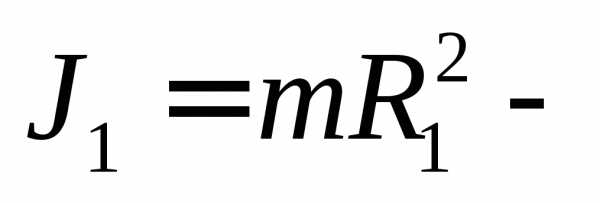 момент
инерции кометы при наибольшем
момент
инерции кометы при наибольшем
удалении.
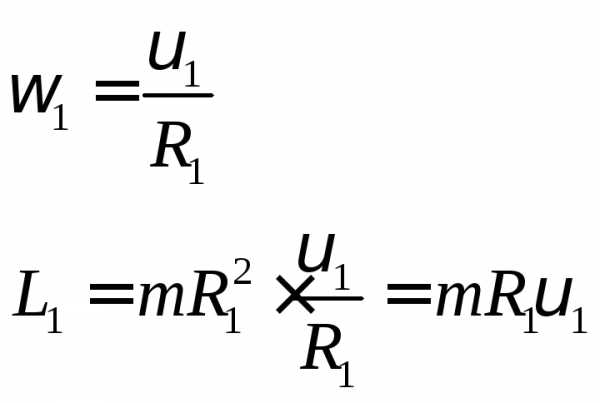
момент импульса кометы при
минимальном удалении.
L1 = L2 – закон сохранения момента импульса.
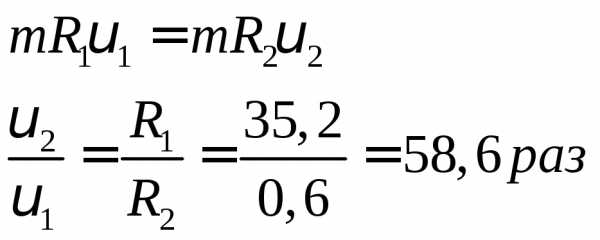
Ответ: 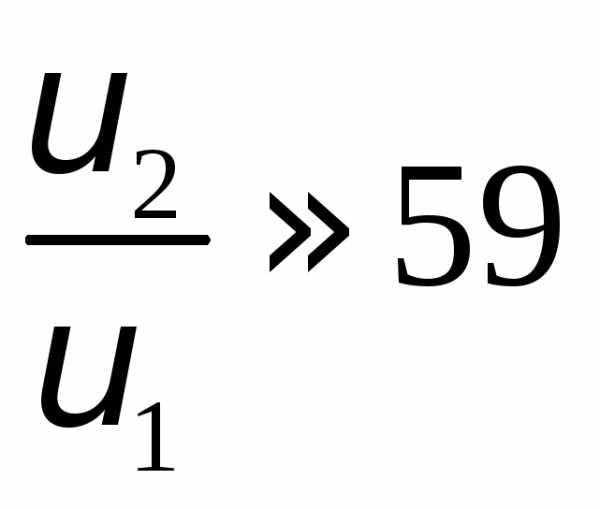
Человек стоит на вращающейся с некоторой угловой скоростью платформе. В вытянутых в сторону руках он держит по гире, массой каждой из них m = 5 кг. Расстояние от гирь до оси вращения R1=0,71м. Во сколько раз изменится частота вращения человека, если он прижмет к себе руки так, что расстояние от оси вращения до гири станет R2= 0,2 м. Момент инерции человека считайте в обоих случаях равным J0 = 1 кг м.²
Дано: Решение:
m = 5 кг Момент импульса в первом случае
R1=0,71м 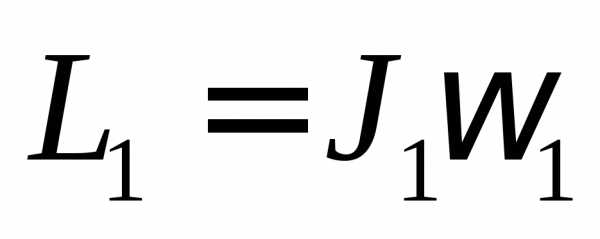
R2= 0,2 м момент инерции в первом случае.
J0 = 1 кг м² 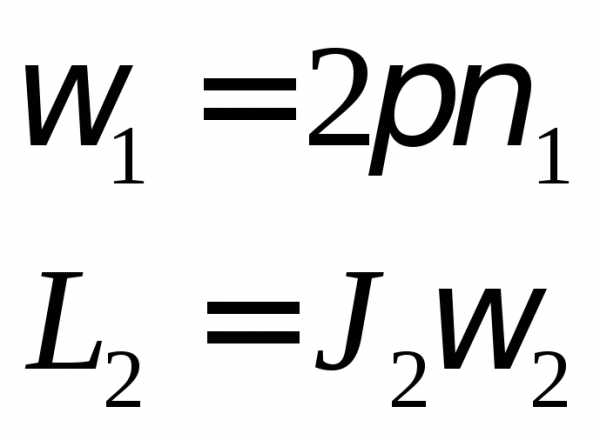
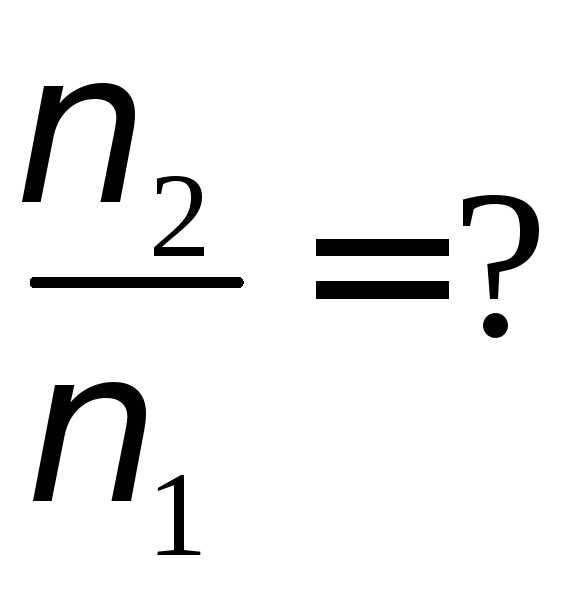 момент
инерции во втором случае.
момент
инерции во втором случае.
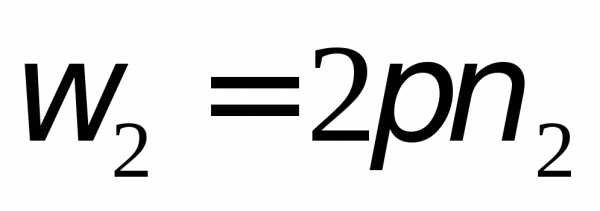
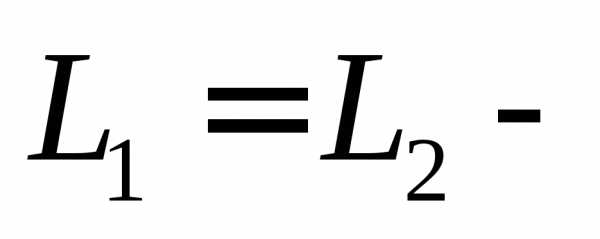 закон
сохранения момента импульса.
закон
сохранения момента импульса.
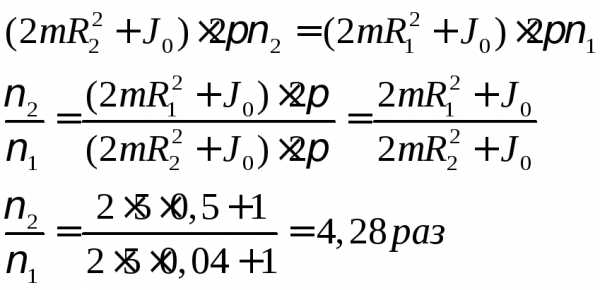
Ответ: 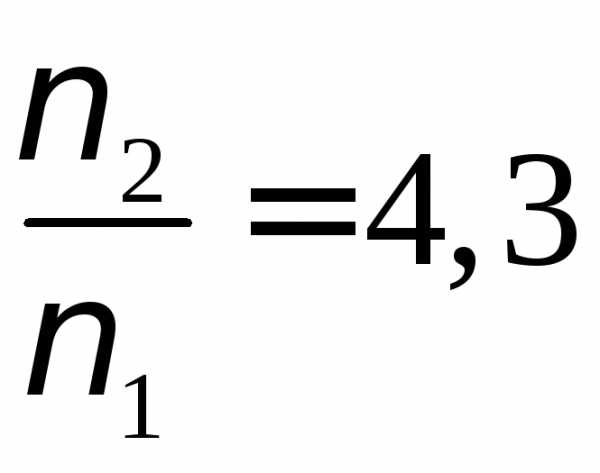
Человек массой m1 = 60 кг находится на неподвижной круглой платформе радиусом R2= 10м и массой m2 = 120 кг, которая может вращаться вокруг своей вертикальной оси. С какой угловой скоростью будет вращаться платформа, если человек станет двигаться по окружности радиусом R1= 5м с линейной скоростью υ1= 2 м/с относительно платформы.
Дано: Решение:
m1 = 60 кг момент импульса человека;
R2= 10м момент инерции человека.
m2 = 120 кг 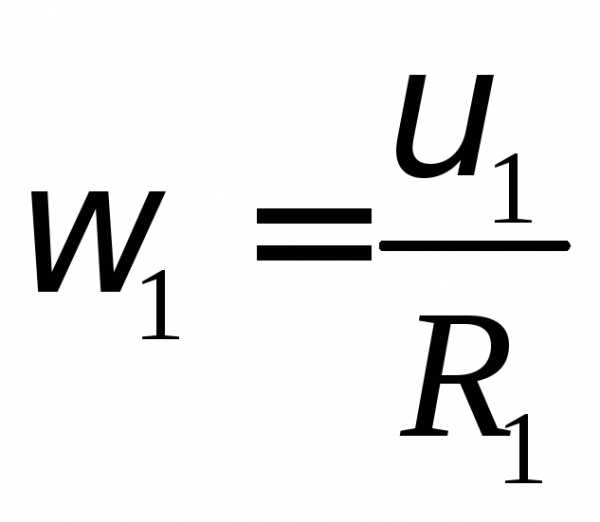
R1= 5м
υ1= 2 м/с момент импульса платформы
ω = ? и человека.
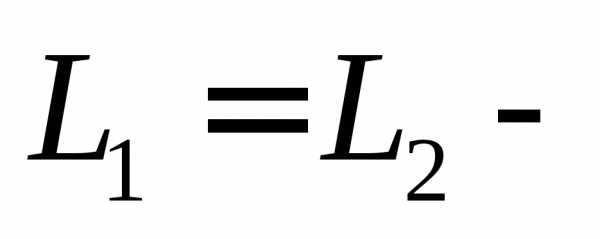 закон
сохранения импульса.
закон
сохранения импульса.
Ответ: 0, 08 с-1
Считая Солнце однородным шаром, оцените минимальный радиус и период вращения вокруг своей оси пульсара, который мог бы образоваться после сжатия Солнца под действием силы тяготения при исчерпании внутренних источников энергии, поддерживающих высокую температуру газа. Радиус Солнца Rc= 7·108 м, период вращения вокруг оси Тс = 2,2·106 с. Масса Солнца Мс = 2·10³º кг.
Дано: Решение:
Rc= 7·108 м Момент импульса Солнца
Тс = 2,2·106 с 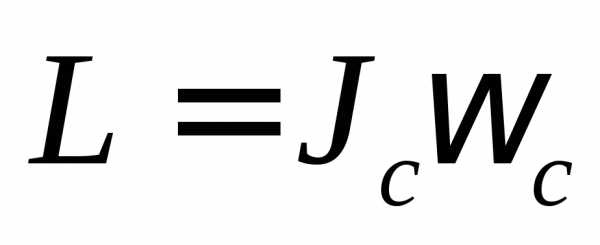
Мс = 2·10³º кг момент инерции Солнца
Rп = ? Тп = ? 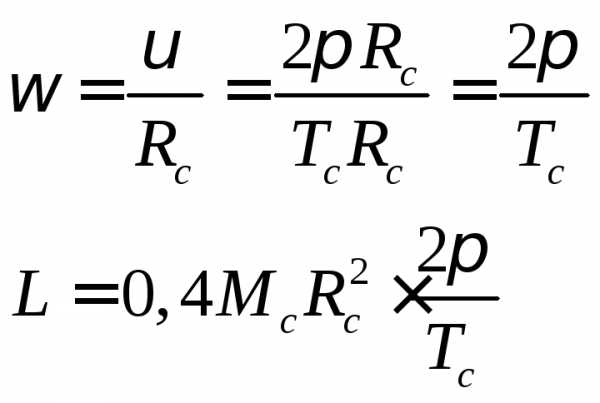
Момент импульса образовавшегося пульсара
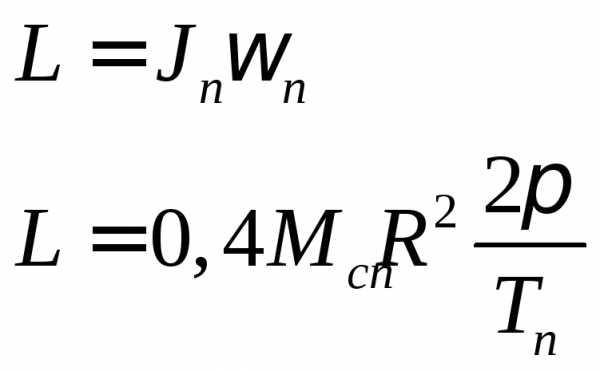
По закону сохранения импульса
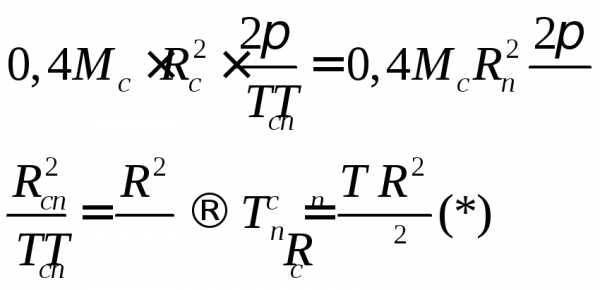
Вращение пульсара происходит под действием силы тяготения.
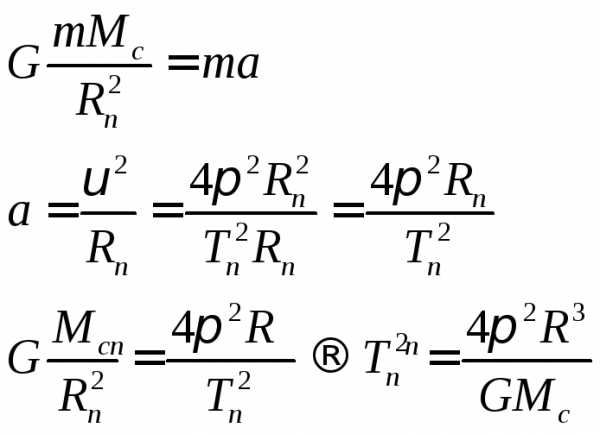
Для удобства расчета (*) возведем в квадрат
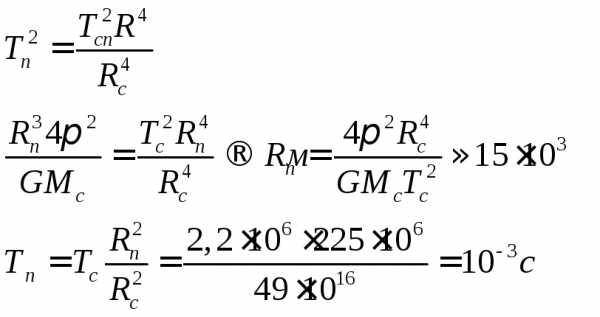
Ответ: Rп =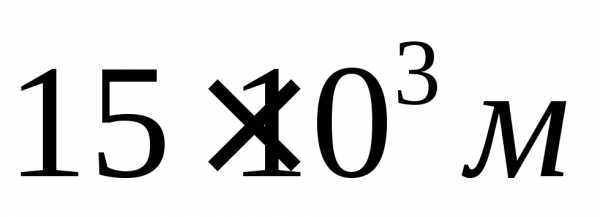
Tп = 10-3 с
studfiles.net
Примеры решения задач
Пример 1. Вычислить
момент инерции Jz молекулы NО2 относительно оси z,
проходящей через центр масс молекулы
перпендикулярно плоскости, содержащей
ядра атомов. Межъядерное расстояние d этой молекулы равно
0,118 нм,
валентный угол  =140°.
=140°.
Решение. Молекулу NO2 можно рассматривать как систему, состоящую из трех материальных точек общей массой
m=2m1+m2, (1)
где m1 — масса атома кислорода; m2— масса атома азота.
Расположим молекулу относительно координатных осей так, как это указано на рис. 3.1 (начало координат совместим с центром
масс С молекулы, ось z направим перпендикулярно плоскости чертежа «к нам».)
Для определения Jz воспользуемся теоремой Штейнера:
J=Jc+ma2.
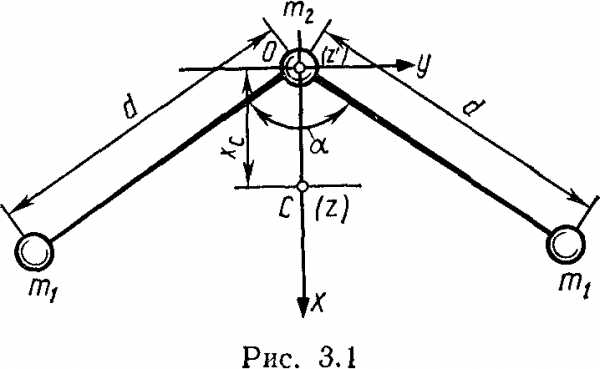
Jz = Jz‘ –ma2 (2)
Момент инерции Jz‘ находим как сумму моментов инерции двух материальных точек (атомов кислорода):
Jz‘ = 2m1 d2 (3)
Расстояние а между осями z и z‘ равно координате xс центра масс системы и поэтому может быть выражено по формуле (см. § 2, с. 20) В данном случае
а=хс=
(2m1x1+m2x2)/(2m1+m2),
или, учитывая, что x1=d cos
( /2)
и х2=0,
/2)
и х2=0,
(4)
Подставив в формулу (2) значения Jz‘, т, а соответственно из выражений (3), (1), (4), получим
или после преобразований
(5)
Найдем в табл. 23 относительные атомные массы кислорода (AO=16) и азота (АN==14) и запишем массы атомов этих элементов в атомных единицах массы (а.е.м.), а затем выразим в килограммах (1 а.е.м. =1,66 •10-27 кг, см. табл. 9):
m1= 16 1,66 10-27 кг=2,66 10-26 кг;
m2 = 14 1,66 10–27 кг = 2,32 10-26 кг.
Значения m1,
т1, d и  подставим
* в формулу
(5) и произведем
вычисления:
подставим
* в формулу
(5) и произведем
вычисления:
Jz=6,80 10-46 кг.м2.
Пример 2. Физический маятник представляет собой стержень длиной l=1 м и массой m1=l кг с прикрепленным к одному из его
*Для вычисления выражения, стоящего в скобках, вместо масс атомов можно подставить их относительные атомные массы, так как здесь массы входят в виде отношения.
концов диском массой т2=0,5 m1. Определить момент инерции Jz такого маятника относительно оси Оz, проходящей через точку О на стержне перпендикулярно плоскости чертежа (рис. 3.2).
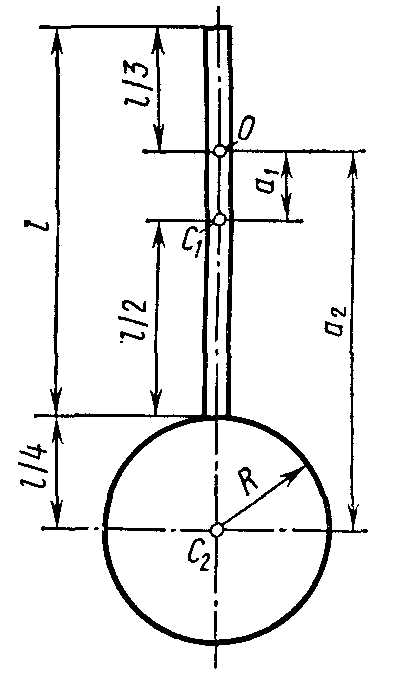
Jz = Jz1 + Jz2 (1)
Формулы, по которым вычисляются моменты инерции стержня Jz1 и диска Jz2 относительно осей, проходящих через их центры масс, даны в табл. на с. 41. Чтобы определить моменты инерции Jz1 и Jz2, надо воспользоваться теоремой Штейнера:
J=Jc+ma2. (2)
Выразим момент инерции стержня согласно формуле (2):
Jz1=l/12m1l2+m1a12.
Расстояние a1 между осью Оz и параллельной ей осью, проходящей через центр масс C1 стержня, как следует из рис. 3.2, равно 1/2l—l/3l=l/6l. С учетом этого запишем
Jz1=l/12m1l2+m1 (l/6l )2=1/9m1l2=0,111m1l2.
Момент инерции диска в соответствии с формулой (2) равен рис. 3.2
Jz2=l/2m2R2+m2a22.
где R — радиус диска; R=1/4l. Расстояние а2 между осью Оz и параллельной ей осью, проходящей через центр масс диска, равно (рис. 3.2) 2/3l—l/4l=l1/12l. С учетом этого запишем
Jz2=l/2m2 (1/4l)2+m2(l1/12l)2= 0,0312 m1l2 + 0,840 m1l2= 0,871 m1l2.
Подставив полученные выражения Jz1 и Jz2 в формулу (1), найдем
Jz=0,111m1l2+0,871 m1l2=)0,111m1+0,871 m1)l2,
или, учитывая, что т2=0,5 m1,
Jz=0,547m1l2.
Произведя вычисления, получим значение момента инерции физического маятника относительно оси Оz:
Jz =0,547.1.1 кг м2=0,547 кг м2.
Пример 3. Вал в виде сплошного цилиндра массой m1=10 кг насажен на горизонтальную ось. На цилиндр намотан шнур, к свободному концу которого подвешена гиря массой m2=2 кг (рис. 3.3). С каким ускорением а будет опускаться гиря, если ее предоставить самой себе?
Решение. Линейное ускорение а гири равно тангенциальному ускорению точек вала, лежащих на его цилиндрической поверхности,
и связано с угловым ускорением s вала соотношением
а= , (1)
, (1)
где r — радиус вала.
Угловое ускорение вала выражается основным уравнением динамики вращающегося тела:
 =M/J,
(2)
=M/J,
(2)
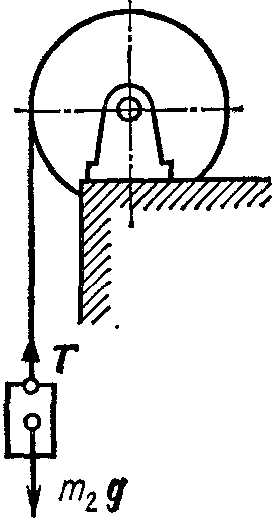
J=1/2m1r2.
Вращающий момент М, действующий на вал, равен произведению силы натяжения Т шнура на радиус вала: М=Тr.
Силу натяжения шнура найдем из следующих соображений. На гирю действуют две силы: сила тяжести m2g, направленная вниз, и сила натяжения Т шнура, направленная вверх. Равнодействующая этих сил вызывает равноускоренное движение гири. По второму закону Ньютона, m2g-T=m2a, откуда T=m2(g-а). Таким образом, вращающий момент M=m2(g—а)r.
Подставив в формулу (2) полученные выражения М и J, найдем угловое ускорение вала:
Для определения линейного ускорения гири подставим это
рис.
3.3 выражение  в формулу
(1).
Получим
в формулу
(1).
Получим
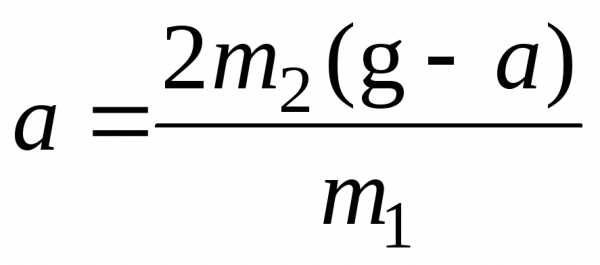 ,
,
откуда
Пример 4. Через блок в виде диска, имеющий массу m=80 г, перекинута тонкая гибкая нить, к концам которой подвешены грузы массами m1=100 г и m2=200 г (рис. 3.4). С каким ускорением будут двигаться грузы, если их предоставить самим себе? Трением пренебречь.
Решение. Применим к решению задачи основные законы поступательного и вращательного движения. На каждый из движущихся грузов действуют две силы: сила тяжести mg, направленная вниз, и сила Т натяжения нити, направленная вверх.
Так как вектор ускорения а груза m1 направлен вверх, то T1>m1g. Равнодействующая этих сил вызывает равноускоренное движение и, по второму закону Ньютона, равна T1 — т1g=т1а, откуда
T1=m1g+m1a. (1)
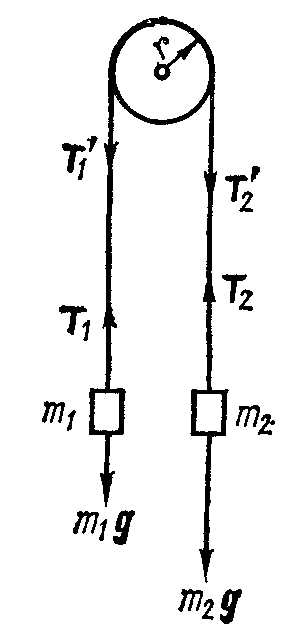
Рис. 3.4
Вектор ускорения а груза т2 направлен вниз; следовательно, T2<m2g. Запишем формулу второго закона для этого груза:m2g — T2=m2a , откуда
T2=m2g– m2а. (2)
Согласно основному
закону динамики вращательного движения,
вращающий момент М, приложенный к диску, равен
произведению момента инерции J диска на его угловое ускорение  :
:
M=J .
(3)
.
(3)
Определим вращающий
момент. Силы натяжения нитей действуют
не только на грузы, но и на диск. По
третьему закону Ньютона, силы 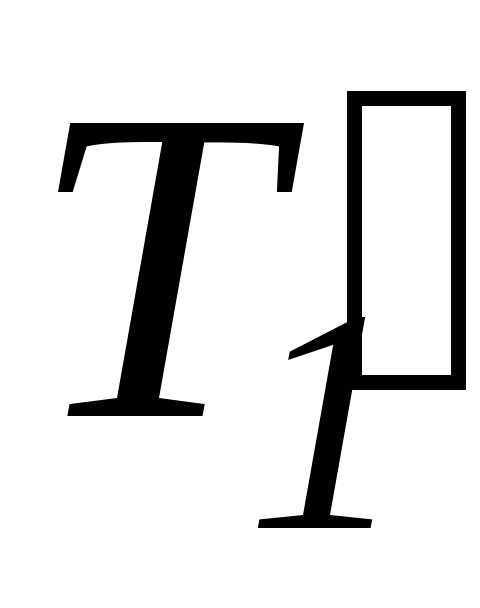 и
и  ,
приложенные к ободу диска, равны
соответственно силам T1 и Т2,
но по направлению им противоположны.
При движении грузов диск ускоренно
вращается по часовой стрелке; следовательно,
,
приложенные к ободу диска, равны
соответственно силам T1 и Т2,
но по направлению им противоположны.
При движении грузов диск ускоренно
вращается по часовой стрелке; следовательно,  >
>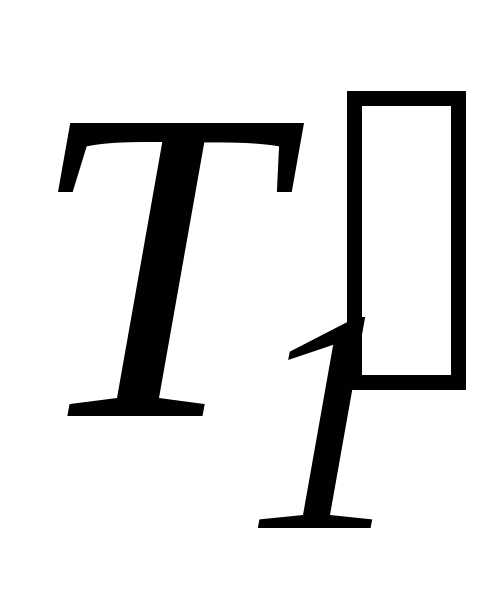 . Вращающий момент, приложенный к диску,
равен произведению разности этих сил
на плечо, равное радиусу диска, т. е.
M=(
. Вращающий момент, приложенный к диску,
равен произведению разности этих сил
на плечо, равное радиусу диска, т. е.
M=( –
– 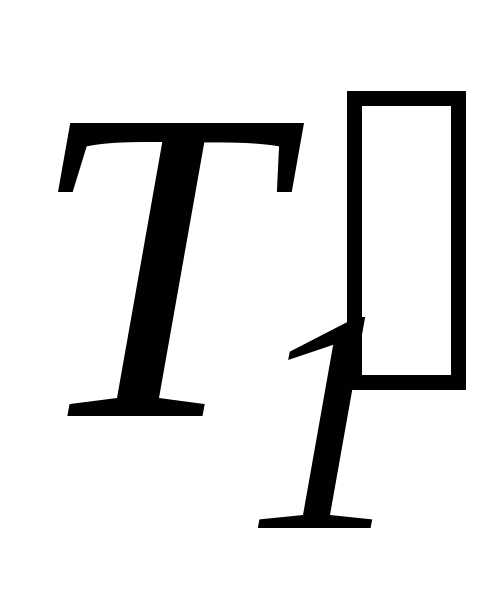 )r. Момент инерции
диска J=mr2/l, угловое ускорение связано с линейным
ускорением грузов соотношением
S=a/r. Подставив в формулу
(3) выражения М, J и
)r. Момент инерции
диска J=mr2/l, угловое ускорение связано с линейным
ускорением грузов соотношением
S=a/r. Подставив в формулу
(3) выражения М, J и  ,
получим
,
получим
( –
– 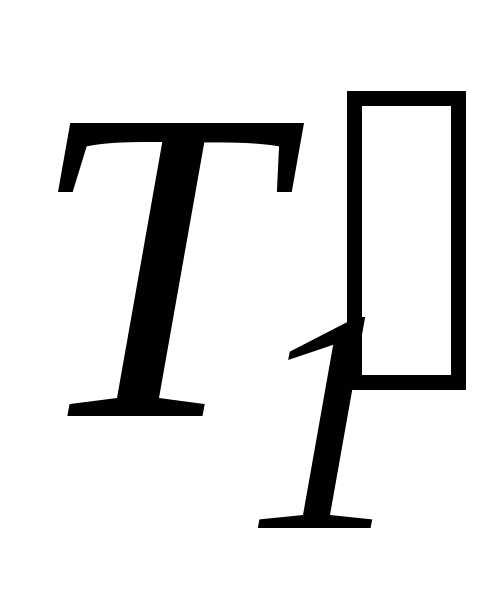 )r =
)r =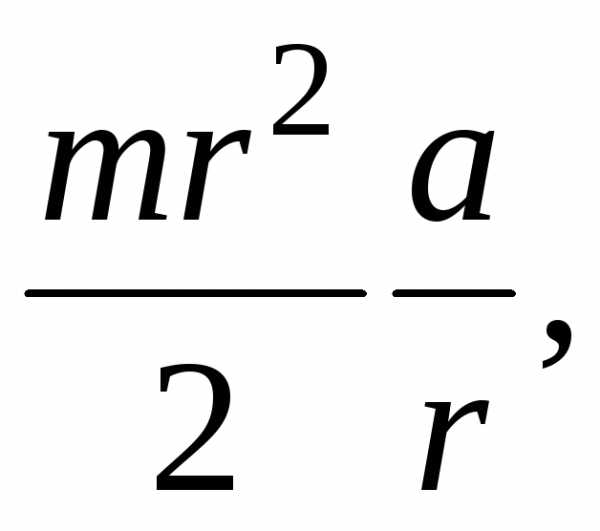 .
.
откуда
 –
– 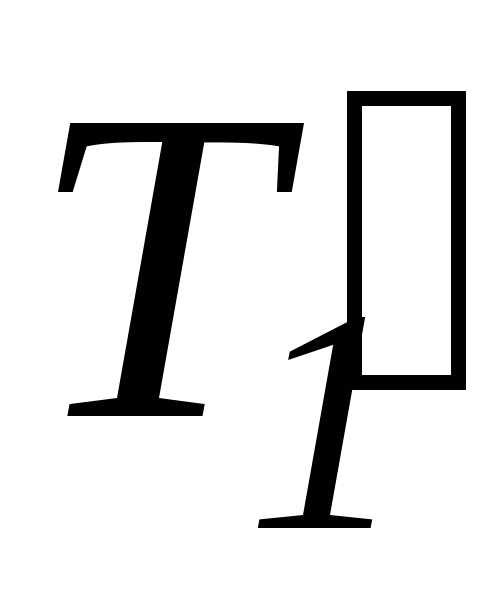 =(т/2)а.
=(т/2)а.
Так как 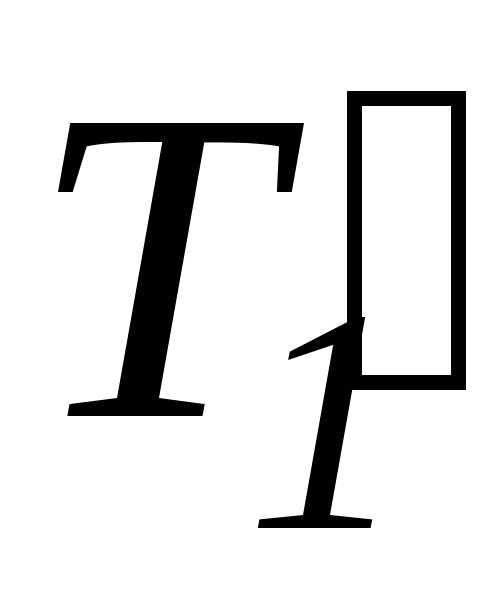 =T1 и
=T1 и  =Т2, то можно заменить силы
=Т2, то можно заменить силы 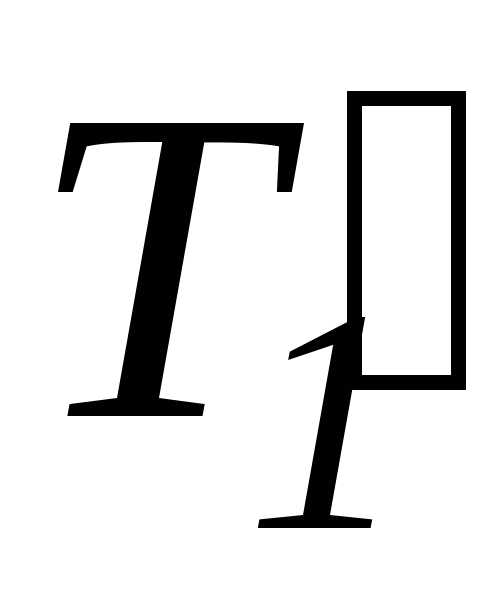 и
и  выражениями по формулам
(1) и
(2), тогда
выражениями по формулам
(1) и
(2), тогда
m2g—m2a—m1g—m1=(m/2)a, или
(m2—m1) g=(m2+m1+m/2)a
откуда
(4)
Отношение масс в правой части формулы (4) есть величина безразмерная. Поэтому значения масс m1, m2 и m можно выразить в граммах, как они даны в условии задачи. После подстановки
получим
Пример 5. Маховик в виде диска массой m=50 кг и радиусом г=20 см был раскручен до частоты вращения n1=480 мин”1 и затем предоставлен самому себе. Вследствие трения маховик остановился. Найти момент М сил трения, считая его постоянным для
двух случаев: 1) маховик остановился через t=50 с; 2) маховик до полной остановки сделал N=200 оборотов.
Решение. 1.По второму закону динамики вращательного движения, изменение момента импульса вращающегося тела равно произведению момента силы, действующего на тело, на время действия этого момента:
M t=J
t=J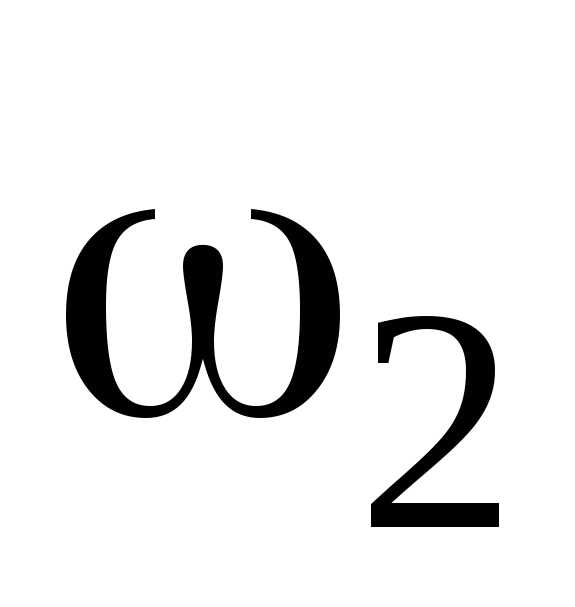 — J
— J ,
,
где J — момент
инерции маховика;  и
и 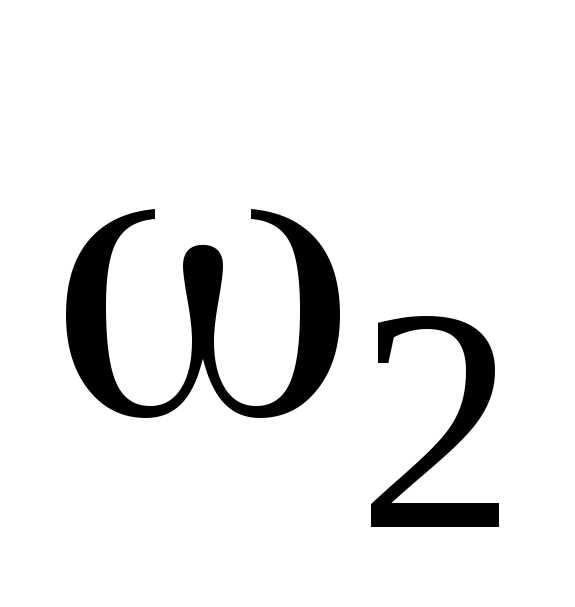 — начальная
и конечная угловые скорости. Так как
— начальная
и конечная угловые скорости. Так как 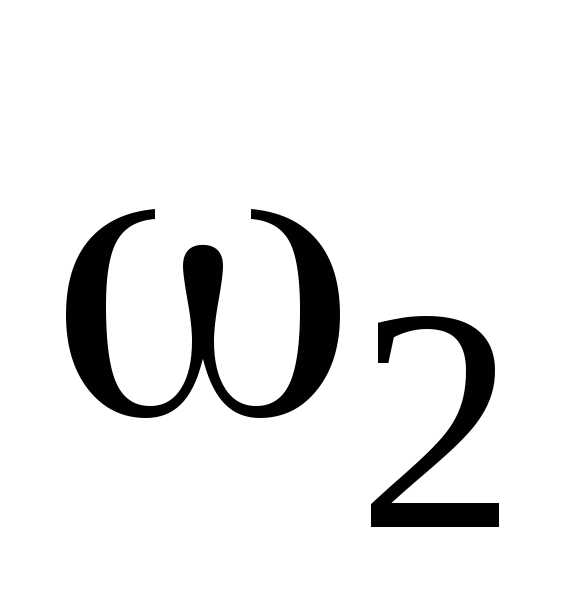 =0
и
=0
и  t=t , то Mt=—J
t=t , то Mt=—J ,
откуда
,
откуда
M= —J /t. (1)
/t. (1)
Момент инерции диска относительно его геометрической оси равен J=1/2mr2. Подставив это выражение в формулу (1), найдем
M=—mr2 /(2t). (2)
/(2t). (2)
Выразив угловую
скорость  через частоту вращения n1 и произведя вычисления по формуле
(2), найдем
через частоту вращения n1 и произведя вычисления по формуле
(2), найдем
М= —1 Н м.
2. В условии задачи дано число оборотов, сделанных маховиком до остановки, т. е. его угловое перемещение. Поэтому применим формулу, выражающую связь работы с изменением кинетической энергии:
или,
учтя, что 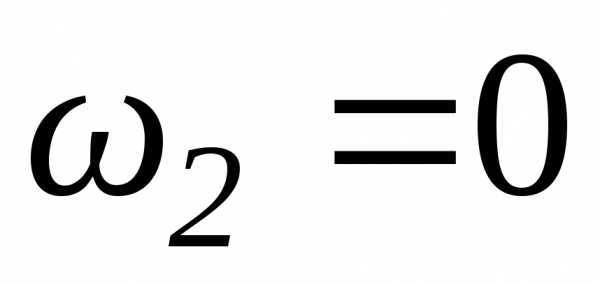 ,
,
. (3)
Работа при вращательном движении определяется по формуле A=M. Подставив выражения работы и момента инерции диска в формулу (3), получим
M = —mr2
= —mr2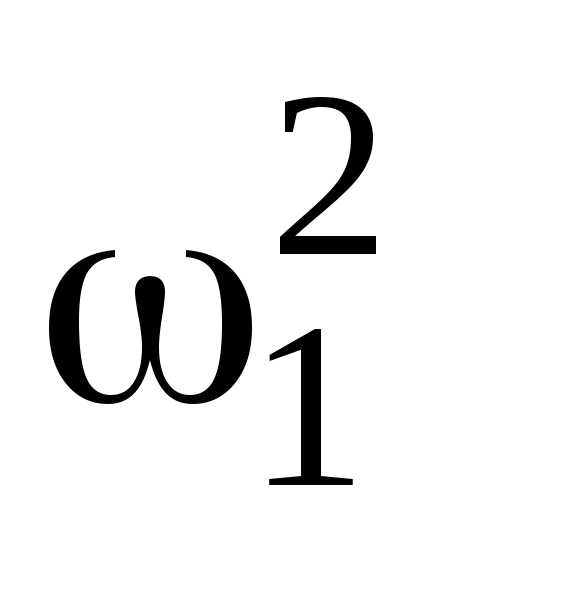 /4.
/4.
Отсюда момент силы трения
М= —mr2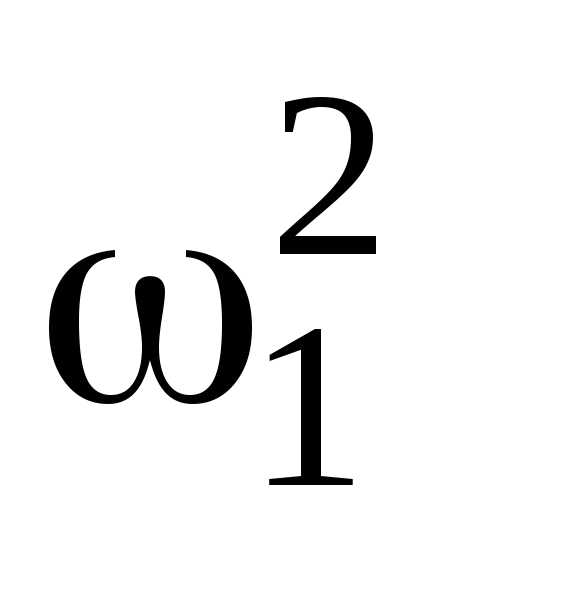 /4
/4 . (4)
. (4)
Угол поворота =2лN=2 3,14 200 рад=1256 рад. Произведя вычисления по формуле (4), получим
М= —1 Н м.
Знак минус показывает, что момент силы трения оказывает тормозящее действие.
Пример 6. Платформа в виде диска радиусом R= 1,5 м и массой m1=180 кг вращается по инерции около вертикальной оси с частотой n=10 мин-1. В центре платформы стоит человек массой т2=60 кг. Какую линейную скорость относительно пола помещения будет иметь человек, если он перейдет на край платформы?
Решение. По закону сохранения момента импульса,
(1)
где J1 — момент
инерции платформы; J2 — момент
инерции человека, стоящего в центре
платформы;  — угловая
скорость платформы с человеком, стоящим
в ее центре; J2‘
— момент
инерции
— угловая
скорость платформы с человеком, стоящим
в ее центре; J2‘
— момент
инерции
человека, стоящего
на краю платформы; 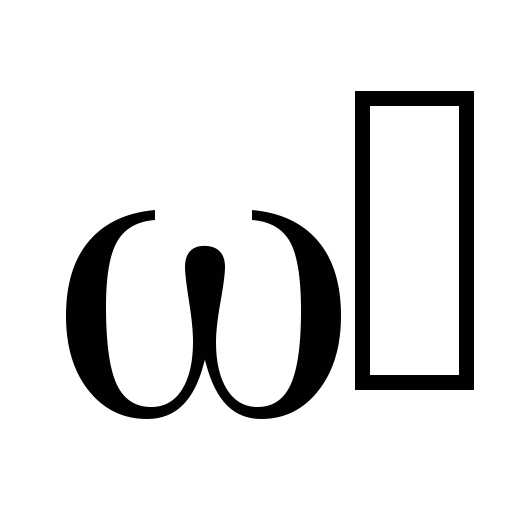 — угловая
скорость платформы с человеком, стоящим
на ее краю.
— угловая
скорость платформы с человеком, стоящим
на ее краю.
Линейная скорость человека, стоящего на краю платформы, связана с угловой скоростью соотношением
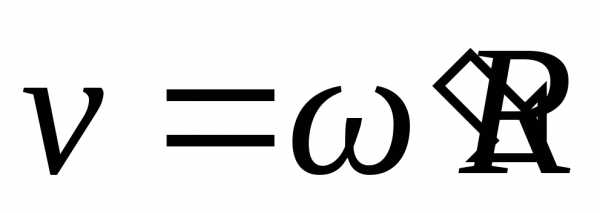 . (2)
. (2)
Определив 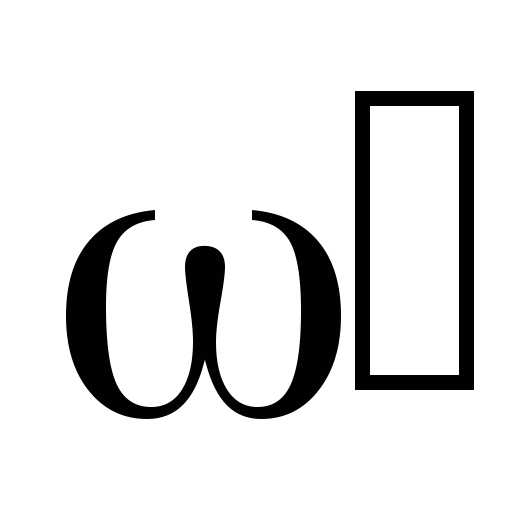 из уравнения
(1) и подставив
полученное выражение в формулу
(2), будем
иметь
из уравнения
(1) и подставив
полученное выражение в формулу
(2), будем
иметь
v=(J1+J2) R/(J1+J‘2). (3)
R/(J1+J‘2). (3)
Момент инерции платформы рассчитываем как для диска; следовательно, J1=112m1R2 • Момент инерции человека рассчитываем как для материальной точки. Поэтому J2=0, J’2=m2R2. Угловая скорость платформы до перехода человека равна .
Заменив в формуле
(3) величины J1, J2, J‘2. и  их выражениями, получим
их выражениями, получим
Сделав подстановку
значений т1,
т2,
п, R и  , найдем линейную скорость человека:
, найдем линейную скорость человека:
Пример 7. Человек стоит в центре скамьи Жуковского и вместе с ней вращается по инерции. Частота вращения n1=0,5 c-1. Момент инерции joтела человека относи-
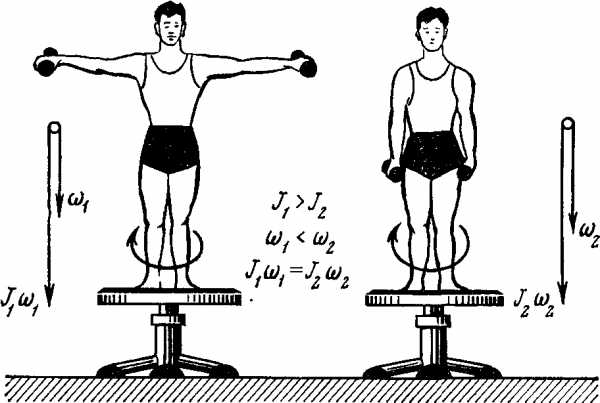
Рис. 3.5
тельно оси вращения равен 1,6 кг м2. В вытянутых в стороны руках человек держит по гире массой m=2 кг каждая. Расстояние между гирями l1=l,6 м. Определить частоту вращения n2, скамьи с человеком, когда он опустит руки и расстояние l2 между гирями станет равным 0,4 м. Моментом инерции скамьи пренебречь.
Решение. Человек, держащий гири (рис. 3.5), составляет
вместе со скамьей
замкнутую механическую систему
*, поэтому
момент импульса J этой системы должен иметь постоянное
значение. Следовательно, для данного
случая
этой системы должен иметь постоянное
значение. Следовательно, для данного
случая
J1 = J2
= J2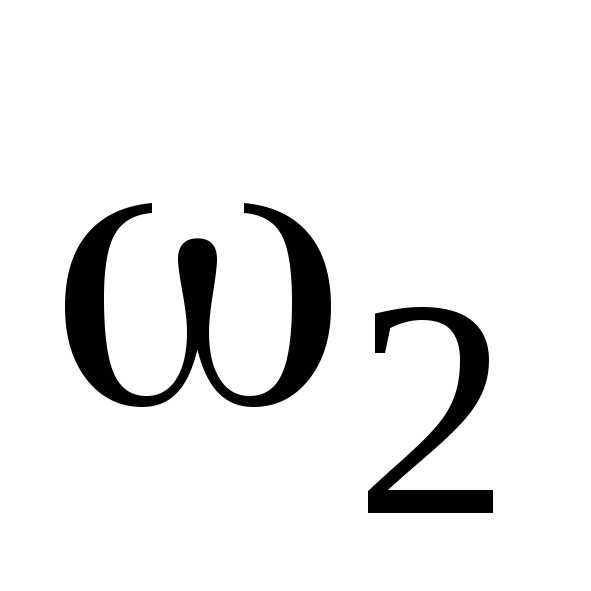 ,
,
где J и  — момент инерции тела человека и угловая
скорость скамьи и человека с вытянутыми
руками; J2 и
— момент инерции тела человека и угловая
скорость скамьи и человека с вытянутыми
руками; J2 и 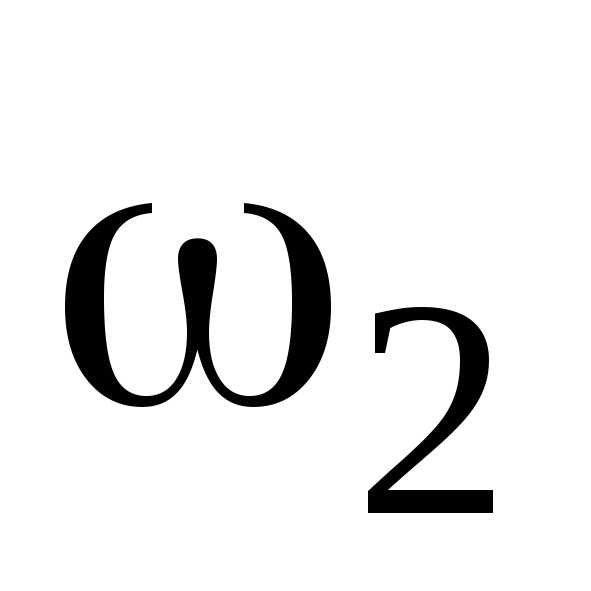 —
момент инерции тела человека и угловая
скорость скамьи и человека с опущенными
руками. Отсюда
—
момент инерции тела человека и угловая
скорость скамьи и человека с опущенными
руками. Отсюда
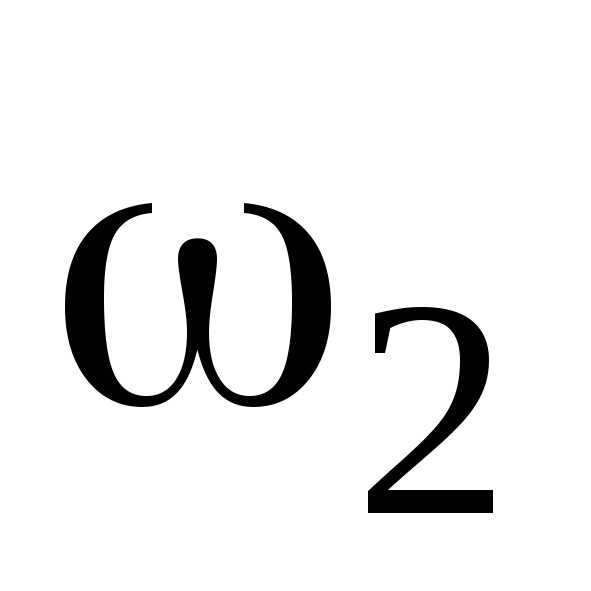 = (J1/J2)
= (J1/J2)  .
.
Выразив
в этом уравнении угловые скорости  и
и 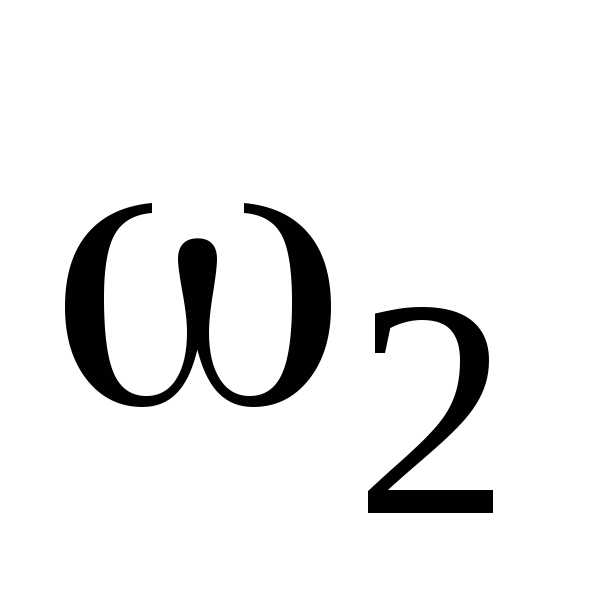 через частоты вращения n1 и n2(
через частоты вращения n1 и n2( =2
=2 n)
и сократив на 2
n)
и сократив на 2 ,
получим
,
получим
n2=(J1/J2)n1. (1)
Момент инерции системы, рассматриваемой в данной задаче, равен сумме момента инерции тела человека J0 и момента инерции гирь в руках человека. Так как размер гирь много меньше расстояния их от оси вращения, то момент инерции гирь можно определить по формуле момента инерции материальной точки: J=mr2. Следовательно **,
J1=J0+2m(l1/2)2;
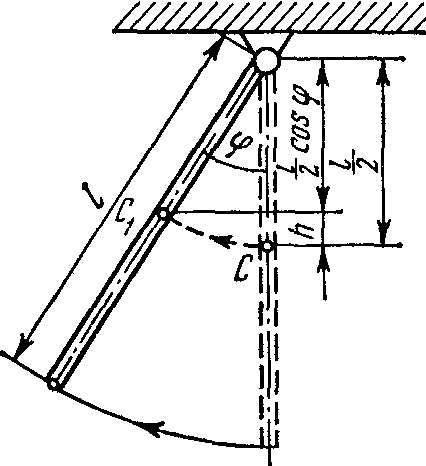
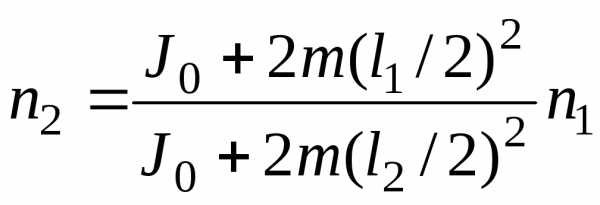 (2)
(2)
Выполнив вычисления по формуле (2), найдем
n2==1,18 с-1.
Пример 8. Стержень длиной l=1,5 м и массой М=10 кг может вращаться вокруг неподвижной оси, проходящей через верхний конец стержня (рис. 3.6). В середину стержня ударяет пуля массой m=10 г, летящая в горизонтальном направлении со скоростью vo=500 м/с, и
Рис.
3.6
застревает в стержне. На какой угол  отклонится стержень после удара?
отклонится стержень после удара?
Решение. Удар пули следует рассматривать как неупругий: после удара и нуля, и соответствующая точка стержня будут двигаться с одинаковыми скоростями.
Рассмотрим подробнее явления, происходящие при ударе. Сначала пуля, ударившись о стержень, за ничтожно малый промежу-
* Предполагается, что моменты всех внешних сил (сил тяжести и сил реакции), действующих на эту систему по отношению к оси вращения, являются уравновешенными. Трением пренебречь.
** В действительности с изменением положения рук человека (без гирь) изменяется момент инерции его тела относительно оси вращения, однако ввиду сложности учета этого изменения будем считать момент инерции Jо тела человека постоянным.
ток времени приводит его в движение с угловой скоростью и сообщает ему кинетическую энергию
(1) где — момент инерции стержня относительно оси вращения.
Затем стержень поворачивается на искомый угол , причем центр масс его поднимается на высоту. В от- клоненном положении стержень будет обладать потенциальной энергией
(2) Потенциальная энергия получена за счет кинетической энергии и равна ей по закону сохранения энергии. Приравняв правые части равенств (1) и (2), получим
Отсюда
Подставив в эту формулу выражение для момента инерции стержня , получим
(3)
Чтобы из выражения (3) найти , необходимо предварительно определить значение. В момент удара на пулю и на стержень действуют силы тяжести, линии действия которых проходят через ось вращения и направлены вертикально вниз. Моменты этих сил относительно оси вращения равны нулю. Поэтому при ударе пули о стержень будет справедлив закон сохранения момента импульса. В начальный момент удара угловая скорость стержня=0,поэтому его момент импульса. Пуля коснулась стержняи начала углубляться в стержень, сообщая ему угловое ускорение и участвуя во вращении стержня около оси. Начальный момент импульса пули, где— расстояние точки попадания от оси вращения. В конечный момент удара стержень имел угловую скорость, а пуля — линейную скорость, равную линейной скорости точек стержня, находящихся на расстояниит от оси вращения. Так как , то конечный момент импульса пули
studfiles.net
Примеры решения задач по теме «Динамика вращательного движения абсолютно твёрдого тела»
Примеры решения задач по теме «Динамика вращательного движения абсолютно твёрдого тела»
«Физика – 10 класс»
При решении задач на эту тему следует иметь в виду, что моменты силы, инерции и импульса зависят от выбора оси вращения. Кроме этого, нужно обращать внимание на то, что моменты импульса всех тел записываются относительно одной и той же системы отсчёта.
Задача 1.
На блок радиусом r и массой m1 намотана нить, к концу которой привязан груз массой m2 (рис. 6.12).
Груз отпускают, и он движется вниз, раскручивая нить. Определите ускорение груза. Массой нити можно пренебречь.
Р е ш е н и е.
Обозначим на рисунке силы, действующие на блок и груз.
На блок действуют сила тяжести m1, сила реакции опоры и сила натяжения нити.
На груз действуют сила тяжести m2 и сила натяжения ‘.
Согласно второму закону Ньютона в проекции на ось Y для груза запишем:
m2a = m2g – T’. (1)
Согласно основному закону динамики вращательного движения для блока запишем:
Iε = Tr. (2)
Момент инерции блока Связь углового и линейного ускорений а = εr.
Так как по условию задачи нить невесома, то Т = Т’.
Преобразуем уравнение (2): тогда
Подставив это выражение в уравнение (1), получим
Окончательно
Задача 2.
Скамья Жуковского радиусом 1 м со стоящим в центре человеком вращается, делая 2 об/с. Человек переходит на край скамьи. Определите изменение угловой скорости вращения скамьи. Масса человека 50 кг, момент инерции скамьи 30 кг • м2.
Р е ш е н и е.
Так как внешние силы — сила тяжести и сила реакции опоры, направленные параллельно оси вращения, не могут изменить момент импульса системы тел «скамья—человек», то согласно закону сохранения импульса
I1ω1 = I2ω2. (1)
Когда человек находится в центре скамьи, то момент инерции системы равен только моменту инерции скамьи: I1 = Iск.
После того как человек перешёл на край скамьи, момент инерции системы стал равен I2 = Iск + mr2.
Угловая скорость связана с числом оборотов в секунду соотношением ω1 = 2πn.
Подставив найденные выражения в уравнение (1), получим Iск2πn = (Iск + mr2)ω2. Тогда
Изменение угловой скорости
Задача 3.
На наклонную плоскость вкатывается колесо, двигавшееся по горизонтальной поверхности со скоростью 4 м/с. Вся масса колеса сосредоточена в ободе. Определите максимальную высоту, на которую поднимется колесо. Работой силы трения можно пренебречь.
Р е ш е н и е.
Выберем нулевой уровень отсчёта потенциальной энергии так, как показано на рисунке 6.13. Учтём, что момент инерции колеса-обруча I = mR2, а угловая скорость вращения ω = υ/R. Механическая энергия колеса на горизонтальной поверхности равна сумме кинетических энергий поступательного и вращательного движений колеса:
На максимальной высоте механическая энергия равна потенциальной энергии Е2 = mgh. Согласно закону сохранения механической энергии получим Е1 = Е2, или mυ2 = mgh, откуда h = υ2/g = 1,6 м.
Задача 4.
Сплошной цилиндр раскрутили до угловой скорости ω и положили на пол к стенке. Коэффициент трения между стенкой, полом и цилиндром μ, радиус цилиндра R. Определите, сколько оборотов сделает цилиндр до остановки.
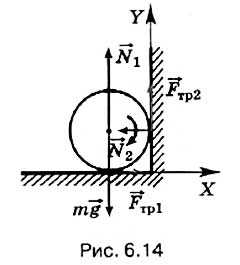
Р е ш е н и е.
Решаем задачу, используя теорему об изменении кинетической энергии. При этом учтём, что ось вращения цилиндра неподвижна, момент инерции цилиндра относительно этой оси равен соответственно кинетическая энергия цилиндра вначале равна
Изменение кинетической энергии равно алгебраической сумме работ сил, действующих на него:
На цилиндр (рис. 6.14) действуют силы тяжести m реакции опоры 1, 2 и силы трения тр1, тр2.
Так как перемещается относительно стенок угла только точка приложения сил трения, то работу совершают только силы трения. В связи с этим справедливо уравнение
Работы сил трения равны Aтp1 = -Fтp12πRn; Aтp2 = -Fтp12πRn, где n — число полных оборотов цилиндра до остановки, а силы трения определяются силами реакции опоры стенок на цилиндр: Fтp1 = μN1; Fтp2 = μN2.
Найдём силы реакции опоры.
По условию задачи цилиндр только вращается, его центр тяжести не движется, следовательно, векторная сумма сил, действующих на него, равна нулю:
m + 1 + 2 + тp1 + тp2 = 0.
В проекциях на оси ОХ и OY имеем
Fтp1 – N2 = 0; (2)
N1 + Fтp2 – mg = 0. (3)
Подставив в уравнения (2) и (3) выражения для сил трения, получим
μN1 – N2 = 0; (4)
N1 + μN2 – mg = 0. (5)
Решая систему уравнений (4) и (5), найдём силы реакции опоры:
Тогда число оборотов до остановки цилиндра
Источник: «Физика – 10 класс», 2014, учебник Мякишев, Буховцев, Сотский
Законы сохранения в механике – Физика, учебник для 10 класса – Класс!ная физика
Импульс материальной точки — Закон сохранения импульса — Реактивное движение. Успехи в освоении космоса — Примеры решения задач по теме «Закон сохранения импульса» — Механическая работа и мощность силы — Энергия. Кинетическая энергия — Примеры решения задач по теме «Кинетическая энергия и её изменение» — Работа силы тяжести. Консервативные силы — Работа силы упругости. Консервативные силы — Потенциальная энергия — Закон сохранения энергии в механике — Работа силы тяготения. Потенциальная энергия в поле тяготения — Примеры решения задач по теме «Закон сохранения механической энергии» — Основное уравнение динамики вращательного движения — Закон сохранения момента импульса. Кинетическая энергия абсолютно твёрдого тела, вращающегося относительно неподвижной оси — Примеры решения задач по теме «Динамика вращательного движения абсолютно твёрдого тела»
class-fizika.ru
23. Механика твердого тела. Момент импульса: задачи с ответами
(Все задачи по статике и гидростатике и ответы к ним находятся в zip-архиве (615 кб), который можно скачать и открыть на своем компьютере. Попробуйте решать задачи самостоятельно и только потом сравнивать свои ответы с нашими. Желаем успехов!)23.1. Легкая металлическая бочка, полностью заполненная водой, скатывается без проскальзывания с наклонной плоскости. Как изменится ускорение бочки, если вода замерзнет? [смотрите ответ в общем файле темы]
23.2. Тонкий обруч раскрутили до угловой скорости w и вертикально поставили на горизонтальную поверхность. Какая угловая скорость будет у обруча в установившемся движении? [смотрите ответ в общем файле темы]
23.3. Чему равна кинетическая энергия тонкого обруча массой m, катящегося по горизонтальной поверхности со скоростью v? [смотрите ответ в общем файле темы]
23.4. Тонкий обруч скатывается без проскальзывания с наклонной плоскости с углом наклона α. Найти ускорение центра обруча. Каким должен быть коэффициент трения, чтобы не было проскальзывания? [смотрите ответ в общем файле темы]
23.5. Тонкий обруч радиусом R раскрутили до угловой скорости w и плашмя положили на стол. Через время t обруч остановился. Определить коэффициент трения между обручем и столом. [ μ = wR/(gt) ]
23.6. Два маленьких шарика массами m1 и m2 находятся на расстоянии l друг от друга. Определить момент инерции системы относительно ее центра масс. [смотрите ответ в общем файле темы]
23.7. Определить момент инерции однородного стержня относительно оси, проходящей через середину стержня и составляющей угол α со стержнем. Длина стержня равна l, его масса – m. [смотрите ответ в общем файле темы]
23.8. Прямоугольник со сторонами a и b сделан из однородной проволоки. Масса единицы длины проволоки равна μ. Определить момент инерции прямоугольника относительно оси, совпадающей со стороной, длина которой равна а. [смотрите ответ в общем файле темы]
23.9. Система состоит из двух, скрепленных между собой, однородных, взаимно перпендикулярных стержней массами m1 и m2 и длиной l1 и l2. Найти момент инерции системы относительно оси, проходящей через точку O и перпендикулярной плоскости системы. [смотрите ответ в общем файле темы]
23.10. Система состоит из двух, скрепленных между собой, однородных, взаимно перпендикулярных стержней массами m1 и m2 и длиной l1 и l2. Найти момент инерции системы относительно оси, проходящей через точку O и перпендикулярной плоскости системы. [смотрите ответ в общем файле темы]
23.11. Из однородного диска радиусом R вырезано круглое отверстие радиусом r. Расстояние между центрами диска и отверстия равно а, а масса фигуры — m. Определить момент инерции фигуры относительно оси, проходящей через центр диска и перпендикулярной его плоскости. [указания к решению и ответ смотрите в общем файле темы]
23.12. Из однородной проволоки сделан правильный треугольник. Масса стороны треугольника равна m, его длина равна l. Определить момент инерции треугольника относительно оси: а) проходящей через центр треугольника и перпендикулярной его плоскости; б) совпадающей с одной из сторон треугольника; в) проходящей через вершину и параллельной противоположной стороне треугольника. [смотрите ответ в общем файле темы]
23.13. Однородный шар скатывается с наклонной плоскости с углом наклона а. Найти ускорение центра шара. Каким должен быть коэффициент трения, чтобы шар не скользил? [смотрите ответ в общем файле темы]
23.14. В вагоне, движущемся с постоянной скоростью v, к потолку шарнирно подвешен стержень длиной l. На какой максимальный угол от вертикали отклонится стержень, если вагон резко остановить? [смотрите ответ в общем файле темы]
23.15. Однородный тонкий стержень длиной l поставили вертикально на горизонтальную гладкую поверхность, слегка вывели из положения равновесия и отпустили. Какую скорость будет иметь верхний конец стержня в момент удара стержня о поверхность? [ v = √(3gl) ]
23.16. Тонкий стержень AB массой m = 1 кг движется поступательно с ускорением a = 1 м/с2 под действием двух сил F1 и F2. Расстояние между точками приложения сил АС = 20 см. Сила F2 = 5 Н. Найти длину стержня. [ 100 см ]
23.17. Неподвижный блок представляет собой однородный цилиндр массой m, подвешенный на нити к потолку. На цилиндр намотана нить, к которой подвешен груз такой же массы m. Найти силу натяжения верхней нити при свободном движении системы. Трения нет. [ T = 4mg/3 ]
23.18. На однородный диск массой m намотана нить. Свободный конец нити привязали к потолку и диск отпустили. Определить силу натяжения нити в процессе опускания диска. Считать, что нить все время вертикальна. [ T = mg/3 ]
23.19. Однородный стержень массой m подвешен горизонтально за концы на двух вертикальных нитях. Одна из нитей обрывается. Какова сила натяжения второй нити в момент обрыва? [ T = mg/4 ]
23.20. Неподвижный блок представляет собой однородный цилиндр массой m. Через блок перекинута невесомая нить, к концам которой привязаны грузы массами m1 и m2. Определить ускорение грузов и силу натяжения нити слева и справа от блока при свободном движении системы. Проскальзывания нити и трения в блоке нет. [смотрите ответ в общем файле темы]
23.21. На однородный цилиндр массой m и радиусом R, лежащий на горизонтальной поверхности, намотана тонкая нить. За нить тянут горизонтальной силой F. При каком значении коэффициента трения цилиндр не будет проскальзывать по поверхности? [смотрите ответ в общем файле темы]
23.22. Однородный цилиндр лежит на горизонтальной поверхности. Второй такой же цилиндр катится на первый со скоростью v. Оси цилиндров параллельны. Между цилиндрами происходит абсолютно упругий удар. Определить конечные установившиеся скорости движения цилиндров. [указания к решению и ответ смотрите в общем файле темы]
23.23. Тонкостенную трубу радиусом R раскрутили вокруг оси до угловой скорости w и положили в угол между полом и стеной параллельно ребру угла. Коэффициент трения между трубой и стеной равен μ, а между трубой и полом — 2μ. Сколько оборотов сделает труба до остановки? [смотрите ответ в общем файле темы]
23.24. Горизонтально расположенный деревянный стержень массой М и длиной l может вращаться вокруг вертикальной оси, проходящей через его середину. В конец стержня попадает и застревает в нем пуля массой m, летящая со скоростью v перпендикулярно стержню и оси его вращения. С какой угловой скоростью начнет вращаться стержень? [смотрите ответ в общем файле темы]
23.25. По гладкой горизонтальной поверхности по окружности движется небольшое тело, привязанное к нити. Нить продета в маленькое отверстие в поверхности. Нить начинают медленно втягивать в отверстие, уменьшая радиус окружности движения тела. Как зависит сила натяжения нити от радиуса окружности? Масса тела равна m. Считать, что при радиусе равном Ro угловая скорость движения тела была равна wo. [смотрите ответ в общем файле темы]
23.26. На массивный неподвижный блок в виде цилиндра радиусом R намотана нить, к свободному концу которой подвешен груз массой m. В момент t = 0 систему отпускают. Написать зависимость момента импульса системы относительно оси блока от времени. Трения нет. [смотрите ответ в общем файле темы]
23.27. Стержень, расположенный горизонтально, падает без начальной скорости с высоты h и ударяется одним концом о край стола. Определить скорость центра масс стержня сразу после удара. Удар абсолютно упругий. [указания к решению и ответ смотрите в общем файле темы]
23.28. Шарик массой m влетает в спиральный лабиринт, который может свободно двигаться в пространстве, и останавливается в его центре. Начальная скорость шарика равна v, радиус лабиринта R, масса лабиринта М, его момент инерции J. Определить угловую скорость вращения лабиринта после того как шарик остановится. Размерами шарика и внешними силами пренебречь. [указания к решению и ответ смотрите в общем файле темы]
23.29. Два диска, имеющие моменты инерции J1 и J2, вращаются на одной оси с угловыми скоростями w1 и w2. Диски прижимают друг к другу. Определить установившуюся угловую скорость вращения и количество теплоты, выделившееся при трении дисков. [смотрите ответ в общем файле темы]
23.30. Тонкий стержень длиной l и массой M стоит вертикально на гладкой горизонтальной поверхности. В его верхний конец попадает горизонтально летящая пуля массой m (m << М) и застревает в нем. При какой минимальной скорости пули стержень сразу оторвется от поверхности? [указания к решению и ответ смотрите в общем файле темы]
Далее: 30 задач по механическим колебаниям. | Вернуться к списку разделов СТАТИКИ и ГИДРОСТАТИКИ.
www.afportal.ru
Закон сохранения момента импульса задачи с решением — Ваше право
Задачи по теме: «Момент инерции. Закон сохранения момента инерции и момента импульса».
На барабан радиусом R=0,5 м и с горизонтальной осью вращения намотан шнур, к концу которого привязан груз массой m = 10 кг. Найдите момент инерции барабана, если известно, что его угловое ускорение равно . Тернием пренебречь.
M = J? – момент силы через момент инерции для вращающегося тела.
К ободу однородного диска радиусом R=0,2м массой m=1,2 кг приложена постоянная сила 100 Н, при вращении на диск действует момент силы трения, равный 5 нм. Чему равно угловое ускорение диска?
R = 0, 2 м Из оснавного управления динамики вращательного
F = 100 Н Сила действующая на обод F`= F — Fтр. Из M = 5 нм момента силы трения Fтр = M\R = 25 Н
Шарик, диаметр которого равен 6 см, катится по полу и останавливается через t = 2с, пройдя расстояние S = 70 см. Определите коэффициент трения качения, считая его постоянным.
d = 0, 06 м М=?J — основное уравнение вращательного движения.
Во сколько раз уменьшится угловая скорость вращения человека, если момент инерции изменится от 1 кг м? до 1,25 кг м??
Найти момент импульса Земного шара М3 = 6·10 24 кг, R3 = 6,4·10? км, если точки поверхности Земли вращаются со скоростью 36 км/ ч.
Комета Галлея движется вокруг солнца по вытянутому эллипсу. Наибольшее удаление от солнца равно 35,2 а. е., а наименьшее удаление — 0,6 а.е.. Найти отношение максимальной скорости кометы к минимальной.
Человек стоит на вращающейся с некоторой угловой скоростью платформе. В вытянутых в сторону руках он держит по гире, массой каждой из них m = 5 кг. Расстояние от гирь до оси вращения R1=0,71м. Во сколько раз изменится частота вращения человека, если он прижмет к себе руки так, что расстояние от оси вращения до гири станет R2= 0,2 м. Момент инерции человека считайте в обоих случаях равным J0 = 1 кг м.?
Человек массой m1 = 60 кг находится на неподвижной круглой платформе радиусом R2= 10м и массой m2 = 120 кг, которая может вращаться вокруг своей вертикальной оси. С какой угловой скоростью будет вращаться платформа, если человек станет двигаться по окружности радиусом R1= 5м с линейной скоростью ?1= 2 м/с относительно платформы.
Считая Солнце однородным шаром, оцените минимальный радиус и период вращения вокруг своей оси пульсара, который мог бы образоваться после сжатия Солнца под действием силы тяготения при исчерпании внутренних источников энергии, поддерживающих высокую температуру газа. Радиус Солнца Rc = 7·10 8 м, период вращения вокруг оси Тс = 2,2·10 6 с. Масса Солнца Мс = 2·10?? кг.
Вращение пульсара происходит под действием силы тяготения.
gigabaza.ru
Моментом импульса относительно неподвижной оси z называется скалярная величина Lz, равная проекции на эту ось вектора момента импульса, определенного относительно произвольной точки 0 данной оси. Значение момента импульса Lz не зависит от положения точки 0 на оси z.
При вращении абсолютно твердого тела вокруг неподвижной оси каждая отдельная точка тела движется по окружности постоянного радиуса с некоторой скоростью . Скорость и импульс перпендикулярны этому радиусу, т.е. радиус является плечом вектора . Поэтому можно записать, что момент импульса отдельной точки относительно оси z равен
Момент импульса твердого тела относительно оси есть сумма моментов импульса отдельных его точек:
Учитывая связь между линейной и угловой скоростями ( ), получим следующее выражение для момента импульса тела относительно неподвижной оси:
т.е. момент импульса твердого тела относительно оси равен произведению момента инерции тела относительно той же оси на угловую скорость.
Продифференцировав выражение (4.12) по времени, получим:
Это еще одна форма уравнения динамики вращательного движения твердого тела относительно неподвижной оси: скорость изменения момента импульса тела относительно неподвижной оси вращения равна результирующему моменту относительно этой оси всех внешних сил, действующих на тело.
Закон сохранения момента импульса вытекает из основного уравнения динамики вращательного движения тела, закрепленного в неподвижной точке (уравнение 4.8), и состоит в следующем:
pred64.ru

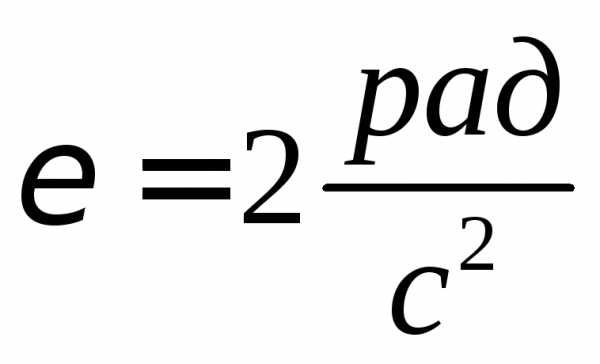 .
Тернием пренебречь.
.
Тернием пренебречь.