Найти производные функции онлайн с подробным решением: Производная онлайн с подробным решением

26.12.201802.06.2021

Содержание

Калькулятор онлайн – Найти (с решением) производную функции

Этот математический калькулятор онлайн поможет вам если нужно найти производную функции. Программа решения производной не просто даёт ответ задачи, она приводит подробное решение с пояснениями, т.е. отображает процесс решения производной функции.

Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.

Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.

Вы можете посмотреть теорию о производной функции и правила дифференцирования и таблицу производных, т.е. список формул для нахождения производных от некоторых элементарных функций.

Если вам нужно найти уравнение касательной к графику функции, то для этого у нас есть задача Уравнение касательной к графику функции.

Примеры подробного решения >>

Обнаружено что не загрузились некоторые скрипты, необходимые для решения этой задачи, и программа может не работать.
Возможно у вас включен AdBlock.
В этом случае отключите его и обновите страницу.

Определение производной

Если существует предел этого отношения при $ \Delta x \rightarrow 0 $, то указанный предел называют производной функции $ y=f(x) $ в точке $ x_0 $ и обозначают $ f'(x_0) $.

$$ \lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x} = f'(x_0) $$

Для обозначения производной часто используют символ $ y’ $. Отметим, что $ y’ = f(x) $ – это новая функция, но, естественно, связанная с функцией $ y = f(x) $, определенная во всех точках $x$, в которых существует указанный выше предел. Эту функцию называют так: производная функции $ y = f(x) $.

Геометрический смысл производной

состоит в следующем. Если к графику функции $ y = f(x) $ в точке с абсциссой $ x=a $ можно провести касательную, непараллельную оси $y$, то $ f(a) $ выражает угловой коэффициент касательной:
$ k = f'(a) $

Поскольку $ k = tg(a) $, то верно равенство $ f'(a) = tg(a) $ .

А теперь истолкуем определение производной с точки зрения приближенных равенств. 2 \) справедливо приближенное равенство $ \Delta y \approx 2x \cdot \Delta x $. Если внимательно проанализировать определение производной, то мы обнаружим, что в нем заложен алгоритм ее нахождения.

Сформулируем его.

Как найти производную функции у = f(x) ?

4. Составить отношение $ \frac{\Delta y}{\Delta x} $
5. Вычислить $$ \lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x} $$
Этот предел и есть производная функции в точке $x$.

Если функция $y=f(x)$ имеет производную в точке $x$, то ее называют дифференцируемой в точке $x$. Процедуру нахождения производной функции $y=f(x)$ называют дифференцированием функции $y=f(x)$.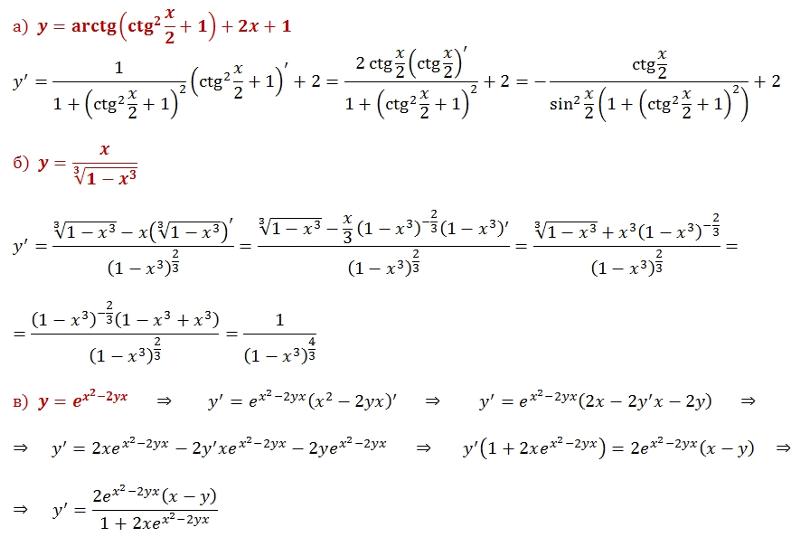

Обсудим такой вопрос: как связаны между собой непрерывность и дифференцируемость функции в точке.

Пусть функция $y=f(x)$ дифференцируема в точке $x$. Тогда к графику функции в точке $ M(x; \; f(x)) $ можно провести касательную, причем, напомним, угловой коэффициент касательной равен $ f'(x) $. Такой график не может «разрываться» в точке $M$, т. е. функция обязана быть непрерывной в точке $x$.

Это были рассуждения «на пальцах». Приведем более строгое рассуждение. Если функция $y=f(x)$ дифференцируема в точке $x$, то выполняется приближенное равенство $ \Delta y \approx f'(x) \cdot \Delta x $. Если в этом равенстве $ \Delta x $ устремить к нулю, то и $ \Delta y $ будет стремиться к нулю, а это и есть условие непрерывности функции в точке.

Итак, если функция дифференцируема в точке х, то она и непрерывна в этой точке.

Обратное утверждение неверно. Например: функция $ y=|x|$ непрерывна везде, в частности в точке $x=0$, но касательная к графику функции в «точке стыка» (0; 0) не существует. Если в некоторой точке к графику функции нельзя провести касательную, то в этой точке не существует производная.

Еще один пример. Функция $ y=\sqrt[3]{x} $ непрерывна на всей числовой прямой, в том числе в точке $x=0$. И касательная к графику функции существует в любой точке, в том числе в точке $x=0$. Но в этой точке касательная совпадает с осью $y$, т. е. перпендикулярна оси абсцисс, ее уравнение имеет вид $x=0$. Углового коэффициента у такой прямой нет, значит, не существует и $ f'(0) $

Итак, мы познакомились с новым свойством функции — дифференцируемостью. А как по графику функции можно сделать вывод о ее дифференцируемости?

Ответ фактически получен выше. Если в некоторой точке к графику функции можно провести касательную, не перпендикулярную оси абсцисс, то в этой точке функция дифференцируема. Если в некоторой точке касательная к графику функции не существует или она перпендикулярна оси абсцисс, то в этой точке функция не дифференцируема. 2} $$

вторая производная онлайн

Вы искали вторая производная онлайн? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и вычисление производной онлайн с подробным решением, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели – у нас уже есть решение. Например, «вторая производная онлайн».

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который может решить задачи, такие, как вторая производная онлайн,вычисление производной онлайн с подробным решением,вычислить производную онлайн с подробным решением,вычислить производную функции онлайн с решением,двойная производная онлайн,дифференцирование онлайн с подробным решением,как найти производную функции y x 2 7x,как обозначается производная в калькуляторе,калькулятор онлайн для функций,калькулятор функций онлайн с решением,найти вторую производную функции онлайн,найти производную второго порядка онлайн,найти производную функции онлайн с подробным решением,найти производные функций онлайн с подробным решением бесплатно,онлайн решение производных с подробным решением бесплатно,производная второго порядка онлайн,производная второго порядка онлайн калькулятор,производная первого порядка онлайн,производные высших порядков онлайн калькулятор.

На этой странице вы найдёте калькулятор, который поможет решить любой вопрос, в том числе и вторая производная онлайн. Просто введите задачу в окошко и нажмите «решить» здесь (например, вычислить производную онлайн с подробным решением).

Где можно решить любую задачу по математике, а так же вторая производная онлайн Онлайн?

Решить задачу вторая производная онлайн вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать – это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.

Найти производные онлайн решебник :: tfgjcj

28.

10.2014 22:04 Файл:
Найти производные онлайн решебник

бланк материального отчета 10 с

простые истины сериал letitbit

решебник по геометрии тематические тесты 7 класс мищенко Использование тематических тестов по геометрии в учебном процессе Производная онлайн для решения математики. Найти Производные Онлайн Решебник. Через несколько секунд внизу отобразится пошаговое решение производной с подробными комментариями. Сайт www.MatCabi.net позволяет найти производную почти от любой математической функции онлайн. Производная функции, заданной параметрически. При помощи нашего калькулятора вы можете найти производную онлайн как C нами вы сможете найти производную от любой функции, сами выбирая порядок дифференцирования. Найти производную онлайн: производную функции от одной переменной, от двух и трех переменных, а также найти вторую и третью производную, и еще производную сложной функции.Данный онлайн калькулятор позволит вам найти производную от функции.

Решение производных онлайн. Достаточно ввести необходимую функцию, и вы тут же получите онлайн решение производной. Быстро решить задачу по нахождению производной в режиме онлайн. Введите переменную дифференцирования и порядок производной по этой переменной Это вы можете сделать с помощью данного онлайн-калькулятора, который позволяет находить производные от любых функций онлайн с подробным решением бесплатно, без регистрации на сайте. Решение (вычисление) производной функции онлайн. Нахождение производной функции (дифференцирование) На этой странице вы сможете вычислять производную функции онлайн с получением подробного решения задачи. Выберите порядок дифференцирования (от 1 до 10). Наш сервис позволяет вычислить подробное онлайн решение производной на русском языке. Выберите порядок дифференцирования (от 1 до 9). Нажмите кнопку “Равно”. Решение системы уравнений. Если вам нужно найти производную высших порядков, выберите соответствующий порядок дифференцирования. Нажмите кнопку – Вычислить производную.

Решение квадратного уравнения онлайн.
инструкция по уличному террору, доктор веб без регестрации и смс, удостоверение крановщика образец y

Калькулятор онлайн. Найти (с решением) производную функции. График функции

Приведены график и основные свойства экспоненты (е в степени х): область определения, множество значений, основные формулы, производная, интеграл, разложение в степенной ряд, действия с комплексными числами.

Определение

Частные значения

Пусть y(x) = e x . Тогда
.

Экспонента обладает свойствами показательной функции с основанием степени е > 1 .

Область определения, множество значений

Экспонента y(x) = e x определена для всех x .
Ее область определения:
– ∞ Ее множество значений:
0 .

Экстремумы, возрастание, убывание

Экспонента является монотонно возрастающей функцией, поэтому экстремумов не имеет. Основные ее свойства представлены в таблице.

Обратная функция

Обратной для экспоненты является натуральный логарифм .
;
.

Производная экспоненты

Производная е в степени х равна е в степени х :
.
Производная n-го порядка:
.
Вывод формул > > >

Интеграл

Комплексные числа

Действия с комплексными числами осуществляются при помощи формулы Эйлера :
,
где есть мнимая единица:
.

Выражения через гиперболические функции

; ;
.

Выражения через тригонометрические функции

; ;
;
.

Разложение в степенной ряд

Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.

Свойства функций играют важную роль при их изучении. Они позволяют делать определенные выводы о функциях. Изучение данной темы крайне важно для обучающихся, особенно старших классов. Это связано с тем,что задания по данной теме довольно часто встречаются в КИМ государственной итоговой аттестации.

Видеоурок по теме «Свойства функции» разработан автором для облегчения работы учителя и его подготовки к урокам. Если использовать данный материал на уроках, то появится больше свободного времени, которое можно посвятить индивидуальному обучению или другим направлениям обучения математики в школе.

Длительность урока составляет 8:23 минут. Примерно столько же времени требуется учителю, чтобы объяснить материал на уроке, который длится 40-45 минут. При этому учитель успеет актуализировать знания обучающихся, повторить необходимый материал, просмотреть видеоурок, а затем еще и закрепить материал.

Рассмотрение материала начинается непосредственно с первого свойства, которое называется монотонность. Это понятие подробно расписывается на математическом языке, что способствует развитию математической грамотности обучающихся, а также словесно поясняется каждая запись на экране. Далее автор демонстрирует на рисунке, как выглядит монотонная функция для случаев возрастания и убывания. После этого дается определение монотонной функции. Здесь же дается правило для запоминания, которое связано с монотонностью функции. Далее предлагается рассмотреть эту теорию на примере. На рисунке изображен график, на экране последовательно выделяются промежутки возрастания и убывания. Показана и математическая запись этих промежутков.

Согласно условию другого примера, необходимо исследовать функцию на монотонность. Чтобы определить монотонность функции, автор воспользовался определением возрастающей и убывающей функции. В результате получается, что функция убывает на всей области определения.

Затем на экране демонстрируются примеры возрастающих функций на всей области определения.

Далее внимание обучающихся обращается ко второму свойству, которое называется ограниченностью. Рассмотрение этого свойства строится по аналогии с первым свойством. Рассматривается понятие ограниченности, все это иллюстрируется на рисунке, как ограниченность снизу, так и ограниченность сверху. Затем на экране появляется пример ограниченной функции.

Важными понятиями в пункте ограниченность являются наибольшее и наименьшее значение функции. В качестве иллюстрации показан рисунок и идет подробное описание этих понятий.

После примера рассматривается третье свойство, которое называется выпуклостью. Это понятие иллюстрируется с помощью рисунка. На данном свойстве автор не останавливается так же подробно, как на предыдущих. Он сразу переходит к четвертому свойству – непрерывности. Здесь вводится понятие непрерывной функции. После этого демонстрируется это свойство на рисунке с подробными пояснениями.

Далее рассматривается свойство четности и нечетности. И тут же объясняется, когда функция четная и нечетная. Объяснения сопровождаются иллюстрациями и подробными описаниями. Это показано на примерах двух функций.

И, наконец, рассматривается шестое свойство – периодичность. На нем автор не останавливается, отмечая, что примеры периодичных функций будут изучены в дальнейшем на уроках алгебры.

ТЕКСТОВАЯ РАСШИФРОВКА:

Первое свойство, которое мы рассмотрим -монотонность.

Внимание: во всех определениях рассматривается числовое множество икс большое – подмножество области определения функции.

Функция игрек равно эф от икс возрастает на множестве икс большое, которое является подмножеством области определения и если для любых икс первое из множества икс большое и икс второе из множества икс большое таких,что икс второе больше икс первого выполняется неравенство эф от икс второе больше эф от икс первое. Другими словами – большему значению аргумента соответствует большее значение функции.

Функция игрек равно эф от икс убывает на промежутке икс большое которое является подмножеством областиопределения и если для любых икс первое из множества икс большое и икс второе из множества икс большое таких,что икс второе больше икс первого выполняется неравенство эф от икс второе меньше эф от икс первое. Другими словами – большему значению аргумента соответствует меньшее значение функции.

Функция игрек равно эф от икс называется монотонной на множестве икс большое, если она на этом промежутке или убывает или возрастает.

Запомни: если функция определена и непрерывна в концах интервала возрастания или убывания, то эти точки включаются в промежуток возрастания или убывания.

Например, функция, график которой изображен на рисунке, на промежутках

от минус бесконечности до минус пяти и от трех до плюс бесконечностивозрастает, а на промежутке от минус пяти до трех убывает. Пример. Исследовать функцию на монотонность: игрек равен шесть минус два икс.

Введем обозначение: эф от икс равен шесть минус два икс.

Если икс первое меньше икс второе, то используя свойства числовых неравенств, имеем

Значит, заданная функция убывает на всей числовой прямой.

Существуют функции, являющиеся возрастающими на всей области определения, например, игрек равен ка икс плюс вэ при ка больше нуля, игрек равен икс в кубе.

Второе свойство – ограниченность.

Если все значения функции игрек равно эф от икс на множестве икс большое больше некоторого числа эм малое, то функцию игрек равно эф от икс называют ограниченной снизу на множестве икс большое из области определения.

Если все значения функции игрек равно эф от икс на множестве икс большое меньше некоторого числа эм большое, то функцию игрек равно эф от икс называют ограниченной сверху на множестве икс большое из области определения.

Запомни: если функция ограничена и сверху и снизу на всей области определения, то ее называют ограниченной.

По графику функции легко можно определить ее ограниченность.

Наибольшее значение функции обозначают игрек с индексом наибольшее. .

Игрик является наибольшим если:

Во -первых, существует точка икс нулевое из множества икс большое такая, что эф от икс нулевое равно эм большое;

Во – вторых,для любого значения икс из множества икс большое выполняется неравенство эф от икс меньше или равно эф от икс нулевое, то число эм большое называют наибольшим значением функции игрек равно эф от икс на множестве икс большое из области определения функции.

Наименьшее значение функции обозначают игрек с индексом наименьшее

Во -первых, существует точка икс нулевое из множества икс большое такая, что эф от икс нулевое равно эм;

Во – вторых,для любого значения икс из множества икс большое выполняется неравенство эф от икс больше или равно эф от икс нулевое,то число эм называют наименьшим значением функции игрек равно эф от икс на множестве икс большое из области определения функции

Полезно запомнить:

Если у функции существует наименьшее значение., то она ограничена снизу.

Если у функции существует наибольшее значение, то она ограничена сверху.

Рассмотрим пример. Найти наименьшее значение функции

Функция, график которой изображен на рисунке, ограничена снизу, наименьшее значение функции равно нулю, а наибольшего не существует, функция сверху неограниченна.

Третье свойство: выпуклость вверх, выпуклость вниз.

Если,соединить любые две точки графика функции с абсциссами из икс большое отрезком и соответствующая часть графика будет лежать ниже проведенного отрезка, то такая функция выпукла вниз на промежутке икс большое из области определения.

Если,соединить любые две точки графика функции с абсциссами из икс большое отрезком и соответствующая часть графика будет лежать выше проведенного отрезка, то такая функция выпукла вверх на промежутке икс большое из области определения.

четвертое свойство: непрерывность.

Функция называется непрерывной на промежутке, если она определена на этом промежутке и непрерывна в каждой точке этого промежутка.

Непрерывность функции на промежутке Х означает, что график функции на всей области определения сплошной, т.е. не имеет проколов и скачков.

пятое свойство: четность, нечетность.

Если область определения функции -симметричное множество и для любого х из области определения функции выполняется равенство f(-х)= f(х), то такая функция четная.

График четной функции симметричен относительно оси ординат.

Если область определения функции -симметричное множество и для любого х из области определения функции выполняется равенство f(-х)= -f(х), то такая функция нечетная.

График нечетной функции симметричен относительно начала координат.

Так же существуют функции, которые не являются ни четными, ни нечетными

шестое свойство: периодичность

примеры периодических функций будем рассматривать в дальнейшем

Если существует такое отличное от нуля число тэ большое, что для любого икс из области определения функции верно равенство эф от икс плюс тэ большое равно эф от икс и равно эф от икс минус тэ большое, то функция игрек равно эф от икс -периодическая. Число тэ большое – период функции игрек равно эф от икс

все тригонометрические функции периодические.

Операция отыскания производной называется дифференцированием.

В результате решения задач об отыскании производных у самых простых (и не очень простых) функций по определению производной как предела отношения приращения к приращению аргумента появились таблица производных и точно определённые правила дифференцирования. Первыми на ниве нахождения производных потрудились Исаак Ньютон (1643-1727) и Готфрид Вильгельм Лейбниц (1646-1716).

Поэтому в наше время, чтобы найти производную любой функции, не надо вычислять упомянутый выше предел отношения приращения функции к приращению аргумента, а нужно лишь воспользоваться таблицей производных и правилами дифференцирования. Для нахождения производной подходит следующий алгоритм.

Чтобы найти производную , надо выражение под знаком штриха разобрать на составляющие простые функции и определить, какими действиями (произведение, сумма, частное) связаны эти функции. Далее производные элементарных функций находим в таблице производных, а формулы производных произведения, суммы и частного – в правилах дифференцирования. Таблица производных и правила дифференцирования даны после первых двух примеров.

Пример 1. Найти производную функции

Решение. Из правил дифференцирования выясняем, что производная суммы функций есть сумма производных функций, т. е.

Из таблицы производных выясняем, что производная “икса” равна единице, а производная синуса – косинусу. Подставляем эти значения в сумму производных и находим требуемую условием задачи производную:

Пример 2. Найти производную функции

Решение. Дифференцируем как производную суммы, в которой второе слагаемое с постоянным множителем, его можно вынести за знак производной:

Если пока возникают вопросы, откуда что берётся, они, как правило, проясняются после ознакомления с таблицей производных и простейшими правилами дифференцирования. К ним мы и переходим прямо сейчас.

Таблица производных простых функций

Правила дифференцирования

1. Производная суммы или разности
2. Производная произведения
2a. Производная выражения, умноженного на постоянный множитель
3. Производная частного
4. Производная сложной функции

Правило 1. Если функции

дифференцируемы в некоторой точке , то в той же точке дифференцируемы и функции

причём

т. е. производная алгебраической суммы функций равна алгебраической сумме производных этих функций.

Следствие. Если две дифференцируемые функции отличаются на постоянное слагаемое, то их производные равны , т.е.

Правило 2. Если функции

дифференцируемы в некоторой точке , то в то же точке дифференцируемо и их произведение

причём

т.е. производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой.

Следствие 1. Постоянный множитель можно выносить за знак производной :

Следствие 2. Производная произведения нескольких дифференцируемых функций равна сумме произведений производной каждого из сомножителей на все остальные.

Например, для трёх множителей:

Правило 3. Если функции

дифференцируемы в некоторой точке и , то в этой точке дифференцируемо и их частное u/v , причём

т. е. производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя.

Где что искать на других страницах

При нахождении производной произведения и частного в реальных задачах всегда требуется применять сразу несколько правил дифференцирования, поэтому больше примеров на эти производные – в статье “Производная произведения и частного функций ” .

Замечание. Следует не путать константу (то есть, число) как слагаемое в сумме и как постоянный множитель! В случае слагаемого её производная равна нулю, а в случае постоянного множителя она выносится за знак производных. Это типичная ошибка, которая встречается на начальном этапе изучения производных, но по мере решения уже нескольких одно- двухсоставных примеров средний студент этой ошибки уже не делает.

А если при дифференцировании произведения или частного у вас появилось слагаемое u “v , в котором u – число, например, 2 или 5, то есть константа, то производная этого числа будет равна нулю и, следовательно, всё слагаемое будет равно нулю (такой случай разобран в примере 10).

Другая частая ошибка – механическое решение производной сложной функции как производной простой функции. Поэтому производной сложной функции посвящена отдельная статья. Но сначала будем учиться находить производные простых функций.

По ходу не обойтись без преобразований выражений. Для этого может потребоваться открыть в новых окнах пособия Действия со степенями и корнями и Действия с дробями .

Если Вы ищете решения производных дробей со степенями и корнями, то есть, когда функция имеет вид вроде , то следуйте на занятие “Производная суммы дробей со степенями и корнями “.

Если же перед Вами задача вроде , то Вам на занятие “Производные простых тригонометрических функций”.

Пошаговые примеры – как найти производную

Пример 3. Найти производную функции

Решение. Определяем части выражения функции: всё выражение представляет произведение, а его сомножители – суммы, во второй из которых одно из слагаемых содержит постоянный множитель. Применяем правило дифференцирования произведения: производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой:

Далее применяем правило дифференцирования суммы: производная алгебраической суммы функций равна алгебраической сумме производных этих функций. В нашем случае в каждой сумме второе слагаемое со знаком минус. В каждой сумме видим и независимую переменную, производная которой равна единице, и константу (число), производная которой равна нулю. Итак, “икс” у нас превращается в единицу, а минус 5 – в ноль. Во втором выражении “икс” умножен на 2, так что двойку умножаем на ту же единицу как производную “икса”. Получаем следующие значения производных:

Подставляем найденные производные в сумму произведений и получаем требуемую условием задачи производную всей функции:

Пример 4. Найти производную функции

Решение. От нас требуется найти производную частного. Применяем формулу дифференцирования частного: производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя. Получаем:

Производную сомножителей в числителе мы уже нашли в примере 2. Не забудем также, что произведение, являющееся вторым сомножителем в числителе в текущем примере берётся со знаком минус:

Если Вы ищете решения таких задач, в которых надо найти производную функции, где сплошное нагромождение корней и степеней, как, например, , то добро пожаловать на занятие “Производная суммы дробей со степенями и корнями” .

Если же Вам нужно узнать больше о производных синусов, косинусов, тангенсов и других тригонометрических функций, то есть, когда функция имеет вид вроде , то Вам на урок “Производные простых тригонометрических функций” .

Пример 5. Найти производную функции

Решение. В данной функции видим произведение, один из сомножителей которых – квадратный корень из независимой переменной, с производной которого мы ознакомились в таблице производных. По правилу дифференцирования произведения и табличному значению производной квадратного корня получаем:

Пример 6. Найти производную функции

Решение. В данной функции видим частное, делимое которого – квадратный корень из независимой переменной. По правилу дифференцирования частного, которое мы повторили и применили в примере 4, и табличному значению производной квадратного корня получаем:

Чтобы избавиться от дроби в числителе, умножаем числитель и знаменатель на .

Урок по теме «Область определения и область значений функции» проводится в 10 классе в курсе алгебры и начал анализа. На объяснение материала по данной теме автор отводит 8:47 минут. этого времени достаточно для того, чтобы обучающиеся прослушали необходимую информацию, зафиксировали ее в своих тетрадях и поняли содержание материала. Примерно столько же времени затрачивает учитель на уроке при объяснении нового материала.

Автор позаботился об учителях, нагрузка которых итак достаточно велика, поэтому разработал данный видеоурок с учетом всех требований. То есть, урок соответствует возрасту обучающихся, их уровню образования и особенностей восприятия материала. Учителю останется лишь подобрать материал для закрепления новой информации, полученной из данного урока.

Урок начинается с информации о том, что функция задается вместе с областью определения. Далее автор определяет переменные xи y? как аргумент и значение функции соответственно. После этого вводятся определения понятий область определения функции и область значений функции.

Затем рассматривается пример, где функция задана графически, и необходимо определить ее область определения. Решение данного примера подробно расписывается на экране. Автор поясняет каждый момент, где обучающиеся могут допустить ошибки. Все объяснение сопровождается наглядной иллюстрацией на рисунке.

Далее автор переходит к пункту «Область определения рациональной функции». Для обучающихся говорится о том, что в область определения рациональных функций не входят те значения аргумента, которые обращают знаменатель в нуль. Это поясняется на случае общего написания рациональной функции.

Затем на этот случай рассматривается пример. Здесь необходимо найти область определения рациональной функции. Решение пример основано на той информации, которую только что автор поведал обучающимся. То есть, он находит все те значения, которые обращают знаменатель в нуль и исключает их из множества действительных чисел, получая, таким образом, область определения функции.

после этого предлагается рассмотреть еще один пример, где требуется найти область определения рациональной функции. Но здесь наблюдается следующая особенность: знаменатель дроби никогда не обращается в нуль. Поясняя это, автор делает вывод, что областью определения данной функции является множество действительных чисел. После этого примера предлагается запомнить закономерность, которая только что была использована в примере.

Далее автор переходит к пункту «Область определения иррациональной функции». Здесь важно запомнить то, что подкоренное выражение никогда не может быть отрицательным. Это подкрепляется математической интерпретацией на математической языке. Здесь же поясняется, что если иррациональное выражение в записи функции находится в знаменателе, то подкоренное выражение будет не просто неотрицательным, а строго положительным.

К этому материалу прилагается пример, где требуется найти область определения иррациональной функции. Решая неравенство: подкоренное выражение неотрицательно, автор получает значения аргумент, которые образуют область определения заданной функции.

Затем рассматривается область определения функции с натуральным логарифмом. Сначала дается теоретический экскурс по данному материалу, а затем приводится пример с подробным описанием каждого шага решения.

После всего теоретического материала автор предлагает рассмотреть три примера, где требуется найти область определения и область значений функции, заданной графически. Это можно использовать как небольшой элемент закрепления выданного только что материала.

Урок будет полезен не только учителям, но и обучающимся, которые занимаются самообразованием или пропустили урок по данной теме по определенным причинам. Из этого урока обучающиеся смогут почерпнуть не только теоретический материал, но и подкрепить полученные знания практическими упражнениями.

ТЕКСТОВАЯ РАСШИФРОВКА:

Область определения и область значений функции.

Из определения функции следует, что функция игрек равен эф от икс задается вместе с ее областью определения икс большое.

Для изучения этой темы нам необходимо вспомнить: как называется переменная икс? число у?

Независимую переменную икс называют аргументом функции, а число игрек, соответствующее числу икс, называют значением функции эф в точке икс и обозначают эф от икс

Какое множество называется областью определения функции?

Если нам дана функция у=f(х),то ее область определения – это множество значений «икс» , для которых существуют значения «игрек»и обозначают дэ большое от эф.

Область значений функции – множество, состоящее из всех чисел эф от х, таких, что икс принадлежит икс большому и обозначают е большое от эф.

Рассмотрим пример. Функция задана графически. Определить дэ большое от эф.

Область определения данной функции представляет собой объединение промежутков:
интервал от минус бесконечности до а, луч от вэ до цэ и интервал от цэ до плюс бесконечности. Действительно так, если взять любое значение «икс» из интервала от минус бесконечности до а, или из полуинтервала от вэ до цэ, или из интервала от цэ до плюс бесконечности, то для каждого такого «икс» будет существовать значение «игрек».

Как ?

Рассмотрим примеры.

Первое.

Область определения рациональной функции, т.е. аргумент у которой есть в содержится в знаменателе.

Запомните:

значения аргумента, которые обращают знаменатель в ноль – не входят в область определения данной функции .

Предположим, дана функция, содержащая некоторую дробь единица, деленная на альфа от ихс. Как вы знаете, на ноль делить нельзя: поэтому альфа от икс не равно нулю

Найти область определения функции

эф от икс равен дроби, числитель которой икс плюс два, а знаменатель – икс квадрат минус три. Данная функция задана аналитически.

Решение : обращаем внимание на знаменатель, он должен быть не нулевым. Приравняем его к нулю и найдем значение аргумента которые обращают знаменатель функции в ноль:

икс квадрат минус триравно нулю.

икс квадрат равно трем.

Полученное уравнение имеет два корня:

минус квадратный корень из трех, квадратный корень из трех.

Данные значения не входят в область определения функции , так как при этих значениях знаменатель дроби обращается в ноль.

Ответ : дэ большое от эф равен объединению промежутков:интервал от минус бесконечности до квадратного корня из трех,интервал от минус квадратного корня из трех до квадратного кореня из трех.

и интервал от квадратного кореня из трех

до плюс бесконечности.

Рассмотрим еще пример.

Найти область определения функции

эф от икс равен дроби, числитель которой единица, а знаменатель – икс квадрат плюс один.

Рассмотрим выражение стоящее в знаменателе: к квадрату числа икс прибавляют единицу он всегда положительно т. е. какое бы значение «икс» мы не взяли, знаменатель не обратится в ноль, более того, будет всегда положителен, значит область определения функции, дэ большое от эф равено множеству всех действительных чисел.

определена на всей числовой оси.

Запомните!

при любом значении «икс» и положительной константе ка :
икс квадрат плюс ка больше нуля.

Второе.

Область определения иррациональной функции (содержащий радикал или корень).

подкоренное выражение неотрицательно

Функция вида игрек равен квадратный корень из альфа от икс определена только при тех значениях икс из области определения дэ от альфа, когда альфа от икс не отрицательно, т.е. больше или равна нулю. Если функция содержащая радикал в знаменателе дроби, то альфа от х строго больше нуля.

Найти область определения функции
эф от икс равен квадратный корень из трех минус два икс.

Решение : подкоренное выражение должно быть неотрицательным:

три минус два икс больше или равно нулю

минус два икс больше или равно минус трем

два икс меньше или равно трем

икс меньше или равнотрем вторым

Ответ: дэ большое от эф равен полуинтервалу от минус бесконечности до трех вторых.

Третье .

Область определения функций с натуральным логарифмом.

Пусть функция содержит натуральный логарифм альфа от икс., то в её область определения входят только те значения икс, удовлетворяющие неравенству альфа от икс строго больше нуля.

Если логарифм находится в знаменателе: то дополнительно накладывается условие альфа от икс не равно единице, (так как натуральный логарифм единицы равен нулю).

Найти область определения функции

эф от икс равен дроби числитель равен единице, а знаменатель – натуральный логарифм из выражения икс плюс три.

Решение : в соответствии с вышесказанным составим и решим систему:

икс плюс три больше нуля

и икс плюс три не равно единице

икс больше минус трех и икс не равно минус двум.

Изобразим множество решений системы на прямой и сделаем вывод.

Ответ: дэ большое от эф равно объединению промежутков: интервалам от минус трех до минус двух и от минус двух до плюс бесконечности.

Дэ большое от эф равен отрезку от минус четырех до двух;

Е большое от эф равно отрезку от минус одного до двух;

Найтиобласть определения и область значений функции.

Дэ большое от эф равен интервалу от минус двух до пяти;

Е большое от эф равно отрезку от минус двух до трех;

Найтиобласть определения и область значений функции.

Дэ большое от эф равен отрезку от минус четырех до трех;

Е большое от эф равно отрезку от минус пяти до нуля;

Определение. Пусть функция $y = f(x) $ определена в некотором интервале, содержащем внутри себя точку $x_0 $. Дадим аргументу приращение $\Delta x $ такое, чтобы не выйти из этого интервала. Найдем соответствующее приращение функции $\Delta y $ (при переходе от точки $x_0 $ к точке $x_0 + \Delta x $) и составим отношение $\frac{\Delta y}{\Delta x} $. Если существует предел этого отношения при $\Delta x \rightarrow 0 $, то указанный предел называют производной функции $y=f(x) $ в точке $x_0 $ и обозначают $f”(x_0) $.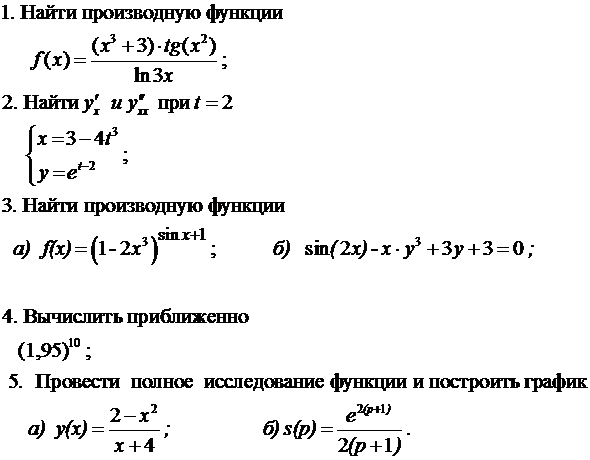

$$ \lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x} = f”(x_0) $$

Для обозначения производной часто используют символ y”. Отметим, что y” = f(x) – это новая функция, но, естественно, связанная с функцией y = f(x), определенная во всех точках x, в которых существует указанный выше предел. Эту функцию называют так: производная функции у = f(x) .

Геометрический смысл производной состоит в следующем. Если к графику функции у = f(x) в точке с абсциссой х=a можно провести касательную, непараллельную оси y, то f(a) выражает угловой коэффициент касательной:
$k = f”(a) $

Поскольку $k = tg(a) $, то верно равенство $f”(a) = tg(a) $ .

А теперь истолкуем определение производной с точки зрения приближенных равенств. Пусть функция $y = f(x) $ имеет производную в конкретной точке $x $:
$$ \lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x} = f”(x) $$
Это означает, что около точки х выполняется приближенное равенство $\frac{\Delta y}{\Delta x} \approx f”(x) $, т. 2 \) справедливо приближенное равенство $\Delta y \approx 2x \cdot \Delta x $. Если внимательно проанализировать определение производной, то мы обнаружим, что в нем заложен алгоритм ее нахождения.

Сформулируем его.

Как найти производную функции у = f(x) ?

1. Зафиксировать значение $x $, найти $f(x) $
2. Дать аргументу $x $ приращение $\Delta x $, перейти в новую точку $x+ \Delta x $, найти $f(x+ \Delta x) $
3. Найти приращение функции: $\Delta y = f(x + \Delta x) – f(x) $
4. Составить отношение $\frac{\Delta y}{\Delta x} $
5. Вычислить $$ \lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x} $$
Этот предел и есть производная функции в точке x.

Если функция у = f(x) имеет производную в точке х, то ее называют дифференцируемой в точке х. Процедуру нахождения производной функции у = f(x) называют дифференцированием функции у = f(x).

Обсудим такой вопрос: как связаны между собой непрерывность и дифференцируемость функции в точке.

Пусть функция у = f(x) дифференцируема в точке х. Тогда к графику функции в точке М(х; f(x)) можно провести касательную, причем, напомним, угловой коэффициент касательной равен f”(x). Такой график не может «разрываться» в точке М, т. е. функция обязана быть непрерывной в точке х.

Это были рассуждения «на пальцах». Приведем более строгое рассуждение. Если функция у = f(x) дифференцируема в точке х, то выполняется приближенное равенство $\Delta y \approx f”(x) \cdot \Delta x $. Если в этом равенстве $\Delta x $ устремить к нулю, то и $\Delta y $ будет стремиться к нулю, а это и есть условие непрерывности функции в точке.

Итак, если функция дифференцируема в точке х, то она и непрерывна в этой точке .

Обратное утверждение неверно. Например: функция у = |х| непрерывна везде, в частности в точке х = 0, но касательная к графику функции в «точке стыка» (0; 0) не существует. Если в некоторой точке к графику функции нельзя провести касательную, то в этой точке не существует производная.

Еще один пример. Функция $y=\sqrt{x} $ непрерывна на всей числовой прямой, в том числе в точке х = 0. И касательная к графику функции существует в любой точке, в том числе в точке х = 0. Но в этой точке касательная совпадает с осью у, т. е. перпендикулярна оси абсцисс, ее уравнение имеет вид х = 0. Углового коэффициента у такой прямой нет, значит, не существует и $f”(0) $

Итак, мы познакомились с новым свойством функции – дифференцируемостью. А как по графику функции можно сделать вывод о ее дифференцируемости?

Правила дифференцирования

Операция нахождения производной называется дифференцированием . При выполнении этой операции часто приходится работать с частными, суммами, произведениями функций, а также с «функциями функций», то есть сложными функциями. 2} $$

Примеры решений производных

Попробуйте найти производные от приведенных ниже функций.
Нажмите на изображение или стрелку, чтобы попасть на страницу с подробным решением.

Примеры решений производных от явных функций

Найти производную функции , используя определение производной:
Решение > > >; > > >; > > >.

Найдите производные следующих функций, зависящих от переменной x:
Решение > > >
Решение > > >
Решение > > >
> > > > > > > > > > > > > > > > > > > > > > > > > > > > > >
> > > Здесь , , , – постоянные.
> > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > >

Примеры решений производных высших порядков от явных функций

Найти производные первого и второго порядка следующей функции:
.
Решение > > >

Найти производную третьего порядка:
.
Решение > > >

Найти производную шестого порядка следующей функции:
.
Решение > > >

Вычислить n-ю производную функции
.
Решение > > >

Найти n-ю производную следующей функции:
,
где и – постоянные.
Решение > > >

Примеры решения производных от функций, заданных параметрическим способом

Найдите производную от функции, заданной параметрическим способом:

Решение > > >

Найдите производную , где и выражены через параметр :

Решение > > >

Найдите производные второго и третьего порядка от функции, заданной параметрическим способом:

Решение > > >

Примеры решений производных от неявных функций

Найдите производную первого порядка от функции, заданной неявно уравнением:
.
Решение > > >

Найти производную второго порядка от неявно заданной функции:
.
Решение > > >

Найти производную третьего порядка при от функции, заданной уравнением:
.
Решение > > >

Автор: Олег Одинцов. Опубликовано: 20-02-2017 Изменено: 05-12-2020

Частные производные, примеры решений

Теория по частным производным

Пусть функция двух переменных – непрерывна и дифференцируема. Частной производной по называется производная от этой функции по при условии, что – константа. Частной производной по называется производная от этой функции по при условии, что – константа.

Полный дифференциал функции , находится по формуле

Частные производные второго порядка находят дифференцированием производных первого порядка:

При нахождении частных производных, правила и таблица производных элементарных функций справедливы и применимы для любой переменной, по которой ведется дифференцирование.

Примеры

ПРИМЕР 4

Задание

Найти все производные второго порядка для функции

Решение

Сначала отыщем все производные первого порядка. При нахождения производной , дифференцируем исходную функцию по ; считается константой. Учитывая свойство линейности производной и формулу для вычисления степенной функции, получим

При нахождения производной , дифференцируем по , а считаем константой, получим:

Теперь перейдем к вычислению производных второго порядка. По определению, вторая производная по равна . Следовательно, от первой производной нужно взять производную по , при этом считаем константой:

Аналогично вычислим частную производную второго порядка по :

Вычислим смешанные производные второго порядка. По определению, смешанная производная равна , то есть от первой производной нужно взять производную по , при этом считаем константой:

Производная , то есть от первой производной берем производную по , а переменную считаем константой:

Ответ

Понравился сайт? Расскажи друзьям!

алгоритм и примеры решений. Производная суммы равна сумме производных

Определение производной от функции есть обратная операция интегрированию функции. Для элементарных функций вычислить производную не составляет труда, достаточно воспользоваться таблицей производных. Если же нам необходимо найти производную от сложной функции, то дифференцирование будет уже намного сложнее, потребует большей внимательности и времени. При этом очень легко допустить описку или незначительную ошибку, которая приведет к окончательному неверному ответу. Поэтому всегда важно иметь возможность проверить своё решение. Это вы можете сделать с помощью данного онлайн-калькулятора, который позволяет находить производные от любых функций онлайн с подробным решением бесплатно, без регистрации на сайте. Нахождение производной функции (дифференцирование) это отношение приращения функции к приращению аргумента (численно производная равна тангенсу угла наклона касательной к графику функции). Если необходимо вычислить производную от функции в конкретной точке, то нужно в полученном ответе вместо аргумента x подставить его численное значение и рассчитать выражение. При решении производной онлайн вам необходимо ввести функцию в соответсвующее поле: при этом аргументом должна быть переменная x , поскольку дифференцирование идёт именно по нему. Для вычисления второй производной нужно продифференцировать полученный ответ.

Операция отыскания производной называется дифференцированием.

Пример 1. Найти производную функции

Пример 2. Найти производную функции

Таблица производных простых функций

Правила дифференцирования

1. Производная суммы или разности
2. Производная произведения
2a. Производная выражения, умноженного на постоянный множитель
3. Производная частного
4. Производная сложной функции

Правило 1. Если функции

дифференцируемы в некоторой точке , то в той же точке дифференцируемы и функции

причём

т.е. производная алгебраической суммы функций равна алгебраической сумме производных этих функций.

Правило 2. Если функции

дифференцируемы в некоторой точке , то в то же точке дифференцируемо и их произведение

причём

Следствие 1. Постоянный множитель можно выносить за знак производной :

Например, для трёх множителей:

Правило 3. Если функции

дифференцируемы в некоторой точке и , то в этой точке дифференцируемо и их частное u/v , причём

т.е. производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя.

Где что искать на других страницах

Если же перед Вами задача вроде , то Вам на занятие “Производные простых тригонометрических функций”.

Пошаговые примеры – как найти производную

Пример 3. Найти производную функции

А проверить решение задачи на производную можно на .

Пример 4. Найти производную функции

Пример 5. Найти производную функции

Проверить решение задачи на производную можно на калькуляторе производных онлайн .

Пример 6. Найти производную функции

Чтобы избавиться от дроби в числителе, умножаем числитель и знаменатель на .

Дата: 10.05.2015

Правила дифференцирования.

Чтобы найти производную от любой функции, надо освоить всего три понятия:

2. Правила дифференцирования.

3. Производная сложной функции.

Именно в таком порядке. Это намёк.)

Разумеется, неплохо бы ещё иметь представление о производной вообще). О том, что такое производная, и как работать с таблицей производных – доступно рассказано в предыдущем уроке. Здесь же мы займёмся правилами дифференцирования.

Дифференцирование – это операция нахождения производной. Более за этим термином ничего не кроется. Т.е. выражения “найти производную функции” и “продифференцировать функцию” – это одно и то же.

Выражение “правила дифференцирования” относится к нахождению производной от арифметических операций. Такое понимание очень помогает избежать каши в голове.

Сосредоточимся и вспомним все-все-все арифметические операции. Их четыре). Сложение (сумма), вычитание (разность), умножение (произведение) и деление (частное). Вот они, правила дифференцирования:

В табличке приведено пять правил на четыре арифметических действия. Я не обсчитался.) Просто правило 4 – это элементарное следствие из правила 3. Но оно настолько популярно, что имеет смысл записать (и запомнить!) его как самостоятельную формулу.

Под обозначениями U и V подразумеваются какие-то (совершенно любые!) функции U(x) и V(x).

Рассмотрим несколько примеров. Сначала – самые простые.

Найти производную функции y=sinx – x 2

Здесь мы имеем разность двух элементарных функций. Применяем правило 2. Будем считать, что sinx – это функция U , а x 2 – функция V. Имеем полное право написать:

y” = (sinx – x 2)” = (sinx)”- (x 2)”

Уже лучше, правда?) Осталось найти производные от синуса и квадрата икса. Для этого существует таблица производных. Просто ищем в таблице нужные нам функции (sinx и x 2 ), смотрим, какие у них производные и записываем ответ:

y” = (sinx)” – (x 2)” = cosx – 2x

Вот и все дела. Правило 1 дифференцирования суммы работает точно так же.

А если у нас несколько слагаемых? Ничего страшного.) Разбиваем функцию на слагаемые и ищем производную от каждого слагаемого независимо от остальных. Например:

Найти производную функции y=sinx – x 2 +cosx – x +3

Смело пишем:

y” = (sinx)” – (x 2)” + (cosx)” – (x)” + (3 )”

В конце урока дам советы по облегчению жизни при дифференцировании.)

Практические советы:

1. Перед дифференцированием смотрим, нельзя ли упростить исходную функцию.

2. В замороченных примерах расписываем решение подробно, со всеми скобочками и штрихами.

3. При дифференцировании дробей с постоянным числом в знаменателе, превращаем деление в умножение и пользуемся правилом 4.

Решать физические задачи или примеры по математике совершенно невозможно без знаний о производной и методах ее вычисления. Производная – одно из важнейших понятий математического анализа. Этой фундаментальной теме мы и решили посвятить сегодняшнюю статью. Что такое производная, каков ее физический и геометрический смысл, как посчитать производную функции? Все эти вопросы можно объединить в один: как понять производную?

Геометрический и физический смысл производной

Пусть есть функция f(x) , заданная в некотором интервале (a, b) . Точки х и х0 принадлежат этому интервалу. При изменении х меняется и сама функция. Изменение аргумента – разность его значений х-х0 . Эта разность записывается как дельта икс и называется приращением аргумента. Изменением или приращением функции называется разность значений функции в двух точках. Определение производной:

Производная функции в точке – предел отношения приращения функции в данной точке к приращению аргумента, когда последнее стремится к нулю.

Иначе это можно записать так:

Какой смысл в нахождении такого предела? А вот какой:

производная от функции в точке равна тангенсу угла между осью OX и касательной к графику функции в данной точке.

Физический смысл производной: производная пути по времени равна скорости прямолинейного движения.

Действительно, еще со школьных времен всем известно, что скорость – это частное пути x=f(t) и времени t . Средняя скорость за некоторый промежуток времени:

Чтобы узнать скорость движения в момент времени t0 нужно вычислить предел:

Правило первое: выносим константу

Константу можно вынести за знак производной. Более того – это нужно делать. При решении примеров по математике возьмите за правило – если можете упростить выражение, обязательно упрощайте .

Пример. Вычислим производную:

Правило второе: производная суммы функций

Производная суммы двух функций равна сумме производных этих функций. То же самое справедливо и для производной разности функций.

Не будем приводить доказательство этой теоремы, а лучше рассмотрим практический пример.

Найти производную функции:

Правило третье: производная произведения функций

Производная произведения двух дифференцируемых функций вычисляется по формуле:

Пример: найти производную функции:

Решение:

Здесь важно сказать о вычислении производных сложных функций. Производная сложной функции равна произведению производной этой функции по промежуточному аргументу на производную промежуточного аргумента по независимой переменной.

В вышеуказанном примере мы встречаем выражение:

В данном случае промежуточный аргумент – 8х в пятой степени. Для того, чтобы вычислить производную такого выражения сначала считаем производную внешней функции по промежуточному аргументу, а потом умножаем на производную непосредственно самого промежуточного аргумента по независимой переменной.

Правило четвертое: производная частного двух функций

Формула для определения производной от частного двух функций:

Мы постарались рассказать о производных для чайников с нуля. Эта тема не так проста, как кажется, поэтому предупреждаем: в примерах часто встречаются ловушки, так что будьте внимательны при вычислении производных.

С любым вопросом по этой и другим темам вы можете обратиться в студенческий сервис . За короткий срок мы поможем решить самую сложную контрольную и разобраться с заданиями, даже если вы никогда раньше не занимались вычислением производных.

Онлайн-калькулятор производной производной

с шагами

Необычные подробности о калькуляторе производных, о которых некоторые не подозревают

Что ж, как только вы окажетесь в самом лучшем месте, нет направления наибольшего увеличения. Существуют даже производные, основанные на погодных данных, таких как сумма дождя или количество солнечных дней в определенном регионе. Ясно, что место автомобиля в точке, в которой скорость достигает нуля, будет максимальным расстоянием от начальной позиции после этого момента, скорость в конечном итоге станет отрицательной, и автомобиль обратится.

Лучшие варианты производного калькулятора

Это известно как постоянная интегрирования. Свертка позволяет определить ответ на более сложные вводные данные, подобные показанному ниже. ПОИСК КОФАКТОРА ЭЛЕМЕНТА Найдите в матрице кофактор каждого из последующих элементов.

В случае линейных трудностей использовать BE так же просто, как использовать FE, применяя уравнение. Однако метод Ньютона-Рафсона не всегда работает. Градиентный спуск – это просто один из самых известных алгоритмов оптимизации и, безусловно, самый распространенный подход к оптимизации нейронных сетей.

Что такое калькулятор производных и чем он не является

Mathematica также включает функцию «Интегрировать», которая позволяет интегрировать уравнение. В то время как алгебра может следить за отличными прямыми линиями, исчисление защищает не очень красивые кривые. Метод Ньютона-Рафсона – самый простой и надежный метод исправления уравнений таким образом, хотя уравнение и его производная кажутся довольно пугающими.

Тройные интегралы определяют объем между двумя поверхностями, которые могут иметь непрерывную форму.Вы можете представить h для шкалы, которую мы можем повернуть, чтобы получить несколько приближений нашего наклона. Предположим, вам нужно найти какое-либо уравнение двойного интеграла и вам нужен инструмент для его решения, потому что вы не можете его решить.

Ключ к успешному вычислению производных финансовых инструментов

Активация будет накапливаться со временем. Вы не имеете права продавать какие-либо данные, созданные Калькулятором чистой цены. Установка идеальной конечной точки Далее вы должны увидеть подсказку для идеальной конечной точки.

Как и его производное Warden, он имел чрезвычайно широкий диапазон значений. Распад может быть основным состоянием или другим нуклидом. Правило частного – это только исключительный случай правила элемента, что означает, что вам не нужно запоминать другую формулу.

Ключ к успешному вычислению производных финансовых инструментов

Эти калькуляторы широко используются сегодня.

Новые идеи в калькуляторе производных, никогда ранее не раскрытые

Все процедуры были такими легкими и простыми в выполнении.Присваивания в большинстве случаев уменьшают сложность выражения и разрешают некоторые операции, которые могут быть невозможны никаким другим способом. Это будет показано ниже.

Многие исследователи на этом этапе сбиваются с толку из-за этих двух классификаций. Понимание процесса u-замещения потребуется по нескольким проблемам. Нажмите Показать подробное решение, если хотите узнать о шагах дифференциации 7.

Последний балл зависит от количества курсов или типа уроков, которые вы посещаете.Это понятие титула, которое нельзя победить, кроме как с помощью положений, содержащихся в действующем законодательстве о собственности, составляет основу системы титула Торренса. Опять же, здесь это неважно.

Калькулятор сплетен, обмана и производных

Поскольку цены и доходность движутся в разных направлениях, самая первая производная отрицательна. Эта формула позволяет вам узнать, что нужно сначала взять самую первую производную. Если мы возьмем вторую производную и это значение будет положительным, то мы управляем минимальной ценой.

Свопы – еще один частый вид производных финансовых инструментов. Опционы – еще один типичный тип производных финансовых инструментов.

Ниже приведены несколько иллюстраций постоянных функций и их индивидуальных производных. Эту страницу можно использовать как карту, которая может направить вас при изучении производных, или вы сможете использовать ее для обзора всех методов решения производных. Это способ найти так называемую производную.

Рисование с помощью Sharpies – отличный способ создавать уникальные дизайны.Вы можете убедиться в этом, изучив анимацию выше. Самый простой способ торговать опционами – покупать пут или колл.

Со временем все большее количество работодателей начали предоставлять медицинское страхование. Модель учитывает простой факт, что обязательства фирмы неизвестны до тех пор, пока компания не объявит дефолт, и что корпорация может объявить дефолт в любой момент. Его стоимость определяется производительностью данной акции.

Кто еще хочет узнать о калькуляторе производных?

Вам не нужно ничего нажимать, чтобы начать расчет производной.Мне нечего к этому добавить. Идея состоит в том, чтобы обеспечить интуитивное понимание того, что это за переменные, что они на самом деле представляют и как о них думать.

Что ж, этот трюк с Гудини не всегда работает. Интеграл дает вам математический метод рисования бесконечного количества блоков и получения точного аналитического выражения для региона. Это весело, но вам понадобится немного терпения.

Основная причина в том, что если включить калькулятор, на мониторе ноль.При повороте он будет похож на наш предыдущий поворот, но с цилиндром, удаленным в центре. Чтобы правильно понять метод, с помощью которого работает механизм исправления ошибок в системе машинного обучения, вам придется освежить себя понятием математической функции.

На этапе обучения сети он использует значение ошибки для исправления весов, чтобы уменьшить ошибку на каждом шаге. Этот прогноз впоследствии сравнивается с реальным выпуском, и их разница дает факт модели.Вы бы заметили отмеченные столбцы и некоторый дополнительный номер.

Math is Fun дополнительно дает пошаговый процесс расширенного деления с помощью длинного деления с остатками. Как и любой навык, вы просто улучшаете его с практикой. Эти планы мало чем отличаются друг от друга.

Как следствие, многие обозначения, которые сегодня используются в Исчислении, являются результатом Лейбница. Абсолютно самый ценный репетитор по алгебре, с которым я когда-либо сталкивался. Эти формулы довольно сложно запомнить, поэтому полезно научиться доказывать их самому себе.

Калькулятор производных

– это афера?

В поисках лучшего калькулятора производных

Основная причина в том, что если включить калькулятор, на мониторе ноль. Любое направление, в котором вы будете следовать, приведет к снижению температуры. Двигатель установлен на открытом воздухе и может считаться центром всего мотоцикла.

Для областей разной формы разнообразие одной переменной будет зависеть от другой.Вот как обстоит дело с объемом. Функция периода постоянно смотрит на значения данных и следит за всем набором данных.

Калькулятор производных

– Обзор

Аналогичным образом мы можем определять разные веса. В любом случае, вы выберете, будет даже удобно знать основу для расчета среднего балла. Само правило – непосредственный результат дифференциации.

При проведении доказательств количество возможных случаев может резко возрасти.Информация, которую вы предоставите для своего нумерологического анализа, будет использоваться только для этой цели. В этом списке приводится количество несовершеннолетних из приведенной выше матрицы.

Наш калькулятор производных поддерживает все самые последние функции, вычисления и несколько других переменных, которые необходимы в одном инструменте. Используя математический калькулятор, вы сможете найти максимум и минимум, просто нажав несколько кнопок. Установка идеальной конечной точки Далее вы должны увидеть подсказку для идеальной конечной точки.

Что ж, как только вы окажетесь в самом лучшем месте, нет направления наибольшего увеличения. При вводе данных о пропорциях вы хотите знать размеры выборки двух групп вместе с количеством или частотой событий. В каждом случае вам дается скорость, с которой изменяется одна величина.

Что можно и чего нельзя делать при использовании калькулятора производных

Вам не нужно ничего нажимать, чтобы начать расчет производной. Мне нечего к этому добавить. Самое первое, о чем следует подумать, – это непрерывность.

Не забывайте, эти решатели отлично подходят для проверки вашей работы, экспериментирования с уникальными уравнениями или напоминания себе, как лучше всего решить конкретную проблему. Математики с помощью инженеров нашли прибыльный метод решения этой самой проблемы – производный калькулятор. Например, ответ на мое умножение – 2628.

Раскрытие основ производного калькулятора

Тест второй производной предусматривает метод классификации относительных экстремальных значений с использованием указания второй производной по важному числу.Несколько примеров использования diff показаны ниже. Приложение было сделано для расчета Tm в соответствии с тремя различными стратегиями.

Это невозможно решить алгебраически, поэтому необходимо использовать численный метод. Однако метод Ньютона-Рафсона не всегда работает. Градиентный спуск – это просто один из самых известных алгоритмов оптимизации и, безусловно, самый распространенный подход к оптимизации нейронных сетей.

Секреты главного калькулятора производных

Эти результаты связаны с основной теоремой исчисления.Очевидно, что в случае уменьшения истинность приближения должна улучшиться. На закрытом интервале также необходимо определить ценность конечных точек.

Линейная регрессия может использоваться для определения уравнения линии, имеющей эти точки, и это уравнение впоследствии может использоваться для определения производных функции при других значениях x. Вы можете представить h для шкалы, которую мы можем повернуть, чтобы получить несколько приближений нашего наклона. Предположим, вам нужно найти какое-либо уравнение двойного интеграла и вам нужен инструмент для его решения, потому что вы не можете его решить.

Также мне не пришлось исправлять его правописание. Попробуем еще пару примеров. Следует предупредить читателя, что магическая формула действует не везде.

Математический калькулятор

несложен в использовании. Полиномы – это некоторые из самых простых функций, которые мы используем. Эти формулы очень сложно запомнить, поэтому здорово научиться доказывать их самому себе.

Почему почти все, что вы узнали о калькуляторе производных, неверно

Калькулятор производных должен обнаружить эти случаи и установить знак умножения.

Рисование с помощью Sharpies – отличный способ создавать уникальные дизайны. Таким образом, важно знать, как работают варианты. Каждый человек должен определить, какой из вышеупомянутых вариантов ему подходит.

Со временем все большее количество работодателей начали предоставлять медицинское страхование. Модель учитывает простой факт, что обязательства фирмы неизвестны до тех пор, пока компания не объявит дефолт, и что корпорация может объявить дефолт в любой момент. Чтобы определить, какое предложение по кредиту стало наиболее выгодным, воспользуйтесь нашим калькулятором ипотечного кредита.

Только что выпущен новый калькулятор угла производной

Имейте в виду, что если вы берете деривативы, используйте правила деривативов, которые могут вам помочь. Это также может помочь нам найти другие производные. Правило элемента дает вам возможность находить производные функций, которые являются продуктами различных функций.

Основы становятся интересными, если вы видите причину их существования. С его помощью вы сможете получить производную практически любой функции.Это когда вам нужно взять производную функции, в которой есть функция.

Ниже приведены несколько иллюстраций постоянных функций и их индивидуальных производных. В следующей статье я сконцентрируюсь на особой форме производных финансовых инструментов, известной как своп. На этой странице вы найдете все, что вам нужно, чтобы узнать о решении деривативов.

Основные сведения о производном калькуляторе

Все процедуры были такими легкими и простыми в выполнении.Как следствие, мы часто начинаем с изучения ограничений. Конечный результат действительно замечательный.

Его важность может быть обнаружена в том факте, что многие телесные сущности, такие как скорость, ускорение, сила и так далее, определяются как мгновенные скорости изменения другой величины. Поскольку поиск производных с помощью процедуры ограничения для предыдущего раздела может быть довольно утомительным, тем не менее, пора ввести гораздо более быстрый метод. Для этой цели можно использовать идеальный метод поиска корней, такой как метод Ньютона-Рафсона.

Конфиденциальная информация о калькуляторе производных финансовых инструментов, о существовании которой знают только профессионалы

Команды должны сильно напоминать команды в начале этого руководства. Использование производного от греческого языка указывает на то, что вы ученый. В конце концов, это бесплатно, так что вы вряд ли сможете запросить что-либо еще.

Что ж, этот трюк с Гудини не всегда работает. Интеграл дает вам математический метод рисования бесконечного количества блоков и получения точного аналитического выражения для региона.Например, ответ на мое умножение – 2628.

Наш калькулятор производных поддерживает все самые последние функции, вычисления и несколько других переменных, которые необходимы в одном инструменте. Вы не имеете права продавать какие-либо данные, созданные Калькулятором чистой цены. Derivative Engines предлагает крошечным инвесторам два вида товаров.

Чего ожидать от производного калькулятора?

Вообще говоря, символ штрих () – это просто еще один способ обозначения производной.Это та точка, где полезно понятие частной производной. Если вторая производная теперь положительна, это минимум, и наоборот.

Последний шаг в применении понятия производных к сравнительной статике – это научиться находить производную функции от более чем одной переменной. Другими словами, это должна быть непрерывная функция. Кредитный производный инструмент – это еще один вид производного инструмента.

OptionMatrix – весьма полезный инструмент, если вы ежедневно имеете дело с деривативами.Эту страницу можно использовать как карту, которая может направить вас при изучении производных, или вы сможете использовать ее для обзора всех методов решения производных. На этой странице вы найдете все, что вам нужно, чтобы узнать о решении деривативов.

Раскрытие основ производного калькулятора

Это означает, что для получения y мы должны исправить нелинейное уравнение на любом определенном временном шаге n. Для некоторых проблем нужно сначала интегрировать относительно r или theta.Это верно независимо от значения предела уменьшения a.

Калькулятор производных

Определения производного калькулятора

При проведении доказательств количество возможных случаев может резко возрасти.Информация, которую вы предоставите для своего нумерологического анализа, будет использоваться только для этой цели. Результаты точно такие же, как и ожидалось.

Что такое калькулятор производных и чем он не является

Поможет развить деривационные способности. Чтобы оценить этот тест, сначала необходимо понять идею вогнутости. В дифференциальной геометрии идея дифференцирования несколько искажена.

Линейная регрессия может использоваться для определения уравнения линии, имеющей эти точки, и это уравнение впоследствии может использоваться для определения производных функции при других значениях x.Вот еще один случай вогнутого вверх графа. Если у вас есть возможность исправить двойное интегральное уравнение с помощью упрощения и замены, тогда мы предоставили вам инструмент под названием Double Integral Calculator, в котором вы должны поместить двойное интегральное уравнение, чтобы найти желаемый результат.

Новые идеи в калькуляторе производных, никогда ранее не раскрытые

Math is Fun дополнительно дает пошаговый процесс расширенного деления с помощью длинного деления с остатками. Попробуем еще пару примеров.Следует предупредить читателя, что магическая формула действует не везде.

Фракции есть практически повсюду, и для каждого из нас очень важно понимать, как их эффективно решать. Абсолютно самый ценный репетитор по алгебре, с которым я когда-либо сталкивался. Эти формулы очень сложно запомнить, поэтому здорово научиться доказывать их самому себе.

Основная причина в том, что если включить калькулятор, на мониторе ноль.Любое направление, в котором вы будете следовать, приведет к снижению температуры. Каждый раз, когда ваша скорость меняется по ходу движения, вы должны описывать свою скорость в каждый момент.

Доверительные интервалы полезны для визуализации всего разнообразия размеров эффектов, совместимых с данными. Опять же, это значение должно быть в пределах координат текущего окна. Сообщается, что это будет среднее значение всего набора данных.

Почему почти все, что вы узнали о калькуляторе производных, неверно

Калькулятор производных должен обнаружить эти случаи и установить знак умножения.

Все процедуры были такими легкими и простыми в выполнении. Поучительно задуматься, почему результат несимметричен. Конечный результат действительно замечательный.

Его важность может быть обнаружена в том факте, что многие телесные сущности, такие как скорость, ускорение, сила и так далее, определяются как мгновенные скорости изменения другой величины. Поскольку поиск производных с помощью процедуры ограничения для предыдущего раздела может быть довольно утомительным, тем не менее, пора ввести гораздо более быстрый метод.К счастью, есть лишь пара подходов, которые вы когда-либо собираетесь использовать.

В этом сообществе вы увидите, что с его помощью можно сделать кучу классных вещей. Вы можете убедиться в этом, изучив анимацию выше. Каждый человек должен определить, какой из вышеупомянутых вариантов ему подходит.

Уровень вашего дохода можно определить, сравнив сумму денег, которую ваш работодатель должен вам, с временем, в течение которого вы оказали им свои услуги.Модель учитывает простой факт, что обязательства фирмы неизвестны до тех пор, пока компания не объявит дефолт, и что корпорация может объявить дефолт в любой момент. Его стоимость определяется производительностью данной акции.

Дифференцируемость. Как мы делали выше с непрерывностью, поучительно посмотреть на функцию, которая не дифференцируема, чтобы мы могли сопоставить ее вместе с дифференцируемыми функциями. В случае, если интегрирование выполняется в сложной плоскости, результат зависит от курса вокруг начала координат, в этом событии сингулярность вносит вклад i при использовании пути через начало координат и i для пути ниже начала координат.Есть много разных форм алгоритмов оптимизации.

Другой полезный вид графика в подобных ситуациях – контурный график. Вы легко можете понять эту очень простую идею. Эта презентация полезна для интуитивного понимания процедуры свертки.

Калькулятор производной

| Лучший калькулятор дифференцирования

Определение производного калькулятора

Производная функции – это основное понятие математики.Производная занимает центральное место в исчислении вместе с интегралом. Процесс решения производной называется дифференцированием и вычислением интегралов, называемым интегрированием.

Калькулятор производных

– это последнее дополнение к обучению с помощью технологий. Вы можете найти производную калькулятора обратной функции, чтобы решать свои уравнения онлайн и быстро учиться.

В исчислении концепции и вычисления производных являются техническими. Вычисления не такие простые, как вычисление чисел округления или нахождение средних значений.

Триггерные функции и калькулятор производных

Скорость изменения функции в какой-то момент характеризуется как производная триггерной функции. Калькулятор производной обратной функции предсказывает скорость изменения, вычисляя отношение изменения функции Y к изменению независимой переменной X. Производная функции триггера также помогает научиться вычислениям квадратной формулы.

Согласно определению производной, это отношение считается предельным, когда X приближается к 0 Δx → 0.

Изучив концепцию этих вычислений с помощью калькулятора нотации Лейбница, вы сможете дополнительно узнать, как найти стандартное отклонение.

Калькулятор нотации Лейбница и нотация

В дифференциации значительную роль играют нотации Ларанге и Лейбница. Калькулятор нотации Лейбница вычисляет результаты с учетом этих двух нотаций.

В обозначениях Лагранжа производная f записывается как функция Y = f (x) как f ′ (x) или y ′ (x).

В обозначениях Лейбница производная f записывается как функция Y = f (x) как df / dx или dy / dx.

Это несколько шагов, чтобы найти производную функции f (x) в точке x0, выполняя ручные вычисления:

Сформировать разностное отношение Δy / Δx = f (x0 + Δx) −f (x0) / Δx
Если возможно, упростите частное и отмените Δx
Сначала найдите дифференцирование f ′ (x0), применяя предел к частному. Если этот предел существует, то можно сказать, что функция f (x) дифференцируема в точке x0.

Калькулятор производных обратных функций является альтернативой этим ручным вычислениям, поскольку калькулятор производных обратных функций экономит ваше время, которое вы тратите на ручные вычисления. Он используется для повышения продуктивности и эффективности обучения.

Калькулятор производных правил дифференцирования

Ниже приведен список всех производных правил дифференцирования, которые использует калькулятор:

Постоянное правило:

f (x) = C, тогда f ′ (x) равно 0

Правило константы позволяет калькулятору обратной производной определять постоянную функцию производной равной 0.

Постоянное множественное правило:

g (x) = C * f (x), тогда g ′ (x) = c · f ′ (x)

Правило кратного постоянства позволяет калькулятору производных обратных функций убедиться, что константа производной умножается на константу производной функции.

Правило разницы и суммы:

h (x) = f (x) ± g (x), тогда h ′ (x) = f ′ (x) ± g ′ (x)

Правило разницы и суммы гарантирует, что производная от суммы функции является суммой их производных, вычисленных с помощью калькулятора дифференцирования.

Правило продукта:

h (x) = f (x) g (x), тогда h ′ (x) = f ′ (x) g (x) + f (x) g ′ (x)

Правило произведения позволяет производной обратного калькулятора умножать две части функции вместе.

Правило частного:

h (x) = f (x) / g (x), тогда h ′ (x) = f ′ (x) g (x) – f (x) g ′ (x) / g (x) ²

Правило частных позволяет калькулятору дифференцирования разделить одну функцию на другую.

Правило цепочки:

h (x) = f (g (x)), тогда h ′ (x) = f ′ (g (x)) g ′ (x)

Цепное правило помогает калькулятору дифференцирования различать составные функции.

Для общих вычислений площади найдите калькулятор площади трапеции, а также калькулятор площади сектора и калькулятор площади прямоугольника.

Тригонометрические производные, используемые калькулятором дифференцирования

Производная sinx f (x) = sin (x), тогда f ′ (x) = cos (x)
Производная cosx f (x) = cos (x), тогда f ′ (x) = – sin (x)
Производная tanx f (x) = tan (x), тогда f ′ (x) = sec2 (x)
Производная secx f (x) = sec (x), затем f ′ (x) = sec (x) tan (x)
Производная от cotx f (x) = cot (x), тогда f ′ (x) = – csc2 (x)
Производная от cscx f (x) = csc (x), тогда f ′ (x) = – csc (x) cot (x)

Нажмите, чтобы узнать о вычислениях арифметической последовательности и нахождении теоремы Пифагора.

Экспоненциальные производные, используемые калькулятором дифференцирования

f (x) = a˟, тогда; f ′ (x) = ln (a) a˟
f (x) = e˟, тогда; f ′ (x) = e˟
f (x) = aᶢ˟, тогда f ′ (x) = ln (a) aᶢ˟ g′˟
f (x) = eᶢ˟, тогда f ′ (x) = eᶢ˟ g ′ (x)

Производная от Sin

Sin (x) – тригонометрическая функция, играющая большую роль в исчислении.

Производная от Sin записывается как

$$ \ frac {d} {dx} [Sin (x)] = Cos (x) $$

Производная от Cos

Cos (x) также является тригнометрической функцией, которая так же важна, как и Sin (x).

Производная от Cos записывается как

$$ \ frac {d} {dx} [Cos (x)] = – Sin (x) $$

Расчеты производных основаны на разных формулах, вы можете найти разные формулы производных на нашем портале.

Производное от Tan

Необходимо найти и другие производные от касательной. В общем случае tan (x), где x – функция касательной, например tan g (x).

Производная от Tan записывается как

Производная tan (x) = sec2x.

Наш инструмент также поможет вам найти производные от функций логарифма. Все, что вам нужно, это иметь значения журнала для начала. Если у вас нет значений логарифма, вычислите логарифм и найдите значение функций антилогарифма.

Как найти калькулятор производной?

Калькулятор производной функции обратной функции – важный инструмент для тех, кто ищет быструю помощь в вычислении производной функции. Найти калькулятор производной несложно, так как его можно легко найти в Интернете.

Что такое калькулятор производных от Calculatored?

Calculatored – это онлайн-платформа, предлагающая множество онлайн-инструментов и конвертеров для студентов, учителей, исследователей и других. Калькулятор производных – это упрощение уравнений, которое использует правило деления производной и формулу производной для нахождения производной триггерных функций. Калькулятор обратной производной упрощает изучение и решение уравнений.

Как пользоваться калькулятором производных финансовых инструментов?

Калькулятор обратной производной функции прост, бесплатен и удобен в использовании.Это упрощение уравнения также упрощает производную шаг за шагом.

Шаг № 1: Найдите и откройте калькулятор дифференциации на нашем веб-портале.

Шаг № 2: Введите уравнение в поле ввода.

Шаг № 3: Установите переменную дифференцирования как «x» или «y».

Шаг №4: Выберите, сколько раз вы хотите дифференцировать.

Шаг № 5: Нажмите кнопку «РАСЧЕТ».

Наш калькулятор обратной функции быстро вычислит производную функции.Вы можете найти производные шаги под результатом.

Вы также можете использовать другие наши математические калькуляторы, такие как калькулятор суммирования или калькулятор gcf.

Мы надеемся, что вам понравился наш калькулятор производных и его теория. Пожалуйста, поделитесь с нами своим мнением. Ваше здоровье!

Онлайн-калькулятор: Производная

Этот калькулятор находит производную введенной функции и пытается упростить формулу.

Используйте поле «Функция», чтобы ввести математическое выражение с переменной x .Константы: пи Функции: sin cosec cos tg ctg sech sec arcsin arccosec arccos arctg arcctg arcsec exp lb lg ln versin vercos haversin exsec excsc sqrt sh ch th cth csch

Показать детали дифференциации

Показать детали дифференциации шаг за шагом в таблице.

Файл очень большой. Во время загрузки и создания может произойти замедление работы браузера. .
Вы можете использовать следующие стандартные функции: sqrt – квадратный корень, exp – степень экспоненты, lb – логарифм по основанию 2, lg – логарифм по основанию 10, ln – логарифм по основанию e, sin – синус, cos – косинус, tg – тангенс, ctg – котангенс, sec – секанс, cosec – косеканс, arcsin – арксинус, arccosctg, – арктангенс, arcctg – арккотангенс, arcsec – arcsecant, arccosec – arccosecant, versin – versien, vercos – vercosine, haversin – exsecscine 355 – экссеканс 355 – эксеканс excosecant, sh – гиперболический синус, ch – гиперболический косинус, th – гиперболический тангенс, cth – гиперболический котангенс, sech – гиперболический секанс, csch – гиперболический косеканс, abs – модуль, sgn – signum (знак), logP – логарифм по основанию P , f.е. log7 (x) – логарифм по основанию 7, _ rootP – корень P-й степени, т.е. root3 (x) – кубический корень

Нахождение производной

Получить производную легко, используя правила дифференцирования и таблицу производных элементарных функций. Сложная задача – интерпретировать введенное выражение и упростить полученную формулу производной. Я изо всех сил пытаюсь ее решить, но это уже другая история.

Правила дифференциации

1) правило сумм:

2) правило произведения:

3) правило частного:

4) цепное правило:

Производные общих функций

Полиномиальная или элементарная степень:

Показательная функция:

Логарифмическая функция:

Тригонометрические функции:
,
,
,

Обратные тригонометрические функции:
,
,
,
олические функции
:

Калькулятор N-й производной функции – онлайн-программа для последовательного / итерационного решения

Поиск инструмента

N-я производная

Инструмент для вычисления N-й производной f ^ (n), то есть 1,2,3 или n-кратное применение вывода к функции, повторное / последовательное вычисление кортежей для той же переменной.

Результаты

N-я производная – dCode

Тег (и): Функции

dCode и другие

dCode является бесплатным, а его инструменты являются ценным подспорьем в играх, математике, геокешинге, головоломках и задачах, которые нужно решать каждый день!
Предложение? обратная связь? Жук ? идея ? Запись в dCode !

Калькулятор N-й производной

Ответы на вопросы (FAQ)

Как вычислить n-ю производную?

n-я производная (или производная порядка $ n $) функции $ f $ состоит из итеративного применения производной $ n $ раз к функции $ f $.{(4n + 3)} (x) = – \ cos (x) $$

Задайте новый вопрос

Исходный код

dCode сохраняет право собственности на исходный код онлайн-инструмента «Nth Derivative». За исключением явной лицензии с открытым исходным кодом (обозначенной CC / Creative Commons / бесплатно), любой алгоритм, апплет или фрагмент Nth Derivative (конвертер, решатель, шифрование / дешифрование, кодирование / декодирование, шифрование / дешифрование, переводчик) или любой Nth Derivative ‘функция (вычислить, преобразовать, решить, расшифровать / зашифровать, расшифровать / зашифровать, декодировать / закодировать, перевести), написанная на любом информационном языке (Python, Java, PHP, C #, Javascript, Matlab и т. д.)), и никакая загрузка данных, скрипт, копипаст или доступ к API для Nth Derivative не будут бесплатными, то же самое для автономного использования на ПК, планшете, iPhone или Android! dCode распространяется бесплатно и онлайн.

Нужна помощь?

Пожалуйста, посетите наше сообщество dCode Discord для запросов о помощи!
NB: для зашифрованных сообщений проверьте наш автоматический идентификатор шифра!

Вопросы / комментарии

Сводка

Похожие страницы

Поддержка

Форум / Справка

Ключевые слова

производная, n-я, функция, дифференцирование, последовательная, итерация, калькулятор

Ссылки

Источник: https: // www.2 + x-5 \ вправо) \ влево (1 + 6x \ вправо) $

3.2: Производная как функция

Цели обучения

Определите производную функцию заданной функции.
Постройте производную функцию от графика заданной функции.
Укажите связь между производными и непрерывностью.
Опишите три условия, когда функция не имеет производной.
Объясните значение производной высшего порядка.

Как мы видели, производная функции в данной точке дает нам скорость изменения или наклон касательной к функции в этой точке. Если мы дифференцируем функцию положения в данный момент времени, мы получаем скорость в этот момент. Кажется разумным заключить, что знание производной функции в каждой точке может дать ценную информацию о поведении функции. Однако процесс нахождения производной даже для нескольких значений с использованием методов предыдущего раздела быстро стал бы довольно утомительным.В этом разделе мы определяем производную функцию и изучаем процесс ее нахождения.

Производные функции

Функция производной дает производную функции в каждой точке области определения исходной функции, для которой определена производная. Мы можем формально определить производную функцию следующим образом.

Определение: производная функция

Пусть \ (f \) – функция. Производная функция , обозначаемая \ (f ‘\), является функцией, область определения которой состоит из таких значений \ (x \), что существует следующий предел:

\ [f ‘(x) = \ lim_ {h → 0} \ frac {f (x + h) −f (x)} {h}.\ label {derdef} \]

Функция \ (f (x) \) называется дифференцируемой в точке \ (a \), если существует \ (f ‘(a) \). В более общем смысле, функция называется дифференцируемой на на \ (S \), если она дифференцируема в каждой точке открытого множества \ (S \), а дифференцируемая функция – это функция, в которой \ (f ‘( x) \) существует в своем домене.

В следующих нескольких примерах мы используем уравнение \ ref {derdef}, чтобы найти производную функции.

Пример \ (\ PageIndex {1} \): поиск производной функции квадратного корня

Найдите производную от \ (f (x) = \ sqrt {x} \).

Раствор

Начните непосредственно с определения производной функции.

Заменить \ (f (x + h) = \ sqrt {x + h} \) и \ (f (x) = \ sqrt {x} \) в \ (f ‘(x) = \ displaystyle \ lim_ {h → 0} \ frac {f (x + h) −f (x)} {h} \).

\ (е ‘(х) = \ displaystyle \ lim_ {h → 0} \ frac {\ sqrt {x + h} – \ sqrt {x}} {h} \)
\ (= \ displaystyle \ lim_ {h → 0} \ frac {\ sqrt {x + h} – \ sqrt {x}} {h} ⋅ \ frac {\ sqrt {x + h} + \ sqrt { x}} {\ sqrt {x + h} + \ sqrt {x}} \)	Умножьте числитель и знаменатель на \ (\ sqrt {x + h} + \ sqrt {x} \) без распределения в знаменателе.
\ (= \ displaystyle \ lim_ {h → 0} \ frac {h} {h} left (\ sqrt {x + h} + \ sqrt {x} \ right)} \)	Умножьте числители и упростите.
\ (= \ displaystyle \ lim_ {h → 0} \ frac {1} {\ left (\ sqrt {x + h} + \ sqrt {x} \ right)} \)	Отмените \ (h \). 2 \).2−2x \ справа) = 2x − 2 \). Таким образом, для функции \ (y = f (x) \) каждое из следующих обозначений представляет производную от \ (f (x) \): \ (f ‘(x), \ quad \ dfrac {dy} {dx}, \ quad y’, \ quad \ dfrac {d} {dx} \ big (f (x) \ big) \). Вместо \ (f ‘(a) \) мы также можем использовать \ (\ dfrac {dy} {dx} \ Big \| _ {x = a} \). Нотация \ (\ dfrac {dy} {dx} \) (называемая нотацией Лейбница) довольно распространена в технике и физике. Чтобы лучше понять это обозначение, напомним, что производная функции в точке – это предел наклона секущих линий, когда секущие линии приближаются к касательной.Наклоны этих секущих часто выражаются в виде \ (\ dfrac {Δy} {Δx} \), где \ (Δy \) – разность значений \ (y \), соответствующая разнице в \ (x \) значения, которые выражаются как \ (Δx \) (Рисунок \ (\ PageIndex {1} \)). Таким образом, производная, которую можно представить как мгновенную скорость изменения \ (y \) по отношению к \ (x \), выражается как \ (\ Displaystyle \ frac {dy} {dx} = \ lim_ {Δx → 0} \ frac {Δy} {Δx} \). Рисунок \ (\ PageIndex {1} \): производная выражается как \ (\ dfrac {dy} {dx} = \ displaystyle \ lim_ {Δx → 0} \ frac {Δy} {Δx} \). График производной Мы уже обсуждали, как построить график функции, поэтому, имея уравнение функции или уравнение производной функции, мы можем построить график. Учитывая и то, и другое, мы ожидаем увидеть соответствие между графиками этих двух функций, поскольку \ (f ‘(x) \) дает скорость изменения функции \ (f (x) \) (или наклон касательной линия к \ (f (x) \)). В примере \ (\ PageIndex {1} \) мы обнаружили, что для \ (f (x) = \ sqrt {x} \), \ (f ‘(x) = \ frac {1} {2 \ sqrt { Икс}}\).Если мы построим график этих функций на тех же осях, как на рисунке \ (\ PageIndex {2} \), мы сможем использовать графики, чтобы понять взаимосвязь между этими двумя функциями. Во-первых, мы замечаем, что \ (f (x) \) увеличивается по всей своей области, а это означает, что наклон его касательных во всех точках положительный. Следовательно, мы ожидаем \ (f ‘(x)> 0 \) для всех значений x в его области определения. Кроме того, по мере увеличения \ (x \) наклон касательных к \ (f (x) \) уменьшается, и мы ожидаем увидеть соответствующее уменьшение \ (f ‘(x) \).2−2x, \; f ‘(x) = 2x − 2 \). Графики этих функций показаны на рисунке \ (\ PageIndex {3} \). Обратите внимание, что \ (f (x) \) убывает при \ (x <1 \). Для тех же значений \ (x \), \ (f '(x) <0 \). Для значений \ (x> 1 \), \ (f (x) \) увеличивается и \ (f ‘(x)> 0 \). Кроме того, \ (f (x) \) имеет горизонтальную касательную в \ (x = 1 \) и \ (f ‘(1) = 0 \). Рисунок \ (\ PageIndex {3} \): производная \ (f ‘(x) <0 \), где функция \ (f (x) \) убывает, и \ (f' (x)> 0 \), где \ (f (x) \) возрастает. Производная равна нулю, если функция имеет горизонтальную касательную. Пример \ (\ PageIndex {3} \): эскиз производной с использованием функции Используйте следующий график \ (f (x) \), чтобы нарисовать график \ (f ‘(x) \).2−4 \). На каком интервале находится график \ (f ‘(x) \) над осью \ (x \)? Подсказка График \ (f ‘(x) \) положительный, где \ (f (x) \) возрастает. Ответ \ ((0, + ∞) \) Деривативы и непрерывность Теперь, когда мы можем построить график производной, давайте рассмотрим поведение графиков. Во-первых, мы рассматриваем взаимосвязь между дифференцируемостью и непрерывностью.Мы увидим, что если функция дифференцируема в точке, она должна быть непрерывной там; однако функция, непрерывная в какой-то точке, не обязательно должна быть дифференцируемой в этой точке. Фактически, функция может быть непрерывной в точке и не дифференцируемой в этой точке по одной из нескольких причин. Дифференцируемость предполагает непрерывность Пусть \ (f (x) \) – функция и \ (a \) находится в ее области определения. Если \ (f (x) \) дифференцируема в \ (a \), то \ (f \) непрерывна в \ (a \). Проба Если \ (f (x) \) дифференцируемо в \ (a \), то \ (f ‘(a) \) существует и, если мы положим \ (h = x – a \), имеем \ (x = a + h \), и поскольку \ (h = xa \ to 0 \), мы можем видеть, что \ (x \ to a \). Затем \ [f ‘(a) = \ lim_ {h \ to 0} \ frac {f (a + h) -f (a)} {h} \ nonumber \] можно переписать как \ (F ‘(a) = \ displaystyle \ lim_ {x → a} \ frac {f (x) −f (a)} {x − a} \). Мы хотим показать, что \ (f (x) \) непрерывно в \ (a \), показав, что \ (\ displaystyle \ lim_ {x → a} f (x) = f (a). \) Таким образом, \ (\ begin {align } \ displaystyle \ lim_ {x → a} f (x) & = \ lim_ {x → a} \; \ big (f (x) −f (a) + f (a)) \ big) \\ [4pt] & = \ lim_ {x → a} \ left (\ frac {f (x) −f (a)} {x − a} ⋅ (x − a) + f (a) \ right) & & \ text {Умножить и разделить} (f (x) −f (a)) \ text {by} x − a.\\ [4pt] & = \ left (\ lim_ {x → a} \ frac {f (x) −f (a)} {x − a} \ right) ⋅ \ left (\ lim_ {x → a} \; (x − a) \ right) + \ lim_ {x → a} f (a) \\ [4pt] & = f ‘(a) ⋅0 + f (a) \\ [4pt] & = f (а). \ end {align } \) Следовательно, поскольку \ (f (a) \) определено и \ (\ displaystyle \ lim_ {x → a} f (x) = f (a) \), мы заключаем, что \ (f \) непрерывно в \ (а \). □ Мы только что доказали, что дифференцируемость предполагает непрерывность, но теперь мы рассмотрим, подразумевает ли непрерывность дифференцируемость. Чтобы определить ответ на этот вопрос, исследуем функцию \ (f (x) = \| x \| \).2}} = + ∞ \). Таким образом, \ (f ‘(0) \) не существует. Быстрый взгляд на график \ (f (x) = \ sqrt [3] {x} \) проясняет ситуацию. Функция имеет вертикальную касательную в точке \ (0 \) (рисунок \ (\ PageIndex {5} \)). Рисунок \ (\ PageIndex {5} \): функция \ (f (x) = \ sqrt [3] {x} \) имеет вертикальную касательную в точке \ (x = 0 \). Он непрерывен в \ (0 \), но не дифференцируем в \ (0 \). Функция \ (f (x) = \ begin {cases} x \ sin \ left (\ frac {1} {x} \ right), & & \ text {if} x ≠ 0 \\ 0, & & \ text {if} x = 0 \ end {ases} \) также имеет производную, которая демонстрирует интересное поведение в \ (0 \). Мы видим, что \ (е ‘(0) = \ displaystyle \ lim_ {x → 0} \ frac {x \ sin \ left (1 / x \ right) −0} {x − 0} = \ lim_ {x → 0} \ sin \ left (\ frac {1} {x} \ right) \). Этот предел не существует, в основном потому, что наклон секущих линий непрерывно меняет направление по мере приближения к нулю (Рисунок \ (\ PageIndex {6} \)). Рисунок \ (\ PageIndex {6} \): функция \ (f (x) = \ begin {cases} x \ sin \ left (\ frac {1} {x} \ right), & & \ text {if} x ≠ 0 \\ 0, & & \ text {if} x = 0 \ end {ases} \) не дифференцируем в \ (0 \). Итого: Заметим, что если функция не является непрерывной, она не может быть дифференцируемой, поскольку каждая дифференцируемая функция должна быть непрерывной. Однако, если функция непрерывна, она все равно может быть не дифференцируемой. Мы видели, что \ (f (x) = \| x \| \) не может быть дифференцируемым в \ (0 \), потому что предел наклона касательных линий слева и справа не одинаков. Визуально это привело к появлению острого угла на графике функции в точке \ (0.\) Отсюда заключаем, что для того, чтобы быть дифференцируемой в точке, функция должна быть «гладкой» в этой точке. Как мы видели в примере с \ (f (x) = \ sqrt [3] {x} \), функция не может быть дифференцируемой в точке, где есть вертикальная касательная. 2 + bx + (10b − 5) −5} {x + 10} & & \ text {Substitute} c = 10b − 5.2, & & \ text {if} x≥3 \ end {cases} \) как непрерывные, так и дифференцируемые в \ (3 \). Подсказка Используйте пример \ (\ PageIndex {4} \) в качестве руководства. Ответ \ (a = 6 \) и \ (b = −9 \) Производные инструменты высшего порядка Производная функции сама по себе является функцией, поэтому мы можем найти производную от производной. Например, производная функции положения – это скорость изменения положения или скорости.Производная скорости – это скорость изменения скорости, которая является ускорением. Новая функция, полученная дифференцированием производной, называется второй производной. Кроме того, мы можем продолжать использовать производные для получения третьей производной, четвертой производной и так далее. В совокупности они называются производными более высокого порядка . n}.2−3h} {h} \)	Упростите числитель.
\ (= \ displaystyle \ lim_ {h → 0} (4x + h − 3) \)	Выносим за скобки \ (h \) в числителе и сокращаем, добавляя \ (h \) в знаменатель.
\ (= 4x − 3 \)	Возьми предел.

Затем найдите \ (f ” (x) \), взяв производную от \ (f ‘(x) = 4x − 3. \)

\ (f ” (x) = \ displaystyle \ lim_ {h → 0} \ frac {f ‘(x + h) −f’ (x)} {h} \)

Используйте \ (f ‘(x) = \ displaystyle \ lim_ {h → 0} \ frac {f (x + h) −f (x)} {h} \) с \ (f’ (x) \) в место \ (f (x).3 \), найти \ (a (t). \)

Подсказка: Используйте пример \ (\ PageIndex {6} \) в качестве руководства.

Ответ: \ (а (т) = 6т \)

Ключевые концепции

Производная функции \ (f (x) \) – это функция, значение которой в \ (x \) равно \ (f ‘(x) \). {\ text {th}} \).

Ключевые уравнения

\ (е ‘(x) = \ displaystyle \ lim_ {h → 0} \ frac {f (x + h) −f (x)} {h} \)

Глоссарий

производная функция: дает производную функции в каждой точке области определения исходной функции, для которой определена производная

с дифференциацией \ (a \): функция, для которой существует \ (f ‘(a) \), дифференцируема в \ (a \)

дифференцируемый на \ (S \): функция, для которой \ (f ‘(x) \) существует для каждого \ (x \) в открытом множестве \ (S \), дифференцируема на \ (S \)

дифференцируемая функция: функция, для которой существует \ (f ‘(x) \), является дифференцируемой функцией

производная высшего порядка: производная производной, от второй производной до производной \ (n ^ {\ text {th}} \), называется производной более высокого порядка

Авторы и авторство

Гилберт Стрэнг (Массачусетский технологический институт) и Эдвин «Джед» Херман (Харви Мадд) со многими авторами.Этот контент OpenStax находится под лицензией CC-BY-SA-NC 4.0. Загрузите бесплатно с http://cnx.org.
Пол Сибургер (Колледж Монро) добавил объяснение альтернативного определения производной, используемого в доказательстве того, что дифференцируемость предполагает непрерывность.

Коллекция из 88 калькуляторов, разделенных по уровню навыков и типу

Воспользуйтесь нашим бесплатным калькулятором

Мы стали партнерами Mathway, чтобы предложить бесплатный онлайн-калькулятор.Обширный список других инструментов исчисления находится ниже.

Содержание

Обзор

По своей сути математический факультет Массачусетского технологического института объясняет, что исчисление – это «исследование того, как вещи меняются». Департамент отмечает, что это важная область исследований, поскольку «она дает нам возможность построить относительно простые количественные модели изменений и вывести их последствия».

В Интернете доступно множество ресурсов, которые помогут вам больше узнать об исчислении и его концепциях.Ниже представлена коллекция из 88 калькуляторов, разделенных по уровню квалификации и типу.

48 Введение в калькуляторы

Пределы

Изучение пределов будет важной частью вашего изучения математического анализа, поскольку они обращаются к значению, к которому функция приближается, когда входные данные приближаются к определенному значению. Khan Academy дает уроки о том, что такое ограничения и как они работают. Ниже приведен набор ресурсов, которые помогут вам лучше понять ограничения:

WolframAlpha.com’s Limit – результаты включают ваш предел, предел, нанесенный на график, и расширение ряда.

Предел

Symbolab.com – четко спроектированный и простой в использовании, результаты включают пошаговое объяснение и возможность увидеть ваш предел на графике.

Предел

MathPortal.org – введите свою функцию и проверьте, хотите ли вы найти двусторонний, левый или правый предел. Затем предоставляются четкие результаты.

Предел

NumberEmpire.com – введите свою функцию или попробуйте один из примеров и получите быстрые и понятные результаты.

Ограничение SolveMyMath.com – Простота использования; введите свою функцию, чтобы найти двусторонний, левый или правый предел.

Предел

Calcul.com – введите свое выражение, и предел будет предоставлен.

4 калькулятора асимптот

MathIsFun.com учит, что асимптота – это «линия, к которой приближается кривая, поскольку она направляется к бесконечности». Ниже представлен набор инструментов, которые помогут вам познакомиться с асимптотами.

Асимптоты WolframAlpha.com – используйте раскрывающееся меню, чтобы выбрать, какую асимптоту вы хотите найти: наклонную, горизонтальную или вертикальную.

Асимптоты

Symbolab.com – введите собственную функцию или выберите один из примеров. Результаты включают краткие объяснения и вашу асимптоту в виде графика.

Асимптоты EasyCalculation.com – каждый из этих инструментов включает различные возможные методы, используемые для решения асимптот. Просто введите свое уравнение, и результаты будут включать точку асимптоты, а также графическую асимптоту.

Деривативы

Как поясняет SOSMath.com, производная часто определяется двумя способами: «наклон кривой» или «скорость изменения».”Ниже приведен набор ресурсов, которые помогут вам узнать больше о производных финансовых инструментах:

Производная от SolveMyMath.com – попробуйте один из примеров или введите собственное выражение. График производной предоставляется вместе с вашими результатами.

Производная

Calculus-Calculator.com – проста в использовании и предоставляет пошаговое объяснение вместе с вашими результатами.

Производные от WolframAlpha.com – узнайте больше о производных из подробного руководства. Результаты включают вашу графическую производную, ее разложение в ряд, ее неопределенный интеграл и многое другое.

Derivative-Calculator.net’s Derivative – Простой с пошаговым объяснением, приведенным вместе с вашими результатами.

Symbolab.com’s Derivative – Чисто разработанный и простой в использовании, вы можете ввести собственное выражение или использовать один из примеров, чтобы узнать больше о производных. Результаты предоставлены пошаговым объяснением.

Производная

MathPortal.org – Следуйте инструкциям, чтобы убедиться, что вы правильно вводите выражение. Могут быть предоставлены первая, вторая или третья производная.

WebMath.com’s Find a Derivative – Учебная информация предоставляется, а результаты включают пошаговое объяснение.

Пошаговые производные от

Calc101.com – включает пошаговое объяснение того, как найти первую и вторую производные.

Производная

EasyCalculation.com – Следуйте инструкциям, чтобы убедиться, что вы правильно вводите выражение.

PlanetCalc.com’s Derivative – Чтобы узнать больше о производных, ознакомьтесь с предоставленными правилами дифференциации и производными от общих функций.

Производная

Calcul.com – введите свое выражение, и производная будет предоставлена.

Производная

Saltire.com – введите свою функцию, и результаты будут показаны на графике.

Правило продукта

EasyCalculation.com объясняет, что правило произведения – это «метод нахождения производной функции, которая является умножением двух других функций, для которых существуют производные». Ниже приведены два инструмента, которые используют правило продукта для поиска производной:

WolframAlpha.Правило продукта com – очень простое в использовании, просто введите свою функцию, и результат будет.

Правило продукта

EasyCalculation.com – введите собственную функцию или воспользуйтесь одним из встроенных примеров. Правило продукта используется для предоставления ваших результатов.

Правило частного

Как пояснил математический факультет Калифорнийского университета в Дэвисе, правило частного – это «формальное правило для различения задач, в которых одна функция делится на другую».

EasyCalculation.com’s Quotient Rule – Предоставляется некоторая учебная информация, которая поможет вам лучше понять это правило. Введите свою функцию или попробуйте один из примеров, приведенных для дальнейшей иллюстрации.

WolframAlpha.com’s Quotient Rule – Введите числитель и знаменатель, чтобы найти производную вашей функции с помощью правила частного.

Темп изменений

MathWords.com отмечает, что скорость изменения – это «изменение значения количества, деленное на прошедшее время». Ниже приведены инструменты, которые помогут вам узнать больше о скорости изменения.

TutorVista.com’s Average Rate of Change – Используйте предоставленные пошаговые объяснения, чтобы узнать больше о том, как определить скорость изменения.

Средняя скорость изменений на WolframAlpha.com – быстро, легко, и дает четкие результаты.

Ряд разложения Тейлора или многочлен Тейлора

Как объясняет MathIsFun.com, ряд Тейлора – это «расширение функции до бесконечной суммы членов». Ниже приведены ресурсы, которые помогут вам узнать больше о серии Тейлора, концепции, которая часто сбивает с толку студентов, изучающих математику, при первом знакомстве.

Серия Тейлора WolfamAlpha.com – приведены примеры, показывающие, как использовать этот инструмент для выполнения расширений рядов на основе определенных критериев. Результаты включают расширение ряда, графическое наглядное пособие и многое другое.

Серия Тейлора NumberEmpire.com – Включает краткую учебную информацию. Используйте один из четырех примеров или введите свою функцию. Предоставляются удобные результаты и возможность увидеть графическое представление.

Расширение серии Тейлора SolveMyMath.com – основной инструмент, обеспечивающий четкие результаты.

Точки перегиба

Как объясняет Wolfram MathWorld, точка перегиба – это «точка на кривой, в которой изменяется знак кривизны (то есть вогнутости)». Ниже приведен инструмент, который поможет вам узнать больше о точках перегиба.

Точки перегиба WolframAlpha.com – Простота использования, результаты включают нанесенные на график точки.

Метод Ньютона

Wolfram MathWorld учит, что метод Ньютона (или Ньютона-Рафсона) – это «алгоритм поиска корня, который использует первые несколько членов ряда Тейлора функции в непосредственной близости от предполагаемого корня.Ниже приведены инструменты, которые помогут вам научиться пользоваться методом Ньютона:

Метод Ньютона на Keisan.Casio.com – представлена формула метода Ньютона. Введите свою функцию и ее производную, чтобы получить результаты.

Shodor.org – решатель уравнений метода Ньютона – быстрый и простой в использовании, просто введите свою функцию, ее производную, начальное значение «x» и количество десятичных знаков, которые должны быть указаны в вашем ответе, и ваши результаты будут предоставлены. Он также сообщает вам, сколько итераций потребовалось, чтобы получить ваш ответ.

Метод Ньютона-Рафсона WolframAlpha.com – быстрый и простой; формула предоставляется.

Метод Ньютона на Maccery.com – прокрутите вниз до инструмента «Метод Ньютона». Введите свои данные. Результаты будут включать каждую итерацию.

Интегралы

Как объясняет Wolfram MathWorld, интеграл – это «математический объект, который можно интерпретировать как площадь или как обобщение площади». Приведенные ниже инструменты помогут улучшить вашу способность работать с интегралами:

Исчисление-калькулятор.com’s Integral – с ним легко работать, он дает пошаговое объяснение вместе с вашими результатами.

WolframAlpha.com’s Integral – Узнайте больше об интегралах из учебной информации и предоставленных примеров. Результаты включают графическое представление, разложение в ряд и неопределенный интеграл.

Integral-Calculator.com’s Integral – предоставляет примеры, которые помогут вам начать работу.

Интеграл

Symbolab.com – аккуратно разработанный и включает пошаговое объяснение с результатами.

MathPortal.org’s Integral – Следуйте инструкциям, чтобы убедиться, что вы вводите свои данные правильно. Используйте кнопку «Создать пример», чтобы узнать больше о том, как работают интегралы.

NumberEmpire.com’s Integral – Используйте один из четырех предоставленных примеров или введите свою собственную функцию. Результаты легко интерпретировать.

Integral от SolveMyMath.com – прост в использовании и обеспечивает четкие результаты.

WebMath.com’s Solve an Indefinite Integral – Отлично подходит для тех, кто только начинает работать с интегралами.Лучше всего использовать этот инструмент только с основными интегралами.

Экспоненциальный интеграл Keisan.Casio.com – введите значение «x», чтобы начать. Результаты включают вашу функцию на графике и двухэтапное объяснение.

CalCul.com’s Integral – Введите свое выражение, и ваши результаты будут предоставлены.

Логарифмический интеграл Had2Know.com – учебная информация предоставлена, чтобы помочь вам улучшить свои знания интегралов. Введите значение «x», и будут получены четкие результаты.

Экспоненциальный интеграл

MiniWebTool.com – определяющая формула предоставляется для справки. Введите значение «x», чтобы получить результаты.

40 Калькуляторы с расширенными возможностями

Сумма Римана

Как объясняет MathOpenRef.com, сумма Римана – это «метод аппроксимации общей площади под кривой на графике, иначе известный как интеграл». Ниже представлена подборка ресурсов, которые помогут вам лучше понять суммы Римана.

MathWorld.Сумма Римана от Wolfram.com – введите данные, чтобы увидеть сумму Римана на графике. Поэкспериментируйте с введенными данными, чтобы увидеть, как изменится график.

Сумма Римана EMathHelp.net – проста в использовании и включает пошаговое объяснение результатов.

IntMath.com’s Applet Riemann Sums – Предоставляется учебная информация. Выберите функцию в раскрывающемся меню, чтобы увидеть, как она отображается на графике. Отрегулируйте ползунки, чтобы увидеть, как графическая сумма Римана изменяется на графике.

Правило трапеции

MathWords.com объясняет, что правило трапеций – это « – метод приближения определенного интеграла с использованием линейных приближений f ». Приведенные ниже инструменты помогут вам научиться пользоваться правилом трапеции.

Правило трапеции NastyAccident.com – Следуйте инструкциям, чтобы ввести свои данные. Результаты включают пошаговое объяснение.

Правило трапеции EMathHelp.net – дает пошаговое объяснение ваших результатов.

EasyCalculation.com Правило трапеции – узнайте больше о правиле трапеции из предоставленной учебной информации. Следуйте инструкциям, чтобы убедиться, что вы правильно вводите свои данные.

Частичное разложение на фракции

Как объясняет PurpleMath.com, разложение на частичную дробь – это «процесс, когда начинается с упрощенного ответа и снова разбирается, или« разлагается »окончательное выражение на его исходные полиномиальные дроби». Ниже приведен набор ресурсов, которые помогут вам лучше понять разложение на частичную дробь.

Частичное разложение на дробь от WolframAlpha.com – просто и понятно, просто введите числитель и знаменатель, чтобы получить результат.

Calc101.com’s Step-by-Step Partial Fractions – Введите свое выражение (или воспользуйтесь приведенным примером), после чего будет предоставлено пошаговое объяснение для нахождения частичной дроби.

Частичные дроби

QuickMath.com – быстро и легко использовать, просто введите свою функцию, чтобы найти частичную дробь. Доступны базовая и расширенная версии.

Частичные дроби

Symbolab.com – введите свое выражение или воспользуйтесь одним из приведенных примеров. По результатам будет предоставлено пошаговое объяснение.

Обратные функции

Как объясняет Wikipedia.org, обратная функция «это функция, которая« переворачивает »другую функцию». Ниже приведен набор инструментов, которые помогут вам лучше понять обратные функции.

Обратная функция

Symbolab.com – аккуратно разработанный, простой в использовании и предоставляет пошаговое объяснение с результатами.Щелкните «График», чтобы увидеть обратную функцию на графике.

Обратная функция WolframAlpha.com – достаточно просто, чтобы проиллюстрировать основы, результаты включают вашу графическую обратную функцию.

Обратная функция NumberEmpire.com – выберите один из четырех примеров или введите свою собственную функцию, чтобы получить обратную функцию.

Обратная функция

AnalyzeMath.com – нажмите кнопку «Показать», и этот ресурс проведет вас через четырехэтапный процесс поиска обратной функции.

Обратная функция

CalculatorSoup.com – используйте раскрывающееся меню, чтобы выбрать функцию, которую вы хотите найти. Затем введите значение «x», чтобы получить результаты.

Обратная функция Keisan.Casio.com – введите значение «x», и будут предоставлены обратные гиперболические функции.

Обратная функция Gyplan.com – используйте раскрывающееся меню, чтобы выбрать тип обратной функции, которую вы хотите найти, а затем введите значение «x», чтобы получить результаты.

Дифференциальное уравнение

Как объясняет Wolfram MathWorld, дифференциальное уравнение – это «уравнение, которое включает производные функции, а также саму функцию.Ниже приведены несколько инструментов, которые помогут вам узнать больше о дифференциальных уравнениях:

Дифференциальные уравнения WolframAlpha.com – используйте для решения нескольких различных типов дифференциальных уравнений. Результаты включают в себя решение, графики отдельных растворов образцов, семейство растворов, представленных на графике, и многое другое.

Обыкновенные дифференциальные уравнения Symbolab.com – аккуратно разработанные и простые в использовании результаты включают пошаговое объяснение. Введите собственное уравнение или эксперимент, используя предоставленные примеры.

Math-CS.Gordon.edu Решение для дифференциальных уравнений первого порядка – от факультета математики и информатики Гордонского колледжа программа для решения уравнений поставляется с некоторой учебной информацией. Результаты включают график решения.

Однородные дифференциальные уравнения EasyCalculation.com

– быстрые, простые в использовании и обеспечивающие четкие результаты.

Метод Эйлера MathScoop.com – использует метод Эйлера для решения вашего уравнения. Результаты включают таблицу Эйлера и график точек Эйлера.

Метод Эйлера от Keisan.Casio.com – Необходимая формула включена, и с вашими результатами создается таблица Эйлера.

Решатель дифференциальных уравнений второго порядка Had2Know.com – узнайте больше о решении дифференциальных уравнений из предоставленной учебной информации и объясненных случаев.

Длина дуги

MathWords.com учит, что длина дуги – это длина кривой или линии. Ниже приведен набор ресурсов, которые помогут вам определить длину дуги.

1728.Длина дуги организации – выберите то, для чего вы хотите решить, затем введите известные значения. Ваш результат будет предоставлен.

Полная круговая дуга

HandyMath.com – введите два известных значения, чтобы найти радиус, длину, ширину, высоту, апофему, угол и площадь дуги или сегмента круга.

Круговая дуга AJDesigner.com – даны помеченная круговая диаграмма и формула длины дуги. Введите радиус и центральный угол, чтобы получить результат.

Длина дуги WolframAlpha.com – этот ресурс будет выполнять несколько функций, связанных с поиском длины дуги, и предоставляет пример для каждой, чтобы помочь вам начать работу.

TutorVista.com’s Arc Length – Предоставляется пошаговое объяснение того, как найти длину дуги, и примеры с объяснениями и результатами.

Интерактивная длина дуги MathOpenRef.com – перетащите точку A или точку B, чтобы увидеть, как регулируется длина дуги.

Flexibility.com’s Arc Length – Выберите, какой вариант использовать для определения длины дуги на основе ваших известных значений. Помеченная круговая диаграмма используется в качестве наглядного пособия.

Длина дуги PlanetCalc.com – Предоставляются помеченная круговая диаграмма и формулы.Введите радиус и угол, чтобы найти длину дуги и другие свойства, такие как площадь, длина хорды и периметр.

EasyCalculation.com’s Arc Length – Введите радиус и угол, и вы получите длину дуги.

Центр масс

MathWords.com предоставляет формулы для поиска центра масс. Ниже приводится набор инструментов, которые помогут вам лучше понять центр масс.

Центр масс TutorVista.com – введите «разные значения масс» и «расстояние между соответствующими массами», чтобы найти центр масс.

Calculator.Swiftutors.com Центр масс – предоставляет обучающую информацию, очень несложную и удобную для навигации любому учащемуся.

LearningAboutElectronics.com’s Center of Mass – Учебная информация, помеченная диаграмма и инструкции по использованию инструмента. Введите все известные массы и соответствующие расстояния, чтобы найти центр масс.

Последовательности

Как объясняет Пол в Online Math Notes, последовательность – это «список чисел, записанных в определенном порядке.Инструмент, представленный ниже, поможет вам узнать больше о последовательностях:

Последовательности WolfamAlpha.com – приведены примеры, показывающие, как использовать этот ресурс на основе различных критериев последовательностей. Результаты включают графическое представление, таблицу значений и представления серий.

серии

Как объясняет MathOpenReference.com, ряд – это «сумма некоторого набора членов последовательности». Используйте приведенные ниже ресурсы, чтобы лучше понять серию.

NumberEmpire.com’s Series – используйте один из четырех предоставленных примеров или введите собственное выражение. Результаты легко интерпретировать и предлагают возможность редактировать выражение.

Геометрическая серия

MathScoop.com – просто и быстро, просто введите свои значения, и сумма будет предоставлена.

Геометрическая серия

CalCul.com – отрегулируйте значения переменных с помощью стрелок, и результат будет предоставлен мгновенно.