Ряды для чайников mathprofi: Математическое Бюро. Страница 404
Сначала начнем с повторения. Вспомним случаи, когда нужно применять самый ходовойпредельный признак сравнения. Предельный признак сравнения применяется тогда, когда в общем члене ряда:
1) В знаменателе находится многочлен.
2) Многочлены находятся и в числителе и в знаменателе.
3) Один или оба многочлена могут быть под корнем.
Основные же предпосылки для применения признака Даламбера следующие:
1) В общий член ряда («начинку» ряда) входит какое-нибудь число в степени, например, , , и так далее. Причем, совершенно не важно, где эта штуковина располагается, в числителе или в знаменателе – важно, что она там присутствует.
2) В общий член ряда входит факториал. Что такое факториал? Ничего сложного, факториал – это просто свёрнутая запись произведения:
…
…
! При использовании признака Даламбера нам как раз придется расписывать факториал подробно. Как и в предыдущем пункте, факториал может располагаться вверху или внизу дроби.
а) При ряд сходится. В частности, ряд сходится при .
б) При ряд расходится. В частности, ряд расходится при .
в) При признак не дает ответа. Нужно использовать другой признак. Чаще всего единица получается в том случае, когда признак Даламбера пытаются применить там, где нужно использовать предельный признак сравнения.
У кого до сих пор проблемы с пределами или недопонимание пределов, обратитесь к урокуПределы. Примеры решений. Без понимания предела и умения раскрывать неопределенность дальше, к сожалению, не продвинуться.
А сейчас долгожданные примеры.
Пример 1
Исследовать ряд на сходимость
Мы видим, что в общем члене ряда у нас есть , а это верная предпосылка того, что нужно использовать признак Даламбера. Сначала полное решение и образец оформления, комментарии ниже.
Используем признак Даламбера:
Таким образом, исследуемый ряд сходится.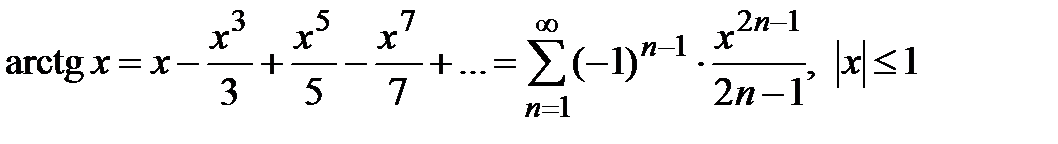
(1) Составляем отношение следующего члена ряда к предыдущему: . Из условия мы видим, что общий член ряда . Для того, чтобы получить следующий член ряда необходимо вместо подставить : .
(2) Избавляемся от четырехэтажности дроби. При определенном опыте решения этот шаг можно пропускать.
(3) В числителе раскрываем скобки. В знаменателе выносим четверку из степени.
(4) Сокращаем на . Константу выносим за знак предела. В числителе в скобках приводим подобные слагаемые.
(5) Неопределенность устраняется стандартным способом – делением числителя и знаменателя на «эн» в старшей степени.
(6) Почленно делим числители на знаменатели, и указываем слагаемые, которые стремятся к нулю.
В рассмотренном примере в общем члене ряда у нас встретился многочлен 2-ой степени. Что делать, если там многочлен 3-ей, 4-ой или более высокой степени? Дело в том, что если дан многочлен более высокой степени, то возникнут трудности с раскрытием скобок. В этом случае можно применять «турбо»-метод решения.
В этом случае можно применять «турбо»-метод решения.
Пример 2
Возьмём похожий ряд и исследуем его на сходимость
Сначала полное решение, потом комментарии:
Используем признак Даламбера:
Таким образом, исследуемый ряд сходится.
(1) Составляем отношение .
(2) Избавляемся от четырехэтажности дроби.
(3) Рассмотрим выражение в числителе и выражение в знаменателе. Мы видим, что в числителе нужно раскрывать скобки и возводить в четвертую степень: , чего делать совершенно не хочется. Кроме того, для тех, кто не знаком с биномом Ньютона, данная задача вообще может оказаться невыполнимой. Проанализируем старшие степени: если мы вверху раскроем скобки , то получим старшую степень . Внизу у нас такая же старшая степень: . По аналогии с предыдущим примером, очевидно, что при почленном делении числителя и знаменателя на у нас в пределе получится единица. Или, как говорят математики, многочлены и – одного порядка роста. Таким образом, вполне можно обвести отношение простым карандашом и сразу указать, что эта штука стремится к единице. Аналогично расправляемся со второй парой многочленов: и , они тоже одного порядка роста, и их отношение стремится к единице.
Таким образом, вполне можно обвести отношение простым карандашом и сразу указать, что эта штука стремится к единице. Аналогично расправляемся со второй парой многочленов: и , они тоже одного порядка роста, и их отношение стремится к единице.
На самом деле, такую «халтуру» можно было провернуть и в Примере №1, но для многочлена 2-ой степени такое решение смотрится всё-таки как-то несолидно. Лично я поступаю так: если есть многочлен (или многочлены) первой или второй степени, я использую «длинный» способ решения Примера 1. Если попадается многочлен 3-ей и более высоких степеней, я использую «турбо»-метод по образцу Примера 2.
Пример 3
Исследовать ряд на сходимость
Полное решение и образец оформления в конце урока
Рассмотрим типовые примеры с факториалами:
Пример 4
Исследовать ряд на сходимость
В общий член ряда входит и степень, и факториал. Ясно, как день, что здесь надо использовать признак Даламбера. Решаем.
Таким образом, исследуемый ряд расходится.
(1) Составляем отношение . Повторяем еще раз. По условию общий член ряда: . Для того чтобы получить следующий член ряда, вместо нужно подставить
, таким образом: .(2) Избавляемся от четырехэтажности дроби.
(3) Отщипываем семерку от степени. Факториалы расписываем подробно. Как это сделать – см. начало урока.
(4) Сокращаем всё, что можно сократить.
(5) Константу выносим за знак предела. В числителе раскрываем скобки.
(6) Неопределенность устраняем стандартным способом – делением числителя и знаменателя на «эн» в старшей степени.
Пример 5
Исследовать ряд на сходимость
Полное решение и образец оформления в конце урока
Пример 6
Исследовать ряд на сходимость
Иногда встречаются ряды, которые в своей начинке содержат «цепь» множителей, этот тип ряда мы еще не рассматривали. Как исследовать ряд с «цепочкой» множителей? Использовать признак Даламбера. Но сначала для понимания происходящего распишем ряд подробно:
Из разложения мы видим, что у каждого следующего члена ряда добавляется дополнительный множитель в знаменателе, поэтому, если общий член ряда , то следующий член ряда:
 Радикальный признак Коши обычно использует в тех случаях, когда общий член ряда ПОЛНОСТЬЮ находится в степени,зависящей от «эн». Либо когда корень «хорошо» извлекается из общего члена ряда. Есть еще экзотические случаи, но ими голову забивать не будем.
Радикальный признак Коши обычно использует в тех случаях, когда общий член ряда ПОЛНОСТЬЮ находится в степени,зависящей от «эн». Либо когда корень «хорошо» извлекается из общего члена ряда. Есть еще экзотические случаи, но ими голову забивать не будем.Пример 7
Исследовать ряд на сходимость
Мы видим, что общий член ряда полностью находится под степенью, зависящей от , а значит, нужно использовать радикальный признак Коши:
Таким образом, исследуемый ряд расходится.
(1) Оформляем общий член ряда под корень.
(2) Переписываем то же самое, только уже без корня, используя свойство степеней .
(3) В показателе почленно делим числитель на знаменатель, указывая, что
(4) В результате у нас получилась неопределенность . Здесь можно было пойти длинным путем: возвести в куб, возвести в куб, потом разделить числитель и знаменатель на «эн» в старшей степени. Но в данном случае есть более эффективное решение: можно почленно поделить числитель и знаменатель прямо под степенью-константой.
(5) Собственно выполняем почленное деление, и указываем слагаемые, которые стремятся к нулю.
(6) Доводим ответ до ума, помечаем, что и делаем вывод о том, что ряд расходится.
А вот более простой пример для самостоятельного решения:
Пример 8
Исследовать ряд на сходимость
И еще пара типовых примеров.
Полное решение и образец оформления в конце урока
Пример 9
Исследовать ряд на сходимость
Используем радикальный признак Коши:
Таким образом, исследуемый ряд сходится.
(1) Помещаем общий член ряда под корень.
(3) В показателе почленно делим числитель на знаменатель и указываем, что .
(4) Получена неопределенность вида . Здесь можно прямо в скобке почленно поделить числитель на знаменатель на «эн» в старшей степени.
 Нечто подобное у нас встречалось при изучении второго замечательного предела. Но здесь ситуация другая. Если бы коэффициенты при старших степенях были одинаковыми, например: , то фокус с почленным делением уже бы не прошел, и надо было бы использовать второй замечательный предел. Но у нас эти коэффициенты разные (5 и 6), поэтому можно (и нужно) делить почленно (кстати, наоборот – второй замечательный предел при разных коэффициентах при старших степенях уже не прокатывает).
Нечто подобное у нас встречалось при изучении второго замечательного предела. Но здесь ситуация другая. Если бы коэффициенты при старших степенях были одинаковыми, например: , то фокус с почленным делением уже бы не прошел, и надо было бы использовать второй замечательный предел. Но у нас эти коэффициенты разные (5 и 6), поэтому можно (и нужно) делить почленно (кстати, наоборот – второй замечательный предел при разных коэффициентах при старших степенях уже не прокатывает).(5) Собственно выполняем почленное деление и указываем, какие слагаемые у нас стремятся к нулю.
(6) Неопределенность устранена, у нас остался простейший предел: . Почему в бесконечно большой степени стремится к нулю? Потому-что основание степени удовлетворяет неравенству . Если у кого есть сомнения в справедливости предела , то я не поленюсь, возьму в руки калькулятор:
Если , то
Если , то
Если , то
Если , то
Если , то
… и т.д. до бесконечности – то есть, в пределе:
(7) Указываем, что и делаем вывод о том, что ряд сходится.
 является тот факт, что в общем члене ряда есть некоторая функция и её производная. Из темы Производная вы наверняка запомнили простейшую табличную вещь: , и у нас как раз такой канонический случай.
является тот факт, что в общем члене ряда есть некоторая функция и её производная. Из темы Производная вы наверняка запомнили простейшую табличную вещь: , и у нас как раз такой канонический случай.Как использовать интегральный признак? Сначала берем значок интеграла и переписываем со «счётчика» ряда верхний и нижний пределы: . Затем под интегралом переписываем «начинку» ряда с буковкой «хэ»: . Чего-то не хватает…, ах, да, еще в числителе нужно прилепить значок дифференциала: .
Теперь нужно вычислить несобственный интеграл . При этом возможно два случая:
1) Если выяснится, что интеграл сходится, то будет сходиться и наш ряд .
2) Если выяснится, что интеграл расходится, то наш ряд тоже будет расходиться.
Повторюсь, если материал запущен, то чтение параграфа будет трудным и малопонятным, поскольку применение признака по сути дела сводится к вычислениюнесобственного интеграла первого рода.
Полное решение и оформление примера должно выглядеть примерно так:
Используем интегральный признак:
Подынтегральная функция непрерывна на
Таким образом, исследуемый ряд расходится вместе с соответствующим несобственным интегралом.
Пример 12
Исследовать ряд на сходимость
Решение и образец оформления в конце урока
В рассмотренных примерах логарифм также мог находиться под корнем, это не изменило бы способа решения.
И еще два примера на закуску
Пример 13
Исследовать ряд на сходимость
По общим «параметрам» общий член ряда вроде бы подходит для использования предельного признака сравнения. Нужно всего лишь раскрыть скобки и сразу сдать на кандидата предельно сравнить данный ряд со сходящимся рядом . Впрочем, я немного слукавил, скобки можно и не раскрывать, но всё равно решение через предельный признак сравнения будет выглядеть довольно вычурно.
Поэтому мы используем интегральный признак Коши:
Подынтегральная функция непрерывна на
Получено конечное число, значит, исследуемый ряд сходится вместе с соответствующим несобственным интегралом.
! Примечание: полученное число – не является суммой ряда!!!
Пример 14
Исследовать ряд на сходимость
Решение и образец оформления в конце урока, который подходит к концу.
Таким образом, исследуемый ряд расходится.
Примечание: Можно было использовать и «турбо»-метод решения: сразу обвести карандашом отношение , указать, что оно стремится к единице и сделать пометку: «одного порядка роста».
Пример 5: Используем признак Даламбера:
Таким образом, исследуемый ряд сходится.
Пример 8:
Используем радикальный признак Коши.
Таким образом, исследуемый ряд сходится.
Пример 10:
Используем радикальный признак Коши.
Таким образом, исследуемый ряд расходится.
Примечание: Здесь основание степени , поэтому
Пример 12:
Используем интегральный признак.
Подынтегральная функция непрерывна на .
Получено конечное число, значит, исследуемый ряд сходится вместе с соответствующим несобственным интегралом.
Пример 14:
Используем интегральный признак. {n}}{n !}$
{n}}{n !}$
Читать дальше: разложение в ряд Маклорена элементарных функций.
- Смех без причины признак Даламбера
- Ряды Фурье
- Дисперсионный анализ ANOVA понятным языком
- Норден А.П. Краткий курс дифференциальной геометрии ОНЛАЙН
- Собственные числа и вектора матриц. Методы их нахождения
- Судоку для чайников – Уровень 3 // Обзор
- python – создает фиктивные закодированные столбцы для столбца и объединяет их с набором данных
- Работа с таблицами Excel для чайников: пошаговая инструкция
Смех без причины признак Даламбера
Подборка по базе: изм. 1 Реферат. Вредные привычки в детском возрасте общая характ, Таблица характерных неисправностей контакторов электромагнитного, Мировой финансовый кризис причины и последствия..docx, Оценка связи между качественными признаками.docx, Реферат 2020 Понятие государства и его признаки.docx, 37. Инфляция сущность, причины, социально-экономические последст, Статистика практическая Смехов.doc, Статистика практическая Смехов.doc, Виды и признаки переломов.docx, ПАМЯТКА ПРИЧИНЫ НЕВЫНАШИВАНИЯ БЕРЕМЕННОСТИ.docx
Смех без причины – признак Даламбера
Вот и пробил час функциональных рядов. Для успешного освоения темы, и, в частности, этого урока, нужно хорошо разбираться в обычных числовых рядах. Следует хорошо понимать, что такое ряд, уметь применять признаки сравнения для исследования ряда на сходимость. Таким образом, если Вы только-только приступили к изучению темы или являетесь чайником в высшей математике, необходимо последовательно проработать три урока: Ряды для чайников,Признак Даламбера. Признаки Коши и Знакочередующиеся ряды. Признак Лейбница. Обязательно все три! Если есть элементарные знания и навыки решения задач с числовыми рядами, то справиться с функциональными рядами будет довольно просто, поскольку нового материала не очень и много.
Таким образом, если Вы только-только приступили к изучению темы или являетесь чайником в высшей математике, необходимо последовательно проработать три урока: Ряды для чайников,Признак Даламбера. Признаки Коши и Знакочередующиеся ряды. Признак Лейбница. Обязательно все три! Если есть элементарные знания и навыки решения задач с числовыми рядами, то справиться с функциональными рядами будет довольно просто, поскольку нового материала не очень и много.
На данном уроке мы рассмотрим понятие функционального ряда (что это вообще такое), познакомимся со степенными рядами, которые встречаются в 99%-ах практических заданий, и научимся решать распространенную типовую задачу на нахождение радиуса сходимости, интервала сходимости и области сходимости степенного ряда. Далее можно будет рассмотреть материал о сумме степенного ряда и разложении функций в степенные ряды.
Понятие функционального ряда и степенного ряда
Обычный числовой ряд, вспоминаем, состоит из чисел:
Все члены ряда – это ЧИСЛА.
Функциональный же ряд состоит из ФУНКЦИЙ:
В общий член ряда помимо многочленов, факториалов и других подарков непременновходит буковка «икс». Выглядит это, например, так: . Как и числовой ряд, любой функциональный ряд можно расписать в развернутом виде:
Как видите, все члены функционального ряда – это функции.
Наиболее популярной разновидностью функционального ряда является степенной ряд.
Определение:
Степенной ряд – это ряд, в общий член которого входят целые положительные степени независимой переменной . Упрощенно степенной ряд во многих учебниках записывают так: , где – это старая знакомая «начинка» числовых рядов (многочлены, степени, факториалы, зависящие только от «эн»). Простейший пример:
Посмотрим на это разложение и еще раз осмыслим определение: члены степенного ряда содержат «иксы» в целых положительных (натуральных) степенях.
Очень часто степенной ряд можно встретить в следующих «модификациях»: или , где – константа. Например:
Например:
Строго говоря, упрощенные записи степенного ряда , или не совсем корректны. В показателе степени вместо одинокой буквы «эн» может располагаться более сложное выражение, например:
Или такой степенной ряд:
Лишь бы показатели степеней при «иксАх» были натуральными.
Сходимость степенного ряда.
Интервал сходимости, радиус сходимости и область сходимости
Не нужно пугаться такого обилия терминов, они идут «рядом друг с другом» и не представляют особых сложностей для понимания. Лучше выберем какой-нибудь простой подопытный ряд и сразу начнём разбираться.
Прошу любить и жаловать степенной ряд .
Переменная может принимать любое действительное значение от «минус бесконечности» до «плюс бесконечности». Подставим в общий член ряда несколько произвольных значений «икс»:
Если , то
Если , то
Если , то
Если , то
И так далее.
Очевидно, что, подставляя в то или иное значение «икс», мы получаем различные числовые ряды. Некоторые числовые ряды будут сходиться, а некоторые расходиться. И наша задача найти множество значений «икс», при котором степенной ряд будетсходиться. Такое множество и называется областью сходимости ряда.
Некоторые числовые ряды будут сходиться, а некоторые расходиться. И наша задача найти множество значений «икс», при котором степенной ряд будетсходиться. Такое множество и называется областью сходимости ряда.
Для любого степенного ряда (временно отвлекаемся от конкретного примера) возможны три случая:
1) Степенной ряд сходится абсолютно на некотором интервале . Иными словами, если мы выбираем любое значение «икс» из интервала и подставляем его в общий член степенного ряда, то у нас получается абсолютно сходящийся числовой ряд. Такой интервал и называется интервалом сходимости степенного ряда.
Радиус сходимости, если совсем просто, это половина длины интервала сходимости:
Геометрически ситуация выглядит так:
В данном случае, интервал сходимости ряда: , радиус сходимости ряда:
Широко распространен тривиальный случай, когда интервал сходимости симметричен относительно нуля:
>
Здесь интервал сходимости ряда: , радиус сходимости ряда:
А что будет происходить на концах интервала ? В точках , степенной рядможет, как сходиться, так и расходится, и для выяснения этого необходимо проводить дополнительное исследование. После такого исследования речь идёт уже об области сходимости ряда:
После такого исследования речь идёт уже об области сходимости ряда:
– Если установлено, что степенной ряд расходится на обоих концах интервала, то область сходимости ряда совпадает с интервалом сходимости:
– Если установлено, что степенной ряд сходится на одном конце интервала и расходится на другом, то область сходимости ряда представляет собой полуинтервал: или .
– Если установлено, что степенной ряд сходится на обоих концах интервала, то область сходимости ряда представляет собой отрезок:
Термины очень похожи, область сходимости ряда – это чуть более детализированныйинтервал сходимости ряда.
С двумя оставшимися случаями всё короче и проще:
2) Степенной ряд сходится абсолютно при любом значении . То есть, какое бы значение «икс» мы не подставили в общий член степенного ряда – в любом случае у нас получитсяабсолютно сходящийся числовой ряд. Интервал сходимости и область сходимости в данном случае совпадают: . Радиус сходимости: . Рисунок приводить не буду, думаю, нет необходимости.
Радиус сходимости: . Рисунок приводить не буду, думаю, нет необходимости.
3) Степенной ряд сходится в единственной точке. Если ряд имеет вид , то он будет сходиться в единственной точке . В этом случае интервал сходимости и область сходимости ряда тоже совпадают и равны единственному числу – нулю: . Если ряд имеет вид , то он будет сходиться в единственной точке , если ряд имеет вид , то, понятно, – в точке «минус а». Радиус сходимости ряда во всех случаях, естественно, нулевой: .
Других вариантов нет. Область сходимости степенного ряда – это всегда либо единственная точка, либо любое «икс», либо интервал (возможно полуинтервал, отрезок). Подчеркиваю, что данная классификация справедлива для степенных рядов. Для произвольного функционального ряда она в общем случае является неверной.
Исследование степенного ряда на сходимость
После небольшой порции теоретического материала переходим к рассмотрению типового задания, которое практически всегда встречается на зачетах и экзаменах по высшей математике.
Пример 1
Найти область сходимости степенного ряда
Задание часто формулируют эквивалентно: Найти интервал сходимости степенного ряда и исследовать его сходимость на концах найденного интервала.
Алгоритм решения довольно прозрачен и трафаретен.
На первом этапе находим интервал сходимости ряда. Почти всегда необходимо использовать признак Даламбера и находить предел . Технология применения признака Даламбера точно такая же, как и для числовых рядов, с ней можно ознакомиться на урокеПризнак Даламбера. Признаки Коши. Единственное отличие – все дела у нас происходят под знаком модуля.
Итак, решаем наш предел:
(1) Составляем отношение следующего члена ряда к предыдущему.
(2) Избавляемся от четырехэтажности дроби.
(3) В числителе по правилу действий со степенями «отщипываем» один «икс». В знаменателе возводим двучлен в квадрат.
(4) Выносим оставшийся «икс» за знак предела, причем, выносим его вместе со знаком модуля. Почему со знаком модуля? Дело в том, что наш предел и так будет неотрицательным, а вот «икс» вполне может принимать отрицательные значения. Поэтому модуль относится именно к нему.
Кстати, почему можно вообще вынести за знак предела? Потому-что «динамической» переменной в пределе у нас является «эн», и от этого нашему «иксу» ни жарко ни холодно.
(5) Устраняем неопределенность стандартным способом.
После того, как предел найден, нужно проанализировать, что у нас получилось.
Если в пределе получается ноль, то алгоритм решения заканчивает свою работу, и мы даём окончательный ответ задания: «Область сходимости степенного ряда: » (любое действительное число – случай №2 предыдущего параграфа). То есть, степенной ряд сходится при любом значении «икс». Ответ можно записать эквивалентно: «Ряд сходится при » (значок в математике обозначает принадлежность).
Если в пределе получается бесконечность, то алгоритм решения также заканчивает свою работу, и мы даём окончательный ответ задания: «Ряд сходится при » (или при либо »). Смотрите случай №3 предыдущего параграфа.
Если в пределе получается не ноль и не бесконечность, то у нас самый распространенный на практике случае №1 – ряд сходится на некотором интервале.
В данном случае предел равен . Как найти интервал сходимости ряда? Составляем неравенство:
В ЛЮБОМ задании данного типа в левой части неравенства должен находиться результат вычисления предела, а в правой части неравенства – строго единица. Не буду объяснять, почему именно такое неравенство и почему справа единица. Уроки носят практическую направленность, и уже очень хорошо, что от моих рассказов не повесился профессорско-преподавательский состав стали понятнее некоторые теоремы.
Техника работы с модулем и решения двойных неравенств подробно рассматривалась на первом курсе в статье Область определения функции, но для удобства я постараюсь максимально подробно закомментировать все действия. Раскрываем неравенство с модулем по школьному правилу . В данном случае:
– интервал сходимости исследуемого степенного ряда.
Половина пути позади.
На втором этапе необходимо исследовать сходимость ряда на концах найденного интервала.
Сначала берём левый конец интервала и подставляем его в наш степенной ряд :
При
Получен числовой ряд, и нам нужно исследовать его на сходимость (уже знакомая из предыдущих уроков задача).
Используем признак Лейбница:
1) Ряд является знакочередующимся.
2) – члены ряда убывают по модулю. Каждый следующий член ряда по модулю меньше, чем предыдущий, значит, убывание монотонно.
Вывод: ряд сходится.
Исследуем ряд на абсолютную сходимость:
– сходится (случай обобщенного гармонического ряда).
Таким образом, полученный числовой ряд сходится абсолютно.
Далее рассматриваем правый конец интервала , подставляем это значение в наш степенной ряд :
При – сходится.
Таким образом, степенной ряд сходится на обоих концах найденного интервала.
Ответ: Область сходимости исследуемого степенного ряда:
Имеет право на жизнь и другое оформление ответа: Ряд сходится, если
Иногда в условии задачи требуют указать радиус сходимости. Очевидно, что в рассмотренном примере .
Пример 2
Найти область сходимости степенного ряда
Решение: Найдем интервал сходимости данного ряда. Используем признак Даламбера:
Составляем стандартное неравенство:
Ряд сходится при
Слева нам нужно оставить только , поэтому умножаем обе части неравенства на 3:
И раскрываем неравенство с модулем по правилу :
– интервал сходимости исследуемого степенного ряда.
Исследуем сходимость степенного ряда на концах найденного интервала.
1) При
Обратите внимание, что при подстановке значения в степенной ряд у нас сократилась степень . Это верный признак того, что мы правильно нашли интервал сходимости ряда.
Исследуем полученный числовой ряд на сходимость.
Используем признак Лейбница.
– Ряд является знакочередующимся.
– – члены ряда убывают по модулю. Каждый следующий член ряда по модулю меньше, чем предыдущий, значит, убывание монотонно.
Вывод: Ряд сходится.
Исследуем ряд на абсолютную сходимость:
Сравним данный ряд с расходящимся рядом .
Используем предельный признак сравнения:
Получено конечное число, отличное от нуля, значит, ряд расходится вместе с рядом .
Таким образом, ряд сходится только условно.
2) При – расходится (по доказанному).
Ответ: Область сходимости исследуемого степенного ряда: . При ряд сходится только условно.
В рассмотренном примере областью сходимости степенного ряда является полуинтервал, причем во всех точках интервала степенной ряд сходится абсолютно (см. предыдущий параграф), а в точке , как выяснилось – сходится только условно.
Пример 3
Найти интервал сходимости степенного ряда и исследовать его сходимость на концах найденного интервала
Это пример для самостоятельного решения.
Рассмотрим пару примеров, которые встречаются редко, но встречаются.
Пример 4
Найти область сходимости ряда:
Решение: Найдем интервал сходимости данного ряда. Используем признак Даламбера:
(1) Составляем отношение следующего члена ряда к предыдущему.
(2) Избавляемся от четырехэтажности дроби.
(3) Кубы и по правилу действий со степенями подводим под единую степень. В числителе хитро раскладываем степень , т.е. раскладываем таким образом, чтобы на следующем шаге сократить дробь на . Факториалы расписываем подробно.
(4) Под кубом почленно делим числитель на знаменатель, указывая, что . В дроби сокращаем всё, что можно сократить. Множитель выносим за знак предела, его можно вынести, поскольку в нём нет ничего, зависящего от «динамической» переменной «эн». Обратите внимание, что знак модуля не нарисован – по той причине, что принимает неотрицательные значения при любом «икс».
В пределе получен ноль, а значит, можно давать окончательный ответ:
Ответ: Ряд сходится при
А сначала-то казалось, что этот ряд со «страшной начинкой» будет трудно решить. Ноль или бесконечность в пределе – почти подарок, ведь решение заметно сокращается!
Пример 5
Найти область сходимости ряда
Это пример для самостоятельного решения. Будьте внимательны 😉 Полное решение ответ в конце урока.
Рассмотрим еще несколько примеров, содержащих элемент новизны в плане использования технических приемов.
Пример 6
Найти интервал сходимости ряда и исследовать его сходимость на концах найденного интервала
Решение: В общий член степенного ряда входит множитель , обеспечивающий знакочередование. Алгоритм решения полностью сохраняется, но при составлении предела мы игнорируем (не пишем) этот множитель, поскольку модуль уничтожает все «минусы».
Найдем интервал сходимости данного ряда. Используем признак Даламбера:
Составляем стандартное неравенство:
Ряд сходится при
Слева нам нужно оставить только модуль, поэтому умножаем обе части неравенства на 5:
Теперь раскрываем модуль уже знакомым способом:
В середине двойного неравенства нужно оставить только «икс», в этих целях из каждой части неравенства вычитаем 2:
– интервал сходимости исследуемого степенного ряда.
Исследуем сходимость ряда на концах найденного интервала:
1) Подставляем значение в наш степенной ряд :
Будьте предельно внимательны, множитель не обеспечивает знакочередование, при любом натуральном «эн» . Полученный минус выносим за пределы ряда и забываем про него, поскольку он (как и любая константа-множитель) никак не влияет на сходимость или расходимость числового ряда.
Еще раз заметьте, что в ходе подстановки значения в общий член степенного ряда у нас сократился множитель . Если бы этого не произошло, то это бы значило, что мы либо неверно вычислили предел, либо неправильно раскрыли модуль.
Итак, требуется исследовать на сходимость числовой ряд . Здесь проще всего использовать предельный признак сравнения и сравнить данный ряд с расходящимся гармоническим рядом. Но, если честно, предельный признак сравнения до ужаса мне надоел, поэтому внесу некоторое разнообразие в решение.
Используем интегральный признак.
Подынтегральная функция непрерывна на .
Таким образом, полученный числовой ряд расходится вместе с соответствующим несобственным интегралом.
2) Исследуем второй конец интервала сходимости.
При
Используем признак Лейбница:
– Ряд является знакочередующимся.
– – члены ряда убывают по модулю. Каждый следующий член ряда по модулю меньше, чем предыдущий, значит, убывание монотонно.
Вывод: ряд сходится
Рассматриваемый числовой ряд не является абсолютно сходящимся поскольку – расходится (по доказанному).
Ответ: – область сходимости исследуемого степенного ряда, при ряд сходится только условно.
Пример 7
Найти интервал сходимости ряда и исследовать его сходимость на концах найденного интервала
Это пример для самостоятельного решения.
Кто утомился, может сходить покурить, а мы рассмотрим еще два примера.
Пример 8
Найти интервал сходимости ряда и исследовать его сходимость на концах найденного интервала
Решение: Найдем интервал сходимости данного ряда. Используем признак Даламбера:
Предел по той причине, что числитель и знаменатель одного порядка роста. Более подробно об этом моменте и «турбо»-методе решения читайте в статьеПризнак Даламбера. Признаки Коши.
Итак, ряд сходится при
Умножаем обе части неравенства на 9:
Извлекаем из обеих частей корень, при этом помним старый школьный прикол :
Раскрываем модуль:
И прибавляем ко всем частям единицу:
– интервал сходимости исследуемого степенного ряда.
Исследуем сходимость степенного ряда на концах найденного интервала:
1) Если , то получается следующий числовой ряд:
Множитель бесследно пропал, поскольку при любом натуральном значении «эн» .
И в третий раз обращаю внимание на то, что в результате подстановки сократились степени , а значит, интервал сходимости найден правильно.
По всем признакам для полученного числового ряда следует применить предельный признак сравнения. Какой ряд подобрать для сравнения? Об этой методике я уже рассказывал на уроке Ряды для чайников. Повторим.
Определяем старшую степень знаменателя, для этого мысленно или на черновике отбрасываем под корнем всё, кроме самого старшего слагаемого: . Таким образом, старшая степень знаменателя равна . Старшая степень числителя, очевидно, равна 1. Из старшей степени знаменателя вычитаем старшую степень числителя: .
Таким образом, наш ряд нужно сравнить со сходящимся рядом .
Используем предельный признак сравнения:
Получено конечное, отличное от нуля число, значит, ряд сходится вместе с рядом .
2) Что происходит на другом конце интервала?
При – сходится.
А вот и вознаграждение за мучения в предыдущем пункте! Получился точно такой же числовой ряд, сходимость которого мы только что доказали.
Ответ: область сходимости исследуемого степенного ряда:
Чуть менее сложный пример для самостоятельного решения:
Пример 9
Найти область сходимости ряда
Достаточно для начала =)
В заключение остановлюсь на одном моменте. Во всех примерах мы использовали признак Даламбера и составляли предел . Всегда ли при решении заданий такого типа нужно применять признак Даламбера? Почти всегда. Однако в редких случаях невероятно выгодно использовать радикальный признак Коши и составлять предел , при этом техника и алгоритм решения задачи остаются точно такими же! Что это за случаи? Это те случаи, когда из общего члена степенного ряда «хорошо» (полностью) извлекается корень «энной» степени.
Следующий урок по теме – Разложение функций в степенные ряды. Примеры решений.
Желаю успехов!
Решения и ответы:
Пример 3: Решение: Найдем интервал сходимости данного ряда. Используем признак Даламбера:
Ряд сходится при
Слева нужно оставить только модуль, поэтому умножаем обе части неравенства на 7
– интервал сходимости исследуемого степенного ряда.
Исследуем сходимость ряда на концах найденного интервала.
1) При
Используем признак Лейбница.
– Ряд является знакочередующимся.
– члены ряда не убывают по модулю.
Вывод: Ряд расходится
2) При
Ряд расходится, так как не выполнен необходимый признак сходимости ряда.
Ответ: – область сходимости исследуемого степенного ряда
Пример 5: Решение: Найдем интервал сходимости данного ряда. Используем признак Даламбера:
Ответ: Ряд сходится при
Почему получилась двойка, а не ноль? Перечитайте классификацию области сходимости степенного ряда. Хотя, наверное, многие уже понимают, почему.
Пример 7: Решение: Найдем интервал сходимости данного ряда. Используем признак Даламбера:
Ряд сходится при
Слева нужно оставить только модуль, умножаем обе части неравенства на :
В середине нужно оставить только «икс», вычитаем из каждой части неравенства 3:
– интервал сходимости исследуемого степенного ряда.
Исследуем сходимость ряда на концах найденного интервала:
1) При
Степень сократилась, значит, мы на верном пути.
Используем признак Лейбница.
Ряд является знакочередующимся.
– члены ряда убывают по модулю. Каждый следующий член ряда по модулю меньше, чем предыдущий, значит, убывание монотонно.
Ряд сходится по признаку Лейбница.
Исследуем ряд на абсолютную сходимость:
Используем интегральный признак.
Подынтегральная функция непрерывна на .
Таким образом, ряд расходится вместе с соответствующим несобственным интегралом. Ряд сходится только условно.
2) При – расходится (по доказанному).
Ответ: Область сходимости исследуемого степенного ряда: , при ряд сходится только условно.
Область сходимости окончательно можно записать так:, или даже так: .
Примечание: Ряд можно было исследовать на сходимость с помощью предельного признака сравнения.
Пример 9: Решение: Найдем интервал сходимости данного ряда. Используем признак Даламбера:
Ряд сходится при
– интервал сходимости исследуемого степенного ряда.
Исследуем сходимость ряда на концах найденного интервала.
1) При
Сравним данный ряд с расходящимся гармоническим рядом . Используем предельный признак сравнения.
Получено конечное число, отличное от нуля, значит, полученный числовой ряд расходится вместе с гармоническим рядом.
2) При – расходится (по доказанному).
Ответ: область сходимости исследуемого степенного ряда:
Ряды Фурье
Отрицательный аргумент дела не меняет: . Пожалуй, достаточно.
И, в-третьих, уважаемый отряд космонавтов, необходимо уметь… интегрировать.
В частности, уверенно подводить функцию под знак дифференциала, интегрировать по частям и быть в ладах с формулой Ньютона-Лейбница. Начнём важные предполётные упражнения. Категорически не рекомендую пропускать, чтобы потом не плющило в невесомости:
Пример 1 Вычислить определённые интегралы
где принимает натуральные значения.
Решение: интегрирование проводится по переменной «икс» и на данном этапе дискретная переменная «эн» считается константой. Во всех интегралах подводим функцию под знак дифференциала:
а)
Перед применением формулы Ньютона-Лейбница полезно мысленно либо на черновике выполнить проверку. Используя правило дифференцирования сложной функции и не забывая, что – это константа, находим производную от первообразной:
– получена исходная
подынтегральная функция, как оно и должно быть.
После интегрирования константа сразу выносится за скобки, и стандартная подстановка
проходит без её участия: сначала в вместо «икс» подставляем верхний предел (ноль), затем нижний предел («минус пи»). Синус нуля равен нулю, и как только что отмечалось, при любом натуральном «эн».
Кстати, результат тут виден сразу – интеграл от нечётной функции по симметричному относительно нуля отрезку равен нулю.
Не забываем о промежуточной проверке первообразной:
И на завершающем этапе даже лучше не проводить замены , а воспользоваться чётностью косинуса:
Крайне желательно научиться выполнять некоторые действия в уме и записывать решение сокращённо:
Желательно потому, что в рядах Фурье и без этого гелевый стержень опустеет. Следующие два пункта отличаются усложнённой константой:
Проверка:
Подстановку распишу очень подробно:
Здесь на последнем этапе внесли «минус» в скобку и сделали ответ более компактным, возьмите на заметку этот приём. Также обратите внимание, что в результате применения формулы Ньютона-Лейбница, получено не число, а числовая последовательность.
Короткая версия решения, к которой хорошо бы пристреляться, выглядит так:
Привыкаем:
Четыре оставшихся пункта самостоятельно. Постарайтесь добросовестно отнестись к заданию и оформить интегралы коротким способом. Образцы решений в конце урока.
После КАЧЕСТВЕННОГО выполнения упражнений надеваем скафандры и готовимся к старту!
Разложение функции в ряд Фурье на промежутке
Рассмотрим некоторую функцию , которая определена по крайне мере на промежутке (а, возможно, и на бОльшем промежутке). Если данная функция
интегрируема на отрезке | , то её можно разложить в тригонометрический ряд Фурье: |
, где – так называемые коэффициенты Фурье.
При этом число называют периодом разложения, а число –
полупериодом разложения.
Очевидно, что в общем случае ряд Фурье состоит из синусов и косинусов:
Действительно, распишем его подробно:
Нулевой член ряда принято записывать в виде | . |
Коэффициенты Фурье рассчитываются по следующим формулам:
Прекрасно понимаю, что начинающим изучать тему пока малопонятны новые термины:
период разложения, полупериод, коэффициенты Фурье и др. Без паники, это не сравнимо с волнением перед выходом в открытый космос. Во всём разберёмся в ближайшем примере, перед выполнением которого логично задаться насущными практическими вопросами:
Что нужно сделать в нижеследующих заданиях?
Разложить функцию | в ряд Фурье. Дополнительно нередко требуется изобразить | |
график функции | , график суммы ряда | , частичной суммы и в случае изощрённых |
профессорский фантазий – сделать что-нибудь ещё.
Как разложить функцию в ряд Фурье?
По существу, нужно найти коэффициенты Фурье , то есть, составить и вычислить три определённых интеграла.
Пожалуйста, перепишите общий вид ряда Фурье и три рабочие формулы к себе в тетрадь. Я очень рад, что у некоторых посетителей сайта прямо на моих глазах осуществляется детская мечта стать космонавтом =)
Поехали: Пример 2
Разложить функцию | в ряд Фурье на промежутке | . Построить график |
, график суммы ряда | и частичной суммы | . |
Решение: первая часть задания состоит в разложении функции в ряд Фурье. Начало стандартное, обязательно записываем, что:
В данной задаче период разложения , полупериод . Разложим функцию в ряд Фурье на промежутке :
Используя соответствующие формулы, найдём коэффициенты Фурье. Теперь нужно составить и вычислить три определённых интеграла. Для удобства я буду нумеровать пункты:
1)Первый интеграл самый простой, однако и он уже требует глаз да глаз:
2)Используем вторую формулу:
Данный интеграл хорошо знаком и берётся он по частям:
При нахождении использован метод подведения функции под знак дифференциала. В рассматриваемом задании сподручнее сразу использовать формулу интегрирования по
частям в определённом интеграле | : |
Пара технических замечаний. Во-первых, после применения формулы всё выражение нужно заключить в большие скобки, так как перед исходным интегралом находится
константа . Не теряем её! Скобки можно раскрыть на любом дальнейшем шаге, я это сделал в самую последнюю очередь. В первом «куске» проявляем крайнюю аккуратность в подстановке, как видите, константа не при делах, и пределы
интегрирования подставляются в произведение | . Данное действие выделено |
квадратными скобками. Ну а интеграл | второго «куска» формулы вам хорошо |
знаком из тренировочного задания 😉
Исамое главное – предельная концентрация внимания!
3)Ищем третий коэффициент Фурье:
Получен родственник предыдущего интеграла, который тоже интегрируется по частям:
Этот экземпляр чуть сложнее, закомментирую дальнейшие действия пошагово:
(1) Выражение полностью заключаем в большие скобки. Не хотел
показаться занудой, слишком уж часто теряют константу .
(2) В данном случае я немедленно раскрыл эти большие скобки. Особое внимание
уделяем первому «куску»: константа | курит в сторонке и не участвует в подстановке | ||
пределов интегрирования ( и | ) в произведение | . Ввиду загромождённости | |
записи это действие снова целесообразно выделить квадратными скобками. Со вторым
«куском» | всё проще: здесь дробь | появилась после раскрытия больших |
скобок, а константа | – в результате интегрирования знакомого интеграла 😉 | |
(3)В квадратных скобках проводим преобразования , а в правом интеграле – подстановку пределов интегрирования.
(4)Выносим «мигалку» из квадратных скобок:
,после чего раскрываем внутренние скобки:
.
(5) Сокращаем 1 и –1 в скобках, проводим окончательные упрощения. Наконец-то найдены все три коэффициента Фурье:
Подставим их в формулу :
При этом не забываем разделить пополам. На последнем шаге константа («минус два»), не зависящая от «эн», вынесена за пределы суммы.
Таким образом, мы получили разложение функции в ряд Фурье на промежутке
:
Изучим вопрос сходимости ряда Фурье. Я объясню теорию, в частности теорему Дирихле, буквально «на пальцах», поэтому если вам необходимы строгие формулировки, пожалуйста, обратитесь к учебнику по математическому анализу (например, 2-й том Бохана; или 3-й том Фихтенгольца, но в нём труднее).
Во второй части задачи требуется изобразить график , график суммы ряда и график частичной суммы .
График функции представляет собой обычную прямую на плоскости, которая проведена чёрным пунктиром:
Разбираемся с суммой ряда . Как вы знаете, функциональные ряды сходятся к функциям. В нашем случае построенный ряд Фурье при любом
значении «икс» сойдётся к функции , которая изображена красным цветом. Данная функция терпит разрывы 1-го рода в точках , но определена и в них (красные точки на чертеже)
Таким образом: . Легко видеть, что заметно отличается от
исходной функции , именно поэтому в записи ставится значок «тильда», а не знак равенства.
Изучим алгоритм, по которому удобно строить сумму ряда.
На центральном интервале ряд Фурье сходится к самой функции (центральный красный отрезок совпадает с чёрным пунктиром линейной функции).
Теперь немного порассуждаем о природе рассматриваемого тригонометрического разложения. В ряд Фурье входят только периодические функции (константа, синусы и косинусы), поэтому сумма ряда
тоже представляет собой периодическую функцию.
После выполнения чертежа завершаем задание:
Ответ:
Во многих задачах функция терпит разрыв 1-го рода прямо на периоде разложения: Пример 3
Разложить в ряд Фурье функцию | , заданную на отрезке | . Начертить график |
функции и полной суммы ряда. |
|
|
Предложенная функция задана кусочным образом (причём, заметьте, только на отрезке
) и терпит разрыв 1-го рода в точке | . Можно ли вычислить коэффициенты | ||
Фурье? Без проблем. И левая | и правая | части функции интегрируемы на | |
своих промежутках, поэтому интегралы в каждой из трёх формул следует представить в виде суммы двух интегралов. Посмотрим, например, как это делается у нулевого коэффициента:
Второй интеграл оказался равным нулю, что убавило работы, но так бывает далеко не всегда.
Аналогично расписываются два других коэффициента Фурье. |
| |||
Как изобразить сумму ряда? На левом интервале | чертим отрезок прямой | |||
, а на интервале | – отрезок прямой | (жирно-жирно выделяем | ||
участок оси | ). То есть, на промежутке разложения | сумма ряда | совпадает с | |
функцией | везде, кроме трёх «нехороших» точек. В точке разрыва функции | |||
ряд Фурье сойдётся к изолированному значению, которое располагается ровно посередине
«скачка» разрыва. Его нетрудно увидеть и устно: левосторонний предел: |
| ||
| , правосторонний предел: |
| и, очевидно, |
что ордината средней точки равна 0,5. |
|
| |
В силу периодичности суммы | , картинку необходимо «размножить» на соседние | ||
периоды, в частности изобразить то же самое на интервалах | и | . При этом, | |
в точках | ряд Фурье сойдётся к срединным значениям. | ||
По сути-то ничего нового здесь нет.
Постарайтесь самостоятельно справиться с данной задачей. Примерный образец чистового оформления и чертёж в конце урока.
Далее возникает закономерный вопрос: если схема работает на отрезке | , то почему |
бы её не применить к разложению функций в ряд Фурье на промежутках |
|
или на каком-нибудь другом периоде? |
|
Разложение функции в ряд Фурье на произвольном периоде
Для произвольного периода разложения , где «эль» – любое положительное число, формулы ряда Фурье и коэффициентов Фурье отличаются немного усложнённым аргументом синуса и косинуса:
Если , то получаются формулы промежутка , с которых мы начинали.
Алгоритм и принципы решения задачи полностью сохраняются, но возрастает техническая сложность вычислений:
Пример 4 Разложить функцию в ряд Фурье и построить график суммы.
Решение: фактически аналог Примера №3 с разрывом 1-го рода в точке . В данной задаче период разложения , полупериод . Функция определена только на полуинтервале , но это не меняет дела – важно, что оба куска функции интегрируемы.
Разложим функцию в ряд Фурье:
Поскольку функция разрывна в начале координат, то каждый коэффициент Фурье очевидным образом следует записать в виде суммы двух интегралов:
1)Первый интеграл распишу максимально подробно:
2)Тщательным образом вглядываемся в поверхность Луны:
Второй интеграл берём по частям:
На что следует обратить пристальное внимание, после того, как мы звёздочкой открываем продолжение решения?
Во-первых, не теряем первый интеграл , где сразу же выполняем
подведение под знак дифференциала. Во-вторых, не забываем злополучную константу перед большими скобками и не путаемся в знаках при использовании формулы
. Большие скобки, всё-таки удобнее раскрывать сразу же на следующем
шаге.
Остальное дело техники, затруднения может вызвать только недостаточный опыт решения интегралов.
Да, не зря именитые коллеги французского математика Фурье возмущались – как это тот посмел раскладывать функции в тригонометрические ряды?! =) К слову, наверное, всем интересен практический смысл рассматриваемого задания. Сам Фурье работал над математической моделью теплопроводности, а впоследствии ряд, названный его именем стал применяться для исследования многих периодических процессов, коих в окружающем мире видимо-невидимо. Сейчас, кстати, поймал себя на мысли, что не случайно сравнил график второго примера с периодическим ритмом сердца. Желающие могут ознакомиться с практическим применением преобразования Фурье в сторонних источниках. …Хотя лучше не надо – будет вспоминаться, как Первая Любовь =)
3) Учитывая неоднократно упоминавшиеся слабые звенья, разбираемся с третьим коэффициентом:
Интегрируем по частям:
Подставим найдённые коэффициенты Фурье | в | ||
формулу |
| , не забывая поделить нулевой коэффициент | |
пополам: |
|
|
|
Построим график суммы ряда. Кратко повторим порядок действий: на интервале | |||
строим прямую | , а на интервале | – прямую | . При нулевом |
значении «икс» ставим точку посередине «скачка» разрыва | и «тиражируем» | ||
график на соседние периоды: |
|
| |
На «стыках» периодов | сумма также будет равна серединам |
«скачка» разрыва | . |
Готово. Напоминаю, что сама функция по условию определена только на полуинтервале и, очевидно, совпадает с суммой ряда на интервалах
Ответ:
Иногда кусочно-заданная функция бывает и непрерывна на периоде разложения. Простейший образец: . Решение (см. 2-й том Бохана) такое же,
как и двух предыдущих примерах: несмотря на непрерывность функции в точке , каждый коэффициент Фурье выражается суммой двух интегралов.
На промежутке разложения точек разрыва 1-го рода и/или точек «стыка» графика может быть и больше (две, три и вообще любое конечное количество). Если функция интегрируема на каждой части, то она также разложима в ряд Фурье. Но из практического опыта такую жесть что-то не припоминаю. Тем не менее, встречаются более трудные задания, чем только что рассмотренное, и в конце статьи для всех желающих есть ссылки на ряды Фурье повышенной сложности.
А пока расслабимся, откинувшись в креслах и созерцая бескрайние звёздные просторы: Пример 5
Разложить функцию в ряд Фурье на промежутке и построить график суммы ряда.
В данной задаче функция непрерывна на полуинтервале разложения, что упрощает решение. Всё очень похоже на Пример №2. С космического корабля никуда не деться – придётся решать =) Примерный образец оформления в конце урока, график прилагается.
Разложение в ряд Фурье чётных и нечётных функций
С чётными и нечётными функциями процесс решения задачи заметно упрощается. И вот почему. Вернёмся к разложению функции в ряд Фурье на периоде «два пи»
и произвольном периоде «два эль»
| . |
Предположим, что наша функция | чётна. Общий же член ряда, как вы видите, |
содержит чётные косинусы и нечётные синусы. А если мы раскладываем ЧЁТНУЮ функцию, то зачем нам нечётные синусы?! Давайте обнулим ненужный коэффициент: .
Таким образом, чётная функция раскладывается в ряд Фурье только по косинусам:
Поскольку интегралы от чётных функций по симметричному относительно нуля отрезку интегрирования можно удваивать, то упрощаются и остальные коэффициенты Фурье.
Для промежутка :
Для произвольного промежутка:
К хрестоматийным примерам, которые есть практически в любом учебнике по матанализу,
относятся разложения чётных функций | . Кроме того, они неоднократно | |
встречались и в моей личной практике: |
| |
Пример 6 |
|
|
Дана функция | . Требуется: |
|
1)разложить функцию в ряд Фурье с периодом , где – произвольное положительное число;
2)записать разложение на промежутке , построить функцию и график полной суммы ряда .
Решение: в первом пункте предлагается решить задачу в общем виде, и это очень удобно! Появится надобность – просто подставьте своё значение.
1) В данной задаче период разложения | , полупериод . В ходе дальнейших действий, | |
в частности при интегрировании, «эль» считается константой | ||
Функция | является чётной, а значит, раскладывается в ряд Фурье только по | |
косинусам: | . |
|
Коэффициенты Фурье ищем по формулам | . Обратите | |
внимание на их безусловные преимущества. Во-первых, интегрирование проводится по положительному отрезку разложения, а значит, мы благополучно избавляемся от модуля
, рассматривая из двух кусков только «икс». И, во-вторых, заметно упрощается интегрирование.
Раз:
Два:
Интегрируем по частям:
Таким образом:
|
| , при этом |
константу , которая не зависит от «эн», выносим за пределы суммы. | ||
Ответ: |
|
|
2) Запишем разложение | на промежутке | , для этого в общую формулу |
подставляем нужное значение полупериода | : | |
В данном случае сумма ряда непрерывна, и, разумеется, чётна. Построение графика вряд ли нуждается в комментариях:
Хотел ещё построить частичную сумму
, но её график практически совпал
с «красной пилой» – настолько хорошо уже такое малое количество слагаемых приближает полную сумму.
Ответ:
Думаю, все представили, как «водят хороводы» параболы при разложении функции
. И, чтобы никому не было обидно, я прикреплю этот пример к дополнительным
материалам. |
|
| |
Если | – нечётная функция, то в разложениях Фурье | , | |
|
| оказываются лишними чётные косинусы, из чего |
|
следует равенство | . Более того, коэффициент тоже равен нулю, в чём легко |
| |
убедиться аналитически: интеграл от нечётной функции по симметричному относительно
нуля отрезку равен нулю: .
Таким образом, нечётная функция раскладывается в ряд Фурье только по синусам:
на промежутке | или | на произвольном периоде. |
При этом необходимо вычислить единственный коэффициент Фурье: | ||
или |
| соответственно. |
Небольшая миниатюра для самостоятельного решения: Пример 7
Разложить функцию в ряд Фурье и построить график суммы ряда не менее чем на трёх периодах
Решение и ответ в конце урока.
Разложение чётной функции часто маскируют типовой формулировкой, пример:
Разложить функцию | в ряд Фурье по косинусам на промежутке | . |
Если по условию не нужно чертежа, тихой сапой применяем формулы |
| |
| и даём ответ в виде | . Про |
чётность можно скромно умолчать 😉
Но если дополнительно требуется построить график суммы, то необходимо понимать
следующее: разложение по косинусам отобразит отрезок прямой | (чёрная | ||
линия) чётным образом (симметрично относительно оси | ) на интервал | ||
(зелёная линия), и, очевидно, функция | будет иметь непрерывный пилообразный | ||
график: |
|
|
|
В ряде случаев симметричное продолжение функции надо записать аналитически.
Начинающим рекомендую графический метод: сначала на промежутке | чертим отрезок | ||
прямой | , затем, симметрично относительно оси ординат – его «зелёного» | ||
коллегу. Находим уравнение прямой | , которая содержит зелёный отрезок | ||
(устно, или, например, по двум точкам). |
|
| |
Таким образом, эта же задача может быть сформулирована по-другому: |
| ||
Разложить функцию | в ряд Фурье. |
| |
Кстати, эта интерпретация вообще коварно умалчивает о чётности функции и может наказать двойным объёмом работы по общим формулам 😉 Поэтому в случае подозрительной похожести кусков функции (а чайникам – в любом случае!) имеет смысл сразу же изобразить её на чертеже.
Условие чётности | нетрудно проверить и аналитически. В левую часть функции |
подставляем «минус икс»: | – в результате чего «на выходе» |
получаем правую часть. |
|
Решение данного примера есть в соответствующем архиве (Папка Ряды_7), который можно бесплатно закачать на странице Готовые задачи по высшей математике.
Аналогично вуалируется нечётность: |
|
| |
Разложить функцию | в ряд Фурье по синусам на промежутке | . | |
Если чертёж не нужен, ищем коэффициент | и записываем ответ в виде | ||
. О нечётности снова молчок 😉 Однако в любом случае полезно знать | |||
следующее: разложение по синусам отобразит отрезок прямой |
| (чёрная линия) | |
нечётным образом (симметрично относительно начала координат) на интервал
(зелёная линия). И внимательный читатель статьи без труда изобразит график суммы ряда:
Составим уравнение «зелёного» продолжения (например, по предложенному в предыдущем пункте алгоритму) и перепишем задачу в эквивалентной формулировке:
Разложить функцию в ряд Фурье.
Выглядит опять провокационно, и если вам встретилось похожее условие, то сначала постройте график функции и изучите его на предмет симметрии – чтобы не пришлось использовать общие формулы разложения.
Проверим условие нечётности | аналитически, для этого в левый кусок |
функции подставляем «минус икс»: | – в результате |
чего «на выходе» получается правый кусок с противоположным знаком.
Вот, пожалуй, и все основные сведения о рядах Фурье, которых должно хватить для решения многих практических примеров. Надо сказать, что материал был непростой, причём изложить его доступно тоже было далеко не просто. Но вроде получилось неплохо.
Наш полёт подошёл к концу, и есть такое подозрение, что немалая часть экипажа хочет отправиться в экспедицию на Марс =) Дополнительные задачи с решениями можно закачать в Банке готовых работ, причём среди них есть и более редкие задания по теме –
нахождение спектра амплитуд, суммы ряда в различных точках и т.д. Кроме того, я создал дополнительную pdf-ку, в которую включил примеры, не вошедшие в статью (всётаки нужно соблюдать разумные рамки), а также ряды Фурье повышенной сложности, в своё время решённые на заказ студентам солидного технического ВУЗа.
Удачного путешествия – и обязательно возвращайтесь! Решения и ответы:
Пример 1: Решение:
Пример 3: Решение: В данной задаче период разложения | , полупериод | . |
Разложим функцию в ряд Фурье: | . |
|
Используя соответствующие формулы, вычислим коэффициенты Фурье:
Интегрируем по частям:
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)
Как можно отблагодарить автора?
Профессиональная помощь по любому предмету – Zaochnik.com
Дисперсионный анализ ANOVA понятным языком
Кирилл Сергеевич Мильчаков
В данной статье пойдет речь о сути применения дисперсионного анализа и смысле это процесса. Казалось бы зачем мне нужен дисперсионный анализ (ANOVA) если существует такой прекрасный и понятный статистический критерий, как т-критерий Стьюедента? Однако, здесь стоит внимательно разобраться. Главное ограничение т-критерия перед дисперсионным анализом состоит в том, что первый предназначен для парных сравнений, то есть ситуации, когда у нас есть только две группы и он нуждается в поправках на множественные сравнения, в случае, если у нас более двух групп, во-вторых представим, если у нас 6 групп и мы ищем статистически значимые различия между ними, сколько попарных сравнений в таком случае нужно сделать? Много 🙂
В таком случае гораздо проще использоваться критерий, который предназначен для ситуаций, когда много групп и который нам даст единый ответ на все изучаемые группы — дисперсионный анализ.
Условия применения дисперсионного анализа ANOVA
Перед тем как приступить к применению дисперсионного анализа, который предназначен для минимизации риска неправильной оценки ошибки 1 рода в случае множественных сравнений необходимо убедиться в соблюдении ряда условий:
- Количественный непрерывный тип данных, дискретные данные менее желательны.
- Независимые между собой выборки.
- Нормальное распределение признака в статистических совокупностях, из которых извлечены выборки.
- Равенство (гомогенность) дисперсий изучаемого признака в статистических совокупностях из которых извлечены выборки, проверяется с помощью критерия Levene.
- Независимые наблюдения в каждой из выборок.
Статистическая информация для применения однофакторного дисперсионного анализа
Ho в случае однофакторного дисперсионного анализа (ANOVA) подразумевает, что средние генеральных совокупностей из которых были извлечены выборки равны, другими словами все они относятся к одной генеральной совокупности и различия носят случайный характер. Для проверки теорий в случае дисперсионного анализа используется F-распределение. F-статистика принимает только положительные или нулевые значения.
Процедура дисперсионного анализа состоит в определении соотношения систематической (межгрупповой) дисперсии к случайной (внутригрупповой) дисперсии в измеряемых данных. В качестве показателя изменчивости используется сумма квадратов отклонения значений параметра от среднего: SS (от англ. Sum of Squares). Общая сумма квадратов SSTotal раскладывается на межгрупповую сумму квадратов SSBG[1] и внутригрупповую сумму квадратов SSWG[2]:
SSTotal = SSBG + SSWG
В случае если верна Ho, то как внутригрупповая, так и межгрупповая дисперсии служат оценками одной и той же дисперсии и должны быть приблизительно равны.
Исходя из этого значение F должно быть близко к 1 в случае, если статистически значимых различий все-таки нет. Критическое значение F определяется уровнем значимости (обычно 0,05 или 0,01) и внутригрупповым и межгрупповым числом степеней свободы (ν). Оно достаточно сложно для вычисления, поэтому чаще используются табличные значения с указанием α, νBG, νWG.
Межгрупповое число степеней свободы:
νBG = m – 1.
m – число групп
Внутригрупповое число степеней свободы:
νWG = n – m
n – количество наблюдений в каждой из групп
Апостериорные значения
Однако, при обнаружении статистически значимых отличий мы не сможем сказать лишь об их наличии, но какие именно группы отличаются друг от друга мы определить не сможем, для этого производят так называемые процедуры апостериорных сравнений. Апостериорные сравнения представляют собой попарные сравнения изучаемых групп для обнаружения различий между ними.
Апостериорные сравнения могут быть проведены с помощью критерия Стьюдента для независимых выборок, что может показаться странным, учитывая сказанное ранее о проблеме множественных сравнений. Однако в отличие от простых попарных сравнений при проведении апостериорных сравнений рассчитываются новые критические уровни значимости для удержания ошибки 1 типа в пределах 5 %.
Наиболее простым и наиболее популярным способом коррекции ошибки 1 типа является поправка Бонферрони (Bonferroni), при которой уровень ошибки 1 типа делится на количество сравнений для получения нового критического уровня значимости. Так, если имеется 3 сравнения, то новый критический уровень должен быть 0,05 / 3 = 0,017. Поправка Бонферрони хорошо контролирует ошибку 1 типа, но является очень консервативной и приводит к повышению вероятности ошибки 2 типа (вероятности принятия решения об отсутствии различий там, где они на самом деле есть). Либеральные критерии, (например критерий Тьюки) в свою очередь, завышают вероятность ошибки 1 типа, то есть вероятность принятия решения о наличии различий там, где их нет.
Таким образом, при выборе статистического критерия для апостериорных сравнений необходимо принимать во внимание, как критерии контролируют ошибки 1 и 2 типов и как они работают при несоблюдении необходимых условий применения дисперсионного анализа.
Если данные не подчиняются нормальному распределению, то при анализе можно использовать два способа: применением различных арифметических преобразований до достижения нормальности распределения и дальше уже применять дисперсионный анализ, или использовать критерий Краскела-Уоллиса (Kruskal-Wallis H-test), иногда его также называют непараметрическим дисперсионным анализом. Как и в большинстве непараметрических методов, работающих с количественными данными, исходный набор данных преобразуется в ранги и обрабатывается уже он. При обнаружении статистически значимых различий между группами стоит дальше проводить апостериорные сравнения с использованием критерия Манна-Уитни.
Пример
В условиях крупной городской клинической больницы было решено провести исследование по оценке влияния возраста на длительность госпитализации после лапароскопической холецистектомии. 9 пациентов были разделены на 3 группы в зависимости от возраста
Длительность госпитализации
после лапароскопической холецистектомии в зависимости от возраста, дни
| Группа №1Младше 45 лет | Группа №245-55 лет | Группа №3Старше 55 лет |
| 3 | 5 | 7 |
| 1 | 3 | 6 |
| 2 | 4 | 5 |
| x̄=2 | x̄=4 | x̄=6 |
Сделайте выводы о влиянии возраста на длительности госпитализации после лапароскопической холецистектомии.
- Постановка нулевой гипотезы
H0 указывает на отсутствие различий между группами, иными словами все группы по возрасту относятся к одной генеральной совокупности и соответственно средние равны друг другу
µ1= µ2= µ3
Альтернативная гипотеза выдвигает предположение, что длительно госпитализации зависит от возраста и средние в этих группах на самом деле не равны
µ1≠ µ2≠ µ3
- Найдем общую сумму квадратов
Для этого нам нужно знать общую среднюю по всем выборкам, найдем ее:
x̄= (2+3+6)=4
SST =2 = (3-4)2+(1-4) 2+(2-4) 2+(5-4) 2+(4-4) 2+(3-4) 2+(7-4) 2+
+(6-4) 2+(5-4) 2=30
- Найдем сумму квадратов внутри групп последовательно вычитая из каждого значения в группе групповую среднюю:
SSWG = (3-2)2 + (1-2) 2 + (2-2) 2 + (5-4) 2 + (3-4) 2 + (4-4) 2 + (7-6) 2 + (6-6) 2 + (5-6)2 =2+2+2=6
- Найдем внутригрупповую сумму квадратов.
Для этого нам необходимо найти квадрат отклонения каждой из выборочных средних относительно общей вредней:
SSBG =3(2-4)2+3(4-4)2+3(6-4)2=24
- Найдем значение критерия Фишера, исходя из средних квадратов отклонений внутри групп и между ними и соответствующих степеней свободы:
νBG = m – 1 = 3-1 = 2
νWG = n – m = 9 – 3 = 6
F= 12, Fкрит. = 5,143 при α = 0,05
F > Fкрит
- Делаем вывод о наличии статистически значимых отличий между группами:
так как наше значение F больше критического значения при заданном количестве наблюдений и количестве групп, иными словами наша дисперсия между группами вносит больший вклад в любую сумму дисперсий, чем таковая внутри самих групп.
Возраст влияет на длительность госпитализации после холецистектомии.
[1] Sum of squares between groups
[2] Sum of squares within groups
[3]MSBG — Средний квадрат отклонения между группами и MSWG — Средний квадрат отклонения внутри групп
Если Вам понравилась статья и оказалась полезной, Вы можете поделиться ею с коллегами и друзьями в социальных сетях:
Норден А.П. Краткий курс дифференциальной геометрии ОНЛАЙН
Норден А.П. Краткий курс дифференциальной геометрии. – М., 1958. – 244 с.
Курс построен в соответствии с программами механико-математических и физико-математических факультетов университетов и пединститутов.
Главы: Векторная функция скалярного аргумента Кривая и касательная Длина дуги и сопровождающий трехгранник кривой Натуральные уравнения кривой Развертывающиеся поверхности Поверхность и ее линейный элемент Кривизна линий на поверхности Замечательные сети и линии на поверхности Внутренняя геометрия поверхности Параллельное перенесение.
ОГЛАВЛЕНИЕ
Предисловие ………………………..7
ЧАСТЬ 1
ГЛАВА I. ВЕКТОРНАЯ ФУНКЦИЯ СКАЛЯРНОГО АРГУМЕНТА
§ 1. Введение ………………………………………………9
§ 2. Бесконечно малые векторы………………………………..9
§ 3. Предел переменного вектора………………И
§ 4. Векторная функция скалярного аргумента…………12
§ 5. Годограф векторной функции………………13
§ 6. Производная векторной функции …………….15
§ 7. Правила дифференцирования вектора…………..15
§ 8. Формула Тейлора……………………18
§ 9. Вектор постоянной длины и вектор постоянного направления . .19
§ 10. Вектор, параллельный неизменной плоскости………..20
§ 11. Векторные круговые функции ……………..21
§ 12. Интеграл от векторной функции ………… . . . 22
ГЛАВА II. КРИВАЯ И КАСАТЕЛЬНАЯ
§ 13. Понятие кривой линии …………… . . . . . 24
§ 14. Параметрическое уравнение кривой……………24
§ 15. Касательная прямая кривой……………….26
§ 16. Винтовая линия…………………….30
§ 17. Неявное уравнение плоской кривой………….. . 30
§ 18. Особые точки кривой, заданной неявным уравнением……32
§ 19. Асимптоты………………………36
§ 20. Касательная и асимптота алгебраической кривой………37
§ 21. Огибающая семейства плоских кривых ………… . 39
§ 22. Поверхность и ее касательные. Нормаль поверхности……43
§ 23. Цилиндрические и конические поверхности ………..45
§ 24. Особая точка поверхности ……………….46
§ 25. Неявное задание пространственной кривой………..48
§ 26. Семейство кривых, зависящих от п параметров………49
§ 27. Соприкосновение кривых………………..50
§ 28. Соприкосновение кривой и поверхности………….53
ГЛАВА III. ДЛИНА ДУГИ И СОПРОВОЖДАЮЩИЙ ТРЕХГРАННИК КРИВОЙ
§ 29. Длина дуги …………………….. 55
§ 30. Длина дуги как параметр……………………..58
§ 31. Соприкасающаяся плоскость……………….60
§ 32. Уравнение соприкасающейся плоскости ………….62
§ 33. Сопровождающий трехгранник кривой …………64
§ 34. Формулы Серре — Френе…………………66
§ 35. Другой вывод формул Серре—Френе…………..69
§ 36. Лемма о единичном векторе ………………70
§ 37. Кривизна……………………….70
§ 38. Кручение ………………………71
§ 39. Формулы для вычисления кривизны и кручения………72
§ 40. Взаимное расположение кривой и плоскости……….75
§ 41. Проекция кривой на соприкасающуюся плоскость ……..78
§ 42. Проекция кривой на спрямляющую плоскость ……….78
§ 43. Вид кривой вблизи данной точки …………….80
§ 44. Вид кривой вблизи точки уплощения……………82
§ 45. Эволюта плоской кривой …………………83
§ 46. Соприкасающаяся окружность плоской кривой……….85
§ 47. Эвольвента………………………86
§ 48. Трактриса и цепная линия ……………….88
ГЛАВА IV. НАТУРАЛЬНЫЕ УРАВНЕНИЯ КРИВОЙ
§ 49. Натуральные уравнения ………………..91
§ 50. Кривые с общими натуральными уравнениями……….93
§ 51. Дифференциальные уравнения ……………..95
52. Векторные дифференциальные уравнения…………98
53.
59. Линейная зависимость между кривизной и кручением ……113
60. Кривые постоянной кривизны………………114
ГЛАВА V. РАЗВЕРТЫВАЮЩИЕСЯ ПОВЕРХНОСТИ
§ 61. Огибающая семейства поверхностей……………116
§ 62. Характеристика семейства поверхностей …………. 118
§ 63. Ребро возврата…………………….119
§ 64. Развертывающиеся поверхности……………..121
§ 65. Полярная поверхность …………………124
§ 66. Характеристическая точка полярной поверхности ……..126
§ 67. Соприкасающаяся сфера ……………….127
§ 68. Огибающая касательных плоскостей……………129
§ 69. Параллельные кривые…………………130
§ 70. Пространственная эволюта……………….132
ЧАСТЬ II
ГЛАВА VI. ПОВЕРХНОСТЬ И ЕЕ ЛИНЕЙНЫЙ ЭЛЕМЕНТ
§ 71. Понятие поверхности……………… . . 134
§ 72. Криволинейные координаты и параметрическое уравнение поверхности
§ 73. Примеры параметризованных поверхностей
§ 74. Касательная прямая поверхности …….140
§ 75. Касательная плоскость …………………141
§ 76. Огибающая семейства плоскостей, зависящих от двух параметров 142
§ 77. Длина дуги………………….. . . 143
§ 78. Первая квадратичная форма…………..144
§ 79. Угол между двумя линиями ………….. 145
§ 80. Ортогональные траектории . .. . ……….. 147
§ 81. Площадь поверхности …………. . . 148
§ 82. Поверхность вращения ……….151
§ 83. Косая и развертывающаяся линейчатые поверхности 153
§ 84. Криволинейные координаты в пространстве .. . . . . 156
ГЛАВА VII. КРИВИЗНА ЛИНИЙ НА ПОВЕРХНОСТИ
§ 85. Нормальная кривизна . . . ………….. …. 159
§ 86. Вторая квадратичная форма ………………159
§ 87. Кривизна кривой и ее соприкасающаяся плоскость …….161
§ 88. Нормальное сечение ………………………….163
§ 89. Теорема Менье…….. . . . . . ……. . 163
§ 90. Индикатриса Дюпена……… 165
§ 91. Формула Эйлера…………………. 167
§ 92. Характеристическое уравнение поверхности. Полная и средняя
кривизны………………….. 168
§ 93. Кривизны поверхности вращения………… … 170
§ 94. Кривизна линий на сфере ………………. 171
§ 95. Классификация точек поверхности . . ……………….171
§ 96. Строение поверхности вблизи эллиптической точки ……… 173
§ 97. Строение поверхности вблизи гиперболической точки ………174
§ 98. Строение поверхности вблизи параболической точки 176
§ 99. Линия пересечения поверхности с ее касательной плоскостью . . 178
100. Точки поверхностей второго порядка…………..179
§ 101. Сферическое отображение……………….180
§ 102. Знак полной кривизны…………………182
ГЛАВА VIII. ЗАМЕЧАТЕЛЬНЫЕ СЕТИ И ЛИНИИ НА ПОВЕРХНОСТИ
§ 103. Сопряженные направления……………….185
§ 104. Сопряженная сеть…………………..187
§ 105. Поверхности переноса…………………188
§ 106. Асимптотические линии ………………..189
§ 107. Линии кривизны……………………191
§ 108. Теорема Иоахимсталя …………………193
§ 109. Уравнение линий кривизны ………………194
§ 110. Поверхности нулевой кривизны …………….197
§ 111. Поверхность, состоящая из омбилических точек………198
ГЛАВА IX. ВНУТРЕННЯЯ ГЕОМЕТРИЯ ПОВЕРХНОСТИ
§ 112. Изгибание и наложимость ……………….200
§ 113. Признак наложимости…………………200
§ 114. Внутренняя геометрия поверхности ………….. 202
§ 115. Изгибание развертывающихся поверхностей ……….203
§ 116. Сопровождающий трехгранник поверхности………..204
§ 117. Дифференциал единичного касательного вектора поверхности …. 206
§ 118. Геодезическая кривизна………………..207
§ 119. Геодезические линии …………………209
§ 120. Геодезические линии поверхности вращения ……….211
§ 121. Полугеодезические координаты……………..212
§ 122. Геодезическая линия как кратчайшая…………..214
§ 123. Окончание подсчета коэффициентов сопровождающего трехгранника ………………………..215
§ 124. Основные квадратичные формы определяют поверхность …. 216
§ 125. Теорема Гаусса……………………218
§ 126. Конформное отображение……………….220
§ 127. Стереографическая проекция………………221
§ 128. Линейный элемент поверхности постоянной гауссовой кривизны 223
§ 129. Наложимость поверхностей постоянной кривизны……..224
§ 130. Псевдосфера ……………………225
131. Геодезические линии псевдосферы …………..226
ГЛАВА X. ПАРАЛЛЕЛЬНОЕ ПЕРЕНЕСЕНИЕ
§ 132. Векторы, принадлежащие поверхности………….228
§ 133. Внутреннее параллельное перенесение………….229
§ 134. Навертывание кривой на плоскость …………..231
§ 135. Геодезическая кривизна и геодезические линии ……… 232
§ 136. Площадь сферического многоугольника………….233
§ 137. Параллельный обвод вектора по замкнутому сферическому контуру ……………………….235
§ 138. Параллельный обвод вектора по произвольной поверхности . . . 236
§ 139. Теорема Гаусса—Бонне………………..238
§ 140. Геодезический треугольник ……………..240
§ 141. Теорема Гаусса—Бонне для многосвязной области……..241
§ 142. Интегральная кривизна замкнутой поверхности………243
Собственные числа и вектора матриц. Методы их нахождения
Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.
Пусть число $\lambda$ и вектор $x\in L, x\neq 0$ таковы, что $$Ax=\lambda x.\qquad\qquad\qquad\qquad\qquad(1)$$ Тогда число $\lambda$ называется собственным числом линейного оператора $A,$ а вектор $x$ собственным вектором этого оператора, соответствующим собственному числу $\lambda.$
В конечномерном пространстве $L_n$ векторное равенство (1) эквивалентно матричному равенству $$(A-\lambda E)X=0,\,\,\,\, X\neq 0.\qquad\qquad\quad\quad (2)$$
Отсюда следует, что число $\lambda$ есть собственное число оператора $A$ в том и только том случае, когда детерминант $det(A-\lambda E)=0,$ т. е. $\lambda$ есть корень многочлена $p(\lambda)=det(A-\lambda E),$ называемого характеристическим многочленом оператора $A.$ Столбец координат $X$ любого собственного вектора соответствующего собственному числу $\lambda$ есть нетривиальное решение однородной системы (2).
Примеры.
Найти собственные числа и собственные векторы линейных операторов, заданных своими матрицами.4.134. $A=\begin{pmatrix}2&-1&2\\5&-3&3\\-1&0&-2\end{pmatrix}.$
Решение.
Найдем собственные вектора заданного линейного оператора. Число $\lambda$ есть собственное число оператора $A$ в том и только том случае, когда $det(A-\lambda E)=0.$ Запишем характеристическое уравнение:
$$A-\lambda E=\begin{pmatrix}2&-1&2\\5&-3&3\\-1&0&-2\end{pmatrix}-\lambda\begin{pmatrix}1&0&0\\0&1&0\\0&0&1\end{pmatrix}=$$ $$=\begin{pmatrix}2-\lambda&-1&2\\5&-3-\lambda&3\\-1&0&-2-\lambda\end{pmatrix}.3=0\Rightarrow \lambda=-1.$$
Собственный вектор для собственного числа $\lambda=-1$ найдем из системы $$(A-\lambda E)X=0, X\neq 0, \Rightarrow (A+E)X=0, X\neq 0$$
$$(A+E)X=\begin{pmatrix}2+1&-1&2\\5&-3+1&3\\-1&0&-2+1\end{pmatrix}\begin{pmatrix}x_1\\x_2\\x_3\end{pmatrix}=$$ $$=\begin{pmatrix}3x_1-x_2+2x_3\\5x_1-2x_2+3x_3\\-x_1-x_3\end{pmatrix}=0.$$
Решим однородную систему уравнений:
$$\left\{\begin{array}{lcl}3x_1-x_2+2x_3=0\\ 5x_1-2x_2+3x_3=0\\-x_1-x_3=0\end{array}\right.$$
Вычислим ранг матрицы коэффициентов $A=\begin{pmatrix}3&-1&2\\5&-2&3\\-1&0&-1\end{pmatrix}$ методом окаймляющих миноров:
Фиксируем минор отличный от нуля второго порядка $M_2=\begin{vmatrix}3&-1\\5&-2\end{vmatrix}=-6+5=-1\neq 0.$
Рассмотрим окаймляющий минор третьего порядка: $\begin{vmatrix}3&-1&2\\5&-2&3\\-1&0&-1\end{vmatrix}=6+3-4-5=0;$
Таким образом ранг матрицы $A$ равен двум.
Выберем в качестве базисного минор $M=\begin{vmatrix}3&-1\\5&-2\end{vmatrix}=-1\neq 0.$ Тогда, полагая $x_3=c,$ получаем: $$\left\{\begin{array}{lcl}3x_1-x_2+2с=0\\ 5x_1-2x_2+3с=0\end{array}\right.\Rightarrow\left\{\begin{array}{lcl}3x_1-x_2=-2c\\5x_1-2x_2=-3c\end{array}\right.$$
По правилу Крамера находим $x_1$ и $x_2:$
$\Delta=\begin{vmatrix}3&-1\\5&-2\end{vmatrix}=-6+5=-1;$
$\Delta_1=\begin{vmatrix}-2c&-1\\-3c&-2\end{vmatrix}=4c-3c=c;$
$\Delta_2=\begin{vmatrix}3&-2c\\5&-3c\end{vmatrix}=-9c+10c=c;$
$x_1=\frac{\Delta_1}{\Delta}=\frac{c}{-1}=-c;$ $x_2=\frac{\Delta_2}{\Delta}=\frac{c}{-1}=-c.$
Таким образом, общее решение системы $X(c)=\begin{pmatrix}-c\\-c\\c\end{pmatrix}.$
Из общего решения находим фундаментальную систему решений: $E=X(1)=\begin{pmatrix}-1\\-1\\1\end{pmatrix}.$
С использованием фундаментальной системы решений, общее решение может быть записано в виде $X(c)=cE.$
Ответ: $\lambda=-1;$ $X=c\begin{pmatrix}-1\\-1\\1\end{pmatrix}, c\neq 0.2-\lambda-1)=0\Rightarrow \lambda=2.$$
Собственный вектор для собственного числа $\lambda=2$ найдем из системы $$(A-\lambda E)X=0, X\neq 0, \Rightarrow (A-2E)X=0, X\neq 0$$
$$(A-2E)X=\begin{pmatrix}-2&-1&0\\1&-1&-2\\1&-1&-2\end{pmatrix}\begin{pmatrix}x_1\\x_2\\x_3\end{pmatrix}=$$ $$=\begin{pmatrix}-2x_1-x_2\\x_1-x_2-2x_3\\x_1-x_2-2x_3\end{pmatrix}=0.$$
Решим однородную систему уравнений:
$$\left\{\begin{array}{lcl}-2x_1-x_2=0\\ x_1-x_2-2x_3=0\\x_1-x_2-2x_3=0\end{array}\right.$$
Вычислим ранг матрицы коэффициентов $A=\begin{pmatrix}-2&-1&0\\1&-1&-2\\1&-1&-2\end{pmatrix}$ методом окаймляющих миноров:
Фиксируем минор отличный от нуля второго порядка $M_2=\begin{vmatrix}-2&-1\\1&-1\end{vmatrix}=2+1=3\neq 0.$
Рассмотрим окаймляющий минор третьего порядка: $\begin{vmatrix}-2&-1&0\\1&-1&-2\\1&-1&-2\end{vmatrix}=0;$
Таким образом ранг матрицы $A$ равен двум.
Выберем в качестве базисного минор $M=\begin{vmatrix}-2&-1\\1&-1\end{vmatrix}=3\neq 0.$ Тогда, полагая $x_3=c,$ получаем: $$\left\{\begin{array}{lcl}-2x_1-x_2=0\\ x_1-x_2-2с=0\end{array}\right.\Rightarrow\left\{\begin{array}{lcl}-2x_1-x_2=0\\x_1-x_2=2c\end{array}\right.$$
По правилу Крамера находим $x_1$ и $x_2:$
$\Delta=\begin{vmatrix}-2&-1\\1&-1\end{vmatrix}=2+1=3;$
$\Delta_1=\begin{vmatrix}0&-1\\2c&-1\end{vmatrix}=2c;$
$\Delta_2=\begin{vmatrix}-2&0\\1&2c\end{vmatrix}=-4c;$
$x_1=\frac{\Delta_1}{\Delta}=\frac{2c}{3};$ $x_2=\frac{\Delta_2}{\Delta}=\frac{-4c}{3}.$
Таким образом, общее решение системы $X(c)=\begin{pmatrix}\frac{2c}{3}\\-\frac{4c}{3}\\c\end{pmatrix}.$
Из общего решения находим фундаментальную систему решений: $E=X(1)=\begin{pmatrix}\frac{2}{3}\\-\frac{4}{3}\\1\end{pmatrix}.$
С использованием фундаментальной системы решений, общее решение может быть записано в виде $X(c)=cE.$ Переобозначив постоянную, $\alpha=3c,$ получаем собственный вектор $X=\alpha\begin{pmatrix}2\\-4\\3\end{pmatrix}, \alpha\neq 0.$
Ответ: $\lambda=2;$ $X=\alpha\begin{pmatrix}2\\-4\\3\end{pmatrix}, \alpha\neq 0.$
Домашнее задание.
Найти собственные числа и собственные векторы линейных операторов, заданных своими матрицами.
4.135. $A=\begin{pmatrix}0&1&0\\-4&4&0\\-2&1&2\end{pmatrix}.$
Ответ: $\lambda=2;$ $X=c_1\begin{pmatrix}1\\2\\0\end{pmatrix}+c_2\begin{pmatrix}0\\0\\1\end{pmatrix}, $c_1$ и $ c_2$ не равны одновременно нулю.
4.142. $A=\begin{pmatrix}1&-3&1\\3&-3&-1\\3&-5&1\end{pmatrix}.$
Ответ: $\lambda_1=-1,$ $X(\lambda_1)=c\begin{pmatrix}1\\1\\1\end{pmatrix};$ $\lambda_2=2,$ $X(\lambda_2)=c\begin{pmatrix}4\\1\\7\end{pmatrix};$ $\lambda_3=-2,$ $X(\lambda_3)=c\begin{pmatrix}2\\3\\3\end{pmatrix}, c\neq 0.$
{jumi[*4]}
Судоку для чайников – Уровень 3 // Обзор
Поздравляем Уилла Норриса ’19 с прохождением уровня босса 2! Если у вас есть вопросы, напишите ему по адресу [email protected]
.Что касается уровня 3, я с сожалением должен сообщить вам, что я натягиваю на вас Дары смерти Гарри Поттера. Да, я разбиваю его на две части… Я понял, что мне нужно многое осветить. Я также пишу это в Info Commons за день до публикации, потому что мой домашний компьютер сломался…
Без лишних слов!
Этот урок действительно должен быть с 2.2. Забыл. Я такой бездельник 🙁
В любом случае, 2.2 была Naked Pair , 3.1 – Hidden Pair
Название подсказки Hidden Pair, говорит само за себя. Взгляните на третий ряд – может, у вас получится без объяснения причин.
Обратите внимание, что 6-й и 9-й столбцы – единственные поля в строке 3, которые имеют как 1, так и 3.
Поскольку это в основном то же самое, что и 2.2, я не собираюсь тратить много времени на объяснение этого:
- Если столбец 6 равен 1, столбец 9 должен быть равен 3, и наоборот.
- Единственные единицы и тройки в строке 3 находятся в столбцах 6 и 9.
- Итак, вы можете исключить всех остальных кандидатов из этих двух ящиков.
А теперь пора повышать уровень. Я не слишком часто использую эту следующую стратегию, когда решаю головоломки в Dallas Morning News или в этом приложении, но это действительно помогает понять более жесткие стратегии. Он называется X-Wing.
Для этого парня мы сосредоточимся на семерках. Особенно в строках 2 и 6.
Обратите внимание, что есть только два возможных места для 7 в каждой из этих строк.
Удобно, что эти возможности сочетаются друг с другом!
Очень важно, чтобы это были единственные семерки в ряду. Если в ряду больше 7 кандидатов, попытка выполнить X-Wing вас испортит.
Поскольку их всего две, у нас остается по две возможности для каждой строки. Либо цифра 7 находится в столбце 4, либо в столбце 8.
Давайте рассмотрим эти возможности так же, как мы это делали в 2.2.
Теперь, когда у нас есть два случая, мы можем исключить некоторых кандидатов.Помните, что то, что вычеркнуто в обоих случаях, должно быть верным, несмотря ни на что.
Красными крестиками отмечены кандидаты, которые не могут быть верными, потому что мы поместили 7 в строку 6 столбца 4.
Мы исключили одного из двух 7 кандидатов в строке 2. Таким образом, строка 2 в столбце 8 должна быть 7 (написано зеленым).
Синие крестики обозначают выбывших кандидатов из-за зеленой 7.
Ниже я проделал то же самое для второй возможности.
Как видите, многие из X являются общими, что означает, что они верны, несмотря ни на что:
Стрела !!!
Твердые 8 кандидатов уничтожены!
Как это круто!
Резюме 3.2
- Должно быть ровно два кандидата числа в строке
- В разных строках должно быть ровно два кандидата с одинаковым номером
- Кандидаты из этих двух рядов должны выстроиться в линию.
- Вы можете удалить всех кандидатов из этих двух столбцов, кроме двух исходных строк
То же самое верно, если вы меняете строки и столбцы
Трудно говорить кратко, не вдаваясь в технические подробности. Так что я много написал для урока простыми, надеюсь, словами и сложил их в сложный список.Но это должно иметь смысл, если вы до сих пор следили за мной.
Я не получала писем о том, что это сложно понять. Но я не думаю, что многие люди читали прошлые уроки, потому что они были такими простыми с самого начала … Сейчас самое время начать читать уроки, потому что более сложные трюки слишком сложно понять, если вы этого еще не знаете.
Итак, мы снова смотрим на семерки.
Ряды 3 и 7.
К сожалению, X-Wing отсутствует, потому что в строке 7 есть четыре кандидата 7.
Но давайте представим, что это X-wing, поддельный X-Wing, более известный как X-Wing с ребрами .
Вот наш первый случай. Давайте представим себе, что столбцов 7 и 8 не существует ни на секунду (если это все еще кажется вам неестественным и неправильным, вам придется привыкнуть к гипотетическим случаям. Они никуда не денутся…)
Поскольку эти столбцы исчезли, у нас есть крестовина между 7 кандидатами в строках 3 и 7 (обведены синим).
Если вы не знаете, откуда берутся эти красные крестики, прочтите 3.2 первый.
Но эти красные крестики не обязательно соответствуют действительности. Мы сделали предположение, но не рассмотрели все случаи…
Значит, либо X-Wing верен… Или есть 7 в строке 7, столбце 7 или 8.
Итак, мы рассмотрели все случаи. Что у них общего?
Ага… Мы просто проделали всю эту работу, только чтобы избавиться от единственного кандидата… Извини, если это было немного анти-кульминационным для тебя.
Это действительно здорово, потому что X-Wings намного более универсальны.
Извините, что немного понизил уровень на этой неделе. Я пытался отдать ему должное. Надеюсь, вы не думаете, что это было столь же бесполезно и неактуально, как Дары Смерти. Часть 1…
Обещаю, в следующий раз все будет хорошо!
Удачи, решая эту проблему, мои растущие кузнечики!
Опять же, первый человек, который напишет мне по электронной почте ([email protected]) правильное решение, будет показан в выпуске на следующей неделе.
Если вы сможете решить эту проблему и уровень босса 2 без посторонней помощи, я уверен, что вы сможете решить все 5-звездочные судоку в Dallas Morning News.Остался только один уровень (5 обведенных звездочек)! Хорошая работа 🙂
Счастливого судоку, до встречи на следующей неделе в The Roundup!
python – создает фиктивные закодированные столбцы для столбца и объединяет их с набором данных
.Я работаю с набором данных об уровне оттока сотовых телефонов. Я пытаюсь создать фиктивный код для столбца аббревиатур состояний в наборе данных с формой 3333 строки × 20 столбцов. Мне нужно исключить один из столбцов с фиктивным кодом состояния, который будет служить «справочным» столбцом для использования при моделировании.Я думаю, должно произойти создание столбца для каждой строки и установка 1 в строке, соответствующей вновь созданному фиктивному столбцу. В настоящее время я получаю 0 в каждой строке, кроме первой, которая заполнена всеми единицами. Мне нужно каким-то образом заставить фиктивные переменные включать маркер в соответствующий столбец для каждой строки. Я также думаю, что мне следует объединить столбцы, чтобы они были только уникальными столбцами (в данном случае по одному для каждого состояния), но я не уверен, что это испортит точку фиктивного кодирования?
В настоящее время у меня есть следующий код:
1.Создание фиктивных переменных для ‘состояния’ и исключение первого фиктивного столбца:
churn_dummies = pd.get_dummies (churn, columns = 'state', prefix = 'st'). Iloc [:, 20:]
Возвращает фрейм данных размером 3333×3332.
st_OH st_NJ st_OH st_OK st_AL st_MA st_MO st_LA st_WV st_IN st_RI
0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0
1 NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
2 NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
3 NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
4 NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
Этот результат, кажется, продолжается во всем созданном гигантском фрейме данных, и при выборочной проверке строки, похоже, не содержат соответствующих единиц, отмеченных соответствующим столбцом.Я использовал следующий документ pandas: https://pandas.pydata.org/pandas-docs/stable/reference/api/pandas.get_dummies.html
2. Затем объединение столбцов во фрейм данных:
churn = pd.concat ([churn, churn_dummies], axis = 1)
Работа с таблицами Excel для чайников: пошаговая инструкция
Microsoft Excel удобен для создания таблиц и выполнения расчетов. Его рабочая область представляет собой набор ячеек, которые необходимо заполнить данными.Следовательно, данные можно форматировать, использовать для построения графиков, диаграмм, сводных отчетов.
Для новичка работа с таблицами в Excel на первый взгляд может показаться сложной. Это существенно отличается от принципов построения таблиц в Word. Однако давайте начнем с самых основ: создание и форматирование таблиц. К тому времени, когда вы дойдете до конца этой статьи, вы поймете, что нет лучшего инструмента для создания таблиц, чем Excel.
Взаимодействие с другими людьмиСоздание таблицы в Excel: манекен
Работа с таблицами Excel для чайников не терпит спешки.Есть разные способы создать стол для определенной цели, и каждый из них имеет свои преимущества. Поэтому начнем с визуальной оценки ситуации.
Посмотрите внимательно на рабочий лист настольного процессора:
Это набор ячеек в столбцах и строках. По сути, это стол. Столбцы отмечены буквами. Строки обозначены цифрами. Нет границ.
Прежде всего, научимся работать с ячейками, строками и столбцами.
Как выбрать столбец и строку
Чтобы выделить весь столбец, щелкните левой кнопкой мыши по отмеченной букве.
Чтобы выбрать строку, щелкните номер, которым она обозначена.
Чтобы выбрать несколько столбцов или строк, щелкните имя левой кнопкой мыши, удерживайте кнопку и перетащите указатель.
Чтобы выбрать столбец с помощью горячих клавиш, поместите курсор в любую ячейку столбца и нажмите Ctrl + Пробел. Комбинация клавиш Shift + Пробел используется для выбора строки.
Как изменить размер ячеек
Если ваша информация не помещается в таблице, вам необходимо изменить размер ячеек.
- Вы можете перемещать их вручную, захватывая границу ячейки левой кнопкой мыши.
- Если ячейка содержит длинное слово, вы можете дважды щелкнуть границу столбца / строки. Программа автоматически расширит свои границы.
- Если вам необходимо увеличить высоту строки с сохранением ширины столбца, воспользуйтесь кнопкой «Перенести текст» на панели инструментов.
Чтобы изменить ширину столбца и высоту строки в определенном диапазоне, измените размер 1 столбца / строки (путем перетаскивания его границ вручную) – и размер всех выбранных столбцов и строк будет изменен автоматически.
Важное примечание. Чтобы вернуться к предыдущему размеру, вы можете нажать кнопку «Отменить ввод» или комбинацию горячих клавиш CTRL + Z. Однако он работает только при немедленном использовании. В дальнейшем это не поможет.
Чтобы привести строки к их исходным границам, откройте меню инструментов: «HOME» – «Format» и выберите «AutoFit Row Height».
Этот метод не работает для столбцов. Нажмите «Формат» – «Автоподбор ширины ряда». Запомните это число. Выберите любую ячейку в столбце, размер которой должен вернуться к исходному.Снова нажмите «Формат» – «Ширина столбца» и введите значение, предложенное программой (как правило, это 8,43 – количество знаков в шрифте Calibri, размер 11 pt). ОК.
Как вставить столбец или строку
Выберите столбец / строку справа от / под местом, где должна быть сделана вставка. То есть новый столбец появится слева от выбранной ячейки. Над ним будет вставлена новая строка.
Щелкните ячейку правой кнопкой мыши и в раскрывающемся меню выберите «Вставить» (или нажмите комбинацию горячих клавиш CTRL + SHIFT + «=»).
Выберите «Весь столбец» и нажмите ОК.
Подсказка. Чтобы быстро вставить новый столбец, выберите столбец в нужном месте и нажмите CTRL + SHIFT + PLUS.
Все эти навыки пригодятся при построении таблицы в Excel. Вам нужно будет изменить размер ячеек и вставить строки / столбцы в процессе.
Пошаговое создание таблицы с формулами
- Заполните заголовок вручную, указав заголовки столбцов. Заполните строки, введя свои данные.Применяйте полученные знания на практике: расширяйте границы столбцов, регулируйте высоту строк.
- Для заполнения столбца «Сумма» установите курсор в его первую ячейку. Введите «=». Таким образом мы информируем Excel: здесь будет формула. Выделите ячейку B2 (с первой ценой). Введите символ умножения (*). Выделите ячейку C2 (с количеством). Нажмите Ввод.
- При наведении указателя мыши на ячейку, содержащую формулу, в ее правом нижнем углу появится крестик.Он указывает на маркер автозаполнения. Захватите его левой кнопкой мыши и перетащите в конец столбца. Формула будет скопирована в каждую ячейку.
- Обозначьте границы вашего стола. Выберите диапазон, содержащий ваши данные. Нажмите кнопку «ГЛАВНАЯ» – «Граница» (на главной странице в меню «Шрифт»). И нажмите «Все границы».
Теперь границы столбца и строки будут видны при печати таблицы.
Меню «Шрифт» позволяет форматировать данные в таблице Excel так, как если бы вы это делали в Word.
Например, измените размер шрифта и выделите заголовок жирным шрифтом. Вы также можете применить выравнивание по центру, перенос слов и т. Д.
Взаимодействие с другими людьмиСоздание таблицы в Excel: пошаговая инструкция
Вы уже знаете простейший способ создания таблиц. Однако Excel может предложить более удобный вариант (с точки зрения последующего форматирования и работы с данными).
Построим умную (динамическую) таблицу:
- Перейти на вкладку «ВСТАВИТЬ» – инструмент «Таблица» (или нажать комбинацию горячих клавиш CTRL + T).
- Откроется диалоговое окно, в котором необходимо ввести диапазон данных. Установите флажок для таблицы с заголовками. Щелкните ОК. Ничего страшного, если вы не войдете в правильный диапазон с первой попытки. Умный стол гибкий, динамичный.
Важное примечание. Вы также можете пойти по альтернативному пути: сначала выделите диапазон ячеек, а затем нажмите кнопку «Таблица».
Теперь введите свои данные в готовый фреймворк. Если вам нужен дополнительный столбец, поместите курсор в ячейку заголовка.Сделайте запись и нажмите ENTER. Ассортимент расширится автоматически.
Если вам нужны дополнительные строки, возьмите маркер автозаполнения в правом нижнем углу и перетащите его вниз.
Как работать с таблицей в Excel
С выходом новых версий программы работа с таблицами в Excel стала более интересной и динамичной. После формирования умной таблицы на электронной таблице становится доступен инструмент «ИНСТРУМЕНТЫ ТАБЛИЦЫ» – «ДИЗАЙН».
Здесь вы можете назвать таблицу или изменить ее размер.
Вам доступны различные стили, а также возможность трансформировать таблицу в обычный диапазон или сводный лист.
Динамические электронные таблицыMS Excel открывают огромные возможности. Начнем с базовых навыков ввода данных и автозаполнения:
- Выберите ячейку, щелкнув по ней левой кнопкой мыши. Введите текстовое / числовое значение. Нажмите Ввод. Если вам нужно изменить значение, снова поместите курсор в ячейку и введите новые данные.
- При повторном вводе значения Excel распознает его. Вам нужно будет всего лишь ввести несколько символов и нажать Enter.
- В интеллектуальной таблице, чтобы применить формулу ко всему столбцу, введите ее в первую ячейку. Программа автоматически скопирует формулу в другие ячейки.
- Для подсчета итогов выделите столбец, содержащий значения плюс пустую ячейку для будущего итога, и нажмите кнопку «Сумма» (группа инструментов «Редактирование» на вкладке «ГЛАВНАЯ», либо нажмите комбинацию горячих клавиш ALT + ” знак равно
Щелкнув маленькую стрелку справа от каждого подзаголовка в заголовке, вы получите доступ к дополнительным инструментам для работы с данными в таблице.
Иногда пользователю приходится работать с огромными таблицами, в которых нужно прокрутить несколько тысяч строк, чтобы увидеть итоги. Удаление строк невозможно (данные вам понадобятся позже). Однако вы можете их скрыть. Для этого используйте числовые фильтры (изображенные на изображении выше). Снимите флажки со значений, которые необходимо скрыть.
.
