03.05.202008.07.2019

Задачи по физике простые – Задачи по физике с решениями и ответами по всем разделам

• by alexxlab
• Комментариев к записи Задачи по физике простые – Задачи по физике с решениями и ответами по всем разделам нет
• Разное

Сборник задач по различным темам физики с подробным решением и анализом

В данном разделе собраны темы, на которые в школьном курсе собрано достаточно большое количество задач. В каждом из подразделов рассмотрены условные планы, по которым достаточно просто «увидеть» ход решения задачи. К сожалению, эти планы не являются универсальными, но достаточно много типовых задач можно решить, если прибегнуть к ним.

Кроме того, есть ряд рекомендаций для всех физических задач в целом:

• правильно прочитать условие задачи (часть условия часто намекает на дальнейшее решение, некоторые слова задачи могут иметь чёткий физический смысл)
• оформить дано (чем более ясно оформлено дано, тем меньше нужно возвращаться к условию задачи, что уменьшает время её решения)
• нарисовать рисунок и выставить все элементы из дано на него (чёткий рисунок даёт представление о физической природе рассматриваемого процесса и подсказывает дальнейшее решение)
• рассмотреть сам физический процесс и относящиеся к нему закономерности (законы и формулы, относящиеся именно к рассматриваемому физическому явлению)
• решение начинается с вопроса (обязательно первая формула должна содержать переменную, которую необходимо найти)

Кинематические задачи:

1. Траектория. Путь. Перемещение.
2. Средняя скорость
3. Равномерное движение
4. Неравномерное прямолинейное движение (равноускоренное/равнозамедленное)
5. Движение тела, брошенного под углом к горизонту
6. Кинематика вращательного движения
7. Относительное движение/скорость

Задачи на динамику и статику:

1. Динамика
2. Вес тела
3. Статика
4. Блоки
5. Давление

Задачи на импульс, механическую энергию, законы сохранения импульса и энергии:

1. Импульс
2. Механическая работа
3. Механическая мощность

Задачи на механические колебания

1. Уравнение гармонических колебаний
2. Энергия гармонических колебаний
3. Пружинный и математический маятники

Задачи на гидростатику и гидродинамику

1. Закон Архимеда
2. Гидростатическое давление

Задачи на электростатику

1. Заряд. Закон сохранения заряда
2. Закон Кулона
3. Напряжённость электростатического поля
4. Потенциал электростатического поля
5. Работа поля по переносу заряда
6. Электроёмкость плоского конденсатора

Задачи на постоянный ток

1. Сила тока
2. Закон Ома для участка цепи
3. Закон Ома для полной цепи

Задачи на релятивистские эффекты и СТО

1. Элементы релятивистской динамики

Задачи на квантовые эффекты (фотон, фотоэффект)

1. Элементы квантовой физики

Задачи на термодинамику и молекулярную физику:

1. Химическое количество вещества
2. Кинематические характеристики газа (скорость, пробег)
3. Работа и внутренняя энергия идеального газа
4. Процессы, происходящие в идеальном газе
5. Первое начало термодинамики
6. КПД (коэффициент полезного действия) цикла
7. Фазовые превращения. Нагревание/охлаждение. Уравнение теплового баланса
8. Поверхностное натяжение
9. Относительная и абсолютная влажность

Поделиться ссылкой:

www.abitur.by

Простые механизмы. Задачи по физике Григория Остера – 7 класс

Простые механизмы. Задачи по физике Григория Остера – 7 класс

Посмейся и сообрази!

Перед тобой занимательные задачи по физике Григория Остера!

195. Пете нечего было делать. От скуки Петя, чтобы провести свободное время, подсунул швабру под шкаф, надавил на ручку и, совершенно неожиданно для самого себя, опрокинул шкаф на пол. Как называют физики швабру, подсунутую под шкаф?

Ответ. Швабра под шкафом — это механизм: приспособление для преобразования силы. Механизм, с помощью которого Петя проводил свободное время, называется рычаг. Но придумал его не Петя. Еще три тысячи лет назад местное население Египта использовало рычаг в тех же целях и добивалось хороших результатов.

196. Что напоминает вам твердое тело, которое вращается вокруг неподвижной и несмазанной точки опоры, скрипя и рыча?

Ответ. Рычаг.

197. Все друзья любили Силантия Филимоновича, звали его запросто — Сила и, при встрече, приветствовали оригинальным способом: изо всех сил лупили по части тела, которая называется точно так же, как называют кратчайшее расстояние между точкой опоры и прямой, вдоль которой действует на рычаг сила. Как называется эта таинственная часть тела Силантия Филимоновича?

Ответ. Плечо Силы. А у рычага эту часть называют с маленькой буквы: плечо силы.

198. Близнецы Митя и Витя, живущие на третьем этаже, положили на подоконник длинную доску так, чтобы середина доски пришлась на середину подоконника, и стоят на разных концах доски. Митя стоит снаружи, а Витя в комнате. «Иди сюда» — говорит Витя. «Нет, ты иди», — спорит Митя. Стоит ли Мите спорить с братом?

Ответ. Не стоит, потому что стоит только Вите сделать шаг к Мите и условие, при котором доска-рычаг находится в равновесии, будет нарушено: расстояние между точкой опоры доски и прямой, вдоль которой действует на доску сила, равная витиному весу, сократится. В этот же момент оба брата вместе со своей доской окажутся на свежем воздухе.

199. Сможет ли нечистая сила в 1000 н с помощью рычага, большее плечо которого 2 м, а меньшее 0,5 м, поднять из гроба покойника, масса которого 120 кг?

Ответ.Ой, сможет! Спасайся, кто хочет!

200. Одна агрессивная сила хотела оккупировать рычаг, но в этот момент, с другой стороны рычага, подоспела миротворческая. Миротворческая сила в 200 Н имела плечо 4 метра, а агрессивная сила в 300 Н — плечо 2 метра. Вычисли моменты этих двух сил и скажи кто победит, когда одна сила начнет действовать по часовой стрелке, а другая против.

Ответ. Момент миротворческой силы равен 800 ньютон-метров, а момент агрессивной только 600 ньютон- метров. Миротворческая сила победит, отлупит агрессивную и заставит ее кричать: «Миру-мир!»

201. Молодой трепетный рычаг, имевший широкие плечи: правое 5 метров, а левое 3 метра, познакомился с двумя юными силами — блондинкой и шатенкой. У блондинки был маленький курносый модуль величиной в 300 Н, а у шатенки длинный и кривой величиной 500 Н. Удастся ли молодому рычагу сохранить равновесие, когда на его правом плече повиснет блондинка, а на левом шатенка? Как долго будет сохранять равновесие рычаг?

Ответ. Рычаг не склонится ни к шатенке, ни к брюнетке и будет сохранять равновесие, пока не появится третья сила с каким-нибудь более симпатичным модулем.

202. Парикмахер стрижет клиента, купившего сто лотерейных билетов. Кто: парикмахер или клиент наверняка получит выигрыш?

Ответ. Выиграют ли лотерейные билеты — неизвестно, а вот парикмахер непременно получит выигрыш в силе, потому что ножницы — это рычаг, ось вращения которого проходит через винтик, соединяющий две острые половинки.

203. Длина опытной сотрудницы физической лаборатории белой мышки Мушки от кончика носа до кончика хвоста 20 см. За кончик хвоста сотрудницу в научных целях прицепили к маленькому подвижному блоку и, применяя комбинацию подвижного блока с неподвижным, стали вдумчиво поднимать на ниточке. Свободный конец ниточки вытянули на 35 см. Оторвался от пола нос опытной сотрудницы или не оторвался?

Ответ. Не оторвался. Мышка Мушка от всей души была благодарна эксперементаторам за то, что ее не стали поднимать еще выше.

204. Один азартный строительный рабочий целый день играл с двумя блоками подвижным и неподвижным. К вечеру строительный рабочий выиграл в силе много ньютонов. Какой из двух блоков отдал азартному рабочему его выигрыш: подвижный или неподвижный?

Ответ. Подвижный. Неподвижный блок никому никогда никакого выигрыша в силе не даст. Юноши, не играйте в азартные игры с неподвижными блоками!

205. Пете велели покрасить забор. На покраску забора Петя израсходовал ведро зеленой краски и 55 Дж энергии. Однако вместе с забором Петя за это же время нечаянно покрасил и всех своих друзей. Всего на покраску друзей и забора Петя израсходовал три ведра зеленой краски и 165 Дж энергии. Каков коэффициент полезного действия Пети?

Ответ. Величина петиной полезной работы равна энергии, затраченной на покраску забора. А полная работа, проделанная Петей, равна энергии, которую Петя затратил на покраску друзей и забора вместе взятых. КПД Пети, если рассматривать этого старательного мальчика как очень простой механизм, будет примерно 33 %.

206. Какой из простых механизмов: рычаг, блок, ворот, наклонную плоскость, клин или винт должен использовать лентяй, чтобы получить выигрыш в работе. Не лучше ли лентяю использовать для своей вожделенной цели более сложный механизм?

Ответ. Ни один из механизмов не даст выигрыш в работе лентяю. К сожалению, не даст и честному труженику. Во сколько раз лентяй с тружеником, используя механизм, выиграют в силе, во столько раз проиграют в расстоянии. И наоборот.

207. Ученый с мировым именем Иннокентий долго рассматривал неподвижный блок как равноплечий рычаг, у которого плечи сил равны радиусу колеса. В свою очередь неподвижный блок тоже благосклонно смотрел на талантливого ученого и хотя ничего ему не дал, кое-что все-таки позволил. Чего не дали и что позволили Иннокентию?

Ответ. Известному ученому не дали выигрыша в силе, зато позволили изменить направление силы. «С паршивой овцы хоть шерсти клок», — сказал ученый.

208. Во время ремонта родной школы, который проводился собственными силами учеников, Вовочка нашел незнакомый механизм и с его помощью совершил полезную работу, равную 20 Джоулям. Совершая эту полезную работу, незнакомый механизм с помощью Вовочки нанес родной школе урон Джоулей на 200. Таким образом полная работа, проделанная механизмом в умелых вовочкиных руках, оказалась равна 220 Джоулям. Вычисли коэффициент полезного действия незнакомого механизма в руках у Вовочки.

Ответ. Коэффициент полезного действия всегда равен отношению полезной работы к полной. В данном случае КПД — 11 %. Родной школе еще повезло.

209. Прилагая силу в 50 Н Коля с помощью подвижного блока, вес которого 4 Н, равномерно поднял над дверью ведро с водой и ждет, когда войдет Толя. Вычисли массу этого ведра с водой. Трение, так и быть, можешь не учитывать.

Ответ. Подвижный блок осчастливил Колю выигрышем в силе. В два раза. 100 Н — 2 Н = 98 Н: 9,8 = 10 кг. Скоро Коля в свою очередь осчастливит Толю ведром с водой, общая масса которых 10 кг.

210. Когда Коля попросил Толю поднять его с помощью подвижного блока, Толя послал Колю подальше и сказал, что он не так глуп, чтобы делать двойную работу и вместе с Толей поднимать еще и блок. Действительно ли работа, совершенная при поднятии груза с помощью подвижного блока, больше, чем без блока? Зачем тогда блок?

Ответ. Да, подвижный блок не дает выигрыш в работе. Полная работа, совершенная с его помощью, даже больше полезной. Зато получается выигрыш в силе.

class-fizika.ru

Примеры решения задач по физике для 7 класса – смешные и серьезные

Примеры решения задач по физике для 7 класса – смешные и серьезные

Задачи по физике – это просто!

Серьезные задачи по физике для 7 класса

Средняя скорость. Решение задач ………. смотреть
Плотность. Решение задач. 7 класс ………. смотреть
Механическое движение. Решение задач. 7 класс ………. смотреть
Сила тяжести, вес тела, сила упругости. Решение задач. 7 класс ………. смотреть

Смешные задачи для юных физиков Григория Остера

Как решить задачу по физике? ………. смотреть
Воздухоплавание ………. смотреть
Что изучает физика? ………. смотреть
Наблюдения, опыты, физические величины ………. смотреть
Строение вещества ………. смотреть
Диффузия. Агрегатные состояния ………. смотреть
Взаимодействие тел. Движение ………. смотреть
Взаимодействие тел ………. смотреть
Масса. Плотность ………. смотреть

Сила. Вес тела ………. смотреть
Силы в физике ………. смотреть
Трение ………. смотреть
Давление ………. смотреть
Сила тяжести ………. смотреть
Давление в жидкости и газе ………. смотреть
Давление. Барометр. Манометр. Насос ………. смотреть
Выталкивающая сила. Плавание тел ………. смотреть
Механическая работа ………. смотреть
Механическая мощность ………. смотреть
Простые механизмы ………. смотреть
Энергия ………. смотреть
Лабораторные работы ………. смотреть

Знаете ли вы?

Физиологи установили

… что работа дыхательных органов человека в течение суток достигает 20 тыс. килограммометров. 1 ватт-час соответствует 367 килограммометрам. Следовательно, суточной работы легких достаточно для накаливания 10-вт электрической лампы в течение 5,5 часа.

За сутки человек выдыхает в среднем 1—2 кг углекислого газа, а в год примерно полтонны. Таким образом, все человечество выдыхает ежегодно в атмосферу Земли около миллиарда тонн углекислого газа.

Возможно ли это?

Два человека рассуждали о том, какое светило, солнце или луна, заслуживает преимущества.
Один, не колеблясь, назвал солнце, но другой глубокомысленно заметил: а я так думаю, что луне принадлежит эта честь; что за важность светить, когда солнце, днем, когда и без того светло, а ведь месяц светит ночью, когда темно.

Скажи, могла бы светить луна, если бы не было солнца?

Некто утверждает, что в полдень 22 июня видел радугу на небе.
Возможно ли это?

Оказывается, радуга видна лишь тогда, когда высота солнца над горизонтом не превышает 42 градусов.
22 июня в полдень солнце стоит на небе выше, и нет возможности увидеть радугу.

Интересно, что с земли радуга выглядит обычно как часть окружности, а с самолета она может представлять собой и целую окружность!

class-fizika.ru

Подготовка к ЕГЭ по физике онлайн. Раскрываем секреты простых решений сложных задач.

Зная хорошо теорию по физике, можно быстро, практически устно решать некоторые задачи. Разберём задачу по кинематике и 2 способа её решения.

Итак, задача.

За какую секунду от начала движения, путь, пройденный телом при равноускоренном движении, в 1,4 раза больше его пути, пройденного им за предыдущую секунду, если  в начальный момент времени тело покоилось?

Решение.

1 способ. Обозначим искомую секунду  движения Δt, а предшествующую ей  секунду Δt – 1. Тогда, путь, пройденный за время Δt – это разность путей, пройденных телом за время t и время t – 1. Смотрим внимательно на рис. 1.

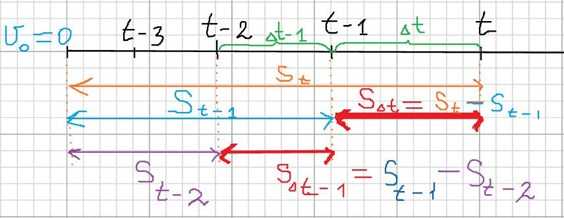
S_Δt = S_t – S_t-1 = at²/2 – a(t – 1)²/2 = 0,5a(t² – (t – 1)²) = 0,5a(t² – ( t² – 2t + 1)) = 0,5a(t² – t² + 2t – 1) = 0,5a(2t – 1)  (*)

Аналогично размышляя, глядя на рисунок 1, запишем, какой путь пройдёт тело за предыдущую секунду Δt-1.

S_Δt-1 = S_t-1 – S_t-2 = a(t – 1)²/2 – a(t – 2)²/2 = 0,5a((t – 1)²– (t – 2)²) = 0,5a(t² – 2t + 1 – (t² – 4t + 4)) =

= 0,5a(t² – 2t + 1 – t² + 4t – 4) = 0,5a(-2t + 1 + 4t – 4) = 0,5a(2t – 3)  (**)

Исходя из условия задачи, составим отношение S_Δt / S_Δt-1 = 1,4. Решим это отношение, подставив вместо S_Δt  ответ, обозначенный (*), а вместо S_Δt-1 ответ, обозначенный (**).

0,5a(2t – 1) / 0,5a(2t – 3) = 1,4

2t – 1/2t – 3 = 1,4

2t – 1 = 1,4(2t – 3)

2t – 1 = 2,8t – 4,2

3,2 = 0,8t

Получаем t = 4 (сек). Проверим себя, подставив данные в выражение  (*) и в выражение  (**)

S₄ = S₄ – S₃ = 0,5a(2 · 4 – 1) = 0,5a 7 = 3,5a

S₃ = S₃ – S₂ = 0,5a(2 · 3 – 1) = 0,5a 5 = 2,5a

Найдём отношение S₄/S₃  =  3,5a/2,5a = 1,4.

Всё правильно, задача решена верно!

Ответ: 4 сек.

Этот способ довольно трудоёмкий, и трудность заключается в правильном прочтении условия , составления и решения  уравнений (*) и (**).

Но есть 2 способ решения этой задачи. Он намного проще. Используя этот способ, подобные задачи можно решить практически устно. Посмотрим внимательно на рис. 2.

И вспомним, что при равноускоренном движении, при условии начала движения из состояния покоя (как раз как в нашей задаче), тело за последовательные промежутки времени  Δt = 1 секунде, проходит пути, которые относятся как последовательные нечётные числа.

S₁: S₂: S₃: S₄: S₅: S₆ … = 1: 3: 5: 7: 9: 11: … Теперь посмотрим, отношение  какой пары последовательных нечётных чисел даёт нам 1,4? Это числа 7 и 5. Глядя на рисунок 2, видим, что граница отрезка, подписанного числом 7, заканчивается справа точкой  t₄ = 4 (сек). Мы получили такой же ответ, как и в способе 1. А вот какой способ решения будете использовать Вы, решать Вам.

Остались вопросы? Не знаете, как решать задачи по физике?
Чтобы получить помощь репетитора – зарегистрируйтесь.
Первый урок – бесплатно!

Зарегистрироваться

© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.

blog.tutoronline.ru

Задачи по статике с подробными решениями

Задачи по статике с решениями

Равновесие тел

3.1.1 Человек стоит на полу. Масса его 60 кг. Площадь подошв 400 см2. Какое давление
3.1.2 На тело действуют силы 4 и 5 Н, направленные под углом 90 градусов друг к другу
3.1.3 На аэростат в горизонтальном направлении действует ветер с силой 3000 Н. Натяжение
3.1.4 Какую силу необходимо приложить, чтобы приподнять за один конец бревно
3.1.5 Шар массой 6 кг висит на веревке, прикрепленной к гладкой стене. С какой силой шар
3.1.6 На обод колеса вагона действует тормозящая сила 500 Н. Определить момент этой силы
3.1.7 Два одинаковых шарика, масса и радиусы которых равны соответственно 100 г и 3 см
3.1.8 К тросу длиной 3 м, концы которого закреплены на одной высоте, на расстоянии 1 м
3.1.9 Шар массой 5 кг опирается на две гладкие плоскости, образующие угол, причем
3.1.10 В ящике находится шар массой 3 кг. Ящик наклоняют так, что его дно составляет
3.1.11 На двух взаимно перпендикулярных наклонных плоскостях, из которых одна наклонена
3.1.12 При подвеске контактного провода троллейбусной сети провес опорного троса
3.1.13 Два шара, алюминиевый и цинковый, одинакового объема и радиуса 10 см скреплены
3.1.14 Три однородных шара массой 1, 2 и 2 кг укреплены на легко стержне. Центр 2-ого шара
3.1.15 На одном из концов однородного стержня прикреплен груз массой 3 кг. Если стержень
3.1.16 Однородная доска массой 10 кг подперта на расстоянии 0,25 её длины от конца. Какую
3.1.17 Рабочий удерживает за один конец доску массой 50 кг. С горизонтальной поверхностью
3.1.18 Два человека несут груз на невесомом стержне длиной 3 м. Нагрузка (усилие) одного
3.1.19 На тело массой 2 кг, покоящееся на гладкой наклонной плоскости с углом при основании
3.1.20 Каков должен быть коэффициент трения, чтобы заколоченный в бревно клин
3.1.21 К стене приставлена лестница массой 60 кг. Центр тяжести лестницы находится
3.1.22 Лестница массой 15 кг и длиной 3 м стоит, упираясь верхним концом в гладкую стену
3.1.23 Подъемное устройство состоит из однородного стержня длиной L=2,5 м и массой m=5 кг
3.1.24 Лестница составляет с землей угол 70 градусов и опирается о вертикальную гладкую
3.1.25 Стержень длиной l и массой m одним концом упирается в вертикальную стенку
3.1.26 К вертикальной гладкой стене подвешен на тросе AB однородный шар массы M
3.1.27 К вертикальной гладкой стене подвешен на тросе AB однородный шар массы M. Определите
3.1.28 Расстояние между двумя опорами 8 м. На эти опоры положили горизонтальную балку
3.1.29 Однородная балка длины 2 м и массы 1000 кг удерживается в горизонтальном положении
3.1.30 Расстояние между двумя опорами 8 м. На эти опоры положили горизонтальную
3.1.31 С помощью каната, перекинутого через неподвижный блок, укрепленный под потолком
3.1.32 Под каким наименьшим углом a к горизонту может стоять лестница, прислоненная
3.1.33 Какой тормозящий момент относительно оси вращающегося колеса диаметра 40 см
3.1.34 На барабан лебедки диаметра 20 см намотан трос. К тросу подвесили груз массы 20 кг
3.1.35 В две сообщающиеся трубки разного сечения налили сначала ртуть, а потом в широкую
3.1.36 В одном из двух одинаковых заполненных водой сообщающихся сосудов плавает шарик
3.1.37 В сосуд с водой вставлена трубка сечением 2 см2. В трубку налили 72 г масла. Найти
3.1.38 В колено U-образной трубки площадью 1 см2, содержащей ртуть, налили 7,2 г воды
3.1.39 В сообщающиеся сосуды налили сначала ртуть. Затем в один сосуд налили масло высотой
3.1.40 В сообщающихся сосудах находится ртуть. Площадь сечения одного сосуда в 4 раза
3.1.41 Две трубки диаметром 4 см представляют собой сообщающиеся сосуды. В одно колено
3.1.42 Поршень весом 30 Н представляет собой круглый диск радиусом 4 см с отверстием
3.1.43 Определить массу груза, который можно поднять с помощью гидравлического поршня
3.1.44 В гидравлическом прессе площадь малого поршня 20 см2, а большого 500 см2. С какой
3.1.45 К малому поршню гидравлического пресса приложена сила 196 Н, под действием
3.1.46 Малый поршень гидравлического пресса за один ход опускается на 0,2 м, а большой
3.1.47 Столб воды в сообщающихся сосудах высотой 17,2 см уравновешивает столб дизельного

Давление в жидкостях и газах

3.2.1 Во сколько раз давление столбика ртути высотой 10 см больше давления столбика
3.2.2 С какой силой давит на дно стакана слой воды толщиной 10 см? Радиус дна
3.2.3 В сосуд налито воды высотой 20 см. Определить среднее давление воды на стенку
3.2.4 Аквариум имеет форму куба со стороной 0,6 м. До какой высоты следует налить в него
3.2.5 Аквариум наполнен доверху водой. С какой средней силой давит вода на стенку
3.2.6 В сосуд, имеющий форму прямоугольной призмы, шириной 15 см и длиной 35 см налита
3.2.7 На сколько отличается давление столбика ртути высотой 10 мм от давления столбика
3.2.8 Найти давление в озере на глубине 4,5 м. Атмосферное давление
3.2.9 Чему равно давление воды на глубине 2 м?
3.2.10 С какой силой действует вода на прямоугольную плотину высотой 75 м и шириной 120 м
3.2.11 Барометр показывает в воздухе давление 75 см ртутного столба. Найти давление на глубине
3.2.12 В узкую мензурку вода налита до уровня 10 см. Определите давление на дно мензурки
3.2.13 В цилиндрический сосуд налиты равные по массе количества воды и ртути. Общая
3.2.14 В цилиндрическое ведро с площадью дна 0,02 м2 налита вода. Найдите массу воды
3.2.15 Какова сила давления на поршень насоса при высоте подачи воды 25 м, если
3.2.16 На какой глубине в пресной воде давление в 3 раза больше нормального
3.2.17 На какой глубине моря гидростатическое давление воды равно 4,9 МПа? Плотность
3.2.18 Образовавшееся на дне нефтяного бака отверстие в 5 см2 заделано пробкой
3.2.19 Поверхность воды в водонапорной башне находится на 30 м выше водопроводного
3.2.20 С какой силой выталкивается вода из иглы медицинского шприца, если на поршень
3.2.21 Цистерна с бензином имеет высоту 6 м. Найти давление на высоте 2,5 м от дна
3.2.22 Высота воды в открытом сосуде 5 м. Стенка сосуда имеет ширину 1,5 м и наклонена
3.2.23 Плоскодонная баржа на глубине 1,8 м от уровня воды в реке получила пробоину
3.2.24 С какой силой давит атмосферный воздух на обложку книги размером 12×20 см2

Закон Архимеда

3.3.1 В воде плавает шар, погрузившись на 0,25 своего объема. Определить плотность
3.3.2 Брусок дерева плавает в воде. Объем погруженной части бруска 36 см3. Определить
3.3.3 Льдина плавает на поверхности воды. Часть её объема, равная 150 м3, находится
3.3.4 На тело, находящееся в воде, действует выталкивающая сила 2 Н. С какой силой это тело
3.3.5 Цилиндр высотой 40 см плавает в вертикальном положении в сосуде с водой. Определить
3.3.6 В воде плавает шар, погрузившись на 2/3 объема. Определите плотность
3.3.7 В стакане, наполненном до краев водой, плавает кусок льда. Как изменится давление
3.3.8 В цилиндрический сосуд с водой, с площадью дна 150 см2, опускают тело массой 1 кг
3.3.9 Вес куска железа в воде 1,67 Н. Найти его объем
3.3.10 Груз какой массы может поднять аэростат объемом 100000 м3 на высоту 40 км?
3.3.11 Деревянный брусок массой 1,4 кг плавает на поверхности воды. Какой массы груз
3.3.12 Дубовый шар лежит в сосуде с водой, причем половина его находится в воде. С какой
3.3.13 К телу, сделанному из пробки, привязали веревку, другой конец которой закрепили
3.3.14 Кусок дерева плавает в воде, погружаясь на 0,75 своего объема. Какова плотность
3.3.15 Кусок металла массой 0,78 кг весит в воде 6,8 Н, а в бензине — 7,1 Н. Определить
3.3.16 Кусок пробки плавает в банке с керосином. Какая часть объема пробки погружена
3.3.17 На плоту, состоящем из 20 одинаковых бревен, можно перевозить груз максимальной
3.3.18 Надводная часть айсберга имеет объем 1000 м3. При какой плотности льда объем
3.3.19 Пробковый спасательный круг имеет массу 3,2 кг. Определить подъемную силу
3.3.20 Шарик плавает в сосуде, в котором находятся вода и масло. При этом 2/3 объема
3.3.21 Вес тела в воде в 5 раз меньше, чем в воздухе. Какова плотность вещества тела?
3.3.22 Льдина равномерной толщины, плавает в воде, выступая над её поверхностью на 2 см
3.3.23 Из воды с глубины 5 м поднимают на поверхность камень объемом 0,6 м3. Плотность
3.3.24 Доска толщиной 5 см плавает в воде, погрузившись на 70%. Поверх воды разливается
3.3.25 Один конец нити закреплен на дне, а второй прикреплен к пробковому поплавку
3.3.26 Плотность жидкости в 3 раза больше плотности материала тела. Какая часть объема
3.3.27 Полый цинковый шар, внешний объем которого 200 см3, плавает так, что половина его
3.3.28 Стеклянный шарик объемом 0,5 см3 равномерно тонет в воде. Какое количество
3.3.29 Тело массой 2 кг и объемом 1 л находится в озере на глубине 5 м. Какую необходимо
3.3.30 Шарик массой 20 г всплывает с постоянной скоростью в жидкости, плотность которой
3.3.31 Шарик на нити, уравновешенный на весах, опускают в воду. Когда шарик на 0,3 своего
3.3.32 В сосуд налили ртуть и сверху неё масло. Шар в сосуде плавает так, что он ровно
3.3.33 Деревянный шар лежит на дне сосуда с водой, причем половина его находится в воде
3.3.34 На рычажных весах уравновешен сосуд с водой. На сколько нужно увеличить массу гирь
3.3.35 Поверх жидкости плотностью 1000 кг/м3 налита большим слоем жидкость плотностью
3.3.36 Полый железный шар взвешивают в воздухе и керосине. Показания динамометра
3.3.37 Пустая цилиндрическая пробирка, опущенная вертикально в воду, оказалась погруженной
3.3.38 С какой высоты должно падать тело плотностью 400 кг/м3, чтобы оно погрузилось
3.3.39 Чашки равноплечих весов находятся в воде плотностью 1 г/см3. Найти массу гирь
3.3.40 Человек прыгает в воду со скалы высотой 10 м. На какую глубину он опустится
3.3.41 Шарик подвесили на упругой пружине и опустили в воду. Во сколько раз уменьшилось
3.3.42 В цилиндрическом сосуде диаметром 50 см плавает льдинка объемом 12 дм3. В льдинку
3.3.43 Однородный конус массой 48 кг плавает в воде вершиной вниз. Определить высоту
3.3.44 Цилиндр плавает в вертикальном положении в сосуде с водой. В сосуд подливают более
3.3.45 Шарик от настольного тенниса диаметром 4 см и массой 8 г удерживается под водой
3.3.46 В воде плавает льдина с площадью поперечного сечения 5 м2 и высотой 0,5 м. Какую
3.3.47 Однородный куб плавает в воде, на 0,75 своего объема погрузившись в воду. Если
3.3.48 Однородный пробковый брусок квадратного сечения со стороной 10 см и длиной 40 см
3.3.49 Однородный стержень длиной 1 м и площадью сечения 1 см2 плавает в вертикальном
3.3.50 Шарик для игры в настольный теннис радиусом 15 мм и массой 5 г погружен в воду
3.3.51 Два деревянных шара одинакового объема, полностью находящиеся в жидкости
3.3.52 В сосуде находятся две несмешивающиеся жидкости с различными плотностями
3.3.53 Плотность воды 1000 кг/м3, а плотность пробки 200 кг/м3. Пробковый шар массы 100 г
3.3.54 Плотность воды 1000 кг/м3, а плотность камня 2500 кг/м3. Если не учитывать
3.3.55 Палочка массы 400 г наполовину погружена в воду, как показано на рисунке. Угол
3.3.56 Палочка массы m наполовину погружена в воду, как показано на рисунке. Угол наклона

Поверхностные явления

3.4.1 На какую высоту поднимается вода в капиллярной трубке диаметром
3.4.2 В капиллярной трубке радиусом 0,5 мм жидкость поднялась на 11 мм. Определить
3.4.3 Определить массу воды, поднявшейся по капиллярной трубке диаметром
3.4.4 На проволочной рамке с подвижной перекладиной длиной 10 см натянута мыльная пленка
3.4.5 При лужении оловом с конца проволоки диаметром 1 мм оторвалось 20 капель олова

easyfizika.ru

Сила тяжести, вес тела, сила упругости. Примеры решения задач по физике. 7 класс

Сила тяжести, вес тела, сила упругости. Примеры решения задач по физике. 7 класс

Задачи по физике – это просто!

Вспомним

Изображение сил на чертеже:

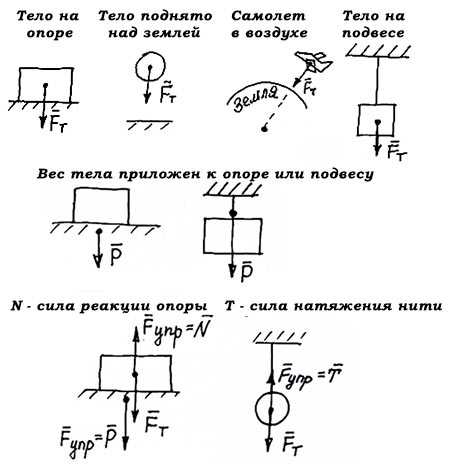
Формула для расчета силы тяжести, действующей на тело:

Формула для расчета веса тела:

Форула для расчета силы упругости:

Здесь единица измерения массы – 1 кг,
единица измерения силы – 1 Н,
единица измерения жесткости пружины – 1 Н/м,
единица измерения величины деформации пружины (удлинения) – 1 м.
Все задачи решаем в системе СИ!

А теперь к задачам!

Элементарные задачи для 7 класса из курса школьной физики на расчет силы тяжести, веса тела и силы упругости.

Задача 1

Определить силу тяжести, действующую на тело массой 100 кг.

Задача 2

Определить вес тела массой 600 г.

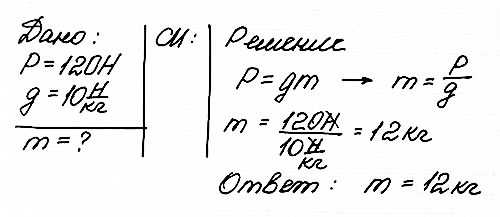
Задача 3

Определить массу тела весом 120 Н.

Задача 4

На полу стоит ящик массой 1 тонна. Определить силу тяжести и силу упругости, действующие на ящик, а также вес ящика.
(Здесь N – сила реакции опоры, на которой стоит ящик, приложена к ящику, является силой упругости.
Если тело стоит неподвижно, т.е. не проваливается сквозь опору, то сила реакции опоры численно равна силе тяжести, действующей на тело.
Вес тела приложен к опоре и численно равен силе тяжести, действующей на тело.)

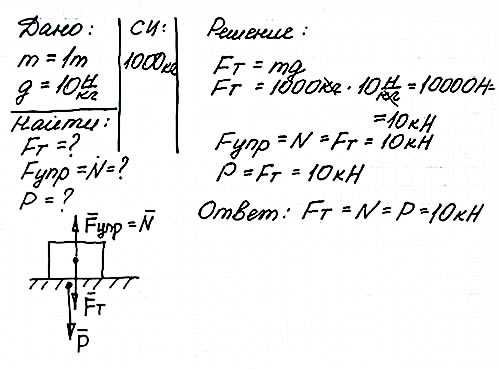
Задача 5

Определить вес алюминиевого бруска объемом 200 см³.

Задача 6

Определить силу упругости, возникающую при сжатии пружины на 10 см, если жесткость пружины равна 400 Н/м.

Задача 7

Определить максимальную силу упругости, возникающую при растяжении резины грузом массой 5 кг.

Задача 7

Найти удлинение пружины, возникающее под действием подвешенного к ней груза массой 200 г, если жесткость пружины равна 1000 Н/м.
(в этой задаче Х -это удлинение пружины, иначе величина деформации пружины, равна изменению длины пружины при деформации)

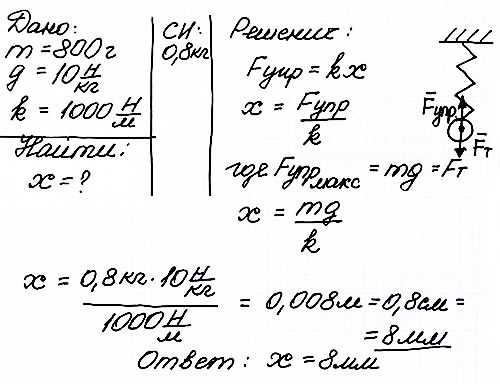
class-fizika.ru

Обучение физики через решение задач

Разделы: Физика

---

Чтобы научить решать задачи,
надо их решать.
Д.Пойа

После введения цикличности в школьном курсе физики, возникла серьезная проблема: на изучение механики отводился один год, в данный момент одна четверть. В первые два года приходилось тратить на этот раздел все первое полугодие, что приводило к проблемам с изучением материала в конце учебного года.

В итоге решение проблемы было найдено в следующем виде:

• единый подход к решению всех физических задач;
• алгоритмы на типовые задачи.

Решение любой физической задачи может быть разбито на четыре этапа:

1. На основе анализа физического процесса составляется система уравнений.
2. Математическое решение системы уравнений. (Предварительно решить вопрос о совместности уравнений).
3. Анализ полученных результатов с точки зрения физики процесса.
4. Вычисления и оценка реальности результатов.

С другой стороны все задачи можно разделить на задачи двух типов:

1. Тренировочные задачи. Условие такой задачи содержит все необходимые величины и четко сформулированный вопрос. Проблема решения такой задачи – проблема выполнения определенного алгоритма действий.
2. Задачи, требующие анализа, результатом которого является разбиение условия на конечное число подзадач 1 типа. Уровень сложности такой задачи определяется соотношением между объемами аналитической и алгоритмической части.

Особое положение занимают «эвристические» задачи, решение которых не может быть сведено к выполнению конечного числа алгоритмов.

В данном материале мы будем рассматривать базовые алгоритмы раздела «Механика».

Решение тренировочных задач темы «Равноускоренное движение»

В идеале задачи этой темы должны решаться на основе только двух формул:

• закона движения 
• определения ускорения
• и вспомогательной формулы S_x = x – x₀

которая используется, если скорость тела в интересующий нас промежуток времени не изменяла своего направления. Решение задачи начинаться с задания начальных условий (Н.У.) движения (r, v, a при t = 0) и с выбора системы отсчета (если она не задана в условии задачи).

Но это в идеале. За один, два урока при данном подходе с проблемой не справиться, тем более что задача отягощается математическими проблемами при выводе формул  и заданием Н.У.

Решим проблему с начальными условиями:

Пример 1. Мячик бросили вертикально вверх с высоты h₀ = 6 м со скоростью v₀ = 20 м/с. Определите, через сколько секунд мячик окажется на высоте h = 1 м.

Опустим начало решения и запишем закон движения в проекции на ось Oy:

Зачеркиванием введем Н.У. и при необходимости К.У.

в итоге получаем частный случай закона движения для нашей задачи:

Разрешить проблему времени позволяет алгоритм, в основе которого лежат шесть формул:

Формула №1 используется в редких случаях, если в условии задачи задается положение тела.

Формулу № 6 необходимо пробовать в первую очередь если выполняется условие . Для случая v₀ = 0 это очевидное следствие формулы №3. Для случая v = 0 требует вывода.

• Краткая запись условия.
• Рисунок
  
• Анализ краткой записи условия.
• Математическое решение.
• Анализ полученного результата.
• Вычисления.
• Ответ.

При краткой записи условия необходимо обратить особое внимание на скрытые условия, т.е. величины заданные вербально. На первых этапах достаточно при чтении условия делать остановки в трудных местах условия.

Рисунок необходим для определения знака ускорения через выбор системы координат и проекцию. Проще на этом этапе рисунок заменить комментарием: «разгон», «торможение» или «равноускоренное движение», «равнозамедленное движение». Но во многих методических источниках не рекомендуется использовать термин «равнозамедленное движение» т.к. он сужает границы применения термина «равноускоренное движение» и приводит к невозможности единого описания некоторых видов движения, например  движения под действием силы тяжести. При дальнейшей работе возникают следующие проблемы: учащиеся делят движение под действием силы тяжести на два участка и не воспринимают его как единое целое, описываемое с точки зрения математики одним уравнением, т.е. данный подход не удается обобщить и тему приходится изучать с «нуля».

Анализ краткой записи условия проще объяснить на примере.

Пример 2. На пути  45 метров скорость тела изменилась от 10 м/с до 40 м/с. Определите ускорение тела.

Дано: S = 45 v = 10 м/с v0 = 40 м/с	В условии не упоминается время, следовательно необходимо применить формулу
а = ?

Математическое решение. Не первоначальном этапе изучения физики много времени приходится уделять математической обработки результатов. В основном возникают следующие проблемы:

• Работа с тригонометрическими функциями.
  • В основном мы используем два тригонометрических равенства: cos²α + sin²α = 1 и sin²α = 2 sinα cosα
  • Основные тригонометрические функции:
•  Работа с уравнениями.   

Мы обычно ругаем математиков за недостаточную подготовку, но некоторые действия, допустимые при решении задач по физике, недопустимы в общей математической практике. Например, с уравнениями можно производить те же действия, что и с числами: сложение, вычитание, умножение и деление. Операция деления ограничена условием – делитель не может быть нулевым, но с точки зрения физического смысла мы уверены, что функция не может быть нулевой или нули функции нам не нужны.

Пример 3.

быстрее, чем выразить и подставить.

Те же проблемы возникают и при решении квадратных уравнений. Часто до квадратного уравнения можно не доводить, теряя, отрицательные корни, не имеющие физического смысла. Т.е. с учетом физического смысла можно сильно сузить ОДЗ и упростить решение.

Пример 4. Определите внутреннее сопротивление источника тока, если при сопротивлении R₁ во внешней цепи выделяется такая же мощность, как и при сопротивлении R₂.

т.к. P₁ = P₂, следовательно

Анализ полученного результата включает в себя:

• проверку размерности как проверку правильности полученной формулы;
• анализ зависимости искомой величины от данных особенно при их критических значениях;
• оценку реальности результата.

Вычисления значительно упрощаются при освоении инженерного калькулятора:

• набора чисел в форме x × 10ⁿ;
• вычисления прямых и обратных тригонометрических функций;
• вычисления на калькуляторе без дополнительных записей в тетради.

В профильном классе в обязательном порядке проводится зачет, основным вопросом которого является доказательство формул №1–№6.

Алгоритм решения задач на применение законов Ньютона

Алгоритм II.

• Краткая запись условия;
• первичный рисунок;
• Как движется тело? – рисуем скорость и ускорение;
• С какими телами взаимодействует? – рисуем силы;
• Если в условии задачи рассматривается вес тела:

Опора                        –         «по 3 з. Ньютона                  Р = N»

Подвес                      –         «по 3 з. Ньютона                  P = T»

Невесомость            –         «по 3 з. Ньютона                  P = 0 = T или Р = 0 = N»

• Есть ли ускорение?

Да                              –          «по 2 з. Ньютона                »

Нет                            –          «по 1 з. Ньютона                »

• Сколько на рисунке сил?
• Запись векторная 1 или 2 з. Ньютона (расширенная).
• Выбор СО (системы отсчета).
• Если есть силы не параллельные осям – рисунок их проекций
• Запись законов Ньютона в проекции на оси СК

F ↑↑ оси        –          знак не меняем

F ↑↓ оси        –          знак меняем

F  оси        –          не пишем (проекция равна нулю)

Или смотри рисунок.

• При необходимости применение закона Гука, закона всемирного тяготения, частных формул для сил….
• Если в условии есть скорость путь время, применяем формулы кинематики.
• математическое решение.
• анализ полученного результата.
• вычисления.
• ответ.

Первичный рисунок – на этом этапе часто на рисунке изображаются детали, отсутствующие в условии задачи.

Пример 5. В первых задачах на применение второго закона Ньютона в условии часто написано «На тело массой mдействует сила F». Учащиеся рисуют опору и силу тяжести, хотя в условии их нет и происхождение силы не оговаривается.

Неверно	Верно

На рисунке желательно придать силе произвольное направление, что подчеркнет свободное условие задачи и даст повод обсудить связь между силой,  ускорением и скоростью с точки зрения причинно – следственной связи.

Пример 6. Тело под действием силы F поднимается вверх с ускорением а.

Не верно	Верно

(очень распространенная ошибка).

Данные примеры подчеркивают необходимость выполнения рисунка в строгом соответствии с условием задачи и отступления не допустимы.

Рисунок должен занимать не менее трети тетрадного листа.

Сила – это величина, характеризующая взаимодействие тел. Здесь возможны следующие нюансы:

• Взаимодействие может осуществляется без непосредственного контакта (на первоначальном этапе только взаимодействие с Землей – сила тяжести). По сути это действие на тело гравитационного поля. На профильном уровне имеет смысл ввести понятие поля вместе с понятием силы, рассмотрев теории близкодействия и дальнодействия. Тогда вопрос, «С какими телами взаимодействует тело?» можно сразу разбить на два:

1. С какими телами взаимодействует тело?
2. В каких полях находится тело?

В 10 классе возможно рассмотреть гравитационное и электромагнитное поле и подчеркнуть, что взаимодействие при непосредственном контакте на макроуровне это на микроуровне так же действие поля на микрообъект (в случае сил упругости и сил трения – взаимодействия электромагнитного поля одной молекулы с другой молекулой как системой зарядов).

• Взаимодействие при непосредственном контакте тел.

Есть контакт – есть взаимодействие – есть сила.

Итоги

Описанные алгоритмы, при их активном использовании на уроках позволяют существенно сократить время на приобретения учащимися навыка решения задач. Алгоритмы универсальны и могут применяться в любой теме, что позволяет провести единую линию решения задач по всему школьному курсу физики. Позволяет один раз, затратив учебное время на обучение решению задач, в дальнейшем вводить только новые законы и закономерности подчеркивая единые способы и методы их применения в задачах.

В основе выше приведенного материала лежат следующие общеизвестные технологии:

• Технология обучения математике на основе решения задач (Р.Г. Хазанкин)
• Проблемное обучение.
• Уровневая дифференциация обучения на основе обязательных результатов (В.В. Фирсов)

22.07.2010

urok.1sept.ru

---