Закон ньютона 2 3: Физические основы механики
- Второй закон Ньютона и «Три богатыря» Васнецова
- Сила. Три закона Ньютона | LAMPA
- Взаимодействие тел, третий закон Ньютона — ЗФТШ, МФТИ
- Об извращённом толковании Первого закона Ньютона в современной физике / Хабр
- Третий закон Ньютона — урок. Физика, 9 класс.
- 1 2 и 3 закон ньютона – Третий закон Ньютона определение. Формула третьего закона Ньютона. Третий закон Ньютона, сила
- Второй закон Ньютона
- Второй закон движения Ньютона
- Второй закон движения Ньютона: концепция системы
- Научный эксперимент: Второй закон Ньютона…
- 4.3 Второй закон движения Ньютона – Физика
- Задачи обучения раздела
- Поддержка учителей
- Раздел Основные термины
- Описание второго закона движения Ньютона
- Поддержка учителей
- Применение второго закона Ньютона
- Поддержка учителей
- Snap Lab
- Проверка захвата
- Советы для успеха
- Watch Physics
- Проверка захвата
- Рабочий пример
- Стратегия
- Рабочий пример
- Стратегия
- Практические задачи
- Проверьте свое понимание
- Поддержка учителя
- Что такое второй закон движения Ньютона? | Исаак Ньютон
- Второй закон Ньютона – Силы, ускорение и законы движения Ньютона – Eduqas – GCSE Combined Science Revision – Eduqas
- Движение и силы: второй закон движения Ньютона
Второй закон Ньютона и «Три богатыря» Васнецова
Статьи
Линия УМК А. В. Грачева. Физика (7-9)
Физика
Как думаете, какая связь существует между картиной Васнецова «Три богатыря» и вторым законом Ньютона?
27 августа 2019
Ответ на загадку найдете в конце статьи, а пока давайте вспомним вклад Ньютона в классическую физику.
Галилей, Гюйгенс, Кеплер, множество других исследователей, чьи имена остались похоронены под слоем пыли в темных библиотеках средневековых замков, проводили опыты и эксперименты, пытаясь открыть законы движения предметов в окружающей среде.
Исаак Ньютон, опираясь на знания и эксперименты предшественников и собственные наблюдения, смог подытожить накопленный колоссальный опыт и сформулировать законы, по которым движутся физические тела.
В 1867 году увидел свет его научный труд: «Математические начала натуральной философии», где английский физик представил известные законы механики и закон всемирного тяготения.С того времени классическая механика базируется на законах Ньютона.
Физика. 8 класс. Учебник.
Учебнипк рассчитан на учащихся общеобразовательных организаций. Настоящее издание вместе с рабочими тетрадями, тетрадью для лабораторных работ и методическим пособием для учителей составляет учебно-методический комплект по физике для 8 класса. В учебнике представлены разделы «Тепловые явления» и «Электромагнитные явления».
Купить
Первый закон, или закон инерции гласит: «Всякое тело продолжает удерживаться в состоянии покоя или равномерного и прямолинейного движения, пока и поскольку оно не понуждается приложенными силами изменить это состояние.» Подробно данный закон разбирается в учебнике «Физика 9 класс» под редакцией Л.
Цель нашей статьи — второй закон Ньютона.
Как вы заметили, первый закон определяет, что происходит с телом в покое, т.е. когда на него не действуют силы. Но в реальном мире движение повсюду.Играете ли вы в футбол, нога футболиста с силой ударяет по мячу, придавая нужное ускорение и траекторию, чтобы забить победный гол. Отбивает ли мама на кухне мясо — рука передает кухонному молотку также определенную силу, чтобы получился вкусный стейк.
И именно эти взаимодействия объясняет второй закон Ньютона, который звучит так: «Величина силы, действующая на тело, равна произведению массы тела на ускорение, которое получает тело, когда на него начинает действовать сила.»
Если представить этот закон математически, формула второго закона Ньютона выглядит следующим образом:
F=m*a, где:
- m- масса тела,
- а — ускорение, которое получает тело под воздействием приложенной силы,
- F — Это результирующая всех сил приложенных к телу (велосипедисту, паровозу, самолету и т.
 д.)
д.)
Однако, эта формула вводит в небольшое заблуждение, потому что глядя на нее, кажется, что ускорение вызывает силу, а такого в живой природе быть не может.
Преобразовав уравнение таким образом:
а=F/m
приходим к выводу, что сила определяет ускорение, а не наоборот.
Чем большая сила действует на тело, тем больше ускорение он получит, и наоборот, чем больше масса, тем меньше ускорит свое движение тело.
Физика. 9 класс. Учебник.
Настоящее издание является завершением линии учебников для учащихся 7-9 классов общеобразовательных организаций (авт. А.В.Грачёв, В.А. Погожев и др.). Учебник рассматривает разделы «Механические явления», «Электромагнитные явления», «Оптические явления» и «Квантовые явления». В учебник включены материалы для учащихся, интересующихся физикой, задания для внеклассной работы.
Купить
А сейчас ответим на вопрос, заданный в начале статьи, о том, что общего между богатырями с картины Васнецова и вторым законом Ньютона.
Представьте: ратное поле и три красавца коня ноздря в ноздрю бьют копытом землю. Как думаете, чья силушка богатырская будет больше, если кони сорвутся в бой с одинаковым ускорением? Конечно у того богатыря, чья масса больше.
А вот и ответ. Картина Васнецова напоминает простое мнемоническое правило для лучшего запоминания второго закона Ньютона: сила богатыря равна богатырской массе умноженной на богатырское ускорение.
Что ещё почитать?
#ADVERTISING_INSERT#Сила. Три закона Ньютона | LAMPA
Три закона Ньютона
Три закона Ньютона определяют “правила жизни” в механике. Обычно в школе их излагают в прямой последовательности — от первого закона к третьему. Мы поступим по-другому. Мы изложим их в обратном порядке. Нам кажется, что так будет понятнее. Приступим.
Третий закон Ньютона. Попробуйте надавить рукой на стол. При этом ладонью своей руки вы почувствуете поверхность стола. И вы также почувствуете некоторое сопротивление со стороны стола. Будто и сам стол давит на вас. При этом, если бы вы не давили на стол, а держали руку неподвижно, а поверхность стола приближалась бы к вашей руке и сама давила на вашу руку, то ощущения были бы точно такими же.
При этом ладонью своей руки вы почувствуете поверхность стола. И вы также почувствуете некоторое сопротивление со стороны стола. Будто и сам стол давит на вас. При этом, если бы вы не давили на стол, а держали руку неподвижно, а поверхность стола приближалась бы к вашей руке и сама давила на вашу руку, то ощущения были бы точно такими же.
Можно предположить, что когда тело А воздействует на другое тело — тело B (например, вы действуете на стол), — то и тело B действует на тело А.
Рассмотрим другой пример. Девочка А и девочка B стоят на коньках на льду. Девочка А начинает толкать девочку B. Наш жизненный опыт подсказывает нам, что девочка B будет двигаться в ту сторону, куда ее толкает девочка А. Но! Жизненный опыт нам подсказывает, что и девочка А начнет двигаться так, будто ее толкнула девочка B.
Это подтверждает нашу догадку, что когда тело А действует с некоторой силой на тело B, то и тело B действует на тело А.
Оказывается, что наше предположение — верное. Более того, силы, с которыми тела действуют друг на друга, одинаковые (!).
Итак, третий закон Ньютона звучит следующим образом:
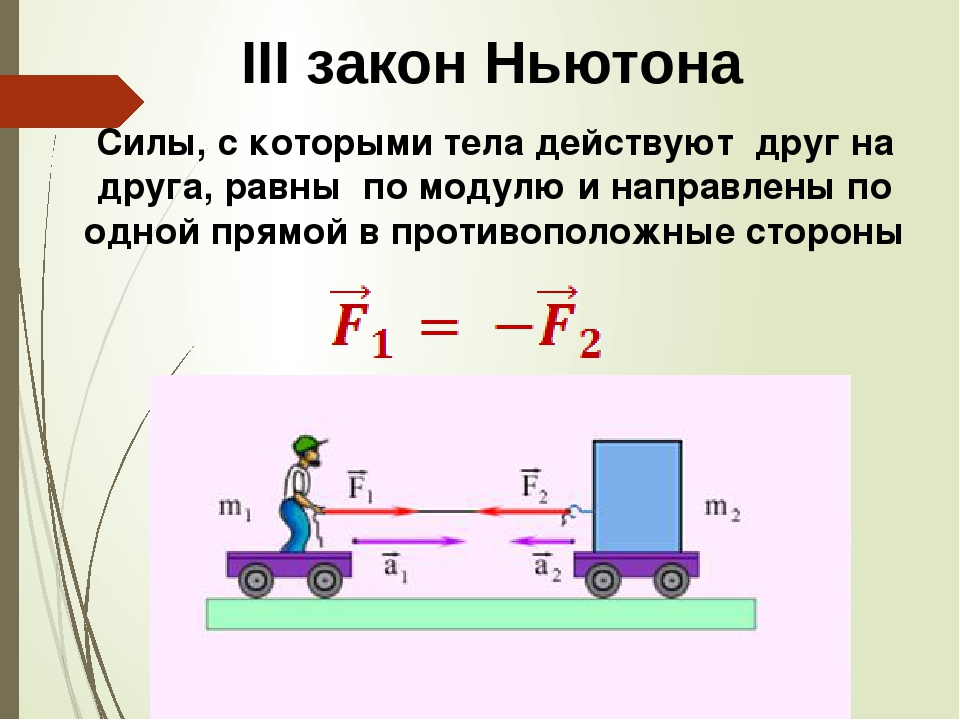
Силы, с которыми тела действуют друг на друга, равны по модулю и противоположны по направлению: F⃗1→2=−F⃗2→1.\vec{F}_{1\to 2}=-\vec{F}_{2\to 1}{.}F⃗1→2=−F⃗2→1.
Второй закон Ньютона. Представьте себе ситуацию: на столе неподвижно стоит мячик. Мы толкаем его, то есть мы действуем силой. При этом мячик начинает двигаться. Значит, у него появилась скорость.
Итак, сначала мячик покоился и у него была нулевая скорость: V1=0V_1=0V1=0. А затем мячик двигался, и его скорость была уже не нулевой: V2≠0V_2\neq 0V2≠0. То есть скорость изменилась (!). У нас есть изменение скорости. А это значит, что есть ускорение.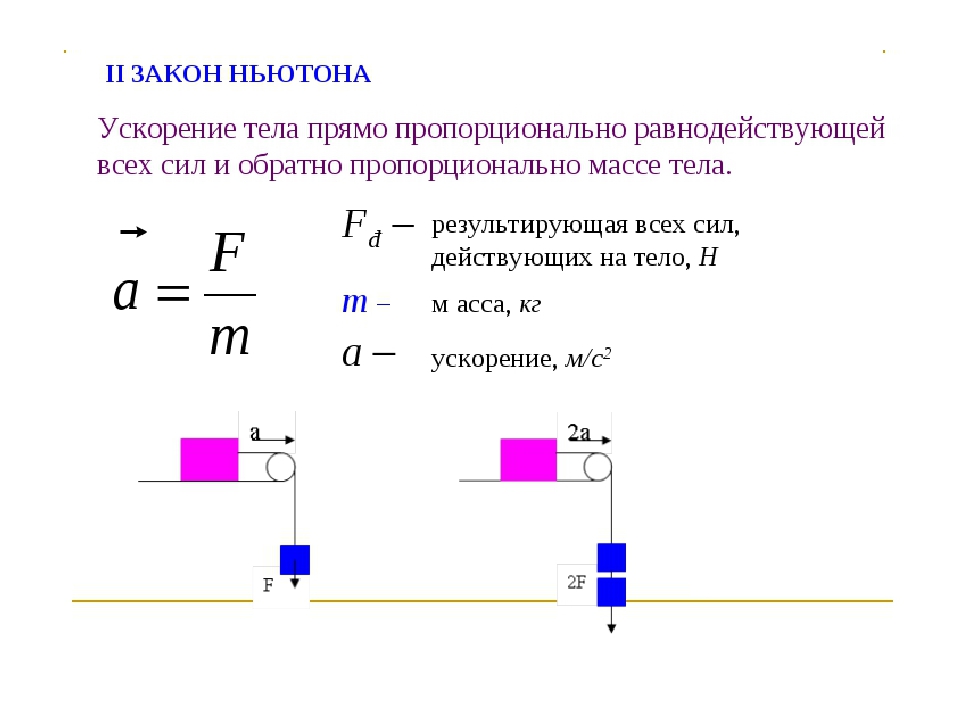
Итак, можно сделать вывод, что сила придает телу ускорение, она “создает” ускорение тела. Логично будет предположить, что бОльшая сила даст мячику бОльшее ускорение: ускорение тела тем больше, чем больше сила. Но это еще не все.
Возьмем два мячика: легкий шарик для пинг-понга и тяжелый железный шарик из подшипника. Подействуем на них одинаковой силой. Оба они получат ускорение. Но ускорение будет разное. Это подсказывает нам жизненный опыт.
Более тяжелый (массивный, с большей массой) стальной шарик получит небольшую скорость; его ускорение будет небольшим.
Легкий (с меньшей массой) шарик для пинг-понга получит большую скорость; ускорение у него будет большим.
Само собой у нас получилось ввести некоторую величину — массу mmm. Получается, что масса показывает, насколько неохотно тело изменяет свою скорость. Если масса тела велика, то ускорение тела — мало. То есть, если величина силы неизменна (сила зафиксирована по величине), то чем больше масса — тем меньше ускорение, которое получает тело.
То есть, если величина силы неизменна (сила зафиксирована по величине), то чем больше масса — тем меньше ускорение, которое получает тело.
Взаимодействие тел, третий закон Ньютона — ЗФТШ, МФТИ
Из анализов многочисленных опытов, как уже отмечалось, было получено соотношение масс взаимодействующих тел и их ускорений:
\[\frac{m_2}{m_1} = \frac{a_1}{a_2},\quad или \quad m_1a_1 = m_2a_2.\]
Но мы знаем из опытов, что при взаимодействии всегда ускорения тел противоположны друг другу: a→1↑↓a→2\vec a_1 \uparrow \downarrow \vec a_2, следовательно, m1a→1=-m2a→2m_1\vec a_1 = – m_2 \vec a_2.
Но произведение массы тела на ускорение этого тела равна действующей на это тело силе. Тогда
F→1=-F→2\boxed{\vec F_1 = -\vec F_2}.
Данное утверждение и представляет собой третий закон Ньютона.
Третий закон Ньютона: При взаимодействии тела действуют друг на друга с силами, равными по величине, противоположными по направлению, одинаковыми по природе и лежащими на прямой, проходящей через центры тел.
Данные проявления встречаются всюду:
1) при столкновении (упругом или неупругом) тела деформируются, при этом появляются силы упругости. Первое тело действует на второе с силой F21F_{21}, а второе на первое с силой F12F_{12}. Причём обе силы по природе своей являются силами упругости – силами взаимодействия между молекулами (электромагнитными). Силы лежат на одной прямой, лежащей на линии точек приложения сил. Силы противоположны.
2) при гравитационном взаимодействии двух тел (Земля и Луна, или Солнце и Юпитер и т. д.) возникают две гравитационные силы, которые тоже противоположны и равны друг другу.
3) при взаимодействии прямоугольного тела, стоящего на поверхности стола, то же возникают две силы упругости: сила возникает потому, что стол деформировался (прогнулся, деформация изгиба см. далее), а сила возникает потому, что прямоугольное тело тоже деформировалось (сжалось под действием силы тяжести, подробнее см. далее). Обе силы равны друг другу и противоположны.
Рассмотрение примеров позволяет сформулировать следующие свойства сил, возникающих при взаимодействии:
силы всегда появляются (или исчезают) парами;
силы не компенсируют друг друга, т. к. приложены к разным телам;
силы одинаковой природы.
Пример 3. Для растяжения пружины жёсткостью 50 Н/м50\ \mathrm{Н}/\mathrm{м}, закреплённой одним концом на стене, на 20 см20\ \mathrm{см} требуется сила 10 Н10\ \mathrm{Н}. Какую силу нужно приложить к этой пружине, чтобы растянуть её на 20 см20\ \mathrm{см}, прикладывая силу с двух сторон и действуя в противоположных направлениях?
Решение. В первом случае в растянутом состоянии пружина находилась в состоянии покоя. Следовательно, по второму закону Ньютона сила, приложенная к пружине со стороны руки, скомпенсирована силой, приложенной к пружине со стороны стены. Значит, стена действует на пружину с силой 10 Н10\ \mathrm{Н}. а) Первая пара сил: точка приложения силы со стороны руки неподвижна и находится в пружине, а сила упругости пружины приложена к точке, находящейся в руке, и тоже неподвижна. Эти две силы равны и противоположны по третьему закону Ньютона. б) Вторая пара сил: во второй паре взаимодействующих тел (стены и пружины) силы тоже равны и противоположны по тому же закону.
Эти две силы равны и противоположны по третьему закону Ньютона. б) Вторая пара сил: во второй паре взаимодействующих тел (стены и пружины) силы тоже равны и противоположны по тому же закону.
Во втором случае пружина тоже находится в покое. Только теперь одна из сил создаётся одной рукой, а вторая сила второй рукой. Сила, создаваемая стеной в первом случае, заменяется силой, создаваемой второй рукой, во втором. Понятно, что неподвижной пружина останется во втором случае только тогда, когда величина силы тоже сохранит первоначальное значение. Следовательно, во втором случае к пружине нужно приложить силу 10 Н10\ \mathrm{Н} с обеих сторон.
Об извращённом толковании Первого закона Ньютона в современной физике / Хабр
В начале ХХ века в физике появились умники-недоучки, не признающие саму методологию научного творчества и объявившие о неких «ограничениях», сужающих область применимости механики Ньютона (I. Newton).Начнём с того, как трактуются законы Ньютона в современных учебниках по физике. Например, в книге А.В. Перышкина и Е.М. Гутника [1] на стр.42 написано следующее:
Например, в книге А.В. Перышкина и Е.М. Гутника [1] на стр.42 написано следующее:
<…> с точки зрения современных представлений первый закон Ньютона формулируется так:Сравним это убожество с формулировкой самого Ньютона [2], кстати, приведённого в той же книжке страницей ранее:существуют такие системы отсчёта, относительно которых тела сохраняют свою скорость неизменной, если на них не действуют другие тела или действия других тел компенсируются.
Всякое тело продолжает удерживаться в состоянии покоя или равномерного прямолинейного движения, пока и поскольку оно не понуждается приложенными силами изменить это состояние.Как видим, ни о какой системе отсчёта нет и речи. И что? Ньютон был «глупее» современных «умников», «улучшающих» его законы? Да нет же! Ньютон подробно рассматривает вопрос о…: «кажущихся» и «истинных» движениях! Вот что он пишет в «Поучении» в разделе «Определения» (см. книгу[2]):
Причины происхождения, которыми различаются истинные и кажущиеся движения, суть те силы, которые надо к телам приложить, чтобы произвести эти движения.Т.е., Ньютон рассматривал вопрос о системах отсчёта очень скрупулёзно и сумел абстрагироваться от кажущихся (относительных) движений, мешающих понять первопричину всех движений и изменения движений – действие силы.Истинное абсолютное движение не может ни произойти, ни измениться иначе, как от действия сил, приложенных непосредственно к самому движущемуся телу, тогда как относительное движение тела может быть и произведено, и изменено без приложения сил к этому телу; достаточно, чтобы силы были приложены к телам, по отношению к которым это движение определяется.
В этом умении абстрагироваться от, искажающих суть, факторов и заключается гениальность Ньютона и его предшественников – коперниканцев, отвергнувших теорию движения планет Птолемея (Πτολεμαΐος), основанную только на описании относительных, кажущихся движений, и, именно поэтому, бессильной в определении причин, приводящих к таким движениям. Получается, что «поправляющие» Ньютона пытаются отбросить нас в эпоху Птолемея и Аристотеля (Αριστοτέλης)…
Кстати, вся теория относительности Эйнштейна рассматривает именно относительные, кажущиеся движения и неудивительно, что следствиями этой теории являются неразрешимые парадоксы.
Также следует отметить, что в теории Эйнштейна абсолютизируется состояние покоя, что, опять же, является возвратом к временам Аристотеля и Птолемея. А Ньютон, своим Первым законом, специально подчёркивает, что v = 0 = const не имеет никаких преимуществ по сравнению с v = const > 0.
Включение в формулировку Первого закона инерциальной системы отсчёта неприемлемо и в том смысле, что физический закон реализуется независимо от того – наблюдаем мы за процессом или нет, измеряем что-либо или нет… Тем более, что определение инерциальной системы отсчёта дают через Первый закон Ньютона (см., например, на стр.13 в [3]), а потом переформулируют этот же закон, используя понятие «инерциальной системы отсчёта»… Очень «научный» подход…
Итак, одна из главных идей Первого закона Ньютона заключается в том, что «состояние покоя» не является особым случаем, а как раз наоборот, это – частный случай «состояния прямолинейного равномерного движения», когда скорость равна нулю, т. е. любое другое число, равноправно во всех отношениях с нулём!
е. любое другое число, равноправно во всех отношениях с нулём!
Именно эта мысль – главный удар по теории Аристотеля, которая недалеко ушла (точнее: никуда не ушла) от обыденного представления о движении, когда считается, что для того, чтобы привести в движение физическое тело и поддерживать это движение в дальнейшем, требуется всё время прикладывать усилие (силу). Разумеется, те примеры движения, такие как «полёт брошенного камня», «полёт стрелы после прекращения действия тетивы», где не видно, «поддерживающей движение», силы, ставят в тупик эти представления о движении.
Второй важный момент. Утверждают, что Ньютон «искал» какую-то абсолютную точку отсчёта и, в конце концов, «закончил» эти поиски в центре Солнца. Как бы то ни было, но Первый закон, как раз, отрицает абсолютность нулевой скорости, а, следовательно, и абсолютность какой-либо точки отсчёта… Вполне возможно, что эти «поиски» (если они, на самом деле, были…) – другое проявление самого Ньютона, не как физика, а как теолога. Ведь, само утверждение «существуют такие системы отсчёта» в корне неверно! При точных измерениях мы всегда обнаружим ускорения. Даже корабль, двигающийся с постоянной скоростью при полном штиле не является инерциальной системой отсчёта, потому что Земля шарообразная и корабль движется по кривой поверхности моря, не говоря уже о том, что сама Земля вращается…
Ведь, само утверждение «существуют такие системы отсчёта» в корне неверно! При точных измерениях мы всегда обнаружим ускорения. Даже корабль, двигающийся с постоянной скоростью при полном штиле не является инерциальной системой отсчёта, потому что Земля шарообразная и корабль движется по кривой поверхности моря, не говоря уже о том, что сама Земля вращается…
И ещё. Что бы ни говорили «квантомеханики»: нет ни одного эксперимента, показывающего, что в микромире этот закон не выполняется!.. Наоборот, то же Броуновское движение доказывает «дословное» (т.е. без дополнительных пояснений) выполнение закона: микрочастица движется от одного столкновения до другого по прямой и с постоянной скоростью.
Т.е., утверждая выше об отсутствии инерциальных систем отсчёта я немного погорячился? В микромире они существуют? Похоже на то!
Но, в то же время в микромире отсутствуют… ускорения (!), потому что там нет «полей» как в макромире и все взаимодействия происходят только посредством «столкновений» в очень малой области пространства за очень короткое время… Для подтверждения этого тезиса сошлюсь на авторитет Ричарда Фейнмана (Richard Feynman), утверждавшего в [4]:
Хочу особенно подчеркнуть, что свет существует именно в виде частиц – это очень важно знать.Кстати, сами фейнмановские диаграммы изначально строились как «траектории» частиц до и после взаимодействия в одной пространственной и одной временной осях координат, но потом «увлеклись» математикой и об этом «забыли», опять же, потому что решили «ограничить» применимость Законов Ньютона…Это особенно важно знать тем из вас, кто ходил в школу, где, возможно, что-то говорили о волновой природе света. Я говорю вам, как он на самом деле ведёт себя – как частицы
Литература
- Перышкин А.В. Физика. 9 кл.: учебник / А.В. Перышкин, Е.М. Гутник. – М.: Дрофа, 2014. – 319,[1] с.: ил.
- Ньютон Исаак. Математические начала натуральной философии. – М.: Наука, 1989. (перевод с латинского и комментарии А.Н. Крылова).
- Ландау Л.Д., Лифшиц Е.М. Теоретическая физика: Учеб.пособ.: Для вузов. В 10т. Т. II. Теория поля.— 8-е изд., стереот.-М.: ФИЗМАТЛИТ, 2003.-536 с
- Фейнман Ричард. КЭД – странная теория света и вещества: Пер. с англ.—М.: Наука.
 Гл. ред. физ.-мат. лит., 1988.—144с.—(Б-чка «Квант». Вып.66.)
Гл. ред. физ.-мат. лит., 1988.—144с.—(Б-чка «Квант». Вып.66.)
Третий закон Ньютона — урок. Физика, 9 класс.
Взаимодействие двух тел — это всегда двусторонний процесс.
Пример:
Рассмотрим процесс вбивания гвоздя молотком (рис. \(1\)). Изменение энергии молотка, позволяет совершать работу по забиванию гвоздя. Металлическая часть молотка воздействует на шляпку гвоздя, что вызывает сопротивление бруска при забивании гвоздя. Эта сила противодействует силе молотка. Поэтому молоток останавливается.
Рис. 1. Изображение гвоздя и молотка
Проведём опыт.
Сцепим два динамометра вместе. Показания динамометров будут одинаковы (рис. \(2\)). Следовательно, динамометры взаимодействуют равными по модулю и противоположно направленными силами.
Рис. 2. Изображения динамометров
Обрати внимание!
Тела действуют друг на друга с равными по модулю силами и в том случае, если взаимодействие происходит на расстоянии.
К одному из динамометров прикрепим металлический брусок, а к другому — магнит (рис. \(3\)).
Рис. 3. Изображение взаимодействия
Сначала динамометры разведём на такое расстояние, при котором силы взаимодействия магнита и металлического бруска практически равны нулю. В данный момент оба динамометра будут показывать «0».
Если начинать сближать динамометры (перемещать один из них или оба сразу), то стрелки динамометров начнут отклоняться. Интересен тот факт, что отклонение от нуля происходит в разные стороны. Это означает, что силы взаимодействия магнита и металлического бруска противоположны по направлению. Показания динамометров в данном случае будут одинаковы.
Третий закон Ньютона
Силы взаимодействия двух тел равны по величине, противоположно направлены, и действуют вдоль прямой, соединяющей эти тела:
F→1=−F→2.
Знак равенства обозначает, что действие равно противодействию, силы возникают попарно. Знак минуса означает, что силы действуют противонаправленно, их векторная сумма равна нулю.
Как этот закон применяется для объяснения явлений?
Например, метеорит падает на землю, поскольку Земля притягивает его с силой тяжести F=mg. Однако, метеорит притягивает Землю с точно такой же по величине силой. Поскольку масса Земли чрезвычайно велика, её перемещение под действием этой силы пренебрежимо мало.
Обрати внимание!
Силы, возникающие в результате взаимодействия тел, являются силами одной природы.
Пример:
Все тела действуют на опору или подвес благодаря гравитации — силе притяжения между телом и Землёй. Под действием силы тяжести опора деформируется: скамейка изгибается, полка под весом книг провисает. Опора стремится вернуть исходное положение, что вызывает силы упругости, с которыми опора воздействует на тело (рис. \(4\)).
Рис. 4. Изображение сил
Вес тела P→ приложен к опоре и направлен вертикально вниз к центру Земли.
Противодействует весу сила реакции опоры N→, поэтому она направлена перпендикулярно поверхности опоры.
Источники:
Рис. 1: Указание авторства не требуется: промышленность/ремесла, 2020-06-19, бесплатно для коммерческого использования, https://clck.ru/UuTPu.
1 2 и 3 закон ньютона – Третий закон Ньютона определение. Формула третьего закона Ньютона. Третий закон Ньютона, сила
Кратко и понятно о первом, втором и третьем законах Ньютона: формулировки, примеры и формулы
Три закона Ньютона — это основа классической механики. В 1867 году Ньютон опубликовал работу под названием «Математические начала натуральной философии». Там были все знания, накопленные до него другими учёными, а также новые, открытые самим Ньютоном. Его считают одним из самых первых основоположником современной физики. Благодаря систематизированным знаниям, которые были описаны в вышеуказанном труде, он открыл множество законов механики, Закон всемирного тяготения и многое другое.
Кратко о законах Ньютона
Первый закон Ньютона
- Формулировка. В наше время встречаются несколько формулировок, вот одна из самых современных: «Существуют такие инерциальные системы отсчёта, относительно которых тело, если на него не действуют другие силы (либо действие других сил компенсируется), находится в покое либо движется равномерно и прямолинейно».
 Этот закон иногда называют Законом инерции.
Этот закон иногда называют Законом инерции. - Трактовка. Если описать это утверждение простыми словами, то можно увидеть, что всё достаточно просто: если какое-то тело находится в покое относительно чего-либо, то оно и будет оставаться в покое до тех пор, пока на него не подействует какой-либо предмет. То же самое, если тело движется равномерно прямолинейно, то оно будет продолжать так двигаться, пока на него не подействует какая-либо сила. До Ньютона его открыл Галилео Галилей, но он не совсем точно его описал. Теперь осталось только разобраться, что такое инерциальные системы отсчёта. Проще говоря, это такая система, для которой выполняется Первый закон Ньютона.
- Пример действия. Представьте себе парашютиста, который движется прямолинейно равномерно к Земле. Это будет продолжаться до тех пор, пока притяжение к поверхности Земли будет компенсироваться сопротивлением воздуха. Если же сопротивление станет меньше либо больше, то тогда на тело начнёт действовать сила притяжения, и оно станет двигаться прямолинейно равноускоренно.

- История открытия. Существует легенда об открытии этого утверждения. Когда-то Ньютон сидел под деревом, и рядом с ним упало яблоко. Это подтолкнуло его на размышления о том, почему яблоко упало перпендикулярно земле, каковы были причины данного явления. По крайней мере, так описывал этот эпизод знаменитый биограф Уильям Стьюкли.
- Формулы у него нет.
Это интересно: система отсчета в физике – определение и ее виды.
Второй закон Ньютона
Он описывает поведение тела при действии на него других объектов. Что с ним происходит, как он начинает двигаться и прочее.
- Формулировка. «В инерциальных системах отсчёта ускорение тела с постоянной массой прямо пропорционально равнодействующей всех сил и обратно пропорционально его массе».
- Формула. Математическое описание этого утверждения такое: а = F/m, где a — это ускорение, F — равнодействующая всех сил, приложенных к телу, m — масса тела.

- Трактовка. Из формулы мы видим, что ускорение тела зависит от силы, приложенной к этому телу, и массы. А также можно увидеть, что чем больше равнодействующая всех сил, то тем больше ускорение, и чем больше масса тела, тем ускорение меньше. Говоря простым языком, если равнодействующая всех сил не равна нулю и не меньше нуля, то выполняется данное утверждение. Можно сказать ещё проще, если на тело действует сила, то оно приобретает ускорение.
- Пример действия. Возьмём бейсбольную биту и мяч. Если ударить битой по мячу, и удар будет сильнее действия всех других сил, то мяч приобретёт ускорение равное отношению равнодействующей всех сил к массе.
Это интересно: формула всемирного тяготения – определение закона.
Третий закон Ньютона
- Формулировка. «Тела взаимодействуют друг на друга с силами одинаковой природы, направленными вдоль прямой, которая соединяет центры масс этих тел, а силы равны по модулю и разнонаправленны».

- Трактовка. Это значит, что на каждое действие есть своё противодействие.
- Пример действия. Более понятно это можно рассмотреть на таком примере: представьте пушку, из которой стреляют ядром. Ядро будет действовать на пушку с той же силой, с какой пушка вытолкала ядро. Поэтому при выстреле пушка откатится чуть-чуть назад, это происходит из-за того, что размеры пушки и ядра разные. Примерно то же самое происходит и при падении яблока на землю. Земля действует на яблоко с некой силой и яблоко тоже действует на Землю. Только из-за того, что масса Земли в миллионы раз больше яблока этого действия не видно. Еще один пример действия Третьего закона для закрепления усвоенного. Возьмём довольно сложный пример: притяжение планет. Луна вертится вокруг Земли благодаря тому, что она притягивается к Земле, но по Третьему закону Ньютона Луна тоже притягивает Землю к себе. Однако, из-за того, что их массы разные, Луна не может притянуть Землю, но у неё получается вызвать отливы и приливы в морях и океанах.

- Формула. Математически это утверждение можно записать так: F1 = -F2, где F1 — это сила, с которой первое тело действует на второе, а F2 — сила, с которой второе тело действует на первое.
obrazovanie.guru
Законы ньютона 1 2 3 кратко определение
Они могут узнать его, пользуясь такой «цепочкой». Им известно начальное положение корабля на стартовой площадке и его начальная скорость. Им известны и силы, которые действуют на корабль в любой точке траектории. Пользуясь этими данными, они и решают задачу механики применительно к космическому полету. Но так как силы, действующие на корабль, все время изменяются, то вычисления настолько сложны, что приходится привлекать на помощь вычислительные машины. Мы все время говорили, что основная задача механики — определение положения движущегося тела в любой момент времени.
Он равномерно приближается к земле, когда действие силы тяжести компенсируется силой натяжения строп парашюта, которая в свою очередь обусловлена сопротивлением воздуха. 1 -ая формулировка — ускорение, приобретаемое телом в инерциальной системе отсчета прямо пропорционально действующей на него силе и обратно пропорциональна его массе a = F
1 -ая формулировка — ускорение, приобретаемое телом в инерциальной системе отсчета прямо пропорционально действующей на него силе и обратно пропорциональна его массе a = F
1.2. Законы ньютона
1.2.1. Формулировка
законов
До сих
пор мы
пользовались статическим определением
силы, полученным на основе уравновешивания
сил, приложенных к телу, с помощью силы,
возникающей от динамометра. Опыт
показывает, что если сумма всех сил,
приложенных к телу, не равна нулю, то
тело придет в движение. Для изучения
динамических
свойств силы
мы должны обратиться к законам Ньютона.
Первый закон.
Всякое тело продолжает удерживаться в
своем состоянии покоя или равномерного
и прямолинейного движения, пока и
поскольку оно не вынуждается приложенными
силами изменить это состояние. Современную
формулировку этого закона следует
повторить
еще раз:
Существуют такие
системы отсчета, называемые инерциальными,
относительно которых свободное
тело находится
в состоянии покоя или равномерного и
прямолинейного движения.
Второй закон.
Изменение
количества движения пропорционально
приложенной движущей силе и происходит
по направлению той прямой, по которой
действует эта сила.
Третий закон.
Действию
всегда есть равное и противоположное
противодействие, иными словами,
взаимодействия двух тел равны между
собой и направлены в противоположные
стороны.
Определение.
Под
количеством
движения
понимается векторная
величина, равная произведению массы
тела на его скорость
(1.2.1)
где
— масса тела. Мы ввели новую физическую
величину – массу, которую пока точно
не определили. Это мы сделаем в следующем
разделе,
а здесь нам достаточно
обыденного понимания этого понятия.
Строгая формулировка второго закона
имеет следующий вид:
(1.2.2)
Из (1. 2.2) видно, что
2.2) видно, что
при равенстве суммы сил нулю скорость
тела будет постоянной, т. е. мы приходим
к математической формулировке первого
закона. Однако ни в коей мере нельзя
полагать, что все физическое содержание
первого закона является тривиальным
следствием второго закона. Мы
воспользовались гелиоцентрической
системой отсчета, в которой всякая сила
— есть результат воздействия на данное
тело какого-то другого тела. Чтобы это
было очевидно, рассмотрим следующий
пример.
Пример.
Представьте
себе, что вы находитесь в закрытом вагоне
поезда, идущего плавно по рельсам. К
потолку вагона прикреплен с помощью
нити шарик (рис. 1.2.1). Другой шарик
находится на идеально гладком полу. Вы
наблюдаете, что нить расположена
вертикально относительно пола, другой
шарик покоится на полу. Сами вы чувствуете
себя спокойно. Вдруг вы замечаете, что
нить отклонилась от вертикали, шарик
на полу пришел в движение. Вы же сами
Вы же сами
стали испытывать некоторые ощущения
и предпринимаете
определенные усилия, чтобы удержаться
в кресле. С вашей точки зрения (в системе
отсчета, связанной с вагоном) шарик на
полу пришел в движение. Задайте себе
вопрос: если сила, действующая на тело,
есть результат воздействия на это тело
какого-то другого тела, то какое тело
внутри вагона
заставляет шарик двигаться? Какое тело
внутри вагона заставляет шарик на нити
отклониться от вертикали? Сколько
бы ни искали, вы таких тел не найдете.
Рис.
1.2.1. Рассматриваемая экспериментальная
ситуация
В то же время с
точки зрения наблюдателя, находящегося
на платформе, все обстоит достаточно
просто. Он видит (измеряет), что вагон
движется с ускорением и, следовательно,
результирующая сила, действующая на
висящий шарик, должна быть направлена
в сторону ускорения вагона. Именно
поэтому нить и отклонится от положения
равновесия,
а шарик на идеально гладком
полу в этой системе остается неподвижным
относительно наблюдателя на платформе.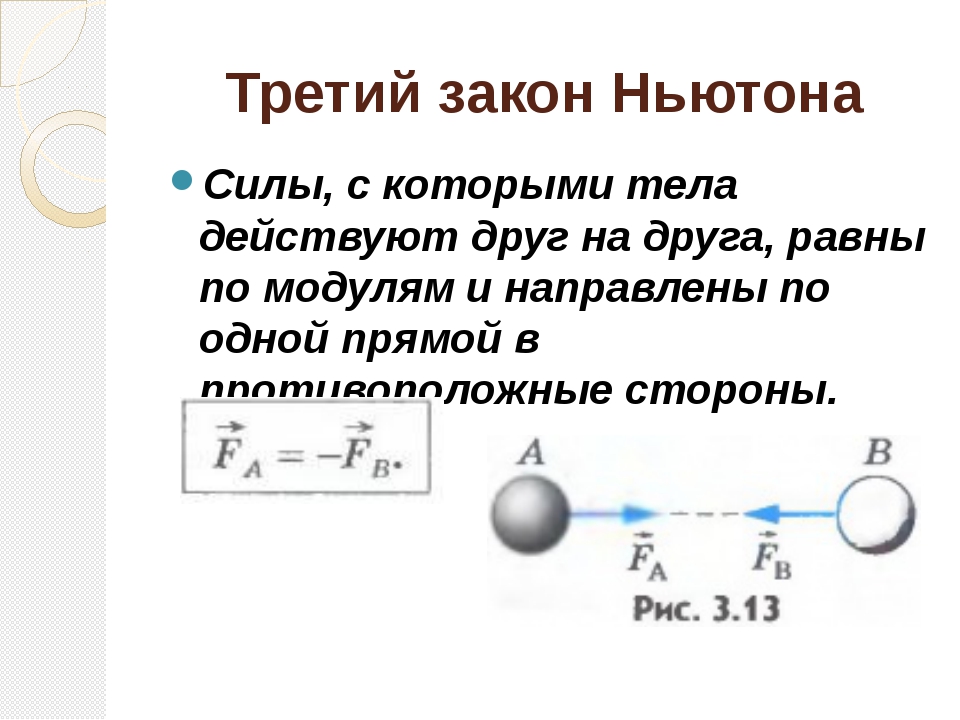
Вернемся ко второму
закону Ньютона. В школьном курсе физики
этот закон обычно дается в виде:
studfiles.net
Математические начала натуральной философии»
Ньютон был современником Петра 1 и Людовика XIV. Окончив университет, Ньютон получил ученое звание бакалавра, затем магистра. С 1669 года стал во главе кафедры физики и математики в Кембриджском университете. Внешне жизнь Ньютона протекала спокойно, мирно и однообразно.
Но ее заполняли непрестанный труд, математические изыскания, физические и химические опыты, вызывавшие восхищение его современников.
С высокой степенью точности инерциальной системой считается система отсчета, связанная с Солнцем (гелиоцентрическая). Если рассматриваемое время движения невелико, то инерциальной можно считать систему отсчета, связанную с Землей (геоцентрическая).
Пример. В качестве примера выполнения 1 закона Ньютона можно рассмотреть движение парашютиста (см. рис. 2). Он равномерно приближается
Он утверждает, что существуют такие системы отсчета, в которых любое тело, что не подверглось воздействию внешних сил, сохраняет состояние покоя или прямолинейного равномерного движения.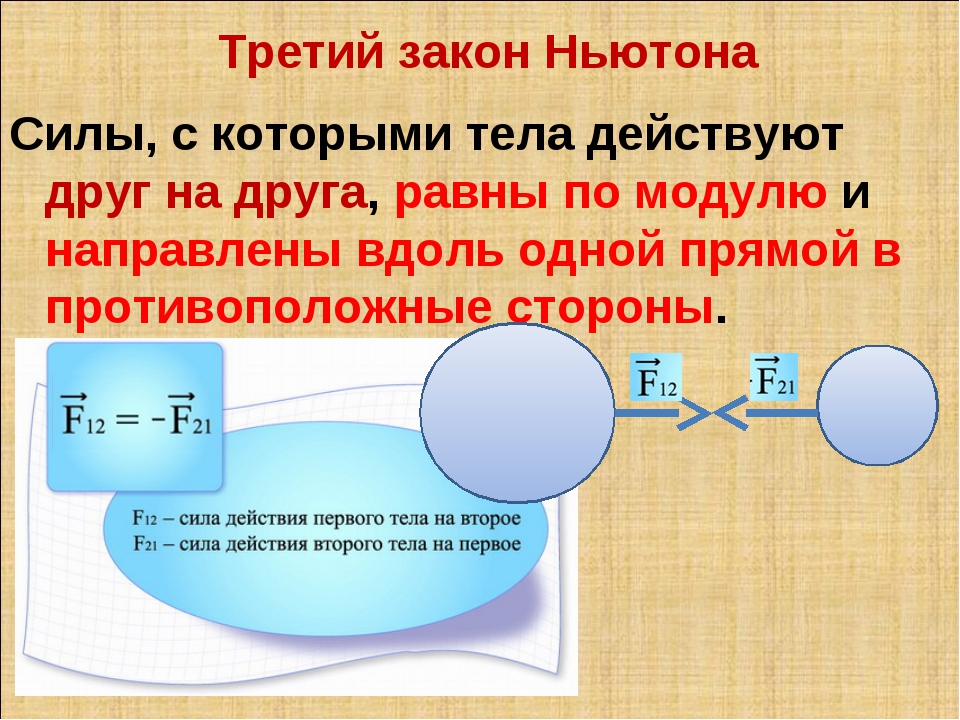 Закон говорит, что в этой же системе любые другие свободные тела должны вести себя абсолютно одинаково.
Закон говорит, что в этой же системе любые другие свободные тела должны вести себя абсолютно одинаково.
Состояние покоя или равномерного движения являются вполне равноправными и не требуют объяснения. Любая система, которая находится в поступательном движении, прямолинейно и равномерно по отношению к инерциальной также является инерциальной. Второй закон Ньютона говорит, что причиной изменения скорости тел, которые находятся в состоянии равномерного движения, может изменить свою скорость только при воздействии посторонних тел.
Второй закон Ньютона
Определение 1Второй закон Ньютона представляет собой основной закон динамики. Данный закон может выполняться только в инерциальных системах отсчета.
Формулируя второй закон, стоит обратить внимание на то, что в динамике вводятся масса тела m и сила F→, а также способы их измерения. Масса является количественной характеристикой инертных свойств тела и показывает реакцию тела на внешнее воздействие.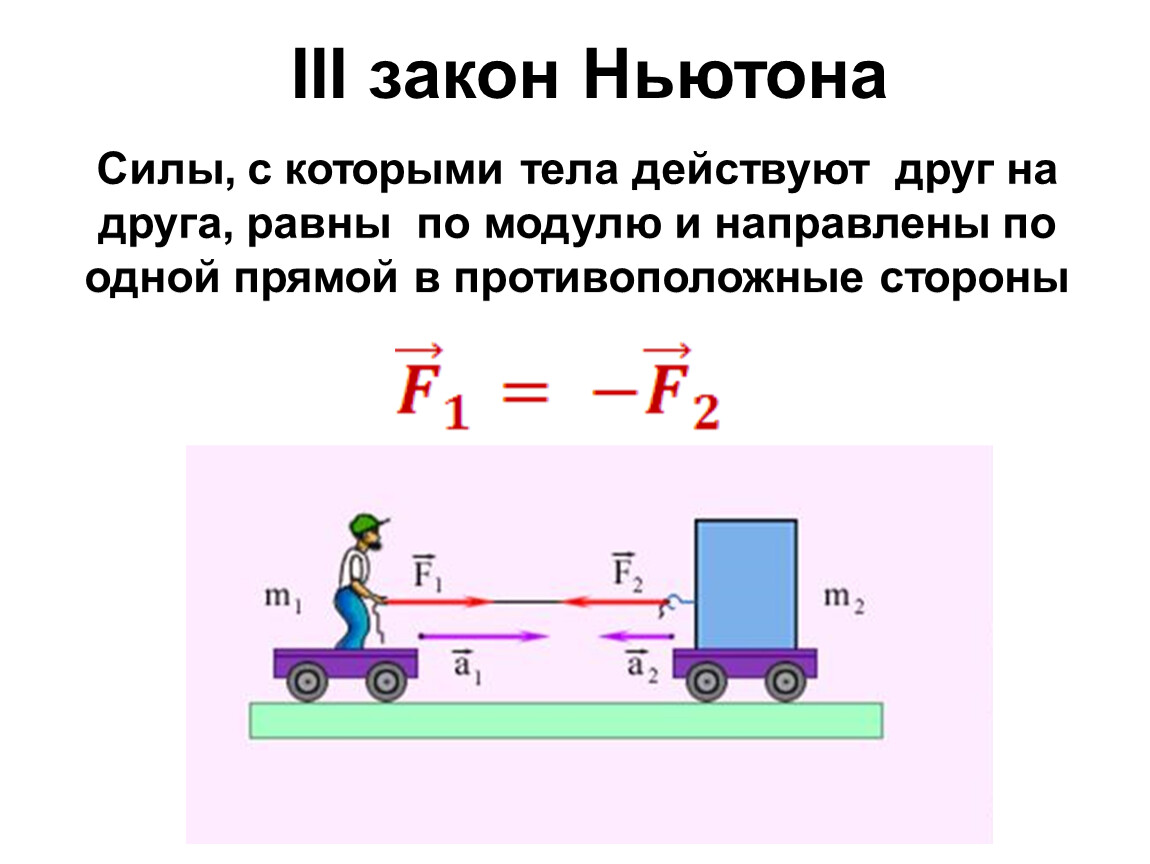 Сила же F→ представляет из себя количественную меру действия одного объекта на другой.
Сила же F→ представляет из себя количественную меру действия одного объекта на другой.
2-ой закон Ньютона, определение и формула
Второй закон Ньютона – фундаментальный закон природы, являющийся обобщением опытных фактов, подразделяющихся на две категории:
- Если на обладающие разной массой тела подействовать одной и той же силой, то приобретаемые телами ускорения окажутся обратно пропорциональны их массам:
a~1m, при F=const.
- Если силами различной величины подействовать на одно тело, то ускорения тела окажутся прямо пропорциональными приложенным силам:
a→~F→, при m=const.
Основной закон динамики был сформулирован Ньютоном путем обобщения данных фактов:
Определение 2Сила, которая оказывает воздействие на тело, эквивалентна произведению массы тела на сообщаемое данной силой ускорение:
F→=ma→.
Приведенное выражение и представляет собой второй закон Ньютона.
С помощью него стало возможным вычисление ускорение тела в случае, если известна его масса m и действующая на него сила F→:
a→=F’m.
В Международной системе единиц (СИ) в качестве единицы силы считают такую силу, которая сообщающая телу массой 1 кг ускорение 1 м/с2. Данная единица называется ньютоном (Н). В (СИ) ее принимают за эталон силы.
1 Н=1кг·мс2.
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать заданиеРавнодействующая сила
В том случае, если на тело одновременно воздействуют несколько сил, как например, F1→, F2→ и F3→, то силой F→ в формуле второго закона Ньютона считается равнодействующая всех сил это величина, выражающаяся в виде формулы:
F→=F1→+F2→+F3→.
Рисунок 1.8.1. Сила F→ – равнодействующая силы тяжести F→Т и силы нормального давления FN→, действующих на лыжницу на гладкой горе. Сила F→ вызывает ускорение лыжника.
В случае же, когда равнодействующая сила F→=0, тело будет пребывать в состоянии покоя или равномерного прямолинейного движения. Выходит, что формально второй закон Ньютона включает в себя в качестве частного случая первый закон Ньютона. Но первый закон Ньютона обладает более глубоким физическим значением. Он обуславливает существование инерциальных систем отсчета.
Но первый закон Ньютона обладает более глубоким физическим значением. Он обуславливает существование инерциальных систем отсчета.
Рисунок 1.8.1. Модель движения тел на легком блоке.
Второй закон движения Ньютона
Первый закон движения Ньютона предсказывает поведение объектов, для которых все существующие силы уравновешены. Первый закон – иногда называемый законом инерции – гласит, что если силы, действующие на объект, уравновешены, то ускорение этого объекта будет 0 м / с / с. Объекты в равновесии (состояние, при котором все силы уравновешены) не будут ускоряться. Согласно Ньютону, объект будет ускоряться только в том случае, если на него действует чистая или неуравновешенная сила.Присутствие неуравновешенной силы ускоряет объект, изменяя его скорость, направление или одновременно скорость и направление.
Второй закон движения Ньютона относится к поведению объектов, для которых все существующие силы не уравновешены. Второй закон гласит, что ускорение объекта зависит от двух переменных – чистой силы, действующей на объект, и массы объекта. Ускорение объекта напрямую зависит от чистой силы, действующей на объект, и обратно – от массы объекта.По мере увеличения силы, действующей на объект, ускорение объекта увеличивается. По мере увеличения массы объекта ускорение объекта уменьшается.
Второй закон гласит, что ускорение объекта зависит от двух переменных – чистой силы, действующей на объект, и массы объекта. Ускорение объекта напрямую зависит от чистой силы, действующей на объект, и обратно – от массы объекта.По мере увеличения силы, действующей на объект, ускорение объекта увеличивается. По мере увеличения массы объекта ускорение объекта уменьшается.
Второй закон движения Ньютона можно формально сформулировать следующим образом:
Ускорение объекта, создаваемое чистой силой, прямо пропорционально величине чистой силы в том же направлении, что и результирующая сила, и обратно пропорционально массе объекта.
Это словесное утверждение можно выразить в виде уравнения следующим образом:
a = F нетто / м Приведенное выше уравнение часто преобразовывается в более знакомую форму, как показано ниже.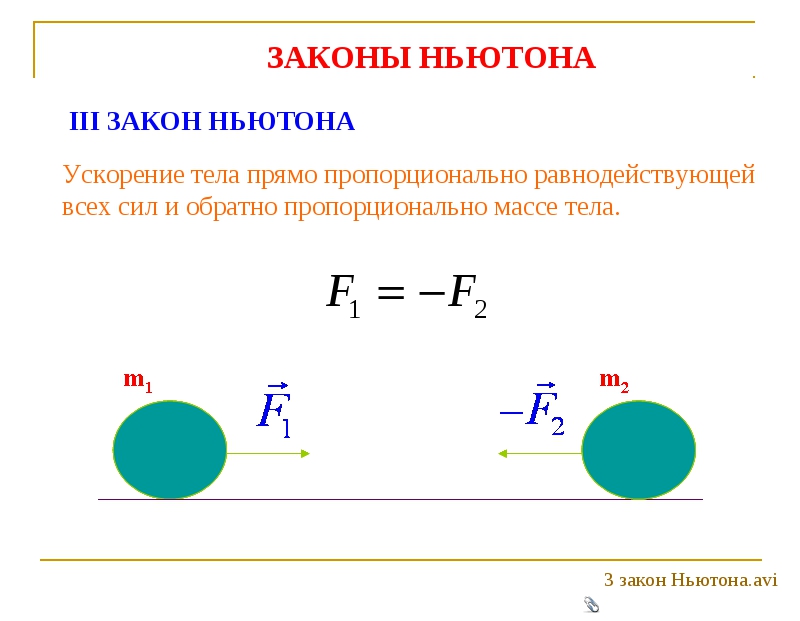 Чистая сила равна произведению массы на ускорение.
Чистая сила равна произведению массы на ускорение.
Во всем этом обсуждении упор был сделан на чистую силу .Ускорение прямо пропорционально чистой силе ; чистая сила равна массе, умноженной на ускорение; ускорение в том же направлении, что и чистая сила ; ускорение создается чистой силой . СЕТЕВАЯ СИЛА. Важно помнить об этом различии. Не используйте в приведенном выше уравнении значение просто «какой-либо старой силы». Это чистая сила, связанная с ускорением. Как обсуждалось в предыдущем уроке, результирующая сила – это векторная сумма всех сил.Если известны все индивидуальные силы, действующие на объект, то можно определить результирующую силу. При необходимости просмотрите этот принцип, вернувшись к практическим вопросам в Уроке 2.
В соответствии с приведенным выше уравнением единица силы равна единице массы, умноженной на единицу ускорения. Подставив стандартные метрические единицы для силы, массы и ускорения в приведенное выше уравнение, можно записать следующую эквивалентность единиц.
Подставив стандартные метрические единицы для силы, массы и ускорения в приведенное выше уравнение, можно записать следующую эквивалентность единиц.
Определение стандартной метрической единицы силы определяется приведенным выше уравнением.Один ньютон определяется как количество силы, необходимое для придания 1 кг массы ускорения в 1 м / с / с.
Ваша очередь практиковаться Сеть F = m • уравнение часто используется при решении алгебраических задач. Приведенную ниже таблицу можно заполнить, подставив в уравнение и решив неизвестную величину. Попробуйте сами, а затем используйте кнопки, чтобы просмотреть ответы.
| Чистая сила (н.) | Масса (кг) | Разгон (м / с / с) | |
1. | 10 | 2 | |
| 2. | 20 | 2 | |
| 3. | 20 | 4 | |
| 4. | 2 | 5 | |
| 5. | 10 | 10 |
Числовая информация в таблице выше демонстрирует некоторые важные качественные отношения между силой, массой и ускорением.Сравнивая значения в строках 1 и 2, можно увидеть, что удвоение чистой силы приводит к удвоению ускорения (если масса остается постоянной). Точно так же сравнение значений в строках 2 и 4 демонстрирует, что уменьшение вдвое чистой силы приводит к уменьшению вдвое ускорения (если масса остается постоянной). Ускорение прямо пропорционально чистой силе.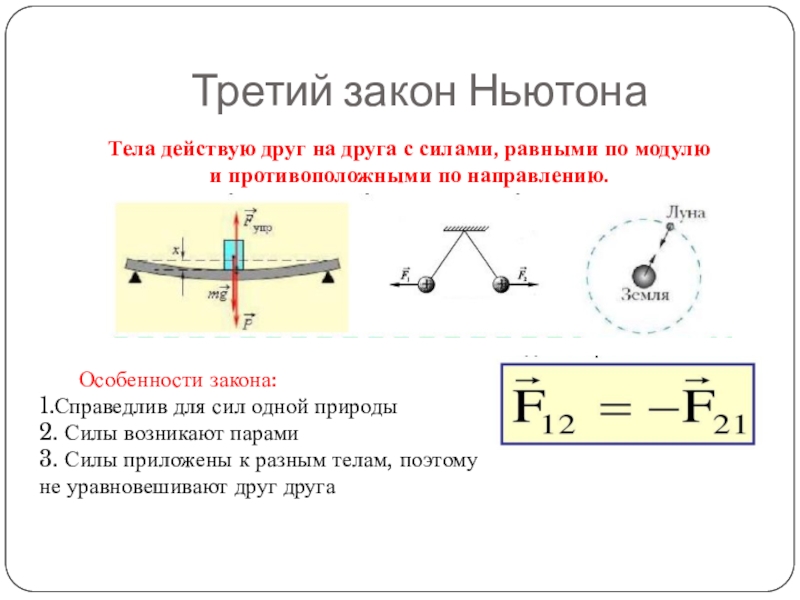
Кроме того, качественную взаимосвязь между массой и ускорением можно увидеть, сравнив числовые значения в приведенной выше таблице.Обратите внимание на строки 2 и 3, что удвоение массы приводит к уменьшению вдвое ускорения (если сила остается постоянной). Точно так же строки 4 и 5 показывают, что уменьшение массы на вдвое приводит к удвоению ускорения (если сила остается постоянной). Ускорение обратно пропорционально массе.
Анализ табличных данных показывает, что такое уравнение, как F net = m * a, может быть руководством к размышлениям о том, как изменение одной величины может повлиять на другую величину.Какое бы изменение ни производилось в чистой силе, такое же изменение произойдет и с ускорением. Удвойте, утроите или учетверите чистую силу, и ускорение будет делать то же самое. С другой стороны, какое бы изменение массы ни произошло, с ускорением произойдет противоположное или обратное изменение. Удвойте, утроите или учетверите массу, и ускорение составит половину, одну треть или одну четвертую от первоначального значения.
Направление чистой силы и ускорения
Как указано выше, направление результирующей силы совпадает с направлением ускорения.Таким образом, если известно направление ускорения, то известно и направление результирующей силы. Рассмотрим две диаграммы падения масла ниже для ускорения автомобиля. По диаграмме определите направление чистой силы, действующей на автомобиль. Затем нажмите кнопки, чтобы просмотреть ответы. (При необходимости проверьте ускорение по сравнению с предыдущим блоком.)
В заключение, второй закон Ньютона дает объяснение поведения объектов, на которых силы не уравновешиваются.Закон гласит, что неуравновешенные силы заставляют объекты ускоряться с ускорением, которое прямо пропорционально чистой силе и обратно пропорционально массе.
 Вы должны взаимодействовать с ним! И это именно то, что вы делаете, когда используете один из интерактивных материалов The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего Force Interactive.Вы можете найти его в разделе Physics Interactives на нашем сайте. Force Interactive позволяет учащемуся исследовать влияние изменений приложенной силы, чистой силы, массы и трения на ускорение объекта.
Вы должны взаимодействовать с ним! И это именно то, что вы делаете, когда используете один из интерактивных материалов The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего Force Interactive.Вы можете найти его в разделе Physics Interactives на нашем сайте. Force Interactive позволяет учащемуся исследовать влияние изменений приложенной силы, чистой силы, массы и трения на ускорение объекта.
1. Определите ускорения, возникающие при приложении чистой силы 12 Н к объекту массой 3 кг, а затем к объекту массой 6 кг.
2. К энциклопедии прилагается чистая сила 15 Н, которая заставляет ее ускоряться со скоростью 5 м / с 2 .Определите массу энциклопедии.
3. Предположим, что салазки ускоряются со скоростью 2 м / с 2 . Если чистая сила утроится, а масса – вдвое, то каково новое ускорение салазок?
4. Предположим, что салазки ускоряются со скоростью 2 м / с 2 . Если чистая сила утроится, а масса уменьшится вдвое, то каково новое ускорение салазок?
Второй закон движения Ньютона: концепция системы
Цели обучения
К концу этого раздела вы сможете:
- Определите чистую силу, внешнюю силу и систему.
- Поймите второй закон движения Ньютона.
- Примените второй закон Ньютона для определения веса объекта.
Второй закон движения Ньютона тесно связан с первым законом движения Ньютона. Он математически устанавливает причинно-следственную связь между силой и изменениями в движении. Второй закон движения Ньютона является более количественным и широко используется для расчета того, что происходит в ситуациях, связанных с действием силы. Прежде чем мы сможем записать второй закон Ньютона в виде простого уравнения, дающего точное соотношение силы, массы и ускорения, нам необходимо отточить некоторые идеи, которые уже упоминались.
Он математически устанавливает причинно-следственную связь между силой и изменениями в движении. Второй закон движения Ньютона является более количественным и широко используется для расчета того, что происходит в ситуациях, связанных с действием силы. Прежде чем мы сможем записать второй закон Ньютона в виде простого уравнения, дающего точное соотношение силы, массы и ускорения, нам необходимо отточить некоторые идеи, которые уже упоминались.
Во-первых, что мы подразумеваем под изменением движения? Ответ заключается в том, что изменение движения эквивалентно изменению скорости. Изменение скорости по определению означает наличие ускорения . Первый закон Ньютона гласит, что чистая внешняя сила вызывает изменение движения; таким образом, мы видим, что чистая внешняя сила вызывает ускорение .
Сразу возникает еще один вопрос. Что мы подразумеваем под внешней силой? Интуитивное представление о внешнем является правильным – внешняя сила действует извне из интересующей системы . Например, на рис. 1 (а) интересующая система – это вагон плюс ребенок в нем. Две силы, действующие со стороны других детей, – это внешние силы. Между элементами системы действует внутренняя сила. Снова посмотрев на рисунок 1 (а), сила, которую ребенок в повозке прикладывает, чтобы повиснуть на повозке, является внутренней силой между элементами интересующей системы. Согласно первому закону Ньютона, только внешние силы влияют на движение системы. (Внутренние силы фактически отменяются, как мы увидим в следующем разделе.) Необходимо определить границы системы, прежде чем вы сможете определить, какие силы являются внешними . Иногда система очевидна, тогда как в других случаях определение границ системы более тонкое. Концепция системы является фундаментальной для многих областей физики, как и правильное применение законов Ньютона. Эта концепция будет неоднократно пересматриваться в нашем путешествии по физике.
Например, на рис. 1 (а) интересующая система – это вагон плюс ребенок в нем. Две силы, действующие со стороны других детей, – это внешние силы. Между элементами системы действует внутренняя сила. Снова посмотрев на рисунок 1 (а), сила, которую ребенок в повозке прикладывает, чтобы повиснуть на повозке, является внутренней силой между элементами интересующей системы. Согласно первому закону Ньютона, только внешние силы влияют на движение системы. (Внутренние силы фактически отменяются, как мы увидим в следующем разделе.) Необходимо определить границы системы, прежде чем вы сможете определить, какие силы являются внешними . Иногда система очевидна, тогда как в других случаях определение границ системы более тонкое. Концепция системы является фундаментальной для многих областей физики, как и правильное применение законов Ньютона. Эта концепция будет неоднократно пересматриваться в нашем путешествии по физике.
Рис. 1. Различные силы, действующие на одну и ту же массу, вызывают разное ускорение. а) Двое детей толкают тележку с ребенком в ней. Показаны стрелки, представляющие все внешние силы. Интересующая система – это повозка и ее водитель. Вес системы w и опора земли N также показаны для полноты и, как предполагается, отменяют. Вектор f представляет трение, действующее на вагон, и действует влево, противодействуя движению вагона. (b) Все внешние силы, действующие на систему, в сумме образуют чистую силу, F net .На диаграмме свободного тела показаны все силы, действующие на интересующую систему. Точка представляет собой центр масс системы. Каждый вектор силы простирается от этой точки. Поскольку справа действуют две силы, мы рисуем векторы коллинеарно. (c) Большая чистая внешняя сила вызывает большее ускорение ( a ‘> a ), когда взрослый толкает ребенка.
а) Двое детей толкают тележку с ребенком в ней. Показаны стрелки, представляющие все внешние силы. Интересующая система – это повозка и ее водитель. Вес системы w и опора земли N также показаны для полноты и, как предполагается, отменяют. Вектор f представляет трение, действующее на вагон, и действует влево, противодействуя движению вагона. (b) Все внешние силы, действующие на систему, в сумме образуют чистую силу, F net .На диаграмме свободного тела показаны все силы, действующие на интересующую систему. Точка представляет собой центр масс системы. Каждый вектор силы простирается от этой точки. Поскольку справа действуют две силы, мы рисуем векторы коллинеарно. (c) Большая чистая внешняя сила вызывает большее ускорение ( a ‘> a ), когда взрослый толкает ребенка.
Теперь кажется разумным, что ускорение должно быть прямо пропорционально и в том же направлении, что и чистая (полная) внешняя сила, действующая на систему.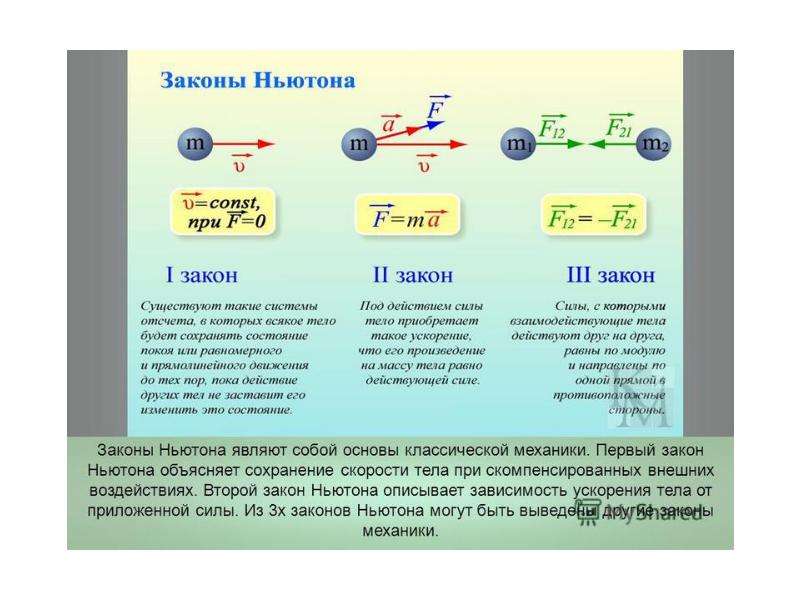 Это предположение было проверено экспериментально и показано на рисунке 1. В части (а) меньшая сила вызывает меньшее ускорение, чем большая сила, показанная в части (с). Для полноты картины также показаны вертикальные силы; предполагается, что они отменяются, поскольку нет ускорения в вертикальном направлении. Вертикальные силы – это вес w и опора на землю N , а горизонтальная сила f представляет собой силу трения. Они будут обсуждаться более подробно в следующих разделах.А пока мы определим трение как силу, которая противодействует движению мимо друг друга соприкасающихся объектов. На рисунке 1 (b) показано, как векторы, представляющие внешние силы, складываются, чтобы получить результирующую силу,
Это предположение было проверено экспериментально и показано на рисунке 1. В части (а) меньшая сила вызывает меньшее ускорение, чем большая сила, показанная в части (с). Для полноты картины также показаны вертикальные силы; предполагается, что они отменяются, поскольку нет ускорения в вертикальном направлении. Вертикальные силы – это вес w и опора на землю N , а горизонтальная сила f представляет собой силу трения. Они будут обсуждаться более подробно в следующих разделах.А пока мы определим трение как силу, которая противодействует движению мимо друг друга соприкасающихся объектов. На рисунке 1 (b) показано, как векторы, представляющие внешние силы, складываются, чтобы получить результирующую силу,
F net .
Чтобы получить уравнение для второго закона Ньютона, сначала запишем соотношение ускорения и чистой внешней силы как пропорциональность
[латекс] \ text {a} \ propto {\ text {F} _ {net}} \\ [/ latex]
, где символ ∝ означает «пропорционально», а F net – это чистая внешняя сила . (Чистая внешняя сила представляет собой векторную сумму всех внешних сил и может быть определена графически, используя метод “голова к хвосту”, или аналитически, используя компоненты. Методы такие же, как и для сложения других векторов, и рассматриваются в двумерной кинематике.) Эта пропорциональность выражает то, что мы сказали словами: ускорение прямо пропорционально чистой внешней силе . После выбора интересующей системы важно определить внешние силы и игнорировать внутренние.Это огромное упрощение – не учитывать многочисленные внутренние силы, действующие между объектами внутри системы, такие как мышечные силы в теле ребенка, не говоря уже о мириадах сил между атомами в объектах, но, делая это, мы можем легко решить некоторые очень сложные проблемы с минимальной ошибкой благодаря нашему упрощению.
(Чистая внешняя сила представляет собой векторную сумму всех внешних сил и может быть определена графически, используя метод “голова к хвосту”, или аналитически, используя компоненты. Методы такие же, как и для сложения других векторов, и рассматриваются в двумерной кинематике.) Эта пропорциональность выражает то, что мы сказали словами: ускорение прямо пропорционально чистой внешней силе . После выбора интересующей системы важно определить внешние силы и игнорировать внутренние.Это огромное упрощение – не учитывать многочисленные внутренние силы, действующие между объектами внутри системы, такие как мышечные силы в теле ребенка, не говоря уже о мириадах сил между атомами в объектах, но, делая это, мы можем легко решить некоторые очень сложные проблемы с минимальной ошибкой благодаря нашему упрощению.
Теперь также кажется разумным, что ускорение должно быть обратно пропорционально массе системы. Другими словами, чем больше масса (инерция), тем меньше ускорение, создаваемое данной силой. И действительно, как показано на рисунке 2, та же самая чистая внешняя сила, приложенная к автомобилю, вызывает гораздо меньшее ускорение, чем при приложении к баскетбольному мячу. Пропорциональность записывается как
И действительно, как показано на рисунке 2, та же самая чистая внешняя сила, приложенная к автомобилю, вызывает гораздо меньшее ускорение, чем при приложении к баскетбольному мячу. Пропорциональность записывается как
[латекс] \ text {a} \ propto {\ frac {1} {m}} \\ [/ latex]
, где м – масса системы. Эксперименты показали, что ускорение прямо обратно пропорционально массе, точно так же, как оно прямо линейно пропорционально чистой внешней силе.
Рис. 2. Одна и та же сила, действующая на системы разной массы, вызывает разное ускорение.(а) Баскетболист толкает баскетбольный мяч, чтобы сделать передачу. (Влияние силы тяжести на мяч игнорируется.) (B) Тот же игрок оказывает идентичную силу на остановившийся внедорожник и производит гораздо меньшее ускорение (даже если трение незначительно). (c) Диаграммы свободного тела идентичны, что позволяет напрямую сравнить две ситуации. По мере того, как вы будете решать больше задач, появится серия паттернов для диаграммы свободного тела.
Было обнаружено, что ускорение объекта только зависит от чистой внешней силы и массы объекта.Объединение двух только что приведенных пропорциональностей дает второй закон движения Ньютона.
Второй закон движения Ньютона
Ускорение системы прямо пропорционально чистой внешней силе, действующей на систему, и в том же направлении, и обратно пропорционально ее массе. В форме уравнения второй закон движения Ньютона равен
.[латекс] {\ text {a}} = \ frac {{{\ text {F}}} _ {\ text {net}}} {m} \\ [/ latex].
Это часто записывается в более знакомой форме
F нетто = м a .
Если рассматривать только величину силы и ускорения, это уравнение просто
F net = ma.
Хотя эти последние два уравнения на самом деле одинаковы, первое дает больше понимания того, что означает второй закон Ньютона. Закон – это причинно-следственная связь между тремя величинами, которая не просто основана на их определениях.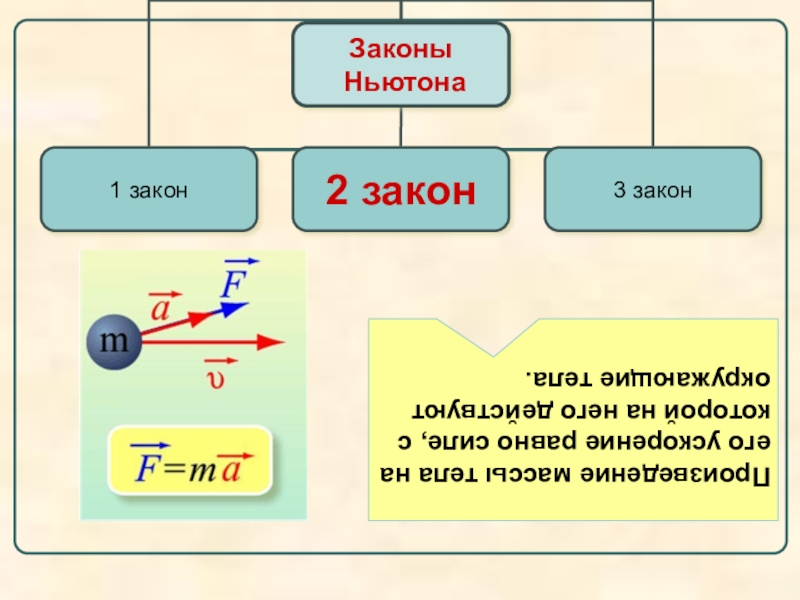 Справедливость второго закона полностью основана на экспериментальной проверке.
Справедливость второго закона полностью основана на экспериментальной проверке.
F net = м используется для определения единиц силы в терминах трех основных единиц массы, длины и времени. Единица силы в системе СИ называется ньютон (сокращенно Н) и представляет собой силу, необходимую для ускорения системы массой 1 кг со скоростью 1 м / с 2 . То есть, поскольку F net = m a ,
1 Н = 1 кг ⋅ м / с 2 .
В то время как почти весь мир использует ньютон в качестве единицы силы, в Соединенных Штатах наиболее известной единицей силы является фунт (фунт), где 1 N = 0.225 фунтов
Вес и гравитационная сила
Когда объект падает, он ускоряется к центру Земли. Второй закон Ньютона гласит, что общая сила, действующая на объект, отвечает за его ускорение. Если сопротивление воздуха незначительно, результирующая сила, действующая на падающий объект, – это сила тяжести, обычно называемая его массой масс Вт. Вес можно обозначить как вектор w, потому что он имеет направление; вниз – это, по определению, направление силы тяжести, и, следовательно, вес – это сила, направленная вниз.Величина веса обозначается как w . Галилей показал, что при отсутствии сопротивления воздуха все объекты падают с одинаковым ускорением g . Используя результат Галилея и второй закон Ньютона, мы можем вывести уравнение для веса.
Вес можно обозначить как вектор w, потому что он имеет направление; вниз – это, по определению, направление силы тяжести, и, следовательно, вес – это сила, направленная вниз.Величина веса обозначается как w . Галилей показал, что при отсутствии сопротивления воздуха все объекты падают с одинаковым ускорением g . Используя результат Галилея и второй закон Ньютона, мы можем вывести уравнение для веса.
Рассмотрим объект массой м , падающий на Землю. Он испытывает только направленную вниз силу тяжести, величина которой составляет w . Второй закон Ньютона гласит, что величина чистой внешней силы, действующей на объект, составляет F net = ма .Поскольку объект испытывает только направленную вниз силу тяжести, F net = w . Мы знаем, что ускорение объекта под действием силы тяжести составляет g , или a = g . Подставляя их во второй закон Ньютона, получаем
МассаЭто уравнение для веса – силы тяжести, действующей на массу m:
w = мг
Так как g = 9,80 м / с 2 на Земле, вес 1. 0 кг объекта на Земле составляет 9,8 Н, как мы видим:
0 кг объекта на Земле составляет 9,8 Н, как мы видим:
w = мг = (1,0 кг) (9,80 м / с 2 ) = 9,8 Н.
Напомним, что g может принимать положительное или отрицательное значение в зависимости от положительного направления в системе координат. Обязательно учтите это при решении задач с весом.
Когда чистая внешняя сила, действующая на объект, равна его весу, мы говорим, что оно находится в состоянии свободного падения . То есть единственная сила, действующая на объект, – это сила тяжести.В реальном мире, когда объекты падают вниз к Земле, они никогда не находятся в состоянии свободного падения, потому что на объект всегда действует некоторая восходящая сила из воздуха.
Ускорение свободного падения g незначительно меняется по поверхности Земли, поэтому вес объекта зависит от местоположения и не является внутренним свойством объекта. Вес резко меняется, если человек покидает поверхность Земли. На Луне, например, ускорение свободного падения всего 1. 67 м / с 2 . Таким образом, масса в 1,0 кг имеет вес 9,8 Н на Земле и всего около 1,7 Н на Луне.
67 м / с 2 . Таким образом, масса в 1,0 кг имеет вес 9,8 Н на Земле и всего около 1,7 Н на Луне.
Самое широкое определение веса в этом смысле состоит в том, что вес объекта – это сила тяжести, действующая на него со стороны ближайшего большого тела , такого как Земля, Луна, Солнце и так далее. Это наиболее распространенное и полезное определение веса в физике. Однако оно кардинально отличается от определения веса, используемого НАСА и популярными СМИ в отношении космических путешествий и исследований.Когда они говорят о «невесомости» и «микрогравитации», они на самом деле имеют в виду явление, которое в физике мы называем «свободным падением». Мы будем использовать приведенное выше определение веса и проведем тщательное различие между свободным падением и фактической невесомостью.
Важно знать, что вес и масса – очень разные физические величины, хотя они тесно связаны. Масса – это количество материи (сколько «вещества») и не изменяется в классической физике, тогда как вес – это сила тяжести, которая зависит от силы тяжести.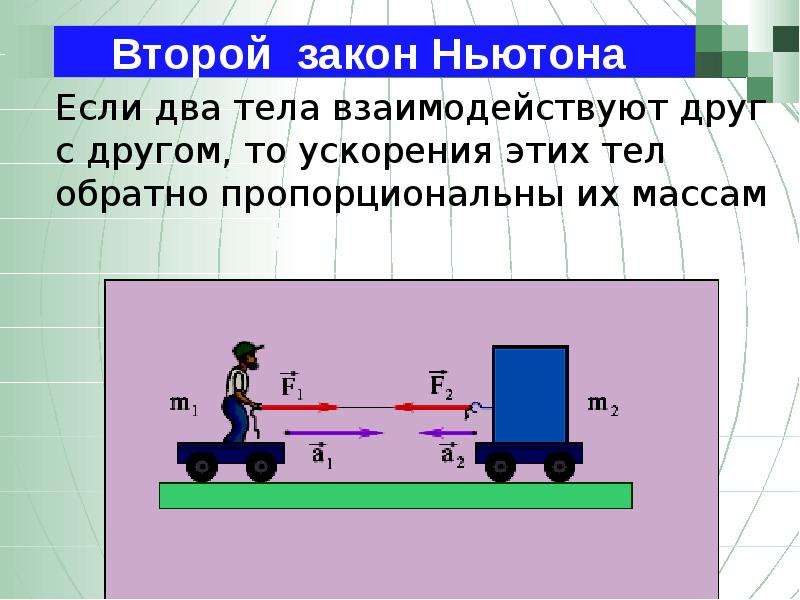 Заманчиво приравнять эти два понятия, поскольку большинство наших примеров имеет место на Земле, где вес объекта лишь немного зависит от его местоположения. Кроме того, в повседневном языке термины масса и масса используются взаимозаменяемо; например, в наших медицинских записях наш «вес» часто указывается в килограммах, но никогда в правильных единицах – ньютонах.
Заманчиво приравнять эти два понятия, поскольку большинство наших примеров имеет место на Земле, где вес объекта лишь немного зависит от его местоположения. Кроме того, в повседневном языке термины масса и масса используются взаимозаменяемо; например, в наших медицинских записях наш «вес» часто указывается в килограммах, но никогда в правильных единицах – ньютонах.
В повседневной речи масса и вес часто используются как синонимы.Однако в науке эти термины существенно отличаются друг от друга. Масса – это мера количества вещества в объекте. Типичной мерой массы является килограмм (или «пуля» в английских единицах измерения). С другой стороны, вес – это мера силы тяжести, действующей на объект. Вес равен массе объекта (м), умноженной на ускорение свободного падения (g). Как и любая другая сила, вес измеряется в ньютонах (или фунтах в английских единицах). Предполагая, что масса объекта остается неизменной, она останется неизменной независимо от его местоположения. Однако, поскольку вес зависит от ускорения свободного падения, вес объекта может измениться на , когда объект входит в область с большей или меньшей силой тяжести. Например, ускорение свободного падения на Луне составляет 1,67 м / с 2 (что намного меньше ускорения свободного падения на Земле, 9,80 м / с 2 ). Если вы измерили свой вес на Земле, а затем измерили свой вес на Луне, вы бы обнаружили, что «весите» гораздо меньше, хотя и не выглядите стройнее.Это потому, что сила тяжести на Луне слабее. Фактически, когда люди говорят, что они «худеют», они на самом деле имеют в виду, что они теряют «массу» (что, в свою очередь, заставляет их весить меньше).
Однако, поскольку вес зависит от ускорения свободного падения, вес объекта может измениться на , когда объект входит в область с большей или меньшей силой тяжести. Например, ускорение свободного падения на Луне составляет 1,67 м / с 2 (что намного меньше ускорения свободного падения на Земле, 9,80 м / с 2 ). Если вы измерили свой вес на Земле, а затем измерили свой вес на Луне, вы бы обнаружили, что «весите» гораздо меньше, хотя и не выглядите стройнее.Это потому, что сила тяжести на Луне слабее. Фактически, когда люди говорят, что они «худеют», они на самом деле имеют в виду, что они теряют «массу» (что, в свою очередь, заставляет их весить меньше).
Эксперимент на вынос: масса и вес
Что измеряют весы для ванной? Когда вы стоите на весах в ванной, что происходит с весами? Слегка угнетает. Весы содержат пружины, которые сжимаются пропорционально вашему весу – подобно резиновым лентам, расширяющимся при натяжении.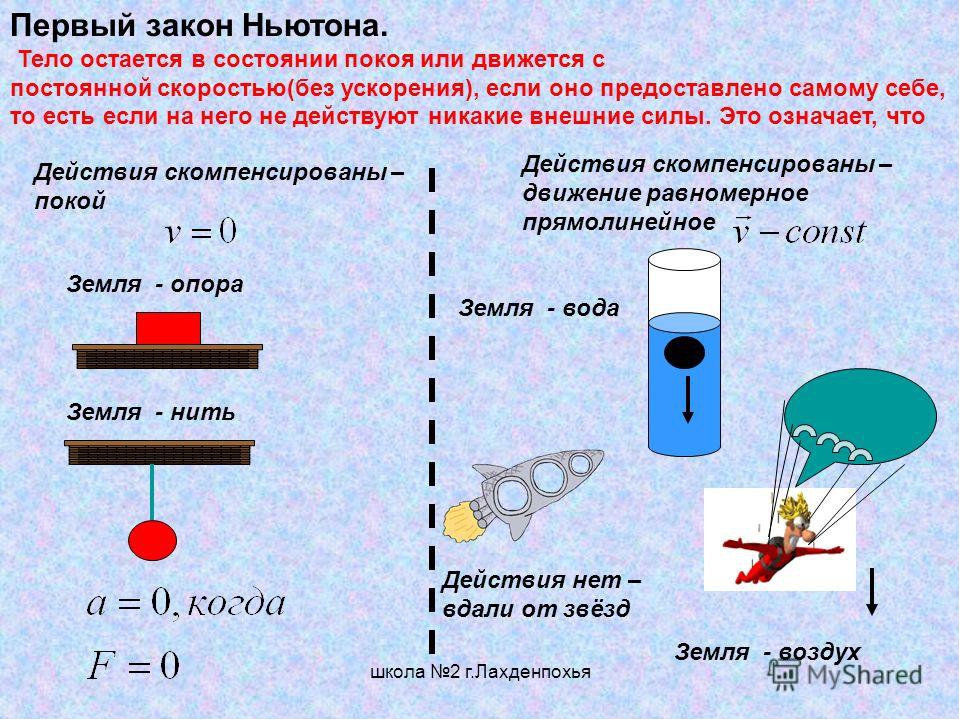 Пружины позволяют измерить ваш вес (для объекта, который не ускоряется). Это сила в ньютонах (или фунтах). В большинстве стран результат делится на 9,80, чтобы получить значение в килограммах. Весы измеряют вес, но откалиброваны для предоставления информации о массе. Стоя на весах в ванной, нажмите на соседний стол. Что происходит с чтением? Почему? Будет ли ваша шкала измерять ту же «массу» на Земле, что и на Луне?
Пружины позволяют измерить ваш вес (для объекта, который не ускоряется). Это сила в ньютонах (или фунтах). В большинстве стран результат делится на 9,80, чтобы получить значение в килограммах. Весы измеряют вес, но откалиброваны для предоставления информации о массе. Стоя на весах в ванной, нажмите на соседний стол. Что происходит с чтением? Почему? Будет ли ваша шкала измерять ту же «массу» на Земле, что и на Луне?
Пример 1.Какое ускорение может дать человек, толкая газонокосилку?
Предположим, что чистая внешняя сила (толчок минус трение), действующая на газонокосилку, составляет 51 Н (около 11 фунтов) параллельно земле. Масса косилки 24 кг. Какое у него ускорение?Рис. 3. Сила полезного действия на газонокосилку справа составляет 51 Н. С какой скоростью газонокосилка ускоряется вправо?
Стратегия Поскольку даны F net и m, ускорение можно вычислить непосредственно из второго закона Ньютона, как указано в F net = m a . {2} \\ [/ латекс].
{2} \\ [/ латекс].
Направление ускорения совпадает с направлением результирующей силы, параллельной земле. В этом примере нет информации об отдельных внешних силах, действующих на систему, но мы можем кое-что сказать об их относительных величинах. Например, сила, прикладываемая человеком, толкающим косилку, должна быть больше, чем трение, препятствующее движению (поскольку мы знаем, что косилка движется вперед), а вертикальные силы должны нейтрализоваться, если не должно быть ускорения в вертикальном направлении ( косилка движется только горизонтально).Обнаруженное ускорение достаточно мало, чтобы быть приемлемым для человека, толкающего косилку. Такое усилие не будет длиться слишком долго, потому что человек скоро наберет максимальную скорость.
Пример 2. Какая ракетная тяга разгоняет салазки?
До пилотируемых космических полетов ракетные сани использовались для испытания самолетов, ракетного оборудования и физиологических воздействий на людей на высоких скоростях. Они состояли из платформы, которая была установлена на одной или двух направляющих и приводилась в движение несколькими ракетами.Вычислите величину силы, прилагаемой каждой ракетой, которая называется ее тягой T, для четырехракетной двигательной установки, показанной на рисунке 4. Начальное ускорение салазок составляет 49 м / с2, масса системы – 2100 кг, а сила трения. противодействие движению, как известно, составляет 650 Н.
Они состояли из платформы, которая была установлена на одной или двух направляющих и приводилась в движение несколькими ракетами.Вычислите величину силы, прилагаемой каждой ракетой, которая называется ее тягой T, для четырехракетной двигательной установки, показанной на рисунке 4. Начальное ускорение салазок составляет 49 м / с2, масса системы – 2100 кг, а сила трения. противодействие движению, как известно, составляет 650 Н.Рис. 4. Салазки испытывают ракетную тягу, которая ускоряет их вправо. Каждая ракета создает одинаковую тягу T. Как и в других ситуациях, когда есть только горизонтальное ускорение, вертикальные силы нейтрализуются.Земля оказывает на систему направленную вверх силу N, равную по величине и противоположную по направлению ее весу w. Система здесь – сани, его ракеты и всадник, поэтому никакие силы между этими объектами не рассматриваются. Стрелка, обозначающая трение (f), нарисована крупнее шкалы.
Стратегия Несмотря на то, что существуют силы, действующие вертикально и горизонтально, мы предполагаем, что вертикальные силы компенсируются, поскольку нет вертикального ускорения. Это оставляет нам только горизонтальные силы и более простую одномерную задачу.Направления указываются знаками плюс или минус, при этом вправо принимается за положительное направление. См. Диаграмму свободного тела на рисунке.
Это оставляет нам только горизонтальные силы и более простую одномерную задачу.Направления указываются знаками плюс или минус, при этом вправо принимается за положительное направление. См. Диаграмму свободного тела на рисунке.
Поскольку ускорение, масса и сила трения даны, мы начнем со второго закона Ньютона и ищем способы найти тягу двигателей. Поскольку мы определили направление силы и ускорения как действующие «вправо», нам нужно учитывать в расчетах только величины этих величин.Следовательно, мы начинаем с
F net = ma,
, где F net – чистая сила в горизонтальном направлении. Из рисунка 4 видно, что тяга двигателя увеличивается, а трение противодействует тяге. В форме уравнения чистая внешняя сила равна
.Подставляя это во второй закон Ньютона, получаем
Используя небольшую алгебру, мы решаем общую тягу 4 T :
Подстановка известных значений дает
[латекс] 4T = \ text {ma} + f = \ left (\ text {2100 кг} \ right) \ left ({\ text {49 м / с}} ^ {2} \ right) + \ text { 650 Н} \ [/ латекс]
[латекс] 4Т = 1. {4} \ text {N} \\ [/ latex].
{4} \ text {N} \\ [/ latex].
Цифры довольно большие, поэтому результат может вас удивить. Подобные эксперименты проводились в начале 1960-х годов для проверки пределов человеческой выносливости и установки, предназначенной для защиты людей при аварийных выбросах реактивных истребителей. Была получена скорость 1000 км / ч с ускорением 45 g. (Напомним, что g, ускорение свободного падения, составляет 9,80 м / с 2 . Когда мы говорим, что ускорение составляет 45 g, это 45 × 9.80 м / с 2 , что составляет примерно 440 м / с 2 .) Хотя живые предметы больше не используются, с помощью ракетных саней была получена сухопутная скорость 10 000 км / ч. В этом примере, как и в предыдущем, интересующая система очевидна. В следующих примерах мы увидим, что выбор интересующей системы имеет решающее значение, и выбор не всегда очевиден.
Второй закон движения Ньютона – это больше, чем определение; это соотношение между ускорением, силой и массой.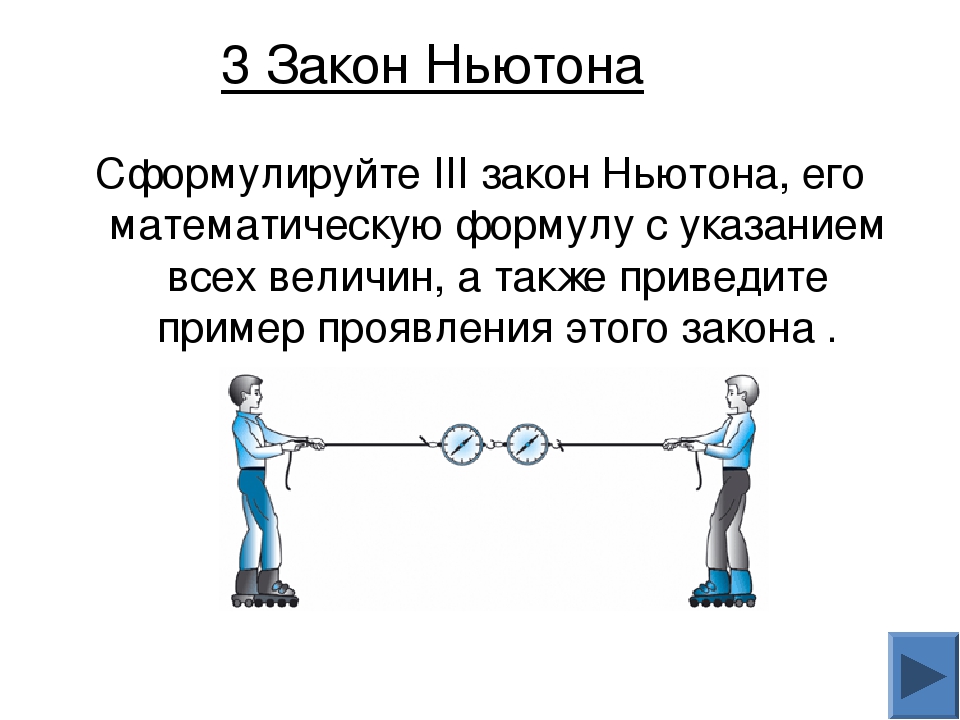 Это может помочь нам делать прогнозы. Каждую из этих физических величин можно определить независимо, поэтому второй закон говорит нам что-то основное и универсальное о природе. В следующем разделе представлен третий и последний закон движения.
Это может помочь нам делать прогнозы. Каждую из этих физических величин можно определить независимо, поэтому второй закон говорит нам что-то основное и универсальное о природе. В следующем разделе представлен третий и последний закон движения.
Сводка раздела
- Ускорение, a , определяется как изменение скорости, означающее изменение ее величины или направления, или и того, и другого.
- Внешняя сила – это сила, действующая на систему извне, в отличие от внутренних сил, которые действуют между компонентами внутри системы.
- Второй закон движения Ньютона гласит, что ускорение системы прямо пропорционально и в том же направлении, что и чистая внешняя сила, действующая на систему, и обратно пропорционально ее массе.
- В форме уравнения второй закон движения Ньютона выглядит так: [latex] {\ text {a}} = \ frac {{{\ text {F}}} _ {\ text {net}}} {m} \\ [/ латекс].
- Это часто записывается в более привычной форме: F net = m a .

- Вес объекта w определяется как сила тяжести, действующая на объект массой м .Объект испытывает ускорение свободного падения g :
w = м г .
- Если единственная сила, действующая на объект, вызвана гравитацией, объект находится в свободном падении.
- Трение – это сила, которая препятствует движению соприкасающихся объектов друг за другом.
Концептуальные вопросы
1. Какое утверждение верно? (а) Чистая сила вызывает движение. (b) Чистая сила вызывает изменение движения. Объясните свой ответ и приведите пример.
2. Почему мы можем пренебрегать такими силами, как силы, удерживающие тело вместе, когда мы применяем второй закон движения Ньютона?
3. Объясните, как выбор «интересующей системы» влияет на то, какие силы необходимо учитывать при применении второго закона движения Ньютона.
4. Опишите ситуацию, в которой чистая внешняя сила, действующая на систему, не равна нулю, но ее скорость остается постоянной.
5. Система может иметь ненулевую скорость, в то время как чистая внешняя сила, действующая на нее , равна нулю.Опишите такую ситуацию.
6. Камень брошен вверх. Какая чистая внешняя сила действует на скалу, когда она находится на вершине своей траектории?
7. (a) Приведите пример различных чистых внешних сил, действующих на одну и ту же систему, вызывая разные ускорения. (б) Приведите пример одной и той же чистой внешней силы, действующей на системы разной массы, вызывая разные ускорения. (c) Какой закон точно описывает оба эффекта? Сформулируйте это словами и в виде уравнения.
8. Если ускорение системы равно нулю, не действуют ли на нее внешние силы? А как насчет внутренних сил? Объясни свои ответы.
9. Если к объекту приложена постоянная ненулевая сила, что вы можете сказать о скорости и ускорении объекта?
10. Сила тяжести, действующая на баскетбольный мяч на рисунке 2, игнорируется. Если принять во внимание гравитацию и , каково направление чистой внешней силы на баскетбольный мяч – выше горизонтали, ниже горизонтали или все еще горизонтально?
Задачи и упражнения
Вы можете предположить, что данные, взятые с иллюстраций, имеют точность до трех цифр.
1. Спринтер весом 63,0 кг начинает забег с ускорением 4,20 м / с. 2 . Какая чистая внешняя сила действует на него?
2. Если спринтер из предыдущей задачи разгоняется с такой скоростью на 20 м, а затем сохраняет эту скорость до конца 100-метрового рывка, сколько у него времени для забега?
3. Пылесос толкает тележку для белья весом 4,50 кг таким образом, чтобы чистая внешняя сила, действующая на нее, составляла 60,0 Н. Вычислите величину ее ускорения.
4. Поскольку астронавты на орбите явно невесомые, необходим умный метод измерения их массы, чтобы отслеживать прирост или потерю массы для корректировки рациона. Один из способов сделать это – приложить известную силу к космонавту и измерить возникающее ускорение. Предположим, что действует чистая внешняя сила 50,0 Н и измеренное ускорение астронавта составляет 0,893 м / с 2 . (а) Рассчитайте ее массу. (b) При приложении силы к космонавту, аппарат, в котором он движется по орбите, испытывает равную и противоположную силу.Обсудите, как это повлияет на измерение ускорения космонавта. Предложите метод, позволяющий избежать отдачи автомобиля.
5. На рис. 3 чистая внешняя сила на газонокосилке 24 кг заявлена равной 51 Н. Если сила трения, препятствующая движению, равна 24 Н, то какую силу F (в ньютонах) прикладывает человек косилка? Предположим, косилка движется со скоростью 1,5 м / с при снятии усилия F . Как далеко уйдет косилка до остановки?
6.Те же ракетные салазки, изображенные на рисунке 5, замедляются со скоростью 196 м / с 2 . Какая сила необходима, чтобы вызвать это замедление? Предположим, что ракеты выключены. Масса системы 2100 кг.
Рисунок 5.
7. (a) Если салазки ракеты, показанные на рисунке 6, запускаются с горящей только одной ракетой, какова величина ее ускорения? Предположим, что масса системы составляет 2100 кг, тяга T составляет 2,4 × 10 4 Н, а сила трения, препятствующая движению, известна как 650 Н.б) Почему ускорение не в четыре раза меньше, чем у всех горящих ракет?
Рисунок 6.
8. Какое замедление у ракетных санок, если они останавливаются за 1,1 с со скорости 1000 км / ч? (Из-за такого замедления один испытуемый потерял сознание и временно потерял сознание.)
9. Предположим, двое детей толкают третьего ребенка в повозке горизонтально, но в противоположных направлениях. Первый ребенок прикладывает силу 75,0 Н, второй – 90.{2} \\ [/ latex] при скорости 90,0 км / ч. На этой скорости силы сопротивления движению, включая трение и сопротивление воздуха, составляют в сумме 400 Н. (Сопротивление воздуха аналогично трению воздуха. Оно всегда противодействует движению объекта). Какова величина силы, которую мотоцикл оказывает на мотоцикл в обратном направлении. земля, чтобы произвести его ускорение, если масса мотоцикла с водителем составляет 245 кг?
11. Ракетные салазки, показанные на рисунке 8, ускоряются со скоростью 49,0 м / с. 2 . Его пассажирский вес 75.0 кг. (а) Рассчитайте горизонтальную составляющую силы, которую сиденье оказывает на его тело. Сравните это с его весом, используя соотношение. (b) Рассчитайте направление и величину общей силы, которую сиденье оказывает на его тело.
Рисунок 8.
12. Повторите предыдущую задачу для ситуации, когда салазки ракеты замедляются со скоростью 201 м / с 2 . В этой задаче силы прилагаются к сиденью и удерживающим ремням.
13. Вес космонавта вместе с его скафандром на Луне составляет всего 250 Н.Сколько они весят на Земле? Какая масса на Луне? На земле?
14. Предположим, масса полностью загруженного модуля, в котором космонавты взлетают с Луны, составляет 10 000 кг. Тяга его двигателей составляет 30 000 Н. (а) Рассчитайте величину ускорения при вертикальном взлете с Луны. б) Может ли он взлететь с Земли? Если нет, то почему? Если бы это было возможно, вычислите величину его ускорения.
Глоссарий
- ускорение:
- скорость, с которой скорость объекта изменяется за период времени
- свободное падение:
- ситуация, в которой единственной силой, действующей на объект, является сила тяжести
- трение:
- – сила соприкасающихся объектов друг с другом; примеры включают шероховатую поверхность и сопротивление воздуха
- чистая внешняя сила:
- векторная сумма всех внешних сил, действующих на объект или систему; заставляет массу ускоряться
- Второй закон движения Ньютона:
- чистая внешняя сила F чистая на объекте с массой m пропорциональна и в том же направлении, что и ускорение объекта, a , и обратно пропорциональна массе; математически определяется как [latex] \ mathbf {\ text {a}} = \ frac {{\ mathbf {\ text {F}}} _ {\ text {net}}} {m} \\ [/ latex]
- система
- определяется границами наблюдаемого объекта или набора объектов; все силы, возникающие извне системы, считаются внешними силами
- вес
- сила w из-за силы тяжести, действующей на объект массой [латекс] м [/ латекс]; математически определяется как: w = mg , где g – величина и направление ускорения свободного падения
Избранные решения проблем и упражнения
1.265 N
3. 13,3 м / с 2
7. (a) 12 м / с 2 (b) Ускорение не в четверть от того, что было при горящих ракетах, потому что сила трения все еще такая же большая, как и при всех горящих ракетах.
9. (a) Система – это ребенок в вагоне плюс вагон.
Рисунок 9
(б)
(c) a = 0,130 м / с 2 в направлении толчка второго ребенка.
(г) a = 0,00 м / с 2
11.(а) 3,68 × 10 3 Н. Эта сила в 5,00 раз превышает его вес. (b) 3750 Н; 11,3º над горизонтом
13. 1,5 × 10 3 Н, 150 кг, 150 кг
Научный эксперимент: Второй закон Ньютона…
Сэр Исаак Ньютон был английским ученым. Он родился в 1642 году и умер в 1727 году. Это было примерно во время ранней колонизации Северной Америки, во время основания некоторых из первоначальных 13 колоний, войн во Франции и Индиане и судебных процессов над салемскими ведьмами.Он жил незадолго до американской революции.
Ньютон наиболее известен тремя очень важными принципами физики, называемыми классической механикой. Эти принципы описывают движение вещей и сегодня называются его именем – Законы движения Ньютона. Их три: Первый, Второй и Третий закон движения Ньютонов.
Второй закон движения Ньютона гласит, что ускорение (увеличение скорости) происходит, когда сила действует на массу (объект). Езда на велосипеде – хороший пример того, как действует этот закон движения.Ваш велосипед – это масса. Мышцы ваших ног, толкающие педали велосипеда, – это сила. Когда вы нажимаете на педали, ваш велосипед ускоряется. Вы увеличиваете скорость велосипеда, прикладывая усилие к педалям.
Второй закон Ньютона также гласит, что чем больше масса ускоряемого объекта, тем большее количество силы необходимо для ускорения объекта. Допустим, у вас есть два одинаковых велосипеда, у каждого из которых есть корзина. У одного велосипеда пустая корзина. У одного велосипеда есть корзина, полная кирпичей.Если вы попытаетесь ездить на каждом велосипеде и будете нажимать на педали с одинаковой силой, вы сможете ускорить велосипед с пустой корзиной БОЛЬШЕ, чем велосипед с корзиной, полной кирпичей. Кирпичи добавляют массы второму велосипеду. С кирпичами в корзине вам придется прикладывать больше усилий к педалям, чтобы велосипед с кирпичами в корзине двигался.
Эксперименты по исследованию второго закона движения Ньютона:
Сайтов, мероприятий и печатных форм:
Вы можете попросить помощи с домашним заданием у эксперта по математике и естественным наукам, позвонив на горячую линию Ask Rose Homework.Они предоставляют БЕСПЛАТНУЮ помощь в выполнении домашних заданий по математике и естественным наукам учащимся из Индианы 6-12 классов.
Книг:
Используйте свою библиотечную карту indyPL, чтобы искать книги в любом из наших мест или проверять электронные книги и электронные аудиокниги из дома прямо на свое устройство.
Нужна помощь? Позвоните или спросите сотрудника библиотеки в любом из наших офисов или напишите библиотекарю по телефону 317 333-6877.
4.3 Второй закон движения Ньютона – Физика
Задачи обучения раздела
К концу этого раздела вы сможете делать следующее:
- Опишите второй закон Ньютона, как словесно, так и математически
- Используйте второй закон Ньютона для решения проблем
Поддержка учителей
Поддержка учителей
Цели обучения в этом разделе помогут учащимся освоить следующие стандарты:
- (4) Научные концепции.Учащийся знает и применяет законы движения в различных ситуациях. Ожидается, что студент:
- (D) вычисляет влияние сил на объекты, включая закон инерции, соотношение между силой и ускорением и характер пар сил между объектами.
Перед тем, как начать этот раздел, просмотрите силы, ускорение, ускорение свободного падения (g), трение, инерцию и первый закон Ньютона.
Раздел Основные термины
| в свободном падении | Второй закон движения Ньютона | вес |
Описание второго закона движения Ньютона
Поддержка учителей
Поддержка учителей
[BL] [OL] Просмотрите концепции инерции и первый закон Ньютона.Объясните: согласно первому закону Ньютона изменение движения вызывается внешней силой. Например, подброшенный мяч меняет свою скорость и направление, когда по нему попадает летучая мышь.
[BL] [OL] [AL] Напишите уравнение для второго закона Ньютона и покажите, как его можно решить для всех трех переменных: F , m и a . Объясните практическое значение для каждого случая. Спросите студентов, как бы вели себя две другие переменные, если бы одна величина оставалась постоянной.
Предупреждение о заблуждении
Студенты могут перепутать термины , равные , и , пропорциональные .
Первый закон Ньютона рассматривал тела в покое или тела, движущиеся с постоянной скоростью. Другое состояние движения, которое следует учитывать, – это когда объект движется с изменяющейся скоростью, что означает изменение скорости и / или направления движения. Этот тип движения рассматривается во втором законе движения Ньютона, который гласит, как сила вызывает изменения в движении.Второй закон движения Ньютона используется для расчета того, что происходит в ситуациях, связанных с силами и движением, и показывает математическую взаимосвязь между силой, массой и ускорением . Математически второй закон чаще всего записывается как
Fnet = maorΣF = ma, Fnet = maorΣF = ma,4,2
, где F net (или ∑ F ) – чистая внешняя сила, м – масса системы, а – – ускорение. Обратите внимание, что F net и ∑ F одинаковы, поскольку чистая внешняя сила является суммой всех внешних сил, действующих на систему.
Во-первых, что мы подразумеваем под изменением движения ? Изменение движения – это просто изменение скорости: скорость объекта может стать медленнее или быстрее, направление, в котором движется объект, может измениться, или обе эти переменные могут измениться. Изменение скорости по определению означает, что произошло ускорение. Первый закон Ньютона гласит, что только ненулевая чистая внешняя сила может вызвать изменение движения, поэтому чистая внешняя сила должна вызывать ускорение. Обратите внимание, что ускорение может относиться к замедлению или ускорению.Ускорение также может относиться к изменению направления движения без изменения скорости, потому что ускорение – это изменение скорости, деленное на время, необходимое для того, чтобы это изменение произошло, скорость и определяется скоростью и направлением .
Из уравнения Fnet = ma, Fnet = ma мы видим, что сила прямо пропорциональна как массе, так и ускорению, что имеет смысл. Чтобы ускорить два объекта из состояния покоя до одной и той же скорости, можно ожидать, что для ускорения более массивного объекта потребуется больше силы.Точно так же для двух объектов одинаковой массы приложение большей силы к одному ускорит его до большей скорости.
Теперь давайте изменим второй закон Ньютона, чтобы найти ускорение. Получаем
a = Fnetmora = ΣFm.a = Fnetmora = ΣFm.4.3
В этой форме мы видим, что ускорение прямо пропорционально силе, которую мы записываем как
, где символ ∝∝ означает , пропорциональный .
Эта пропорциональность математически выражает то, что мы только что сказали словами: ускорение прямо пропорционально чистой внешней силе.Когда две переменные прямо пропорциональны друг другу, тогда, если одна переменная удваивается, другая переменная должна удваиваться. Аналогичным образом, если одна переменная уменьшается вдвое, другая переменная также должна быть уменьшена вдвое. Как правило, когда одна переменная умножается на число, другая переменная также умножается на то же число. Кажется разумным, что ускорение системы должно быть прямо пропорционально и в том же направлении, что и чистая внешняя сила, действующая на систему. Объект испытывает большее ускорение, когда на него действует большая сила.
Из уравнения a = Fnet / ma = Fnet / m также ясно, что ускорение обратно пропорционально массе, которую мы записываем как
a 1m.a ∝ 1m.4,5
Обратно пропорциональный означает, что если одна переменная умножается на число, другая переменная должна быть разделена на на то же число. Теперь также кажется разумным, что ускорение должно быть обратно пропорционально массе системы. Другими словами, чем больше масса (инерция), тем меньше ускорение, создаваемое данной силой.Эта взаимосвязь проиллюстрирована на рис. 4.5, который показывает, что заданная чистая внешняя сила, приложенная к баскетбольному мячу, вызывает гораздо большее ускорение, чем при приложении к автомобилю.
Рис. 4.5 Одна и та же сила, действующая на системы разной массы, вызывает разное ускорение. (а) Мальчик толкает баскетбольный мяч, чтобы сделать передачу. Влияние силы тяжести на мяч игнорируется. (б) Тот же мальчик, толкающий с одинаковой силой заглохшую машину, дает гораздо меньшее ускорение (трение незначительно).Обратите внимание, что диаграммы свободного тела для мяча и для автомобиля идентичны, что позволяет нам сравнивать эти две ситуации.
Применение второго закона Ньютона
Поддержка учителей
Поддержка учителей
[BL] Узнайте, как преобразовывать единицы измерения.
[OL] [AL] Попросите студентов привести примеры второго закона Ньютона.
Предупреждение о заблуждении
Учащиеся могут спутать вес, который представляет собой силу, и г, , что означает ускорение свободного падения.
[BL] [OL] [AL] Спросите студентов, думают ли они, что космонавт весит на Луне столько же, сколько они на Земле. Поговорим о разнице между массой и весом.
Прежде чем применять второй закон Ньютона, важно рассмотреть единицы измерения. Уравнение Fnet = maFnet = ma используется для определения единиц силы в терминах трех основных единиц массы, длины и времени (напомним, что ускорение состоит из единиц длины, разделенных на квадрат времени). Единица силы в системе СИ называется ньютон (сокращенно Н) и представляет собой силу, необходимую для ускорения системы массой 1 кг со скоростью 1 м / с 2 .То есть, поскольку Fnet = ma, Fnet = ma, мы имеем
1N = 1 кг × 1 м / с2 = 1 кг⋅мс2,1N = 1 кг × 1 м / с2 = 1 кг⋅мс2.4,6
Одним из наиболее важных применений второго закона Ньютона является вычисление веса (также известного как сила тяжести), который математически обычно представляется как W . Когда люди говорят о гравитации, они не всегда понимают, что это ускорение. Когда объект падает, он ускоряется к центру Земли. Второй закон Ньютона гласит, что чистая внешняя сила, действующая на объект, ответственна за его ускорение.Если сопротивление воздуха незначительно, чистая внешняя сила на падающий объект – это только сила тяжести (т. Е. Вес объекта).
Вес может быть представлен вектором, потому что он имеет направление. Вниз определяется как направление, в котором тянет сила тяжести, поэтому вес обычно считается направленной вниз силой. Используя второй закон Ньютона, мы можем вычислить уравнение веса.
Рассмотрим объект массой м , падающий на Землю. Он испытывает только силу тяжести (т.е., гравитационная сила или вес), который представлен вторым законом У. Ньютона, согласно которому Fnet = ma.Fnet = ma. Поскольку единственная сила, действующая на объект, – это сила тяжести, мы имеем Fnet = W.Fnet = W. Мы знаем, что ускорение объекта под действием силы тяжести составляет g , поэтому мы имеем a = g.a = g. Подставляя эти два выражения во второй закон Ньютона, получаем
Это уравнение для веса – силы тяжести на массу м . На Земле g = 9,80 м / с2, g = 9.80 м / с2, поэтому вес (без учета направления веса) объекта массой 1,0 кг на Земле составляет
Вт = mg = (1,0 кг) (9,80 м / с2) = 9,8 NW = mg = (1,0 кг) (9,80 м / с2) = 9,8 Н.4,8
Хотя в большинстве стран мира в качестве единицы силы используется ньютон, в Соединенных Штатах наиболее известной единицей силы является фунт (фунт), где 1 Н = 0,225 фунта.
Напомним, что хотя сила тяжести действует вниз, ей можно присвоить положительное или отрицательное значение, в зависимости от того, какое положительное направление находится в выбранной вами системе координат.Обязательно учтите это при решении задач с весом. Когда направление вниз считается отрицательным, как это часто бывает, ускорение свободного падения становится равным
g = -9,8 м / с 2 .
Когда чистая внешняя сила, действующая на объект, равна его весу, мы говорим, что он находится в свободном падении. В этом случае единственной силой, действующей на объект, является сила тяжести. На поверхности Земли, когда объекты падают вниз по направлению к Земле, они никогда не находятся в истинном свободном падении, потому что всегда существует некоторая восходящая сила из-за сопротивления воздуха, которое действует на объект (и есть также сила плавучести воздуха, которая аналогична сила плавучести в воде, которая удерживает лодки на плаву).
Гравитация незначительно меняется на поверхности Земли, поэтому вес объекта очень мало зависит от его местоположения на Земле. Вес резко меняется от поверхности Земли. На Луне, например, ускорение свободного падения составляет всего 1,67 м / с 2 . Поскольку вес зависит от силы тяжести, масса в 1,0 кг весит 9,8 Н на Земле и всего около 1,7 Н на Луне.
Важно помнить, что вес и масса очень разные, хотя они тесно связаны.Масса – это количество материи (сколько материала ) в объекте и не меняется, но вес – это сила тяжести на объекте, пропорциональная силе тяжести. Их легко спутать, потому что наш опыт ограничен Землей, а вес объекта по существу одинаков, независимо от того, где вы находитесь на Земле. Путаницу усугубляет то, что в повседневном языке термины масса и вес часто используются как синонимы; например, наши медицинские записи часто показывают наш вес в килограммах, но никогда в правильных единицах измерения – ньютонах.
Snap Lab
Масса и вес
Поддержка учителя
Поддержка учителя
Объясните: хотя весы показывают массу, они фактически измеряют вес. Весы откалиброваны, чтобы показывать правильную массу на Земле. На Луне они дадут разные результаты, потому что на Луне сила тяжести слабее.
В этом упражнении вы будете использовать весы для определения массы и веса.
- Что измеряют весы для ванной?
- Когда вы стоите на весах в ванной, что происходит с весами? Слегка угнетает.Весы содержат пружины, которые сжимаются пропорционально вашему весу – подобно резиновым лентам, расширяющимся при натяжении.
- Пружины определяют ваш вес (при условии, что вы не ускоряетесь). Это сила в ньютонах (или фунтах). В большинстве стран измерение теперь делится на 9,80, чтобы получить значение в килограммах, что соответствует массе. Весы определяют вес, но откалиброваны для отображения массы.
- Если вы отправитесь на Луну и встанете на свои весы, обнаружит ли он ту же массу , что и на Земле?
Проверка захвата
Стоя на весах в ванной, нажмите на соседний стол.Что происходит с чтением? Почему?
- Показание увеличивается, потому что часть вашего веса прикладывается к столу, и стол оказывает на вас соответствующую силу, действующую в направлении вашего веса.
- Показание увеличивается, потому что часть вашего веса приложена к столу, и стол оказывает на вас соответствующую силу, которая действует в направлении, противоположном вашему весу.
- Показание уменьшается, потому что часть вашего веса прикладывается к столу, и стол оказывает на вас соответствующую силу, действующую в направлении вашего веса.
- Показание уменьшается, потому что часть вашего веса приложена к столу, и стол оказывает на вас соответствующую силу, действующую в направлении, противоположном вашему весу.
Советы для успеха
Только чистая внешняя сила влияет на ускорение объекта. Если на объект действует более одной силы, и вы вычисляете ускорение, используя только одну из этих сил, вы не получите правильное ускорение для этого объекта.
Watch Physics
Второй закон движения Ньютона
В этом видео рассматривается второй закон движения Ньютона и то, как чистая внешняя сила и ускорение связаны друг с другом и с массой.Он также охватывает единицы силы, массы и ускорения и рассматривает отработанный пример.
Проверка захвата
Верно или неверно. Если вы хотите уменьшить ускорение объекта до половины от его первоначального значения, вам нужно будет уменьшить чистую внешнюю силу вдвое.
- Истинно
- Ложь
Рабочий пример
Какое ускорение может вызвать человек, толкая газонокосилку?
Предположим, что чистая внешняя сила (толчок минус трение), действующая на газонокосилку, составляет 51 Н, параллельную земле.Масса косилки 240 кг. Какое у него ускорение?
Рисунок 4.6
Стратегия
Поскольку даны F net и м , ускорение можно рассчитать непосредственно по второму закону Ньютона: F net = м a .
Решение
Решая второй закон Ньютона для ускорения, мы находим, что величина ускорения, a , равна a = Fnetm.а = Fnetm. Ввод данных значений чистой внешней силы и массы дает
a = 51 N240 kga = 51 N240 кг4,9
Вставка единиц кг⋅м / с2кг⋅м / с2 для N дает
a = 51 кг⋅м / с2240 кг = 0,21 м / с2. A = 51 кгм / с2240 кг = 0,21 м / с2.4,10
Обсуждение
Ускорение происходит в том же направлении, что и чистая внешняя сила, которая параллельна земле и направо. В этом примере нет информации об отдельных внешних силах, действующих на систему, но мы можем кое-что сказать об их относительных величинах.Например, сила, прилагаемая человеком, толкающим косилку, должна быть больше, чем трение, препятствующее движению, потому что нам дано, что чистая внешняя сила направлена в направлении, в котором толкает человек. Кроме того, вертикальные силы должны нейтрализоваться, если нет ускорения в вертикальном направлении (косилка движется только горизонтально). Найденное ускорение приемлемо для человека, толкающего косилку; скорость косилки должна увеличиваться на 0,21 м / с каждую секунду, что возможно. Время, в течение которого газонокосилка разгоняется, не будет очень долгим, потому что скоро человек достигнет максимальной скорости.На этом этапе человек может толкать немного меньше, потому что ему нужно только преодолеть трение.
Рабочий пример
Какая ракетная тяга ускоряет эти салазки?
До пилотируемых космических полетов ракетные сани использовались для проверки самолетов, ракетного оборудования и физиологических воздействий на человека при высоких ускорениях. Ракетные сани представляли собой платформу, установленную на одной или двух рельсах и приводимую в движение несколькими ракетами. Вычислите величину силы, прилагаемой каждой ракетой, которая называется ее тягой, T , для четырехракетной двигательной установки, показанной ниже.Начальное ускорение саней составляет 49 м / с2,49 м / с2, масса системы – 2100 кг, сила трения, препятствующая движению, – 650 Н.
Рисунок 4.7
Стратегия
Интересующая система – ракетные сани. Хотя силы действуют на систему вертикально, они должны нейтрализоваться, поскольку система не ускоряется вертикально. Остается рассмотреть только горизонтальные силы. Мы назначим направление вправо как положительное. См. Диаграмму свободного тела на рисунке 4.8.
Решение
Начнем со второго закона Ньютона и ищем способы определить тягу T двигателей. Поскольку все силы и ускорения линейны, нам нужно учитывать только величины этих величин в расчетах. Начнем с
, где FnetFnet – чистая внешняя сила в горизонтальном направлении. Из рисунка 4.8 видно, что тяга двигателя в одном направлении (которое мы называем положительным направлением), тогда как трение противодействует тяге.В форме уравнения чистая внешняя сила равна
. Fnet = 4T − f. Fnet = 4T − f.4,12
Второй закон Ньютона говорит нам, что F net = м a , поэтому мы получаем
После небольшой алгебры решаем общую тягу 4 T :
, что означает, что индивидуальная тяга составляет
Вставка известных значений дает
T = (2100 кг) (49 м / с2) +650 N4 = 2,6 × 104 N.T = (2100 кг) (49 м / с2) +650 N4 = 2,6 × 104 N.4,16
Обсуждение
Цифры довольно большие, поэтому результат может вас удивить.Подобные эксперименты проводились в начале 1960-х годов, чтобы проверить пределы человеческой выносливости и проверить устройство, предназначенное для защиты летчиков-истребителей от аварийных катапультирований. Были получены скорости 1000 км / ч, с ускорением 45 g . (Напомним, что g, ускорение свободного падения, составляет 9,80 м / с2,9,80 м / с2. Ускорение 45 g составляет 45 × 9,80 м / с2,45 × 9,80 м / с2, что составляет примерно 440 м / с. s2,440 м / с2.) Живые предметы больше не используются, и теперь с помощью ракетных саней была получена сухопутная скорость 10 000 км / ч.В этом примере, как и в предыдущем примере, интересующая система ясна. В последующих примерах мы увидим, что выбор интересующей системы имеет решающее значение и что этот выбор не всегда очевиден.
Практические задачи
9.Если 1 Н равен 0,225 фунта, сколько фунтов составляют 5 Н силы?
- 0,045 фунта
- 1,125 фунта
- 2,025 фунта
- 5.000 фунтов
Какое усилие необходимо приложить к объекту массой 5 кг, чтобы он разогнался со скоростью 20 м / с 2 ?
- 1 н.
- 10 N
- 100 N
- 1,000 N
Проверьте свое понимание
Поддержка учителя
Поддержка учителя
Используйте вопросы в Проверьте свое понимание , чтобы оценить, достигли ли учащиеся целей обучения по разделу.Если учащиеся не справляются с какой-либо конкретной целью, экзамен Check Your Understanding поможет определить, что вызывает проблему, и направит учащихся к соответствующему содержанию.
11.Каково математическое утверждение второго закона движения Ньютона?
- F = м a
- F = 2 м a
- F = maF = ma
- F = м a 2
Второй закон Ньютона описывает взаимосвязь между какими величинами?
- Сила, масса и время
- Сила, масса и перемещение
- Сила, масса и скорость
- Сила, масса и ускорение
Что такое ускорение?
- Ускорение – это скорость изменения рабочего объема.
- Ускорение – это скорость изменения силы.
- Ускорение – это скорость изменения скорости.
- Ускорение – это скорость изменения массы.
Что такое второй закон движения Ньютона? | Исаак Ньютон
Законы движения Исаака Ньютона впервые были изложены в его Principia Mathematica Philosophiae Naturalis в 1687 году.Первый закон гласит, что объект будет оставаться в покое или двигаться с постоянной скоростью, если на него не действует внешняя сила. Третий – это хорошо известная (хотя и не совсем понятная) идея о том, что каждое действие (сила) имеет равную, но противоположную реакцию – если вы толкнете дверь, дверь оттолкнется от вас.
Второй закон говорит вам, как рассчитать значение силы. Сила (измеряемая в Ньютонах) – одно из фундаментальных физических свойств системы, которое может принимать разные формы.Вы можете почувствовать это как толчок или притяжение (механическую силу), в то время как это величина вашего веса (гравитационная сила Земли, притягивающая вас), и ее можно увидеть в отталкивании или притяжении магнитов или электрических зарядов (электромагнитных сила). Сила может быть результатом любого количества фундаментальных физических взаимодействий между частицами материи, но второй закон Ньютона позволяет вам выяснить, как сила, когда она присутствует, повлияет на движение объекта.
В форме, изображенной выше, говорится, что сила (F) равна скорости изменения количества движения (p) во времени (t).Маленькие буквы «d» – это дифференциальная система обозначений, еще одно изобретение Ньютона, которое появляется в бесчисленных физических уравнениях и позволяет математически предсказать, как что-то изменится по мере постепенного изменения другого связанного параметра – в данном случае времени.
Импульс – это масса (в килограммах) объекта, умноженная на его скорость (в метрах в секунду). В большинстве ситуаций масса чего-либо не изменяется при движении, поэтому уравнение можно упростить до массы (m), умноженной на скорость изменения скорости, которую мы знаем как ускорение (a).Это дает нам более знакомую версию второго закона из школьных учебников: F = ma.
Как и остальная часть физики Ньютона, второй закон движения применим в огромном количестве повседневных ситуаций и является рабочей лошадкой в современной науке и технике. Используя его законы движения, можно определить способ движения почти всего: сколько силы потребуется, чтобы разогнать поезд, достигнет ли пушечное ядро своей цели, как движутся воздушные и океанские течения или будет ли летать самолет – все это приложения. второго закона Ньютона.Он даже использовал законы движения в сочетании со своим универсальным законом тяготения, чтобы объяснить, почему планеты движутся именно так.
Вес – это сила, равная массе объекта, умноженной на гравитационное ускорение, вызываемое Землей (равное 10 метрам в секунду в секунду), в направлении центра планеты. Причина, по которой вы не проваливаетесь под землю, конечно же, объясняется третьим законом движения Ньютона, который гласит, что поверхность Земли толкается к вашим ногам с силой, равной, но противоположной вашему весу.
Модифицированная версия второго закона применяется, когда масса объекта изменяется, например ракеты, которая сжигает топливо и становится легче при прохождении через атмосферу.
Все мы знаем второй закон на практике, если не в математике. Чтобы передвинуть тяжелый рояль, нужно приложить больше силы (и, следовательно, больше энергии), чем передвигать по полу небольшой табурет. Когда вы ловите быстро движущийся мяч для крикета, вы знаете, что вам будет меньше больно, если вы отодвинете руку назад, когда поймаете его – если дать движущемуся мячу больше времени, чтобы замедлить ход, ваша рука должна оказывать меньшее противодействующее усилие на мяч.
Пример мяча для крикета демонстрирует, что силы не только имеют размер, но и действуют в определенном направлении. Силы относятся к категории физических свойств, в которую входят импульс и скорость, известные как векторы. Они контрастируют со скалярами, которые имеют размер, но не имеют направления, например температуру или массу.
Буква F во втором законе Ньютона относится к чистой силе, действующей на объект. Таким образом, выяснение того, что происходит с объектом, на который действует несколько сил, требует учета как направления, так и размера каждой силы.Две силы могут иметь одинаковые размеры, но, если они направлены прямо напротив друг друга, они уменьшатся до нуля.
Игра в перетягивание каната – хороший способ подумать об этом. Когда две команды тянут в противоположных направлениях, движение веревки (рассчитанное по второму закону Ньютона) будет определяться чистой силой, действующей на веревку. Размер этой чистой силы – это разница в размерах сил, прилагаемых двумя командами. Направление чистой силы будет в направлении той команды, которая работает сильнее.
Для описания атомов и даже более мелких объектов физики используют версии силы и импульса в уравнениях, которые включают квантово-механические описания времени, а также пространства. В этом масштабе силы – это математические побочные продукты, возникающие, когда фундаментальные частицы материи, такие как электроны и кварки, обмениваются частицами, такими как фотоны, глюоны или частицы W или Z, которые «переносят» силы и в совокупности известны как калибровочные бозоны.
Второй закон Ньютона работает как способ описания движения всего в квантово-механической системе до тех пор, пока частицы не движутся со скоростью, близкой к скорости света.
Когда объект движется со скоростью, близкой к скорости света, мы попадаем в сферу специальной теории относительности, которая говорит нам, что масса объекта будет увеличиваться по мере того, как он движется быстрее. Это необходимо учитывать при расчете сил на этих скоростях.
Действительно, большая часть классической физики Ньютона нуждается в модификации в экстремальных ситуациях – второй закон не является точным, когда присутствуют огромные гравитационные силы, например, вокруг черной дыры или в контексте огромных масс целых галактик, где обычно Относительность становится лучшим способом описания движения в системе.
Второй закон Ньютона – Силы, ускорение и законы движения Ньютона – Eduqas – GCSE Combined Science Revision – Eduqas
Сила, масса и ускорение
Второй закон движения Ньютона можно описать следующим уравнением:
- равнодействующая сила = масса × ускорение
- F = ma
Это когда:
- результирующая сила (F) измеряется в ньютонах (Н)
- масса (м) измеряется в килограммах (кг)
- ускорение (a) равно измеряется в метрах в секунду в квадрате (м / с²)
Уравнение показывает, что ускорение объекта:
- пропорционально равнодействующей силе, действующей на объект
- , обратно пропорционально массе объекта
In Другими словами, ускорение объекта увеличивается, если результирующая сила, действующая на него, увеличивается, и уменьшается, если масса объекта увеличивается.
Второй закон Ньютона можно выразить как «результирующая сила = масса × ускорение» или «Ускорение объекта прямо пропорционально результирующей (или чистой) силе в том же направлении, что и сила, и обратно пропорционально масса объекта “.
Инерционная масса – Высшая
Отношение силы к ускорению – это определение инерционной массы. Инерционная масса – это мера того, насколько сложно изменить скорость объекта. Он определяется как «отношение силы к ускорению».Объекты с большей массой имеют большую инерцию, поэтому для того же ускорения потребуется большая результирующая сила.
Пример
Рассчитайте силу, необходимую для ускорения 22-килограммового гепарда со скоростью 15 м / с².
\ [F = m \ a \]
\ [F = 22 \ times 15 \]
\ [\ underline {F = 330 \ N} \]
- Вопрос
Рассчитайте усилие, необходимое для разогнать газель массой 15 кг со скоростью 10 м / с².
- Показать ответ
\ [F = m \ a \]
\ [F = 15 \ times 10 \]
\ [\ underline {F = 150 \ N} \]
Оценка скорости , ускорения и силы
Важно уметь оценивать скорость, ускорения и силы, задействованные в дорожных транспортных средствах.Символ ~ используется для обозначения приблизительного значения или ответа. В таблице приведены некоторые примеры.
| Автомобиль | Максимальная разрешенная скорость на одинарной проезжей части в м / с | Масса в кг | Ускорение в м / с2 |
|---|---|---|---|
| Семейный автомобиль | ~ 27 | ~ 1,600 | 9 3|
| Грузовик | ~ 22 | ~ 36000 | ~ 0,4 |
Пример
Оцените силу, необходимую для разгона семейного автомобиля до максимальной скорости на одинарной проезжей части.Используя значения ~ 1600 кг и ~ 3 м / с 2 , и F = m a:
- \ [1600 \ times 3 = \ underline {\ sim 4800 \ N} \]
- Вопрос
Оцените силу, необходимую для разгона грузовика до максимальной скорости на одной проезжей части.
- Показать ответ
Используя значения ~ 36 000 кг и ~ 0,4 м / с 2 , и F = ma:
\ [\ underline {Force (F) \ is \ sim 14400 \ N} \]
Движение и силы: второй закон движения Ньютона
Первую часть деятельности, описанной ниже, также можно использовать для иллюстрации инерции.Во второй части упражнения игрушечной машинке добавляется масса, чтобы проиллюстрировать Второй закон Ньютона. Дайте ученику с нарушением зрения возможность почувствовать вес машины до и после добавления глины.
Конечно, трение – это еще одна сила, влияющая на движение, но она не принимается во внимание как фактор активности.
Словарь
Ньютон – единица силы СИ 
Эффекты несбалансированных сил
Несбалансированные силы вызывают ускорение.Когда на объект действует неуравновешенная сила, движение объекта изменяется. Если объект находится в состоянии покоя, сила заставляет его двигаться. Если объект находится в движении, сила меняет его скорость. Любое изменение скорости – это ускорение.
Сила, масса и ускорение
Величина, на которую ускоряется объект, зависит от трех вещей. Это размер силы, направление, в котором действует сила, и масса объекта. Если две силы действуют на один и тот же объект, большая сила вызовет большее ускорение, чем меньшая сила.
Второй закон Ньютона
Второй закон Ньютона описывает соотношение между силой, массой и ускорением. Второй закон Ньютона гласит, что несбалансированная сила, действующая на объект, равна массе объекта, умноженной на его ускорение. Второй закон Ньютона можно описать этим уравнением
F = mxa
В этом уравнении F – сила, m – масса, а – ускорение.Когда масса измеряется в килограммах, а ускорение измеряется в метрах в секунду в секунду, сила измеряется в ньютонах (Н). Ньютон – это единица силы в системе СИ. Неуравновешенная сила в 1 Н ускоряет массу в 1 кг со скоростью 1 м / с2. Один Ньютон силы равен одному килограмм-метру в секунду в секунду (1 кг-м / с2).
Использование второго закона Ньютона
Если трение отсутствует, какое усилие нужно приложить к объекту массой 10 кг, чтобы он разогнался со скоростью 45 м / с2? Поначалу это может показаться сложной проблемой.Однако, если вы воспользуетесь уравнением второго закона Ньютона, это станет легко.
F = mxa
F = 10 кг x 45 м / с2
F = 450 кг м / с2
Вам потребуется приложить силу 450 кг м / с2 или 450 Н.
Сэр Исаак Ньютон (1642-1727)
Исаак Ньютон родился в Англии 25 декабря 1642 года. Он был физиком, астрономом и математиком. В возрасте 45 лет Ньютон опубликовал свои теории движения и гравитации.Великую книгу Ньютона обычно называют «Начала». Считается одним из важнейших произведений в истории науки.
В «Началах» Ньютон объяснил свои три закона движения и свою теорию гравитации. Ньютон также изобрел раздел математики, называемый исчислением, чтобы предсказывать движение, используя свои три закона. Ньютон также сделал много важных открытий, касающихся света и цвета.
Ньютон был профессором математики в Кембриджском университете и членом Королевского общества.Он был посвящен в рыцари королевой Анной в 1705 году.

 д.)
д.) Истинное абсолютное движение не может ни произойти, ни измениться иначе, как от действия сил, приложенных непосредственно к самому движущемуся телу, тогда как относительное движение тела может быть и произведено, и изменено без приложения сил к этому телу; достаточно, чтобы силы были приложены к телам, по отношению к которым это движение определяется.
Истинное абсолютное движение не может ни произойти, ни измениться иначе, как от действия сил, приложенных непосредственно к самому движущемуся телу, тогда как относительное движение тела может быть и произведено, и изменено без приложения сил к этому телу; достаточно, чтобы силы были приложены к телам, по отношению к которым это движение определяется. Это особенно важно знать тем из вас, кто ходил в школу, где, возможно, что-то говорили о волновой природе света. Я говорю вам, как он на самом деле ведёт себя – как частицы
Это особенно важно знать тем из вас, кто ходил в школу, где, возможно, что-то говорили о волновой природе света. Я говорю вам, как он на самом деле ведёт себя – как частицы Гл. ред. физ.-мат. лит., 1988.—144с.—(Б-чка «Квант». Вып.66.)
Гл. ред. физ.-мат. лит., 1988.—144с.—(Б-чка «Квант». Вып.66.)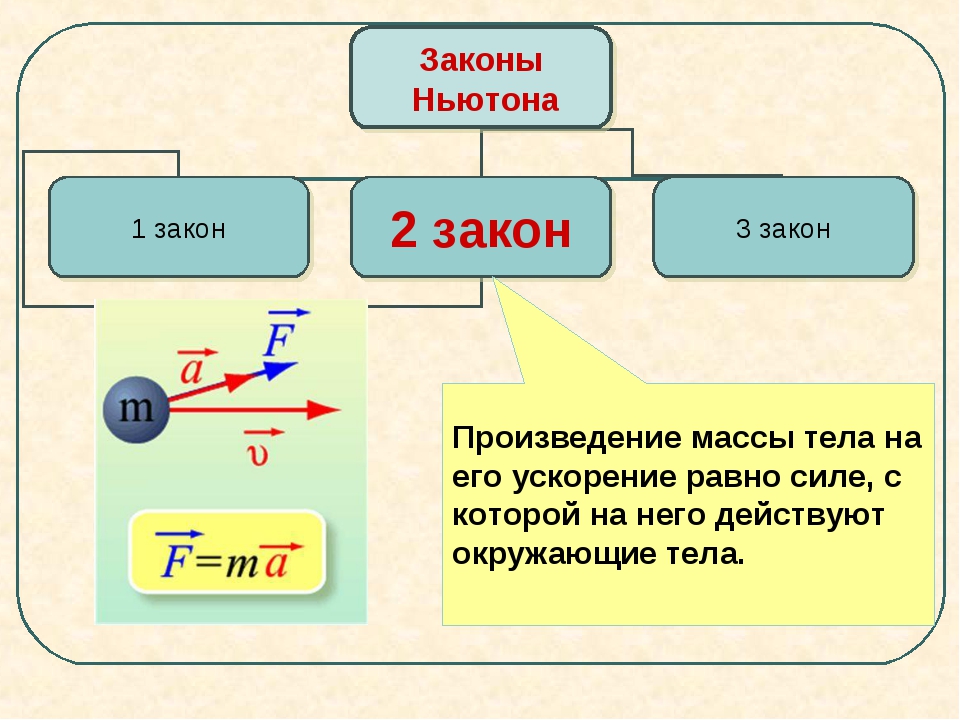 Этот закон иногда называют Законом инерции.
Этот закон иногда называют Законом инерции.