Формула кинематики – .
Основные понятия кинематики
Определение 1Кинематика − это раздел механики, который рассматривает движение тел без объяснения вызывающих его причин.
Определение 2Механическое движение тела − это изменение положения данного тела в пространстве относительно других тел во времени.
Как мы сказали, механическое движение тела относительно. Движение одного и того же тела относительно разных тел может быть разным.
Определение 3Для характеристики движения тела указывается, по отношению к какому из тел рассматривается это движение. Это будет тело отсчета.
Определение 4Система отсчета − система координат, которая связана с телом отсчета и временем для отсчета. Она позволяет определить положение передвигающегося тела в любой отрезок времени.
В СИ единицей длины выступает метр, а единицей времени – секунда.
У каждого тела есть определенные размеры. Разные части тела расположены в разных пространственных местах. Но в большинстве задач механики не нужно указывать положение отдельных частей тела. Если размеры тела маленькие в сравнении с расстояниями до остальных тел, тогда заданное тело считается его материальной точкой. Таким образом поступают при изучении перемещения планет вокруг Солнца.
Механическое движение называют поступательным, в случае если все части тела перемещаются одинаково.
Пример 1Поступательное движение наблюдается у кабин в аттракционе «Колесо обозрения» или у автомобиля на прямолинейном участке пути.
При поступательном движении тела его также рассматривают в качестве материальной точки.
Определение 6Материальная точка − это тело, размерами которого при заданных условиях можно пренебречь.
Материальная точка в механике
Термин “материальная точка” имеет важное значение в механике.
Определение 7Траектория движения тела
− некоторая линия, которую тело или материальная точка описывает, перемещаясь во времени от одной точки до другой.Местонахождение материальной точки в пространстве в любой временной отрезок (закон движения) определяют, используя зависимость координат от времени x=x(t), y=y(t), z=z(t) или зависимость от времени радиус-вектора r→=r→(t), проведенного от начала координат до заданной точки. Наглядно это представлено на рисунке
zaochnik.com
2. Элементы кинематики Основные формулы
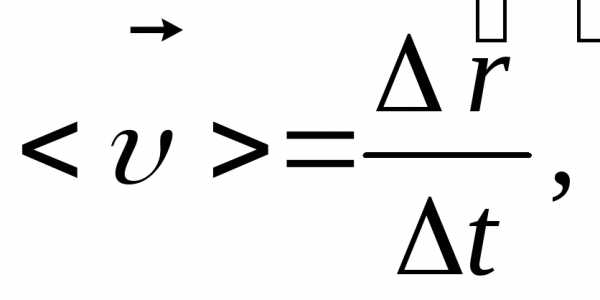
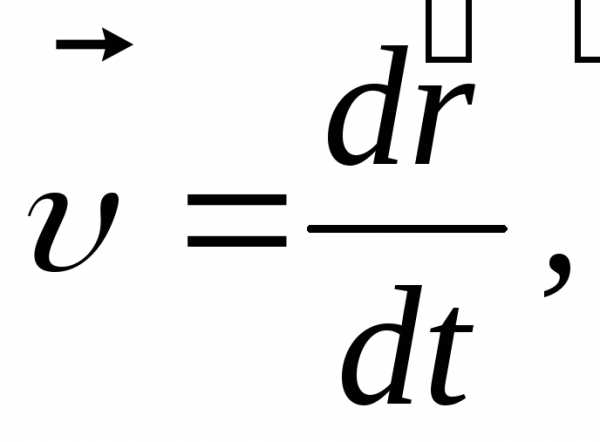
где 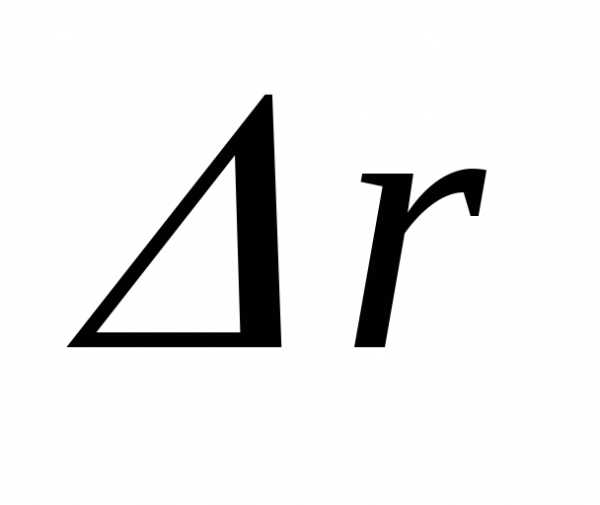 – перемещение точки за время
– перемещение точки за время 
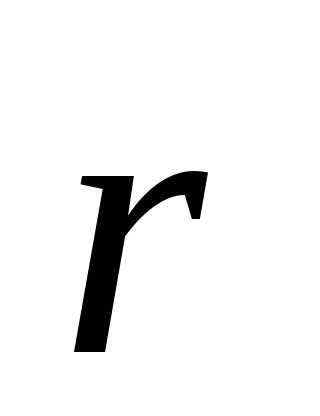 –
радиус-вектор, определяющий положение
точки.
–
радиус-вектор, определяющий положение
точки. 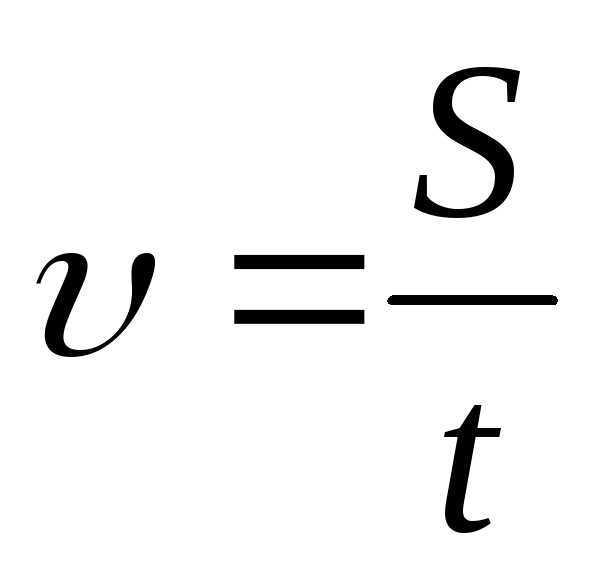 ,
,
где  –
путь, пройденный точкой за время
–
путь, пройденный точкой за время  .
.
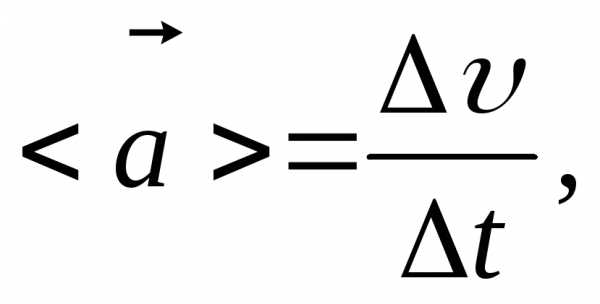
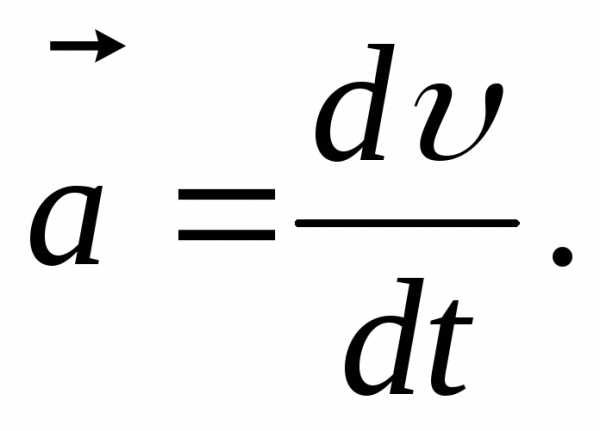
где 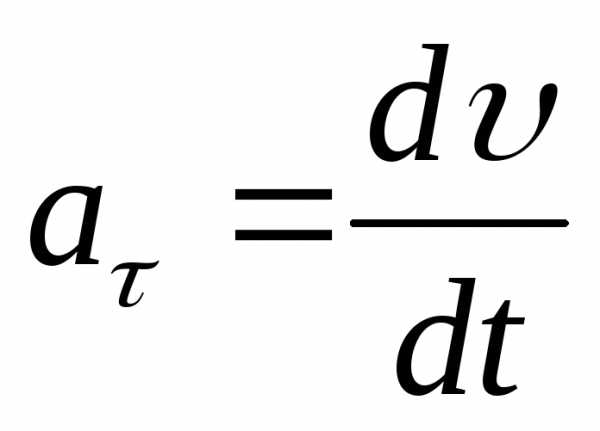 –
тангенциальная составляющая ускорения,
направленная по касательной к траектории;
–
тангенциальная составляющая ускорения,
направленная по касательной к траектории; 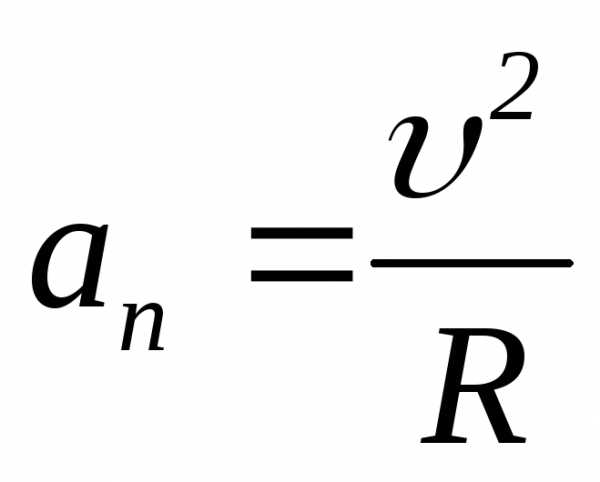 –
нормальная составляющая ускорения,
направленная к центру кривизны траектории
(
–
нормальная составляющая ускорения,
направленная к центру кривизны траектории
(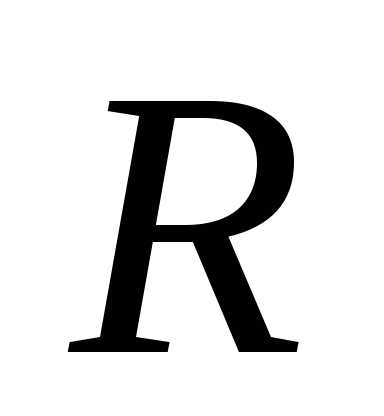 –
радиус кривизны траектории в данной
точке).
–
радиус кривизны траектории в данной
точке).
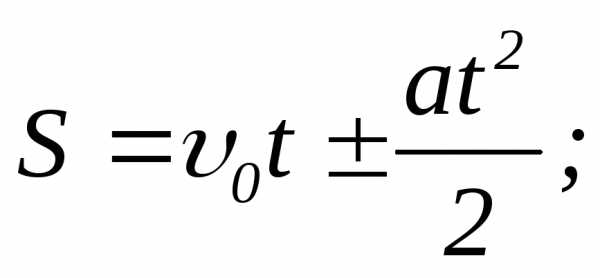
где 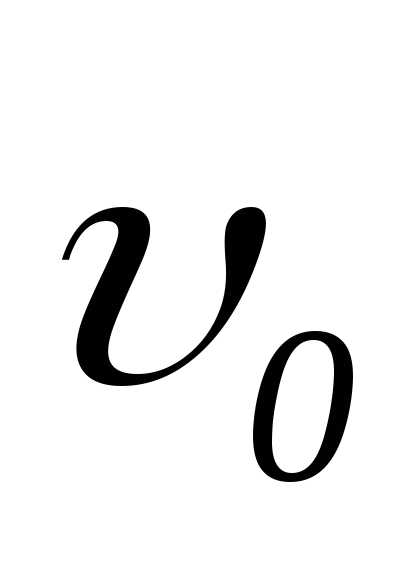 –
начальная скорость, «+» соответствует
равноускоренному движению, «-» –
равнозамедленному.
–
начальная скорость, «+» соответствует
равноускоренному движению, «-» –
равнозамедленному.
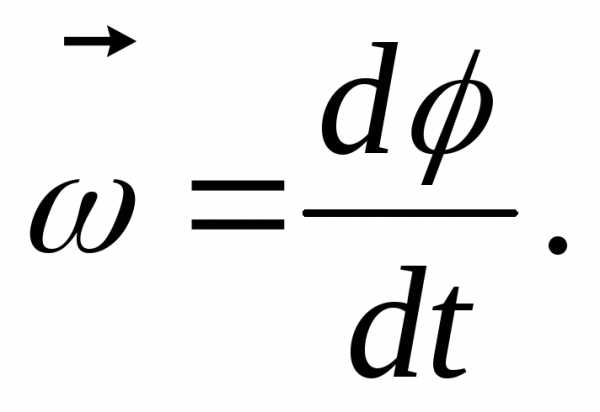
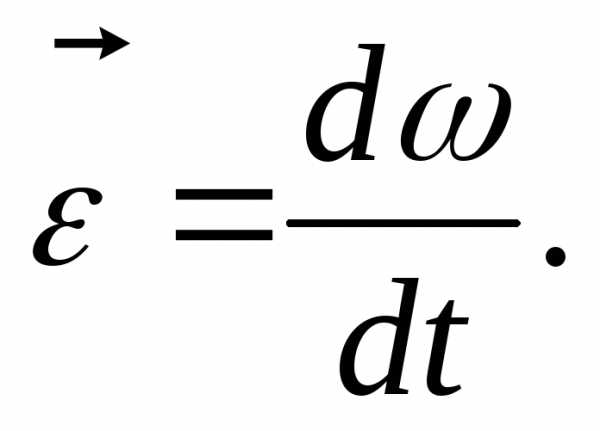
где  –
угол поворота тела,
–
угол поворота тела, 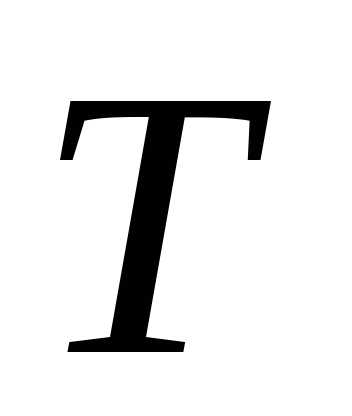 –
период вращения;
–
период вращения; 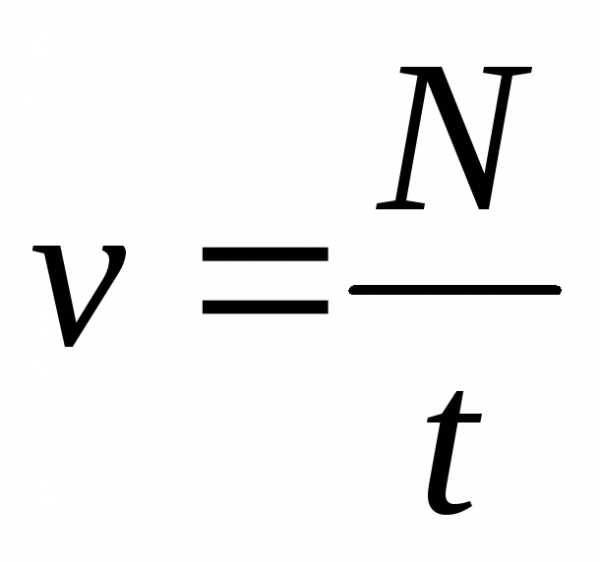 – частота вращения (
– частота вращения (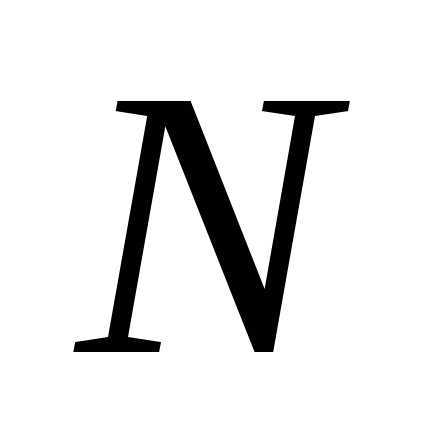 –
число оборотов, совершаемых телом за
время
–
число оборотов, совершаемых телом за
время  ).
).
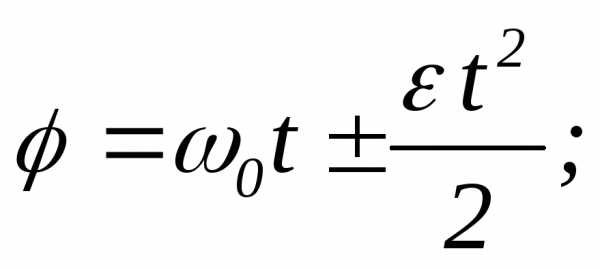
где 
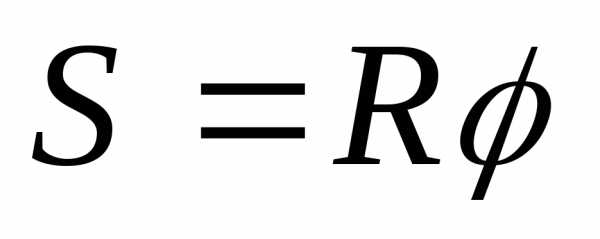 ;
; 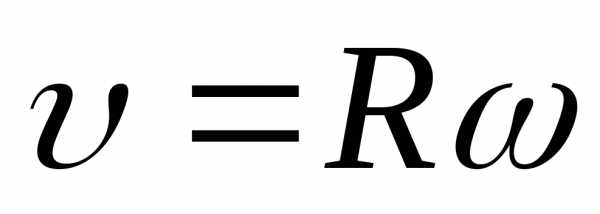 ;
; 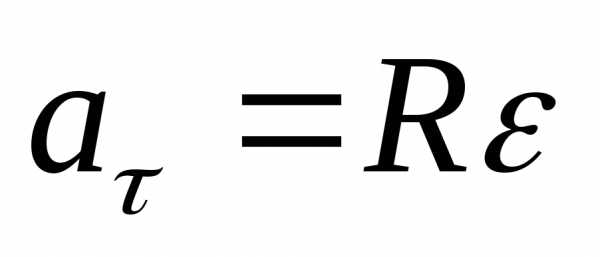 ;
; 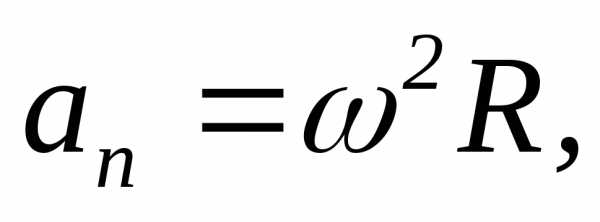
где 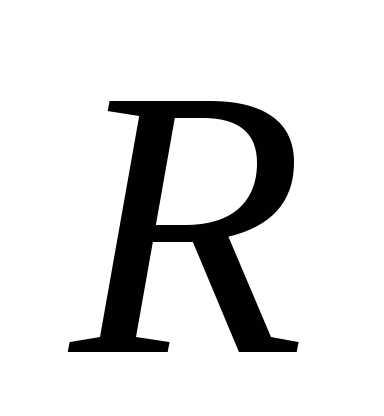 –
расстояние от точки до мгновенной оси
вращения.
–
расстояние от точки до мгновенной оси
вращения.
Примеры решения задач
Задача
1.
Зависимость пройденного телом пути  от времени
от времени  выражается уравнением (
= 2 м/с,
выражается уравнением (
= 2 м/с,  = 3 м/с2,
= 3 м/с2, 
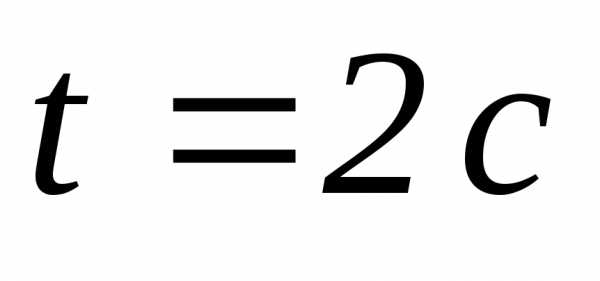 после начала движения пройденный путь,
скорость и ускорение.
после начала движения пройденный путь,
скорость и ускорение.Дано: ;
| Решение: Для определения зависимости скорости движения тела от времени определяем первую производную от пути по времени: , или после подстановки Для определения зависимости ускорения движения тела от времени определяем первую производную от скорости по времени: , или после подстановки . Пройденный путь определяется как разность . |
Ответ: 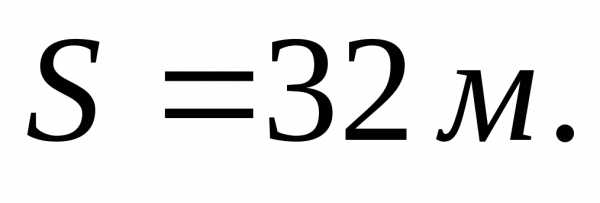
Задача
2. Тело
брошено со скоростью под углом 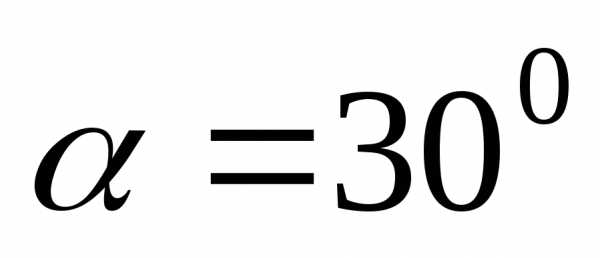 к горизонту. Принимая тело за материальную
точку, определите нормальное
к горизонту. Принимая тело за материальную
точку, определите нормальное 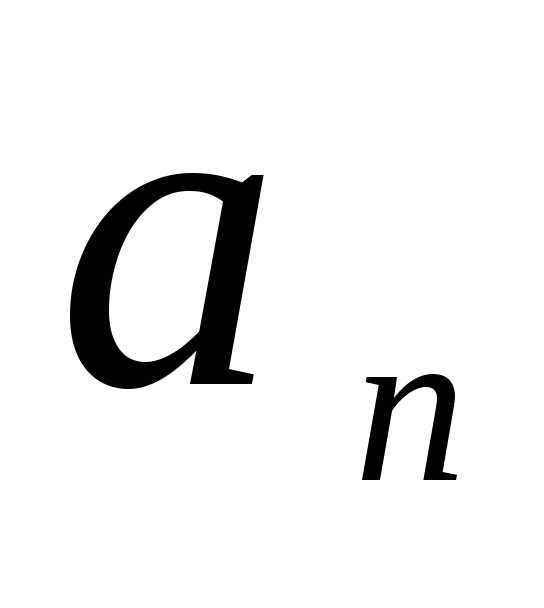 и
тангенциальное
и
тангенциальное 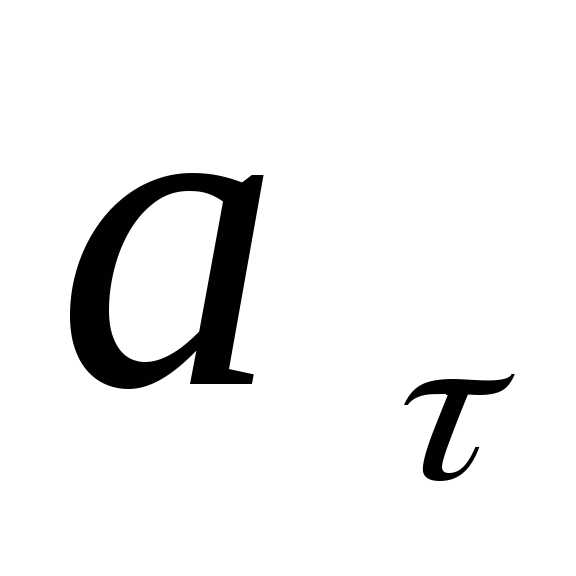 ускорение тела через 1,2 с после начала
движения.
ускорение тела через 1,2 с после начала
движения.
Дано: ;
. | Решение Построим чертеж и определим проекции скорости , . 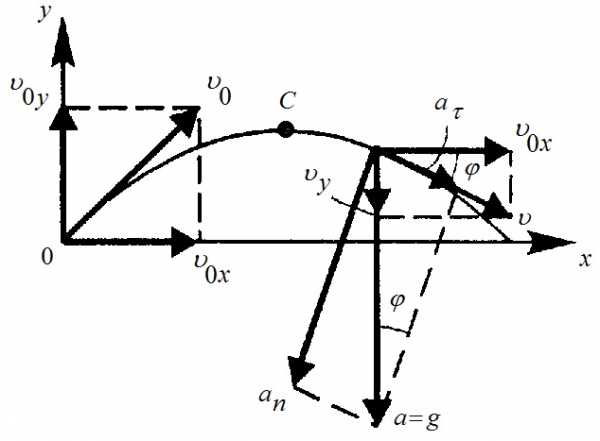 Рис.1.1 |
|
Проекция 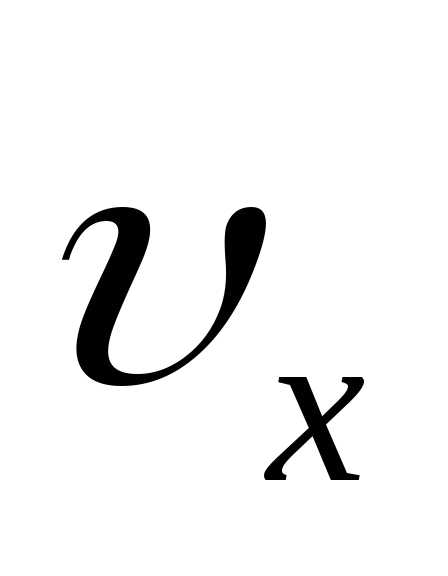
Проекция 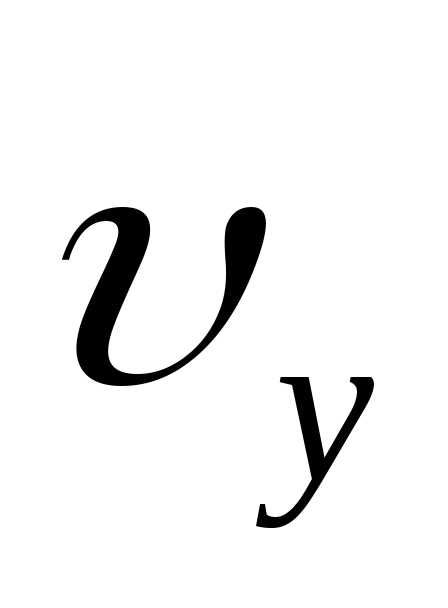 на
ось
на
ось 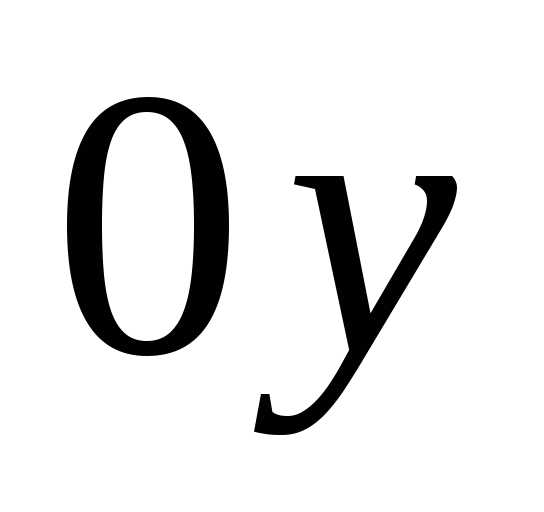 изменяется. В точке С (рис 1.1) скорость
направлена горизонтально, т.е.
изменяется. В точке С (рис 1.1) скорость
направлена горизонтально, т.е. 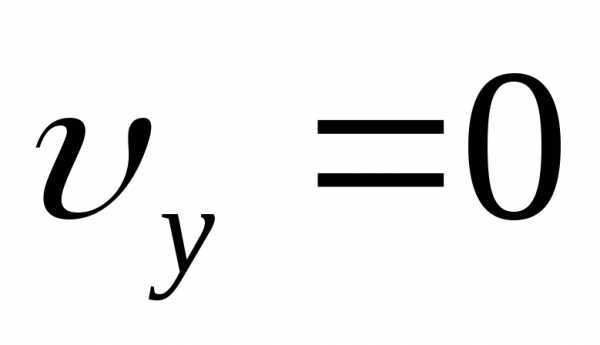 .
Это означает, что
,
где
.
Это означает, что
,
где 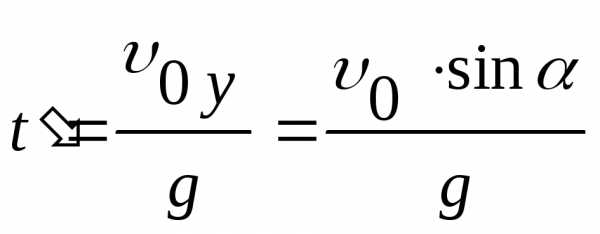 – время, в течение которого материальная
точка поднимается до максимальной
высоты, или после подстановки
– время, в течение которого материальная
точка поднимается до максимальной
высоты, или после подстановки 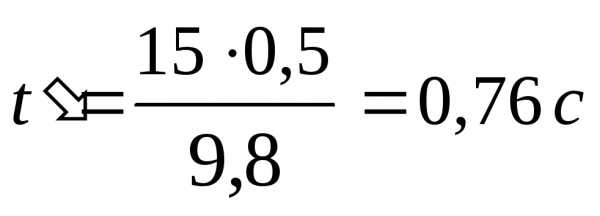 .
.
К
моменту времени 1,2 с тело будет находиться
на спуске. Полное ускорение в процессе
движения направлено вертикально вниз
и равно ускорению свободного падения 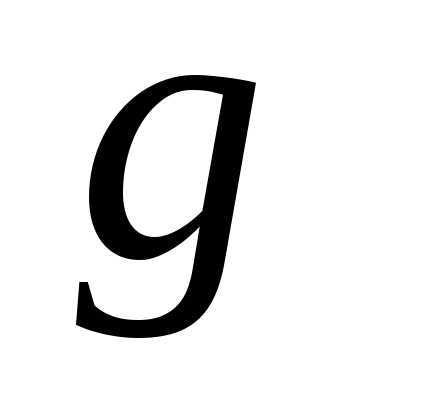 .
Нормальное ускорение равно проекции
ускорения свободного падения на
направление радиуса кривизны, а
тангенциальное ускорение – проекции
ускорения свободного падения на
направление скорости движения (см.
рис.1.1).
.
Нормальное ускорение равно проекции
ускорения свободного падения на
направление радиуса кривизны, а
тангенциальное ускорение – проекции
ускорения свободного падения на
направление скорости движения (см.
рис.1.1).
Из треугольников скоростей и ускорений имеем:
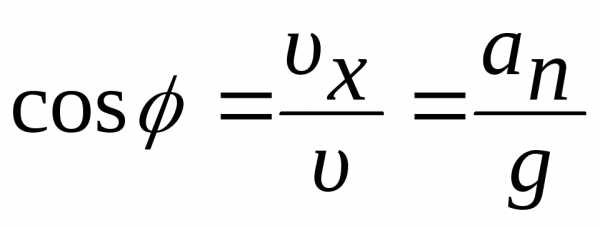 ,
, 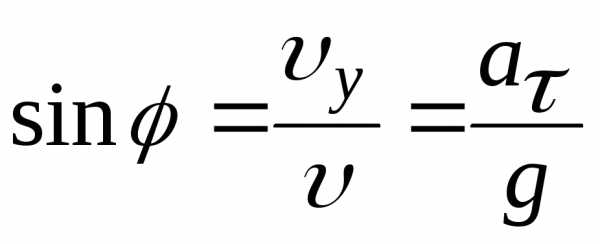 ,
,
откуда 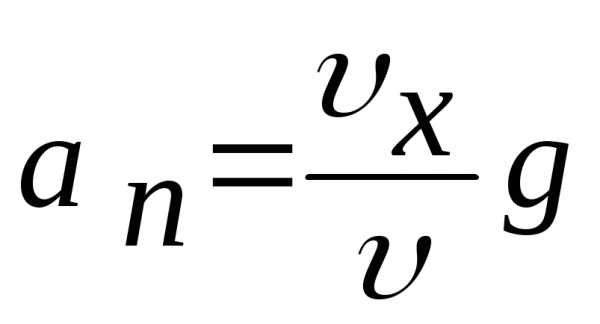 ,
, 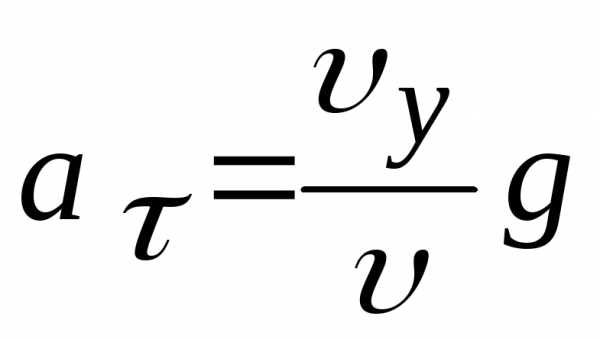 ,
,
где – скорость в момент времени
После подстановки получаем:
.
.
Ответ: ,.
Задача 3. Колесо автомобиля вращается равнозамедленно. За время 2 мин оно изменило частоту вращения от 240 до 60 мин-1. Определите: 1) угловое ускорение колеса; 2) число полных оборотов, сделанных колесом за это время.
Дано:
| Решение: Запишем формулы для угла поворота и угловой скорости при равнозамедленном вращении:
|
(2) |
где 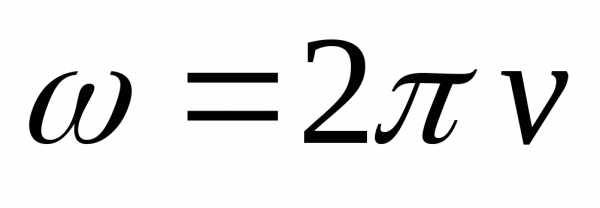 –
угловые скорости в начальный и конечный
моменты времени соответственно.
–
угловые скорости в начальный и конечный
моменты времени соответственно.
Из уравнения (2) получаем:
.
Угол поворота . Поэтому выражение (1) можно записать так: .
Отсюда: .
Ответ: ;  .
.
Задача 4. Точка движется по окружности радиусом так, что зависимость угла поворота радиуса от времени дается уравнением, где,. Определите к концу второй секунды вращения: а) угловую скорость; б) линейную скорость; в) угловое ускорение; г) нормальное ускорение; д) тангенциальное ускорение.
studfiles.net
Координата и перемещение при равномерном движении по прямой x = xo + vxt,Sx = x − xo = vxt, где xo − начальная координата. Закон сложения скоростей (для поступательного движения системы отсчета) где v1 − скорость первого тела (например, относительно земли), v12 − скорость первого тела относительно второго тела (подвижной системы отсчета), v2 − скорость второго тела (относительно земли). Аналогичный вид имеют закон сложения перемещений S1 = S12 + S2 и закон сложения ускорений a1 = a12 + a2. Эту формулу в виде v12 = v1 − v2 называют формулой для относительной скорости двух тел. Средняя скорость при неравномерном движении по прямой Два последовательных этапа с разными скоростями: vcp = (S1 + S2)/(t1 + t2), где S1 = v1t1, S2 = v2t2. Скорость и перемещение при равноускоренном движении по прямой Sx = voxt + axt2/2, где vox − начальная скорость. Связь между скоростями и перемещением: vx2 − vox2 = 2axSx. Средняя скорость при равноускоренном движении: Sx = (vox + vx)t/2. Свободное падение (vo = 0). Скорость и перемещение (ось y направлена вниз, ay = g) Высота в момент времени t h(t) = H − gt2/2, где H − начальная высота. Время падения и конечная скорость: t = √{2H/g}, v = √{2gH}. Бросок вертикально вверх с начальной скоростью vo. Скорость и перемещение (ось y направлена вверх, voy = vo, ay = −g): Sy = vot − gt2/2. Время подъема до высшей точки (где vy = 0) и высота подъема t1 = vo/g, hmax = vo2/(2g). Полное время полета (до возврата в точку броска) t2 = 2t1 = 2vo/g. Горизонтальный бросок со скоростью vo. Проекции скорости и перемещения (ось x направлена горизонтальна, ось y − вертикально вниз): vx = vo, Sx = vot, vy = gt, Sy = gt2/2, (по горизонтали − равномерное движение со скоростью vo, по вертикали − свободное падение). Модули скорости и угол наклона скорости к горизонту: v = √{vx2 + vy2} = √{vo2 + (gt)2} tgβ = vy/vx = gt/vo. Время до падения на землю (начальная высота H) и дальность полета: t = √{2H/g} S = vo√{2H/g}. Бросок под углом к горизонту с начальной скоростью vo. Проекция скорости и перемещения (ось x направлена горизонтально, ось y − вертикально вверх): vy = vosinα − gt, Sy = votsinα − gt2/2, (по горизонтали − равномерное движение со скоростью vocosα, по вертикали − бросок вертикально вверх с начальной скоростью voy = vosinα). Время подъема до высшей точки (vy = 0) и максимальная высота t1 = vosinα/g, hmax = (vosinα)2/(2g). Полное время и дальность полета t2 = 2t1 = 2vosinα/g, S = vxt2 = vo2sin(2α)/g. Равномерное вращение с угловой скоростью ω. Угол поворота (в рад) и число оборотов: φ = ωt, N = φ/(2π) = νt, где ν − частота вращения (ν = ω/(2π)). Период вращения: T = 1/ν = 2π/ω. Связь между угловыми и линейными перемещениями l = φR, v = ωR, где l − длина дуги. Центростремительное ускорение: aц = v2/R = ω2R. Объем и масса (жидкости, газа), проходящие через сечение S струи за время Δt (уравнение расхода): Δm = ρΔV = ρSvΔt, где v − скорость струи, ρ − плотность (жидкости, газа). | |
abpbrf.ucoz.ru
Глава 4. Кинематика твердого тела
Твердым телом будем называть тело, расстояния между точками которого не изменяются в процессе движения.
Если в качестве модели реального объекта рассматривается тело, состоящее из тел-точек, положение которых описывается не только вектором положения, а и ориентацией (т.е. тела-точки могут вращаться), то в определение следует добавить слова « и взаимная ориентация не изменяется».
4.1 Кинематика плоского движения.
Плоским движением называется движение, при котором траектории (а, следовательно, и скорости) всех точек тела лежат в плоскостях, параллельных одной фиксированной плоскости. Таково, например, движение книги по ровному столу. Ясно, что достаточно изучить движение одного лишь сечения – плоской фигуры (одного листа книги).
4.1.1 Основная формула кинематики твердого тела. Формула Эйлера
Положение твердого тела вообще и плоской фигуры в частности описывается вектором положения какой-либо точки А, называемой полюсом, и ориентацией, которую удобно описывать с помощью жестко связанной с телом тройки векторов. Для простоты возьмем ортонормированную тройку векторов, которые в отсчетном положении обозначаются , а в актуальном в момент времени. В качестве отсчетного положения чаще всего удобно взять положение в момент времени, тогда, но иногда в качестве отсчетного удобнее взять положение, которое тело никогда не занимало в прошлом и, возможно, никогда не займет в будущем.
При плоском движении ориентация задается одним углом (t). Введем вектор угловой скорости где единичный векторперпендикулярен плоской фигуре, а его направление согласовано с положительным направлением отсчета угла(t) в соответствии с принятой ориентацией пространства. Так, в правоориентированном пространстве направлен так, что с его с конца положительное направление отсчета угла(t) видно происходящим против часовой стрелки, т.е. « на нас» (рис 4.1). Заметим, что независимо от выбора положительного направления отсчета угла (t) вектор направлен « на нас», если фигура в данный момент времени вращается против часовой стрелки.
Запишем очевидное равенство . (4.1)
Обозначим для краткости и разложимпо актуальному базису :
, где координаты постоянные.
Разложим по отсчетному базисуи продифференцируем по времени:. Нетрудно убедиться, что=. Совершенно аналогично , откуда следует или
(4.2)
Эта формула называется формулой Эйлера и она справедлива не только для плоского, но и для произвольного движения твердого тела.
Дифференцируя (4.1), получим с учетом (4.2) или
(4.3)
Эту формулу будем называть основной формулой кинематики твердого тела.
Слагаемое называют вращательной скоростью точкиB вокруг полюса A.
Направление этого перпендикулярного к слагаемого легко получить, вращая фигуру вокруг полюса А – отсюда и его название.
На рисунке – круговой вектор угловой скорости, которому сопоставляется прямой.
4.1.2 Мгновенный центр скоростей и способы его нахождения.
Из основной формулы кинематики твердого тела (4.3) ясно, что если , то можно найти такую точкуP , скорость которой равна нулю – эта точка и называется мгновенным центром скоростей.
Для определения неизвестного вектора из уравненияумножим его слева векторно наи, раскрывая двойное векторное произведение, будем иметь
, откуда
(4.4)
Формула (4.4) предполагает, разумеется, известными , но во многих случаях мгновенный центр скоростей можно найти другими способами. Наиболее часто встречаются случаи:
1. Тело катится без проскальзывания.
Мгновенный центр скоростей находится в точке касания тела с неподвижной поверхностью.
Следующие случаи следуют из основной формулы, где в качестве полюса выбран мгновенный центр скоростей: ( 4.5)
Отсюда следует, что: a) – скорость всякой точки В перпендикулярна ,
b) – скорость всякой точки В пропорциональна расстоянию до точкиP.
2. Если известна скорость одной точки A и линия, вдоль которой может быть направлена скорость другой точки B, то мгновенный центр скоростей находится на пересечении перпендикуляров к скоростям. В этом случае вычисляется величина угловой скорости , определяется ее направление и, соответственно, скорость точки В (см. рис 4.2).
Если перпендикуляры не пересекаются, то (мгновенно- поступательное движение) и скорости всех точек равны.
Если перпендикуляры слились, то мгновенный центр скоростей находится на пересечении линии, соединяющей концы векторов скорости и общего перпендикуляра.
studfiles.net

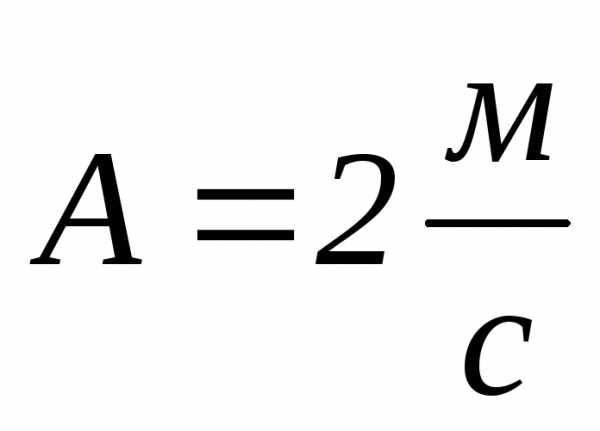 ;
;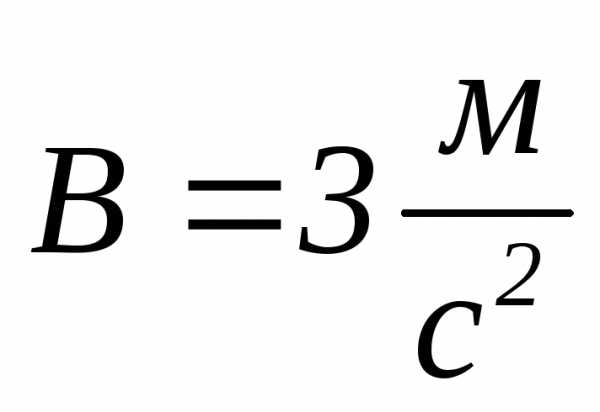 ;
;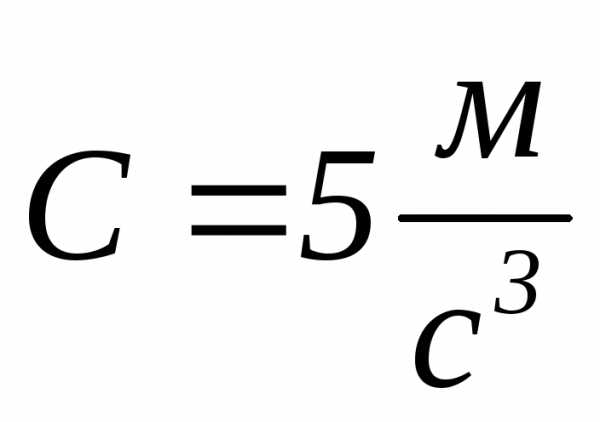 ;
; 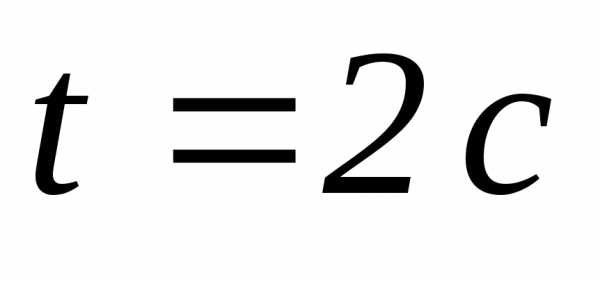 .
.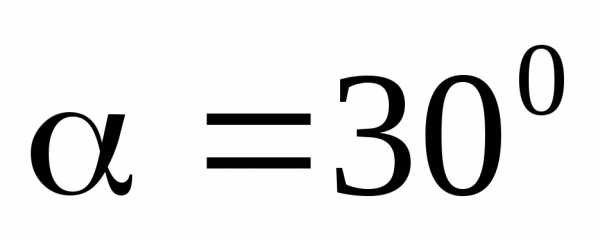 ;
;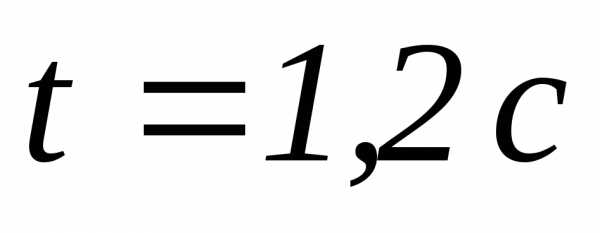 ;
;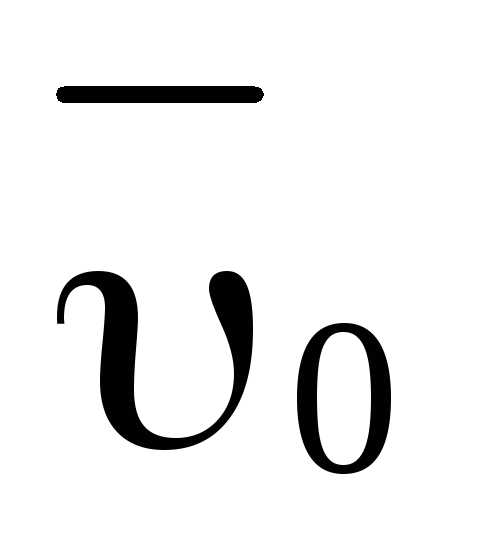 в начальный момент времени:
в начальный момент времени:
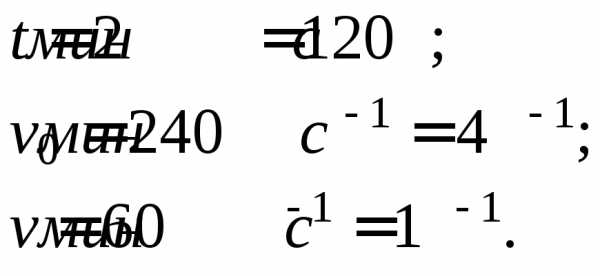
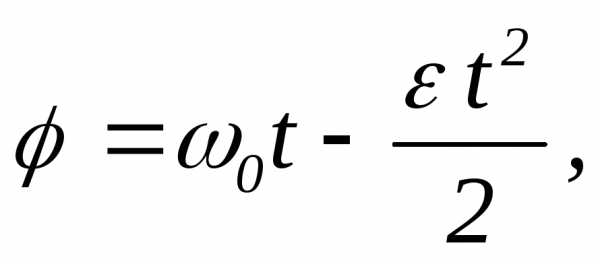 (1)
(1)