M формула физика: Формула массы тела в физике
В классической механике считают:
- масса тела не является зависимой от движения тела, от воздействия других тел, расположения тела;
- выполняется закон сохранения массы: масса замкнутой механической системы тел неизменна во времени.
- Формула массы тела в физике
- Формула массы тела в физике
- Плотность – Физика
- Урок 21. релятивистские эффекты – Физика – 11 класс
- Инвариантная масса • Физика элементарных частиц • LHC на «Элементах»
- Потенциальная энергия: определение, виды, формулы
- Линейный импульс и сила | Физика
- Формула моментума
- Импульс
- Мощность (физика): определение, формула, единицы измерения, как найти (с примерами)
- Gravity
- Что такое формула массы?
- 2.1: Релятивистский импульс, сила и энергия
Инертная масса
Свойство инертности материальной точки состоит в том, что если на точку действует внешняя сила, то у нее возникает конечное по модулю ускорение. Если внешних воздействий нет, то в инерциальной системе отсчета тело находится в состоянии покоя или движется равномерно и прямолинейно. Масса входит во второй закон Ньютона:
$$\bar{F}=m \bar{a}(2)$$где масса определяет инертные свойства материальной точки (инертная масса).
Гравитационная масса
Масса материальной точки входит в закон всемирного тяготения, при этом она определяет гравитационные свойства данной точки.при этом она носит название гравитационной (тяжелой) массы.
Эмпирически получено, что для всех тел отношения инертных масс к гравитационным являются одинаковыми.
Слишком сложно?
Формула массы тела не по зубам? Тебе ответит эксперт через 10 минут!
Пример
Задание. Какова масса 2м3 меди?
Решение. Будем считать, что медь однородна и для решения задачи используем формулу:
$$m=\rho V$$При этом если известно вещество (медь), то можно при помощи справочника найти ее плотность. Плотность меди будем считать равной $\rho$ Cu=8900 кг/м3 . Для расчета все величины известны. Проведем вычисления:
$m=8900 \cdot 2=17800$ (кг)
Ответ. $m=8900 \cdot 2=17800$ (кг)
Читать дальше: Формула момента силы.
Формула массы тела в физике
Содержание:
Определение и формула массы тела
Определение
В механике Ньютона массой тела называют скалярную физическую величину, которая является мерой инерционных его свойств и
источником гравитационного взаимодействия. {n} m_{i}(1)$$
{n} m_{i}(1)$$
В классической механике считают:
- масса тела не является зависимой от движения тела, от воздействия других тел, расположения тела;
- выполняется закон сохранения массы: масса замкнутой механической системы тел неизменна во времени.
Инертная масса
Свойство инертности материальной точки состоит в том, что если на точку действует внешняя сила, то у нее возникает конечное по модулю ускорение. Если внешних воздействий нет, то в инерциальной системе отсчета тело находится в состоянии покоя или движется равномерно и прямолинейно. Масса входит во второй закон Ньютона:
$$\bar{F}=m \bar{a}(2)$$Гравитационная масса
Масса материальной точки входит в закон всемирного тяготения, при этом она определяет гравитационные свойства данной точки.при этом она носит название гравитационной (тяжелой) массы.
Эмпирически получено, что для всех тел отношения инертных масс к гравитационным являются одинаковыми. {2}}}}$$
{2}}}}$$
Слишком сложно?
Формула массы тела не по зубам? Тебе ответит эксперт через 10 минут!
Пример
Задание. Какова масса 2м3 меди?
Решение. Будем считать, что медь однородна и для решения задачи используем формулу:
$$m=\rho V$$При этом если известно вещество (медь), то можно при помощи справочника найти ее плотность. Плотность меди будем считать равной $\rho$ Cu=8900 кг/м3 . Для расчета все величины известны. Проведем вычисления:
$m=8900 \cdot 2=17800$ (кг)
Ответ. $m=8900 \cdot 2=17800$ (кг)
Читать дальше: Формула момента силы.
Формула массы тела в физике
Содержание:
Определение и формула массы тела
Определение
В механике Ньютона массой тела называют скалярную физическую величину, которая является мерой инерционных его свойств и
источником гравитационного взаимодействия. {n} m_{i}(1)$$
{n} m_{i}(1)$$
В классической механике считают:
- масса тела не является зависимой от движения тела, от воздействия других тел, расположения тела;
- выполняется закон сохранения массы: масса замкнутой механической системы тел неизменна во времени.
Инертная масса
Свойство инертности материальной точки состоит в том, что если на точку действует внешняя сила, то у нее возникает конечное по модулю ускорение. Если внешних воздействий нет, то в инерциальной системе отсчета тело находится в состоянии покоя или движется равномерно и прямолинейно. Масса входит во второй закон Ньютона:
где масса определяет инертные свойства материальной точки (инертная масса).
Гравитационная масса
Масса материальной точки входит в закон всемирного тяготения, при этом она определяет гравитационные свойства данной точки.при этом она носит название гравитационной (тяжелой) массы.
Эмпирически получено, что для всех тел отношения инертных масс к гравитационным являются одинаковыми. {2}}}}$$
{2}}}}$$
Слишком сложно?
Формула массы тела не по зубам? Тебе ответит эксперт через 10 минут!
Пример
Задание. Какова масса 2м3 меди?
Решение. Будем считать, что медь однородна и для решения задачи используем формулу:
$$m=\rho V$$При этом если известно вещество (медь), то можно при помощи справочника найти ее плотность. Плотность меди будем считать равной $\rho$ Cu=8900 кг/м3 . Для расчета все величины известны. Проведем вычисления:
$m=8900 \cdot 2=17800$ (кг)
Ответ. $m=8900 \cdot 2=17800$ (кг)
Читать дальше: Формула момента силы.
Плотность – Физика
Для обозначения плотности обычно используется символ (ро).Пло́тность — скалярная физическая величина, определяемая как отношение массы тела к занимаемому этим телом объёму или площади (поверхностная плотность).
Более точное определение плотности требует уточнение формулировки:
- Средняя плотность тела — отношение массы тела к его объёму.
 Для однородного тела она также называется просто плотностью тела.
Для однородного тела она также называется просто плотностью тела. - Плотность вещества — это плотность тел, состоящих из этого вещества.
- Плотность тела в точке — это предел отношения массы малой части тела (), содержащей эту точку, к объёму этой малой части (), когда этот объём стремится к нулю[1], или, записывая кратко, . При таком предельном переходе необходимо помнить, что на атомарном уровне любое тело неоднородно, поэтому необходимо остановиться на объёме, соответствующем используемой физической модели.
Виды плотности и единицы измерения
Исходя из определения плотности, её размерность кг/м³ в системе СИ и в г/см³ в системе СГС.
Для сыпучих и пористых тел различают:
- истинную плотность, определяемую без учёта пустот;
- удельную (кажущуюся) плотность, рассчитываемую как отношение массы вещества ко всему занимаемому им объёму.
Истинную плотность из кажущейся получают с помощью величины коэффициента пористости — доли объёма пустот в занимаемом объёме.
Формула нахождения плотности
Плотность (плотность однородного тела или средняя плотность неоднородного) находится по формуле:
где m — масса тела, V — его объём; формула является просто математической записью определения термина «плотность», данного выше.
- При вычислении плотности газов эта формула может быть записана и в виде:
- где М — молярная масса газа, — молярный объём (при нормальных условиях равен 22,4 л/моль).
Зависимость плотности от температуры
Как правило, при уменьшении температуры плотность увеличивается, хотя встречаются вещества, чья плотность ведёт себя иначе, например, вода, бронза и чугун. Так, плотность воды имеет максимальное значение при 4 °C и уменьшается как с повышением, так и с понижением температуры относительно этого значения.
При изменении агрегатного состояния плотность вещества меняется скачкообразно: плотность растёт при переходе из газообразного состояния в жидкое и при затвердевании жидкости.
 Вода, кремний, германий и некоторые другие вещества являются исключениями из данного правила, так как их плотность при переходе в твердую фазу уменьшается.
Вода, кремний, германий и некоторые другие вещества являются исключениями из данного правила, так как их плотность при переходе в твердую фазу уменьшается.
Урок 21. релятивистские эффекты – Физика – 11 класс
Физика, 11 класс
Урок №21. Релятивистские эффекты
На уроке рассматриваются понятия: энергия покоя, полная энергия частиц; связь массы и энергии в специальной теории относительности; релятивистский импульс частицы, релятивистская кинетическая энергия; принцип соответствия.
Глоссарий урока:
Релятивистская механика – раздел физики, где описывается движение частиц со скоростями близкими к скорости света.
Закон взаимосвязи энергии и массы – тело обладает энергией и при нулевой скорости, такую энергию называют
Релятивистская энергия составляет сумму собственной энергии частицы и релятивистской кинетической энергии.
Безмассовыми называют частицы массы, которых в состоянии покоя равны нулю, они существуют только в движении, при этом во всех инерциальных системах отсчёта их импульс и энергия не равны нулю.
Массовыми называют частицы, для которых масса является важной характеристикой, мерой инертности тела.
Принцип соответствия – это подтверждение законов Ньютона и классических представлений о пространстве и времени, рассматриваются как частный случай релятивистских законов при скоростях намного меньших скорость света.
Согласно принципу соответствия любая теория, претендующая на более глубокое описание явлений и на более широкую сферу применимости, должна включать предыдущую теорию, как предельный случай.
Обязательная литература:
- Мякишев Г.Я., Буховцев Б.Б., Сотский Н.Н. Физика.11 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2017. – С. 239 – 241.
- Рымкевич А.П. Физика. Задачник. 10-11 классы. – М.
 : Дрофа, 2013. — С. 147 – 149
: Дрофа, 2013. — С. 147 – 149
Дополнительная литература:
- Анциферов Л.И., Физика: электродинамика и квантовая физика. 11кл. Учебник для общеобразовательных учреждений – М.: Мнемозина, 2001. – С. 253-260.
- Кирик Л.А., Генденштейн Л.Э., Гельфгат И.М.. Задачи по физике. 10-11 классы для профильной школы. – М.: Илекса, 2010. – С. 311-315.
- Айзексон У., Эйнштейн. Жизнь гения; пер. с анг. А.Ю. Каннуниковой. – М: АСТ, 2016 – С.144-157
Основное содержание темы
«Основы физики претерпели неожиданные и радикальные изменения благодаря смелости молодого и революционно мыслящего гения.»
Вернер Гейзенберг
Эти слова и множество других восхищённых эпитетов будут высказаны в адрес гениального учёного Альберта Эйнштейна. Эйнштейн не боялся опровергать общепринятые утверждения. Он разрушил представление об абсолютном времени и незыблемости пространства. Его теория утверждала, что есть движущиеся системы координат со своим относительным временем. А пространство существует, пока в нём существует всё материальное. Время идёт тем медленнее, если быстрее движется тело. Такие удобные и понятные принципы классической физики: о постоянстве массы, длины, времени, скорости – опровергаются следствиями из постулатов специальной теории относительности Эйнштейна.
А пространство существует, пока в нём существует всё материальное. Время идёт тем медленнее, если быстрее движется тело. Такие удобные и понятные принципы классической физики: о постоянстве массы, длины, времени, скорости – опровергаются следствиями из постулатов специальной теории относительности Эйнштейна.
Альберт (Einstein) Эйнштейн
14 марта 1879 г. – 18 апреля 1955 г.
Физик-теоретик, один из основателей современной теоретической физики, лауреат Нобелевской премии по физике 1921 года, общественный деятель-гуманист.
По законам классической физики: масса – это мера инертности тела. Но Эйнштейн утверждает другое: масса – это мера энергии, содержащейся в теле.
Любое тело обладает энергией уже в силу своего существования. Альбертом Эйнштейном была установлена пропорциональность между энергией и массой:
На первый взгляд, простая формула, является фундаментальным законом природы, законом взаимосвязи энергии и массы.
Согласно этой формуле тело обладает энергией даже при нулевой скорости, в таком случае энергию называют E энергией покоя. А массу, которая входит в формулу Эйнштейна назовём m0 массой покоя.
А массу, которая входит в формулу Эйнштейна назовём m0 массой покоя.
Как же будет выглядеть закон взаимосвязи массы и энергии для движущегося тела? К нему добавляем радикал (релятивистский множитель) из преобразований Лоренца:
Такую формулу называют
Релятивистская механика – раздел физики, где описываются движения тел и частиц со скоростями близкими к скорости света, где используются преобразования Лоренца, перехода из одной инерциальной системы в другую, когда одна система движется относительно другой со скоростью вдоль оси ОХ.
Любые изменения физических величин, связанные с сокращением размеров:
эффект замедления времени:
изменение массы тела при изменении энергии:
закон сложения скоростей:
в специальной теории относительности называют релятивистскими изменениями.
По законам классической физики полная энергия равна сумме кинетической и потенциальной энергий тела или частицы
Отсюда выразим кинетическую энергию тела
Релятивистская энергия составляет сумму собственной энергии частицы и релятивистской кинетической энергии
В классической физике кинетическая энергия вычисляется по формуле
Получим ещё одно выражение
Выразим кинетическую энергию из формулы релятивистской энергии:
Поставим релятивистский радикал, который можно преобразовать при малых скоростях и получим релятивистскую кинетическую энергию частицы:
Или другой способ выражения кинетической энергии, если использовать классическую кинетическую энергию, то получим
– выражение для определения релятивистской кинетической энергии.
Путём не сложных математических вычислений можно доказать, что формула определения кинетической энергии в классической физикеи формула кинетической энергии в релятивистской физике равны между собой.
Давайте проверим работают ли главные законы механики – законы Ньютона в релятивистской физике.
Первый закон Ньютона: существуют системы отсчёта, называемые инерциальными, относительно которых тело движется прямолинейно и равномерно, если на него не действуют другие тела.
Первый постулат СТО Эйнштейна: все физические явления протекают одинаково во всех инерциальных системах отсчёта, или никакими опытами, проводимыми в инерциальной системе отсчёта, невозможно установить её движение относительно других инерциальных систем.
Внимание! Они не противоречат друг другу!
Третий закон Ньютона: силы с которыми тела действуют друг на друга равны по модулю и направлены вдоль одной прямой в противоположные стороны. Этот закон тоже работает в релятивистской физике (смотрите первый постулат СТО).
А что же со вторым законом классической механики? Второй закон Ньютона: ускорение тела прямо пропорционально силе и обратно пропорционально его массе.
Рассмотрим предельный случай: если на тело долгое время t (время стремится к бесконечности) действовать с постоянной силой F = const, то ускорение будет постоянным a = const. Ускорение в свою очередь, зависит от скорости, с которой движется тело:
Отсюда скорость тоже будет стремиться к бесконечности, а это невозможно (смотрите второй постулат СТО), так как скорость тела или частицы не может быть больше предельного значения скорости света ()!
Но давайте рассмотрим другую формулировку второго закона Ньютона, когда сила прямо пропорциональна изменению импульсов тела ко времени этого изменения:
В классической механике импульс равен произведению массы тела или частицы на его скорость: , где m – постоянная величина, мера инертности тела.
В релятивистской механике выражение импульса можно записать, используя преобразования Лоренца:
При скоростях намного меньших, чем скорость света 𝟅с, формула принимает вид классической механики Ньютона
Эти проявления – подтверждение законов Ньютона и классических представлений о пространстве и времени, рассматривают как частный случай релятивистских законов при скоростях намного меньших скорости света и называют принципом соответствия. Согласно принципу соответствия любая теория, претендующая на более глубокое описание явлений и на более широкую сферу применимости, должна включать предыдущую теорию, как предельный случай. То есть законы классической механики подтверждаются релятивистской, но только для частиц или тел, движущихся с малыми скоростями.
Согласно принципу соответствия любая теория, претендующая на более глубокое описание явлений и на более широкую сферу применимости, должна включать предыдущую теорию, как предельный случай. То есть законы классической механики подтверждаются релятивистской, но только для частиц или тел, движущихся с малыми скоростями.
В природе существуют такие частицы (фотоны, мюоны, нейтрино), скорость которых равна или близка к скорости света. Массы таких частиц в состоянии покоя равны нулю, эти частицы называют безмассовыми. Они существуют только в движении, но во всех инерциальных системах отсчёта их импульс и энергия не равны нулю. Тогда подтверждается утверждение Эйнштейна, что масса – это мера энергии тела. Частицы, для которых масса является важной характеристикой – мерой инертности, называют массовыми.
Найдём соотношение между энергией и импульсом:
Взаимно уничтожаются подкоренные выражения, сокращается произведение массы на скорость света, и мы получим простое соотношение энергии и импульса, где нет зависимости от массы.
Энергия и импульс связаны соотношением
Поэтому во всех инерциальных системах отсчёта импульс и энергия не равны нулю. При превращениях элементарных частиц, обладающих массой покоя , в частицы у которых , их энергия покоя целиком превращается в кинетическую энергию вновь образовавшихся частиц. Этот факт является наиболее очевидным экспериментальным доказательством существования энергии покоя.
Во всех инерциальных системах отсчёта импульс частицы и её энергия связаны соотношением:
или
– эта формула является фундаментальным соотношением энергии и импульса для массовых частиц релятивистской механики. Эти соотношения экспериментально подтверждены.
Следовательно, для безмассовых частиц, где или , выражение примет вид
Основное выражение энергии через её импульс записывают так:
Отсюда, масса, движущейся частицы, будет равна
Если частица покоится, то её значение можно определить из основной формулы Эйнштейна взаимосвязи массы и энергии:
В обычных условиях, при нагревании тела или его охлаждении, при химической реакции, эти приращения массы происходят, их можно вычислить, но изменения массы не так заметны. Энергию, полученную из расщепления ядер на атомных электростанциях, используют на благо человека, где незначительные массы радиоактивного топлива вырабатывают энергию, питающую электроэнергией огромные города. Но, к сожалению, такую энергию, высвобождающуюся при цепной реакции, люди использовали и военных целях, для уничтожения городов, людей. Поэтому, только в последствии, понимая ответственность за свои открытия, учёные искренне становятся общественными деятелями: правозащитниками и борцами за мир.
Энергию, полученную из расщепления ядер на атомных электростанциях, используют на благо человека, где незначительные массы радиоактивного топлива вырабатывают энергию, питающую электроэнергией огромные города. Но, к сожалению, такую энергию, высвобождающуюся при цепной реакции, люди использовали и военных целях, для уничтожения городов, людей. Поэтому, только в последствии, понимая ответственность за свои открытия, учёные искренне становятся общественными деятелями: правозащитниками и борцами за мир.
Рассмотрим задачи тренировочного блока урока:
1. Чтобы выработать количество энергии, которой обладает тело массой 1 кг, Красноярской ГЭС потребуется времени _________ суток (1,5·107; 173,6; 182,3). Мощность Красноярской ГЭС 6000МВт.
Дано:
m = 1 кг
P = 6000 МВт = 6·109 Вт
t – ? (сутки)
Воспользуемся выражением, описывающим зависимость энергии тела от массы:
И зависимостью мощности от работы и времени:
Выразим секунды в часах, а затем в сутках:
Ответ: 173,6 суток.
2. Чему равен импульс протона, летящего со скоростью 8,3·107 м/с? На сколько будет допущена ошибка, если пользоваться формулами классической физики? Данные поученных вычислений занесите в таблицу:
Физические величины | Показатели |
Масса покоя протона, m | 1,67·10-27 кг |
Скорость света, с | 3·108 м/с |
Скорость движения протона, 𝟅 | 8,3·107 м/с |
Импульс протона по классическим законам, рк | ? |
Импульс протона по релятивистским законам, рр | ? |
Разница в вычислениях импульса протона, | ? |
Воспользуемся формулами для определения импульса релятивистским и классическим способами:
Вычислим разницу показаний:
Физические величины | Показатели |
Масса покоя протона, m | 1,67·10-27кг |
Скорость света, с | 3·108 м/с |
Скорость движения протона, 𝟅 | 8,3·107 м/с |
Импульс протона по классическим законам, рк | 1,38·10-19кг·м/с |
Импульс протона по релятивистским законам, рр | 5,2·10-19 кг·м/с |
Разница в вычислениях импульса протона, | в 3,8 раза |
Инвариантная масса • Физика элементарных частиц • LHC на «Элементах»
Инвариантная масса — исключительно важная характеристика коллектива частиц, описывающая их разлет относительно друг друга.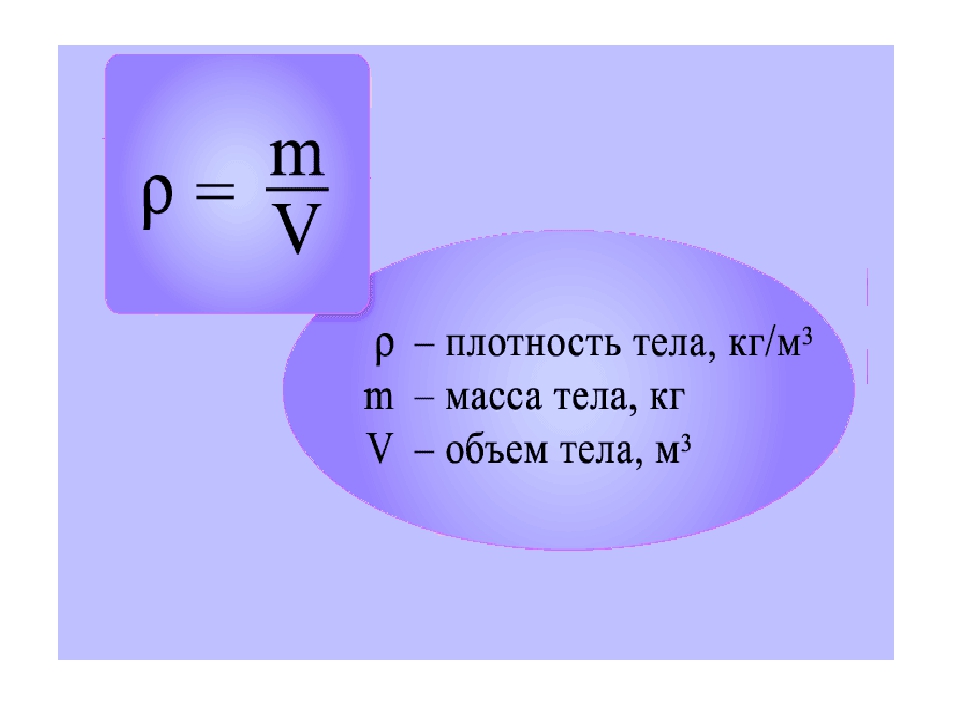 Без измерения и обсуждения инвариантной массы не обходится практически никакой анализ современных коллайдерных данных. Однако прежде, чем рассказывать об инвариантной массе, начнем с одного недоразумения, касающегося понятия массы.
Без измерения и обсуждения инвариантной массы не обходится практически никакой анализ современных коллайдерных данных. Однако прежде, чем рассказывать об инвариантной массе, начнем с одного недоразумения, касающегося понятия массы.
Масса не растет со скоростью!
Есть широко распространенное убеждение, что масса растет со скоростью; ее часто называют «релятивистской массой». Это убеждение основано на неправильной интерпретации связи между энергией и массой: мол, раз с увеличением скорости растет энергия, значит растет и масса. Это утверждение встречается не только во многих популярных книжках, но и в школьных и даже в вузовских учебниках физики.
Это утверждение неверно (для пущей педантичности см. приписку ниже мелким шрифтом). Масса — в том виде, в котором это слово понимает современная физика, и в особенности физика элементарных частиц, — от скорости не зависит. От скорости зависит энергия частицы и ее импульс, при околосветовых скоростях меняются законы динамики и кинематики. Но масса частицы — величина, которая связана с полной энергией E и импульсом p формулой
Но масса частицы — величина, которая связана с полной энергией E и импульсом p формулой
m2 = E2/c4 – p2/c2,
остается неизменной. В популярных материалах эту величину называют «массой покоя» и противопоставляют ее «релятивистской массе», но подчеркнем еще раз: это разделение проводится только в популярных материалах и в некоторых курсах физики. В современной физике нет никакой «релятивистской массы», в ней есть только «масса», определенная этим уравнением. Термин «релятивистская масса» — это неудачный прием популяризации физики, давным-давно уже от настоящей физики оторвавшийся.
Для читателя, который уже наслышан об этой проблеме, а может быть, даже поучаствовал в спорах по поводу нее, такая точка зрения может показаться несколько «экстремистской». Ведь формально мы можем ввести понятие релятивистской массы и переписать все уравнения с помощью нее, а не настоящей массы, и никакой математической ошибки мы при этом не совершим.
Так почему же «релятивистскую массу» лишают права на существование?
Дело в том, что этот термин бесплоден с научной точки зрения и вреден с педагогической. Во-первых, опыт показывает, что он вовсе не упрощает понимание теории относительности (если под пониманием подразумевать что-то большее, чем просто знание нескольких слов). Во-вторых, он сбивает с толку «житейскую интуицию» непосвященного читателя и часто приводит его к ошибочным умозаключениям (например, о том, что тело, движущееся со скоростью, достаточно близкой к скорости света, неизбежно превратится в черную дыру из-за «возросшей массы»). Этот термин подспудно настраивает интуицию читателя на принятие выводов о том, что с частицей могут происходить изменения, зависящие от системы отсчета. И наконец, — повторим снова! — «релятивистская масса» не соответствует ни одной реальной характеристике частицы, которые знает современная физика; это исключительно прием популяризации физики.
Поэтому с образовательной точки зрения намного полезнее вообще не вводить этот термин.
Подробнее про происхождение и вред этого заблуждения см. в многочисленных публикациях выдающегося физика Льва Борисовича Окуня, например в заметке «Релятивистская» кружка.
Инвариантная масса
Пусть у нас есть две частицы с энергиями E1 и E2 и импульсами p1 и p2 (жирный шрифт указывает на то, что импульс — вектор). Это могут быть две сталкивающиеся или две разлетающиеся частицы, неважно. Их массы, разумеется, вычисляются по энергиям и импульсам в соответствии с приведенной выше формулой.
Мы хотим теперь что-то узнать о свойстве этой пары частиц как единой системы. Мы можем написать полную энергию E12 и полный импульс p12 этой системы, E12 = E1 + E2, p12 = p1 + p2, при этом импульсы суммируются как вектора. А значит, мы можем вычислить и некую похожую на массу величину m12 по формуле
m122 = E122/c4 – p122/c2.
Эта величина m12 и называется инвариантной массой пары частиц. Ее важнейшее свойство состоит как раз в том, что она инвариантна, то есть не зависит от системы отсчета, в которой мы проводим вычисление (хотя энергии и импульсы зависят).
Обратим внимание, что инвариантная масса вовсе не равна сумме масс двух частиц! Более того, несложно доказать, что m12 ≥ m1 + m2, причем равенство возможно только тогда, когда две частицы движутся с одинаковыми скоростями (то есть первая частица покоится с точки зрения второй). Итак, для пары частиц у нас имеются три независимых характеристики, не зависящие от системы отсчета: m1, m2 и m12.
Если мы изучаем не две частицы, а больше, то инвариантные массы по этим правилам можно сосчитать не только для всей системы целиком, но и для любой пары, тройки и вообще любой комбинации этих частиц. Заметьте, что сосчитав эти массы, мы еще ничего не утверждаем про сами частицы, про их происхождение, про то, в каких «отношениях» они состоят друг с другом. Это просто дополнительные кинематические величины, которые не зависят от системы отсчета.
Инвариантная масса как «метка» происхождения частиц
Инвариантная масса характеризует, насколько бурно частицы разлетаются друг от друга, насколько интенсивен этот разлет (или их столкновение, если речь идет о сталкивающихся частицах). Говоря совсем упрощенно, если разлет частиц представить себе как «микровзрыв» коллектива частиц, то инвариантная масса характеризует «энергетический баланс» этого микровзрыва. Для примера на рис. 1 показаны две ситуации, в которых энергии двух частиц E1 и E2 и модули их импульсов |p1| и |p2| одни и те же, но инвариантные массы разные.
Главная польза от инвариантной массы в том, что она помогает узнать происхождение этих частиц: получились ли они от распада какой-то одной промежуточной нестабильной частицы или же родились в разных процессах. В первом случае их инвариантная масса примерно совпадает с массой этой нестабильной частицы, а во втором случае она может быть произвольной. Этот прием сплошь и рядом используется при анализе результатов столкновений элементарных частиц; именно с помощью него мы узнаем о быстротечном существовании нестабильных частиц и умеем отделять разные типы событий друг от друга.
Возьмем ставший уже знаменитым пример: поиск хиггсовского бозона на Большом адронном коллайдере через его распад на два фотона. Если хиггсовский бозон рождается в столкновении, он может распасться на два фотона (рис. 2, слева). Но такая же пара фотонов может получиться и сама по себе, безо всяких промежуточных частиц, просто за счет излучения фотонов кварками (рис. 2, справа). Детектор в обоих случаях увидит пару фотонов и не сможет сказать, за счет чего они появились. Просто детектируя фотоны, мы не сможем доказать, что у нас действительно иногда происходит рождение и распад бозона Хиггса.
На помощь приходит изучение инвариантной массы двух фотонов mγγ. В каждом конкретном событии с двумя фотонами надо вычислить эту инвариантную массу, а затем подсчитать, сколько событий с какой инвариантной массой у нас получилось, и построить график: количество событий в зависимости от mγγ. Если хиггсовского бозона в данных нет (или пока не видно), эта зависимость будет плавной — ведь энергии и импульсы двух фотонов не связаны, поэтому инвариантная масса может получиться какой угодно. Если же хиггсовский бозон есть, на графике должен проступить бугорок. Этот бугорок — это те дополнительные события, которые получились именно за счет рождения бозона Хиггса и его распада на два фотона. Положение бугорка укажет на массу бозона, а его высота — на интенсивность этого процесса.
На рис. 3 показаны данные детектора ATLAS по результатам 2011-го и 2012 года в области инвариантной массы двух фотонов от 100 до 160 ГэВ. Виден более-менее плавный фон, уменьшающийся с ростом mγγ и вызванный как раз независимым рождением двух фотонов. И на этом фоне хорошо заметен нужный бугорок в районе 125 ГэВ. Он не слишком сильный, но благодаря маленьким погрешностям у него большая статистическая значимость, а значит, существование новой частицы, распадающейся на два фотона, можно считать экспериментально доказанным.
Дополнительная литература:
Потенциальная энергия: определение, виды, формулы
Определение потенциальной энергии
Энергия, говоря простым языком, это возможность что-либо сделать, возможность совершить работу. То есть, если какое-либо тело может совершить какую-либо работу, то про это тело можно сказать, что оно обладает энергией. По сути, энергия — это мера различных форм движения и взаимодействия материи, а её изменение происходит при совершении некоторой работы. Таким образом, совершённая работа всегда равна изменению какой-либо энергии. А значит, рассматривая вопрос о совершённой телом работе, мы неизбежно приходим к изменению какого-либо вида энергии. Вспомним также и тот факт, что работа совершается только в том случае, когда тело под действием некоторой силы движется, и при этом сама работа определяется как скалярное произведение вектора этой силы и вектора перемещения, то есть А = F*s*cosa, где а — угол между вектором силы и вектором перемещения. Это нам пригодится в дальнейшем для вывода формул различных видов энергии.
Энергию, связанную с взаимодействием тел, называют ПОТЕНЦИАЛЬНОЙ ЭНЕРГИЕЙ. Иначе говоря, если тело за счёт взаимодействия с другим телом может совершить некоторую работу, то оно будет обладать потенциальной энергией, и при совершении работы будет происходить изменение этой энергии. Обозначают механическую потенциальную энергию чаще всего — Еп.
Виды потенциальной энергии
Существуют различные виды потенциальной энергии. К примеру, любое тело на Земле находится в гравитационном взаимодействии с Землёй, а значит обладает потенциальной энергией гравитационного взаимодействия. И ещё пример — витки растянутой или сжатой пружины находятся в упругом взаимодействии друг с другом, а значит сжатая или растянутая пружина будет обладать потенциальной энергией упругого взаимодействия.
Далее мы рассмотрим только виды механической потенциальной энергии и формулы, по которым их можно рассчитать. Но в дальнейшем вы узнаете и о других видах потенциальной энергии — к примеру, о потенциальной энергии электрического взаимодействия заряженных тел, о потенциальной энергии взаимодействия электрона с атомным ядром.
Знакомьтесь: наш мир. Физика всего на свете.
Книга адресована школьникам старших классов, студентам, преподавателям и учителям физики, а также всем тем, кто хочет понять, что происходит в мире вокруг нас, и воспитать в себе научный взгляд на все многообразие явлений природы. Каждый раздел книги представляет собой, по сути, набор физических задач, решая которые читатель укрепит свое понимание физических законов и научится применять их в практически интересных случаях.
КупитьФормулы потенциальной энергии
Перед тем как приступить к выводу формул потенциальной энергии, ещё раз вспомним, что совершённая телом или над телом работа равна изменению его энергии. При этом, если само тело совершает работу, то его энергия уменьшается, а если над телом совершают работу, то его энергия увеличивается. К примеру, если спортсмен поднимает штангу, то он сообщает ей потенциальную энергию гравитационного взаимодействия, а если он отпускает штангу и она падает, то потенциальная энергия гравитационного взаимодействия штанги с Землёй уменьшается. Также, если вы открываете дверь, растягивая пружину, то вы сообщаете пружине потенциальную энергию упругого взаимодействия, но если потом дверь закрывается, благодаря сжатию пружины в начальное состояние, то и энергия упругой деформации пружины уменьшается до нуля.
А) Чтобы вывести формулу потенциальной энергии гравитационного взаимодействия, рассмотрим, какую работу совершает тело, двигаясь под действием силы тяжести:
А = F*s = mg*s = mg*(h1 — h2) = mgh1 — mgh2 = Eп1 — Еп2, то есть, мы получили, что потенциальная энергия гравитационного взаимодействия тела с Землёй может быть вычислена по формуле: Еп = mgh.
Здесь важно отметить, что поверхность Земли принимается за начало отсчёта высоты, то есть для тела, находящегося на поверхности Земли Еп = 0, для тела, поднятого над Землёй Еп > 0, а для тела, находящегося в яме глубиной h, Еп < 0.
Отметим также и то, что в формуле работы отсутсвовал cosa. Это не случайно. Ведь если тело движется по сложной траектории, то, какой бы сложной она ни была, её можно разбить на множество вертикальных и горизонтальных участков. Но на горизонтальных участках работа силы тяжести будет равна нулю, так как угол между силой тяжести и перемещением будет прямым, а значит работа будет совершаться только на вертикальных участках траектории, для которых cosa = 1 или cosa = −1.
Тогда можно сделать ещё один важный вывод — работа силы тяжести не зависит от формы траектории, а только от расположения начальной и конечной точки. А это не случайность — это свойство любых сил, сообщающих телам потенциальную энергию. Такие силы называют потенциальными и сила тяжести — одна из них. К потенциальным силам относится и сила упругости.
Б) Чтобы вывести формулу потенциальной энергии упругой деформации, рассмотрим, какую работу нужно совершить, чтобы растянуть пружину, изменив её длину на х (х = l — l0):
А = –Fупр(ср.)*s,
Во-первых, знак минус в формуле стоит потому, что угол между силой упругости и перемещением свободного конца пружины равен 180 градусов и cosa = −1.
Во-вторых, возникающая при растяжении пружины сила упругости является переменной силой, в отличие от силы тяжести, поэтому в формуле работы стоит средняя сила упругости. При этом величина силы упругости, в соответствии с законом Гука, прямо пропорциональна изменению длины пружины, а значит её среднее значение можно определить так:
Fупр(ср.) = (Fупр(нач.) + Fупр(конеч.))/2
И так как Fупр(нач.) = 0, а Fупр(конеч.) = kх, то:
А = —kх*s/2
Но s = x, поэтому: А = —kx2/2 = 0 — kх2/2 = Еп1 — Еп2.
В итоге, мы получили формулу потенциальной энергии упругой деформации: Еп = kx2/2.
Что еще почитать?
Методические советы учителям
1) Обязательно обратите внимание учащихся на связь энергии и работы.
2) Не давайте учащимся формулы потенциальной энергии без вывода.
3) Обратите внимание учащихся на то, что оба вида потенциальной энергии зависят от выбора начальной точки, то есть от системы координат.
4) При выводе формул потенциальной энергии обязательно поясните учащимся почему отсутствует cosa в формуле работы.
5) Отметьте, что и работа силы тяжести, и работа силы упругости не зависят от формы траектории и, следовательно равны нулю на замкнутой траектории — это общее и важное свойство всех потенциальных сил.
#ADVERTISING_INSERT#Линейный импульс и сила | Физика
Цели обучения
К концу этого раздела вы сможете:
- Определите количество движения.
- Объясните взаимосвязь между импульсом и силой.
- Укажите второй закон движения Ньютона с точки зрения количества движения.
- Вычислить импульс с учетом массы и скорости.
Линейный импульс
Научное определение количества движения согласуется с интуитивным пониманием количества движения большинства людей: большой, быстро движущийся объект имеет больший импульс, чем меньший и более медленный объект. Линейный импульс определяется как произведение массы системы на ее скорость. В символах линейный импульс выражается как p = м v .
Импульс прямо пропорционален массе объекта, а также его скорости. Таким образом, чем больше масса объекта или чем больше его скорость, тем больше его импульс. Импульс p – это вектор, имеющий то же направление, что и скорость v . Единица измерения количества движения в системе СИ – кг · м / с.
Линейный импульс
Линейный импульс определяется как произведение массы системы на ее скорость:
p = м v
Пример 1. Расчет импульса: футболист и футбол
- Рассчитайте импульс футболиста весом 110 кг, бегущего со скоростью 8,00 м / с.
- Сравните импульс игрока с импульсом сильно брошенного футбольного мяча весом 0,410 кг, который имеет скорость 25,0 м / с.
Стратегия
Никакой информации относительно направления не дается, поэтому мы можем вычислить только величину импульса, p .(Как обычно, курсивом обозначена величина, а курсивом, полужирным шрифтом и стрелкой – вектор.) В обеих частях этого примера величина импульса может быть вычислена непосредственно из определения импульс, заданный в уравнении, который становится p = mv , если рассматривать только величины.
Решение для части 1
Чтобы определить импульс игрока, подставьте известные значения массы и скорости игрока в уравнение.
p игрок = (110 кг) (8,00 м / с) = 880 кг · м / с
Решение для части 2
Чтобы определить импульс мяча, подставьте известные значения массы и скорости мяча в уравнение.
p мяч = (0,410 кг) (25,0 м / с) = 10,3 кг · м / с
Отношение импульса игрока к импульсу мяча составляет
.[латекс] \ displaystyle \ frac {p _ {\ text {player}}} {p _ {\ text {ball}}} = \ frac {880} {10.3} = 85,9 \ [/ латекс]
Обсуждение
Хотя мяч имеет большую скорость, игрок имеет гораздо большую массу. Таким образом, как вы могли догадаться, импульс игрока намного больше, чем импульс футбола. В результате, если игрок ловит мяч, это лишь незначительно влияет на его движение. В следующих разделах мы дадим количественную оценку тому, что происходит при таких столкновениях, с точки зрения количества движения.
Импульс и второй закон Ньютона
Важность импульса, в отличие от энергии, была признана на раннем этапе развития классической физики.Импульс считался настолько важным, что его называли «количеством движения». Ньютон фактически сформулировал свой второй закон движения в терминах количества движения: Чистая внешняя сила равна изменению количества движения системы, деленному на время, в течение которого он изменяется. Используя символы, это закон
.[латекс] \ displaystyle {\ mathbf {F}} _ {\ text {net}} = \ frac {\ Delta \ mathbf {p}} {\ Delta t} [/ latex],
, где F net – чистая внешняя сила, Δp – изменение количества движения, а Δ t – изменение во времени.
Второй закон движения Ньютона с точки зрения количества движения
Чистая внешняя сила равна изменению количества движения системы, деленному на время, в течение которого он изменяется.
[латекс] \ displaystyle {\ mathbf {F}} _ {\ text {net}} = \ frac {\ Delta \ mathbf {p}} {\ Delta t} [/ latex]
Установление связей: сила и импульс
Сила и импульс тесно связаны. Сила, действующая с течением времени, может изменять импульс, и второй закон движения Ньютона может быть сформулирован в его наиболее широко применимой форме с точки зрения количества движения.Импульс продолжает оставаться ключевым понятием при изучении атомных и субатомных частиц в квантовой механике.
Это утверждение второго закона движения Ньютона включает более знакомую F net = m a как частный случай. Мы можем получить эту форму следующим образом. Во-первых, обратите внимание, что изменение импульса Δp определяется как Δp = Δ ( м v).
Если масса системы постоянна, то Δ ( м v) = м Δv.
Таким образом, для постоянной массы второй закон движения Ньютона принимает вид
.[латекс] \ displaystyle {\ mathbf {F}} _ {\ text {net}} = \ frac {\ Delta \ mathbf {p}} {\ Delta t} = \ frac {m \ Delta \ mathbf {v} } {\ Delta {t}} [/ latex]
Поскольку [latex] \ frac {\ Delta \ mathbf {v}} {\ Delta {t}} = \ mathbf {a} \\ [/ latex], мы получаем знакомое уравнение F net = m a при постоянной массе системы .
Второй закон движения Ньютона, выраженный в терминах количества движения, более широко применим, потому что его можно применять к системам с изменяющейся массой, таким как ракеты, а также к системам с постоянной массой. Рассмотрим подробнее системы с разной массой; однако связь между импульсом и силой остается полезной, когда масса постоянна, как в следующем примере.
Пример 2. Расчетное усилие: ракетка Винус Уильямс
Во время Открытого чемпионата Франции 2007 года Винус Уильямс показала самую быструю подачу в женском матче, достигнув скорости 58 м / с (209 км / ч).Какова средняя сила, прилагаемая ракеткой Винус Уильямс к теннисному мячу весом 0,057 кг, если предположить, что скорость мяча сразу после удара составляет 58 м / с, что начальная горизонтальная составляющая скорости до удара пренебрежимо мала и что мяч оставался в контакте с ракеткой в течение 5,0 мс (миллисекунд)?
Стратегия
Эта проблема включает только одно измерение, потому что мяч не имеет горизонтальной составляющей скорости до удара. Второй закон Ньютона, выраженный в единицах количества движения, записывается как
[латекс] \ displaystyle {\ mathbf {F}} _ {\ text {net}} = \ frac {\ Delta \ mathbf {p}} {\ Delta t} [/ latex]
Как отмечалось выше, когда масса постоянна, изменение количества движения определяется выражением Δ p = м Δ v = м ( v f – v i ).
В этом примере даны скорость сразу после удара и изменение во времени; таким образом, после вычисления Δ p можно использовать [latex] {\ mathbf {F}} _ {\ text {net}} = \ frac {\ Delta {p}} {\ Delta t} [/ latex] найти силу.
Решение
Чтобы определить изменение количества движения, подставьте значения начальной и конечной скоростей в приведенное выше уравнение.
[латекс] \ begin {array} {lll} \ Delta {p} & = & m (v _ {\ text {f}} – v {\ text {i}}) \\ & = & (0,057 \ text {кг }) (58 \ текст {м / с} -0 \ текст {м / с}) \\ & = & 3.{-3} \ text {s}} \\ & = & 661 \ text {N} \ приблизительно660 \ text {N} \ end {array} \\ [/ latex]
, где на последнем этапе мы оставили только две значащие цифры.
Обсуждение
Эта величина представляла собой среднюю силу, прилагаемую ракеткой Винус Уильямс к теннисному мячу во время его кратковременного удара (обратите внимание, что мяч также испытал силу тяжести 0,56 Н, но эта сила возникла не из-за ракетки). Эту проблему также можно решить, сначала найдя ускорение, а затем используя F net = ma , но потребуется один дополнительный шаг по сравнению со стратегией, использованной в этом примере.
Сводка раздела
- Линейный импульс (импульс для краткости) определяется как произведение массы системы на ее скорость.
- В символах, линейный импульс p определен как p = m v , где m – масса системы, а v – ее скорость.
- Единица измерения количества движения в системе СИ – кг · м / с.
- Второй закон движения Ньютона с точки зрения количества движения гласит, что чистая внешняя сила равна изменению количества движения системы, деленному на время, в течение которого он изменяется.
- В символах второй закон движения Ньютона определяется как [latex] {\ mathbf {F}} _ {\ text {net}} = \ frac {\ Delta \ mathbf {p}} {\ Delta t} \\ [/ latex], F net – чистая внешняя сила, Δ p – изменение количества движения и Δ t – время изменения.
Концептуальные вопросы
- Объект с малой массой и объект с большой массой имеют одинаковый импульс. Какой объект имеет наибольшую кинетическую энергию?
- Объект с малой массой и объект с большой массой имеют одинаковую кинетическую энергию.Какая масса имеет наибольший импульс?
- Профессиональное приложение. Футбольные тренеры советуют игрокам блокировать, бить и отбиваться ногами на земле, а не прыгать в воздухе. Используя концепции импульса, работы и энергии, объясните, как футболист может быть более эффективным, стоя на земле.
- Как малая сила может передать объекту такой же импульс, что и большая сила?
Задачи и упражнения
- (a) Вычислите импульс 2000-кг слона, который атакует охотника со скоростью 7.50 м / с. (б) Сравните импульс слона с импульсом дротика с транквилизатором весом 0,0400 кг, выпущенного со скоростью 600 м / с. (c) Каков импульс 90-килограммового охотника, бегущего со скоростью 7,40 м / с после того, как пропустил слона?
- (а) Какова масса большого корабля с импульсом 1,60 × 10 9 кг · м / с, когда корабль движется со скоростью 48,0 км / ч? (b) Сравните импульс корабля с импульсом артиллерийского снаряда массой 1100 кг, выпущенного со скоростью 1200 м / с.
- (a) С какой скоростью будет 2.00 × 10 4 -кг самолет должен лететь, чтобы иметь импульс 1,60 × 10 9 кг · м / с (такой же, как импульс корабля в задаче выше)? (b) Какова инерция самолета, когда он взлетает со скоростью 60,0 м / с? (c) Если корабль является авианосцем, который запускает эти самолеты с помощью катапульты, обсудите последствия вашего ответа на (b), поскольку он относится к эффектам отдачи катапульты на корабль.
- (a) Каков импульс мусоровоза, который составляет 1,20 × 10 4 кг и движется со скоростью 10.0 м / с? (b) На какой скорости мусор весом 8 кг может иметь такую же скорость, что и грузовик?
- Неуправляемый вагон массой 15 000 кг движется по рельсам со скоростью 5,4 м / с. Вычислите время, необходимое для того, чтобы заставить автомобиль остановиться, приложив усилие в 1500 Н.
- Масса Земли составляет 5,972 × 10 24 кг, а радиус ее орбиты в среднем составляет 1,496 × 10 11 м. Рассчитайте его импульс.
Глоссарий
Количество движения: произведение массы на скорость
второй закон движения: физический закон, который гласит, что чистая внешняя сила равна изменению количества движения системы, деленному на время, в течение которого оно изменяется
Избранные решения проблем и упражнения
1.а) 1,50 × 10 4 кг м / с; (б) 625 к 1; (в) 6,66 × 10 2 кг ⋅ м / с
3. (а) 8.00 × 10 4 м / с; (б) 1,20 × 10 6 кг · м / с; (c) Поскольку импульс самолета на 3 порядка меньше, чем у корабля, корабль не будет сильно отскакивать. Отдача составит -0,0100 м / с, что, вероятно, не заметно.
5. 54 с
Формула моментума
Формула моментума Вопросы:
1) Общая масса мотоцикла и человека, едущего на нем, составляет 200.0 кг. Если гонщик движется с постоянной скоростью 30,0 м / с, каков импульс мотоцикла и гонщика?
Ответ: Импульс можно найти по формуле:
p = mv
p = (200,0 кг) (30,0 м / с)
p = 6000 кг · м / с
Импульс мотоцикла и гонщика 6000 кг · м / с.
2) Хоккейная шайба скользит по льду со скоростью 43,80 м / с. Имеет массу 0,165 кг.Шайба попадает в камень для керлинга весом 19,10 кг, который изначально находится в состоянии покоя. Хоккейная шайба отскакивает от камня и скользит в противоположном направлении со скоростью 43,0 м / с. Какова скорость скручивающейся скалы после столкновения?
Ответ: Этот вопрос зависит от сохранения количества движения при упругих столкновениях. Общий импульс до равен общему импульсу после:
p шайба, перед + p скала, перед = p шайба, после + p скала, после
м шайба v шайба, до + м скала v скала, до = м шайба v шайба, после + м скала v скала, после
Масса шайбы м шайба = 0.165 кг . Масса породы м, порода = 19,10 кг. Скорость шайбы до столкновения v шайба, до = +43,80 м / с. Скорость породы перед столкновением составляет v камень, до = 0,0 м / с, потому что она находилась в состоянии покоя. Скорость шайбы после столкновения отрицательна, потому что она двигалась в противоположном направлении, как и до столкновения: v шайба, после = -43,0 м / с.
(0,165 кг) (43,80 м / с) + (19,10 кг) (0.0 м / с) = (0,165 кг) (- 43,0 м / с) + (19,10 кг) v порода, после
(0,165 кг) (43,80 м / с) = – (0,165 кг) (43,0 м / с) + (19,10 кг) v скала, после
Теперь уравнение можно изменить, чтобы найти камень v после .
(0,165 кг) (43,80 м / с) + (0,165 кг) (43,0 м / с) = (19,10 кг) против породы , после
v скала, после = +0,750 м / с
Скорость керлинга после столкновения с хоккейной шайбой плотностью льда равна v рок, после = +0.750 м / с.
Импульс
Спортивный диктор говорит: «Перед перерывом на все звезды Чикаго Уайт Сокс имеют импульс ». Заголовки гласят: «Чикаго Буллз набирает оборотов в ». Тренер накачивает своей команде в перерыве между таймами, говоря: «У вас есть импульс ; критическая необходимость состоит в том, чтобы вы использовали импульс и похоронили их в этой третьей четверти».
Momentum – широко используемый термин в спорте.Команда, у которой есть импульс, находится на шаге и , и ей нужно приложить некоторые усилия, чтобы остановиться. Команда, которая имеет большой импульс, на самом деле на ходу и будет трудно остановить . Импульс – это физический термин; это относится к количеству движения, которое имеет объект. Спортивная команда, которая движется , имеет импульс. Если объект находится в движении ( в движении ), то он имеет импульс.
Импульс можно определить как «массу в движении».”Все объекты имеют массу; поэтому, если объект движется, у него есть импульс – его масса находится в движении. Количество импульса, которое имеет объект, зависит от двух переменных: сколько движется материала и насколько быстро материал движется. Импульс зависит от переменных массы и скорости. В терминах уравнения импульс объекта равен массе объекта, умноженной на его скорость.
Импульс = масса • скоростьВ физике символом количества импульса является строчная буква p .Таким образом, приведенное выше уравнение можно переписать как
p = m • v, где м, – масса, а v – скорость. Уравнение показывает, что импульс прямо пропорционален массе объекта и прямо пропорционален его скорости.
Единицами количества движения будут единицы массы, умноженные на единицы скорости. Стандартная метрическая единица импульса – кг • м / с. Хотя кг • м / с является стандартной метрической единицей количества движения, существует множество других единиц, которые являются приемлемыми (хотя и не традиционными) единицами количества движения.Примеры включают кг • миль / час, кг • км / час и г • см / с. В каждом из этих примеров единица массы умножается на единицу скорости, чтобы получить единицу количества движения. Это согласуется с уравнением для импульса.
Импульс как векторная величина
Momentum – это векторная величина . Как обсуждалось в предыдущем разделе, векторная величина – это величина, которая полностью описывается как величиной, так и направлением. Чтобы полностью описать импульс шара для боулинга весом 5 кг, движущегося на запад со скоростью 2 м / с, вы должны включить информацию как о величине, так и о направлении шара для боулинга. недостаточно, чтобы сказать, что мяч имеет импульс 10 кг • м / с; импульс мяча равен , а не полностью, пока не будет дана информация о его направлении. Направление вектора импульса совпадает с направлением скорости мяча. В предыдущем разделе было сказано, что направление вектора скорости совпадает с направлением движения объекта. Если шар для боулинга движется на запад, то его импульс можно полностью описать, сказав, что он составляет 10 кг • м / с на запад.Как векторная величина, импульс объекта полностью описывается величиной и направлением .
Уравнение момента как руководство к мышлению
Из определения количества движения становится очевидным, что объект имеет большой импульс, если и его масса, и его скорость велики. Обе переменные одинаково важны для определения количества движения объекта. Представьте грузовик Mack и роликовые коньки, движущиеся по улице с одинаковой скоростью.Значительно большая масса грузовика Mack придает ему значительно большую динамику. И все же, если бы грузовик Mack был в состоянии покоя, то импульс наименее массивных роликовых коньков был бы самым большим. Импульс любого объекта, который находится в состоянии покоя, равен 0. Объекты в состоянии покоя не обладают импульсом – у них нет “массы в движении”. Обе переменные – масса и скорость – важны при сравнении количества движения двух объектов.
Уравнение импульса может помочь нам подумать о том, как изменение одной из двух переменных может повлиять на импульс объекта.Рассмотрим физическую тележку массой 0,5 кг, загруженную одним кирпичом массой 0,5 кг и движущуюся со скоростью 2,0 м / с. Полная масса загруженной тележки составляет 1,0 кг, а ее импульс – 2,0 кг • м / с. Если вместо этого тележка была загружена тремя кирпичами по 0,5 кг, то общая масса загруженной тележки составила бы 2,0 кг, а ее импульс – 4,0 кг • м / с. Удвоение массы приводит к удвоению количества движения.
Аналогично, если бы тележка массой 2,0 кг имела скорость 8,0 м / с (вместо 2.0 м / с), то тележка будет иметь импульс 16,0 кг • м / с (вместо 4,0 кг • м / с). Учетверенное значение на скорости приводит к увеличению в четырехкратного увеличения на количества движения. Эти два примера иллюстрируют, как уравнение p = m • v служит «руководством к размышлению», а , а не просто , « готовый рецепт для решения алгебраических задач».
Проверьте свое понимание
Выразите свое понимание концепции и математики импульса, ответив на следующие вопросы.Нажмите кнопку, чтобы просмотреть ответы.
1. Определите импульс …
а. 60-кг полузащитник движется на восток со скоростью 9 м / с.
г. Автомобиль весом 1000 кг движется на север со скоростью 20 м / с.
г. Первокурсник весом 40 кг движется на юг со скоростью 2 м / с.
2. Автомобиль имеет 20 000 единиц количества движения.Каким будет новый импульс автомобилю, если …
а. его скорость была увеличена вдвое.
г. его скорость увеличилась втрое.
г. его масса увеличена вдвое (за счет увеличения количества пассажиров и груза)
г. его скорость и масса увеличились вдвое.
3. По футбольному полю бегут полузащитник (m = 60 кг), тута (m = 90 кг) и линейный игрок (m = 120 кг).Рассмотрим их образцы тикерной ленты ниже.
Сравните скорости этих трех игроков. Во сколько раз скорость полузащитника и тугого конца больше, чем скорость лайнмена?
Какой игрок имеет наибольшую динамику? Объяснять.
Мощность (физика): определение, формула, единицы измерения, как найти (с примерами)
Обновлено 28 декабря 2020 г.
Автор Эми Дусто
Бодибилдер и пятиклассник могли носить все книги с полки вверх по лестнице, но вряд ли они справятся с задачей за то же время.Бодибилдер, вероятно, будет быстрее, потому что у нее рейтинг мощности выше , чем у пятиклассника.
Точно так же гоночный автомобиль с высокой мощностью лошадиных сил сможет проехать дальше намного быстрее, чем лошадь.
TL; DR (слишком долго; не читал)
Мощность – это мера того, сколько работы выполнено за временной интервал.
Краткое замечание о лошадиных силах: этот термин предназначен для сравнения мощности парового двигателя с мощностью лошади, так как двигатель мощностью 700 лошадиных сил может выполнять примерно в 700 раз больше работы, чем одна лошадь.Это восходит к тому времени, когда паровые двигатели были новыми, и один из самых выдающихся изобретателей, работавших над повышением их эффективности, Джеймс Ватт, придумал этот термин как способ убедить среднего человека в их ценности.
Формулы для мощности
Есть два способа рассчитать мощность в зависимости от того, какая информация доступна. Кроме того, есть две единицы мощности, которые одинаково действительны.
1. Мощность в единицах работы и времени:
P = \ frac {W} {t}
Где работа Вт измеряется в Ньютон-метрах (Нм), а время т измеряется в секундах (с).
2. Мощность в единицах силы и скорости:
P = Fv
Где сила F выражается в Ньютонах (Н), а скорость v выражается в метрах в секунду (м / с). .
Эти уравнения не эквивалентны случайным образом. Второе уравнение может быть получено из первого следующим образом:
Обратите внимание, что работа совпадает с усилие на перемещение:
W = Fd
Подставьте это в первое уравнение мощности:
Затем, поскольку смещение в любую единицу времени равно скорости (v = d / t), перепишите члены в конце как v , чтобы получить второе уравнение мощности.
Единицы мощности
Единица мощности в системе СИ p обычно представлена как Вт (Вт) , названная в честь того же Джеймса Ватта, который проектировал двигатели и сравнивал их с лошадьми. На бирках лампочек и других бытовых приборов этот блок обычно указывается.
Однако рассмотрение второй формулы мощности приводит к другой единице. Сила, умноженная на скорость, дает измерение в единицах ньютон-метров в секунду (Нм / с). Затем, поскольку единица энергии Джоуль также определяется как один Ньютон-метр (Нм), первую часть этой величины можно переписать как Джоуль, в результате чего получится вторая единица мощности СИ: Джоуль в секунду (Дж. / с).
Как стать сильным
Рассмотрение определения силы и двух способов ее нахождения дает несколько способов увеличить силу чего-то : увеличить его силу (использовать больше силы ) или получить та же работа выполняется быстрее (уменьшение т или увеличение т ). Мощная машина – это сильная и быстрая , а слабая – ни то, ни другое. легче и быстрее может работать , более мощный объект, выполняющий работу.
Это также означает, что очень сильная машина, скажем, очень мускулистый бодибилдер, может все еще испытывать недостаток в мощности . Человек, который может поднять очень тяжелый груз, но только очень медленно, менее силен, чем тот, кто может поднять его быстро.
Точно так же очень быстрая машина или человек, который мало что делает, кто-то быстро крутится на месте, но ни к чему не приходит, на самом деле не является мощным.
Пример расчета мощности
1. Усэйн Болт выработал мощность около 25 Вт в своем рекордном спринте на 100 м, который занял 9 человек.58 секунд. Сколько работы он проделал?
Поскольку указаны P и t , а W неизвестно, используйте первое уравнение:
P = \ frac {W} {t} \ подразумевает 25 = \ frac { W} {9.58} \ подразумевает W = 239.5 \ text {Nm}
2. С какой средней силой он давил на землю во время бега?
Так как работа в Нм уже известна, как и рабочий объем в метрах, деление на длину гонки даст усилие (иными словами, работа то же самое, что сила, умноженная на смещение: W = F × d):
\ frac {239.5} {100} = 2.395 \ text {N}
3. Какую мощность вырабатывает человек весом 48 кг, который тратит 6 секунд на подъем по 3-метровой лестнице?
В этой задаче указаны смещение и время, что позволяет быстро вычислить скорость:
v = \ frac {d} {t} = \ frac {3} {6} = 0,5 \ text {м / с}
Второе уравнение мощности учитывает скорость, но также включает силу. Человек, поднимающийся по лестнице, пытается противостоять силе тяжести. Итак, силу в этом случае можно найти, используя их массу и ускорение свободного падения, которое на Земле всегда равно 9.8 м / с 2 .
F_ {grav} = mg = 48 \ times 9,8 = 470,4 \ text {N}
Теперь сила и скорость укладываются во вторую формулу мощности:
= Fv = 470,4 \ times 0,5 = 235,2 \ text {J / s}
Обратите внимание, что решение оставить здесь единицы измерения Дж / с, а не ватты, является произвольным. Столь же приемлемый ответ – 235,2 Вт.
4. Одна лошадиная сила в единицах СИ составляет около 746 Вт, что основано на нагрузке, которую подходящая лошадь могла бы выдержать в течение одной минуты. Сколько работы проделала лошадь-пример за это время?
Единственный шаг перед включением значений мощности и времени в первое уравнение – убедиться, что время указывается в правильных единицах СИ – секундах, переписав одну минуту как 60 секунд.Тогда:
P = \ frac {W} {t} \ подразумевает 746 = \ frac {W} {60} \ implies W = 44,670 \ text {Nm}
Киловатт и электричество
Многие коммунальные предприятия взимают плату с клиентов плата основана на использовании киловатт-часов и киловатт-часов. Чтобы понять значение этой общей единицы электроэнергии, начните с разбивки единиц.
Префикс килограмм означает 1000, поэтому киловатт (кВт) равен 1000 ватт. Таким образом, киловатт-час (кВтч) – это количество киловатт, используемое за один час времени.
Для подсчета киловатт-часов умножьте количество киловатт на использованные часы. Таким образом, если кто-то использует 100-ваттную лампочку в течение 10 часов, он в общей сложности израсходует 1000 ватт-часов или 1 кВт-ч электроэнергии.
Киловатт-час Примеры проблем
1. Электроэнергетика взимает 0,12 доллара за киловатт-час. Очень мощный вакуум 3000 Вт используется в течение 30 минут. Сколько стоит это количество энергии домовладельцам?
3 \ text {кВт} \ times 0.5 \ text {h} = 1,5 \ text {кВтч} \ text {и} 1,5 \ text {кВтч} \ times 0,12 \ text {долларов / кВтч} = \ 0,18 доллара США
2. Та же коммунальная компания кредитует домашнее хозяйство 10 долларов каждые 4 кВтч электроэнергии возвращается в сеть. Солнце дает около 1000 Вт мощности на квадратный метр. Если солнечный элемент площадью два квадратных метра в доме собирает энергию в течение 8 часов, сколько денег он приносит?
Учитывая информацию в задаче, солнечный элемент должен быть способен собирать 2 000 Вт от Солнца или 2 кВт. За 8 часов это 16 кВтч.
\ frac {\ $ 10} {4 \ text {kWh}} \ times 16 \ text {kWh} = \ $ 40
Gravity
Падающее яблоко
Гравитация повсюду вокруг нас. Он может, например, заставить яблоко упасть на землю:
Гравитация постоянно действует на яблоко, поэтому оно движется все быстрее и быстрее … другими словами, оно ускоряется.
Игнорируя сопротивление воздуха, его скорость увеличивается на 9,8 метра в секунду каждую секунду . То есть два лота «в секунду» и пишется:
9.8 м / с 2
9,8 м / с 2 – ускорение под действием силы тяжести у поверхности Земли. Почти все в нашей жизни происходит вблизи поверхности Земли, поэтому это значение часто используется и записывается как small g :
г = 9,8 м / с 2
Среднее значение г составляет 9,80665 м / с 2 , но значения в разных странах разные, например, в Калькутте 9.78548, Лондон 9.81599 и Токио 9.79805.
Таким образом, большинство людей просто используют 9,8 м / с 2
Чтобы удержать яблоко против силы тяжести, нужна сила.
Сила – это масса, умноженная на ускорение ( F = m a ), и в этом случае ускорение составляет g :
F = m g
Пример: сколько силы удерживать яблоко массой 0.1 кг?
F = m g
F = 0,1 кг × 9,8 м / с 2
F = 0,98 кг м / с 2
Сила измеряется в Ньютонах ( Н ), что совпадает с кг м / с 2
F = 0,98 N
Итак, чтобы удерживать яблоко, требуется сила около 1 Ньютона .
Мы также говорим, что вес яблока равен 0.98 Н.
Чтобы преобразовать массу в кг в силу в Ньютонах, умножьте на 9,8 м / с 2
Другой пример:
Пример: стальная балка весом 100 кг равномерно установлена на двух опорах. Сколько силы приходится на каждую опору?
На балку действует сила тяжести, направленная вниз:
F = m g
F = 100 кг × 9,8 м / с 2 = 980 Н
Поскольку каждая опора равномерно расположена на опоре, она несет половину веса (980/2 = 490):
Но что такое гравитация?
Теперь вы знаете, как справиться с гравитацией здесь, на Земле (просто умножьте массу на 9.8 м / с 2 , чтобы получить силу), но что такое гравитация на самом деле?
Что ж, масса и энергия делают пространство искривленным (или искаженным), поэтому для объектов естественно следовать по пути друг к другу.
Здесь объект естественным образом следует за пространством-временем в направлении
Земля
Это приводит к тому, что объекты притягиваются друг к другу , что мы называем Гравитацией .
Гравитация : притяжение объектов с массой или энергией друг к другу.
Это притяжение проявляется в виде силы:
- На
- меньше для удаленных объектов На
- больше для объектов большей массы (например, Солнца)
Представьте себе всего два шара:
Каждый шар состоит из множества кусочков массы и энергии, которые притягиваются друг к другу:
(На самом деле нужно лотов на частиц больше!)
Но мы обычно упрощаем это, представляя, что масса и энергия каждого шара находятся в его центре, называемом Центром тяжести.
(Но помните, что мы просто представляем, что вся масса находится в центре, чтобы упростить вычисления.)
Ньютон разработал формулу силы притяжения:
- F – сила (в Ньютонах), равная, но противоположная по направлению для обоих объектов
- G – гравитационная постоянная, приблизительно 6,674 × 10 -11 Н · м 2 / кг 2
- м 1 и м 2 – две массы (в кг)
- d – расстояние между центрами каждой массы (в метрах)
Пример: две машины массой 800 кг и 1500 кг находятся на расстоянии 3 м друг от друга
Гравитационное притяжение между двумя автомобилями составляет:
F = G м 1 м 2 д 2
F = 6.674 × 10 -11 Н м 2 / кг 2 × 800 кг × 1500 кг (3 м) 2
F ≈ 0,000009 N
Они очень слабо (всего 9 миллионных долей Ньютона) притягиваются друг к другу!
Пример: Яблоко и Земля
Яблоко массой 0,1 кг
Земля имеет массу 5,972 × 10 24 кг
От центра яблока до центра Земли составляет 6371 км (6.371 × 10 6 м)
F = G м 1 м 2 д 2
F = 6,674 × 10 -11 Н м 2 / кг 2 × 0,1 кг × 5,972 × 10 24 кг (6,371 × 10 6 м) 2
F = 0,98 N
(Это то же значение, что и в предыдущем расчете, так что это кажется вполне правильным!)
В обе стороны
Яблоко тянет и Землю!
Но Земля настолько невероятно массивна, что почти не влияет на нее.
Рассчитаем ускорение для яблока и для Земли:
Пример (продолжение): Зная, что сила равна 0,98 Н, каково ускорение яблока
и Земли?Для яблока :
| F = m a | ||
| Мы знаем, что F составляет 0,98 Н, а m равно 0,1 кг | 0.98 Н = 0,1 кг a | |
| Разделите обе стороны на 0,1 кг | 0,98 N / 0,1 кг = a | |
| Поменять местами | a = 0,98 Н / 0,1 кг | |
| Ответ: | a = 9,8 м / с 2 |
Это ускорение свободного падения g, которое мы все испытываем каждый день.
А для Земли :
| F = m a | ||
| F составляет 0,98 Н, а m равно 5,972 × 10 24 кг | 0,98 N = 5,972 × 10 24 кг a | |
| Разделите обе стороны на 5,972 × 10 24 кг | 0,98 Н / 5,972 × 10 24 кг = a | |
| Поменять местами | = 0.98 Н / 5.972 × 10 24 кг | |
| Ответ: | a = 1,64 × 10 -25 м / с 2 |
Это очень маленькое ускорение , неудивительно, что мы не замечаем, как Земля движется из-за яблока.
Но гораздо более крупный объект, такой как Луна (с массой 7.342 × 10 22 кг ), действительно оказывает заметное влияние на Землю.
Луна вращается вокруг Земли на расстоянии около 384 000 км каждые 27,3 дня
И Земля также имеет “орбиту” (больше похожую на колебание) с Луной около 5000 км (что на самом деле меньше радиуса Земли), также каждые 27,3 дня.
Ваша очередь: попробуйте вычислить силу притяжения между Землей и Луной.
Играй
Поиграйте с гравитацией в Gravity Freeplay.
Сводка
- Пространство кривой массы и энергии, которое естественным образом заставляет объекты двигаться навстречу друг другу
- этот аттракцион мы называем гравитацией
- это постоянное притяжение заставляет объекты ускоряться навстречу друг другу
- ускорение имеет соответствующую силу ( F = m a )
- у поверхности Земли ускорение свободного падения составляет 9.8 м / с 2
- , так что массой 1 кг испытывает гравитационное притяжение 9,8 Ньютона силы
Что такое формула массы?
Масса – это свойство физических объектов и мера устойчивости этого тела к ускорению. Можно рассматривать массу объекта как меру того, сколько физического «вещества» составляет этот объект.
В отличие от реляционных свойств, таких как положение, скорость или потенциальная энергия, которые всегда должны определяться по отношению к другому объекту или контрольной точке, масса является внутренним свойством , которое объект имеет независимо от его отношения к другим вещам.Массу объекта можно рассчитать несколькими способами:
- масса = плотность × объем (m = ρV) . Плотность – это мера массы на единицу объема, поэтому массу объекта можно определить, умножив плотность на объем.
- масса = сила ÷ ускорение (м = F / a) . Согласно второму закону Ньютона (F = ma) ускорение объекта прямо пропорционально приложенной к нему силе. Следовательно, величина ускорения, сопровождающая приложение постоянной силы, обратно пропорциональна массе.
- масса = вес ÷ ускорение свободного падения (м = Вт / г). Вес – это произведение ускорения массы в гравитационном поле. В зависимости от силы ускорения свободного падения вес будет разным.
Все три формулы являются способом определения массы объекта. Поскольку масса является фундаментальным свойством, она не определяется в других единицах, как джоуль (Дж) ньютона (Н). Есть и другие способы вычисления массы объекта, но эти три формулы являются наиболее распространенными.
m = ρV
m = W / g
m = F / a
Единицы массы
Принятая в системе СИ единица измерения массы килограмм (кг). Килограмм – единственная основная единица СИ, имеющая в названии префикс (килограмм). Первоначально один килограмм определялся как масса одного кубического децилитра (дл) воды при температуре плавления. В 1889 году килограмм был переопределен как масса International Kilogram Prototype (IPK), физического артефакта, который должен был быть универсальной эталонной массой для килограмма.Первоначально ИПК представлял собой чугунную гирю. В настоящее время принятый ИПК представляет собой цилиндр высотой 39 мм из специального сплава платины.
«Слова тоже имеют подлинную сущность – массу, вес и удельный вес». – Тим О’Брайен
По состоянию на 2018 год килограмм является единственной единицей СИ, в которой физический объект используется в качестве эталонного значения. Все остальные единицы СИ были переопределены с точки зрения фундаментальных физических констант, таких как скорость света или постоянная Планка.В ноябре 2018 года Генеральная конференция мер и весов (GCPM) проголосовала за пересмотр определения килограмма с точки зрения фундаментальных физических констант, и это изменение вступит в силу 20 мая 2019 года.
Способы расчета массы
На основе плотности и объема
Плотность объекта, иногда обозначаемая греческой буквой «ρ», является мерой массы на единицу объема. По сути, плотность говорит вам, насколько плотно упакована масса объекта. Чем плотнее объект, тем больше у него массы на единицу объема.
Например, вода имеет плотность 977 кг / м 3 при стандартной температуре и давлении. То есть один кубометр воды имеет массу 977 кг. Если мы знаем плотность и объем вещества, мы также можем вычислить массу этого вещества. Допустим, у нас есть образец воды размером 0,7 м 3 . Какова масса этого образца?
Решение для массы дает:
m = ρV
m = (0,7 м 3 ) (977 кг / м 3 ) = 683 кг
0.5 кубометров воды при стандартной температуре и давлении имели бы массу 683 кг.
Некоторые объекты невероятно плотные. Например, нейтронная звезда имеет среднюю плотность 1,1 x 10 18 кг / м 3 . Одна чайная ложка нейтронной звезды на Земле будет весить около 100 миллионов тонн.
«Масса становится неподвижной; он не может маневрировать и, следовательно, не может одерживать победы, он может сокрушить только своим весом ». – Hans Von Seeckt
От силы и ускорения
Свойство массы также понимается как мера сопротивления физического объекта ускорению под действием внешней силы.Это понятие массы иногда называют инертной массой . Инерция – это тенденция движущегося тела продолжать движение в постоянном состоянии, поэтому инерционная масса – это мера того, сколько инерции имеет тело и насколько сложно изменить его состояние движения. Связь между массой, силой и ускорением выражается вторым законом движения Ньютона F = ma. Это математическое соотношение говорит нам, что перед лицом постоянной силы более массивное тело будет ускоряться медленнее.Измеряя силу, приложенную к телу, и измеряя наблюдаемое ускорение, мы можем вычислить массу тела.
Например, предположим, что мы прикладываем силу 748 Н к металлическому кубу и измеряем его ускорение как 21 м / с 2 . Какая масса у металлического куба? Мы можем вычислить массу, разделив величину силы на величину ускорения так:
м = F / a
м = (748 Н) / (21 м / с 2 ) ≈ 35,62 кг
Итак, мы знаем, что металлический куб должен иметь массу 35.62 кг.
Вес
Строго говоря, вес и масса – это разные вещи. В английском языке два слова «вес» и «масса» являются синонимами, но в физических науках они имеют разные значения. Масса – неизменное свойство, которое не меняется от места к месту. Вес – это мера силы гравитационного поля, действующего на массивное тело. Поскольку напряженность гравитационного поля может различаться, то есть Луна имеет более слабую напряженность гравитационного поля, чем Земля, вес объекта может различаться в разных средах.
Связь между массой и весом определяется выражением W = mg, где g – мера ускорения свободного падения. Точное значение g различается в зависимости от местоположения. На Земле g имеет значение приблизительно 9,81 м / с 2 , а на Луне g составляет около 1,6 м / с 2 . Выражение W = mg дает вес в ньютонах, в то время как повседневное понимание веса дано в фунтах (фунтах), коэффициент преобразования из ньютонов в фунты составляет около 1 N = 0,22 фунта.
Например, на поверхности Земли где g = 9.81 м / с 2 , объект весом 50 кг будет иметь вес в фунтах:
W = (50 кг) (9,81 м / с 2 ) = 490,5N
Преобразование ньютонов в фунты дает:
490,5 Н (0,22 фунта / 1 Н) ≈ 108 фунтов
И наоборот, на Луне, где g имеет значение 1,6 м / с 2 , объект весом 50 кг будет весить:
W = 50 (кг) ( 1,6 м / с 2 ) (0,22 фунта / 1 Н) ≈ 18 фунтов
Тот же объект весом 50 кг весит 108 фунтов на Земле и 18 фунтов на Луне.
Точно так же, если мы знаем вес объекта, мы можем работать в обратном направлении, чтобы вычислить его массу. Скажем, объект весит 160 фунтов Земли. мы можем рассчитать массу объекта как:
180 фунтов (1N / 0,22 фунта) = 818,18N
818,18N = м (9,81 м / с 2 )
м = 818,18N / (9,81 м / с 2 ) ≈ 83,4 кг
Итак, тело весом 180 фунтов на Земле имеет массу около 84,3 кг.
Эквивалентность массы и энергии
В течение очень долгого времени ученые считали, что массу объекта можно считать полностью независимой от других его свойств.Однако в начале 20 века специальная теория относительности Эйнштейна показала, что масса и энергия на самом деле являются двумя разными названиями одной и той же физической величины. В частности, масса объекта и его полная энергия связаны знаменитым уравнением Эйнштейна E = mc 2 , где c – скорость света в вакууме.
E = mc 2 говорит нам, что полная энергия неподвижного тела прямо пропорциональна его массе с коэффициентом c 2 . Поскольку c = 3 000 000 м / с, c 2 является чрезвычайно большим фактором.Следовательно, даже крошечный кусочек массы содержит огромное количество внутренней энергии. Чтобы рассмотреть вопрос в перспективе, общее количество энергии от полного преобразования 1 грамма вещества в энергию примерно равно 21,5 килотоннам в тротиловом эквиваленте – силе атомной бомбы в Хиросиме.
«Любой дурак может знать. Дело в том, чтобы понять ». – Альберт Эйнштейн
В определенных физических процессах, таких как ядерное деление или движение тела в сильном гравитационном поле, материя преобразуется в энергию и выделяется в виде большого количества света и тепла.В частности, уравнение Эйнштейна говорит нам, как мы можем рассчитать количество энергии, выделяющейся во время таких реакций.
Скажем, 30 кг урана (Ur) загружают в ядерный реактор. Во время деления примерно 0,1% этой массы полностью превращается в энергию. Сколько энергии получается?
0,1% от 30 кг составляет 0,3 кг. Подставив это в уравнение Эйнштейна, мы получим:
E = (0,3 кг) (3,000,000) 2 = (0,3) (8,98755179 × 10 16 ) = 2,69626554 × 10 16 J
Полное преобразование всего 0 .3 кг (0,6 фунта) вещества превращаются в энергию, выделяя 2,69626554 × 10 16 Дж энергии. Это примерно столько же, сколько взорвано более 6 миллионов тонн тротила (12 миллиардов фунтов), чего достаточно, чтобы полностью сравнять с землей даже самые большие города.
Мы также можем работать в обратном направлении от некоторого количества энергии, чтобы определить количество преобразованной массы. Скажем, некоторая реакция деления высвобождает 1,6178 × 10 16 джоулей энергии. Сколько массы было преобразовано в энергию во время этого процесса? Используя нашу удобную формулу эквивалентности массы и энергии, мы можем определить:
1.6178 × 10 16 J = м (8,98755179 × 10 16 )
(1,6178 × 10 16 ) / 8,98755179 × 10 16 ) = м
м ≈ 0,18 кг
Таким образом, примерно 0,18 кг масса была преобразована в энергию.
Почему объекты имеют массу?
Только недавно ученые начали открывать ответ на вопрос, почему частицы вообще имеют массу. В 1960-х годах несколько ученых заметили некоторые проблемы со своими уравнениями, описывающими поведение элементарных частиц.В частности, их уравнения предсказывали, что определенные частицы, генерируемые во время высокоскоростных столкновений, не будут иметь массы. Однако экспериментальное наблюдение показало, что эти частицы действительно имели ненулевую массу.
Ученые предположили, что масса бозона может быть образована взаимодействием между этими бозонами и всепроникающим полем, называемым полем Хиггса (в честь одного из его теоретиков Питера Хиггса). Когда безмассовые бозоны движутся против этого поля, их импульс замедляется, и они теряют некоторую энергию.Поле Хиггса преобразует эту энергию в массу-энергию, которая проявляется как масса свойства, которую мы измеряем. Было предсказано, что это взаимодействие между бозонами и полем Хиггса приведет к созданию новой частицы, крошечного бозона, получившего название бозона Хиггса. Ускоритель элементарных частиц в ЦЕРНе наконец продемонстрировал существование частицы Хиггса в 2013 году, а 8 октября 2013 года Питер Хиггс и Франсуа Энглерт были удостоены Нобелевской премии по физике за их теоретические работы по частице.
Была ли эта статья полезной?
😊 ☹️ Приятно слышать! Хотите больше научных тенденций? Подпишитесь на нашу рассылку новостей науки! Нам очень жаль это слышать! Мы любим отзывы 🙂 и хотим, чтобы вы внесли свой вклад в то, как сделать Science Trends еще лучше.2.1: Релятивистский импульс, сила и энергия
Когда Эйнштейн произвел революцию в нашем понимании пространства и времени, перед физиками встала грандиозная задача. Вся физика до Эйнштейна была основана на идее абсолютного пространства и времени. Как только эти концепции оказались ошибочными, всю классическую физику пришлось пересмотреть в этом свете. В этом разделе мы «повторно исследуем» наше понимание импульса, силы и энергии.
Релятивистский импульс
В классической физике импульс определяется как
\ [\ vec {p} = m \ vec {v} \]
Однако использование этого определения количества движения приводит к количеству, которое не сохраняется во всех системах отсчета во время столкновений.Однако, если импульс будет переопределен как
\ [\ vec {p} = \ gamma m \ vec {v} \ label {eq2} \]
это – это , сохраняющееся во время столкновений частиц. Следовательно, экспериментально релятивистский импульс определяется уравнением \ ref {eq2}.
Релятивистская сила
Когда природа подсказывает нам правильную формулу для вычисления количества движения, математика подсказывает нам, как измерить силу и энергию. Сила определяется как производная от импульса
по времени.\ [\ vec {F} = \ dfrac {d \ vec {p}} {dt} \ label {eq5} \]
Уравнение \ ref {eq5} является скалярной формой этого отношения и справедливо только для движения в одном измерении.Полная векторная трактовка силы сложнее, чем она того стоит.
(В классической физике, где \ (\ vec {p} = m \ vec {v} \), уравнение \ ref {eq5} сводится к \ (\ vec {F} = m \ vec {a} \).) Подставляя правильное соотношение для импульса (уравнение \ ref {eq2}) в уравнение \ ref {eq5}, получаем
\ [\ begin {align} F & = \ dfrac {d (\ gamma m \ vec {v})} {dt} \\ [5pt] & = \ left (\ dfrac {d \ gamma} {dt} \ справа) mv + \ gamma m \ left (\ dfrac {dv} {dt} \ right) \\ [5pt] & = mv \ dfrac {d} {dt} \ left [\ left (1- \ dfrac {v ^ 2} {c ^ 2} \ right) ^ {- 1/2} \ right] + \ gamma ma \ end {align} \]
Используйте цепное правило для вычисления производной от \ (\ gamma \)
\ [\ begin {align} F & = mv \ left [- \ dfrac {1} {2} \ left (1 – \ dfrac {v ^ 2} {c ^ 2} \ right) »^ {- 3/2 } \ left (- \ dfrac {2v} {c ^ 2} \ right) \ left (\ dfrac {dv} {dt} \ right) \ right] + \ gamma ma \\ [5pt] & = mv \ left [ \ dfrac {v} {c ^ 2} \ left (1 – \ dfrac {v ^ 2} {c ^ 2} \ right) ^ {- 3/2} a \ right] + \ gamma ma \ end {align} \]
Выносим за скобки общий множитель \ (\ gamma ma \),
\ [F = \ gamma ma \ left [\ dfrac {\ dfrac {v ^ 2} {c ^ 2}} {1- \ dfrac {v ^ 2} {c ^ 2}} + 1 \ right] \]
Найдите общий знаменатель и упростите,
\ [\ begin {align} F & = \ gamma ma \ left [\ dfrac {\ cancel {\ dfrac {v ^ 2} {c ^ 2}} + 1 – \ cancel {\ dfrac {v ^ 2} { c ^ 2}}} {1- \ dfrac {v ^ 2} {c ^ 2}} \ right] \\ [5pt] & = \ gamma ma \ left [\ dfrac {1} {1- \ dfrac {v ^ 2} {c ^ 2}} \ right] \\ [5pt] & = \ gamma ^ 3 ma \ label {Force5} \ end {align} \]
Уравнение \ ref {Force5} – это релятивистски правильная форма Второго закона Ньютона для движения, ограниченного в одном измерении.2 \) как полная энергия частицы. Таким образом, полная энергия – это сумма кинетической энергии и совершенно новой формы энергии, энергии покоя . Частицы обладают энергией покоя только благодаря своей массе. На самом деле масса – это просто форма энергии.
\ [E_ {total} = KE + E_ {Rest} \]
Использование импульса и энергии
Электрон ускоряется через разность потенциалов 80 киловольт. Найдите кинетическую энергию, полную энергию, импульс и скорость электрона.2 \ label {Etot} \]
Уравнение \ ref {Etot} особенно полезно, поскольку оно позволяет установить прямую связь между энергией и импульсом без необходимости вычислять скорость. Доказательство этой связи оставлено в качестве упражнения.
Из электродинамики кинетическая энергия заряда, ускоренного разностью потенциалов \ (V \), является просто произведением заряда (\ (q \)) и разности потенциалов (\ (V \)),
\ [\ begin {align} KE & = qV \\ [5pt] & = e (80 \ times 10 ^ {3} V) = 80 \, кэВ \ end {align} \]
Вместо того, чтобы подставлять числовое значение заряда на электрон
\ [q = -e = -1.

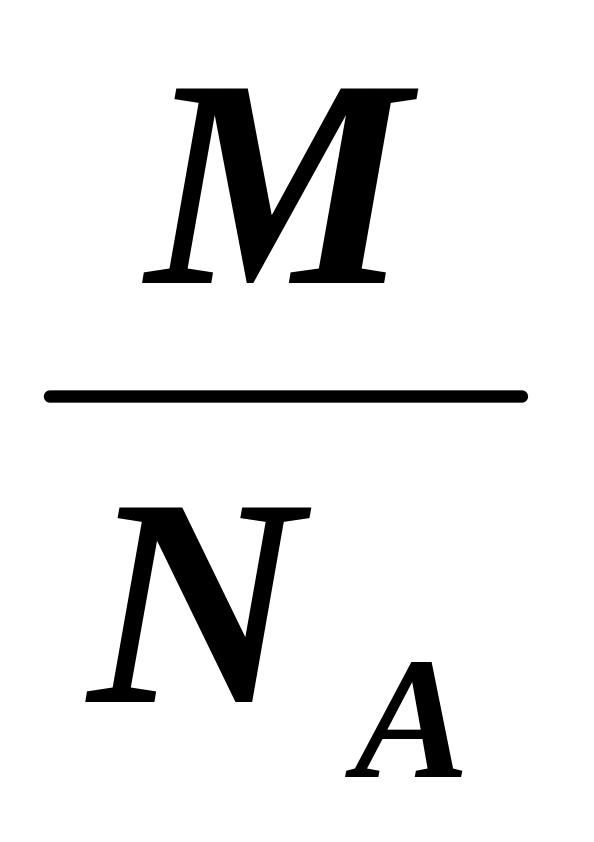 Вода, кремний, германий и некоторые другие вещества являются исключениями из данного правила, так как их плотность при переходе в твердую фазу уменьшается.
Вода, кремний, германий и некоторые другие вещества являются исключениями из данного правила, так как их плотность при переходе в твердую фазу уменьшается.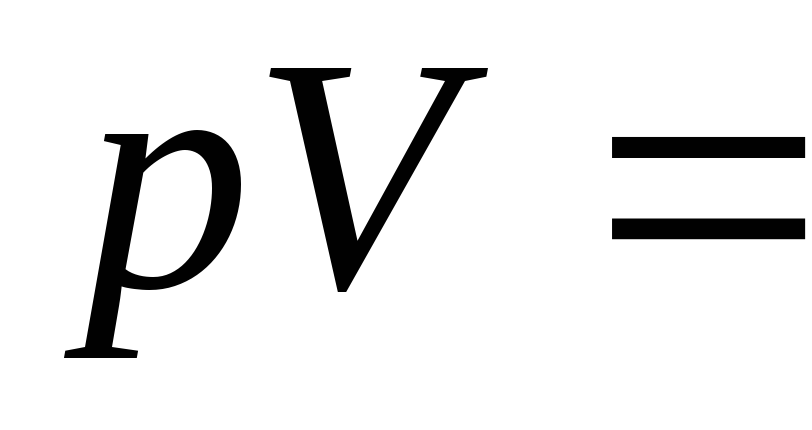 : Дрофа, 2013. — С. 147 – 149
: Дрофа, 2013. — С. 147 – 149 Так почему же «релятивистскую массу» лишают права на существование?
Так почему же «релятивистскую массу» лишают права на существование?