09.03.201924.12.2018

Что называется моментом инерции тела – Момент инерции — Википедия

• by alexxlab
• Комментариев к записи Что называется моментом инерции тела – Момент инерции — Википедия нет
• Советы абитуриенту

№03определение момента инерции тел

4

Лабораторная работа № 3

определение момента инерции тел и

проверка основного зАкона динамики

вращательного движения

Цель работы: определить момент инерции маятника Обербека, изучить зависимости углового ускорения от момента инерции при неизменном моменте силы.

Приборы и принадлежности: маятник Обербека, двухметровая линейка, секундомер, штангенциркуль, шнур длиной 2,5 м, грузы массой 100 г и 200 г.

Теория работы

Момент инерции I_i материальной точки с массой Δm_i , находящейся на расстоянии r_i от оси вращения, численно равен произведению массы математической точки на квадрат расстояния её от оси, т.е. I_i = Δm_ir_i² (рис.1).

Тело можно представить состоящим изnтаких элементарных масс. Тогда момент инерции тела:

I= .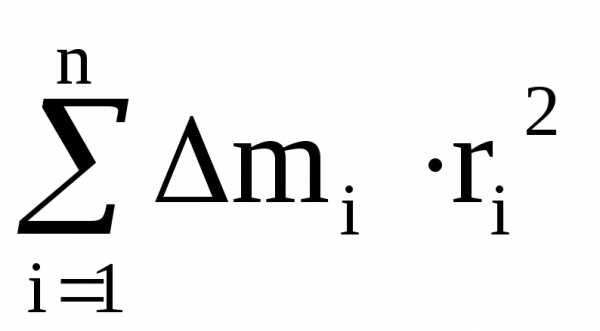

Единица измерения момента инерции в СИ: [I] = кг·м². Вращение тела вокруг оси вызывается вращающим моментом или просто моментом силы. Моментом М силы относительно оси вращения называют векторную величину, численно равную произведению силыFна длинуdперпендикуляра, опущенного из центра вращения на направление действия силы, называемого плечом силы:

М = F·d.

Под действием момента силы закрепленное на оси твердое тело приобретает угловое ускорение β:

β = ,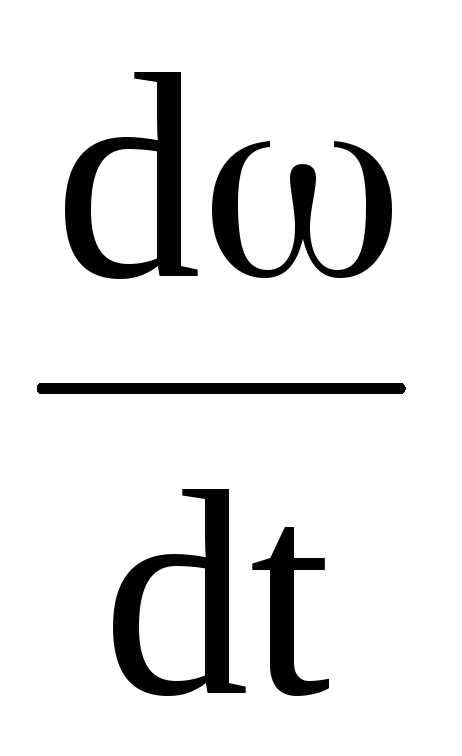

где ω – угловая скорость.

Зависимость углового ускорения β вращающегося тела от момента М действующей на тело силы и момента инерции Iтела относительно оси, вокруг которой происходит вращение, определяется основным уравнением (законом) динамики вращательного движения:

М = I β = I.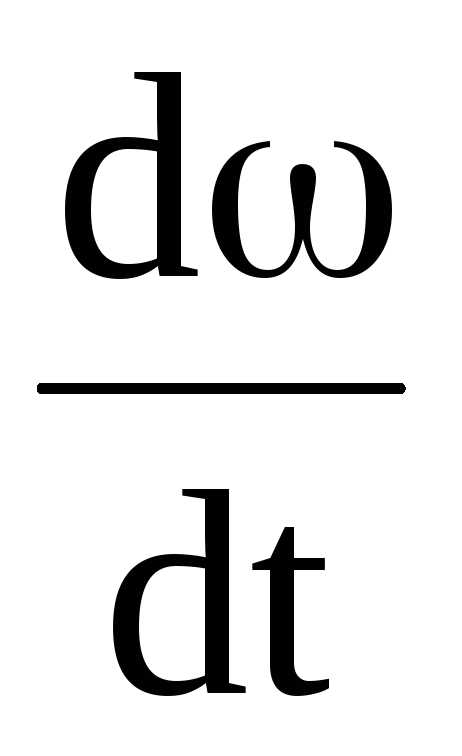

Формула закона для вращательного движения аналогична формуле закона Ньютона для поступательного движения:

F=ma.

Силе Fсоответствует момент силы М; ускорению а – угловое ускорение β; массеm– момент инерцииI. Подобно тому, как массаmхарактеризует инерционные свойства тела при поступательном движении, момент инерцииIхарактеризует инерционные свойства тел при вращательном движении.

Знание момента инерции тел, а также основного закона динамики вращательного движения необходимо во многих областях науки и технике. В некоторых разделах космической и спортивной медицины, ортопедии, бионики возникает необходимость измерения момента инерции тела человека и отдельных его частей. Момент инерции при вращательном движении туловища человека или его конечностей вычисляют приблизительно по формулам момента инерции цилиндра и круглого стержня или определяют из опыта. В молекулярной биологии определяют моменты инерции сложных молекул. По их значениям классифицируют молекулы многих исследуемых веществ. Знание моментов инерции молекул необходимо также при определении вращательной энергии молекул в квантовой механике.

Описание установки

Момент инерции тела может быть определен из закона динамики вращательного движения: I= 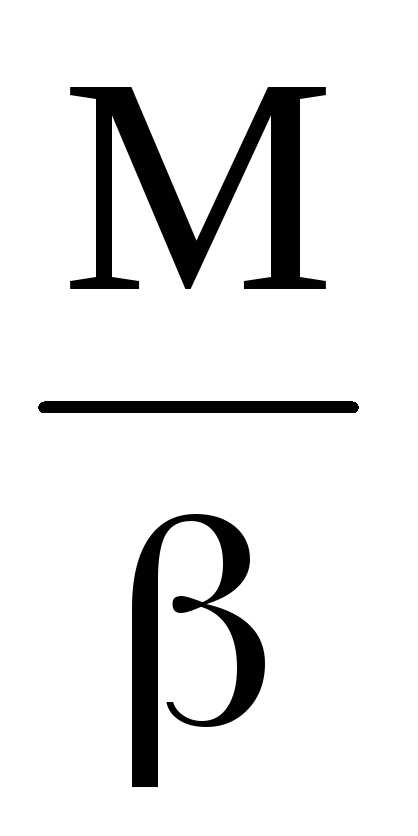. (1)

Для измерения действующего на тело момента силы и сообщенного этому телу углового ускорения применяют крестообразный маятник Обербека (рис.2).

Прибор состоит из шкива Lрадиусомr, закреплённого на осиO; четырёх стержней, расположенных под углом 90º друг к другу и четырёх одинаковых цилиндрических грузовm

0, которые можно перемещать вдоль стержней и закреплять на определённых расстояниях.

Грузы закрепляются симметрично, т.е. так, чтобы центр тяжести маятника находился на оси вращения.

Прибор приводится во вращательное движение грузом, масса которого m. Груз прикрепляется к концу шнура, намотанного на шкив.

Если груз, подвешенный на нити, падает с высоты hза времяt, тоh= 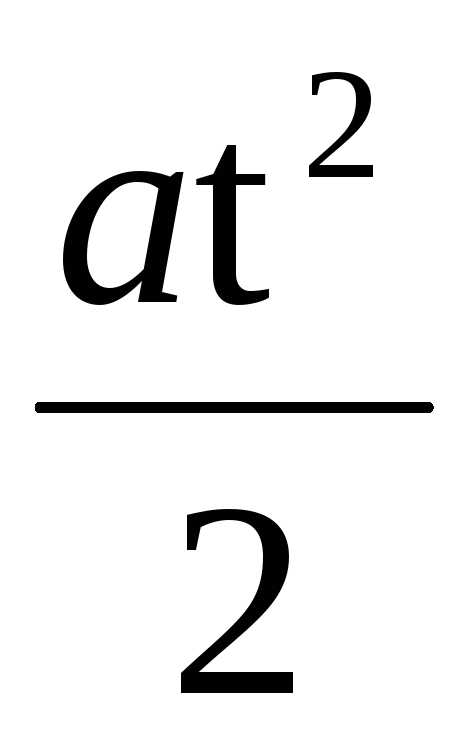, гдеа– линейное ускорение на ободе шкива. Тогда:

а=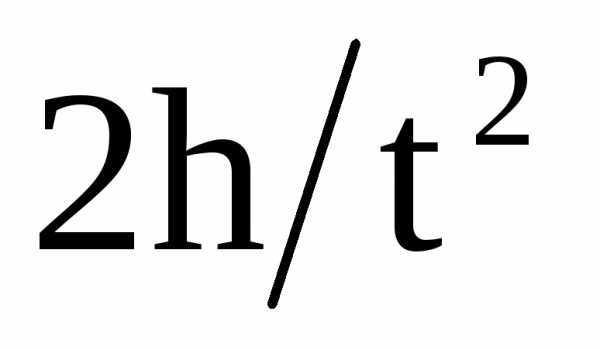. (2)

При этом шкив со стержнями и расположенными на нём грузами будет вращаться с угловым ускорением β:

β =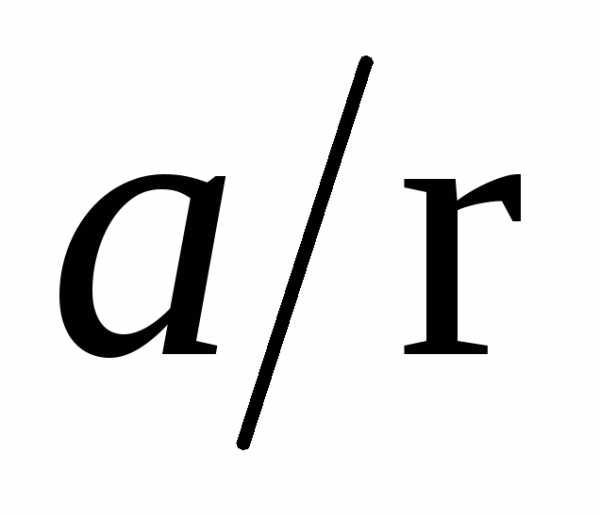

. (3)

Из (2) и (3) следует, что:

β = 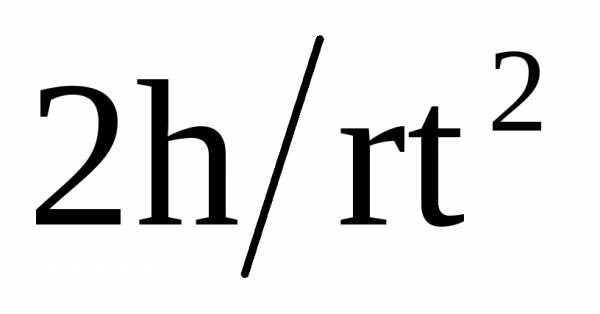. (4)

Вращающий момент найдем по формуле: М = Т·r, где Т – сила натяжения нити,r– плечо этой силы.

Силу натяжения нити найдем из IIзакона Ньютона для груза массойm:

ma= 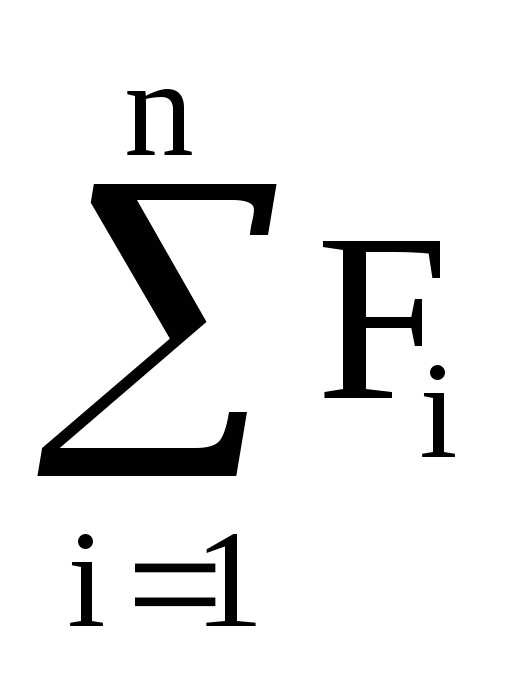, ноma=mg–T, откуда Т =mg–ma.

Тогда: М = (mg–ma) ·r=m(g-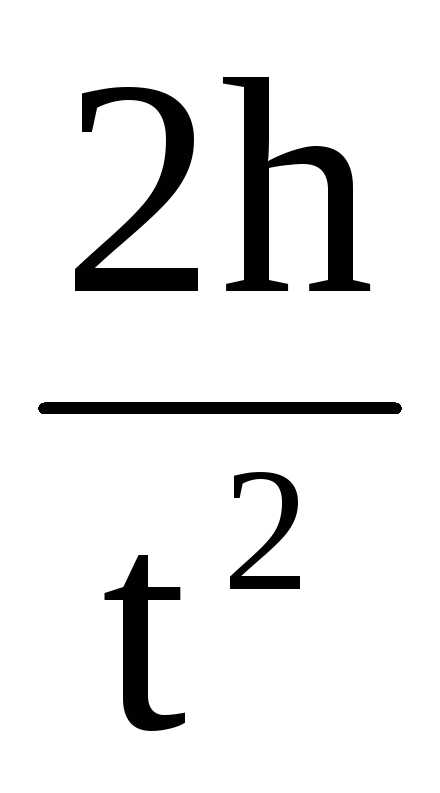) ·r. (5)

Подставив в формулу (1), формулы (4) и (5) получим:

I=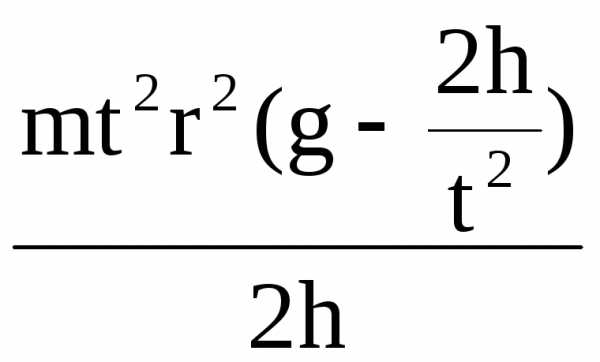

. (6)

Для определения момента инерции Iнеобходимо определить опытным путём все величины, стоящие в правой части формулы (6).

Порядок выполнения работы

1. Определение момента инерции маятника.

1. Переместить грузы к концам стержней и закрепить их винтами на последних делениях, нанесенных на стержнях. При этом маятник не должен поворачиваться, если систем правильно сбалансирована.

2. К концу нити прикрепить груз. Намотать равномерно нить на шкив.

3. На линейке нанести две метки на расстоянии, соответствующем высоте падения h.

4. С помощью штангенциркуля определить радиус шкива.

5. Предоставив возможность грузу mпадать, по секундомеру определить время падения. Секундомер включить в момент начала падения груза от верхней метки на линейке и остановить в момент прохождения нижней метки.

6. Опыт повторить для двух разных грузов (например, 100 и 200 г). Данные опытов занести в таблицу 1.

Таблица 1

№ п/п	m, кг	r, м	h, м	t, c	I, кг·м2	<I>, кг·м2
1
2

7. Определить дважды моменты инерции маятника по формуле (6) и найти его среднее значение.

2. Исследование законов вращательного движения.

1. Последовательно закрепить грузы симметрично на размеченных на стержнях делениях и описанным в первом опыте способом найти время tдля различных положений грузов.

2. Маятник приводить в движение с помощью одного и того же груза, т.е. m=const.

3. Полученные данные занести в таблицу 2.

Таблица 2

№ п/п	h, м	t, c	M, Н·м	β , c-2	I, кг·м2	Приложение
1 2						m= r=

3. По формулам (5), (4) и (1) определить: момент силы, угловое ускорение и момент инерции маятника для каждого случая.

Контрольные вопросы

1. Что называется моментом инерции материальной точки тела? Какие свойства тел он характеризует?

2. В каких единицах в системе СИ изменяется момент инерции?

3. Что называется моментом силы? В каких единицах он измеряется?

4. В каких областях медицины необходимо знание моментов инерции тел?

5. Сформулировать и записать уравнение динамики вращательного движения. Сравнить его со IIзаконом Ньютона для поступательного движения.

6. Вывести расчетную формулу для определения момента инерции маятника Обербека.

7. Какая зависимость между угловым ускорением и моментом инерции маятника при постоянном значении момента силы?

studfiles.net

Что называется моментом инерции твердого тела относительно оси вращения?

Рассмотрим твёрдое тело, которое может вращаться вокруг неподвижной вертикальной оси. Чтобы удержать ось от перемещений в пространстве, заключим её в подшипники. Опирающийся па нижний подшипник фланец Фл , предотвращает передвижение оси в вертикальном направлении .

Абсолютно твёрдое тело можно рассматривать как систему материальных точек с неизменным расстоянием между ними. Линейная скорость элементарной массы равна , где -расстояние массы от оси вращения. Следовательно, для кинетической энергии элементарной массы получается выражение

Кинетическая энергия вращающегося твёрдого тела складывается из кинетических энергий его частей.

Сумму, входящую в правую часть этого соотношения назовём моментом инерции I тела относительно оси вращения

– момент инерции твёрдого тела.

27. Получите выражение для момента импульса твердого тела относительно непод­вижной оси вращения.

28. Выведите формулу для момента инерции однородного тонкого стержня длиной / и массы т относительно оси, проходящей через центр масс стержня и перпен­дикулярной стержню.

29. Выведите формулу для момента инерции однородного тонкого стержня дли­ной / и массы т относительно оси, проходящей через конец стержня и перпен-^ \ дикулярной стержню.

30 Выведите формулу для момента инерции однородного тонкого диска радиуса и массы т относительно оси, проходящей через центр масс диска и перпендику лярной плоскости диска.

31. Выведите формулу для момента инерции тонкого обруча радиуса К и массы т относительно оси, проходящей через центр масс обруча и перпендикулярной плоскости обруча.

Пример 1: Вычисление момента инерции тонкого стержня массы m и длинной l, вращающегося вокруг оси перпендикулярной стержню и проходящей через центр масс.

Будем считать стержень однородным, тогда

Другие примеры значений моментов инерции для некоторых тел правильной формы приведём без вычислений .

Пример 2:Полый тонкостенный цилиндр, тонкое кольцо :

 

– момент инерции цилиндра или

тонкого кольца

 

 

Пример 3: Сплошной цилиндр, диск.

 

– момент инерции сплошного

цилиндра или диска

 

Пример 4: Сплошной шар .

 

– момент инерции шара.

 

 

Заметим, что во всех приведённых примерах, тела предполагаются однородными, и вычисляются моменты инерции относительно центральных осей,

т.е. осей проходящих через центр масс.

32. Получите закон сохранения момента импульса твердого тела относительно оси _вращения.

В случае главной оси вращения при суммарном моменте внешней силы, действующем на тело, равном нулю, имеет место закон сохранения момента импульса твёрдого тела: – закон сохранения момента импульса твёрдого тела.

Если суммарный момент внешних сил , то он совершает работу, которая приводит к увеличению кинетической энергии вращающегося твёрдого тела (в этом случае потенциальная энергия ).

 

33. Получите формулу кинетической энергии вращающегося твердого тела. Кинетическая энергия(или энергия движения) определяется массами и скоростями рассматриваемых тел. Рассмотрим материальную точку, движущуюся под действием силы . Работа этой силы увеличивает кинетическую энергию материальной точки . Вычислим в этом случае малое приращение (дифференциал) кинетической энергии:

.

При вычислении использован второй закон Ньютона , а также – модуль скорости материальной точки. Тогда можно представить в виде:

–

– кинетическая энергия движущейся материальной точки.

cyberpedia.su

Определение момента инерции твердого тела — Мегаобучалка

 

Цель работы: определить момент инерции крестовины с грузами, используя законы динамики вращательного движения и сохранения энергии.

 

Приборы и принадлежности: маятник Обербека, грузы, масштабная линейка, секундомер, штангенциркуль.

 

Схема экспериментальной установки:

 

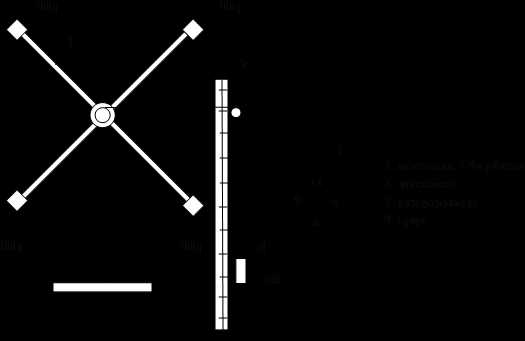Методика исследования и описание установки

Момент инерции твердого тела является физической величиной, характеризующей инертность тела при изменении угловой скорости вращения этого тела ω под действием вращающего момента М.

Моментом инерции твердого тела называется скалярная физическая величина равная:

, (1)

где dV – элемент объема;

ρ – плотность;

r – расстояние от этого элемента до оси вращения.

Из формулы (1) видно, что момент инерции не зависит от характера движения, а зависит от размеров, форм и плотности тела. Момент инерции твердого тела во вращательном движении выполняет ту же роль, что и масса тела при поступательном движении.

Проектирование машин и механизмов, имеющих вращающиеся при работе детали, ведется с учетом моментов инерции этих деталей.

Для однородного тела правильной геометрической формы момент инерции может быть вычислен теоретически (1). При сложной форме тела и неравномерном распределении плотности вещества в нем теоретическое вычисление момента инерции может быть достаточно сложной задачей. В этих случаях момент инерции определяют опытным путем. В настоящей работе определяется момент инерции крестовины маятника Обербека методом вращения.

Подвижная часть маятника Обербека (крестовина) состоит из двухступенчатого блока, насаженного на ось, и четырех спиц с одинаковыми цилиндрическими грузами с массами m₁. Грузы m₁ можно перемещать, закрепляя в том или ином положении, меняя этим момент инерции крестовины.

Центр тяжести системы должен находиться на оси вращения. Крестовина приводится в движение при помощи груза массой m, прикрепленного на нити, накрученной на шкив.

Итак, если груз опустить с высоты h, то он будет двигаться с линейным ускорением:

, (2)

где t – время движения груза на участке длиной h.

Крестовина же при этом будет вращаться с угловым ускорением:

, (3)

где r – радиус шкива, на который наматывается нить.

С другой стороны, это ускорение по закону динамики вращательного движения:

, (4)

, (5)

где g – ускорение свободного падения.

На основании (2), (3), (4), (5) получаем:

. (6)

Порядок выполнения работы

1. По указанию преподавателя откройте программу, содержащую блок лабораторных работ по физике, раздел «механика, статистическая физика и термодинамика». Выберите нужную вам лабораторную работу.

2. Еще раз внимательно прочитайте теорию и методику проведения работы. Для этого щелкните левой клавишей мыши на экране кнопку «Теория и методика проведения работы».

3. Откройте flash – анимацию, для этого щелкните кнопку «Эксперимент».

4. По указанию преподавателя с помощью мыши задайте параметры экспериментальной установки.

5. Запишите полученные данные в таблицу.

6. Щелкните кнопку «Пуск» для начала эксперимента. Остановите секундомер с помощью мыши в момент касания грузом нулевого уровня.

7. Занесите полученное значение времени в таблицу.

8. Повторите опыт 10 раз, каждый раз вводя параметры установки.

9. При помощи калькулятора произведите вычисления предлагаемых величин.

10. Сделайте вывод о проделанной работе.

11. Ответьте на контрольные вопросы.

Обработка результатов измерений

1. Абсолютные погрешности времени определить либо как погрешность многократных измерений, либо как погрешность секундомера (по указанию преподавателя)

2. Момент инерции рассчитывается по формуле (6).

3. Относительные погрешности опытов определяются по формуле

.

4. Абсолютные погрешности опытов рассчитать по формуле

.

Таблица измерений

 

Номер опыта	m…	h…	t…	Dt…	r…	Dr…	…	…	…
Среднее значение	-	-			-	-

 

Контрольные вопросы:

 

1) Что называется моментом инерции материальной точки и абсолютно твердого тела?

2) Что называется моментом силы относительно неподвижной точки и неподвижной оси, как он направлен, как определяется его модуль?

3) Записать основной закон динамики вращательного движения.

4) Как меняется отношение линейных ускорений груза m, если грузы m₁ сдвинуть к центру?

5) Что изменится, если изменить диаметр шкива, на который наматывается нить?

 

Лабораторная работа №4

 

megaobuchalka.ru

5.4. Момент инерции твердого тела

Чтобы найти момент инерции тела, надо просуммировать момент инерции всех материальных точек, составляющих данное тело

(5.4)

В общем случае, если тело сплошное, оно представляет собой совокупность множества точек с бесконечно малыми массами , и моменты инерции тела определяется интегралом

(5.5)

о где – расстояние от элемента до оси вращения.

Распределение массы в пределах тела можно охарактеризовать с помощью
плотности

(5.5)

где m – масса однородного тела, V – его объем. Для тела с неравномерно распределенной массой это выражение даетсреднюю плотность.

Плотность в данной точке в этом случае определяется следующим образом

и тогда

(5.6)

Пределы интегрирования зависят от формы и размеров тела Интегрирование уравнения (5.5) наиболее просто осуществить для тех случаев, когда ось вращения проходит через центр тяжести тела. Рассмотрим результаты интегрирования для простейших (геометрически правильных) форм твердого тела, масса которого равномерно распределена по объему.

Момент инерции полого цилиндра с тонкими стенками, радиуса R.

Для полого цилиндра с тонкими стенками

Сплошной однородный диск. Ось вращения является осью диска радиуса . и массы m с плотностью Высота диска h. Внутри диска на расстоянии вырежем пустотелый цилиндр с толщиной стенки и массой . Для него

Весь диск можно разбить на бесконечное множество цилиндров, а затем просуммировать:

Момент инерции шара относительно оси, проходящей через центр тяжести.

Момент инерции стержня длиной L и массой m относительно оси, проходящей:

а) через центр стержня –

б) через начало стержня –

Теорема Штейнера. Имеем тело, момент инерции которого относительно оси, проходящей через его центр масс известен. Необходимо определить момент инерции относительно произвольно оси параллельной оси . Согласно теореме Штейнера, момент инерции тела относительно произвольной оси равен сумме момента инерции тела относительно оси, проходящей через центр масс и параллельной данной оси, плюс произведение массы тела на квадрат расстояния между осями:

(5.7)

physics-lectures.ru

---