Определение пределы – Определение предела по Коши и по Гейне, их эквивалентность — ПриМат
- Комментариев к записи Определение пределы – Определение предела по Коши и по Гейне, их эквивалентность — ПриМат нет
- Советы абитуриенту
Лекция 12. Предел функции
Лекция 12. Предел функции.
12.1. Определения предела функции.
Пусть задана
функция 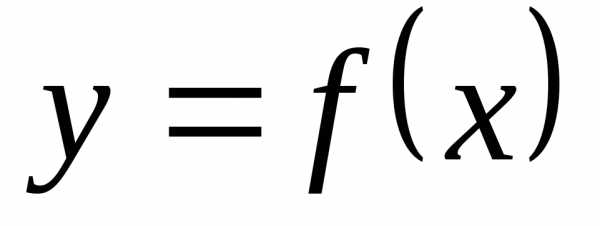 ,
определённая на множестве
,
определённая на множестве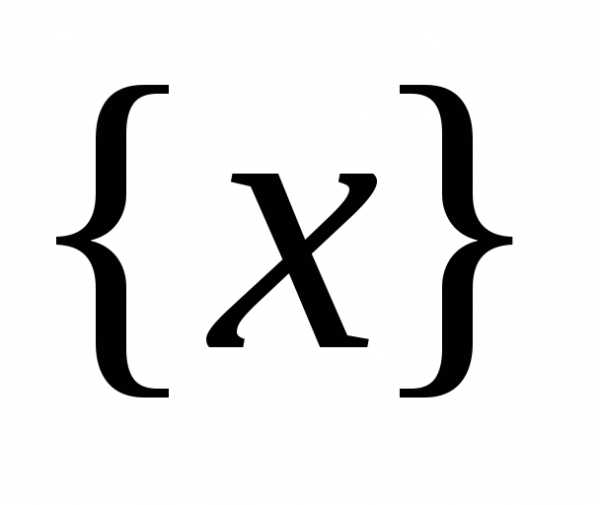 .
Пусть имеется точкаa,
быть может и не принадлежащая
.
Пусть имеется точкаa,
быть может и не принадлежащая 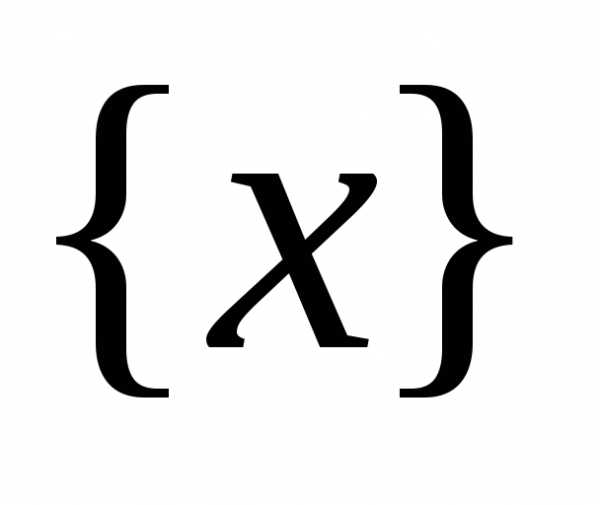 ,
но такая, что в любой
,
но такая, что в любой -окрестности
точкиa имеются точки множества
-окрестности
точкиa имеются точки множества 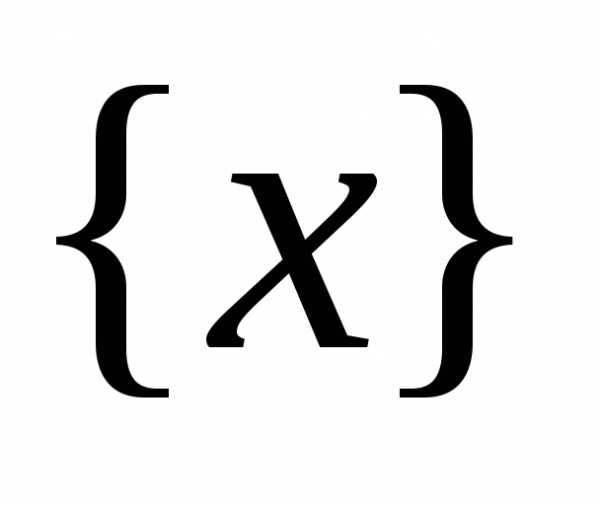 ,
отличные отa.
Например:
,
точкаa не принадлежит
,
отличные отa.
Например:
,
точкаa не принадлежит 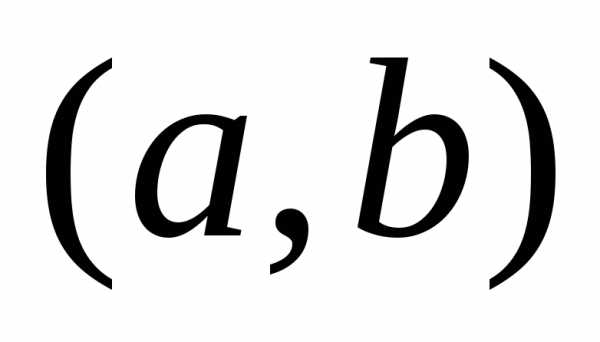 ,
но любая
,
но любая -окрестностьсодержит точки, принадлежащие
-окрестностьсодержит точки, принадлежащие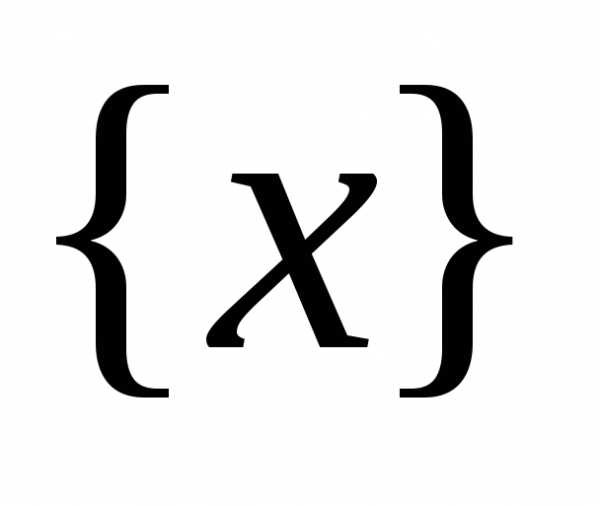
Определение 12.1 (определение
предела функции по Гейне). Число b называется пределом (или предельным
значением) функции 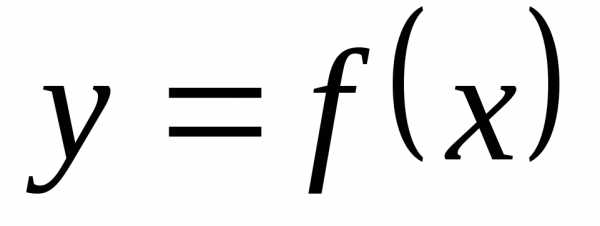 в точке a (или при
),
если для любой последовательности
значений аргумента,
сходящейся кa и состоящей из чисел
в точке a (или при
),
если для любой последовательности
значений аргумента,
сходящейся кa и состоящей из чисел 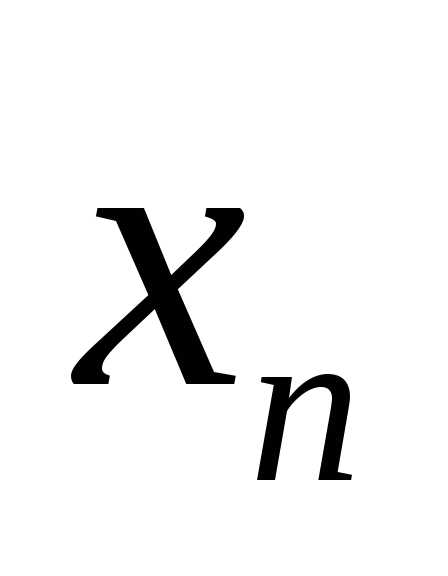 ,
отличных отa,
соответствующая последовательность
значений функции
сходится к числуb.
,
отличных отa,
соответствующая последовательность
значений функции
сходится к числуb.
Определение 12.2 (определение
предела функции по Коши). Число b называется пределом
функции 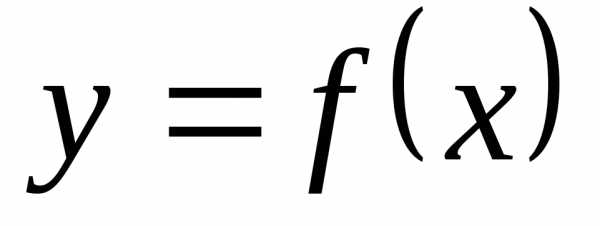 в точке a,
если для любого сколь угодно малого
положительного числа
в точке a,
если для любого сколь угодно малого
положительного числа  найдётся отвечающее ему положительное
число
найдётся отвечающее ему положительное
число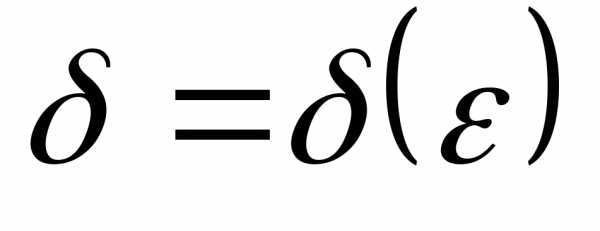 такое, что для всех значений аргументаx,
удовлетворяющих условию
,
справедливо неравенство.
такое, что для всех значений аргументаx,
удовлетворяющих условию
,
справедливо неравенство.
Обозначается предел функции следующим образом:
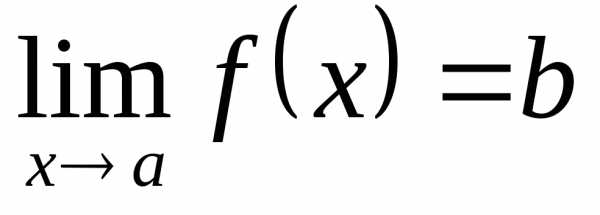 или
или 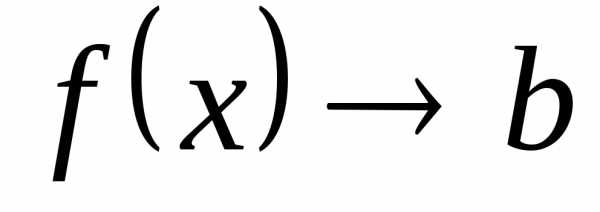 при.
при.
♦ Утверждение 12.1. Определения 12.1 и 12.2 эквивалентны.
☼ Замечание 12.1. Элементы последовательности 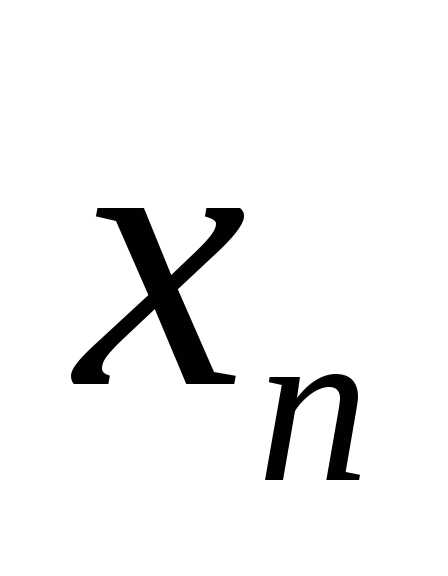 должны быть отличны отa:
функция
должны быть отличны отa:
функция 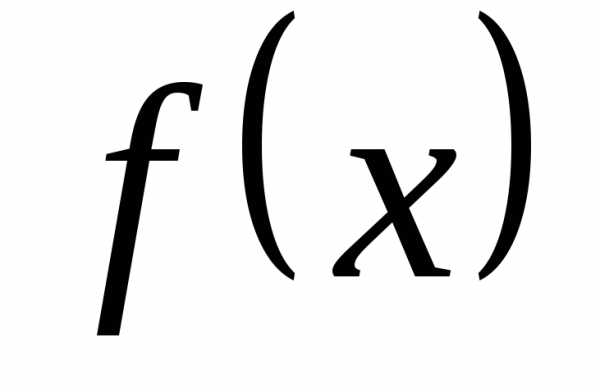 может быть не определена в точке
может быть не определена в точке
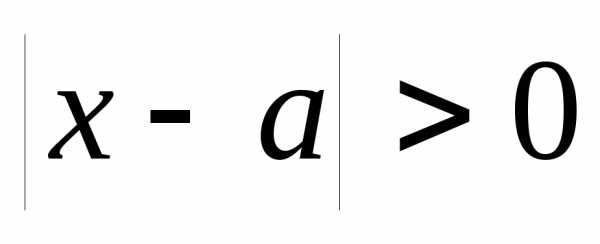 означает
означает 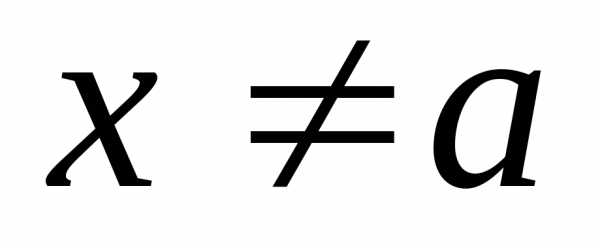 . ☼
. ☼ Пример 12.1. 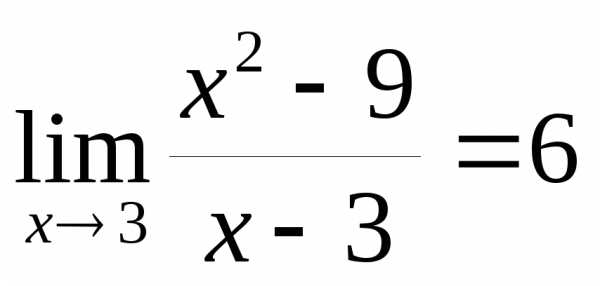 .
.
☼ Замечание 12.2.
Функция 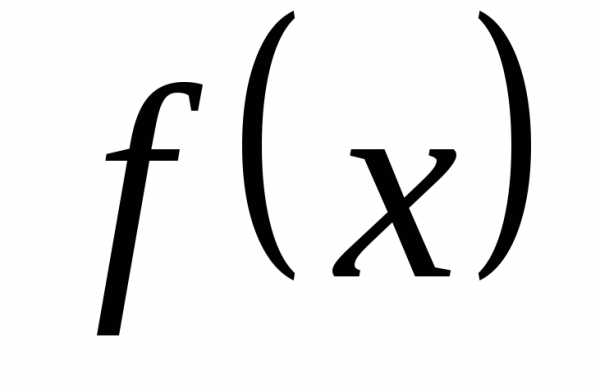 может иметь в точке a только один предел, так как имеется
единственный предел последовательности
может иметь в точке a только один предел, так как имеется
единственный предел последовательности 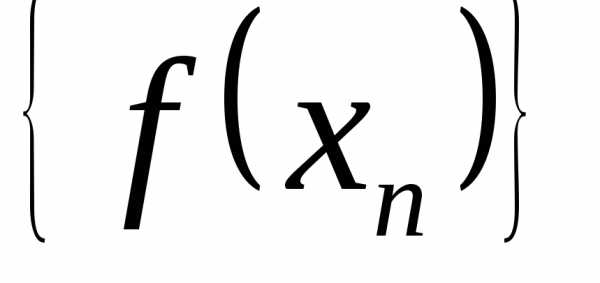 в определении 12.1, а определение 12.2
эквивалентно определению 12.1.☼
в определении 12.1, а определение 12.2
эквивалентно определению 12.1.☼
Пример 12.2. 1) 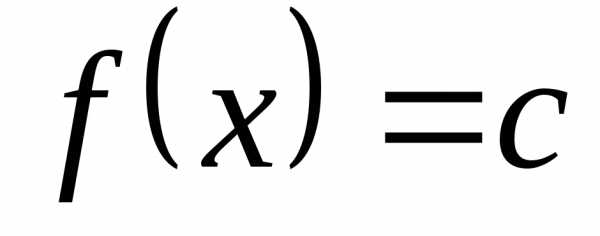 .
.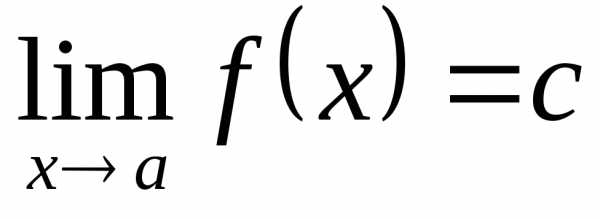 ,
так как любая последовательность ,
сходящаяся к числу a,
порождает последовательность
.
,
так как любая последовательность ,
сходящаяся к числу a,
порождает последовательность
.
2) 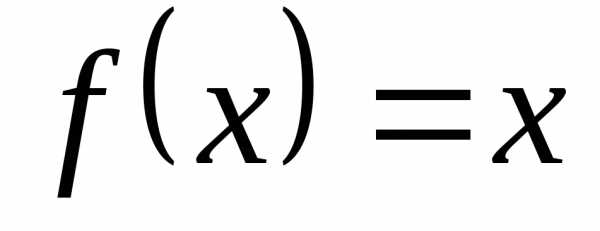 .
.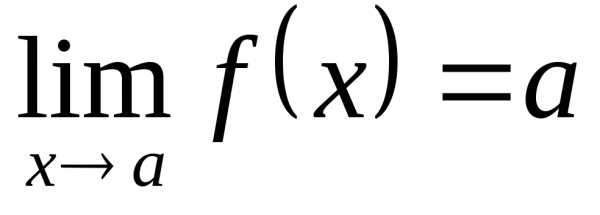 ,
так как последовательности и совпадают.
,
так как последовательности и совпадают.
3) 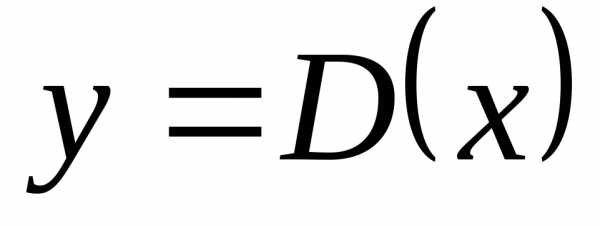 – функция Дирихле, – не имеет предела:
для рациональных чисел при,
для иррациональных при
– функция Дирихле, – не имеет предела:
для рациональных чисел при,
для иррациональных при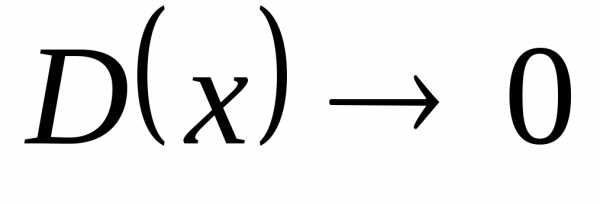 .
Это противоречит определению 12.1.
.
Это противоречит определению 12.1.
Определение 12.3. Число b называется правым
(левым) предельным значением функции 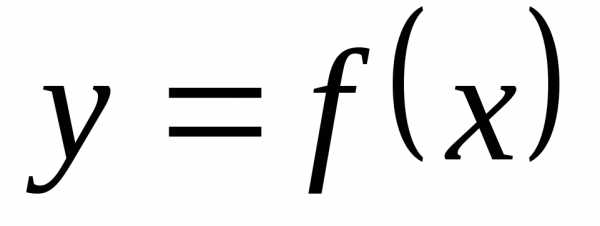 в точке
в точке 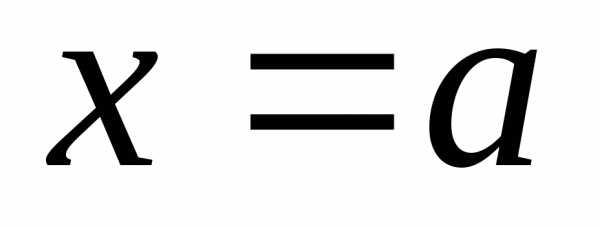 ,
если для любой последовательности
значений аргумента ,
сходящейся к a,
элементы
,
если для любой последовательности
значений аргумента ,
сходящейся к a,
элементы 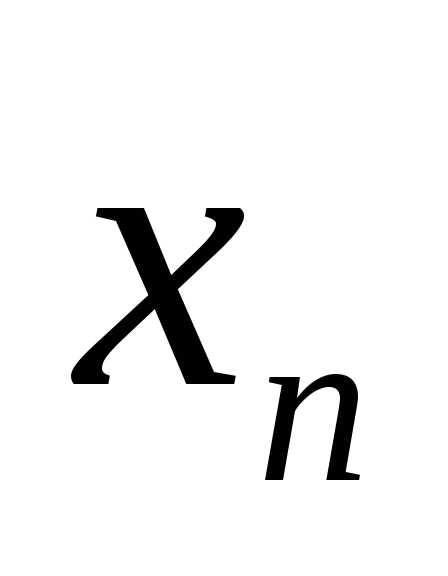 которой больше (меньше)
которой больше (меньше)
Обозначения: илидля правого предельного значения,
или для левого предельного значения.
Пример 12.3. Для функции правое предельное значениеи левое предельное значение.
♦ Утверждение 12.2. Если в
точке a правое и левое предельные значения
функции 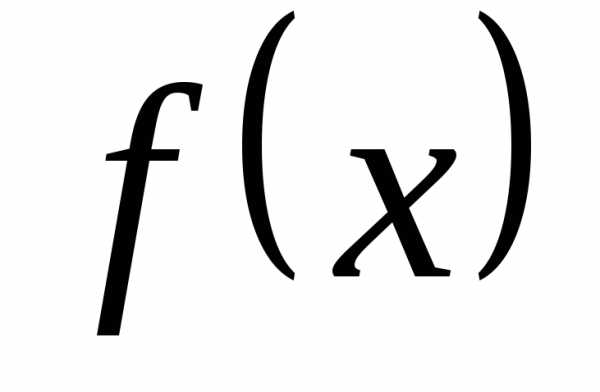 равны, то в точкеa существует предельное значение этой
функции, равное указанным односторонним
предельным значениям.
равны, то в точкеa существует предельное значение этой
функции, равное указанным односторонним
предельным значениям.
Доказательство. Пусть
последовательность 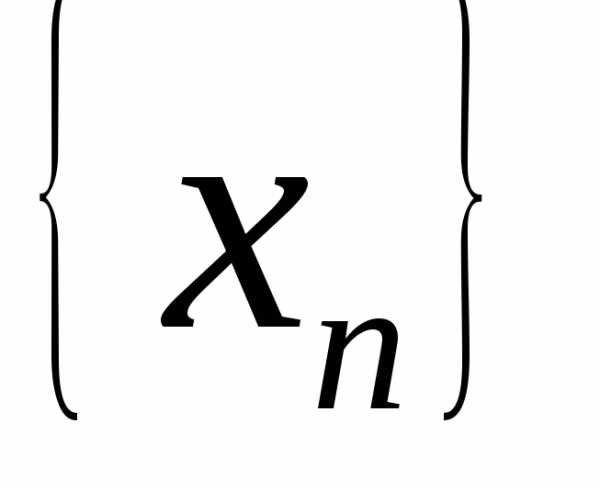 :
: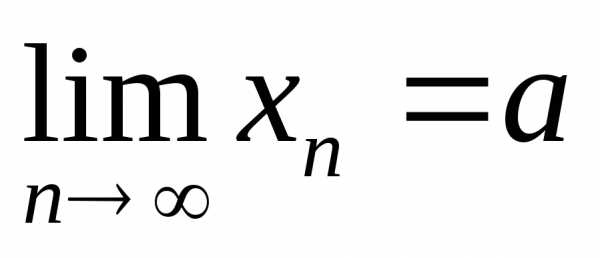 (
(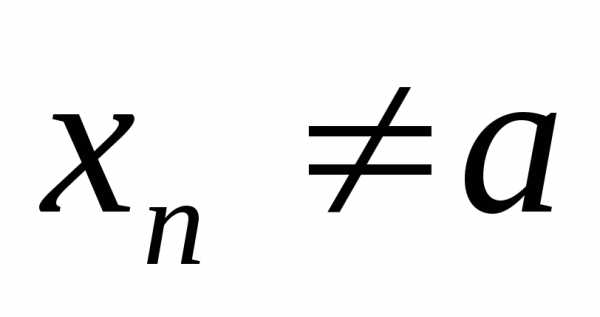 для любогоn). Пусть
подпоследовательность
для любогоn). Пусть
подпоследовательность 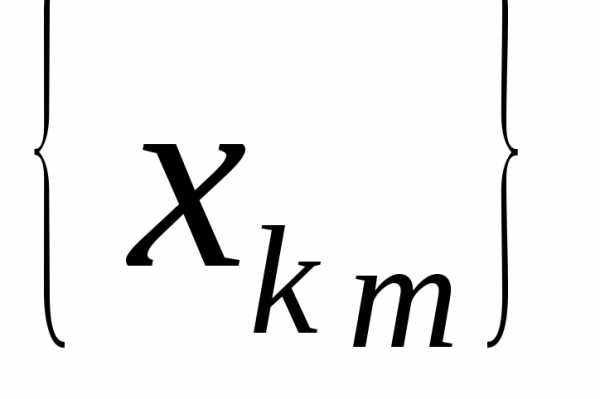
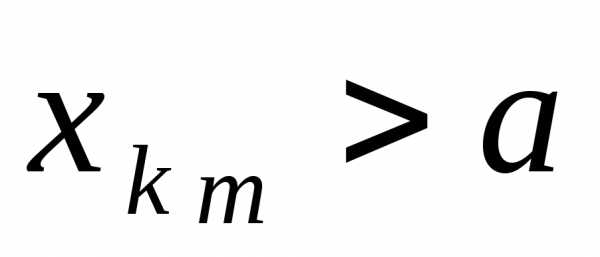 ,
а подпоследовательность
,
а подпоследовательность 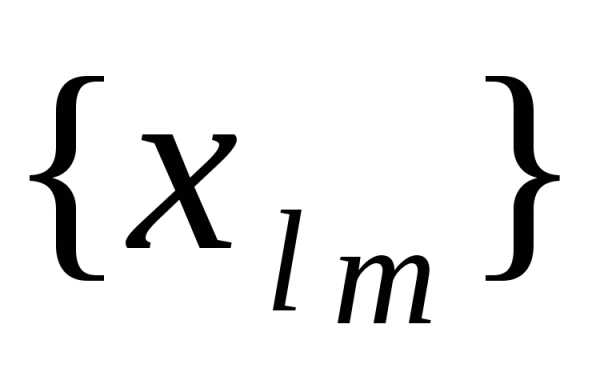 из всех
из всех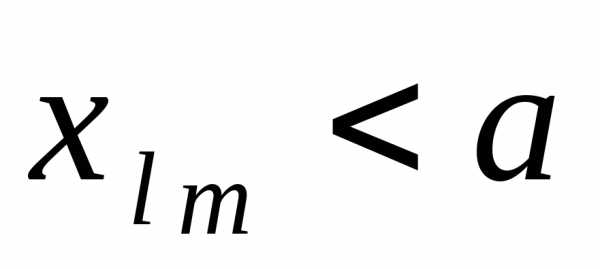 . По условию:
:
. По условию:
: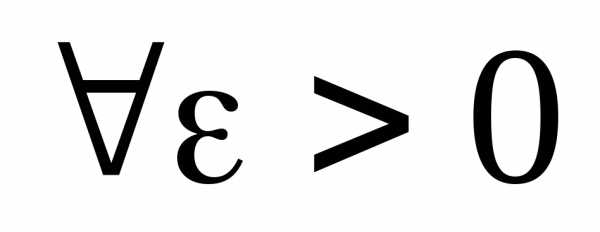 ; ,
; ,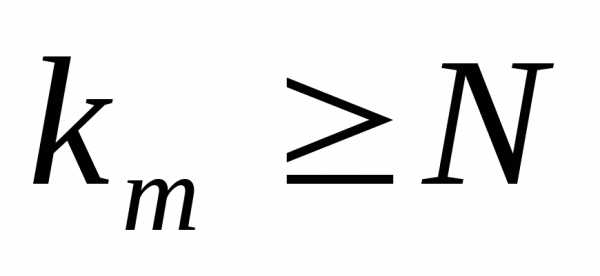 ;,
;,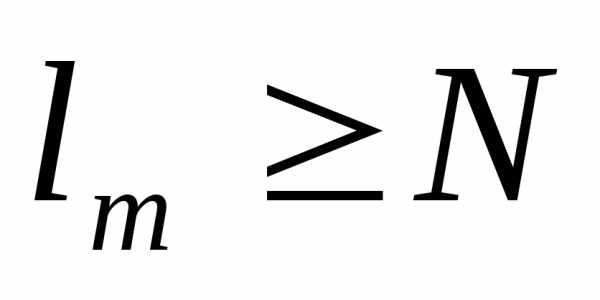 . Так как
и
. Так как
и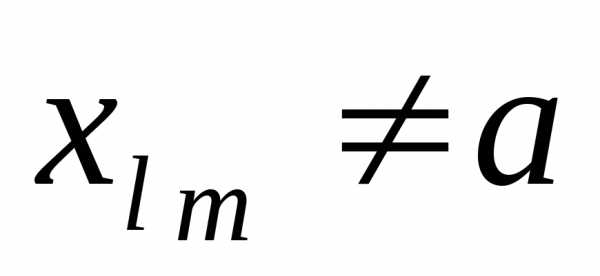 ,
то есть неравенствами охвачены все
элементы
,
то есть неравенствами охвачены все
элементы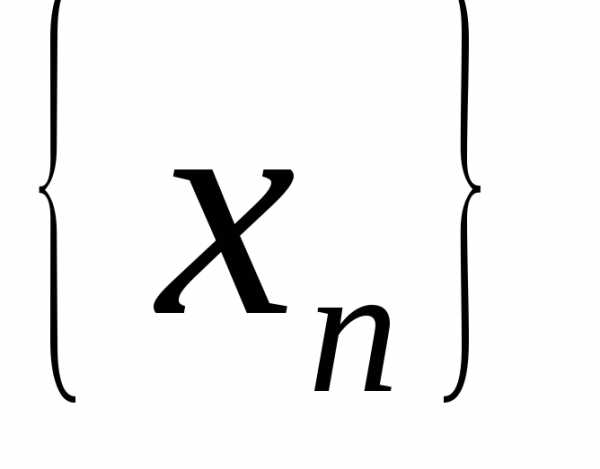 ,
то при всех
,
то при всех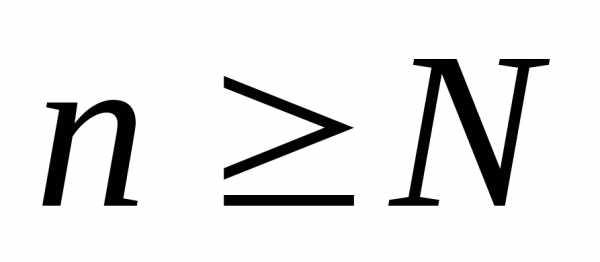 выполняется неравенство .
■
выполняется неравенство .
■Определение 12.4. Число b называется пределом функции при , если для любой бесконечно большой последовательности значений аргумента соответствующая последовательность значений функции сходится к
Обозначение: 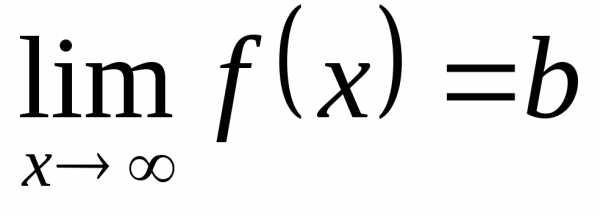 .
.
Определение 12.5. Число b называется предельным
значением функции 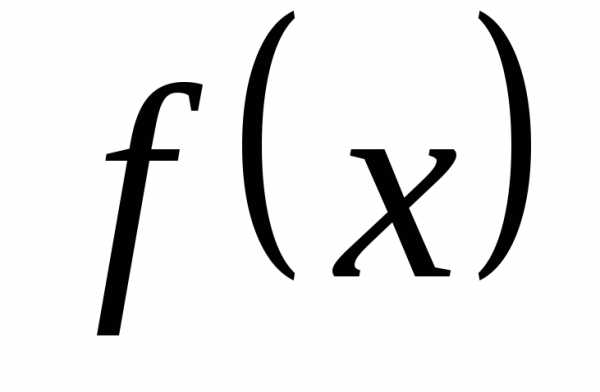 при
стремлении аргумента x к положительной (отрицательной)
бесконечности,
если для любой бесконечно большой
последовательности значений аргумента,
элементы которой, начиная с некоторого
номера, положительны (отрицательны),
соответствующая последовательность
сходится к b.
при
стремлении аргумента x к положительной (отрицательной)
бесконечности,
если для любой бесконечно большой
последовательности значений аргумента,
элементы которой, начиная с некоторого
номера, положительны (отрицательны),
соответствующая последовательность
сходится к b.
Обозначение: 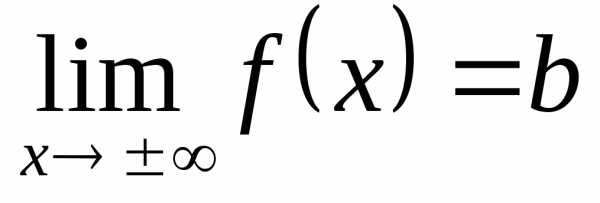 .
.
♦ Теорема 12.1 (критерий
Коши существования предела функции в
точке a). Для того,
чтобы функция 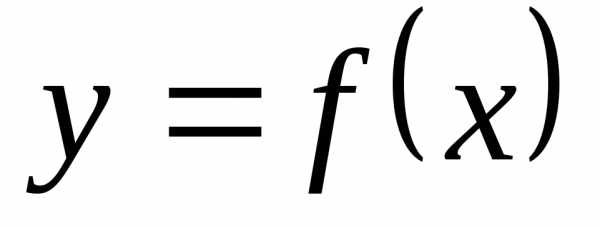 имела в точкеa конечный предел, необходимо и достаточно,
чтобы в точке a функция
имела в точкеa конечный предел, необходимо и достаточно,
чтобы в точке a функция 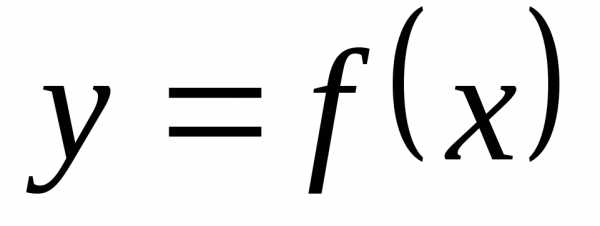 удовлетворяла условию Коши: для любого
сколь угодно малого
удовлетворяла условию Коши: для любого
сколь угодно малого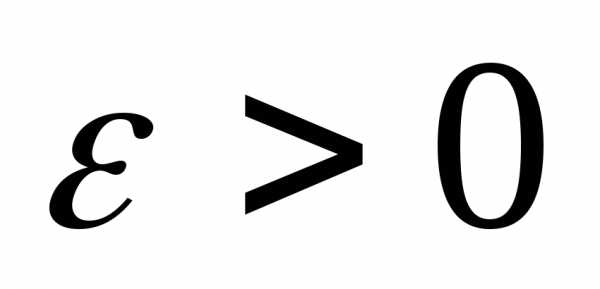 найдется
найдется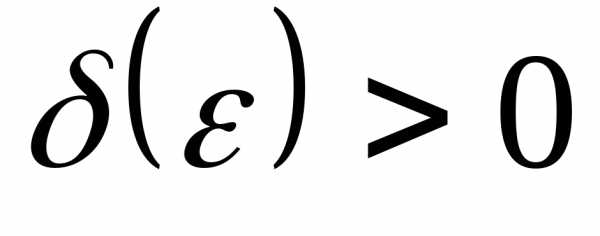 такое, что для любых двух значений
аргумента
такое, что для любых двух значений
аргумента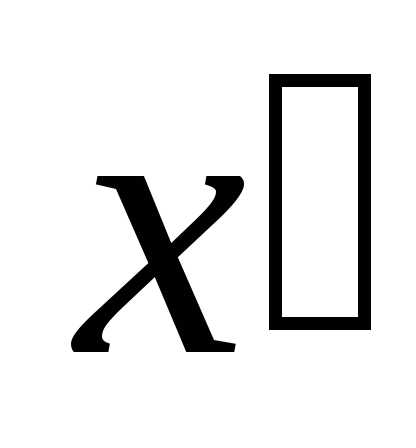 и
и ,
удовлетворяющих условиям;,
справедливо неравенство.
,
удовлетворяющих условиям;,
справедливо неравенство.
12.2. Арифметические операции над функциями, имеющими предельные значения.
Арифметические операции над функциями, имеющими предел в точке a, приводят к функциям, также имеющим предел в точке a
♦ Теорема 12.2. Пусть две
функции 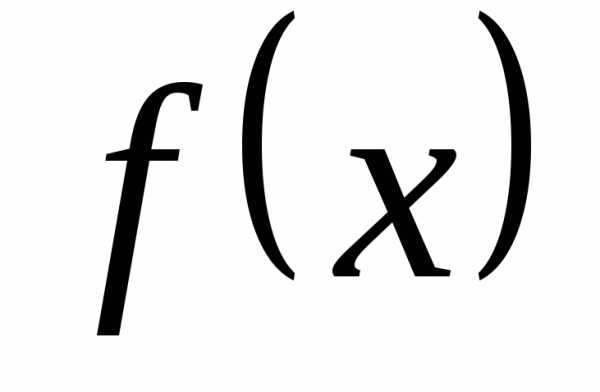 и
и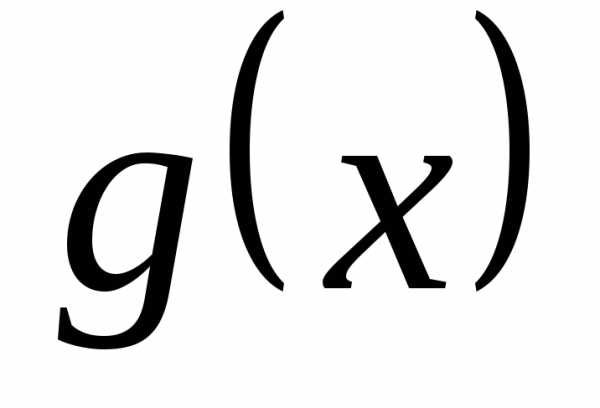 заданы на одном и том же множестве
заданы на одном и том же множестве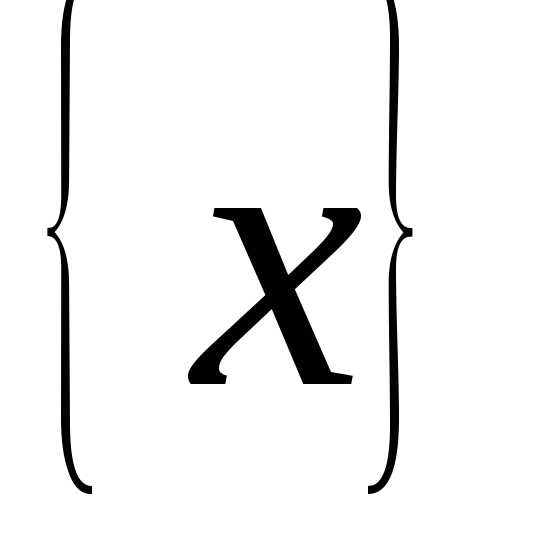 и имеют в точкеa пределы, равные b и c.
Тогда
и имеют в точкеa пределы, равные b и c.
Тогда
,
,
.
Доказательство. Пусть
– произвольная, сходящаяся ка последовательность значений аргумента
функций 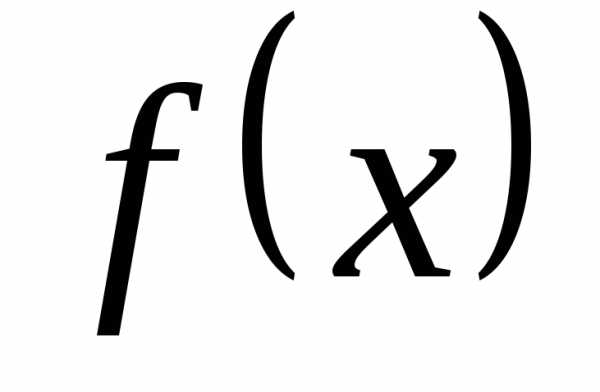 и
и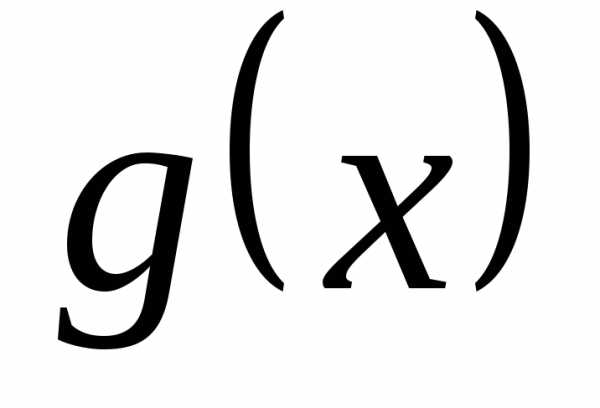 .
Соответствующие последовательности
.
Соответствующие последовательности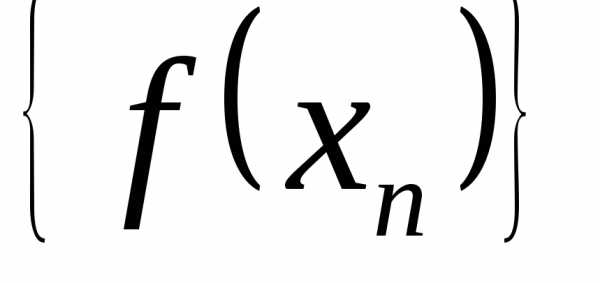 и
и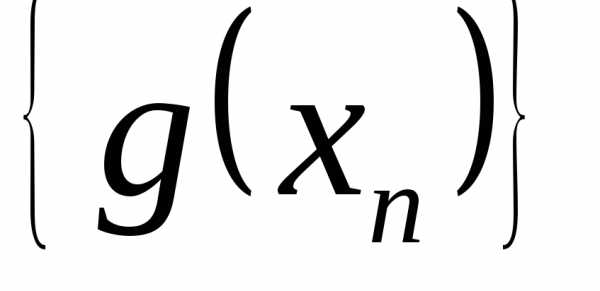 значений этих функций имеют пределыb и c.
Но тогда, в силу теорем 9.3-9.5, последовательности
,и
значений этих функций имеют пределыb и c.
Но тогда, в силу теорем 9.3-9.5, последовательности
,и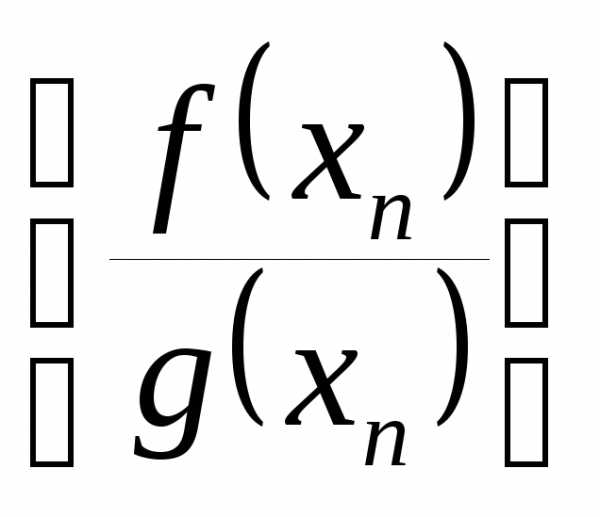
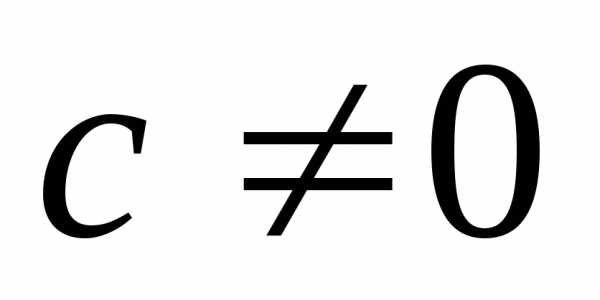 имеют пределы, соответственно равные
имеют пределы, соответственно равные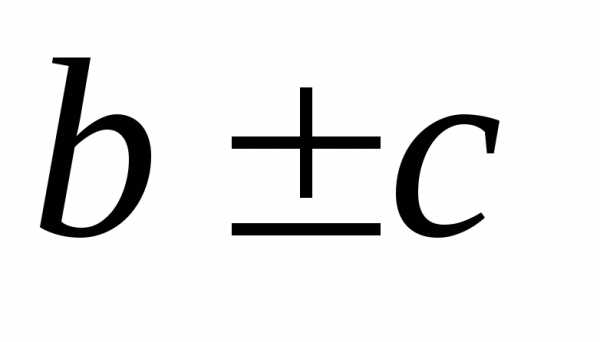 ,
,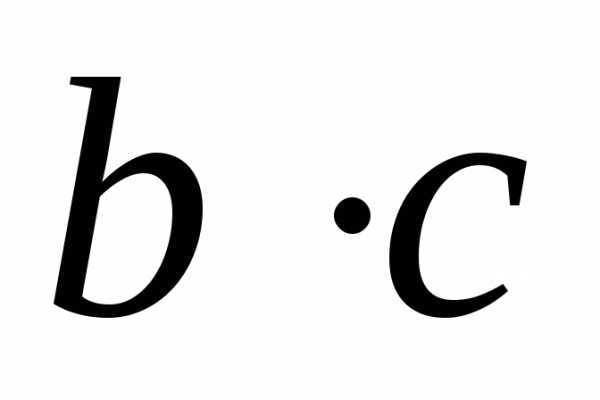 и.
Согласно определению 12.1 предела функции,
это означает, что , , . ■
и.
Согласно определению 12.1 предела функции,
это означает, что , , . ■♦ Утверждение 12.3. Многочлен степени n , где, имеет предел в любой точке, причём этот пределравен частному значению многочлена в точкеa.
Доказательство: Так как 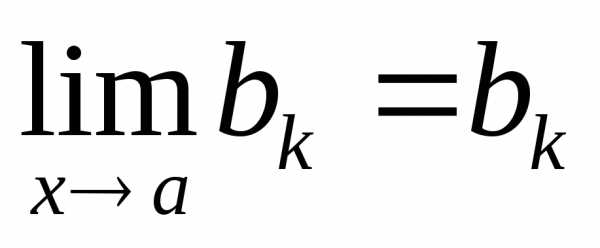 ,
,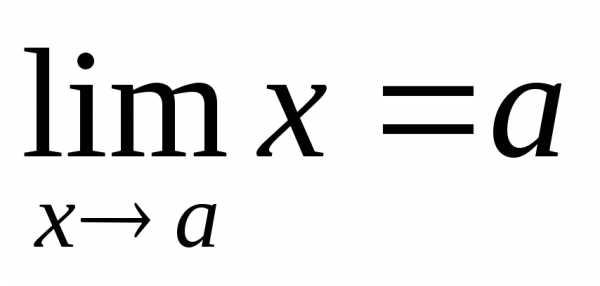 ,
то
,
то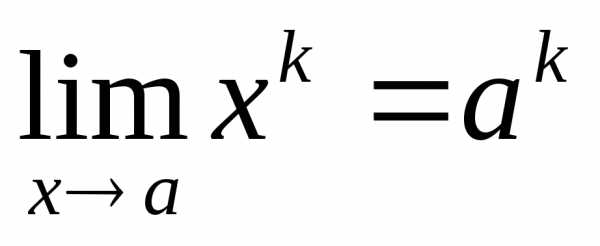 и. ■
и. ■
♦ Утверждение 12.4. Рациональная
дробь (частное 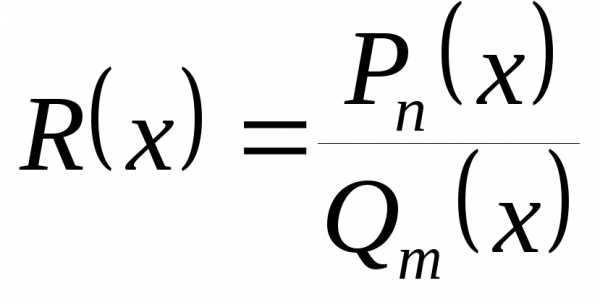 )
имеет предел в любой точке,
не являющейся корнем её знаменателя,
причём
)
имеет предел в любой точке,
не являющейся корнем её знаменателя,
причём
.
12.3. Бесконечно малые и бесконечно большие функции.
Определение 12.6. Функция 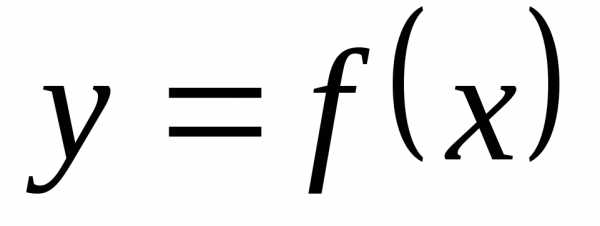 называетсябесконечно
малой в точке
называетсябесконечно
малой в точке 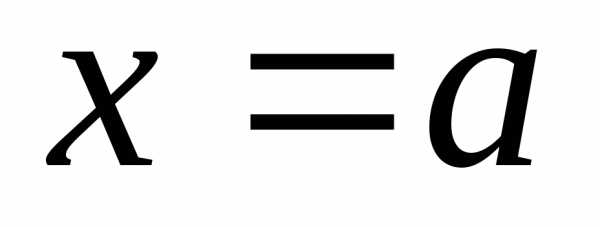 (при),
если
(при),
если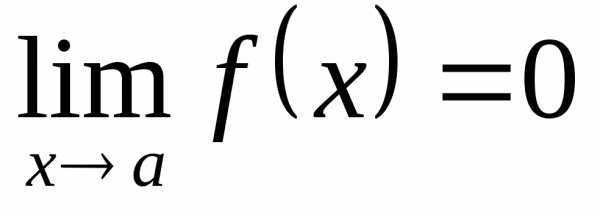 .
.
Например,
,
где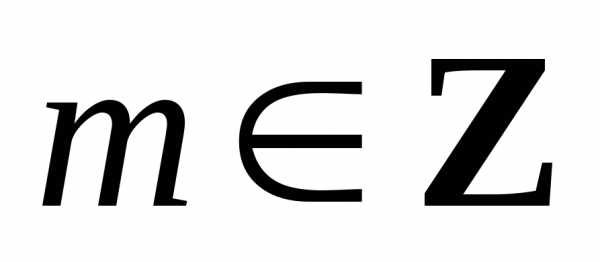 ,
– бесконечно малая функция в любой
точке,
в силу утверждения 12.3:
,
– бесконечно малая функция в любой
точке,
в силу утверждения 12.3:
.
☼ Замечание 12.3. Если 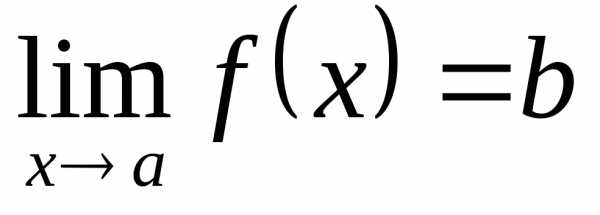 ,
то
– бесконечно малая в точкеa.
Отсюда следует специальное представление
функции
,
где
,
то
– бесконечно малая в точкеa.
Отсюда следует специальное представление
функции
,
где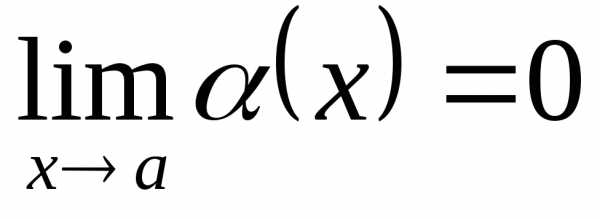 .
Говорят, что функция
.
Говорят, что функция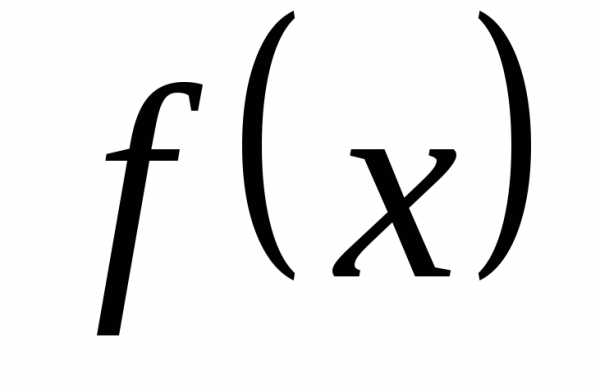 асимптотически равнаb при
.☼
асимптотически равнаb при
.☼
Определение 12.7. Функция 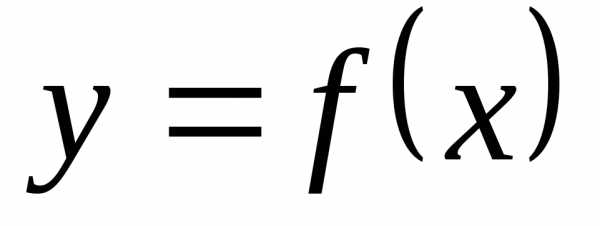 называетсябесконечно
большой в точке
называетсябесконечно
большой в точке 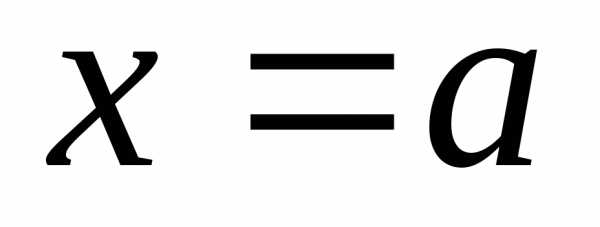 справа
(слева),
если для любой последовательности
справа
(слева),
если для любой последовательности 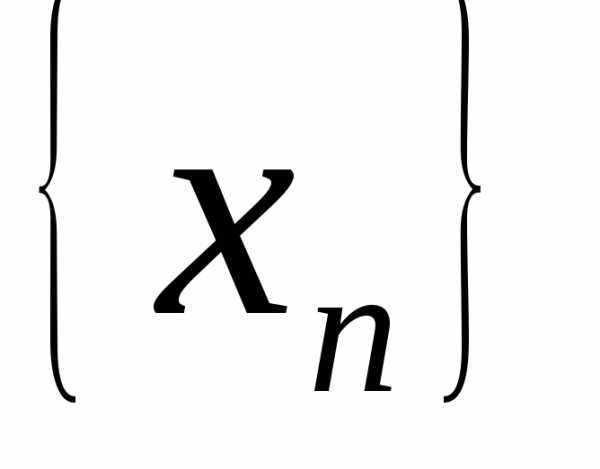 :
: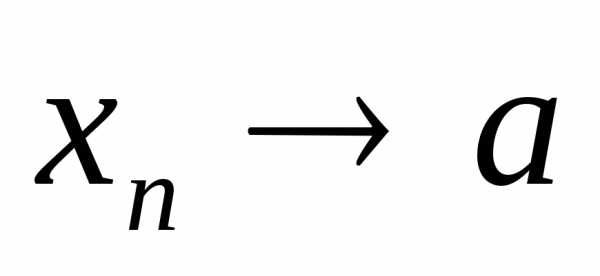 при,
при,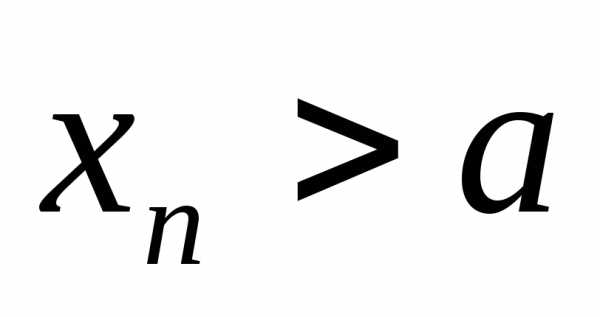 (
(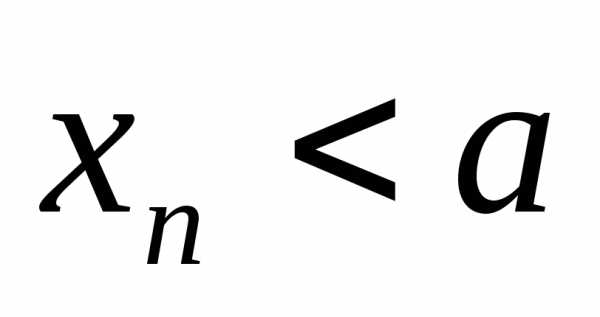 ),
соответствующая последовательность
),
соответствующая последовательность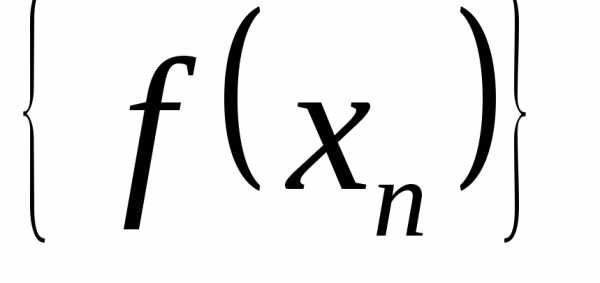 значений функции является бесконечно
большой последовательностью определённого
знака.
значений функции является бесконечно
большой последовательностью определённого
знака.
Например, функция 
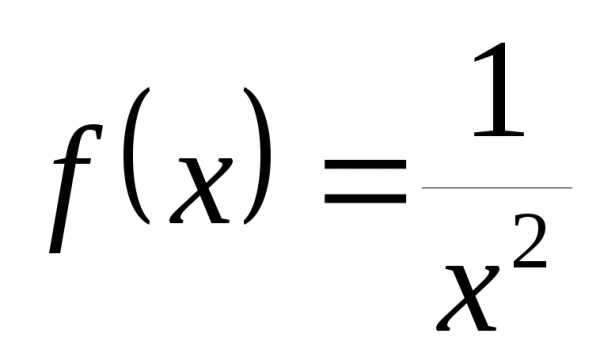 является бесконечно большой при
является бесконечно большой при ,
,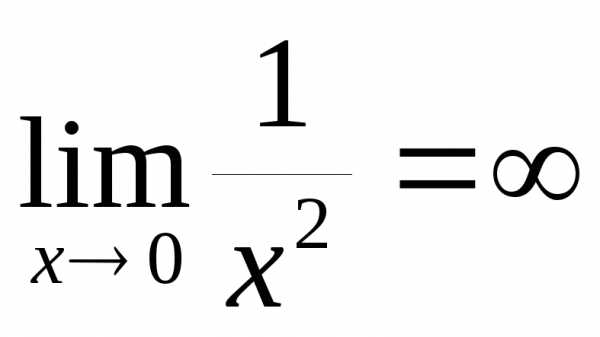 .
.
Возможны ситуации и для случая односторонних пределов:
; .
Рассмотрим функцию 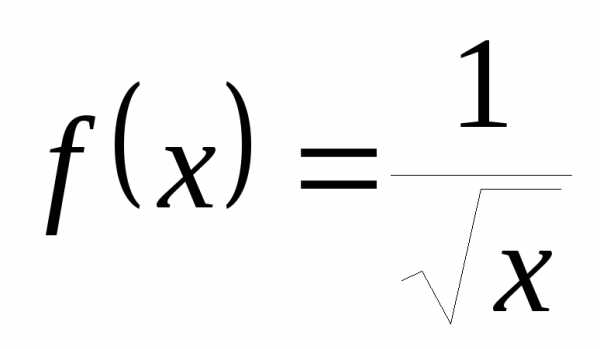 вблизи точки
вблизи точки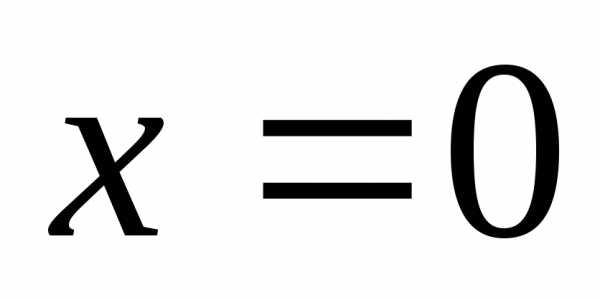 .
Так как она определена лишь при
.
Так как она определена лишь при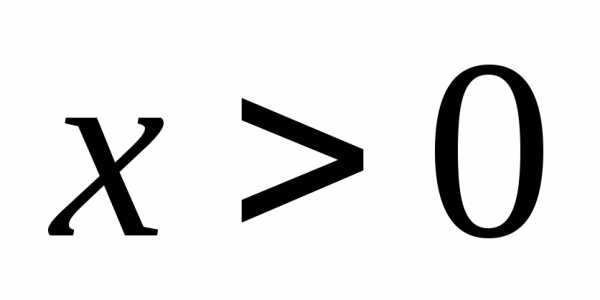 ,
то вблизи
,
то вблизи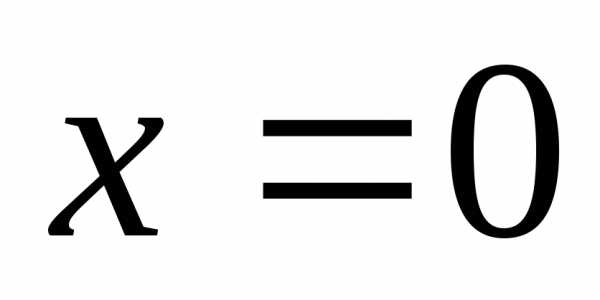 её можно исследовать только при:
её можно исследовать только при: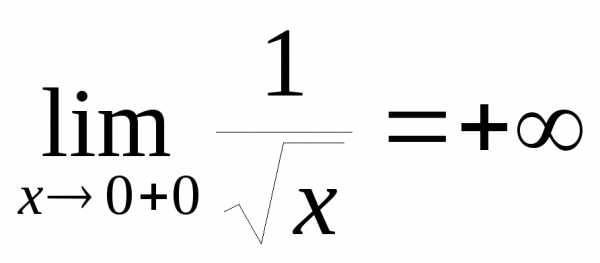 .
То есть функция
.
То есть функция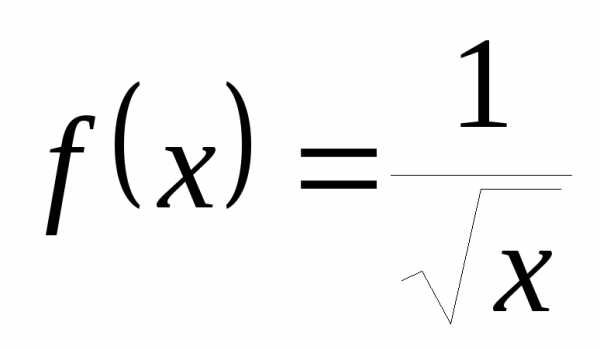 – положительная бесконечно большая
при.
– положительная бесконечно большая
при.
12.4. Сравнение бесконечно малых и бесконечно больших функций.
Определение 12.8. Пусть 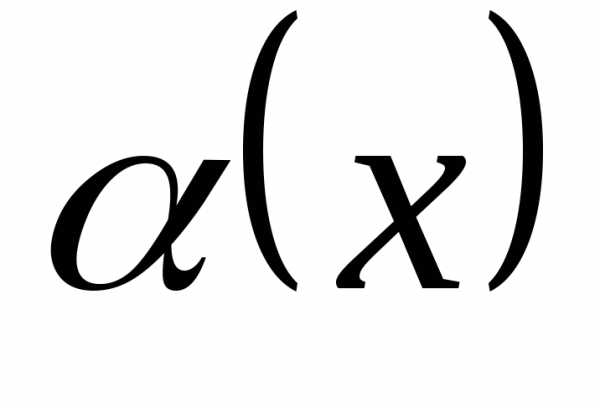 и
и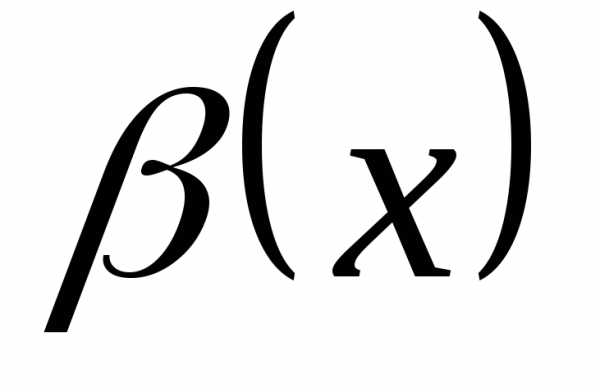 – две бесконечно малые в точке
– две бесконечно малые в точке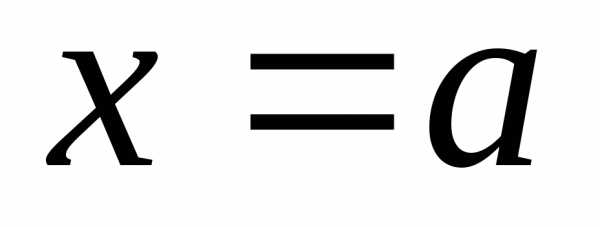 функции и пусть существует
функции и пусть существует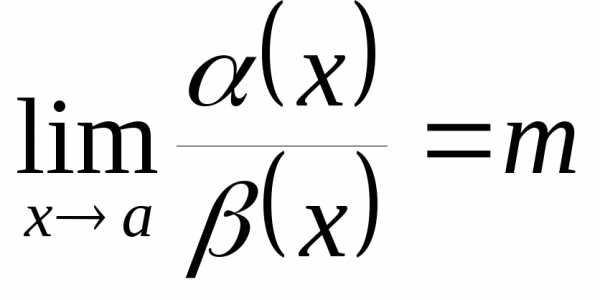 .
Если
.
Если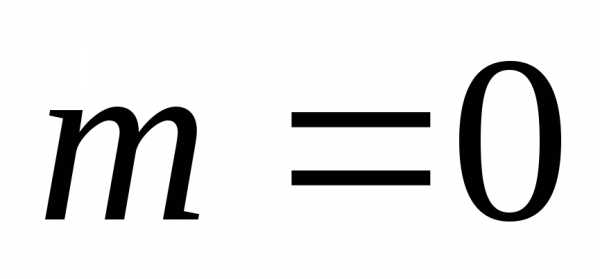 ,
то
,
то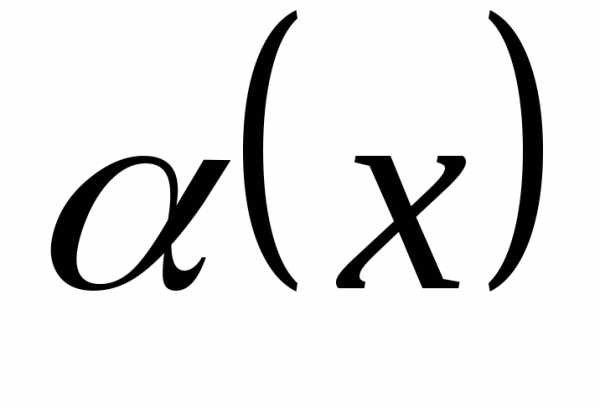 –бесконечно
малая более высокого порядка,
чем
–бесконечно
малая более высокого порядка,
чем 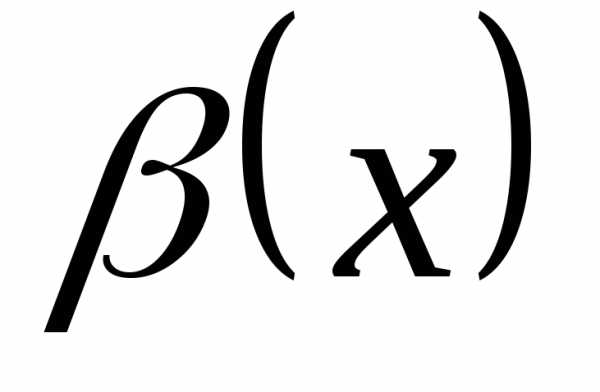 . Если
. Если 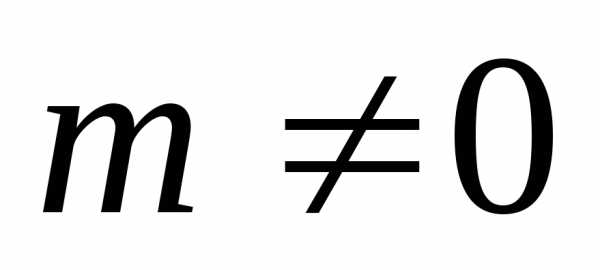 ,
то
,
то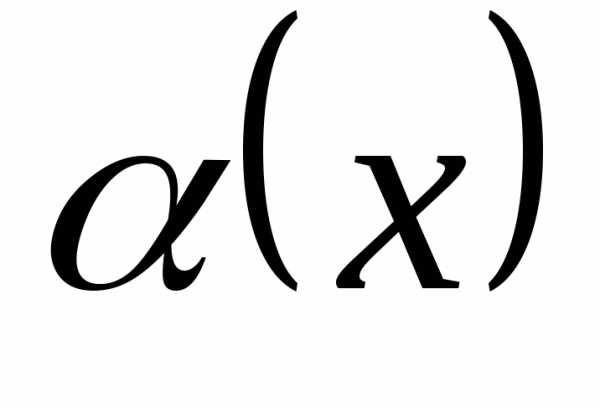 и
и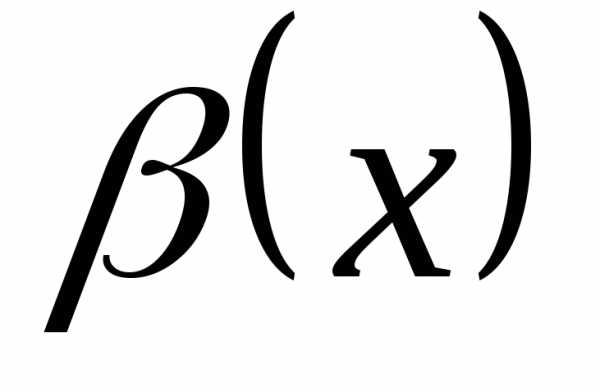 –бесконечно
малые одного порядка. Если
–бесконечно
малые одного порядка. Если 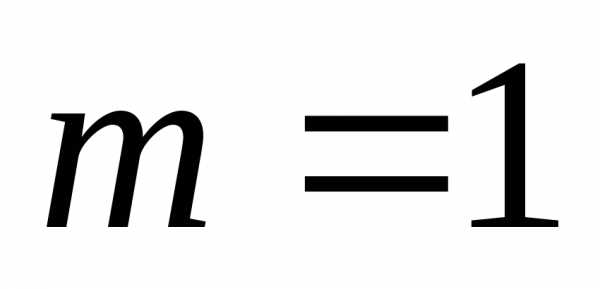 ,
то
,
то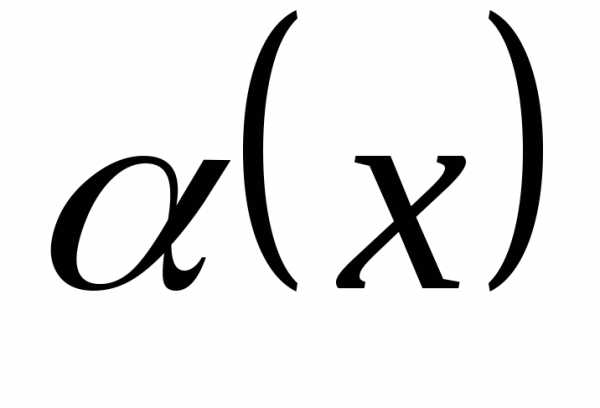 и
и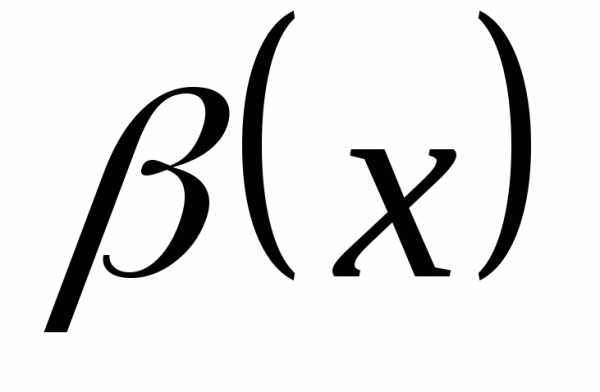 –эквивалентные
бесконечно малые.
–эквивалентные
бесконечно малые.
В качестве стандартной функции сравнения берут функцию .
Говорят, что
бесконечно малая функция 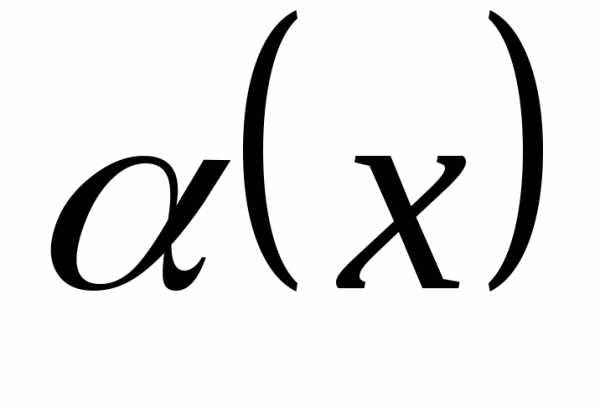 имеет порядок малостиm,
если
имеет порядок малостиm,
если 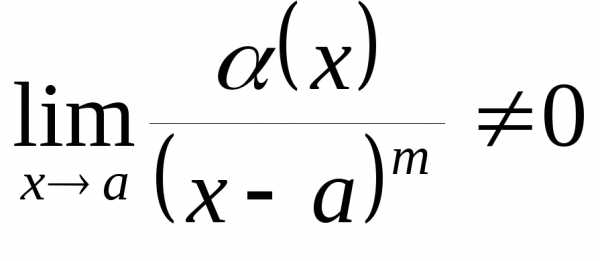 .
.
Используется
следующая символика: 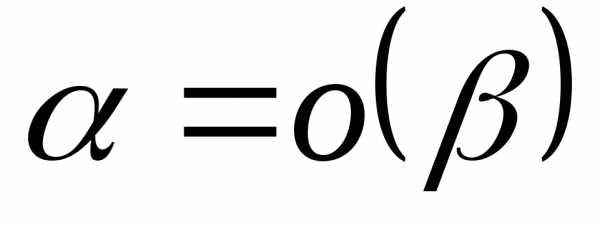 (
( равноo малое от
равноo малое от  ),
если
),
если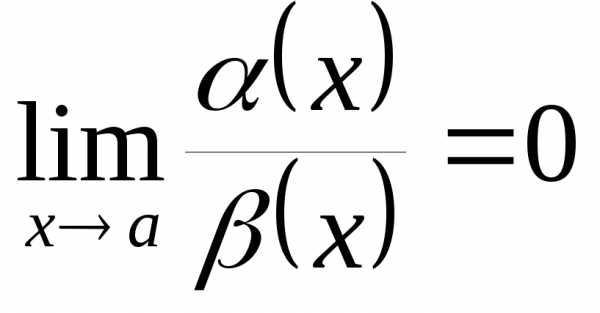 .
.
Пример 12.4. 1) и 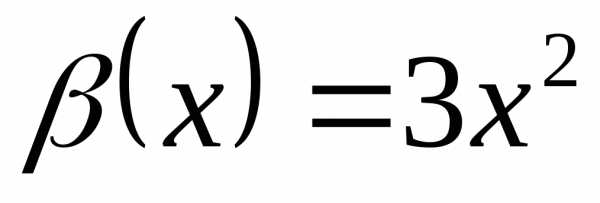 – бесконечно малые одного порядка при
– бесконечно малые одного порядка при  ,
так как
,
так как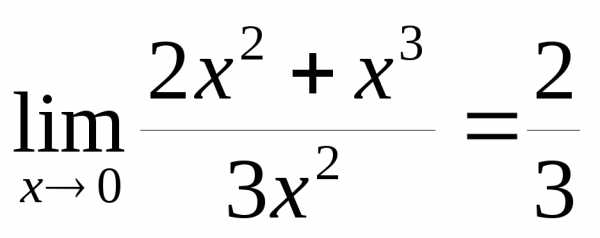 .
.
2) и 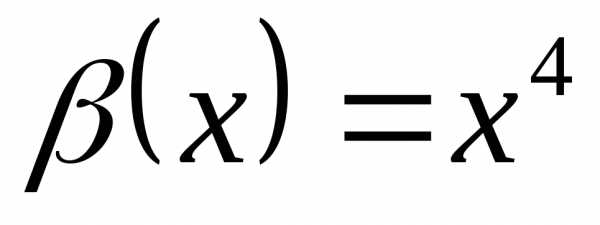 – эквивалентные бесконечно малые при
– эквивалентные бесконечно малые при  ,
так как
,
так как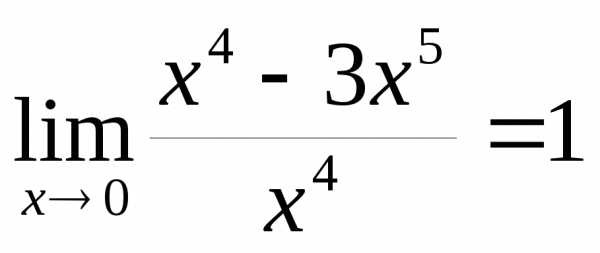 .
.
3) 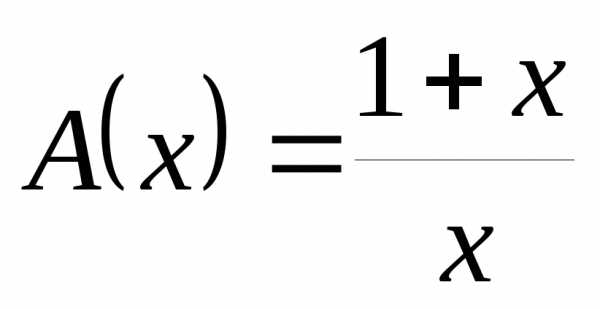 и
и 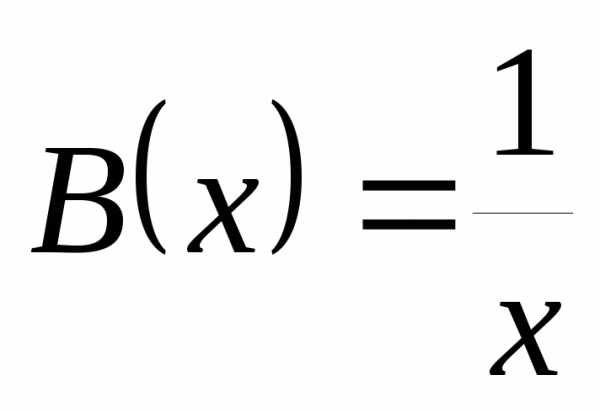 имеют одинаковый порядок роста при
имеют одинаковый порядок роста при  справа и слева, так как
справа и слева, так как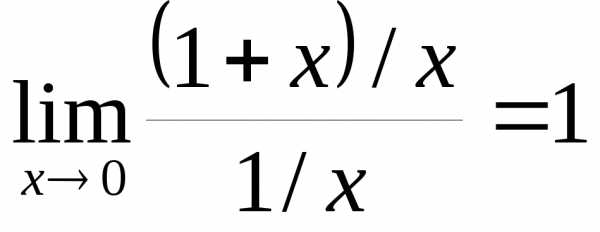 .
.
Аналогично сравниваются бесконечно большие функции.
Определение 12.9. Пусть 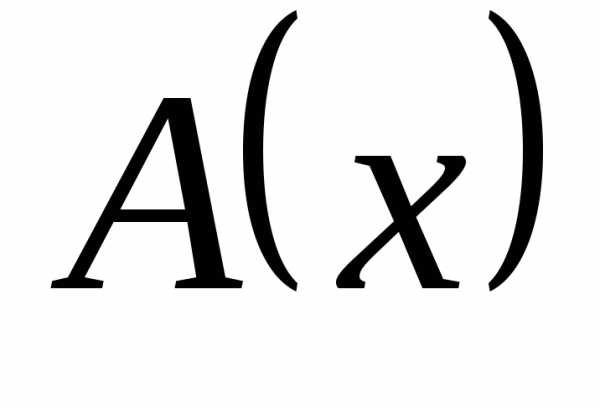 и
и 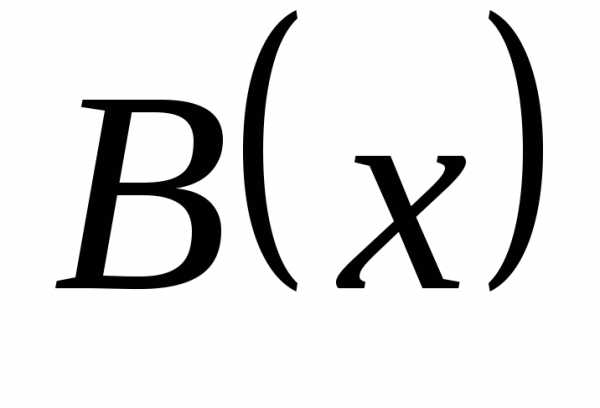 – бесконечно большие в точке
– бесконечно большие в точке 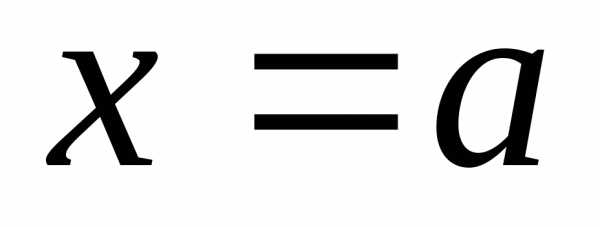 справа функции одного знака: , .
Если
справа функции одного знака: , .
Если 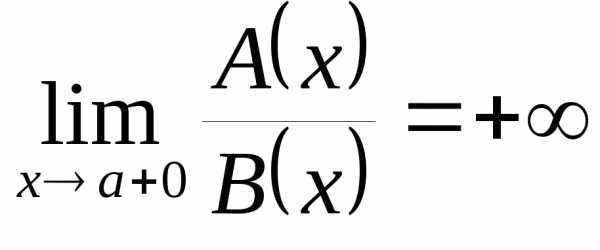 ,
то
,
то 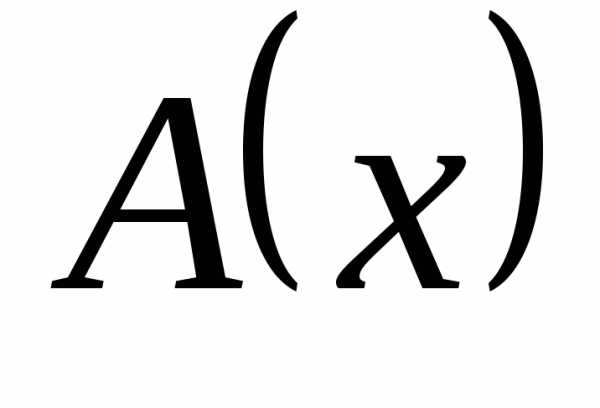 имеет
более высокий порядок роста в точке a справа, чем
имеет
более высокий порядок роста в точке a справа, чем 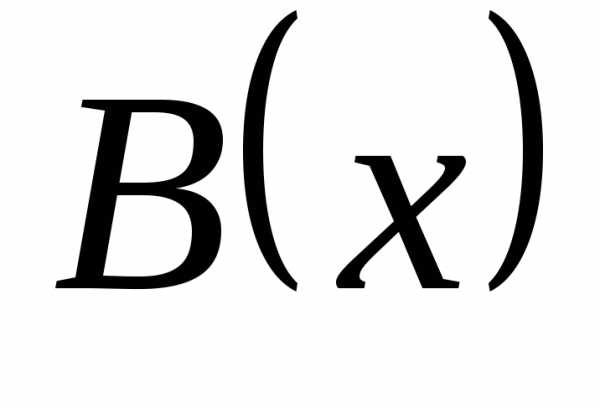 .
Если
.
Если 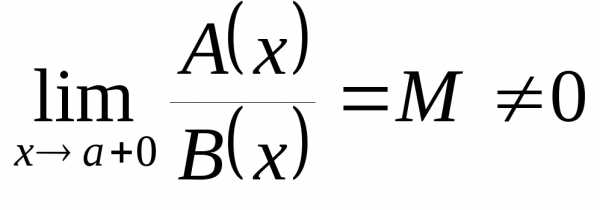 ,
то
,
то 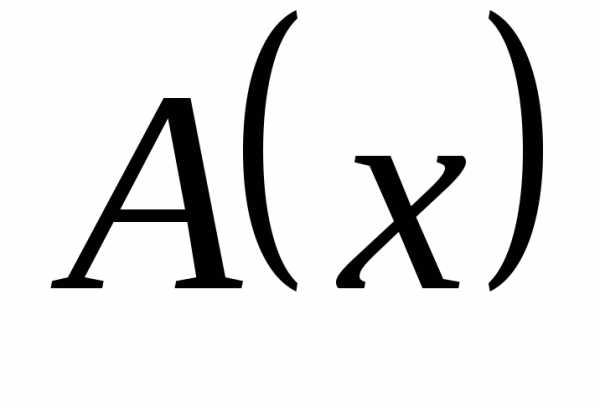 и
и 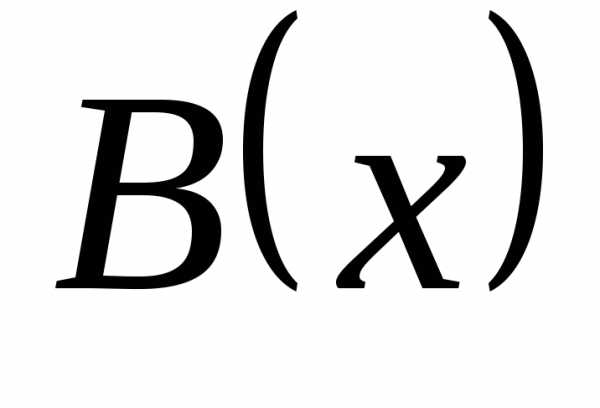 имеют в точке a справа одинаковый порядок роста. Если
имеют в точке a справа одинаковый порядок роста. Если 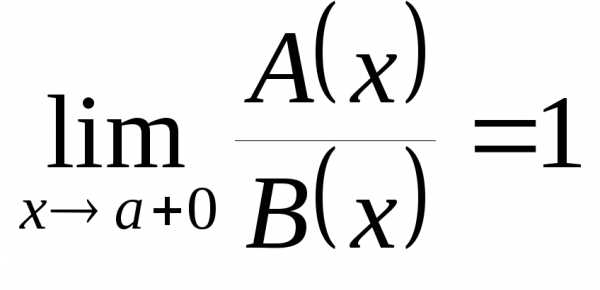 ,
то
,
то 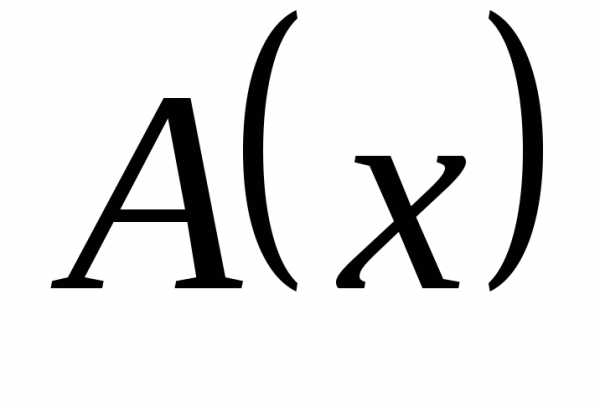 и
и 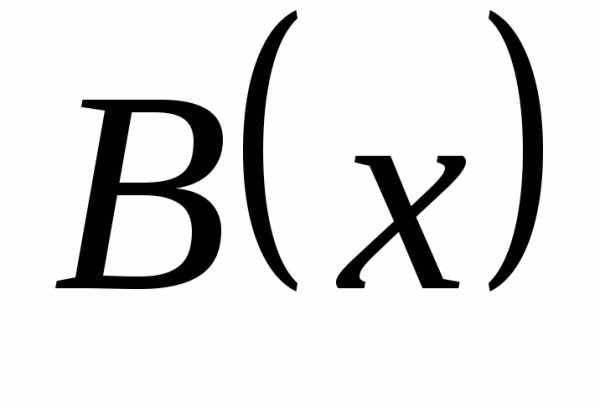 – эквивалентные
бесконечно большие функции.
– эквивалентные
бесконечно большие функции.
Таковы же правила сравнения бесконечно больших функций и при .
Пример 12.5. 1)
, .
Так как 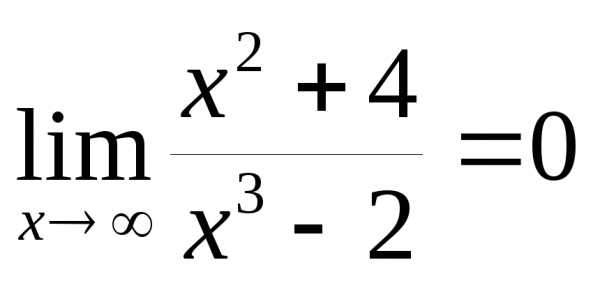 ,
то
,
то 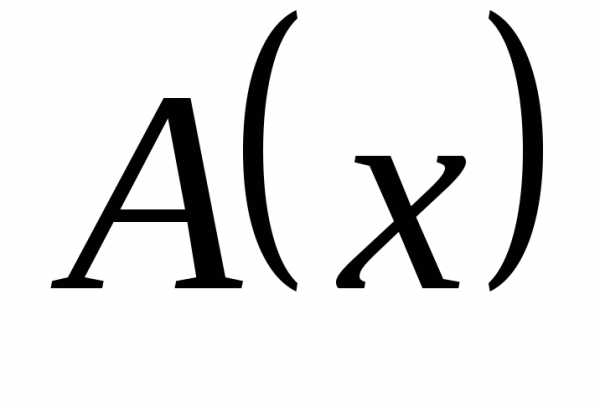 – бесконечно большая более низкого
порядка, чем
– бесконечно большая более низкого
порядка, чем 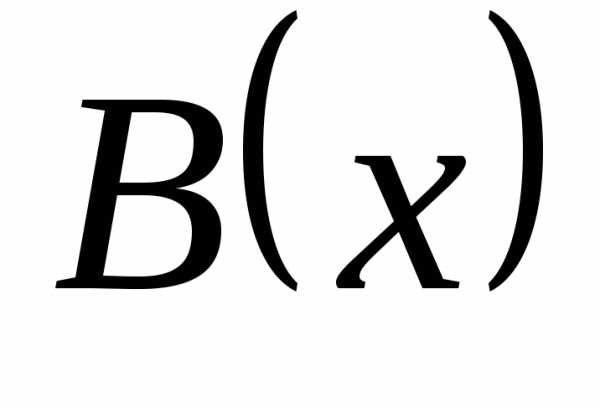 .
А
.
А 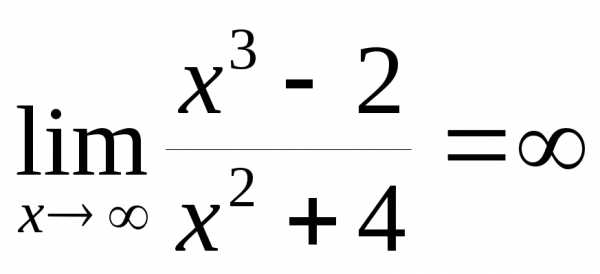 ,
поэтому
,
поэтому 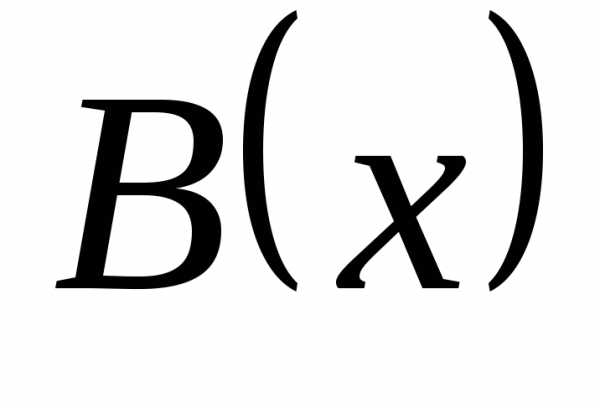 – бесконечно большая более высокого
порядка, чем
– бесконечно большая более высокого
порядка, чем 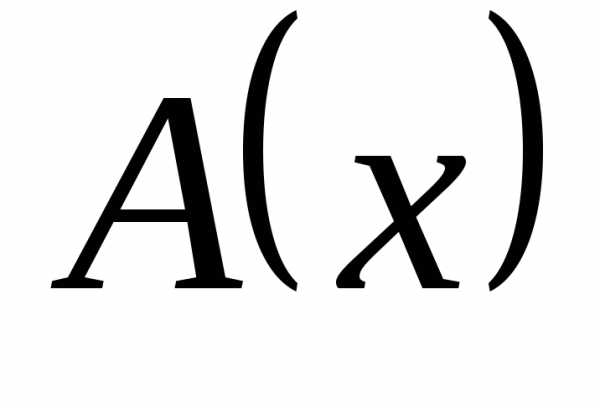 .
.
2)
, . 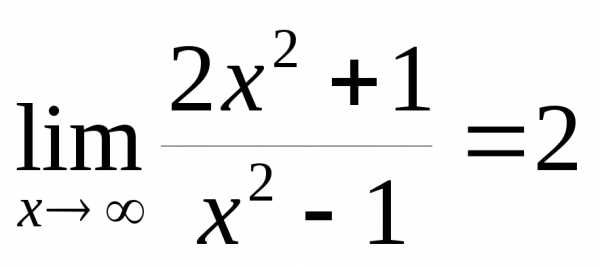 – таким образом,
– таким образом, 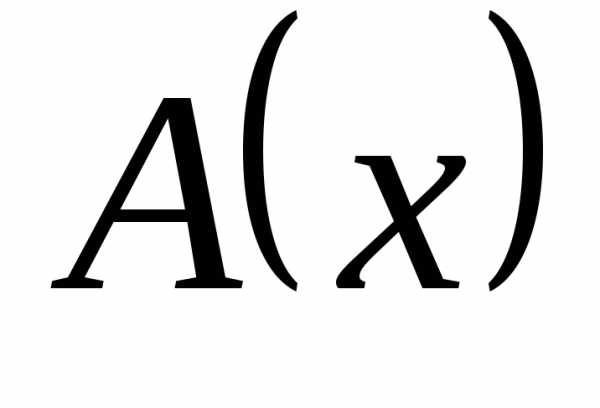 и
и 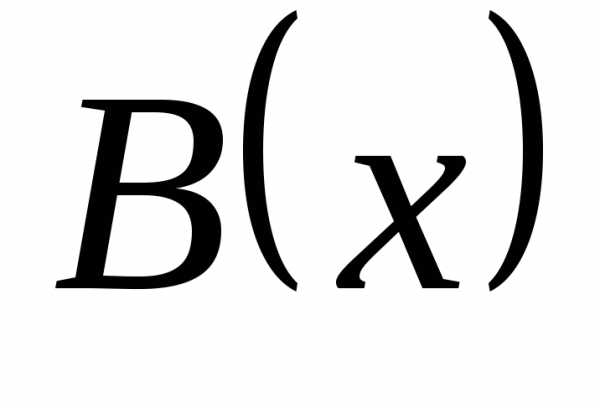 – бесконечно большие одного порядка
(один порядок роста).
– бесконечно большие одного порядка
(один порядок роста).
3)
, .
Здесь 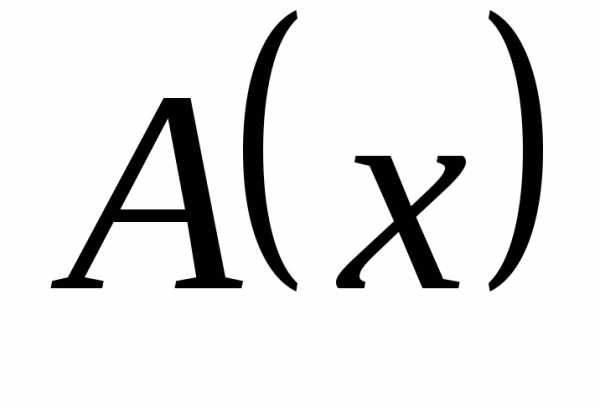 – бесконечно большая второго порядка
по отношению к
– бесконечно большая второго порядка
по отношению к 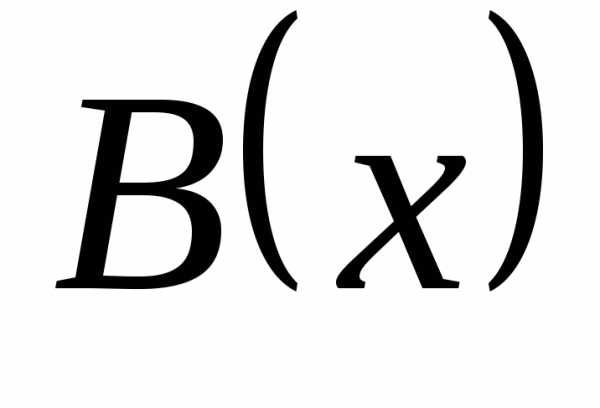 .
.
Таким образом, при вычислении предела отношения члены отношения можно заменять на эквивалентные.
Пример 12.6. 1)  .
.
2) .
3) .
Таким образом,
если 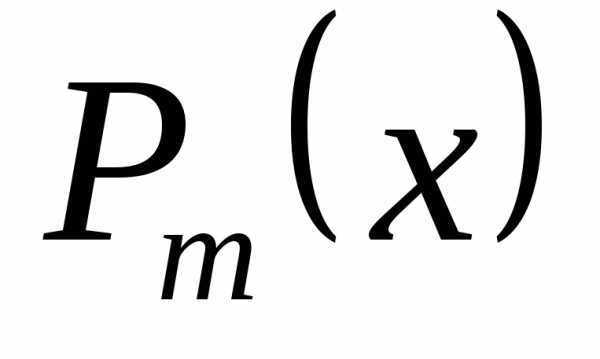 ,
,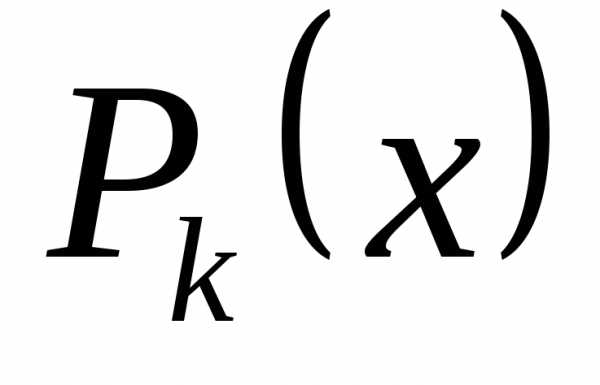 – многочлены степенейm и k соответственно, то
– многочлены степенейm и k соответственно, то 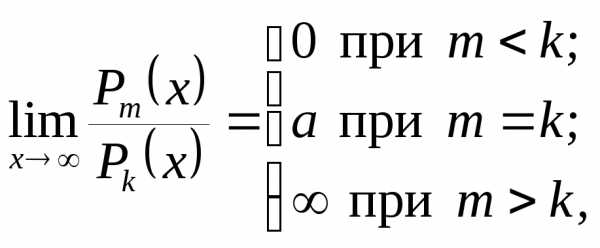 гдеа – отношение коэффициентов при старших
степенях многочленов.
гдеа – отношение коэффициентов при старших
степенях многочленов.
12.5. Связь между бесконечно малыми и бесконечно большими величинами.
♦ Теорема 12.3. 1) Если
функция 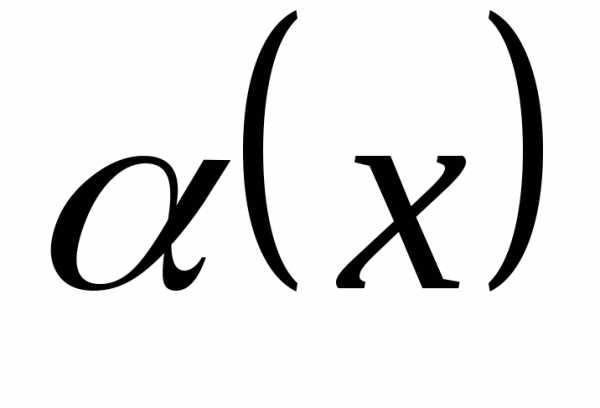 – бесконечно малая при
– бесконечно малая при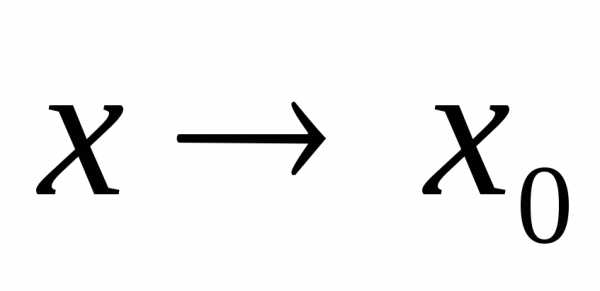
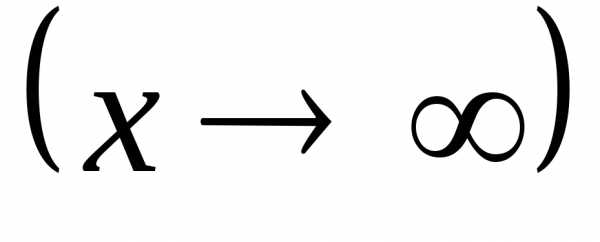 ,
то функция
,
то функция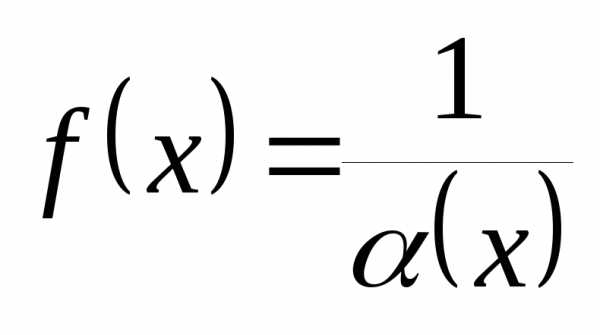 является бесконечно большой при
является бесконечно большой при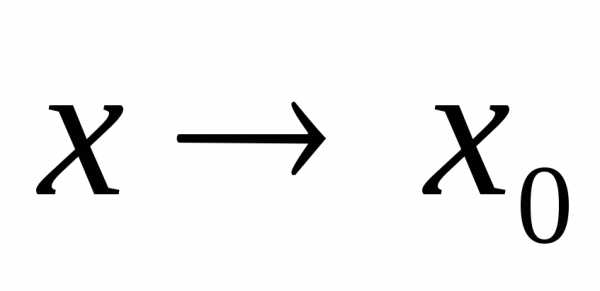
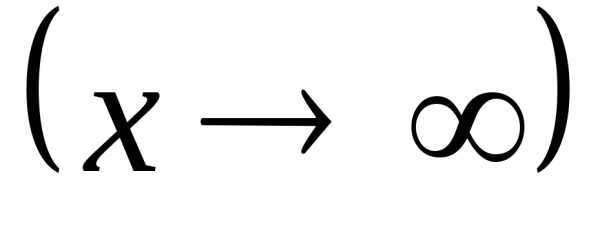 .
.
2) Если функция 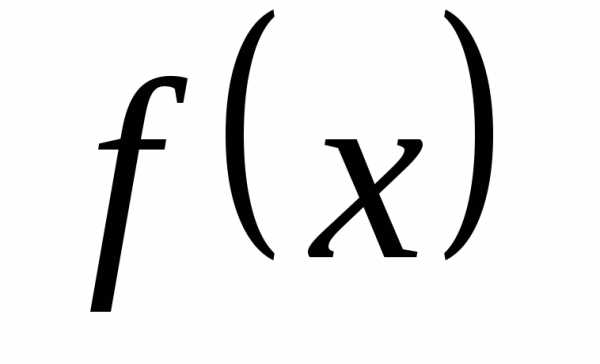 – бесконечно большая при
– бесконечно большая при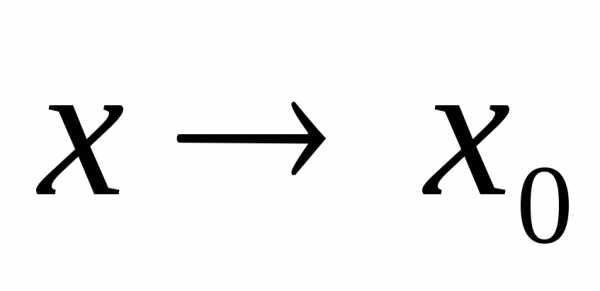
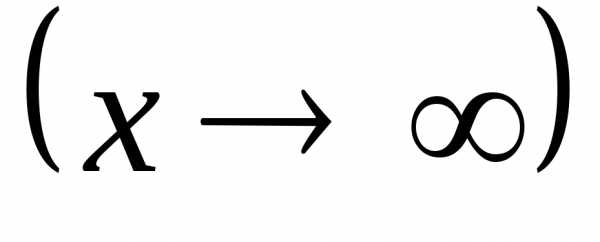 ,
то функция
,
то функция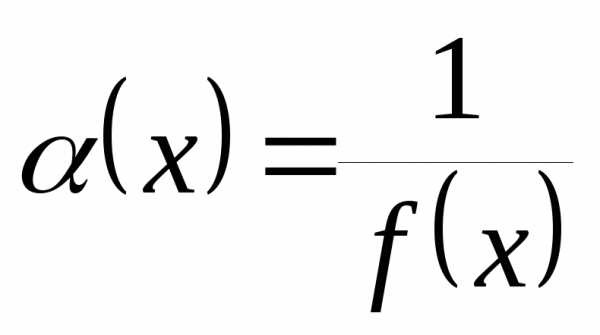 является бесконечно малой при
является бесконечно малой при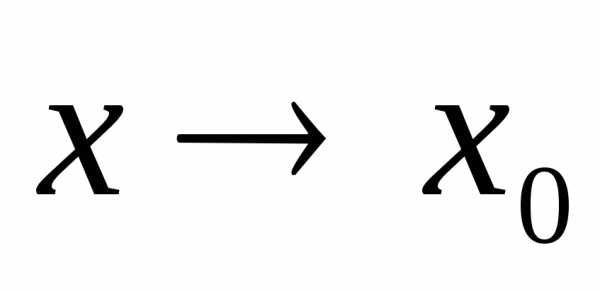
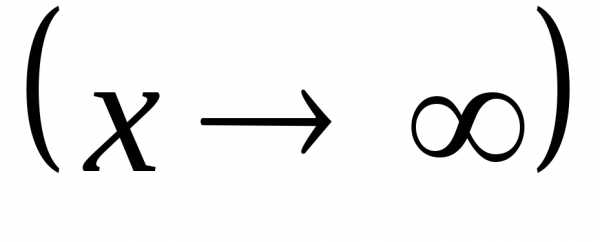 .
.
Доказательство. 1) Пусть при 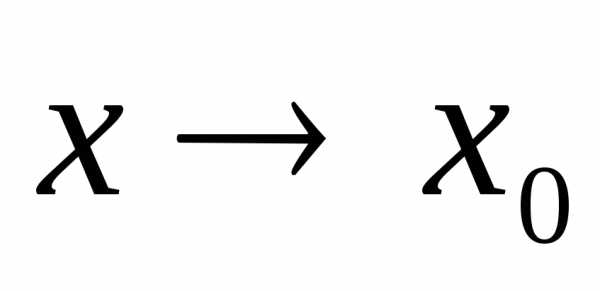
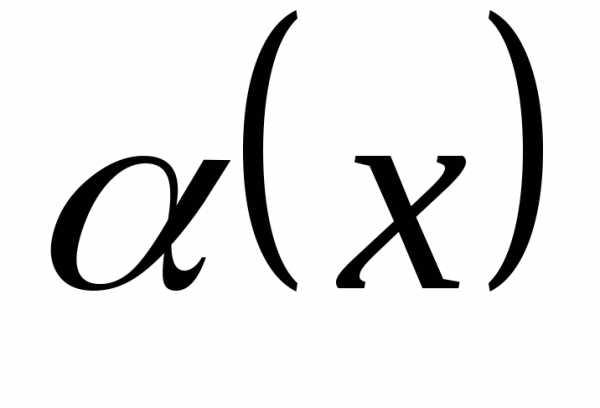 – бесконечно малая, то есть
.
Таким образом,
– бесконечно малая, то есть
.
Таким образом, 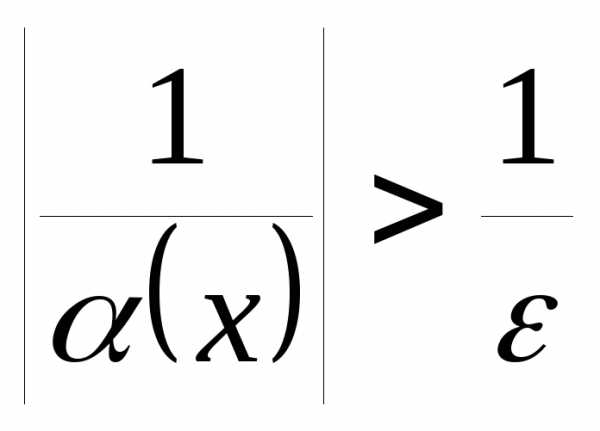 ,
отсюда
,
отсюда 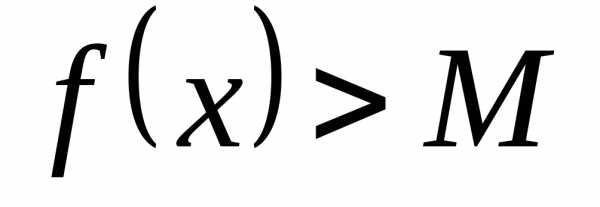 ,
где
,
где 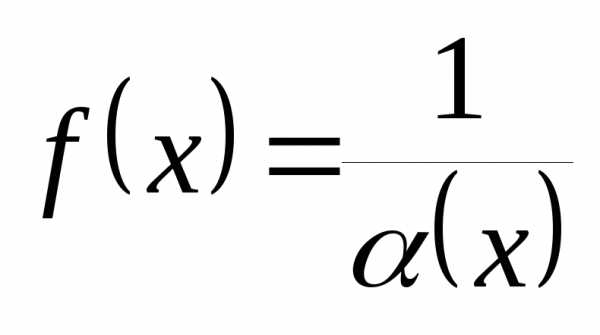 ,
, 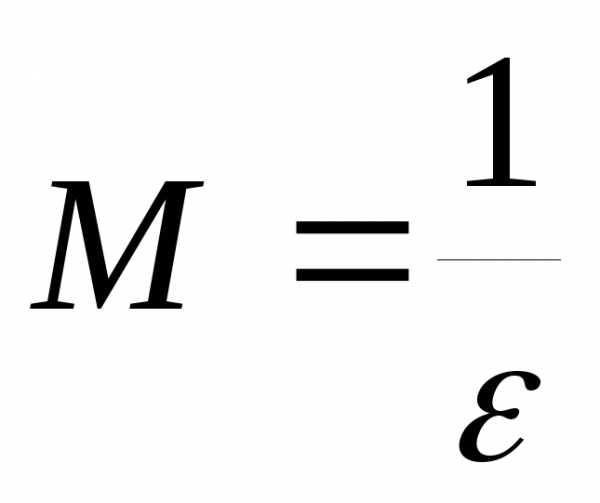 .
Получаем, что функция
.
Получаем, что функция 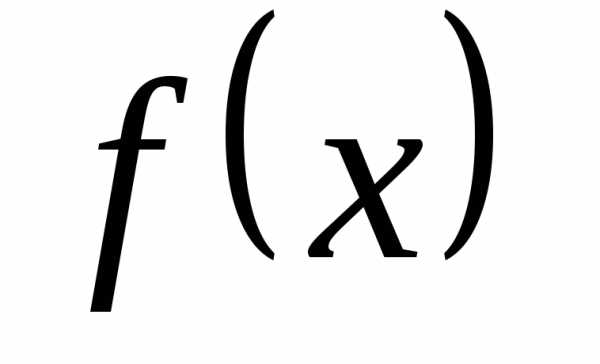 – бесконечно большая.
– бесконечно большая.
2) Доказательство проводится аналогичным образом. ■
Пример 12.7. 1)
при– бесконечно малая, а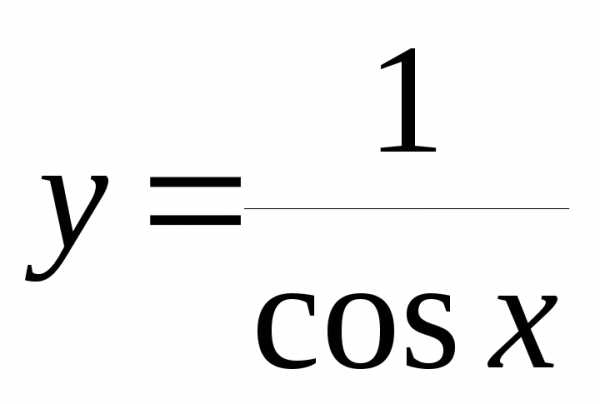 – бесконечно большая величина. При
– бесконечно большая величина. При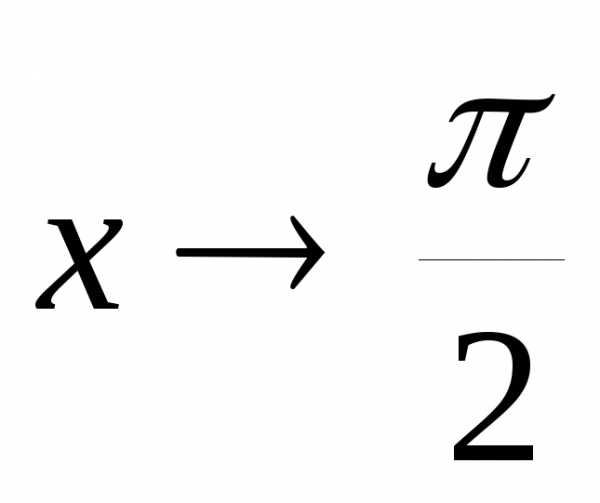 функция
функция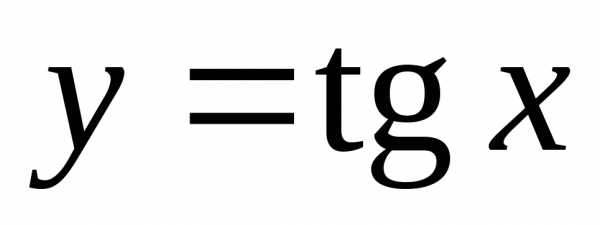 – бесконечно большая, а– бесконечно малая.
– бесконечно большая, а– бесконечно малая.
2) 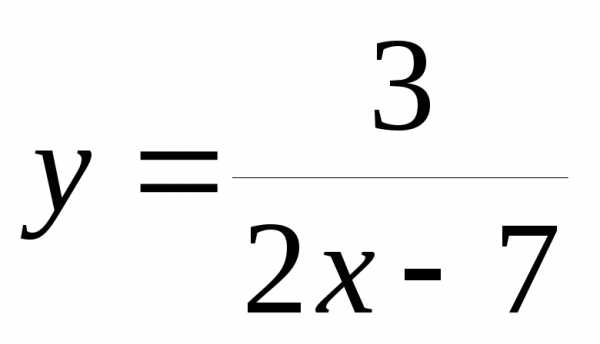 при– бесконечно малая, а
при– бесконечно малая, а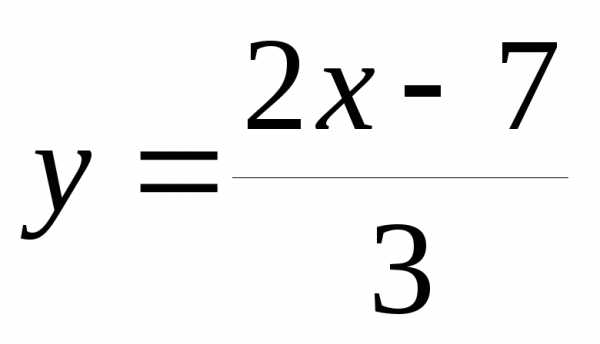 – бесконечно большая.
– бесконечно большая.
3)
при– бесконечно большая, а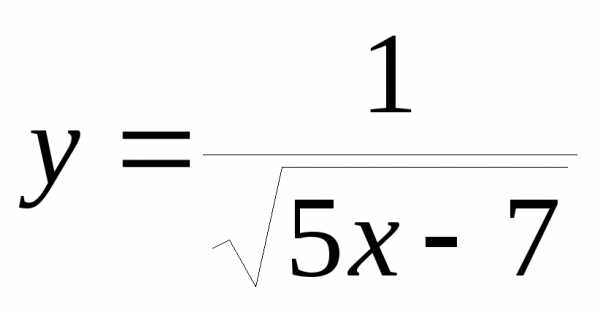 – бесконечно малая.
– бесконечно малая.
57
studfiles.net
Определение предела функции (по Гейне и Коши)
Первое определение предела функции (по Гейне)
Пусть функция f(x) определена на некоторой проколотой окрестности точки x0.
Число a называется пределом функции f(x) в точке x0:
,
если для любой последовательности {xn}, сходящейся к x0:
,
элементы которой принадлежат окрестности ,
последовательность {f(xn)} сходится к a:
.
Здесь x0 и a могут быть как конечными числами, так и бесконечно удаленными точками. Окрестность может быть как двусторонней, так и односторонней.
Запишем это определение с помощью логических символов существования и всеобщности:
.
Второе определение предела функции (по Коши)
Пусть функция f(x) определена на некоторой проколотой окрестности точки x0.
Число a называется пределом функции f(x) в точке x0:
,
если для любого положительного числа ε > 0 существует такое число δε> 0, зависящее от ε, что для всех x, принадлежащих проколотой δε – окрестности точки x0:
,
значения функции f(x) принадлежат ε – окрестности точки a:
.
Точки x0 и a могут быть как конечными числами, так и бесконечно удаленными точками. Окрестность также может быть как двусторонней, так и односторонней.
Запишем это определение с помощью логических символов существования и всеобщности:
.
В этом определении используются окрестности с равноудаленными концами. Можно дать и эквивалентное определение, используя произвольные окрестности точек.
Определение с использованием произвольных окрестностей
Пусть функция f(x) определена на некоторой проколотой окрестности точки x0.
Число a называется пределом функции f(x) в точке x0:
,
если для любой окрестности U(a) точки a существует такая проколотая окрестность точки x0, что для всех x, принадлежащих проколотой окрестности точки x0:
,
значения функции f(x) принадлежат окрестности U(a) точки a:
.
С помощью логических символов существования и всеобщности это определение можно записать так:
.
На странице «Окрестность точки» мы показали, что определение предела функции с использованием более простой окрестности с равноудаленными концами эквивалентно определению, в котором используется произвольная окрестность. Формулировка второго определения по Коши имеет более общий вид, и оно часто используется при доказательстве теорем. Первое определение, в математическом смысле, проще. Его удобно применять в вычислениях.
Более подробно определение Коши для конечных точек рассматривается на странице «Определение предела функции в конечной точке»; для бесконечно удаленных точек – на странице «Определение предела функции на бесконечности».
Односторонние и двусторонние пределы
Приведенные выше определения универсальны в том смысле, что их можно использовать для любых типов окрестностей. Если, в качестве мы используем левостороннюю проколотую окрестность конечной точки, то получим определение левостороннего предела . Если в качестве окрестности использовать окрестность бесконечно удаленной точки, то получим определение предела на бесконечности.
Для определения предела по Гейне это сводится к тому, что на произвольную, сходящуюся к , последовательность накладывается дополнительное ограничение – ее элементы должны принадлежать соответствующей проколотой окрестности точки .
Для определения предела по Коши нужно в каждом случае преобразовать выражения и в неравенства, используя соответствующие определения окрестности точки.
См. «Окрестность точки».
Определение, что точка a не является пределом функции
Часто возникает необходимость использовать условие, что точка a не является пределом функции при . Построим отрицания к изложенным выше определениям. В них мы предполагаем, что функция f(x) определена на некоторой проколотой окрестности точки x0. Точки a и x0 могут быть как конечными числами, так и бесконечно удаленными. Все сформулированное ниже относится как к двусторонним, так и к односторонним пределам.
По Гейне.
Число a не является пределом функции f(x) в точке x0: ,
если существует такая последовательность {xn}, сходящаяся к x0:
,
элементы которой принадлежат окрестности ,
что последовательность {f(xn)} не сходится к a:
.
.
По Коши.
Число a не является пределом функции f(x) в точке x0:
,
если существует такое положительное число ε > 0, так что для любого положительного числа δ > 0, существует такое x, принадлежащее проколотой δ – окрестности точки x0:
,
что значение функции f(x) не принадлежит ε – окрестности точки a:
.
.
Разумеется, если точка a не является пределом функции при , то это не означает, что у нее не может быть предела. Возможно, существует предел , но он не равен a. Также возможен случай, когда функция определена в проколотой окрестности точки , но не имеет предела при .
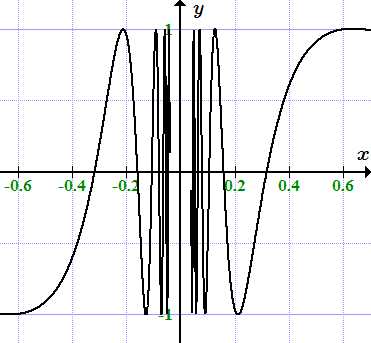
Функция f(x) = sin(1/x) не имеет предела при x → 0.
Например, функция определена при , но предела не существует. Для доказательства возьмем последовательность . Она сходится к точке 0: . Поскольку , то .
Возьмем последовательность . Она также сходится к точке 0: . Но поскольку , то .
Тогда предел не может равняться никакому числу a. Действительно, при , существует последовательность , с которой . Поэтому любое отличное от нуля число не является пределом. Но также не является пределом, поскольку существует последовательность , с которой .
Эквивалентность определений предела по Гейне и по Коши
Теорема
Определения предела функции по Гейне и по Коши эквивалентны.
Доказательство
При доказательстве мы предполагаем, что функция определена в некоторой проколотой окрестности точки (конечной или бесконечно удаленной). Точка a также может быть конечной или бесконечно удаленной.
Доказательство Гейне ⇒ Коши
Пусть функция имеет в точке предел a согласно первому определению (по Гейне). То есть для любой последовательности , принадлежащей окрестности точки и имеющей предел
(1) ,
предел последовательности равен a:
(2) .
Покажем, что функция имеет предел в точке по Коши. То есть для любого существует , что для всех .
Допустим противное. Пусть условия (1) и (2) выполнены, но функция не имеет предела по Коши. То есть существует такое , что для любого существует , так что
.
Возьмем , где n – натуральное число. Тогда существует , причем
.
Таким образом мы построили последовательность , сходящуюся к , но предел последовательности не равен a. Это противоречит условию теоремы.
Первая часть доказана.
Доказательство Коши ⇒ Гейне
Пусть функция имеет в точке предел a согласно второму определению (по Коши). То есть для любого существует , что
(3) для всех .
Покажем, что функция имеет предел a в точке по Гейне.
Возьмем произвольное число . Согласно определению Коши, существует число , так что выполняется (3).
Возьмем произвольную последовательность , принадлежащую проколотой окрестности и сходящуюся к . По определению сходящейся последовательности, для любого существует , что
при .
Тогда из (3) следует, что
при .
Поскольку это выполняется для любого , то
.
Теорема доказана.
Использованная литература:
Л.Д. Кудрявцев. Курс математического анализа. Том 1. Москва, 2003.
Автор: Олег Одинцов. Опубликовано: Изменено:
1cov-edu.ru
Определение предела функции в точке
Определение предела функции по Коши
Конечный предел функции в конечной точке
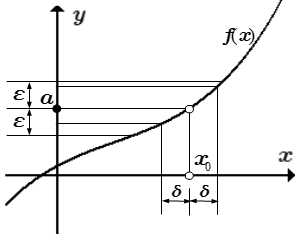
Предел функции в точке:
|f(x) – a| < ε при 0 < |x – x0| < δ
Определение конечного предела функции по Коши
Пусть функция f(x) определена в некоторой проколотой окрестности конечной точки x0. Число a называется пределом функции f(x) в точке x0, если для любого сколь угодно малого положительного числа ε > 0 существует такое число δε> 0, зависящее от ε, что для всех x, принадлежащих проколотой δε – окрестности точки x0: 0 < |x – x0| < δε, значения функции принадлежат ε – окрестности точки a:
|f(x) – a| < ε.
Предел функции обозначается так:
.
Или при .
С помощью логических символов существования и всеобщности определение предела функции можно записать следующим образом:
.
Односторонние пределы
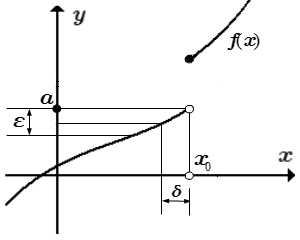
Левый предел функции в точке:
|f(x) – a| < ε при 0 < x0 – x < δ
Функция может быть определена не с двух сторон от точки , а в некоторой левой окрестности точки , при или в некоторой правой окрестности, при . Также функция может иметь разрыв в точке . Тогда используют односторонние пределы.
Левый предел в точке (левосторонний предел):
.
Правый предел в точке (правосторонний предел):
.
Пределы слева и справа часто обозначают так:
; .
Бесконечный предел функции в конечной точке
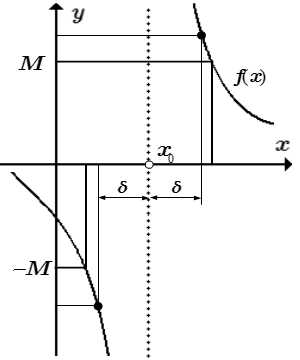
Бесконечный предел функции в точке:
|f(x)| > M при 0 < |x – x0| < δ
Определение бесконечного предела функции по Коши
Пусть функция f(x) определена в некоторой проколотой окрестности конечной точки x0. Предел функции f(x) при x → x0 равен бесконечности, если для любого, сколь угодно большого числа M > 0, существует такое число δM > 0, зависящее от M, что для всех x, принадлежащих проколотой δM – окрестности точки x0: 0 < |x – x0| < δM, значения функции принадлежат окрестности бесконечно удаленной точки:
|f(x)| > M.
Бесконечный предел обозначают так:
.
Или при .
С помощью логических символов существования и всеобщности определение бесконечного предела функции можно записать так:
.
Также можно ввести определения бесконечных пределов определенных знаков, равных и :
.
.
Аналогичным образом вводятся определения односторонних пределов.
Левые пределы.
.
.
.
Правые пределы.
.
.
.
Определение предела функции по Гейне
Пусть функция f(x) определена на некоторой проколотой окрестности точки x0.
Число a (конечное или бесконечно удаленное) называется пределом функции f(x) в точке x0:
,
если для любой последовательности {xn}, сходящейся к x0: ,
элементы которой принадлежат окрестности , последовательность {f(xn)} сходится к a:
.
Если в качестве окрестности взять левостороннюю окрестность точки x0, то получим определение левого предела. Если правостороннюю – то получим определение правого предела.
Определения предела по Гейне и Коши эквивалентны.
Примеры
Пример 1
Используя эпсилон и дельта – рассуждения показать, что
.
Решение
Введем обозначения:
.
Выпишем определение конечного предела функции в точке по Коши:
.
Преобразуем разность:
.
Пусть
.
Тогда
;
;
.
Итак, мы нашли, что при ,
.
Вводим положительные числа и :
.
Отсюда следует, что
при , и .
Поскольку всегда можно уменьшить, то возьмем . Тогда для любого ,
при .
Это означает, что .
Пример 2
Используя определение предела по Коши показать, что
.
Решение
Введем обозначение:
.
Выпишем определение предела функции в точке , равного бесконечности, по Коши:
.
Выразим многочлены в числителе и знаменатели через многочлены от .
;
.
Пусть
.
Тогда
;
;
.
Итак, мы нашли, что при ,
.
Вводим положительные числа и :
.
Отсюда следует, что
при , и .
Поскольку всегда можно уменьшить, то возьмем . Тогда для любого ,
при .
Это означает, что .
Пример 3
Используя определение предела по Коши показать, что
.
Решение
Введем обозначение:
.
Выпишем определение левого предела в точке , равного , по Коши:
.
В нашем случае .
Выразим многочлены в числителе и знаменатели через многочлены от .
;
.
Пусть
.
Тогда
; );
;
;
.
Итак, мы нашли, что при ,
.
Вводим положительные числа и :
.
Отсюда следует, что
при , и .
Поскольку всегда можно уменьшить, то возьмем . Тогда для любого ,
при .
Это означает, что .
Использованная литература:
С.М. Никольский. Курс математического анализа. Том 1. Москва, 1983.
Автор: Олег Одинцов. Опубликовано:
1cov-edu.ru
Определение предела по Коши и по Гейне, их эквивалентность — ПриМат
Определение 1.1. (определение по Коши или на языке ):
— предел функции в точке (и пишут \(\lim\limits_{x\rightarrow a } f(x) = A\)), если:
В определении допускается, что , то есть может не принадлежать области определения функции.
Определение 1.2. (определение по Гейне):
называется пределом функции в точке , если , то есть , соответствующая последовательность значений , то есть .
Замечание 1.1.
Из определения предела функции по Гейне следует, что функция не может иметь в точке два разные предела.
Замечание 1.2.
Понятие предела функции в точке есть локальное понятие: существование и значение предела полностью определяется значениями функции в как угодно малой окрестности этой точки.
Замечание 1.3.
Данную запись в определении можно сформулировать иначе: точка принадлежит проколотой -окрестности точки ()
2. Эквивалентность определений
Пусть число является пределом функции в точке по Коши. Выберем произвольную подходящую последовательность , , то есть такую, для которой . Покажем, что является пределом по Гейне.
Зададим произвольное и укажем для него такое , что для всех из условия следует неравенство . В силу того, что , для найдётся такой номер , что будет выполняться неравенство , то есть .
Докажем теперь обратное утверждение: предположим, что по Гейне, и покажем, что число является пределом функции в точке по Коши. Предположим, что это неверно, то есть: . В качестве рассмотрим , а соответствующие значения будем обозначать . Тогда при любом выполняются условия и . Отсюда следует, что последовательность является подходящей, но число не является пределом функции в точке . Получили противоречие.
Пример 3.1.
а)
, например
б)
Пример 3.2.
Доказать, что не имеет предела в точке 0.
Вывод: последовательность по Гейне не имеет предела.
Лимит времени: 0
Информация
Тест по теме Определение предела по Коши и по Гейне, их эквивалентность.
Желаем удачи!
Вы уже проходили тест ранее. Вы не можете запустить его снова.
Тест загружается…
Вы должны войти или зарегистрироваться для того, чтобы начать тест.
Вы должны закончить следующие тесты, чтобы начать этот:
Правильных ответов: 0 из 5
Ваше время:
Время вышло
Вы набрали 0 из 0 баллов (0)
| Средний результат |
|
| Ваш результат |
|
Рубрики
- Математический анализ 0%
Спасибо Вам за прохождение данного теста, надеюсь вы узнали для себя что-нибудь новое!
| Место | Имя | Записано | Баллы | Результат |
|---|---|---|---|---|
| Таблица загружается | ||||
| Нет данных | ||||
- С ответом
- С отметкой о просмотре
Навигация по записям
ib.mazurok.com
Определение предела функции
17
Число  называетсяпределомфункции
называетсяпределомфункции при
при ,
если для любого сколь угодно малого
,
если для любого сколь угодно малого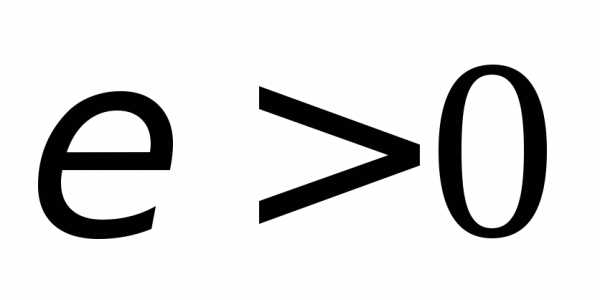 найдется
найдется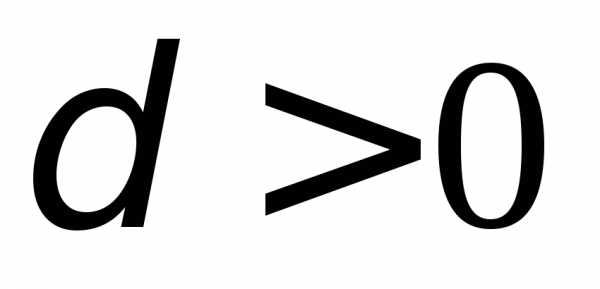 ,
такое что для всех значений
,
такое что для всех значений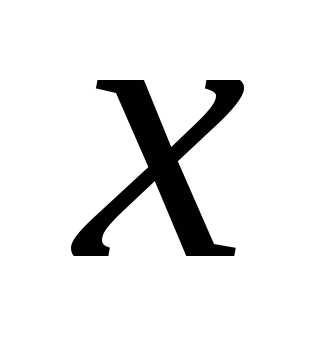 ,
удовлетворяющих неравенству,
выполнено неравенство.
,
удовлетворяющих неравенству,
выполнено неравенство.
При этом пишут 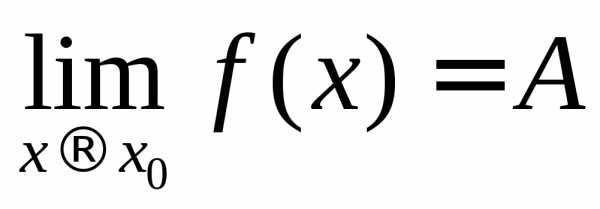 или
или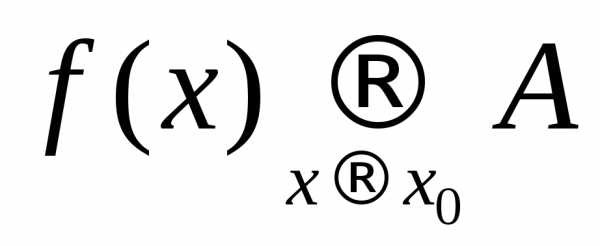 .
В символах математического анализа
определение может быть записано так:
.
В символах математического анализа
определение может быть записано так:
.
Выше приведено
определение для случая конечных значений  и
и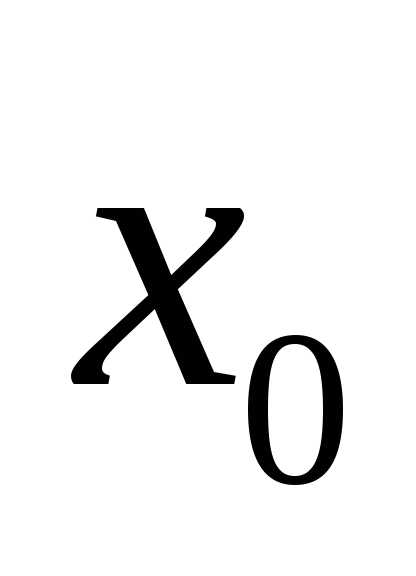 .
Оно может быть переделано для случаев,
когда
.
Оно может быть переделано для случаев,
когда или
или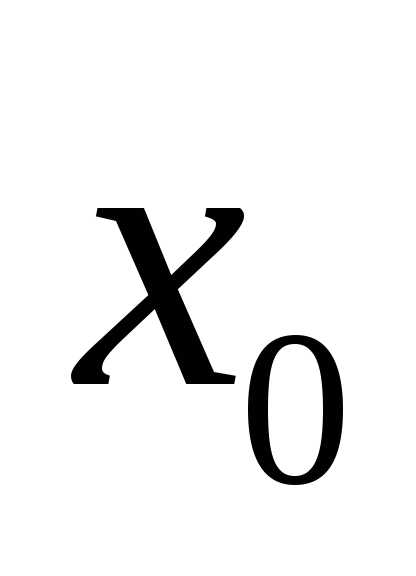 обращаются в бесконечность
обращаются в бесконечность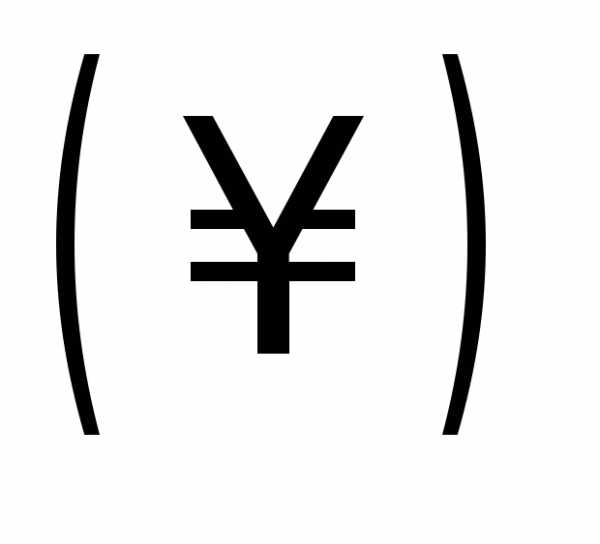 .
При этом соответствующие неравенства
должны быть заменены на неравенства
типа
.
При этом соответствующие неравенства
должны быть заменены на неравенства
типа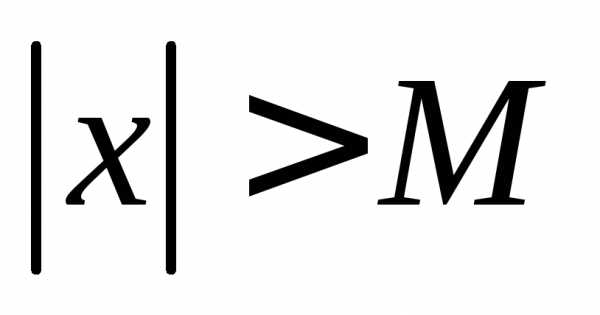 ,
если,
,
если,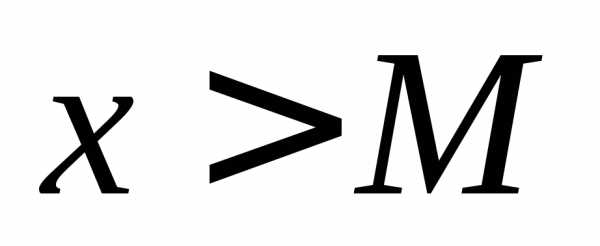 ,если,
,если,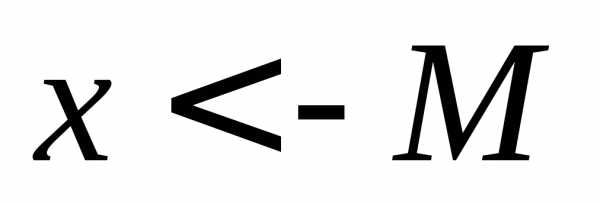 ,
еслии т.п.
,
еслии т.п.
Переменная величина 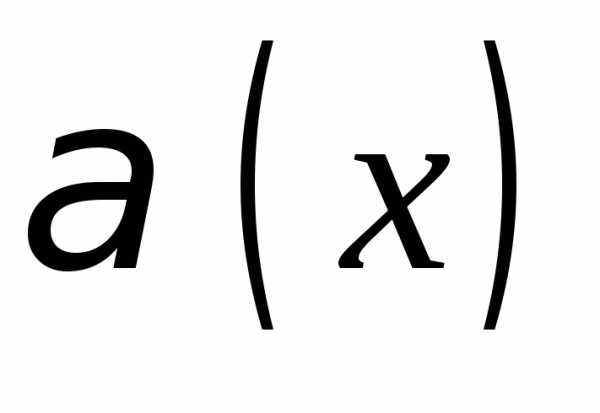 называетсябесконечно малой
величинойпри
называетсябесконечно малой
величинойпри ,
если
,
если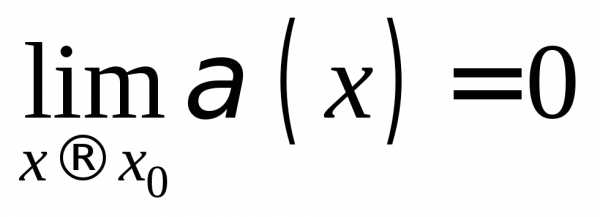 .
.
Пусть
,
где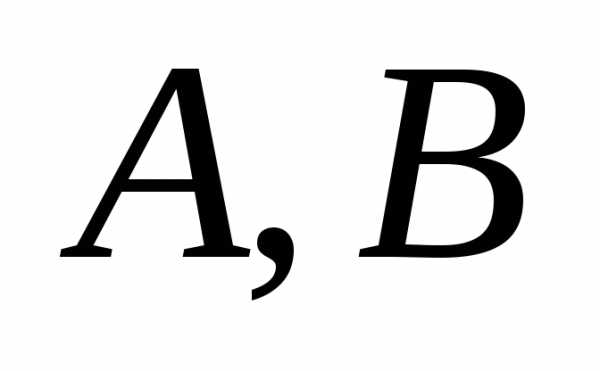 –
конечные числа,
–
конечные числа,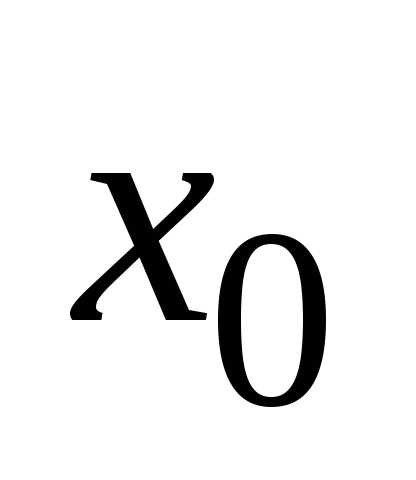 –
любое конечное число или бесконечность.
–
любое конечное число или бесконечность.
Теоремыо пределах:
.
.
Если .
Пусть – конечное число. Тогда:
а)
б)
в) .
5. Пусть
,
тогда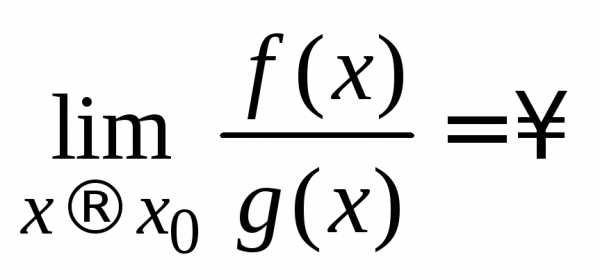 .
●
.
●
Функция 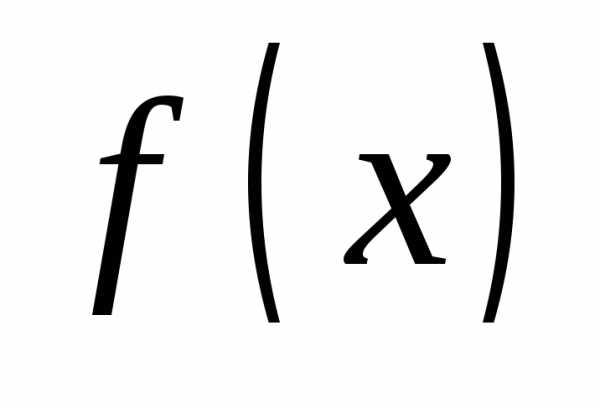 называетсянепрерывнойв точке
называетсянепрерывнойв точке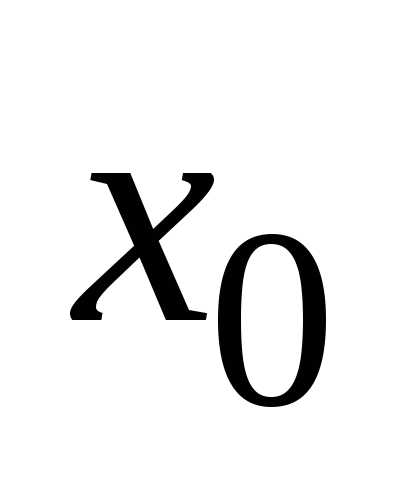 ,
если она определена в этой точке и.
Для непрерывной функции возможен переход
к пределу под знаком функции.
,
если она определена в этой точке и.
Для непрерывной функции возможен переход
к пределу под знаком функции.
Предельные переходы, содержащие нуль или бесконечность, при кратко можно записать так:
, (1)
где выражение, заключенное в квадратные скобки, понимается как предельное значение. Выражения вида:
, (2)
─ называются неопределенностями,
что означает, что нельзя дать ответ,
используя правила (1), Например, рассмотрим
три функции:при .
Отношение любых двух функций из
указанных трех приводит к неопределенности
.
Отношение любых двух функций из
указанных трех приводит к неопределенности .
Однако, пределы этих отношений различны,
например:
.
Однако, пределы этих отношений различны,
например:
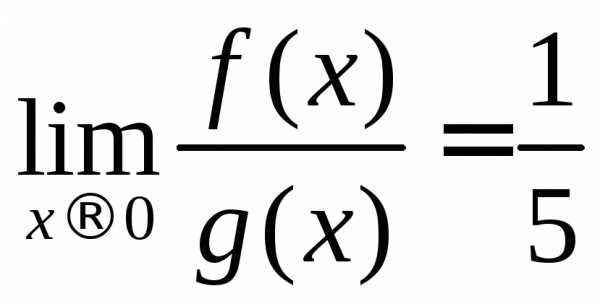 ,
,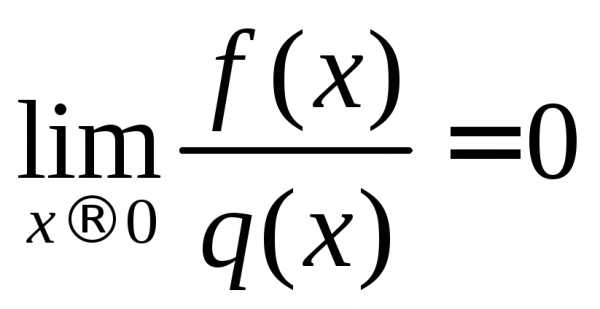 ,
,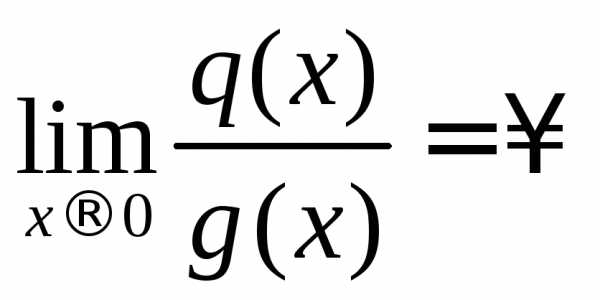 .
.
Неопределенности (2) всегда можно перевести из одной в другую. Кроме указанных выражений неопределенностями являются предельные выражения:
.
При вычислении пределов сначала подставляется предельное значение переменной. Если выполнены условия теорем, то сразу получаем ответ. Если при подстановке получается неопределенность, то следует предварительно преобразовать выражение, а затем подставить предельное значение.
Рассмотрим несколько примеров на вычисление пределов.
1. 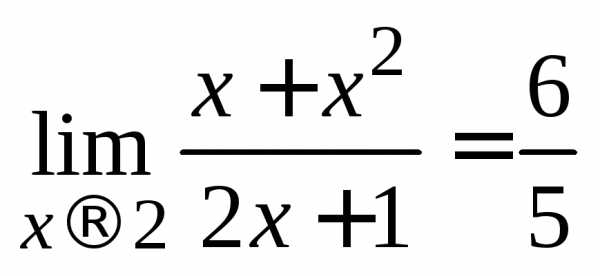 .
.
2. 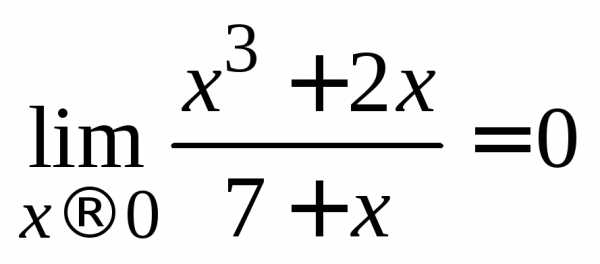 .
.
3. .
4. .
5. .
6. 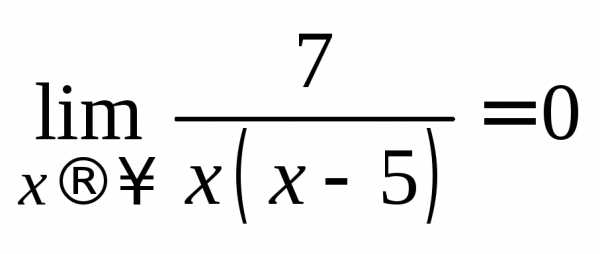 .
.
7. 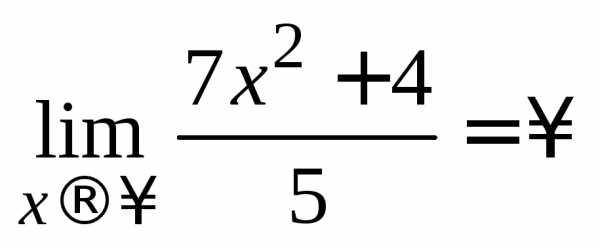 .
.
8. 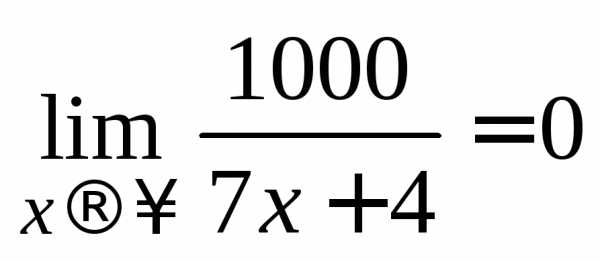 .
.
9. .
10..
11. .
12. .
13.
В примерах 1─3,6─8 можно сразу записать
ответ. В остальных примерах первая
подстановка приводит к неопределенности,
поэтому: сначала проводим преобразование.
Так в примере 13 мы умножили числитель
и знаменатель на сопряженное выражение,
что позволило затем сократить дробь.
Обратите внимание, что выражение
,
и это позволило вынести множитель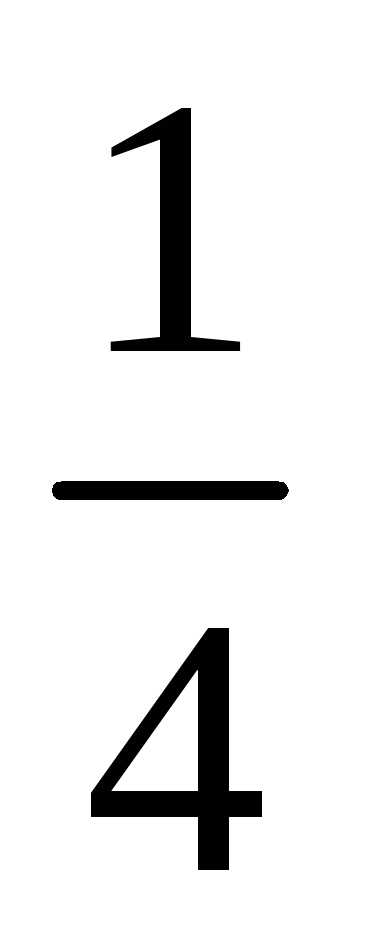 за знак предела.
за знак предела.
Проанализировав решения примеров 9–11, замечаем, что при вычислении пределов типа , приходим к пределу отношения членов со старшими степенями. Окончательный ответ зависит от соотношения степеней. Аналогичная ситуация и для выражений, содержащих дробные степени или радикалы.
Например, вычисляя 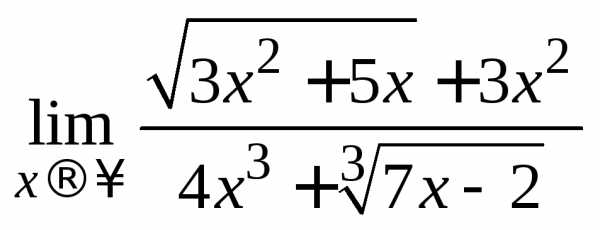 ,
приходим к неопределенности
,
приходим к неопределенности .
Выбрав в числителе и знаменателе
слагаемые со старшими степенями
.
Выбрав в числителе и знаменателе
слагаемые со старшими степенями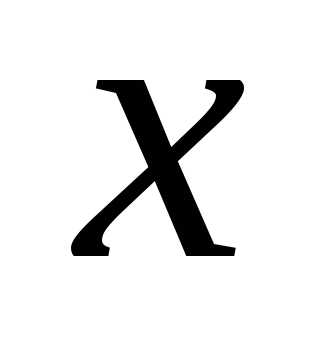 .
получаем решение:
.
получаем решение:
.
2. Односторонние пределы
Если  ,
оставаясь больше (или меньше)
,
оставаясь больше (или меньше)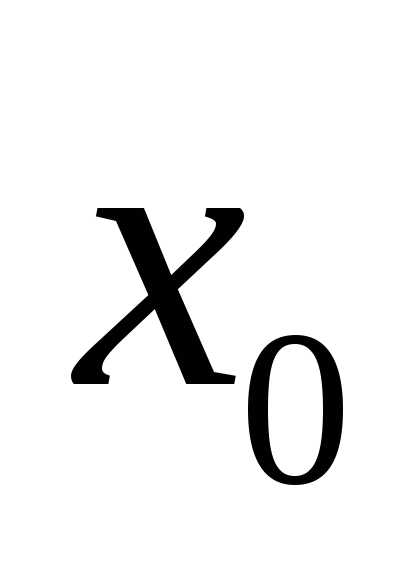 ,
то такие пределы называютсяодносторонними пределами или пределами справа
(слева). Стремление переменной к
предельному значению слева будем
записыватьпри стремлении справа,
а сами предельные значения функции
,
то такие пределы называютсяодносторонними пределами или пределами справа
(слева). Стремление переменной к
предельному значению слева будем
записыватьпри стремлении справа,
а сами предельные значения функции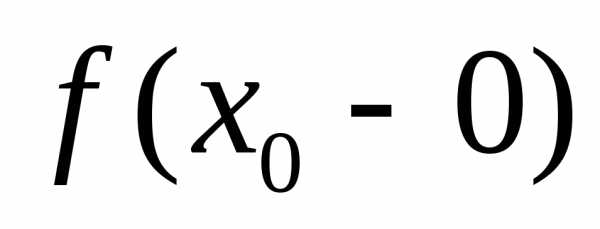 или
или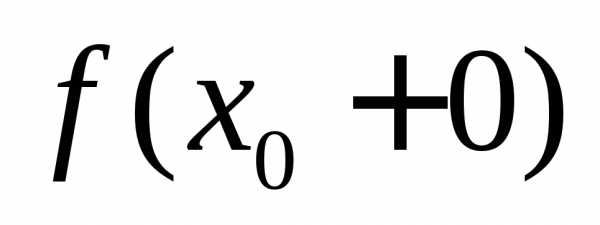 .
Приилитакже имеем односторонние пределы:
.
Приилитакже имеем односторонние пределы: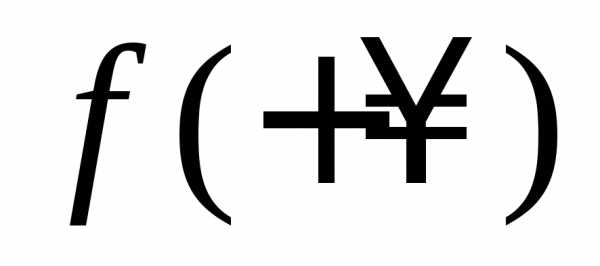 и
и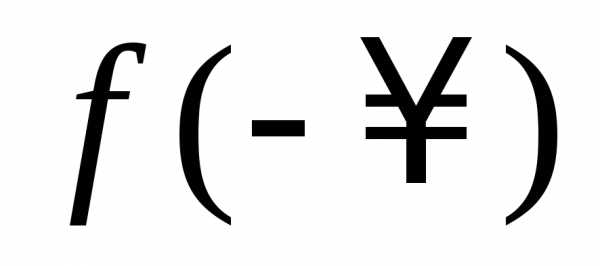 .
Сравните два предела
.
Сравните два предела
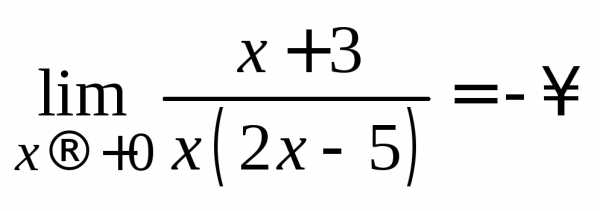 ,
,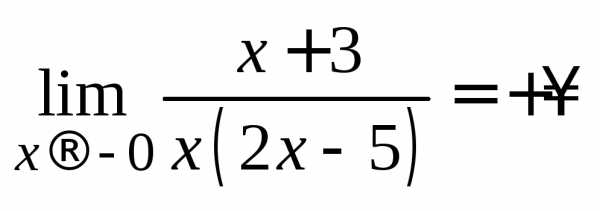 .
.
Как указано в первом разделе: функция 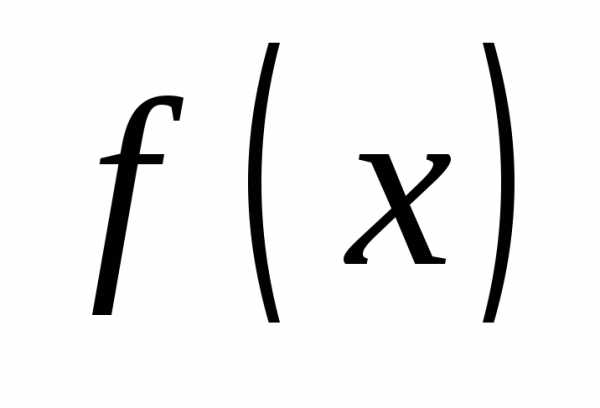 называетсянепрерывнойв точке
называетсянепрерывнойв точке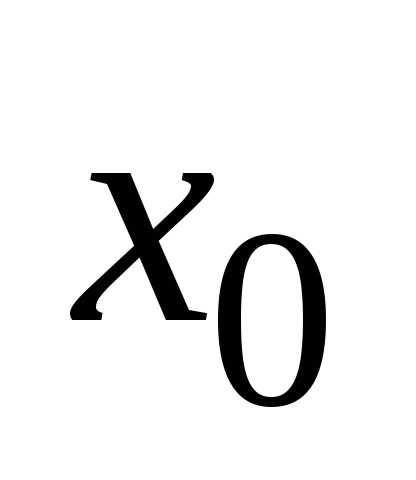 ,
если она определена в этой точке и.
Если функция не является непрерывной
в точке
,
если она определена в этой точке и.
Если функция не является непрерывной
в точке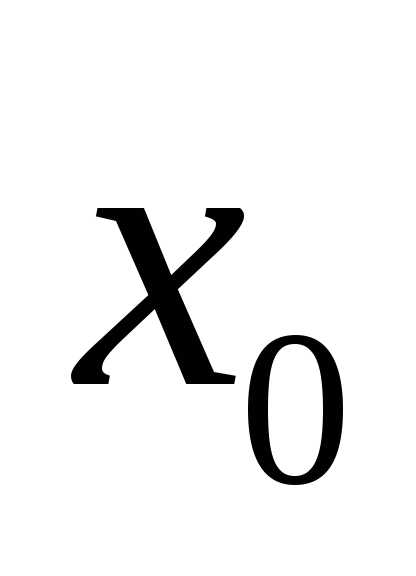 ,
то говорят, что функция имеет разрыв в
точке
,
то говорят, что функция имеет разрыв в
точке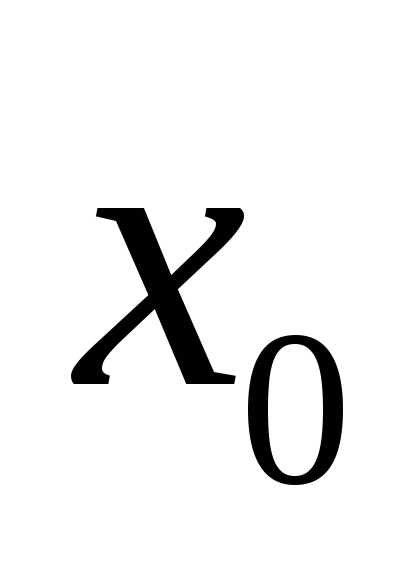 .
Разрывы функции имеют три типа и связаны
с поведением функции слева и справа от
точки разрыва.
.
Разрывы функции имеют три типа и связаны
с поведением функции слева и справа от
точки разрыва.
1. Устранимый
разрыв. Существуют левосторонний
и правосторонний пределы, оба предела
конечны, равны между собой, а функция
не определена в точке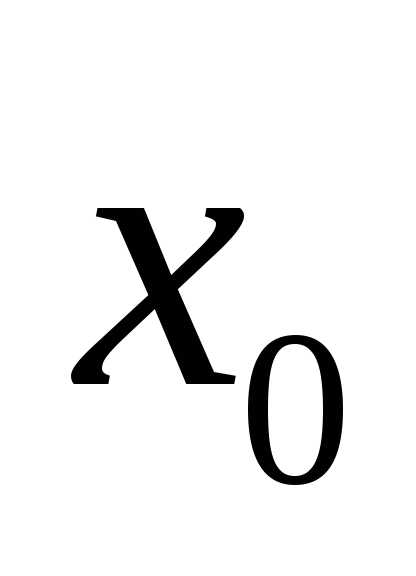 :
:
.
2. Разрыв первого рода(скачок). Существуют левосторонний и правосторонний пределы, оба предела конечны, но они не равны между собой.
3. Разрыв второго рода. Один из пределов или оба обращаются в бесконечность или не существуют.
Все элементарные функции непрерывны в области своего определения.
Пример 1. Исследовать поведение функциина границе ее области определения.
Решение..
Определим пределы функции в граничных
точках
и при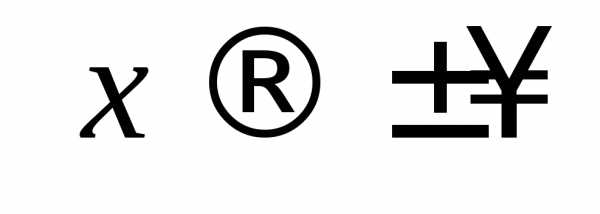 :
:
Пример 2.Исследовать поведение
функции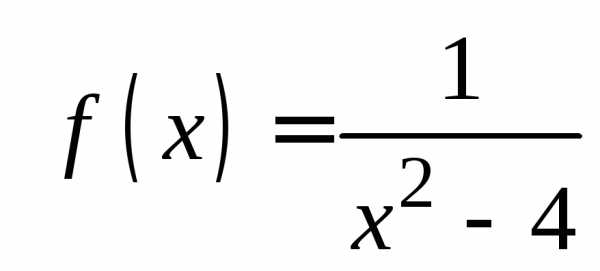 на границе ее области определения.
на границе ее области определения.
Решение..
Определим пределы функции в граничных
точках
и при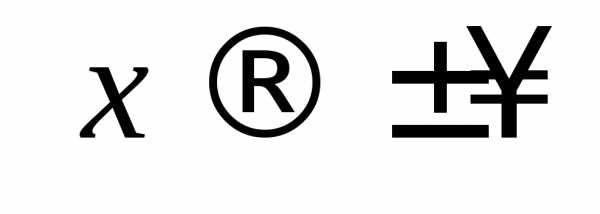 .
Заметим, что каждая из точекграничной точкой является дважды.
Поэтому в этих точках вычислим
односторонние пределы:
.
Заметим, что каждая из точекграничной точкой является дважды.
Поэтому в этих точках вычислим
односторонние пределы:
studfiles.net
Предел функции.Определения. Свойства предела
Материал из Википедии — свободной энциклопедии
Перейти к: навигация, поиск
Преде́л фу́нкции— одно из основных понятий математического анализа. Функцияf(x) имеет пределAв точкеx0если для всех значенийx, достаточно близких кx0, значениеf(x) близко кA.
Определения
(определение по Коши, ε−δ—определение) Пусть дана функция и— предельная точка множестваM. Числоназывается пределом функцииfприx, стремящемся кa, если
при
Замечания
Все данные выше определения предела функции в точке эквивалентны.
Если предел функции fприсуществует и равенA, пишут
Предел вдоль фильтра
Определение фильтра
Основная статья:Фильтр (математика)
Пусть дано множество A. Система множествназывается фильтром наA, если
Определение предела
Пусть и— фильтр наM. Числоявляется пределом функцииfпо фильтруесли
Пишут:
Примеры
Обычный предел
Пусть дано топологическое пространство , иПустьТогда система множеств
является фильтром и обозначается Данное выше определение предела совпадает с пределом по фильтру
Односторонние пределы
Основная статья:Односторонние пределы
является фильтром и обозначается илиПределназывается правосторонним пределом функцииfприxстремящемся кa.
является фильтром и обозначается илиПределназывается левосторонним пределом функцииfприxстремящемся кa.
Пределы на бесконечности
Основная статья:Пределы функции на бесконечности
является фильтром и обозначается илиПределназывается пределом функцииfприxстремящемся к бесконечности.
является фильтром и обозначается Пределназывается пределом функцииfприxстремящемся к минус-бесконечности.
Предел последовательности
Основная статья:Предел последовательности
Система множеств где
является фильтром и обозначается Функцияназывается числовой последовательностью, а пределпределом этой последовательности.
Интеграл Римана
Основная статья:Интеграл Римана
Пусть Назовём размеченным разбиением отрезка [a,b] коллекцию точекНазовём диаметром разбиенияTчислоТогда система множеств
является фильтром в пространстве всех размеченных разбиений [a,b]. Определим функциюравенством
Тогда предел называется интегралом Римана функцииfна отрезке [a,b].
Свойства пределов числовых функций
Пусть даны функции иТогда
где – проколотая окрестность точкиa.
В частности, функция, сходящаяся к положительному (отрицательному) пределу, остаётся положительной (отрицательной) в некоторой окрестности предельной точки:
studfiles.net