Что такое колебания в физике – Величины, характеризующие колебательное движение. Гармонические колебания :: Класс!ная физика
- Комментариев к записи Что такое колебания в физике – Величины, характеризующие колебательное движение. Гармонические колебания :: Класс!ная физика нет
- Советы абитуриенту
- Физика
- Физика – Колебания и волны
- Виды колебаний в физике и их характеристика
- Основные определения
- Разновидности колебательных процессов
- Особенности классификации
- По варианту взаимодействия с окружающей средой
- Основные параметры колебательных движений
- Характеристика гармонических колебаний
- Основные отличия между вынужденными и свободными колебаниями
- Электромагнитные колебания
- Значение колебаний в науке и технике
- Заключение
- Ответы@Mail.Ru: что такое колебание
- Колебания – это… Что такое Колебания?
- Основные понятия теории колебаний
- Колебания – это… Что такое Колебания?
Физика
1.Определение колебательного движения
Колебательное движение – это движение, точно или приблизительно повторяющееся через одинаковые промежутки времени. Учение о колебательном движении в физике выделяют особо. Это обусловлено общностью закономерностей колебательного движения различной природы и методов его исследования. Механические, акустические, электромагнитные колебания и волны рассматриваются с единой точки зрения. Колебательное движение свойственно всем явлениям природы. Внутри любого живого организма непрерывно происходят ритмично повторяющиеся процессы, например биение сердца.
Механические колебания Колебания – это любой физический процесс, характеризующийся повторяемостью во времени.
Волнение моря, качание маятника часов, вибрации корпуса корабля, биение человеческого сердца, звук, радиоволны, свет, переменные токи — все это колебания.
В процессе колебаний значения физических величин, определяющих состояние системы, через равные или неравные промежутки времени повторяются. Колебания называются периодическими, если значения изменяющихся физических величин повторяются через равные промежутки времени.
Наименьший промежуток времени Т, черезкоторый значение изменяющейся физической величины повторяется (по величине и направлению, если эта величина векторная, по величине и знаку, если она скалярная), называетсяпериодом колебаний.
Число полных колебаний n , совершаемых за единицу времени, называется частотой колебаний этой величины и обозначается через ν . Период и частота колебаний связаны соотношением :
Любое колебание обусловлено тем или иным воздействием на колеблющуюся систему. В зависимости от характера воздействия, вызывающего колебания, различают следующие виды периодических колебаний: свободные, вынужденные, автоколебания, параметрические.
Свободные колебания — это колебания, происходящие в системе, предоставленной самой себе, после выведения ее из состояния устойчивого равновесия (например, колебания груза на пружине).
Вынужденные колебания — это колебания, обусловленные внешним периодическим воздействием (например, электромагнитные колебания в антенне телевизора).
Механические колебания
Автоколебания — свободные колебания, поддерживаемые внешним источником энергии, включение которого в нужные моменты времени осуществляет сама колеблющаяся система (например, колебания маятника часов).
Параметрические колебания — это колебания, в процессе которых происходит периодическое изменение какого-либо параметра системы (например, раскачивание качелей: приседая в крайних положениях и выпрямляясь в среднем положении, человек, находящийся на качелях, изменяет момент инерции качелей).
Различные по своей природе колебания обнаруживают много общего: они подчиняются одним и тем же закономерностям, описываются одними и теми же уравнениями, исследуются одними и теми же методами. Это дает возможность создать единую теорию колебаний.
Простейшими из периодических колебаний
являются гармонические колебания.
Гармонические колебания- это колебания, в процессе совершения которых значения физических величин изменяются с течением времени по закону синуса или косинуса. Большинство колебательных процессов описываются этим законом или может быть приставлено в виде суммы гармонических колебаний.
Возможно и другое «динамическое» определение гармонических колебании как процесса, совершаемого под действием упругой или «квазиупругой»
силы.
2. Периодическими называются колебания, при которых происходит точное повторение процесса через равные промежутки времени.
Периодом периодических колебаний называется минимальное время, через которое система возвращается в первоначальное
х — колеблющаяся величина (например, сила тока в цепи, состояние и начинается повторение процесса. Процесс, происходящий за один период колебаний, называется «одно полное колебание».
периодических колебаний называется число полных колебаний за единицу времени (1 секунду) — это может быть не целое число.
Т — период колебаний Период — время одного полного колебания.
Чтобы вычислить частоту v, надо разделить 1 секунду на время Т одного колебания (в секундах) и получится число колебаний за 1 секунду или координата точки) t — время
Гармоническое колебание
Это периодическое колебание, при котором координата, скорость, ускорение, характеризующие движение, изменяются по закону синуса или косинуса.
График гармонического колебания
График устанавливает зависимость смещения тела со временем. Установим к пружинному маятнику карандаш, за маятником бумажную ленту, которая равномерно перемещается. Или математический маятник заставим оставлять след. На бумаге отобразится график движения.
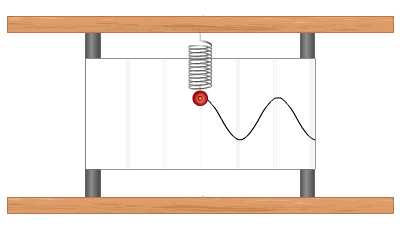
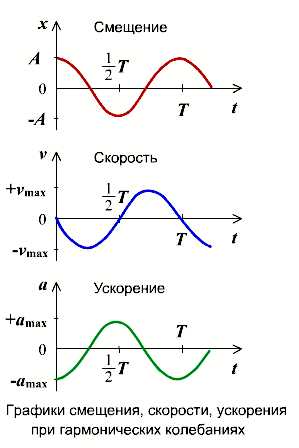
Графиком гармонического колебания является синусоида (или косинусоида). По графику колебаний можно определить все характеристики колебательного движения.
Уравнение гармонического колебания
Уравнение гармонического колебания устанавливает зависимость координаты тела от времени

График косинуса в начальный момент имеет максимальное значение, а график синуса имеет в начальный момент нулевое значение. Если колебание начинаем исследовать из положения равновесия, то колебание будет повторять синусоиду. Если колебание начинаем рассматривать из положения максимального отклонения, то колебание опишет косинус. Или такое колебание можно описать формулой синуса с начальной фазой .
Изменение скорости и ускорения при гармоническом колебании
Не только координата тела изменяется со временем по закону синуса или косинуса. Но и такие величины, каксила, скорость и ускорение, тоже изменяются аналогично. Сила и ускорение максимальные, когда колеблющееся тело находится в крайних положениях, где смещение максимально, и равны нулю, когда тело проходит через положение равновесия. Скорость, наоборот, в крайних положениях равна нулю, а при прохождении телом положения равновесия – достигает максимального значения.
Если колебание описывать по закону косинуса
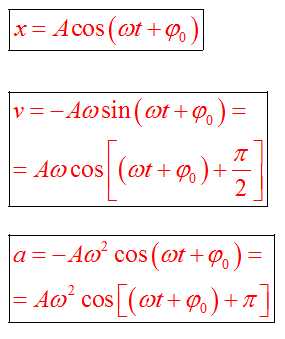
Если колебание описывать по закону синуса
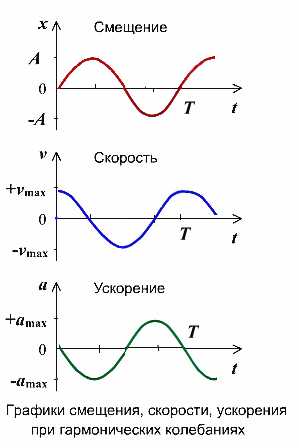
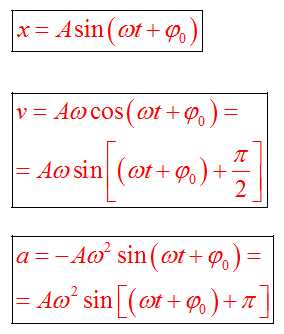
Максимальные значения скорости и ускорения
Проанализировав уравнения зависимости v(t) и a(t), можно догадаться, что максимальные значения скорость и ускорение принимают в том случае, когда тригонометрический множитель равен 1 или -1. Определяются по формуле
Как получить зависимости v(t) и a(t)
studfiles.net
Физика – Колебания и волны
II семестр
Механические колебания и волны
Общая черта колебательных процессов – высокая степень повторяемости процесса.
Колебания подразделяются:
по природе: механические, электромагнитные;
по степени повторяемости: периодические, непериодические;
по свойствам: гармонические, ангармонические;
по способу возникновения: свободные, вынужденные.
Механические колебания
Колебательные системы
Колебания – физические процессы, которые происходят с определённой повторяемостью во времени.
Периодические колебания – колебания, при которых значения характерных параметров системы повторяются через равные промежутки времени.
Полное колебание – процесс, проходящие в системе за период.
Период – минимальный период времени, через который все параметры системы повторяются.
Частота – число полных колебаний, происходящих в единицу времени.
Циклическая частота – число
полных колебаний за 
Гармонические колебания – колебания, происходящие по закону изменения гармонических функций.
Линейные колебания – колебания, возникающие в линейных системах.
Линейная система – система, реакция которой линейно зависит от воздействия.
Свободные (собственные) колебания – колебания, которые происходят в отсутствие внешних воздействий на колебательную систему и возникают вследствие какого-либо начального отклонения этой системы из состояния её устойчивого равновесия под действием внутренних сил системы.
Вынужденные колебания – колебания, возникающие в какой-либо системе под влиянием переменного внешнего воздействия.
Равновесие в механических системах и возникновение колебаний
Условие равновесия точечного
тела: 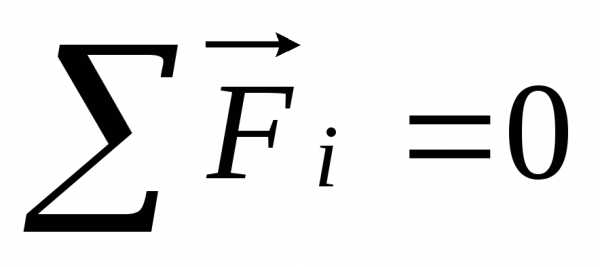
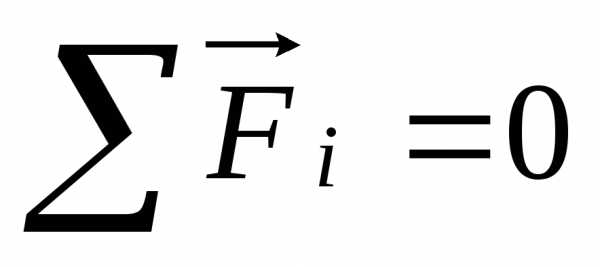 ,.
,.Характерным свойством колебательной системы является наличие возвращающей (квазиупругой) силы.
,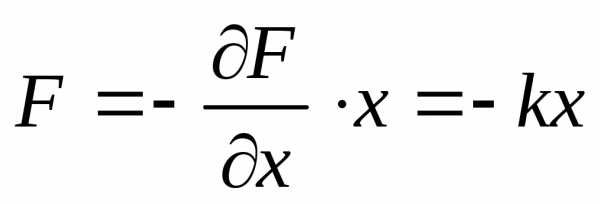 ;
;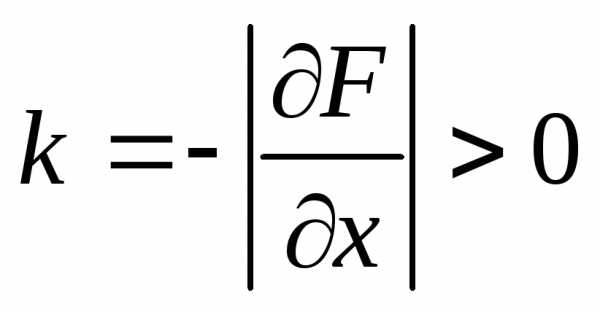 .
Необходимое условие колебательной
системы:.
Достаточность:
.
Необходимое условие колебательной
системы:.
Достаточность: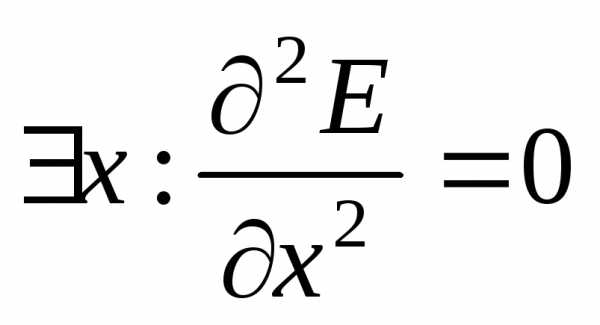 .
.
Свободные незатухающие колебания
у
Пружинный маятник:
, ,
,,
где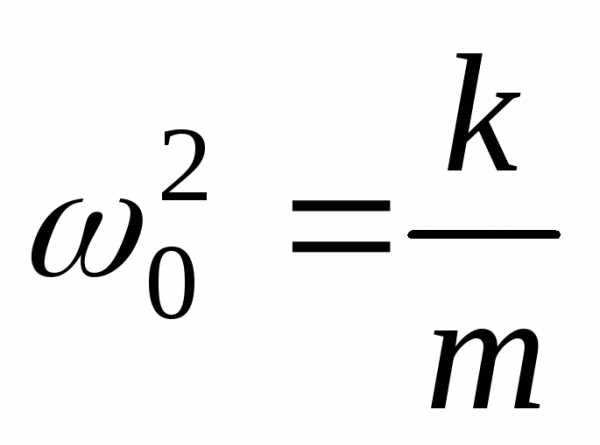 .
.
Математический маятник:
.,.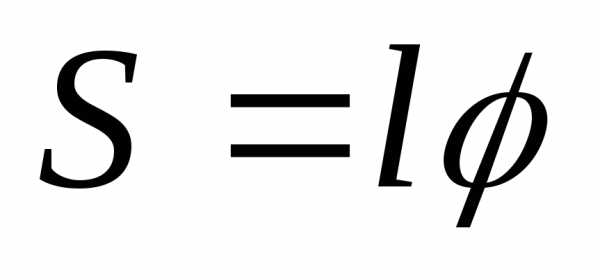 ,,,,
,,,,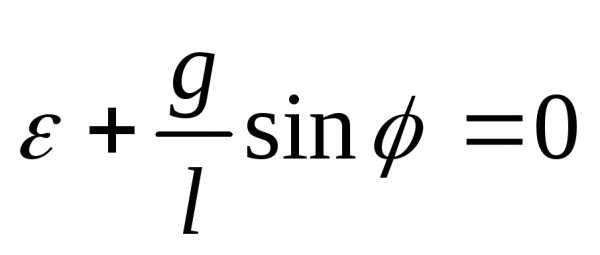 ,,
где
,,
где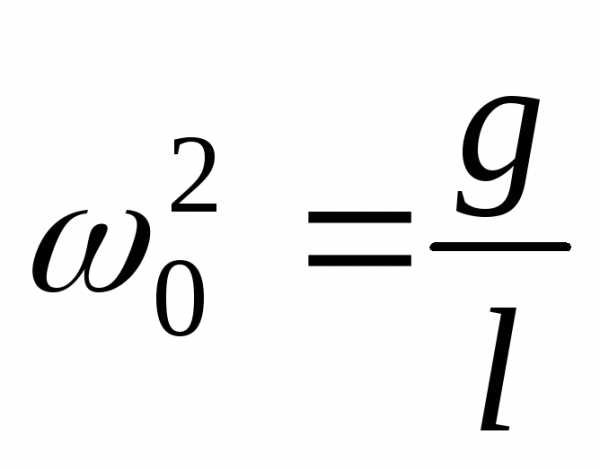
Физический маятник: 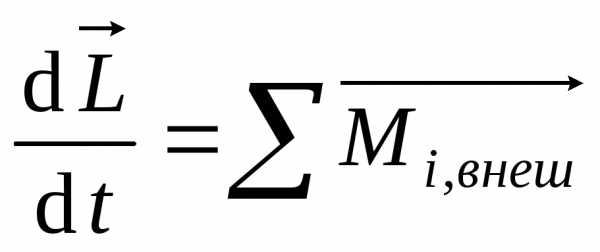 ,
,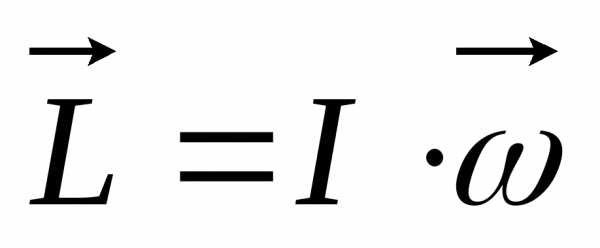 ,,
,,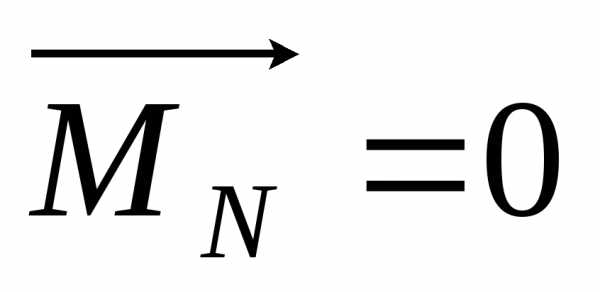 ,,,,
где
,,,,
где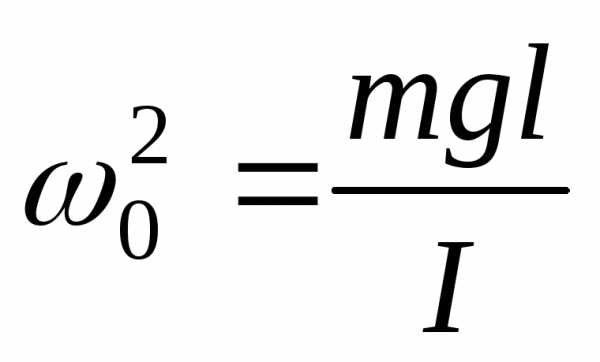 .
.
Приведённая длина физического
маятника – длина математического
маятника, период колебаний которого
равен периоду колебаний физического
маятника, 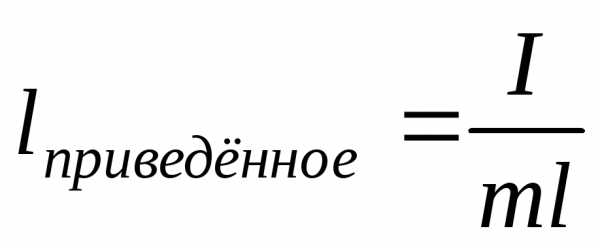 .
.
Центр качания – математическая точка, отстоящая от точки подвеса на приведённую длину и лежащая на маятнике.
Если физический и математический маятники с приведённой длиной колеблются около одной оси, то материальная точка математического и центр качания физического маятника движутся синхронно, если вначале их отклонили на одинаковый угол и одновременно отпустили.
Точка подвеса и центр качания обратимы (можно подвесить за любую из них, период колебаний будет одинаков).
Уравнение колебаний
Все системы описываются
уравнением 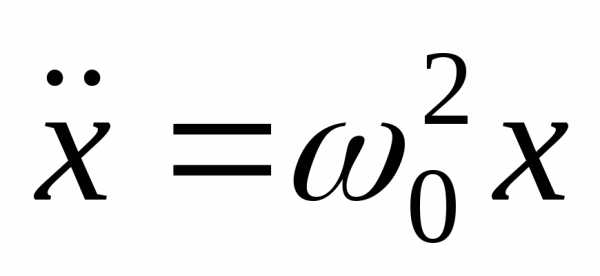 ,
где
,
где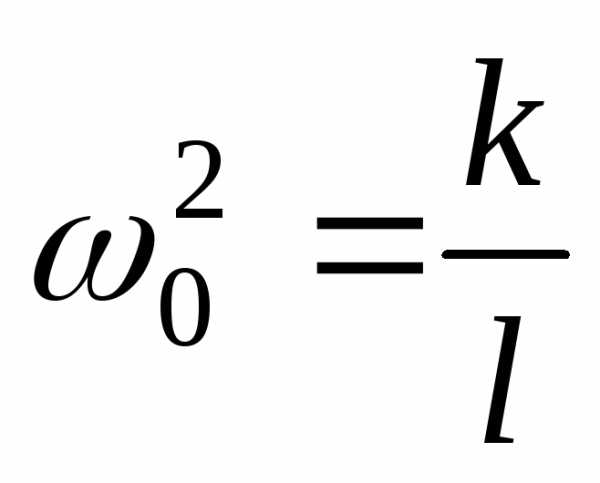 (пружинный),
(пружинный),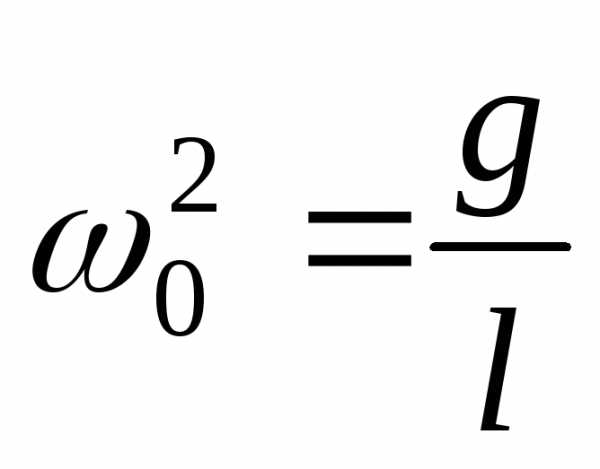 (математический),
(математический),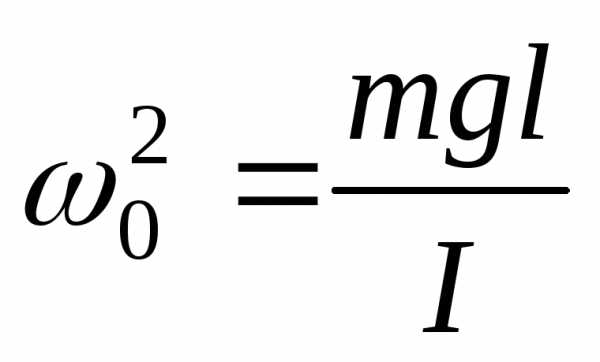 (физический).
(физический).
Переменная колебаний – параметр, характеризующий отклонение системы от положения равновесия. (x).
Решение уравнения колебаний.
.
Линейный гармонический осциллятор – любая колебательная система, в которой возникают малые линейные гармонические колебания.
Основные характеристики гармонических колебаний
Амплитуда – максимальное значение переменной колебания (максимальное отклонение системы от положения равновесия). Амплитуда всегда положительна. ,A – амплитуда.
Фаза – параметр, характеризующий
относительное значения отклонения
системы от положения равновесия (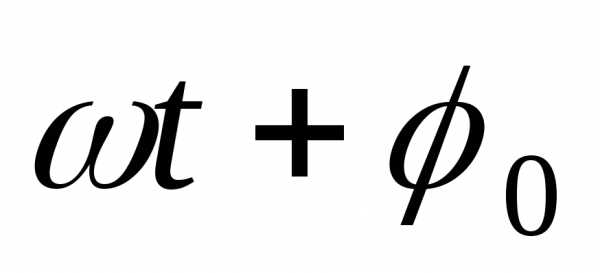 ).
).
Начальная фаза – значение
фазы в начальный момент времени (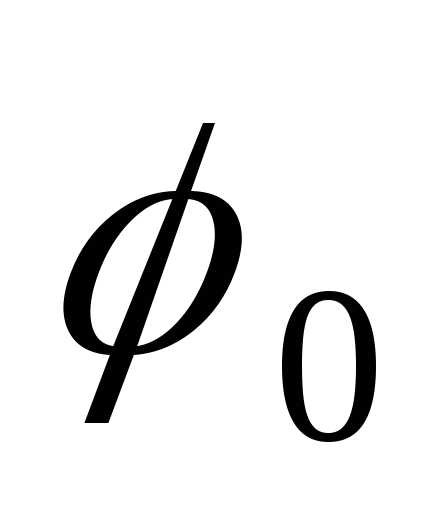 ).
).
Период: 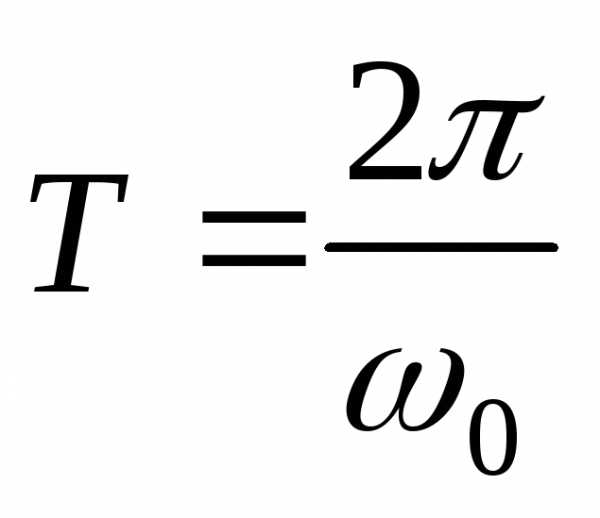 ,
частота
,
частота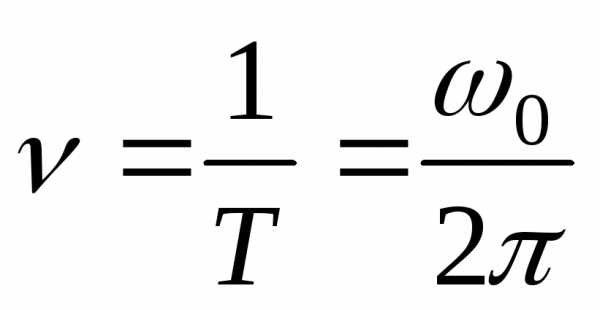 ,
,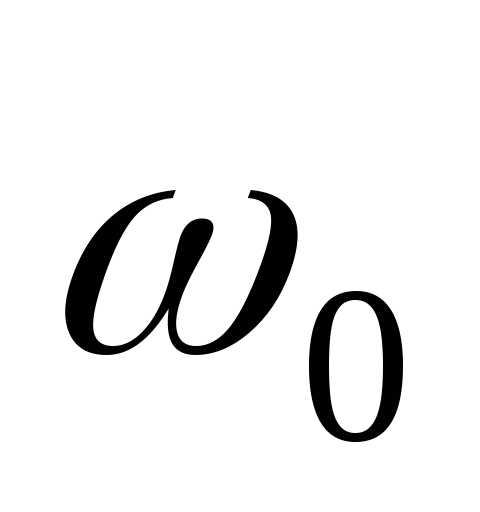 – циклическая частота.
– циклическая частота.
Свойства гармонических колебаний:
Частота и период гармонических колебаний определяются свойствами самой системы.
Амплитуда и начальная фаза зависят от способа возбуждения колебаний.
Период и частота не зависят от амплитуды.
Скорость и ускорение при колебаниях:
Пусть . Тогда,.
Начальные условие – задание смещение и скорости в начальный момент времени.
 ,,- колебания отсутствуют.
,,- колебания отсутствуют. ,,.
,,. ,
, ,.
,. ,
, ,
, .
.
Задание начальных условий определяет амплитуду и начальную фазу.
Кинетическая и потенциальная энергия системы:
. Для пружинного маятника- закон сохранения энергии при свободных незатухающих колебаниях.
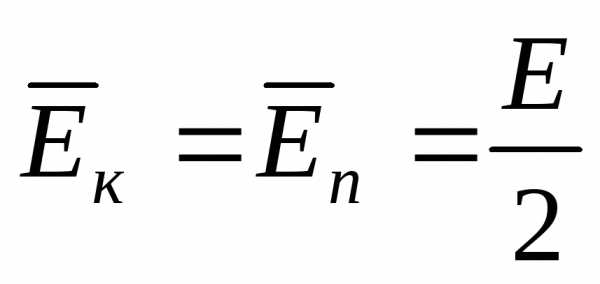 .,.
.,.
Э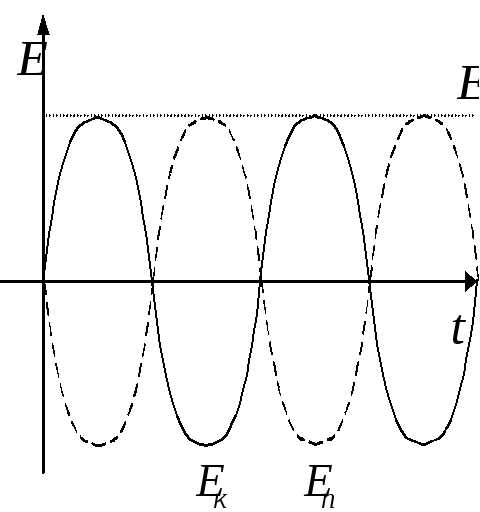 нергия
и вычисление периода колебаний:
нергия
и вычисление периода колебаний:
..
Пружинный маятник: .
Математический маятник:
 /
/
Представление колебаний с помощью векторных диаграмм и комплексных чисел.
П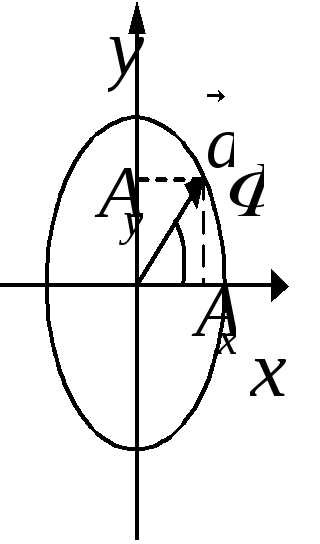 усть,
где.
Возьмём,.
Тогда
усть,
где.
Возьмём,.
Тогда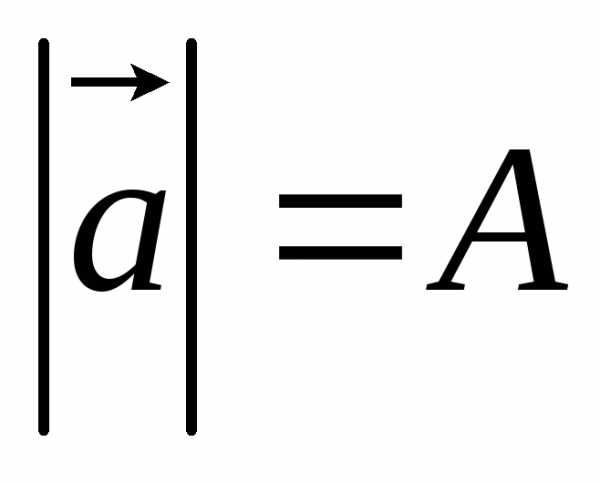 ,
а уравнение
,
а уравнение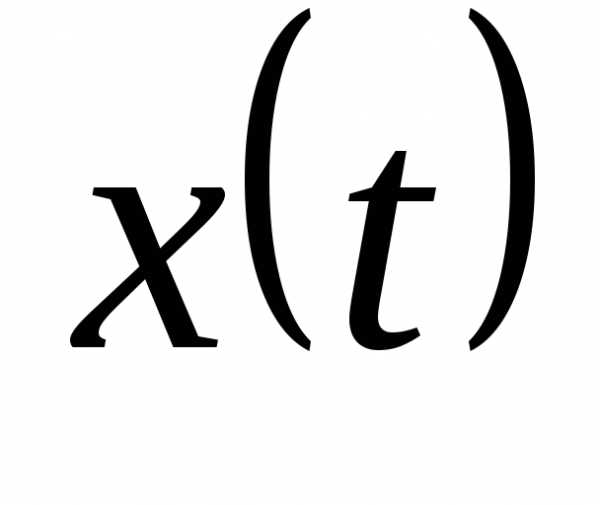 описывает движение проекций конца
вектора по соответствующим осям. Пусть
теперьxy – комплексная плоскость. Тогда
.
описывает движение проекций конца
вектора по соответствующим осям. Пусть
теперьxy – комплексная плоскость. Тогда
.
Фазовая плоскость
(пространство) – геометрический образ,
представимый множеством состояний
системы 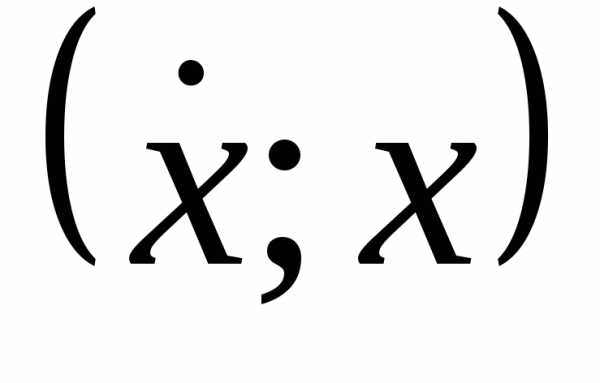 или
или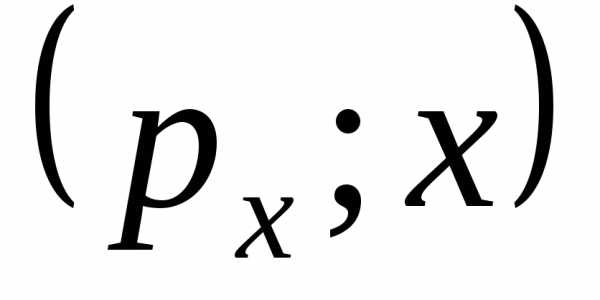 .
.
Фазовая точка – точка фазовой плоскости, определяемая скоростью и координатой и соответствующая определённому состоянию системы.
Фазовая траектория – линия, которую описывает точка на фазовой плоскости при изменении состояния системы.
Фазовый портрет маятника
– фазовая траектория маятника: 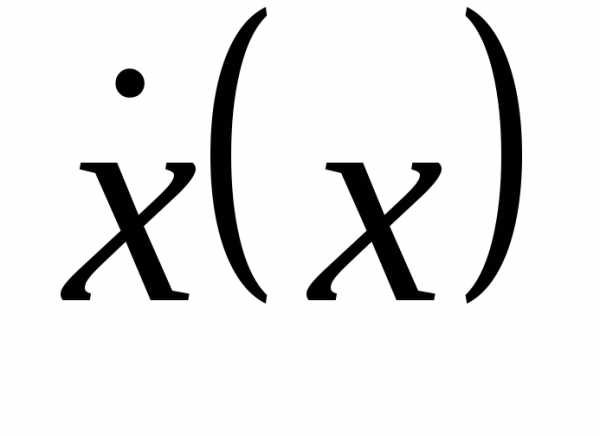 или
или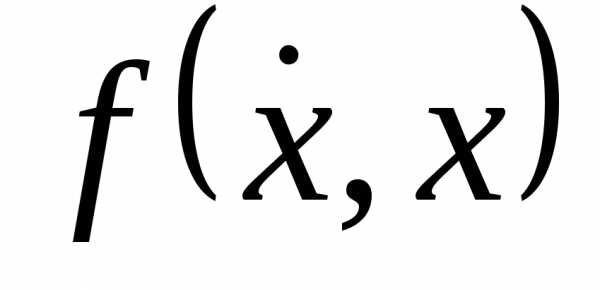 (
(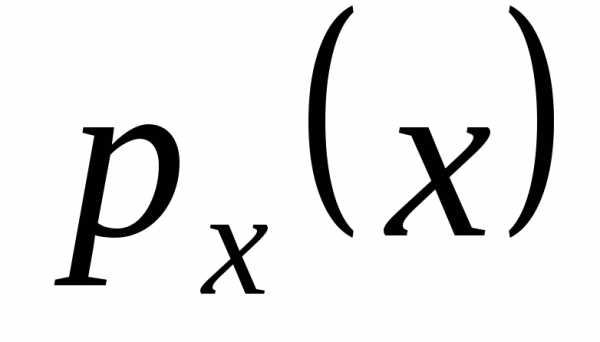 или
или 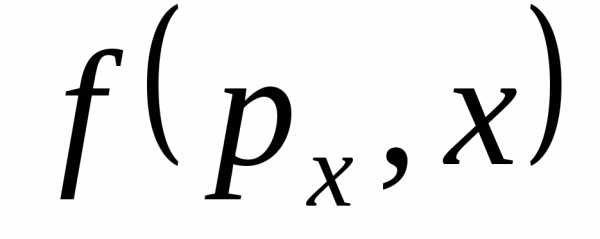 ).
).
Ф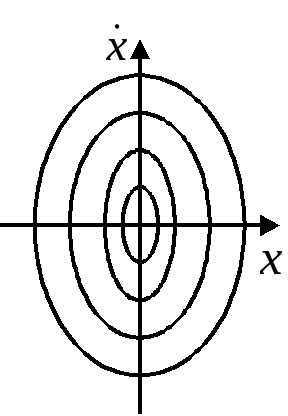 азовый
портрет для гармонических колебаний:
азовый
портрет для гармонических колебаний: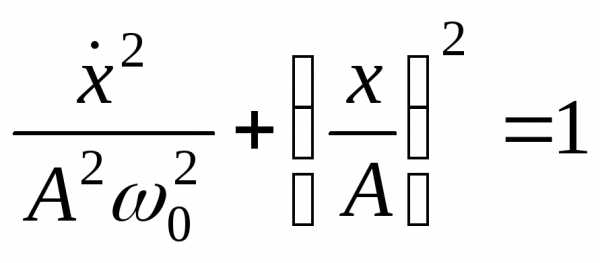 .
.
Свободные затухающие колебания
Пружинный маятник:
.,
где – параметр (коэффициент) затухания, 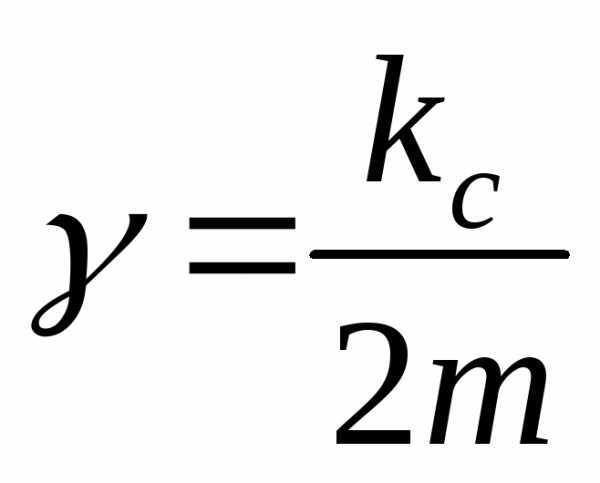 .
.
Математический маятник: .
Решение уравнения свободных затухающих колебаний:
Предположим, что 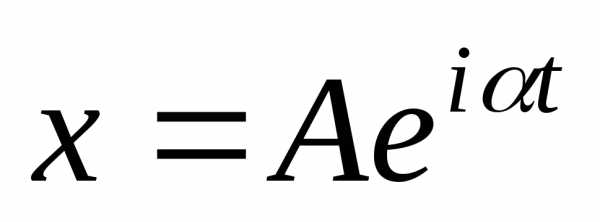 .
Тогда,.,.
Отсюда.
Обозначив,
получим:- решение уравнения свободных затухающих
колебаний.
.
Тогда,.,.
Отсюда.
Обозначив,
получим:- решение уравнения свободных затухающих
колебаний.
Если трение мало  ,
то
,
то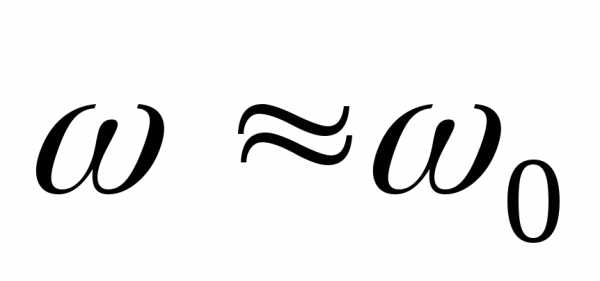 .
.
Основные характеристики затухающих колебаний.
В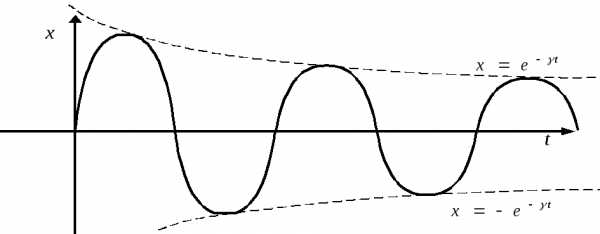 ремя
релаксации – время, в течение которого
значение параметра убывает вe раз:
.
ремя
релаксации – время, в течение которого
значение параметра убывает вe раз:
.
Декремент затухания
характеризует, во сколько раз амплитуда
колебаний убывает за один период: 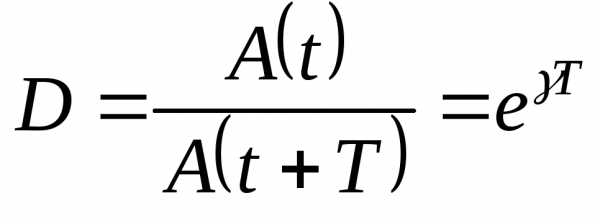 .
.
Логарифмический декремент затухания характеризует, во сколько раз изменяется логарифм убывания амплитуды: .
Пусть
и совершаетсяN колебаний, т.е.
.
Тогда,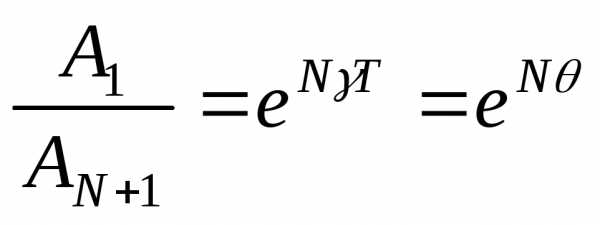 .
.
Скорость и ускорение затухающих колебаний: ,,.
Добротность системы 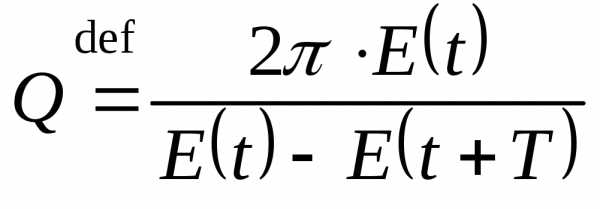 .
.
Э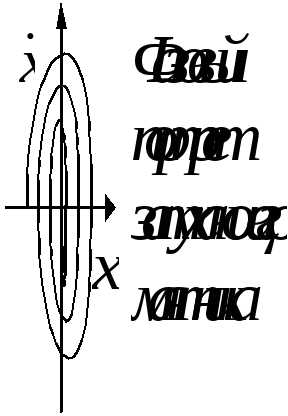 нергия,.
нергия,.
.
При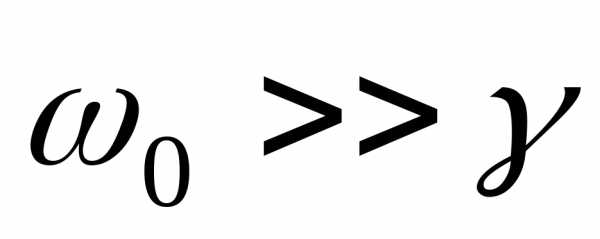
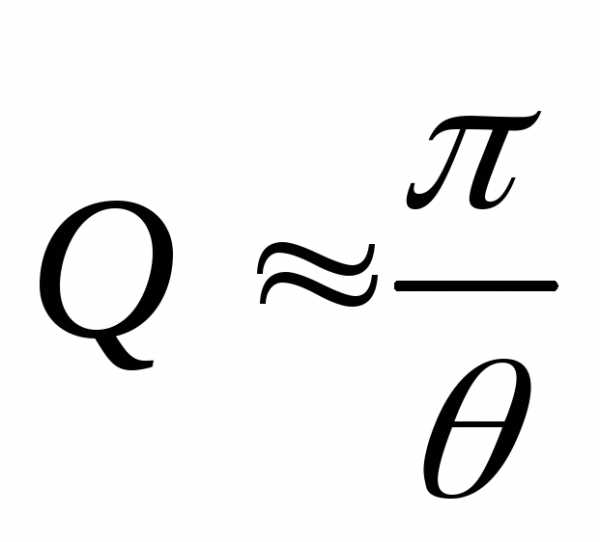 .
.
Вынужденные колебания
Д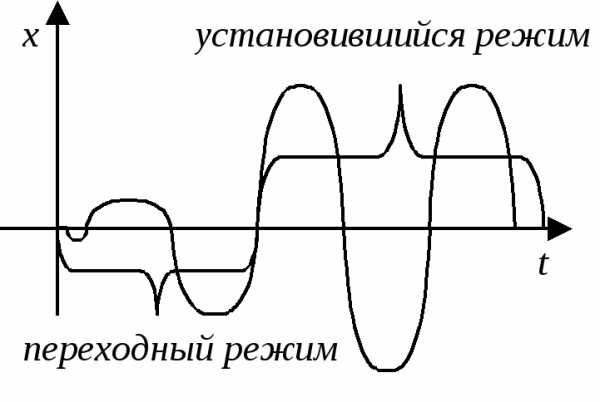 ля
пружинного маятника:,
гдеm – масса тела, F – амплитуда силы, – циклическая частота
силы.
ля
пружинного маятника:,
гдеm – масса тела, F – амплитуда силы, – циклическая частота
силы.
Для математического маятника: .
Длительность переходного режима совпадает со временем релаксации.
– амплитудно-частотная характеристика
вынужденных колебаний,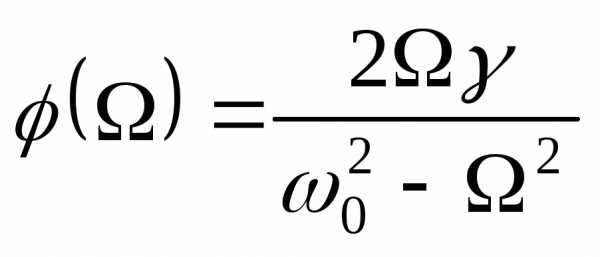 – фазо-частотная характеристика
вынужденных колебаний.
– фазо-частотная характеристика
вынужденных колебаний.
Общее уравнение: , где первое слагаемое представляет собой начальное колебаний системы, которое из-за затухания постепенно сходит на нет, а второе – установившийся режим вынужденных колебаний.
Резонанс.
Н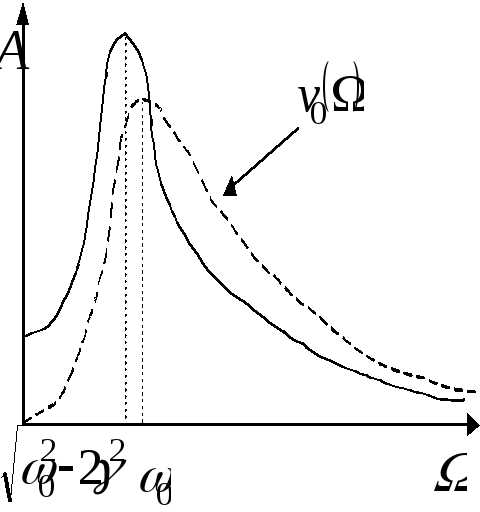 айдём
максимум амплитуды колебаний в зависимости
от частоты воздействующей силы. Для
этого решим уравнение
айдём
максимум амплитуды колебаний в зависимости
от частоты воздействующей силы. Для
этого решим уравнение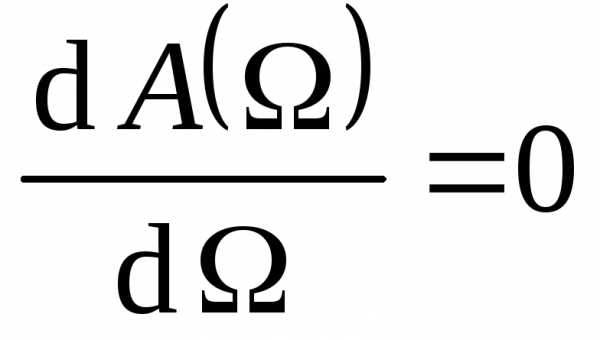 .
Получим:.
.
Получим:.
Резонанс – явление резкого
возрастания (убывания) амплитуды
вынужденных колебаний при стремлении
частоты воздействия внешней силы к
частоте собственных колебаний (точнее,
к величине 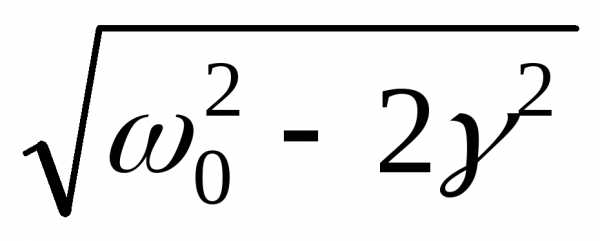 ,
где – коэффициент затухания, но обычно
,
где – коэффициент затухания, но обычно 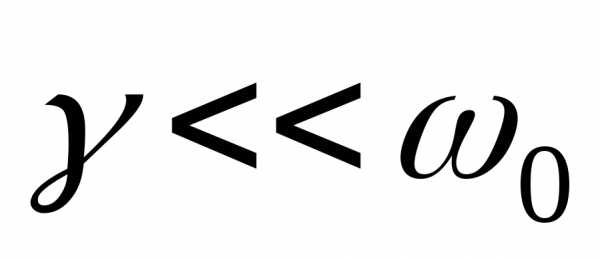 ).
).
Резонансная частота – частота внешней возбуждающей силы, при которой достигается максимум амплитуды вынужденных колебаний.
Наложение колебаний
Сложение колебаний одного направления
Пусть,. Тогда.
Векторная диаграмма:
 ,
,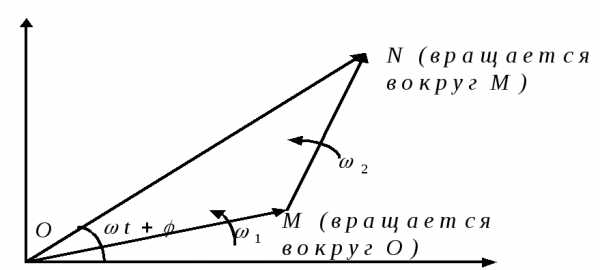
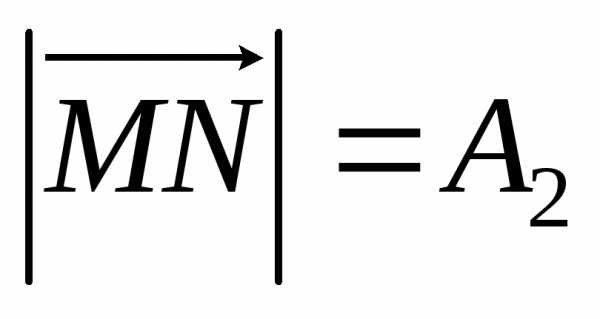 ,.
Тогда,
,.
Тогда,
.
Таким образом, .
Б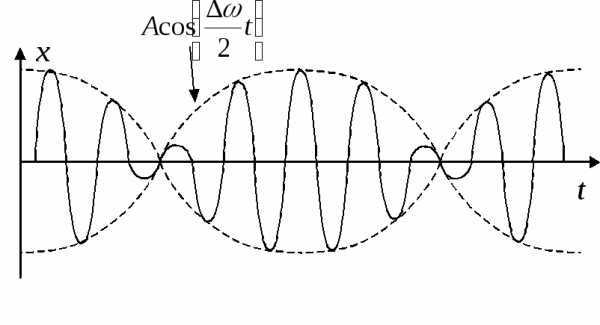 иения:
Рассмотри два колебания:и,
где.
Результирующее колебания будет
описываться уравнением.
иения:
Рассмотри два колебания:и,
где.
Результирующее колебания будет
описываться уравнением.
Частота биения: 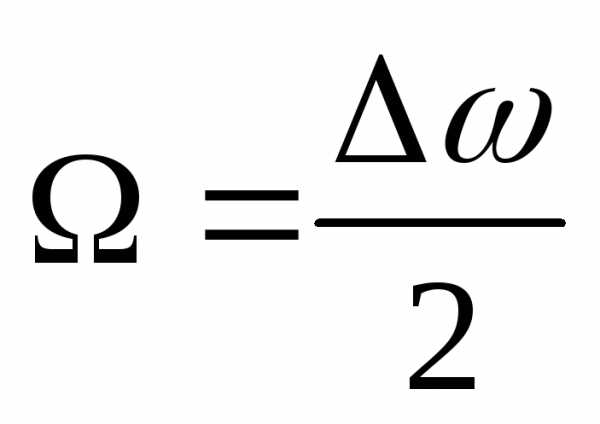 ,
период
,
период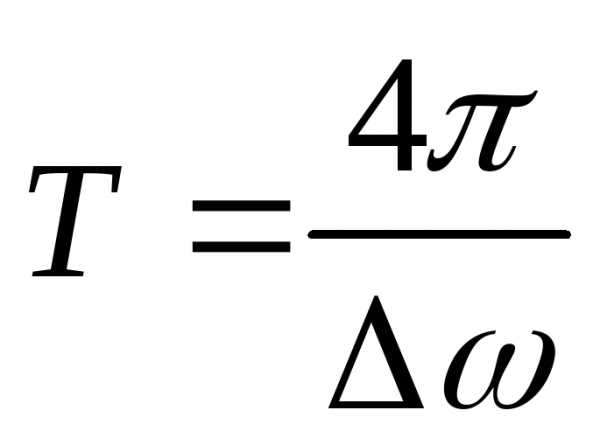 .
.
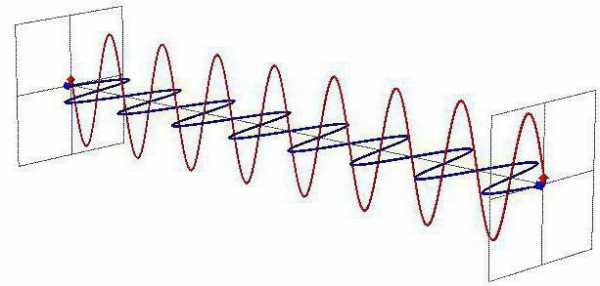
Взаимно перпендикулярные колебания
Рассмотрим два колебания, происходящие во взаимно перпендикулярных направлениях: ,.
Если
 и
и ,
то график
,
то график представляет собой прямую, проходящую
через начало координат.
представляет собой прямую, проходящую
через начало координат.Если
 ,
, и
и ,
то график
,
то график представляет собой эллипс, полуоси
которого равныA и B.
представляет собой эллипс, полуоси
которого равныA и B. ,
, – график
– график представляет собой параболу.
представляет собой параболу.Общий случай: ,.
Фигура Лиссажу – эта линия, которую описывает тело, одновременно колеблющееся в двух взаимно перпендикулярных направлениях.
Свойства фигур Лиссажу:
Если колебания происходят с амплитудами A и B, то фигуру Лиссажу можно вписать в прямоугольник со сторонами
 и
и .
.Если
 – величина рациональная, то фигура
Лиссажу замкнута, иначе – незамкнута.
– величина рациональная, то фигура
Лиссажу замкнута, иначе – незамкнута.Отношение частот колебаний в горизонтальном и вертикальном направлениях равно отношению числа касаний фигуры вертикальных и горизонтальных сторон.
Механические волны
Распространение волн в упругой среде
Волны – процесс распространения колебаний в пространстве с течением времени.
Упругие волны – волны, распространяющиеся в упругой среде.
Волновая поверхность – геометрическое место точек среды, колеблющихся в одной фазе.
Волновой фронт – поверхность, разделяющая возмущённую и невозмущённую части среды.
Виды волн:
Поперечные – колебания в которых происходят поперёк направления распространения.
Продольные – колебания в которых происходят вдоль направления распространения.
В газообразной и жидкой среде колеблется плотность или, что то же, давление. В твёрдой среде и на границе раздела фаз – деформация или, что то же, механическое напряжение.
Волновое уравнение
И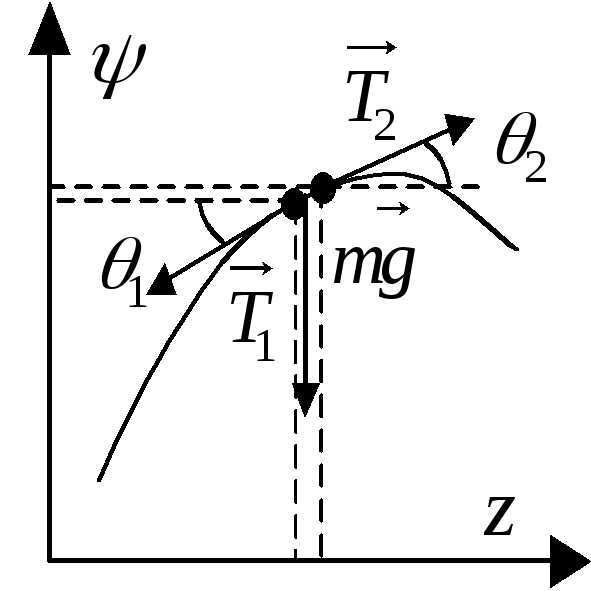 сследуем
колебания струны. Пусть в какой-то момент
времени струна деформирована так, как
показано на рисунке. Тогда уравнение
движения для этой струны выглядит так:.
Т.к.
сследуем
колебания струны. Пусть в какой-то момент
времени струна деформирована так, как
показано на рисунке. Тогда уравнение
движения для этой струны выглядит так:.
Т.к. и
и ,
то.
Спроектируем это уравнение на ось:
и на осьz:
.
Т.к.
,
то.
Спроектируем это уравнение на ось:
и на осьz:
.
Т.к. и
и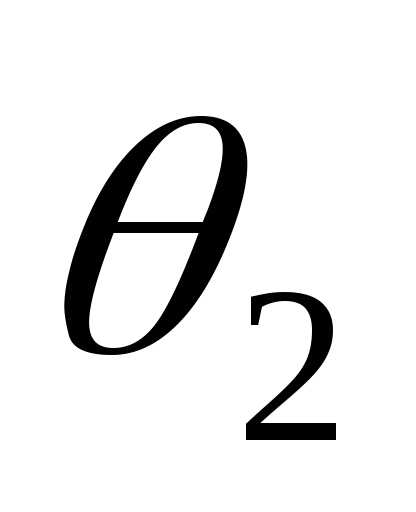 очень малы, то,.
Тогда.
Введём линейную плотность
очень малы, то,.
Тогда.
Введём линейную плотность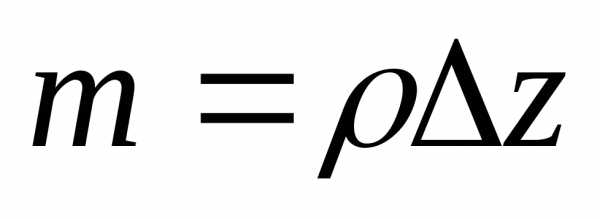 ,
тогда.
Таким образом мы получили волновое
уравнение поперечной волны:,
где
,
тогда.
Таким образом мы получили волновое
уравнение поперечной волны:,
где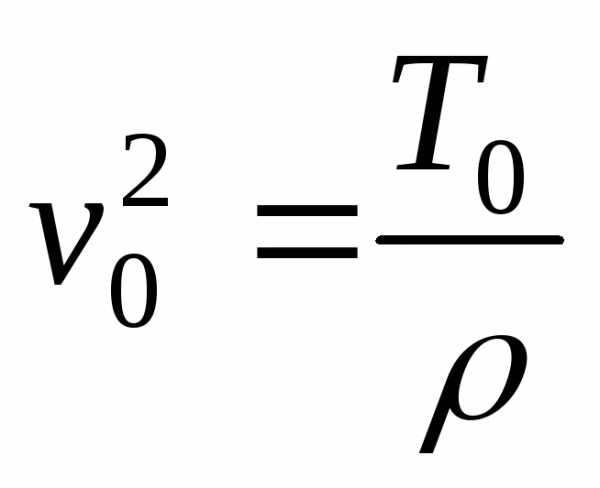 .
.
Волновое уравнение для
продольной волны выглядит так: 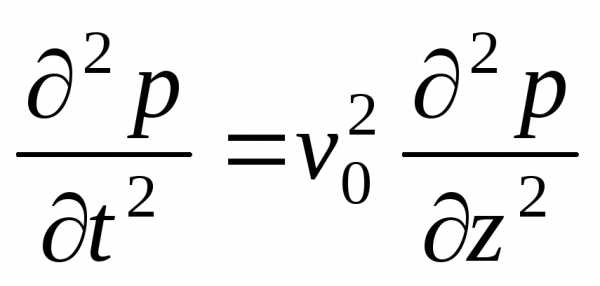 ,
где
,
где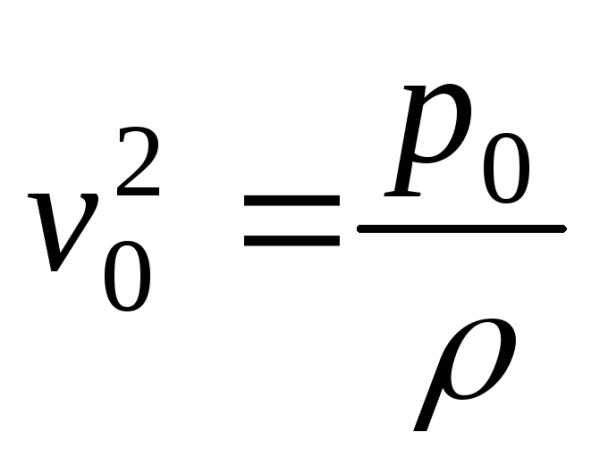 ,p – давление в среде распространения
волны.
,p – давление в среде распространения
волны.
Анализ механических волн
Пусть 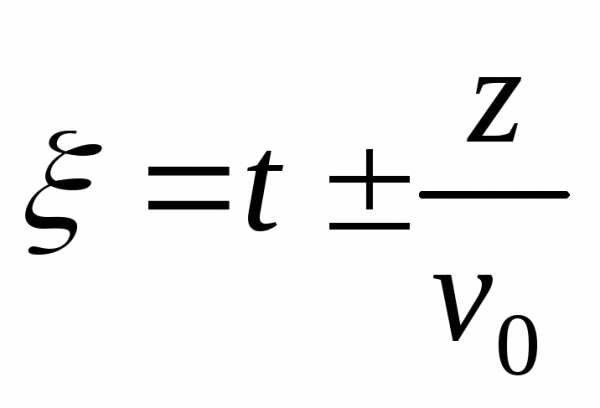 .
Тогда
.
Тогда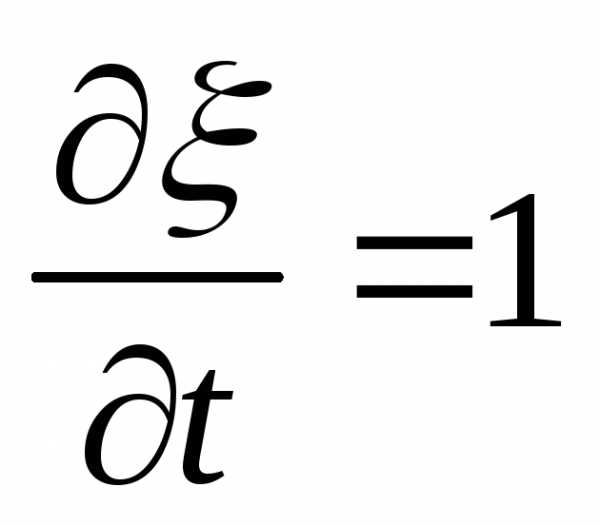 ,
,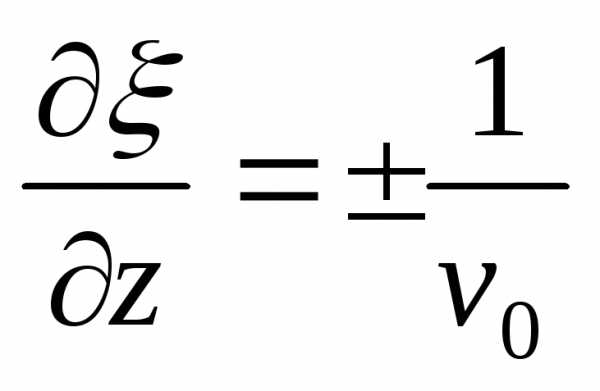 и,
и,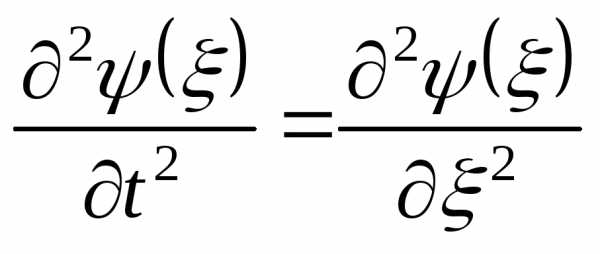 ,
, ,
,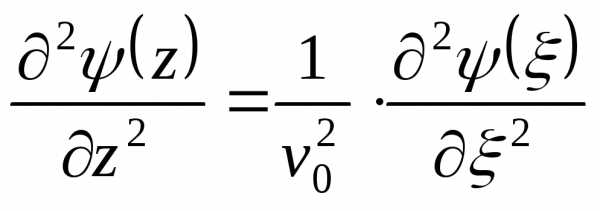 .
Подставим это в волновое уравнение:
.
Подставим это в волновое уравнение: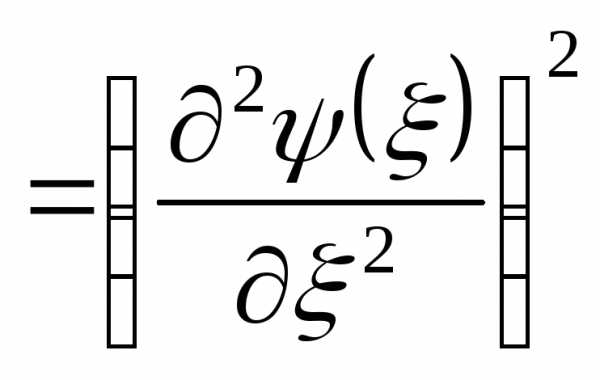 .
.
Общее решение волнового
уравнения:
,
где и
и – произвольные функции.
– произвольные функции.
Гармоническое решение волнового уравнения: .
Период волны 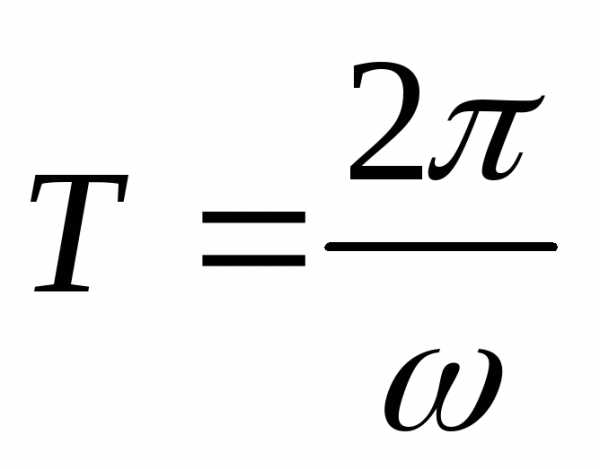 ,
фаза волны.
,
фаза волны.
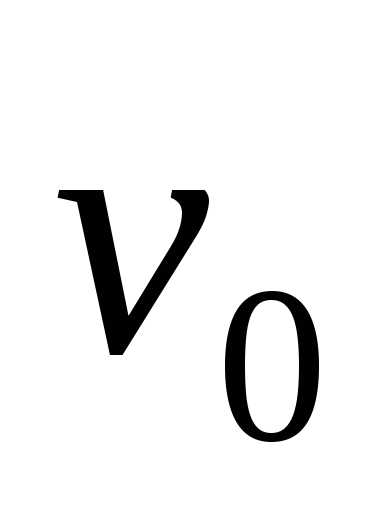 – фазовая скорость волны.
– фазовая скорость волны.
Длина волны – расстояние,
на которое распространяется волна за
один период, 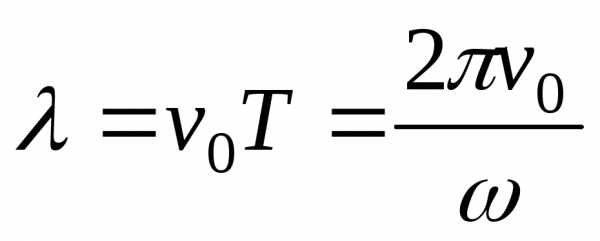
Волновое число 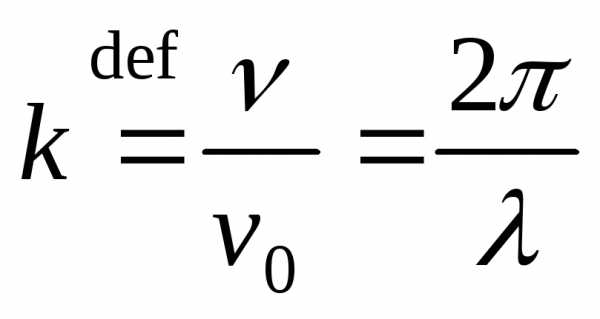 .
.
Волновой вектор: 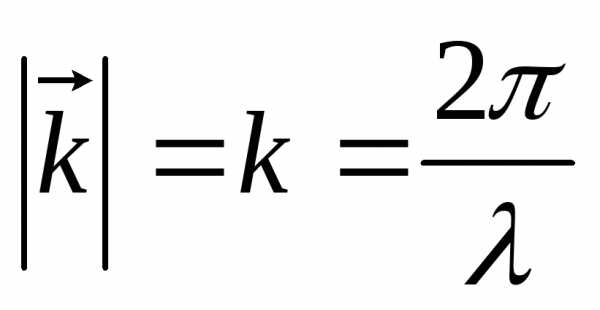 ,
,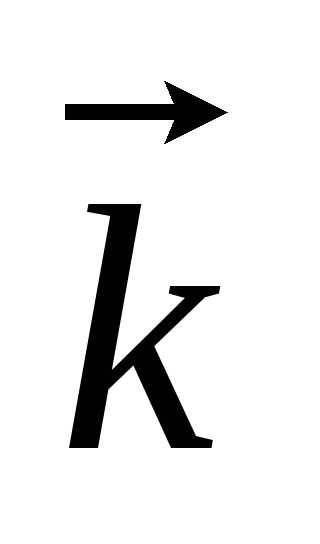 сонаправлен с направлением распространения
волны.
сонаправлен с направлением распространения
волны.
Фазовая скорость волны –
скорость, с которой движутся точки
волны, колеблющиеся в одной фазе. 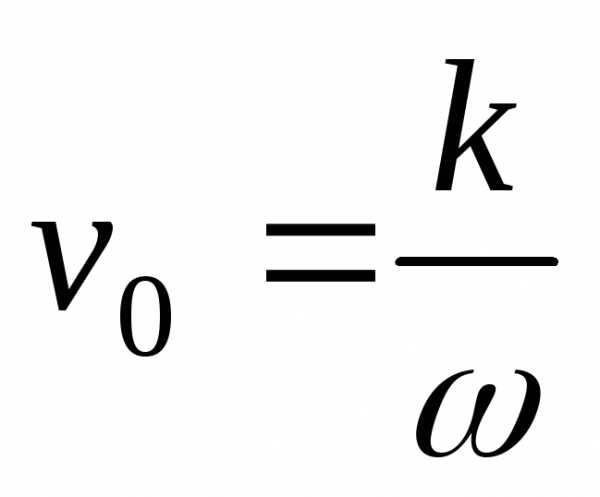 .
.
Геометрические свойства волн
Для трёхмерного случая
выражение 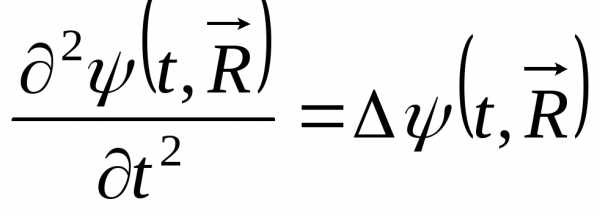 ,
где
– это оператор Лапласа, в декартовой
системе координат
.
,
где
– это оператор Лапласа, в декартовой
системе координат
.
Плоские, цилиндрические и сферические волны – волны, волновой фронт которых представляет собой соответственно плоскость, цилиндр и сферу.
В случае плоской волны в
волновом уравнении достаточно заменить 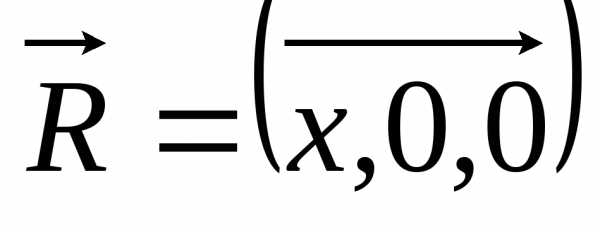 ,
т.е..
,
т.е..
Для цилиндрической волны
или, для гармонических колебаний,.
Здесь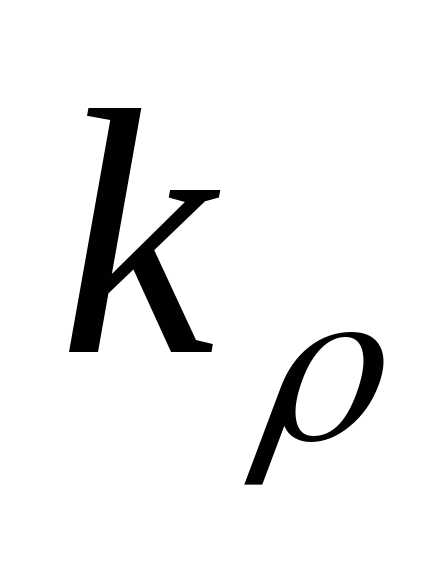 – проекция волнового вектора на ось
– проекция волнового вектора на ось .
.
Уравнение сферической
волны:
,
.
Здесь 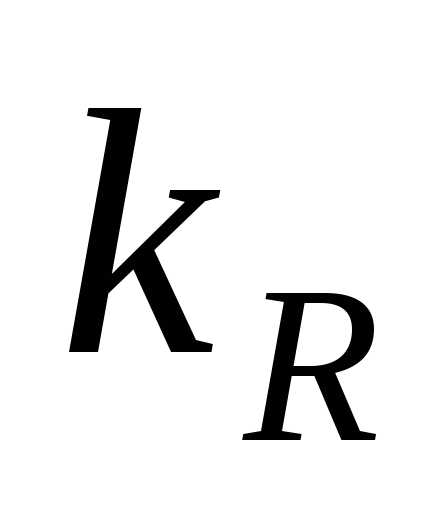 – проекция волнового вектора на
радиус-вектор.
– проекция волнового вектора на
радиус-вектор.
Бегущие и стоячие волны
Если , то направление распространения волны сонаправленно с осьюz. Если же , то направление распространения волны противоположно направлено осиz.
Рассмотрим сложение двух одинаковых волн, двигающихся навстречу друг другу. Т.е. пусть ,. Тогда- уравнение стоячей волны.
Узлы – это точки, амплитуда колебаний которых равна 0 (т.е. ).
Пучности – это точки, амплитуда колебаний которых максимальна (т.е. ).
Длина стоячей волны 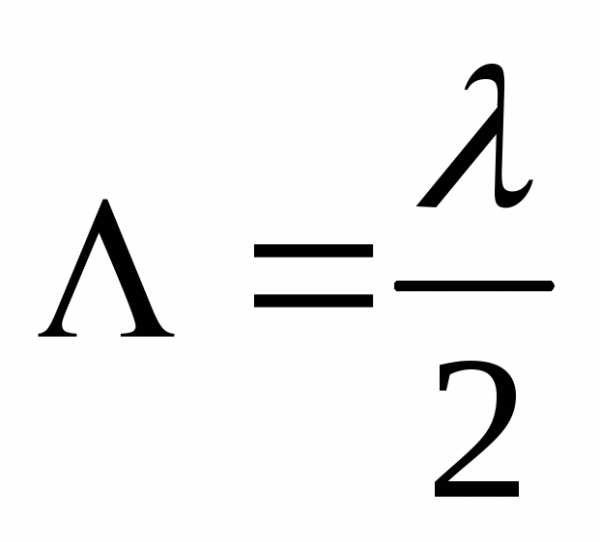 .
.
studfiles.net
Виды колебаний в физике и их характеристика
Существуют разные виды колебаний в физике, характеризующиеся определенными параметрами. Рассмотрим их основные отличия, классификацию по разным факторам.
Основные определения
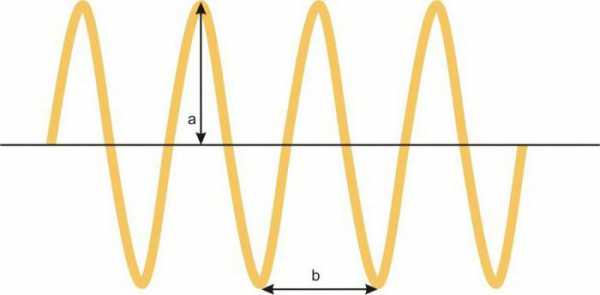
Под колебанием подразумевают процесс, в котором через равные промежутки времени основные характеристики движения имеют одинаковые значения.
Периодическими называют такие колебания, при которых значения основных величин повторяются через одинаковые промежутки времени (период колебаний).
Разновидности колебательных процессов
Рассмотрим основные виды колебаний, существующие в фундаментальной физике.
Свободными называют колебания, которые возникают в системе, не подвергающейся внешним переменным воздействиям после начального толчка.
В качестве примера свободных колебаний является математический маятник.
Те виды механических колебаний, которые возникают в системе под действием внешней переменной силы.

Особенности классификации
По физической природе выделяют следующие виды колебательных движений:
- механические;
- тепловые;
- электромагнитные;
- смешанные.
По варианту взаимодействия с окружающей средой
Виды колебаний по взаимодействию с окружающей средой выделяют несколько групп.
Вынужденные колебания появляются в системе при действии внешнего периодического действия. В качестве примеров такого вида колебаний можно рассмотреть движение рук, листья на деревьях.
Для вынужденных гармонических колебаний возможно появление резонанса, при котором при равных значениях частоты внешнего воздействия и осциллятора при резком возрастании амплитуды.
Собственные это колебания в системе под воздействием внутренних сил после того, когда она будет выведена из равновесного состояния. Простейшим вариантом свободных колебаний является движение груза, который подвешен на нити, либо прикреплен к пружине.
Автоколебаниями называют виды, при которых у системы есть определенный запас потенциальной энергии, идущей на совершение колебаний. Отличительной чертой их является тот факт, что амплитуда характеризуется свойствами самой системы, а не первоначальными условиями.
Для случайных колебаний внешняя нагрузка имеет случайное значение.
Основные параметры колебательных движений
Все виды колебаний имеют определенные характеристики, о которых следует упомянуть отдельно.
Амплитудой называют максимальное отклонение от положения равновесия отклонение колеблющейся величины, измеряется она в метрах.
Период является время одного полного колебания, через который повторяются характеристики системы, вычисляется в секундах.
Частота определяется количеством колебаний за единицу времени, она обратно пропорциональна периоду колебаний.
Фаза колебаний характеризует состояние системы.

Характеристика гармонических колебаний
Такие виды колебаний происходят по закону косинуса или синуса. Фурье удалось установить, что всякое периодическое колебание можно представить в виде суммы гармонических изменений путем разложения определенной функции в ряд Фурье.
В качестве примера можно рассмотреть маятник, имеющий определенный период и циклическую частоту.
Чем характеризуются такие виды колебаний? Физика считает математический маятник идеализированной системой, которая состоит из материальной точки, которая подвешена на невесомой нерастяжимой нити, колеблется под воздействием силы тяжести.
Такие виды колебаний обладают определенной величиной энергии, они распространены в природе и технике.
При продолжительном колебательном движении происходит изменение координаты его центра масс, а при переменном токе меняется значение тока и напряжения в цепи.
Выделяют разные виды гармонических колебаний по физической природе: электромагнитные, механические и др.
В качестве вынужденных колебаний выступает тряска транспортного средства, которое передвигается по неровной дороге.
Основные отличия между вынужденными и свободными колебаниями
Эти виды электромагнитных колебаний отличаются по физическим характеристикам. Наличие сопротивления среды и силы трения приводят к затуханию свободных колебаний. В случае вынужденных колебаний потери энергии компенсируются ее дополнительным поступлением от внешнего источника.
Период пружинного маятника связывает массу тела и жесткость пружины. В случае математического маятника он зависит от длины нити.
При известном периоде можно вычислить собственную частоту колебательной системы.
В технике и природе существуют колебания с разными значениями частот. К примеру, маятник, который колеблется в Исаакиевском соборе в Петербурге, имеет частоту 0,05 Гц, а у атомов она составляет несколько миллионов мегагерц.
Через некоторый промежуток времени наблюдается затухание свободных колебаний. Именно поэтому в реальной практике применяют вынужденные колебания. Они востребованы в разнообразных вибрационных машинах. Вибромолот является ударно-вибрационной машиной, которая предназначается для забивки в грунт труб, свай, иных металлических конструкций.

Электромагнитные колебания
Характеристика видов колебаний предполагает анализ основных физических параметров: заряда, напряжения, силы тока. В качестве элементарной системы, которая используется для наблюдения электромагнитных колебаний, является колебательный контур. Он образуется при последовательном соединении катушки и конденсатора.
При замыкании цепи, в ней возникают свободные электромагнитные колебания, связанные с периодическими изменениями электрического заряда на конденсаторе и тока в катушке.
Свободными они являются благодаря тому, что при их совершении нет внешнего воздействия, а используется только энергия, которая запасена в самом контуре.
Если считать сопротивление катушки нулевым, а период колебаний взять за Т, можно рассмотреть одно полное колебание, совершаемое системой.
При отсутствии внешнего воздействия, через определенный промежуток времени, наблюдается затухание электромагнитного колебания. Причиной подобного явления будет постепенная разрядка конденсатора, а также сопротивление, которым в реальности обладает катушка.
Именно поэтому в реальном контуре происходят затухающие колебания. Уменьшение заряда на конденсаторе приводит к снижению значения энергии в сравнении с ее первоначальным показателем. Постепенно она выделится в виде тепла на соединительных проводах и катушке, конденсатор полностью разрядится, а электромагнитное колебание завершится.

Значение колебаний в науке и технике
Любые движения, которые обладают определенной степенью повторяемости, являются колебаниями. Например, математический маятник характеризуется систематическим отклонением в обе стороны от первоначального вертикального положения.
Для пружинного маятника одно полное колебание соответствует его движению вверх-вниз от начального положения.
В электрическом контуре, который обладает емкостью и индуктивностью, наблюдается повторение заряда на пластинах конденсатора. В чем причина колебательных движений? Маятник функционирует благодаря тому, что сила тяжести заставляет его возвращаться в первоначальное положение. В случае пружиной модели подобную функцию осуществляет сила упругости пружины. Проходя положение равновесия, груз имеет определенную скорость, поэтому по инерции движется мимо среднего состояния.
Электрические колебания можно объяснить разностью потенциалов, существующей между обкладками заряженного конденсатора. Даже при его полной разрядке ток не исчезает, осуществляется перезарядка.
В современной технике применяются колебания, которые существенно различаются по своей природе, степени повторяемости, характеру, а также «механизму» появления.
Механические колебания совершают струны музыкальных инструментов, морские волны, маятник. Химические колебания, связанные с изменением концентрации реагирующих веществ, учитывают при проведении различных взаимодействий.
Электромагнитные колебания позволяют создавать различные технические приспособления, например, телефон, ультразвуковые медицинские приборы.
Колебания яркости цефеид представляют особый интерес в астрофизике, их изучением занимаются ученые из разных стран.
Заключение
Все виды колебаний тесно связаны с огромным количеством технических процессов и физических явлений. Велико их практическое значение в самолетостроении, строительстве судов, возведении жилых комплексов, электротехнике, радиоэлектронике, медицине, фундаментальной науке. Примером типичного колебательного процесса в физиологии выступает движение сердечной мышцы. Механические колебания встречаются в органической и неорганической химии, метеорологии, а также во многих иных естественнонаучных областях.
Первые исследования математического маятника были проведены в семнадцатом веке, а к концу девятнадцатого столетия ученым удалось установить природу электромагнитных колебаний. Русский ученый Александр Попов, которого считают «отцом» радиосвязи, проводил свои эксперименты именно на основе теории электромагнитных колебаний, результатах исследований Томсона, Гюйгенса, Рэлея. Ему удалось найти практическое применение электромагнитным колебаниям, использовать их для передачи радиосигнала на большое расстояние.
Академик П. Н. Лебедев на протяжении многих лет проводил эксперименты, связанные с получение электромагнитных колебаний высокой частоты с помощью переменны электрических полей. Благодаря многочисленным экспериментам, связанные с различными видами колебаний, ученым удалось найти области их оптимального использования в современной науке и технике.
fb.ru
Ответы@Mail.Ru: что такое колебание
http://ru.wikipedia.org/wiki/КолебанияКолебания
Материал из Википедии — свободной энциклопедии
(Перенаправлено с Колебание)
Колеба́ния — повторяющийся в той или иной степени во времени процесс изменения состояний системы. Например, при колебаниях маятника повторяются отклонения его в ту и другую сторону от вертикального положения; при колебаниях в электрическом колебательном контуре повторяются величина и направление тока, текущего через катушку.
Колебания почти всегда связаны с попеременным превращением энергии одной формы проявления в другую форму.
Отличие колебания от волны.
Колебания различной физической природы имеют много общих закономерностей и тесно взаимосвязаны c волнами. Поэтому исследованиями этих закономерностей занимается обобщённая теория колебаний и волн. Принципиальное отличие от волн: при колебаниях не происходит переноса энергии, это, так сказать, «местные» преобразования энергии. Содержание [убрать]
1 Классификация
1.1 По физической природе
1.2 По характеру взаимодействия с окружающей средой
2 Характеристики
3 См. также
4 Литература
[править]
Классификация
Выделение разных видов колебаний зависит от подчёркиваемых свойств колеблющихся систем (осцилляторов)
[править]
По физической природе
Механические (звук, вибрация)
Электромагнитные (свет, радиоволны, тепловые)
Смешанного типа — комбинации вышеперечисленных
[править]
По характеру взаимодействия с окружающей средой
Вынужденные — колебания, протекающие в системе под влиянием внешнего периодического воздействия
Собственные (или свободные) — колебания при отсутствии внешних сил, когда система, после первоначального воздействия внешней силы, предоставляется самой себе (в реальных условиях свободные колебания всегда затухающие)
Автоколебания — колебания, при которых система имеет запас потенциальной энергии, расходующейся на совершение колебаний (пример такой системы — механические часы) .
[править]
Характеристики
Амплитуда — максимальное отклонение колеблющейся величины от некоторого усреднённого её значения для системы, (м)
Период — промежуток времени, через который повторяются какие-либо показатели состояния системы (система совершает одно полное колебание) , (сек)
Частота — число колебаний в единицу времени, (Гц, сек−1).
Период колебаний и частота — обратные величины;
и
В круговых или циклических процессах вместо характеристики «частота» используется понятие круговая (циклическая) частота (рад/сек, Гц, сек−1), показывающая число колебаний за 2π единиц времени:
Фаза колебаний — определяет смещение в любой момент времени, то есть определяет состояние колебательной системы. Циклическая частота показывает изменение фазы колебаний, выраженное в радианах, за секунду времени.
otvet.mail.ru
Колебания – это… Что такое Колебания?
Отличие колебания от волныКолеба́ния — повторяющийся в той или иной степени во времени процесс изменения состояний системы около точки равновесия. Например, при колебаниях маятника повторяются отклонения его в ту и другую сторону от вертикального положения; при колебаниях в электрическом колебательном контуре повторяются величина и направление тока, текущего через катушку.
Колебания почти всегда связаны с попеременным превращением энергии одной формы проявления в другую форму.
Колебания различной физической природы имеют много общих закономерностей и тесно взаимосвязаны c волнами. Поэтому исследованиями этих закономерностей занимается обобщённая теория колебаний и волн. Принципиальное отличие от волн: при колебаниях не происходит переноса энергии, это, так сказать, «местные» преобразования энергии.
Классификация
Выделение разных видов колебаний зависит от подчёркиваемых свойств колеблющихся систем (осцилляторов)
По физической природе
По характеру взаимодействия с окружающей средой
- Вынужденные — колебания, протекающие в системе под влиянием внешнего периодического воздействия. Примеры: листья на деревьях, поднятие и опускание руки. При вынужденных колебаниях может возникнуть явление резонанса: резкое возрастание амплитуды колебаний при совпадении собственной частоты осциллятора и частоты внешнего воздействия.
- Свободные (или собственные) — это колебания в системе под действием внутренних сил, после того как система выведена из состояния равновесия (в реальных условиях свободные колебания всегда затухающие). Простейшими примерами свободных колебаний являются колебания груза, прикреплённого к пружине, или груза, подвешенного на нити.
- Автоколебания — колебания, при которых система имеет запас потенциальной энергии, расходующейся на совершение колебаний (пример такой системы — механические часы). Характерным отличием автоколебаний от свободных колебаний является, то что их амплитуда определяется свойствами самой системы, а не начальными условиями.
- Параметрические — колебания, возникающие при изменении какого-либо параметра колебательной системы в результате внешнего воздействия.
- Случайные — колебания, при которых внешняя или параметрическая нагрузка является случайным процессом.
Характеристики
- Амплитуда — максимальное отклонение колеблющейся величины от некоторого усреднённого её значения для системы, (м)
- Период — промежуток времени, через который повторяются какие-либо показатели состояния системы (система совершает одно полное колебание), (с)
- Частота — число колебаний в единицу времени, (Гц, с−1).
Период колебаний и частота — обратные величины;
иВ круговых или циклических процессах вместо характеристики «частота» используется понятие круговая (циклическая) частота (рад/с, Гц, с−1), показывающая число колебаний за единиц времени:
- Смещение — отклонение тела от положения равновесия. Обозначение Х, Единица измерения метр.
- Фаза колебаний — определяет смещение в любой момент времени, то есть определяет состояние колебательной системы.
См. также
Литература
- Физика. Большой энциклопедический словарь/Гл. ред. А. М. Прохоров. — 4-е изд. — М.: Большая Российская энциклопедия, 1999. — С. 293—295. ISBN 5-85270-306-0 (БРЭ)
biograf.academic.ru
Основные понятия теории колебаний
Колебания — это процессы, которые имеют какую либо степень повторяемости во времени.
Свободные (собственные) колебания — это колебания, которые предоставляют сами себе системы, вызванные первоначальным кратковременным внешним возбуждением.
Колебательная система — это такая система, которая способная производить свободные колебания.
Колебательная система соответствует следующим условиям:
- необходимо положение устойчивого равновесия;
- необходим фактор, не позволяющий системе остановиться в положении равновесия в процессе колебаний;
- трение в системе должно быть небольшим, а собственная частота колебательной системы обусловливается только параметрами системы.
Амплитуда колебаний — это максимальное значение величины (для механических колебаний это смещение), которая совершает колебания.
Период колебаний — это самый маленький отрезок времени, через который система совершает колебания, снова возвращается в исходное состояние, т. е. в начальный момент.
Частота колебаний — это физическая величина, равная числу колебаний, которые совершаются в единицу времени.
Циклическая частота — это характеристика гармонических колебаний, совершаемых за
Фаза колебаний — это аргумент функции, который периодически изменяется.
Затухающие колебания — это собственные колебания, у которых амплитуда уменьшается со временем, что обусловлено потерями энергии колебательной системой.
Коэффициент затухания и логарифмический декремент затухания — это характеристика быстроты уменьшения амплитуды в случае механических колебаний, где энергия убывает за счет действия сил трения и других сил сопротивления.
Декремент затухания — это количественная характеристика быстроты затухания колебаний, которая определяется натуральным логарифмом отношения двух последовательных максимальных отклонений , колеблющейся величины в одну сторону:
Декремент затухания — величина, обратная числу колебаний, по истечении которых амплитуда убывает в: е раз е = 2,71828). Промежуток времени, необходимый для этого, называется временем релаксации.
Дифференциальное уравнение малых затухающих колебаний системы:
Вынужденные колебания — это колебания, которые возникают под действием внешней периодической силы.
Дифференциальное уравнение вынужденных колебаний:
Резонанс — это процесс резкого возрастания амплитуды вынужденных колебаний при приближении циклической частоты , вынуждающей силы к собственной циклической частоте колебательной системы.
Автоколебания — это незатухающие колебания физической системы, которые способны существовать без воздействия на нее внешних сил.
Автоколебательная система — это физическая система, где имеет место существовать автоколебания.
Автоколебательная система состоит из следующих частей:
- колебательная система, в которой параметры определяют частоту автоколебаний;
- источник энергии, который способствует поддержанию колебаний;
- клапан, который регулирует поступление энергии в колебательную систему;
- положительная обратная связь, которая способна управлять клапаном в колебательной системе.
Обратная связь — это воздействие результатом какого-либо процесса на его протекание.
Обратная связь бывает:
- положительная — это связь, которая приводит к увеличению отклонения;
- отрицательная — это связь, которая приводит к уменьшению отклонения.
Периодические колебания — это колебания, которые имеют изменяющиеся значения физических величин, но которые повторяются через равные отрезки времени.
Смещение — это физическая величина, которая является характеристикой колебаний, равная отклонению тела от положения равновесия в данный момент времени.
Математический, физический, пружинный маятники.
Математический маятник — это тело малых размеров, подвешенное на тонкой нерастяжимой нити, масса которой ничтожно мала по сравнению с массой тела. В положении равновесия, когда маятник висит по отвесу, сила тяжести уравновешивается силой натяжения нити .
Составляющая силы тяжести при отклонении маятника из положения равновесия на некоторый угол ф , где знак «минус» означает, что касательная составляющая на- правлена в сторону, противоположную отклонению маятника. Второй закон Ньютона для математического маятника запишется: , где x — линейное смещение маятника от положения равно- весия по дуге окружности, l — радиус.
Угловое смещение будет равно
Для малых колебаний математического маятника второй закон Ньютона записывается в виде:
Если математический маятник совершает малые колебания, то он является гармоническим осциллятором. Собственная частота малых колебаний математического маятника:
Период малых колебаний математического маятника определяется:
Физический маятник — это тело, которое является твердым, производящее колебания в поле каких-либо сил относительно точки, которая не является центром масс этого тела, или горизонтальной оси.
Второй закон Ньютона для физического маятника принимает вид:
Собственная частота малых колебаний физического маятника:
Период малых колебаний физического маятника определяется:
Круговая частота свободных колебаний физического маятника определяется выражением:
Центр качания физического маятника — это точка, где необходимо сосредоточить всю массу физического маятника, чтобы его период колебаний оставался постоянным.
Физический маятник обладает следующим замечательным свойством: если физический маятник подвесить за центр качания, то его период колебаний будет постоянным, а прежняя точка подвеса станет новым центром качания.
Пружинный маятник — это колебательная система, которая состоит из груза, подвешенного к абсолютно упругой пружине.
Пружинный маятник совершает гармонические колебания с циклической частотой:
, где k — коэффициент жесткости.
Период пружинного маятника определяется:
Уравнение движения пружинного маятника при этом имеет вид:
xn—-7sbfhivhrke5c.xn--p1ai
Колебания – это… Что такое Колебания?
T называется периодом. Число К. в единицу времени ν = 1/Т называется частотой К.
Частными случаями периодических К. являются К. прямоугольные (), пилообразные (), синусоидальные (или гармонические,). В последнем случае s=Acos (ωt— φ),
где А, ω, φ — постоянные. Величина А (максимальное значение s) называется амплитудой. Так как значения cos (ωf — φ) повторяются при возрастании аргумента на 2π, то ωТ =2π и, следовательно,
ω=2π/Т=2πν.
Величина ω называется круговой, пли циклической, частотой, равна числу К. за 2π единиц времени. Функция времени ωt — (называется фазой К., постоянная φ — начальной фазой (часто её называют просто фазой). На изображено затухающее К.
s = Ae-δtcos (ωt — φ),
где А, δ, ω,φ — постоянные. А называется начальной амплитудой, Ae-δt — мгновенным значением амплитуды. δ — коэффициент затухания, τ=1/δ — временной постоянной (см. также Декремент затухания). Величина δ здесь положительна. При отрицательном знаке δ К. является нарастающим. Величины ωt — (,ω, φ имеют те же названия, что и в случае синусоидального К. Хотя затухающее К. не является точно периодическим, величина Т = 2 π/ω также называется периодом.В физике и радиотехнике большое значение имеют модулированные К., то есть К. вида
s=A (t) cos [ωt— ω(t)],
причём функции A (t), ω(t) меняются медленно по сравнению с cosωt (ω — постоянная). Если φ(t) = const. то К. называются амплитудно-модулированным (рис. 3, ж), если A (t) = const (рис. 3, з) — модулированным по фазе (или по частоте; см. Модуляция колебаний). В общем случае () К. модулированы как по амплитуде, так и по фазе. соответствуют периодической амплитудной и фазовой модуляции: A (t) и φ(t) — периодические функции. Важное значение в технике (радиотелефония, телевидение) и в физике имеет случай, когда A (t) или φ(t), или же обе одновременно являются так называемыми случайными функциями (). Часто в природе и технике встречаются беспорядочные К. (), например белый свет, акустический и электрический «белый» шум и т.п. Ни в природе, ни в технике никогда не встречаются строго периодические (в частности, строго гармонические) К. Тем не менее гармонические К. весьма важны по двум причинам. 1) В природе и технических устройствах часто возникают К., мало отличающиеся на протяжении достаточно большого времени от гармонических. 2) Многие физические системы, принадлежащие к классу спектральных приборов в широком смысле этого слова или гармонических анализаторов, преобразуют произвольные К. в набор К., близких к гармоническим. Когда говорят о гармонических К., всегда имеют в виду К., лишь близкие к гармоническим. Гармонические К. даже одинаковой физической природы (К. давления воздуха, напряженности электрического поля), но различной частоты могут обладать (наряду с аналогичными) резко различающимися свойствами; они могут совершенно по-разному воздействовать на те или иные физические системы и живые организмы и, в частности, на органы чувств человека и животных (см. Слух, Зрение). Возникновение колебаний. Здесь рассматривается возникновение К. в системе, не получающей К. извне, а являющейся источником К. В случае, когда система приходит в К. под действием К., подводимых извне, говорят не о возникновении К., а о воздействии К. на систему и о преобразовании их системой. В пассивных (не содержащих источников энергии) системах такое воздействие вызывает Вынужденные колебания. Существует 3 основных типа К. в системах, являющихся источниками К. 1) Свободные (или собственные) К., происходящие, когда система предоставлена самой себе после нарушения равновесия вмешательством извне, например К. пружинного маятника (рис. 1, б) и К. тока в электрическом контуре (рис. 2). Свободные К. пружинного маятника и колебательного контура относятся к частному типу свободных К. в линейных колебательных системах (то есть системах, обладающих параметрами, практически неизменными, и описываемых с достаточной точностью линейными дифференциальными уравнениями) с одной степенью свободы. В линейных системах с N степенями свободы (N>1) свободные К. в каждой точке являются суперпозицией N К. (см. Нормальные колебания). В линейных распределённых системах (если отвлечься от атомистической структуры вещества), например струне, стержне, трубе, а также в электрическом кабеле, объемном резонаторе, свободные К. в каждой точке являются суперпозицией бесконечного числа К. Если восстанавливающая сила, т. е. сила, возвращающая систему к положению равновесия, не пропорциональна отклонению от него, свободные К. описываются нелинейным дифференциальным уравнением, например в случае маятника, когда амплитуду нельзя считать очень малой. Такие системы называются нелинейными. Здесь, в отличие от линейных систем, свободные К. (даже если не учитывать затухания) не синусоидальны, и, кроме того, период их зависит от начальных условий, например у маятника период свободных К. тем больше, чем больше амплитуда. Лишь в пределе, когда она стремится к нулю, система становится линейной, а её К. — изохронными: период не зависит от амплитуды. 2) Флуктуационные К., происходящие в результате теплового движения вещества. Поскольку маятник, груз, контур участвуют в тепловом движении материи, они совершают никогда не прекращающиеся флуктуационные К. (см. Флуктуации) — один из видов броуновского движения (См. Броуновское движение). Эти К. особенно легко обнаружить и наблюдать в случае колебательного контура, в котором происходят флуктуации напряжения и тока, применяя усилитель с большим коэффициентом усиления и Осциллограф. Флуктуационные К. в колебательных контурах, антеннах и т.д. — важнейший фактор, ограничивающий чувствительность радиоприёмников. 3) Автоколебания — незатухающие К., которые могут существовать при отсутствии переменного внешнего воздействия, причем амплитуда и период К. определяются только свойствами самой системы и в определенных пределах не зависят от начальных условий. Примерами являются: К. маятника или баланса часов, поддерживаемые опусканием гири или раскручиванием спиральной пружины, звучание духовых и смычковых музыкальных инструментов, К. всевозможных электронных ламповых генераторов, применяемых в радиотехнике, и др. Подробнее см. Автоколебания.Распространение колебаний. Колеблющийся маятник () приводит в движение раму, на которой он подвешен; рама приводит в движение стол и так далее. Таким образом, К. не остаются локализованными, а распространяются, охватывая все окружающие тела. Явление распространения К. гораздо сильнее выражено в случае более быстрых механических (звуковых) К. — струны, колокола, воздуха в трубах музыкальных духовых инструментов и тому подобное. Здесь распространение К. происходит главным образом через воздух. Вокруг источников электрических К. возникают переменные электрические и магнитные поля, распространяющиеся вдаль от точки к точке через диэлектрики (в том числе вакуум). Процессы распространения К. (а также всяких возмущений) называются волнами.
Общий характер колебательных воздействий. Прогиб балки под действием постоянной нагрузки тем больше, чем больше нагрузка; сила тока, возникающего под действием постоянной эдс, тем больше, чем больше эдс, и так далее. В случае колеблющейся нагрузки, переменной эдс и др. колебательных воздействий дело обстоит гораздо сложнее — здесь имеют место вынужденные колебания. Результат воздействия в этом случае зависит не только от его интенсивности, но также в большой степени от его темпа, от того, как оно изменяется со временем. В этом состоит одна из основных и характерных черт К.
Пусть на груз пружинного маятника действует ряд периодически повторяющихся кратковременных толчков снизу вверх. В силу линейности системы для неё справедлив Суперпозиции принцип: действия отдельных толчков складываются. Вообще говоря, действие очередного толчка будет одинаково часто как усиливать, так и ослаблять действие всех предыдущих; амплитуда К. будет то увеличиваться, то уменьшаться, оставаясь сравнительно небольшой. Но если период толчков равен или кратен периоду собственных К., то каждый толчок, действуя «в такт» с К., будет усиливать действие предыдущих и пружинный маятник раскачается до очень большой амплитуды. Рост амплитуды прекратиться только благодаря тому, что существенное значение при большой раскачке приобретает затухание К. за время между двумя толчками. Раскачка линейной колебательной системы под влиянием периодических толчков, ограниченная только затуханием, представляет собой так называемое явление Резонанса. Другой важный случай резонанса наступает при действии на такую систему непрерывной силы, изменяющейся по синусоидальному закону, если частота её изменения совпадает с частотой ω0 свободных К. системы. При периодическом изменении параметра колебательной системы, например, длины нити маятника, емкости колебательного контура и так далее, вообще говоря, маятник не будет раскачиваться, в контуре не будет возникать электрических К. и так далее. Но и здесь при подходящем темпе воздействия (лучше всего, если параметр меняется с частотой, равной 2ω) могут возникнуть К. В любой колебательной системе вследствие воздействия на неё различных случайных факторов всегда существуют флуктуационные К., которые имеют сплошной спектр со всевозможными фазами гармонических составляющих. Поэтому периодические изменения параметра системы всегда совпадут по фазе с одной из гармонических составляющих и ее амплитуда будет возрастать, при этом маятник начнет раскачиваться около вертикали, в контуре появляются нарастающие электромагнитные К. (см. Параметрическое возбуждение колебаний).Частоты некоторых важнейших К. Вращение есть суперпозиция двух взаимно перпендикулярных гармонических К. Обращение планет вокруг Солнца совершается с частотами от 1,28∙10-9гц (Плутон, период 250 лет) до 1,32∙10-7 гц (Меркурий, период 88 сут). Сутки — период обращения Земли вокруг её оси — соответствуют частоте около 1,16∙10-5гц. Морские приливы и отливы происходят с частотой того же порядка. Морские волны, возникающие под действием ветра, имеют частоту Колебания10-1гц. К. сооружений, К. b вращение машин имеют частоты от долей до Колебания10-4гц. Механические К., воспринимаемые нормальным человеческим ухом как звук, совершаются с частотами от 20 гц до Колебания2∙104гц. Более быстрые (неслышимые) упругие К. с частотой до 109гц называются ультразвуковыми, а с частотами до 1012 — 1013гц называются гиперзвуковыми. К. атомов, из которых складывается тепловое движение твёрдых и жидких тел, а также К. атомов в молекулах присущи частоты порядка 1013гц.
Переменный ток, вырабатываемый электростанциями, имеет в СССР и большинстве др. стран стандартную частоту 50 гц. Радиотехника использует электромагнитные К. и волны с частотой от 105гц (длинные волны) до 1011гц (миллиметровые волны). Оптика имеет дело с электромагнитными волнами, в которых К. напряжённости электрического и магнитного полей происходит с частотой от 1012гц до 1017гц. К этому интервалу относится видимый свет (красный: 0,4∙1014гц, фиолетовый: 0,75∙1014гц). Интервал от 1012 до 1014гц соответствует инфракрасному, от 1015 до 1017гц — ультрафиолетовому излучениям. Далее в порядке повышения частоты идут рентгеновское излучение (1018 — 1019гц), гамма-излучение (1020гц), электромагнитное излучение, входящее в состав космических лучей (до 1022гц и более).
Лит.: Элементарный учебник физики, под ред. Г. С. Ландсберга, 7 изд., т. 1, М., 1971; Красильников В. А., Звуковые волны в воздухе, воде и твердых телах, М.— Л.,1951; Стрэтт Дж. В. (Рэлей), Теория звука, пер. с англ., т. 1—2, М.— Л., 1940—44; Андронов А. А. и Хайкин С. Э., Теория колебаний, ч. 1, М.— Л., 1937; Стрелков С. П., Введение и теорию колебаний, М.— Л., 1951; Горелик Г. С., Колебания и волны, 2 изд., М.—Л., 1959.
Г. С. Горелик.
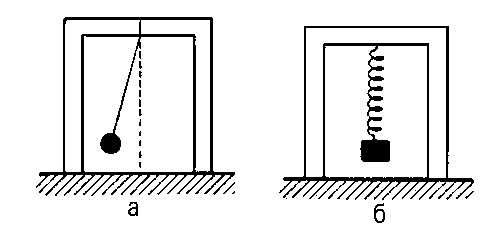
Рис. 1. а — колебания маятника; б — колебания груза на пружине.
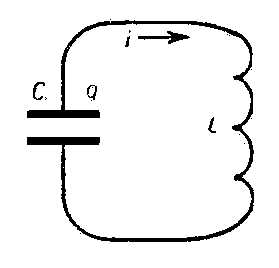
Рис. 2. Электрический колебательный контур: С — ёмкость; L — индуктивность; q — заряд на обкладках конденсатора; i — ток в цепи.
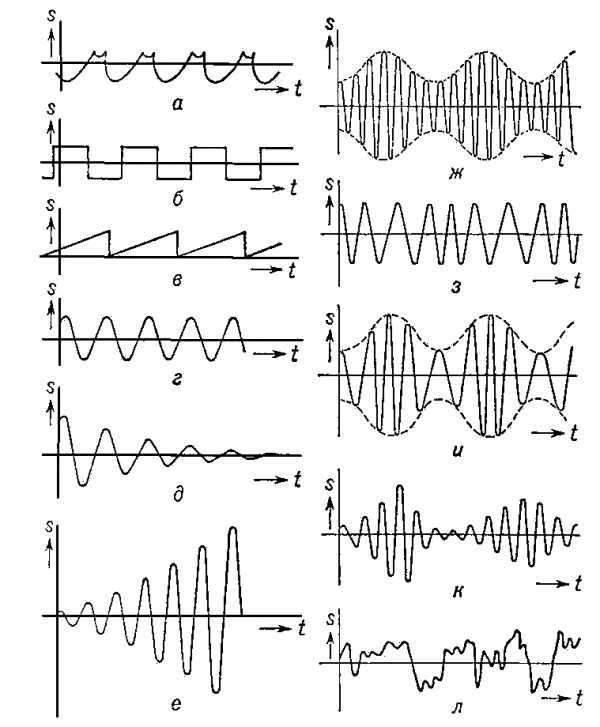
Рис. 3. Различные виды колебаний: а — общий случай периодического колебания; б — прямоугольные колебания; в — пилообразные; г — синусоидальные; д — затухающие; е — нарастающие; ж — амплитудно-модулированные; з — частотно-модулированные; и — колебания, модулированные по амплитуде и по фазе; к — колебания, амплитуда и фаза которых — случайные функции; л — беспорядочные колебания; s — колеблющаяся величина.
Большая советская энциклопедия. — М.: Советская энциклопедия. 1969—1978.
dic.academic.ru

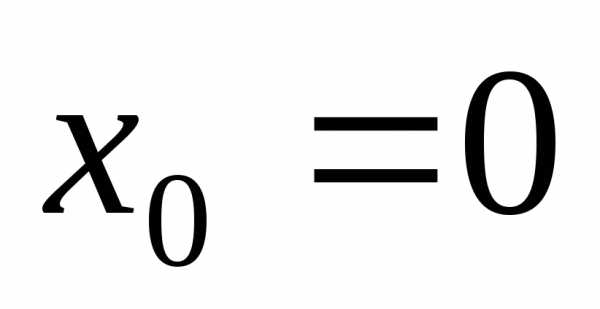 ,,- колебания отсутствуют.
,,- колебания отсутствуют.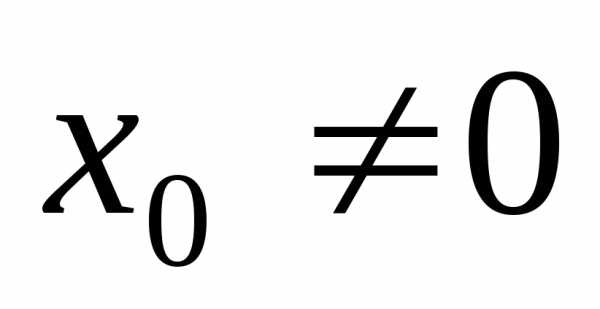 ,,.
,,.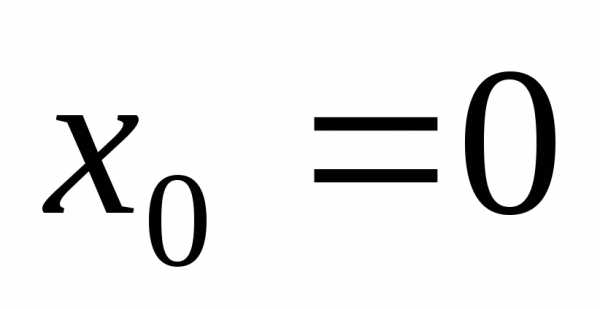 ,
,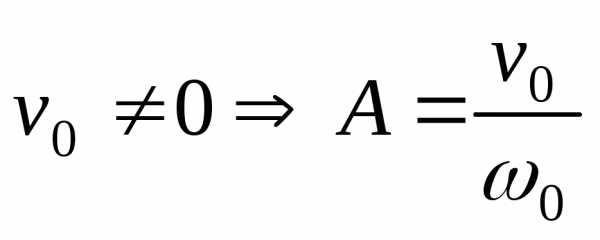 ,.
,.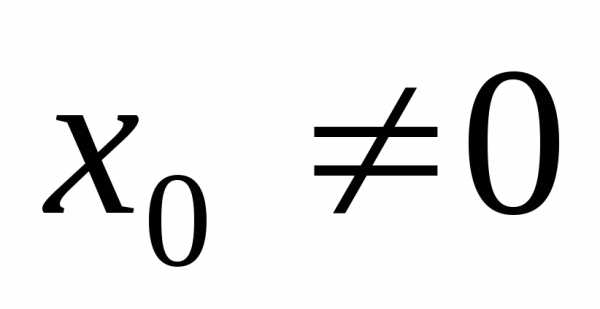 ,
,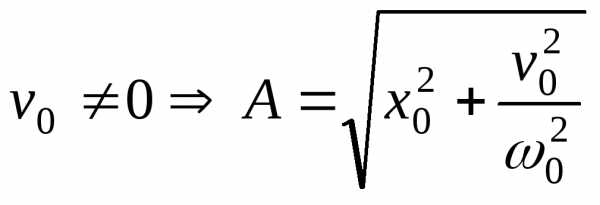 ,
,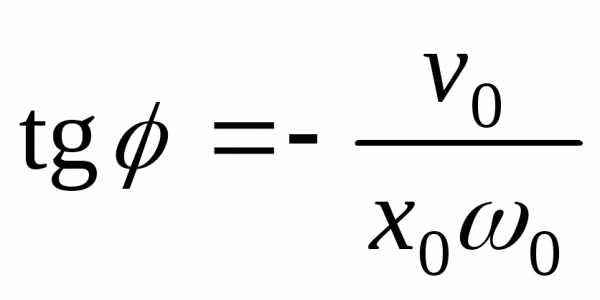 .
.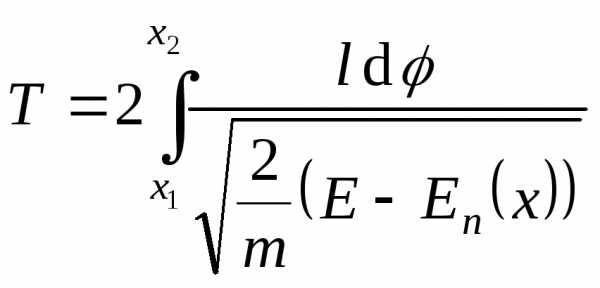 /
/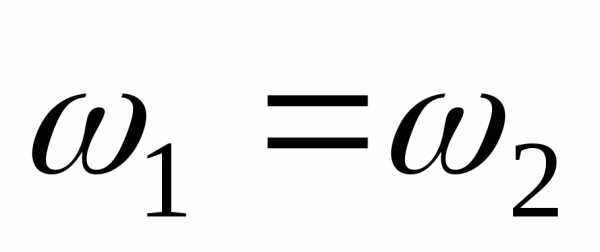 и
и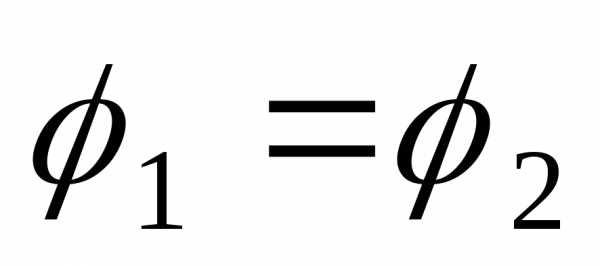 ,
то график
,
то график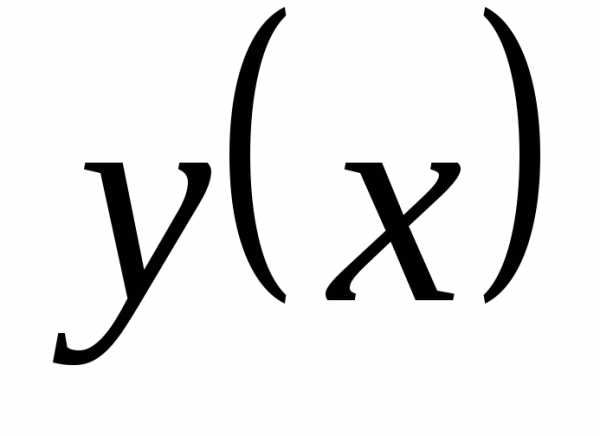 представляет собой прямую, проходящую
через начало координат.
представляет собой прямую, проходящую
через начало координат.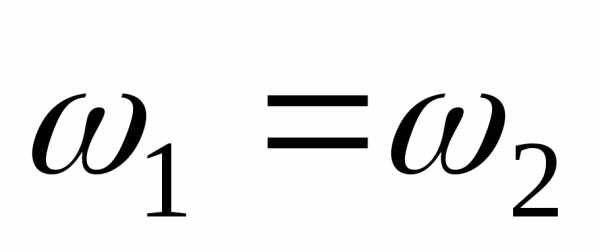 ,
,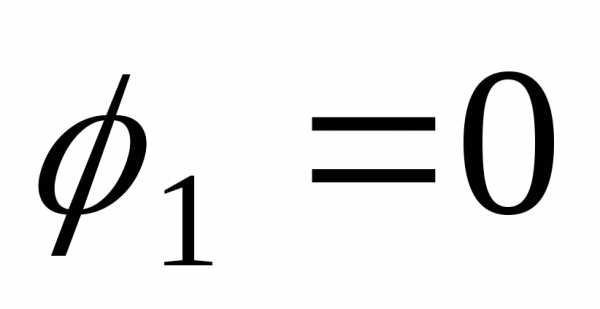 и
и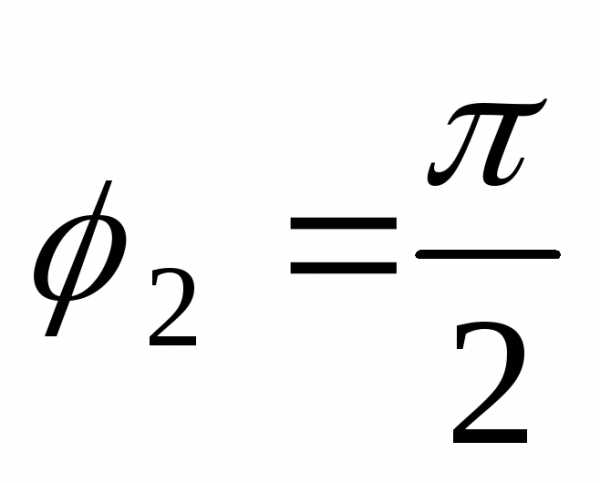 ,
то график
,
то график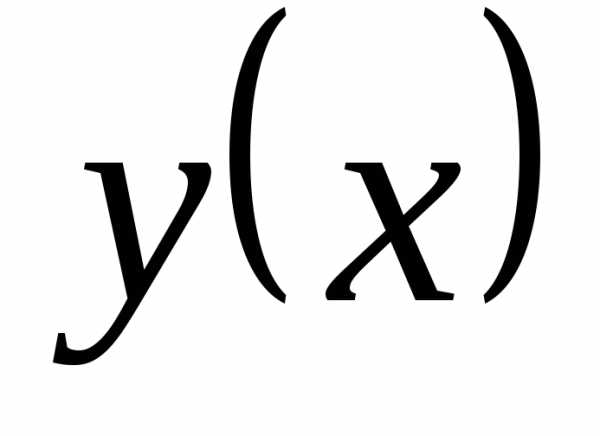 представляет собой эллипс, полуоси
которого равныA и B.
представляет собой эллипс, полуоси
которого равныA и B.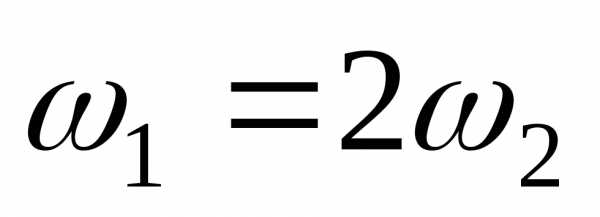 ,
,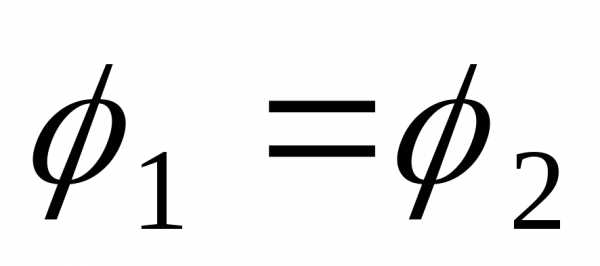 – график
– график представляет собой параболу.
представляет собой параболу. и
и .
.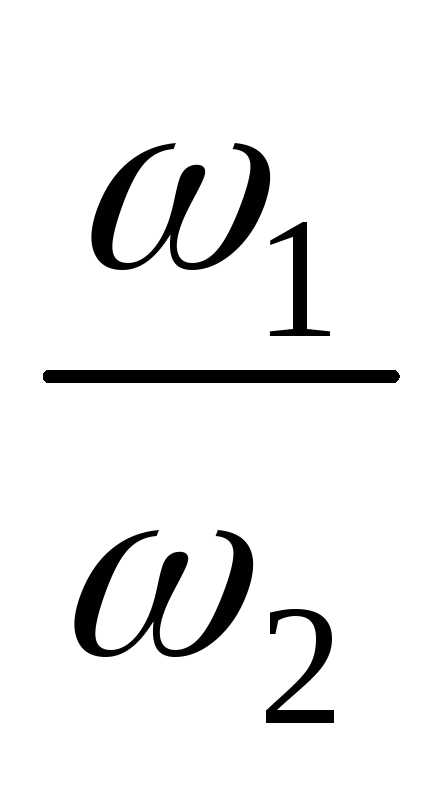 – величина рациональная, то фигура
Лиссажу замкнута, иначе – незамкнута.
– величина рациональная, то фигура
Лиссажу замкнута, иначе – незамкнута.

