01.01.201917.11.2018

Что такое производная функция – Что такое производная функции? | New-Best.com Самый простой поиск ответов на наилучшие вопросы

• by alexxlab
• Комментариев к записи Что такое производная функция – Что такое производная функции? | New-Best.com Самый простой поиск ответов на наилучшие вопросы нет
• Советы абитуриенту

Производная функции – это… Что такое Производная функции?

У этого термина существуют и другие значения, см. Производная. Иллюстрация понятия производной

Произво́дная (функции в точке) — основное понятие дифференциального исчисления, характеризующее скорость изменения функции (в данной точке). Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если такой предел существует. Функцию, имеющую конечную производную (в некоторой точке), называют дифференцируемой (в данной точке).

Процесс вычисления производной называется дифференци́рованием. Обратный процесс — нахождение первообразной — интегрирование.

История

В классическом дифференциальном исчислении производная чаще всего определяется через понятия теории пределов, однако исторически теория пределов появилась позже дифференциального исчисления.

Русский термин «производная функции» впервые употребил В. И. Висковатов.^[1]

Определение

Пусть в некоторой окрестности точки определена функция Производной функции называется такое число , что функцию в окрестности можно представить в виде

если существует.

Определение производной функции через предел

Пусть в некоторой окрестности точки определена функция Производной функции в точке называется предел, если он существует,

Общепринятые обозначения производной функции в точке

Заметим, что последнее обычно обозначает производную по времени (в теоретической механике).

Дифференцируемость

Производная функции в точке , будучи пределом, может не существовать или существовать и быть конечной или бесконечной. Функция является дифференцируемой в точке тогда и только тогда, когда её производная в этой точке существует и конечна:

Для дифференцируемой в функции в окрестности справедливо представление

при

Замечания

Геометрический и физический смысл производной

Тангенс угла наклона касательной прямой

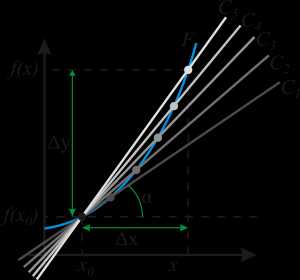Геометрический смысл производной. На графике функции выбирается абсцисса

x₀ и вычисляется соответствующая ордината f(x₀). В окрестности точки x₀ выбирается произвольная точка x. Через соответствующие точки на графике функции F проводится секущая (первая светло-серая линия C₅). Расстояние Δx = x — x₀ устремляется к нулю, в результате секущая переходит в касательную (постепенно темнеющие линии C₅ — C₁). Тангенс угла α наклона этой касательной — и есть производная в точке x₀.

Если функция имеет конечную производную в точке то в окрестности её можно приблизить линейной функцией

Функция называется касательной к в точке Число является угловым коэффициентом или тангенсом угла наклона касательной прямой.

Скорость изменения функции

Пусть  — закон прямолинейного движения. Тогда выражает мгновенную скорость движения в момент времени Вторая производная выражает мгновенное ускорение в момент времени

Вообще производная функции в точке выражает скорость изменения функции в точке , то есть скорость протекания процесса, описанного зависимостью

Производные высших порядков

Понятие производной произвольного порядка задаётся рекуррентно. Полагаем

Если функция дифференцируема в , то производная первого порядка определяется соотношением

Пусть теперь производная -го порядка определена в некоторой окрестности точки и дифференцируема. Тогда

Если функция имеет в некоторой области D частную производную по одной из переменных, то названная производная, сама являясь функцией от   может иметь в некоторой точке частные производные по той же или по любой другой переменной. Для исходной функции эти производные будут частными производными второго порядка (или вторыми частными производными).

  или  

  или  

Частная производная второго или более высокого порядка, взятая по различным переменным, называется смешанной частной производной. Например,

Способы записи производных

В зависимости от целей, области применения и используемого математического аппарата используют различные способы записи производных. Так, производная n-го порядка может быть записана в нотациях:

• Лагранжа , при этом для малых n часто используют штрихи и римские цифры:

и т. д.

Такая запись удобна своей краткостью и широко распространена; однако штрихами разрешается обозначать не выше третьей производной.

• Лейбница, удобная наглядной записью отношения бесконечно малых (только в случае, если  — независимая переменная; в противном случае обозначение верно лишь для производной первого порядка):

• Ньютона, которая часто используется в механике для производной по времени функции координаты (для пространственной производной чаще используют запись Лагранжа). Порядок производной обозначается числом точек над функцией, например:

 — производная первого порядка по при , или  — вторая производная по в точке и т. д.

, или иногда .

• В вариационном исчислении и математической физике часто применяется обозначение , ; для значения производной в точке — . Для частных производных обозначение то же, поэтому смысл обозначения определяют из контекста.

Конечно, при этом необходимо не забывать, что служат все они для обозначения одних и тех же объектов:

Примеры

• Пусть . Тогда

• Пусть . Тогда если то

где обозначает функцию знака. Если то а следовательно не существует.

Правила дифференцирования

Операция нахождения производной называется дифференцированием. При выполнении этой операции часто приходится работать с частными, суммами, произведениями функций, а также с «функциями функций», то есть сложными функциями. Исходя из определения производной, можно вывести правила дифференцирования, облегчающие эту работу. Если

C — постоянное число и f=f(x), g=g(x) — некоторые дифференцируемые функции, то справедливы следующие правила дифференцирования:

, то

• Формулы производной произведения и отношения обобщаются на случай n-кратного дифференцирования (формула Лейбница):

где  — биномиальные коэффициенты.

Следующие свойства производной служат дополнением к правилам дифференцирования:

Доказательство  

Таблица производных некоторых функций

Производная вектор-функции по параметру

Определим производную вектор-функции по параметру:

.

Если производная в точке существует, вектор-функция называется дифференцируемой в этой точке. Координатными функциями для производной будут .

Свойства производной вектор-функции (всюду предполагается, что производные существуют):

См. также

Примечания

Литература

• В. Г. Болтянский, Что такое дифференцирование?, «Популярные лекции по математике», Выпуск 17, Гостехиздат 1955 г., 64 стр.
• В. А. Гусев, А. Г. Мордкович «Математика»
• Г. М. Фихтенгольц «Курс дифференциального и интегрального исчисления», том 1
• В. М. Бородихин, Высшая математика, учеб. пособие, ISBN 5-7782-0422-1

dic.academic.ru

Производная — Циклопедия

Математика – Производная // Skill up

Производная — это математический термин, обозначающий некую функцию, соответствующую скорости изменения функции. Нахождение производной от функции называется дифференцированием.

[править] Производная от функции

1. Определение производной через понятие дифференциала.

Производная от функции y=f(x) равна отношению дифференциалов функции и аргумента.

[math]y'(x)=\frac{dy}{dx}[/math]

2. Определение производной от функции через понятие предела.

Производная от функции y=f(x) равна пределу отношения приращения функции Δy к приращению аргумента Δx, когда приращение аргумента стремиться к нулю Δx→0.

[math]y'(x)=\lim_{\Delta x \to 0}\frac{\Delta y}{\Delta x} \Leftrightarrow y'(x)=\lim_{\Delta x \to 0}\frac{y(x+\Delta x)-y(x)}{\Delta x}[/math]

[math]f'(x)=\lim_{\Delta x \to 0}\frac{\Delta f}{\Delta x} \Leftrightarrow f'(x)=\lim_{\Delta x \to 0}\frac{f(x+\Delta x)-f(x)}{\Delta x}[/math]

[править] Свойства производных

Для функций u=f(x) и v=g(x)

верны правила:

При f(x) и g(x)=C получаем:

При f(x)=C и g(x) получаем:

[править] Виды производных:

Производные элементарных функций — это производные (табличные) от элементарных функций.

Производные сложных функций — это производные от функций, состоящих из внешней функции и внутренней функции (функция от функции).

Формулы производных сложных функций

[math]\left[f(g(x))\right]’_x = f’_g(g(x)) \cdot g’_x(x) \Leftrightarrow \left[u(v)\right]’_x=u’_v \cdot v’_x[/math]

[math]\left[f(x)^{g(x)})\right]’_x = f(x)^{g(x)} \cdot \left[f’_x(x)\cdot\frac{g(x)}{f(x)}+g’_x(x) \cdot \ln f(x)\right] \Leftrightarrow \left[u^v\right]’_x=u^v\cdot \left(u’_x\frac{v}{u}+v’_x\ln u\right)[/math]

[править] Другие понятия:

• Корн Г., Корн Т. Справочник по математике для научных работников и инженеров — М.: Наука, 1970.

cyclowiki.org

Производная

II.Производная

1.Определение производной. Производной функции в точке называется предел отношения приращения функции к вызвавшему его приращению аргумента, когда приращение аргумента стремится к нулю, и при условии, что этот предел существует.

2.Дифференцируемая функция. Если в опр.1 – конечная, то функция называется дифференцируемой от .

3.Функция дифференцируема на интервале, если она дифференцируема в каждой его точке.

Теорема о непрерывности дифференцируемой функции.

Теорема. Если – дифференцируема в точке , то она является непрерывной в этой точке.

Доказательство.

По лемме о функции, имеющий конечный предел:

Тогда:

По второму определению единственности предела функция непрерывна в точке .

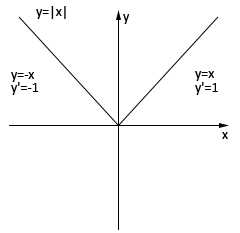
Пример:

В силу единственности предела в точке 0

предела нет (рисунок справа).

Дифференциал функции 1-го порядка.

Определение. Дифференциалом функции называется величина, пропорциональная бесконечно малому приращению аргумента и отличающаяся от соответсвующего приращения функции на бесконечно малую величину более высокого порялка, чем .

Если , то дифференциал 1-го порядка составляет главную часть функции.

Правила дифференцирования.

Пусть функции и дифференцируемы в точке .

Тогда:

4. если – постоянная;

Доказательства.

Посчитаем предел:

Так как функция дифференцирцема в точке , то она непрерывна, то есть ее приращение равно нулю.

Переходим к пределу:

4. если – постоянная;

Таблица элементарных производных

Вывод производных.

Теорема о производной обратной функции

Пусть – дифференцируема в точке , и – монотонная функция в достаточно малой окрестности точки . Тогда имеет обратную функцию , которая также является непрерывной и монотонной по , дифференцируемой по , и ее производная находится по формуле:

Доказательство:

Выведем все оставшиеся производные обратных функций через эту формулу.

10. Используем тождество:

Гиперболические функции и их производные.

Теорема о производной сложной функции.

Пусть функция дифференцируема в точке , , а функция дифференцируема в точке .

Тогда, если то ;

Доказательство:

Если в данной формуле .

Поделим обе части формулы на , и перейдем к пределу при , т.е. устремим к нулю.

;

Производная показательно-степенной функции.

Тогда:

Вывод формулы:

Логарифмируем:

Что и требовалось доказать.

Геометрический смысл производной и дифференциала.

– дуга графика

Рассмотрим треугольник :

Если , то ,

Если дифференцируема в точке , то

т.е. производная функции равна тангенсу угла наклона касательной.

Уравнения касательной и нормальной прямой.

– прямая, проходящая через точку ;

;

Тогда уравнение касательной к этой прямой записывается следующим образом:

– уравнение касательной;

Нормальная прямая (нормаль) в точке – это прямая, проходящая через эту точку перпендикулярно касательной.

Найти коэффициент можно и другим способом:

Тогда уравнение нормали к этой прямой записывается следующим образом:

– уравнение нормальной прямой;

Дифференциал функции и его свойства.

Пусть дифференцируемы по при некотором

Справедливы свойства:

1. ;

Для независимой переменной ее приращение равно дифференциалу;

3. – некоторая постоянная;

Арифметические свойства:

Инвариантность дифференциала 1-го порядка.

Дифференциал сложной функции записывается так же, как дифференциал внешней функции.

– внутренняя функция;

– внешняя функция;

Пусть эти функции дифференцируемы, тогда

1. ;

Дифференциалы более высоких порядков этим свойством не обладают.

Производная функции, заданной параметрически.

задана параметрически, если ее можно записать в виде:

При этом, функция – монотонная, и – обратная функция.

Доказательство:

Функция – монотонная, следовательно:

По теореме о производной сложной функции, получим:

Пример:

Параметрическое задание:

Это окружность с радиусом .

Покажем, что

Параметрическое задание эллипса

– полуоси эллипса,

Циклоида.

Уравнение циклоиды:

Вывод параметрического задания циклоиды:

Из треугольника :

Найдем угловой коэффициент в точке циклоиды:

Производная функции, заданной неявно.

Пример 1.

– задана неявно,

Продифференцируем левую и правую части уравнения:

Выразим

Пример 2.

Выразим

Основные теоремы дифференциального исчисления:

Теоремы Ролля, Лагранжа, Коши и Ферма.

Понятие локального максимума и локального минимума.

Точка – точка локального максимума, если:

Точка – точка локального минимума, если :

Точки локального минимума и локального максимума называются точками экстремума.

Критическими точками функции называются внутренние точки области определения этой функции, в которых производная равна нулю, или не существует.

Малая теорема Ферма (1601-1665)

Пусть – экстремальная точка функции , и в этой точке функция дифференцируема, тогда производная в этой точке равна нулю.

Пусть – точка локального максимума,

Рассмотрим левостороннюю производную:

studfiles.net

Что такое производная функции? | New-Best.com Самый простой поиск ответов на наилучшие вопросы

Производная функции – основное понятие дифференциального исчисления, характеризующее скорость конфигурации функции. Определяется как предел дела приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, в том случае такой предел существует. Функцию, имеющую конечную производную, именуют дифференцируемой. Процесс вычисления производной именуется дифференци?рованием.

Производной в определенной точке неведомого интервала является наибольшее либо малое значение, к которому стремится отношение приращения функции в этой точке к соответственному приращению аргумента, в случае в том случае значение последнего стремится к нулю.

В арифметике конфигурации функций изучаются в согласовании с производной либо переменной. Производные являются основой для решения задач, связанных с вычислением либо решением дифференциальных уравнений.

Производная как математический парадокс берет свое начало с воплощения попыток построения касательной полосы к кривой, определение скорости неравномерного движения, нахождение площади криволинейного геометрического тела. Теоретическое оформление математического парадокса производной отыскало свое проявление в трудах подобных величавых ученых, как Исаак Ньютон, Вильгельм Лейбниц. В собственных работах они отразили суть математических действий интегрирования и дифференцирования функций. Парадокс производной является обширно применяемым в рамках воплощения математического анализа, в базе которого, в свою очередь, лежит понятие предела, другими словами определение наибольшего и малого значений функций. В первый раз такие математические определения были применены французским ученым Остеаном Луи Коши.

В геометрическом контексте, производная функции может быть интерпретирована как угловой коэффициент графика функции либо, выражаясь более точно, угловой коэффициент касательной полосы в определенной точке. Практически же, производная представляет собой вычисления, приобретенные из формулы тангенса угла наклона для прямой полосы. В качестве особенности есть возможность именовать тот факт, что переход к лимиту может быть осуществим только по отношению к кривой.

Определение геометрического значения производной делается в согласовании с построением касательной полосы к графику определенной функции. Проведение таковой математической операции спровоцировало разработку и развитие дифференциального вычисления. Геометрический смысл производной также зависит и от определения угла наклона касательной к кривой. В том случае провести касательную к определенному графику, к примеру, в точке х, то сама функция окажется близкой к линейной с угловым коэффициентом.

Исходя из убеждений физики, производная представляет собой секундную скорость определенной перемещающейся точки при движении по прямой, а именно. В том случае давать общую характеристику, то в данном контексте под производной понимается очевидная скорость движения.

Парадокс производной

В том случае подвергать рассмотрению парадокс производной в рамках практического значения, то она представляется самой функцией со специфичными качествами возрастания и убывания.

Чаше всего, на всех функциях простого нрава есть возможность найти производную, в итоге чего, такая функция будет считаться дифференцируемой. Стоит отметить, что в математической практике есть и недифференцируемые функции, в главном они представляют собой кривую линию, которая образует угол, где модуль графика функции равен нулю.

В арифметике может быть не только лишь определение производной функции при помощи графического изображения, что носит заглавие дифференциации, да и построение графика уникальной функции, используя график ее производной. Этот процесс, оборотный дифференциации, именуется интегрированием функции.

Понятие производной применяется не только лишь в математических отраслях, да и в других научных и технологических направлениях, к примеру, в физике простых частиц и квантовой механике.

Первоисточники

wikipedia.org – определение производной в Википедии;

cadzone.ru – геометрический смысл производной;

naukoved.ru – производная, как математичсекий парадокс.

Источник материала Интернет-сайт www.genon.ru

new-best.com

Полная производная функции – это… Что такое Полная производная функции?

Полная производная функции — производная функции по времени вдоль траектории.

Расчёт полной производной функции по времени t, (в отличие от частной производной, ) не подразумевает, что другие аргументы (т.е. иные нежели аргумент, t, по которому ведётся полное дифференцирование: x и y) постоянны при изменяющемся t. Полная производная включает в себя эти непрямые зависимости от t (т.е. x(t) и y(t)) для описания зависимости f от t.

Пример №1

Например, для упомянутой функции f = f(t, x(t), y(t)) полная производная функции вычисляется по следующему правилу:

что упрощается до

где  — частные производные.

Следует отметить, что обозначение является условным и не означает деления дифференциалов. Кроме того, полная производная функции зависит не только от самой функции, но и от траектории.

Пример №2

Например, полная производная функции :

Здесь нет так как сама по себе («явно») не зависит от .

Приложения

См. также

dikc.academic.ru

Производная функции – это… Что такое Производная функции?

У этого термина существуют и другие значения, см. Производная. Иллюстрация понятия производной

Произво́дная (функции в точке) — основное понятие дифференциального исчисления, характеризующее скорость изменения функции (в данной точке). Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если такой предел существует. Функцию, имеющую конечную производную (в некоторой точке), называют дифференцируемой (в данной точке).

Процесс вычисления производной называется дифференци́рованием. Обратный процесс — нахождение первообразной — интегрирование.

История

В классическом дифференциальном исчислении производная чаще всего определяется через понятия теории пределов, однако исторически теория пределов появилась позже дифференциального исчисления.

Русский термин «производная функции» впервые употребил В. И. Висковатов.^[1]

Определение

Пусть в некоторой окрестности точки определена функция Производной функции называется такое число , что функцию в окрестности можно представить в виде

если существует.

Определение производной функции через предел

Пусть в некоторой окрестности точки определена функция Производной функции в точке называется предел, если он существует,

Общепринятые обозначения производной функции в точке

Заметим, что последнее обычно обозначает производную по времени (в теоретической механике).

Дифференцируемость

Производная функции в точке , будучи пределом, может не существовать или существовать и быть конечной или бесконечной. Функция является дифференцируемой в точке тогда и только тогда, когда её производная в этой точке существует и конечна:

Для дифференцируемой в функции в окрестности справедливо представление

при

Замечания

Геометрический и физический смысл производной

Тангенс угла наклона касательной прямой

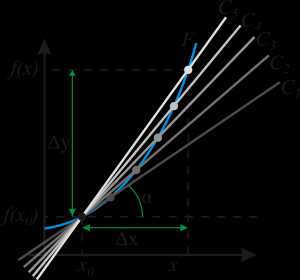Геометрический смысл производной. На графике функции выбирается абсцисса x₀ и вычисляется соответствующая ордината f(x₀). В окрестности точки x₀ выбирается произвольная точка x. Через соответствующие точки на графике функции F проводится секущая (первая светло-серая линия C₅). Расстояние Δx = x — x₀ устремляется к нулю, в результате секущая переходит в касательную (постепенно темнеющие линии C₅ — C₁). Тангенс угла α наклона этой касательной — и есть производная в точке x₀.

Если функция имеет конечную производную в точке то в окрестности её можно приблизить линейной функцией

Функция называется касательной к в точке Число является угловым коэффициентом или тангенсом угла наклона касательной прямой.

Скорость изменения функции

Пусть  — закон прямолинейного движения. Тогда выражает мгновенную скорость движения в момент времени Вторая производная выражает мгновенное ускорение в момент времени

Вообще производная функции в точке выражает скорость изменения функции в точке , то есть скорость протекания процесса, описанного зависимостью

Производные высших порядков

Понятие производной произвольного порядка задаётся рекуррентно. Полагаем

Если функция дифференцируема в , то производная первого порядка определяется соотношением

Пусть теперь производная -го порядка определена в некоторой окрестности точки и дифференцируема. Тогда

Если функция имеет в некоторой области D частную производную по одной из переменных, то названная производная, сама являясь функцией от   может иметь в некоторой точке частные производные по той же или по любой другой переменной. Для исходной функции эти производные будут частными производными второго порядка (или вторыми частными производными).

  или  

  или  

Частная производная второго или более высокого порядка, взятая по различным переменным, называется смешанной частной производной. Например,

Способы записи производных

В зависимости от целей, области применения и используемого математического аппарата используют различные способы записи производных. Так, производная n-го порядка может быть записана в нотациях:

• Лагранжа , при этом для малых n часто используют штрихи и римские цифры:

и т. д.

Такая запись удобна своей краткостью и широко распространена; однако штрихами разрешается обозначать не выше третьей производной.

• Лейбница, удобная наглядной записью отношения бесконечно малых (только в случае, если  — независимая переменная; в противном случае обозначение верно лишь для производной первого порядка):

• Ньютона, которая часто используется в механике для производной по времени функции координаты (для пространственной производной чаще используют запись Лагранжа). Порядок производной обозначается числом точек над функцией, например:

 — производная первого порядка по при , или  — вторая производная по в точке и т. д.

, или иногда .

• В вариационном исчислении и математической физике часто применяется обозначение , ; для значения производной в точке — . Для частных производных обозначение то же, поэтому смысл обозначения определяют из контекста.

Конечно, при этом необходимо не забывать, что служат все они для обозначения одних и тех же объектов:

Примеры

• Пусть . Тогда

• Пусть . Тогда если то

где обозначает функцию знака. Если то а следовательно не существует.

Правила дифференцирования

Операция нахождения производной называется дифференцированием. При выполнении этой операции часто приходится работать с частными, суммами, произведениями функций, а также с «функциями функций», то есть сложными функциями. Исходя из определения производной, можно вывести правила дифференцирования, облегчающие эту работу. Если C — постоянное число и f=f(x), g=g(x) — некоторые дифференцируемые функции, то справедливы следующие правила дифференцирования:

, то

• Формулы производной произведения и отношения обобщаются на случай n-кратного дифференцирования (формула Лейбница):

где  — биномиальные коэффициенты.

Следующие свойства производной служат дополнением к правилам дифференцирования:

Доказательство  

Таблица производных некоторых функций

Производная вектор-функции по параметру

Определим производную вектор-функции по параметру:

.

Если производная в точке существует, вектор-функция называется дифференцируемой в этой точке. Координатными функциями для производной будут .

Свойства производной вектор-функции (всюду предполагается, что производные существуют):

См. также

Примечания

Литература

• В. Г. Болтянский, Что такое дифференцирование?, «Популярные лекции по математике», Выпуск 17, Гостехиздат 1955 г., 64 стр.
• В. А. Гусев, А. Г. Мордкович «Математика»
• Г. М. Фихтенгольц «Курс дифференциального и интегрального исчисления», том 1
• В. М. Бородихин, Высшая математика, учеб. пособие, ISBN 5-7782-0422-1

xzsad.academic.ru

Полная производная функции – это… Что такое Полная производная функции?

Полная производная функции — производная функции по времени вдоль траектории.

Расчёт полной производной функции по времени t, (в отличие от частной производной, ) не подразумевает, что другие аргументы (т.е. иные нежели аргумент, t, по которому ведётся полное дифференцирование: x и y) постоянны при изменяющемся t. Полная производная включает в себя эти непрямые зависимости от t (т.е. x(t) и y(t)) для описания зависимости f от t.

Пример №1

Например, для упомянутой функции f = f(t, x(t), y(t)) полная производная функции вычисляется по следующему правилу:

что упрощается до

где  — частные производные.

Следует отметить, что обозначение является условным и не означает деления дифференциалов. Кроме того, полная производная функции зависит не только от самой функции, но и от траектории.

Пример №2

Например, полная производная функции :

Здесь нет так как сама по себе («явно») не зависит от .

Приложения

См. также

dik.academic.ru

---