Физический смысл ускорения – В чем физический смысл ускорения?
- Комментариев к записи Физический смысл ускорения – В чем физический смысл ускорения? нет
- Советы абитуриенту
4.5 Теорема сложения ускорений
Возьмем
производную по времени от векторного
равенства (4.11), зная, что постоянными
являются только вектора  по правилам высшей математики.
по правилам высшей математики.
Сравнив слагаемые, входящие в формулу (4.13) с формулами (4.5), (4.7), (4.9), видим, что только выражение не имеет названия. Его называютКориолисовым или поворотным ускорением; названо в честь французского механика Гюстава Гаспара Кориолиса (1792–1843 гг.), который в 1833 г. вывел теорему сложения ускорений *). Итак, ускорение Кориолиса равно:
. (4.14)
Векторное равенство (4.13), учитывая названия входящих в него слагаемых, согласно формулам (4.5), (4.7), (4.9), (4.14), имеет вид:
. (4.15)
Эта формула выражает
Абсолютное ускорение точки, совершающей сложное движение, равняется геометрической сумме ее переносного, относительного и Кориолисового ускорений. |
Рассмотрим случай,
когда переносное
движение поступательное.
Тогда оси  не
меняют свою ориентацию (рис. 4.3), можно
их выбрать так, что они остаются
параллельными осям
не
меняют свою ориентацию (рис. 4.3), можно
их выбрать так, что они остаются
параллельными осям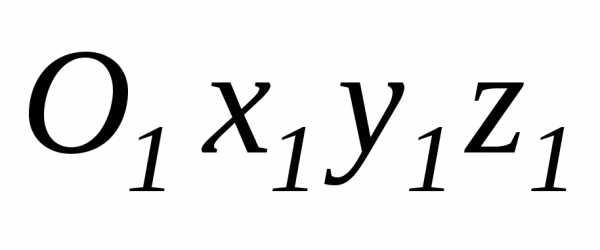 .
В этом случае ускорение Кориолиса равно
нулю, т. к.в формуле (4.14).
.
В этом случае ускорение Кориолиса равно
нулю, т. к.в формуле (4.14).
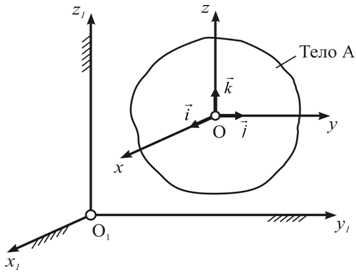
Рисунок 4.3
Теорема сложения ускорений при переносном поступательном движении формулируется так: при переносном поступательном движении абсолютное ускорение точки равно геометрической сумме двух ускорений: переносного и относительного |
. (4.16)
4.6 Ускорение Кориолиса и его физический смысл
В предыдущем пункте для ускорения Кориолиса получено выражение (4.14)
.
Для
практического вычисления ускорения
Кориолиса выполним некоторые
преобразования. Так как вектора 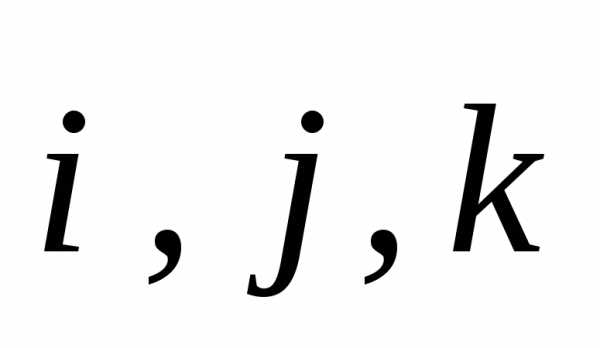 изменяются только по направлению,
рассмотрим частный случай, когдапереносное
движение – вращательное вокруг оси
изменяются только по направлению,
рассмотрим частный случай, когдапереносное
движение – вращательное вокруг оси 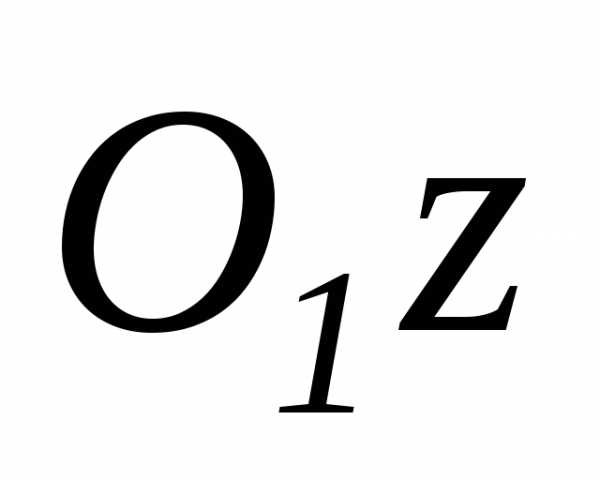 с угловой скоростью
.
Оси
с угловой скоростью
.
Оси связаны
с телом (рис. 4.4).
связаны
с телом (рис. 4.4).
Изучим,
чему равна производная от орта 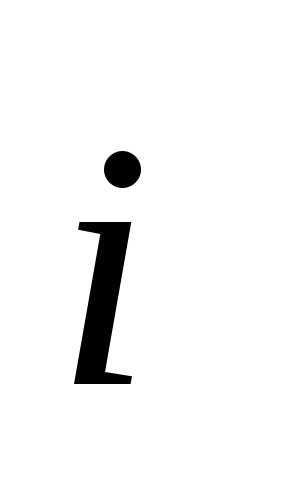
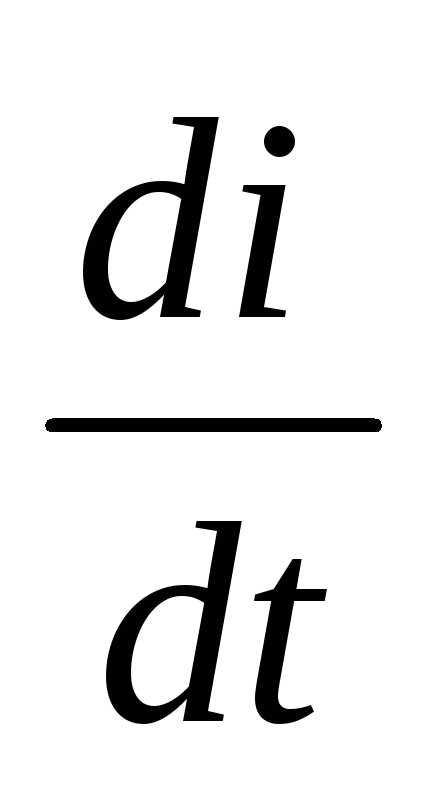 .
Вектор
.
Вектор можно рассматривать как радиус-вектор
точкиА,
т. е.
можно рассматривать как радиус-вектор
точкиА,
т. е. 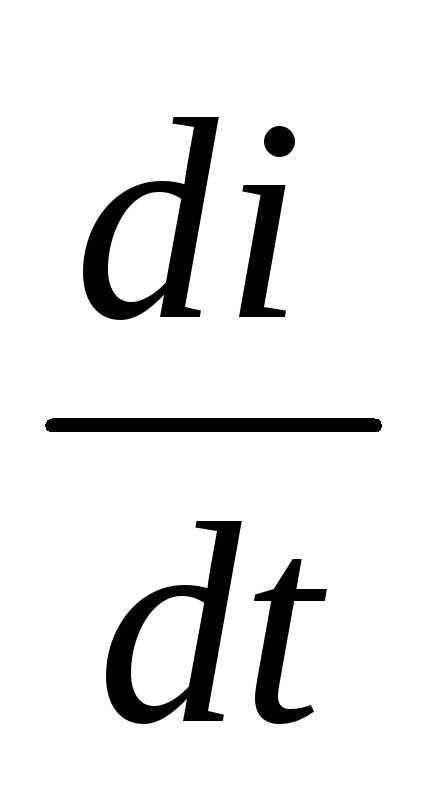 есть скорость точкиA.
есть скорость точкиA. 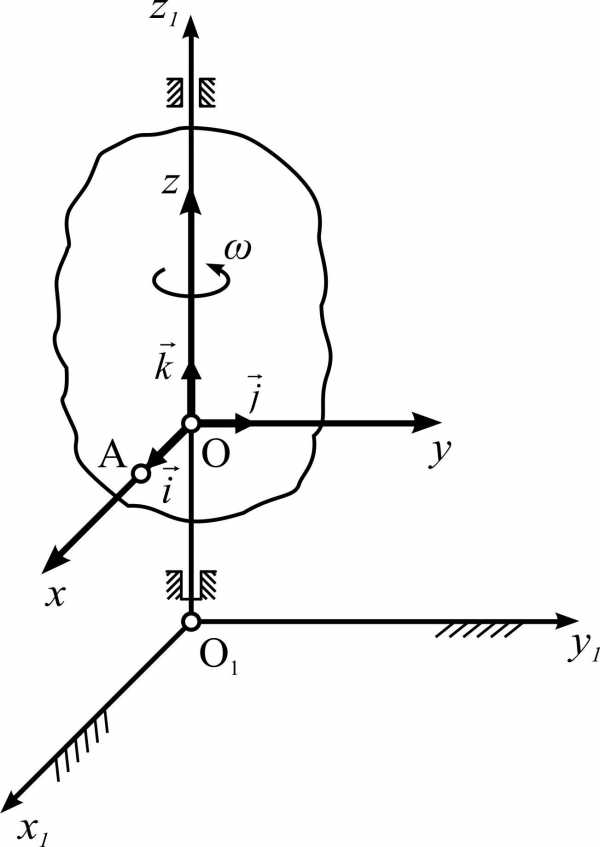
Рисунок 4.4
Применив
формулу Эйлера (2.16), имеем скорость
точки А: 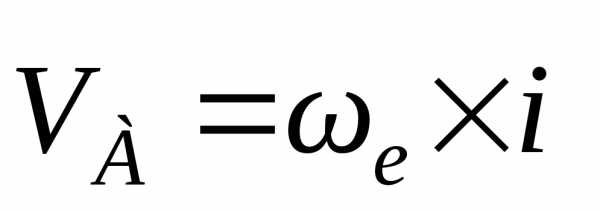 ,
т.е.
,
т.е.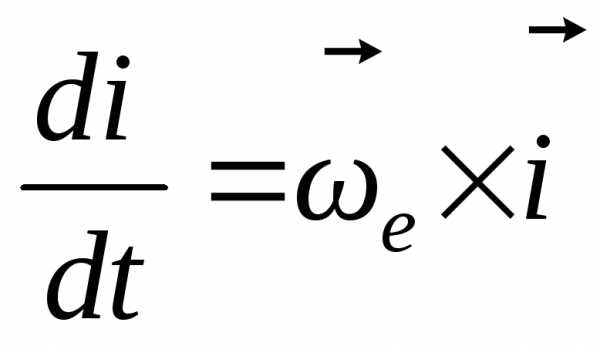 .
Аналогично, можно убедиться в том, что
производная от орта
.
Аналогично, можно убедиться в том, что
производная от орта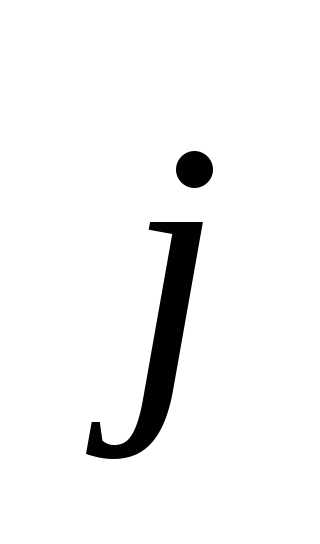 будет равна
будет равна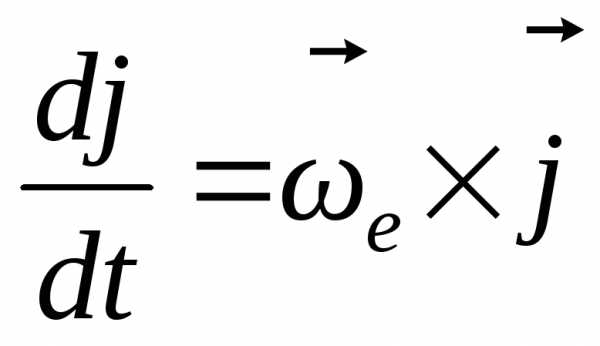 .
Если ось вращения
.
Если ось вращения
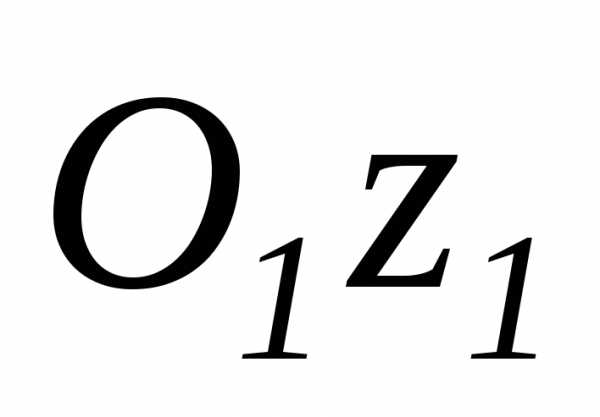 ,
а тоже движется, то можно убедиться в
том, что
,
а тоже движется, то можно убедиться в
том, что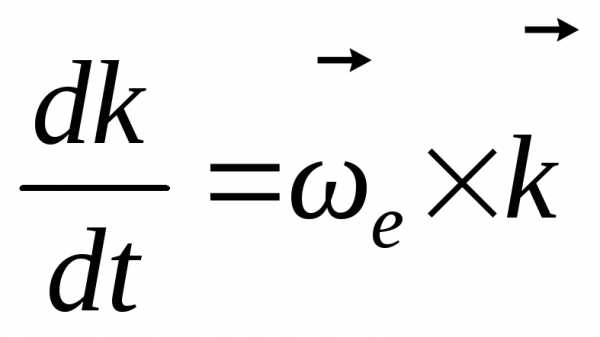 .
. Подставив
значения производных от единичных
векторов в формулу (4.14), получим
.
Скобка, стоящая в этой формуле, – это
относительная скорость 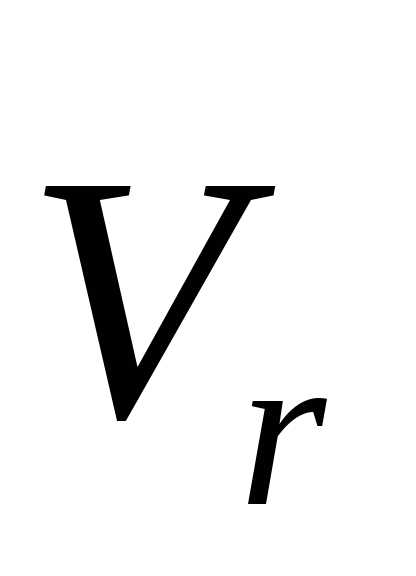 (формула (4.4)). Поэтому
(формула (4.4)). Поэтому
. (4.17)
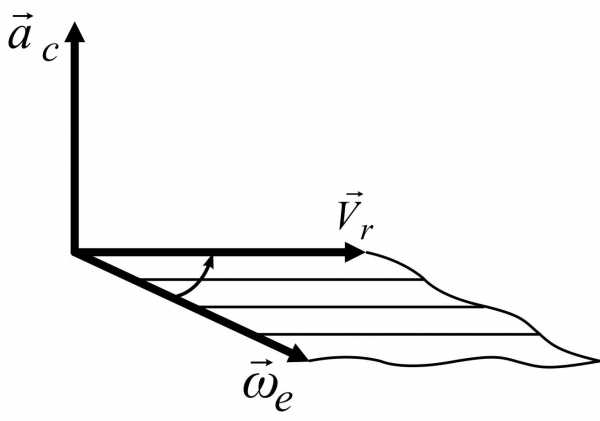
Вектор ускорения Кориолиса геометрически равняется удвоенному векторному произведению вектора переносной угловой скорости на вектор относительной скорости точки. |
Эта формула дает возможность определить как модуль, так и направление ускорения Кориолиса. Исходя из свойств векторного произведения, имеем:
1) модуль ускорения Кориолиса равен:
. (4.18)
2) вектор ускорения 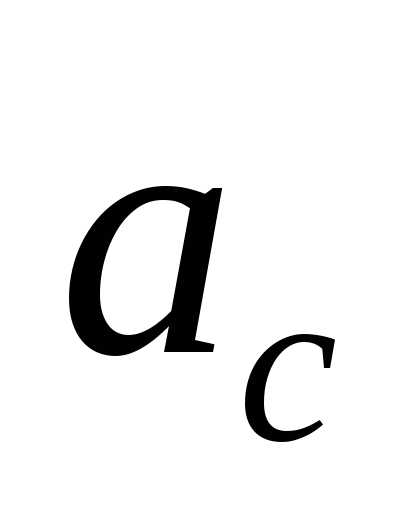 направлен перпендикулярно плоскости,
в которой расположены вектора
направлен перпендикулярно плоскости,
в которой расположены вектора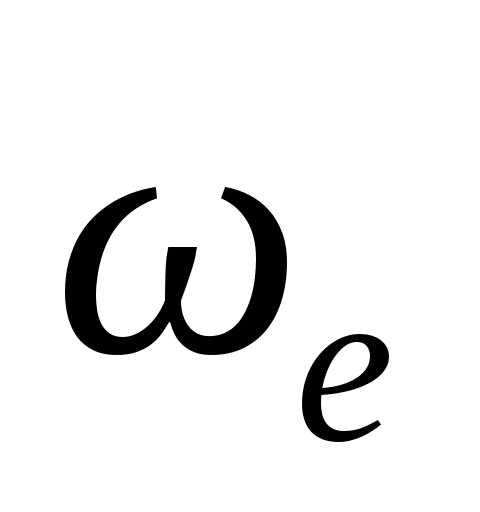 и
и 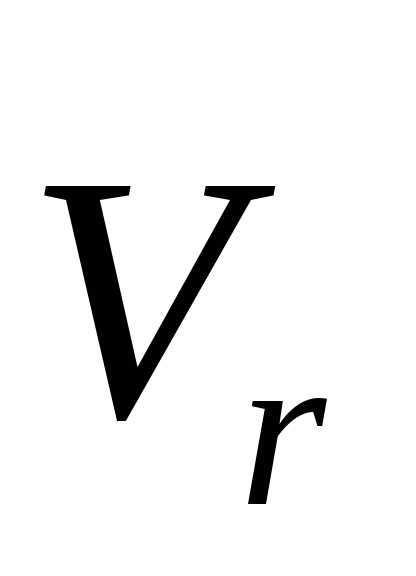 в сторону, откуда поворот вектора
в сторону, откуда поворот вектора 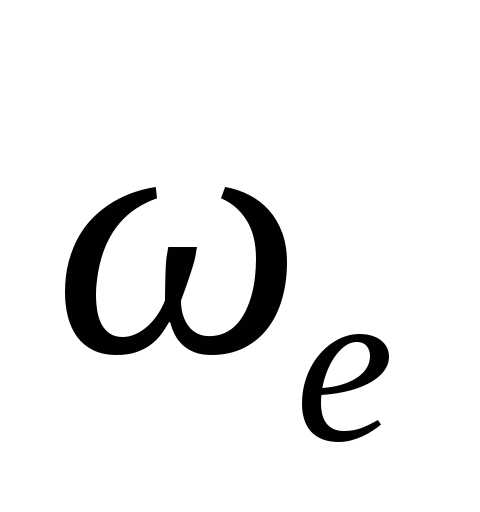 к вектору
к вектору 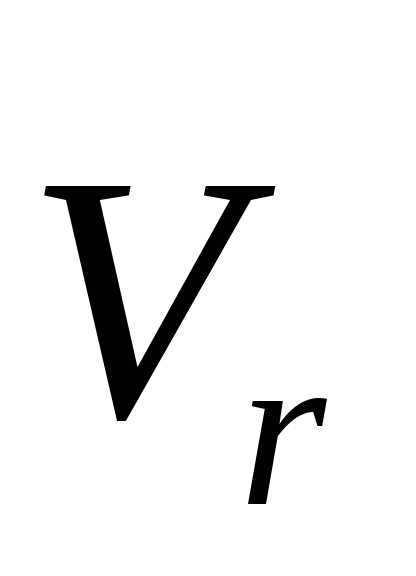 по меньшему углу (чтобы их совместить)
видим против хода часовой стрелки (рис.
4.5).
по меньшему углу (чтобы их совместить)
видим против хода часовой стрелки (рис.
4.5).
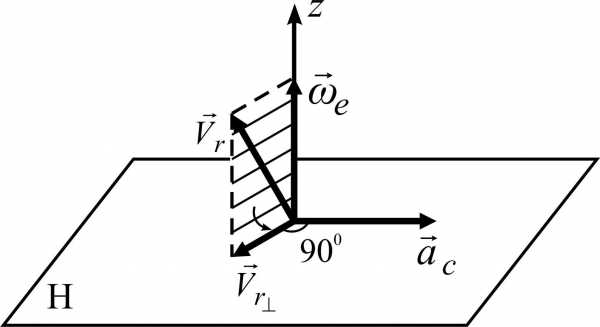
Направление
вектора ускорения Кориолиса можно
определять по
правилу Н. Е. Жуковского).
Для этого необходимо вектор относительной
скорости 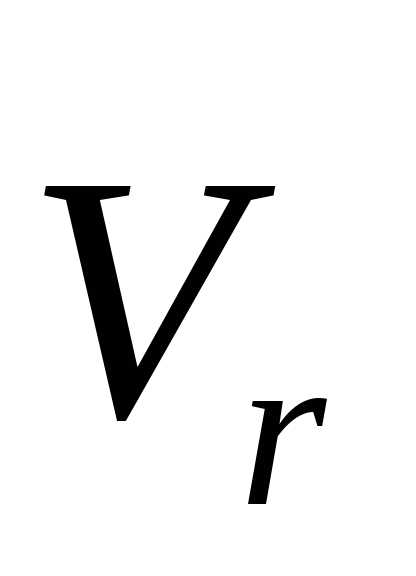 (рис. 4.6) спроецировать на плоскость H,
перпендикулярную к оси переносного
вращения и полученную проекцию
(рис. 4.6) спроецировать на плоскость H,
перпендикулярную к оси переносного
вращения и полученную проекцию 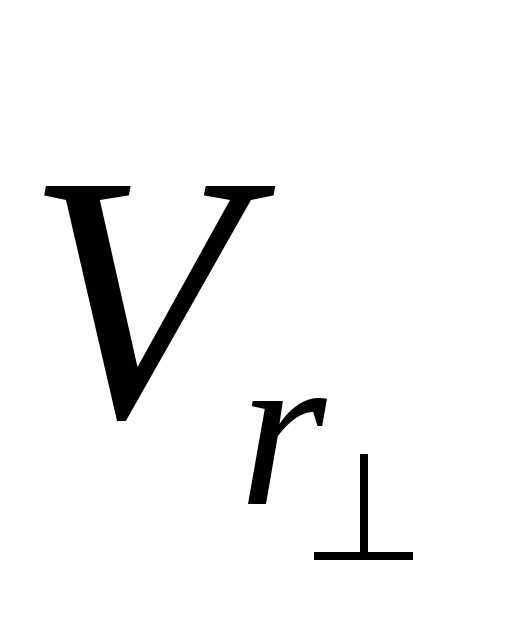
Рисунок 4.5 | Рисунок 4.6 |
Для выяснения
физического смысла ускорения Кориолиса рассмотрим такой пример. Диск вращается
вокруг оси  ,
перпендикулярной к плоскости диска с
постоянной угловой скоростью
,
перпендикулярной к плоскости диска с
постоянной угловой скоростью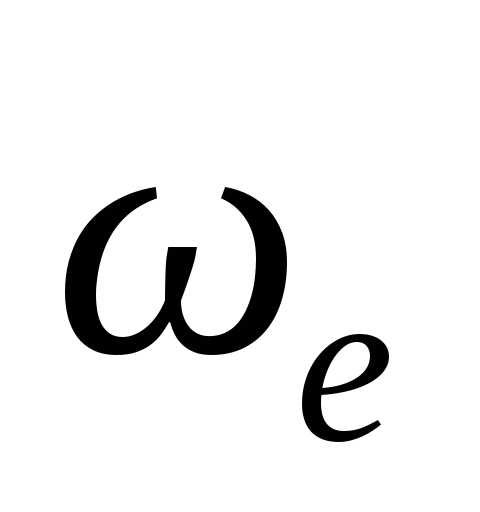 (рис. 4.7,а).
По диску от его центра к ободу с постоянной
скоростью
(рис. 4.7,а).
По диску от его центра к ободу с постоянной
скоростью 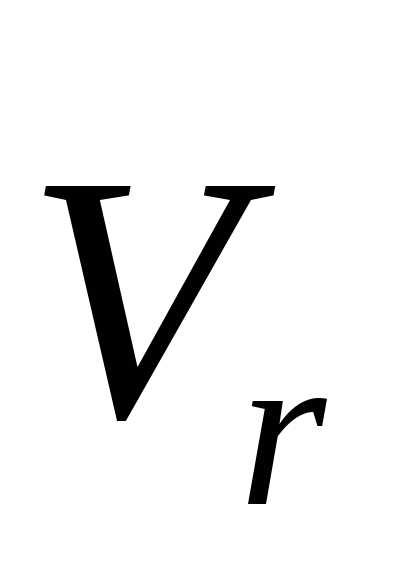 движется точка
движется точка
а) б) в)
Рисунок 4.7
Представим себе, что для изучения относительного и переносного движений имеется два разных секундомера.
1. Включим секундомер
для изучения переносного движения.
Выясним, как изменится относительная
скорость 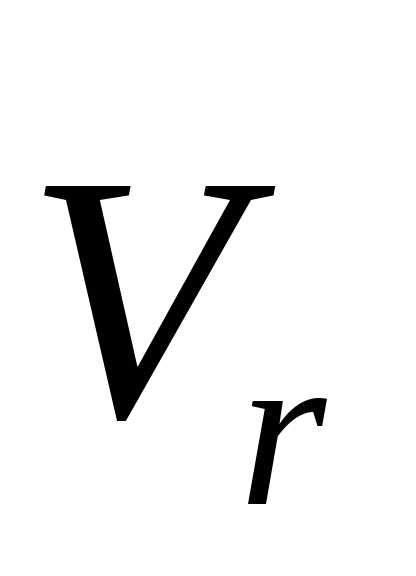 при остановленном относительном
секундомере за время
при остановленном относительном
секундомере за время 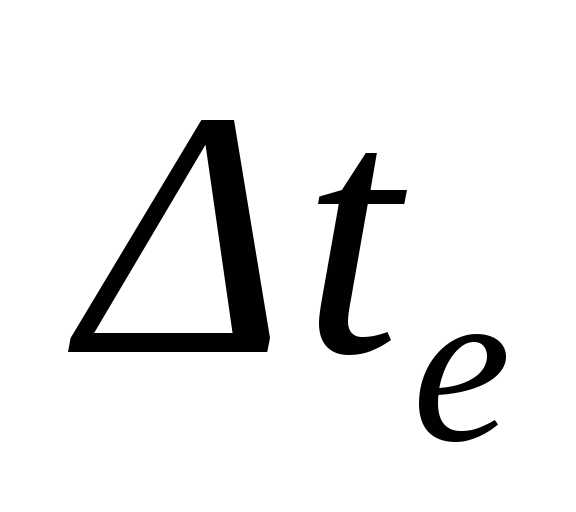 .
Тогда вектор
.
Тогда вектор 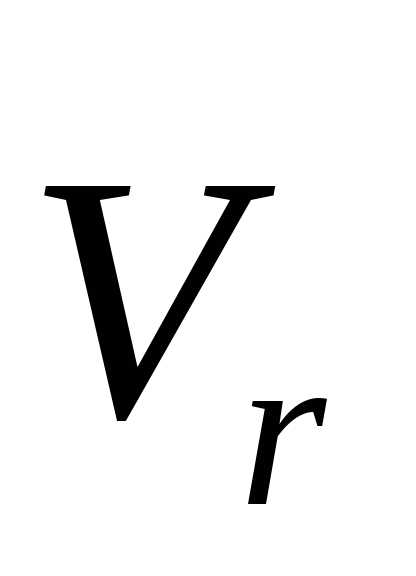 в положении
в положении 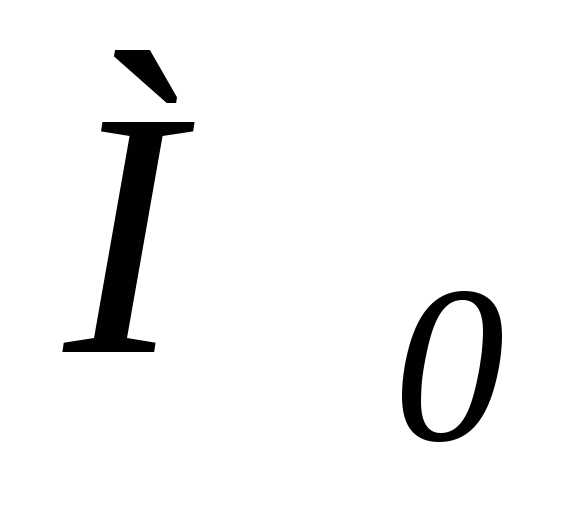 сохранит свой модуль, но приложен будет
в точке
сохранит свой модуль, но приложен будет
в точке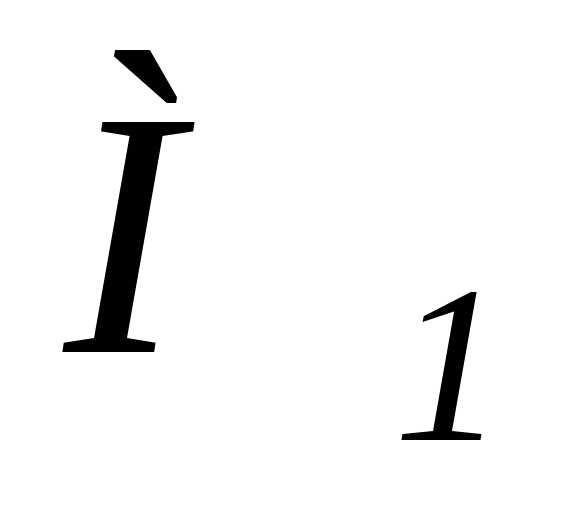 ,
куда переместится точка
,
куда переместится точка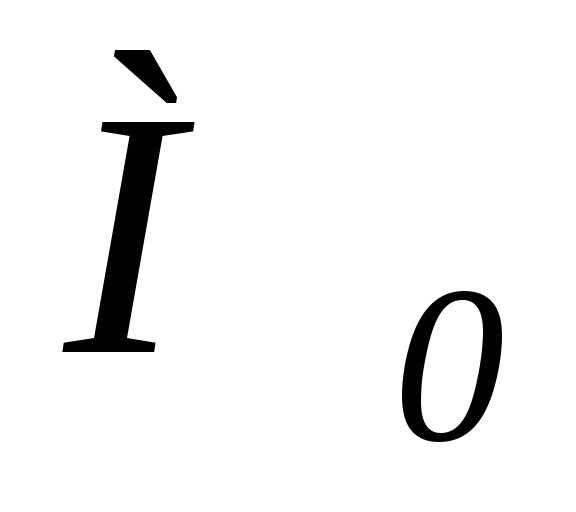
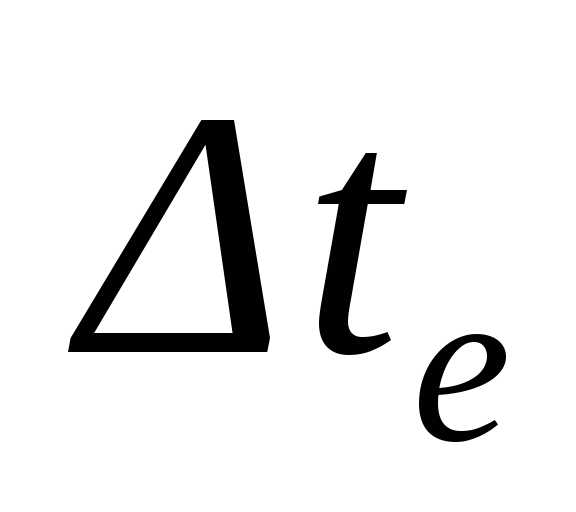 (рис.
4.7,б).
Модуль разности векторов
(рис.
4.7,б).
Модуль разности векторов 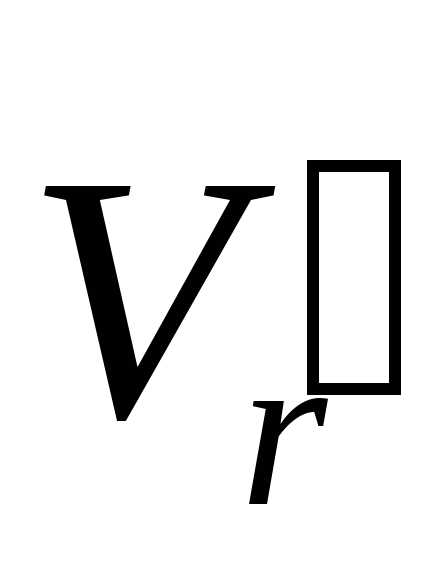 и
и 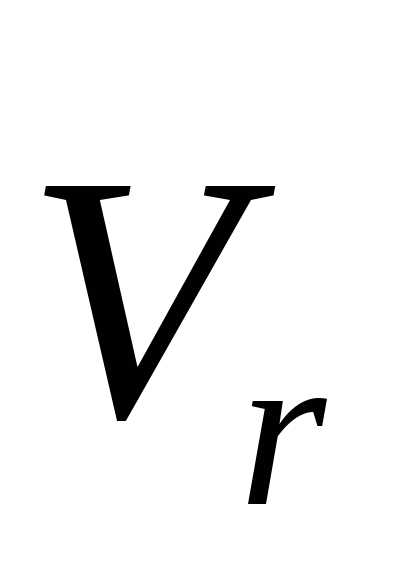 равен
равен 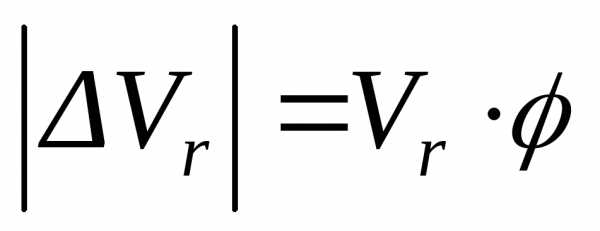 ,
где
,
где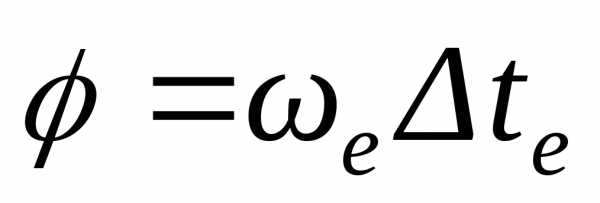 – угол поворота диска за время
– угол поворота диска за время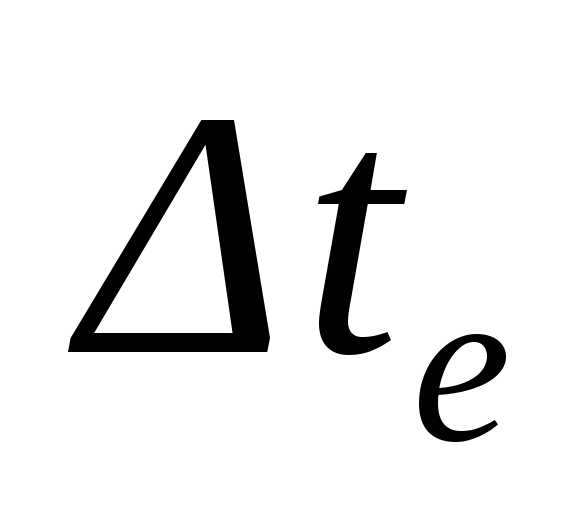 ,
т.е.
,
т.е.. (4.19)
Изменилась
относительная скорость только за счет
переносного движения (т. к. 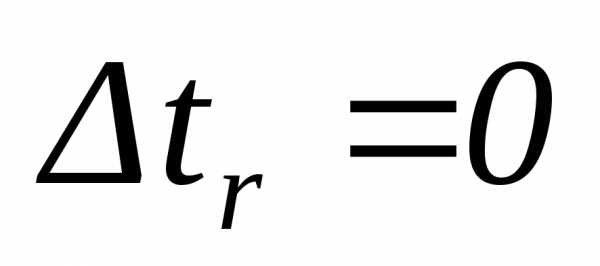 ).
).
2.
Включим секундомер для изучения
относительного движения. Выясним, как
изменится переносная скорость 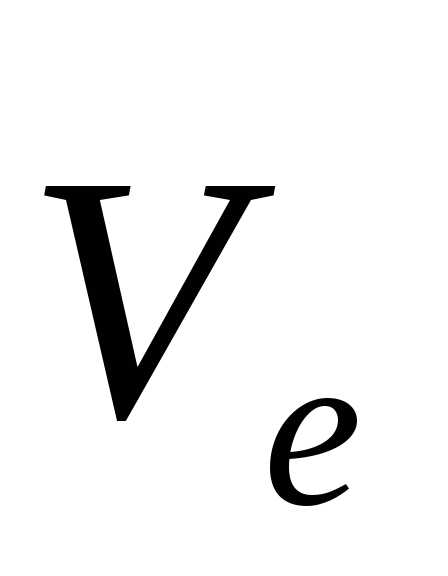 ,
если точка переместилась из положения
,
если точка переместилась из положения 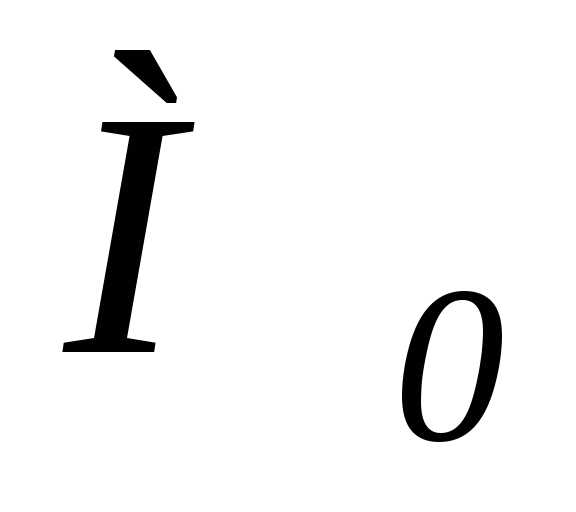
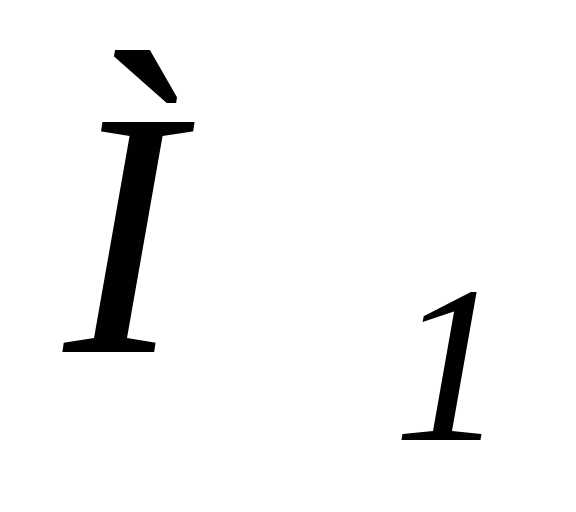 на расстояние(рис. 4.7,в).
Переносная скорость точки
на расстояние(рис. 4.7,в).
Переносная скорость точки 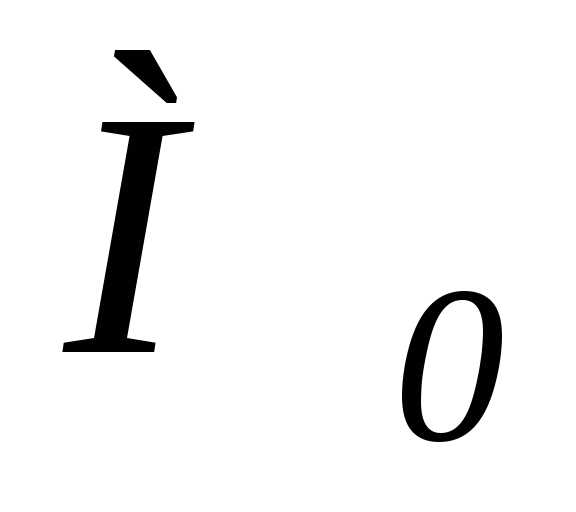 равна,
переносная скорость точки
равна,
переносная скорость точки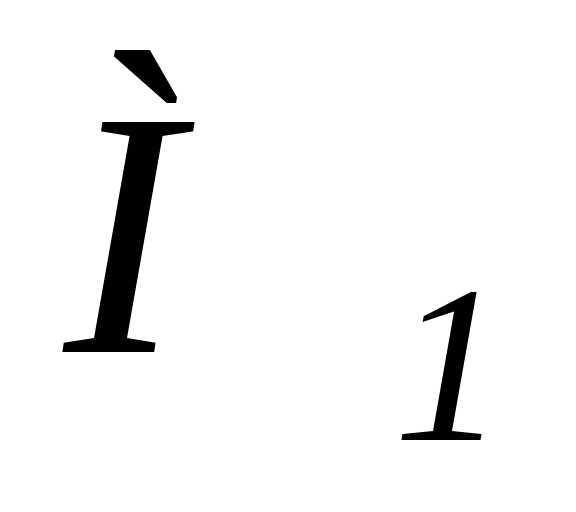 равна.
Модуль разности векторов
равна.
Модуль разности векторов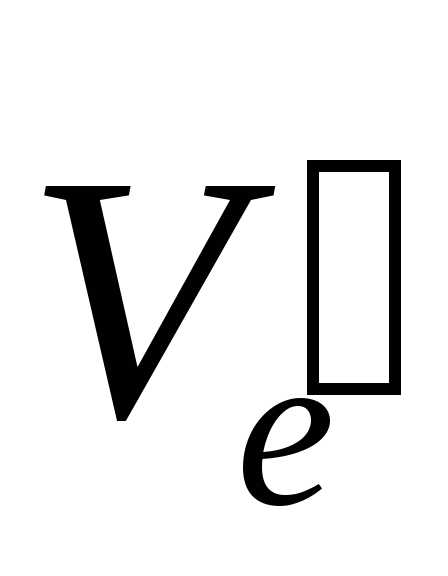 и
и 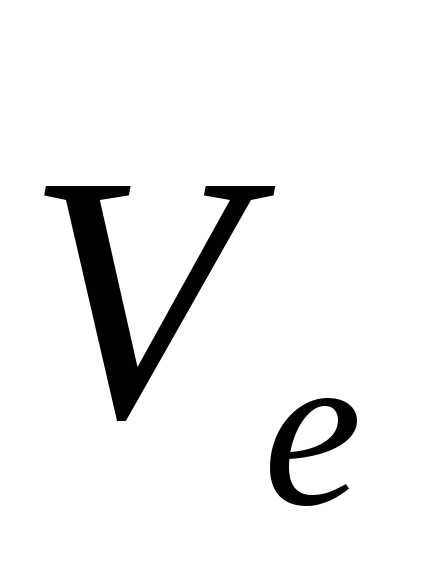 равен
равен. (4.20)
Изменилась
переносная скорость только за счет
относительного движения за время 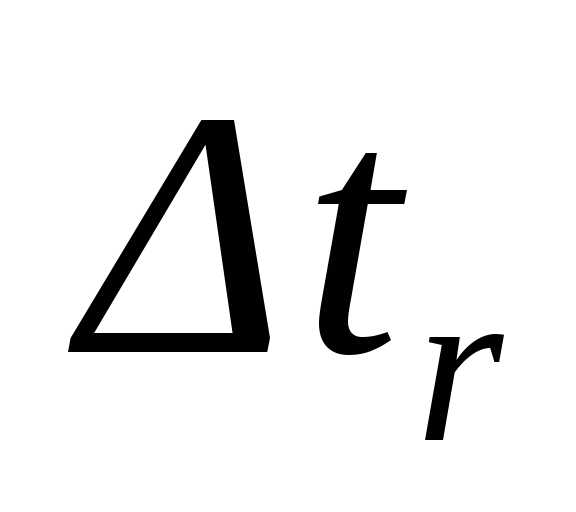 (т. к.
(т. к.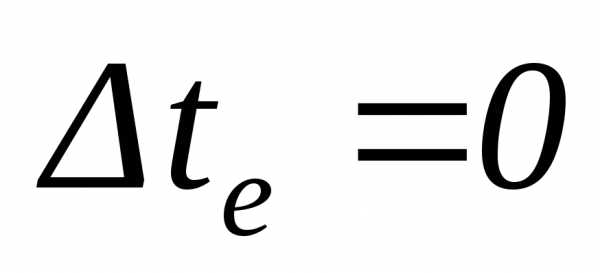 ).
).
3. На самом деле нет двух секундомеров для изучения относительного и переносного движений. Есть один секундомер и оба движения происходят одновременно. Выясним, какое ускорение получила точка М на самом деле.
Учитывая формулы (4.19) и (4.20), оно равно
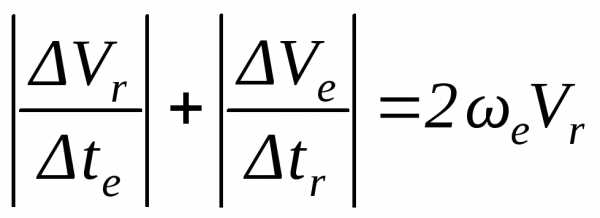 . (4.21)
. (4.21)
Если определить ускорение Кориолиса в данном примере по формуле (4.18), получим:
. (4.21′)
Значит, полученное точкой в данном примере ускорение, есть ускорение Кориолиса.
Имеем физический смысл ускорения Кориолиса: ускорение Кориолиса измеряет изменение вектора относительной скорости в переносном движении и изменение вектора переносной скорости в относительном движении. |
Ускорение Кориолиса
еще называют поворотным; при переносном
поступательном движении оно не возникает.
Есть еще один случай сложного движения,
при котором ускорение Кориолиса равно
нулю: если векторы 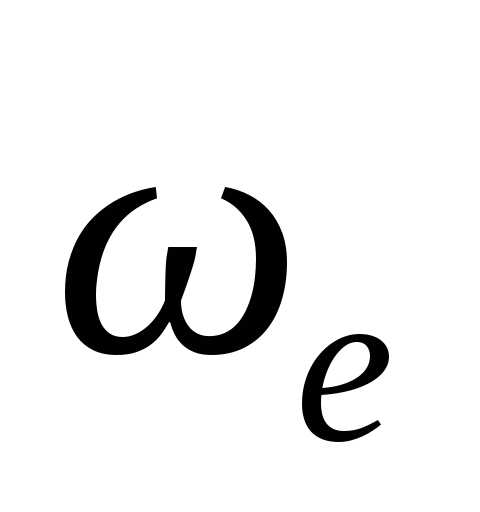
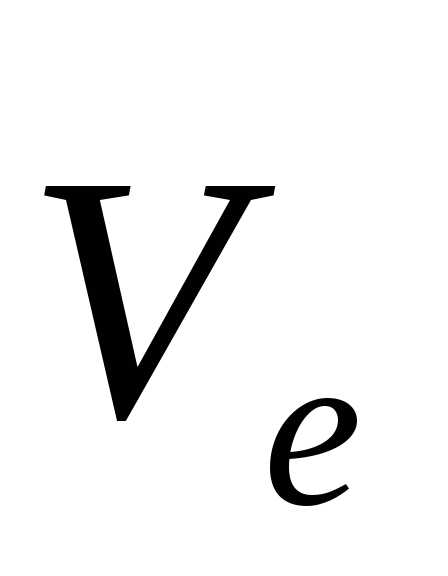 параллельны, т. к.
,.
параллельны, т. к.
,.В качестве примера, иллюстрирующего определение ускорения Кориолиса, рассмотрим вопрос о том, почему правый берег реки Волга более крутой, чем левый?
Пример.
Некоторая частица воды М движется со
скоростью  (рис. 4.8) по меридиану Земли с севера на
юг. Определить величину и направление
ускорения Кориолиса этой частицы, зная
угловую скорость вращения Земли
(рис. 4.8) по меридиану Земли с севера на
юг. Определить величину и направление
ускорения Кориолиса этой частицы, зная
угловую скорость вращения Земли  вокруг вертикальной оси.
вокруг вертикальной оси.
Зная угловую скорость вращения Земли вокруг вертикальной оси
и географическую
широту местоположения точки М,
а также скорость  ,
с которой движется частица по Земле,
можно найти величину ускорения Кориолиса
по формуле (4.18). Направлен вектор ускорения
Кориолиса перпендикулярно медиональной
плоскости по параллели с запада на
восток.
,
с которой движется частица по Земле,
можно найти величину ускорения Кориолиса
по формуле (4.18). Направлен вектор ускорения
Кориолиса перпендикулярно медиональной
плоскости по параллели с запада на
восток.
В разделе «Динамика» будет доказано, что в относительном движении по поверхности Земли ускорению Кориолиса соответствует сила Кориолиса, направленная в сторону, противоположную этому ускорению. В нашем примере частицы воды будут прижиматься к правому берегу реки. Наблюдающееся в двухколесных железных дорогах преимущественное истирание правого рельса также объясняется действием Кориолисовой силы.
В этом заключается известный закон Бэра: Кориолисова сила вызывает дополнительное давление частиц воды к правому берегу в северном полушарии и к левому берегу в южном полушарии. |
studfiles.net
В чём физический смысл Скорости?
Скорость – это хорошо XDDDDDDD
v=ds/dt приращение расстояния по времени…
интересно отвечает на сей вопрос “институт ритмодинамики”
в физике нет смысла
Параметр “скорость” показывает, как быстро изменяется расстояние, пройденное телом.
Скорости относительной. Это концентрация энергии во времени. Это тоже адронный коллайдер. Получив большую скорость мы концентрируем энергию сообщенную во времени долго. и впрыскиваем за время столкновения. тоесть сообщаем энергию в пространстве блольшом, и времени долгом, и используем в сумме мгновенно. Относительная скорость для нас это энергия, которую можно использовать по нашему желанию где хотим.
touch.otvet.mail.ru
Ускорение Кориолиса и его физический смысл.
Формула (71) выражает теорему Кориолиса: абсолютное ускорение точки равно сумме переносного, относительного ускорений и кориолисова, равного
. (72)
Модуль ускорения Кориолиса , а направление определяется по правилу векторного произведения.
Ускорение Кориолиса равно нулю, если:
– (переносное движение поступательное либо равенство справедливо в некоторые моменты времени) ,
– ( равенство справедливо в некоторые моменты времени),
– (векторы, входящие в (72) параллельны).
Заметим, что в формулах (59) для вычисления ускорения точки при плоскопараллельном движении тела имеет место первый из оговоренных случаев.
После формулы (68) наличие последнего слагаемого в формуле (71) может вызвать недоумение. Ниже на простом примере показано, что в общем случае .
Рассмотрим круглую платформу радиуса R, вращающуюся вокруг своего центра О с постоянной угловой скоростью (рис.81). По краю платформы пустим точку М так, чтобы она все время находилась напротив маяка А, установленного на неподвижном основании. Очевидно, что в неподвижной системе отсчета точка М покоится, т.е. ее абсолютные скорость и ускорение равны нулю.

Принимая движение точки М по платформе за относительное, а движение совпадающей с ней точки – за переносное, имеем
; ; .
Ускорения точки М в указанных движениях будут равны своим нормальным составляющим. Последние направлены от точки М к центру платформы и равны . Их сумма не равна нулю, что противоречит здравому смыслу (неподвижность точки М).
Появление ускорения Кориолиса объясняется взаимовлиянием переносного и относительного движений, которое отсутствует при независимом рассмотрении картин составляющих движений.
Задачи на сложное движение точки подразделяются на два типа: в первом по известным переносному и относительному движениям определяют абсолютное, во втором известное абсолютное движение раскладывают на интересующие составляющие.
ПРИМЕР 29 (продолжение решения ПРИМЕРА 27). Шайба М движется по горизонтальному стержню ОА так, что . В то же время стержень вращается вокруг вертикальной оси, проходящей через точку О, по закону . Определить радиальную и трансверсальную составляющие абсолютного ускорения шайбы в момент времени .
РЕШЕНИЕ. Примем за относительное движение шайбы ее движение вдоль стержня ОА по закону ; картина этого движения (КОД) и его кинематические характеристики, вычисленные для момента времени , изображены на рис.82.а.

;
Переносным движением шайбы М будет движение точки стержня, находящейся в рассматриваемый момент времени под шайбой. Тогда ; .
Картина переносного движения (КПД) и вычисленные для него кинематические характеристики изображены на рис.82.б.
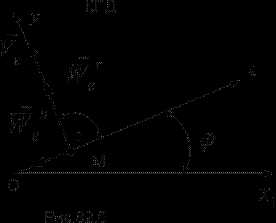
Ускорение Кориолиса равно , его направление см. на рис.82.а.
Теперь вычислим радиальную (проекции на ось Оx подвижной координатной системы) составляющую абсолютного ускорения:
.
Трансверсальная (проекции на ось Oy подвижной координатной системы) составляющая абсолютного ускорения будет
.
При необходимости можно найти величину абсолютного ускорения шайбы как геометрическую сумму ее составляющих.
ПРИМЕР 30. Кривошип кривошипно-кулисного механизма вращается с постоянной угловой скоростью вокруг оси . На расстоянии по вертикали вниз расположена ось вращения кулисы, длина которой . Найти скорость и ускорение точки В кулисы, когда кривошип занимает горизонтальное положение (рис 83.а).

РЕШЕНИЕ. Задание движения кривошипа позволяет рассчитать скорость и ускорение центра ползуна А, как
.
Движение точки А по окружности представим как сложное движение, состоящее из относительного движения вдоль кулисы и переносного движения вместе с точкой кулисы , совпадающей в данный момент времени с точкой А.
Такой подход позволяет рассмотреть независимо картины относительного (рис.83.б) и переносного (рис.83.в) движений точки А, находя интересующие нас глобальные кинематические характеристики переносного движения.

Построим треугольник скоростей (см. рис.84.а) :
.
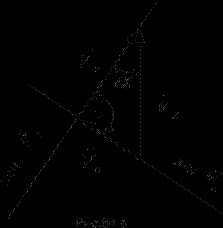
Из треугольника находим, что
Построим многоугольник ускорений (см. рис.84.б):
;
при этом учтено, что
.
Направление ускорения Кориолиса указано на картине относительного движения (рис.83.б).
. 
Проецируя многоугольник на оси выбранной координатной системы, получим два уравнения для вычисления неизвестных составляющих и :
.
Вычислив тангенциальную составляющую переносного ускорения
,
найдем угловое ускорение кулисы .
Теперь вычислить кинематические характеристики точки В не представляет затруднений:
.
Вопросы и задачи для самоконтроля
1. Дайте определения абсолютного, относительного и переносного движений точки.
2. Что происходит с параметрами переносного движения при рассмотрении картины относительного движения (и наоборот)?
3. В каком случае производные, вычисленные в неподвижной и подвижной координатных системах, оказываются равными?
4. Запишите формулы, связывающие скорости и ускорения в подвижной и неподвижной системах отсчета.
5. Запишите формулу для вычисления ускорения Кориолиса. В каких случаях оно обращается в нуль?
6. Диск равномерно вращается вокруг оси, перпендикулярной его плоскости и проходящей через точку О обода. По ободу с постоянной по величине скоростью движется точка А. Найти ускорение точки А в указанном положении.
Лекция 9
Рекомендуемые страницы:
lektsia.com
В чем физический смысл ускорения?
тэги:
ускорение,
физика
категория:
наука и техника
ответить
комментировать
в избранное
бонус
5 ответов:
старые выше
новые выше
по рейтингу
2
Грустный Роджер
[189K]
4 дня назад
Как и всякая производная, ускорение показывает скорость изменения какой-то другой физической величины. В данном случае — скорость изменения скорости.
комментировать
в избранное
ссылка
отблагодарить
1
Алексей Цемахович
[133K]
4 дня назад
Физическим смыслом ускорения тела, является то, что оно является следствием силы, или равнодействующей сил, приложенных к этому телу.
Причем ускорение — это не только изменение скорости, но и любое изменение направления движения.
комментировать
в избранное
ссылка
отблагодарить
0
Maksim Vyrskii
[21.6K]
4 дня назад
Физическим смыслом ускорения является скорость, с которой изменяется скорость объекта. Возьмём для примера и рассмотрим ускорение свободного падения, оно, как всем известно, равно 9,81 м/c^2. И будет означать, что при падении объекта (тела) без сопротивления воздуха, его скорость будет увеличиваться на 9,81 м/с каждую секунду.
комментировать
в избранное
ссылка
отблагодарить
0
bezdelnik
[26.4K]
4 дня назад
Ускорение тела — это следствие, а не физический смысл. Физический смысл ускорения — наличие неуравновешенной силы.
комментировать
в избранное
ссылка
отблагодарить
0
Трифон Ли
[19.5K]
4 дня назад
Наверно буду неправ, но моя т.з. на том, что ускорение это ситуация неуравновешенности действующих на тело сил.
комментировать
в избранное
ссылка
отблагодарить
roypchel.com
Ускорение Кориолиса | Лекции и примеры решения задач механики
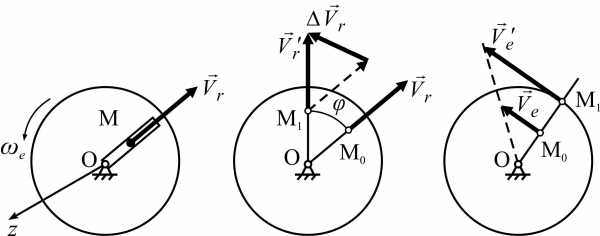
Согласно теореме Кориолиса, абсолютное ускорение точки в сложном движении определяется как геометрическая сумма относительного, переносного и кориолисова ускорений (рис. 3)
aa = ar + ae + aC
Рис. 3
Поскольку, в данном случае, относительное движение происходит по прямой линии, относительное ускорение ar направлено вдоль этой прямой и определяется выражением
Переносным ускорением точки M является ускорение точки M диска. Диск совершает вращательное движение, следовательно, переносное ускорение определяется выражением
ae = aeвр + aeцс
где aeвр= ε ⋅ OM — вращательное ускорение точки M, направленное перпендикулярно отрезку OM;
aeцс= ω2⋅ OM — центростремительное ускорение точки M, направленное к центру диска.
Ускорение Кориолиса или поворотное ускорение определяется по формуле
aC = 2 ωe × νr
где ωe — переносная угловая скорость,
νr — относительная скорость точки.
Направление ускорения Кориолиса определяется по правилу векторного произведения или по правилу Жуковского.
Величина ускорения Кориолиса определяется выражением
aC = 2 ωe νr sinα
где α – угол между векторами ωe и νr.
Рассмотрим, какой физический смысл заложен в ускорение Кориолиса. Для простоты будем считать, что диск вращается с постоянной угловой скоростью, а точка M движется относительно диска с постоянной относительной скоростью (рис.4).
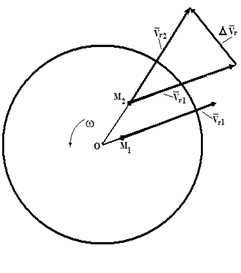
Рис. 4
Пусть в момент времени t1 точка M занимала положение M1 и имела относительную скорость νr1. За промежуток времени Δt точка M переместится в положение M2, при этом направление скорости νr изменится вследствие вращения диска. Вектор νr получит приращение Δνr. Отношение Δνr/Δt определяет среднее ускорение точки за промежуток времени Δt. Предел отношения Δνr / Δt при Δt→ 0 есть производная dνr /dt, как производная от вектора постоянного по величине.
Рассмотрим, как изменяется переносная скорость в зависимости от относительного движения. В моменты времени t1 и t2 переносная скорость определяется выражениями νe1= ω × OM1 и νe2= ω × OM2. Тогда приращение вектора νe за счет относительного движения будет равно
Δνe = ω × OM2 — ω × OM1 =
= ω ×(OM2 — OM1) = ω × νr⋅ Δt
Отношение Δνe/ Δt в пределе при Δt→ 0 дает производную dνe / dt = ω × νr.
Таким образом, ускорение Кориолиса с одной стороны характеризует изменение относительной скорости по направлению за счет переносного вращения и, с другой стороны, изменение величины переносной скорости за счет относительного движения.
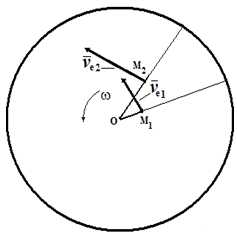
Рис. 5
Абсолютное ускорение точки в сложном движении в общем случае определяется геометрической суммой пяти слагаемых
Для определения величины абсолютного ускорения удобнее пользоваться аналитическим методом сложения векторов:
>> Сферическое движение и способы его задания
isopromat.ru
в чем заключается физический смысл понятия-ускорение свободного падения
в чем заключается физический смысл понятия-ускорение свободного падения – Умные вопросыв чем заключается физический смысл понятия-ускорение свободного падения и одинаково ли его значение на планетах Солнечной системы? 6 годов назад от Черная Экономика
3 Ответы
Это ускорение, которое тело приобретают под действием исключительно силы тяжести (т. е. когда никакие другие силы на него не действуют) .Физически этот параметр характеризует напряжённость гравитационного поля в данной точке.
Вестимо, его величина зависит от того, где именно оно измеряется. На планетах Солнечной системы оно отличается от того, что имется на поверхности Земли. 6 годов назад от svb
В том что, тело набирает скорость при падении десять метров в секунду за секунду. А про ускорение свободного падения на других планетах – читайте Перельмана, “Занимательную физику”. Лучше его никто про это не написал. 6 годов назад от Ату
самое тут печальное, что оно ни хрена не определено.
точне определено в разных местах по разному.
в одних определениях задано, что на поверхности планеты, в других – в любой точке пространства, в одних учитывается центробежная сила, в других нет. 6 годов назад от Венд
Связанные вопросы
1 ответ
2 годов назад от Влад Комаров1 ответ
2 годов назад от Александр я2 ответов
3 годов назад от Илюшка Левойengangs.ru