Формулы математика производные – Таблица производных – Дифференциальное исчисление – Высшая математика – Каталог статей
- Комментариев к записи Формулы математика производные – Таблица производных – Дифференциальное исчисление – Высшая математика – Каталог статей нет
- Советы абитуриенту
таблица производных | математика-повторение
На этом занятии мы будем учиться применять формулы и правила дифференцирования.
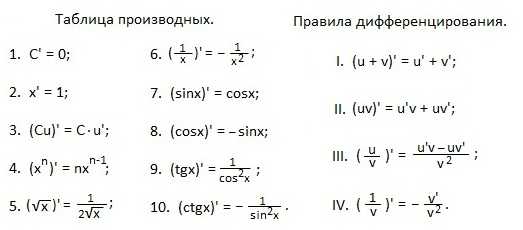
Примеры. Найти производные функций.
1. y=x7+x5-x4+x3-x2+x-9. Применяем правило I, формулы 4, 2 и 1. Получаем:
y’=7x6+5x4-4x3+3x2-2x+1.
2. y=3x6-2x+5. Решаем аналогично, используя те же формулы и формулу 3.
y’=3∙6x5-2=18x5-2.
Применяем правило I, формулы 3, 5 и 6 и 1.
Применяем правило IV, формулы 5 и 1.
В пятом примере по правилу I производная суммы равна сумме производных, а производную 1-го слагаемого мы только что находили (пример
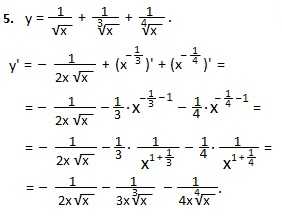Дифференцируем 2-ое и 3-е слагаемые по формуле 4. Для этого преобразуем корни третьей и четвертой степеней в знаменателях к степеням с отрицательными показателями, а затем, по 4 формуле, находим производные степеней.
Посмотрите на данный пример и полученный результат. Уловили закономерность? Хорошо. Это означает, что мы получили новую формулу и можем добавить ее в нашу таблицу производных.
Решим шестой пример и выведем еще одну формулу.
Используем правило IV и формулу 4. Получившиеся дроби сократим.
Смотрим на данную функцию и на ее производную. Вы, конечно, поняли закономерность и готовы назвать формулу:Учим новые формулы!
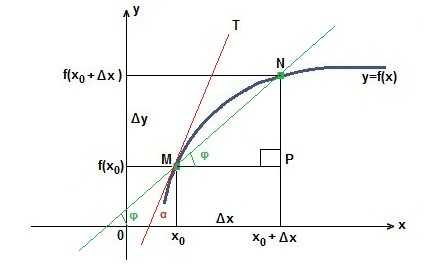В координатной плоскости хОу рассмотрим график функции y=f (x). Зафиксируем точку М(х0; f (x0)). Придадим абсциссе х0 приращение Δх. Мы получим новую абсциссу х0+Δх. Это абсцисса точки N, а ордината будет равна f (х0+Δх). Изменение абсциссы повлекло за собой изменение ординаты. Это изменение называют приращение функции и обозначают Δy.
Δy=f (х0+Δх) — f (x0). Через точки M и N проведем секущую MN, которая образует угол
Пусть Δх стремится к нулю. Тогда секущая MN будет стремиться занять положение касательной МТ, а угол φ станет углом α. Значит, тангенс угла α есть предельное значение тангенса угла φ:
Определение производной. Предел отношения приращения функции к приращению аргумента, при стремлении последнего к нулю, называют производной функции в данной точке:
Геометрический смысл производной заключается в том, что численно производная функции в данной точке равна тангенсу угла, образованного касательной, проведенной через эту точку к данной кривой, и положительным направлением оси Ох:
Смотрите видео 10.3. Определение производной. Геометрический смысл производной.
Примеры.
1. Найти приращение аргумента и приращение функции y=x2, если начальное значение аргумента было равно 4, а новое –4,01.
Решение.
Новое значение аргумента х=х0+Δx. Подставим данные: 4,01=4+Δх, отсюда приращение аргумента Δх=4,01-4=0,01. Приращение функции, по определению, равно разности между новым и прежним значениями функции, т.е. Δy=f (х0+Δх) – f (x0). Так как у нас функция y=x2, то Δу=(х0+Δx)2— (х0)2=(х0)2+2x0 · Δx+(Δx)2— (х0)2=2x0 · Δx+(Δx)2=
Ответ: приращение аргумента Δх=0,01; приращение функции Δу=0,0801.
Можно было приращение функции найти по-другому: Δy=y (х0+Δx) -y (х0)=у(4,01) -у(4)=4,012-42=16,0801-16=0,0801.
2. Найти угол наклона касательной к графику функции y=f (x) в точке х0, если f ‘(х0) = 1.
Решение.
Значение производной в точке касания х0 и есть значение тангенса угла наклона касательной (геометрический смысл производной). Имеем: f ‘(х0) = tgα = 1 → α = 45°, так как tg45°=1.
Ответ: касательная к графику данной функции образует с положительным направлением оси Ох угол, равный 45°.
3. Вывести формулу производной функции y=xn.
Смотрите видео: «10.3.0. Вывод формулы производной степени».
Дифференцирование — это действие нахождения производной функции.
При нахождении производных применяют формулы, которые были выведены на основании определения производной, так же, как мы вывели формулу производной степени: (xn)’ = nxn-1.
Вот эти формулы.
Таблицу производных легче будет заучить, проговаривая словесные формулировки:
1. Производная постоянной величины равна нулю.
2. Икс штрих равен единице.
3. Постоянный множитель можно вынести за знак производной.
4. Производная степени равна произведению показателя этой степени на степень с тем же основанием, но показателем на единицу меньше.
5. Производная корня равна единице, деленной на два таких же корня.
6. Производная единицы, деленной на икс равна минус единице, деленной на икс в квадрате.
7. Производная синуса равна косинусу.
8. Производная косинуса равна минус синусу.
9. Производная тангенса равна единице, деленной на квадрат косинуса.
10. Производная котангенса равна минус единице, деленной на квадрат синуса.
Учим правила дифференцирования.
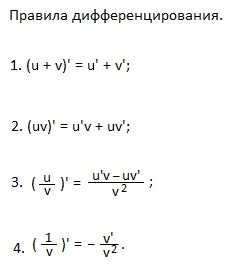1. Производная алгебраической суммы равна алгебраической сумме производных слагаемых.
2. Производная произведения равна произведению производной первого множителя на второй плюс произведение первого множителя на производную второго.
3.
Производная «у», деленного на «вэ» равна дроби, в числителе которой “у штрих умноженный на «вэ» минус «у, умноженный на вэ штрих», а в знаменателе — «вэ в квадрате».4. Частный случай формулы 3.
Учим вместе!
www.mathematics-repetition.com
Формулы производных
Что такое производная функция – это основное математическое понятие, находится на одном уровне с интегралами, при анализе. Данная функция в определенной точке дает характеристику скорости изменений функции в данной точке.
Такие понятия как дифференцирование и интегрирование, первое расшифровывается как действие поиска производной, второе наоборот, восстанавливает функцию отталкиваясь от данной производной.
Вычислениям производной отводится важная часть в дифференциальных расчетах.
Для наглядного примера, изобразим производную на координатной плоскости.
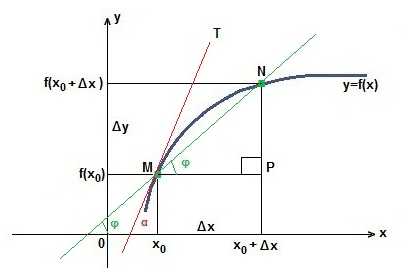
в функции у=f(х) фиксируем точки М в которой (х0; f(X0)) и N f (x0+?x) к каждой абсциссе есть приращение в виде ?x. Приращением называется процесс когда изменяется абсцисса, тогда меняется и ордината. Обозначается как ?у.
Найдем тангенс угла в треугольнике MPN используя для этого точки М и N.
tg? = NP/MP = ?у/?x.
При ?x идущем к 0. Пересекающая МN все ближе к касательной МТ и угол ? будет ?. Следовательно, tg ? максимальное значение для tg ?.
tg ? = lim от ?x-0 tg ? = lim от ?x-0 ?у/?x
Таблица производныхЕсли проговаривать формулировку каждой формулы производных. Таблица будет проще запоминаться.
1) Производная от постоянного значения равняется 0.
2) Х со штрихом равняется единице.
3) Если есть постоянный множитель, просто выносим ео за производную.
5) Поиск корня равен одному, деленному 2 этих корня.
6) Производная одного, деленного на Х равняется одному разделенному на Х возведенный в квадрат, со знаком минус.
7) П синус равняется косинусу
8) П косинус равняется синусу со знаком минус.
9) П тангенс равняется одному, деленному на косинус в квадрате.
10) П котангенс равняется одному со знаком минус, деленная на синус в квадрате.
В дифференцировании также существуют правила, которые тоже проще выучить проговаривая их в слух.
1) Очень просто, п. слагаемых равняется их сумме.
2) Производная в умножении равняется умножению первого значения на второе, прибавляя к себе умножение второго значения на первое.
4) Формулировка является частным случаем третьей формулы.
Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:
reshit.ru
Формулы производных функции
Рассмотрим функцию которая определена и непрерывна на некотором интервале произвольную точку и соответствующее значение функции в этой точке Зададим аргументу функции приращение в точке В результате получим величину и соответствующее значение функции
ОПРЕДЕЛЕНИЕ Производной функции в точке называется предел отношения приращения функции к вызвавшему его приращению аргумента в этой точке, при условии, что последний стремится к нулю:
Если данный предел конечен, то рассматриваемая функция называется дифференцируемой в точке .
Дифференцирование – это процесс нахождения производной функции. Его проводят с использованием таблицы производных и правил дифференцирования. На этой странице разобраны все формулы производных функции.
Таблица производных, список формул
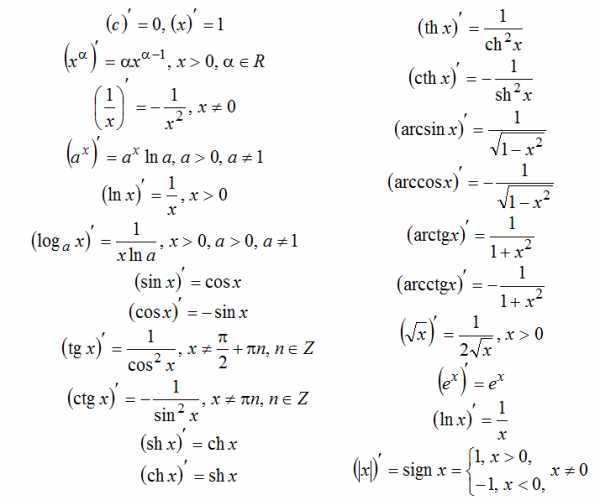
Правила дифференцирования
ПРИМЕР 1
| Задание | Найти производную функции |
| Решение | Искомая производная равна:
|
| Ответ |
| Задание | Продифференцировать функцию
|
| Решение | Искомая производная
Производная разности равна разности производных:
Производную первого слагаемого найдем по таблице производных, второго – как производную частного:
|
| Ответ |
ru.solverbook.com
| (Ф. Хаусдорф.) ‘ quotes[1]='”Математика – это язык, на котором написана книга природы.”(Г. Галилей) ‘ quotes[2]='”Кто с детских лет занимается математикой, тот развивает внимание, тренирует свой мозг, свою волю, воспитывает настойчивость и упорство в достижении цели.”(А. Маркушевич) ‘ quotes[3]='”Рано или поздно всякая правильная математическая идея находит применение в том или ином деле.”(А.Н. Крылов) ‘ quotes[4]='”Если вы хотите участвовать в большой жизни, то наполняйте свою голову математикой. Она окажет вам потом огромную помощь во всей вашей работе.”(М.И. Калинин) ‘ quotes[5]='”Разве ты не заметил, что способный к математике изощрен во всех науках в природе?”(Платон) ‘ quotes[6]='”Математика есть лучшее и даже единственное введение в изучение природы.”(Д.И. Писарев) ‘ quotes[7]='”Вдохновение нужно в геометрии не меньше, чем в поэзии.”(А.С. Пушкин) ‘ quotes[8]='”Геометрия полна приключений, потому что за каждой задачей скрывается приключение мысли. Решить задачу – это значит пережить приключение.”(В. Произволов) ‘ quotes[9]='”В математике есть своя красота, как в живописи и поэзии.”(Н.Е. Жуковский) ‘ quotes[10]='”Химия – правая рука физики, математика – ее глаз.”(М.В. Ломоносов) ‘ quotes[11]='”Математику уже затем учить надо, что она ум в порядок приводит.”(М.В. Ломоносов) ‘ quotes[12]='”Математика – это язык, на котором говорят все точные науки.”(Н.И. Лобачевский) ‘ quotes[13]='”Именно математика дает надежнейшие правила: кто им следует – тому не опасен обман чувств.”(Л. Эйлер) ‘ quotes[14]='”Числа не управляют миром, но они показывают, как управляется мир.”(И. Гете) ‘ quotes[15]='”Было бы легче остановить Солнце, легче было сдвинуть Землю, чем уменьшить сумму углов в треугольнике или свести параллели к схождению…”(В.Ф. Каган) ‘ quotes[16]='”Счет и вычисления – основа порядка в голове.”(Песталоцци) ‘ quotes[17]='”Величие человека – в его способности мыслить.”(Б. Паскаль) ‘ quotes[18]='”Если вы хотите научиться плавать, то смело входите в воду, а если хотите научиться решать задачи, то решайте их.”(Д.Пойа) ‘ quotes[19]='”Предмет математики столь серьезен, что не следует упускать ни одной возможности сделать его более занимательным.”(Б. Паскаль) ‘ quotes[20]='”В математических вопросах нельзя пренебрегать даже самыми мелкими ошибками.”(И. Ньютон) ‘ quotes[21]='”Первое условие, которое надлежит выполнять в математике, – это быть точным, второе – быть ясным и, насколько можно, простым.”(Л. Карно) ‘ quotes[22]='”Много из математики не остается в памяти, но когда поймешь ее, тогда легко при случае вспомнить забытое.”(М.В. Остроградский) ‘ quotes[23]='”Математика – это цепь понятий: выпадет одно звенышко – и не понятно будет дальнейшее.”(Н.К. Крупская) ‘ quotes[24]='”Математика уступает свои крепости лишь сильным и смелым.”(А.П. Конфорович) ‘ quotes[25]='”Доказательство – это рассуждение, которое убеждает.”(Ю.А. Шиханович) ‘ quotes[26]='”В каждой естественной науке заключено столько истины, сколько в ней есть математики.”(И. Кант) ‘ var whichquote= Math.floor(Math.random()*(quotes.length)) document.write(quotes[whichquote]) |
free-math.ru
Формулы дифференцирования функций
Далее разобраны основные правила и формулы дифференцирования функций:
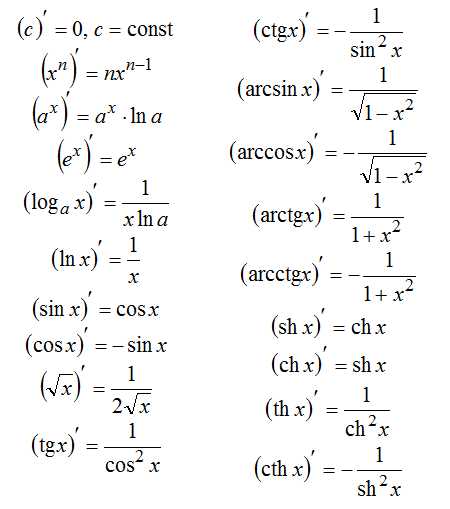
Правила дифференцирования:
Константу можно выносить за знак производной:
Производная суммы равна сумме производных:
Производная произведения равна сумме произведений производной первого слагаемого на второе и первого слагаемого на производную второго:
Производная частного находится по формуле:
| Понравился сайт? Расскажи друзьям! | |||
ru.solverbook.com
Правила дифференцирования в математике | univer-nn.ru
Производная алгебраической суммы функций
выражается следующей теоремой.
Теорема 1. Производная суммы (разности) двух дифференцируемых функций равна сумме (разности) производных этих функций:
(u±v)’ = u’±v’Следствие. Производная конечной алгебраической суммы дифференцируемых функций равна такой же алгебраической сумме производных слагаемых. Например,
(u — v + w)’ = u’ — v’ + w’Производную произведения функций определяет
Теорема 2. Производная произведения двух дифференцируемых функций равна произведению первой функции на производную второй плюс произведение второй функции на производную первой, т. е.
(uv)’ = u’v + uv’Следствие 1. Постоянный множитель можно выносить за знак производной (cv)’ = cv’ (с = const).
Следствие 2. Производная произведения нескольких дифференцируемых функций равна сумме произведений производной каждой из них на все остальные.
Например, (uvw)’ = u’vw + uv’w + uvw’Производная частного двух функций
выражается следующей теоремой.
Теорема 3. Производная частного двух дифференцируемых функций определяется формулой
Производную сложной функции выражает
Теорема 4. Если y = f(u) и и = (ф(х)) — дифференцируемые функции своих аргументов, то производная сложной функции у = f (ф(х)) существует и равна произведению производной этой функции по промежуточному аргументу на производную промежуточного аргумента по независимой переменной, т. е.
Очень часто в задачах по математике на производные даются сложные функции, например, y = sin(cos5x). Производная такой функции равна -5sin5x*sin(cos5x)Смотрите пример вычисления сложной функции на следующем видео
Производная обратной функции
Еели у = f(x) и х = ф (у) — взаимно обратные дифференцируемые функции, то
univer-nn.ru
Формулы производных функций y (x)
Производные линейной функции.
Производные степенной функции.
Производные показательной функции.
Производные логарифмической функции.
Производные тригонометрической функции.
Производные обратной тригонометрической функции.
- Подробности
- Автор: Administrator
www-formula.ru
