Интеграл решение примеров – Примеры решений интегралов по частям, содержащих логарифм и обратные тригонометрические функции
- Комментариев к записи Интеграл решение примеров – Примеры решений интегралов по частям, содержащих логарифм и обратные тригонометрические функции нет
- Советы абитуриенту
- 11-а, Решение интегралов
- Методы вычисления интеграла | Высшая математика
- Примеры решений интегралов по частям, содержащих логарифм и обратные тригонометрические функции
- Двойные интегралы, примеры решений
- Неопределенный интеграл. Примеры решений
11-а, Решение интегралов
Решение интегралов. Рассказываем, как решать интегралы.
Интеграл – расширенное математическое понятие суммы. Решение интегралов или их нахождение называется интегрированием. Пользуясь интегралом можно найти такие величины, как площадь, объем, массу и другое. Решение интегралов (интегрирование) есть операция обратная диференциированию. Чтобы лучше представлять, что есть интеграл, представим его в следующей форме. Представьте. У нас есть тело, но пока не можем описать его, мы только знаем какие у него элементарные частицы и как они расположены. Для того, чтобы собрать тело в единое целое необходимо проинтегрировать его элементарные частички – слить части в единую систему. В геометрическом виде для функции y=f(x), интеграл представляет собой площадь фигуры ограниченной кривой, осью х, и 2-мя вертикальными линиями х=а и х=b .
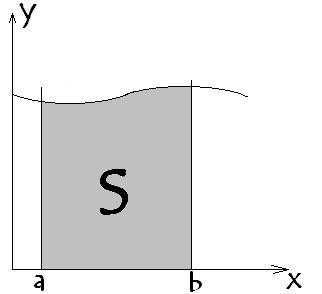
Так
вот площадь закрашенной области, есть
интеграл от функции в пределах от a до
b.
Не верится? Проверим на любой функции.
Возьмем простейшую у=3. Ограничим функцию
значениями а=1 и b=2. Построим: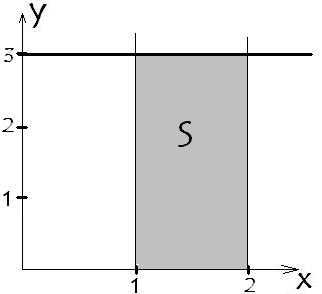 Итак
ограниченная фигура прямоугольник.
Площадь прямоугольника равна произведению
длины на ширину. В наше случае длина 3,
ширина 1, площадь 3*1=3.
Попробуем решить
тоже самое не прибегая к построению,
используя интегрирование:Как
видите ответ получился тот же. Решение
интегралов – это собирание во едино
каких-либо элементарных частей. В случае
с площадью суммируются полоски бесконечно
малой ширины. Интегралы могут быть
определенными и неопределенными.
Решить
определенный интеграл значит найти
значение функции в заданных границах.
Решение неопределенного интеграла
сводиться к нахождению первообразной.F(x)
– первообразная. Дифференцируя
первообразую, мы получим исходное
подинтегральное выражение. Чтобы
проверить правильно ли мы решили
интеграл, мы дифференциируем полученный
ответ и сравниваем с исходным
выражением.
Основные функции и
первообразные для них приведены в
таблице:
Итак
ограниченная фигура прямоугольник.
Площадь прямоугольника равна произведению
длины на ширину. В наше случае длина 3,
ширина 1, площадь 3*1=3.
Попробуем решить
тоже самое не прибегая к построению,
используя интегрирование:Как
видите ответ получился тот же. Решение
интегралов – это собирание во едино
каких-либо элементарных частей. В случае
с площадью суммируются полоски бесконечно
малой ширины. Интегралы могут быть
определенными и неопределенными.
Решить
определенный интеграл значит найти
значение функции в заданных границах.
Решение неопределенного интеграла
сводиться к нахождению первообразной.F(x)
– первообразная. Дифференцируя
первообразую, мы получим исходное
подинтегральное выражение. Чтобы
проверить правильно ли мы решили
интеграл, мы дифференциируем полученный
ответ и сравниваем с исходным
выражением.
Основные функции и
первообразные для них приведены в
таблице:
Таблица первообразных для решения интегралов
 Основные
приемы решения интегралов:
Решить
интеграл, значит проинтегрировать
функцию по переменной. Если интеграл
имеет табличный вид, то можно сказать,
что вопрос, как решить интеграл, решен.
Если же нет, то основной задачей при
решении интеграла становиться сведение
его к табличному виду.
Сначала следует
запомнить основные свойства интегралов:
Основные
приемы решения интегралов:
Решить
интеграл, значит проинтегрировать
функцию по переменной. Если интеграл
имеет табличный вид, то можно сказать,
что вопрос, как решить интеграл, решен.
Если же нет, то основной задачей при
решении интеграла становиться сведение
его к табличному виду.
Сначала следует
запомнить основные свойства интегралов: 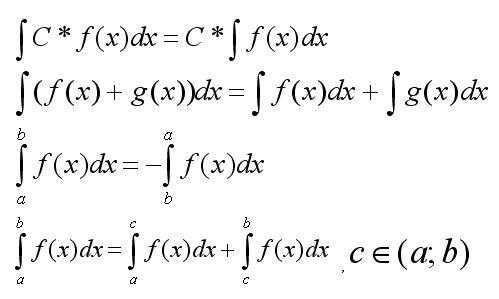
Знание только этих основ позволит решать простые интегралы. Но следует понимать, что большинство интегралов сложные и для их решения необходимо прибегнуть к использованию дополнительных приемов. Ниже мы рассмотрим основные примеры решения интегралов. Приемы будет даны для общего ознакомления
Основные приемы решения интегралов
1.
Замена переменной. 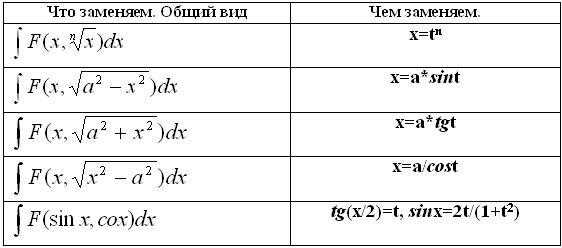 Для
выполнения данного приема потребуется
хороший навык нахождения производных.
Для
выполнения данного приема потребуется
хороший навык нахождения производных.
2. Интегрирование по частям. Пользуются следующей формулой. Применения этой формулы позволяет казалось бы нерешаемые интегралы привести к решению.
3. Интегрирование дробно-рациональных функций. – разложить дробь на простейшие- выделить полный квадрат.- создать в числителе дифференциал знаменателя.
4. Интегрирование дробно-иррациональных функций. – выделить под корнем полный квадрат- создать в числителе дифференциал подкоренного выважения. 5. Интегрирование тригонометрических функций.При интегрировании выражений вида применяет формулы разложения для произведения. Для выраженийm-нечетное, n –любое, создаем d(cosx). Используем тождество sin 2+cos2=1 m,n – четные, sin2x=(1-cos2x)/2 и cos2x=(1+cos2x)/2 Для выражений вида: – Применяем свойство tg2x=1/cos2x – 1
1. Разобраться в сути интегралов. Необходимо понять базовую сущность интеграла и его решения. Интеграл по сути есть сумма элементарных частей объекта интегрирования. Если речь идет об интегрирование функции, то интеграл есть площадь фигуры между графиком функции, осью х и границами интегрирования. Если интеграл неопределенный, то есть границы интегрирования не указаны, то решение сводиться к нахождению первобразной. Если интеграл определенный, то необходимо подставить значения границ в найденную функцию. 2. Отработать использование таблицы первообразных и основным свойства интегралов
Примеры решения интегралов
Пример 1: Решить интеграл: Интеграл неопределенный. Находим первообразную. Для этого интеграл суммы разложим на сумму интегралов.Каждый из интегралов табличного вида. Смотрим первообразные по таблице. Решение интеграла:Проверим решение(найдем производную):
Пример 2. Решаем интеграл Интеграл неопределенный. Находим первообразную. Сравниваем с таблицей. В таблице нет. Разложить, пользуясь свойствами, нельзя. Смотрим приемы. Наиболее подходит замена переменной. Заменяем х+5 на t5. t5 = x+5 . Получаем. Но dx нужно тоже заменить на t. x= t5 – 5, dx = (t5 – 5)’ = 5t4. Подставляем: Интеграл из таблицы. Считаем:Подставляем в ответ вместо t ,Решение интеграла:
Пример 3. Решение интеграла: Для решения в этом случае необходимо выделить полный квадрат. Выделяем:
В данном случае коэфециент ½ перед интегралом получился в результате замены dx на ½*d(2x+1). Если вы найдете производные x’ = 1 и ½*(2x+1)’= 1, то поймете почему так. В результате мы привели интеграл к табличному виду. Находим первообразную. В итоге получаем:
studfiles.net
Методы вычисления интеграла | Высшая математика
Формулы и уравнения неопределенных интегралов здесь.
Пример. Метод непосредственного интегрирования неопределенного интеграла.
Дано: интеграл
Найти:
Вычислить неопределенный интеграл методом непосредственного интегрирования.
Решение:
Метод непосредственного интегрирования: воспользовавшись свойством линейности
применяя тождественные преобразования подынтегрального выражения, исходный интеграл сводится к нескольким более простым, которые могут быть вычислены непосредственно по таблице интегралов.
Используя вышеприведенное, применив основное тригонометрическое тождество , получим следующее:
Далее, разделив каждое слагаемое числителя подынтегрального выражения на знаменатель и воспользовавшись таблицей интегралов от элементарных функций (ссылка) получим следующее:
Ответ:
Пример. Метод интегрирования по частям неопределенного интеграла.
Дано: интеграл
Найти:
Вычислить неопределенный интеграл методом интегрирования по частям.
Решение:
Метод интегрирования по частям: подынтегральное выражение представляем в виде произведения некоторой функции u на дифференциал другой функции dv: . Далее, используя формулу интегрирования по частям заменяем исходный интеграл другим который, как правило, более простой для вычисления.
Применим вышесказанное к нашему интегралу. Считаем , тогда
Воспользовавшись вышеприведенной формулой, в итоге получим следующее:
Пример. Метод замены переменной неопределенного интеграла.
Дано: интеграл
Найти:
Вычислить неопределенный интеграл методом замены переменной.
Решение:
Метод замены переменной: вместо исходной переменной x, вводится новая переменная k, связанная с x соотношением: , где — дифференцируемая функция переменной x.
Применяем вышеприведенное к нашему интегралу, обозначаем через новую переменную интегрирования k выражение, стоящее в знаменателе подинтегральной функции значит, . Получаем преобразованный интеграл:
Вычисляем полученный интеграл по переменной k и возвращаемся к старой переменной x, с учетом того, что
Ответ:
matematika.electrichelp.ru
Примеры решений интегралов по частям, содержащих логарифм и обратные тригонометрические функции
Формула интегрирования по частям
Ниже, при решении примеров, применяется формула интегрирования по частям:
;
.
Подробнее >>>
Примеры интегралов, содержащих логарифм и обратные тригонометрические функции
Вот примеры интегралов, которые интегрируются по частям:
, , , , , , .
При интегрировании ту часть подынтегрального выражения, которая содержит логарифм или обратные тригонометрические функции обозначают через u, остальное – через dv.
Ниже приведены примеры с подробными решениями этих интегралов.
Простой пример с логарифмом
Вычислим интеграл, содержащий произведение многочлена и логарифма:
Решение
Здесь подынтегральное выражение содержит логарифм. Делаем подстановки
u = ln x, dv = x2 dx. Тогда
,
.
Интегрируем по частям.
.
Вычисляем оставшийся интеграл:
.
Тогда
.
В конце вычислений добавим постоянную C.
Ответ
Пример логарифма в степени 2
Рассмотрим пример, в котором в подынтегральное выражение входит логарифм в целочисленной степени. Такие интегралы также могут интегрироваться по частям.
Решение
Делаем подстановки
u = (ln x)2, dv = x dx. Тогда
,
.
.
Оставшийся интеграл также вычисляем по частям:
.
Подставляем
.
Ответ
Пример, в котором аргумент логарифма является многочленом
По частям могут вычисляться интегралы, в подынтегральное выражение которого входит логарифм, аргумент которого является многочленом, рациональной или иррациональной функцией. В качестве примера, вычислим интеграл с логарифмом, аргумент которого является многочленом.
.
Решение
Делаем подстановки
u = ln( x2 – 1), dv = x dx.
Тогда
,
.
.
Вычисляем оставшийся интеграл:
.
Мы здесь не пишем знак модуля ln |x2 – 1|, поскольку подынтегральное выражение определено при x2 – 1 > 0. Подставляем
.
Ответ
Пример с арксинусом
Рассмотрим пример интеграла, в подынтегральное выражение которого входит арксинус.
.
Решение
Делаем подстановки
u = arcsin x,
.
Тогда
,
.
.
Далее замечаем, что подынтегральное выражение определено при |x| < 1. Раскроем знак модуля под логарифмом, учитывая что 1 – x > 0 и 1 + x > 0.
Ответ
Пример с арктангенсом
Решим пример с арктангенсом:
.
Решение
Интегрируем по частям.
.
Выделим целую часть дроби:
x8 = x8 + x6 – x6 – x4 + x4 + x2 – x2 – 1 + 1 = (x2 + 1)(x6 – x4 + x2 – 1) + 1;
.
Интегрируем:
.
Окончательно имеем:
.
Ответ
Еще один пример с арксинусом
Решить интеграл:
.
Решение
Интегрируем по частям.
.
Вычисляем оставшийся интеграл. При x > 0 имеем:
.
.
.
При x < 0 сделаем подстановку x = – t, t > 0:
.
Окончательно имеем:
Ответ
.
Автор: Олег Одинцов. Опубликовано:
1cov-edu.ru
Двойные интегралы, примеры решений
Теория по двойным интегралам
Двойной интеграл от функции двух переменных по области G обозначается
Для вычисления двойного интеграла, его нужно свести к повторному интегралу. Возможны два случая. Пусть область интегрирования – элементарна относительно оси (рис. 1). Тогда двойной интеграл по области выражается через повторные по формуле:
Если же область интегрирования – элементарна относительно оси (рис. 2), то двойной интеграл по области выражается через повторные следующим образом:
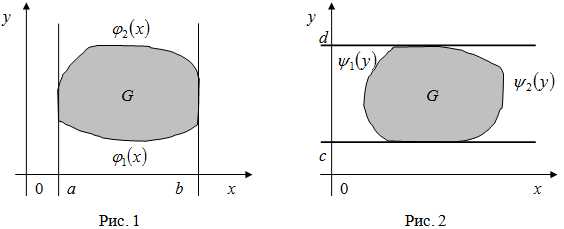
При решении задач иногда полезно разбить исходную область интегрирования на две или более областей и вычислять двойной интеграл в каждой области отдельно.
Примеры
ПРИМЕР 3| Задание | Вычислить двойной интеграл, если область – единичный круг с центром в начале координат. Интеграл:
|
| Решение | Если область, по которой вычисляется интеграл, является кругом или его частью, то интеграл проще вычислять в полярных координатах. Перейдем к полярным координатам:
В декартовых координатах уравнение единичной окружности с центром в начале координат имеет вид: ; запишем его в полярной системе координат:
Учитывая, что по определению , получим, что лежит в пределах . Так как интегрирование производится по всей окружности, то лежит в пределах . Подынтегральная функция в полярной системе координат примет вид:
Подставляя эту замену в исходный интеграл и переходя от двойного к повторному, получим:
Так как внутренний интеграл не зависит от , то его можно вычислить отдельно , осталось вычислить внутренний интеграл по :
|
| Ответ |
| Задание | С помощью двойного интеграла, вычислить площадь фигуры, ограниченной линиями: |
| Решение | Сделаем рисунок (рис. 4).
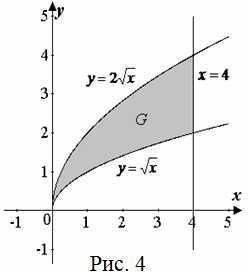
Площадь с помощью двойного интеграла вычисляется по формуле
Перейдем от двойного интеграла к повторному:
Вычислим этот интеграл, начиная с внутреннего:
(кв. ед.) |
| Ответ |
| Понравился сайт? Расскажи друзьям! | |||
ru.solverbook.com
Неопределенный интеграл. Примеры решений
На данном уроке мы познакомимся с одним из самых важных и наиболее распространенных приемов, который применяется в ходе решения неопределенных интегралов – методом замены переменной. Для успешного освоения материала требуются начальные знания и навыки интегрирования. Если есть ощущение пустого полного чайника в интегральном исчислении, то сначала следует ознакомиться с материалом Неопределенный интеграл. Примеры решений, где я объяснил в доступной форме, что такое интеграл и подробно разобрал базовые примеры для начинающих.
Технически метод замены переменной в неопределенном интеграле реализуется двумя способами:
– ^
– Собственно замена переменной.
По сути дела, это одно и то же, но оформление решения выглядит по-разному.
Начнем с более простого случая.
^
На уроке Неопределенный интеграл. Примеры решений мы научились раскрывать дифференциал, напоминаю пример, который я приводил:
То есть, раскрыть дифференциал – это почти то же самое, что найти производную.
Пример 1
Найти неопределенный интеграл. Выполнить проверку.
Смотрим на таблицу интегралов и находим похожую формулу: . Но проблема заключается в том, что у нас под синусом не просто буковка «икс», а сложное выражение. Что делать?
Подводим функцию под знак дифференциала:
Раскрывая дифференциал, легко проверить, что:
Фактически и – это запись одного и того же.
Но, тем не менее, остался вопрос, а как мы пришли к мысли, что на первом шаге нужно записать наш интеграл именно так: ? Почему так, а не иначе?
Формула (и все другие табличные формулы) справедливы и применимы НЕ ТОЛЬКО для переменной , но и для любого сложного выражения ЛИШЬ БЫ АРГУМЕНТ ФУНКЦИИ ( – в нашем примере) ^ ОДИНАКОВЫМИ.
Поэтому мысленное рассуждение при решении должно складываться примерно так: «Мне надо решить интеграл . Я посмотрел в таблицу и нашел похожую формулу . Но у меня сложный аргумент и формулой я сразу воспользоваться не могу. Однако если мне удастся получить и под знаком дифференциала, то всё будет нормально. Если я запишу , тогда . Но в исходном интеграле множителя-тройки нет, поэтому, чтобы подынтегральная функция не изменилась, мне надо ее домножить на ». В ходе примерно таких мысленных рассуждений и рождается запись:
Теперь можно пользоваться табличной формулой :
Готово
Единственное отличие, у нас не буква «икс», а сложное выражение .
Выполним проверку. Открываем таблицу производных и дифференцируем ответ:
Получена исходная подынтегральная функция, значит, интеграл найден правильно.
Обратите внимание, что в ходе проверки мы использовали правило дифференцирования сложной функции . ^ – это два взаимно обратных правила.
Пример 2
Найти неопределенный интеграл. Выполнить проверку.
Анализируем подынтегральную функцию. Здесь у нас дробь, причем в знаменателе линейная функция (с «иксом» в первой степени). Смотрим в таблицу интегралов и находим наиболее похожую вещь: .
Подводим функцию под знак дифференциала:
Те, кому трудно сразу сообразить, на какую дробь нужно домножать, могут быстренько на черновике раскрыть дифференциал: . Ага, получается , значит, чтобы ничего не изменилось, мне надо домножить интеграл на .
Далее используем табличную формулу :
Проверка:
Получена исходная подынтегральная функция, значит, интеграл найден правильно.
Пример 3
Найти неопределенный интеграл. Выполнить проверку.
Это пример для самостоятельного решения. Ответ в конце урока.
Пример 4
Найти неопределенный интеграл. Выполнить проверку.
Это пример для самостоятельного решения. Ответ в конце урока.
При определенном опыте решения интегралов, подобные примеры будут казаться лёгкими, и щелкаться как орехи:
И так далее.
В конце данного параграфа хотелось бы еще остановиться на «халявном» случае, когда в линейной функции переменная входит с единичным коэффициентом, например:
Строго говоря, решение должно выглядеть так:
Как видите, подведение функции под знак дифференциала прошло «безболезненно», без всяких домножений. Поэтому на практике таким длинным решением часто пренебрегают и сразу записывают, что . Но будьте готовы при необходимости объяснить преподавателю, как Вы решали! Поскольку интеграла в таблице вообще-то нет.
^
Переходим к рассмотрению общего случая – метода замены переменных в неопределенном интеграле.
Пример 5
Найти неопределенный интеграл.
В качестве примера я взял интеграл, который мы рассматривали в самом начале урока. Как мы уже говорили, для решения интеграла нам приглянулась табличная формула , и всё дело хотелось бы свести к ней.
Идея метода замены состоит в том, чтобы сложное выражение (или некоторую функцию) заменить одной буквой.
В данном случае напрашивается:
Вторая по популярности буква для замены – это буква .
В принципе, можно использовать и другие буквы, но мы всё-таки будем придерживаться традиций.
Итак:
Но при замене у нас остаётся ! Наверное, многие догадались, что если осуществляется переход к новой переменной , то в новом интеграле всё должно быть выражено через букву , и дифференциалу там совсем не место.
Следует логичный вывод, что нужно превратить в некоторое выражение, которое зависит только от .
Действие следующее. После того, как мы подобрали замену, в данном примере, , нам нужно найти дифференциал . С дифференциалами, думаю, дружба уже у всех налажена.
Так как , то
После разборок с дифференциалом окончательный результат рекомендую переписать максимально коротко:
Теперь по правилам пропорции выражаем нужный нам :
В итоге:
Таким образом:
А это уже самый что ни на есть табличный интеграл (таблица, интегралов, естественно, справедлива и для переменной ).
В заключении осталось провести обратную замену. Вспоминаем, что .
Готово.
Чистовое оформление рассмотренного примера должно выглядеть примерно так:
“
Проведем замену:
“
Значок не несет никакого математического смысла, он обозначает, что мы прервали решение для промежуточных объяснений.
Также всем рекомендую использовать математический знак вместо фразы «из этого следует это». И коротко, и удобно.
При оформлении примера в тетради надстрочную пометку обратной замены лучше выполнять простым карандашом.
Внимание! В следующих примерах нахождение дифференциала расписываться подробно не будет.
А теперь самое время вспомнить первый способ решения:
В чем разница? Принципиальной разницы нет. Это фактически одно и то же. ^
Возникает вопрос. Если первый способ короче, то зачем тогда использовать метод замены? Дело в том, что для ряда интегралов не так-то просто «подогнать» функцию под знак дифференциала.
Пример 6
Найти неопределенный интеграл.
Проведем замену: (другую замену здесь трудно придумать)
Как видите, в результате замены исходный интеграл значительно упростился – свёлся к обычной степенной функции. ^ .
Ленивые продвинутые люди запросто решат данный интеграл методом подведения функции под знак дифференциала:
Другое дело, что такое решение очевидно далеко не для всех студентов. Кроме того, уже в этом примере использование метода подведения функции под знак дифференциалазначительно повышает риск запутаться в решении.
Пример 7
Найти неопределенный интеграл. Выполнить проверку.
Это пример для самостоятельного решения. Ответ в конце урока.
Пример 8
Найти неопределенный интеграл.
Замена:
Осталось выяснить, во что превратится
Хорошо, мы выразили, но что делать с оставшимся в числителе «иксом»?!
Время от времени в ходе решения интегралов встречается следующий трюк: мы выразим из той же замены !
Готово.
Пример 9
Найти неопределенный интеграл.
Это пример для самостоятельного решения. Ответ в конце урока.
Пример 10
Найти неопределенный интеграл.
Наверняка некоторые обратили внимание, что в моей справочной таблице нет правила замены переменной. Сделано это сознательно. Правило внесло бы путаницу в объяснение и понимание, поскольку в вышерассмотренных примерах оно не фигурирует в явном виде.
Настало время рассказать об основной предпосылке использования метода замены переменной: в подынтегральном выражении должна находиться некоторая функция и её производная : (функции , могут быть и не в произведении)
В этой связи при нахождении интегралов довольно часто приходится заглядывать в таблицу производных.
В рассматриваемом примере замечаем, что степень числителя на единицу меньше степени знаменателя. В таблице производных находим формулу , которая как раз понижает степень на единицу. А, значит, если обозначить за знаменатель, то велики шансы, что числитель превратится во что-нибудь хорошее.
Замена:
Кстати, здесь не так сложно подвести функцию под знак дифференциала:
Следует отметить, что для дробей вроде, такой фокус уже не пройдет (точнее говоря, применить нужно будет не только прием замены). Интегрировать некоторые дроби можно научиться на уроке Интегрирование некоторых дробей.
Вот еще пара типовых примеров для самостоятельного решения из той же оперы:
Пример 11
Найти неопределенный интеграл.
Пример 12
Найти неопределенный интеграл.
Решения в конце урока.
Пример 13
Найти неопределенный интеграл.
Смотрим в таблицу производных и находим наш арккосинус: . У нас в подынтегральном выражении находится арккосинус и нечто похожее на его производную.
Общее правило:
За обозначаем саму функцию (а не её производную).
В данном случае: . Осталось выяснить, во что превратится оставшаяся часть подынтегрального выражения .
В этом примере нахождение я распишу подробно поскольку – сложная функция.
Или короче:
По правилу пропорции выражаем нужный нам остаток:
Таким образом:
Вот здесь подвести функцию под знак дифференциала уже не так-то просто.
Пример 14
Найти неопределенный интеграл.
Пример для самостоятельного решения. Ответ совсем близко.
Внимательные читатели заметили, что я рассмотрел мало примеров с тригонометрическими функциями. И это не случайно, поскольку под интегралы от тригонометрических функцийотведён отдельный урок. Более того, на указанном уроке даны некоторые полезные ориентиры для замены переменной, что особенно актуально для чайников, которым не всегда и не сразу понятно, какую именно замену нужно проводить в том или ином интеграле. Также некоторые типы замен можно посмотреть в статье Определенный интеграл. Примеры решений.
Более опытные студенты могут ознакомиться с типовой заменой в интегралах с иррациональными функциями. Замена при интегрировании корней является специфической, и её техника выполнения отличается от той, которую мы рассмотрели на этом уроке.
Желаю успехов!
Решения и ответы:
Пример 3: Решение:
Пример 4: Решение:
Пример 7: Решение:
Пример 9: Решение:
Замена:
Пример 11: Решение:
Проведем замену:
Пример 12: Решение:
Проведем замену:
Пример 14: Решение:
Проведем замену:
Я выполнил проверку, а Вы? 😉
Автор: Емелин Александр
izlov.ru