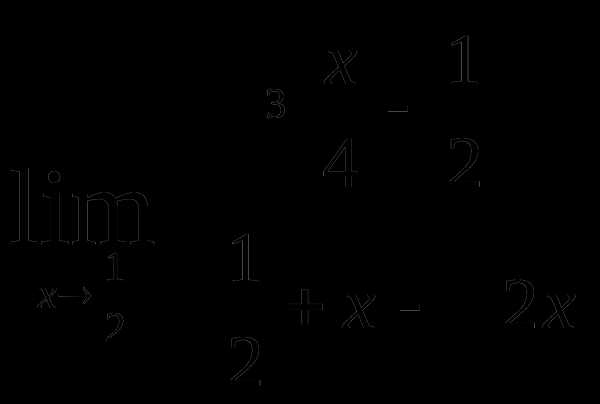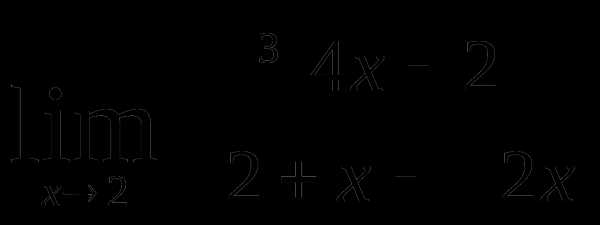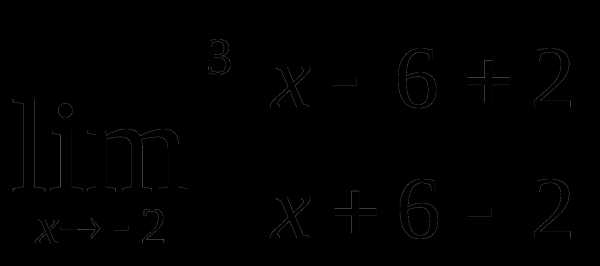Используя правило лопиталя найти предел онлайн – Как вычислить пределы функций, не пользуясь средствами дифференциального исчисления 🚩 вычислить предел не пользуясь правилом лопиталя 🚩 Математика
- Комментариев к записи Используя правило лопиталя найти предел онлайн – Как вычислить пределы функций, не пользуясь средствами дифференциального исчисления 🚩 вычислить предел не пользуясь правилом лопиталя 🚩 Математика нет
- Советы абитуриенту
Нахождение предела функции в точке по правилу Лопиталя
Калькулятор ниже находит предел функции по правилу Лопиталя (через производные числителя и знаменателя). Описание правила смотри ниже.
Допустимые операции: + – / * ^ Константы: pi Функции: sin cosec cos tg ctg sech sec arcsin arccosec arccos arctg arcctg arcsec exp lb lg ln versin vercos haversin exsec excsc sqrt sh ch th cth csch
Точка в которой необходимо посчитать предел
Точность вычисленияЗнаков после запятой: 2
Правило Лопиталя
Предел функции в точке
Сохранить share extension
Правило Лопиталя
Если выполняются следующие условия:
- пределы функций f(x) и g(x) равны между собой и равны нулю или бесконечности:
или ; - функции g(x) и f(x) дифференцируемы в проколотой окрестности a;
- производная функции g(x) не равна нулю в проколотой окрестности a
- и существует предел отношения производной f(x) к производной g(x):
Тогда существует предел отношения функций f(x) и g(x):
,
И он равен пределу отношения производной функции f(x) к производной функции g(x):
В формуле допускается использование числа пи (pi), экспоненты (e), следующих математических операторов:
+ — сложение
– — вычитание
* — умножение
/ — деление
^ — возведение в степень
и следующих функций:
- sqrt — квадратный корень
- rootp — корень степени p, например root3(x) – кубический корень
- exp — e в указанной степени
- lb — логарифм по основанию 2
- lg — логарифм по основанию 10
- ln — натуральный логарифм (по основанию e)
- logp — логарифм по основанию p, например log7(x) — логарифм по основанию 7
- sin — синус
- cos — косинус
- tg — тангенс
- ctg — котангенс
- sec — секанс
- cosec — косеканс
- arcsin — арксинус
- arccos — арккосинус
- arctg — арктангенс
- arcctg — арккотангенс
- arcsec — арксеканс
- arccosec — арккосеканс
- versin — версинус
- vercos — коверсинус
- haversin — гаверсинус
- exsec — экссеканс
- excsc — экскосеканс
- sh — гиперболический синус
- ch — гиперболический косинус
- th — гиперболический тангенс
- cth — гиперболический котангенс
- sech — гиперболический секанс
- csch — гиперболический косеканс
- abs — абсолютное значение (модуль)
- sgn — сигнум (знак)
skokaskoka.ru
§ 6 Вычисление пределов функций с помощью правила Лопиталя 6 1 Неопределенности и Правило Лопиталя – Решение
§6. Вычисление пределов функций
с помощью правила Лопиталя
6.1. Неопределенности и .
Правило Лопиталя: Предел отношения двух бесконечно малых или бесконечно больших функций равен пределу отношения их производных, если последний предел существует.
Буква над знаком равенства означает, что для вычисления предела применяется правило Лопиталя. В этих формулах х может стремиться и к бесконечности . Если после применения правила Лопиталя непределенность или сохраняется , то следует применить еще раз правило Лопиталя.
Пример 6.1. С помощью правила Лопиталя найти пределы.
Решение. 1)
.
2)
3)
4) Здесь лучше в знаменателе (в числителе нельзя!) использовать эквивалентность бесконечно малых, а затем применить правило Лопиталя.
Буква Э над знаком равенства означает применение эквивалентности бесконечно малых.
В последнем примере показано как разумно сочетать эквивалентность бесконечно малых и правило Лопиталя.
5)
6.2. Другие неопределенности.
а) Неопределенность приводится к виду с помощью равенства или к виду с помощью равенства .
б) Неопределенность приводят с помощью преобразования к виду , если . Если же , то предел равен (или ).
в) Непределенность 00 или приводятся к вышерассмотренным с помощью преобразования:
Неопределенность также можно раскрывать с помощью последнего преобразования, но лучше пользоваться формулами, приведенными в §2.
Пример 6.2. Найти пределы:
Решение. 1) Здесь неопределенность . Представим ее в виде .
2)
Здесь неопределенность мы преобразовали в неопределенность , затем использовали эквивалентность и правило Лопиталя.
3)
4)
.
Пример 6.3. Найти предел .
Решение. Здесь мы имеем неопределенность . Попробуем применить правило Лопиталя.
Последний предел не существует, то есть не существует . Это означает, что в данном случае мы имеем неопределенность , но мы не имеем право применять правило Лопиталя. Этот предел вычисляется так:
Так как , а , то
Пример 6.4. Найти пределы:
а) Найти пределы:
а) | б) |
Решение. В обоих примерах имеем неопределенность .
а) Здесь надо применить формулу
.
б) Здесь лучше применить формулу .
Задачи к §6.
Используя правило Лопиталя и эквивалентность, найти пределы.
241. | 242. | ||
243. | 244. | ||
245. | 246. | ||
247. | |||
248. | |||
249. | 250. | ||
251. | 252. | ||
253. | 254. | ||
255. | 256. | ||
257. | 258. | ||
259. | 260. | ||
261. | 262. | ||
263. | 264. | ||
265. | 266. | ||
§7. Индивидуальное домашнее задание (ИДЗ) по теме: “Предел и непрерывность”
Задача 1. Найти пределы:
1.1. | 1.2. |
1.3. | 1.4. |
1.5. | 1.6. |
1.7. | 1.8. |
1.9. | 1.10 |
1.11 | 1.12. |
1.13. | 1.14. |
1.15. | 1.16. |
1.17. | 1.18. |
1.19. | 1.20. |
1.21. | 1.22. |
1.23. | 1.24. |
1.25. | 1.26. |
1.27. | 1.28. |
1.29. | 1.30. |
Задача 2. Найти пределы.
2.1. | 2.2. | |||
2.3. | 2.4. | |||
2.5. | 2.6. | |||
2.7. | 2.8. | |||
2.9. | 2.10. | |||
2.11. | ||||
2.13. | ||||
2.14. | ||||
2.15. | ||||
2.16. | ||||
2.17. | ||||
2.18. | ||||
2.19. | ||||
2.20. 2.21. | ||||
2.22. | ||||
2.23. | ||||
2.25. | ||||
2.26. 2.27. | ||||
2.28. | ||||
2.29. | ||||
2.30. | ||||
Задача 3. Доказать непрерывность функции f(x) в точке x0.
3.1. f(x)=6-x2, x0=2 | 3.2. f(x)=3x2-2, x0=-2 |
3.3. f(x)=-2x2-3, x0=3 | 3.4. f(x)=2x2+5, x0=-3 |
3.5. f(x)=5x2-1, x0=4 | 3.6. f(x)=2-3x2, x0=4 |
3.7. f(x)=4x2-3, x0=-1 | 3.8. f(x)=4x2+5, x0=2 |
3.9. f(x)=x2+7, x0=-3 | 3.10. f(x)=7-2x2, x0=3 |
3.11. f(x)=-2x2-7, x0=2 | 3.12. f(x)=3x2+2, x0=4 |
3.13. f (x)=5x2+3, x0=-2 | 3.14. f(x)=4x2-1, x0=-3 |
3.15. f(x)=7x2-1, x0=4 | 3.16. f(x)=-8x2-1, x0=1 |
3.17. f(x)=2x2+11, x0=5 | 3.18. f(x)=10x2-3, x0=5 |
3.19. f(x)=13-2x2, x0=3 | 3.20. f(x)=3-10x2, x0=4 |
3.21. f(x)=4x2-11, x0=-2 | 3.22. f(x)=1-5x2, x0=2 |
3.23. f(x)=3-4x2, x0=1 | 3.24. f(x)=-7-x2, x0=1 |
3.25. f(x)=x2-6, x0=3 | 3.26. f(x)=9-5x2, x0=-2 |
3.27. f(x)=7-5x2, x0=-2 | 3.28. f(x)=-2x2-1, x0=3 |
3.29. f(x)=11-3x2, x0=2 | 3.30. f(x)=4x2-15, x0=-1 |
Задача 4. Найти пределы разложением на множители и по правилу Лопиталя.
4.1. | 4.2. |
4.3. | 4.4. |
4.5. | 4.6. |
4.7. | 4.8. |
4.9. | 4.10. |
4.11. | 4.12. |
4.13. | 4.14. |
4.15. | 4.16. |
4.17. | 4.18. |
4.19. | 4.20. |
4.21. | 4.22. |
4.23. | 4.24. |
4.25. | 4.26. |
4.27. | 4.28. |
4.29. | 4.30. |
Задача 5. Найти пределы, используя метод освобождения от иррациональности.
5.1. | 5.2. | |
5.3. | 5.4. | |
5.5. | 5.6. | |
5.7. | 5.8. | |
5.9. | 5.10. | |
5.11. | 5.12. | |
5.13. | 5.14. | |
5.15. | 5.16. | |
5.17. | 5.18. | |
5.19. | 5.20. | |
5.21. | ||
5.22. | 5.23. | |
5.24. | 5.25. | |
5.26. | 5.27. | |
5.28. | 5.29. | |
5.30. | ||
textarchive.ru
Пример 1. Найти предел
$$\lim _{x\rightarrow 1}\frac{x^2-1+\ln x}{e^x-e}.$$
Числитель и знаменатель стремится к нулю при \(x\rightarrow 1\) , а потому имеет неопределенность вида 0/0. Воспользуемся правилом Лопитоля, т.е. рассмотрим предел отношения производных заданных функций :
$$\lim _{x\rightarrow 1}\frac{x^2-1+\ln x}{e^x-e}=\lim _{x\rightarrow 1}\frac{2x+1/x}{e^x}=\frac{3}{e}.$$
Пример 2. Найти предел
$$\lim _{x\rightarrow 1}\frac{x-\sin x}{x^3}.$$
Это неопределенность вида 0/0. Имеем
$$\lim _{x\rightarrow 1}\frac{x-\sin x}{x^3}=\lim _{x\rightarrow 1}\frac{1-\cos x}{3x^2}=\lim _{x\rightarrow 1}\frac{\sin x}{6x}=\frac{1}{6},$$
так как \(\lim _{x\rightarrow 1}\frac{\sin x}{x}=1\) . Здесь правило Лопиталя применено дважды.
Пример 3. Найти предел
\(\lim _{x\rightarrow 1}\frac{x^n}{e^x}\), если \(n\) – целое положительно число.
Это – неопределенность вида \(\infty/\infty\) . Применим правило Лопиталя \(n\) раз :
$$\lim _{x\rightarrow 1}\frac{x^n}{e^x}=\lim _{x\rightarrow 1}\frac{nx^{n-1}}{e^x}=\lim _{x\rightarrow 1}\frac{n(n-1)x^{n-2}}{e^x}=…=\lim _{x\rightarrow 1}\frac{n(n-1)(n-2)…1}{e^x}=0.$$
Пример 4. Найти предел
$$\lim _{x\rightarrow \infty}\frac{xe^{x/2}}{x+e^x}$$
В данном случае так же имеет место неопределенность вида \(\infty/\infty\). Находим
$$\lim _{x\rightarrow \infty}\frac{xe^{x/2}}{x+e^x}=\lim _{x\rightarrow \infty}\frac{e^{x/2}(1+\frac{x}{2})}{1+e^x}=\lim _{x\rightarrow \infty}\frac{\frac{1}{2}e^{x/2}(2+\frac{x}{2})}{e^x}=$$
$$=\frac{1}{2}\lim _{x\rightarrow \infty}\frac{2+\frac{x}{2}}{e^{x/2}}=\frac{1}{2}\lim _{x\rightarrow \infty}\frac{1/2}{(1/2)e^{x/2}}=0.$$
Пример 5. Найти предел \(\lim _{x\rightarrow 0}(x^2\ln x).\)
Здесь мы имеем неопределенность вида \(0\cdot \infty.\) Представим произведение функций в виде частного, а затем, получив неопределенность вида \(\infty/ \infty\) , применим правило Лопиталя :
$$\lim _{x\rightarrow 0}(x^2\ln x)=\lim _{x\rightarrow 0}\frac{\ln x}{1/x^2}=\lim _{x\rightarrow 0}\frac{1/x}{-2/x^3}=-\frac{1}{2}\lim _{x\rightarrow 0}x^2=0.$$
Пример 6.Найти предел \(\lim _{x\rightarrow 0}(1+x)^{\ln x}.\)
Это неопределенность вида \(1^\infty\) . Логарифмируя и применяя правило Лопиталя, полчим
$$\lim _{x\rightarrow 0}\ln y=\lim _{x\rightarrow 0}(\ln x\ln (1+x))=\lim _{x\rightarrow 0}\frac{\ln (1+x)}{1/\ln x}=\lim _{x\rightarrow 0}\frac{1/(1+x)}{-1/(x\ln ^2x)}=$$
$$=-\lim _{x\rightarrow 0}\frac{x\ln ^2x}{x+1}=-\lim _{x\rightarrow 0}\frac{\ln ^2x}{1+1/x}=-\lim _{x\rightarrow 0}\frac{(2\ln x)/x}{-1/x^2}=2\lim _{x\rightarrow 0}\frac{\ln x}{1/x}=2\lim _{x\rightarrow 0}\frac{1/x}{-1/x^2}=0.$$
Таким образом, \(\lim _{x\rightarrow 0}y=e^0=1.\)
Пример 7. Найти предел \(\lim _{x\rightarrow \infty}(\sin x)^x.\)
Это неопределенность вида \( 0^0\) . Обозначив данную функцию через \(y\) , т.е. \(y=(\sin x)^x\) , и прологарифмируем ее:
$$\ln y=x\ln \sin x=\frac{\ln \sin x}{1/x}.$$
Вычислив предел логарифма данной функции, применяя правило Лопиталя (здесь имеем неопределенность вида \(\infty/\infty\) :
$$\lim _{x\rightarrow 0}\ln y=\lim _{x\rightarrow 0}\frac{\ln \sin x}{1/x}=\lim _{x\rightarrow 0}\frac{\cos x/ \sin x}{-1/x^2}=$$
$$=-\lim _{x\rightarrow 0}\frac{x^2\cos x}{\sin x}=-\lim _{x\rightarrow 0}(x\cdot \cos x\cdot \frac{x}{\sin x)}=0.$$
Следовательно, \(\lim _{x\rightarrow 0}y=e^0=1.\)
primat.org
Вычислить предел, используя правило Лопиталя
Поиск ЛекцийПервое правило Лопиталя
Рассмотрим функции , которые бесконечно малЫв некоторой точке . Если существует предел их отношений , то в целях устранения неопределённости можно взять две производные – от числителя и от знаменателя. При этом: , то есть при дифференцировании числителя и знаменателя значение предела не меняется.
Примечание: предел тоже должен существовать, в противном случае правило не применимо.
Что следует из вышесказанного?
Во-первых, необходимо уметь находить производные функций, и чем лучше – тем лучше =)
Во-вторых, производные берутся ОТДЕЛЬНО от числителя и ОТДЕЛЬНО от знаменателя. Пожалуйста, не путайте с правилом дифференцирования частного !!!
И, в-третьих, «икс» может стремиться куда угодно, в том числе, к бесконечности – лишь бы была неопределённость .
Вернёмся к Примеру 5 первой статьи о пределах, в котором был получен следующий результат:
К неопределённости 0:0 применим первое правило Лопиталя:
Как видите, дифференцирование числителя и знаменателя привело нас к ответу с пол оборота: нашли две простые производные, подставили в них «двойку», и оказалось, что неопределённость бесследно исчезла!
Не редкость, когда правила Лопиталя приходится применять последовательно два или бОльшее количество раз (это относится и ко второму правилу). Вытащим на ретро-вечер Пример 2 урока о замечательных пределах
:На двухъярусной кровати снова прохлаждаются два бублика. Применим правило Лопиталя:
Обратите внимание, что на первом шаге в знаменателе берётся производная сложной функции. После этого проводим ряд промежуточных упрощений, в частности, избавляемся от косинуса, указывая, что он стремится к единице. Неопределённость не устранена, поэтому применяем правило Лопиталя ещё раз (вторая строчка).
Я специально подобрал не самый простой пример, чтобы вы провели небольшое самотестирование. Если не совсем понятно, как найдены производные, следует усилить свою технику дифференцирования, если не понятен фокус с косинусом, пожалуйста, вернитесь к замечательным пределам. Не вижу особого смысла в пошаговых комментариях, так как о производных и пределах я уже рассказал достаточно подробно. Новизна статьи состоит в самих правилах и некоторых технических приёмах решения.
Как уже отмечалось, в большинстве случаев правила Лопиталя использовать не нужно, но их зачастую целесообразно применять для черновой проверки решения. Зачастую, но далеко не всегда. Так, например, только что рассмотренный пример значительно выгоднее проверить через
Второе правило Лопиталя
Брат-2 борется с двумя спящими восьмёрками . Аналогично:
Если существует предел отношения бесконечно большихв точке функций: , то в целях устранения неопределённости можно взять две производные – ОТДЕЛЬНО от числителя и ОТДЕЛЬНО от знаменателя. При этом: , то есть при дифференцировании числителя и знаменателя значение предела не меняется.
Примечание: предел должен существовать
Опять же, в различных практических примерах значениеможет быть разным , в том числе, бесконечным. Важно, чтобы была неопределённость .
Проверим Пример №3 первого урока: . Используем второе правило Лопиталя:
Однако для Примера №2 той же статьи проверка данным способом будет весьма муторна. Тут придётся использовать правило Лопиталя три раза подряд (экспериментаторы могут попробовать). На самом деле ответ лежит на поверхности и почти мгновенно определяется устно (см. статью Методы решения пределов).
Коль скоро речь зашла о великанах, разберём два каноничных предела:
Пример 1
Вычислить предел
Получить ответ «обычными» методами непросто, поэтому для раскрытия неопределённости «бесконечность на бесконечность» используем правило Лопиталя:
Таким образом, линейная функцияболее высокого порядка роста, чем логарифм с основанием бОльшим единицы( и т.д.). Разумеется, «иксы» в старших степенях тоже будут «перетягивать» такие логарифмы. Действительно, функция растёт достаточно медленно и её
Пример 2
Вычислить предел
Ещё один примелькавшийся кадр. В целях устранения неопределённости , используем правило Лопиталя, причём, два раза подряд:
Показательная функция, с основанием, бОльшим единицы( и т.д.)более высокого порядка роста, чем степенная функция с положительной степенью.
Похожие пределы встречаются в ходе полного исследования функции, а именно, при нахождении асимптот графиков. Также замечаются они и в некоторых задачах по теории вероятностей. Советую взять на заметку два рассмотренных примера, это один из немногих случаев, когда лучше дифференцирования числителя и знаменателя ничего нет.
Далее по тексту я не буду разграничивать первое и второе правило Лопиталя, это было сделано только в целях структурирования статьи. Вообще, с моей точки зрения, несколько вредно излишне нумеровать математические аксиомы, теоремы, правила, свойства, поскольку фразы вроде «согласно следствию 3 по теореме 19…» информативны только в рамках того или иного учебника. В другом источнике информации то же самое будет «следствием 2 и теоремой 3». Такие высказывания формальны и удобны разве что самим авторам. В идеале лучше ссылаться на суть математического факта. Исключение – исторически устоявшиеся термины, например, первый замечательный предел или второй замечательный предел.
Продолжаем разрабатывать тему, которую нам подкинул член Парижской академии наук маркиз Гийом Франсуа де Лопиталь. Статья приобретает ярко выраженную практическую окраску и в достаточно распространённом задании требуется:
Вычислить предел, используя правило Лопиталя
Пример 3
Вычислить предел по правилу Лопиталя
Предел можно предварительно упростить, избавившись от косинуса, однако проявим уважение к условию и сразу продифференцируем числитель и знаменатель:
В самом процессе нахождения производных нет чего-то нестандартного, так, в знаменателе использовано обычное правило дифференцирования произведения .
Пример 4
Вычислить предел по правилу Лопиталя
Пример 4
Пример 5
Вычислить предел, используя правило Лопиталя
Напрашивается применение замечательной эквивалентности, но путь жёстко предопределён по условию:
После дифференцирования настоятельно рекомендуюизбавляться от многоэтажности дробии проводить максимальные упрощения. Конечно, более подготовленные студенты могут пропустить последний шаг и сразу записать: , но в некоторых пределах запутаются даже отличники.
Пример 6
Вычислить предел, используя правило Лопиталя
Пример 6
Пример 7
Вычислить предел, используя правило Лопиталя
Пример 7
Пример 8
Вычислить предел, используя правило Лопиталя
Поехали:
Интересно, что первоначальная неопределённость после первого дифференцирования превратилась в неопределённость , и правило Лопиталя невозмутимо применяется дальше. Также заметьте, как после каждого «подхода» устраняется четырёхэтажная дробь, а константы выносятся за знак предела. В более простых примерах константы удобнее не выносить, но когда предел сложный, упрощаем всё-всё-всё. Коварство решённого примера состоит ещё и в том, что при , а , поэтому в ходе ликвидации синусов немудрено запутаться в знаках. В предпоследней строчке синусы можно было и не убивать, но пример довольно тяжелый, простительно.
На днях мне попалось любопытное задание:
Пример 9
Вычислить предел функции, используя правило Лопиталя
Если честно, немного засомневался, чему будет равен данный предел. Как демонстрировалось выше, «икс» более высокого порядка роста, чем логарифм, но «перетянет» ли он логарифм в кубе? Постарайтесь выяснить самостоятельно, за кем будет победа.
Да, правила Лопиталя – это не только пальба по воробьям из пушки, но ещё и кропотливая работа….
В целях применения правил Лопиталя к бубликам или уставшим восьмёркам сводятся неопределённости вида .
Расправа с неопределённостью подробно разобрана в Примерах №№9-13 урока Методы решения пределов. Давайте для проформы ещё один:
Пример 10
Вычислить предел функции, используя правило Лопиталя
На первом шаге приводим выражение к общему знаменателю, трансформируя тем самым неопределённость в неопределённость . А затем заряжаем правило Лопиталя:
Здесь, к слову, тот случай, когда четырёхэтажное выражение трогать бессмысленно.
Неопределённость тоже не сопротивляется превращению в или :
Пример 11
Вычислить предел функции с помощью правила Лопиталя
Предел здесь односторонний, и о таких пределах уже шла речь в методичке Графики и свойства функций. Как вы помните, графика «классического» логарифма не существует слева от оси , таким образом, мы можем приближаться к нулю только справа.
Правила Лопиталя для односторонних пределов работают, но сначала необходимо разобраться с неопределённостью . На первом шаге делаем дробь трёхэтажной, получая неопределённость , далее решение идёт по шаблонной схеме:
После дифференцирования числителя и знаменателя избавляемся от четырёхэтажной дроби, чтобы провести упрощения. В результате нарисовалась неопределённость . Повторяем трюк: снова делаем дробь трёхэтажной и к полученной неопределённости применяем правило Лопиталя ещё раз:
Готово.
Исходный предел можно было попытаться свести к двум бубликам:
Но, во-первых, производная в знаменателе труднее, а во-вторых, ничего хорошего из этого не выйдет.
Таким образом, перед решением похожих примеров нужно проанализировать (устно либо на черновике), К КАКОЙ неопределённости выгоднее свести – к «нулю на ноль» или к «бесконечности на бесконечность».
В свою очередь на огонёк подтягиваются собутыльники и более экзотические товарищи . Метод трансформации прост и стандартен:
Пример 12
Вычислить предел функции с помощью правила Лопиталя
Для устранения неопределённости используем основное логарифмическое тождество: . В данном случае :
На предпоследнем шаге, согласно известному школьному свойству, «сносим» синус из степени за пределы логарифма, получая произведение . На последнем шаге перемещаем значок предела в показатель (поскольку экспоненциальная функция непрерывна, да и предел относится, прежде всего, к верхнему этажу).
Чтобы не мельчить, вычислим предел показателя отдельно:
С неопределённостью разбираемся уже знакомым способом – делаем дробь трёхэтажной, получая долгожданную неопределённость , к которой применимо правило Лопиталя:
Метаморфозы продолжаются, теперь вылезла неопределённость «ноль на ноль». В принципе, можно избавиться от косинуса, указав, что он стремится к единице. Но мудрая стратегия заключается в том, чтобы никто ни до чего не докопался. Поэтому сразу применим правило Лопиталя, как этого требует условие задачи:
Не торопитесь, предел не равен нулю! Мы вычислили только предел показателя. В конце решения главное не забыть про экспоненту, я сейчас сам чуть про неё не забыл =) Окончательно:
В ряде случаев после использование основного логарифмического тождества удаётся миновать неопределённость :
Пример 13
Вычислить предел по правилу Лопиталя
Очередной папуас тоже сдаётся перед формулой . В данном случае :
В результате сразу получена неопределённость , что облегчает задачу. Предел показателя для удобства вычислим отдельно:
В итоге:
Аналогичное задание для самостоятельного решения:
Пример 14
Вычислить предел по правилу Лопиталя
Полное решение и ответ в конце урока.
Предел с неопределённостью по правилу Лопиталя, если честно, у себя не нашёл, но для полноты картины решим многострадальный шестой пример урока Замечательные пределы:
Пример 15
Вычислить с помощью правила Лопиталя
Рекомендуемые страницы:
poisk-ru.ru