Как умножить матрицы – Как умножить вектор на матрицу 🚩 умножение матрица на вектор 🚩 Математика

Как умножать матрицы

Матрицы, действия с матрицами

Операции над матрицами, свойства операций.


В этой статье мы разберемся как проводится операция сложения над матицами одного порядка, операция умножения матрицы на число и операция умножения матриц подходящего порядка, аксиоматически зададим свойства операций, а также обсудим приоритет операций над матрицами. Параллельно с теорией будем приводить подробные решения примеров, в которых выполняются операции над матрицами.

Сразу заметим, что все нижесказанное относится к матрицам, элементами которых являются действительные (или комплексные) числа.


Операция сложения двух матриц.

Определение операции сложения двух матриц.

Операция сложения определена ТОЛЬКО ДЛЯ МАТРИЦ ОДНОГО ПОРЯДКА. Другими словами, нельзя найти сумму матриц разной размерности и вообще нельзя говорить о сложении матриц разной размерности. Также нельзя говорить о сумме матрицы и числа или о сумме матрицы и какого-нибудь другого элемента.

Как умножить матрицы

Таким образом, результатом операции сложения двух матриц является матрица того же порядка.

Свойства операции сложения матриц.

Какими же свойствами обладает операция сложения матриц? На этот вопрос достаточно легко ответить, отталкиваясь от определения суммы двух матриц данного порядка и вспомнив свойства операции сложения действительных (или комплексных) чисел.

  1. Для матриц А, В и С одного порядка характерно свойство ассоциативности сложения А+(В+С)=(А+В)+С.
  2. Для матриц данного порядка существует нейтральный элемент по сложению, которым является нулевая матрица. То есть, справедливо свойство А+О=А.
  3. Для ненулевой матрицы А данного порядка существует матрица (–А), их суммой является нулевая матрица: А+(-А)=О.
  4. Для матриц А и В данного порядка справедливо свойство коммутативности сложения А+В=В+А.

Следовательно, множество матриц данного порядка порождает аддитивную группу Абеля (абелеву группу относительно алгебраической операции сложения).

Сложение матриц — решения примеров.

Рассмотрим несколько примеров сложения матриц.

Найдите сумму матриц и .

Порядки матриц А и В совпадают и равны 4 на 2, поэтому мы можем проводить операцию сложения матриц и в результате должны получить матрицу порядка 4 на 2. Согласно определению операции сложения двух матриц, сложение производим поэлементно:

Найдите сумму двух матриц и элементами которых являются комплексные числа.

Так как порядки матриц равны, то мы можем выполнить сложение.

Выполните сложение трех матриц .

Сначала сложим матрицу А с В, затем к полученной матрице прибавим С:

Получили нулевую матрицу.

К началу страницы

Операция умножения матрицы на число.


Определение операции умножения матрицы на число.

Операция умножения матрицы на число определена ДЛЯ МАТРИЦ ЛЮБОГО ПОРЯДКА.

Таким образом, результатом умножения матрицы на число является матрица того же порядка.

Свойства операции умножения матрицы на число.

  1. Для матриц одного порядка А и В, а также произвольного действительного (или комплексного) числа справедливо свойство дистрибутивности умножения относительно сложения .
  2. Для произвольной матрицы А и любых действительных (или комплексных) чисел и выполняется свойство дистрибутивности .
  3. Для произвольной матрицы А и любых действительных (или комплексных) чисел и справедливо свойство ассоциативности умножения .
  4. Нейтральным числом по умножению на произвольную матрицу А является единица, то есть, .

Из свойств операции умножения матрицы на число следует, что умножение нулевой матрицы на число ноль даст нулевую матрицу, а произведение произвольного числа и нулевой матрицы есть нулевая матрица.

Умножение матрицы на число — примеры и их решение.

Разберемся с проведением операция умножения матрицы на число на примерах.

Найдите произведение числа 2 и матрицы .

Чтобы умножить матрицу на число, нужно каждый ее элемент умножить на это число:

Выполните умножение матрицы на число .

Умножаем каждый элемент заданной матрицы на данное число:

К началу страницы

Операция умножения двух матриц.

Определение операции умножения двух матриц.

Операция умножения двух матриц А и В определяется только для случая, когда ЧИСЛО СТОЛБЦОВ МАТРИЦЫ А РАВНО ЧИСЛУ СТРОК МАТРИЦЫ В.

Таким образом, результатом операции умножения матрицы порядка на матрицу порядка является матрица порядка .

Умножение матрицы на матрицу — решения примеров.

Разберемся с умножением матриц на примерах, после этого перейдем к перечислению свойств операции умножения матриц.

Выполните умножение матриц и .

Порядки исходных матриц позволяют провести операцию умножения. В результате мы должны получить матрицу порядка 2 на 3.

Даны матрицы и . Найдите произведение матриц А и В, а также матриц В и А.

Так как порядок матрицы А равен 3 на 1, а матрицы В равен 1 на 3, то А⋅В будет иметь порядок 3 на 3, а произведение матриц В и A будет иметь порядок 1 на 1.

Как видите, . Это одно из свойств операции умножения матриц.

Свойства операции умножения матриц.

Если матрицы А, В и С подходящих порядков, то справедливы следующие свойства операции умножения матриц.

  1. Свойство ассоциативности умножения матриц .
  2. Два свойства дистрибутивности и .
  3. В общем случае операция умножения матриц некоммутативна .
  4. Единичная матрица Е порядка n на n является нейтральным элементом по умножению, то есть, для произвольной матрицы А порядка p на n справедливо равенство , а для произвольной матрицы А порядка n на p — равенство .

Следует отметить, что при подходящих порядках произведение нулевой матрицы О на матрицу А дает нулевую матрицу. Произведение А на О также дает нулевую матрицу, если порядки позволяют проводить операцию умножения матриц.

Среди квадратных матриц существуют так называемые перестановочные матрицы, операция умножения для них коммутативна, то есть . Примером перестановочных матриц является пара единичной матрицы и любой другой матрицы того же порядка, так как справедливо .

К началу страницы

Приоритет операций над матрицами.

Операции умножения матрицы на число и умножения матрицы на матрицу наделены равным приоритетом. В то же время эти операции имеют приоритет выше, чем операция сложения двух матриц. Таким образом, сначала выполняется умножение матрицы на число и умножение матриц, а уже потом производится сложение матриц. Однако, порядок выполнения операций над матрицами может быть задан явно с помощью скобок.

Итак, приоритет операций над матрицами аналогичен приоритету, присвоенному операциям сложения и умножения действительных чисел.

К началу страницы

Следует заметить, что операции вычитания матриц одного порядка А и В как таковой не существует. Разность двух матриц по сути есть сумма матрицы А и матрицы В, предварительно умноженной на минус единицу: .

Операция возведения квадратной матрицы в натуральную степень так же не самостоятельна, так как является последовательным умножением матриц.

Подведем итог.

На множестве матриц определены три операции: сложение матриц одного порядка, умножение матрицы на число и умножение матриц подходящих порядков. Операция сложения на множестве матриц данного порядка порождает группу Абеля.

Некогда разбираться?

Закажите решение

Профиль автора статьи в Google+

К началу страницы

Сумма двух матриц и — это матрица, элементы которой равны сумме соответствующих элементов матриц А и В, то есть, .

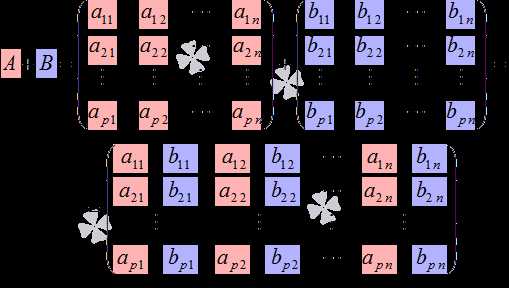
Произведение матрицы и действительного (или комплексного) числа — это матрица, элементы которой получаются умножением соответствующих элементов исходной матрицы на число , то есть, .

Произведение матрицы А порядка и матрицы В порядка — это такая матрица С порядка , каждый элемент которой равен сумме произведений элементов i-ой строки матрицы А на соответствующие элементы j-ого столбца матрицы В, то есть,

laservirta.ru

Как умножить три матрицы?

Как умножить три матрицы?

Прежде всего, ЧТО должно получиться в результате умножения трёх матриц ? Кошка не родит мышку. Если матричное умножение осуществимо, то в итоге тоже получится матрица. М-да, хорошо мой преподаватель по алгебре не видит, как я объясняю замкнутость алгебраической структуры относительно её элементов =)

Произведение трёх матриц можно вычислить двумя способами:

1) найти , а затем домножить на матрицу «цэ»: ;

2) либо сначала найти , потом выполнить умножение .

Результаты обязательно совпадут, и в теории данное свойство называют ассоциативностью матричного умножения

:

Пример 6

Перемножить матрицы двумя способами

Алгоритм решения двухшаговый: находим произведение двух матриц, затем снова находим произведение двух матриц.

1) Используем формулу

Действие первое:

Действие второе:

2) Используем формулу

Действие первое:

Действие второе:

Ответ:

Более привычен и стандартен, конечно же, первый способ решения, там «как бы всё по порядку». Кстати, по поводу порядка. В рассматриваемом задании часто возникает иллюзия, что речь идёт о каких-то перестановках матриц. Их здесь нет. Снова напоминаю, что в общем случае ПЕРЕСТАВЛЯТЬ МАТРИЦЫ НЕЛЬЗЯ. Так, во втором пункте на втором шаге выполняем умножение , но ни в коем случае не . С обычными числами такой бы номер прошёл, а с матрицами – нет.

Свойство ассоциативности умножения справедливо не только для квадратных, но и для произвольных матриц – лишь бы они умножались:

Пример 7

Найти произведение трёх матриц

Это пример для самостоятельного решения. В образце решения вычисления проведены двумя способами, проанализируйте, какой путь выгоднее и короче.

Свойство ассоциативности матричного умножения имеет место быть и для бОльшего количества множителей.

Теперь самое время вернуться к степеням матриц. Квадрат матрицы рассмотрен в самом начале и повестке дня вопрос:

Дата добавления: 2015-08-27; просмотров: 52 | Нарушение авторских прав

Свойства определителя | При транспонировании матрицы величина её определителя не меняется | Если две строки (или два столбца) определителя поменять местами, то определитель сменит знак | Из строки (столбца) определителя можно вынести общий множитель | Если две строки (столбца) определителя пропорциональны (как частный случай – одинаковы), то данный определитель равен нулю | К строке определителя можно прибавить другую строку, умноженную на ненулевое число. При этом величина определителя не изменится | К столбцу определителя можно прибавить другой столбец, умноженный на ненулевое число. При этом величина определителя не изменится | Можно ли к матрице прибавить число? | Как возвести матрицу в квадрат? | Немного о некоммутативности матричного умножения и единичной матрице |
mybiblioteka.su – 2015-2018 год. (0.006 сек.)

mybiblioteka.su

Как умножить матрицу на матрицу

Умножение матриц отличается от обычного умножения чисел или переменных из-за структуры участвующих в операции элементов, поэтому здесь есть свои правила и особенности.

Спонсор размещения P&G Статьи по теме “Как умножить матрицу на матрицу” Как перемножать матрицы Как считать матрицы Как находить ранг матрицы

Инструкция

1

Самая простая и краткая формулировка этой операции такова: матрицы перемножаются по алгоритму “строка на столбец”.

Теперь подробнее об этом правиле, а также о возможных ограничениях и особенностях.

Умножение на единичную матриц переводит исходную матрицы саму в себя (эквивалентно умножению чисел, где один из элементов 1). Аналогично, умножение на нулевую матрицу даёт нулевую матрицу.

Главное условие, накладываемое на участвующие в операции матрицы вытекает из способа выполнения умножения: строк в первой матрице должно быть столько же, сколько столбцов во второй. Нетрудно догадаться, что в противном случае умножать будет просто не на что.

Также стоит отметить ещё один важный момент: у умножения матриц нет свойства коммутативности (или “перестановочности”), иначе говоря, А умножить на B не равняется B умножить на А. Запомните это и не путайте с правилом для умножения чисел.

2

Теперь, собственно сам процесс умножения.

Пусть мы умножаем матрицу А на матрицу B справа.

Берём первую строчку матрицы А и ее i-ый элемент умножаем на i-ый элемент первого столцба матрицы B. Все полученные произведения складываем и записываем на место а11 в итоговую матрицу.

Далее первую строку матрицы А аналогичным образом умножаем на второй столбец матрицы В, а получившийся результат записываем справа от первого полученного числа в итоговую матрицу, то есть на позицию а12.

Затем также поступаем с первой строкой матрицы А и 3-им, 4-ым и т.д. столбцами матрицы Б, заполнив, таким образом, первую строчку итоговой матрицы.

3

Теперь переходим ко второй строке и снова перемножаем её последовательно на все столбцы, начиная с первого. Записываем результат во вторую строку итоговой матрицы.

Затем к 3-ей, 4-ой и т.д.

Повторяем действия, пока не перемножим все строки в матрице А со всеми столбцами матрицы В.

Как просто

masterotvetov.com

Как умножать матрицы Как? Так!

Содержимое:

Матрица представляет собой прямоугольное расположение чисел, символов или выражений в строках и столбцах. Чтобы умножить матрицы, вам нужно умножить элементы (или числа) в строках первой матрицы на элементы в столбцах второй матрицы и сложить полученные значения. Для умножения матриц потребуется умножение, сложение и правильная расстановка результатов.

Шаги

  1. 1 Умножение матриц. В данной статье рассматривается умножение матриц равных размеров, то есть таких, у которых число строк первой матрицы равно числу строк второй матрицы.
    • На рисунке: первая матрица А имеет две строки, и вторая матрица B имеет два столбца.
  2. 2 Обозначьте размеры конечной матрицы. Нарисуйте новую пустую матрицу, которая будет конечной матрицей – результатом произведения первой матрицы на вторую. Конечная матрица имеет столько же строк, как матрица А, и столько же столбцов, как матрица В.
    • Матрица А имеет 2 строки, поэтому конечная матрица будет иметь 2 строки.
    • Матрица B имеет 2 столбца, поэтому конечная матрица будет иметь 2 столбца.
    • Конечная матрица будет иметь 2 строки и 2 столбца.
  3. 3 Найдите первое скалярное произведение. Для этого умножьте первый элемент первой строки на первый элемент первого столбца, второй элемент первой строки на второй элемент первого столбца, третий элемент первой строки на третий элемент первого столбца. Потом сложите полученные значения. Например, умножим вторую строку на второй столбец (и найдем четвертое скалярное произведение):
    • 6 x -5 = -30
    • 1 x 0 = 0
    • -2 x 2 = -4
    • -30 + 0 + (-4) = -34
    • Четвертое скалярное произведение равно (-34) и оно записывается в правом нижнем углу конечной матрицы.
      • Результат скалярного произведения записывается согласно номерам умножаемой строки и столбца. Например, когда вы нашли скалярное произведение второй строки (матрица А) и второго столбца (матрица B), результат (-34) записывается на пересечении второй строки и второго столбца конечной матрицы.
  4. 4 Найдите второе скалярное произведение. Для этого умножьте элементы второй строки первой матрицы на элементы первого столбца второй матрицы, а затем сложите результаты.
    • 6 x 4 = 24
    • 1 x (-3) = -3
    • (-2) x 1 = -2
    • 24 + (-3) + (-2) = 19
    • Второе скалярное произведение равно (-19), и оно записывается на пересечении второй строки и первого столбца конечной матрицы.
  5. 5 Найдите оставшиеся скалярные произведения. Первое скалярное произведение вычисляется умножением элементов первой строки на элементы первого столбца:
    • 2 x 4 = 8
    • 3 x (-3) = -9
    • (-1) x 1 = -1
    • 8 + (-9) + (-1) = -2
    • Первое скалярное произведение равно (-2), и оно записывается на пересечении первой строки и первого столбца конечной матрицы.
      • Третье скалярное произведение вычисляется умножением элементов первой строки на элементы второго столбца:
    • 2 x (-5) = -10
    • 3 x 0 = 0
    • (-1) x 2 = -2
    • -10 + 0 + (-2) = -12
    • Третье скалярное произведение равно (-12), и оно записывается на пересечении первой строки и второго столбца конечной матрицы.
  6. 6 Убедитесь, что результаты всех четырех скалярных произведений правильно расставлены.

Советы

  • Результат произведения двух матриц имеет столько же строк, как первая матрица, и столько же столбцов, как вторая матрица.
  • Записывайте ваши вычисления. Умножение матриц включает много расчетов, в которых легко запутаться.

Прислал: Николаева Кристина . 2017-11-12 13:11:10

kak-otvet.imysite.ru

Related Posts

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *