Квантовая механика для начинающих – Квантовая механика для всех, даром, и пусть никто не уйдёт обиженным: часть первая / Хабр
- Комментариев к записи Квантовая механика для начинающих – Квантовая механика для всех, даром, и пусть никто не уйдёт обиженным: часть первая / Хабр нет
- Советы абитуриенту
Квантовая механика для всех, даром, и пусть никто не уйдёт обиженным: часть первая / Хабр
Здравствуйте! Я хотел бы представить вашему вниманию отличное введение в квантовую механику, написанное Элиезером Юдковским; быть может, он известен вам по своему сайту lesswrong.com, посвящённому рационализму, предрассудкам, когнитивным парадоксам и ещё многим интересным вещам.читать вторую часть →
Предупреждаю сразу: этот цикл статей заметно отличается от традиционного введения в квантовую механику.
Во-первых, я не буду цитировать Ричарда Фейнмана, однажды заявившего, что «это нормально — не понимать квантовую механику, потому что никто её не понимает». Когда-то это было так, но времена меняются.
Я не скажу: «Квантовую механику невозможно понять, к ней просто нужно привыкнуть». (Эту цитату приписывают Джону фон Нейману; он жил в те дремучие времена, когда никто и в самом деле не понимал квантовую механику.)
Нельзя заканчивать объяснение словами «Если что-то непонятно, так и должно быть». Нет, так не должно быть
Я не буду говорить, что квантовая механика — это нечто странное, запутанное или недоступное для человеческого понимания. Да, она контринтуитивна — но это беда исключительно нашей интуиции. Квантовая механика возникла задолго до Солнца, планеты Земля или человеческой цивилизации. Она не собирается меняться ради вас. Вообще, не существует обескураживающих фактов, есть только теории, обескураженные фактами; а если теория не совпадает с практикой, это не делает ей чести.
Всегда стоит рассматривать реальность как совершенно обыденную вещь. С начала времён во Вселенной не случилось ничего необычного.
Наша цель — научиться чувствовать себя как дома в этом квантовом мире. Потому что мы и так дома.
На протяжении всего этого цикла я буду говорить о квантовой механике как о самой обычной теории; а там, где интуитивное представление о мире не совпадает с ней, я буду высмеивать интуицию за несоответствие реальности.
Во-вторых, я не собираюсь следовать традиционному порядку изучения квантовой механики, копирующему порядок, в котором её открывали.
Обычно всё начинается с рассказа о том, что материя иногда ведёт себя как кучка маленьких бильярдных шаров, сталкивающихся между собой, а иногда — как волны на поверхности бассейна. Это сопровождается несколькими примерами, иллюстирующими оба взгляда на материю.
Раньше, когда всё это только зарождалось и никто не имел ни малейшего понятия о математических основах физики, учёные всерьёз считали, что всё состоит из атомов, ведущих себя примерно как бильярдные шары. А потом они стали считать, что всё состоит из волн. А потом они опять вернулись к бильярдным шарам. Всё это привело к тому, что учёные
Если применить этот исторический достоверный подход к обучению современных студентов (как сейчас и поступают), с ними закономерно случится то же, что случилось с ранними учёными, а именно — они впадут в полное и абсолютное замешательство. Рассказывать студентам, изучающим физику, о корпускулярно-волновом дуализме, это то же самое, что начинать курс химии лекцией о четырёх стихиях.
Электрон не похож ни на бильярдный шар, ни на гребень океанской волны. Электрон — это совершенно другой объект с математической точки зрения, и он остаётся таким при любых обстоятельствах. А если вы будете упорствовать в своём стремлении считать его и тем, и тем, как вам удобнее, предупреждаю: за двумя зайцами погонишься — ни одного не поймаешь.
Это не единственная причина, по которой исторический порядок — не лучший выбор. Давайте проследим за гипотетическим процессом с самого начала: люди замечают, что они окружены другими животными — внутри животных, оказывается, есть органы — а органы, если присмотреться внимательнее, состоят из тканей — под микроскопом видно, что ткани состоят из клеток — клетки состоят из протеинов и прочих химических соединений — химические соединения состоят из атомов — атомы состоят из протонов, нейтронов и электронов — а последние гораздо проще и понятнее животных, с которых всё началось, но были открыты на десятки тысяч лет позже.
Физику не начинают проходить с биологии. Тогда почему её нужно начинать с обсуждения лабораторных экспериментов и их результатов, которые даже в случае простейших опытов являются следствием множества сложных и запутанных процессов?
С одной стороны, я могу понять, почему во главу угла ставится эксперимент. Мы же о физике говорим, в конце концов.
С другой стороны, давать студентам в руки сложный математический аппарат только для того, чтобы они могли проанализировать простой опыт —
Классическая механика не следует явным образом из квантовой механики. Более того, классическая механика находится на гораздо более высоком уровне. Сравните атомы и молекулы с кварками: миллионы известных науке химических веществ, сотня химических элементов, и всего шесть кварков. Сначала лучше понять простое, а только потом переходить к сложному.
Наконец, я буду рассматривать квантовую механику со строго реалистической позиции — наш мир является квантовым, наши уравнения описывают территорию, а не её карту, и привычный нам мир неявным образом существует в квантовом мире. Если среди моих читателей есть антиреалисты — пожалуйста, придержите свои комментарии. Квантовую механику гораздо труднее понять и представить, если сомневаешься в её справедливости. Я поговорю об этом подробнее в одной из следующих статей.
Я думаю, что той точки зрения, которую я буду излагать в этом введении, придерживается большинство физиков-теоретиков. Но вы всё же должны знать, что это не единственная возможная точка зрения, и немалая доля учёных сомневается в верности реалистической позиции. Хоть я и не собираюсь уделять внимание каким-либо другим теориям прямо сейчас, я чувствую себя обязанным упомянуть о том, что они есть.
Подводя итог, моя цель — научить вас думать как коренной житель квантового мира, а не как турист поневоле.
Покрепче вцепитесь в реальность. Мы начинаем.
Посмотрите на рис. 1. В точке A находится полупосеребрённое зеркало, а в точках B и C — два детектора фотонов.
Этот простой эксперимент в своё время заставил учёных поломать головы. Дело в том, что в половине случаев фотон, выпущенный в сторону зеркала, регистрировался первым детектором, а в половине — на вторым. И учёные — внимание, приготовьтесь смеяться — предполагали, что зеркало то пропускало фотон, то отражало его.
Ха-ха-ха, представьте себе зеркало, которое может само выбирать, пропускать ему фотон или не пропускать! Если вы и можете это представить, то все равно не делайте этого — а не то вы запутаетесь так же, как и те учёные. Зеркало ведёт себя абсолютно одинаково в обоих случаях.
Если бы мы попробовали написать компьютерную программу, симулирующую этот эксперимент (а не просто предсказывающую результат), она бы выглядела примерно так…
В начале программы мы объявляем переменную, хранящую в себе определённый математический объект — конфигурацию. Она представляет некое описание состояния мира — в данном случае, «один фотон летит в точку А».
На самом деле конфигурация описывается комплексным числом (напомню, что комплексные числа имеют вид (a + b i), где a и b — действительные числа, а i — мнимая единица, т.е. такое число, что i² = -1). Нашей конфигурации «фотон летит в точку A» тоже соответствует какое-то число. Пусть это будет (-1 + 0i). В дальнейшем мы будем называть число, соответствующее конфигурации, её амплитудой.
Введём ещё две конфигурации: «фотон летит из A в точку B» и «фотон летит из A в точку C». Мы пока не знаем амплитуды этих конфигураций; им будут присвоены значения в ходе выполнения программы.
Посчитать амплитуды можно, применив правило, по которому работает зеркало, к начальной конфигурации. Не вдаваясь в подробности, можно считать, что правило выглядит так: «умножить на 1, когда фотон пролетает; умножить на i, когда фотон отражается». Применим правило: амплитуда конфигурации «фотон летит в
В принципе, можно считать «первый детектор регистрирует фотон» и «второй детектор регистрирует фотон» отдельными конфигурациями, но это ничего не меняет; их амплитуды будут равны амплитудам двух предыдущих конфигураций соответственно. (На самом деле их ещё надо домножить на множитель, равный расстоянию от A до детекторов, но мы просто предположим, что все расстояния в нашем эксперименте являются множителями единицы.)
Итак, вот конечное состояние программы:
- «фотон летит в A»: (-1 + 0i)
- «фотон летит из A в B»: (0 + –i)
- «фотон летит из A в C»: (-1 + 0i)
И, возможно:
- «сработал первый детектор»: (0 + –i)
- «сработал второй детектор»: (-1 + 0i)
Разумеется, сколько бы раз мы ни запускали программу, конечное состояние останется таким же.
Теперь, по довольно сложным причинам, в которые я пока не буду вдаваться, не существует простого способа измерить амплитуду конфигурации. Состояние программы скрыто от нас.
Что же делать?
Хоть мы и не можем измерить амплитуду непосредственно, кое-что у нас есть — а именно, волшебная измерительная штуковина, которая может сообщить нам квадрат модуля амплитуды конфигурации. Другими словами, для амплитуды (a + bi) штуковина ответит числом (a² + b²).
Точнее было бы сказать, что волшебная штуковина находит всего лишь отношение квадратов модулей друг к другу. Но даже этой информации оказывается достаточно, чтобы понять, что происходит внутри программы и по каким законам она работает.
С помощью штуковины мы можем легко узнать, что квадраты модулей конфигураций «сработал первый детектор» и «сработал второй детектор» равны. А проведя некоторые более сложные эксперименты, мы сможем также узнать отношение самих амплитуд — i к 1.
Кстати, а что это за волшебная измерительная штуковина такая?
Ну, когда такие эксперименты проводят в реальной жизни, в качестве волшебной штуковины служит то, что эксперимент проводят пару тысяч раз и просто считают, сколько раз фотон оказался в первом детекторе, а сколько — во втором. Отношение этих значений и будет отношением квадратов модулей амплитуд. Почему это будет так — вопрос другой, гораздо более сложный. А пока можно пользоваться штуковиной и без понимания того, как да почему она работает. Всему своё время.
Вы можете спросить: «А зачем вообще нужна квантовая теория, если её предсказания совпадают с предсказаниями „бильярдной” теории?» Есть две причины. Во-первых, реальность, что бы вы там ни думали, всё-таки подчиняется квантовым законам — амплитуды, комплексные числа и всё такое. А во-вторых, «бильярдная» теория не работает для любого мало-мальски сложного эксперимента. Хотите пример? Пожалуйста.
На рис. 2 вы можете видеть два зеркала в точках B и C, и два полу-зеркала в точках A и D. Позже я объясню, почему отрезок DE проведён пунктиром; на расчётах это никак не скажется.
Давайте применим правила, которые мы уже знаем.
В начале у нас есть конфигурация «фотон летит в A», её амплитуда — (-1 + 0i).
Считаем амплитуды конфигураций «фотон летит из A в B» и «фотон летит из A в C»:
- «фотон летит из A в B» = i × «фотон летит в A» = (0 + –i)
- «фотон летит из A в C» = 1 × «фотон летит в A» = (-1 + 0i)
Интуитивно ясно, что обычное зеркало ведёт себя как половина полу-зеркала: всегда отражает фотон, всегда умножает амплитуду на i. Итак:
- «фотон летит из B в D» = i × «фотон летит из A в B» = (1 + 0i)
- «фотон летит из C в D» = i × «фотон летит из A в C» = (0 + –i)
Важно понять, что «из B в D» и «из C в D» — это две разные конфигурации. Нельзя просто написать «фотон летит в D», потому что от угла, под которым этот фотон приходит в D, зависит то, что с ним случится дальше.
Считаем дальше:
- амплитуда конфигурации «фотон летит из B в D», равная (1 + 0i):
- умножается на i, и результат (0 + i) засчитывается в пользу конфигурации «фотон летит из D в E»
- умножается на 1, и результат (1 + 0i) засчитывается в пользу конфигурации «фотон летит из D в F»
- амплитуда конфигурации «фотон летит из C в D», равная (0 + –i):
- умножается на i, и результат (1 + 0i) засчитывается в пользу конфигурации «фотон летит из D в F»
- умножается на 1, и результат (0 + –i) засчитывается в пользу конфигурации «фотон летит из D в E»
Итого:
- «фотон летит из D в E» = (0 + i) + (0 + –i) = (0 + 0i) = 0
- «фотон летит из D в F» = (1 + 0i) + (1 + 0i) = (2 + 0i)
Отношение квадратов модулей амплитуд — 0 к 4; из расчётов следует, что первый детектор вообще не будет срабатывать! Поэтому-то отрезок DE и был проведён пунктиром на рис. 2.
Если бы полу-зеркала отражали или пропускали фотон случайным образом, оба детектора реагировали бы примерно с одинаковой частотой. Но это не совпадает с результатами экспериментов. Вот и всё.
Вы могли бы возразить: «А вот и не всё! Предположим, например, что когда зеркало отражает фотон, с ним происходит что-то такое, что второй раз он уже не отразится? И, наоборот, когда зеркало пропускает фотон, в следующий раз ему придётся отразиться.»
Во-первых, бритва Оккама. Не стоит выдумывать сложное объяснение, если уже существует простое (если, конечно, считать квантовую механику простой…) А во-вторых, я могу придумать другой опыт, который опровергнет и эту альтернативную теорию.
Поместим маленький непрозрачный объект между B и D, чтобы амплитуда конфигурации «фотон летит из B в D» всегда равнялась нулю.
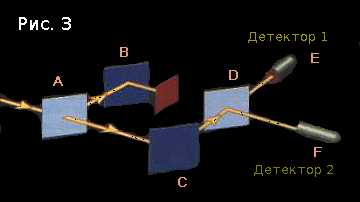
Теперь амплитуда конфигурации «фотон летит из D в F» равна (1 + 0i), а амплитуда конфигурации «фотон летит из D в E» — (0 + –i). Квадраты модулей равны 1. Это значит, что в половине случаев будет срабатывать первый детектор, а в половине — второй.
Это невозможно объяснить, если считать, что фотон — это маленький бильярдный шарик, который отражается от зеркал.
Дело в том, что об амплитуде нельзя думать, как о вероятности. В теории вероятностей, если событие X может произойти или не произойти, то вероятность события Z равна P(Z|X)P(X) + P(Z|¬X)P(¬X), где все вероятности положительны. Если вы знаете, что вероятность Z при условии, что X случилось, равна 0.5, а вероятность X — 0.3, то полная вероятность Z по меньшей мере 0.15, независимо от того, что произойдёт, если X не случится. Не бывает отрицательных вероятностей. Возможные и невозможные события не могут аннулировать друг друга. А амплитуды — могут.
Вот пример неправильного мышления: «Фотон летит в B или в C, но он мог полететь по-другому, и это влияет на вероятность того, что он полетит в E…»
События, которые не случились, не имеют никакого влияния на мир. Единственное, что может повлиять на мир — это наше воображение. «О боже, эта машина чуть не сбила меня», думаете вы, и решаете уйти в монастырь, чтобы больше никогда не встречаться с опасными машинами. Но реально по-прежнему не само событие, а лишь ваше воображение, содержащееся в вашем мозгу — который можно из вас достать, пощупать и положить назад, чтобы убедиться, что он вполне реален.
Реально всё, что влияет на мир. (Если вы полагаете, что это не так, попробуйте дать определение слову «реальный».) Конфигурации и амплитуды непосредственно влияют на мир, так что они тоже реальны. Сказать, что конфигурация — это «то, что могло случиться», так же странно, как сказать, что стул — это «то, что могло случиться».
А что это тогда — конфигурация?
Продолжение следует.
На самом деле всё немного сложнее, чем вам могло показаться после прочтения этой статьи.
Каждая конфигурация описывает все частицы во Вселенной. Амплитуда — это непрерывное распределение по всему пространству конфигураций, а не дискретное, как мы рассматривали сегодня. И в самом деле, фотоны же не телепортируются из одного места в другое мгновенно, а каждое различное состояние мира описывается новой конфигурацией. В конце концов мы и до этого доберёмся.
Если вы ничего не поняли из этого абзаца, не беспокойтесь, я всё объясню. Потом.
читать вторую часть →
Автор: Eliezer Yudkowsky. Вольный и сокращённый (совсем чуть-чуть) перевод: я. Ссылки на оригиналы: lesswrong.com/lw/pc/quantum_explanations, lesswrong.com/lw/pd/configurations_and_amplitude.
habr.com
“Квантовая механика для чайников” | Физика
Как работает квантовая механика или почему наблюдаемый мир классичен?
Апрель 15, 2011 в 12:51 дп · Filed under Физика и техника ·Отмечено квантовая-механика, наука, физика, эверетт, эвереттика, эвереттчина
Врага надо знать в лицо.
Любая сложная задача имеет простое, всем понятное неправильное решение.
Этот креатив предназначается для тех, кто хочет быстро разобраться в том, что из себя представляет квантовая механика, как она описывает окружающий мир. По поводу квантовой механики у учёных есть разногласия, в том числе в том, может ли она вообще описывать окружающий мир, поэтому изучать её по учебникам довольно сложно: в учебниках, как правило, описан формализм, его «вывод» (если это безобразие можно так назвать), разобрано несколько очень частных случаев применения формализма с кучей пренебрежений и упрощений, и всё остальное место занято математическими методами. Вопрос же о том, как из этого «формализма» может получиться нечто похожее на реальный мир, который мы наблюдаем, рассматривается очень плохо. Если человек по каким-то причинам решил изучить квантовую механику (например, для общего образования), он столкнётся со следующими проблемами:
- Материал учебника требует кучу предварительных знаний, как математических, так и физических.
- Учебник огромен и читается очень медленно по причине большого количества сложных математических выкладок.
- Даже, если человек осилил учебник (потратив год или больше), у него может остаться непонимание («а о чём это вообще?», «где здесь картина мира?»), квантовая механика будет ему казаться набором эвристических правил, которые работают в некоторых частных случаях.
Прочтение этого креатива позволит читателю перейти по отношению к квантовой механике из состояния «что за неведомая хрень?» в состояние «в целом осознаю и могу изучать дальше с чувством понимания». При этом от читателя требуется только знание школьной программы по математике и самое базовое представление о классической механике, правда, нужно будет самостоятельно изучить некоторые математические факты хотя бы на физическом уровне строгости (см. начало второй части), например, по википедиям. Этот креатив можно было бы назвать «квантовая механика для чайников», но для чайников с развитым математическим мышлением. Придётся немало потрудиться, в этом креативе много формул, читателю желательно не только их формально проверять, но и пытаться воспринимать идеи, которые в них заложены, пытаться их улучшать и обобщать. Вообще, квантовую механику невозможно объяснить без формул. Если кто-то пытается это сделать, то он банально вешает лапшу на уши. Но, в любом случае, проще изучить 10 страниц, насыщенных формулами, потратить на это, скажем, две недели, и поиметь понимание сути, чем изучить столь же насыщенные 1000 страниц, потратить год или больше, и нихрена не понять.
Надо помнить, что квантовая механика — это не конкретная теория. Это — некоторая база, на которой строятся разные теории. Здесь мы будем делать наше рассмотрение на примере одной конкретной теории — нерелятивистской Шрёдингеровской механики. Даже сама эта теория не является полностью фиксированной: мы можем произвольным образом задать потенциальную энергию взаимодействия как функцию координат частиц (да и по поводу того, что делать с получившимся результатом, существует много разных мнений, но мы рассмотрим здесь один конкретный самый тупой подход).
Физики по своему отношению к квантовой механике делятся на два типа:
- Те, кто думает, что в рамках квантовой механики в принципе возможно описание всего мира.
- Те, кто так не думает.
Как обычно, у вторых нет какой-либо чёткой картины мира, поэтому они обычно молчат в тряпочку и мирно занимаются своим делом, первые же такую «картину» имеют, поэтому не прочь её активно пропагандировать, бессовестно дезинформируя население.
Здесь мы будем пытаться встать в позицию первых и разобраться, почему они так думают. Большинство физиков первого типа являются сторонниками так называемой многомировой (эвереттовской) интерпретации квантовой механики, поэтому именно с её точки зрения мы будем делать наше рассмотрение.
Конечно, основная проблема эвереттчины — это полное отсутствие научных оснований для неё, и полное противоречие элементарному здравому смыслу, поэтому сторонников этой теории трудно назвать учёными, это скорее научные тролли, основная задача которых — впарить ложь максимальному количеству людей, да ещё так, чтобы они не смогли её опровергнуть. Это лирическое отступление.
При первом рассмотрении кажется, что многомировая теория противоречит всему, чему только можно, но если присмотреться более внимательно, то выяснится, что найти какие-либо проверяемые (передаваемые) противоречия крайне трудно, и основными подвисающими проблемами остаются только научность, здравый смысл и почему так происходит. Одна из задач креатива — помочь читателю понять, чему многомировая теория НЕ ПРОТИВОРЕЧИТ, чтобы читатель мог искать настоящие дыры в теории, а не заниматься ерундой, на которую уже давно придуманы отмазки.
Многомировая теория (интерпретация) не является единственным взглядом на квантовую механику, но она оптимальна с педагогической точки зрения. Можно сказать, что понимать квантовую механику — это значит понимать многомировую теорию. К тому же, она наиболее популярна среди «теоретиков всего». Конечно, никто не заставляет в неё верить, но ты можешь знать, что говорит многомировая теория о результате того или иного эксперимента, и пытаться придумать теорию, которая даёт те же предсказания, но уже не страдает подобным фантастическим дебилизмом. Это как стена, от которой можно оттолкнуться. Понимание многомировой интерпретации избавит тебя от многих вопросов, которые задают люди, изучающие квантовую механику по классическим учебникам (в которых, как правило, даётся копенгагенский подход).
Главный вопрос, связанный с квантовой механикой, на котором свет клином не сошёлся, — это как она переходит в классическую на макромасштабах, т.е., почему мы наблюдаем мир, подчиняющийся почти классическим законам. Именно этому вопросу посвящается бОльшая часть креатива, и именно про это ниже сформулирована и доказана теорема.
Кроме всего прочего, я хочу обратить внимание на многие тонкие моменты, связанные с многомировой интерпретацией и квантовой механикой вообще, которые многие не замечают, и которые показывают, что всё далеко не так просто, как кажется, и из которых, возможно, вылезут настоящие противоречия с реальностью, понятные даже троллям-формалистам.
Хотелось бы заметить, что квантовая механика с многомировой теорией — это вещь очень красивая, но читателю настоятельно рекомендуется не попадаться в плен этой красоты. Вовсе необязательно верить во всю эту хрень! Всегда нужно помнить, что, скорее всего, никакого макроскопического мультиверса в природе не существует. Многомировая теория настолько противоречит здравому смыслу, что нормальный человек станет её сторонником только тогда, когда у него не останется ни одной альтернативы, нынешняя же экспериментальная база оставляет кучу таких альтернатив. К сожалению, «ненормальных», таких, у которых желание сменить парадигму намного сильнее желания узнать истину, довольно много, и некоторые их них имеют очень высокий учёный статус. Хотелось бы порекомендовать читателю не поддаваться стадному инстинкту и влиянию авторитетов, как можно больше внимания уделять анализу существующей экспериментальной базы и вопросу о том, как из неё можно получить теорию, чему можно доверять, а чему — нет (это относится в том числе к таким фундаментальным вещам, как принцип относительности и закон сохранения энергии). Всегда нужно помнить, что основная задача физика — это описывать реальный мир, а не придумывать красивые теории, которые трудно опровергнуть.
Формулировка квантовой механики.
Считаем, что у нас есть n частиц с заданными массами. Тогда вселенная (мультиверс) полностью описывается функцией
,
где — координаты k-ой частицы, — время (всё вещественные числа). Функция принимает комплексные значения.
Для упрощения записи координаты всех частиц будем обозначать , где . Множество всех возможных векторов называется конфигурационным пространством. Через будем обозначать массу частицы, соответствующей -ой координате.
Эволюция волновой функции полностью описывается уравнением Шрёдингера:
,
здесь , Дж*с — приведённая постоянная Планка, — потенциальная энергия взаимодействия частиц (которую нужно найти из классической физики, например, можно взять энергию кулоновского взаимодействия), — мнимая единица 🙂
Теперь про физический смысл. Миром будем называть набор координат . Мультиверс в каждый момент времени нужно представлять как совокупность всех возможных миров, причём каждому миру соответствует плотность . Плотность имеет смысл, аналогичный количеству миров, т.е., если, например, A и B — два множества миров,
, ,
то в момент времени в множестве A в раз больше миров, чем в B. Иными словами, вероятность того, что «наш» мир лежит в A, ровно во столько раз больше, чем, что лежит в B. Вот и всё.
Некоторые пояснения.
Оказывается, что такая простая «теория всего» позволяет объяснить как знаменитые эксперименты, из которых родилась квантовая механика, такие, как, например, двухщелевой с электронами, так и наблюдаемую классичность вселенной.
Конечно, такая теория очень далека от реальности, потому что в ней нет даже полей, но её вполне достаточно для понимания основных идей квантовой механики и её перехода в классическую на макромасштабах. Более современные квантовомеханические теории устроены похожим образом: в них тоже есть комплекснозначная функция (только с другой областью определения), эта функция подчиняется уравнению с такой же левой частью, но другой правой (но справа тоже линейный оператор, применённый к ).
Куда делись скорости?
Мы привыкли, что в классической механике состояние системы — это не только координаты частиц, но и их скорости, а здесь почему-то только координаты. Дело тут вот в чём. То, что мы наблюдаем, записано у нас в виде состояния мозга, для описания которого вполне достаточно координат (по крайней мере, опровергнуть это будет очень сложно). Например, если мы видим движущийся объект, то мозг преобразует это движение в состояние нейронов, в котором движение уже не играет роли (просто статически записана информация «объект движется»). Конечно, можно было бы назвать миром что-то, содержащее как координаты, так и скорости, но здесь нужно было бы принять во внимание принцип неопределённости Гейзенберга, выбрать базис, обосновать, почему именно такой, а не другой, короче, куча геморроя, совершенно ненужного для понимания ключевых идей.
Почему мы не рассматриваем измерения других, отличных от координат, физических величин, таких, как скорости, угловые моменты?
Потому что любой такой величине в реальности должен соответствовать прибор, который её измеряет, и даёт о результате измерения знать сознанию наблюдателя, состояние которого зависит только от координат (как мы договорились). Измерение других величин (а также операторы, собственные значения и т.д.) нужны для практического использования, чтобы не рассматривать систему объект-прибор-сознание (и ещё желательно окружающую среду), а ограничиться чем-то более простым. Для «теории всего» это не нужно. Да и мы вообще не рассматриваем измерений, мы просто говорим, как нам трактовать волновую функцию.
Может ли мультиверс состоять из макроскопически различимых миров, которыми нельзя пренебречь?
Да, может. Более того, состоит. Всегда. И это гораздо более масштабно, чем может показаться! Любые квантовомеханические эксперименты, в которых появляются вероятности, приводят к появлению таких суперпозиций миров. Например, знаменитый «кот Шрёдингера» реально (с точки зрения многомировой теории, естественно) находится в суперпозиции живого и мёртвого состояния, как и наблюдатель находится в суперпозиции «вижу живого кота» и «вижу мёртвого кота», причём эти суперпозиции никуда не исчезают, а продолжают жить своей жизнью. И если кто-то другой, даже инопланетяне, ставят подобный эксперимент, то происходит образование таких вот суперпозиций различимых миров.
Но и это не самое главное. Дело в том, что волновая функция непрерывно расплывается, причём делает это она очень быстро, и везде (НАПОМИНАЮ, ЧТО ЭТА «РЕАЛЬНОСТЬ» — ТОЛЬКО С ТОЧКИ ЗРЕНИЯ МНОГОМИРОВОЙ ТЕОРИИ). Макроскопические параметры, такие, как положения и форма тел, «расплываются» не так быстро, но тоже вполне ощутимо, особенно это хорошо проявляется, по-видимому, в различных макроскопических свойствах газов и жидкостей, формах разных облаков, положении вихрей, воздействии газов на тела и так далее. То, есть, если в течение суток образовалась суперпозиция человека и его же, отстоящего на метр, с приличной вероятностью, это вполне нормально, для этого не нужны никакие специальные «квантовомеханические» эксперименты. Если в какой-то момент времени волновая функция была хорошо локализованным пятном, то со временем пятно будет расплываться, и становиться огромным, ведь уравнение Шрёдингера не даёт никакого механизма схлопывания такого пятна (и сейчас оно огромно, потому что вселенная существует давно 🙂 ). Более того, разные части пятна будут вторично расплываться, и, тем самым, взаимодействовать друг с другом, создавая интерференции и т.п. Объяснить, почему мы не наблюдаем таких интерференций и прочих продуктов этого взаимодействия, да и вообще, почему, вопреки всему безобразию, мы наблюдаем почти классическую эволюцию мира — довольно непростая задача (и в учебниках этого обычно нет), об этом будет сказано ниже (и теорема будет доказана). Подробнее про бытовое макроскопическое расплывание волновой функции см. здесь.
Рассмотрим иллюстрацию (анимированный gif).
Здесь изображено поведение волновой функции. Линии — изолинии потенциальной энергии. Яркость — это модуль, цвет — фаза (красный — от 0 до пи, зелёный — остальное). Вначале в.ф. была почти классическим локализованным волновым пакетом, скорость «закодирована» в нём градиентом фазы (то есть, чем меньше длина волны, тем выше скорость). Потом пакет начал расплываться, и через некоторое время интерферировать сам с собой (можно заметить интерференционные полосы). Каждая точка здесь — это мир. Конечно, здесь у нас всего две координаты , в реальности должно быть как минимум порядка , но основные идеи понять можно, нечто подобное будет происходить и с волновой функцией настоящего мультиверса.
Для сравнения, вот иллюстрация для аналогичного классического объекта:
Почему мы не наблюдаем суперпозиций живых и мёртвых котов и вообще суперпозиций макроскопически различимых состояний?
По определению. Потому что мы договорились, что всё, что мы наблюдаем, зависит только от классического состояния, то есть, координат . Но в разных мирах находятся разные копии нас, которые могут наблюдать разные вещи, например, в одном мире мы видим живого кота, а в другом другая копия нас — мёртвого.
Почему от учёных иногда доносятся заявления о том, что они наблюдали суперпозиционные состояния, например, электрон, проходящий одновременно через две щели?
Они их не наблюдали, они по косвенным признакам сделали вывод о существовании таких состояний, например, в случае с электронами в щелях, по интерференционной картине в распределении вероятностей попадания электронов в разные места детектора.
Почему мы не наблюдаем скачков сознания между далеко стоящими макроскопически различимыми мирами?
Ответ очень прост: потому что всё, что мы наблюдаем и когда-либо наблюдали, записано в виде состояния мозга (т.е., координат его частиц) в ДАННЫЙ МОМЕНТ ВРЕМЕНИ. А там нет никакой информации о таких скачках. Более того, вопрос о том, наблюдаем мы их или нет, не имеет смысла. Даже, если мы их наблюдаем, то ничего о них не помним.
Есть ли у объектов траектории, хотя бы приблизительные?
Нету. Волновая функция — это очень жирное движущееся пятно, в котором нельзя различить каких-либо траекторий, даже приблизительных. Всё, что мы знаем о траекториях объектов, записано в виде состояния мозга в ДАННЫЙ МОМЕНТ ВРЕМЕНИ, ничего другого нет. То есть, вопрос о том, что было у нас в прошлом, довольно бессмысленен, мы что-то помним и всё, больше ничего нет. Конечно, можно высосать из пальца какое-то вероятностное распределение на траекториях, и некоторые так делают, но надо всегда помнить, что это именно высасывание из пальца, в самой волновой функции такой информации нет.
Как появляются вероятности?
Допустим, что мы 1000000 раз поставили какой-то квантовомеханический эксперимент, в котором с вероятностью 1/2 выпадает либо 0, либо 1. Каждый такой эксперимент расщепляет мультиверс на две группы миров — в одной выпало 0, в другой 1, причём веса, соответствующие этим группам, равны. В итоге, после 1000000 экспериментов у нас мультиверс расщепился на групп миров, каждой соответствует свой набор исходов. Прямой подсчёт показывает, что в подавляющем бльшинстве миров количество выпавших нулей отличается от количества единиц не более, чем на 1%, поэтому с вероятностью, близкой к 1, мы попали именно в такой мир, где будет примерно равное количество исходов 0 или 1, то есть нам будет казаться, что результат получается случайно, и исходы 0 и 1 имеют равную вероятность. А философский вопрос о том, как вообще получается вероятностное распределение из модуля волновой функции, естественно, не имеет ответа.
Если наблюдаемые вероятности — вещь чисто субъективная, то как утверждения об их существовании попали в учебники?
Точно также: в подавляющем большинстве миров в учебниках будет содержаться правильная информация о вероятностях исходов квантовомеханических экспериментов, однако, будет небольшая доля миров, где такая информация будет ложной.
Как работает квантовая механика и многомировая интерпретация (на примере двухщелевого эксперимента, вкратце).
Пусть у нас есть летящая частица, попадающая на пластину из двух щелей, после которой стоит пластина-детектор частиц (который определяет, в какое место пластины попал электрон). Эксперименты говорят, что детектор всегда регистрирует одну частицу, попавшую в одну конкретную точку (корпускулярная природа), но распределение вероятностей попадания в разные точки имеет характерные интерференционные полосы (волновая природа). Эти полосы исчезают, если поставить пролётный детектор, который регистрирует, через какую щель пролетела частица.
Как объясняется этот эксперимент с точки зрения многомировой интерпретации?
Пусть — волновая функция, здесь — часть, соответствующая частице, а — детектору (а также смотрящему на него человеку и всему остальному, но всё это мы будем называть детектором). Пластину с щелями будем для простоты считать состоящей из бесконечно тяжёлых частиц, поэтому мы не будем их включать в модель, считая их просто добавкой к потенциальной энергии. Ещё, для простоты будем считать, что в начальные моменты (когда частица ещё далеко от детектора и с ним не взаимодействует): , при этом множители удовлетворяют уравнениям
,
,
где — масса летящей частицы, — потенциальная энергия детектора без учёта взаимодействия с летящей частицей, — потенциальная энергия взаимодействия летящей частицы и пластины с щелями. — это волновой пакет, который движется в сторону пластины с щелями и проходит её, при этом после прохождения в нём появляются интерференционные полосы (можно проверить решением соответствующего уравнения, для трёх переменных это ещё возможно). Назовём зоной детектирования область конфигурационного пространства, в которой находится достаточно близко к детектору, образованному точками , чтобы детектор начал срабатывание. Волновую функцию в нашем эксперименте можно представить как волновой пакет, который постепенно движется в сторону зоны детектирования. Зона детектирования устроена так, что она с огромной скоростью в некотором направлении выбрасывает всё, что в неё попадает (направление зависит от того, в какую точку зоны мы попали). Связано это с тем, что при попадании частицы на детектор возникает лавинообразный процесс, затрагивающий огромное количество частиц, которые существенно изменяют своё положение, в терминах конфигурационного пространства это означает очень быстрое перемещение, намного более быстрое, чем движение волнового пакета до детектирования. Направление этого выбрасывания очень сильно зависит от того, в какую точку зоны мы попали, хотя бы из-за того, что при попадании частицы в разные точки процесс детектирования происходит по-разному (и от исходного расположения частиц в детекторе это сильно зависит). Всё это означает, что, когда волновой пакет (который с интерференционными полосами) попадает в зону детектирования, он разлетается в разные стороны настолько, что точки, соответствующие не очень близким местам попадания частицы на детектор, можно считать практически невзаимодействующими эвереттовскими мирами (то есть, после детектирования между ними уже никаких интерференций не будет). В каждом таком мире детектор поймал электрон в какой-то конкретной точке, и вероятности будут вполне соответствовать (потому что разбрызгиватель-зона детектирования разбрасывает те миры, что в неё попадают, в том же «количестве»). Формулу для вероятностей здесь выводить не будем.
Почему при установлении пролётного детектора после одной из щелей интерференционная картина пропадает? Предположим теперь, что после одной из щелей стоит пролётный детектор, то есть такой детектор, который засекает прохождение частицы, но при этом даёт ей возможность лететь дальше, не поглощает её. Эксперимент показывает, что в этом случае интерференционная картина пропадает. Попытаемся дать этому объяснение. Для простоты не будем включать в картину основной детектор (который ловит частицы), вместо этого будем считать распределение вероятностей обнаружить частицу в точках пространства. При этом волновая функция у нас будет иметь вид , где — частичная часть, — пролётно-детекторная. Ещё для упрощения будем считать, что , где — то, что получается, если частица проходит через первую щель, а — только через вторую (на самом деле так делать нельзя, но для понимания идеи достаточно). Имеем плотность вероятности:
(звёздочкой обозначается комплексное сопряжение). Поскольку для разных щелей пролётный детектор срабатывает по-разному (причём макроскопически по-разному), выпуклости (в смысле, области, где модуль значения функции достаточно велик) волновых функций и будут приходиться на разные , причём очень далёкие друг от друга. Иными словами, для каждых и одно из значений и очень близко к нулю, следовательно, последнее слагаемое в формуле для вероятности — практически нуль. Вероятность равна сумме вероятностей для отдельных щелей. Этот процесс, в результате которого из-за квантового запутывания с окружающими объектами исчезает интерференционная картина, называется декогеренцией.
Продолжение про наблюдаемую классичность с формулами здесь
maxpark.com
Квантовая физика для чайников – Хочу всё знать…
Если рассматривать успешную научную теорию как средство для разрешения запущеных проблем, то квантововую физику можно рассматривать как чудодейственное лекарство 20 века.Именно она успешно объяснила такие феномены как радиоактивность и антиматерия, и никакая другая теория не способна дать описание тому, как ведёт себя свет и частицы материи в микромире.
Но, в то же время квантовая физика ошеломляет и срывает крышу. Квантовые объекты могут существовать одновременно в нескольких состояниях и в нескольких местах, требуя загадочные методы статистики для своего описания. Полная неопределённости и кишащая парадоксами, эта теория критикуется за то, что бросает вызов самому понятию объективной реальности, факт, оказавшийся не по зубам многим физикам, в том числе и Альберту Эйнштейну.
Сегодня учёные сражаются с этими философскими головоломками, стараясь применить странные свойства квантов для развития технологии, а также объединить квантовую физику и общую теорию относительности в единую теорию квантовой гравитации.
Зарождение идеи
Теория квантов зародилась в начале 20 века, когда идеи классической физики не смогли объяснить некоторые наблюдения. Предыдущие теории дозволяли атомам вибрировать на любой частоте, что привело к ошибочному выводы о том, что атом может излучать бесконечные величины энергии — проблема, известная как ультрафиолетовая катастрофа.
В 1900 году Макс Планк решил эту задачу, допустив, что атомы могут вибрировать только на специфических, квантованных частотах. Затем в 1905 году Эйнштейн раскрыл тайну фотоэффекта, когда свет, падая на металл, высвобождает электроны лишь с определёнными значениями энергии. Существующая тогда теория света как волны не смогла объяснить этот эффект, но Эйнштейн предложил эллегантное решание, допустив, что свет распространяется отдельными порциями энергии, названными фотонами – гениальная идея, вознагражденная в 1921 Нобелевской премией по физике.
(Продолжение следует)
kraoly.livejournal.com
Квантовая механика в повседневной жизни, или туннель в другую реальность
Читать все новости ➔
Однажды наступят волшебные времена. Однажды у нас будет мобильный телефон, который надо заряжать раз в год. Банковская карточка, с которой невозможно украсть деньги. Микротермометр, который почувствует первую же заболевшую клетку и вылечит ее. Однажды это все станет реальностью. Осталось разобраться в квантовой механике, которая сделает чудеса возможными.
Обычная квантовая магия
Постулаты квантовой механики кажутся удивительными, потому что они противоречат нашей интуиции и бытовым знаниям. Но если бы мы с детства росли в мире, живущем по квантово-механическим законам, то эти чудеса были для нас обыденными.
Например…
1. В макромире — том мире, который нас окружает, — вы читаете этот текст, сидя на диване или стуле, и он стоит точно под вами и нигде больше. «Если бы в нашем мире работали законы квантовой механики, то диван мог бы одновременно быть и под вами, и на ближайшей автобусной остановке. Такое квантовое состояние дивана называется суперпозицией», — объясняет профессор Гарвардского университета, член Международного консультативного совета Российского квантового центра физик Михаил Лукин.
2. На автобусной остановке диван могут испачкать или украсть, и вообще вас раздражает неопределенность его местоположения. Чтобы «вернуть» мебель домой, достаточно потрогать ту «ипостась» дивана, которая стоит у вас в квартире, ведь в мире квантовой механики он одновременно существует и там и там! Стоит вам коснуться обивки, суперпозиция дивана разрушится и он останется только в квартире. Впрочем, с некоторой вероятностью диван может оказаться и только на остановке. Поэтому мебельные магазины в квантовом мире продают диваны, для которых после разрушения суперпозиции выше вероятность очутиться у вас дома, а не где-то еще.
3. Есть более простой способ разобраться с диваном. «Суперпозиция — очень хрупкое состояние, и при попытке измерить ее, она тут же разрушается, — объясняет Лукин. — Причем не обязательно использовать приборы, достаточно просто посмотреть. В теории макроскопический диван может находиться в суперпозиции, но этого не происходит, так как с ним сталкиваются атомы воздуха, его «чувствует» пол, на него смотрят люди. Можно сказать, что таким образом внешний мир как бы измеряет суперпозицию и тем самым убивает ее. Но в микромире суперпозиция — самое обычное дело».
4. В нашем привычном мире, собираясь пойти пообедать с коллегами, вы спрашиваете, голодны ли они. В квантовом мире все проще: если в офисе все сотрудники особым образом связаны друг с другом (физики говорят «запутанны»), то вы и так знаете, как они себя ощущают. Более того, если кто-то из коллег пошел обедать, то в момент, когда он поест, вы тоже почувствуете насыщение. Если некто спросит у любого из связанных с вами коллег, сыт он или голоден, то, получив ответ, узнает и ваше состояние. Такой феномен мгновенного перемещения информации на любые расстояния получил название квантовой телепортации.
Знание о том, голоден или сыт связанный с вами коллега, никак не путешествует в пространстве: оно не передается ни по проводам, ни по радио, ни по телеграфу, но вы оба моментально узнаете обо всех изменения друг друга. «Это звучит как магия, но это и есть магия, особая квантовая магия», — говорит швейцарский физик и основатель компании id Quantique Николя Гизен.
5. В макромире, где работают квантовые законы, нет пробок. В привычной реальности, чтобы переместить автомобиль из точки А в точку Б, нужно затратить энергию. В квантовом макромире автомобиль может занять ее у Вселенной и попасть в точку Б сам собой. Этот феномен называют квантовым туннелированием, и он возможен благодаря принципу неопределенности Гейзенберга. Постулат, сформулированный немецким физиком Вернером Гейзенбергом в 1927 году, гласит, что мы не можем с одинаковой точностью измерить положение квантовой частицы и ее импульс. Из скучной фразы следует: если мы точно знаем, что автомобиль находится в гараже в точке А, его импульс оказывается неопределенным и может случайно стать достаточно большим для того, чтобы «подтолкнуть» машину на парковку в точку Б.
Так выглядит квантовый компьютер изнутри. Это запчасти машины, созданной компанией D-Wave. Ее первый компьютер содержал 16 кубитов, а более поздняя модель — уже 28. Фото:J CHUNG, © 2006-2007 D-WAVE SYSTEMS, INC. (X4)
Дырявые алмазы и суперсенсоры
Благодаря квантовой механике можно создать приборы, которые невозможны в рамках классической физики. Например, построить компьютеры, которые будут считать в миллионы раз быстрее самых мощных нынешних суперкомпьютеров. Квантовые компьютеры используют странное для людей состояние суперпозиции, которое позволяет совершенно иначе проводить вычисления.
В обычном компьютере информация хранится в виде двоичного кода, который состоит из двух значений — 0 и 1. Каждая цифра кода «лежит» в специальной ячейке памяти, и ее значение называется битом. Таким образом, бит может иметь только два состояния — 0 либо 1. «Квантовый компьютер — это вычислительная система, которая может находиться одновременно во многих состояниях. Благодаря суперпозиции квантовый бит, или кубит, может принимать бесконечное множество значений, а не два, — объясняет Лукин. — Это дает возможность делать вычисления параллельно. Если вы что-то делаете с этим битом, то изменяются сразу и 0, и 1. То есть мы можем одновременно проводить вычисления с начальным состоянием 0 и с начальным состоянием 1».
Пока ученые смогли построить только самые простые квантовые компьютеры, которые содержат от одного до тысячи кубитов. Чаще всего в качестве квантовых битов выступают атомы различных веществ, охлажденные почти до абсолютного нуля (–273,15 °С) — температуры, ниже которой не может остыть ничто во Вселенной. Поэтому даже самый маленький квантовый компьютер занимает целую комнату. Но недавно группе Михаила Лукина удалось создать кубит размером с пылинку. Это алмазный нанокристалл с вкраплениями атомов азота, которые имеют те же характеристики, что и сверххолодные кубиты. Алмазно-азотные кубиты работают при комнатной температуре и могут хранить информацию несколько секунд — для квантовых компьютеров это очень долго.
Пока квантовые компьютеры — это гигантские приборы, но не исключено, что скоро они будут стоять в любом смартфоне.
Термометр для раковой клетки
Пока одни разработчики квантовых компьютеров ломают голову, как удержать квантовые системы в чрезвычайно хрупком состоянии суперпозиции, другие придумали, как использовать эту неустойчивость во благо. Они создают квантовые системы, которые чувствительны к специфическим воздействиям, например к изменениям температуры. Точность подобных систем достигает миллионных долей градуса. Один из прототипов термометра будущего — те самые алмазные кубиты — сконструировали Лукин и его коллеги. Ученые шприцем вводят нанокристаллы в живые клетки и определяют, как сильно прогрелась та или иная их часть. Например, исследователи могут сравнить, насколько правая половина клетки горячее левой.
«Используя алмазные кубиты, мы можем искать в организме раковые клетки, потому что их температура отличается от температуры здоровых клеток. Кроме того, мы сможем в реальном времени следить, как работают те или иные гены, — говорит Лукин. — При этом локально слегка меняется температура, и «засечь» ее другими методами невозможно. Наконец, в чуть более отдаленном будущем при помощи таких нанотермомет ров можно будет определять многие болезни на самых ранних стадиях. В этот момент в клетках уже запустились специфические биохимические реакции, но внешне никаких признаков заболевания нет. Однако место в клетке, где проходят такие реакции, слегка нагревается, и мы сможем это увидеть».
При помощи сверхчувствительных квантовых датчиков можно измерять не только температуру. Квантовые состояния могут реагировать, например, на малейшие изменения давления, электромагнитных полей и прочее. У таких сенсоров будет колоссальная чувствительность к изменениям в окружающей среде, потому что квантовое состояние разрушается от малейших воздействий извне.
Исследования квантовых систем — та область, где специалисты ждут прорывов в ближайшие годы. Фото:PHOTONONSTOP/AFP/EAST NEWS
Батарейка вместо нефти
Владельцам смартфонов приходится искать розетку минимум раз в день. Благодаря достижениям в квантовой механике скоро можно будет уезжать в отпуск и не брать с собой зарядку. «Человеческие системы хранения и передачи энергии в разы уступают тому, что придумала природа, — рассказывает профессор Массачусетского технологического института (MIT), специалист по квантовым алгоритмам Сет Ллойд. — Процессы, которые идут в живых клетках, например фотосинтез, чрезвычайно эффективны, и в них используются примерно те же принципы, которые мы применяем для квантовых вычислений».
Постепенно ученые все лучше понимают квантово-механические процессы и начинают потихоньку разбираться, как именно протекает фотосинтез на этом уровне. Они даже конструируют искусственные системы, которые были бы сравнимы с ним по эффективности. «Моя коллега Анджела Белчер из MIT создает генетически модифицированные вирусы, на поверхности которых «торчат» особые молекулы, похожие на те, что задействованы в фотосинтезе у растений. Белчер и ее коллеги научились закреплять вирусные частицы на подложке так, что в итоге получился прототип чрезвычайно энергоэффективной батарейки, копирующей механизм фотосинтеза. Пока ученые дорабатывают изобретение, но уже нашлась компания, которая создает для Белчер вирусы в промышленном масштабе», — рассказывает Ллойд.
Многие компьютерные игры, например покер, основаны на случайных событиях. Но сегодня играющие с людьми в карты компьютеры жульничают, потому что создают псевдослучайные события, используя специальные алгоритмы. Квантовая механика, благодаря которой можно сделать раздачу карт по-настоящему случайной, наконец превратит механических соперников в честных игроков.
Квантовая телепортация и банковские счета
Пока у нас мало алгоритмов, которые позволили бы создать квантовые компьютеры, работающие намного быстрее классических. Самый перспективный — квантовой алгоритм факторизации Питера Шора, названный по имени создателя, выдающегося математика из США. Используя этот алгоритм, квантовый компьютер из семи кубитов разложил число 15 на множители 3 и 5. «И если нам удастся приспособить алгоритм для работы с большими квантовыми системами, то безопасному Интернету придет конец — квантовый компьютер вскроет любой шифр за секунды», — рисует картину близкого апокалипсиса Сет Ллойд.
Впрочем, взамен мы получим шифрование, разгадать которое невозможно физически. Навсегда защитить человечество от киберворовства поможет квантовая запутанность. Запутанные частицы настолько тесно связаны друг с другом, что мгновенно «чувствуют» изменения, которые происходят с «напарницей», даже если они разнесены на десятки километров.
«Волшебные технологии шифрования, основанные на этом принципе, существуют уже сегодня», — рассказывает Николя Гизен. Компания работает уже несколько лет и при помощи квантового шифрования защищает данные клиентов. Пока рынок небольшой, но у него есть все шансы вырасти — просто потому, что спрос на квантовые, принципиально невскрываемые шифры будет увеличиваться.
Так выглядел первый работающий транзистор, который в 1947 году изобрели в Bell Labs — американской копорации, знаменитой своим исследовательским подразделением. Прародитель современных транзисторов представлял собой пластину из германия, к которой были припаяны два контакта. В 1956 году его создатели получили Нобелевскую премию. Современные транзисторы настолько малы, что на их работу уже влияют законы квантовой механики.
Конец Сноудена и вселенная в триста кубитов
Когда бывший сотрудник американских спецслужб Эдвард Сноуден рассказал, что Агентство национальной безопасности (АНБ) США читает электронную почту доброй половины жителей Земли, многие почувствовали себя неуютно. Но бояться, что суровый лейтенант сейчас изучает именно вашу переписку, не стоит — никакие суперкомпьютеры не могут справиться с тем потоком данных, который сваливается на АНБ каждый день, и как следует рассортировать письма.
Волноваться можно начинать после того, как в дело вступят специалисты по квантовой механике: «Даже маленький квантовый компьютер, состоящий из нескольких десятков кубитов, способен за несколько секунд проверить все сообщения, написанные сегодня, на слово «тротил». Чтобы проанализировать все письма, написанные с момента появления электронной почты, потребуется компьютер из нескольких сотен кубитов. С переводом в квантовое состояние всей информации, которая образовалась во Вселенной с момента Большого взрыва, за доли секунды справится компьютер из трех сотен кубитов», — говорит Ллойд.
При этом благодаря природе квантовых состояний спецслужбы не смогут «вытянуть» из собранных данных персональные сведения пользователей, потому что вернуть данные, записанные в квантовой форме, к привычному виду невозможно. То есть квантовые системы позволят анализировать колоссальные массивы информации, не нарушая тайну переписки.
Решение без проблемы
Пока рынок квантовых технологий не очень велик. Не в последнюю очередь слабый интерес предпринимателей объясняется тем, что они не понимают, в чем же суть квантовых процессов. Некоторые маловеры и вовсе считают, что квантовая механика нужна для решения только очень специфических задач и неприменима к повседневной жизни. Впрочем, когда-то лазеры тоже считались всего лишь хитроумным изобретением, сделанным учеными для ученых. «Это решение, к которому еще нужно придумать проблему», — говорили скептики. Сегодня без лазеров трудно представить обычную жизнь — они работают в оптоволоконных системах, благодаря которым, например, домашний компьютер выходит в Интернет. Так что очень может быть, что лет через 20 отличным подарком внуку окажется телефон, работающий на удивительных принципах квантовой механики.
vk.cc/2nYJ7y
Возможно, Вам это будет интересно:
meandr.org
Квантовая физика для начинающих — Портал профессионального образования Чеченской республики
Квантовая физика это достаточно сложная дисциплина, которая не всем легко подается усвоению. Тем не менее, физика как предмет интересная и полезная, поэтому и квантовая физика находит своих фанатов, которые готовы ее изучить и получить в итоге практическую пользу. Для того, чтобы было проще усвоить материал, нужно начинать с самого начала, то есть с раздела квантовая физика для начинающих. Это позволит получить хорошую базу для знаний, и в то же время хорошо структурировать свои знания в голове.Начинать самостоятельное обучение нужно с хорошей литературы. Именно литература является решающим фактором в процессе получения знаний и обеспечивает их качество. Особый интерес вызывает квантовая механика, и многие начинают свои изучения именно с нее. Физику должен знать каждый, потому что это наука о жизни, которая объясняет многие процессы, и делает их понятными для окружающих.
Учтите, что когда приступите к изучению квантовой физики, вы должны обладать знаниями математики и физики, так как без них вы просто не справитесь. Будет хорошо, если у вас будет возможность обращаться к преподавателю, чтобы найти ответы на возникшие вопросы. Если такой возможности не будет, можете попробовать разъяснить ситуацию на специализированных форумах. Форумы тоже могут сильно пригодиться в обучении.
Когда определитесь с выбором учебника, вы должны быть готовы к тому, что он достаточно сложный и его придется не просто читать, а вникать во всем том, что в нем написано. Чтобы по окончании обучения не возникла мысль, что это все ненужные никому знания, пытайтесь связать каждый раз теорию с практикой. Еще важно определить заранее цель с которой вы начали учить квантовую физику, для того чтобы предотвратить появление мысли о бесполезности полученных знаний. Люди делятся на две категории: люди, которые считают квантовую физику интересным и полезным предметом и те, которые так не считают. Выберите для себя, к какой категории относитесь вы и соответственно определите, есть ли квантовой физике место в вашей жизни или же нет. Можно всегда остаться на уровне начинающего в изучении квантовой физики, а можно добиться реальных успехов, все в ваших руках
proffi95.ru
Что интересного происходит в науке: Учебники по теоретической физике
В продолжение постов про рекомендуемые учебники и про рекомендуемые книжки для знакомства с физикой. Чаще всего меня просят порекомендовать учебники по университетским курсам физики, и как правило — теоретической физики. Перед тем, как что-то рекомендовать, снова несколько оговорок (вдобавок к общим оговоркам).Первое. Иногда люди хотят найти хороший курс теоретической физики и изучать по нему все разделы физики. Я, честно говоря, это желание не одобряю. Курсы теоретической физики существуют, тот же Ландау-Лифшиц, но брать их за основу (а тем более, изучать физику только по ним) не надо. Тот же Ландау-Лифшиц это не чисто учебник, а скорее учебник-справочник. Он очень неровный с педагогической точки зрения: иногда он вполне обучательный, а иногда уходит в такие специализированные вопросы, которые при первом изучении курса вообще не нужны. Поэтому лучше всего, как мне кажется, взять по каждому университетскому курсу 2-3 учебника плюс хороший задачник.
Впрочем, в виде исключения я могу порекомендовать тут одну вещь — так называемый Теоретический минимум Леонарда Сасскинда. Это видеолекции Сасскинда по нескольким курсам теоретической физики. То немногое, что я там посмотрел, изложено совершенно замечательно.
Второе. Параллельно с теоретической физикой надо изучать математику. Причем перед многими разделами физики есть какие-то определенные разделы математики, которые надо бы изучить. Стандартное соотношение «раздел физики» – «необходимые разделы математики» примерно такие:
- Механика — производные, интегралы, обыкновенные дифуры, основы функционального анализа (для лагранжевой и гамильтоновой механики),
- Электродинамика — векторное и тензорное исчисление,
- Квантовая механика — функциональный анализ, в частности, операторы в гильбертовых пространствах, дифуры в частных производных, спецфункции,
- Физика сплошных сред — дифуры в частных производных,
- Квантовая теория поля — теория групп (и хоть немного абстрактной алгебры), немного дифференциальной геометрии и топологии.
В общем-то с такими списками мне дальше предлагать нечего. Но раз люди иногда интересуются именно моими рекомендациями, то вот моя субъективная подборка по некоторым темам (которая во многом отражает лично мое обучение и преподавание) — плюс рекомендации, которые мне подсказали в комментариях. Подчеркну еще раз — это примеры начальных учебников для соответствующих курсов; если после них возникло желание углубить предмет, то есть огромное число учебников и монографий по частным вопросам.
Классическая механика
- Ландау-Лифшиц, т.1 — на редкость краткий и доступный том ЛЛ.
- Задачник: Коткин, Сербо, Сборник задач по классической механике.
- Голдстейн, Классическая механика.
Электродинамика и оптика
- Зарубежные универы почти исключительно учат по учебнику Джексон, Классическая электродинамика. Он очень объемный и содержит большое число тем, которые в учебники обычно не входит. Лучше ли он других или нет, я оценить не берусь.
- Задачник: Батыгин, Топтыгин, Сборник задач по электродинамике. — с подробными решениями.
- Топтыгин, Современная электродинамика, в 2 частях. — это и современный учебник, и огромное количество задач.
- В университете мне понравилась небольшая, но довольно оригинальная книжка Мешков, Чириков, Электромагнитное поле, в 2 частях.
- Матвеев, Оптика — это 4й том из курса общей физики Матвеева.
Квантовая механика
- Ландау-Лифшиц, Краткий курс теоретической физики, т.2 отлично покрывает нужды стандартного годового университетского курса, как по объему, так и по уровню. Их же третий том Полного курса содержит больше дополнительных глав и технически сложных моментов, но держать его под рукой тоже полезно.
- Стандартные зарубежные учебники: Коэн-Таннуджи и др. Квантовая механика, Мессиа, Квантовая механика, Сакураи, Modern Quantum Mechanics (не уверен, переводилась ли на русский). Можно заниматься и по ним, они чуть проще Ландау-Лифшица. Старые советские ученибки типа Блохинцева или Давыдова мне как-то не приглянулись. Ну и разумеется ни в коем случае нельзя использовать последний том какого-нибудь курса общей физики.
- Отдельно рекомендуется Фейнман, Хиббс, Квантовая механика и интегралы по траекториям.
- Иванов М.Г. Как понимать квантовую механику — я внимательно не изучал, но по отдельным главам впечатление очень хорошее.
- Задачники: Галицкий, Карнаков, Коган, Сборник задач по квантовой механике — толстенный задачник с подробными решениями, — и двухтомник Флюгге, Задачи по квантовой механике, там задач поменьше, но разжеваны они очень основательно.
Квантовая теория поля
- Классические учебники: Ициксон, Зюбер, Квантовая теория поля и Бьёркен, Дрелл, Релятивистская квантовая теория. Советская классика: Боголюбов, Ширков, Квантовые поля (потоньше и попроще) и Введение в теорию квантованных полей (потолще и потруднее). Можно учиться по ним, но я лично всё же порекомендовал бы более современный курс, даже в качестве первого учебника.
- Недавние хорошие учебники: Пескин, Шрёдер, Введение в квантовую теорию поля, Зи, Квантовая теория поля в двух словах и Средницки, Квантовая теория поля.
- Существуют монструозные учебники типа трехтомника Вайнберга или Fields Зигеля, но наверно подавляющему большинству начинать изучение с них не стоит.
igorivanov.blogspot.com
Книга «Квантовая механика. Теоретический минимум»
Классическая механика интуитивна: она ежедневно и многократно используется людьми для выживания. Но до двадцатого века никто и никогда не использовал квантовую механику. Она описывает вещи столь малые, что они полностью выпадают из области восприятия человеческих органов чувств. Единственный способ понять эту теорию, насладиться ее красотой — перекрыть нашу интуицию абстрактной математикой.Леонард Сасскинд — известный американский ученый — приглашает вас отправиться в увлекательное путешествие в страну квантовой механики. В пути вам пригодятся базовые знания из школьного курса физики, а также основы математического анализа и линейной алгебры. Также необходимо знать кое-что о вопросах, которые рассматривались в первой книге «теоретического минимума» Сасскинда — «Все, что нужно знать о современной физике». Но нестрашно, если эти знания несколько подзабылись. Многое автор напомнит и пояснит по ходу дела.
Квантовая механика — необычная теория: согласно ее постулатам, например, мы можем знать все о системе и ничего о ее отдельных частях. По поводу этого и других противоречий в свое время много спорили Эйнштейн и Нильс Бор. Если вы не боитесь сложностей, обладаете пытливым умом, технически грамотны, искренне и глубоко интересуетесь физикой, то этот курс лекций Леонарда Сасскинда придется вам по душе. Книга концентрируется на логических принципах квантовой теории и ставит целью не сгладить парадоксальность квантовой логики, а вытащить ее на дневной свет и попытаться разобраться с непростыми вопросами, которые она поднимает.
Обзор волновой функции
В этой лекции мы будем использовать язык волновых функций, поэтому давайте перед погружением сделаем небольшой обзор материала. Мы обсуждали в лекции 5 волновые функции абстрактных объектов, не объясняя, какое они имеют отношение к волнам или функциям. Прежде чем восполнить этот пробел, я напомню то, что мы обсуждали ранее.
Начнем с того, что выберем наблюдаемую L с собственными значениями l и собственными векторами |l〉. Пусть |Y〉 будет вектором состояния. Поскольку собственные векторы эрмитова оператора образуют полный ортонормированный базис, вектор |Y〉 можно разложить по этому базису:
Как вы помните из разделов 5.1.2 и 5.1.3, величины Y(l) называются волновой функцией системы. Но заметьте: конкретная форма Y(l) зависит от конкретной наблюдаемой L, которую мы первоначально выбрали. Если выбрать другую наблюдаемую, волновая функция (наряду с базисными векторами и собственными значениями) окажется иной, несмотря на то что мы по-прежнему говорим о том же самом состоянии. Таким образом, мы должны сделать оговорку о том, что Y(l) является волновой функцией, связанной с |Yñ. Если быть точными, мы должны сказать, что Y(l) является волновой функций в L-базисе. Если использовать свойства ортонормированности этого базиса векторов 〈li|lj〉 = dij, то волновая функция в этом L-базисе может быть также задана с помощью внутренних произведений (или проекций) вектора состояния |Y〉 на собственные векторы |l〉: Y(l) = 〈l|Y〉
О волновой функции можно думать двумя способами. Прежде всего, это набор компонент вектора состояния в конкретном базисе. Эти компоненты можно выписать в форме вектора столбца:
Другой способ думать о волновой функции — это рассматривать ее как функцию l. Если вы задали любое допустимое значение l, то функция Y(l) дает комплексное число. Можно, таким образом, сказать, что Y(l) —это комплекснозначная функция дискретной переменной l. При таком рассмотрении линейные операторы становятся операциями, которые применяются к функциям и дают новые функции.
И еще одно, последнее напоминание: вероятность того, что эксперимент даст результат l, равна P(l) = Y*(l)Y(l).
Функции и векторы
До сих пор системы, которые мы изучали, имели конечномерные векторы состояния. Например, простой спин описывается двумерным пространством состояний. По этой причине наблюдаемые имели только конечное число возможных наблюдаемых значений. Но существуют более сложные наблюдаемые, которые могут иметь бесконечное число значений. Примером служит частица. Координаты частицы являются наблюдаемыми, но в отличие от спина координаты имеют бесконечное число возможных значений. Например, частица, движущаяся вдоль оси x, может находиться у любой вещественной отметки x. Другими словами, x является непрерывной бесконечной переменной. Когда наблюдаемые системы непрерывны, волновая функция становится полноценной функцией непрерывной переменной. Для применения квантовой механики к системам такого рода мы должны расширить представление о векторах так, чтобы включить в него функции.
Функции являются функциями, а векторы — векторами; они кажутся совершенно разными сущностями, так в каком же смысле функции являются векторами? Если вы думаете о векторах как о стрелках в трехмерном пространстве, то они, конечно, совсем не то же самое, что функции. Но если вы взглянете на векторы шире, как на математические объекты, удовлетворяющие некоторым постулатам, функции в действительности образуют векторное пространство. Такое векторное пространство часто называют гильбертовым пространством в честь математика Давида Гильберта.
Рассмотрим набор комплексных функций Y(x) одной вещественной переменной x. Под комплексной функцией я имею в виду, что каждому x она сопоставляет комплексное число Y(x). С другой стороны, независимая переменная x является обычной вещественной переменной. Она может принимать любые вещественные значения от –∞ до +∞.
Теперь сформулируем точно, что мы имеем в виду, говоря, что «функции являются векторами». Это не поверхностная аналогия или метафора. При некоторых ограничениях (к которым мы еще вернемся) такие функции, как Y(x), удовлетворяют математическим аксиомам, которые определяют векторное пространство. Мы вскользь упоминали эту идею в разделе 1.9.2, а теперь используем ее в полную силу. Оглядываясь назад, на аксиомы комплексного векторного пространства (в разделе 1.9.1), мы видим, что комплексные функции удовлетворяют им всем.
1. Сумма любых двух функций является функцией.
2. Сложение функций коммутативно.
3. Сложение функций ассоциативно.
4. Существует единственная нулевая функция такая, что при ее сложении с любой функцией получается та же самая функция.
5. Для любой данной функции Y(x) существует единственная функция –Y(x), такая что Y(x) + (–Y(x)) = 0.
6. Умножение функции на любое комплексное число дает функцию и является линейным.
7. Соблюдается дистрибутивное свойство, означающее что
z[Y(x) + j(x)] = zY(x) + zj(x),
[z + w]Y(x) = zY(x) + wY(x),
где z и w — комплексные числа.
Все это подразумевает, что мы можем идентифицировать функцию Y(x) с кет-вектором |Y〉 в абстрактном векторном пространстве. Неудивительно, что мы также можем определить бра-векторы. Бра-вектор 〈Y|, соответствующий кету |Y〉, отождествляется с комплексно сопряженной функцией Y*(x).
Для эффективного использования этой идеи нам необходимо обобщить некоторые предметы из нашего набора математических инструментов. В предыдущих лекциях метки, которые идентифицировали волновые функции, были членами некоего конечного дискретного множества, например собственными значениями определенной наблюдаемой. Но теперь независимая переменная непрерывна. Среди прочего это означает, что мы не можем суммировать по ней, пользуясь обычными суммами. Я думаю, вы знаете, что надо делать. Вот ориентированные на функции заменители для трех наших векторных понятий, с двумя из которых вы уже знакомы.
• Суммы заменяются интегралами.
• Вероятности заменяются плотностями вероятности.
• Дельта-символ Кронекера заменяется дельта-функцией Дирака.
Присмотримся к этим инструментам внимательнее.
Суммы заменяются интегралами. Если мы по-настоящему хотели бы сохранить строгость, то начали бы с замены оси x дискретным набором точек, разделенных очень малыми интервалами ε, а затем перешли бы к пределу ε → 0. Понадобилось бы несколько страниц на то, чтобы обосновать каждый шаг. Но мы можем избежать этих хлопот с помощью нескольких интуитивных определений, таких как замена сумм интегралами. Схематически этот подход можно записать так:
Например, если надо вычислить площадь под кривой, ось x делится на крошечные отрезки, затем складываются площади большого числа прямоугольников, в точности как это делается в элементарном математическом анализе. Когда мы даем отрезкам сжиматься до нулевого размера, сумма становится интегралом.
Рассмотрим бра 〈Y| и кет |Y〉 и определим их внутреннее произведение. Очевидный способ сделать это состоит в замене суммирования в уравнении (1.2) на интегрирование. Мы определим внутреннее произведение так:
Вероятности заменяются плотностями вероятности. Далее, мы отождествим P(x) = Y*(x)Y(x) с плотностью вероятности для переменной x. Почему именно с плотностью вероятности, а не просто с вероятностью? Если x является непрерывной переменной, то вероятность, что она примет любое точно заданное значение, обычно равна нулю. Поэтому правильнее ставить вопрос так: какова вероятность того, что x лежит между двумя значениями x = a и x = b? Плотность вероятности определяется так, что эта вероятность дается интегралом
Поскольку полная вероятность должна быть 1, мы можем определить нормировку вектора как
Дельта-символ Кронекера заменяется дельта-функцией Дирака. До сих пор все было очень знакомо. Дельта функция Дирака — это что-то новенькое. Дельта-функция является аналогом дельта-символа Кронекера dij, который по определению равен 0, если i ≠ j, и 1, если i = j. Но его можно определить и по-другому. Рассмотрим любой вектор Fi в конечномерном пространстве. Легко заметить, что дельта-символ Кронекера удовлетворяет условию
Это связано с тем, что в данной сумме ненулевыми являются только члены с j = i. В ходе суммирования символ Кронекера отфильтровывает все компоненты F кроме Fi. Очевидным обобщением этого будет определить новую функцию, которая обладает таким же фильтрующим свойством, когда используется под интегралом. Другими словами, нам нужна новая сущность d(x – x’), обладающая тем свойством, что для любой функции F(x)
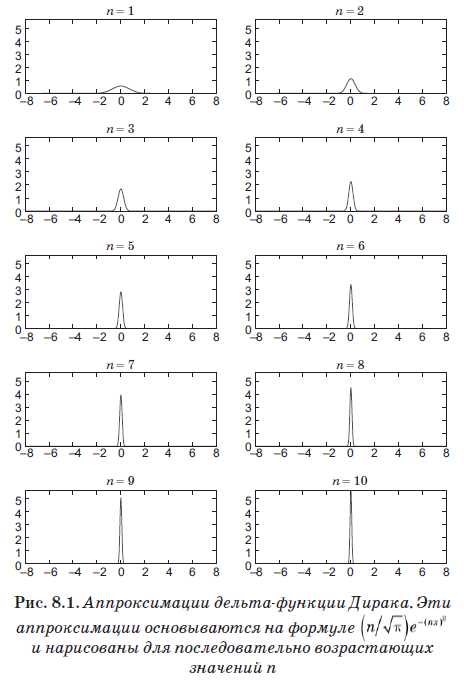
Уравнение (8.4) определяет новую сущность, называемую дельта-функцией Дирака, которая оказалась важнейшим инструментом в квантовой механике. Но несмотря на ее название, это в действительности не функция в обычном смысле. Она равна нулю везде, где x ≠ x’, но когда x = x’ она обращается в бесконечность. Фактически она бесконечна ровно настолько, чтобы площадь под d(x) была равна 1. Грубо говоря, эта функция отлична от нуля на бесконечно малом интервале ε, но на этом интервале имеет значение 1/ε. Таким образом, площадь под ней равна 1, и, что важнее, она удовлетворяет уравнению (8.4). Функция
достаточно хорошо аппроксимирует дельта-функцию при очень больших значениях n. На рис. 8.1 показана эта оптимизация при увеличивающихся значениях n. Несмотря на то что мы остановились на n = 10, то есть очень небольшом значении, обратите внимание, что график уже стал очень узким и резким пиком.
» Более подробно с книгой можно ознакомиться на сайте издательства
» Оглавление
» Отрывок
Для читателей данного блога скидка 20% по купону — Сасскинд
habr.com
