Линейные дифференциальные уравнения первого порядка примеры решений – Линейные дифференциальные уравнения первого порядка, примеры, решение – смотреть онлайн видео урок бесплатно! Автор: alWEBra – Дифференциальные уравнения
- Комментариев к записи Линейные дифференциальные уравнения первого порядка примеры решений – Линейные дифференциальные уравнения первого порядка, примеры, решение – смотреть онлайн видео урок бесплатно! Автор: alWEBra – Дифференциальные уравнения нет
- Советы абитуриенту
Тема 6. Дифференциальные уравнения
177
Программный объем темы:
Дифференциальные уравнения 1-го порядка. Задача Коши. Теорема существования и единственности решения задачи Коши. Понятие об особых решениях дифференциальных уравнений. Основные классы уравнений, интегрируемых в квадратурах.
Дифференциальные уравнения высших порядков. Задача Коши. Понятие о краевых задачах для дифференциальных уравнений. Теорема существования и единственности решения задачи Коши. Уравнения, допускающие понижение порядка.
Линейные дифференциальные уравнения с постоянными коэффициентами (однородные и неоднородные). Понятие общего решения. Метод вариации произвольных постоянных.
Линейные дифференциальные уравнения с постоянными коэффициентами с правой частью специального вида.
Задача Коши для нормальной системы дифференциальных уравнений. Теорема существования и единственности решения задачи Коши. Метод исключения. Векторно-матричная запись нормальной системы. Структура общего решения.
Нормальные системы линейных дифференциальных уравнений с постоянными коэффициентами. Решение в случае простых корней характеристического уравнения.
Дифференциальное уравнение 1-го порядка – уравнение, связывающее независимую переменную, искомую функцию и ее первую производную
.
Решением
дифференциальных уравнений называется
любая действительная функция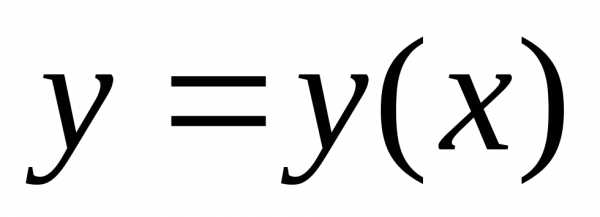
, определенная
на некотором интервале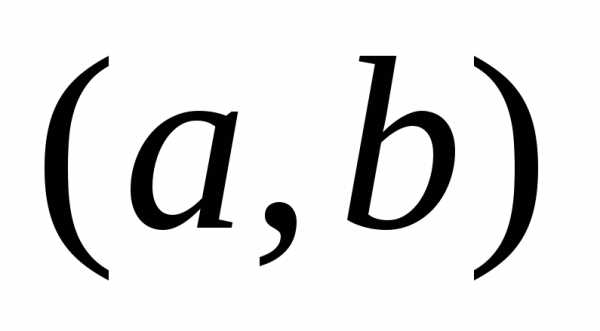 
Если функция, являющаяся решением дифференциального уравнения, определена в неявном виде: , то называется интегралом данного дифференциального уравнения.
Рассмотрим некоторые типы дифференциальных уравнений 1-го порядка:
Уравнения с разделяющимися переменными
,
или .
Разделение переменных производится следующим образом:
,
которые интегрируются
;
.
Пример. Найти общее решение дифференциального уравнения
,
,
,
,
,
,
– общий интеграл уравнения.
Пример. Найти частное решение дифференциального
уравнения.
,
удовлетворяющее начальному условию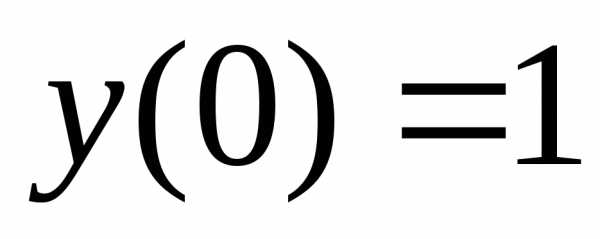
,
,
,
,
,
.
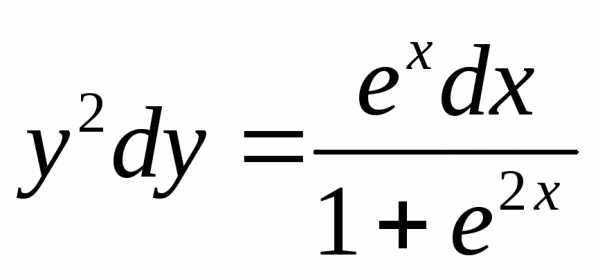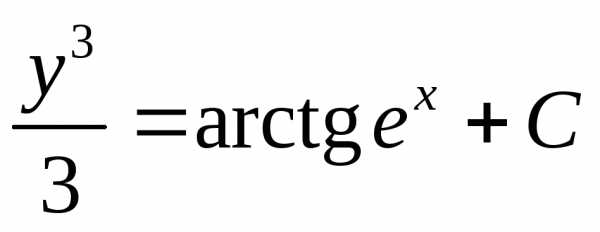Общее решение.
Используем начальные условия, определим значение произвольной постоянной:
,
.
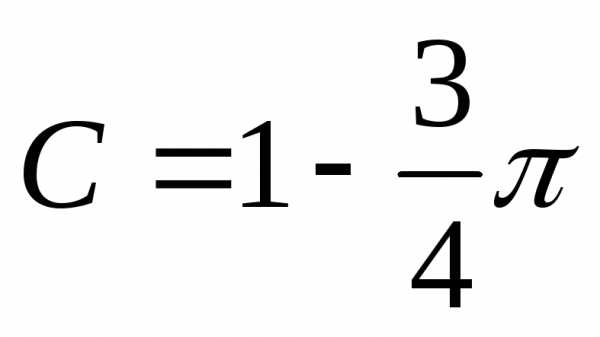Следовательно, частное решение:
.
Однородные дифференциальные уравнения 1-го порядка
Уравнение называется
однородным, если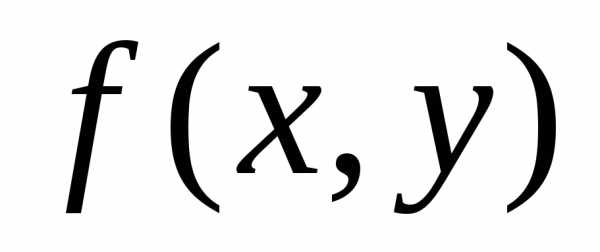 
–
однородная функция нулевого измерения
относительно своих аргументов, т.е.
.
Решение
выполняется с помощью замены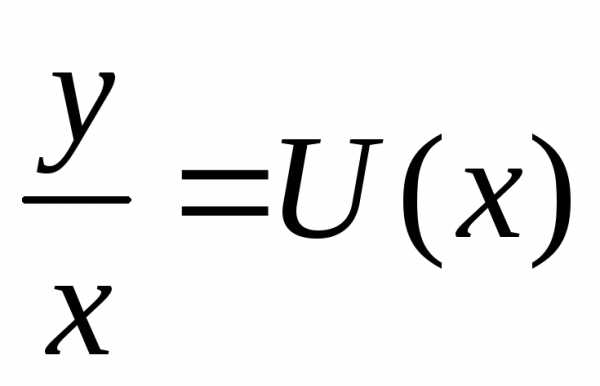 
.
и сводится к уравнению с разделяющимися переменными.
Пример.
,
,
замена ,
,
,
,
,
,
,
;
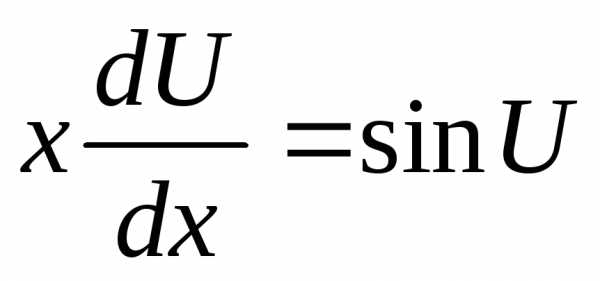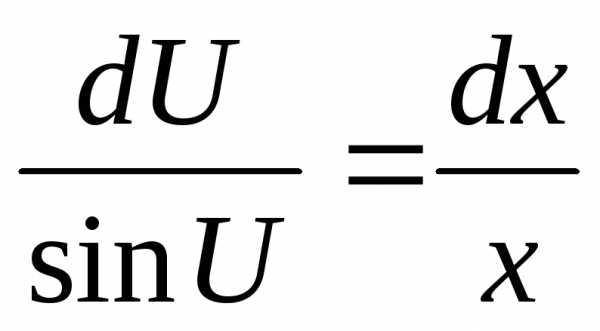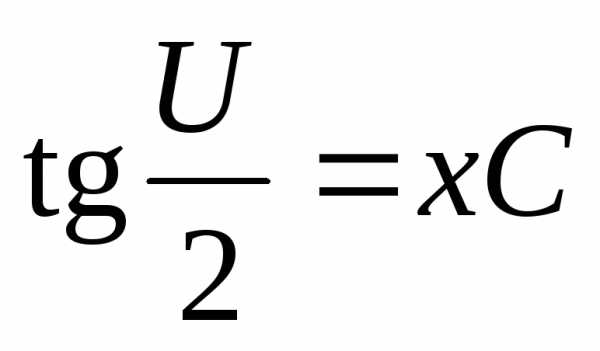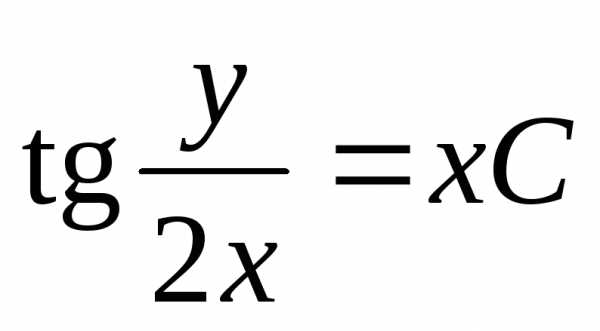– общее решение.
Найдем
,
используя начальное условие
–
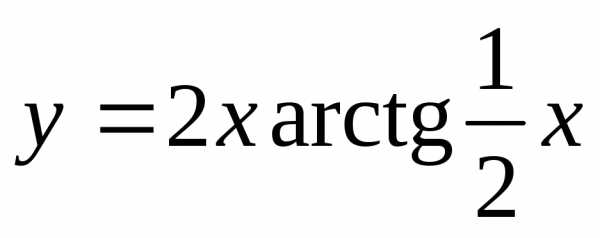частное решение.
Линейные дифференциальные уравнения 1-го порядка. Уравнение Бернулли
Уравнение
,
линейное относительно неизвестной
функции и ее производной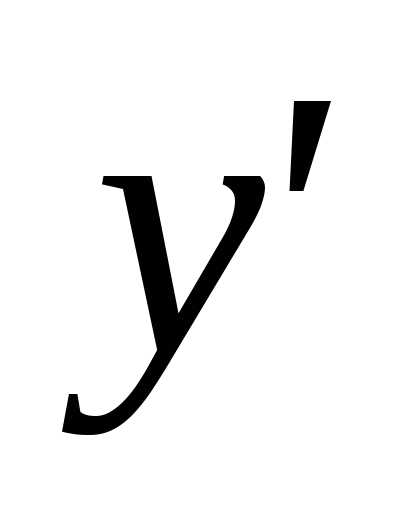
, называется
неоднородным линейным дифференциальным
уравнением первого порядка. Функции 
и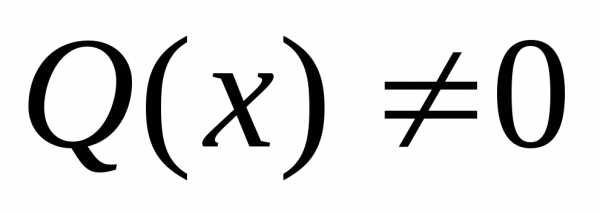
должны
быть непрерывными на отрезке
для того,
чтобы выполнились условия теоремы
Коши существования и единственности
решения.
Для решения выполняем замену
,
т.е. общее решение всегда можно записать в виде
Пример:
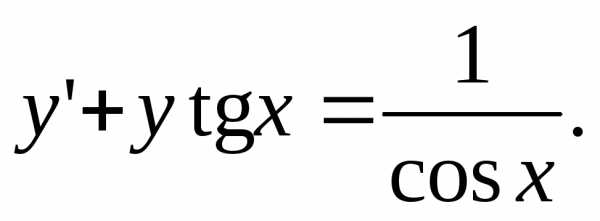
Ищем
решение в виде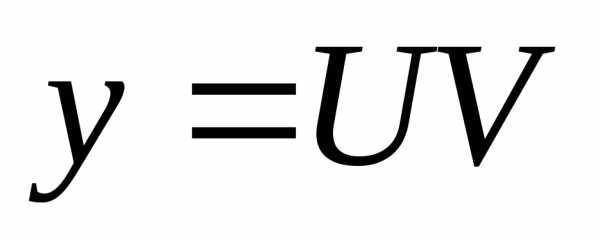
, где
,
,
.
Пример:
,
,
,
,
,
.
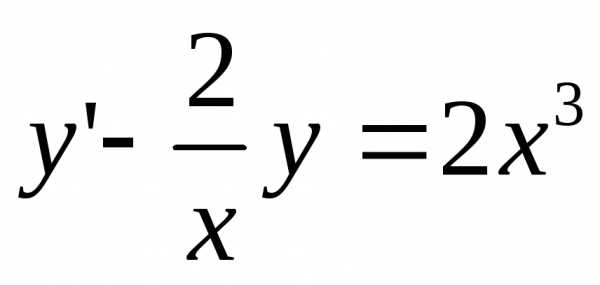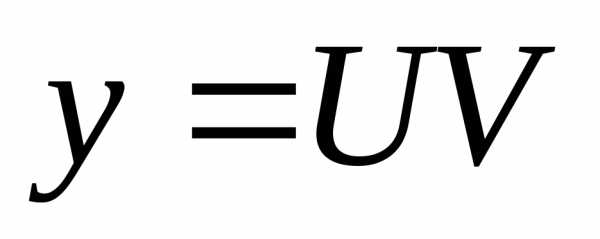Уравнение Бернулли
,
замена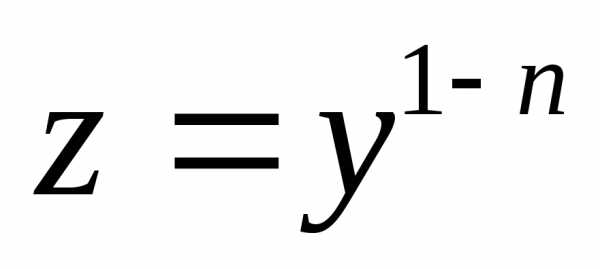 
Пример:
или ,
,
,
,
,
,
,
,
.
Пример решения задачи на составления дифференциальных уравнений.
Задача. Записать уравнения кривой, проходящей
через т. 
и обладающей следующим свойством:
площадь треугольника, образованного
радиус-вектором любой точки кривой,
касательной в этой точке и осью абсцисс,
равна 2.
Как видно из рисунка, .
Из 
получаем
,
,
,
,
.
Поставим
в это равенство выражение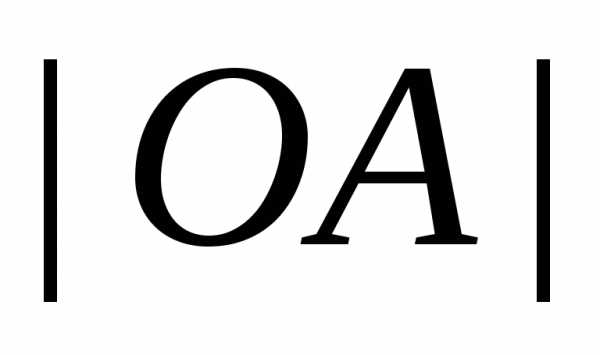 
и
и
придем к дифференциальному уравнению
,
,
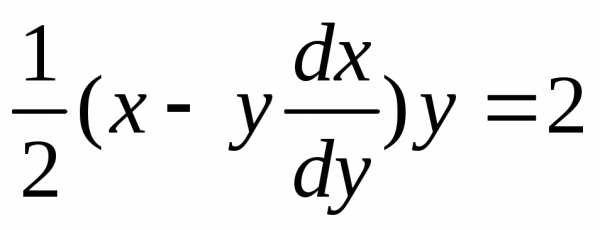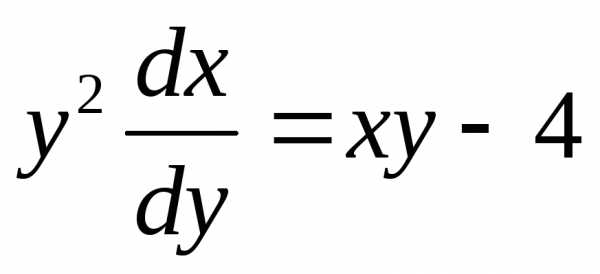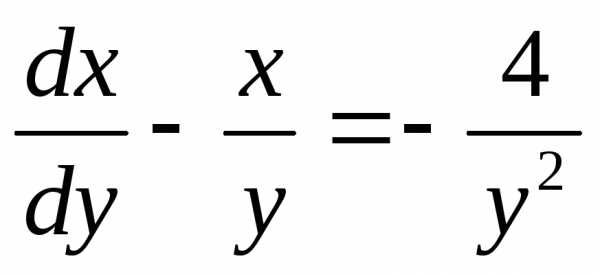-линейное
уравнение 1-го порядка. Решаем его с
помощью подстановки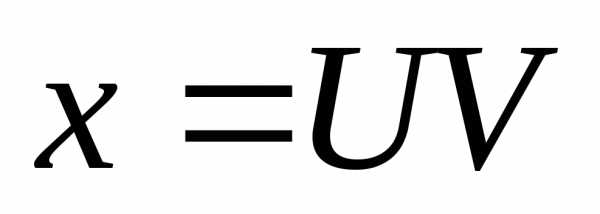 
,
,
,
,
,
,
,
,
.
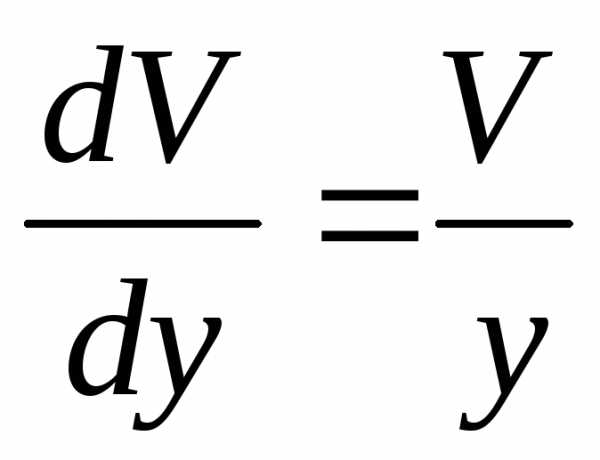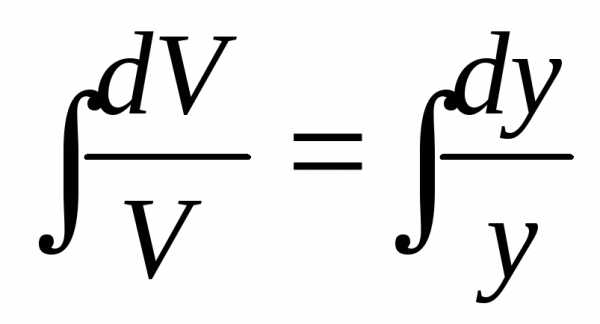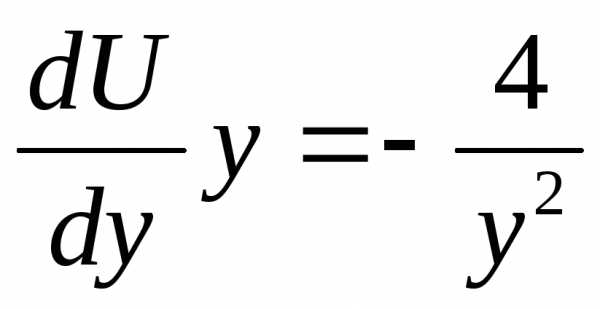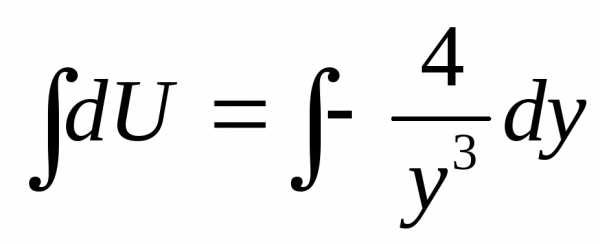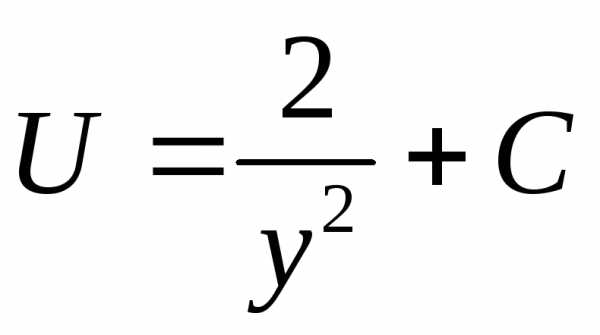
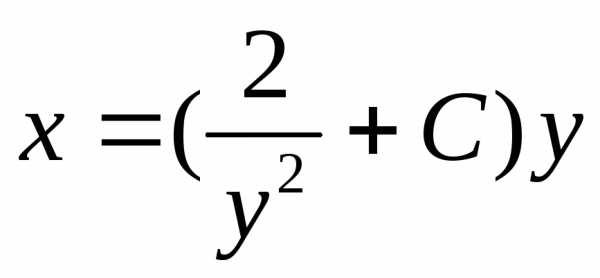Ответ: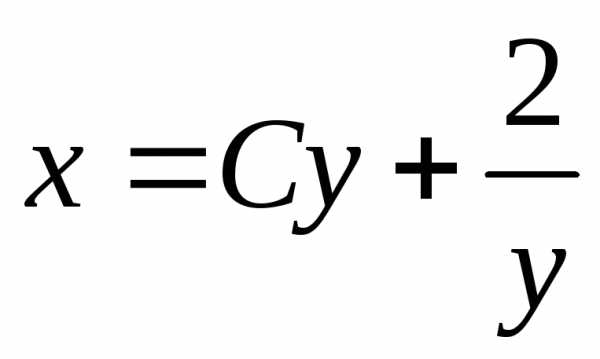 
,
искомая кривая проходит через точку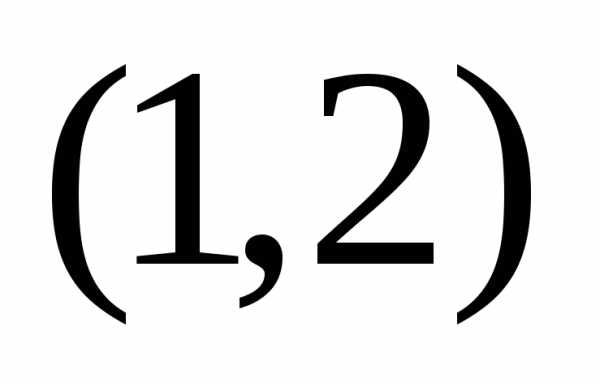
поэтому;
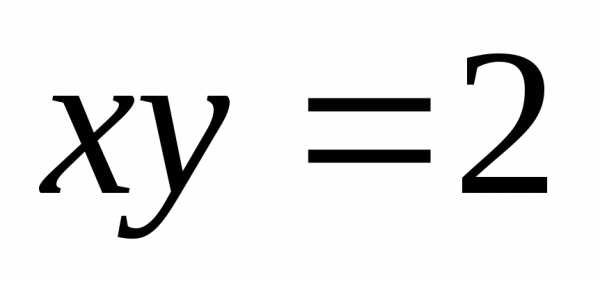-данная
кривая гипербола.
Перейдем теперь к дифференциальным уравнениям 2-го порядка, допускающим понижения порядка.
-общее решение такого вида находим методом 2-кратного интегрирования.
Пусть дифференциальное уравнение 2-го порядка не содержит искомой функции .
В этом случае выполняется замена и уравнение становиться уравнениемпервого порядка.
После
нахождения
находим
.
Пример.,
,
-уравнение 1-го порядка с разделяющимися переменными.
,
,
.
Дифференциальное уравнение 2-го порядка не содержит независимую переменную .
В этом случае выполняется замена
,
После чего уравнение сводится к уравнению 1-го порядка.
Пример:,
,
.
Далее рассмотрим линейные дифференциальные уравнения с постоянными коэффициентами.
–
не-однородное уравнение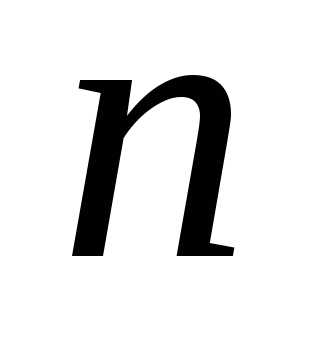 
-го
порядка.
–
однородное уравнение,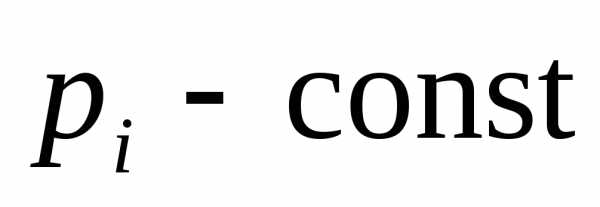
.
Составляется характеристическое уравнение
.
Пример:
Характеристическое уравнение ,
Находятся его корни: .
Корни характеристического уравнения могут быть:
различные действительные;
действительные равные;
комплексные сопряженные.
Пусть – линейное однородное дифференциальное уравнение 2-го порядка с постоянными коэффициентами.
-характеристическое уравнение.
1)
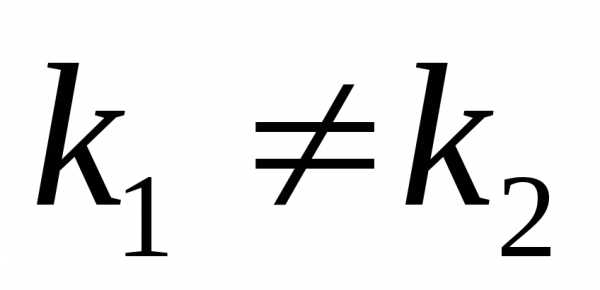-действительные,
решение запишется в виде
.
2) 
-корни
равные, решение имеет вид
.
3) – решение имеет вид
.
Примеры:
1),
,
,
.
2),
,
,
.
3),
,
,
.
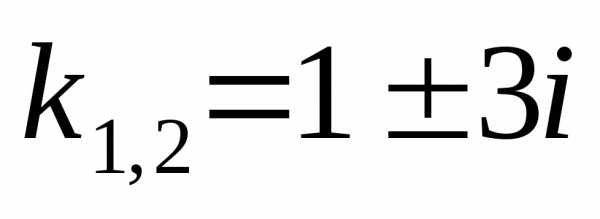4),
,
,
.
Если уравнение с постоянными коэффициентами неоднородное, то его решение состоит из суммы решений: общего решения однородного уравнения и частного решения неоднородного уравнения, которое ищем по виду правой части.
Пусть
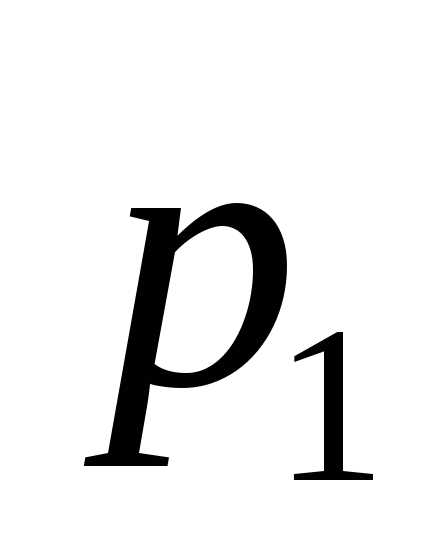и
-сonst,
то
,
где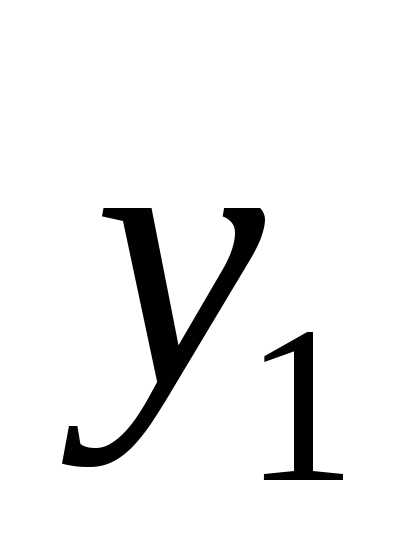
-общее
решение однородного уравнения,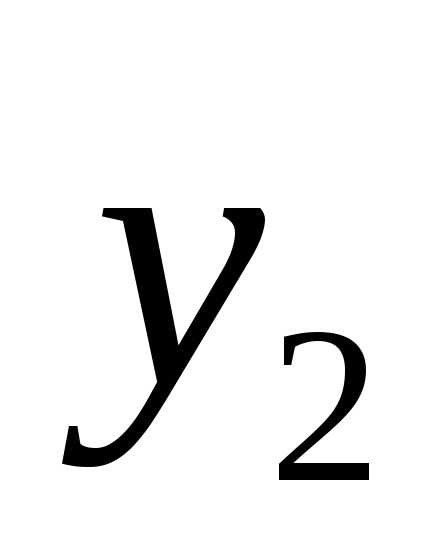
-частное решение, которое ищем в
зависимости от вида, а именно:
1),
где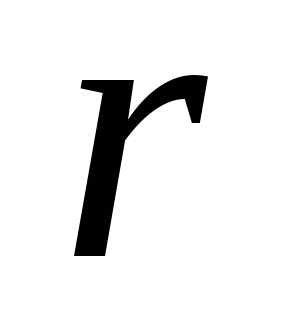 
–
число коней характеристического
уравнения, равных 0;
2) ,
где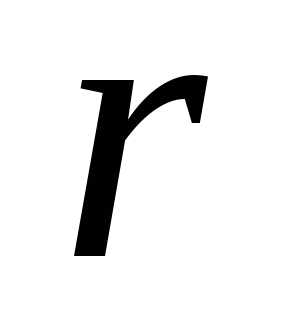 
–
число корней характеристического
уравнения, равных;
3),
где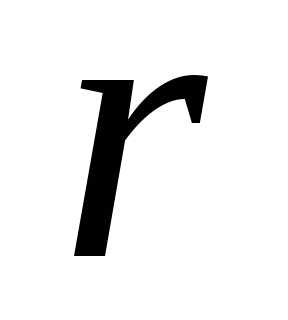 
–
число корней характеристического
уравнения, равных
;
4) ,
,
где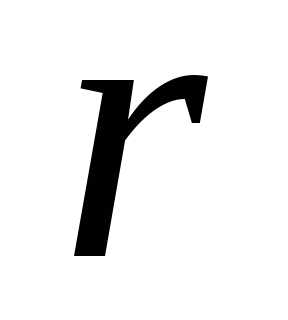 
– число корней характеристического
уравнения, равных
.
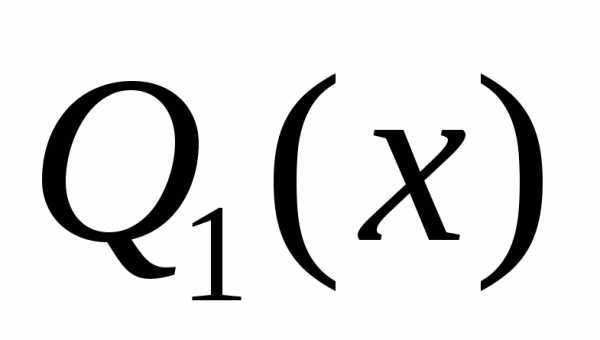и
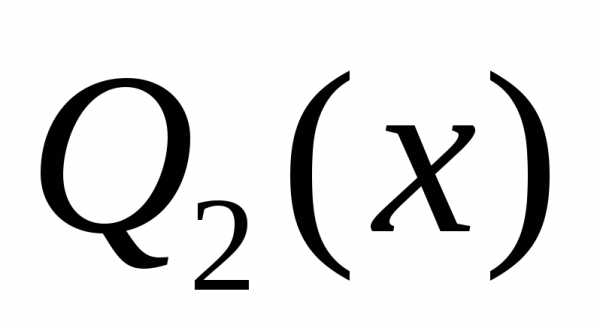многочлены
степени
,
где
.
Пример:
,
,
,
,
,
, так как ;
, так как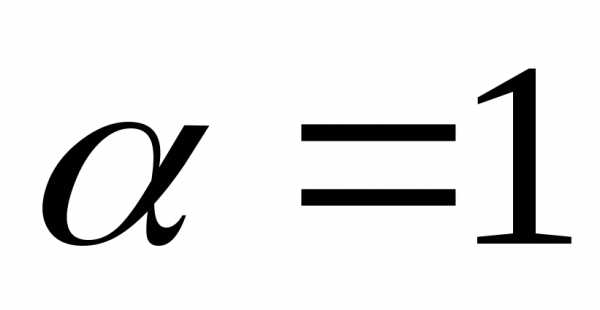 
и корень характеристического уравнения
,
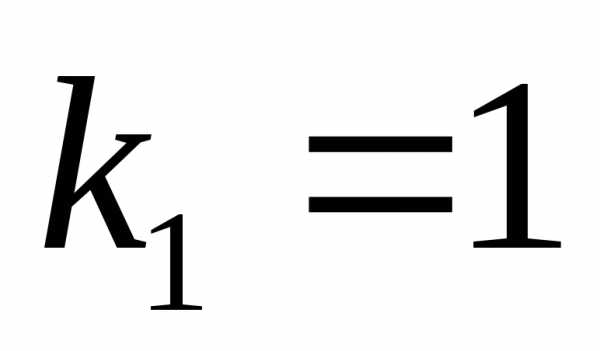то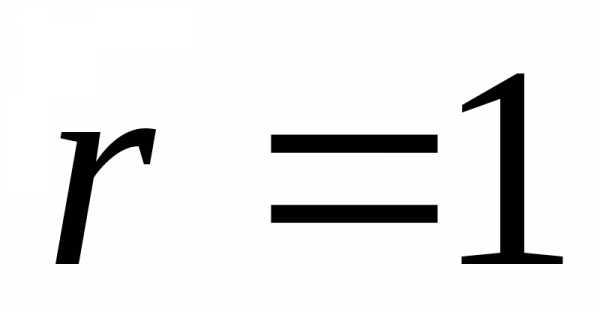
,
.
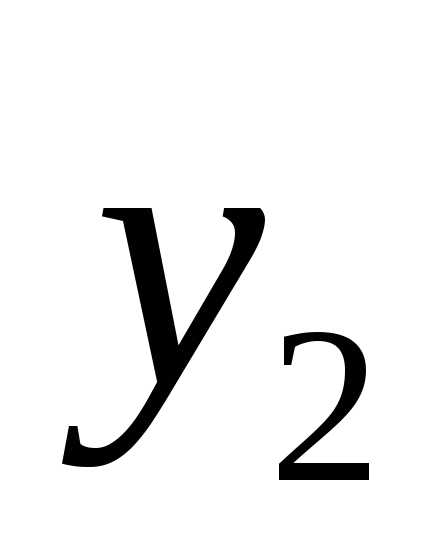-решение,
подставляем его в уравнение и находим
неизвестные коэффициенты 
и
:
.
Подставив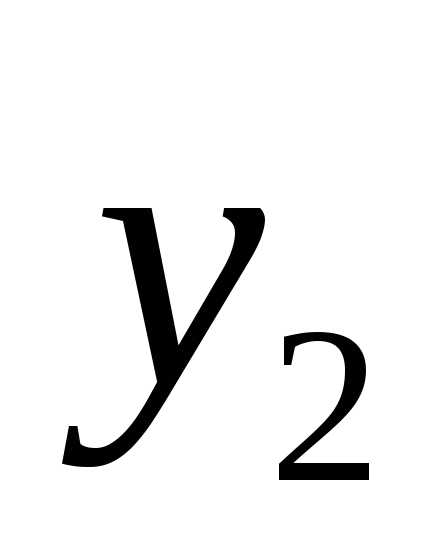
,
,
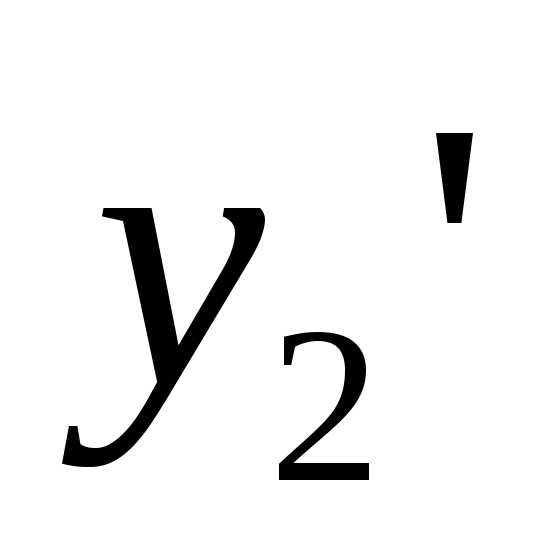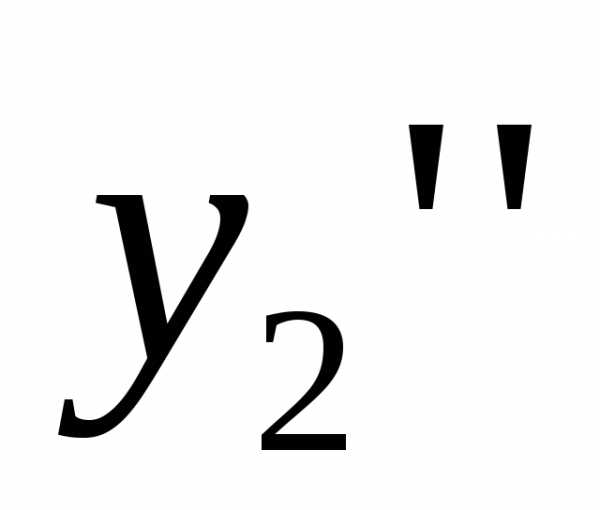в
исходное уравнение и приравнивая
коэффициенты в левой и правой частях
при одинаковой степени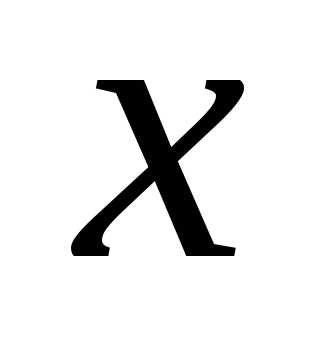
,
получаем систему для нахождения
и
.
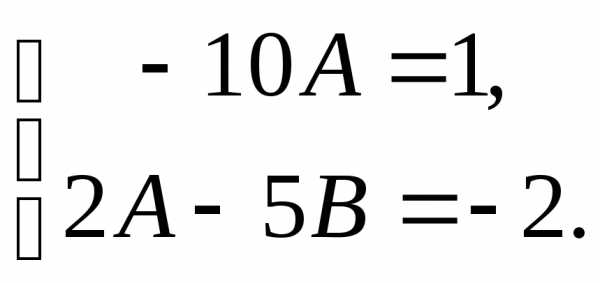
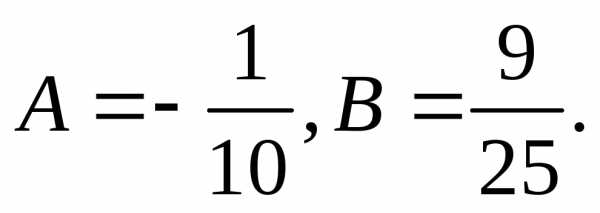
Записываем решение
.
Общим решением уравнения будет
,т.е.
.
Решение дифференциального уравнения методом вариаций
произвольных постоянных
.
Решаем соответствующее однородное уравнение
.
Общее решение однородного уравнения будет
.
Считая,
что 
и
– функции, зависимые от
,
.
Определим 
и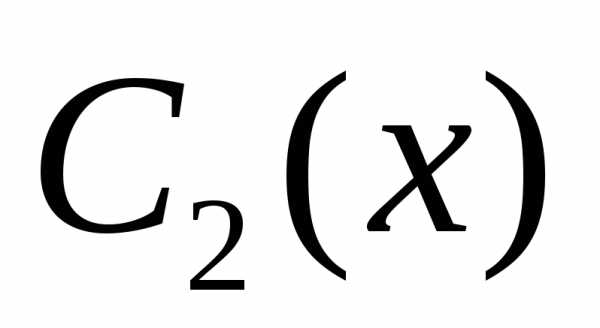
из
системы
которая для данного уравнения имеет вид
находим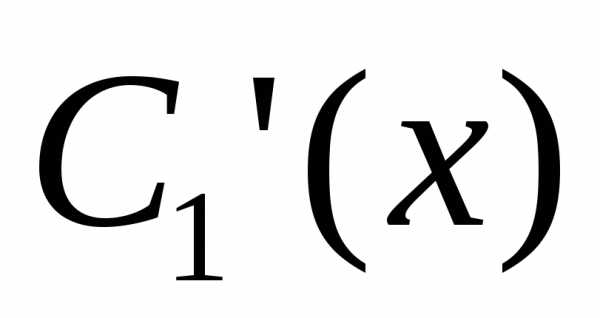 
и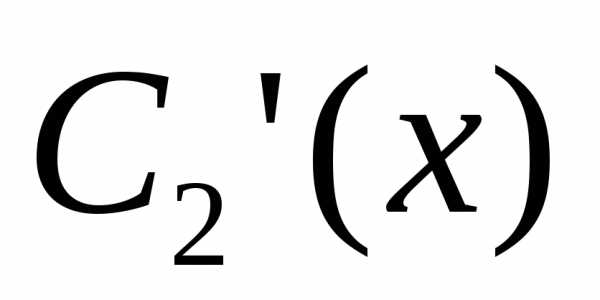
из
этой системы, а затем
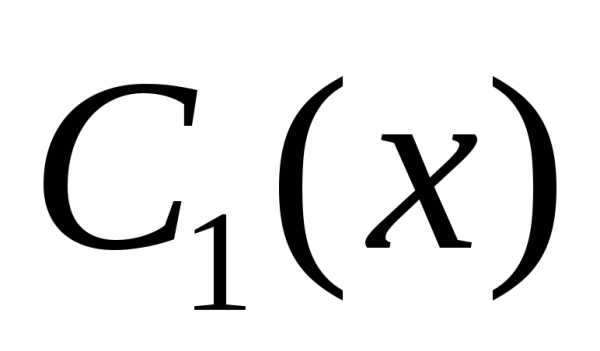и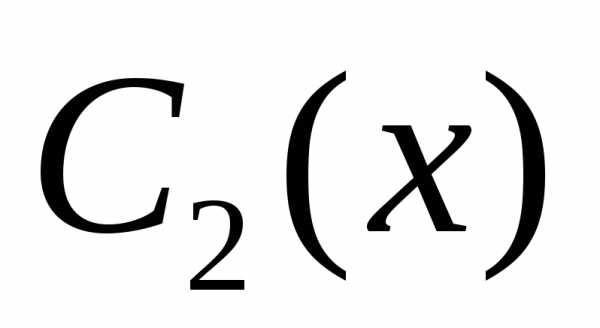
:
;
.
Общее
решение будет выглядеть 
:
.
Пример: решить систему дифференциальных уравнений:
.
Продифференцируем
первое уравнение по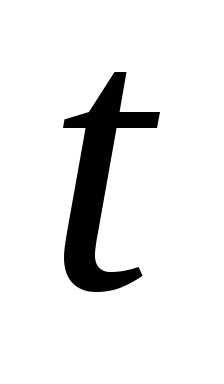 
:
и
заменим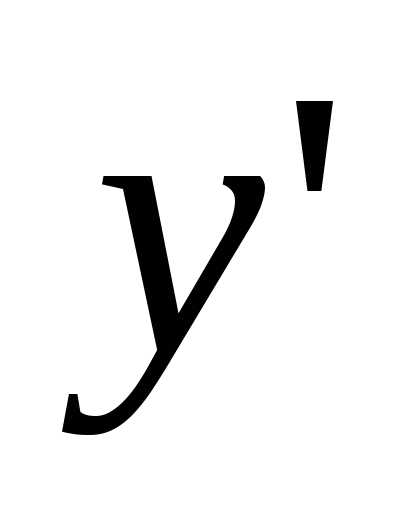
из
второго уравнения:
.
Окончательно ,
-однородное линейное уравнение с постоянными коэффициентами.
.
Следовательно, решение
,
из первого уравнения,
поэтому найдём
и подставим
,
.
Контрольная работа №6 по теме
studfiles.net
Линейные дифференциальные уравнения первого порядка.
Филиппов А. Ф. Сборник задач по дифференциальным уравнениям. Научно-издательский центр “Регулярная и хаотическая динамика”. 2000.
1. Линейные уравнения первого порядка.
Уравнение $$y’+P(x)y=Q(x)\qquad (1)$$ называется линейным. Чтобы его решить, надо сделать замену переменных $y=u(x)v(x),$ где $u(x) – $ решение однородного уравнения $u’+P(x)u=0.$ Это уравнение решается методом разделения переменных.
Далее, делаем обратную замену. $y’=(uv)’=u’v+uv’.$ Следовательно,
$$u’v+v’u+P(x)uv=Q(x)$$
$$v(u’+P(x)u)+v’u=Q(x).$$
Заметим, что $u’+P(x)u=0.$ Следовательно, получили уравнения с разделяющимися переменными $$v’u=Q(x)\\ v’=\frac{Q(x)}{u(x)}\Rightarrow v(x)=\int\frac{Q(x)}{u(x)}dx+C.$$
2. Некоторые уравнения становятся линейными, если поменять местами искомую функцию и независимую переменную. Например, уравнение $y=(2x+y^3)y’,$ в котором $y$ является функцией от $x, -$ нелинейное. Запишем его в дифференциалах: $$ydx-(2x+y^3)dy=0.$$ Так как в это уравнение $x$ и $dx$ входят линейно, то уравнение будет линейным, если $x$ считать искомой функцией, а $y -$ независимым переменным. Это уравнение может быть записано в виде $$\frac{dx}{dy}-\frac{2}{y}x=y^2$$ и решается аналогично уравнению (1).
3. Уравнение Бернулли.
Чтобы решить уравнение Бернулли, то есть уравнение $$y’+a(x)y=b(y)y^n, \qquad (n\neq 1),$$ надо обе его части разделить на $y^n$ и сделать замену $\frac{1}{y^{n-1}}=z.$ После замены получается линейное уравнение, которое можно решить вышеизложенным способом.
4. Уравнение Рикатти.
Уравнение Рикатти, то есть уравнение $$y’+a(x)y+b(x)y^2=c(x),$$ в общем случае не решается в квадратурах. Если же известно одно частное решение $y_1(x),$ то заменой $y=y_1(x)+z$ уравнение Рикатти сводится к уравнению Бернулли и таким образом может быть решено в квадратурах.
Иногда частное решение удобно подобрать, исходя из вида свободного члена уравнения (члена, не содержащего $y$). Например, для уравнения $y’+y^2=x^2-2x$ в левой части будут члены, подобные членам в правой части, если взять $y=ax+b.$ Подставляя в уравнение и приравнивая коэффициенты при подобных членах, найдем $a$ и $b$ (если частное решение указанного вида существует, что вовсе не всегда бывает). Другой пример: для уравнения $y’+2y^2=\frac{6}{x^2}$ те же рассуждения побуждают нас искать частное решение в виде $y=\frac{a}{x}.$ Подставляя $y=\frac{a}{x}$ в уравнение, найдем постоянную $a.$
mathportal.net
Приводящиеся к линейным дифференциальные уравнения первого порядка
Рассмотрены дифференциальные уравнения, приводящиеся к линейным дифференциальным уравнениям первого порядка. Дан пример подробного решения дифференциального уравнения, приводящегося к линейному уравнению.
К линейным уравнениям первого порядка приводится уравнения вида:
(1) ,
где z – функция от y; p и q – функции от x.
Действительно, по правилу дифференцирования сложной функции:
.
Подставляя в (1), получаем уравнение, линейное относительно z:
.
Дифференциальные уравнения, линейные относительно переменной x
Ранее мы рассматривали уравнения, линейные относительно переменной y. То есть мы считали, что x является независимой переменной, а y является зависимой переменной. Однако, всегда стоит иметь в виду, что возможен противоположный подход. То есть можно считать переменную y независимой переменной, а x – зависимой переменной. На практике часто встречаются задачи, в которых уравнение линейно относительно переменной x, а не y. В общем виде такое уравнение можно записать так:
(2) ,
где P, Q, R –функции от y.
Покажем, что это уравнение линейно относительно переменной x. Для этого выполняем преобразования. Представим производную в виде отношения дифференциалов:
.
Тогда уравнение (2) примет вид:
.
Умножаем на и выполняем алгебраические преобразования:
;
.
Разделив на R(y), приводим уравнение к виду:
,
где .
Это – линейное относительно x дифференциальное уравнение.
Пример решения дифференциального уравнения, приводящегося к линейному уравнению первого порядка
Решить уравнение:
(П.1) .
Решение
Подставим в (П.1):
.
Считаем, что y – это независимая переменная, а x – зависимая. То есть x – это функция от y. Умножим на :
(П.2) .
Делаем подстановку:
.
Здесь z – сложная функция от y, .
Дифференцируем по y. По правилу дифференцирования сложной функции:
.
Подставляем в (П.2):
;
.
Это линейное, относительно z, дифференциальное уравнение. Решаем его с помощью интегрирующего множителя. Умножаем уравнение на интегрирующий множитель e y:
;
;
.
Интегрируем по частям:
;
;
;
.
Переходим к переменной x:
;
.
Ответ
.
Использованная литература:
Н.М. Гюнтер, Р.О. Кузьмин, Сборник задач по высшей математике, «Лань», 2003.
Автор: Олег Одинцов. Опубликовано: Изменено:
1cov-edu.ru
Линейные дифференциальные уравнения первого порядка. Метод Бернулли
Все кто ищет готовые ответы на линейные дифференциальные уравнения пришли по правильному адресу. У нас Вы сможете не только получить быстрый ответ, но и научиться методике решения уравнений. Будет ли сложной схема Бернулли для линейных уравнений зависит от Вашего уровня подготовки. Разберите внимательно приведенные ответы и сделайте выводы, что и как Вам нужно углубленно изучить.
Линейным дифференциальным уравнением первого порядканазывается уравнение вида y’+p(x)*y=g(x), где p(x) и g(x) – непрерывные на определенном промежутке функции.
Алгоритм метода Бернулли
1. Решение линейного дифференциального уравнения необходимо представить в виде произведения двух неизвестных функций y=u*v от аргумента u=u(x),v=v(x). Одну из этих функций можно выбрать произвольно, а вторая определяется из дифференциального уравнения.
2. По правилу производная произведения равна y=u*v,то y’=u’v+uv’.
3. Подставим запись функции y=u*v и производной y’=u’v+uv’ в уравнение y’+p(x)*y=g(x) и получим u’v+uv’+p(x)*u*v= g(x). Сгруппируем второй и третий слагаемые, вынеся общий множитель (u) за скобки и придем к диф. уравнению u’v+u(v’+p(x)*v)=g(x).
4. Сперва определяем частное решение v=v(x), для этого решаем диф. уравнения v’+p(x)*v=0 и за произвольную постоянную интегрирования берем ноль (С=0). Данное уравнение является дифференциальным уравнением с разделяющимися переменными.
5. Далее подставим найденную функцию v=v(x) в исходное диф. уравнение u’v+uv’+p(x)*u*v= g(x), которое при этом упростится до вида u’v+u*0=g(x), то есть к дифференциальному уравнению с разделяющимися переменными u’v(х)=g(x) относительно u(x). Из этого уравнения находим u=u(x)+С.
6. Имея u=u(x) и v=v(x) находим общее решение ДУ через произведение y=u*v=( u(x)+С)* v(x).
7. Если задана задача Коши то с дополнительной условия на решение y(x0)=y0 определяем сталую С.
Пример 1. Найти решение задачи Коши
Решение:Имеем неоднородное дифференциальное уравнение первого порядка. Запишем его в правильном виде, для этого перенесем в правую сторону функцию
Далее по схеме Бернулли делаем замену переменных y=u*v, y’=u’v+uv’, где u=u(x) і v=v(x).
Учитывая что множители в левой части уровне
и y2=u2v2
получим следующее уравнение
Согласно алгоритму Бернулли уравнение разделим на 2, для этого дужку слева (выделена черным) приравняем к нулю
Сводим к дифференциальному уравнению с разделенными переменными
и решаем интегрированием
В результате получили экспоненту с отрицательным показателем синуса. При этом исходное дифференциальное уравнение достаточно упростится для поиска второй неизвестной пока функции
Перенесем экспоненту с отрицательным показателем в правую сторону
и сведем к ДУ с разделенными переменными
Интегрированием уравнения в дифференциалах
находим решение дифференциального уравнения
Как описано в начале, общее решение дифференциального уравнения равно произведению функций
Но это еще не конечная ответ к задаче. Найдем частичное решение дифференциального уравнения (задача Коши), для этого определим постоянную с начального условия на функцию
Сталая равна нулю, это позволяет упростить формулу решения диф. уравнения, хотя мало кто из Вас увидит эту подсказку
Мы нашли частичный решение дифференциального уравнения и он равен экспоненте в степени “икс” y=ex.
Пример 2. Решить дифференциальное уравнение та задачу Коши
Решение:Задано неоднородное дифференциальное уравнение первого порядка, которое перепишем в виде
Выполняем замену переменных в уравнении
, где “у” и “в” принимают функциональные зависимости
Находим выражения которые фигурируют в записи
и подставляем в исходное дифференциальное уравнение
Далее схема вычислений заключается в разделении переменных. По алгоритму Бернулли выражение, содержащее “v” приравняем к нулю
Записываем уравнение в дифференциалах
Видим что имеем уравнение с разделяющимися переменным, поетому целесообразно разделить переменные
Проинтегрировав обе части
получим логарифм и синус.
Далее экспонируем обе части и таким образом находим одну из неизвестных функций
Исходное дифференциальное уравнение при этом упростится к виду
Экспоненту в отрицательном показателе переносим вправо от знака равенства
Далее распишем уравнения через дифференциалы (/2)
и сведем к уравнению с разделенными переменными
Интеграл в правой части выглядит тяжелым для высчисления, но если внести дужку под дифференциал, то получим показатель экспоненты
Окончательно после интегрирования получим
Общий интеграл дифференциального уравнения записываем через произведение функций
Чтобы найти частичное решение дифференциального уравнения (задачи Коши) используем начальное условие
Из него определим постоянную и подставим в уравнение частного решения дифференциального уравнения
На этом и построен алгоритм Бернулли вычислений дифференциальных уравнений такого типа. Используйте алгоритм решения уравнения Бернулли ко всем подобным дифференциальным уравнениям.
yukhym.com
Линейные дифференциальные уравнения первого порядка [wiki.eduVdom.com]
subjects:diffury:линейные_уравнения_первого_порядка
Линейным дифференциальным уравнением 1-ого порядка называется уравнение, линейное относительно неизвестной функции и её производной $$ \frac{dy}{dx} +p(x)y =Q(x) \qquad (1)$$
Решение линейного уравнения ищем в виде $y=u(x)v(x)$
Подставляя в (1), после преобразования получаем $$ u \left ( \frac{dv}{dx} + p(x)v \right ) +V\frac{du}{dx} =Q(x) $$
Выберем v такой чтобы $\frac{dv}{dx} + p(x)v =0$ найдём u(x) , и следовательно получим решение $y=uv$
Пример 1
Решить дифференциальное уравнение: ${xy}’-2y=4x^{4}-x$
Решение дифференциального уравнения:
Пример 2. Решить задачу Коши $$ {y}’-y=-e^{-x} \,,\, y|_{x=0}=2 $$
Решение. Это линейное уравнение. Ищем общее решение в виде $y=u(x)v(x)$ , имеем ${y}’={u}’v+u{v}’$ . Подставляя выражения для y и ${y}’$ в данное уравнение, будем иметь
$$
u({v}’-v)+{u}’v=-e^{-x}
\\
u \left (
\frac{dv}{dx} -v
\right )
+\frac{du}{dx}v
=e^{-x}
\\
\frac{dv}{dx}-v=0
\;;\;
\frac{dv}{v}=dx
\;;\;
\ln{|v|}=x
\;;\;
v=e^{x}
$$
Для определения u имеем уравнение
$$
{u}’v=-e^{-x}
\\
\frac{du}{dx}e^{x}=-e^{-x}
\;;\;
\frac{du}{dx}=-e^{-2x}
\;;\;
u=\frac{ e^{-2x} }{2} +c
\\
y=uv=e^{x} \left(
\frac{ e^{-2x} }{2} +c
\right )
=\frac{ e^{-x} }{2} +Ce^{x}
$$
Найдём C: $2=\frac{1}{2}+c \,,\, c=\frac{3}{2}$;
Итак, решением поставленной задачи Коши будет $$ y=\frac{1}{2} \left ( \frac{1}{e^{x}} +3e^{x} \right ) $$
subjects/diffury/линейные_уравнения_первого_порядка.txt · Последние изменения: 2014/12/15 20:27 — ¶
wiki.eduvdom.com
6.08. Линейные неоднородные дифференциальные уравнения 1-го порядка
Это – уравнения вида
(3.12)
Докажем Теорему:
Общее решение уравнения (3.12), содержащее все его частные решения, может быть получено по формуле
, (3.13)
Где – общее решение линейного однородного уравнения (3.9), а – какое – либо частное решение линейного неоднородного уравнения (3.12).
Доказательство. Пусть – некоторое конкретное частное решение уравнения (3.12), а – любое другое его частное решение. Тогда одновременно имеем:
Вычитая из верхнего уравнения нижнее, получим:
То есть функция удовлетворяет линейному однородному уравнению (3.9), а значит, эта функция входит в его общее решение (3.11). Таким образом,
Теорема доказана.
Согласно формуле (3.13), определяющей структуру общего решения линейного неоднородного уравнения (3.12), получение этого общего решения равносильно решению двух частных проблем.
Проблема 1: решить линейное однородное дифференциальное уравнение (3.9) и получить его общее решение (3.11).
Проблема 2: найти (или подобрать) какое – либо частное решение неоднородного уравнения (3.12).
Схема решения первой из этих проблем указана выше (см. (3.10)). А вторую проблему для произвольной функций можно решить так называемым Методом вариации произвольной постоянной.
Суть этого метода в следующем. Будем искать частное решение неоднородного дифференциального уравнения (3.12) в виде
(3.14)
То есть в виде, аналогичном виду (3.11) общего решения линейного однородного уравнения (3.9), только с заменой произвольной константы С на неизвестную функцию . Находя из (3.14)
(3.15)
И подставляя в уравнение (3.12) вместо и выражения (3.14) и (3.15) для и , получим:
(3.16)
Учитывая, что – одно из частных решений линейного однородного уравнения (3.9), получаем, что квадратная скобка в (3.16) равна нулю. Значит, (3.16) принимает вид:
(3.17)
Отсюда находим , а по ней и :
=
=| отбрасываем С, чтобы получить конкретную функцию | = (3.18)
Подставляя найденную функцию в формулу (3.14), получим искомое частное решение неоднородного уравнения (3.12). А затем, по формуле (3.13), получим и общее решение этого уравнения.
Пример 3. Решить дифференциальное уравнение
(3.19)
Решение. Данное уравнение
(3.20)
Имеет вид (3.12) при и , то есть является линейным неоднородным дифференциальным уравнением первого порядка. Следовательно, его общее решение, содержащее все его частные решения, может быть найдено по формуле (3.13). Найдем оба слагаемых этой формулы. Для этого решим следующие две проблемы.
Проблема 1. Решим соответствующее неоднородному уравнению (3.20) однородное уравнение
(3.21)
И найдем его общее решение . Для этого реализуем схему (3.10):
, где .
Итак,
() (3.22)
– общее решение линейного однородного уравнения (3.21).
Проблема 2. Найдем частное решение линейного неоднородного уравнения (3.20). Функция уже найдена. А функцию найдем по схеме (3.18):
(3.23)
Итак,
(3.24)
– частное решение линейного неоднородного дифференциального уравнения (3.20).
А теперь по формуле (3.13) с учетом (3.22) и (3.24) запишем и искомое общее решение линейного неоднородного уравнения (3.20):
(3.25)
Примечание. Довольно часто частное решение линейного неоднородного уравнения можно подобрать, не применяя метода вариации произвольной постоянной.
Рассмотрим, например, следующие неоднородные дифференциальные уравнения первого порядка (3.12) при постоянном :
1) 2) 3) … (3.26)
Частное решение каждого из таких уравнений можно подобрать, разыскивая его в форме, совпадающей с формой его правой части. То есть соответственно в форме:
1) ; 2) ; 3) ; … (3.27)
Здесь – неизвестные коэффициенты, которые найдутся, если подставить функцию вместе с её производной в соответствующее уравнение (3.26) и сравнить затем коэффициенты в левой и правой частях при одинаковых степенях . Этот метод подбора функции называется Методом неопределенных коэффициентов.
Пример 4. Методом неопределенных коэффициентов подобрать частное решение линейного неоднородного дифференциального уравнения первого порядка
(3.28)
Решение. Правая часть данного уравнения представляет собой квадратный трехчлен вида при А = 6, B = 0, С = -1. Поэтому и частное решение этого уравнения будем искать в виде квадратного трехчлена
(3.29)
Учитывая, что и подставляя и вместо и в уравнение (3.28), получим:
(3.30)
Если – частное решение уравнения (3.28), то после его подстановки в это уравнение должно получаться тождество – равенство, верное при любых Х. Значит, равенство (3.30) должно быть тождеством. А это будет, если
, откуда
Итак,
– частное решение уравнения (3.28). И в этом легко убедиться, сделав проверку.
| < Предыдущая | Следующая > |
|---|
matica.org.ua
