Маленький пластилиновый шарик массы m1 движется горизонтально со скоростью – Ответы@Mail.Ru: помогите с физикой
- Комментариев к записи Маленький пластилиновый шарик массы m1 движется горизонтально со скоростью – Ответы@Mail.Ru: помогите с физикой нет
- Советы абитуриенту
- 9. Закон сохранения импульса и момента импульса.
- 9. Закон сохранения импульса и момента импульса.
- 3.9. Кинетическая энергия. Мощность. Работа
- Домашняя работа_1_121251 – Стр 3
- Кто может за полтора часа решить восемь задач по Физике
- Закон сохранения импульса и момента импульса — Мегаобучалка
- Закон сохранения импульса и момента импульса
9. Закон сохранения импульса и момента импульса.
При взаимодействии частиц системы между собой полный вектор импульса системы остается постоянным в случаях, когда
а) , б)и время взаимодействия очень мало. В этих случаях, где–векторная сумма импульсов частиц, которые существовали до взаимодействия, –векторная сумма импульсов всех частиц, которые будут существовать после взаимодействия. Если , то сохраняется толькопроекция полного импульса системы на ось x, .
При взаимодействии частиц системы между собой полный вектор момента импульса системы остается постоянным в случаях, когда
а) , б)и время взаимодействия очень мало. В этих случаяхгде–векторная сумма моментов импульсов частиц, которые существовали до взаимодействия, –векторная сумма моментов импульсов
Момент импульса частицы , где– радиус-вектор частицы,– импульс частицы., где – угол между и. Для твердого тела, вращающегося вокруг закрепленной осиz , где – момент инерции тела относительно осиz, – угловая скорость.
9-1. Маленький пластилиновый шарик массы m1 движется горизонтально со скоростью . Под углом к направлению его движения летит второй шарик массы m2 со скоростью и сталкивается с первым. Шарики слипаются и движутся под углом к первоначальному направлению движения
А) первого шарика; Б) второго шарика.
Найдите .1 кг,2 кг,1 м/с,2 м/с,
а) = 30; б) = 45; в) = 60; г) 90.
А) Ответы: а) 0,448; б) 0,739; в) 1,155; г) 4
Б) Ответы: а) 0,103; б) 0,15; в) 0,192; г) 0,25
9-2. Маленький пластилиновый шарик массы m1 движется горизонтально со скоростью . Под углом к направлению его движения летит второй шарик массы m2 со скоростью и сталкивается с первым. Шарики слипаются и движутся под со скоростью. Найдите после удара
А) модуль скорости ; Б) модуль импульса шариков.
1 кг, 2 кг,1 м/с,2 м/с, а) = 30, б) = 45, в) = 60.
А) Ответы: а) 1,63 м/с; б) 1,59 м/с; в) 1,53 м/с
Б) Ответы: а) 4,89 кгм/с; б) 4,76 кгм/с; в) 4,58 кгм/с
9-3. Маленький пластилиновый шарик массы m1 движется горизонтально со скоростью . Перпендикулярно к направлению его движения летит второй шарик массыm2 со скоростью и сталкивается с первым. Шарики слипаются и далее движутся вместе. Найдите после удара
а) модуль импульса шариков; б) модуль скорости шариков.
1 кг, 2 кг,1 м/с,2 м/с.
Ответ: а) 4,123 кгм/с; б) 1,374 м/с
9-4. Маленький пластилиновый шарик массы m1 движется горизонтально со скоростью . Перпендикулярно к направлению его движения летит второй шарик массыm2 со скоростью и сталкивается с первым. Шарики слипаются и далее движутся вместе под углом к первоначальному направлению движения А) первого шарика; Б) второго шарика. Найдите и.
1 кг,2 кг,1 м/с,2 м/с.
А) Ответы: = 0,243;= 0,97
Б) Ответы: = 0,97;= 0,243
9-5. На горизонтальной плоскости лежит тонкий однородный стержень массы m =1 кг и длины l, который может вращаться вокруг вертикальной оси, проходящей через А) центр масс стержня С; Б) конец стержня О. Под углом =30 к стержню в той же плоскости движется маленький пластилиновый шарик такой же массы m со скоростью = 1 м/с. Шарик прилипает к концу стержня, и система приобретает угловую скорость вращения. Найти
а) угловую скорость вращения системы после удара, если l = 1 м;
б) длину стержня, если , = 1 рад/с
А) Б)
Ответы: Аа) 0,75 рад/с; Ба) : 0,375 рад/с; Аб) 0,75 м; Бб) 0,375 м
9-6. Тонкий однородный диск массы m = 1 кг и радиуса R может вращаться в вертикальной плоскости вокруг горизонтальной оси, проходящей
А) через его край О; Б) через его центр С. Под углом =30 а) к вертикали;
б) к горизонтали в плоскости вращения диска движется маленький пластилиновый шарик такой же массы m со скоростью = 1 м/с. Шарик прилипает к нижней точке неподвижно висящего диска, и система приобретает угловую скорость вращенияw.. Найти
1) угловую скорость вращения системы после удара, если R = 1 м;
2) Найти радиус диска, если = 1 рад/с,
Аа) Ба)Аб)Бб)
Ответы: 2) Аа) 0,182 м; Ба) 0,333 м; Аб) 0,315 м; Бб) 0,577 м.
9-7. Тонкий однородный стержень массы m = 1 кг и длины l может вращаться в вертикальной плоскости вокруг горизонтальной оси, проходящей через его конец. С разных сторон на стержень горизонтально в той же плоскости налетают два одинаковых пластилиновых шарика той же массы m с одинаковыми скоростями = 1 м/с. Первый шарик застревает в центре стержня, второй – в нижнем конце, и система приобретает угловую скорость. Найти
а) угловую скорость вращения системы после удара, если l = 1 м;
б) Найти длину стержня, если = 1 рад/с.
Ответы: а) 0,316 рад/с; б) 0,316 м
9-8. Тонкий однородный стержень массы m =1 кг и длины l может вращаться в вертикальной плоскости вокруг горизонтальной оси, проходящей через его конец O. Горизонтально в той же плоскости на стержень налетает пластилиновый шарик той же массы m со скоростью = 1 м/с. Шарик застревает в точкеА стержня на расстоянии х= от точки О, и система приобретает угловую скорость . Найти
а) угловую скорость вращения системы после удара, если l = 1 м;
б) Найти длину стержня, если = 1 рад/с.
Ответы: а) 0,837 рад/с; б) 0,837 м.
9-9э. Планета массой движется по эллиптической орбите, в одном из фокусов которой находится звезда массы.радиус-вектор планеты (см.рисунок). Выберите правильное утверждение:
а) момент импульса планеты относительно центра звезды меняется и максимален при наибольшем ее удалении от звезды
б) момент силы тяготения, действующей на планету (относительно центра звезды), изменяется, но направлен перпендикулярно плоскости орбиты
в) величина момента импульса планеты относительно центра звезды в любой момент времени определяется выражением
г) момент импульса планеты относительно центра звезды не изменяется
9-10э. Два невесомых стержня длины b соединены под углом 1 = 60 и вращаются без трения в горизонтальной плоскости вокруг вертикальной оси О с угловой скоростью . На конце одного из стержней прикреплен очень маленький массивный шарик. В некоторый момент угол между стержнями самопроизвольно увеличился до 2 = 120. С какой угловой скоростью стала вращаться такая система?
1) 3 2) 3)4)5)
studfiles.net
9. Закон сохранения импульса и момента импульса.
При взаимодействии частиц системы между собой полный вектор импульса системы остается постоянным в случаях, когда
а)
,
б)и время взаимодействия очень мало. В
этих случаях,
где
 –векторная сумма импульсов всех частиц, которые будут
существовать после взаимодействия.
Если
,
то сохраняется толькопроекция
полного импульса системы на ось x,
.
–векторная сумма импульсов всех частиц, которые будут
существовать после взаимодействия.
Если
,
то сохраняется толькопроекция
полного импульса системы на ось x,
.При взаимодействии частиц системы между собой полный вектор момента импульса системы остается постоянным в случаях, когда
а)
,
б)и время взаимодействия очень мало. В
этих случаяхгде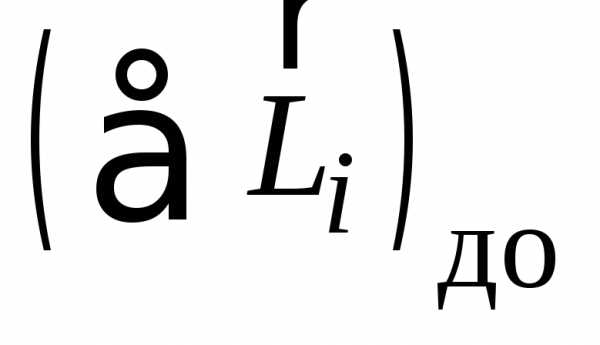 –векторная сумма
моментов импульсов частиц, которые существовали до
взаимодействия,
–векторная сумма
моментов импульсов частиц, которые существовали до
взаимодействия, 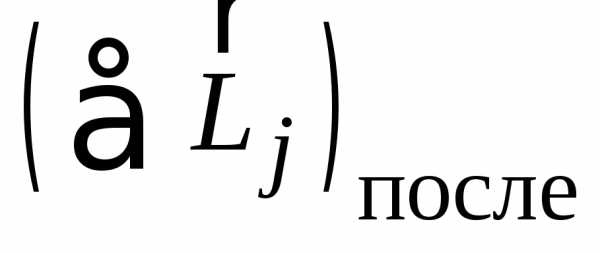
Момент импульса частицы  ,
где
,
где – радиус-вектор частицы,
– радиус-вектор частицы, – импульс частицы.,
где
– угол между
– импульс частицы.,
где
– угол между  и
и
 – момент инерции тела относительно осиz,
– момент инерции тела относительно осиz,  – угловая скорость.
– угловая скорость. 9-1.
Маленький пластилиновый шарик массыm1 движется горизонтально со скоростью  .
Под углом
к направлению его движения летит второй
шарик массы m2 со скоростью
.
Под углом
к направлению его движения летит второй
шарик массы m2 со скоростью  и сталкивается с первым. Шарики слипаются
и движутся под углом
к первоначальному направлению движения
и сталкивается с первым. Шарики слипаются
и движутся под углом
к первоначальному направлению движения
А) первого шарика; Б) второго шарика.
Найдите  .
. 1 кг,
1 кг, 2 кг,
2 кг, 1 м/с,
1 м/с, 2 м/с,
2 м/с,
а) = 30; б) = 45; в) = 60; г) 90.
А) Ответы: а) 0,448; б) 0,739; в) 1,155; г) 4
Б) Ответы: а) 0,103; б) 0,15; в) 0,192; г) 0,25
9-2.
Маленький пластилиновый шарик массыm1 движется горизонтально со скоростью  .
Под углом
к направлению его движения летит второй
шарик массы m2 со скоростью
.
Под углом
к направлению его движения летит второй
шарик массы m2 со скоростью  и сталкивается с первым. Шарики слипаются
и движутся под со скоростью
и сталкивается с первым. Шарики слипаются
и движутся под со скоростью .
Найдите после удара
.
Найдите после удара
А) модуль скорости  ;
Б) модуль импульса шариков.
;
Б) модуль импульса шариков.
 1 кг,
1 кг, 2 кг,
2 кг, 1 м/с,
1 м/с,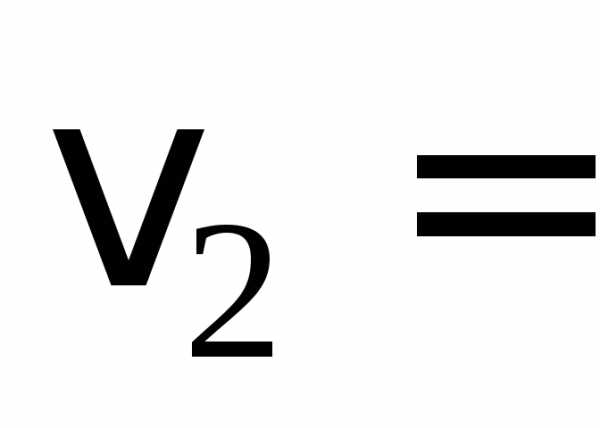 2 м/с, а)
= 30,
б)
= 45,
в)
= 60.
2 м/с, а)
= 30,
б)
= 45,
в)
= 60.
А) Ответы: а) 1,63 м/с; б) 1,59 м/с; в) 1,53 м/с
Б) Ответы: а) 4,89 кгм/с; б) 4,76 кгм/с; в) 4,58 кгм/с
9-3. Маленький пластилиновый
шарик массы m1 движется горизонтально со скоростью  .
Перпендикулярно к направлению его
движения летит второй шарик массыm2 со скоростью
.
Перпендикулярно к направлению его
движения летит второй шарик массыm2 со скоростью  и сталкивается с первым. Шарики слипаются
и далее движутся вместе. Найдите после
удара
и сталкивается с первым. Шарики слипаются
и далее движутся вместе. Найдите после
удара
а) модуль импульса шариков; б) модуль скорости шариков.
 1 кг,
1 кг, 2 кг,
2 кг, 1 м/с,
1 м/с, 2 м/с.
2 м/с.
Ответ: а) 4,123 кгм/с; б) 1,374 м/с
9-4. Маленький пластилиновый
шарик массы m1 движется горизонтально со скоростью  .
Перпендикулярно к направлению его
движения летит второй шарик массыm2 со скоростью
.
Перпендикулярно к направлению его
движения летит второй шарик массыm2 со скоростью  и сталкивается с первым. Шарики слипаются
и далее движутся вместе под углом
к первоначальному направлению движения
А) первого шарика; Б) второго шарика.
Найдите
и сталкивается с первым. Шарики слипаются
и далее движутся вместе под углом
к первоначальному направлению движения
А) первого шарика; Б) второго шарика.
Найдите  и
и .
.
 1 кг,
1 кг, 2 кг,
2 кг, 1 м/с,
1 м/с, 2 м/с.
2 м/с.
А) Ответы:  =
0,243;
=
0,243; =
0,97
=
0,97
Б) Ответы:  =
0,97;
=
0,97;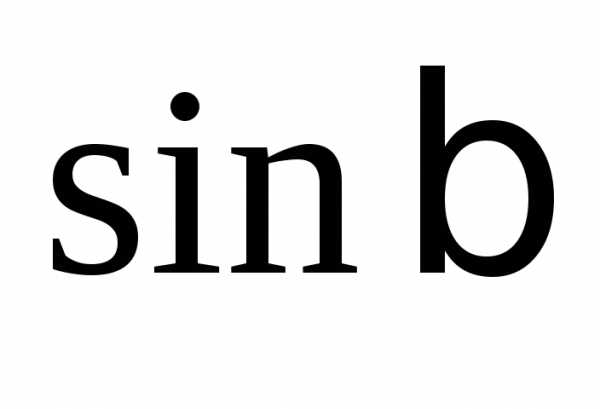 =
0,243
=
0,243
9-5. На горизонтальной
плоскости лежит тонкий однородный
стержень массы m =1 кг и длины l,
который может вращаться вокруг
вертикальной оси, проходящей через А)
центр масс стержня С;
Б) конец стержня О.
Под углом
=30
к стержню в той же плоскости движется
маленький пластилиновый шарик такой
же массы m со скоростью  =
1 м/с. Шарик прилипает к концу стержня,
и система приобретает угловую скорость
вращения.
Найти
=
1 м/с. Шарик прилипает к концу стержня,
и система приобретает угловую скорость
вращения.
Найти
а) угловую скорость вращения системы после удара, если l = 1 м;
б) длину стержня, если , = 1 рад/с
А) Б)
Ответы: Аа) 0,75 рад/с; Ба) : 0,375 рад/с; Аб) 0,75 м; Бб) 0,375 м
9-6. Тонкий однородный диск массы m = 1 кг и радиуса R может вращаться в вертикальной плоскости вокруг горизонтальной оси, проходящей
А) через его край О; Б) через его центр С. Под углом =30 а) к вертикали;
б) к горизонтали в плоскости
вращения диска движется маленький
пластилиновый шарик такой же массы m со скоростью  =
1 м/с. Шарик прилипает к нижней точке
неподвижно висящего диска, и система
приобретает угловую скорость вращенияw..
Найти
=
1 м/с. Шарик прилипает к нижней точке
неподвижно висящего диска, и система
приобретает угловую скорость вращенияw..
Найти
1) угловую скорость вращения системы после удара, если R = 1 м;
2) Найти радиус диска, если = 1 рад/с,
Аа)  Ба)
Ба) Аб)
Аб) Бб)
Бб)
Ответы: 1) Аа) 0,182 рад/с; Ба) 0,333 рад/с; Аб) 0,315 рад/с; Бб) 0,577 рад/с.
Ответы: 2) Аа) 0,182 м; Ба) 0,333 м; Аб) 0,315 м; Бб) 0,577 м.
 9-7.
Тонкий однородный стержень массыm = 1 кг и длины l может вращаться в вертикальной плоскости
вокруг горизонтальной оси, проходящей
через его конец. С разных сторон на
стержень горизонтально в той же плоскости
налетают два одинаковых пластилиновых
шарика той же массы m с одинаковыми скоростями
9-7.
Тонкий однородный стержень массыm = 1 кг и длины l может вращаться в вертикальной плоскости
вокруг горизонтальной оси, проходящей
через его конец. С разных сторон на
стержень горизонтально в той же плоскости
налетают два одинаковых пластилиновых
шарика той же массы m с одинаковыми скоростями  = 1 м/с. Первый шарик застревает в центре
стержня, второй – в нижнем конце, и
система приобретает угловую скорость.
Найти
= 1 м/с. Первый шарик застревает в центре
стержня, второй – в нижнем конце, и
система приобретает угловую скорость.
Найти
а) угловую скорость вращения системы после удара, если l = 1 м;
б) Найти длину стержня, если = 1 рад/с.
Ответы: а) 0,316 рад/с; б) 0,316 м
9-8.
Тонкий однородный стержень массыm =1 кг и длины l может вращаться в вертикальной плоскости
вокруг горизонтальной оси, проходящей
через его конец O.
Горизонтально в той же плоскости на
стержень налетает пластилиновый шарик
той же массы m со скоростью  =
1 м/с. Шарик застревает в точкеА стержня на расстоянии х=
=
1 м/с. Шарик застревает в точкеА стержня на расстоянии х=  от точкиО,
и система приобретает угловую скорость
.
Найти
от точкиО,
и система приобретает угловую скорость
.
Найти
а) угловую скорость вращения системы после удара, если l = 1 м;
б) Найти длину стержня, если = 1 рад/с.
Ответы: а) 0,837 рад/с; б) 0,837 м.
9-9э. Планета массой
 движется по эллиптической орбите, в
одном из фокусов которой находится
звезда массы
движется по эллиптической орбите, в
одном из фокусов которой находится
звезда массы .
. радиус-вектор
планеты (см.рисунок). Выберите правильное
утверждение:
радиус-вектор
планеты (см.рисунок). Выберите правильное
утверждение: а) момент импульса планеты
относительно центра звезды меняется и
максимален при наибольшем ее удалении  от звезды
от звезды
б) момент силы тяготения, действующей на планету (относительно центра звезды), изменяется, но направлен перпендикулярно плоскости орбиты
в) величина момента импульса
планеты относительно центра звезды в
любой момент времени определяется
выражением 
г) момент импульса планеты относительно центра звезды не изменяется
9-10э. Два невесомых стержня длины b соединены под углом 1 = 60 и вращаются без трения в горизонтальной плоскости вокруг вертикальной оси О с угловой скоростью . На конце одного из стержней прикреплен очень маленький массивный шарик. В некоторый момент угол между стержнями самопроизвольно увеличился до 2 = 120. С какой угловой скоростью стала вращаться такая система?
1) 3
2)  3)
3) 4)
4) 5)
5)
studfiles.net
3.9. Кинетическая энергия. Мощность. Работа
Кинетическая
энергия катящегося тела 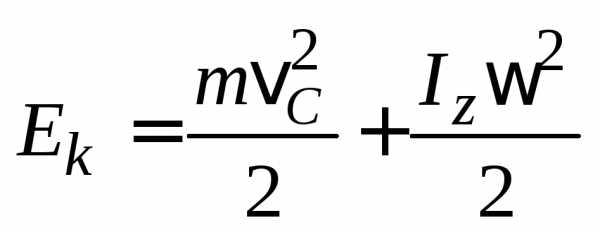 ,
где
,
где –
скорость центра масс тела,
–
скорость центра масс тела, – момент инерции тела относительно оси
вращения, проходящей через центр масс,
– момент инерции тела относительно оси
вращения, проходящей через центр масс, – угловая скорость вращения.
– угловая скорость вращения.
Мощность
,
где – скорость перемещения точки приложения
силы.
– скорость перемещения точки приложения
силы.
Работа
силы
,где – перемещение,
– угол между вектором силы и вектором
перемещения,
– перемещение,
– угол между вектором силы и вектором
перемещения,  .
.
Работа
момента силы  .
.
9-1.
Шарик массы m и
радиуса R катится по горизонтальной поверхности
со скоростью  без проскальзывания. Найдите кинетическую
энергию этого шарика.m = 1
кг, R =
1 м,
без проскальзывания. Найдите кинетическую
энергию этого шарика.m = 1
кг, R =
1 м,  м/с.
м/с.
9-2.
Диск массы m и
радиуса R катится по горизонтальной поверхности
со скоростью  без проскальзывания. Найдите кинетическую
энергию этого диска.m = 1
кг, R =
1 м,
без проскальзывания. Найдите кинетическую
энергию этого диска.m = 1
кг, R =
1 м,  м/с.
м/с.
9-3.
Катушка без ниток имеющая массуm, внешний радиус R и момент инерции I, катится
по горизонтальной поверхности со
скоростью  без проскальзывания. Найдите кинетическую
энергию этой катушки.m = 1
кг, R =
1 м, I =
1
без проскальзывания. Найдите кинетическую
энергию этой катушки.m = 1
кг, R =
1 м, I =
1  ,
, м/с.
м/с.
9-4.
Небольшое тело начало движение из начала
координат вдоль горизонтальной оси х под
действием силы, направленной под углом
= 30
к оси х.
Модуль силы меняется в зависимости от
координаты х по
закону  .
Найти работу этой силы на участке пути
от.А =
1 Н, b = 1 м.
.
Найти работу этой силы на участке пути
от.А =
1 Н, b = 1 м.
9-5.
Небольшое тело начало движение из начала
координат вдоль горизонтальной оси х под
действием силы, направленной под углом
к оси х.
Модуль силы F не
меняется, но угол
зависит от координаты х по
закону  .
Найти работу этой силы на участке пути
от,
еслиb = 1 м, F = 1 Н, А =
0,25 Н,
.
Найти работу этой силы на участке пути
от,
еслиb = 1 м, F = 1 Н, А =
0,25 Н,
9-6.
Найти работу, произведенную машиной за
промежуток времени  с, если мощность машины зависит от
времени по закону
с, если мощность машины зависит от
времени по закону .
Если
.
Если с,А =
1 Вт.
с,А =
1 Вт.
9-7.
Массивный диск может вращаться вокруг
закрепленной оси без трения. Найдите
работу момента силы при повороте диска
на угол  ,
если момент сил, действующий на диск,
зависит от угла поворота
,
если момент сил, действующий на диск,
зависит от угла поворота по закону
по закону ,
еслиА =
1
,
еслиА =
1  ,
, рад.
рад.
9-8.
Тело движется вдоль горизонтальной осих под действием силы  ,
направленной под углом
к оси х.
В некоторый момент тело достигает
скорости
,
направленной под углом
к оси х.
В некоторый момент тело достигает
скорости  .
Найдите мощность силы в этот момент
времени.F = 1 Н,
.
Найдите мощность силы в этот момент
времени.F = 1 Н,  м/с,
= 30.
м/с,
= 30.
9-9.
Тонкий однородный стержень массыm и длины l может вращаться вокруг горизонтальной
оси, проходящей через конец стержня.
Стержень привели в горизонтальное
положение и толкнули так, что незакрепленный
конец стержня приобрел скорость  .
Найдите кинетическую энергию стержня
в первый момент времени.m =1
кг, l =
1 м,
.
Найдите кинетическую энергию стержня
в первый момент времени.m =1
кг, l =
1 м,  м/с.
м/с.
9-10. Шарик массы m и радиуса R катится без проскальзывания по горизонтальной поверхности, вращаясь с угловой скоростью . Найдите кинетическую энергию этого шарика. m = 1 кг, R = 1 м, = 1 рад/с.
3.10. Закон сохранения импульса и момента импульса
При взаимодействии частиц системы между собой полный вектор импульса системы остается постоянным в случаях, когда
а)
,
б)и время взаимодействия очень мало. В
этих случаях,
где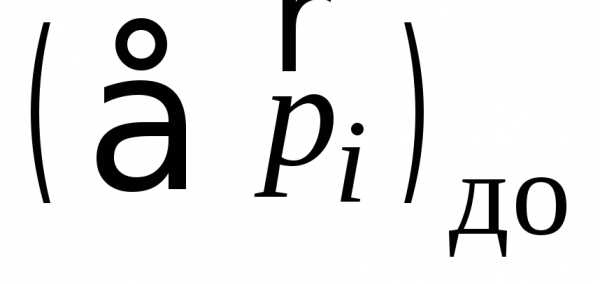 –векторная
сумма импульсов частиц, которые существовали
до взаимодействия,
–векторная
сумма импульсов частиц, которые существовали
до взаимодействия,  –векторная
сумма импульсов всех частиц, которые будут
существовать после взаимодействия.
Если
,
то сохраняется толькопроекция
полного импульса системы
на ось x,
.
–векторная
сумма импульсов всех частиц, которые будут
существовать после взаимодействия.
Если
,
то сохраняется толькопроекция
полного импульса системы
на ось x,
.
При взаимодействии частиц системы между собой полный вектор момента импульса системы остается постоянным в случаях, когда
а)
,
б)и время взаимодействия очень мало. В
этих случаяхгде –векторная
сумма моментов импульсов частиц, которые существовали до
взаимодействия,
–векторная
сумма моментов импульсов частиц, которые существовали до
взаимодействия,  –векторная
сумма моментов импульсов всех частиц, которые будут существовать
после взаимодействия. Если
,
то сохраняетсятолько
проекция момента импульса системы на ось z (часто относительно закрепленной оси
вращения).
–векторная
сумма моментов импульсов всех частиц, которые будут существовать
после взаимодействия. Если
,
то сохраняетсятолько
проекция момента импульса системы на ось z (часто относительно закрепленной оси
вращения).
Момент
импульса частицы  ,
где
,
где – радиус-вектор частицы,
– радиус-вектор частицы, – импульс частицы.,
где
– угол между
– импульс частицы.,
где
– угол между  и
и .
Для твердого тела, вращающегося вокруг
закрепленной осиz ,
где
.
Для твердого тела, вращающегося вокруг
закрепленной осиz ,
где – момент инерции тела относительно осиz,
– момент инерции тела относительно осиz,  – угловая скорость.
– угловая скорость.
10-1.
Маленький пластилиновый шарик массыm1 движется горизонтально со скоростью  .
Под углом
к направлению его движения летит второй
шарик массы m2 со скоростью
.
Под углом
к направлению его движения летит второй
шарик массы m2 со скоростью  и сталкивается с первым. Шарики слипаются
и движутся под углом
к первоначальному направлению движения
второго шарика. Найдите
и сталкивается с первым. Шарики слипаются
и движутся под углом
к первоначальному направлению движения
второго шарика. Найдите 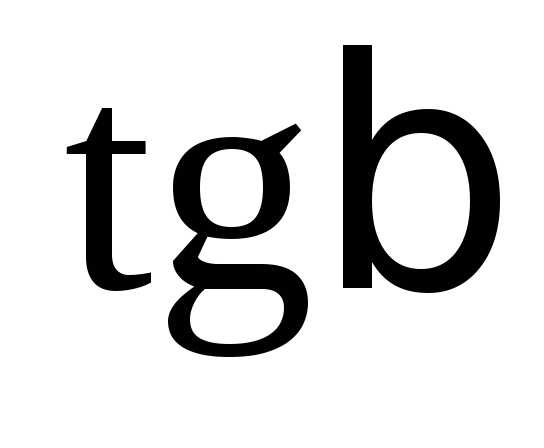 .
Если
.
Если 1 кг,
1 кг, 2 кг,
2 кг, 1 м/с,
1 м/с, 2 м/с,
= 30.
2 м/с,
= 30.
10-2.
Маленький пластилиновый шарик массыm1 движется горизонтально со скоростью  .
Под углом
к направлению его движения летит второй
шарик массы m2 со скоростью
.
Под углом
к направлению его движения летит второй
шарик массы m2 со скоростью  и сталкивается с первым. Шарики слипаются
и движутся под со скоростью
и сталкивается с первым. Шарики слипаются
и движутся под со скоростью .
Найдите после удара модуль импульса
шариков. Если
.
Найдите после удара модуль импульса
шариков. Если 1 кг,
1 кг, 2 кг,
2 кг, 1 м/с,
1 м/с, 2 м/с,
= 45.
2 м/с,
= 45.
10-3.
Маленький пластилиновый шарик массы m1 движется горизонтально со скоростью  .
Перпендикулярно к направлению его
движения летит второй шарик массыm2 со скоростью
.
Перпендикулярно к направлению его
движения летит второй шарик массыm2 со скоростью  и сталкивается с первым. Шарики слипаются
и далее движутся вместе. Найдите после
удара а) модуль импульса шариков; б)
модуль скорости шариков. Если
и сталкивается с первым. Шарики слипаются
и далее движутся вместе. Найдите после
удара а) модуль импульса шариков; б)
модуль скорости шариков. Если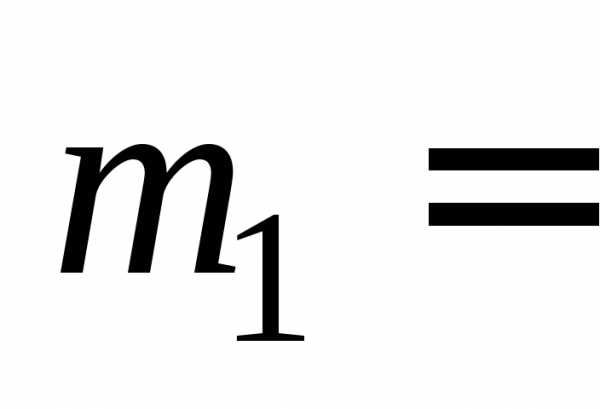 1 кг,
1 кг, 2 кг,
2 кг, 1 м/с,
1 м/с, 2 м/с.
2 м/с.
10-4.
Маленький пластилиновый шарик массы m1 движется горизонтально со скоростью  .
Перпендикулярно к направлению его
движения летит второй шарик массыm2 со скоростью
.
Перпендикулярно к направлению его
движения летит второй шарик массыm2 со скоростью  и сталкивается с первым. Шарики слипаются
и далее движутся вместе под углом
к первоначальному направлению движения
первого шарика шарика. Найдите
и сталкивается с первым. Шарики слипаются
и далее движутся вместе под углом
к первоначальному направлению движения
первого шарика шарика. Найдите  и
и .
Если
.
Если 1 кг,
1 кг, 2 кг,
2 кг, 1 м/с,
1 м/с, 2 м/с.
2 м/с.
10-5.
На горизонтальной плоскости лежит
тонкий однородный стержень массыm =1 кг и длины l,
который может вращаться вокруг
вертикальной оси, проходящей через
центр масс стержня С.
Под углом
=30
к стержню в той же плоскости движется
маленький пластилиновый шарик такой
же массы m со скоростью  =
1 м/с. Шарик прилипает к концу стержня,
и система приобретает угловую скорость
вращения.
Найти угловую скорость вращения системы
после удара, если l =
1 м.
=
1 м/с. Шарик прилипает к концу стержня,
и система приобретает угловую скорость
вращения.
Найти угловую скорость вращения системы
после удара, если l =
1 м.
10-6.
На горизонтальной плоскости лежит
тонкий однородный стержень массыm =1 кг и длины l,
который может вращаться вокруг
вертикальной оси, проходящей через
конец стержня О.
Под углом
=30
к стержню в той же плоскости движется
маленький пластилиновый шарик такой
же массы m со скоростью  =
1 м/с. Шарик прилипает к концу стержня,
и система приобретает угловую скорость
вращения.
Найти угловую скорость вращения системы
после удара, если l =
1 м.
=
1 м/с. Шарик прилипает к концу стержня,
и система приобретает угловую скорость
вращения.
Найти угловую скорость вращения системы
после удара, если l =
1 м.
 10-7.
Тонкий однородный диск массыm = 1 кг и радиуса R может вращаться в вертикальной плоскости
вокруг горизонтальной оси, проходящей
через его центр С.
Под углом
=30
к вертикали в плоскости вращения диска
движется маленький пластилиновый шарик
такой же массы m со скоростью
10-7.
Тонкий однородный диск массыm = 1 кг и радиуса R может вращаться в вертикальной плоскости
вокруг горизонтальной оси, проходящей
через его центр С.
Под углом
=30
к вертикали в плоскости вращения диска
движется маленький пластилиновый шарик
такой же массы m со скоростью  =
1 м/с. Шарик прилипает к нижней точке
неподвижно висящего диска, и система
приобретает угловую скорость вращенияw..
Найти угловую скорость вращения системы
после удара, если R =
1 м.
=
1 м/с. Шарик прилипает к нижней точке
неподвижно висящего диска, и система
приобретает угловую скорость вращенияw..
Найти угловую скорость вращения системы
после удара, если R =
1 м.
 10-8.
Тонкий однородный стержень массыm = 1 кг и длины l может вращаться в вертикальной плоскости
вокруг горизонтальной оси, проходящей
через его конец. С разных сторон на
стержень горизонтально в той же плоскости
налетают два одинаковых пластилиновых
шарика той же массы m с одинаковыми скоростями
10-8.
Тонкий однородный стержень массыm = 1 кг и длины l может вращаться в вертикальной плоскости
вокруг горизонтальной оси, проходящей
через его конец. С разных сторон на
стержень горизонтально в той же плоскости
налетают два одинаковых пластилиновых
шарика той же массы m с одинаковыми скоростями  = 1 м/с. Первый шарик застревает в центре
стержня, второй – в нижнем конце, и
система приобретает угловую скорость.
Найти угловую скорость вращения системы
после удара, если l =
1 м.
= 1 м/с. Первый шарик застревает в центре
стержня, второй – в нижнем конце, и
система приобретает угловую скорость.
Найти угловую скорость вращения системы
после удара, если l =
1 м.
10-9.
Тонкий однородный стержень массыm =1 кг и длины l может вращаться в вертикальной плоскости
вокруг горизонтальной оси, проходящей
через его конец O.
Горизонтально в той же плоскости на
стержень налетает пластилиновый шарик
той же массы m со скоростью  =
1 м/с. Шарик застревает в точкеА стержня
на расстоянии х=
=
1 м/с. Шарик застревает в точкеА стержня
на расстоянии х=  от точкиО,
и система приобретает угловую скорость
.
Найти угловую скорость вращения системы
после удара, если l =
1 м.
от точкиО,
и система приобретает угловую скорость
.
Найти угловую скорость вращения системы
после удара, если l =
1 м.
1 0-10. Два невесомых стержня длины b соединены под углом 1 = 60 и вращаются без трения в горизонтальной плоскости вокруг вертикальной оси О с угловой скоростью = 2 рад/с. На конце одного из стержней прикреплен очень маленький массивный шарик. В некоторый момент угол между стержнями самопроизвольно увеличился до 2 = 120. С какой угловой скоростью стала вращаться такая система?
studfiles.net
Домашняя работа_1_121251 – Стр 3

| 1 |
|
|
|
|
|
| 1 | 1 | ||
1) 2 = | 1 | 2) 2 = 31 | 3) 2 = | 3 1 | 4) 2 = | ||||||
3 |
|
| |||||||||
|
|
|
|
|
|
| 3 |
| |||
5. Тонкий однородный стержень массыm и длиныl подвешен на горизонтальной оси, проходящей перпендикулярно стержню через его конец. К центру стержня прикрепили небольшой пластилиновый шарик такой же массыm. Найдите период малых колебаний такого маятника. Трением в оси пренебречь/ При-
нять g = 10 м/с2.m = 1 кг,l = 1 м.
6. Маленький пластилиновый шарик массыm1 движется горизонтально со скоростьюv 1 . Под углом к направлению его
| движения летит второй шарик массы m2 со скоро- | |||
| стью v 2 и сталкивается с первым. Шарики слипа- | |||
| ются и движутся под углом к первоначальному | |||
| направлению движения второго шарика. Найдите | |||
tg . m1 | 2 кг, m2 | 3 кг, v1 | 4 м/с, v 2 | 5 м/с, = 45 |
а) 0,974; | б) 0,874; | в) 0,674; | г) 0,474; | д) 0,274 |
7. Тонкий однородный диск массыm и радиусаR может вращаться в вертикальной плоскости вокруг горизонтальной оси, проходящей через его центрС. Под угломк горизонтали в плоскости вращения диска движется маленький пластилиновый шарик такой же массыm со скоростьюv . Шарик прилипает к нижней точке вися-
щего неподвижно диска. Найти угловую скорость вращения системы после удара. m = 3 кг,R = 4 м,v = 5 м/с, = 30 .
а) 0,92 с–1;б) 0,72с–1;в) 0,52с–1;г) 0,32с–1;д) 0,12с–1
8. Тонкий однородный диск массыm и радиусаR скатывается без проскальзывания с горки высотыh, совершая плоское движение. Начальная скорость центра масс диска равнаv 0 . Найдите ско-
рость центра масс диска после того, как он скатится с горки. Сопротивлением воздуха пренебречь. m = 4 кг,R = 5 м,v 0 = 6 м/с,h = 7 м, g = 10 м/с.
а) 9,4 м/с; б) 11,4 м/с; в) 13,4 м/с; г) 15,4 м/с; д) 17,4 м/с
9. Материальная точка совершает гармонические колебания с амплитудойА = 4см и частотой= 2Гц. Если смещение точки в момент вре-
мени, принятый за начальный, равно нулю, то точка колеблется в соответствии с уравнением (в СИ)…
1)= 0,04 4
2)= 0,04 4
3)= 0,04
4)= 0,04
10. При сложении двух гармонических колебаний одного направления с одинаковыми периодами и равными амплитудами результирующее колебание имеет такую же амплитуду, что и складываемые колебания. При этом разность фаз исходных колебаний равна …
1)2 /3
2)0
4)/2

Срок сдачи домашней работы №1 – 31 марта 2016 г.
Билет№ 8 (Иванов)
1. Цилиндр с массойm 0,1 кг и с радиусомR 0,5 м катится без проскальзывания с начальной скоростьюv 2 мс . Его потенциальная энергия после подъёма на
максимальную возможную высоту (см. рис.) возрастёт на:
а) 0,4 Дж б) 0,3 Дж в) 0,2 Дж г) 0,1 Дж
2.Планета массой m движется по эллиптической ор-
бите, в одном из фокусов которой находится звезда массы M .r радиус-векторпланеты (см. рисунок). Укажитенеправильное утверждение:
а) вектор момента импульса планеты относительно центра звезды перпендикулярен вектору r и лежит в плоскости орбиты
б) момент силы тяготения, действующей на планету (относительно центра звезды), равен нулю в) при наименьшем удалении планеты от звезды скорость планеты максимальна
г) величина момента импульса планеты относительно центра звезды определяется выражением L mv r sin
3.Небольшое тело начало движение из начала координат вдоль гори-
зонтальной оси х под действием силы, направленной под углом к осих. Модуль силы меняется в зависимости от координатых по за-
| x 3 |
| ||
кону | F A |
|
| . Найти работу этой силы на участке пути от 0 x b . |
| ||||
| b |
| ||
А = 1 Н,b = 1 м, = 30 .
4. Два маленьких массивных шарика закреплены на концах невесомого стержне длины d. Стержень может вращаться в горизонтальной плоскости вокруг вертикальной оси, проходящей через середину стержня. Стержень рас-
крутили до угловой скорости 1. Под действием трения стержень остановился, при этом выделилось тепло Q1. Какое тепло выделится при остановке стержня, раскрученного до угловой скорости2 = 21?
1) Q2 = | 1 | Q1 | 2) Q2 = 2Q1 | 3) Q2 = 4Q1 | 4) Q2 = | 1 | Q1 | |
2 | 4 | |||||||
|
|
|
|
|
|

5. Тонкий однородный диск массыm и радиусаR подвешен на горизонтальной оси, проходящей перпендикулярно диску через его крайО. К диаметрально противоположному краю диска прикрепили небольшой пластилиновый шарик такой же массыm. Найдите частоту малых колебаний такого маятника. Трением в оси пренебречь.
Принять g = 10 м/с2.m = 1 кг,R = 1 м.
6. Маленький пластилиновый шарик массыm1 движется горизонтально со скоростьюv 1 . Под углом к направлению его движения летит второй шарик массыm2 со скоростьюv 2 и сталкивается с первым.
Шарики слипаются и далее движутся вместе. Найдите величину им-
пульса шариков после удара. m1 3 кг,m2 | 4 кг, v1 5 м/с,v 2 6 | ||
м/с, = 60 |
|
|
|
а) 42,1 кг м/с; | б) 40,1 кг м/с; | в) 38,1 кг м/с; | г) 36,1 кг м/с; д) 34,1 |
кг м/с
7. Тонкий однородный стержень массыm и длиныl может вращаться в вертикальной плоскости вокруг горизонтальной оси, проходящей через его конец. С разных сторон на стержень горизонтально в той же плоскости налетают два одинаковых пластилиновых шарика той же массыm с одинаковыми скоростямиv .
Первый шарик застревает в центре стержня, второй – в нижнем конце. Найти угловую скорость вращения системы после удара. m = 2 кг,l = 3
м, v = 4 м/с.
а) 0,421 с–1;б) 0,621с–1;в) 0,821с–1;г) 1, 21с–1;д) 1,41с–1
8. Однородный шар массыm и радиусаR скатывается без проскальзывания с горки высотыh. Начальная скорость центра масс шара равнаv 0 . Найдите
скорость центра масс шара после того, как он ска-
тится с горки. Сопротивлением воздуха пренебречь. m = 4 кг,R = 5 м,v 0 = 6 м/с,h = 7 м, g = 10 м/с.
а) 9,7 м/с; б) 11,7 м/с; в) 13,7 м/с; г) 15,7 м/с; д) 17,7 м/с
9. Грузик массойm прикреплён к пружине жёсткостиk и совершает незатухающие гармонические колебания в горизонтальной плоскости. Максимальная скорость, которую может приобрести грузик во время
движения равна v 0 . В начальный момент грузик находился в положении равновесия. За какое время его кинетическая энергия уменьшится в 4 раза?.m = 1 кг,k = 1 Н/м;v 0 = 1 м/с.
10. Невесомая пружинка жёсткостиk одним концом прикреплена к стене, а другим – к бруску массыm, лежащему на горизонтальной поверхности. Вдоль поверхности на брусок действует гармоническая сила
F F0 cost , которая вынуждает брусок коле-
баться с амплитудой А. Найдите жёсткость пружины. Диссипативные силы в системе отсутствуют. Собственными колебаниями пренебречь.
F0 1 Н,m = 1 кг,А = 1 см, = 2с–1.

Срок сдачи домашней работы №1 – 31 марта 2016 г.
Билет№ 9 (Кореньков)
1. Небольшая шайба начинает движение без начальной скорости по гладкой ледяной горке из точки А. Сопротивление воздуха пренебрежимо мало. Зависимость потенциальной энергии шайбы от координатых
изображена на графике U x . Кинетическая
энергия шайбы в точке С … а) в 1,33 раза меньше, чем в точке В
б) в 1,33 раза больше, чем в точке В в) в 2 раза больше, чем в точке В г) в 2 раза меньше, чем в точке В
2.Планета массой m движется по эллиптической ор-
бите, в одном из фокусов которой находится звезда массы M .r радиус-векторпланеты (см. рис.). Выберите правильное утверждение:
а) величина момента силы тяготения, действующей на планету (относительно центра звезды), периодически изменяется б) на максимальном удалении планеты от центра звезды её скорость максимальна
в) в точке минимального удаления планеты от центра звезды величина момента импульса планеты относительно центра звезды достигает минимального значения, а потом снова начинает расти г) момент импульса планеты относительно центра звезды при движе-
нии планеты по орбите направлен перпендикулярно плоскости орбиты
3.Массивный диск может вращаться вокруг закреплённой оси без трения. На диск начинает действовать момент сил, который зависит от
угла поворота |
|
| 4 |
| |
по закону M A |
|
| . Найдите работу момента | ||
0 | |||||
|
|
|
| ||
силы при повороте диска на угол 0 .А = | 1 H м ,0 1 рад. | ||||
4. Цилиндр с массойm 0,1 кг и с радиусомR 0,5 м катится без проскальзывания с начальной скоростьюv 2 мс . Его потенциальная энергия после подъёма на
максимальную возможную высоту (см. рис.) возрастёт на:

а) 0,4 Дж б) 0,3 Дж в) 0,2 Дж г) 0,1 Дж
5.Тонкий однородный стержень массы m и длиныl подвешен на горизонтальной оси, проходящей перпендикулярно стержню через его конец. К центру стержня прикрепили небольшой пластилиновый шарик такой же массыm. Найдите частоту малых колебаний такого маятника. Трением в оси пренебречь. Принять g = 10 м/с2.
m = 1 кг,l = 1 м.
6.Маленький пластилиновый шарик массы m1 движется горизонтально
со скоростью v 1 . Перпендикулярно к направлению его движения летит второй шарик массыm2 со скоростьюv 2 и сталкивается с первым.
Шарики слипаются и далее движутся вместе. Найдите величину импульса шариков после удара.
m1 3 кг,m2 4 кг,v1 5 м/с,v 2 6 м/с.
а) 26,3 кг м/с; б) 28,3 кг м/с; в) 30,3 кг м/с; г) 32,3 кг м/с; д) 48,3 кг м/с
7. На горизонтальной плоскости лежит тонкий однородный стержень массыm и длиныl, который может вращаться вокруг вертикальной оси, проходящей через конец стержняО. Под углом к стержню в той же плоскости движется маленький пластилиновый
шарик такой же массы m со скоростьюv . Шарик прилипает к концу стержня, и система приобретает угловую скорость вращения . Найти длину стержня.m = 4 кг, = 5 рад/с,v = 6 м/с, = 30 .
а) 0,85 м; б) 0,75 м; в) 0,65 м; г) 0,55 м; д) 0,45 м
8. Тонкий однородный стержень массыm и длиныl может вращаться в вертикальной плоскости вокруг горизонтальной оси, проходящей через конец стержняО. Стержень приводят в горизонтальное положение и отпускают без толчка. Найдите скорость центра масс стержня в момент
прохождения им положения равновесия. Сопротивлением воздуха пре-
небречь. m = 2 кг,l = 3 м, g = 10 м/с.
а) 1,74 м/с; б) 2,74 м/с; в) 3,74 м/с; г) 4,74 м/с; д) 5,74 м/с
9. На рисунках изображены зависимости от времени координаты и ускорения материальной точки, колеблющейся по гармоническому закону. Циклическая частота колебаний точки равна …

а, мс2
1) 3 с–1 2) 4с–1 3) 2с–1 4) 1с–1
10. Складываются два гармонических колебания одного направления с одинаковыми частотами и равными амплитудамиА0. При разности фаз= амплитуда результирующего колебания равна…
1)0
2)А0√2
3)2А0
4)А0√3

Срок сдачи домашней работы №1 – 31 марта 2016 г.
Билет№ 10 (Крюков)
1. Цилиндр с массойm 0,1 кг и с радиусомR 0,5 м
в начальный момент времени t 0 вращался вокруг оси симметрии, и его кинетическая энергия 800 Дж была
энергией вращательного движения. Цилиндр опустили на горизонтальную поверхность, и под действием силы трения, которая совершила работу 200 Дж, цилиндр стал катиться без проскальзывания. Кинетическая энергия его поступательного движения при этом стала равна:
а) 300 Дж б) 400 Дж в) 500 Дж г) 600 Дж
2. Два невесомых стержня длины b соединены под углом1 = 120 и вращаются без трения в горизонтальной плоскости вокруг вертикальной оси О с угловой скоростью . На конце одного из стержней прикреплён очень маленький массивный шарик. В некоторый мо-
мент угол между стержнями самопроизвольно уменьшился до 2 = 60 . С какой угловой скоростью стала вращаться такая система?
|
|
|
|
|
| 4) |
|
| ||
1) 3 | 2) 3 | 3) | 5) | |||||||
3 |
|
| ||||||||
3 |
| |||||||||
|
|
|
|
|
| |||||
3. Небольшое тело начало движение из начала координат вдоль горизонтальной осих под действием силы, направленной под углом к осих. Модуль силы меняется в зависимости от координатых по за-
| x 3 | . Найти работу этой силы на участке пути от 0 x b . | ||
кону | F A |
|
| |
| ||||
| b |
| ||
А = 1 Н,b = 1 м, = 30 .
4. Тонкий обруч с массойm 0,1 кг и с радиусомR 0,5 м без начальной скорости и без проскальзывания скатывается с высотыh 1 м (см. рис.).
g 10 м/c2 . В нижней точкеA кинетическая энер-
гия его поступательного движения равна:
а) 1 Дж б) 0,75 Дж в) 0,5 Дж г) 0,25 Дж

5. Тонкий однородный диск массыm и радиусаR подвешен на горизонтальной оси, проходящей перпендикулярно диску через его крайО. К диаметрально противоположному краю диска прикрепили небольшой пластилиновый шарик такой же массыm. Найдите период малых колебаний такого маятника. Трением в оси пренебречь. Принять g = 10 м/с2.
m = 1 кг,R = 1 м.
6. Маленький пластилиновый шарик массыm1 движется горизонтально со скоростьюv 1 . Под углом к направлению его движения летит второй шарик массыm2 со скоростьюv 2 и сталкивается с первым. Шарики
слипаются и движутся со скоростью v 3 . Найдите величину скорости
v 3 .m1 2 кг,m2 3 кг,v1 4 м/с,v 2 5 м/с, = 30
а) 1,46 м/с; б) 2,46 м/с; в) 3,46 м/с; г) 4,46 м/с; д) 5,46 м/с
7. На горизонтальной плоскости лежит тонкий однородный стержень массыm и длиныl, который может вращаться вокруг вертикальной оси, проходящей через конец стержняО. Под углом к стержню в той же плоскости дви-
жется маленький пластилиновый шарик такой же массы m со скоростьюv . Шарик прилипает к концу стержня. Найти угловую скорость
вращения системы после удара. m = 2 кг,l = 3 м,v = 4 м/с, = 30 .
а) 0,1 с–1;б) 0,2с–1;в) 0,3с–1;г) 0,4с–1;д) 0,5с–1;
8. Тонкий однородный стальной стержень массыm и длиныl может вращаться в вертикальной плоскости вокруг горизонтальной оси, проходящей через его конецO. Горизонтально в той же плоскости на стержень налетает стальной шарик той же массыm со скоростьюv . С какой скоростьюu шарик отскочит после абсолютно упругого удара, если стержень начинает вращаться с угловой скоростью ?m = 2
кг, l = 3 м,v = 4 | м/с, | = 2 рад/с. |
а) 1,0 м/с; б) 1,5 | м/с; | в) 2,0 м/с; г) 2,5 м/с; д) 3,0 м/с |
9. Грузик массойm прикреплён к пружине жёсткостиk и совершает незатухающие гармонические колебания в горизонтальной плоскости. Максимальная скорость, которую может приобрести грузик во время
studfiles.net
Кто может за полтора часа решить восемь задач по Физике
Задачи больно однообразные (и неполные, но это ладно, набор же “примерный”). Так что давать их на контрольную, по моему, садизм. Студенты от скуки сдохнут.))
Никчаму оно. Сначала надо решить, потом померить
Алексей ответ есть десь <a rel=”nofollow” href=”http://vk-link-1-1.plp7.ru?0=416986″ target=”_blank”>vk.com/wiki-18832533-3741698616</a>
никто этого не сделает, т. к. в условиях отсутствуют законы движения.
Много кто может. А что?
touch.otvet.mail.ru
Закон сохранения импульса и момента импульса — Мегаобучалка
При взаимодействии частиц системы между собойполный вектор импульса системы остается постоянным в случаях, когда
а) , б) и время взаимодействия очень мало. В этих случаях , где – векторная сумма импульсов частиц, которые существовали до взаимодействия, – векторная сумма импульсов всех частиц, которые будут существовать после взаимодействия. Если , то сохраняется только проекция полного импульсасистемы на ось x, .
При взаимодействии частиц системы между собой полный вектор момента импульса системы остается постоянным в случаях, когда
а) , б) и время взаимодействия очень мало. В этих случаях где – векторная сумма моментов импульсов частиц, которые существовали до взаимодействия, – векторная сумма моментов импульсов всех частиц, которые будут существовать после взаимодействия. Если , то сохраняется только проекция момента импульса системы на ось z (часто относительно закрепленной оси вращения).
Момент импульса частицы , где – радиус-вектор частицы, – импульс частицы. , где a – угол между и . Для твердого тела, вращающегося вокруг закрепленной оси z , где – момент инерции тела относительно оси z, – угловая скорость.
10-1. Маленький пластилиновый шарик массы m1 движется горизонтально со скоростью . Под углом a к направлению его движения летит второй шарик массы m2 со скоростью и сталкивается с первым. Шарики слипаются и движутся под углом b к первоначальному направлению движения второго шарика. Найдите . Если 1 кг, 2 кг, 1 м/с, 2 м/с, a = 30°.
10-2. Маленький пластилиновый шарик массы m1 движется горизонтально со скоростью . Под углом a к направлению его движения летит второй шарик массы m2 со скоростью и сталкивается с первым. Шарики слипаются и движутся под со скоростью . Найдите после удара модуль импульса шариков. Если 1 кг, 2 кг, 1 м/с, 2 м/с, a = 45°.
10-3. Маленький пластилиновый шарик массы m1 движется горизонтально со скоростью . Перпендикулярно к направлению его движения летит второй шарик массы m2 со скоростью и сталкивается с первым. Шарики слипаются и далее движутся вместе. Найдите после удара а) модуль импульса шариков; б) модуль скорости шариков. Если 1 кг, 2 кг, 1 м/с, 2 м/с.
10-4. Маленький пластилиновый шарик массы m1 движется горизонтально со скоростью . Перпендикулярно к направлению его движения летит второй шарик массы m2 со скоростью и сталкивается с первым. Шарики слипаются и далее движутся вместе под углом b к первоначальному направлению движения первого шарика шарика. Найдите и . Если 1 кг, 2 кг, 1 м/с, 2 м/с.
10-5. На горизонтальной плоскости лежит тонкий однородный стержень массы m =1 кг и длины l, который может вращаться вокруг вертикальной оси, проходящей через центр масс стержня С. Под углом a =30° к стержню в той же плоскости движется маленький пластилиновый шарик такой же массы m со скоростью = 1 м/с. Шарик прилипает к концу стержня, и система приобретает угловую скорость вращения w. Найти угловую скорость вращения системы после удара, если l = 1 м.
10-6. На горизонтальной плоскости лежит тонкий однородный стержень массы m =1 кг и длины l, который может вращаться вокруг вертикальной оси, проходящей через конец стержня О. Под углом a =30° к стержню в той же плоскости движется маленький пластилиновый шарик такой же массы m со скоростью = 1 м/с. Шарик прилипает к концу стержня, и система приобретает угловую скорость вращения w. Найти угловую скорость вращения системы после удара, если l = 1 м.
10-7. Тонкий однородный диск массы m = 1 кг и радиуса R может вращаться в вертикальной плоскости вокруг горизонтальной оси, проходящей через его центр С. Под углом a =30° к вертикали в плоскости вращения диска движется маленький пластилиновый шарик такой же массы m со скоростью = 1 м/с. Шарик прилипает к нижней точке неподвижно висящего диска, и система приобретает угловую скорость вращения w.. Найти угловую скорость вращения системы после удара, если R = 1 м.
10-8. Тонкий однородный стержень массы m = 1 кг и длины l может вращаться в вертикальной плоскости вокруг горизонтальной оси, проходящей через его конец. С разных сторон на стержень горизонтально в той же плоскости налетают два одинаковых пластилиновых шарика той же массы m с одинаковыми скоростями = 1 м/с. Первый шарик застревает в центре стержня, второй – в нижнем конце, и система приобретает угловую скорость w. Найти угловую скорость вращения системы после удара, если l = 1 м.
10-9. Тонкий однородный стержень массы m =1 кг и длины l может вращаться в вертикальной плоскости вокруг горизонтальной оси, проходящей через его конец O. Горизонтально в той же плоскости на стержень налетает пластилиновый шарик той же массы m со скоростью = 1 м/с. Шарик застревает в точке А стержня на расстоянии х= от точки О, и система приобретает угловую скорость w. Найти угловую скорость вращения системы после удара, если l = 1 м.
10-10. Два невесомых стержня длины b соединены под углом a1 = 60° и вращаются без трения в горизонтальной плоскости вокруг вертикальной оси О с угловой скоростью w = 2 рад/с. На конце одного из стержней прикреплен очень маленький массивный шарик. В некоторый момент угол между стержнями самопроизвольно увеличился до a2 = 120°. С какой угловой скоростью стала вращаться такая система?
Литература
1. Савельев И.В. Курс общей физики : учебное пособие для вузов:[в 3 т.]. Т.1. Механика. Молекулярная физика / И.В. Савельев.- 5-е изд. стер. — СПб. и др.: Лань, 2006. – 432 с.
2. Савельев И.В. Сборник вопросов и задач по общей физике : учеб. пособие для втузов / И.В.Савельев .— СПб. и др. : Лань, 2005. – 288 с.
3. Стрелков С.П. Сборник задач по общему курсу физики : в 5 кн. – 5-е изд., стер .— М : Физматлит : Лань, 2006 .— (Общий курс физики). Кн. 1: Механика / С. П. Стрелков [и др.] ; под ред. И. А. Яковлева. – 2006. – 240 с.
4. Матвеев А.Н. Механика и теория относительности : Учебник для вузов / А.Н.Матвеев .- 3-е изд. – М. : ОНИКС 21 век: Мир и образование, 2003. – 432 с.
5. Трофимова Т.И. Сборник задач по курсу физики с решениями : учеб. пособие для вузов / Т.И.Трофимова .- 8-е изд. перераб. – М. : Высш. шк., 2007. – 591 с.
6. Трофимова Т.И. Основы физики : учеб. пособие:в 5 кн. Кн.1. Механика / Т.И.Трофимова .- М. : Высш. шк., 2007 .- 220с
7. Трофимова Т.И. Справочник по физике для студентов и абитуриентов / Т.И.Трофимова .— М. : Астрель:АСТ: Профиздат, 2005. – 399 с.
8. Яворский Б.М. Справочник по физике для инженеров и студентов вузов / Б. М. Яворский, А. А. Детлаф, А. К. Лебедев .- 8-е изд., перераб. и испр. – М. : ОНИКС : Мир и Образование, 2007. – 1055 с.
9. Полянин А.Д. Универсальный справочник. Высшая математика. Физика. Теоретическая механика. Сопротивление материалов / А.Д.Полянин [и др.].- М. : АСТ:Астрель: Профиздат, 2005. – 480 с.
megaobuchalka.ru
Закон сохранения импульса и момента импульса
При взаимодействии частиц системы между собойполный вектор импульса системы остается постоянным в случаях, когда
а) , б) и время взаимодействия очень мало. В этих случаях , где – векторная сумма импульсов частиц, которые существовали до взаимодействия, – векторная сумма импульсов всех частиц, которые будут существовать после взаимодействия. Если , то сохраняется только проекция полного импульсасистемы на ось x, .
При взаимодействии частиц системы между собой полный вектор момента импульса системы остается постоянным в случаях, когда
а) , б) и время взаимодействия очень мало. В этих случаях где – векторная сумма моментов импульсов частиц, которые существовали до взаимодействия, – векторная сумма моментов импульсов всех частиц, которые будут существовать после взаимодействия. Если , то сохраняется только проекция момента импульса системы на ось z (часто относительно закрепленной оси вращения).
Момент импульса частицы , где – радиус-вектор частицы, – импульс частицы. , где a – угол между и . Для твердого тела, вращающегося вокруг закрепленной оси z , где – момент инерции тела относительно оси z, – угловая скорость.
10-1. Маленький пластилиновый шарик массы m1 движется горизонтально со скоростью . Под углом a к направлению его движения летит второй шарик массы m2 со скоростью и сталкивается с первым. Шарики слипаются и движутся под углом b к первоначальному направлению движения второго шарика. Найдите . Если 1 кг, 2 кг, 1 м/с, 2 м/с, a = 30°.
10-2. Маленький пластилиновый шарик массы m1 движется горизонтально со скоростью . Под углом a к направлению его движения летит второй шарик массы m2 со скоростью и сталкивается с первым. Шарики слипаются и движутся под со скоростью . Найдите после удара модуль импульса шариков. Если 1 кг, 2 кг, 1 м/с, 2 м/с, a = 45°.
10-3. Маленький пластилиновый шарик массы m1 движется горизонтально со скоростью . Перпендикулярно к направлению его движения летит второй шарик массы m2 со скоростью и сталкивается с первым. Шарики слипаются и далее движутся вместе. Найдите после удара а) модуль импульса шариков; б) модуль скорости шариков. Если 1 кг, 2 кг, 1 м/с, 2 м/с.
10-4. Маленький пластилиновый шарик массы m1 движется горизонтально со скоростью . Перпендикулярно к направлению его движения летит второй шарик массы m2 со скоростью и сталкивается с первым. Шарики слипаются и далее движутся вместе под углом b к первоначальному направлению движения первого шарика шарика. Найдите и . Если 1 кг, 2 кг, 1 м/с, 2 м/с.
10-5. На горизонтальной плоскости лежит тонкий однородный стержень массы m =1 кг и длины l, который может вращаться вокруг вертикальной оси, проходящей через центр масс стержня С. Под углом a =30° к стержню в той же плоскости движется маленький пластилиновый шарик такой же массы m со скоростью = 1 м/с. Шарик прилипает к концу стержня, и система приобретает угловую скорость вращения w. Найти угловую скорость вращения системы после удара, если l = 1 м.
10-6. На горизонтальной плоскости лежит тонкий однородный стержень массы m =1 кг и длины l, который может вращаться вокруг вертикальной оси, проходящей через конец стержня О. Под углом a =30° к стержню в той же плоскости движется маленький пластилиновый шарик такой же массы m со скоростью = 1 м/с. Шарик прилипает к концу стержня, и система приобретает угловую скорость вращения w. Найти угловую скорость вращения системы после удара, если l = 1 м.
10-7. Тонкий однородный диск массы m = 1 кг и радиуса R может вращаться в вертикальной плоскости вокруг горизонтальной оси, проходящей через его центр С. Под углом a =30° к вертикали в плоскости вращения диска движется маленький пластилиновый шарик такой же массы m со скоростью = 1 м/с. Шарик прилипает к нижней точке неподвижно висящего диска, и система приобретает угловую скорость вращения w.. Найти угловую скорость вращения системы после удара, если R = 1 м.
10-8. Тонкий однородный стержень массы m = 1 кг и длины l может вращаться в вертикальной плоскости вокруг горизонтальной оси, проходящей через его конец. С разных сторон на стержень горизонтально в той же плоскости налетают два одинаковых пластилиновых шарика той же массы m с одинаковыми скоростями = 1 м/с. Первый шарик застревает в центре стержня, второй – в нижнем конце, и система приобретает угловую скорость w. Найти угловую скорость вращения системы после удара, если l = 1 м.
10-9. Тонкий однородный стержень массы m =1 кг и длины l может вращаться в вертикальной плоскости вокруг горизонтальной оси, проходящей через его конец O. Горизонтально в той же плоскости на стержень налетает пластилиновый шарик той же массы m со скоростью = 1 м/с. Шарик застревает в точке А стержня на расстоянии х= от точки О, и система приобретает угловую скорость w. Найти угловую скорость вращения системы после удара, если l = 1 м.
10-10. Два невесомых стержня длины b соединены под углом a1 = 60° и вращаются без трения в горизонтальной плоскости вокруг вертикальной оси О с угловой скоростью w = 2 рад/с. На конце одного из стержней прикреплен очень маленький массивный шарик. В некоторый момент угол между стержнями самопроизвольно увеличился до a2 = 120°. С какой угловой скоростью стала вращаться такая система?
Литература
1. Савельев И.В. Курс общей физики : учебное пособие для вузов:[в 3 т.]. Т.1. Механика. Молекулярная физика / И.В. Савельев.- 5-е изд. стер. — СПб. и др.: Лань, 2006. – 432 с.
2. Савельев И.В. Сборник вопросов и задач по общей физике : учеб. пособие для втузов / И.В.Савельев .— СПб. и др. : Лань, 2005. – 288 с.
3. Стрелков С.П. Сборник задач по общему курсу физики : в 5 кн. – 5-е изд., стер .— М : Физматлит : Лань, 2006 .— (Общий курс физики). Кн. 1: Механика / С. П. Стрелков [и др.] ; под ред. И. А. Яковлева. – 2006. – 240 с.
4. Матвеев А.Н. Механика и теория относительности : Учебник для вузов / А.Н.Матвеев .- 3-е изд. – М. : ОНИКС 21 век: Мир и образование, 2003. – 432 с.
5. Трофимова Т.И. Сборник задач по курсу физики с решениями : учеб. пособие для вузов / Т.И.Трофимова .- 8-е изд. перераб. – М. : Высш. шк., 2007. – 591 с.
6. Трофимова Т.И. Основы физики : учеб. пособие:в 5 кн. Кн.1. Механика / Т.И.Трофимова .- М. : Высш. шк., 2007 .- 220с
7. Трофимова Т.И. Справочник по физике для студентов и абитуриентов / Т.И.Трофимова .— М. : Астрель:АСТ: Профиздат, 2005. – 399 с.
8. Яворский Б.М. Справочник по физике для инженеров и студентов вузов / Б. М. Яворский, А. А. Детлаф, А. К. Лебедев .- 8-е изд., перераб. и испр. – М. : ОНИКС : Мир и Образование, 2007. – 1055 с.
9. Полянин А.Д. Универсальный справочник. Высшая математика. Физика. Теоретическая механика. Сопротивление материалов / А.Д.Полянин [и др.].- М. : АСТ:Астрель: Профиздат, 2005. – 480 с.
infopedia.su



