Матрица гаусс – Метод элементарных преобразований (методы Гаусса и Гаусса-Жордана для нахождения обратных матриц).
- Комментариев к записи Матрица гаусс – Метод элементарных преобразований (методы Гаусса и Гаусса-Жордана для нахождения обратных матриц). нет
- Советы абитуриенту
- Метод элементарных преобразований (методы Гаусса и Гаусса-Жордана для нахождения обратных матриц).
- Вычисление обратной матрицы по схеме Гаусса — КиберПедия
- Матрицы, Метод Гаусса
- Обращение матрицы nхn с использованием метода Гаусса — КиберПедия
- Обратная матрица методом Гаусса | Численные методы на Python
- Матрицы Метод Гаусса
- Матрицы Метод Гаусса
Метод элементарных преобразований (методы Гаусса и Гаусса-Жордана для нахождения обратных матриц).
В первой части был рассмотрен способ нахождения обратной матрицы с помощью алгебраических дополнений. Здесь же мы опишем иной метод нахождения обратных матриц: с использованием преобразований метода Гаусса и Гаусса-Жордана. Зачастую этот метод нахождения обратной матрицы именуют методом элементарных преобразований.
Метод элементарных преобразований
Для применения этого метода в одну матрицу записывают заданную матрицу $A$ и единичную матрицу $E$, т.е. составляют матрицу вида $(A|E)$ (эту матрицу называют также расширенной). После этого с помощью элементарных преобразований, выполняемых со строками расширенной матрицы, добиваются того, что матрица слева от черты станет единичной, причём расширенная матрица примет вид $\left(E| A^{-1} \right)$. К элементарным преобразованиям в данной ситуации относят такие действия:
- Смена мест двух строк.
- Умножение всех элементов строки на некоторое число, не равное нулю.
- Прибавление к элементам одной строки соответствующих элементов другой строки, умноженных на любой множитель.
Применять указанные элементарные преобразования можно разными путями. Обычно выбирают метод Гаусса или метод Гаусса-Жордана. Вообще, методы Гаусса и Гаусса-Жордана предназначены для решения систем линейных алгебраических уравнений, а не для нахождения обратных матриц. Фразу «применение метода Гаусса для нахождения обратной матрицы» здесь нужно понимать как «применение операций, свойственных методу Гаусса, для нахождения обратной матрицы».
Нумерация примеров продолжена с первой части. В примерах №5 и №6 рассмотрено применение метода Гаусса для нахождения обратной матрицы, а в примерах №7 и №8 разобрано использование метода Гаусса-Жордана. Следует отметить, что если в ходе решения все элементы некоторой строки или столбца матрицы, расположенной до черты, обнулились, то обратной матрицы не существует.
Пример №5
Найти матрицу $A^{-1}$, если $A=\left( \begin{array} {ccc} 7 & 4 & 6 \\ 2 & 5 & -4 \\ 1 & -1 & 3 \end{array} \right)$.
Решение
В этом примере будет найдена обратная матрица методом Гаусса. Расширенная матрица, имеющая в общем случае вид $(A|E)$, в данном примере примет такую форму: $ \left( \begin{array} {ccc|ccc} 7 & 4 & 6 & 1 & 0 & 0 \\ 2 & 5 & -4 & 0 & 1 & 0 \\ 1 & -1 & 3 & 0 & 0 & 1 \end{array} \right)$.
Цель: с помощью элементарных преобразований привести расширенную матрицу к виду $\left( E|A^{-1} \right)$. Применим те же операции, что применяются при решении систем линейных уравнений методом Гаусса. Для применения метода Гаусса удобно, когда первым элементом первой строки расширенной матрицы является единица. Чтобы добиться этого, поменяем местами первую и третью строки расширенной матрицы, которая станет такой: $ \left( \begin{array} {ccc|ccc} 1 & -1 & 3 & 0 & 0 & 1 \\ 2 & 5 & -4 & 0 & 1 & 0 \\ 7 & 4 & 6 & 1 & 0 & 0 \end{array} \right)$.
Теперь приступим к решению. Метод Гаусса делится на два этапа: прямой ход и обратный (подробное описание этого метода для решения систем уравнений дано в примерах соответствующей темы). Те же два этапа будут применены и в процессе отыскания обратной матрицы.
Прямой ход
Первый шаг
С помощью первой строки обнуляем элементы первого столбца, расположенные под первой строкой:
Немного прокомментирую выполненное действие. Запись $II-2\cdot I$ означает, что от элементов второй строки вычли соответствующие элементы первой строки, предварительно умноженные на два. Это действие можно записать отдельно следующим образом:

Точно так же выполняется и действие $III-7\cdot I$. Если возникают сложности с выполнением этих операций, их можно выполнить отдельно (аналогично показанному выше действию $II-2\cdot I$), а результат потом внести в расширенную матрицу.
Второй шаг
С помощью второй строки обнуляем элемент второго столбца, расположенный под второй строкой:
Разделим третью строку на 5:
Прямой ход окончен. Все элементы, расположенные под главной диагональю матрицы до черты, обнулились.
Обратный ход
Первый шаг
С помощью третьей строки обнуляем элементы третьего столбца, расположенные над третьей строкой:
Перед переходом к следующему шагу разделим вторую строку на $7$:
Второй шаг
С помощью второй строки обнуляем элементы второго столбца, расположенные над второй строкой:
Преобразования закончены, обратная матрица методом Гаусса найдена: $A^{-1}=\left( \begin{array} {ccc} -11/5 & 18/5 & 46/5 \\ 2 & -3 & -8 \\ 7/5 & -11/5 & -27/5 \end{array} \right)$. Проверку, при необходимости, можно сделать так же, как и в предыдущих примерах. Если пропустить все пояснения, то решение примет вид:

Ответ: $A^{-1}=\left( \begin{array} {ccc} -11/5 & 18/5 & 46/5 \\ 2 & -3 & -8 \\ 7/5 & -11/5 & -27/5 \end{array} \right)$.
Пример №6
Найти матрицу $A^{-1}$, если $A=\left( \begin{array} {cccc} -5 & 4 & 1 & 0 \\ 2 & 3 & -2 & 1 \\ 0 & 7 & -4 & -3 \\ 1 & 4 & 0 & 6 \end{array} \right)$.
Решение
Для нахождения обратной матрицы в этом примере будем использовать те же операции, что применяются при решении систем линейных уравнений методом Гаусса. Подробные пояснения даны в примере №5, здесь же ограничимся краткими комментариями. Запишем расширенную матрицу: $\left( \begin{array} {cccc|cccc} -5 & 4 & 1 & 0 & 1 & 0 & 0 & 0 \\ 2 & 3 & -2 & 1 &0 &1&0 &0 \\ 0 & 7 & -4 & -3 &0 & 0 & 1 & 0\\ 1 & 4 & 0 & 6 &0 &0 & 0 & 1 \end{array} \right)$. Поменяем местами первую и четвёртую строки данной матрицы: $\left( \begin{array} {cccc|cccc} 1 & 4 & 0 & 6 &0 &0 & 0 & 1 \\ 2 & 3 & -2 & 1 &0 &1&0 &0 \\ 0 & 7 & -4 & -3 &0 & 0 & 1 & 0\\ -5 & 4 & 1 & 0 & 1 & 0 & 0 & 0 \end{array} \right)$.
Прямой ход

Преобразования прямого хода завершены. Все элементы, расположенные под главной диагональю матрицы слева от черты, обнулились.
Обратный ход

Обратная матрица методом Гаусса найдена, $A^{-1}=\left( \begin{array} {cccc} -13/14 & -75/8 & 31/8 & 7/2 \\ -19/8 & -117/16 & 49/16 & 11/4 \\ -23/4 & -141/8 & 57/8 & 13/2 \\ 17/8 & 103/6 & -43/16 & -9/4 \end{array} \right)$. Проверку, при необходимости, проводим так же, как и в примерах №2 и №3.
Ответ: $A^{-1}=\left( \begin{array} {cccc} -13/14 & -75/8 & 31/8 & 7/2 \\ -19/8 & -117/16 & 49/16 & 11/4 \\ -23/4 & -141/8 & 57/8 & 13/2 \\ 17/8 & 103/6 & -43/16 & -9/4 \end{array} \right)$.
Пример №7
Найти матрицу $A^{-1}$, если $A=\left( \begin{array} {ccc} 2 & 3 & 4 \\ 7 & 1 & 9 \\ -4 & 5 & -2 \end{array} \right)$.
Решение
Для нахождения обратной матрицы применим операции, характерные методу Гаусса-Жордана. Отличие от метода Гаусса, рассмотренного в предыдущих примерах №5 и №6, состоит в том, что решение осуществляется в один этап. Напомню, что метод Гаусса делится на 2 этапа: прямой ход («делаем» нули под главной диагональю матрицы до черты) и обратный ход (обнуляем элементы над главной диагональю матрицы до черты). Для вычисления обратной матрицы методом Гаусса-Жордана двух стадий решения не потребуется. Для начала составим расширенную матрицу: $(A|E)$:
$$ (A|E)=\left( \begin{array} {ccc|ccc} 2 & 3 & 4 & 1 & 0 & 0\\ 7 & 1 & 9 & 0 & 1 & 0\\ -4 & 5 & -2 &0 & 0 & 1 \end{array} \right) $$Первый шаг
Обнулим все элементы первого столбца кроме одного. В первом столбце все элементы отличны от нуля, посему можем выбрать любой элемент. Возьмём, к примеру, $(-4)$:
Выбранный элемент $(-4)$ находится в третьей строке, посему именно третью строку мы используем для обнуления выделенных элементов первого столбца:
Сделаем так, чтобы первый элемент третьей строки стал равен единице. Для этого разделим элементы третьей строки расширенной матрицы на $(-4)$:
Теперь приступим к обнулению соответствующих элементов первого столбца:
В дальнейших шагах использовать третью строку уже будет нельзя, ибо мы её уже применили на первом шаге.
Второй шаг
Выберем некий не равный нулю элемент второго столбца и обнулим все остальные элементы второго столбца. Мы можем выбрать любой из двух элементов: $\frac{11}{2}$ или $\frac{39}{4}$. Элемент $\left( -\frac{5}{4} \right)$ выбрать нельзя, ибо он расположен в третьей строке, которую мы использовали на предыдущем шаге. Выберем элемент $\frac{11}{2}$, который находится в первой строке. Сделаем так, чтобы вместо $\frac{11}{2}$ в первой строке стала единица:
Теперь обнулим соответствующие элементы второго столбца:
В дальнейших рассуждениях первую строку использовать нельзя.
Третий шаг
Нужно обнулить все элементы третьего столбца кроме одного. Нам надо выбрать некий отличный от нуля элемент третьего столбца. Однако мы не можем взять $\frac{6}{11}$ или $\frac{13}{11}$, ибо эти элементы расположены в первой и третьей строках, которые мы использовали ранее. Выбор невелик: остаётся лишь элемент $\frac{2}{11}$, который находится во второй строке. Разделим все элементы второй строки на $\frac{2}{11}$:
Теперь обнулим соответствующие элементы третьего столбца:
Преобразования по методу Гаусса-Жордана закончены. Осталось лишь сделать так, чтобы матрица до черты стала единичной. Для этого придется менять порядок строк. Для начала поменяем местами первую и третью строки:
Теперь поменяем местами вторую и третью строки:
$$ \left( \begin{array} {ccc|ccc} 1 & 0 & 0 & 47/4 & -13/2 & -23/4 \\ 0 & 1 & 0 & 11/2 & -3 & -5/2 \\ 0 & 0 & 1 & -39/4 & 11/2 & 19/4 \end{array} \right) $$Итак, $A^{-1}=\left( \begin{array} {ccc} 47/4 & -13/2 & -23/4 \\ 11/2 & -3 & -5/2 \\ -39/4 & 11/2 & 19/4 \end{array} \right)$. Естественно, что решение можно провести и по-иному, выбирая элементы, стоящие на главной диагонали. Обычно именно так и поступают, ибо в таком случае в конце решения не придется менять местами строки. Я привел предыдущее решение лишь с одной целью: показать, что выбор строки на каждом шаге не принципиален. Если выбирать на каждом шаге диагональные элементы, то решение станет таким:

Из последней матрицы имеем: $A^{-1}=\left( \begin{array} {ccc} 47/4 & -13/2 & -23/4 \\ 11/2 & -3 & -5/2 \\ -39/4 & 11/2 & 19/4 \end{array} \right)$
Обратная матрица методом Гаусса-Жордана получена, осталось лишь записать ответ.
Ответ: $A^{-1}=\left( \begin{array} {ccc} 47/4 & -13/2 & -23/4 \\ 11/2 & -3 & -5/2 \\ -39/4 & 11/2 & 19/4 \end{array} \right)$.
Пример №8
Найти матрицу $A^{-1}$, если $A=\left( \begin{array} {cccc} 1 & 1 & 1 & 0 \\ 2 & 4 & 0 & 1 \\ 0 & 17 & 2 & -3 \\ -1 & 4 & 0 & -1 \end{array} \right)$.
Решение
Для нахождения обратной матрицы применим операции, характерные методу Гаусса-Жордана. Подробные пояснения были даны в примере №7, посему здесь ограничимся краткими комментариями. Итак, расширенная матрица такова: $A=\left( \begin{array} {cccc|cccc} 1 & 1 & 1 & 0 & 1 & 0 & 0 & 0\\ 2 & 4 & 0 & 1 & 0 & 1 &0 & 0\\ 0 & 17 & 2 & -3 & 0 & 0 & 1 & 0\\ -1 & 4 & 0 & -1 & 0 & 0 & 0 & 1 \end{array} \right)$.
Первый шаг
С помощью первой строки обнуляем соответствующие элементы первого столбца:
Второй шаг
Используя вторую строку обнуляем соответствующие элементы второго столбца:
Третий шаг
Используя третью строку обнуляем соответствующие элементы третьего столбца:
Четвёртый шаг
Используя четвёртую строку обнуляем соответствующие элементы четвёртого столбца:

Итак, $A^{-1}=\left( \begin{array} {cccc} -16/5 & -3/5 & 8/5 & -27/5 \\ 2/5 & 1/5 & -1/5 & 4/5 \\ 19/5 & 2/5 & -7/5 & 23/5 \\ 24/5 & 7/5 & -12/5 & 38/5 \end{array} \right)$. Если пропустить все пояснения, то решение примет вид:

Ответ: $A^{-1}=\left( \begin{array} {cccc} -16/5 & -3/5 & 8/5 & -27/5 \\ 2/5 & 1/5 & -1/5 & 4/5 \\ 19/5 & 2/5 & -7/5 & 23/5 \\ 24/5 & 7/5 & -12/5 & 38/5 \end{array} \right)$.
Примечание
Если в ходе решения диагональный элемент обнулился, то можно поменять местами строки. Например, в матрице $B=\left( \begin{array} {ccccc} 1 & 5 & 11 & 10 & 0\\ 0 & 0 & 9 & 5 & -6\\ 0 & 7 & 1 & -1 & -3\\ 0 & -11 & 8 & -9 & 12\\ 0 & 0 & 6 & -3 & 25 \end{array} \right)$ соответствующие элементы первого столбца обнулены. Нужно переходить к обнулению элементов второго столбца, но $b_{22}=0$. Поменяем местами вторую и третью строки матрицы $B$: $\left( \begin{array} {ccccc} 1 & 5 & 11 & 10 & 0\\ 0 & 7 & 1 & -1 & -3\\ 0 & 0 & 9 & 5 & -6\\ 0 & -11 & 8 & -9 & 12\\ 0 & 0 & 6 & -3 & 25 \end{array} \right)$. Теперь на месте нуля имеем число 7 и далее продолжаем стандартные преобразования метода Гаусса-Жордана.
Если Вас интересует метод вычисления обратной матрицы с помощью алгебраических дополнений, то изложение данного способа находится в первой части.
math1.ru
Вычисление обратной матрицы по схеме Гаусса — КиберПедия
Пусть – неособенная квадратная матрица. Тогда для нее существует обратная матрица . Обозначим через 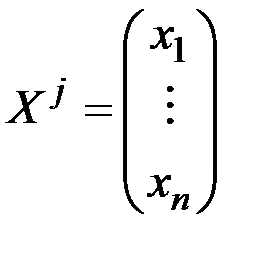 столбец номер обратной матрицы . По определению
столбец номер обратной матрицы . По определению
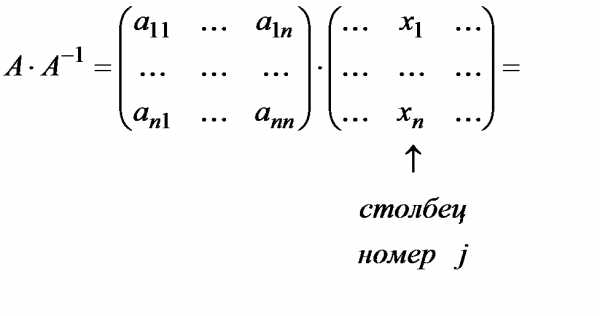

Отсюда, для нахождения -того столбца обратной матрицы необходимо решить систему
 (7.1)
(7.1)
Для нахождения всей матрицы необходимо решить систем вида (7.1) с одинаковыми левыми частями и различными правыми, состоящими из нулей и одной единицы в -й строке.
Таким образом, расширенная матрица имеет вид:
.
С помощью элементарных преобразований метода Гаусса её следует привести к виду
.
Пример 7.1. Методом Гаусса найти матрицу, обратную матрице 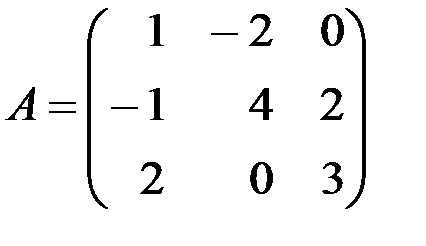 . Используя найденную обратную матрицу, решить систему
. Используя найденную обратную матрицу, решить систему
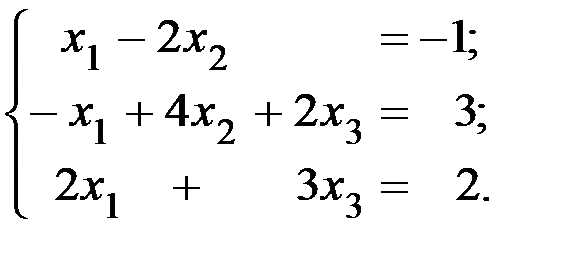
Решение. Составим расширенную матрицу и выполним «прямой ход».
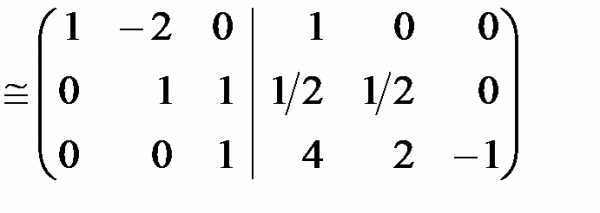
«Прямой ход» завершен. «Обратный ход» выполним также в матричном виде. Умножим третью строку на (–1) и прибавим ко второй строке. Затем вторую строку умножим на 2 и прибавим к первой строке.
.
«Обратный ход» завершен. Слева от черты стоит единичная матрица. Обратная матрица находится в правой части расширенной матрицы за вертикальной чертой. Таким образом,
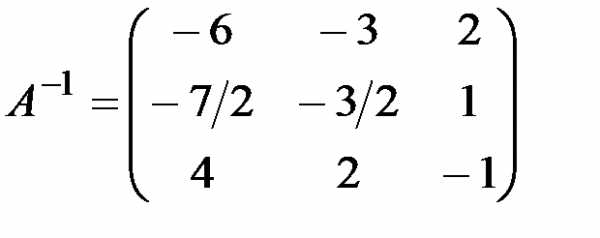 . Решим теперь заданную систему в матричном виде по формуле (2.2):
. Решим теперь заданную систему в матричном виде по формуле (2.2):
.
Ответ:
Проверка. Подставим найденное решение в исходную систему
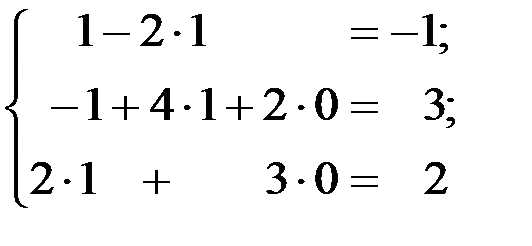
и вычислим левые части уравнений. Тогда имеем
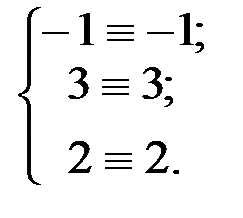
Ранг матрицы
Ранг матрицы является одним из основных понятий при исследовании систем уравнений.
Пусть дана система линейных уравнений, содержащая уравнений и неизвестных
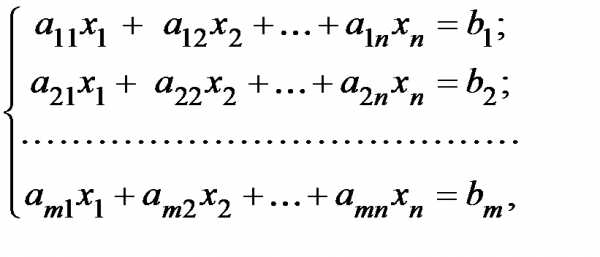
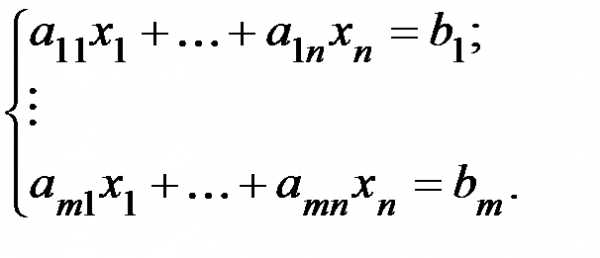 (8.1)
(8.1)
Матрица системы (8.1) имеет вид:
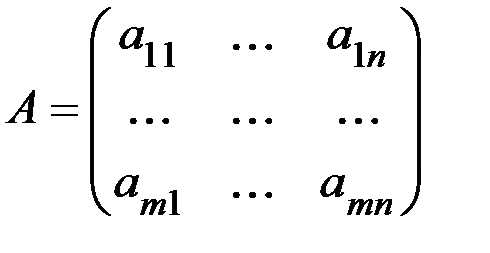 . (8.2)
. (8.2)
В матрице (8.2) выделим произвольных строк и произвольных столбцов. Элементы, стоящие на пересечении этих строк и столбцов, образуют матрицу. Определитель такой матрицы будем называть минором k-го порядка матрицы А.
Минором k-го порядка могут служить как элемент матрицы, так и любая квадратная матрица.
Перебирая значения , где – наименьшее из чисел и , мыможем вычислить все миноры матрицы .
Пример 8.1. Найти все миноры матрицы
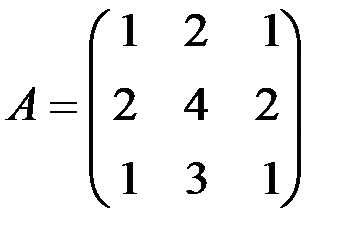 . (8.3)
. (8.3)
Решение.
1, 2, 1, 2, 4, 2, 1, 3, 1.
Миноры второго порядка образуются двумя произвольными строками и столбцами. Их тоже девять:
Наконец, минор третьего порядка – один, и он совпадает с определителем матрицы (8.3):
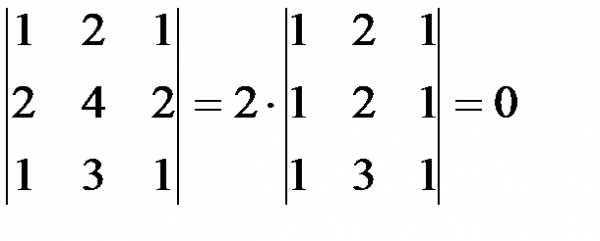 .
.
Рангом матрицы будем называть число, равное наибольшему порядку миноров, отличных от нуля.
Условимся обозначать ранг матрицы через или . Очевидно, что , где – наименьшее из чисел и .
Поскольку в примере 8.1 минор третьего порядка оказался равным нулю и нашлись миноры второго порядка, отличные от нуля, можно сделать вывод, что ранг матрицы (8.3) равен 2, то есть
Пример 8.2. Найти ранг матрицы
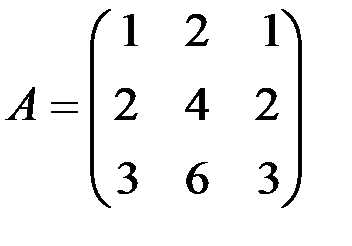 . (8.4)
. (8.4)
Решение. Матрица имеет ненулевые миноры первого порядка, поскольку элементы матрицы не равны нулю.
Вычислим миноры второго порядка:
а затем минор третьего порядка:
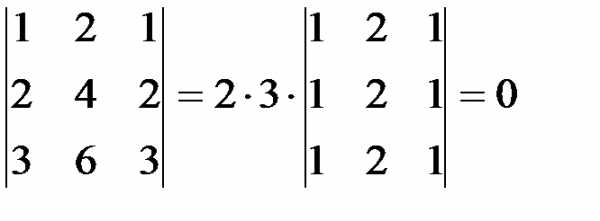 .
.
Из определения ранга матрицы следует, что матрица (8.4) имеет ранг равный единице, потому что обратились в нуль все миноры второго и третьего порядка.
Пример 8.3. Найти ранг матрицы
.
Решение. Матрица имеет только нулевые миноры первого и второго порядка, из чего следует, что .
Если ранг матрицы равен r, то все миноры порядка больше r равны нулю и есть хотя бы один минор порядка r, отличный от нуля.
Вычисление ранга матрицы по определению, то есть через вычисление всех соответствующих миноров, является процессом весьма трудоемким. Поэтому рассмотрим другой способ вычисления ранга, основанный на элементарных преобразованиях матриц.
К элементарным преобразованиям относятся следующие действия:
1) замена местами строк и столбцов матрицы;
2) умножение строки (столбца) на любое число, отличное от нуля;
3) прибавление к любой строке (столбцу) почленно любой другой строки (столбца).
Можно доказать, что указанные элементарные преобразования не меняют ранга матрицы. Первое и второе утверждения – очевидны. Третье – доказывается на основании свойств 4 и 5 определителя.
Для вычисления ранга матрицы (8.2) воспользуемся цепочкой элементарных преобразований и приведём матрицу к виду
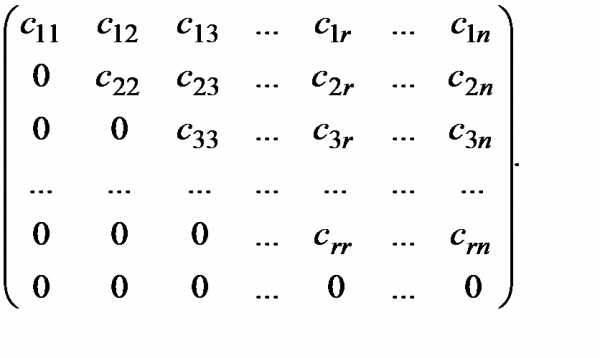 (8.5)
(8.5)
В матрице (8.5) на главной диагонали стоят ненулевые элементы . Элементы матрицы левее главной диагонали и под ней равны нулю. При таком представлении матрицы мы можем утверждать, что её ранг равен .
Итак, , то есть ранг равен числу ненулевых элементов, стоящих на главной диагонали.
Пример 8.4. Найти ранг матрицы
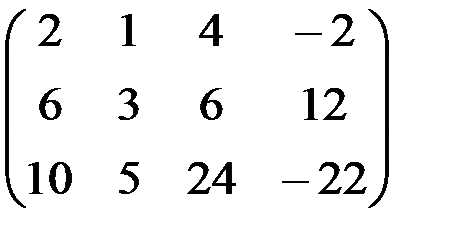 .
.
Решение. Для вычисления ранга матрицы достаточно воспользоваться «прямым ходом» метода Гаусса. Разделим первую строку на 2. Затем умножим первую строку на (–6) и прибавим ко второй строке. Умножим первую строку на (–10) и прибавим к третьей строке.
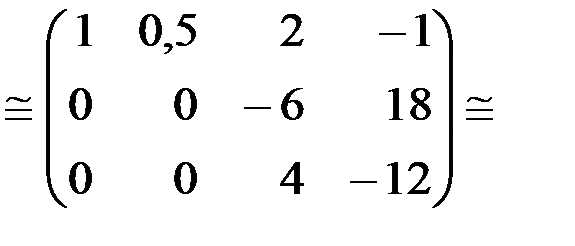
Разделим вторую строку на (–6), а третью – на 4. Получим
Вычтем из третьей строки вторую.
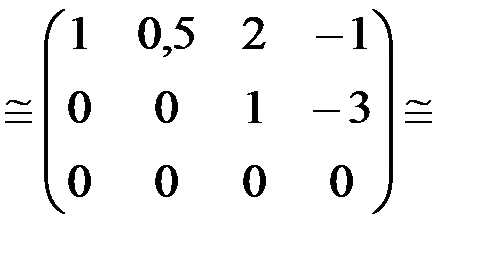
Поменяем местами второй и третий столбец.
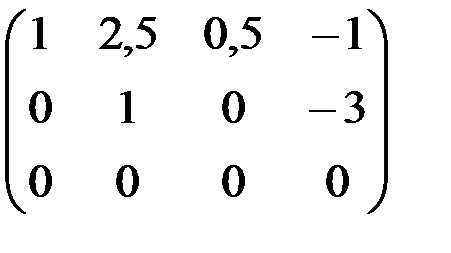 .
.
Из последнего выражения матрицы, содержащего две ненулевые строки с соответствующими ненулевыми элементами на главной диагонали, заключаем, что ранг матрицы равен двум. В приведённом примере мы пользовались методом Гаусса, но на последнем шаге производили элементарные преобразования не только над строками, но и столбцами.
cyberpedia.su
Матрицы, Метод Гаусса
КОСТРОМСКОЙ ФИЛИАЛ ВОЕННОГО УНИВЕРСИТЕТА РХБ ЗАЩИТЫ
Кафедра «Автоматизации управления войсками»
Только для преподавателей
“Утверждаю”
Начальник кафедры № 9
полковник ЯКОВЛЕВ А.Б.
«____»______________ 2004 г.
доцент СМИРНОВА А.И.
“МАТРИЦЫ. МЕТОД ГАУССА”
ЛЕКЦИЯ № 2 / 3
Обсуждено на заседании кафедры № 9
«____»___________ 2003г.
Протокол № ___________
Кострома, 2003
Cодержание
Введение
1. Действия над матрицами.
2. Решение систем линейных уравнений методом Гаусса.
Заключение
Литература
1. В.Е. Шнейдер и др., Краткий курс высшей математики,том I, гл.2,§6, 7.
2. В.С. Щипачев, Высшая математика, гл. 10, § 1, 7.
ВВЕДЕНИЕ
На лекции рассматривается понятие матрицы, действия над над матрицами, а также метод Гаусса для решения систем линейных уравнений. Для частного случая, так называемых квадратных матриц, можно вычислять определители, понятие о которых рассмотрено на предыдущей лекции. Метод Гаусса является более общим, чем рассмотренный ранее метод Крамера решения линейных систем. Разбираемые на лекции вопросы используются в различных разделах математики и в прикладных вопросах.
1-ый учебный вопрос ДЕЙСТВИЯ НАД МАТРИЦАМИ
ОПРЕДЕЛЕНИЕ 1. Прямоугольная таблица из m, n чисел, содержащая m – строк и n – столбцов, вида:
называется матрицей размера m ´ n
Числа, из которых составлена матрица, называются элементами матрицы.
Положение элемента аij в матрице характеризуются двойным индексом:
первый i – номер строки;
второй j – номер столбца, на пересечении которых стоит элемент.
Сокращенно матрицы обозначают заглавными буквами: А, В, С…
Коротко можно записывать так:
ОПРЕДЕЛЕНИЕ 2. Матрица, у которой число строк равно числу столбцов, т.е. m = n , называется квадратной.
Число строк (столбцов) квадратной матрицы называется порядком матрицы.
ПРИМЕР.
ЗАМЕЧАНИЕ 1. Мы будем рассматривать матрицы, элементами которых являются числа. В математике и ее приложениях встречаются матрицы, элементами которых являются другие объекты, например, функции, векторы.
ЗАМЕЧАНИЕ 2. Матрица – специальное математическое понятие. С помощью матриц удобно записывать различные преобразования, линейные системы и т.д., поэтому матрицы часто встречаются в математической и технической литературе.
ОПРЕДЕЛЕНИЕ 3. Матрица размера 1 ´ n, состоящая из одной строки, называется матрицей – строкой.
Матрица размера т ´ 1, состоящая из одного столбца, называется матрицей – столбцом.
ОПРЕДЕЛЕНИЕ 4. Нулевой матрицей называют матрицу, все элементы которой равны нулю.
Рассмотрим квадратную матрицу порядка n:
побочная диагональ
главная диагональ
Диагональ квадратной матрицы, идущая от верхнего левого элемента таблицы к правому нижнему, называется главной диагональю матрицы (на главной диагонали стоят элементы вида а ii).
Диагональ, идущая от правого верхнего элемента к левому нижнему, называется побочной диагональю матрицы.
Рассмотрим некоторые частные виды квадратных матриц.
1) Квадратная матрица называется диагональной, если все элементы, не стоящие на главной диагонали, равны нулю.
2) Диагональная матрица, у которой все элементы главной диагонали равны единице, называется единичной. Обозначается:
3) Квадратная матрица называется треугольной, если все элементы, расположенные по одну сторону от главной диагонали, равны нулю:
верхняя нижняя
треугольная матрица треугольная матрица
Для квадратной матрицы вводится понятие: определитель матрицы. Это определитель, составленный из элементов матрицы. Обозначается:
Ясно, что определитель единичной матрицы равен 1: ½Е½ = 1
ЗАМЕЧАНИЕ. Неквадратная матрица определителя не имеет.
Если определитель квадратичной матрицы отличен от нуля, то матрица называется невырожденной, если определитель равен нулю, то матрица называется вырожденной.
ОПРЕДЕЛЕНИЕ 5. Матрица, полученная из данной заменой ее строк столбцами с теми же номерами, называется транспонированной к данной.
Матрицу, транспонированную к А, обозначают АТ.
ПРИМЕР.
2 3 3 2
ОПРЕДЕЛЕНИЕ. Две матрицы одного и того же размера называются равными, если равны все их соответственные элементы.
Рассмотрим действия над матрицами.
СЛОЖЕНИЕ МАТРИЦ.
Операция сложения вводится только для матриц одинакового размера.
ОПРЕДЕЛЕНИЕ 7. Суммой двух матриц А = (аij) и В = (bij) одинакового размера называется матрица С = (сij) того же размера, элементы которой равны суммам соответствующих элементов слагаемых матриц, т.е. с i j = a i j + b i j
Обозначается сумма матриц А + В.
ПРИМЕР.
УМНОЖЕНИЕ МАТРИЦ НА ДЕЙСТВИТЕЛЬНОЕ ЧИСЛО
ОПРЕДЕЛЕНИЕ 8. Чтобы умножить матрицу на число k, надо умножить на это число каждый элемент матрицы:
если А= (аij), то k · A= (k · aij)
ПРИМЕР.
СВОЙСТВА СЛОЖЕНИЯ МАТРИЦ И УМНОЖЕНИЯ НА ЧИСЛО
1. Переместительное свойство: А + В = В + А
2. Сочетательное свойство: ( А + В ) + С = А + ( В + С )
3. Распределительное свойство: k · ( A + B ) = k A + k B, где k – число
УМНОЖЕНИЕ МАТРИЦ
Матрицу А назовем с о г л а с о в а н н о й с матрицей В , если число столбцов матрицы А равно числу строк матрицы В , т.е. для согласованных матриц матрица А имеет размер m ´ n , матрица В имеет размер n ´ k . Квадратные матрицы согласованы, если они одного порядка.
ОПРЕДЕЛЕНИЕ 9. Произведением матрицы А размера m ´ n на матрицу В размера n ´ k называется матрица С размера m ´ k, элемент которой аij, расположенный в i –ой строке и j – ом столбце, равен сумме произведений элементов i – ой строки матрицы А на соответствующие элементы j – столбца матрицы В, т.е.
cij= a i 1 b 1 j + ai 2 b 2 j +……+ ainbnj
Обозначим: С = А · В.
Если то
Произведение В ´ А не имеет смысла, т.к. матрицы не согласованы.
ЗАМЕЧАНИЕ 1. Если А ´ В имеет смысл, то В ´ А может не иметь смысла.
ЗАМЕЧАНИЕ 2. Если имеет смысл А ´ В и В ´ А, то, вообще говоря
А ´ В ⊃1; В ´ А, т.е. умножение матриц не обладает переместительным законом.
ЗАМЕЧАНИЕ 3. Если А – квадратная матрица и Е – единичная матрица того же порядка, то А ´ Е = Е ´ А = А.
Отсюда следует, что единичная матрица при умножении играет роль единицы.
ПРИМЕРЫ. Найти , если можно, А ´ В и В ´ А.
1.
Решение: Квадратные матрицы одного и того же второго порядка согласованы в томи другом порядке, поэтому А ´ В и В ´ А существуют.
2.
Решение: Матрицы А и В согласованы
Матрицы В и А не согласованы, поэтому В ´ А не имеет смысла.
Отметим, что в результате перемножения двух матриц получается матрица, содержащая столько строк, сколько их имеет матрица–множимое и столько столбцов, сколько их имеет матрица-множитель.
СВОЙСТВА УМНОЖЕНИЯ МАТРИЦ
1. Сочетательное свойство: А ´ ( В ´ С ) = (А ´ В ) ´С
2. Распределительное свойство: (А + В) ´ С = А ´ С + В ´С
Можно показать, что , если А и В – две квадратные матрицы одного порядка с определителями ½ А ½ и ½ В ½, то определитель матрицы С = А ´ В равен произведению определителей перемножаемых матриц, т.е.
½С½ = ½ А ½ ½ В ½
Отметим следующий любопытный факт. Как известно, произведение двух отличных от нуля чисел не равно нулю. Для матриц подобное обстоятельство может и не иметь места, т.е. произведение двух ненулевых матриц может оказаться равным нуль – матрице.
Действие “деление” для матриц не вводится. Для квадратных невырожденных матриц вводится обратная матрица. С понятием обратной матрицы можно познакомиться в рекомендуемой литературе.
2 – ой учебный вопрос РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ
УРАВНЕНИЙ МЕТОДОМ ГАУССА
Метод Гаусса (или метод последовательного исключения неизвестных) применим для решения систем линейных уравнений, в которых число неизвестных может быть либо равно числу уравнений, либо отлично от него.
Система т линейных уравнений с п неизвестными имеет вид:
x1 , x2, …, xn – неизвестные.
aij– коэффициенты при неизвестных.
bi – свободные члены (или правые части)
Система линейных уравнений называется совместной, если она имеет решение, и несовместной, если она не имеет решения.
Совместная система называется определенной, если она имеет единственное решение и неопределенной, если она имеет бесчисленное множество решений.
Две совместные системы называются равносильными, если они имеют одно и то же множество решений.
К элементарным преобразованиям системы отнесем следующее:
1. перемена местами двух любых уравнений;
2. умножение обеих частей любого из уравнений на произвольное число, отличное от нуля;
3. прибавление к обеим частям одного из уравнений системы соответствующих частей другого уравнения, умноженных на любое действительное число.
Элементарные преобразования переводят систему уравнений в равносильную ей.
Элементарные преобразования системы используются в методе Гаусса.
Для простоты рассмотрим метод Гаусса для системы трех линейных уравнений с тремя неизвестными в случае, когда существует единственное решение:
Дана система:
( 1 )
1-ый шаг метода Гаусса.
На первом шаге исключим неизвестное х1 из всех уравнений системы (1), кроме первого. Пусть коэффициент . Назовем его ведущим элементом. Разделим первое уравнение системы (1) на а11. Получим уравнение:
( 2 )
где
Исключим х1 из второго и третьего уравнений системы (1). Для этого вычтем из них уравнение (2), умноженное на коэффициент при х1 (соответственно а21 и а31).
Система примет вид:
( 3 )
Верхний индекс (1) указывает, что речь идет о коэффициентах первой преобразованной системы.
2-ой шаг метода Гаусса.
На втором шаге исключим неизвестное х2из третьего уравнения системы (3). Пусть коэффициент . Выберем его за ведущий элемент и разделим на него второе уравнение системы (3), получим уравнение:
( 4 )
где
Из третьего уравнения системы (3) вычтем уравнение (4), умноженное на Получим уравнение:
Предполагая, что находим
В результате преобразований система приняла вид:
(5)
Система вида (5) называется треугольной.
Процесс приведения системы (1) к треугольному виду (5) (шаги 1 и 2) называют прямым ходом метода Гаусса.
Нахождение неизвестных из треугольной системы называют обратным ходом метода Гаусса.
Для этого найденное значение х3 подставляют во второе уравнение системы (5) и находят х2. Затем х2 и х3 подставляют в первое уравнение и находят х1.
В общем случае для системы т линейных уравнений с п неизвестными проводятся аналогичные преобразования. На каждом шаге исключается одно из неизвестных из всех уравнений, расположенных ниже ведущего уравнения.
Отсюда другое называние метода Гаусса – метод последовательного исключения неизвестных.
Если в ходе преобразований системы получается противоречивое уравнение вида 0 = b, где b ⊃1; 0, то это означает, что система несовместна и решений не имеет.
В случае совместной системы после преобразований по методу Гаусса, составляющих прямой ход метода, система т линейных уравнений с п неизвестными будет приведена или к треугольному или к ступенчатому виду.
Треугольная система имеет вид:
Такая система имеет единственное решение, которое находится в результате проведения обратного хода метода гаусса.
Ступенчатая система имеет вид:
Такая система имеет бесчисленное множество решений. Чтобы найти эти решения, во всех уравнениях системы члены с неизвестными хk+1, … , xk переносят в правую часть. Эти неизвестные называются свободными и придают им произвольные значения. Из полученной треугольной системы находим х1, … , xk, которые будут выражаться через свободные неизвестные. Подробнее об этом можно узнать в рекомендуемой литературе.
Рассмотренный метод Гаусса легко программируется на ЭВМ и является более экономичным (по числу действий), чем другие методы.
ЗАКЛЮЧЕНИЕ
Рассмотренные на лекции матрицы являются удобным инструментом для записи различных математических преобразований и широко используется в научно-технической литературе. Метод Гаусса позволяет решать любые линейные системы, он находит широкое применение и содержится в пакетах стандартных программ для ЭВМ.
доцент Смирнова А.И.
bestreferat.su
Обращение матрицы nхn с использованием метода Гаусса — КиберПедия
По определению, обратная матрица матрицы A размерности n*n должна удовлетворять соотношению:
A×A-1=E (6)
Уравнение (6) представляет собой систему n систем линейных уравнений вида:
(7)
Здесь Z1, Z2,… Zn – столбцы искомой обратной матрицы, E1=(1,0,0,…,0), E2=(0,1,0,…,0), …En=(0,0,…,1) – соответствующие столбцы единичной матрицы.
Решая n систем линейных уравнений (7) получаем столбцы обратной матрицы A.
Находить решение систем линейных уравнений (7) можно любым подходящим численным методом. Основной принцип метода Гаусса – приведение матрицы к треугольному виду – может быть использован для решения задачи нахождения обратной матрицы n*n элементов. Если в методе Гаусса, при каждом проходе по строкам системы в качестве правой части использовать вектор с единственным единичным элементом, соответствующим текущей обрабатываемой строке, то получим алгоритм обращения матрицы n*n с использованием метода Гаусса.
Описание алгоритма вычисления обратной матрицы n*n методом Гаусса:
Задаем коэффициенты исходной системы линейных уравнений a(n,n) и правые части b(n).
Задаем цикл по j от 1 до n.
Задаем цикл по k от 1 до n.
В цикле по k зануляем все значения правой части системы b(k)=0.
Конец цикла по k.
В цикле по j:
Задаем значение для текущего уравнения j значение правой части уравнения равное 1 (b(j)=1).
По имеющейся системе уравнений с помощью метода Гаусса вычисляем решения системы x(1..n).
Задаем цикл по k от 1 до n.
Копируем в цикле по k только что найденные значения x(k=1….k=n) в j-й столбец временной матрицы с(n,n).
Конец цикла по k.
Конец цикла по j.
Задаем цикл по i от 1 до n.
Задаем цикл по j от 1 до n.
В цикле по j копируем найденные значения обратной матрицы, содержащиеся во временной матрице с(n,n), в матрицу a(n,n).
Конец цикла по j.
Конец цикла по i.
Конец алгоритма.
Пример алгоритма вычисления обратной матрицы n×n методом Гаусса на естественном языке:
lb=нижняя_граница_диапазона_случайных_чисел
ub=верхняя_граница_диапазона_случайных_чисел
dec=количество_знаков_после_запятой
n=размерность_системы
Определить Массив a(n,n),x(n),b(n)
* формируем матрицу коэффициентов уравнения и выводим их на печать
Печать ” Матрица коэффициентов a(n,n)”
Вызвать Случ_Матирица(@a,n,lb,ub,dec,1)
* формируем правую часть системы и выводим ее на печать
Печать” Правые частии системы b(n)”
Вызвать Случ_Вектор(@b,n,lb,ub,dec,1)
* “Выводим коэффициенты исходной системы”
Вызвать Печать_Системы(@a,@b,n,dec)
* “Находим обратную матрицу методом Гаусса”
Вызвать Обратить_Матрицу(@a,n)
* “Выводим обратную матрицу”
Вызвать Печать_Системы(@a,@b,n,dec)
Печать” Конец программы “
Определить Процедуру Обратить_Матрицу
Параметры a,n
Определить Локальный Массив c(n,n),b(n),x(n)
Определить Локальную Переменную i,j,k,l,m
Цикл по j от 1 до n
Цикл по k от 1 до n
b(k)=0
Конец Цикла
b(j)=1
Вызвать Метод_Гаусса(@a,@b,@x,n)
FOR k=1 TO n
c(k,j)=x(k)
Конец Цикла
Конец Цикла
Цикл по i от 1 до n
Цикл по j от 1 до n
a(i,j)=c(i,j)
Конец Цикла
Конец Цикла
Конец Определения Процедуры
Определить Функцию Случ_Матирица
Параметры a,n,lb,ub,dec,prnt
Определить Массив a(n,n)
Цикл по i от 1 до n
Цикл по j от 1 до n
a(i,j)=(ub-lb)*Случайный()+lb
a(i,j)=Округлить(a(i,j),dec)
Конец Цикла
Конец Цикла
Если prnt=1 Тогда
Цикл по i от 1 до n
Цикл по j от 1 до n
Печать a(i,j)
Конец Цикла
Печать
Конец Цикла
Конец Если
Возврат
Конец Определения Функции
Определить Функцию Случ_Вектор
Параметры a,n,lb,ub,dec,prnt
Определить Массив a(n)
Цикл по i от 1 до n
a(i)=(ub-lb)*Случайный()+lb
a(i)=Округлить(a(i),dec)
Конец Цикла
Если prnt=1 Тогда
Цикл по i от 1 до n
Печать a(i)
Конец Цикла
Конец Если
Конец Определения Функции
Определить Функцию Метод_Гаусса
Параметры a_tmp,b,x,n
Определить локальный Массив a(n,n)
Цикл по j от 1 до n
Цикл по i от 1 до n
a(i,j)=a_tmp(i,j)
Конец Цикла
Конец Цикла
* приводим к треугольному виду
Цикл по k от 1 до n-1
Цикл по l от k+1 до n
p=a(l,k)/a(k,k)
Цикл по m от k до n
a(l,m)=a(l,m)-a(k,m)*p
Конец Цикла
b(l)=b(l)-b(k)*p
Конец Цикла
Конец Цикла
* вычисляем x
Цикл по k от n до 1 с шагом -1
s=0
Цикл по l от k+1 до n
s=s+a(k,l)*x(l)
Конец Цикла
x(k)=(b(k)-s)/a(k,k)
Конец Цикла
Возврат
Конец Определения Функции
Определить Функцию Печать_Системы
Параметры a,b,n,dec
Цикл по i от 1 до n
Цикл по j от 1 до n
Печать a(i,j)
Конец Цикла
Печать ” :” + b(i)
Конец Цикла
Возврат
Конец Определения Функции
Пример реализации алгоритма вычисления обратной матрицы NxN методом Гаусса на VFP:
CLEAR
lb=-0.5
ub=0.5
dec=6
n=3
DIMENSION a(n,n),x(n),b(n)
* формируем матрицу коэффициентов уравнения и выводим их на печать
? ” Матрица коэффициентов a(n,n)”
CreateRNDMartix(@a,n,lb,ub,dec,1)
?
* формируем правую часть системы и выводим ее на печать
?” Правые частии системы b(n)”
CreateRNDVector(@b,n,lb,ub,dec,1)
?
* “Выводим коэффициенты исходной системы”
PrintSystem(@a,@b,n,dec)
* “Находим обратную матрицу методом Гаусса”
Reverse_Matrix(@a,n)
?
* “Выводим обратную матрицу”
PrintSystem(@a,@b,n,dec)
?
?” Конец программы !!!”
PROCEDURE Reverse_Matrix
LPARAMETERS a,n
LOCAL ARRAY c(n,n),b(n),x(n)
LOCAL i,j,k,l,m
FOR j=1 TO n
FOR k=1 TO n
b(k)=0
ENDFOR
b(j)=1
Gauss_Classic(@a,@b,@x,n)
FOR k=1 TO n
c(k,j)=x(k)
ENDFOR
ENDFOR
FOR i=1 TO n
FOR j=1 TO n
a(i,j)=c(i,j)
ENDFOR
ENDFOR
ENDPROC
FUNCTION CreateRNDMartix
LPARAMETERS a,n,lb,ub,dec,prnt
FOR i=1 TO n
FOR j=1 TO n
a(i,j)=(ub-lb)*RAND()+lb
a(i,j)=ROUND(a(i,j),dec)
ENDFOR
ENDFOR
IF prnt=1 then
?
FOR i=1 TO n
FOR j=1 TO n
?? a(i,j)
ENDFOR
?
ENDFOR
ENDIF
RETURN
ENDFUNC
FUNCTION CreateRNDVector
LPARAMETERS a,n,lb,ub,dec,prnt
FOR i=1 TO n
a(i)=(ub-lb)*RAND()+lb
a(i)=ROUND(a(i),dec)
ENDFOR
IF prnt=1 then
FOR i=1 TO n
? a(i)
ENDFOR
ENDIF
ENDFUNC
FUNCTION Gauss_Classic
LPARAMETERS a_tmp,b,x,n
LOCAL ARRAY a(n,n)
FOR j=1 TO n
FOR i=1 TO n
a(i,j)=a_tmp(i,j)
ENDFOR
ENDFOR
* приводим к треугольному виду
FOR k=1 TO n-1
FOR l=k+1 TO n
p=a(l,k)/a(k,k)
FOR m=k TO n
a(l,m)=a(l,m)-a(k,m)*p
ENDFOR
b(l)=b(l)-b(k)*p
ENDFOR
ENDFOR
* вычисляем x
FOR k=n TO 1 STEP -1
s=0
FOR l=k+1 TO n
s=s+a(k,l)*x(l)
ENDFOR
x(k)=(b(k)-s)/a(k,k)
ENDFOR
RETURN
ENDFUNC
FUNCTION PrintSystem
LPARAMETERS a,b,n,dec
FOR i=1 TO n
?
FOR j=1 TO n
?? STR(a(i,j),dec*2+2,dec)
ENDFOR
?? ” :” + STR(b(i),dec*2+2,dec)
ENDFOR
RETURN
ENDFUNC
В данной реализация использован прием формирования матрицы коэффициентов системы уравнений случайным образом из заданного диапазона, при этом границы диапазона определяются значениями lb (low bound – нижняя граница) и ub (upper bound – верхняя граница).
Запись Округлить() и Случайный() означают соответственно вызовы стандартных встроенных функций округления и возврата псевдослучайного значения из диапазона от 0 до 1.
Пример реализации алгоритма вычисления обратной матрицы nxn методом Гаусса на VBA:
Sub Find_Reverse_Matrix()
Dim a(), b(), x()
n = 3
dec = 4
ReDim a(n, n): ReDim b(n): ReDim x(n)
Call Read_Matrix(“C:\Temp\system.txt”, a(), b(), n)
‘ Выводим на экран исходную систему
Call Print_Matrix(a(), b(), n, dec)
‘ Вычисляем обратную матрицу методом Гаусса
Call Reverse_Matrix(a(), b(), x(), n)
‘ “Выводим обратную матрицу”
Call Print_Matrix(a(), b(), n, dec)
MsgBox “Конец программы !!!”
End Sub
Sub Reverse_Matrix(a(), b(), x(), n)
Dim i, j, k, l, m
Dim c()
ReDim c(n, n)
For j = 1 To n
For k = 1 To n
b(k) = 0
Next k
b(j) = 1
Call Gauss_Classic(a(), b(), x(), n)
For k = 1 To n
c(k, j) = x(k)
Next k
Next j
For i = 1 To n
For j = 1 To n
a(i, j) = c(i, j)
Next j
Next i
End Sub
Sub Gauss_Classic(a_tmp(), b(), x(), n)
Dim i, j, k, l, m
Dim a()
Redim a(n,n)
a()=a_tmp()
‘ приводим к треугольному виду
For k = 1 To n – 1
For l = k + 1 To n
p = a(l, k) / a(k, k)
For m = k To n
a(l, m) = a(l, m) – a(k, m) * p
Next m
b(l) = b(l) – b(k) * p
Next l
Next k
‘ вычисляем x
For k = n To 1 Step -1
s = 0
For l = k + 1 To n
s = s + a(k, l) * x(l)
Next l
x(k) = (b(k) – s) / a(k, k)
Next k
End Sub
Sub Read_Matrix(file_path, a(), b(), n)
Dim s, s1, i, j
nf = FreeFile
Open file_path For Input As #nf
For i = 1 To n
pos1 = 1
Input #nf, s
For j = 1 To n
pos2 = InStr(pos1, s, “;”)
s1 = Mid(s, pos1, pos2 – pos1)
a(i, j) = Val(s1)
pos1 = pos2 + 1
Next j
pos2 = InStr(pos1, s, “;”)
s1 = Mid(s, pos1, pos2 – pos1)
b(i) = Val(s1)
Next i
Close #nf
End Sub
Sub Print_Matrix(a(), b(), n, dec)
Dim i
Dim DStr, str
DStr = “0.”
For i = 1 To dec
DStr = DStr + “0”
Next i
str = “”
For i = 1 To n
str = str & vbCrLf
For j = 1 To n
str = str & Format(a(i, j), DStr) & ” : “
Next j
str = str & ” : ” & Format(b(i), DStr)
Next i
Debug.Print str
End Sub
Данная реализация алгоритма использует чтение коэффициентов системы уравнений из текстового файла. Текстовый файл, например, для системы с тремя уравнениями, должен быть следующего вида:
“0.34;0.71;0.63;2.08;”
“0.71;-0.36;-0.18;0.17;”
“1.17;-2.35;0.75;1.28;”
т.е. в каждой строке файла записываются коэффициенты первой строки системы (i=1, a(i,j), b(i)), при этом вся строка заключена в кавычки (т.е. рассматривается VBA как текстовая строка) и после каждого коэффициента ставиться разделитель – точка с запятой (;).
Контрольные вопросы
1. Что такое система линейных уравнений?
2. Что такое решение системы линейных уравнений?
3. Что такое совместность и полнота системы линейных уравнений?
4. Что такое вырожденная система линейных уравнений?
5. Что такое определитель матрицы системы линейных уравнений?
6. Что такое однородная система линейных уравнений?
7. Что такое собственные значения матрицы?
8. Что такое характеристическая функция системы линейных уравнений?
9. Привести алгоритм табуляции характеристической функции системы линейных уравнений.
10. Как найти собственный вектор системы линейных уравнений?
11. Как найти ненулевое решение однородной системы линейных алгебраических уравнений?
12. Привести алгоритм решения системы линейных уравнений методом простой итерации.
13. В чем состоит условие сходимости метода простой итерации для системы линейных уравнений?
14. Как определить точность вычисления решений системы линейных уравнений методом простой итерации?
15. Привести алгоритмы вычисления разностей векторов и длин разностей векторов (норм).
16. Привести алгоритм определения степени сходимости метода простой итерации для системы линейных уравнений.
17. Привести алгоритм модифицированного (с параметром, улучшающим сходимость) метода простой итерации для системы линейных уравнений.
18. Привести алгоритм метода Гаусса-Зейделя.
19. Привести алгоритм обращения матрицы nxn.
Задания
Методами Зейделя и Гаусса-Зейделя решить с точностью до 0,001 систему линейных уравнений. Численным методом найти обратные матрицы к матрицам коэффициентов систем линейных уравнений. Матрицы коэффициентов и векторы правых частей считывать из:
а) текстовых файлов;
б) dbf-таблицы;
в) MS’Excel;
г) MS’Word.
| №1 | 2,7×1+3,3×2+1,3×3=2,1; 3,5×1–1,7×2+2,8×3=1,7; 4,1×1+5,8×2–1,7×3=0,8. | №2 | 1,7×1+2,8×2+1,9×3=0,7; 2,1×1+3,4×2+1,8×3=1,1; 4,2×1–1,7×2+1,3×3=2,8. |
| №3. | 3,1×1+2,8×2+1,9×3=0,2; 1,9×1+3,1×2+2,1×3=2,1; 7,5×1+3,8×2+4,8×3=5,6. | №4. | 9,1×1+5,6×2+7,8×3=9,8; 3,8×1+5,1×2+2,8×3=6,7; 4,1×1+5,7×2+1,2×3=5,8. |
| №5. | 3,3×1+2,1×2+2,8×3=0,8; 4,1×1+3,7×2+4,8×3=5,7; 2,7×1+1,8×2+1,1×3=3,2. | №6. | 7,6×1+5,8×2+4,7×3=10,1; 3,8×1+4,1×2+2,7×3=9,7; 2,9×1+2,1×2+3,8×3=7,8. |
| №7. | 3,2×1–2,5×2+3,7×3=6,5; 0,5×1+0, 34×2+1,7×3=0,24; 1,6×1+2,3×2–1,5×3=4,3. | №8. | 5,4×1–2,3×2+3,4×3= –3,5; 4,2×1+1,7×2–2,3×3=2,7; 3,4×1+2,4×2+7,4×3=1,9. |
| №9. | 3,6×1+1,8×2–4,7×3=3,8; 2,7×1–3,6×2+1,9×3=0,4; 1,5×1+4,5×2+3,3×3= –1,6. | №10. | 5,6×1+2,7×2–1,7×3=1,9; 3,4×1–3,6×2–6,7×3= –2,4; 0,8×1+1,3×2+3,7×3=1,2. |
| №11. | 2,7×1+0,9×2–1,5×3=3,5; 4,5×1–2,8×2+6,7×3=2,6; 5,1×1+3,7×2–1,4×3= –0,14. | №12. | 4,5×1–3,5×2+7,4×3=2,5; 3,1×1–0,6×2–2,3×3= –1,5; 0,8×1+7,4×2–0,5×3=6,4. |
| №13. | 3,8×1+6,7×2–1,2×3=5,2; 6,4×1+1,3×2–2,7×3=3,8; 2,4×1–4,5×2+3,5×3= –0,6. | №14. | 5,4×1–6,2×2–0,5×3=0,52; 3,4×1+2,3×2+0,8×3= –0,8; 2,4×1–1,1×2+3,8×3=1,8. |
| №15. | 7,8×1+5,4×2+4,8×3=1,8; 3,3×1+1,1×2+1,8×3=2,3; 4,5×1+3,3×2+2,8×3=3,4. | №16. | 3,8×1+4,1×2–2,3×3=4,8; –2,1×1+3,9×2–5,8×3=3,3; 1,8×1+1,1×2–2,1×3=5,8. |
| №17. | 1,7×1–2,2×2+3,0×3=1,8; 2,1×1+1,9×2–2,3×3=2,8; 4,2×1+3,9×2–3,1×3=5,1. | №18. | 2,8×1+3,8×2–3,2×3=4,5; 2,5×1–2,8×2+3,3×3=7,1; 6,5×1–7,1×2+4,8×3=6,3. |
| №19. | 3,3×1+3,7×2+4,2×3=5,8; 2,7×1+2,3×2–2,9×3=6,1; 4,1×1+4,8×2–5,0×3=7,0. | №20. | 7,1×1+6,8×2+6,1×3=7,0; 5,0×1+4,8×2+5,3×3=6,1; 8,2×1+7,8×2+7,1×3=5,8. |
| №21. | 3,7×1+3,1×2+4,0×3=5,0; 4,1×1+4,5×2–4,8×3=4,9; –2,1×1–3,7×2+1,8×3=2,7. | №22. | 4,1×1+5,2×2–5,8×3=7,0; 3,8×1–3,1×2+4,0×3=5,3; 7,8×1+5,3×2–6,3×3=5,8. |
| №23. | 3,7×1–2,3×2+4,5×3=2,4; 2,5×1+4,7×2–7,8×3=3,5; 1,6×1+5,3×2+1,3×3= –2,4. | №24. | 6,3×1+5,2×2–0,6×3=1,5; 3,4×1–2,3×2+3,4×3=2,7; 0,8×1+1,4×2+3,5×3= –2,3. |
cyberpedia.su
Обратная матрица методом Гаусса | Численные методы на Python
Для получения матрицы будем исходить из того, что она является решением уравнения , где – единичная матрица. Представим искомую матрицу как набор векторов-столбцов img а единичную матрицу как набор единичных векторов img Матричное уравнение в соответствии с правилами умножения матриц возможно заменить не связанной между собой системой уравнений img Каждое из этих уравнений может быть решено методом Гаусса. Заметим то обстоятельство, что все СЛАУ имеют одну и ту же матрицу коэффициентов, поэтому
Суть метода Гаусса-Жордана заключается в том, что если с единичной матрицей провести элементарные преобразования, которыми невырожденная квадратная матрица приводится к , то получится обратная матрица . Для отображения всех элементарных преобразований, совершающихся над матрицей , на единичную матрицу , удобно “склеить” две матрицы в одну. Если матрицы и имели размер , то склеенная матрица будет иметь размер . Таким образом, все преобразования над матрицей (перестановка строк, умножение строки на константу) будут автоматически совершаться и над единичной матрицей). Обозначим склеенную матрицу как Приведение матрицы к единичной совершается в два этапа: на первом этапе будем двигаться “сверху-вниз”, получая в итоге треугольную матрицу, с единицами на главной диагонали и нулями ниже. На втором этапе будем двигаться “снизу-вверх”, преобразуя элементы, лежащие выше главной диагонали к нулю, тем самым добиваясь единичной матрицы в результате.
Прямой ход
Пусть матрица имеет размер . Тогда на первом этапе будет совершено шагов. На каждом шаге необходимо совершить три действия.
- Поменять местами строки и , в случае если . Этот шаг необходим для исключения ситуации нахождения на главной диагонали 0.
- Преобразовать элемент, стоящий на главной диагонали к 1. Для этого необохдимо домножить всю строку на .
- Обнулить все нижележащие элементы столбца. Для этого вычтем из каждой нижележащей строки c индексом результат умножения элемента c текущей строкой. Напомним, что в результате шага 2 первый элемент 1, поэтому первым элементом вычитаемой строки будет являться значение первого элемента строки , что и даст 0 в элементе
Обратный ход
Теперь необходимо преобразовать матрицу так, чтобы все элементы n-ого столбца выше стали равны нулю. Для этого прибавляем к n-1 строке соответсвующие элементы n-ой строки, умноженные на . К n-2 строке прибавляем соответсвующие элементы (n-1)-ой строки, умноженные на и т.д. Аналогичные действия необходимо совершить над оставшимися строками.
Реализация
Приведем реализацию функции inverse, принимающей в качестве аргумента исходную матрицу коэффициентов, и возвращающую матрицу, обратную к исходной. Склеим матрицу коэффициентов с единичной матрицей с помощью функции hstack
m = np.hstack((matrix_origin,
np.matrix(np.diag([1.0 for i in range(matrix_origin.shape[0])]))))
Прямой ход
for k in range(n):
swap_row = pick_nonzero_row(m, k)
if swap_row != k:
m[k, :], m[swap_row, :] = m[swap_row, :], np.copy(m[k, :])
if m[k, k] != 1:
m[k, :] *= 1 / m[k, k]
for row in range(k + 1, n):
m[row, :] -= m[k, :] * m[row, k]
Для проверки первгого условия реализуем вспомогательную функцию pick_non_zero_row, возвращающую индекс первой строки, в которой элемент интересующего нас столбца не равен нулю
def pick_nonzero_row(m, k):
while k < m.shape[0] and not m[k, k]:
k += 1
return k
Обратный ход
for k in range(n - 1, 0, -1):
for row in range(k - 1, -1, -1):
if m[row, k]:
m[row, :] -= m[k, :] * m[row, k]
Возвратим преобразованную единичную матрицу, т.е. вторую часть “склееного” массива, воспользовавшись функцией hsplit
return np.hsplit(m, n // 2)[1]
orion1401.gitbooks.io
Матрицы Метод Гаусса
КОСТРОМСКОЙ ФИЛИАЛ ВОЕННОГО УНИВЕРСИТЕТА РХБ ЗАЩИТЫКафедра «Автоматизации управления войсками»
Только для преподавателей
“Утверждаю”
Начальник кафедры № 9
полковник ЯКОВЛЕВ А.Б.
«____»______________ 2004 г.
доцент СМИРНОВА А.И.
“МАТРИЦЫ. МЕТОД ГАУССА”
ЛЕКЦИЯ № 2 / 3
Обсуждено на заседании кафедры № 9
«____»___________ 2003г.
Протокол № ___________
Кострома, 2003
Cодержание
Введение
1. Действия над матрицами.
2. Решение систем линейных уравнений методом Гаусса.
Заключение
Литература
1. В.Е. Шнейдер и др., Краткий курс высшей математики,том I, гл.2,§6, 7.
2. В.С. Щипачев, Высшая математика, гл. 10, § 1, 7.
ВВЕДЕНИЕ
На лекции рассматривается понятие матрицы, действия над над матрицами, а также метод Гаусса для решения систем линейных уравнений. Для частного случая, так называемых квадратных матриц, можно вычислять определители, понятие о которых рассмотрено на предыдущей лекции. Метод Гаусса является более общим, чем рассмотренный ранее метод Крамера решения линейных систем. Разбираемые на лекции вопросы используются в различных разделах математики и в прикладных вопросах.
1-ый учебный вопрос ДЕЙСТВИЯ НАД МАТРИЦАМИ
ОПРЕДЕЛЕНИЕ 1. Прямоугольная таблица из m, n чисел, содержащая m – строк и n – столбцов, вида:
называется матрицей размера m ´ n
Числа, из которых составлена матрица, называются элементами матрицы.
Положение элемента аij в матрице характеризуются двойным индексом:
первый i – номер строки;
второй j – номер столбца, на пересечении которых стоит элемент.
Сокращенно матрицы обозначают заглавными буквами: А, В, С…
Коротко можно записывать так: .zip” v:shapes=”_x0000_i1026″>
ОПРЕДЕЛЕНИЕ 2. Матрица, у которой число строк равно числу столбцов, т.е. m = n , называется квадратной.
Число строк (столбцов) квадратной матрицы называется порядком матрицы.
ПРИМЕР.
ЗАМЕЧАНИЕ 1. Мы будем рассматривать матрицы, элементами которых являются числа. В математике и ее приложениях встречаются матрицы, элементами которых являются другие объекты, например, функции, векторы.
ЗАМЕЧАНИЕ 2. Матрица – специальное математическое понятие. С помощью матриц удобно записывать различные преобразования, линейные системы и т.д., поэтому матрицы часто встречаются в математической и технической литературе.
ОПРЕДЕЛЕНИЕ 3. Матрица размера 1 ´ n, состоящая из одной строки, называется матрицей – строкой.
Матрица размера т ´ 1, состоящая из одного столбца, называется матрицей – столбцом.
ОПРЕДЕЛЕНИЕ 4. Нулевой матрицей называют матрицу, все элементы которой равны нулю.
Рассмотрим квадратную матрицу порядка n:
побочная диагональ
главная диагональ
Диагональ квадратной матрицы, идущая от верхнего левого элемента таблицы к правому нижнему, называется главной диагональю матрицы (на главной диагонали стоят элементы вида а ii).
Диагональ, идущая от правого верхнего элемента к левому нижнему, называется побочной диагональю матрицы.
Рассмотрим некоторые частные виды квадратных матриц.
1) Квадратная матрица называется диагональной, если все элементы, не стоящие на главной диагонали, равны нулю.
2) Диагональная матрица, у которой все элементы главной диагонали равны единице, называется единичной. Обозначается:
3) Квадратная матрица называется треугольной, если все элементы, расположенные по одну сторону от главной диагонали, равны нулю:
верхняя нижняя
треугольная матрица треугольная матрица
Для квадратной матрицы вводится понятие: определитель матрицы. Это определитель, составленный из элементов матрицы. Обозначается:
Ясно, что определитель единичной матрицы равен 1: ½Е½ = 1
ЗАМЕЧАНИЕ. Неквадратная матрица определителя не имеет.
Если определитель квадратичной матрицы отличен от нуля, то матрица называется невырожденной, если определитель равен нулю, то матрица называется вырожденной.
ОПРЕДЕЛЕНИЕ 5. Матрица, полученная из данной заменой ее строк столбцами с теми же номерами, называется транспонированной к данной.
Матрицу, транспонированную к А, обозначают АТ.
ПРИМЕР.
2 3 3 2
ОПРЕДЕЛЕНИЕ. Две матрицы одного и того же размера называются равными, если равны все их соответственные элементы.
Рассмотрим действия над матрицами.
СЛОЖЕНИЕ МАТРИЦ.
Операция сложения вводится только для матриц одинакового размера.
ОПРЕДЕЛЕНИЕ 7. Суммой двух матриц А = (аij) и В = (bij) одинакового размера называется матрица С = (сij) того же размера, элементы которой равны суммам соответствующих элементов слагаемых матриц, т.е. с i j = a i j + b i j
Обозначается сумма матриц А + В.
ПРИМЕР.
УМНОЖЕНИЕ МАТРИЦ НА ДЕЙСТВИТЕЛЬНОЕ ЧИСЛО
ОПРЕДЕЛЕНИЕ 8. Чтобы умножить матрицу на число k, надо умножить на это число каждый элемент матрицы:
если А= (аij), то k · A= (k · aij)
ПРИМЕР.
СВОЙСТВА СЛОЖЕНИЯ МАТРИЦ И УМНОЖЕНИЯ НА ЧИСЛО
1. Переместительное свойство: А + В = В + А
2. Сочетательное свойство: ( А + В ) + С = А + ( В + С )
3. Распределительное свойство: k · ( A + B ) = k A + k B, где k – число
УМНОЖЕНИЕ МАТРИЦ
Матрицу А назовем с о г л а с о в а н н о й с матрицей В , если число столбцов матрицы А равно числу строк матрицы В , т.е. для согласованных матриц матрица А имеет размер m ´ n , матрица В имеет размер n ´ k . Квадратные матрицы согласованы, если они одного порядка.
ОПРЕДЕЛЕНИЕ 9. Произведением матрицы А размера m ´ n на матрицу В размера n ´ k называется матрица С размера m ´ k, элемент которой аij, расположенный в i –ой строке и j – ом столбце, равен сумме произведений элементов i – ой строки матрицы А на соответствующие элементы j – столбца матрицы В, т.е.
cij= a i 1 b 1 j + ai 2 b 2 j +……+ ainbnj
Обозначим: С = А · В.
Если то
Произведение В ´ А не имеет смысла, т.к. матрицы не согласованы.
ЗАМЕЧАНИЕ 1. Если А ´ В имеет смысл, то В ´ А может не иметь смысла.
ЗАМЕЧАНИЕ 2. Если имеет смысл А ´ В и В ´ А, то, вообще говоря
А ´ В ¹ В ´ А, т.е. умножение матриц не обладает переместительным законом.
ЗАМЕЧАНИЕ 3. Если А – квадратная матрица и Е – единичная матрица того же порядка, то А ´ Е = Е ´ А = А.
Отсюда следует, что единичная матрица при умножении играет роль единицы.
ПРИМЕРЫ. Найти , если можно, А ´ В и В ´ А.
1.
Решение: Квадратные матрицы одного и того же второго порядка согласованы в томи другом порядке, поэтому А ´ В и В ´ А существуют.
2.
Решение: Матрицы А и В согласованы
Матрицы В и А не согласованы, поэтому В ´ А не имеет смысла.
Отметим, что в результате перемножения двух матриц получается матрица, содержащая столько строк, сколько их имеет матрица–множимое и столько столбцов, сколько их имеет матрица-множитель.
СВОЙСТВА УМНОЖЕНИЯ МАТРИЦ
1. Сочетательное свойство: А ´ ( В ´ С ) = (А ´ В ) ´С
2. Распределительное свойство: (А + В) ´ С = А ´ С + В ´С
Можно показать, что , если А и В – две квадратные матрицы одного порядка с определителями ½ А ½ и ½ В ½, то определитель матрицы С = А ´ В равен произведению определителей перемножаемых матриц, т.е.
½С½ = ½ А ½ ½ В ½
Отметим следующий любопытный факт. Как известно, произведение двух отличных от нуля чисел не равно нулю. Для матриц подобное обстоятельство может и не иметь места, т.е. произведение двух ненулевых матриц может оказаться равным нуль – матрице.
Действие “деление” для матриц не вводится. Для квадратных невырожденных матриц вводится обратная матрица. С понятием обратной матрицы можно познакомиться в рекомендуемой литературе.
2 – ой учебный вопрос РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ
УРАВНЕНИЙ МЕТОДОМ ГАУССА
Метод Гаусса (или метод последовательного исключения неизвестных) применим для решения систем линейных уравнений, в которых число неизвестных может быть либо равно числу уравнений, либо отлично от него.
Система т линейных уравнений с п неизвестными имеет вид:
x1 , x2, …, xn – неизвестные.
aij– коэффициенты при неизвестных.
bi – свободные члены (или правые части)
Система линейных уравнений называется совместной, если она имеет решение, и несовместной, если она не имеет решения.
Совместная система называется определенной, если она имеет единственное решение и неопределенной, если она имеет бесчисленное множество решений.
Две совместные системы называются равносильными, если они имеют одно и то же множество решений.
К элементарным преобразованиям системы отнесем следующее:
1. перемена местами двух любых уравнений;
2. умножение обеих частей любого из уравнений на произвольное число, отличное от нуля;
3. прибавление к обеим частям одного из уравнений системы соответствующих частей другого уравнения, умноженных на любое действительное число.
Элементарные преобразования переводят систему уравнений в равносильную ей.
Элементарные преобразования системы используются в методе Гаусса.
Для простоты рассмотрим метод Гаусса для системы трех линейных уравнений с тремя неизвестными в случае, когда существует единственное решение:
Дана система:
( 1 )
1-ый шаг метода Гаусса.
На первом шаге исключим неизвестное х1 из всех уравнений системы (1), кроме первого. Пусть коэффициент . Назовем его ведущим элементом. Разделим первое уравнение системы (1) на а11. Получим уравнение:
( 2 )
где
Исключим х1 из второго и третьего уравнений системы (1). Для этого вычтем из них уравнение (2), умноженное на коэффициент при х1 (соответственно а21 и а31).
Система примет вид:
( 3 )
Верхний индекс (1) указывает, что речь идет о коэффициентах первой преобразованной системы.
2-ой шаг метода Гаусса.
На втором шаге исключим неизвестное х2из третьего уравнения системы (3). Пусть коэффициент . Выберем его за ведущий элемент и разделим на него второе уравнение системы (3), получим уравнение:
( 4 )
где
Из третьего уравнения системы (3) вычтем уравнение (4), умноженное на Получим уравнение:
Предполагая, что находим
В результате преобразований система приняла вид:
(5)
Система вида (5) называется треугольной.
Процесс приведения системы (1) к треугольному виду (5) (шаги 1 и 2) называют прямым ходом метода Гаусса.
Нахождение неизвестных из треугольной системы называют обратным ходом метода Гаусса.
Для этого найденное значение х3 подставляют во второе уравнение системы (5) и находят х2. Затем х2 и х3 подставляют в первое уравнение и находят х1.
В общем случае для системы т линейных уравнений с п неизвестными проводятся аналогичные преобразования. На каждом шаге исключается одно из неизвестных из всех уравнений, расположенных ниже ведущего уравнения.
Отсюда другое называние метода Гаусса – метод последовательного исключения неизвестных.
Если в ходе преобразований системы получается противоречивое уравнение вида 0 = b, где b ¹ 0, то это означает, что система несовместна и решений не имеет.
В случае совместной системы после преобразований по методу Гаусса, составляющих прямой ход метода, система т линейных уравнений с п неизвестными будет приведена или к треугольному или к ступенчатому виду.
Треугольная система имеет вид:
Такая система имеет единственное решение, которое находится в результате проведения обратного хода метода гаусса.
Ступенчатая система имеет вид:
Такая система имеет бесчисленное множество решений. Чтобы найти эти решения, во всех уравнениях системы члены с неизвестными хk+1, … , xk переносят в правую часть. Эти неизвестные называются свободными и придают им произвольные значения. Из полученной треугольной системы находим х1, … , xk, которые будут выражаться через свободные неизвестные. Подробнее об этом можно узнать в рекомендуемой литературе.
Рассмотренный метод Гаусса легко программируется на ЭВМ и является более экономичным (по числу действий), чем другие методы.
ЗАКЛЮЧЕНИЕ
Рассмотренные на лекции матрицы являются удобным инструментом для записи различных математических преобразований и широко используется в научно-технической литературе. Метод Гаусса позволяет решать любые линейные системы, он находит широкое применение и содержится в пакетах стандартных программ для ЭВМ.
доцент Смирнова А.И.
referatnatemu.com
Матрицы Метод Гаусса
КОСТРОМСКОЙ ФИЛИАЛ ВОЕННОГО УНИВЕРСИТЕТА РХБ ЗАЩИТЫКафедра «Автоматизации управления войсками»
Только для преподавателей
“Утверждаю”
Начальник кафедры № 9
полковник ЯКОВЛЕВ А.Б.
«____»______________ 2004 г.
доцент СМИРНОВА А.И.
“МАТРИЦЫ. МЕТОД ГАУССА”
ЛЕКЦИЯ № 2 / 3
Обсуждено на заседании кафедры № 9
«____»___________ 2003г.
Протокол № ___________
Кострома, 2003
Cодержание
Введение
1. Действия над матрицами.
2. Решение систем линейных уравнений методом Гаусса.
Заключение
Литература
1. В.Е. Шнейдер и др., Краткий курс высшей математики,том I, гл.2,§6, 7.
2. В.С. Щипачев, Высшая математика, гл. 10, § 1, 7.
ВВЕДЕНИЕ
На лекции рассматривается понятие матрицы, действия над над матрицами, а также метод Гаусса для решения систем линейных уравнений. Для частного случая, так называемых квадратных матриц, можно вычислять определители, понятие о которых рассмотрено на предыдущей лекции. Метод Гаусса является более общим, чем рассмотренный ранее метод Крамера решения линейных систем. Разбираемые на лекции вопросы используются в различных разделах математики и в прикладных вопросах.
1-ый учебный вопрос ДЕЙСТВИЯ НАД МАТРИЦАМИ
ОПРЕДЕЛЕНИЕ 1. Прямоугольная таблица из m, n чисел, содержащая m – строк и n – столбцов, вида:
называется матрицей размера m ´ n
Числа, из которых составлена матрица, называются элементами матрицы.
Положение элемента аij в матрице характеризуются двойным индексом:
первый i – номер строки;
второй j – номер столбца, на пересечении которых стоит элемент.
Сокращенно матрицы обозначают заглавными буквами: А, В, С…
Коротко можно записывать так:
ОПРЕДЕЛЕНИЕ 2. Матрица, у которой число строк равно числу столбцов, т.е. m = n , называется квадратной.
Число строк (столбцов) квадратной матрицы называется порядком матрицы.
ПРИМЕР.
ЗАМЕЧАНИЕ 1. Мы будем рассматривать матрицы, элементами которых являются числа. В математике и ее приложениях встречаются матрицы, элементами которых являются другие объекты, например, функции, векторы.
ЗАМЕЧАНИЕ 2. Матрица – специальное математическое понятие. С помощью матриц удобно записывать различные преобразования, линейные системы и т.д., поэтому матрицы часто встречаются в математической и технической литературе.
ОПРЕДЕЛЕНИЕ 3. Матрица размера 1 ´ n, состоящая из одной строки, называется матрицей – строкой.
Матрица размера т ´ 1, состоящая из одного столбца, называется матрицей – столбцом.
ОПРЕДЕЛЕНИЕ 4. Нулевой матрицей называют матрицу, все элементы которой равны нулю.
Рассмотрим квадратную матрицу порядка n:
побочная диагональ
главная диагональ
Диагональ квадратной матрицы, идущая от верхнего левого элемента таблицы к правому нижнему, называется главной диагональю матрицы (на главной диагонали стоят элементы вида а ii).
Диагональ, идущая от правого верхнего элемента к левому нижнему, называется побочной диагональю матрицы.
Рассмотрим некоторые частные виды квадратных матриц.
1) Квадратная матрица называется диагональной, если все элементы, не стоящие на главной диагонали, равны нулю.
2) Диагональная матрица, у которой все элементы главной диагонали равны единице, называется единичной. Обозначается:
3) Квадратная матрица называется треугольной, если все элементы, расположенные по одну сторону от главной диагонали, равны нулю:
верхняя нижняя
треугольная матрица треугольная матрица
Для квадратной матрицы вводится понятие: определитель матрицы. Это определитель, составленный из элементов матрицы. Обозначается:
Ясно, что определитель единичной матрицы равен 1: ½Е½ = 1
ЗАМЕЧАНИЕ. Неквадратная матрица определителя не имеет.
Если определитель квадратичной матрицы отличен от нуля, то матрица называется невырожденной, если определитель равен нулю, то матрица называется вырожденной.
ОПРЕДЕЛЕНИЕ 5. Матрица, полученная из данной заменой ее строк столбцами с теми же номерами, называется транспонированной к данной.
Матрицу, транспонированную к А, обозначают АТ.
ПРИМЕР.
2 3 3 2
ОПРЕДЕЛЕНИЕ. Две матрицы одного и того же размера называются равными, если равны все их соответственные элементы.
Рассмотрим действия над матрицами.
СЛОЖЕНИЕ МАТРИЦ.
Операция сложения вводится только для матриц одинакового размера.
ОПРЕДЕЛЕНИЕ 7. Суммой двух матриц А = (аij) и В = (bij) одинакового размера называется матрица С = (сij) того же размера, элементы которой равны суммам соответствующих элементов слагаемых матриц, т.е. с i j = a i j + b i j
Обозначается сумма матриц А + В.
ПРИМЕР.
УМНОЖЕНИЕ МАТРИЦ НА ДЕЙСТВИТЕЛЬНОЕ ЧИСЛО
ОПРЕДЕЛЕНИЕ 8. Чтобы умножить матрицу на число k, надо умножить на это число каждый элемент матрицы:
если А= (аij), то k · A= (k · aij)
ПРИМЕР.
СВОЙСТВА СЛОЖЕНИЯ МАТРИЦ И УМНОЖЕНИЯ НА ЧИСЛО
1. Переместительное свойство: А + В = В + А
2. Сочетательное свойство: ( А + В ) + С = А + ( В + С )
3. Распределительное свойство: k · ( A + B ) = k A + k B, где k – число
УМНОЖЕНИЕ МАТРИЦ
Матрицу А назовем с о г л а с о в а н н о й с матрицей В , если число столбцов матрицы А равно числу строк матрицы В , т.е. для согласованных матриц матрица А имеет размер m ´ n , матрица В имеет размер n ´ k . Квадратные матрицы согласованы, если они одного порядка.
ОПРЕДЕЛЕНИЕ 9. Произведением матрицы А размера m ´ n на матрицу В размера n ´ k называется матрица С размера m ´ k, элемент которой аij, расположенный в i –ой строке и j – ом столбце, равен сумме произведений элементов i – ой строки матрицы А на соответствующие элементы j – столбца матрицы В, т.е.
cij= a i 1 b 1 j + ai 2 b 2 j +……+ ainbnj
Обозначим: С = А · В.
Если то
Произведение В ´ А не имеет смысла, т.к. матрицы не согласованы.
ЗАМЕЧАНИЕ 1. Если А ´ В имеет смысл, то В ´ А может не иметь смысла.
ЗАМЕЧАНИЕ 2. Если имеет смысл А ´ В и В ´ А, то, вообще говоря
А ´ В ¹ В ´ А, т.е. умножение матриц не обладает переместительным законом.
ЗАМЕЧАНИЕ 3. Если А – квадратная матрица и Е – единичная матрица того же порядка, то А ´ Е = Е ´ А = А.
Отсюда следует, что единичная матрица при умножении играет роль единицы.
ПРИМЕРЫ. Найти , если можно, А ´ В и В ´ А.
1.
Решение: Квадратные матрицы одного и того же второго порядка согласованы в томи другом порядке, поэтому А ´ В и В ´ А существуют.
2.
Решение: Матрицы А и В согласованы
Матрицы В и А не согласованы, поэтому В ´ А не имеет смысла.
Отметим, что в результате перемножения двух матриц получается матрица, содержащая столько строк, сколько их имеет матрица–множимое и столько столбцов, сколько их имеет матрица-множитель.
СВОЙСТВА УМНОЖЕНИЯ МАТРИЦ
1. Сочетательное свойство: А ´ ( В ´ С ) = (А ´ В ) ´С
2. Распределительное свойство: (А + В) ´ С = А ´ С + В ´С
Можно показать, что , если А и В – две квадратные матрицы одного порядка с определителями ½ А ½ и ½ В ½, то определитель матрицы С = А ´ В равен произведению определителей перемножаемых матриц, т.е.
½С½ = ½ А ½ ½ В ½
Отметим следующий любопытный факт. Как известно, произведение двух отличных от нуля чисел не равно нулю. Для матриц подобное обстоятельство может и не иметь места, т.е. произведение двух ненулевых матриц может оказаться равным нуль – матрице.
Действие “деление” для матриц не вводится. Для квадратных невырожденных матриц вводится обратная матрица. С понятием обратной матрицы можно познакомиться в рекомендуемой литературе.
2 – ой учебный вопрос РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ
УРАВНЕНИЙ МЕТОДОМ ГАУССА
Метод Гаусса (или метод последовательного исключения неизвестных) применим для решения систем линейных уравнений, в которых число неизвестных может быть либо равно числу уравнений, либо отлично от него.
Система т линейных уравнений с п неизвестными имеет вид:
x1 , x2, …, xn – неизвестные.
aij– коэффициенты при неизвестных.
bi – свободные члены (или правые части)
Система линейных уравнений называется совместной, если она имеет решение, и несовместной, если она не имеет решения.
Совместная система называется определенной, если она имеет единственное решение и неопределенной, если она имеет бесчисленное множество решений.
Две совместные системы называются равносильными, если они имеют одно и то же множество решений.
К элементарным преобразованиям системы отнесем следующее:
1. перемена местами двух любых уравнений;
2. умножение обеих частей любого из уравнений на произвольное число, отличное от нуля;
3. прибавление к обеим частям одного из уравнений системы соответствующих частей другого уравнения, умноженных на любое действительное число.
Элементарные преобразования переводят систему уравнений в равносильную ей.
Элементарные преобразования системы используются в методе Гаусса.
Для простоты рассмотрим метод Гаусса для системы трех линейных уравнений с тремя неизвестными в случае, когда существует единственное решение:
Дана система:
( 1 )
1-ый шаг метода Гаусса.
На первом шаге исключим неизвестное х1 из всех уравнений системы (1), кроме первого. Пусть коэффициент . Назовем его ведущим элементом. Разделим первое уравнение системы (1) на а11. Получим уравнение:
( 2 )
где
Исключим х1 из второго и третьего уравнений системы (1). Для этого вычтем из них уравнение (2), умноженное на коэффициент при х1 (соответственно а21 и а31).
Система примет вид:
( 3 )
Верхний индекс (1) указывает, что речь идет о коэффициентах первой преобразованной системы.
2-ой шаг метода Гаусса.
На втором шаге исключим неизвестное х2из третьего уравнения системы (3). Пусть коэффициент . Выберем его за ведущий элемент и разделим на него второе уравнение системы (3), получим уравнение:
( 4 )
где
Из третьего уравнения системы (3) вычтем уравнение (4), умноженное на Получим уравнение:
Предполагая, что находим
В результате преобразований система приняла вид:
(5)
Система вида (5) называется треугольной.
Процесс приведения системы (1) к треугольному виду (5) (шаги 1 и 2) называют прямым ходом метода Гаусса.
Нахождение неизвестных из треугольной системы называют обратным ходом метода Гаусса.
Для этого найденное значение х3 подставляют во второе уравнение системы (5) и находят х2. Затем х2 и х3 подставляют в первое уравнение и находят х1.
В общем случае для системы т линейных уравнений с п неизвестными проводятся аналогичные преобразования. На каждом шаге исключается одно из неизвестных из всех уравнений, расположенных ниже ведущего уравнения.
Отсюда другое называние метода Гаусса – метод последовательного исключения неизвестных.
Если в ходе преобразований системы получается противоречивое уравнение вида 0 = b, где b ¹ 0, то это означает, что система несовместна и решений не имеет.
В случае совместной системы после преобразований по методу Гаусса, составляющих прямой ход метода, система т линейных уравнений с п неизвестными будет приведена или к треугольному или к ступенчатому виду.
Треугольная система имеет вид:
Такая система имеет единственное решение, которое находится в результате проведения обратного хода метода гаусса.
Ступенчатая система имеет вид:
Такая система имеет бесчисленное множество решений. Чтобы найти эти решения, во всех уравнениях системы члены с неизвестными хk+1, … , xk переносят в правую часть. Эти неизвестные называются свободными и придают им произвольные значения. Из полученной треугольной системы находим х1, … , xk, которые будут выражаться через свободные неизвестные. Подробнее об этом можно узнать в рекомендуемой литературе.
Рассмотренный метод Гаусса легко программируется на ЭВМ и является более экономичным (по числу действий), чем другие методы.
ЗАКЛЮЧЕНИЕ
Рассмотренные на лекции матрицы являются удобным инструментом для записи различных математических преобразований и широко используется в научно-технической литературе. Метод Гаусса позволяет решать любые линейные системы, он находит широкое применение и содержится в пакетах стандартных программ для ЭВМ.
доцент Смирнова А.И.
baza-referat.ru



