15.01.202005.12.2018

Мю нулевое равно в магнитном поле – Протон влетает в однородное магнитное поле напряженностью 10^5 A/м перпендикулярно линиям магнитной индукции. Вычислить силу, действующую на протон, и его кинетическую энергию

• by alexxlab
• Комментариев к записи Мю нулевое равно в магнитном поле – Протон влетает в однородное магнитное поле напряженностью 10^5 A/м перпендикулярно линиям магнитной индукции. Вычислить силу, действующую на протон, и его кинетическую энергию нет
• Советы абитуриенту

Магнитная постоянная — WiKi

Численное значение магнитной постоянной вытекает из определения ампера, единицы силы электрического тока, являющегося одной из основных единиц СИ. Согласно определению, принятому IX Генеральной конференцией по мерам и весам (ГКМВ) в 1948 году, «Ампер есть сила неизменяющегося тока, который при прохождении по двум параллельным прямолинейным проводникам бесконечной длины и ничтожно малой площади кругового поперечного сечения, расположенным в вакууме на расстоянии 1 метр один от другого, вызвал бы на каждом участке проводника длиной 1 метр силу взаимодействия, равную 2·10⁻⁷ньютона»^[2][3].

С другой стороны, сила взаимодействия двух расположенных на расстоянии r{\displaystyle r}  друг от друга бесконечных параллельных проводников, по которым текут токи I1{\displaystyle I_{1}}  и I2{\displaystyle I_{2}} , приходящаяся на единицу длины, выражается соотношением:

F=μ04π2I1I2r.{\displaystyle F={\frac {\mu _{0}}{4\pi }}{\frac {2I_{1}I_{2}}{r}}.} 

С учётом определения ампера из этого соотношения следует точное равенство:

μ0=4π×10−7 {\displaystyle \mu _{0}=4\pi \times 10^{-7}\ }  Гн/м

Соответственно выполняется:

μ0≈1,25663706×10−6{\displaystyle \mu _{0}\approx 1,25663706\times 10^{-6}}  Гн/м =1,25663706×10−6{\displaystyle =1,25663706\times 10^{-6}}  Н/А².

В материальных уравнениях, в вакууме, через магнитную проницаемость связаны вектор напряжённости магнитного поля H и вектор магнитной индукции B:

B=μ0 H.{\displaystyle \mathbf {B} =\mu _{0}\ \mathbf {H} .} 

Через магнитную постоянную осуществляется связь между относительной и абсолютной магнитной проницаемостью.

В 2011 году XXIV ГКМВ приняла резолюцию^[4], в которой, в частности, предложено в будущей ревизии Международной системы единиц (СИ) переопределить несколько основных единиц, включая ампер, таким образом, чтобы они были основаны не на созданных человеком артефактах, а на фундаментальных физических постоянных или свойствах атомов.

Предполагается, что в СИ величине элементарного электрического заряда e будет приписано точное значение, равное 1,602 17X·10⁻¹⁹Кл^[5], а новое определение ампера будет основано на этом точном значении элементарного заряда, выраженного в c·А.

Следствием такого подхода к определению ампера станет изменение статуса магнитной постоянной: как отмечается в резолюции ГКМВ, сразу после предполагаемого переопределения ампера значение магнитной постоянной будет равно 4π × 10−7 {\displaystyle 4\pi \ \times \ 10^{-7}\ }  Гн/м, но это значение приобретёт погрешность (неопределённость) и в дальнейшем будет определяться экспериментально^[4].

ru-wiki.org

Численное значение магнитной постоянной

Численное значение магнитной постоянной вытекает из определения ампера, единицы силы электрического тока, являющегося одной из основных единиц СИ. Согласно определению, принятому IX Генеральной конференцией по мерам и весам (ГКМВ) в 1948 году, «Ампер есть сила неизменяющегося тока, который при прохождении по двум параллельным прямолинейным проводникам бесконечной длины и ничтожно малой площади кругового поперечного сечения, расположенным в вакууме на расстоянии 1 метр один от другого, вызвал бы на каждом участке проводника длиной 1 метр силу взаимодействия, равную 2·10⁻⁷ ньютона»^[2][3].

С другой стороны, сила взаимодействия двух расположенных на расстоянии друг от друга бесконечных параллельных проводников, по которым текут токи и , приходящаяся на единицу длины, выражается соотношением:

С учётом определения ампера из этого соотношения следует точное равенство:

 Гн/м

Соответственно выполняется:

 Гн/м Н/А².

В материальных уравнениях, в вакууме, через магнитную проницаемость связаны вектор напряжённости магнитного поля H и вектор магнитной индукции B:

Через магнитную постоянную осуществляется связь между относительной и абсолютной магнитной проницаемостью.

Прежде, чем перейти к примерам расчёта магнитных полей, напомним, что точно тот же самый метод мы использовали и при рассмотрении электростатических полей. Что являлось «элементарным кирпичиком» электростатического поля? Поле точечного заряда. А далее, используя принцип суперпозиции электрических полей, мы получали возможность рассчитать поле любого заряда, разделяя его на составляющие точечные заряды.

Рассмотрим поле, создаваемое током I, текущим по тонкому проводу, имеющему форму окружности радиуса R (рис. 1.7).

Рис. 1.7

      Определим магнитную индукцию на оси проводника с током на расстоянии х от плоскости кругового тока. Векторы перпендикулярны плоскостям, проходящим через соответствующиеи. Следовательно, они образуют симметричный конический веер. Из соображения симметрии видно, что результирующий векторнаправлен вдоль оси кругового тока. Каждый из вектороввносит вклад равный, авзаимно уничтожаются. Но,, а т.к. угол междуиα – прямой, тотогда получим

,

(1.6.1)

      Подставив в (1.6.1) и, проинтегрировав по всему контуру, получим выражение для нахождениямагнитной индукции кругового тока:

,

(1.6.2)

При , получиммагнитную индукцию в центре кругового тока:

,

(1.6.3)

      Заметим, что в числителе (1.6.2)   – магнитный момент контура. Тогда, на большом расстоянии от контура, при, магнитную индукцию можно рассчитать по формуле:

,

(1.6.4)

      Силовые линии магнитного поля кругового тока хорошо видны в опыте с железными опилками.

3. Теорема Гаусса для поля B, отсутствие в природе магнитного монополя. Наглядное представление магнитного поля с помощью картины силовых линий

Как было показано выше, в природе нет магнитных зарядов. В 1931 г. П. Дирак высказал предположение о существовании обособленных магнитных зарядов, названных впоследствии монополи Дирака. Однако до сих пор они не найдены. Это приводит к тому, что линии вектора не имеют ни начала, ни конца. Мы знаем, что поток любого вектора через поверхность равен разности числа линий, начинающихся у поверхности, и числа линий, оканчивающихся внутри поверхности:

 .

В соответствии с вышеизложенным, можно сделать заключение, что поток вектора через замкнутую поверхность должен быть равен нулю.

Таким образом, для любого магнитного поля и произвольной замкнутой поверхности S имеет место условие:

,

(1.7.1)

Это теорема Гаусса для  (в интегральной форме): поток вектора магнитной индукции через любую замкнутую поверхность равен нулю.

Этот результат является математическим выражением того, что 

в природе нет магнитных зарядов – источников магнитного поля, на которых начинались и заканчивались бы линии магнитной индукции.

Заменив поверхностный интеграл в (1.7.1) объемным, получим:

,

(1.7.2)

где – оператор Лапласа.

Это условие должно выполняться для любого произвольного объема V, а это, в свою очередь, возможно, если подынтегральная функция в каждой точке поля равна нулю. Таким образом, магнитное поле обладает тем свойством, что его дивергенция всюду равна нулю:

или

(1.7.3)

В этом его отличие от электростатического поля, которое является потенциальным и может быть выражено скалярным потенциалом φ, магнитное поле – вихревое, или соленоидальное (см. рис. 1.3 и 1.8).

                  

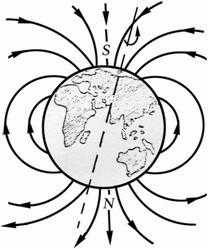
Рис. 1.9

Компьютерная модель магнитного поля Земли, подтверждающая вихревой характер, изображена на рис. 1.9.

Рис 1.10

На рисунке 1.10 показаны магнитное поле постоянного магнита. Линии магнитной индукции замыкаются в окружающем пространстве.

4. Фундаментальное уравнение для циркуляции магнитного поля. Примеры расчёта магнитного поля в случаях высокой симметрии распределения порождающих поле токов.

Теорема о циркуляции магнитного поля — одна из фундаментальных теорем классической электродинамики, сформулированная Андре Мари Ампером в 1826 году. В 1861 году Джеймс Максвелл снова вывел эту теорему, опираясь на аналогии с гидродинамикой, и обобщил ее. Уравнение, представляющее собой содержание теоремы в этом обобщенном виде, входит в число уравнений Максвелла. (Для случая постоянных электрических полей — то есть в принципе вмагнитостатике— верна теорема в первоначальном виде, сформулированном Ампером и приведенном в статье первым; для общего случая правая часть должна быть дополнена членом с производной напряженности электрического поля по времени — см. ниже). Теорема гласит:

Циркуляция магнитного поля постоянных токов по всякому замкнутому контуру пропорциональна сумме сил токов, пронизывающих контур циркуляции.

Эта теорема, особенно в иностранной или переводной литературе, называется также теоремой Ампера или законом Ампера о циркуляции (англ. Ampère’s circuital law). Последнее название подразумевает рассмотрение закона Ампера в качестве более фундаментального утверждения, чем закон Био — Савара — Лапласа, который в свою очередь рассматривается уже в качестве следствия (что, в целом, соответствует современному варианту построения электродинамики).

Для общего случая (классической) электродинамики формула должна быть дополнена в правой части членом, содержащим производную по времени от электрического поля (см. уравнения Максвелла, а также параграф «Обобщение» ниже). В таком дополненном виде она представляет собой четвёртое уравнение Максвелла в интегральной форме.

studfiles.net

Магнитная постоянная

магнитная постоянная, магнитная постоянная равна
Магнитная постоянная — физическая константа, скалярная величина, входящая в выражения некоторых законов электромагнетизма в виде коэффициента пропорциональности при записи их в форме, соответствующей Международной системе единиц (СИ).

Иногда называют магнитной проницаемостью вакуума. Измеряется в генри на метр (или в ньютонах на ампер в квадрате).

Содержание

• 1 Численное значение
• 2 Предполагаемое переопределение
• 3 См. также
• 4 Примечания

Численное значение

Численное значение магнитной постоянной вытекает из определения ампера, единицы силы электрического тока, являющегося одной из основных единиц СИ. Согласно определению, принятому IX Генеральной конференцией по мерам и весам (ГКМВ) в 1948 году, «Ампер есть сила неизменяющегося тока, который при прохождении по двум параллельным прямолинейным проводникам бесконечной длины и ничтожно малой площади кругового поперечного сечения, расположенным в вакууме на расстоянии 1 метр один от другого, вызвал бы на каждом участке проводника длиной 1 метр силу взаимодействия, равную 2·10−7 ньютона».

С другой стороны, сила взаимодействия двух расположенных на расстоянии друг от друга бесконечных параллельных проводников, по которым текут токи и , приходящаяся на единицу длины, выражается соотношением:

С учётом определения ампера из этого соотношения следует точное равенство:

Гн/м

Соответственно выполняется:

Гн/м Н/А2.

В материальных уравнениях, в вакууме, через магнитную проницаемость связаны вектор напряжённости магнитного поля H и вектор магнитной индукции B:

Через магнитную постоянную осуществляется связь между относительной и абсолютной магнитной проницаемостью.

Предполагаемое переопределение

В 2011 году XXIV ГКМВ приняла резолюцию, в которой, в частности, предложено в будущей ревизии Международной системы единиц (СИ) переопределить несколько основных единиц, включая ампер, таким образом, чтобы они были основаны не на созданных человеком артефактах, а на фундаментальных физических постоянных или свойствах атомов.

Предполагается, что в СИ величине элементарного электрического заряда e будет приписано точное значение, равное 1,602 17X·10−19 Кл, а новое определение ампера будет основано на этом точном значении элементарного заряда, выраженного в c·А.

Следствием такого подхода к определению ампера станет изменение статуса магнитной постоянной: как отмечается в резолюции ГКМВ, сразу после предполагаемого переопределения ампера значение магнитной постоянной будет равно Гн/м, но это значение приобретёт погрешность (неопределённость) и в дальнейшем будет определяться экспериментально.

См. также

• Электрическая постоянная
• Скорость света

Примечания

1. ↑ Магнитная постоянная — статья в Физической энциклопедии
2. ↑ Определение ампера на сайте Международного бюро мер и весов (BIPM)
3. ↑ ГОСТ 8.417-2002. Государственная система обеспечения единства измерений. Единицы величин.
4. ↑ 1 2 On the possible future revision of the International System of Units, the SI (англ.) Резолюция XXIV Генеральной конференции по мерам и весам (2011)
5. ↑ Здесь Х заменяет одну или более значащих цифр, которые будут определены в окончательном релизе на основании наиболее точных рекомендаций Комитета по данным для науки и техники (CODATA)

магнитная постоянная, магнитная постоянная равна

---

Магнитная постоянная Информацию О

---

---

Магнитная постоянная Комментарии

Магнитная постоянная
Магнитная постоянная
Магнитная постоянная Вы просматриваете субъект

Магнитная постоянная что, Магнитная постоянная кто, Магнитная постоянная описание

There are excerpts from wikipedia on this article and video

www.turkaramamotoru.com

Магнитная проницаемость — WiKi

Магнитная проницаемость — физическая величина, коэффициент (зависящий от свойств среды), характеризующий связь между магнитной индукцией B{\displaystyle {B}} и напряжённостью магнитного поля H{\displaystyle {H}} в веществе. Для разных сред этот коэффициент различен, поэтому говорят о магнитной проницаемости конкретной среды (подразумевая её состав, состояние, температуру и т. д.).

Впервые встречается в работе Вернера Сименса «Beiträge zur Theorie des Elektromagnetismus» («Вклад в теорию электромагнетизма») в 1881 году^[1].

Обычно обозначается греческой буквой μ{\displaystyle \mu }. Может быть как скаляром (у изотропных веществ), так и тензором (у анизотропных).

В общем, соотношение между магнитной индукцией и напряженностью магнитного поля через магнитную проницаемость вводится как

B→=μH→,{\displaystyle {\vec {B}}=\mu {\vec {H}},}

и μ{\displaystyle \mu } в общем случае здесь следует понимать как тензор, что в компонентной записи соответствует^[2]:

 Bi=μijHj{\displaystyle \ B_{i}=\mu _{ij}H_{j}}

Для изотропных веществ соотношение:

B→=μH→{\displaystyle {\vec {B}}=\mu {\vec {H}}}

можно понимать в смысле умножение вектора на скаляр (магнитная проницаемость сводится в этом случае к скаляру).

В системе СГС магнитная проницаемость — безразмерная величина, в Международной системе единиц (СИ) вводят как размерную (абсолютную), так и безразмерную (относительную) магнитные проницаемости:

μr=μμ0{\displaystyle \mu _{r}={\frac {\mu }{\mu _{0}}}},

где μr{\displaystyle \mu _{r}} — относительная, а μ{\displaystyle \mu } — абсолютная проницаемость, μ0{\displaystyle \mu _{0}} — магнитная постоянная.

Нередко обозначение μ{\displaystyle \mu } используется не так, как здесь, а именно для относительной магнитной проницаемости (при этом μ{\displaystyle \mu } совпадает с таковым в СГС).

Размерность абсолютной магнитной проницаемости в СИ такая же, как размерность магнитной постоянной, то есть Гн/м или Н/А².

Относительная магнитная проницаемость в СИ связана с магнитной восприимчивостью χ соотношением

μr=1+χ,{\displaystyle \mu _{r}=1+\chi ,}

а в Гауссовой системе магнитная проницаемость связана с магнитной восприимчивостью χ соотношением

μ=1+4πχ.{\displaystyle \mu =1+4\pi \chi .}

Вообще говоря, магнитная проницаемость зависит как от свойств вещества, так и от величины и направления магнитного поля (а кроме того от температуры^[3], давления и т.д.).

Также зависит от характера изменения поля со временем, в частности, для синусоидального колебания поля — зависит от частоты этого колебания (в этом случае вводят комплексную магнитную проницаемость чтобы описать влияние среды на сдвиг фазы ‘B’ по отношению к ‘H’). При достаточно низких частотах (небольшой быстроте изменения поля) её можно обычно считать в этом смысле константой.

Схематический график зависимости ‘B’ от ‘H’ (кривая намагничивания) для ферромагнетиков, парамагнетиков и диамагнетиков, а также для вакуума, иллюстрирующий различие магнитной проницаемости (представляющей собою наклон графика) для: ферромагнетиков (μ_f), парамагнетиков (μ_p), вакуума(μ₀) и диамагнетиков (μ_d)

• Магнитная проницаемость сильно зависит от величины поля для нелинейных сред (типичный пример — ферромагнетики, для которых характерен гистерезис). Для таких сред магнитная проницаемость как независящее от поля число может указываться приближенно, в рамках линеаризации^[4].
• Для парамагнетиков и диамагнетиков линейное приближение достаточно хорошо для широкого диапазона величин поля.

Подавляющее большинство веществ относятся либо к классу диамагнетиков (μ⪅1{\displaystyle \mu \lessapprox 1} ), либо к классу парамагнетиков (μ⪆1{\displaystyle \mu \gtrapprox 1} ). Но ряд веществ — (ферромагнетики), например железо, обладают более выраженными магнитными свойствами.

У ферромагнетиков вследствие гистерезиса, понятие магнитной проницаемости, строго говоря, неприменимо. Однако в определенном диапазоне изменения намагничивающего поля (чтобы можно было пренебречь остаточной намагниченностью, но до насыщения) можно в лучшем или худшем приближении всё же представить эту зависимость как линейную (а для магнитомягких материалов ограничение снизу может быть и не слишком практически существенно), и в этом смысле величина магнитной проницаемости бывает измерена и для них.

Магнитная проницаемость сверхпроводников равна нулю.

Абсолютная магнитная проницаемость воздуха приблизительно равна магнитной проницаемости вакуума и в технических расчетах принимается равной^[5] магнитной постоянной = 4π × 10−7{\displaystyle 4\pi \ \times \ 10^{-7}}  Гн/м

ru-wiki.org

При внесении в магнитное поле ферромагнитного бруска магнитная индукция в нем оказалась в 500 раз больше,

Илья Высший разум (200646) 3 года назад Комментарий удален

Илья Высший разум (200646) Поздравляю)))))))

Комментарий удален

Илья Высший разум (200646) Обойдетесь, уважаемый. Научитесь сначала правилам обращения к незнакомому человеку. Мой ответ – полный. То, что Вам он не понятен – для меня тоже говорит о многом. Нечего Вам в вузе делать – пора заменять таджиков своими неучами.

Комментарий удален

Комментарий удален

Илья Высший разум (200646) Вы и остальное сказанное Вам не поняли. Поэтому рекомендую вам ПТУ.

Комментарий удален

Илья Высший разум (200646) А, понятно. Привет коллегам! Я сам фазанку закончил больше 20 лет назад. * – это умножить)))

Комментарий удален

Комментарий удален

Илья Высший разум (200646) Если тыкать перестанешь старшим. Я вообще-то завкафедрой вуза, кандидат наук.

Комментарий удален

Илья Высший разум (200646) Помогу, если смогу.

Комментарий удален

Илья Высший разум (200646) Формулу магнитного сопротивления я не помню, но Rм~L/S (~ – это знак пропорциональности). Длина увеличивается в три раза, значит, сопротивление тоже увеличивается в три раза при таком изменении. Площадь увеличивается в 5 раз, значит, магнитное сопротивление уменьшается в 5 раз при этом изменении.

Комментарий удален

Илья Высший разум (200646) Оформлять я ничего не буду. Свою фазанку я закончил давно) Кстати, по тогдашним правилам нам задания на дом не задавали вообще.

Комментарий удален

Комментарий удален

Илья Высший разум (200646) Да я как-то люблю чистой клавой обходиться, еще после DOS-а. А тут парню оказывается – звездочка была не понятна))) Иногда забываю, что символы можно из Word-a вставлять, но я так не люблю этот чертов Офис, что иногда даже забываю про него…

otvet.mail.ru

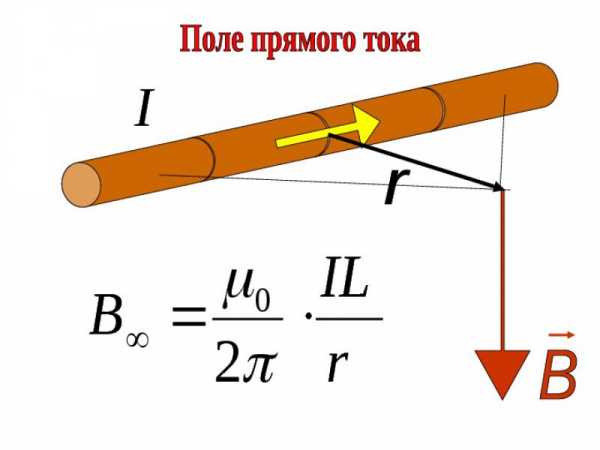
Протон влетает в однородное магнитное поле напряженностью 10^5 A/м перпендикулярно линиям магнитной индукции. Вычислить силу, действующую на протон, и его кинетическую энергию

Протон влетает в однородное магнитное поле напряженностью Н = 10^5 A/м  перпендикулярно линиям магнитной индукции. Вычислить силу, действующую на протон, и его кинетическую энергию, если в магнитном поле он будет двигаться по окружности радиусом R = 2 см .             q – заряд протона (гуглим)                         мю нулевое – магнитная постоянная  (гуглим)             (1)                      (2)                            m – масса протона (гуглим)                                                  (3)
(3) c учетом (2) подставим в (1) и найдем искомую силу:
 

Кинетическая энергия:

                   

ivandriver.blogspot.com

---