Полное нормальное и касательное ускорение – 1.Кинематическое описание движения. Перемещение, скорость. Вычисление пройденного пути. Ускорение.
- Комментариев к записи Полное нормальное и касательное ускорение – 1.Кинематическое описание движения. Перемещение, скорость. Вычисление пройденного пути. Ускорение. нет
- Советы абитуриенту
- 1.Кинематическое описание движения. Перемещение, скорость. Вычисление пройденного пути. Ускорение.
- Тангенциальное, нормальное и полное ускорение
- 3. Нормальное, тангенциальное и полное ускорения.
- 3. Нормальное, тангенциальное и полное ускорения.
- Тангенциальное, нормальное и полное ускорение
- 1.7. Криволинейное движение. Тангенциальное и нормальное ускорения
1.Кинематическое описание движения. Перемещение, скорость. Вычисление пройденного пути. Ускорение.
Кинематика изучает движение без выявления причин, вызывающих это движение. Кинематика является разделом механики. Главной задачей кинематики является математическое определение положения и характеристик движения точек или тел во времени.
Основные кинематические величины:
– Перемещение() –вектор, соединяющий начальную и конечную точки.
r – радиус-вектор, определяет положение МТ в пространстве.
– Скорость – отношение пути ко времени.
– Путь – множество точек через которое прошло тело.
– Ускорение – скорость изменения скорости, то есть первая производная от скорости.
2.Ускорение при криволинейном движении: нормальное и тангенциальное ускорение. Плоское вращение. Угловая скорость, ускорение.
Криволинейное движение – это движение, траектория которого представляет собой кривую линию. Примером криволинейного движения является движение планет, конца стрелки часов по циферблату и т.д.
Криволинейное движение – это всегда ускоренное движение. То есть ускорение при криволинейном движении присутствует всегда, даже если модуль скорости не изменяется, а изменяется только направление скорости.
Изменение величины скорости за единицу времени – это тангенциальное ускорение:
Где 𝛖τ, 𝛖0 – величины скоростей в момент времени t0 + Δt и t0 соответственно. Тангенциальное ускорение в данной точке траектории по направлению совпадает с направлением скорости движения тела или противоположно ему.
Нормальное ускорение – это изменение скорости по направлению за единицу времени:
Нормальное ускорение направлено по радиусу кривизны траектории (к оси вращения). Нормальное ускорение перпендикулярно направлению скорости.
Полное ускорение при равнопеременном криволинейном движении тела равно:
– угловая скорость показывает, на какой угол поворачивается точка при равномерном движении по окружности за единицу времени. Единица измерения в СИ – рад/с.
Плоское вращение – это вращение всех векторов скоростей точек тела в одной плоскости.
3.Связь между векторами скорости и угловой скорости материальной точки. Нормальное, тангенциальное и полное ускорение.
Тангенциальное (касательное) ускорение – это составляющая вектора ускорения, направленная вдоль касательной к траектории в данной точке траектории движения. Тангенциальное ускорение характеризует изменение скорости по модулю при криволинейном движении.
Нормальное (центростремительное) ускорение – это составляющая вектора ускорения, направленная вдоль нормали к траектории движения в данной точке на траектории движения тела. То есть вектор нормального ускорения перпендикулярен линейной скорости движения (см. рис. 1.10). Нормальное ускорение характеризует изменение скорости по направлению и обозначается буквой n. Вектор нормального ускорения направлен по радиусу кривизны траектории.
Полное ускорение при криволинейном движении складывается из тангенциального и нормального ускорений по правилу сложения векторов и определяется формулой:
studfiles.net
Тангенциальное, нормальное и полное ускорение
Криволинейное движение всегда происходит с ускорением, поскольку если даже величина скорости не изменяется, происходит изменение ее направления.
Вектор ускорения < > направлен параллельно вектору изменения скорости в сторону вогнутости траектории (рисунок 1.4).
Рисунок 1.4 – Направление вектора ускорения.
В общем случае мгновенное ускорение направлено под углом к скорости. Зная траекторию, можно определить направление скорости, но не ускорения. Направление ускорения определяется направлением равнодействующей сил, действующих на тело.
Вектор полного ускорения тела при криволинейном движении можно разложить на две составляющие, направленные вдоль скорости – тангенциальное ускорение и перпендикулярно скорости – нормальное ускорение.
Рисунок 1.5 – Касательное и нормальное ускорения.
Тангенциальное ускорение характеризует быстроту изменения величины скорости при криволинейном движении по величине, а нормальное ускорение – быстроту изменения направления вектора скорости.
Как видно из рисунка 1.5, полное ускорение тела есть геометрическая сумма тангенциальной и нормальной составляющих:
.
Модуль полного ускорения равен:
. (1.12)
Похожие статьи:
3. Нормальное, тангенциальное и полное ускорения.
Движение тела характеризуется скоростью и ускорением, которые могут изменяться во времени. Пусть материальная точка движется по плоской криволинейной траектории с переменной по величине и направлению скоростью (рис. 4). Для характеристики степени криволинейности вводится понятие радиуса кривизны в данной точке траектории.
Радиусом кривизны R траектории называют радиус окружности, которая сливается с криволинейной траекторией на бесконечно малом ее участке.
В данной точке траектории касательная всегда перпендикулярна радиусу кривизны.
Пусть и скорость, и ускорение меняются по величине и направлению.
Мы знаем,
что ускорение тела при движении есть 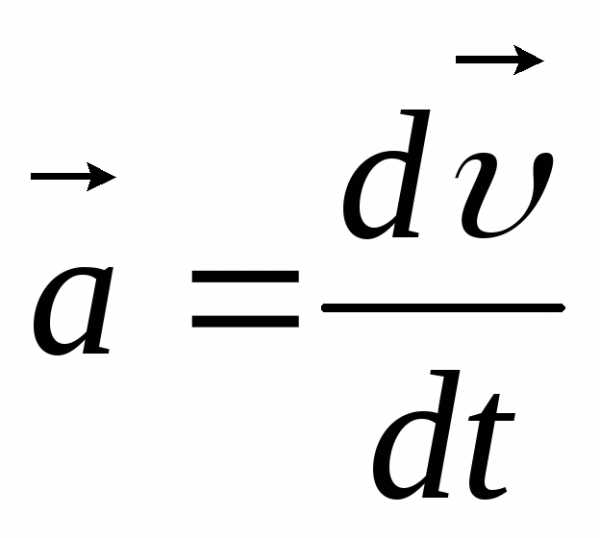
Вектор
скорости 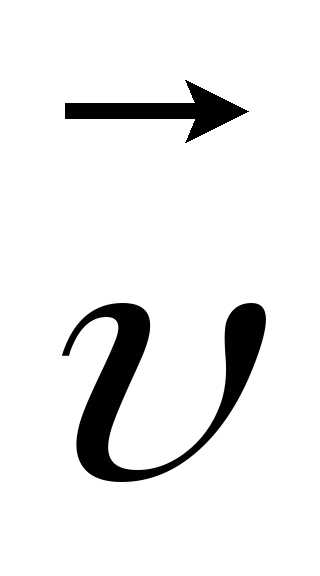 можно представить как произведение
модуля скорости
можно представить как произведение
модуля скорости и некоторого единичного вектора
и некоторого единичного вектора  ,
сонаправленного с вектором линейной
скорости
,
сонаправленного с вектором линейной
скорости 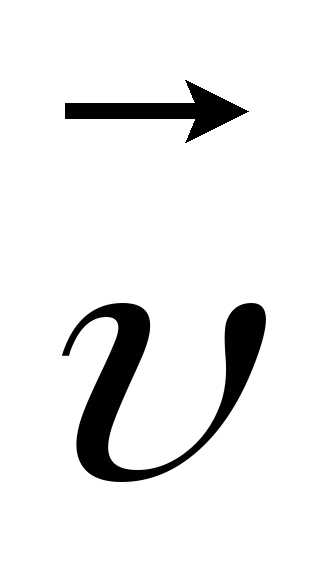 ,
направленного по касательной к траектории.
,
направленного по касательной к траектории.
Таким
образом, полное ускорение материальной
точки при криволинейном движении можно
представить в виде суммы двух слагаемых.
Первое слагаемое 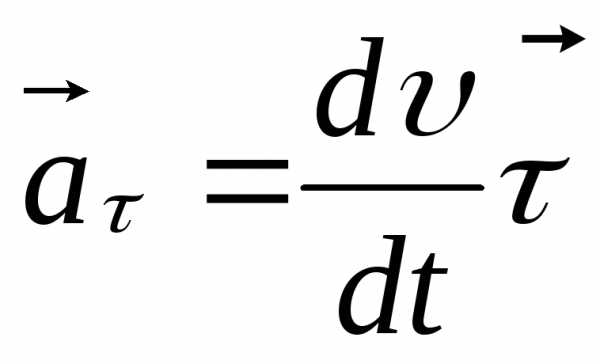 .
.
Вектор 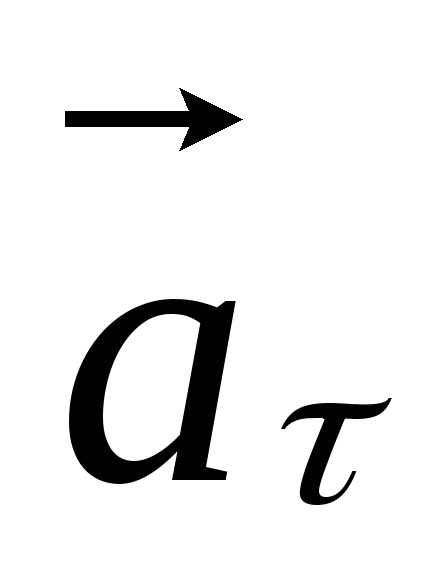 сонаправлен с вектором
сонаправлен с вектором 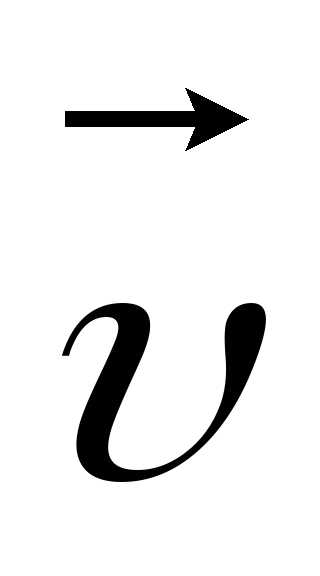
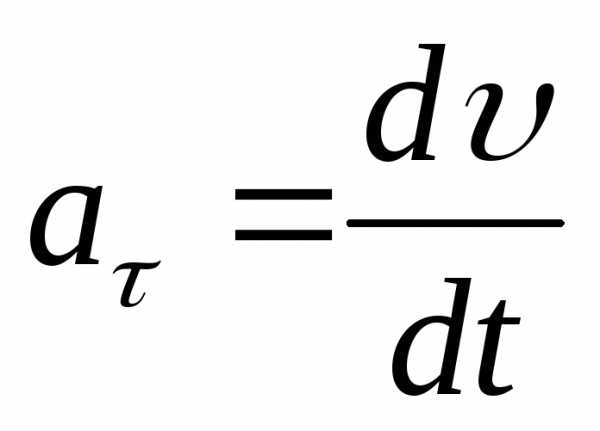 ,
поэтому
,
поэтому 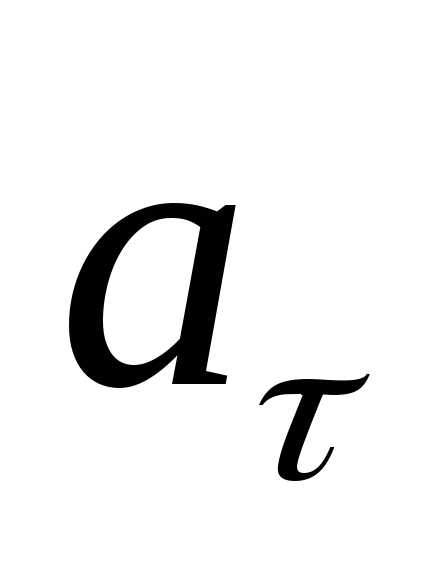 характеризует быстроту изменения
скорости криволинейного движения по
величине, но не направлению, так как
вектор
характеризует быстроту изменения
скорости криволинейного движения по
величине, но не направлению, так как
вектор  не изменяется.
не изменяется. Следовательно,
можно заключить, что 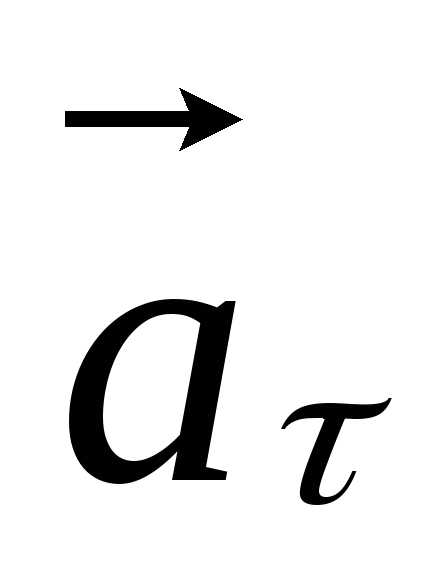 – тангенциальное ускорение, характеризующее
изменение скорости по величине, оно
направлено по касательной к траектории.
– тангенциальное ускорение, характеризующее
изменение скорости по величине, оно
направлено по касательной к траектории.
Второе
слагаемое 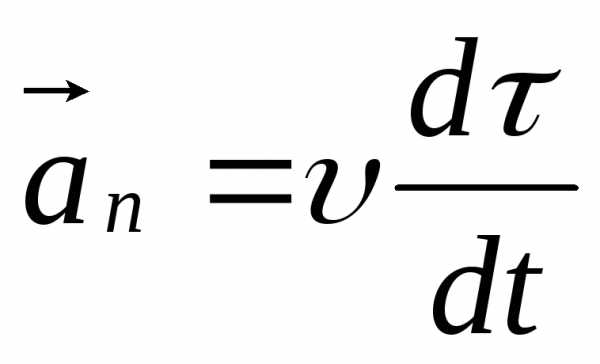 называется нормальным ускорением. Что
характеризует этот вектор, куда направлен,
как его рассчитать?
называется нормальным ускорением. Что
характеризует этот вектор, куда направлен,
как его рассчитать?
Так
как вектор 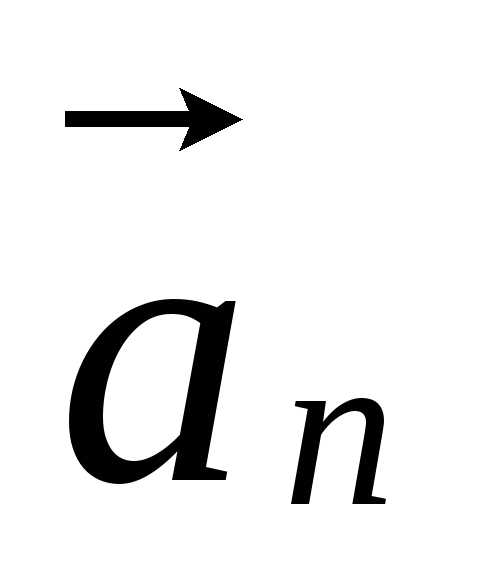 сонаправлен с вектором
сонаправлен с вектором 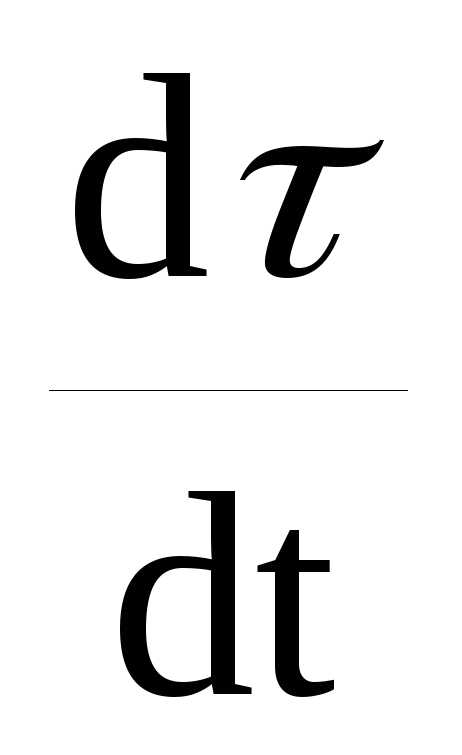 ,
который определяет изменениенаправления вектора линейной скорости, то он
характеризует изменение скорости
криволинейного движения по направлению.
,
который определяет изменениенаправления вектора линейной скорости, то он
характеризует изменение скорости
криволинейного движения по направлению.
О
пределим величину и направление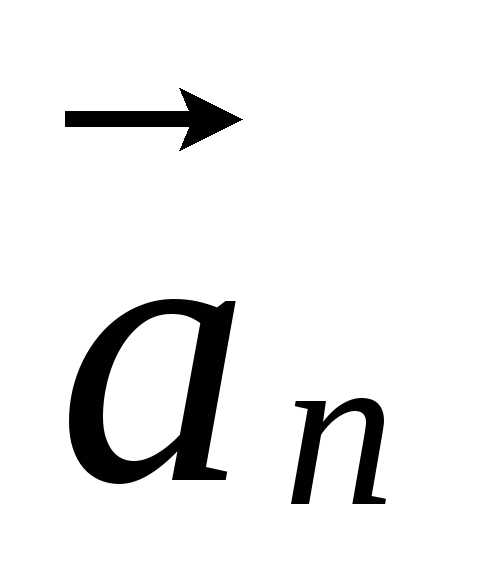 .
Рассмотрим частный случай движения
материальной точки по окружности
радиусом R с постоянной по величине скоростью
.
Рассмотрим частный случай движения
материальной точки по окружности
радиусом R с постоянной по величине скоростью  (рис.5).
Среднее изменение скорости на дуге АВ
отнесем к точке С, лежащей посередине
дуги.
(рис.5).
Среднее изменение скорости на дуге АВ
отнесем к точке С, лежащей посередине
дуги. 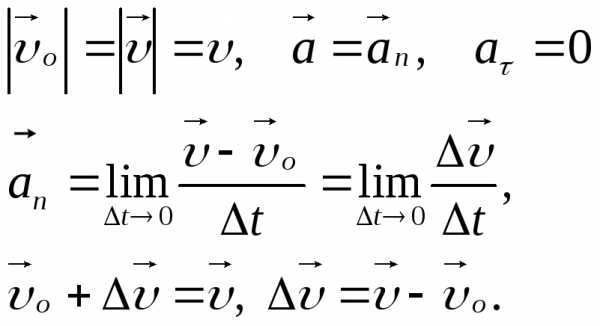
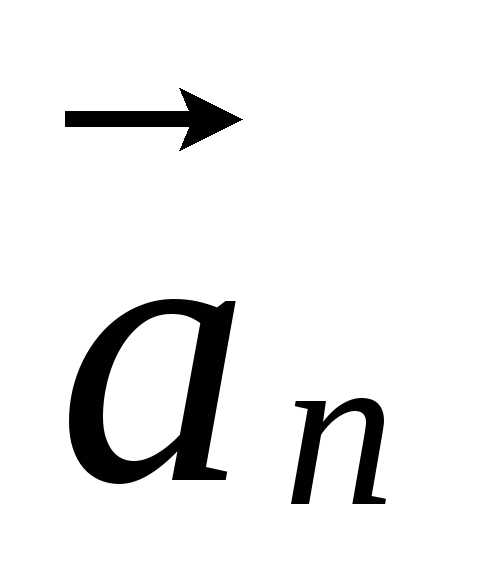
 ∾
∾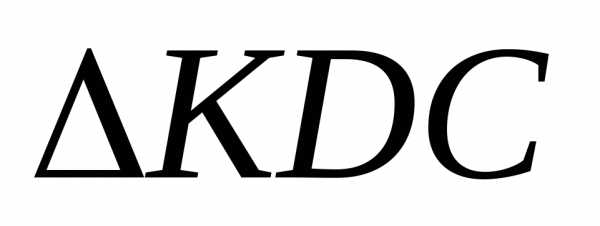 :
:
.
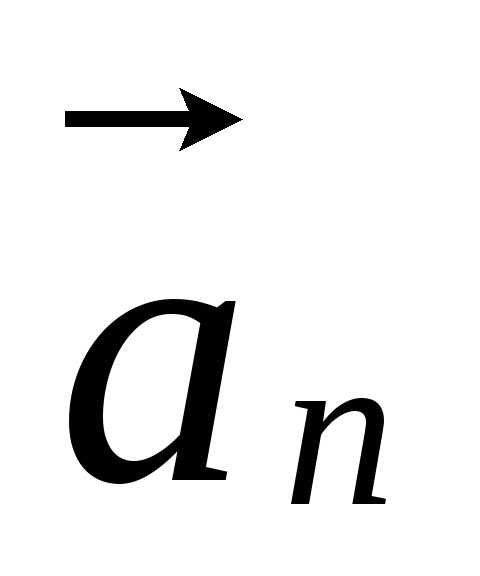 перпендикулярно
скорости, направлено вдоль радиуса к
центру окружности. Его называют
нормальным, радиальным или центростремительным
ускорением.
перпендикулярно
скорости, направлено вдоль радиуса к
центру окружности. Его называют
нормальным, радиальным или центростремительным
ускорением.
Полное ускорение материальной точки при криволинейном движении характеризует быстроту изменения скорости как по величине, так и по направлению (рис.6).
, .
Угловая скорость и угловое ускорение.
Поворот тела на некоторый угол можно задать в виде отрезка, длина которого равна , а направление совпадает с осью, вокруг которой производится поворот. Направление поворота и изображающего его отрезка связано правилом правого винта.
В
математике показывается, что очень
малые повороты можно рассматривать как
векторы, обозначаемые символами 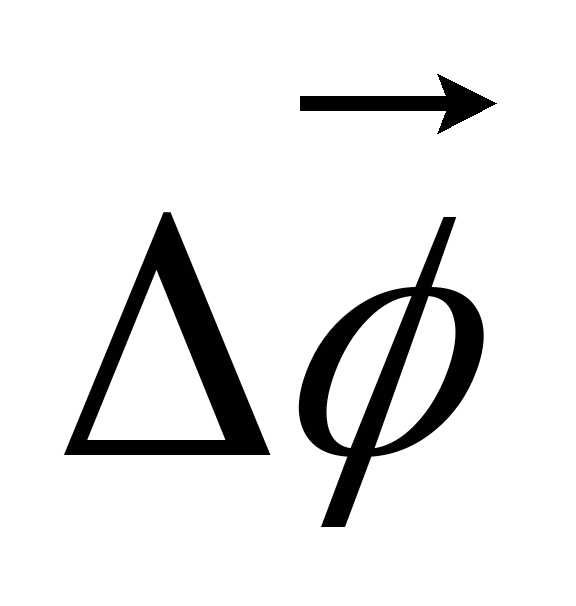 или
или 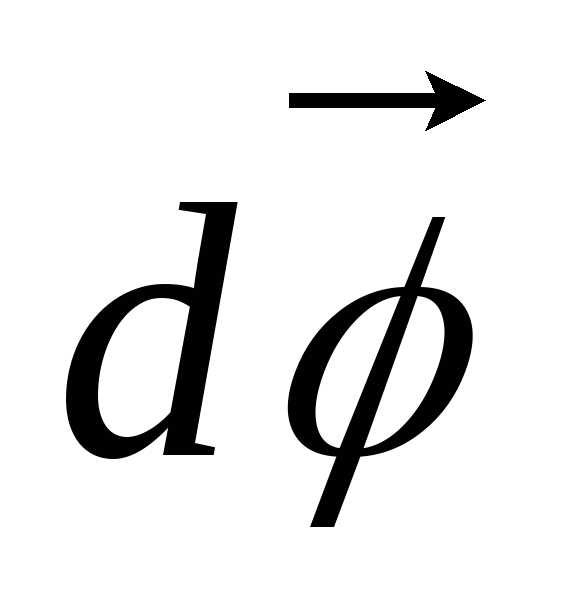 .
Направление вектора поворота связывается
с направлением вращения тела;
.
Направление вектора поворота связывается
с направлением вращения тела; 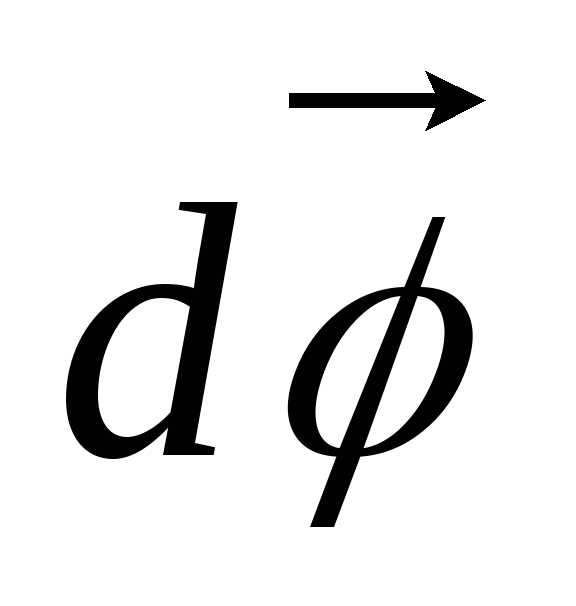 является псевдовектором, так как не
имеет точки приложения.
является псевдовектором, так как не
имеет точки приложения.
При вращательном движении твердого тела каждая точка движется по окружности, центр которой лежит на общей оси вращения (рис. 7). При этом радиус-вектор R, направленный от оси вращения к точке, поворачивается за время t на некоторый угол . Для характеристики вращательного движения вводится угловая скорость и угловое ускорение.
Угловой скоростью
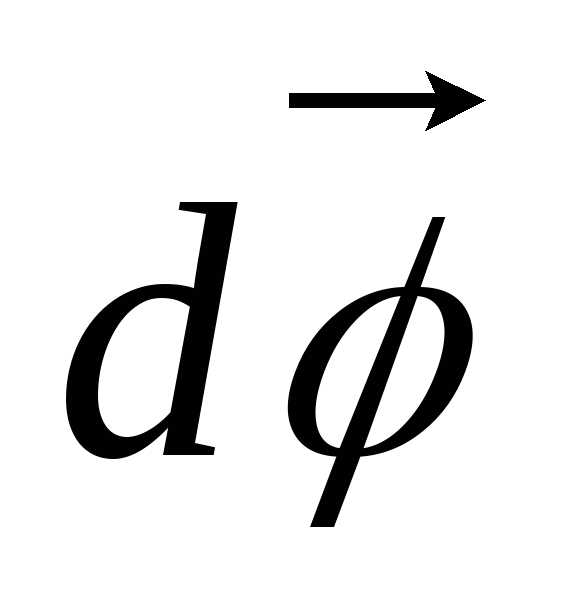 –
вектор элементарного поворота тела.
–
вектор элементарного поворота тела.
Угол в 1 радиан – это центральный угол, длина дуги которого равна радиусу окружности. 360о = 2 рад.
Направление
угловой скорости задается правилом
правого винта: вектор
угловой скорости сонаправлен с 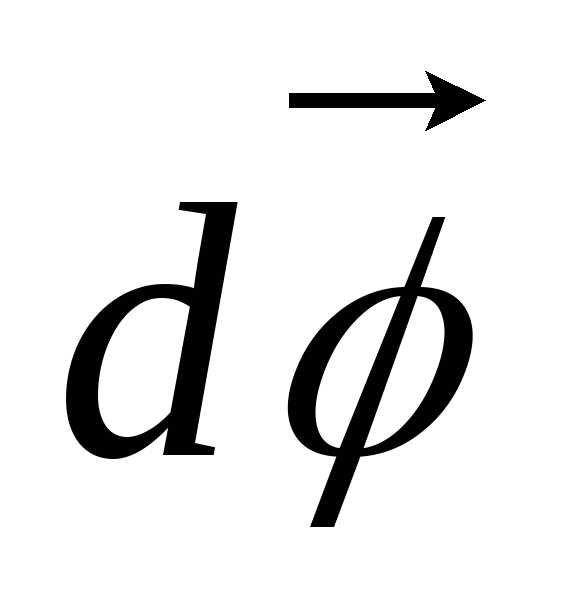 ,
то есть с поступательным движением
винта, головка которого вращается в
направлении движения точки по окружности. Линейная
скорость точки связана с угловой
скоростью:
,
то есть с поступательным движением
винта, головка которого вращается в
направлении движения точки по окружности. Линейная
скорость точки связана с угловой
скоростью:
.
В
векторной форме 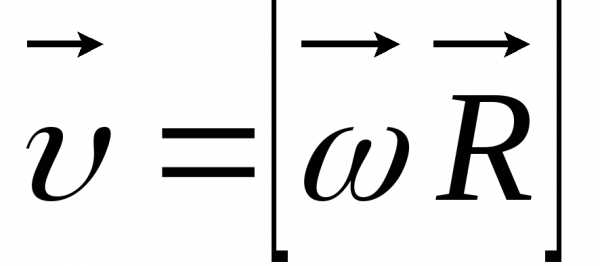 .
.
Если в процессе вращения угловая скорость изменяется, то возникает угловое ускорение:
Угловое
ускорение – векторная величина равная первой
производной угловой скорости по времени.
Вектор угловой скорости сонаправлен с
вектором элементарного изменения
угловой скорости 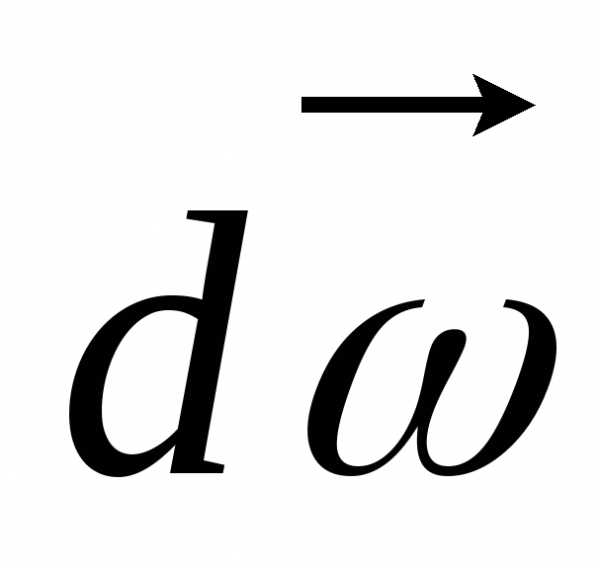 ,
происшедшего за времяdt.
,
происшедшего за времяdt.
При
ускоренном движении вектор 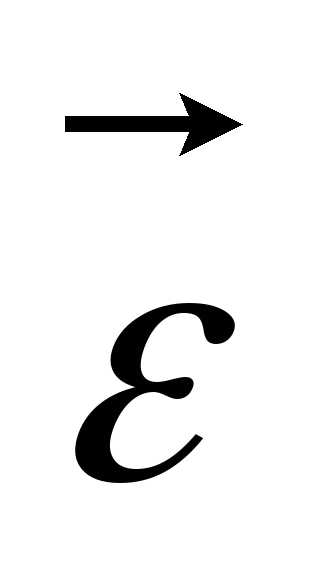 параллелен
параллелен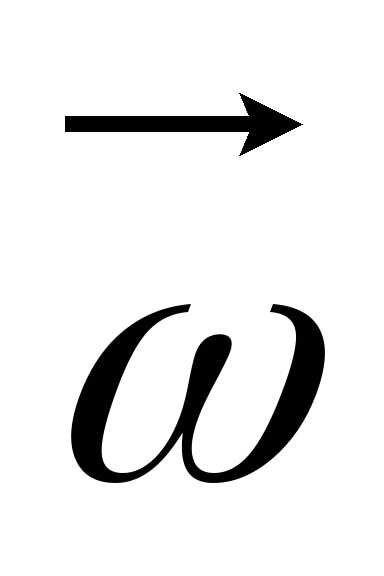 (рис.
8), при замедленном – противонаправлен
(рис. 9).
(рис.
8), при замедленном – противонаправлен
(рис. 9).
Угловое ускорение возникает в системе только тогда, когда происходит изменение угловой скорости, то есть когда линейная скорость движения изменяется по величине. Изменение же скорости по величине характеризует тангенциальное ускорение.
Найдем связь между угловым и тангенциальным ускорениями:
.
Изменение
направления скорости при криволинейном
движении характеризуется нормальным
ускорением 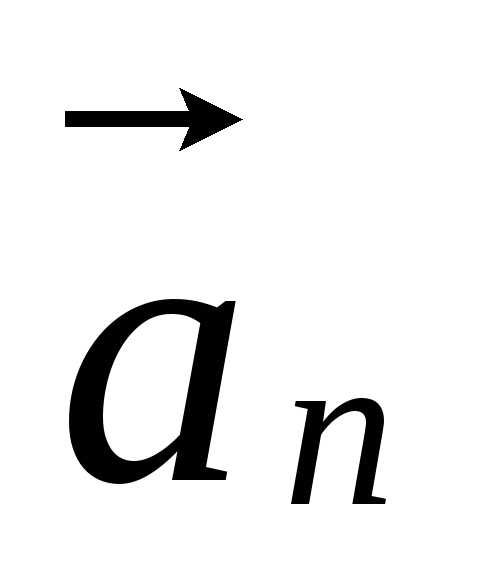 :
:
.
Таким образом, связь между линейными и угловыми величинами выражается следующими формулами:
.
Типы вращательного движения
а) переменное –
движение, при котором изменяются  и
и :
:
б) равнопеременное – вращательное движение с постоянным угловым ускорением:
.
в) равномерное – вращательное движение с постоянной угловой скоростью:
.
Равномерное
вращательное движение можно характеризовать
периодом 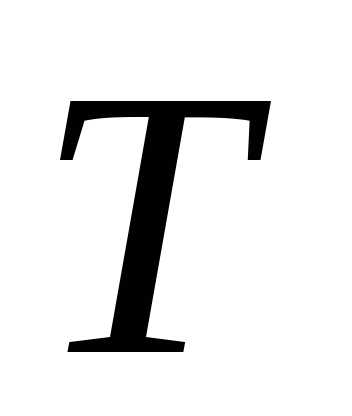 и частотой вращения
и частотой вращения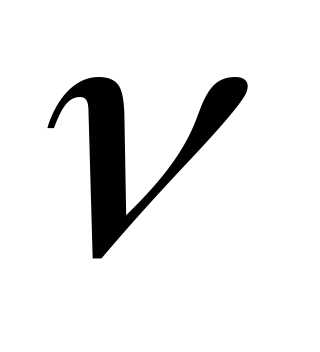 .
.
Период – это время, за которое тело совершает один полный оборот.
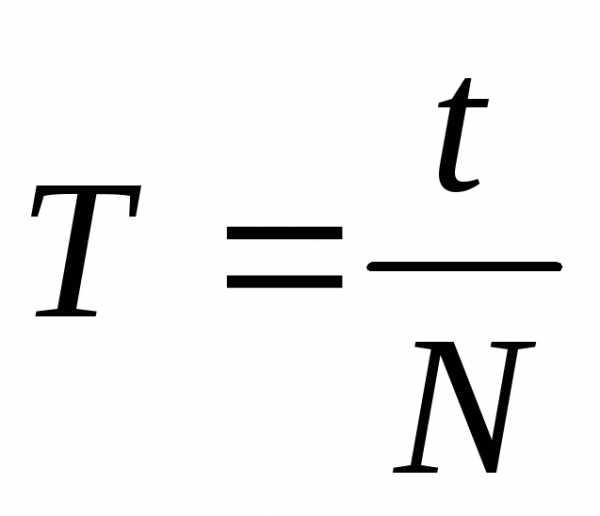 ,
[T]
= c.
,
[T]
= c.
Частота вращения – это число оборотов совершаемых за единицу времени.
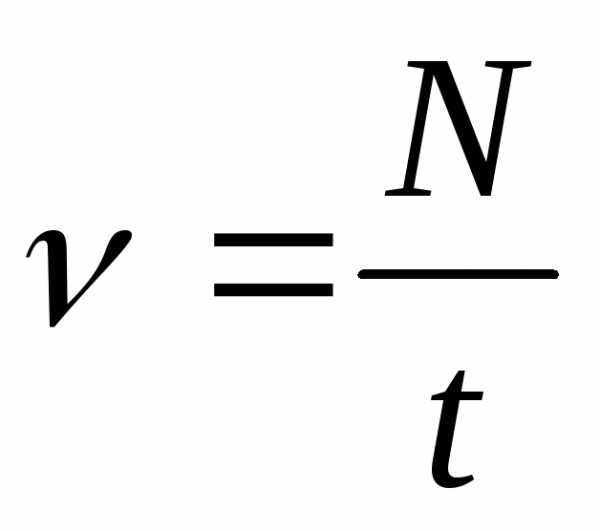 ,
[]
= c-1.
,
[]
= c-1.
За один оборот: ,
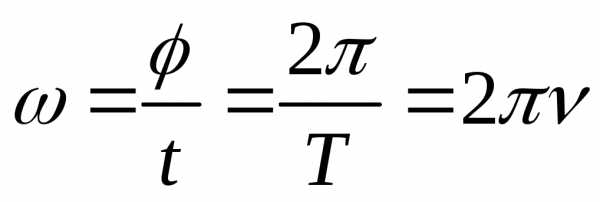 ,
, 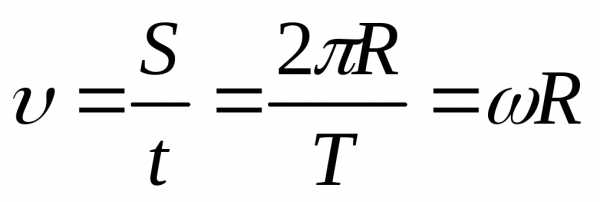 .
.
studfiles.net
3. Нормальное, тангенциальное и полное ускорения.
Движение тела характеризуется скоростью и ускорением, которые могут изменяться во времени. Пусть материальная точка движется по плоской криволинейной траектории с переменной по величине и направлению скоростью (рис. 4). Для характеристики степени криволинейности вводится понятие радиуса кривизны в данной точке траектории.
Радиусом кривизны R траектории называют радиус окружности, которая сливается с криволинейной траекторией на бесконечно малом ее участке.
В данной точке траектории касательная всегда перпендикулярна радиусу кривизны.
Пусть и скорость, и ускорение меняются по величине и направлению.
Мы знаем,
что ускорение тела при движении есть 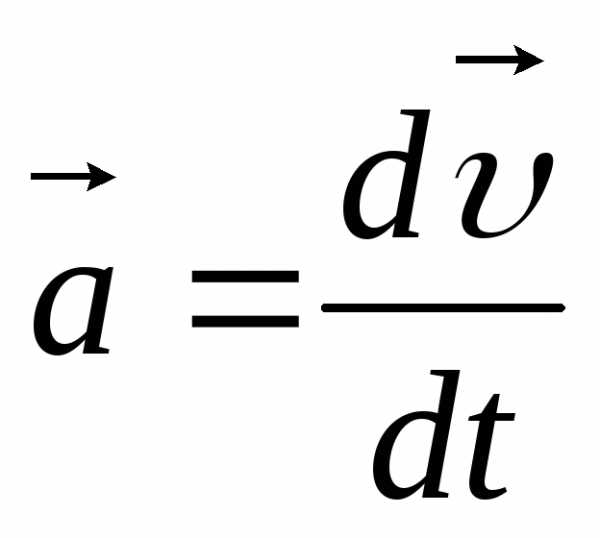 .
.
Вектор
скорости 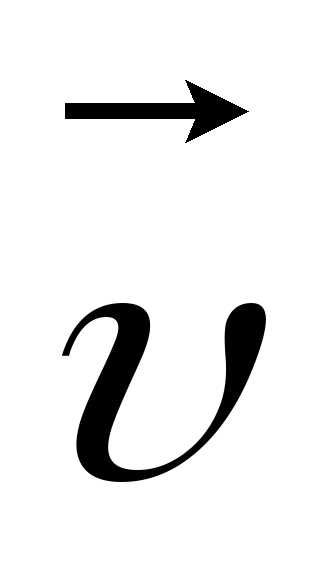 можно представить как произведение
модуля скорости
можно представить как произведение
модуля скорости и некоторого единичного вектора
и некоторого единичного вектора  ,
сонаправленного с вектором линейной
скорости
,
сонаправленного с вектором линейной
скорости 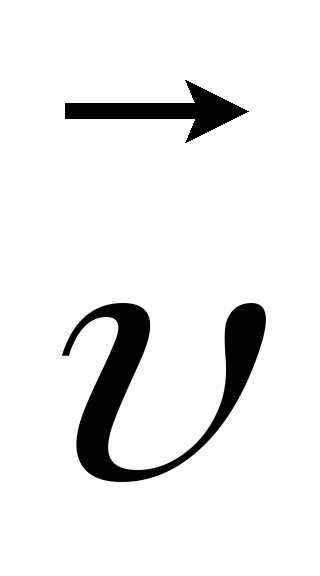 ,
направленного по касательной к траектории.
,
направленного по касательной к траектории.
Таким
образом, полное ускорение материальной
точки при криволинейном движении можно
представить в виде суммы двух слагаемых.
Первое слагаемое 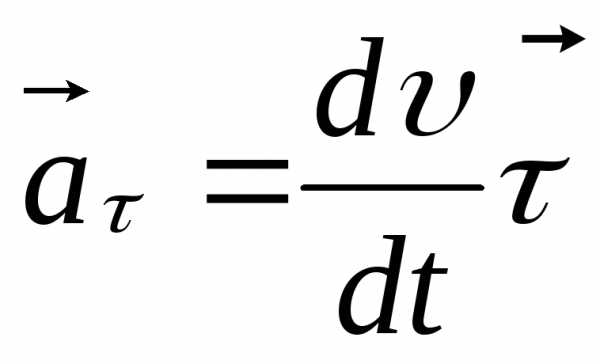 .
.
Вектор 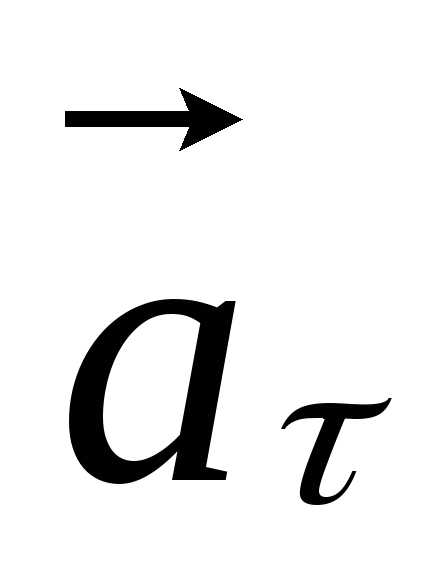 сонаправлен с вектором
сонаправлен с вектором 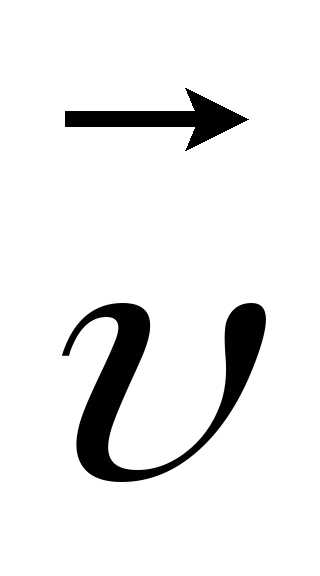 ,
т.е. направлен по касательной к траектории
и называется тангенциальным или касательным ускорением. Его модуль
равен
,
т.е. направлен по касательной к траектории
и называется тангенциальным или касательным ускорением. Его модуль
равен 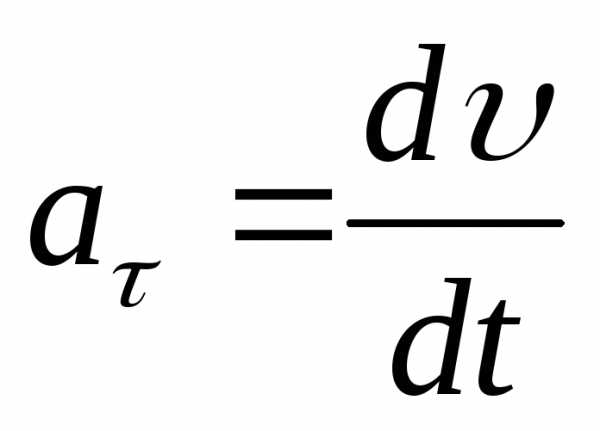 ,
поэтому
,
поэтому 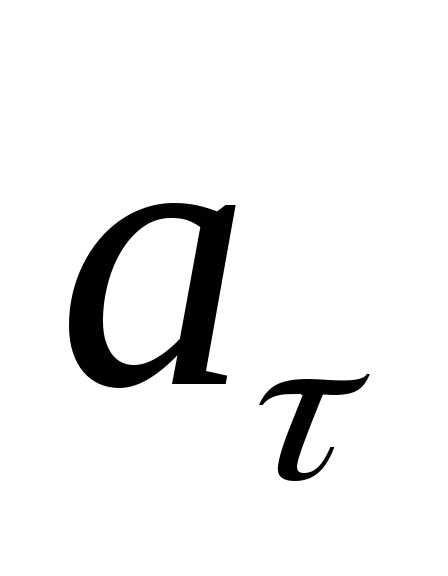 характеризует быстроту изменения
скорости криволинейного движения по
величине, но не направлению, так как
вектор
характеризует быстроту изменения
скорости криволинейного движения по
величине, но не направлению, так как
вектор  не изменяется.
не изменяется.
Следовательно,
можно заключить, что 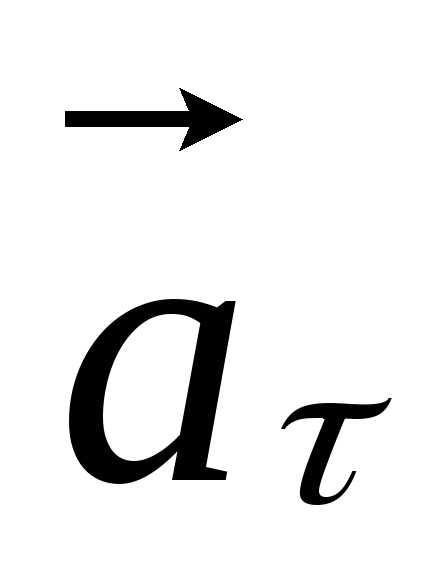 – тангенциальное ускорение, характеризующее
изменение скорости по величине, оно
направлено по касательной к траектории.
– тангенциальное ускорение, характеризующее
изменение скорости по величине, оно
направлено по касательной к траектории.
Второе
слагаемое 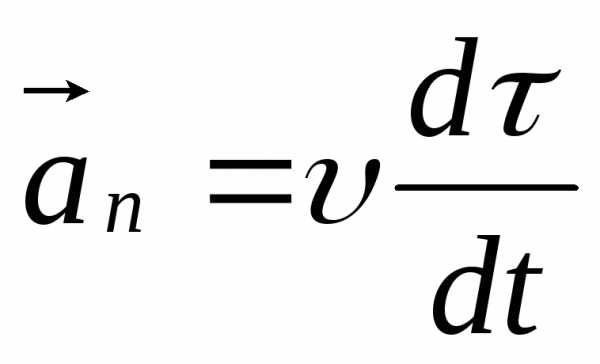 называется нормальным ускорением. Что
характеризует этот вектор, куда направлен,
как его рассчитать?
называется нормальным ускорением. Что
характеризует этот вектор, куда направлен,
как его рассчитать?
Так
как вектор 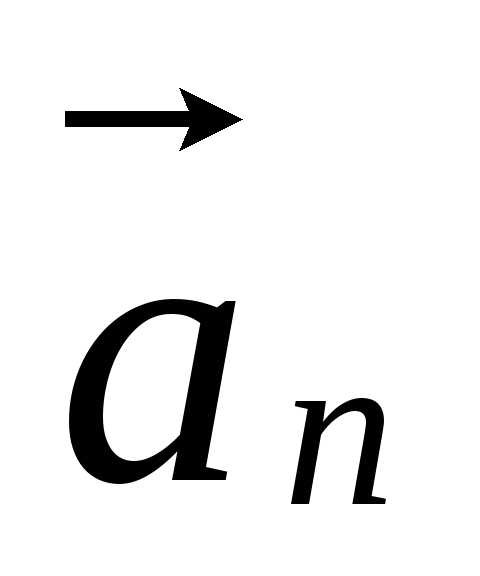 сонаправлен с вектором
сонаправлен с вектором 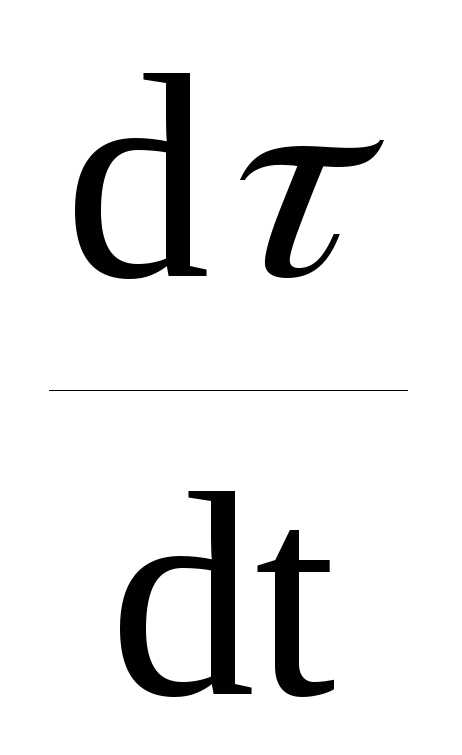 ,
который определяет изменениенаправления вектора линейной скорости, то он
характеризует изменение скорости
криволинейного движения по направлению.
,
который определяет изменениенаправления вектора линейной скорости, то он
характеризует изменение скорости
криволинейного движения по направлению.
О
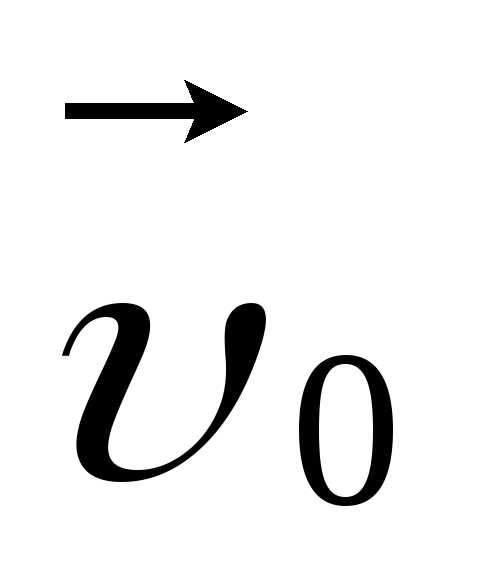
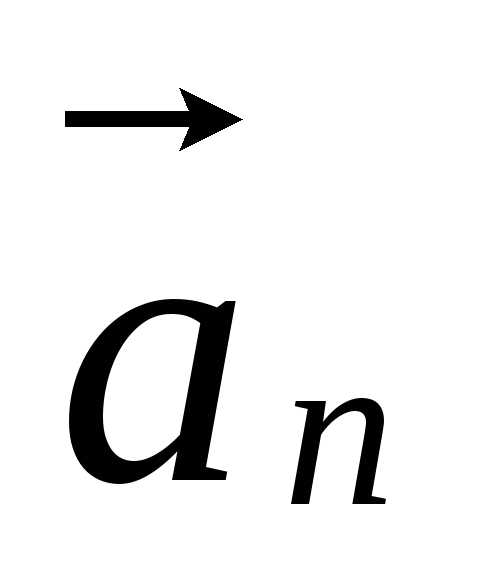 .
Рассмотрим частный случай движения
материальной точки по окружности
радиусом R с постоянной по величине скоростью
.
Рассмотрим частный случай движения
материальной точки по окружности
радиусом R с постоянной по величине скоростью  (рис.5).
Среднее изменение скорости на дуге АВ
отнесем к точке С, лежащей посередине
дуги.
(рис.5).
Среднее изменение скорости на дуге АВ
отнесем к точке С, лежащей посередине
дуги. 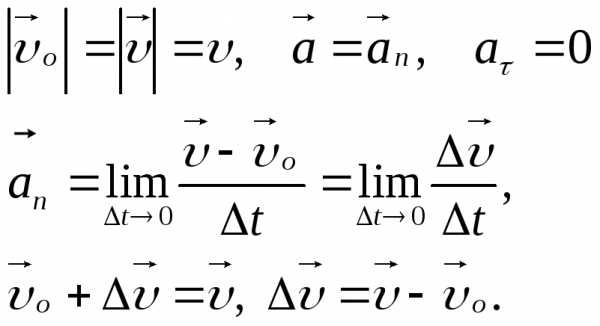
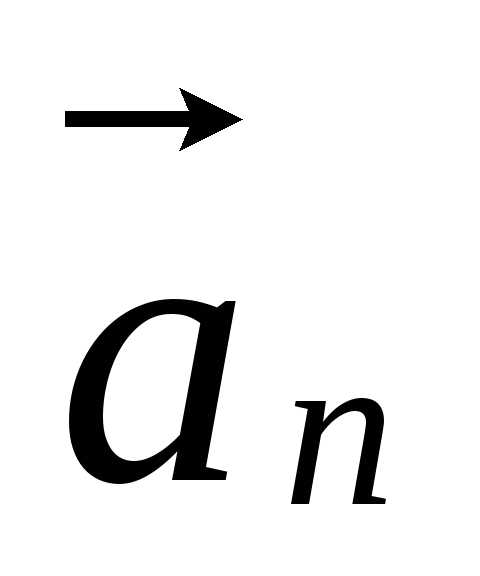 направлено
вдоль R
к центру окружности.
направлено
вдоль R
к центру окружности.
 ∾
∾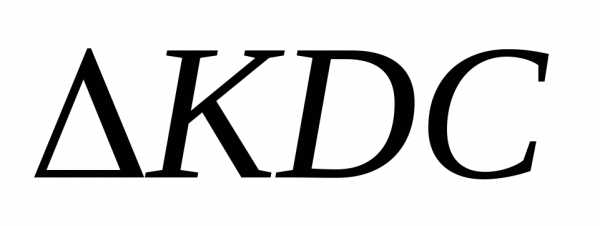 :
:
.
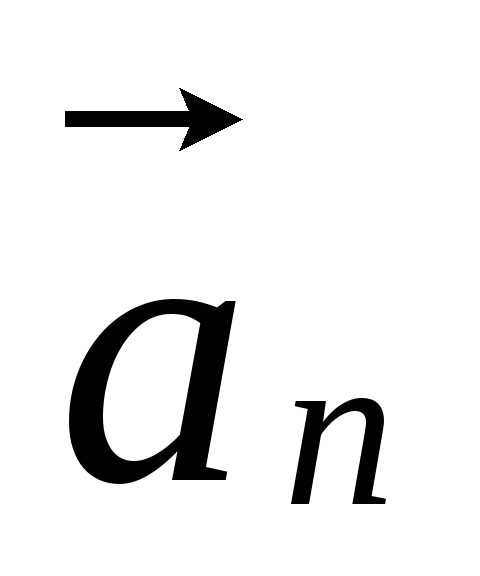 перпендикулярно
скорости, направлено вдоль радиуса к
центру окружности. Его называют
нормальным, радиальным или центростремительным
ускорением.
перпендикулярно
скорости, направлено вдоль радиуса к
центру окружности. Его называют
нормальным, радиальным или центростремительным
ускорением.
Полное ускорение материальной точки при криволинейном движении характеризует быстроту изменения скорости как по величине, так и по направлению (рис.6).
, .
Угловая скорость и угловое ускорение.
Поворот тела на некоторый угол можно задать в виде отрезка, длина которого равна , а направление совпадает с осью, вокруг которой производится поворот. Направление поворота и изображающего его отрезка связано правилом правого винта.
В
математике показывается, что очень
малые повороты можно рассматривать как
векторы, обозначаемые символами 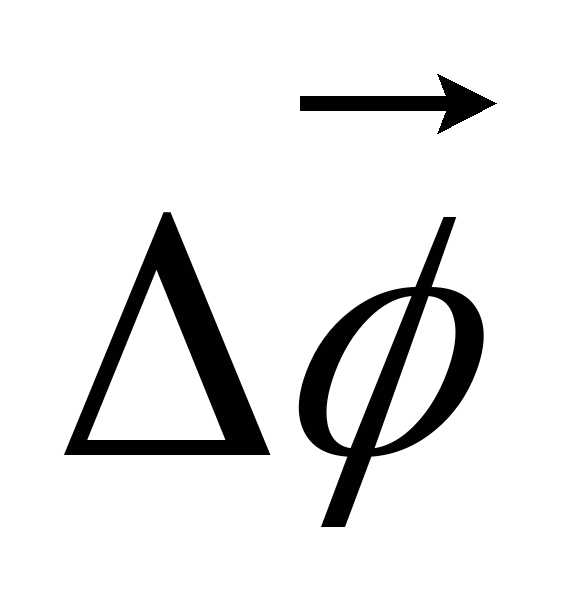 или
или 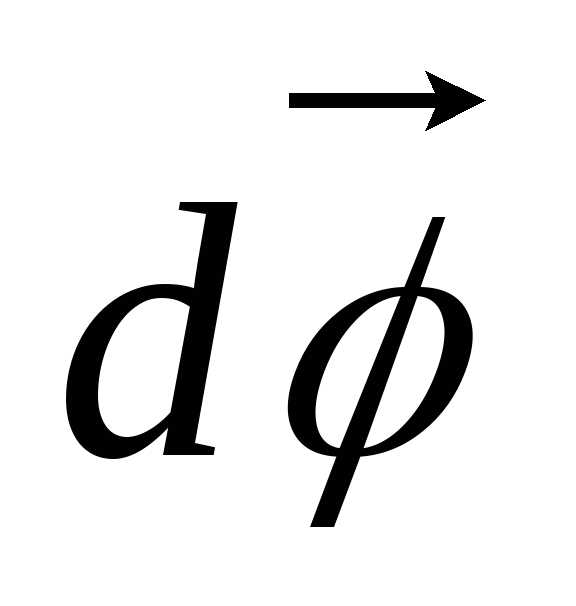 .
Направление вектора поворота связывается
с направлением вращения тела;
.
Направление вектора поворота связывается
с направлением вращения тела; 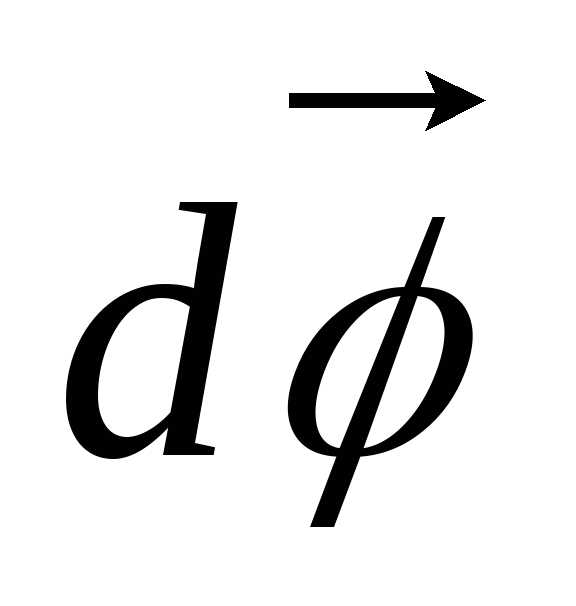 является псевдовектором, так как не
имеет точки приложения.
является псевдовектором, так как не
имеет точки приложения.
При вращательном движении твердого тела каждая точка движется по окружности, центр которой лежит на общей оси вращения (рис. 7). При этом радиус-вектор R, направленный от оси вращения к точке, поворачивается за время t на некоторый угол . Для характеристики вращательного движения вводится угловая скорость и угловое ускорение.
Угловой скоростьюназывается векторная величина, равная первой производной угла поворота тела по времени.
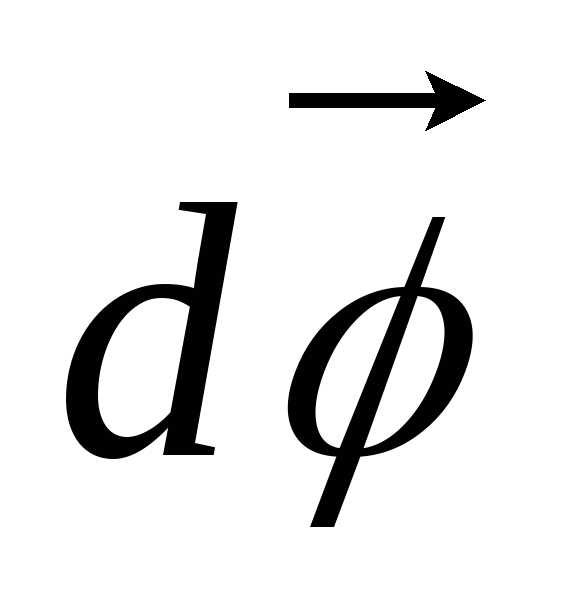 –
вектор элементарного поворота тела.
–
вектор элементарного поворота тела.
Угол в 1 радиан – это центральный угол, длина дуги которого равна радиусу окружности. 360о = 2 рад.
Направление
угловой скорости задается правилом
правого винта: вектор
угловой скорости сонаправлен с 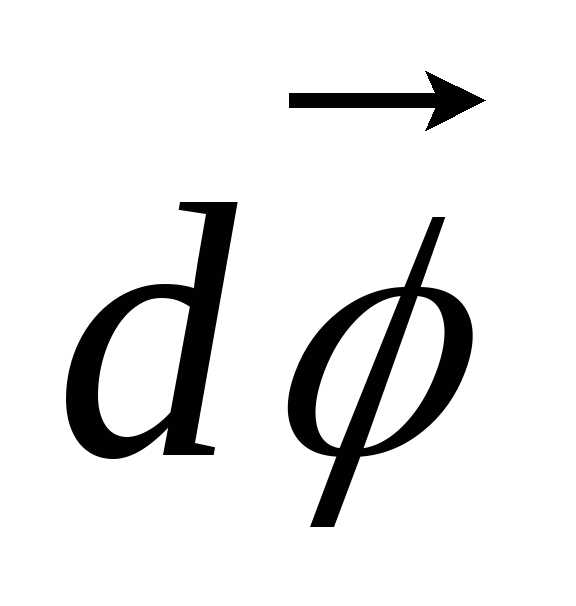 ,
то есть с поступательным движением
винта, головка которого вращается в
направлении движения точки по окружности. Линейная
скорость точки связана с угловой
скоростью:
,
то есть с поступательным движением
винта, головка которого вращается в
направлении движения точки по окружности. Линейная
скорость точки связана с угловой
скоростью:
.
В
векторной форме 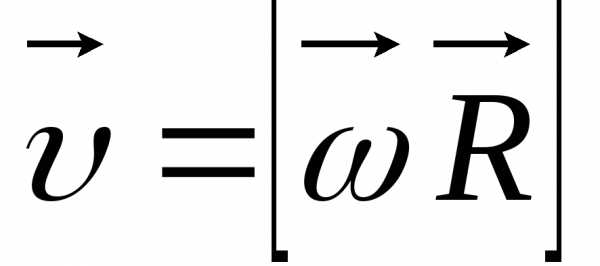 .
.
Если в процессе вращения угловая скорость изменяется, то возникает угловое ускорение:
Угловое
ускорение – векторная величина равная первой
производной угловой скорости по времени.
Вектор угловой скорости сонаправлен с
вектором элементарного изменения
угловой скорости 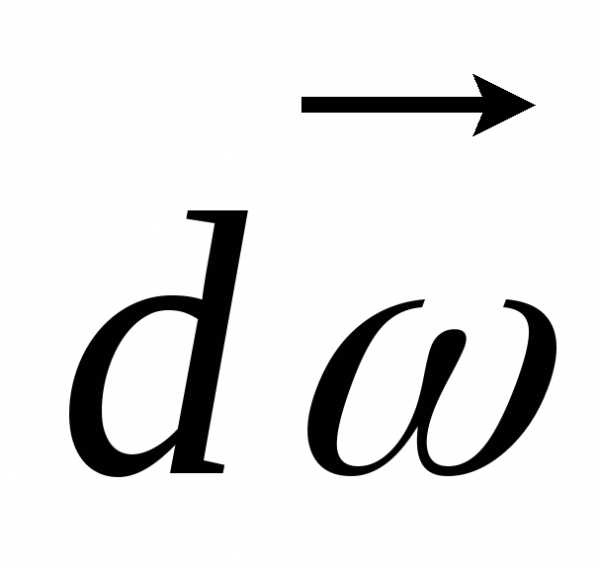 ,
происшедшего за времяdt.
,
происшедшего за времяdt.
При
ускоренном движении вектор 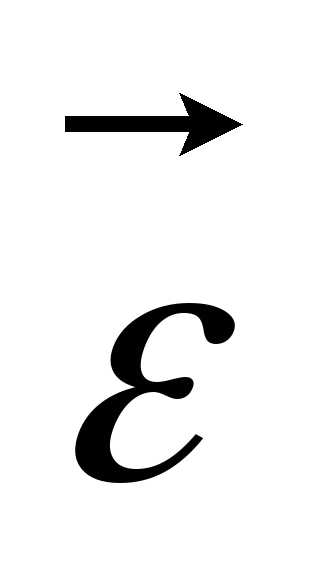 параллелен
параллелен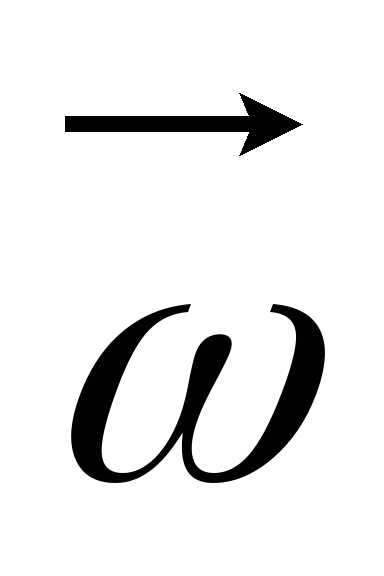 (рис.
8), при замедленном – противонаправлен
(рис. 9).
(рис.
8), при замедленном – противонаправлен
(рис. 9).
Угловое ускорение возникает в системе только тогда, когда происходит изменение угловой скорости, то есть когда линейная скорость движения изменяется по величине. Изменение же скорости по величине характеризует тангенциальное ускорение.
Найдем связь между угловым и тангенциальным ускорениями:
.
Изменение
направления скорости при криволинейном
движении характеризуется нормальным
ускорением 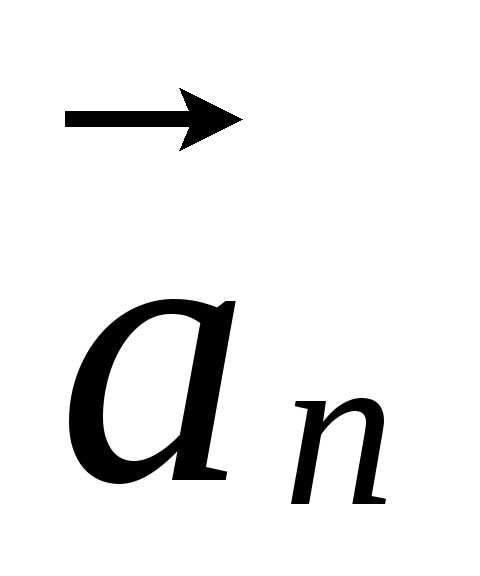 :
:
.
Таким образом, связь между линейными и угловыми величинами выражается следующими формулами:
.
Типы вращательного движения
а) переменное –
движение, при котором изменяются
и :
:
б) равнопеременное – вращательное движение с постоянным угловым ускорением:
.
в) равномерное – вращательное движение с постоянной угловой скоростью:
.
Равномерное
вращательное движение можно характеризовать
периодом 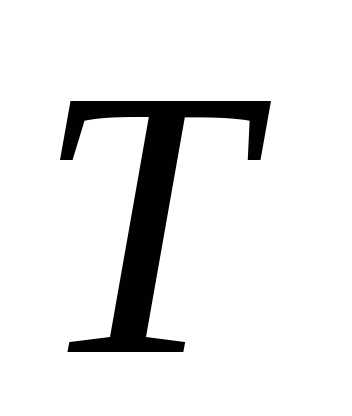 и частотой вращения
и частотой вращения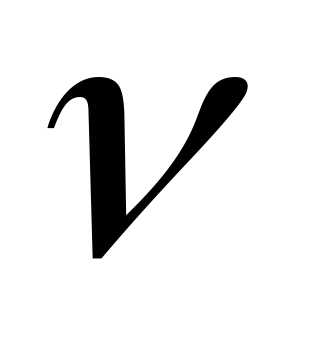 .
.
Период – это время, за которое тело совершает один полный оборот.
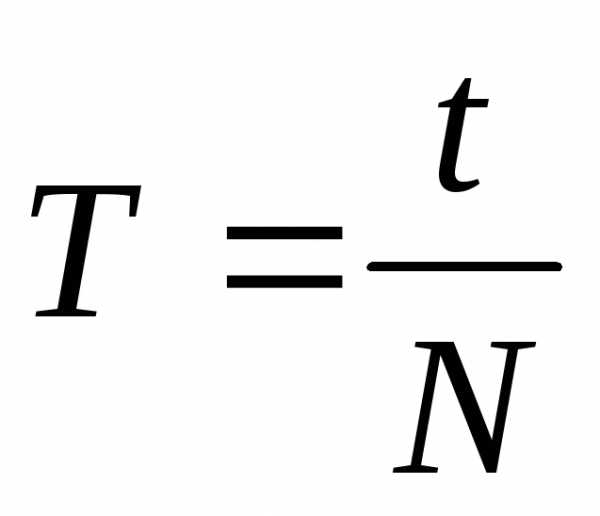 ,
[T]
= c.
,
[T]
= c.
Частота вращения – это число оборотов совершаемых за единицу времени.
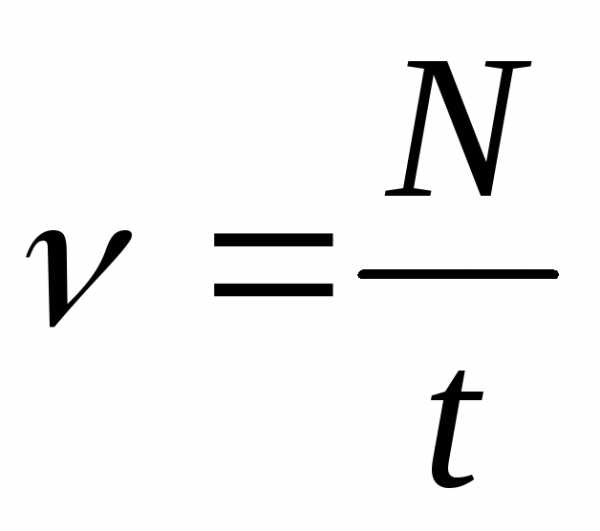 ,
[]
= c-1.
,
[]
= c-1.
За один оборот: ,
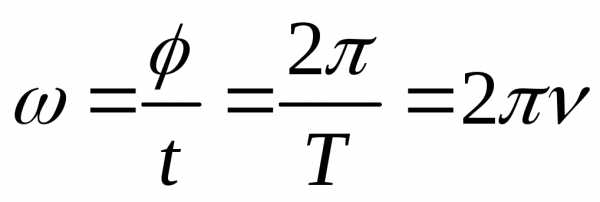 ,
, 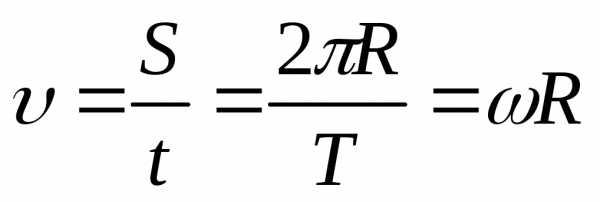 .
.
studfiles.net
Тангенциальное, нормальное и полное ускорение
Количество просмотров публикации Тангенциальное, нормальное и полное ускорение – 200
Тангенциальное (касательное) ускорение – это составляющая вектора ускорения, направленная вдоль касательной к траектории в данной точке траектории движения. Тангенциальное ускорение характеризует изменение скорости по модулю при криволинейном движении.
Рисунок 1 – Тангенциальное ускорение
Направление вектора тангенциального ускорения совпадает с направлением линейной скорости или противоположно ему, из рис. 1. Таким образом вектор тангенциального ускорения лежит на одной оси с касательной окружности, которая является траекторией движения тела.
Нормальное ускорение – это составляющая вектора ускорения, направленная вдоль нормали к траектории движения в данной точке на траектории движения тела. Таким образом вектор нормального ускорения перпендикулярен линейной скорости движения, показано на рис. 1. Нормальное ускорение характеризует изменение скорости по направлению и обозначается n. Вектор нормального ускорения направлен по радиусу кривизны траектории.
Полное ускорение при криволинейном движении складывается из тангенциального и нормального ускорений по правилу сложения векторов и определяется формулой˸
(9)
или
(10)
Направление полного ускорения также определяется правилом сложения векторов˸
(11)
1.1.5 Поступательное и вращательное движение абсолютно твёрдого тела
Движение тела считается поступательным, в случае если любой отрезок прямой линии, жестко связанный с телом, всё время перемещается параллельно самому себе. При поступательном движении все точки тела совершают одинаковые перемещения, проходят одинаковые пути, имеют равные скорости и ускорения, описывают одинаковые траектории.
Вращение твёрдого тела вокруг неподвижной оси – движение, при котором все точки тела описывают окружности, центры которых находятся на одной прямой, перпендикулярной плоскостям этих окружностей. Сама эта прямая является осью вращения.
При вращении тела радиус окружности, описываемой точкой этого тела, повернётся за интервал времени на некоторый угол. Вследствие неизменности взаимного расположения точек тела на такой же угол повернуться за тоже время радиусы окружностей, описываемых любыми другими точками тела. Этот угол является величинои̌, характеризующей вращательное движение всего тела в целом. Отсюда можно сделать вывод, что для описания вращательного движения абсолютно твёрдого тела вокруг неподвижной оси надо знать только одну переменную – угол, на который повернётся тело за определённое время.
Связь между линейной и угловой скоростями для каждой точки твёрдого тела даётся формулой˸
(12)
Также точки твёрдого тела имеют нормальные и тангенциальные ускорения, которые можно задать формулами˸
(13)
Плоскопараллельное движение – движение, при котором каждая точка тела движется постоянно в одной плоскости, при этом все плоскости параллельны между собой. [3, с. 375]
referatwork.ru
1.7. Криволинейное движение. Тангенциальное и нормальное ускорения
При прямолинейном движении векторы скорости и ускорения совпадают с направлением траектории. Рассмотрим движение материальной точки по криволинейной плоской траектории. Вектор скорости в любой точке траектории направлен по касательной к ней. Допустим, что в т.М траектории скорость была , а в т.М1 стала . При этом считаем, что промежуток времени при переходе точки на пути из М в М1 настолько мал, что изменением ускорения по величине и направлению можно пренебречь. Для того, чтобы найти вектор изменения скорости , необходимо определить векторную разность:
Для этого перенесем параллельно самому себе, совмещая его начало с точкой М. Разность двух векторов равна вектору, соединяющему их концы равна стороне АС МАС, построенного на векторах скоростей, как на сторонах. Разложим вектор на две составляющих АВ и АД, и обе соответственно через и . Таким образом вектор изменения скорости равен векторной сумме двух векторов:
По определению:
| (1.15) |
Тангенциальное ускорение характеризует быстроту изменения скорости движения по численному значению и направлена по касательной к траектории.
Следовательно
| (1.16) |
Нормальное ускорение характеризует быстроту изменения скорости по направлению. Вычислим вектор:
Для этого проведем перпендикуляр через точки М и М1 к касательным к траектории (рис. 1.4) Точку пересечения обозначим через О. При достаточно малом участок криволинейной траектории можно считать частью окружности радиуса R. Треугольники МОМ1 и МВС подобны, потому, что являются равнобедренными треугольниками с одинаковыми углами при вершинах. Поэтому:
или
Но , тогда:
Переходя к пределу при и учитывая, что при этом , находим:
,
| (1.17) |
Так как при угол , направление этого ускорения совпадает с направлением нормали к скорости , т.е. вектор ускорения перпендикулярен . Поэтому это ускорение часто называют центростремительным.
Полное ускорение определяется векторной суммой тангенциального нормального ускорений (1.15). Так как векторы этих ускорений взаимноперпендикулярны, то модуль полного ускорения равен:
| (1.18) |
Направление полного ускорения определяется углом между векторам и :
physics-lectures.ru



