Производная функции дроби примеры – Как найти производную от дроби 🚩 Производная от дроби 🚩 Математика
- Комментариев к записи Производная функции дроби примеры – Как найти производную от дроби 🚩 Производная от дроби 🚩 Математика нет
- Советы абитуриенту
- Производная дроби – доказательство – примеры
- Производная дроби
- Производная дроби примеры | Решение задач по математике
- Производная частного двух функций (производная дроби).
- Производная суммы дробей со степенями и корнями
- Как найти производную от дроби
- Производная дроби онлайн · Как пользоваться Контрольная Работа РУ
Производная дроби – доказательство – примеры
Пусть функции и определены в некоторой окрестности точки и имеют в точке производные. И пусть . Тогда их частное имеет в точке производную, которая определяется по формуле:
(1) .
Доказательство
Введем обозначения:
;
.
Здесь и являются функциями от переменных и . Но для простоты записи мы будем опускать обозначения их аргументов.
Далее замечаем, что
;
.
По условию функции и имеют производные в точке , которые являются следующими пределами:
;
.
Из существования производных следует, что функции и непрерывны в точке . Поэтому
;
.
Рассмотрим функцию y от переменной x, которая является дробью из функций и :
.
Рассмотрим приращение этой функции в точке :
.
Умножим на :
.
Отсюда
.
Теперь находим производную:
.
Итак,
.
Формула доказана.
Вместо переменной можно использовать любую другую переменную. Обозначим ее как x. Тогда если существуют производные и , причем , то производная дроби, составленной двух функций, определяется по формуле:
.
Или в более короткой записи
(1) .
Доказательство вторым способом
Примеры
Здесь мы рассмотрим простые примеры вычисления производной дроби, применяя формулу производной частного (1). Заметим, что в более сложных случаях, находить производную дроби проще с помощью логарифмической производной.
Пример 1
Найдите производную дроби
,
где , , , – постоянные.
Решение
Применим правило дифференцирования суммы функций:
.
Производная постоянной
.
Из таблицы производных находим:
.
Тогда
;
.
Заменим на и на :
.
Теперь находим производную дроби по формуле
.
.
Ответ
.
Пример 2
Найти производную функции от переменной x
.
Решение
Применяем правила дифференцирования, как в предыдущем примере.
;
.
Применяем правило дифференцирования дроби
.
.
Раскрываем скобки.
.
Ответ
.
Пример 3
Найти производную дроби
.
Решение
Из таблицы производных находим:
.
Применяем правила дифференцирования суммы и постоянной.
;
.
Применяем формулу для производной дроби:
;
.
Ответ
.
Автор: Олег Одинцов. Опубликовано: Изменено:
1cov-edu.ru
Производная дроби
См. также полную таблицу производных простых функций.
Формулы нахождения производной дроби как для частного случая, так и универсальную, можно посмотреть внизу страницы. Далее, же следует подробное описание вывода этих формул с подробным пояснением, почему именно так.
Для начала, преобразуем выражение для нахождения производной. Как известно, дробь вида 1/х можно представить как х-1.
Таким образом, заменив исходное выражение на тождественное, задачу нахождения производной дроби вида 1/х можно представить как:
(1/x)’ = (x -1)’
Тогда для нахождения производной дроби можно применить правило нахождения производной степенной функции, откуда:
(x -1)’ = -1x-2 = – 1 / х2
Таким образом, производная дроби 1/х равна:
На основании только что показанного принципа преобразования исходного выражения, можно вывести и более универсальную формулу:
Производная дроби с переменной произвольной степени в знаменателе
( 1 / xс )’ = – c / xс+1
Пример нахождения производной дроби:
( 1 / x2 )’ = – 2 / x3 .
(впереди ставим минус, показатель степени переменной поднимаем в числитель дроби, а степень переменной в знаменателе увеличиваем на единичку. Немного “ненаучно”, но подходит для быстрого запоминания)
Формулы нахождения производной дроби:
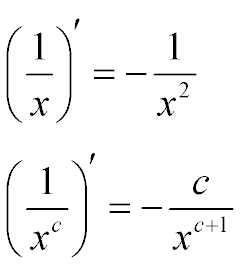
profmeter.com.ua
Производная дроби примеры | Решение задач по математике
Производная дроби примеры
Область определения:
Данная функция определена для:
Решаем вспомогательное уравнение.
Находим дискриминант.
Дискриминант равен нулю, значит уравнение имеет один корень.
Старший коэффициент положителен.
Квадратичная функция принимает только неотрицательные значения.
Следующее неравенство равносильно предыдущему.
Ответ:
Найдем первую производную
Воспользуемся формулой производной частного.
Вторая производная:
Вторая производная это производная от первой производной.
Воспользуемся формулой производной частного.
Воспользуемся свойством степеней, а также воспользуемся правилом нахождения производной для сложной функции. Потом Выносим общий множитель.
Воспользуемся свойством степеней.
Изменим знаки выражений на противоположные.
Точки пересечения с осью x:
Для нахождения точек пересечения с осью абсцисс приравняем функцию к нулю.
Дробь обращается в нуль тогда, когда числитель равен нулю.
Находим дискриминант.
Дискриминант равен нулю, значит уравнение имеет один корень.
Воспользуемся формулой корней квадратного уравнения.
Ответ:
X=3
Точки пересечения с осью
:
Пусть x=0
Вертикальные асимптоты:
Определим значения аргумента, при которых знаменатель функции обращается в ноль
Находим дискриминант.
Дискриминант равен нулю, значит уравнение имеет один корень.
Воспользуемся формулой корней квадратного уравнения.
Горизонтальные асимптоты: y=1
Наклонные асимптоты: нет.
Для нахождения горизонтальных асимптот преобразуем исходное выражение.
Предел данной функции на бесконечности равен числу 1
Критические точки:
X=3
Для нахождения критических точек приравняем первую производную к нулю и решим полученное уравнение.
Дробь обращается в нуль тогда, когда числитель равен нулю.
Следующее уравнение равносильно предыдущему.
Находим дискриминант. Дискриминант положителен, значит уравнение имеет два корня.
Воспользуемся формулой корней квадратного уравнения.
Корень 2 не входит в ОДЗ функции.
Ответ:
Таким образом, окончательный ответ
X=3
Возможные точки перегиба:
X=3.5
Для нахождения возможных точек перегиба приравняем вторую производную к нулю и решим полученное уравнение.
Изменим знаки выражений на противоположные.
Дробь обращается в нуль тогда, когда числитель равен нулю.
Следующее уравнение равносильно предыдущему.
Решаем уравнение методом разложения на множители.
Разложим одночлены в сумму нескольких.
Производим группировку.
Выносим общий множитель.
Выносим общий множитель.
Теперь решение исходного уравнения разбивается на отдельные случаи.
Случай 1
Перенесем известные величины в правую часть уравнения.
Итак,ответ этого случая:
.
Случай 2
Находим дискриминант.
Дискриминант положителен, значит, уравнение имеет два корня.
Воспользуемся формулой корней квадратного уравнения.
Итак,ответ
2 не входит в ОДЗ функции.
Ответ:
X=3.5
Точки разрыва:
X=2
Симметрия относительно оси ординат: нет
Функция f(x) называется четной, если f(-x)=f(x).
Выносим знак минус из произведения. Приводим дроби к общему знаменателю.
Производим сложение дробей с одинаковыми знаменателями. Приводим подобные члены. Выносим знак минус из произведения.
Разложим числитель дроби на множители.
Функция не может быть четной.
Симметрия относительно начала координат: нет
Функция f(x) называется нечетной, если f(-x)-f(x).
Приводим дроби к общему знаменателю. Производим сложение дробей с одинаковыми знаменателями. Приводим подобные члены. Разложим числитель дроби на множители.
Тестовые интервалы:
Результаты исследования функции занесем в таблицу. Относительные экстремумы:
Проходя через точку минимума, производная функции меняет знак с (-) на (+).
Относительный минимум
.
Данные таблицы нанесем на координатную плоскость.
Используя результаты исследования функции, построим ее график.
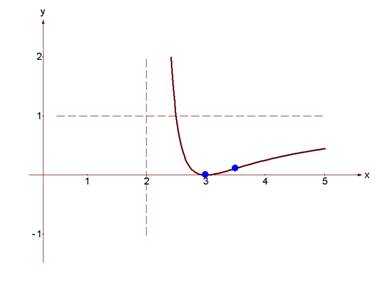
Множество значений функции:
Наименьшее значение:
Наибольшее значение: нет
Запись создана: Понедельник, 20 Август 2018 в 1:24 и находится в рубриках Начала анализа. Вы можете следить за комментариями к этой записи через ленту RSS 2.0. Комментарии и уведомления в настоящее время закрыты.
testmath.ru
Производная частного двух функций (производная дроби).
⇐ ПредыдущаяСтр 5 из 89Следующая ⇒Докажем правило дифференцирования частного двух функций (дроби) . Стоит оговориться, что g(x) не обращается в ноль ни при каких x из промежутка X.
По определению производной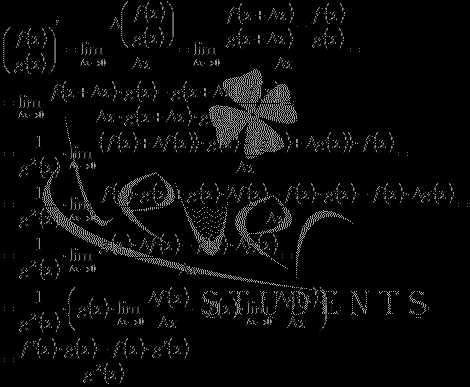
Пример.
Выполнить дифференцирование функции .
Решение.
Исходная функция представляет собой отношение двух выражений sinx и 2x+1. Применим правило дифференцирования дроби:
Не обойтись без правил дифференцирования суммы и вынесения произвольной постоянной за знак производной:
В заключении, давайте соберем все правила в одном примере.
Пример.
Найти производную функции , где a – положительное действительное число.
Решение.
А теперь по порядку.
Первое слагаемое .
Второе слагаемое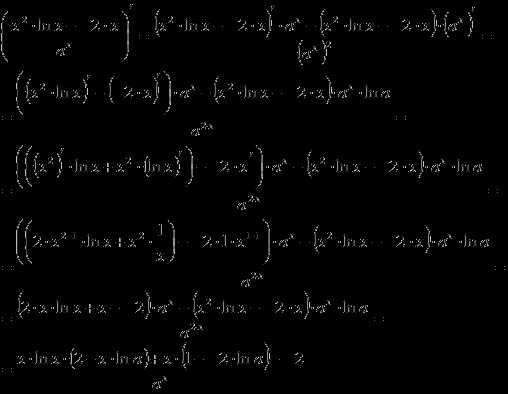
Третье слагаемое
Собираем все вместе:
4.Вопрос.Производные Основных элементарных функций.
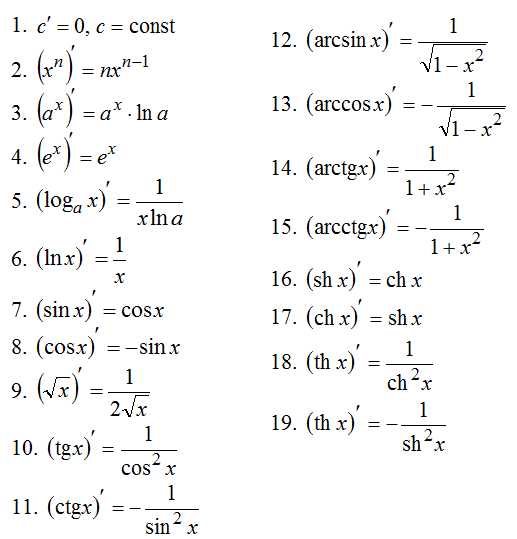
Задание. Найти производную функции
Решение. Используем правила дифференцирования и таблицу производных:
Ответ.
5.Вопрос.Производная сложной функции примеры
Все примеры этого раздела опираются на таблицу производных и теорему о производной сложной функции, формулировка которой такова:
Пусть 1) функция u=φ(x) имеет в некоторой точке x0 производную u′x=φ′(x0), 2) функция y=f(u) имеет в соответствующей точке u0=φ(x0) производную y′u=f′(u). Тогда сложная функция y=f(φ(x)) в упомянутой точке также будет иметь производную, равную произведению производных функций f(u) и φ(x):
(f(φ(x)))′=f′u(φ(x0))⋅φ′(x0)
или, в более короткой записи: y′x=y′u⋅u′x.
В примерах этого раздела все функции имеют вид y=f(x) (т.е. рассматриваем лишь функции одной переменной x). Соответственно, во всех примерах производная y′ берётся по переменной x. Чтобы подчеркнуть то, что производная берётся по переменной x, часто вместо y′ пишут y′x.
В примерах №1, №2 и №3 изложен подробный процесс нахождения производной сложных функций. Пример №4 предназначен для более полного понимания таблицы производных и с ним имеет смысл ознакомиться.
Желательно после изучения материала в примерах №1-3 перейти к самостоятельному решению примеров №5, №6 и №7. Примеры №5, №6 и №7 содержат краткое решение, чтобы читатель мог проверить правильность своего результата.
Пример №1
Найти производную функции y=ecosx.
Решение
Нам нужно найти производную сложной функции y′. Так как y=ecosx, то y′=(ecosx)′. Чтобы найти производную (ecosx)′ используем формулу №6 из таблицы производных. Дабы использовать формулу №6 нужно учесть, что в нашем случае u=cosx. Дальнейшее решение состоит в банальной подстановке в формулу №6 выражения cosx вместо u:
Итак,
y′=(ecosx)′=ecosx⋅(cosx)′(1.1)
Теперь нужно найти значение выражения (cosx)′. Вновь обращаемся к таблице производных, выбирая из неё формулу №10. Подставляя u=x в формулу №10, имеем: (cosx)′=−sinx⋅x′. Теперь продолжим равенство (1.1), дополнив его найденным результатом:
y′=(ecosx)′=ecosx⋅(cosx)′=ecosx⋅(−sinx⋅x′)(1.2)
Так как x′=1, то продолжим равенство (1.2):
y′=(ecosx)′=ecosx⋅(cosx)′=ecosx⋅(−sinx⋅x′)=ecosx⋅(−sinx⋅1)=−sinx⋅ecosx(1.3)
Итак, из равенства (1.3) имеем: y′=−sinx⋅ecosx. Естественно, что пояснения и промежуточные равенства обычно пропускают, записывая нахождение производной в одну строку, – как в равенстве (1.3). Итак, производная сложной функции найдена, осталось лишь записать ответ.
Ответ: y′=−sinx⋅ecosx.
Пример №2
Найти производную функции y=9⋅arctg12(4⋅lnx).
Решение
Нам необходимо вычислить производную y′=(9⋅arctg12(4⋅lnx))′. Для начала отметим, что константу (т.е. число 9) можно вынести за знак производной:
y′=(9⋅arctg12(4⋅lnx))′=9⋅(arctg12(4⋅lnx))′(2.1)
Теперь обратимся к выражению (arctg12(4⋅lnx))′. Чтобы выбрать нужную формулу из таблицы производных было легче, я представлю рассматриваемое выражение в таком виде: ((arctg(4⋅lnx))12)′. Теперь видно, что необходимо использовать формулу №2, т.е. (uα)′=α⋅uα−1⋅u′. В эту формулу подставим u=arctg(4⋅lnx) и α=12:
Дополняя равенство (2.1) полученным результатом, имеем:
y′=(9⋅arctg12(4⋅lnx))′=9⋅(arctg12(4⋅lnx))′=108⋅(arctg(4⋅lnx))11⋅(arctg(4⋅lnx))′(2.2)
Примечание: показать\скрыть
Теперь нужно найти (arctg(4⋅lnx))′. Используем формулу №19 таблицы производных, подставив в неё u=4⋅lnx:
(arctg(4⋅lnx))′=11+(4⋅lnx)2⋅(4⋅lnx)′
Немного упростим полученное выражение, учитывая (4⋅lnx)2=42⋅(lnx)2=16⋅ln2x.
(arctg(4⋅lnx))′=11+(4⋅lnx)2⋅(4⋅lnx)′=11+16⋅ln2x⋅(4⋅lnx)′
Равенство (2.2) теперь станет таким:
y′=(9⋅arctg12(4⋅lnx))′=9⋅(arctg12(4⋅lnx))′==108⋅(arctg(4⋅lnx))11⋅(arctg(4⋅lnx))′=108⋅(arctg(4⋅lnx))11⋅11+16⋅ln2x⋅(4⋅lnx)′(2.3)
Осталось найти (4⋅lnx)′. Вынесем константу (т.е. 4) за знак производной: (4⋅lnx)′=4⋅(lnx)′. Для того, чтобы найти (lnx)′ используем формулу №8, подставив в нее u=x: (lnx)′=1x⋅x′. Так как x′=1, то (lnx)′=1x⋅x′=1x⋅1=1x. Подставив полученный результат в формулу (2.3), получим:
y′=(9⋅arctg12(4⋅lnx))′=9⋅(arctg12(4⋅lnx))′==108⋅(arctg(4⋅lnx))11⋅(arctg(4⋅lnx))′=108⋅(arctg(4⋅lnx))11⋅11+16⋅ln2x⋅(4⋅lnx)′==108⋅(arctg(4⋅lnx))11⋅11+16⋅ln2x⋅4⋅1x=432⋅arctg11(4⋅lnx)x⋅(1+16⋅ln2x).
Напомню, что производная сложной функции чаще всего находится в одну строку, – как записано в последнем равенстве. Поэтому при оформлении типовых расчетов или контрольных работ вовсе не обязательно расписывать решение столь же подробно.
Ответ: y′=432⋅arctg11(4⋅lnx)x⋅(1+16⋅ln2x).
Пример №3
Найти y′ функции y=sin3(5⋅9x)−−−−−−−−−√7.
Решение
Для начала немного преобразим функцию y, выразив радикал (корень) в виде степени: y=sin3(5⋅9x)−−−−−−−−−√7=(sin(5⋅9x))37. Теперь приступим к нахождению производной. Так как y=(sin(5⋅9x))37, то:
y′=((sin(5⋅9x))37)′(3.1)
Используем формулу №2 из таблицы производных, подставив в неё u=sin(5⋅9x) и α=37:
((sin(5⋅9x))37)′=37⋅(sin(5⋅9x))37−1(sin(5⋅9x))′=37⋅(sin(5⋅9x))−47(sin(5⋅9x))′
Продолжим равенство (3.1), используя полученный результат:
y′=((sin(5⋅9x))37)′=37⋅(sin(5⋅9x))−47(sin(5⋅9x))′(3.2)
Теперь нужно найти (sin(5⋅9x))′. Используем для этого формулу №9 из таблицы производных, подставив в неё u=5⋅9x:
(sin(5⋅9x))′=cos(5⋅9x)⋅(5⋅9x)′
Дополнив равенство (3.2) полученным результатом, имеем:
y′=((sin(5⋅9x))37)′=37⋅(sin(5⋅9x))−47(sin(5⋅9x))′==37⋅(sin(5⋅9x))−47cos(5⋅9x)⋅(5⋅9x)′(3.3)
Осталось найти (5⋅9x)′. Для начала вынесем константу (число 5) за знак производной, т.е. (5⋅9x)′=5⋅(9x)′. Для нахождения производной (9x)′ применим формулу №5 таблицы производных, подставив в неё a=9 и u=x: (9x)′=9x⋅ln9⋅x′. Так как x′=1, то (9x)′=9x⋅ln9⋅x′=9x⋅ln9. Теперь можно продолжить равенство (3.3):
y′=((sin(5⋅9x))37)′=37⋅(sin(5⋅9x))−47(sin(5⋅9x))′==37⋅(sin(5⋅9x))−47cos(5⋅9x)⋅(5⋅9x)′=37⋅(sin(5⋅9x))−47cos(5⋅9x)⋅5⋅9x⋅ln9==15⋅ln97⋅(sin(5⋅9x))−47⋅cos(5⋅9x)⋅9x.
Можно вновь от степеней вернуться к радикалам (т.е. корням), записав (sin(5⋅9x))−47 в виде 1(sin(5⋅9x))47=1sin4(5⋅9x)−−−−−−−−−√7. Тогда производная будет записана в такой форме:
y′=15⋅ln97⋅(sin(5⋅9x))−47⋅cos(5⋅9x)⋅9x=15⋅ln97⋅cos(5⋅9x)⋅9xsin4(5⋅9x)−−−−−−−−−√7.
Ответ: y′=15⋅ln97⋅cos(5⋅9x)⋅9xsin4(5⋅9x)−−−−−−−−−√7.
Пример №4
Показать, что формулы №3 и №4 таблицы производных есть частный случай формулы №2 этой таблицы.
Решение
В формуле №2 таблицы производных записана производная функции uα. Подставляя α=−1 в формулу №2, получим:
(u−1)′=−1⋅u−1−1⋅u′=−u−2⋅u′(4.1)
Так как u−1=1u и u−2=1u2, то равенство (4.1) можно переписать так: (1u)′=−1u2⋅u′. Это и есть формула №3 таблицы производных.
Вновь обратимся к формуле №2 таблицы производных. Подставим в неё α=12:
(u12)′=12⋅u12−1⋅u′=12u−12⋅u′(4.2)
Так как u12=u−−√ и u−12=1u12=1u−−√, то равенство (4.2) можно переписать в таком виде:
(u−−√)′=12⋅1u−−√⋅u′=12u−−√⋅u′
Полученное равенство (u−−√)′=12u−−√⋅u′ и есть формула №4 таблицы производных. Как видите, формулы №3 и №4 таблицы производных получаются из формулы №2 подстановкой соответствующего значения α.
Пример №5
Найти y′, если y=arcsin2x.
Решение
Нахождение производной сложной функции в данном примере запишем без подробных пояснений, которые были даны в предыдущих задачах.
Ответ: y′=2xln21−22x−−−−−−√.
Пример №6
Найти y′, если y=7⋅lnsin3x.
Решение
Как и в предыдущем примере, нахождение производной сложной функции укажем без подробностей. Желательно записать производную самостоятельно, лишь сверяясь с указанным ниже решением.
Ответ: y′=21⋅ctgx.
Пример №7
Найти y′, если y=9tg4(log5(2⋅cosx)).
Решение

6 Вопрос. Производная обратной функции примеры.
Производная обратной функции
Формула
Известно свойство степеней, что
тогда
Используя производную степенной функции:
будем иметь:
mykonspekts.ru
Производная суммы дробей со степенями и корнями
При нахождении производной суммы дробей со степенями и корнями во избежание распространённых ошибок следует обращать внимание на следующие моменты:
- применяя формулу дифференцирования произведения и частного, чётко определять разницу между константой, производная которой равна нулю, и постоянным множителем, который просто выносится за знак производной;
- необходимо уверенно пользоваться знаниями из школьного курса по действиям со степенями и корнями, например, что происходит с показателями степени, когда умножаются степени с одинаковыми основаниями;
- что происходит со знаками, когда у производной слагаемого знак противоположен знаку самого слагаемого.
Пример 1. Найти производную функции
.
Решение. Находим производную первого слагаемого:
.
Находим производную второго слагаемого:
.
Находим производную третьего слагаемого:
.
Здесь двойка перед иксом – постоянный множитель, поэтому его просто вынесли за знак производной.
Собираем всё вместе:
.
Если требуется в окончательном решении получить выражение с корнями, то преобразуем степени в корни и получаем искомую производную:
.
Пример 2. Найти производную функции
.
Решение. Находим производную первого слагаемого:
.
Здесь первая двойка в числителе промежуточного выражения была константой, её производная равна нулю.
Находим производную второго слагаемого:
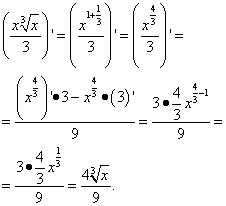
Находим производную третьего слагаемого:
Здесь применяли знания из школьного курса о действиях с дробями, их преобразовании и сокращении.
Собираем всё вместе, обращая внимание на то, что знаки производных первого и третьего слагаемых противоположны знакам слагаемых в исходном выражении:
.
Пример 3. Найти производную функции
.
Решение. Находим производную первого слагаемого:
Здесь потребовались навыки в действиях с дробями.
Находим производную второго слагаемого:
Производная третьего слагаемого – константы 1/2 – равна нулю (бывает, что студенты упорно пытаются найти отличную от нуля производную константы).
Собираем всё вместе, обращая внимание на то, что знак производной второго слагаемого противоположен знаку слагаемого в исходном выражении:
Пример 4. Найти производную функции
.
Решение. Находим производную первого слагаемого:
Находим производную второго слагаемого:
Находим производную третьего слагаемого:
Собираем всё вместе, обращая внимание на то, что знаки производных второго и третьего слагаемых – минусы:
.
Пример 5. Найти производную функции
.
Решение. Находим производную первого слагаемого:
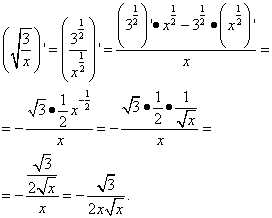
Находим производную второго слагаемого:
Находим производную третьего слагаемого:
Собираем всё вместе, обращая внимание на то, что знак производной второго слагаемого – минус:
.
Поделиться с друзьями
Весь блок “Производная”
function-x.ru
Как найти производную от дроби
Происхождение дифференциального исчисления вызвано необходимостью решать определенные физические задачи. Предполагается, что человек, обладающий дифференциальным исчислением, может брать производные от разных функций. Умеете ли вы брать производную от функции, выраженной дробью?

Инструкция
1. Любая дробь имеет числитель и знаменатель. В процессе нахождения производной от дроби понадобится находить отдельно производную числителя и производную знаменателя.
2. Дабы обнаружить производную от дроби , производную числителя домножьте на знаменатель. Вычтите из полученного выражения производную знаменателя, помноженную на числитель. Итог поделите на знаменатель в квадрате.
3. Пример 1[sin (x) / cos (x)]’ = [sin’ (x) · cos (x) — cos’ (x) · sin (x)] / cos? (x) = [cos (x) · cos (x) + sin (x) · sin (x)] / cos? (x) = [cos? (x) + sin? (x)] / cos? (x) = 1 / cos? (x).
4. Полученный итог является ничем другим, как табличным значением производной функции тангенса. Оно и внятно, чай отношение синуса к косинусу и есть, по определению, тангенс. Выходит,tg (x) = [sin (x) / cos (x)]’ = 1 / cos? (x).
5. Пример 2[(x? — 1) / 6x]’ = [(2x · 6x — 6 · x?) / 6?] = [12x? — 6x?] / 36 = 6x? / 36 = x? / 6.
6. Частным случаем дроби является такая дробь, у которой в знаменателе единица. Обнаружить производную от такого вида дроби проще: довольно представить ее в виде знаменателя со степенью (-1).
7. Пример(1 / x)’ = [x^(-1)]’ = -1 · x^(-2) = -1 / x?.
Обратите внимание!
Дробь может содержать в своем составе еще несколько дробей. В таком случае комфортнее находить вначале отдельно производные «первичных» дробей.
Полезный совет
Когда вы ищите производные знаменателя и числителя, применяйте правила дифференцирования: суммы, произведения, трудных функций. Пригодно удерживать в голове производные простейших табличных функций: линейной, показательной, степенной, логарифмической, тригонометрических и т.д.
jprosto.ru
Производная дроби онлайн · Как пользоваться Контрольная Работа РУ
Для нахождения производных от любых сложный функций, содержащих дробь используйте калькулятор производных на этом сайте. Этот калькулятор находится по ссылке:
https://www.kontrolnaya-rabota.ru/s/proizvodnaya-funktsii/one/
Например, если надо найти производную от дроби, в числителе которой x, в знаминателе (1-x3): x/(1-x^3)
Вводим в форму функцию x/(1-x^3) как изображено на рисунке выше
Нажимаем на кнопку “Найти производную”:
Результат вычисления производной от функции f(x) = x/(1-x^3):
3
3⋅x 1
─────────── + ────────
2 3
⎛ 3 ⎞ - x + 1
⎝- x + 1⎠
|
= |
3*x^3/(-x^3 + 1)^2 + 1/(-x^3 + 1) |
Там же вы можете получить подробное решение производной:
Применим правило производной частного:
и .
Чтобы найти :
В силу правила, применим: получим
Чтобы найти :
дифференцируем почленно:
Производная постоянной равна нулю.
Производная произведения константы на функцию есть произведение этой константы на производную данной функции.
В силу правила, применим: получим
Таким образом, в результате:
В результате:
Теперь применим правило производной деления:
Теперь упростим:
Ответ:
Общее правило
Производную от дроби очень просто посчитать (по-крайней мере от простых дробей)
Производная от дроби “единица, делённая на x” равна минус единице, делённой на x в квадрате.
www.kontrolnaya-rabota.ru



