08.05.201926.12.2018

Путь при ускорении – прямолинейное равноускоренное движение. как найти путь, зная ускорение, время, начальную и конечную скорости?

• by alexxlab
• Комментариев к записи Путь при ускорении – прямолинейное равноускоренное движение. как найти путь, зная ускорение, время, начальную и конечную скорости? нет
• Советы абитуриенту

Скорость и путь при равноускоренном движении — урок. Физика, 9 класс.

Рассмотрим некоторые особенности перемещения тела при прямолинейном равноускоренном движении без начальной скорости. Уравнение, которое описывает это движение, было выведено Галилеем в XVI веке. Необходимо помнить, что при прямолинейном равномерном или неравномерном движении модуль перемещения совпадает по своему значению с пройденным путём. Формула выглядит следующим образом:

s=v0t+at22, где \(а\) — это ускорение.

Сравним графики равномерного и равноускоренного движения:

 

Графики прямолинейного равномерного движения:

  

Зависимость ускорения от времени. Так как при равномерном движении ускорение равно нулю, то зависимость \(a(t)\) — прямая линия, которая лежит на оси времени.

 

Зависимость скорости от времени. Скорость со временем не изменяется, график \(v(t)\) — прямая линия, параллельная оси времени.

 

Правило определения пути по графику \(v(t)\): численное значение перемещения (пути) — это площадь прямоугольника под графиком скорости.

 

Зависимость пути от времени. График \(s(t)\) — наклонная линия.

 

 

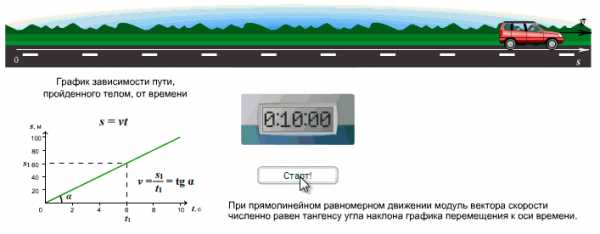
Графики равноускоренного движения:

Зависимость ускорения от времени. Ускорение со временем не изменяется, имеет постоянное значение, график \(a(t)\) — прямая линия, параллельная оси времени.

 

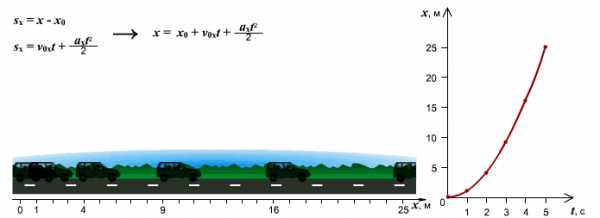
Зависимость скорости от времени. Путь изменяется согласно линейной зависимости .

 

Зависимость пути от времени. При равноускоренном движении путь изменяется согласно квадратной зависимости: s=v0t+at22. В координатах зависимость имеет вид: x=x0+v0xt+axt22.

 

Графиком является ветка параболы.

 

 

Источники:

http://fizmat.by/kursy/kinematika/ravnouskorennoe

www.yaklass.ru

2. Перемещение точки и пройденный путь. Скорость. Вычисление пройденного пути

Расстояние от точки А до точки В, отсчитанное вдоль траектории, называют пройденным путем. Иными словами, пройденный путь – это длина траектории, которую описывает материальная точка за данный промежуток времени.

Перемещением называют вектор, соединяющий начальное положение материальной точки с её конечным положением .

Величины, для задания которых достаточно лишь численного значения, называются скалярами. (Примеры: путь, время, масса, работа, мощность и т.д.)

Величины, характеризующиеся численным значением и направлением, называются векторами. (Примеры: перемещение, скорость, ускорение, сила, импульс и т.д.)

Положение материальной точки в пространстве можно задать при помощи радиуса-вектора .

Если перемещение точки за время будет равно, то под скоростью точки в данный момент времени понимают предел, к которому стремится отношениепри(пристремящемся к нулю).

=.

Вектор скорости направлен по касательной к траектории в соответствующей точке.

При различия между элементарным путеми модулем элементарного перемещенияневелико, поэтому, т.е..

Если задана зависимость скорости от времени, то пройденный путь можно найти, пользуясь формулой

В случае прямолинейного равномерного движения .

Прямолинейное равнопеременное движение. Ускорение. Физический смысл ускорения. Вычисление мгновенной скорости и пройденного пути при равнопеременном движении

Движение, при котором за любые равные промежутки времени скорость тела изменяется на одну и ту же величину, называется равнопеременным.

Быстрота изменения скорости материальной точки характеризуется ускорением

, или , т.е..

Физический смысл ускорения состоит в том, что оно является скоростью изменения скорости.

Если в начальный момент времени скорость тела равна , то в любой момент времени t модуль скорости тела

.

Если ускорение постоянно, то модуль мгновенной скорости

Пройденный путь (при равнопеременном движении) можно найти по формуле:

.

Для нахождения пройденного пути (в случае, если ускорение постоянно) также пользуются формулами:

и .

3. Ускорение при криволинейном движении

Нормальное, тангенциальное и полное ускорение

В случае движения материальной точки по криволинейной траектории различают нормальное и тангенциальное ускорения.

Нормальное (центростремительное) ускорение характеризует изменение скорости по направлению. Оно направлено к центру кривизны траектории.

Модуль нормального ускорения определяют по формуле , где R – радиус кривизны траектории

Тангенциальное (касательное) ускорение характеризует изменение скорости по величине. Оно направлено по касательной к траектории.

Модуль тангенциального ускорения определяют по формуле .

Модуль полного ускорения .

4. Кинематика вращательного движения

Тело, деформациями которого в данных условиях движения, можно пренебречь называют абсолютно твердым телом.

При вращательном движении радиус-вектор каждой точки поворачивается за одно и то время на один и тот же угол.

называют углом поворота тела.

Угловой скоростью тела называют величину

.

– аксиальный вектор (направлен вдоль оси вращения в сторону, определяемую правилом правого винта).

Равномерное вращение характеризуется периодом обращения Т.

Периодом обращения называют промежуток времени, за которое тело делает один полный оборот (поворачивается на угол 2π).

Модуль угловой скорости равномерного движения

.

Частотой обращения называют число оборотов точки за единицу времени .

Таким образом,

Угловое ускорение характеризует быстроту изменения угловой скорости (в случае неравномерного вращения)

.

Линейная скорость тела связана с угловой соотношением .

Модуль нормального ускорения

Модуль тангенциального ускорения .

studfiles.net

Глава 2. Ускорение. Равноускоренное движение

Характеристикой изменения скорости является ускорение. Эта величина определяется как отношение изменения скорости тела к тому интервалу времени, за который это изменение произошло

(2.1)

где и — скорости тела в конце и начале интервала времени . Из определения (2.1) следует, что вектор ускорения тела отличен от нуля только в том в случае, когда изменяется вектор скорости. При этом направление вектора определяется направлением разности , и может не совпадать с направлениями векторов и . Поэтому в задаче 2.1.1 ситуации, перечисленные в ответах 1, 3 и 4, возможны в следующих случаях. В 1 — когда тело, поворачивая на восток, в некоторый момент времени имеет вектор скорости, направленный на север. В 3 — при равноускоренном движении. В 4 — например, в такой ситуации: тело бросили вертикально вверх и в верхней точке траектории оно имеет нулевую скорость и ускорение, равное ускорению свободного падения. Ситуация, сформулированная в ответе

2, невозможна: если у тела постоянная скорость, то у него равное нулю и, следовательно, постоянное ускорение.

В задаче 2.1.2 вектор скорости в конце любого интервала времени меньше вектора скорости в начале этого интервала. Поэтому при направлении вектора скорости на юг вектор изменения скорости, а, следовательно, и вектор ускорения направлены на север (ответ 3).

Если тело движется с постоянной скоростью, координата линейно зависит от времени, причем наклон графика определяется скоростью. Поэтому скорость тела уменьшается, если уменьшается угол наклона графика зависимости координаты от времени к оси времени (задача 2.1.3 — ответ 4).

Движение тела, при котором его ускорение (как величина, так и направление) не изменяется, называется равноускоренным (

задача 2.1.4 — ответ 4). Из определения ускорения (2.1) следует, что при равноускоренном движении зависимость скорости от времени является линейной. Поэтому равноускоренному движению в задаче 2.1.5 отвечает график 1 (несмотря на то, что скорость тела убывает). В этой связи отметим, что равноускоренность означает не то, что тело постоянно разгоняется, а то, что оно имеет «равное ускорение».

При равноускоренном движении зависимости радиус-вектора тела по отношению к произвольной системе координат и скорости тела от времени даются соотношениями

(2.2)

(2.3)

где и — радиус-вектор и скорость тела в момент времени , — ускорение тела. После проецирования на оси координат зависимости (2.2) и (2.3) позволяют находить координаты тела и проекции его скорости на оси в любые моменты времени.

В задаче 2.1.6 зависимость (2.2) в проекциях на ось , которая направлена параллельно ускорению и начало которой находится в точке начала движения, дает

Поскольку тело движется из начала координат и только в одну сторону, то, очевидно, координата тела совпадает с пройденным путем. Поэтому при ускорении через 20 с после начала движения пройденный путь будет равен 100 м (ответ 2). Из этого результата следует, что задача 2.1.7 является обратной по отношению к задаче 2.1.6, поэтому правильный ответ для времени, за которое тело пройдет путь 100 м — 20 с (ответ 1).

В задаче 2.1.8 необходимо использовать зависимость (2.3) для скорости. Так как по условию автомобиль движется из состояния покоя, проекция зависимости (2.3) на ось , направленную вдоль вектора ускорения, имеет вид

где – проекция вектора скорости тела на ось . Так как в момент времени , находим (правильный ответ – 2).

Сравнивая данную в задаче 2.1.9 зависимость координаты от времени с законом (2.2), заключаем, что начальная скорость тела , проекция ускорения тела на ось – . Поэтому из (2.3) получаем зависимость скорости тела от времени .

Из этой зависимости следует, что скорость тела равна нулю при (правильный ответ 2). Можно было также найти скорость как производную координаты по времени. Дифференцируя данную в условии функцию, получим тот же ответ

Зависимость проекции скорости от времени на ось, направленную вертикально вверх, для тела из задачи 2.1.10 имеет вид

где — начальная скорость тела. Подставляя в эту формулу время , находим скорость тела через 0,5 с после броска (ответ 3). Знак «плюс» для проекции скорости на рассматриваемую ось показывает, что через 0,5 c после броска вектор скорости тела все еще направлен вверх.

Чтобы найти время подъема тела, брошенного вертикально вверх, на максимальную высоту (задача 2.2.1) используем то обстоятельство, что в верхней точке траектории скорость тела равна нулю. Поэтому подстановка времени подъема в зависимость скорости от времени дает

где — начальная скорость тела. Отсюда получаем для времени подъема (ответ 4). А самую максимальную высоту подъема (задача 2.2.2) можно найти, подставляя найденное время подъема в зависимость координаты тела по вертикальной оси от времени

Подстановка в эту формулу числовых значений дает (ответ 1).

Пусть время, затраченное телом на прохождение участка пути длиной , отсчитанного от начальной точки, равно , а время, затраченное телом на прохождение участка пути длиной , отсчитанного от этой же точки, равно (

задача 2.2.3). Тогда из уравнения движения (2.2) в проекции на ось, направленную вдоль вектора ускорения тела, имеем

Деля первое уравнение на второе и извлекая из этого отноше-ния квадратный корень, находим

что означает, что время прохождения пути меньше времени прохождения пути в раз (ответ 2).

В некоторых ситуациях приходится применять одновременно обе зависимости — и координаты и скорости. Например, в задаче 2.2.4 зависимости координаты тела по вертикальной оси и проекции скорости на эту ось имеют вид

Из первой зависимости находим время, за которое тело поднимается на высоту

(Два корня для времени получилось, поскольку на рассматриваемой высоте тело побывало дважды — в процессе подъема и в процессе спуска.) Подставляя эти значения времени в уравнение для скорости, получим для проекции скорости на вертикальную ось на высоте :

(«плюс» — на подъеме, «минус» — на спуске). Отсюда находим величину скорости тела на этой высоте — 15 м/с (ответ 3).

Иногда в задачах на равноускоренное движение требуется найти интервалы времени или расстояния, отсчитанные не от момента начала движения или от начального положения тела. Трудность таких задач заключается в том, что такие времена или расстояния сами не входят в уравнения равноускоренного движения. В этом случае искомые интервалы времени или расстояния удобно находить как разность интервалов времени или расстояний, отсчитанных от начала движения. Например, зависимость координаты автомобиля от времени в задаче 2.2.5 дается соотношением

где — ускорение автомобиля, в качестве начала координат выбрана точка начала движения. Из этой зависимости находим, что через 2 с после начала движения автомобиль окажется на расстоянии 4 м от начальной точки, через 3 с после начала движения — на расстоянии 9 м от начальной точки. Поэтому за третью секунду движения автомобиль пройдет путь 5 м — ответ 3.

Аналогично в задаче 2.2.6 из зависимости координаты тела от времени находим, что автомобиль окажется на расстоянии 2 м от начальной точки через время с, на расстоянии 3 м — через время с. Поэтому на прохождение третьего метра пути автомобиль затратит время с (ответ 2).

В задаче 2.2.7 следует из зависимости скорости от времени найти время падения, а затем подставить его в зависимость координаты от времени. Правильный ответ — 1.

При движении тела под углом к горизонту вектор ускорения тела направлен вертикально вниз (ускорение свободного падения — ). Поэтому проекция зависимости скорости от времени (2.3) на горизонтальную ось имеет вид

где – начальная скорость тела, – угол, под которым бросили тело (проекция вектора ускорения тела на горизонтальную ось равна нулю). Из этой формулы следует, что проекция скорости на горизонтальную ось не зависит от времени (задача 2.2.8 – правильный ответ 4).

Дальность полета тела, брошенного под углом к горизонту, определяется из проекции уравнения (2.2) на горизонтальную ось

где — проекция вектора начальной скорости на горизонтальную ось, — полное время движения. По условию задачи 2.2.9 проекции векторов начальной скорости тел на горизонтальную ось одинаковы (это подчеркнуто на рисунке в условии с помощью вертикальной пунктирной прямой). Поэтому дальше улетит то из них, у которого больше время движения. А оно, в свою очередь, определяется проекцией уравнения (2.2) на вертикальную ось

поскольку в момент падения вертикальная координата тела равна нулю. Отсюда следует, что время движения равно , т.е. определяется проекцией вектора начальной скорости на вертикальную ось. А она по условию больше у тела 1, которое, таким образом, и улетит дальше (ответ 1).

Задача 2.2.10 содержит небольшой «подвох». При движении тела по прямой и в одном направлении пройденный путь равен разности координат конца и начала траектории. В этом случае можно, выбрав начало координат в начальной точке, найти пройденный путь, просто подставляя время в уравнение для координаты. В нашем же случае тело движется сначала вверх, потом вниз. Действительно, время подъема для тела, брошенного вертикально вверх со скоростью 20 м/с, равно 2 с. А пройденный путь нужно найти за 3 с после броска. Поэтому пройденный путь складывается из максимальной высоты подъема (для тела, брошенного со скоростью 20 м/с, она равна 20 м) и длины участка пути от верхней точки траектории до точки, в которой тело окажется через 3 с после броска. Координату этой точки в системе координат, начало которой расположено на земле, а ось направлена вертикально вверх, можно найти, подставляя это значение времени в уравнение

(все величины заданы в международной системе единиц СИ). В результате находим, что пройденный телом путь равен 25 м (ответ 3).

online.mephi.ru

Физика. Путь при ускорении тела.

Такой же, как в площади прямоугольного треугольника: катет на катет и пополам. Такой же треугольник получается и для пути, где умножаются время и конечная скорость (которая тоже время, умноженное на ускорение).

По оси абсцисс будем откладывать время, по оси ординат – скорость. Нарисуйте график роста скорости при постоянном ускорении, нулевой начальной скорости, за ограниченное время. Получился треугольник – его физический смысл – это пройденный путь. Попробуйте найти его площадь.

Вначале скорость была: v=0, в конце стала: v=at, причем рост был линейный по времени. Средняя скорость: v1=at/2, путь: s=v1*t=at/2*t=(at^2)/2.

touch.otvet.mail.ru

Определение пути, пройденного автомобилем при разгоне — КиберПедия

 

Путь разгона автомобиля находим, решая уравнение

 

,

интегрируя относительно dS, получим

 

,

тогда

.

 

Интеграл решается графически по графику времени разгона. Значения времени разгона t_p и пути разгона S_p определяются следующим образом:

 

,

 

где t_p^‘ – время, соответствующее участку от 0 до v;

Δt_p – приращение времени разгона на соответствующей передаче, с.

 

,

 

где υ₁^‘ – начальное значение скорости, м/с;

j₁ – ускорение, соответствующее начальному движению на 1

передаче, м/с².

 

,

 

где F_tp – площадь фигуры под кривыми зависимости 1/j = f(υ), мм²;

μ_1/j – масштаб величины, обратной ускорению,

μ_υ – масштаб скорости.

 

По аналогичным формулам ведется расчет пути разгона S_p

 

,

где S – путь, соответствующий участку от 0 до t’, м,

 

S = t₂^‘·υ;

 

ΔS – приращение пути разгона S_p на соответствующей скорости, м,

 

,

 

где F₃ – площадь участков, расположенных между t_p = t(υ) и осью t_p, мм².

Найденные показатели заносятся в таблицу 5.2. По данным таблицы 5.2 строятся графики, примеры которых представлены на рисунках 5.3 и 5.4.

Таблица 5.1

	n0	n, 1/c	υ, м/с	MКР,кНм	Pk, кН	Pw, кН	j, м/с2	1/j, c2/м
I i   δВР
II i   δВР
III i   δВР
IV i   δВР
V i   δВР
VI i   δВР

Таблица 5.2

Передача	υ, м/с	Δυ, м/с	Ft, мм2	Δt, c	t разг, с	Fs, мм2	ΔSp, м	Sp, м
I	tтм
II	tпер
III	tпер
IV	tпер
V	tпер
VI	tпер

 

 

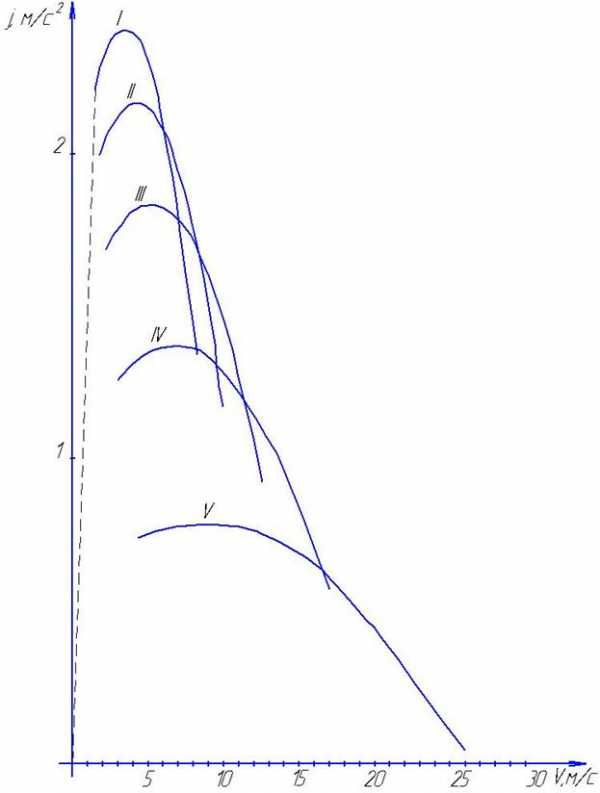
Рисунок 5.1. Пример построения графика ускорений при разгоне автомобиля.

 

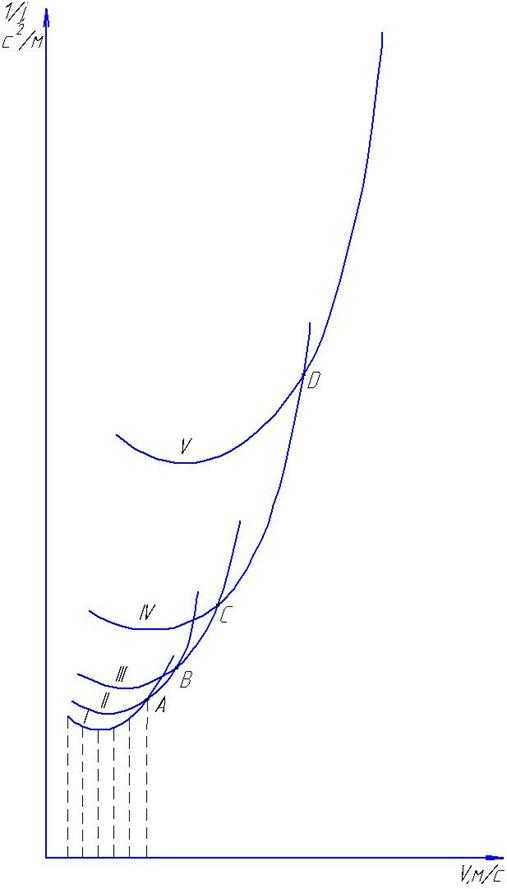
Рисунок 5.2. Пример построения величины, обратной ускорению при разгоне автомобиля.

 

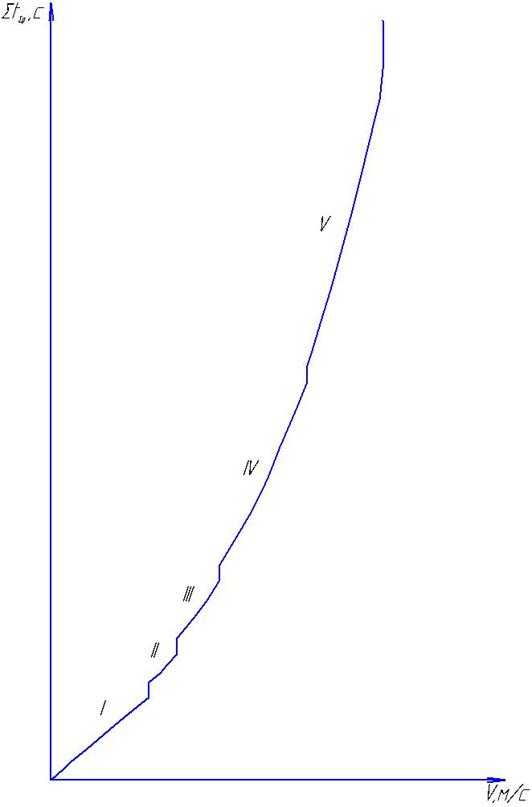
Рисунок 5.3. Пример графика определения времени разгона.

 

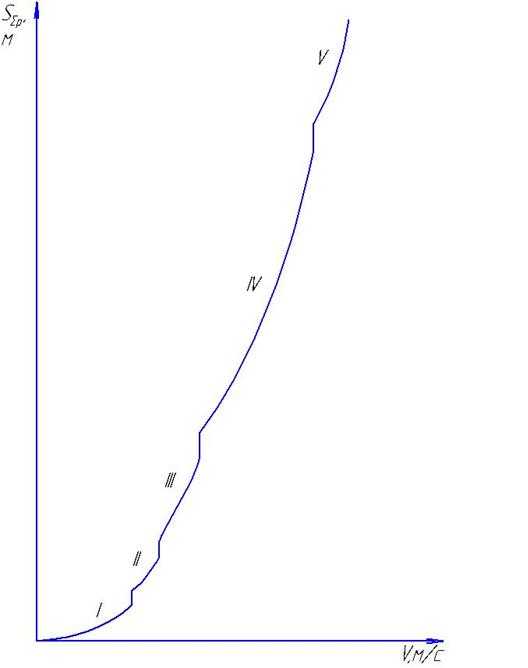
Рисунок 5.4. Пример графика определения пути разгона.

Лабораторная работа №6

 

ДИНАМИЧЕСКИЙ ПАСПОРТ АВТОМОБИЛЯ

Цель работы: построение динамического паспорта автомобиля.

Задачи работы:

1. Построение графика динамического фактора полностью груженого автомобиля;

2. Построение графика динамического фактора частично груженого автомобиля;

3. Определение динамического фактора по условию сцепления ведущих колес.

 

Определение динамического фактора полностью груженого автомобиля

Силовой баланс автомобиля определяется по уравнению:

 

,

или баланс мощности можно записать:

 

,

где Р_к – касательная сила тяги на колесах, Н;

Р_w – сила сопротивления воздуха, Н;

Р_{j рез} – результирующая сила инерции, Н.

 

Из первого выражения выразим избыточную силу тяги:

 

 

Из этого выражения выразим динамический фактор автомобиля:

 

,

.

 

Подставляя в выражение значения Р_к и Р_w при различном режиме и полной загрузке автомобиля, найдем динамический фактор при полной загрузке. Результаты расчетов сведем в таблицу 6.1.

 

По данным таблицы 6.1 строим график зависимости D = f(υ).

 

cyberpedia.su

Богданов К.Ю. – учебник по физике для 10 класса

§ 5. ПРЯМОЛИНЕЙНОЕ ДВИЖЕНИЕ С ПОСТОЯННЫМ УСКОРЕНИЕМ: УРАВНЕНИЕ ДЛЯ СКОРОСТИ И ПРОЙДЕННОГО ПУТИ

Прямолинейное движение с постоянным ускорением называют равноускоренным, если модуль скорости увеличивается со временем, или равнозамедленным, если он уменьшается.

Примером ускоренного движения может быть падение цветочного горшка с балкона невысокого дома. В начале падения скорость горшка равна нулю, но за несколько секунд она успевает вырасти до десятков м/с. Примером замедленного движения является движение камня, брошенного вертикально вверх, скорость которого сначала большая, но потом постепенно уменьшается до нуля в верхней точке траектории. Если пренебречь силой сопротивления воздуха, то ускорение в обоих этих случаях будет одинаково и равно ускорению свободного падения, которое всегда направлено вертикально вниз, обозначается буквой g  и равно примерно 9,8 м/с².

 Ускорение свободного падения, g вызвано силой притяжения Земли. Эта сила ускоряет все тела, движущиеся по направлению к земле, и замедляет те, которые движутся от неё.

 Чтобы найти уравнение для скорости при прямолинейном движении с постоянным ускорением, будем считать, что в момент времени t=0 тело имело начальную скорость v₀. Так как ускорение a постоянно, то для любого момента времени t справедливо следующее уравнение:

где v – скорость тела в момент времени t, откуда после нетрудных преобразований получаем уравнение для скорости при движении с постоянным ускорением:

v = v₀ + at                               (5.1)

 Чтобы вывести уравнение для пути, пройденного при прямолинейном движении с постоянным ускорением, построим сначала график зависимости скорости от времени (5.1). Для a>0 график этой зависимости изображён слева на рис.5 (синяя прямая). Как мы установили в §3, перемещение, совершённое за время t, можно определить, если вычислить площадь под кривой зависимости скорости от времени между моментами t=0 и t. В нашем случае фигура под кривой, ограниченная двумя вертикальными линиями t=0 и t, представляет собой трапецию OABC, площадь которой S, как известно, равна произведению полусуммы длин оснований OA и CB на высоту OC:

 Как видно на рис.5, OA = v₀, CB= v₀ + at, а OC = t. Подставляя эти значения в (5.2), получаем следующее уравнение для перемещения S, совершённого за время t при прямолинейном движении с постоянным ускорением a при начальной скорости v₀ :

Легко показать, что формула (5.3) справедлива не только для движения с ускорением a>0, для которого она была выведена, но и в тех случаях, когда a<0. На рис.5 справа красными линиями показаны графики зависимости S при положительных (верх) и отрицательных (низ) значениях a, построенные по формуле (5.3)  для различных величин v₀. Видно, что в отличие от равномерного движения (см. рис. 3), график зависимости перемещения от времени является параболой, а не прямой, показанной для сравнения пунктирной линией.

Вопросы для повторения:

·        Является ли движение с постоянным ускорением равномерным?

·        Дайте определение равноускоренного и равнозамедленного движения.

·        Чему равно ускорение свободного падения, и чем оно вызвано?

·        По какому закону изменяется скорость при равноускоренном или равнозамедленном движении?

·        Как зависит перемещение при равноускоренном движении от времени, ускорения и начальной скорости?

Рис. 5. Слева – зависимость скорости от времени (синяя прямая) при равноускоренном движении; справа – зависимости перемещения от времени (красные кривые) при равноускоренном (верх) и равнозамедленном движении (низ).

kaf-fiz-1586.narod.ru

---